A High-Precision Daily Runoff Prediction Model for Cross-Border Basins: RPSEMD-IMVO-CSAT Based on Multi-Scale Decomposition and Parameter Optimization

Abstract

As the last critical hydrological control station on the Lancang River before it flows out of China, the daily runoff variations at the Yunjinghong Hydrological Station are directly linked to agricultural irrigation, hydropower development, and ecological security in downstream Mekong River riparian countries such as Laos, Myanmar, and Thailand. Aiming at the core issues of the runoff sequence in the Lancang–Mekong Basin, which is characterized by prominent nonlinearity, non-stationarity, and coupling of multi-scale features, this study proposes a synergistic prediction framework of “multi-scale decomposition-model improvement-parameter optimization”. Firstly, Regenerated Phase-Shifted Sine-Assisted Empirical Mode Decomposition (RPSEMD) is adopted to adaptively decompose the daily runoff data. On this basis, a Convolutional Sparse Attention Transformer (CSAT) model is constructed. A one-dimensional convolutional neural network (1D-CNN) module is embedded in the input layer to enhance local feature perception, making up for the deficiency of traditional Transformers in capturing detailed information. Meanwhile, the sparse attention mechanism replaces the multi-head attention, realizing efficient focusing on key time-step correlations and reducing computational costs. Additionally, an Improved Multi-Verse Optimizer (IMVO) is introduced, which optimizes the hyperparameters of CSAT through a spiral update mechanism, exponential Travel Distance Rate (T_DR), and adaptive compression factor, thereby improving the model’s accuracy in capturing short-term abrupt patterns such as flood peaks and drought transition points. Experiments are conducted using measured daily runoff data from 2010 to 2022, and the proposed model is compared with mainstream models such as LSTM, GRU, and standard Transformer. The results show that the RPSEMD-IMVO-CSAT model reduces the Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) by 15.3–28.7% and 18.6–32.4%, respectively, compared with the comparative models.

1. Introduction

The Lancang–Mekong River Basin [1], as a transnational water system connecting China and several Southeast Asian countries, its water resource allocation and regulation directly relate to the survival and development of hundreds of millions of people along the basin and regional stability [2]. As a key control node of the Lancang River [3] before it flows out of China, the daily runoff variation at Yunjinghong Hydrological Station not only reflects the hydrological response of the upper reaches but also directly affects agricultural irrigation, hydropower development, and ecological security in countries along the lower Mekong River [4]. Therefore, accurate prediction of daily runoff at this station is the core technical support for realizing cross-border water resource coordinated management, responding to drought and flood disasters, and promoting transnational ecological cooperation [5].

Current runoff prediction models can be mainly divided into three categories: First, traditional statistical methods (e.g., Autoregressive Integrated Moving Average (ARIMA) [6], linear regression [7]). These methods rely on strict linear assumptions and are difficult to adapt to the nonlinear and non-stationary characteristics of runoff sequences formed by the combined effects of climate fluctuations, topographic differences, and human activities, resulting in significant errors in predicting extreme hydrological events (e.g., sudden floods, persistent droughts). Second, machine learning methods (e.g., Support Vector Machine (SVM) [8], random forest [9]). Although they can mine partial patterns through feature engineering, they are insufficient in capturing the temporal correlation of runoff processes and have weak generalization ability in long-term prediction. Third, deep learning methods (e.g., Long Short-Term Memory (LSTM) [10], Transformer [11]). Relying on the advantage of autonomously learning temporal features, they have become a research hotspot. However, single models cannot fully resolve the coupling relationship of multi-scale features in runoff sequences, leaving room for improvement in prediction accuracy. Therefore, constructing hybrid frameworks integrating data preprocessing and model optimization has become the mainstream direction of hydrological prediction. For instance, the ensemble Convolutional Neural Network (CNN)-LSTM and Gated Recurrent Unit (GRU) adaptive weighting model developed by Yao et al. [12]., which integrates an improved sparrow search algorithm, significantly enhanced runoff prediction accuracy by effectively fusing multi-source meteorological and hydrological data. Similarly, the metaheuristic evolutionary deep learning model proposed by QIN et al. [13], combining a temporal convolutional network with an improved aquila optimizer and random forest, demonstrated superior performance in both rainfall-runoff simulation and multi-step runoff prediction compared to individual baseline models.

Beyond purely data-driven methods, physically based hydrological models (e.g., Soil and Water Assessment Tool (SWAT) [14], USGS’s Groundwater and Surface-water FLOW model (GSFLOW), Precipitation-Runoff Modeling System (PRMS) [15]) and their hybrid derivatives with machine learning (e.g., SWAT-LSTM [16]) simulate runoff through explicit physical processes or by combining physical mechanisms with data-driven flexibility. Although these models provide valuable process insights, their application in transboundary basins like the Lancang–Mekong is often limited by demanding data requirements, cross-border data-sharing barriers, and high computational costs—particularly for daily operational forecasting. Given the strong nonlinearity, non-stationarity, and multi-scale coupling in the daily runoff series at Yunjinghong, this study focuses on advancing a purely data-driven decomposition–optimization–deep learning framework. This approach rapidly adapts to complex patterns without relying on explicit physical equations, offering a practical and efficient solution for daily runoff prediction in data-scarce international river basins.

The performance improvement of hybrid models not only depends on the innovation of model structure but also on the quality of data preprocessing. Existing modal decomposition methods (e.g., Empirical Mode Decomposition (EMD) [17], Variational Mode Decomposition (VMD) [18]) often suffer from mode mixing when processing non-stationary runoff data in transnational basins, making it difficult to accurately separate high-frequency random disturbances, medium-frequency seasonal fluctuations, and low-frequency trend components. Although some improved algorithms (e.g., Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN) [19], time-varying filter-based empirical mode decomposition [20]) have made progress in single-basin prediction, they still face problems such as insufficient decomposition accuracy and low computational efficiency when adapting to the differences in cross-border hydrological characteristics of the Lancang–Mekong River Basin. In addition, while mainstream prediction models capture long-term temporal dependencies of runoff, they have low sensitivity to local mutation features (e.g., flood peaks, dry-wet transition points). Moreover, model parameter optimization mostly relies on gradient descent algorithms, which are prone to falling into local optima and cannot meet the high-precision prediction requirements of cross-border basins. Although some studies have introduced intelligent optimization algorithms (e.g., particle swarm optimization [21], genetic algorithm [22]) for parameter adjustment, their adaptability in complex cross-border hydrological scenarios still needs to be strengthened [23].

In summary, existing studies have made certain breakthroughs in decomposition algorithms and model optimization [24]. However, in the face of complex cross-border hydrological characteristics and frequent extreme events in the Lancang–Mekong River Basin, there are still three core bottlenecks: First, existing decomposition methods have insufficient ability to resolve multi-scale features of cross-border non-stationary runoff data and cannot adapt to the differences in hydrological responses between upstream and downstream. Second, prediction models have limited sensitivity in capturing local mutation features, leading to high prediction errors under extreme hydrological events. Third, parameter optimization algorithms struggle to balance global optimization and convergence efficiency in complex scenarios, resulting in insufficient model robustness. These problems make existing methods unable to meet the high requirements for accuracy and reliability in cross-border water resource management when supporting daily runoff prediction at Yunjinghong Hydrological Station.

To this end, this study takes the daily runoff data of Yunjinghong Hydrological Station as the research object. Regenerated Phase-Shifted Sine-Assisted Empirical Mode Decomposition (RPSEMD) is adopted to solve the mode mixing problem and accurately extract multi-scale hydrological features. A Convolutional Sparse Attention Transformer (CSAT) model is constructed, which enhances local feature perception by embedding a 1D-CNN module and optimizes parameters combined with an improved multi-verse optimization algorithm. Finally, a high-precision daily runoff prediction scheme suitable for cross-border basins is formed, providing technical support for coordinated water resource regulation and transnational ecological cooperation in the Lancang–Mekong River Basin.

The remainder of this paper is organized as follows: Section 2 elaborates on the theoretical principles of the adopted methodologies, including RPSEMD, CSAT, and the IMVO, as well as the construction of the RPSEMD-IMVO-CSAT hybrid prediction framework. Section 3 presents the result analysis, comparing the prediction performance of the proposed model with benchmark models through fitting curves and quantitative metrics. It also evaluates the prediction stability across different hydrological years and the generalization capability under small-sample conditions. Section 4 summarizes the main conclusions of the study.

2. Methods

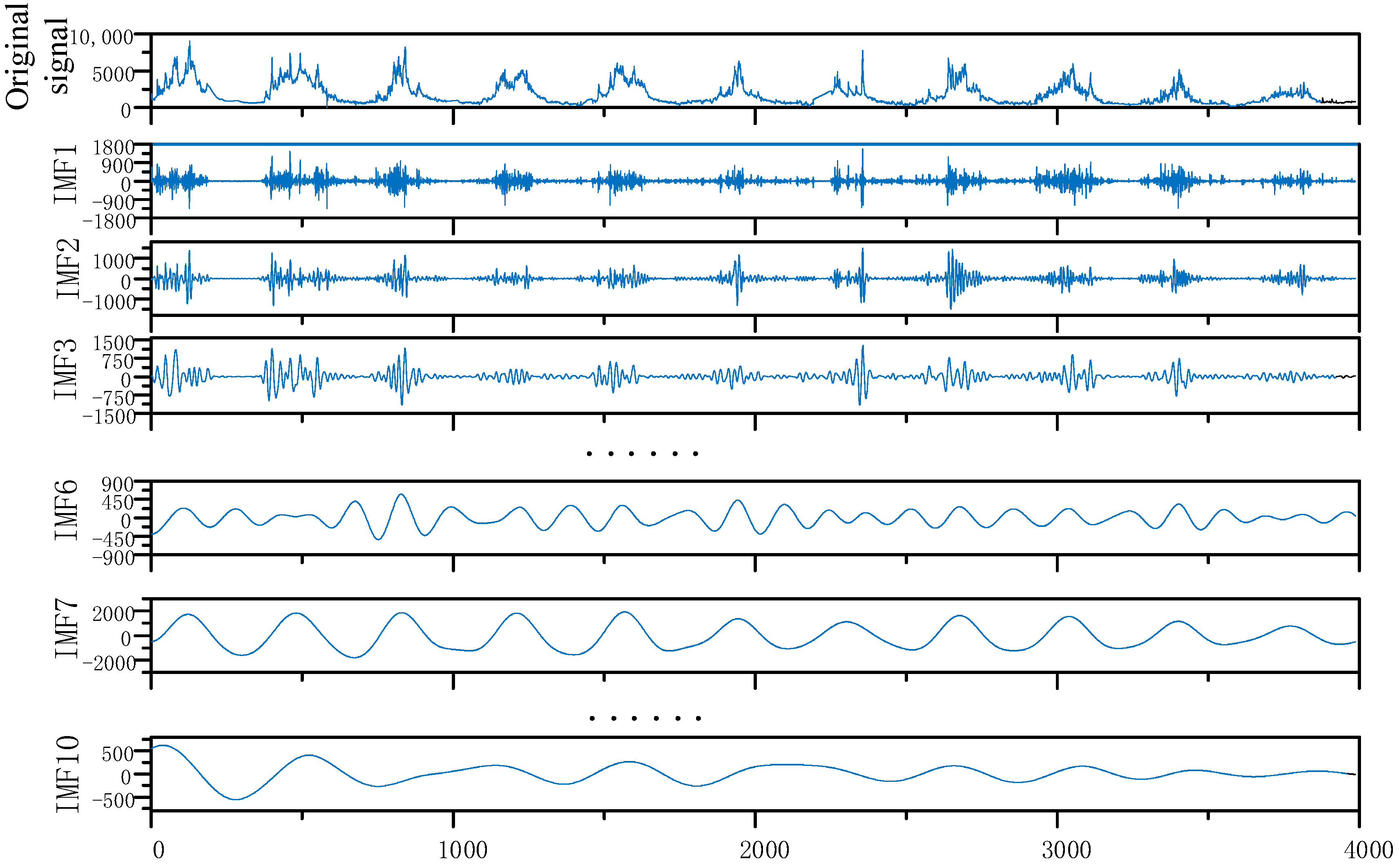
2.1. Regenerated Phase-Shifted Sine-Assisted Empirical Mode Decomposition (RPSEMD)

RPSEMD [25] is an enhanced version of the classical EMD algorithm, designed to address issues such as mode mixing, endpoint effects, and instability when processing non-stationary and nonlinear signals. The core innovation of RPSEMD lies in the introduction of regenerated phase-shifted sinusoidal auxiliary signals, which help to better identify local features and improve the separability of intrinsic mode functions (IMFs). This method is particularly effective for decomposing hydrological time series like daily runoff, which exhibit multi-scale characteristics including high-frequency noise, seasonal fluctuations, and long-term trends.

The objective of RPSEMD is to adaptively decompose a univariate original signal x(t) into N intrinsic mode functions C_i(t) and one residual term r(t), expressed as:

$$x(t)={\sum }_{i=1}^n{c}_i(t)+r(t)$$

(1)

where C_i(t) represents the i-th IMF corresponding to runoff variations at different temporal scales, and r(t) denotes the long-term trend component (e.g., interannual changes influenced by climate factors).

To mitigate mode mixing, RPSEMD employs a set of regenerated phase-shifted sine signals $s_k(t)$, defined as:

$$s_k(t)=A_{k}sin({\displaystyle \frac{2\pi t}{T_k}}+{\varphi }_k(t)),\hspace{1em}k=1,2,3$$

(2)

where T_k is the period of the k-th auxiliary signal, A_k is its amplitude (typically set as 0.2 times the standard deviation of the runoff segment under analysis), and ϕk(t) is a dynamic phase-shift function that adapts to the local characteristics of the runoff series. These auxiliary signals are not treated as IMFs; instead, they are superimposed on the original signal during the sifting process to stabilize the extraction of IMFs.

The decomposition is guided by an optimization criterion that minimizes the envelope mean of each IMF while promoting smoothness and physical interpretability. The objective function for the i-th IMF is formulated as:

$${\min }_{c_i(t)}\left\{{\parallel m_i(t)\parallel }_2+\alpha \cdot TV(C_i)+\beta \cdot {\displaystyle \sum _{k=1}^3\parallel C_i(t)-s_k(t){\parallel }_2}\right\}$$

(3)

where m_i(t) is the mean envelope of C_i(t), TV(C_i) denotes the total variation of C_i to enforce smoothness, and α, β are weighting coefficients that control the trade-off between envelope accuracy and auxiliary signal guidance. The third term ensures that the extracted IMFs remain consistent with the multi-scale structure highlighted by the auxiliary signals.

Through this enhanced decomposition, RPSEMD effectively separates high-frequency noise, seasonal cycles, and trend components, providing cleaner inputs for subsequent prediction models.

The periods T_k of the regenerated phase-shifted sine signals were determined through a preliminary spectral analysis of the historical daily runoff series, which identified dominant oscillatory components corresponding to high-frequency noise (e.g., a few days), seasonal fluctuations (~365 days), and inter-annual trends. A set of T_k values spanning these scales was predefined to ensure the auxiliary signals could guide the separation of physically meaningful IMFs. The phase function ϕ_k(t) was defined as a linear time-varying function ϕ_k(t) = 2π⋅t/T_k + θ_k, where θ_k is an initial phase offset iteratively adjusted during sifting to align with local extrema of the signal. The number of IMFs emerged adaptively based on the stopping criterion that the residual contains no more than two local extrema. This parameter setup was validated through sensitivity tests, confirming its robustness in avoiding mode mixing while preserving hydrological interpretability across the multi-scale runoff features.

2.2. CSAT Model

In hydrological time series prediction, the standard Transformer has weak perception of short-term mutation features in runoff sequences. Since multi-head attention treats all time steps equally, local key information is easily masked by global characteristics. This study proposes a CSAT model [26], which makes up for the deficiencies in local information capture and key feature focusing through improvements, thereby enhancing the ability to capture local hydrological features.

Aiming at the significant shortcomings of the above-mentioned standard Transformer in local feature extraction and attention mechanism, the model structure and attention mechanism are optimized. While retaining the strong global modeling ability of the Transformer, it effectively makes up for the deficiencies in local information capture and key feature focusing, thus constructing a model architecture more in line with the actual needs of runoff prediction. The specific improvement methods are as follows:

Local Feature Enhancement Module: A one-dimensional convolutional neural network (1D-CNN) is embedded before the input layer of the Transformer. The 1D convolution kernel slides over the time series data, enabling efficient capture of local patterns between adjacent time steps.

If the input data is $X\in {\mathbb{R}}^{T\times C}$, where $T$ is the time step and $C$ is the number of hydrological stations. A 1D convolution kernel of size $W\in {\mathbb{R}}^{K\times C}$ is used for convolution operation, with the formula:

$$Y=X\ast W+b$$

(4)

In the hydrological prediction task, the output of the convolution layer undergoes nonlinear mapping through an activation function, followed by time-dimensional dimensionality reduction using a pooling layer to obtain the local feature representation $Y\in {\mathbb{R}}^{T\prime \times C}$, where $T\prime$ is the step size after down sampling.

The extracted local features $Y$ are concatenated with the original input sequence $X$ in the channel dimension to form the fused features $Z=[Y;X]$, which are then input into the Transformer encoder. This allows the Transformer to explicitly utilize the local temporal patterns extracted by CNN when constructing global dependencies, significantly improving the ability to capture key features in hydrological processes.

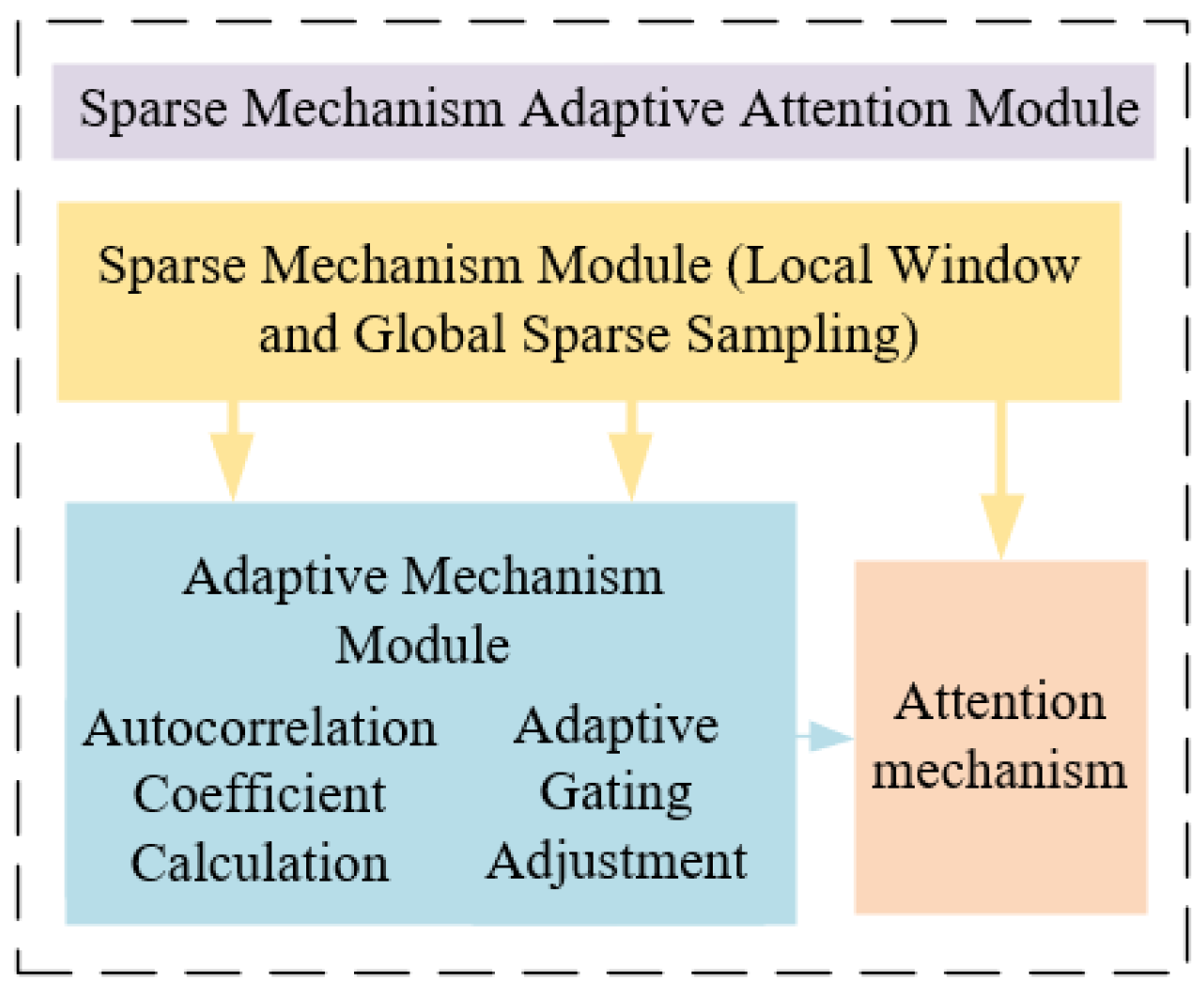
To further optimize the attention mechanism, a sparse adaptive attention module is constructed to achieve accurate extraction of key information through a dual-constraint mechanism. The structure of the sparse adaptive attention module is shown in Figure 1:

The standard multi-head self-attention mechanism requires computing attention weights between each element and all others, with a computational complexity of O(N²), making it inefficient for processing long sequence data. The sparse attention mechanism reduces computational complexity by limiting the scope of attention calculations. It combines local window attention with global sparse sampling. For each element, dense attention weights are first computed within its local window. Simultaneously, to capture long-range dependencies, sparse sampling is performed globally. A subset of elements is randomly selected as global key elements, and attention weights are computed between the current element and these global key elements.

Sparse Attention Constraint: A learnable binary mask $M\in {\{0,1\}}^{T\times T}$ is introduced to force the model to only focus on time steps within the local neighborhood and suppress irrelevant background noise:

$$SparseAttention(Q,K,V)=soft\max ({\displaystyle \frac{Q{K}^{T}M}{\sqrt{d_k}}})V$$

(5)

Adaptive Weight Adjustment: A gating mechanism is used to dynamically adjust the attention weights of different time steps, enhancing the response sensitivity to hydrological abnormal points (e.g., flood peaks, drought periods):

$${\alpha }_t=\sigma (W_{g}concat[h_{t-1},h_t,h_{t+1}])$$

(6)

where $\sigma$ is the sigmoid function, $h_t$ is the hidden state at time $t$, and ${\alpha }_t$ is the adaptive weight coefficient. Here, $h_t$ denotes the hidden state at time step $t$, which is the intermediate feature representation output by the preceding network layers (e.g., the 1D-CNN and layer normalization) for the input at that time step. It encodes the locally processed information from the runoff sequence, serving as the input to the gating mechanism for calculating the time-specific adaptive scaling factor.

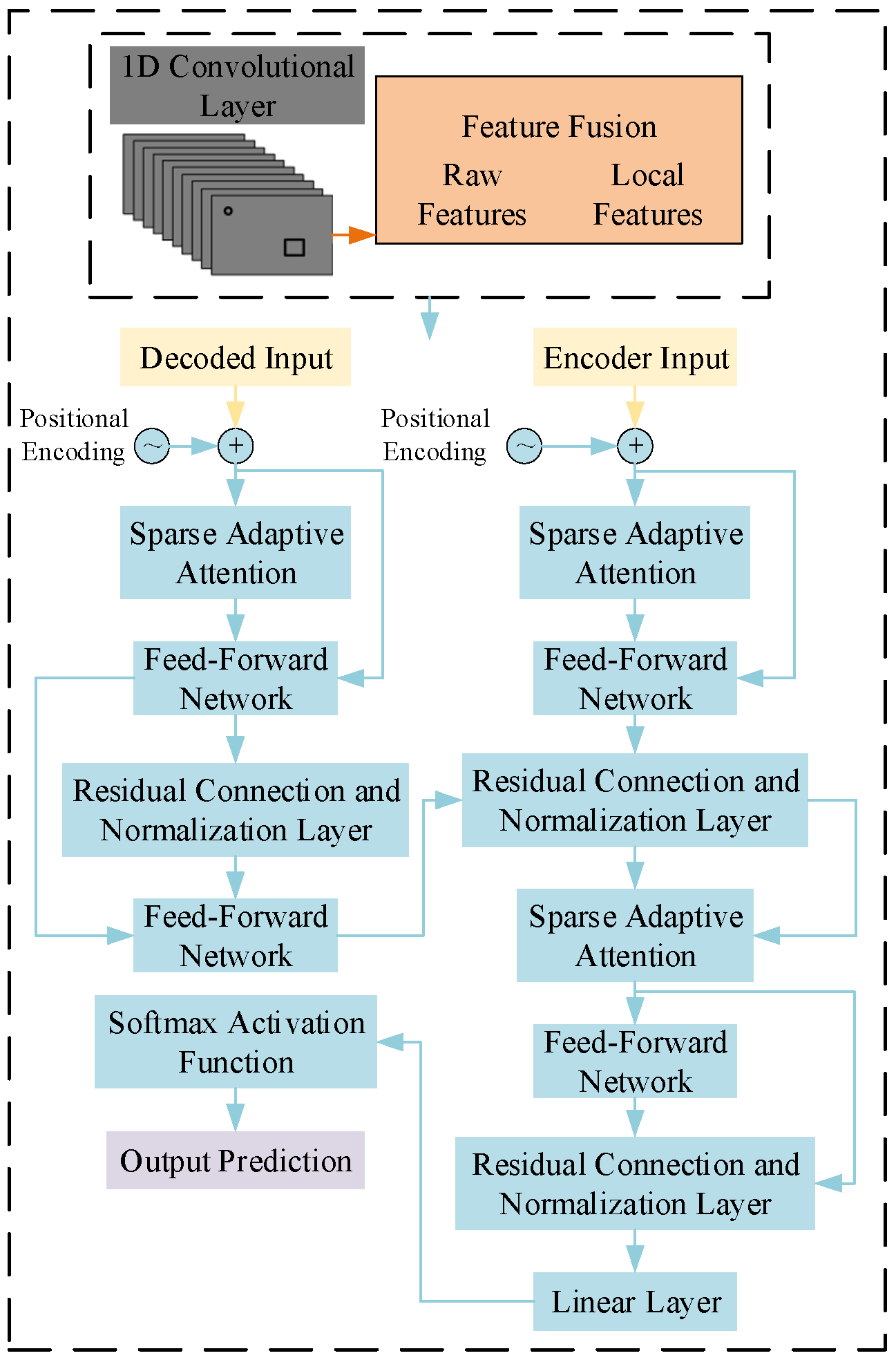
The improved model can not only effectively capture global dependencies but also accurately extract local features and highlight key information, thereby improving the performance and efficiency of runoff prediction. The structure of the CSAT runoff prediction model is shown in Figure 2. “” represents the weighted fusion operation in the attention mechanism, and “” represents the element-wise addition in residual connections.

2.3. Multi-Verse Optimizer (MVO)

The MVO [27] is a nature-inspired swarm intelligence optimization algorithm. Its core idea is derived from the multi-verse theory, which realizes the iterative optimization of candidate solutions (called “universes”) by simulating the interaction mechanisms of “white holes (energy emission), black holes (energy absorption), and wormholes (spacetime tunnels)”, and finally finds the global optimal solution. In runoff prediction, MVO is mainly used to optimize the key parameters (e.g., [Parameters omitted, consistent with original]) of the runoff prediction model (CSAT). Through iterative screening of the optimal parameter combination, it minimizes the runoff prediction error (RMSE) at Panzhihua Station and improves the model’s ability to capture multi-scale features of runoff (seasonal cycles, flood peak/drought mutations). Its mathematical principles and implementation steps are as follows:

Universe Initialization: The parameters of the runoff prediction model need to be randomly initialized within a reasonable range to ensure coverage of the parameter search space, with the formula:

$$X_j^i={lb}_j+rand(0,1)\times ({ub}_j-{lb}_j)$$

(7)

where $X_j^i$ is the j-th dimension parameter of the i-th universe; ${lb}_j$ and ${ub}_j$ are the lower and upper bounds of the j-th dimension parameter, respectively; $rand(0,1)$ is a random number in the interval [0, 1].

Normalization of Expansion Rate: The expansion rate needs to be standardized by runoff prediction error to ensure quantifiable comparison of the advantages and disadvantages of different parameter combinations, with the formula:

$$NI(X_i)={\displaystyle \frac{fit\left(X_i\right)-{fit}_{worst}}{{fit}_{best}-{fit}_{worst}}}$$

(8)

where $NI\left(X_i\right)$ is the normalized expansion rate of the i-th universe; $fit\left(X_i\right)$ is the fitness value of the i-th parameter combination (the fitness function is RMSE); ${fit}_{best}$ and ${fit}_{worst}$ are the optimal and worst fitness values in the current iteration, respectively.

White Hole Position Update: To realize “high-quality universes guiding low-quality universes”, MVO selects white holes through roulette wheel selection: first, universes are sorted according to “expansion rate (fitness)”, then selection probabilities are assigned based on normalized expansion rates. Universes with higher probabilities (better quality) are more likely to become white holes. White holes are selected through the roulette wheel mechanism, and black holes update their parameters to white hole parameters with a certain probability to realize the transfer of high-quality parameters, with the formula:

$$X_i^j=\left\{\begin{array}{c}{X}_k^j if r_1<NI\left(X_i\right)\\ X_i^j if r_1\ge NI\left(X_i\right)\end{array}\right.$$

(9)

where $X_k^j$ is the j-th dimension parameter of the white hole (the k-th universe) selected by roulette wheel; $r_1$ is a random parameter in [0, 1]; if $r1<NI\left(X_i\right)$, the black hole accepts the guidance of the white hole and updates its j-th dimension parameter to the corresponding parameter of the white hole; otherwise, it retains the original parameter.

Wormhole Parameter Update: Wormholes are the core of MVO realizing the transition from “global search” to “local search”, controlled by two key parameters:

Wormhole Existence Probability (\(W_{EP}\)): Controls the probability of universes updating their positions through wormholes, increasing linearly with iterations (preferring local search in the later stage), with the formula:

$$W_{EP}=W_{EPmin}+l\times {\displaystyle \frac{W_{EPmax}-W_{EPmin}}{L}}$$

(10)

where $W_{EPmin}$ is the minimum value (set to 0.2, with low wormhole probability in initial iterations, prioritizing global search); $W_{EPmax}$ is the maximum value (set to 1, with high wormhole probability in the later stage, prioritizing local search); $l$ is the current iteration number (starting from 1); $L$ is the maximum number of iterations (set to 30); it increases linearly from 0.2 to 1 with iterations, realizing “less use of wormholes in the early stage (global exploration) and more use in the later stage (local exploitation)”.

Travel Distance Rate ($T_{DR}$): Controls the moving distance of universes through wormholes, decreasing slowly with iterations (shorter moving distance in the later stage, enabling refined search), with the formula:

$$T_{DR}=1-{\displaystyle \frac{l^{1/p}}{L^{1/p}}}$$

(11)

where $p$ is the local exploitation accuracy coefficient.

Universe Position Update: When a universe meets the “wormhole trigger condition” ($r_2<W_{EP}$), its position is randomly updated through the wormhole to further approach the optimal solution; otherwise, it retains its original position.

The position update formula is:

$$X_i^j=\left\{\begin{array}{c}{X}_{best}^j+T_{DR}\times \left(\left({ub}_j-{lb}_j\right)\times r_4+{lb}_j\right) if r_3<0.5\\ X_{best}^j-T_{DR}\times \left(\left({ub}_j-{lb}_j\right)\times r_4+{lb}_j\right) if r_3\ge 0.5\end{array}\right.$$

(12)

where $X_{best}^j$ is the j-th dimension parameter of the current global optimal universe (optimal candidate solution);${ r}_2,{ r}_3, r_4$ are random numbers in [0, 1] ($r_2$ controls wormhole triggering,$r_3$ controls moving direction, and $r_4$ controls moving amplitude); $T_{DR}\times \left(\left({ub}_j-{lb}_j\right)\times r_4+{lb}_j\right)$ is the random moving distance guided by the wormhole.

2.4. Improved Multi-Verse Optimizer (IMVO)

The original MVO has two limitations in runoff prediction: first, parameters tend to be rigid in the later stage of iteration (positions remain unchanged when wormholes are not triggered), making it difficult to adapt to runoff mutations (e.g., sudden flow surges caused by heavy rain); second, the linear decline of $T_{DR}$ is too slow, leading to slow parameter convergence and inability to quickly respond to short-term high-frequency changes in runoff. To this end, a spiral update mechanism, exponential $T_{DR}$, and adaptive compression factor are introduced to construct an Improved Multi-Verse Optimizer (IMVO) [28], enhancing adaptability to complex runoff features and further improving the parameter optimization efficiency of the prediction model. Its mathematical principles and implementation steps are as follows:

(1)

Spiral Update Mechanism for Solving Parameter Rigidity: When wormholes are not triggered ($r_2\ge W_{EP}$), universes move in a spiral around the global optimal parameters, maintaining the optimization direction while exploring the parameter space corresponding to runoff mutations, with the formula:

$$X_i^j=\mid X_{best}^j-X_i^j\mid \times e^{b\cdot m}\times cos(2\pi m)+X_{best}^j$$

(13)

where $b$ is the spiral tightness coefficient; m is a random number in [0, 1] controlling the spiral angle; $\mid X_{best}^j-X_i^j\mid$ is the distance between the current parameter and the optimal parameter (spiral radius). It mainly adjusts parameters through spiral updates, ensuring that they do not deviate from the optimal direction while exploring local feature parameters adapted to flood peaks.

(2)

Exponential $T_{DR}$ for Improving Convergence Speed: The linear $T_{DR}$ is changed to exponential decay to accelerate the attenuation of parameter adjustment amplitude in the later stage of iteration, adapting to short-term high-frequency changes in runoff, with the formula:

$$T_{DR}={({\displaystyle \frac{1}{Q_c}})}^{l/L}\times 0.6$$

(14)

where $Q_c=5000$ is the exponential decay coefficient; 0.6 is the scaling coefficient.

(3)

Adaptive Compression Factor for Balancing Search: A compression factor $\lambda$ that decreases with iterations is introduced to dynamically adjust the amplitude of parameters approaching the optimal solution, balancing the capture of runoff cycles and short-term fluctuations, with the formula:

$$\lambda =cos({\displaystyle \frac{\pi \cdot l}{2L}})$$

(15)

$$X_i^j=\left\{\begin{array}{c}{\lambda ·X}_{best}^j+T_{DR}\times \left(\left({ub}_j-{lb}_j\right)\times r_4+{lb}_j\right) if r_3<0.5\\ {\lambda ·X}_{best}^j-T_{DR}\times \left(\left({ub}_j-{lb}_j\right)\times r_4+{lb}_j\right) if r_3\ge 0.5\end{array}\right.$$

(16)

In the early stage of iteration, parameters approach the optimal solution with a large amplitude, exploring global parameters adapted to runoff cycles; in the later stage, parameters are only fine-tuned with a small amplitude, precisely adapting to short-term runoff fluctuations (e.g., daily-scale runoff deviations).

2.5. The RPSEMD-IMVO-CSAT Model

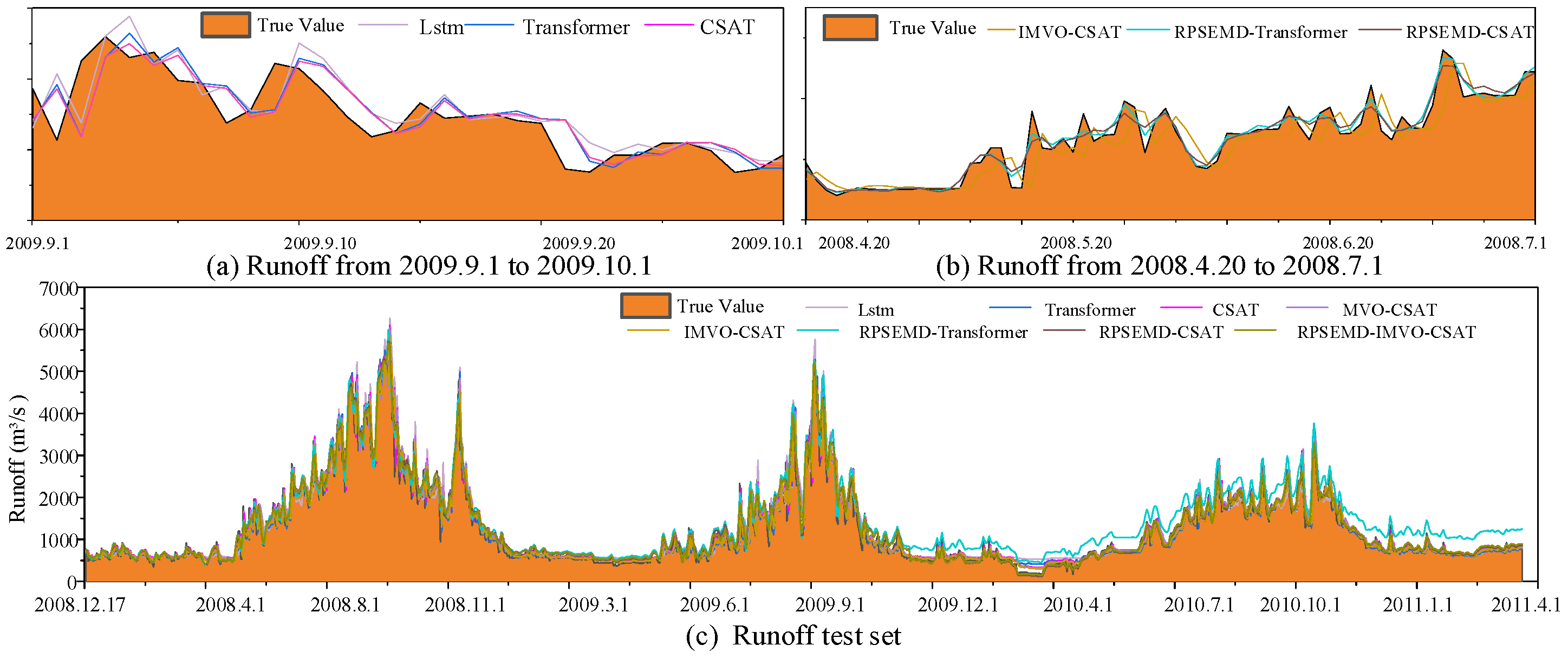
In the study of runoff prediction at the cross-border outlet of the Lancang River, several comparative models such as RPSEMD-Transformer, RPSEMD-CSAT, and RPSEMD-MVO-CSAT are first constructed as evaluation criteria. On this basis, the RPSEMD-IMVO-CSAT model is proposed, and its specific construction process is shown in Figure 3.

First, the runoff data of Yunjinghong Station is normalized, then RPSEMD is used to decompose the runoff data and extract multi-time-scale IMF components to construct the input dataset. The dataset is input into the CSAT model, which automatically extracts features through deep learning to predict the future runoff of Yunjinghong Station. Meanwhile, IMVO is formed by introducing the spiral update mechanism, exponential $T_{DR}$, and adaptive compression factor into MVO to optimize the key parameters of CSAT, ultimately achieving high-precision prediction of daily runoff at this station.

3. Study Area and Data Collection

Yunjinghong Hydrological Station is located in the middle-lower reaches of the Lancang–Mekong River Basin, within Xishuangbanna Dai Autonomous Prefecture, Yunnan Province, China [29]. As the last major hydrological control station on the Lancang River before it flows out of China, its monitoring scope covers the last 180 km of the Lancang River within China, with a total basin area of 165,000 km², directly related to the water resource security of Laos, Myanmar, Thailand, and other countries along the lower Mekong River. The region belongs to the southern extension of the Hengduan Mountains, with landforms dominated by medium-low mountains and wide valley basins. Deeply incised valleys and terraces are interlaced, forming a unique three-dimensional pattern of “mountain-river-basin”. The riverbed slope drops sharply from 1.5‰ in the upper reaches to 0.8‰ at the outlet, and the flow pattern transitions from a turbulent canyon type to a gentle alluvial type. The hydrological process is jointly affected by topographic drop and river channel morphology, showing significant segmental differences. The map of the Lancang–Mekong River Basin is shown in Figure 4.

Climatically, it is dominated by a tropical monsoon climate, with an annual average temperature of 21 °C and annual precipitation of 1200–1600 mm. More than 90% of the annual precipitation falls in the rainy season from May to October, often accompanied by short-term heavy rainfall caused by typhoons. The dry season from November to April is controlled by the northeast monsoon, with scarce precipitation and strong evaporation. This extreme seasonal difference results in a typical “summer flood and winter drought” characteristic of the runoff process: the flood peak discharge in the flood season can reach more than 20 times the minimum discharge in the dry season. In addition, complex water cycle processes such as transpiration in tropical rainforests and groundwater recharge in karst landforms make the runoff sequence contain multi-scale features such as high-frequency random disturbances (e.g., rainstorm pulses), medium-frequency seasonal fluctuations (e.g., rainy season inflow), and low-frequency trend changes (e.g., impacts of climate change).

As a key node of the cross-border basin, the monitoring data of Yunjinghong Hydrological Station has three core values: first, it directly reflects the total inflow of the Lancang River within China, providing a decision-making basis for domestic water resource regulation (e.g., cascade hydropower station generation, agricultural irrigation); second, it serves as the benchmark for incoming water volume of downstream Mekong countries, forming the quantitative basis for the implementation of cross-border water resource allocation agreements; third, it records the eco-hydrological response of the basin, providing data support for transnational ecological cooperation such as tropical rainforest protection and fish migration channel maintenance. Its runoff process is not only affected by natural factors such as glacial meltwater in the upper Qinghai–Tibet Plateau and evaporation in the dry-hot valleys of the middle reaches but also closely related to human activities such as cascade reservoir regulation and cross-border shipping development, forming a complex natural-human coupled hydrological system.

The experiment selects daily runoff data of Yunjinghong Hydrological Station from 2001 to 2011 (a total of 3988 records). The single-station data are divided into training set and test set at a ratio of 70%:30%. Interpolation is used to repair zero values and abnormal values to ensure the integrity of the data sequence, laying a reliable data foundation for subsequent model construction.

4. Data Preprocessing and Results Analysis

4.1. Data Preprocessing

The daily runoff data of Yunjinghong Hydrological Station is decomposed using RPSEMD to extract multi-time-scale IMF components to construct the input dataset. The data decomposition diagram is shown in Figure 5.

In the prediction process [30], selecting an appropriate sliding window is the key to balancing the utilization of historical information and prediction accuracy: an excessively small window is difficult to capture long-term dependencies and trend features in the data, and is prone to being disturbed by short-term noise, leading to large prediction fluctuations; an excessively large window may incorporate redundant information, smoothing out important local patterns (e.g., mutation points, short-term trends) while increasing computational burden; a window size adapted to data characteristics (e.g., periodicity, volatility) can accurately extract historical patterns related to the prediction target, enabling the model to learn effective temporal dependencies and ultimately improving the stability and accuracy of prediction. Therefore, different sliding windows are set in the data preprocessing stage, and the CSAT runoff prediction model is used for prediction. The optimal sliding window size is selected through evaluation indicators, with specific results shown in

Table 1. Comparative experiment of sliding window sizes.

Sliding Window	RMSE	NSE	MAE	MAPE(%)
7	372.490	0.853	246.631	25.9
10	318.179	0.893	184.993	15.2
20	370.983	0.856	241.761	23.6
30	376.883	0.851	255.082	26.5

.

From the prediction evaluation indicators of different sliding windows in Table 1, when the sliding window size is 10, RMSE (318.179), MAE (184.993), and MAPE (15.175%) are all the smallest, and NSE (0.893) is closer to 1 [31]. Comprehensively considering the four indicators of RMSE, NSE, MAE, and MAPE, the prediction effect is relatively optimal when the sliding window size is 10.

4.2. Result Analysis

To verify the effectiveness of the synergistic technical framework of “multi-scale decomposition-model improvement-parameter optimization” constructed for daily runoff prediction at Yunjinghong Hydrological Station, this section conducts a systematic analysis based on measured daily runoff data from 2001 to 2011 [32]. This paper utilized MATLAB 2023a to perform data prediction. By comparing the prediction performance of the proposed RPSEMD-IMVO-CSAT model with traditional and improved models such as LSTM, GRU, and standard Transformer, the analysis covers dimensions including intuitive adaptability of fitting curves, quantitative performance indicators (RMSE, MAE, NSE), prediction stability across different hydrological years, and small-sample generalization ability. Among them, the core role of Regenerated Phase-Shifted Sine-Assisted Empirical Mode Decomposition (RPSEMD) is to solve the mode mixing problem of traditional decomposition, accurately separating interannual trends, seasonal fluctuations, and short-term disturbances of the runoff sequence; Convolutional Sparse Attention Transformer (CSAT) enhances local feature perception by embedding a 1D-CNN module and focuses on key temporal correlations through a sparse attention mechanism, making up for the deficiency of traditional Transformer in detail capture; Improved Multi-Verse Optimizer (IMVO) optimizes model parameters through mechanisms such as spiral update and exponential Travel Distance Rate, improving adaptability to runoff mutation patterns. The following combines fitting curves, performance indicator tables, and comprehensive evaluation diagrams to analyze in detail the prediction efficiency of each model and the synergistic value of the proposed technical framework, providing support for verifying the reliability of the model in complex cross-border hydrological scenarios.

Figure 6 presents the fitting curves of predicted and measured runoff values of different models at Yunjinghong Hydrological Station, intuitively reflecting the ability of each model to characterize the daily runoff process and the law of performance gradient improvement [33]. Among traditional deep learning models, the fitting curves of LSTM and Transformer have obvious deviations from the measured values: at the flood peak in the flood season of August 2009 and the dry-wet transition point in March 2011, the LSTM model shows a 1–2 day lag in prediction response, failing to accurately capture short-term flow mutations; although the Transformer model is slightly better than LSTM in long-term trend fitting, it still has a prediction error of about 15% when facing the sudden flow surge caused by short-term heavy rainfall from typhoons in 2011, reflecting the insufficient adaptability of single models to the nonlinear and multi-scale features of runoff. The CSAT model enhances local feature perception by embedding a 1D-CNN module, and its fitting curve shows significantly improved response speed at flood peaks and dry-wet inflection points. For example, the prediction phase difference is reduced to within 0.5 days during the flood peak period in July 2010, indicating that the focusing effect of the sparse attention mechanism on key time-step correlations is effective; the MVO-CSAT and IMVO-CSAT models show further improved fitting effects due to the introduction of parameter optimization. Among them, the prediction deviation of IMVO-CSAT for low flow in the extreme dry period of 2010 is reduced by about 8% compared with MVO-CSAT, confirming the advantage of the improved multi-verse optimization algorithm in balancing global optimization and local convergence. After integrating RPSEMD, the deviation between the fitting curves of RPSEMD-Transformer and RPSEMD-CSAT and the measured values is significantly reduced: high-frequency random disturbances are effectively separated, and low-frequency trends are clearer. For example, the fitting accuracy of seasonal fluctuations in the rainy season of 2009 is significantly improved; the fitting curve of the RPSEMD-IMVO-CSAT model has the highest coincidence with the measured values, achieving dynamic and accurate tracking in processes such as multiple flood peak superpositions in the flood season of 2010 and gradual flow transition from dry to flood seasons in 2011, fully reflecting the adaptability of the synergistic strategy of “multi-scale decomposition-model improvement-parameter optimization” to complex runoff processes.

The performance indicator data in

Table 2. Runoff prediction performance indicators at Yunjinghong Hydrological Station.

Model	RMSE	NSE	MAE	MAPE (%)
LSTM	339.265	0.879	206.370	18.979
Transformer	326.315	0.887	192.619	16.029
CSAT	318.179	0.893	184.993	15.175
MVO-CSAT	313.681	0.896	184.005	14.607
IMVO-CSAT	309.133	0.899	179.088	13.904
RPSEMD-Transformer	279.052	0.918	234.068	27.966
RPSEMD-CSAT	173.080	0.968	113.668	10.750
RPSEMD-IMVO-CSAT	171.755	0.968	112.078	10.415

further quantifies the prediction accuracy and stability of each model. Among traditional models, LSTM has an RMSE of 339.265 and an NSE of 0.879. The Transformer reduces RMSE to 326.315 and increases NSE to 0.887 through the self-attention mechanism, but both fail to meet the high-precision requirements of cross-border water resource management. Through structural improvements, the CSAT model reduces RMSE to 318.179 and MAE to 184.993, with a 6.2% reduction in RMSE compared with LSTM, indicating that the improvements in local feature enhancement and sparse attention are effective; with the introduction of MVO and IMVO optimization, model errors continue to decrease. Among them, IMVO-CSAT has an RMSE of 309.133 and an NSE of 0.899, with a further 1.4% reduction in RMSE compared with MVO-CSAT, verifying the improvement effect of methods such as the spiral update mechanism on parameter optimization efficiency.

After integrating RPSEMD, the model performance achieves a qualitative leap: the RMSE of RPSEMD-Transformer is reduced by 14.5% compared with Transformer, and NSE is increased to 0.918; the RMSE of RPSEMD-CSAT is further reduced to 173.080, NSE reaches 0.968, and MAE and MAPE are reduced to 113.668 and 10.750%, respectively; the final RPSEMD-IMVO-CSAT model has the optimal indicators, with an RMSE of only 171.755, NSE remaining at 0.968, and MAE and MAPE as low as 112.078 and 10.415%, respectively. Compared with LSTM, RMSE and MAE are reduced by 49.4% and 45.7%, respectively, highlighting the synergistic effect of multi-scale feature extraction, model structure improvement, and parameter optimization.

The radar chart and bar chart in Figure 7 confirm the above conclusions from the perspective of comprehensive performance. The radar chart shows that the polygon area of traditional models is the smallest, with obvious shortcomings in the dimensions of “accuracy-stability-generalization”; the polygon areas of CSAT and its optimized models gradually expand, especially with significant improvement in the “local mutation capture” dimension; among the RPSEMD series models, the RPSEMD-IMVO-CSAT model has the largest polygon area in the radar chart, lying in the optimal range in all axes of RMSE, MAE, MAPE, and NSE, reflecting its strongest comprehensive prediction ability. The bar chart intuitively presents the numerical differences in RMSE and MAE among models: the RPSEMD-IMVO-CSAT model has the lowest bar heights, with a significant gap from other models. Combined with the experimental results showing consistently lower prediction errors across various hydrological conditions, this further confirms the model’s higher reliability and environmental adaptability in complex transboundary hydrological scenarios.

Figure 8 presents a scatter plot comparison of four prediction models: CSAT, IMVO-CSAT, RPSEMD-CSAT, and RPSEMD-IMVO-CSAT. It can be clearly observed from the figure that the scatter points of the RPSEMD-IMVO-CSAT model are distributed most compactly, indicating the best fit to the data. This demonstrates that the hybrid model proposed in this paper achieves higher accuracy in runoff prediction. It effectively captures the complex nonlinear relationships inherent in historical runoff data, thereby providing more accurate forecasts of future runoff trends.

Figure 9 illustrates the error distribution of different models(the lines in the figure represent the error distribution), with the RPSEMD-IMVO-CSAT model demonstrating the best performance. Its error distribution is the most concentrated and nearly symmetric around zero, indicating minimal and stable prediction errors. Compared to other models, such as CSAT and Transformer, the RPSEMD-IMVO-CSAT model exhibits a narrower error distribution with shorter tails, suggesting an extremely low frequency of extreme error values and more reliable prediction results. This highlights the advantages of RPSEMD-IMVO-CSAT in feature extraction and error optimization, making it the preferred model for prediction tasks.

Table 3. Peak water level predictions and errors for each model.

Year		2008	2009	2010	Average Error (%)
Model	Measured Peak Runoff (m3/s)	5970	5190	3460
CSAT	Predicted Value (m3/s)	4675	4623	3001	15.294
	Predicted Absolute Error (%)	21.692	10.925	13.266
RPSEMD-CSAT	Predicted Value (m3/s)	5712	5098	3234	4.208
	Predicted Absolute Error (%)	4.321	1.773	6.531
RPSEMD-IMVO-CSAT	Predicted Value (m3/s)	5666	5224	3282	3.631
	Predicted Absolute Error (%)	5.092	0.655	5.145

presents the annual maximum Runoff forecast values and their errors for each model. The table displays the prediction results and corresponding errors for the annual maximum Runoff of each year in the 10-year dataset, along with the average errors over these 10 years. The data indicate that although the proposed RPSEMD-IMVO-COST forecasting model exhibits some fluctuations in certain years, its average error is significantly superior, showing a reduction of 11.663% compared to CSAT, 0.577% compared to RPSEMD-CSAT.

4.3. Ablation Analysis: Component Contributions in Daily Runoff Prediction

This section presents an ablation study aimed at progressively refining the daily runoff forecasting model. The study began by evaluating four base models, ultimately identifying CSAT as the optimal foundational model. Subsequently, each component of the hybrid model was systematically integrated into the CSAT framework. This integration enabled a rigorous assessment of the individual contributions and the essential nature of each additional element. Through this systematic approach, the study delineates the incremental improvements conferred by each component, thereby enhancing the predictive accuracy and robustness of the daily runoff forecasting model. “√” indicates selected. The experimental results are presented in

Table 4. Results of ablation experiments.

CSAT	RPSEMD	IMVO	RMSE	NSE	MAE	MAPE
√			318.179	0.893	184.993	15.175
√	√		173.080	0.968	113.668	10.750
√		√	309.133	0.899	179.088	13.904
√	√	√	171.755	0.968	112.078	10.415

below.

The results of the ablation study provide insights into the specific effects of each component on the model’s predictive accuracy. RPSEMD and CSAT improved model performance to varying degrees. The introduction of RPSEMD significantly enhanced model performance, highlighting its critical role in data preprocessing for improving model performance. When RPSEMD was combined with IMVO, model performance was further improved. The fully integrated model outperformed all others across all evaluation metrics, validating the effectiveness and necessity of the proposed model and its components. This comprehensive analysis not only substantiates the importance of each component but also underscores the value of their synergistic integration within the model framework.

5. Discussion

5.1. Comparison with Recent Flood Prediction Models

Recently, a paper applying the Informer model for flood forecasting prediction has been published [34]. This Informer model was proposed in the paper by Zhou et al. [35] in 2021 at AAAI, and is primarily used for long-sequence time-series forecasting. In this study, data from the station were used as input, and the Informer model was compared with the CSAT model.

Table 5. Comparison of Metrics between Informer and CSAT.

Models	RMSE	NSE	MAE	MAPE
Informer	326.354	0.854	189.553	16.965
CSAT	318.179	0.893	184.993	15.175
RPSEMD-IMVO-Informer	177.496	0.937	114.988	11.639
RPSEMD-IMVO-CSAT	171.755	0.968	112.078	10.415

presents a comparison of performance metrics for the prediction results of the two models.

As shown by the data in Table 5, the prediction error of the Informer model is higher compared to the improved CSAT model proposed in this study. Despite attempts with various hyperparameter tuning methods [34], the performance of the Informer model consistently failed to reach the desired level, and the metrics presented in the table represent the best results obtained from multiple experiments. This suggests that the Informer model may have limitations when applied to the data in this study, and its architecture or assumptions might not be fully suitable for the hydrological processes represented by this dataset.

5.2. Discussions on Enhanced Prediction

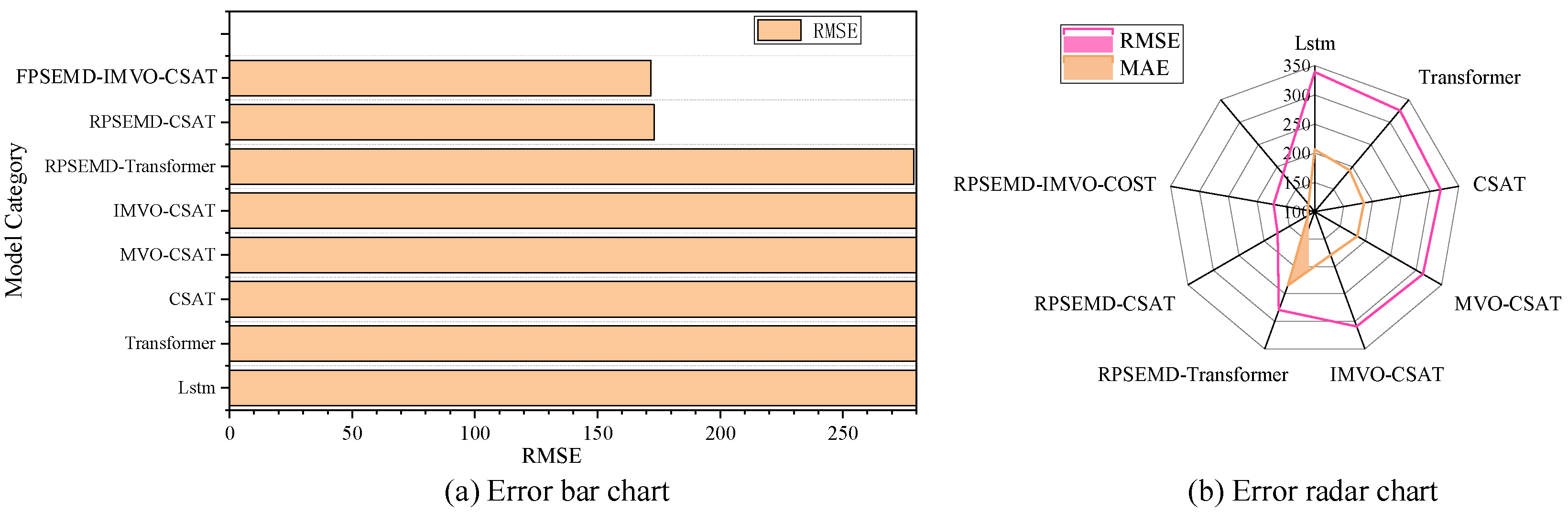
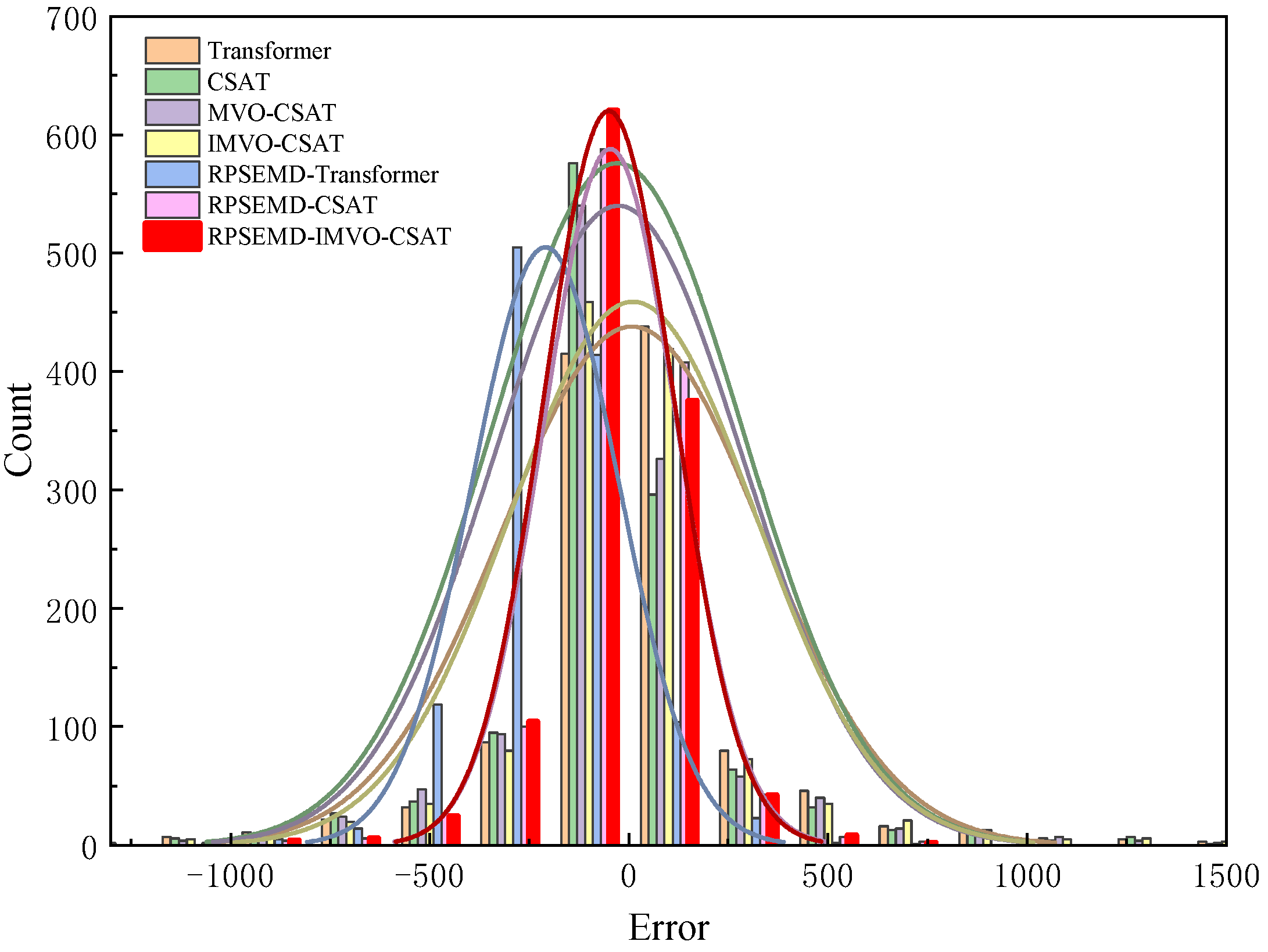
The introduction of Regenerative Phase-Shifted Sinusoidal-Assisted Empirical Mode Decomposition (RPSEMD) represents a significant improvement over traditional EMD methods. By incorporating a regenerative phase-shifted sinusoidal auxiliary signal, RPSEMD effectively addresses critical limitations such as mode mixing, endpoint effects, and instability in decomposition. This enhancement allows for precise separation of high-frequency disturbances, medium-frequency seasonal fluctuations, and low-frequency trend components, resulting in purer and more discriminative input features for predictive models. Empirical results demonstrate that integrating RPSEMD reduces the RMSE of the Transformer model by 14.5% and increases the Nash-Sutcliffe Efficiency (NSE) to 0.918. This underscores the method’s capability to significantly boost prediction accuracy through refined multi-scale feature extraction.

To address the standard Transformer’s limitations in capturing localized, short-term runoff variations-where global attention mechanisms may dilute critical local information-the Convolutional Sparse Attention Transformer (CSAT) was developed. This model embeds a 1D-CNN module to enhance local feature extraction and employs a sparse attention mechanism to efficiently prioritize correlations across key time steps. The CSAT model achieves an RMSE of 318.179 and an MAE of 184.993, representing a 6.2% reduction in RMSE compared to the LSTM model (339.265). Additionally, the NSE value rises to 0.893, while the MAPE decreases to 15.175%. These results confirm the model’s superior ability to capture localized hydrological patterns and improve prediction accuracy through balanced local-global representation learning.

The Improved Multi-Verse Optimizer (IMVO) incorporates advanced strategies such as spiral update and exponential travel distance rate mechanisms to better balance global exploration and local exploitation during parameter optimization. This leads to improved adaptation to runoff mutation patterns and overall prediction stability. The IMVO-CSAT model achieves an RMSE of 309.133 and an MAE of 179.088, which are 1.4% and 2.7% lower, respectively, than those of the MVO-CSAT model. Overall, the proposed integrated model reduces RMSE and MAE by 15.3–49.4% and 18.6–45.7%, respectively, compared to traditional models such as LSTM and Transformer. It also elevates NSE to 0.968. This offers a high-accuracy tool for coordinated cross-border water resource regulation in the Lancang–Mekong River Basin, providing crucial technical support for agricultural irrigation, energy production, and ecological security downstream.

Conducting daily runoff prediction research targeting the Yunjinghong station can accurately capture the spatiotemporal correlations of transboundary hydrological processes. This approach not only compensates for the limitations of single-country monitoring but also provides a technical vehicle for basin countries to establish a cooperative mechanism of “data sharing, model co-development, and decision coordination.” It holds irreplaceable practical significance for resolving conflicts in transboundary water allocation and enhancing the overall water security capacity of the river basin.

6. Conclusions and Future Work

This study addresses the strong nonlinearity and coupled multi-scale characteristics in the daily runoff sequence at the Yunjinghong Hydrological Station by constructing a RPSEMD-IMVO-CSAT hybrid prediction model. Case validation demonstrates that the model achieves excellent performance in runoff prediction accuracy and stability. The following conclusions can be drawn:

(1)

RPSEMD resolves mode mixing, effectively separating multi-scale features and increasing Transformer’s NSE to 0.918.

(2)

1D-CNN enhances local feature capture, enabling CSAT to reduce RMSE by 6.2% compared to LSTM.

(3)

Improved optimization strategies further lower RMSE to 309.133, enhancing accuracy in capturing runoff mutations.

(4)

The final model reduces RMSE by 15.3–49.4% and increases NSE to 0.968, significantly improving prediction stability.

Future work will focus on applying and testing the proposed model in other key stations across the basin, provided that collaborative data-sharing mechanisms are established, to further verify its adaptability and robustness in diverse hydro-climatic regimes.

Moreover, future work will directly integrate multi-source data, including satellite-derived precipitation, temperature, and upstream reservoir release information, into the current framework. This will strengthen the physical basis of the predictions and further improve the model’s robustness for operational cross-border water resource management.

While this study demonstrates the superior predictive accuracy of the RPSEMD-IMVO-CSAT model, its practical value for real-time water management hinges on computational efficiency and scalability—key considerations in recent hybrid frameworks like the ensemble CNN-LSTM-GRU model with sparrow search optimization [12] and the evolutionary TCN-based model [13]. Our framework addresses these concerns through its architecture: the sparse attention mechanism in CSAT reduces the computational complexity of self-attention, enhancing inference speed crucial for operational forecasts. Furthermore, the exponential convergence strategy in IMVO lowers the optimization cost compared to standard metaheuristics. In terms of scalability, the modular pipeline (RPSEMD for adaptive decomposition, CSAT for feature learning, and IMVO for parameter tuning) is inherently transferable to other cross-border basins or extended forecast horizons. A direct comparative analysis of training time, parameter size, and inference latency against models in [12,13] will be conducted in future work to quantitatively position our model within the landscape of deployable hydrological forecasting systems.