A Study on the Deformation Mechanism of a Landslide Reinforced with an Anti-Slip Pile Under the Effect of Reservoir Water Level Decline

Abstract

The fluctuation of reservoir water levels is a critical factor influencing the evolution of reservoir landslide–anti-slide pile systems. To investigate the reinforcement mechanism of anti-slide piles in reservoir landslides under the effect of reservoir water level fluctuations, this study employs numerical simulation methods to establish a three-dimensional slope model, simulating the drawdown process of the reservoir water level from 175 m to 145 m. The displacement and strain fields of the reservoir landslide during the water level drawdown are analyzed. Furthermore, the strain characteristics of the anti-slide pile-reinforced reservoir landslide under stress–seepage coupling are studied, and the prevention effectiveness of the landslide–anti-slide pile interaction system is explored. The results indicate that the drawdown of the reservoir water level can lead to the gradual expansion of the strain and displacement zones in the landslide, as well as a reduction in the safety factor. Under the effect of anti-slide piles, the maximum deformation of the reservoir landslide is significantly reduced. The optimal reinforcement effect is achieved when the anti-slide piles are arranged in the middle of the reservoir landslide, with a pile spacing of four times the pile diameter and an embedded depth reaching the critical depth. The findings of this study can provide a scientific basis for analyzing the instability mechanisms and mitigation of reservoir landslides.

1. Introduction

The long-term cyclical fluctuations in reservoir water levels induce corresponding periodic variations in groundwater levels. This hydrological dynamic leads to intermittent saturation conditions, where portions or even the entire reservoir landslide experience alternating periods of saturation and unsaturation [1,2]. This results in cyclical fluctuations of pore water pressure and shear strength in the soil and rock mass of the landslide, thereby impacting the landslide’s stability. According to the research results, even a 5% cyclical alteration in shear strength parameters can cause a remarkable reduction in the safety factor as compared to the limiting safety factor, thus highlighting the significant effect of reservoir water level changes on the long-term stability of reservoir landslides [3,4]. For example, since the Three Gorges Reservoir impounded water to 175 m in 2008, more than 400 new and old landslide deformations have occurred throughout the reservoir area, with more than 100 collapses and 50 km of unstable reservoir banks, closely related to the cyclical fluctuations of the reservoir water level.

Given the significant impact of reservoir water level fluctuations on the stability of reservoir landslides, scholars both domestically and internationally have conducted relevant research on this issue. Jia et al. [5] conducted model tests to obtain the deformation and failure characteristics and mechanisms of reservoir landslides caused by water level fluctuations. Huang et al. [6] systematically studied monitoring data from a buoyancy-reduced landslide in the Three Gorges Reservoir area, finding that landslide deformations were larger during high water levels and smaller during low water levels. Tang et al. [7] conducted statistical analyses of numerous landslides along the Three Gorges Reservoir, identifying the deformation patterns and mechanisms of landslides with different sliding surfaces and permeabilities under the influence of water level fluctuations. Zhao et al. [8] established a seepage–stress coupling model for the Huangnidaba landslide using the finite element method, indicating that the landslide was significantly affected by the drop in reservoir water levels, exhibiting creep deformation. During the water level decline, the pore water pressure within the landslide decreased, while the effective creep stress increased, accelerating the creep deformation of the landslide. Zangerl et al. [9] investigated the effects of reservoir water level fluctuations on deep-seated landslides at the Gepatsch dam and revealed that the seasonal variation in landslide deformation rates was closely related to the rise in reservoir water levels.

Anti-sliding piles, as an effective landslide support structure, have been widely adopted for landslide stabilization and large landslide remediation in reservoir areas due to their strong deep anti-sliding capability, minimal disturbance to the sliding mass, and ease of construction [10,11,12,13]. Many researchers have conducted extensive studies on the mechanisms of anti-sliding pile reinforcement and design calculation methods. Song et al. [14] revealed the response characteristics of anti-sliding piles and the landslide deformation field under strong rainfall based on field tests and numerical simulations. Through centrifuge model tests, Wang et al. [15] investigated the influence of anti-sliding piles on the deformation field of landslides. Their research demonstrated that anti-sliding piles are capable of efficiently inhibiting the development of sliding surfaces. Zhang et al. [16] highlighted the formation and progressive development of sliding surfaces, noting that the influence of anti-sliding piles decreases as the distance to the failure point increases. Lirer et al. [17] examined the impact of drainage piles on the displacement field of landslides through field monitoring and numerical simulations. Won et al. [18] analyzed the distribution characteristics of earth pressure acting on anti-sliding piles under different parameters using numerical simulations.

As mentioned above, numerous scholars have conducted extensive research on the stability of reservoir landslides under varying water levels, as well as the interaction between anti-slide piles and soil masses. However, there are relatively few studies on the effectiveness of anti-slide piles in reinforcing reservoir landslides under the condition of declining reservoir water levels. This study investigates the interaction mechanism between anti-slide piles and surrounding soil under rapid reservoir drawdown conditions, using a representative landslide in the Three Gorges Reservoir area as a case study through finite element numerical analysis. First, the simulation software ABAQUS [19] was used to explore the variations in the shear strain field, displacement field, and landslide stability of the reservoir landslide in response to water level changes. Subsequently, the effectiveness of anti-sliding piles in reinforcing the reservoir landslide under low reservoir water levels is analyzed. Finally, a sensitivity analysis of the design parameters of the anti-sliding piles is conducted, and an optimized design scheme is proposed.

2. Numerical Methodology

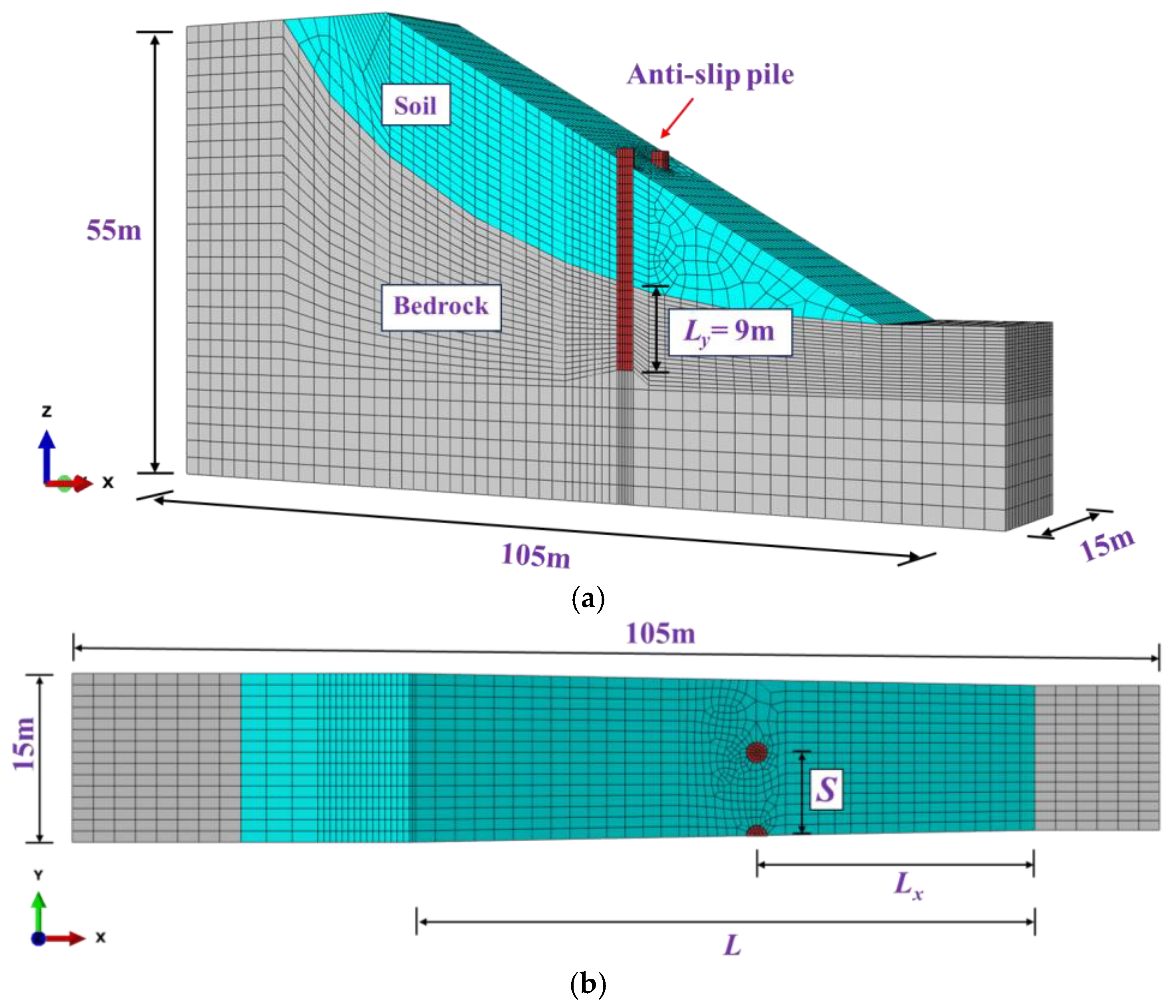
2.1. Numerical Model

(1)

Mathematical formulation

For reservoir landslides, periodic fluctuations in the reservoir water level create a hydraulic head difference between the interior and exterior of the landslide. Periodic water level fluctuations in reservoirs induce hydraulic head differentials between the interior and exterior of landslides. This hydraulic gradient drives seepage flow through the slope body, modifying the groundwater flow regime. Consequently, variations in infiltration pressure and pore water pressure occur, leading to changes in stress distribution and subsequent deformation of the landslide mass. Variations in the stress field exert a profound influence on the soil’s stress–strain behavior, thereby triggering alterations in the soil’s permeability coefficient and porosity. These changes, in turn, further transform the seepage field within the landslide mass. Subsequently, the evolving seepage field prompts additional adjustments to the stress field, giving rise to a fluid–solid coupling effect. This effect represents a dynamic interplay between hydraulic and mechanical processes, playing a pivotal role in governing landslide stability. The equations for stress balance and seepage continuity are presented as follows:

$$I^N-P^N=0$$

(1)

$${\int }_V\delta u_w{\displaystyle \frac{1}{J}}{\displaystyle \frac{d}{dt}}\left(J{p}_w{n}_w\right)dV+{\int }_V\delta u_w{\displaystyle \frac{\partial }{\partial x}}\left[p_w\left(-k{\displaystyle \frac{\partial \psi }{\partial x}}\right)\right]dV$$

(2)

where $I^N$ and $P^N$ are the internal and external force matrices, respectively; $\delta u_w$ represents variable fractions of pore water pressure; $V$ represents the change in volume of the soil; $p_w$ is the density of water; $k$ denotes the permeability coefficient of porous media; $\psi$ is the gauge head, which is the sum of the position head and the pressure head; and ${\displaystyle \frac{\partial \psi }{\partial x}}$ represents the permeability gradient.

(2)

Boundary conditions

Figure 1 presents the built numerical model established in this paper. For the landslide model, the static boundary conditions impose constraints on the displacements of nodes in the X, Y, and Z directions at the bottom. The displacements of nodes in the X direction are restricted at the front and rear boundaries. The displacement of nodes in the Y direction is constrained on both sides. Given that the front edge of the landslide is submerged by the water level of the Yangtze River, the top surface and the front surface of the model are designated as permeable boundaries, while the remaining surfaces are defined as impermeable boundaries.

The entire landslide model is 105 m long, 55 m high, and 15 m wide. The anti-sliding piles are circular piles with a diameter $D$ = 2.0 m. The anti-sliding piles are anchored in the bedrock, with a length $L_p$ = 24 m and an anchoring depth $L_y$ = 9 m in the bedrock layer. The horizontal distance from the anti-sliding piles to the toe of the landslide $L_x$ = 30 m, the horizontal distance from the top of the landslide to the toe of the landslide L = 60 m, and the pile spacing $S$ = 3$D$. By virtue of symmetry, only half of the model needs to be analyzed.

(3)

Element types and sizes

The landslide model (i.e., the slide mass and bedrock model) was discretized into 8-noded Lagrangian brick elements with both displacement and pore pressure degrees of freedom (C3D8P) for coupled flow analysis. The anti-sliding piles were discretized using Lagrangian C3D8R elements. The maximum and minimum mesh sizes for the landslide model were set at 2.2 m and 0.36 m, respectively.

(4)

The landslide parameters

The relevant parameters of the soil and bedrock slopes are shown in

Table 1. Properties of the soil and bedrock.

Material	Density ρ (kN/m3)		Friction Angle φ (°)		Cohesion c (kPa)		Permeability Coefficient k (m/d)	Elasticity Modulus G (MPa)	Poisson’s Ratio υ
	Natural Saturated		Natural Saturated		Natural Saturated
Soil	16.8	22.0	20	18	15	3	7.5	22.0	0.33
Bedrock	26.0	27.0	26	24	40	36	0.01	28,000	0.25

, while the parameters of the anti-sliding piles are presented in

Table 2. Properties of the anti-sliding piles.

Parameter	Symbol	Unit	Value
Diameter	$D$	m	2.0
Density	ρ	kN/m3	24.0
Elasticity modulus	$G$	MPa	26,000
Effective Poisson’s ratio	$\upsilon$		0.13

. It should also be noted that, to date, there has been no experimental research on the unsaturated soil properties of landslides in the Three Gorges Reservoir area. Therefore, the unsaturated permeability coefficient of the landslide can only be derived using an engineering analogy method, which is based on the saturated permeability coefficient and the grain size distribution of the soil to formulate its permeability function.

(5)

Contact surface parameters

The general contact functionality is employed to account for significant sliding and separation between the anti-slip piles and the soil surfaces in this study. The friction coefficient between the anti-slip piles and the soil is set at 0.5.

2.2. Simulation Scheme

Based on the specific geological conditions of the Three Gorges reservoir area and relevant research findings, numerical models were used to study the variations in the shear strain field, displacement field, and landslide stability of the reservoir landslide under declining water levels. The following scenario was simulated using the numerical model: the reservoir water level was initially maintained at a constant height of 175 m until the landslide reached its natural state, after which the water level dropped from 175 m to 145 m. During the numerical calculations, the boundary conditions were as follows: (i) impermeable with no vertical displacement at the bottom; (ii) no horizontal displacement on the left side; and (iii) free drainage and displacement at the slope surface.

3. Results and Discussion

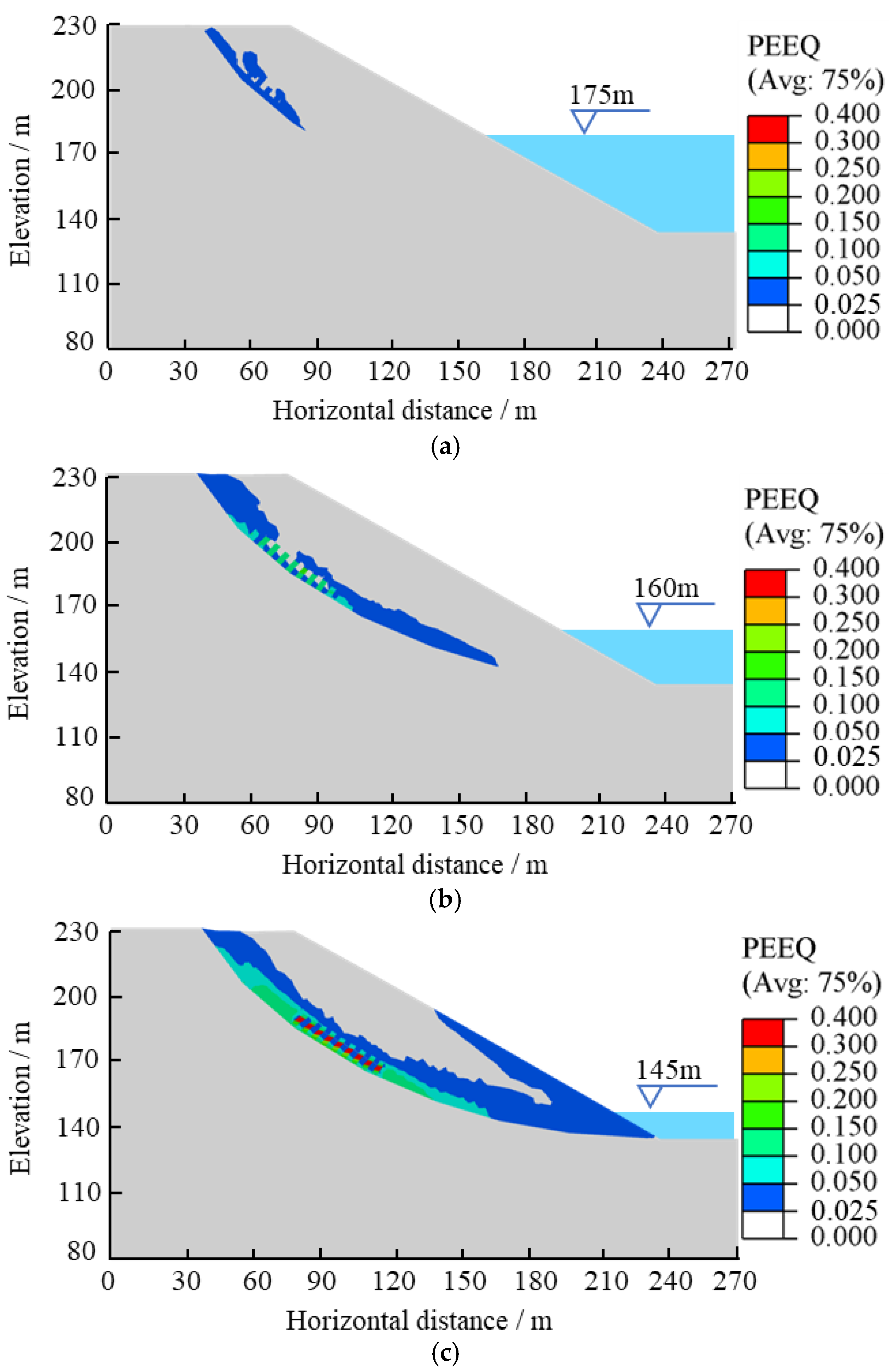
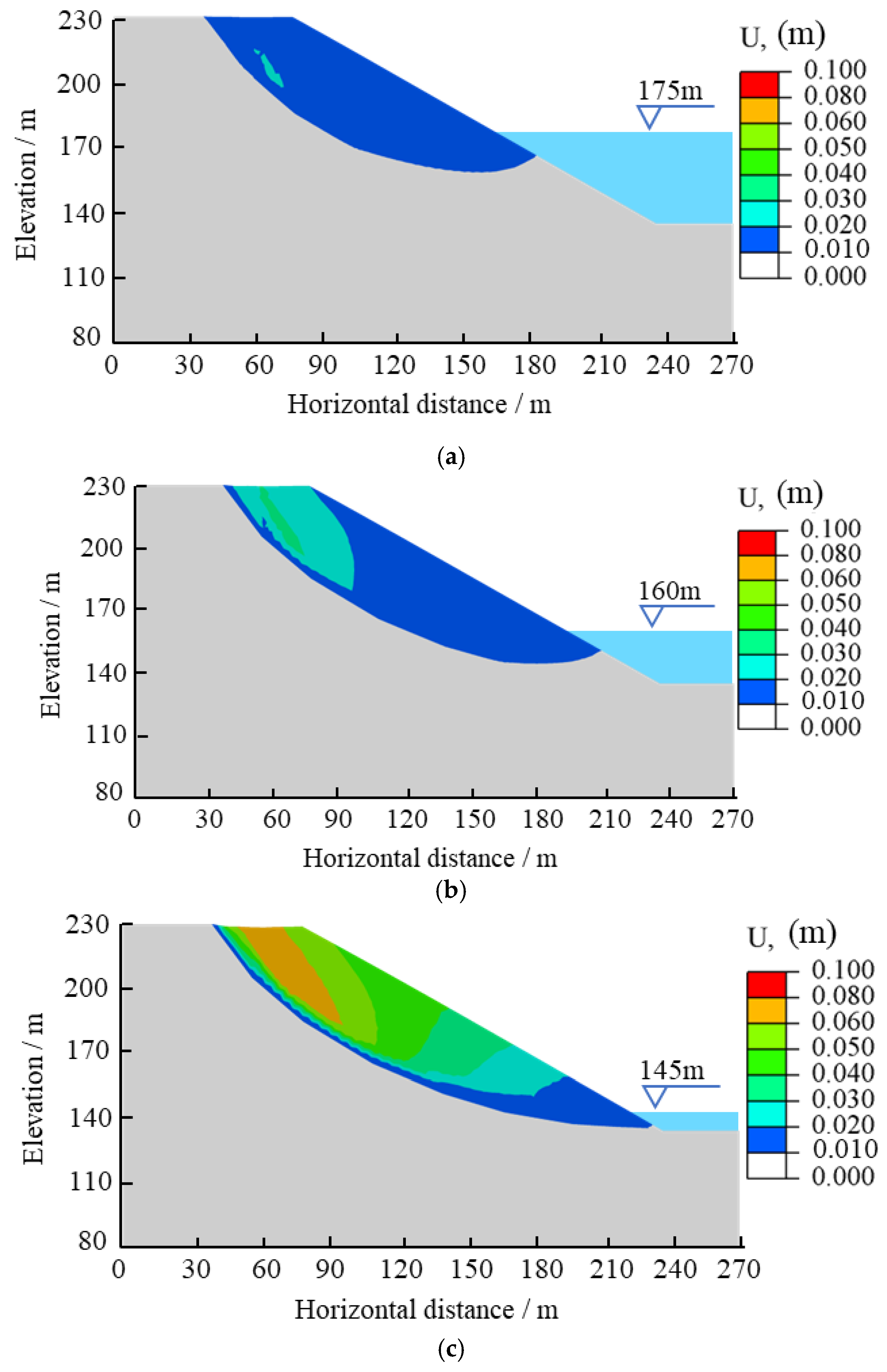
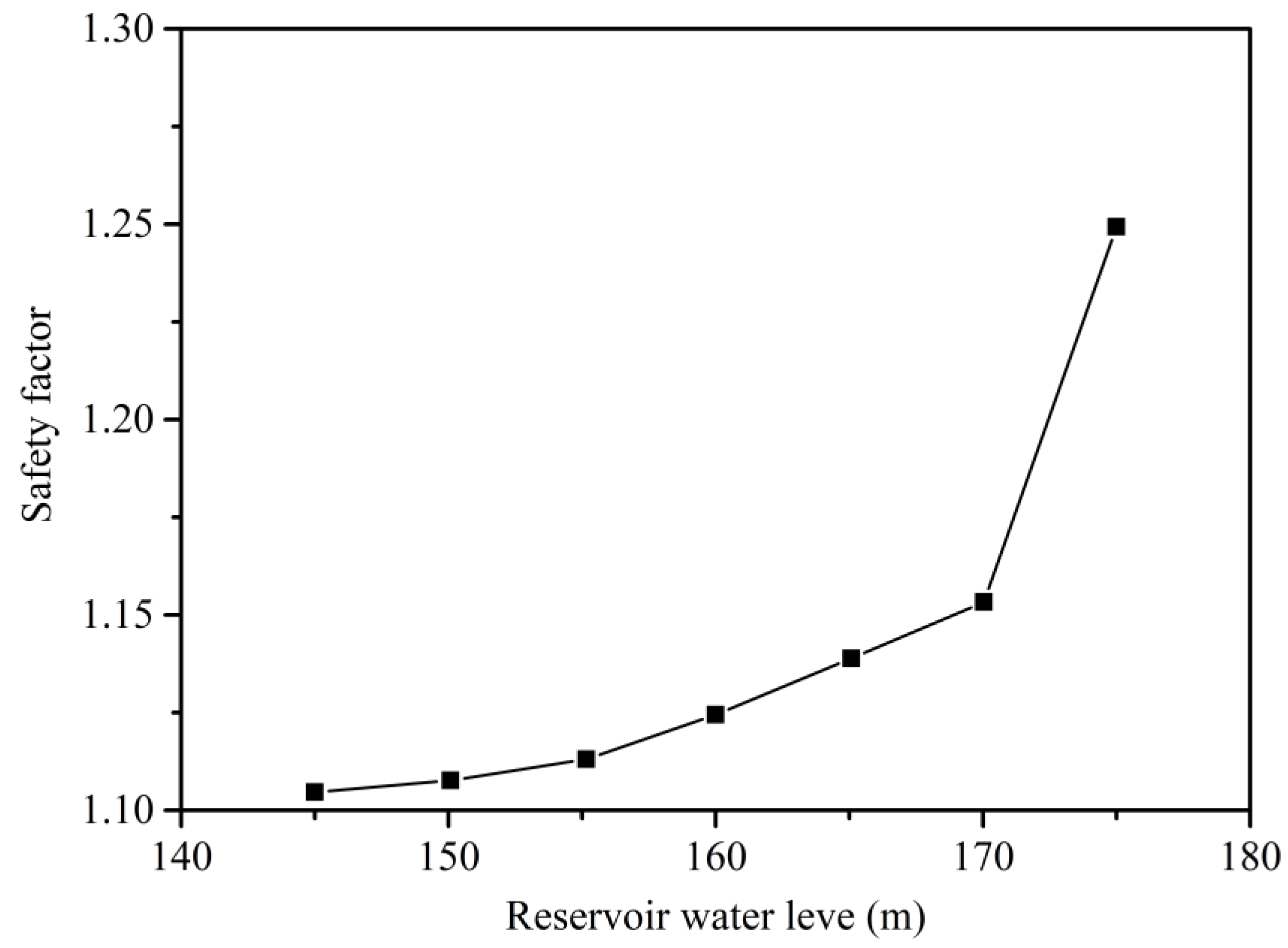
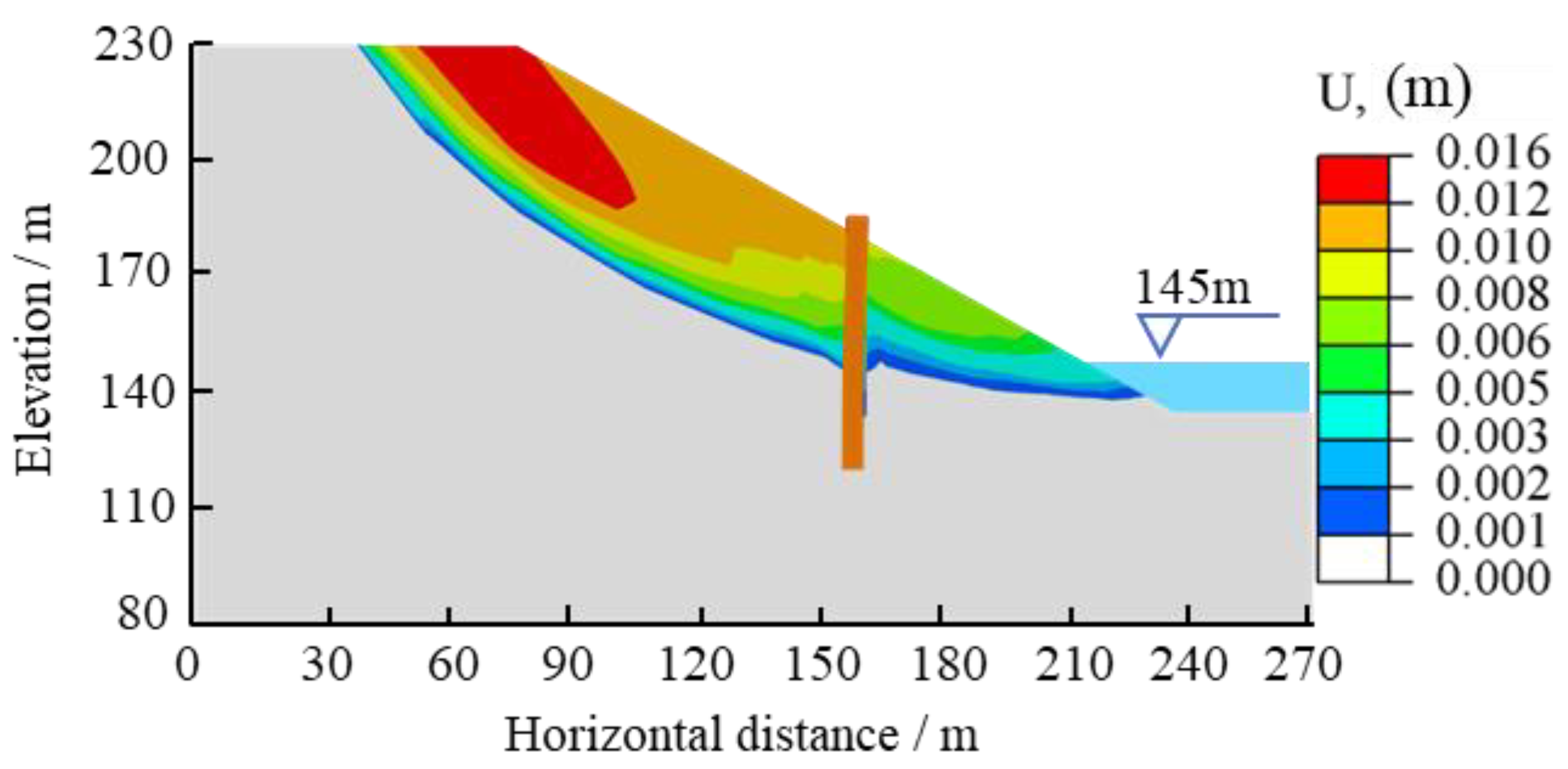
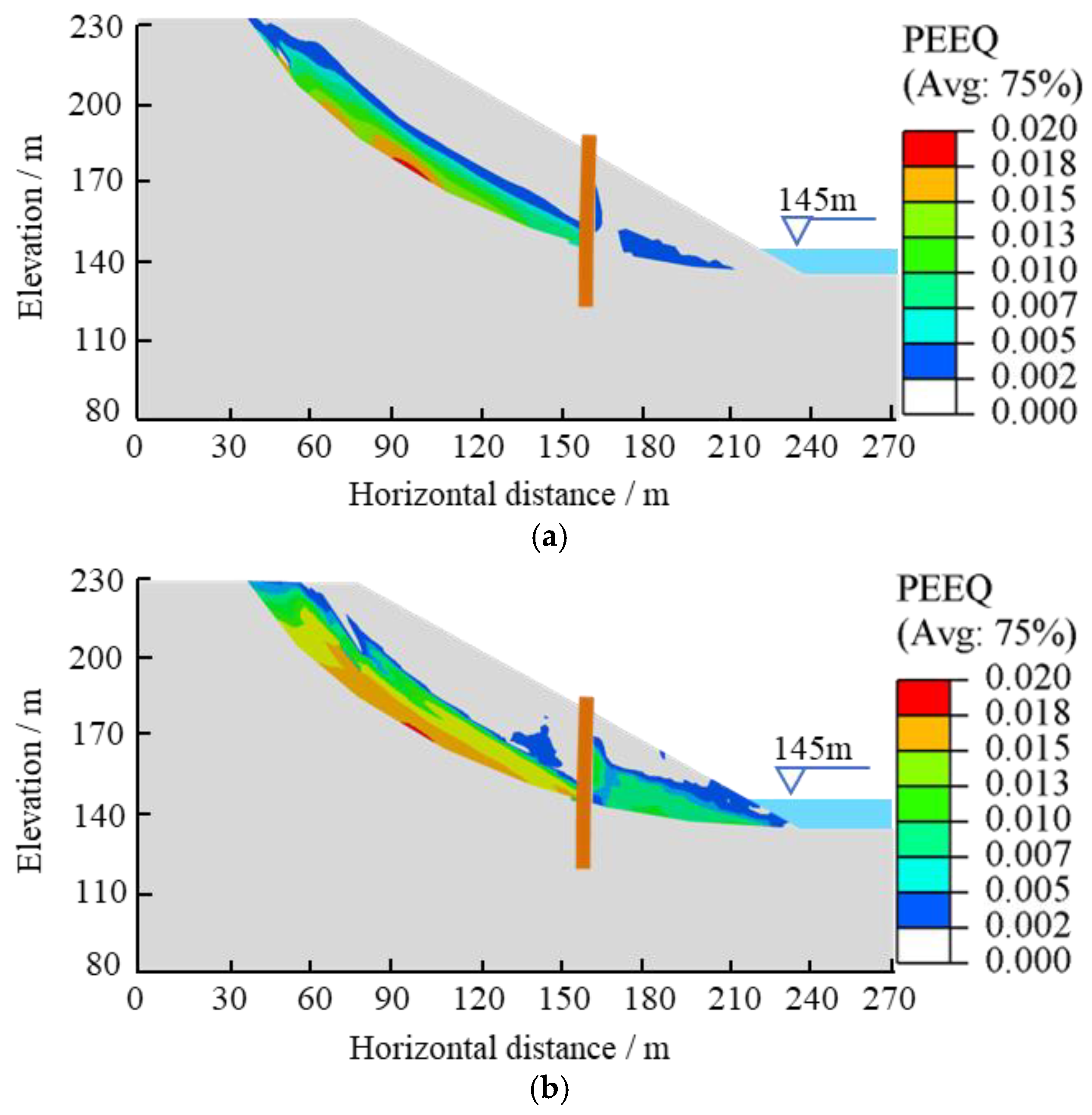
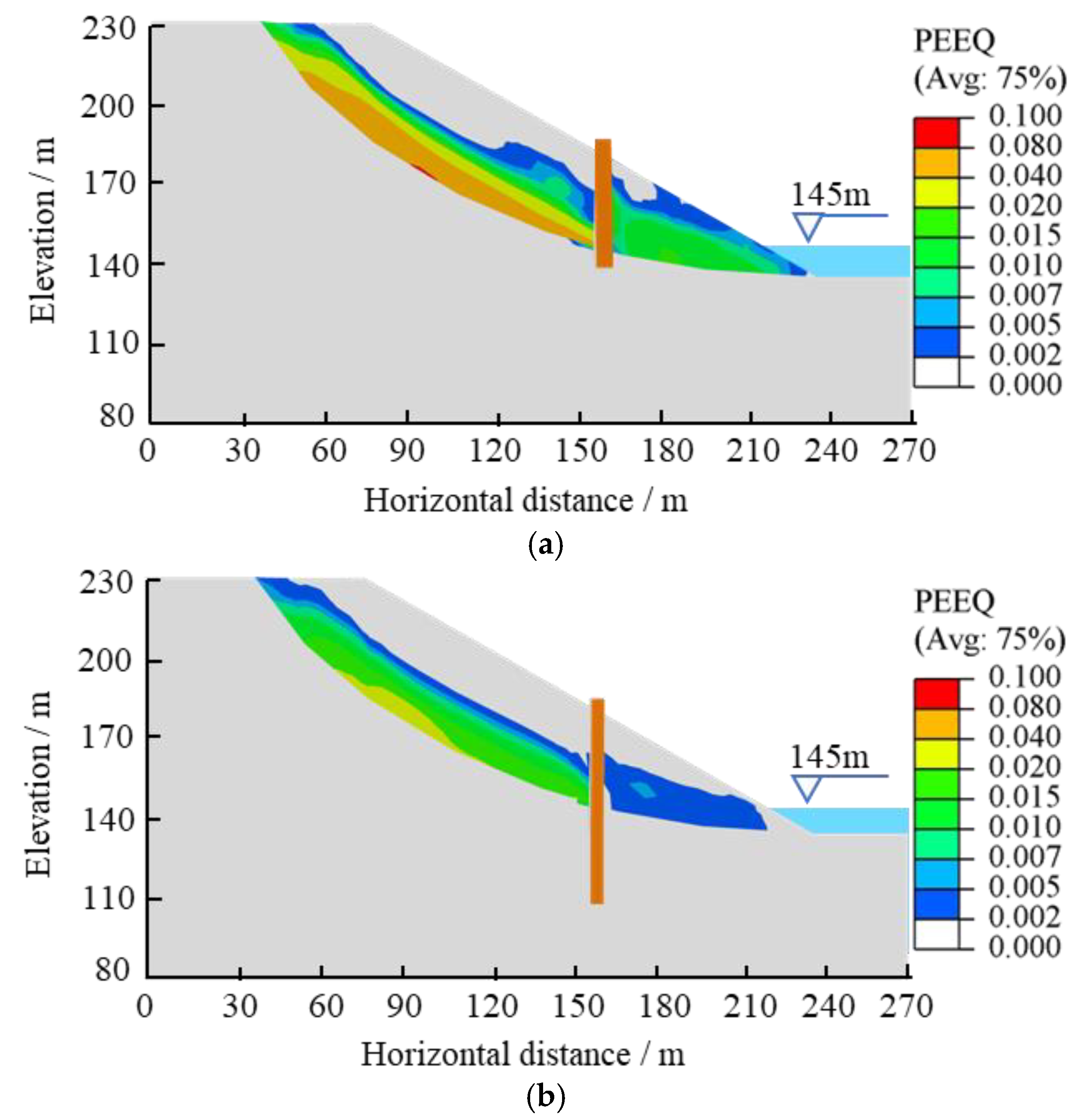
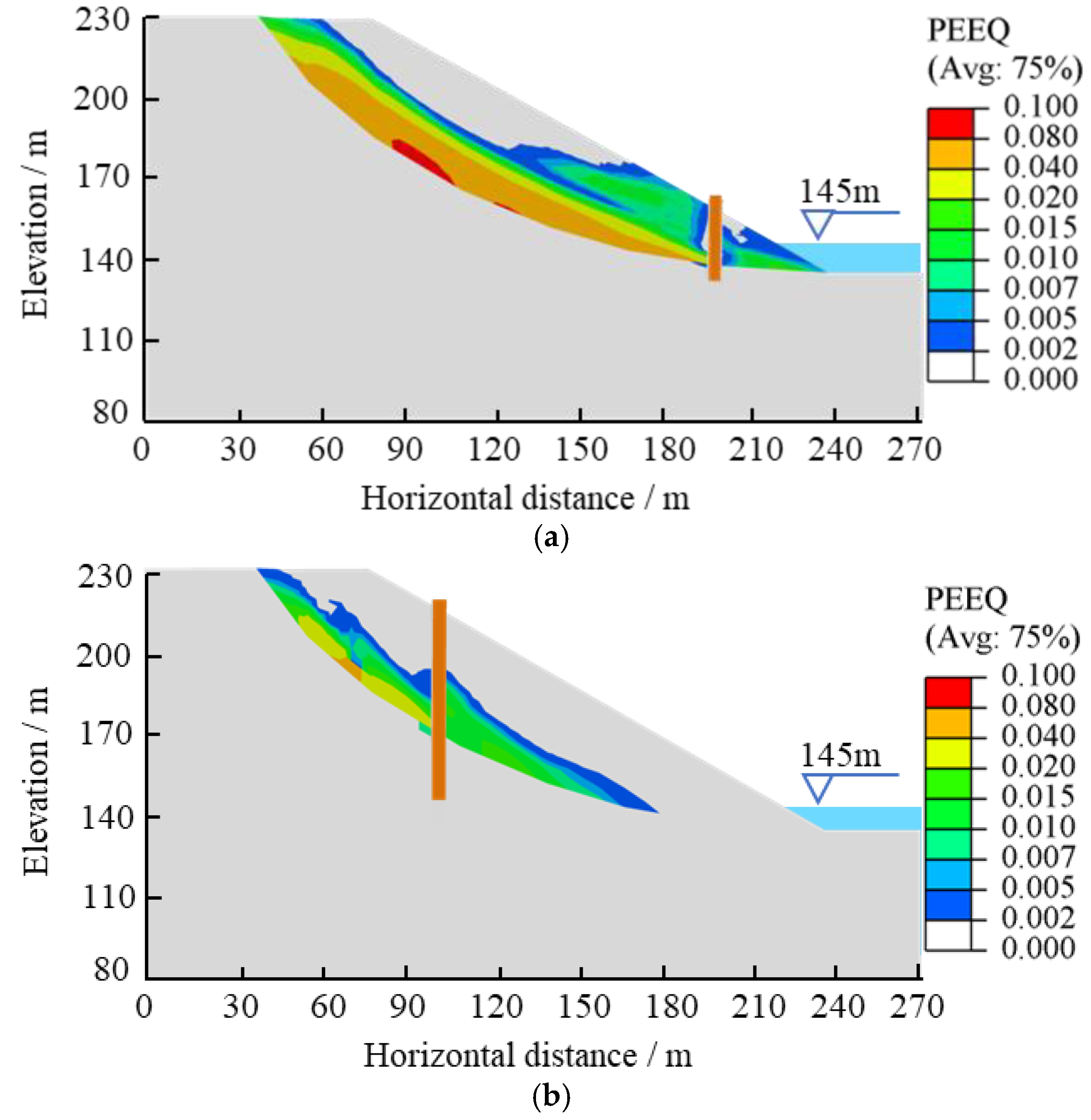
3.1. Analysis of Landslide Deformation Mechanism

During the decline of the reservoir water level, six calculation conditions were established, with the water level decreasing from 175 m to 170 m, 165 m, 160 m, 155 m, 150 m, and 145 m. The calculation results for the landslide displacement field and equivalent plastic strain field are presented for reservoir water levels of 175 m, 160 m, and 145 m, respectively.

Figure 2a illustrates the accumulated equivalent plastic strain (PEEQ) of the landslide when the reservoir level is maintained at 175 m. From this figure, it is evident that numerous shear plastic zones are generated in the middle of the landslide. However, no continuous plastic zone is formed. This is due to the high hydrostatic pressure exerted on the leading edge of the landslide from the 175 m reservoir water level, which prevents plastic deformation in that area. Conversely, the rise in groundwater level, combined with the softening effect on the landslide from prolonged submersion, reduces both the slip resistance and shear strength of the landslide. As a result, plastic damage primarily occurs in the middle section and gradually extends toward the rear edge of the landslide.

Figure 2b,c show the accumulated equivalent plastic strain (PEEQ) of the landslide when the reservoir water level decreases to 160 m and 145 m. As the water level falls, the position of the landslide’s plastic zone progressively shifts toward the base, and its distribution range widens. This is particularly evident in the middle and lower sections of the landslide, where sliding occurs along the slip surface due to changes in effective stress resulting from fluctuations in groundwater level and the effects of infiltration forces. During the decline of the reservoir level, groundwater infiltration into the slope exhibits a hysteresis effect, resulting in the development of larger dynamic water pressure directed toward the critical surface, which increases the instability of the slope. As the hydrostatic pressure acting on the slope surface decreases, the downward forces on the slope increase. Consequently, within the range of water level changes, the slope experiences larger displacements toward the critical surface. Above the water level, the enhancement effect of geotechnical properties exhibits a lagging behavior, resulting in larger horizontal displacements of the slope body during water level fluctuations. As the water level decreases, the pore water pressure within the geotechnical body is reduced, leading to an increase in the effective stress. This results in the compression of the geotechnical body above the water level, contributing to the development of a section of the landslide area that approaches the formation of a continuous plastic zone.

Figure 3 shows the displacement maps of the landslide as the reservoir water level decreases to three different elevations. The maximum total displacements of the landslide are 23 mm, 55 mm, and 85 mm when the water level is at 175 m, 160 m, and 145 m, respectively. As the water level decreases, the distribution of the maximum total displacement of the landslide shifts upward, and the range of displacement distribution continuously expands.

The shear strength reduction method proposed by Zienkiewicz et al. [20] and Dawson et al. [21] is implemented in ABAQUS software (v.6.14) to calculate the slope safety factor. In ABAQUS, the process for obtaining the slope safety factor can be divided into the following steps:

(1)

Define the field variable, usually the strength reduction factor.

(2)

Define the material properties that vary with the field variables.

(3)

Set the boundary conditions and obtain the numerical equilibrium.

(4)

Change and increase the field variable (i.e., the reduction factor) until the numerical calculation does not converge.

The method for calculating the slope safety factor in ABAQUS has been utilized by many scholars and experts to elucidate the effectiveness of landslide reinforcement measures [22,23,24,25,26,27].

The variation curve of the maximum total displacement of the landslide during the decline in water level is shown in Figure 4. It is evident that the lowering of the reservoir water level significantly affects landslide displacement, which increases from 20 mm to 80 mm during the period of water level decline. In contrast, the safety factor of the landslide exhibits an opposite trend. As the water level decreases from 175 m to 145 m, the safety factor shows a downward trend, as illustrated in Figure 5. When the reservoir water level drops to 135 m, the safety factor of the landslide reaches a minimum value of 1.11, representing a reduction of approximately 15% compared to the safety factor at the static water level of 175 m. This indicates an increased risk of instability and failure in the reservoir landslide.

3.2. Analysis of Anti-Slide Pile Reinforcement Effects

From the analysis above, it is evident that a decline in the reservoir water level can lead to significant plastic damage to the landslide. When the water level drops to 145 m, the safety factor of the landslide reaches its minimum. Therefore, in landslide stabilization projects within the reservoir area, it is crucial to consider the impact of lowered water levels on the landslide stability. As an effective landslide retaining structure, anti-slide piles are widely used in landslide disaster mitigation due to their simple design, high stiffness, substantial resistance, and ease of construction. The following section will analyze the effectiveness of anti-slide pile reinforcement on the stability of the reservoir landslide during sudden changes in water level.

Figure 6 and Figure 7 show the distribution contours of the plastic zone and total displacement after reinforcing the reservoir landslide with anti-slide piles at a water level of 145 m, respectively. From Figure 6, it is evident that, after reinforcing the reservoir landslide with anti-slide piles, the maximum shear strain increment is limited near the location of the piles. Additionally, the total displacement of the reservoir landslide has been reduced to 14 mm (see Figure 7), demonstrating a significant decrease compared to the situation without the use of anti-slide piles (see Figure 3c). This is because when anti-slide piles are used for landslide reinforcement, the soil body slides downward relative to the piles. On one hand, the anti-slide piles are embedded in a hard and relatively stable bedrock layer; on the other hand, the physical properties of the piles are stronger than those of the landslide soil. When a portion of the landslide soil experiences uneven deformation or displacement, the cohesion and friction within the sliding mass create frictional resistance against the uneven movement of the soil. This interaction causes soil particles to exert a mutual “wedge effect,” resulting in stress deflection near the anti-slide piles. Consequently, a more pronounced soil arch forms around the base of the neighboring piles, as illustrated in Figure 8. The presence of the soil arch effect causes the anti-slide piles to be embedded in a hard and relatively stable bedrock layer. Additionally, the physical properties of the anti-slide piles are stronger than those of the landslide soil. This soil arch effect makes it difficult for the soil to flow between the piles, thereby inhibiting the downward sliding of the landslide.

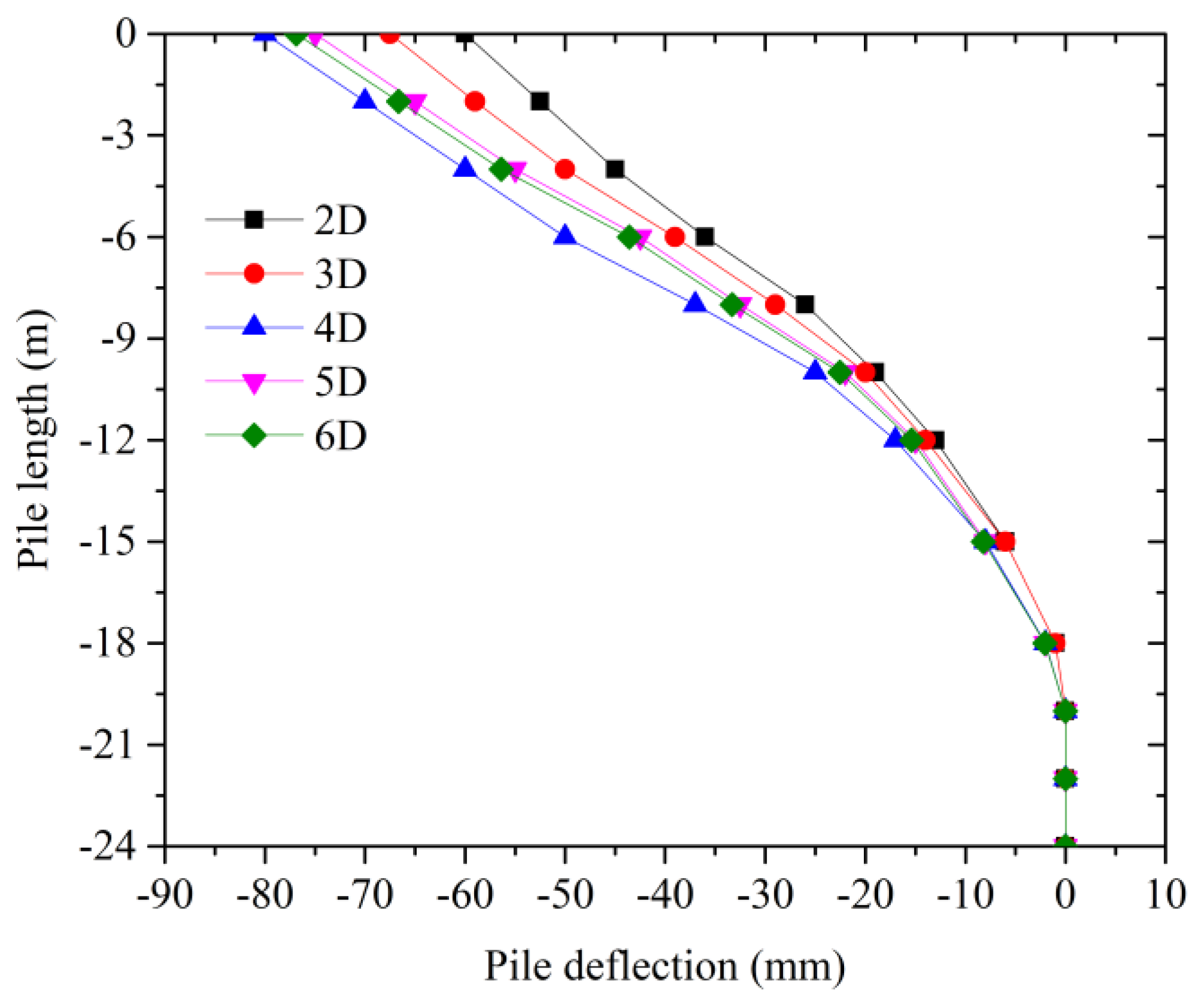
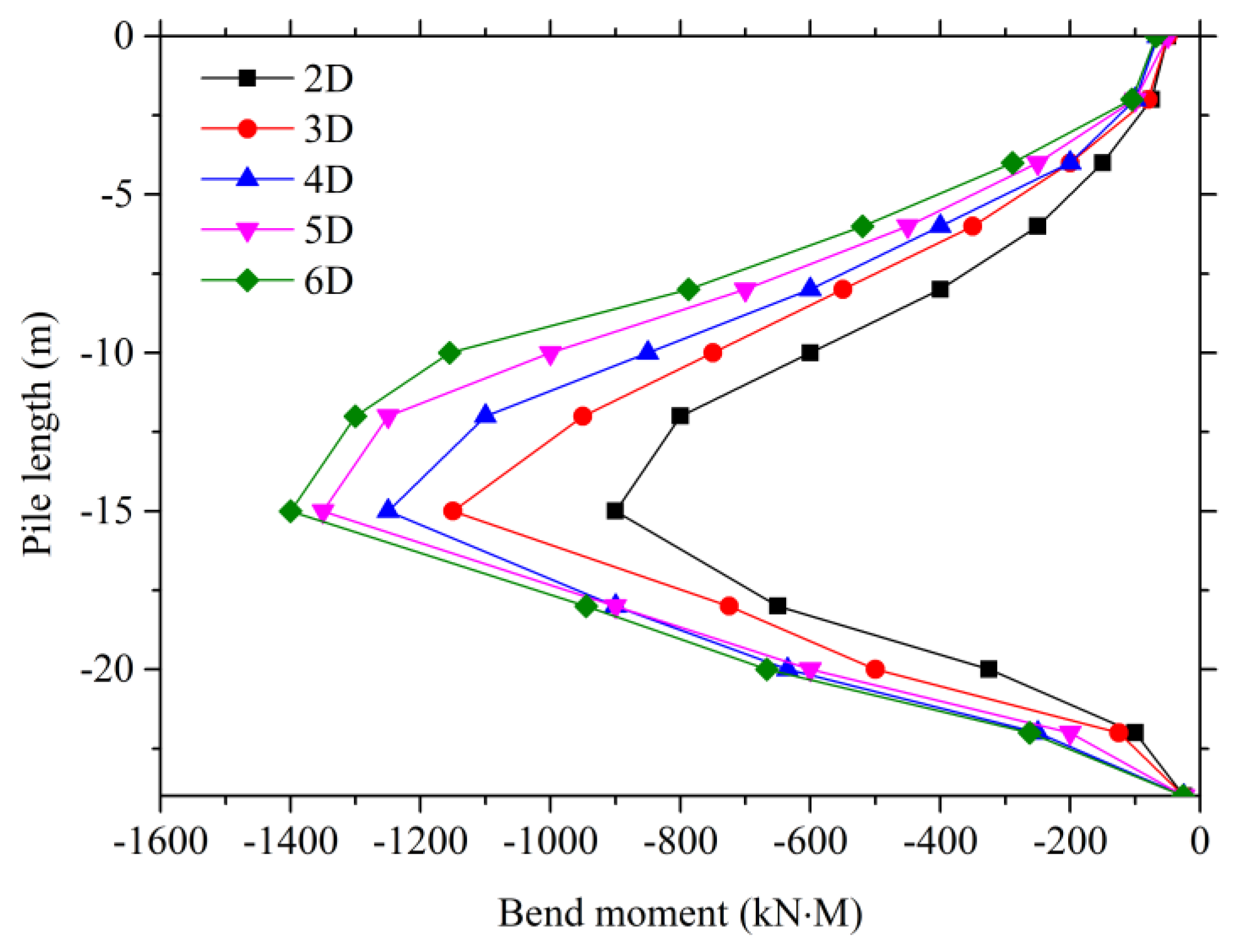
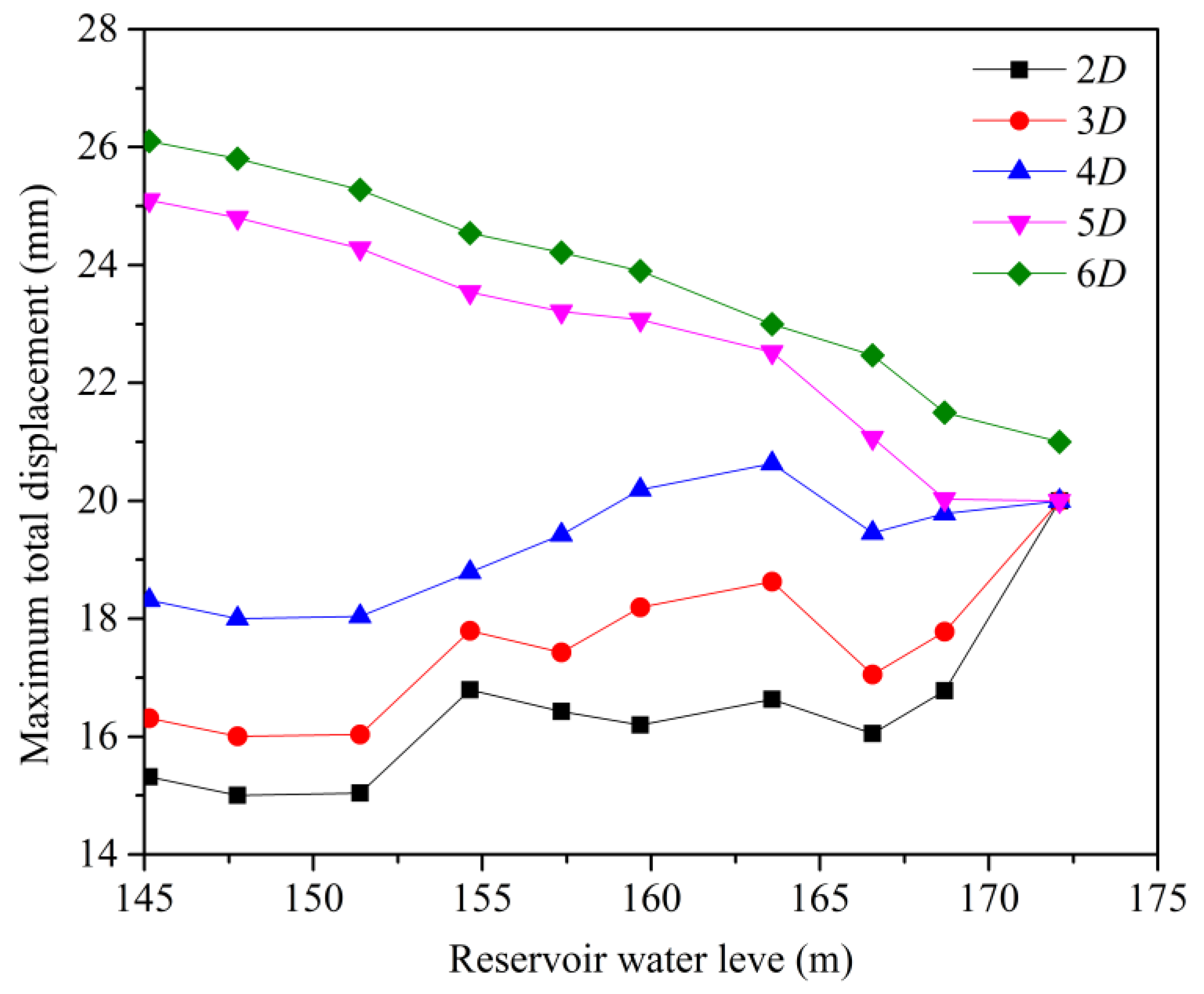
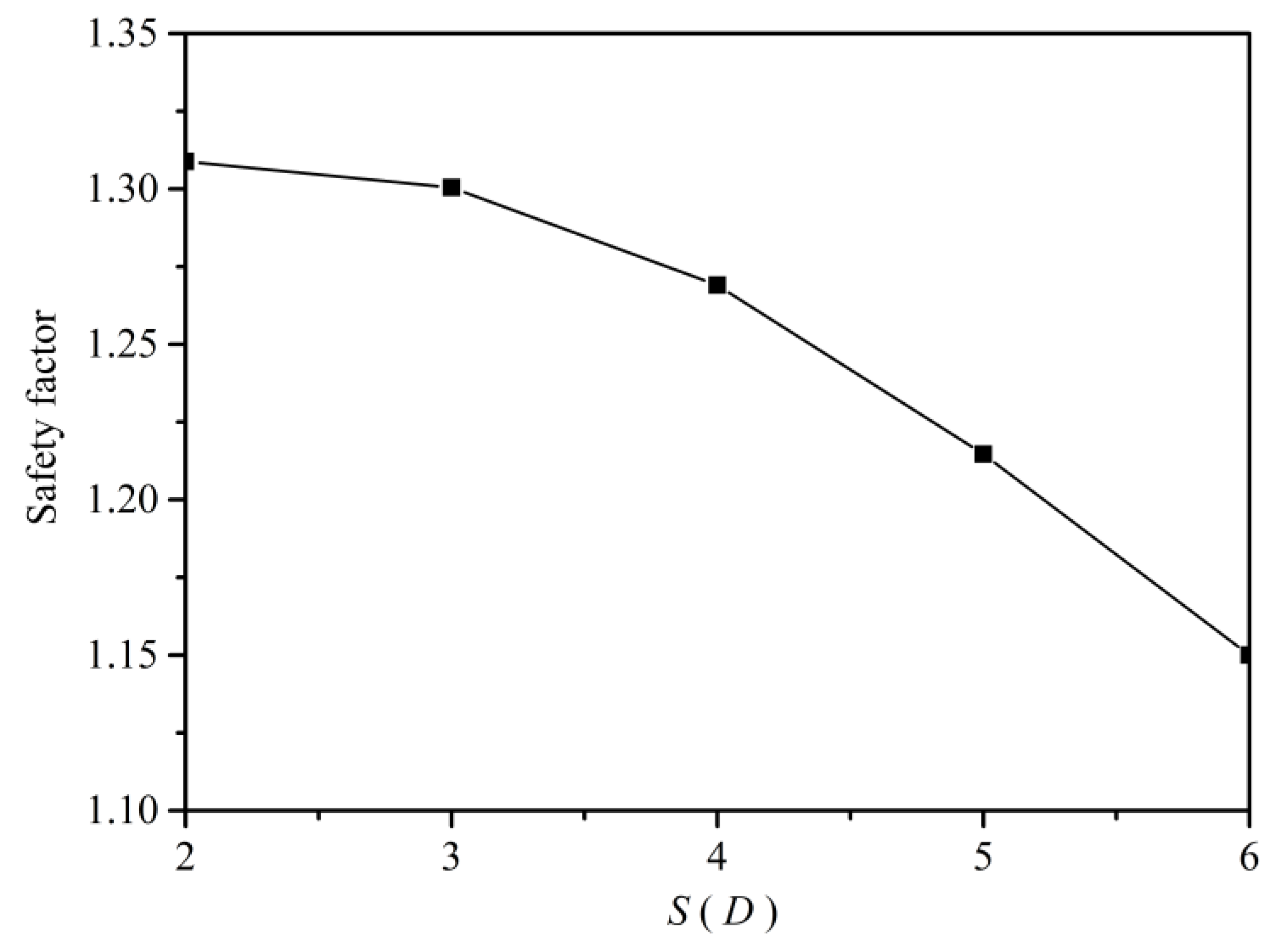
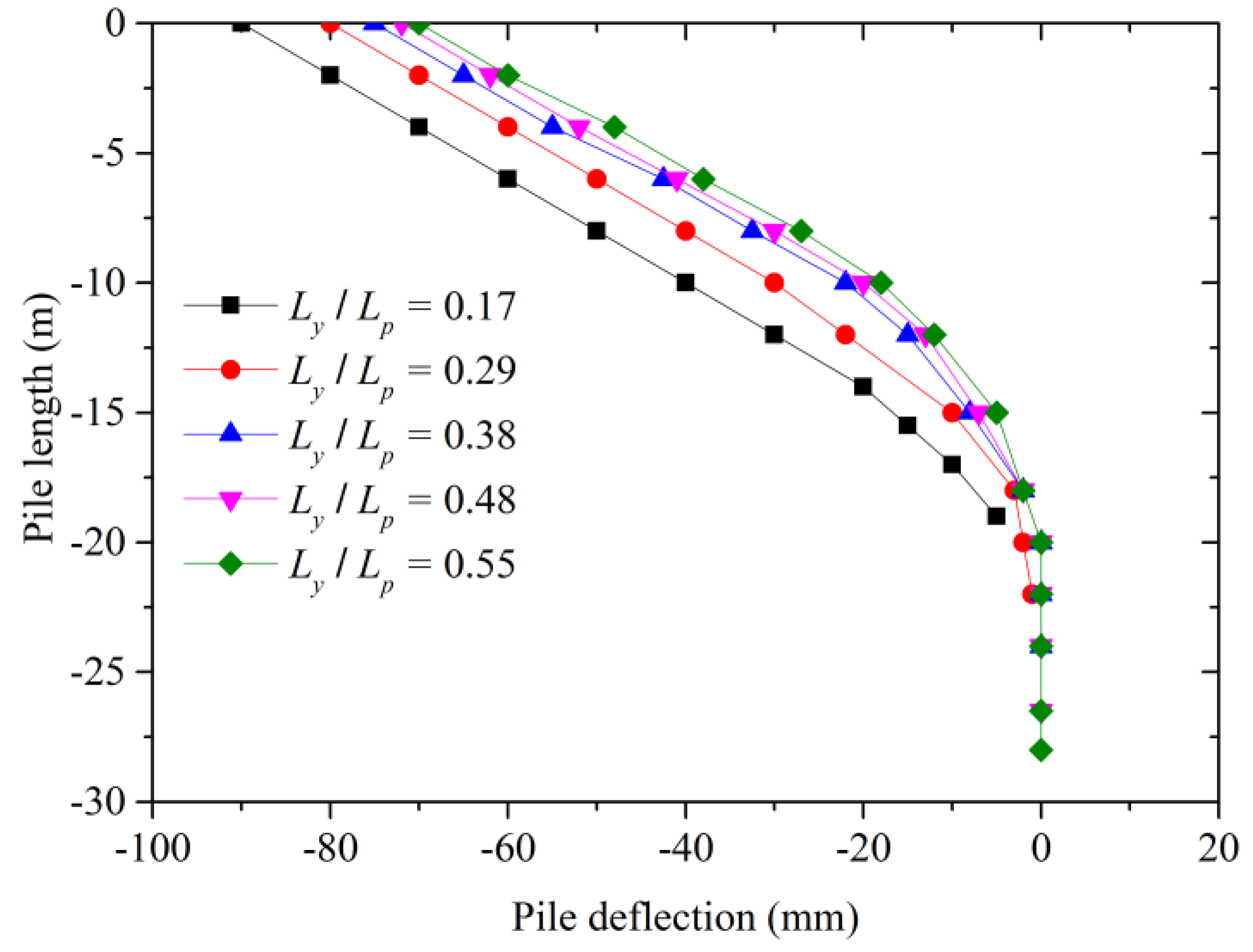
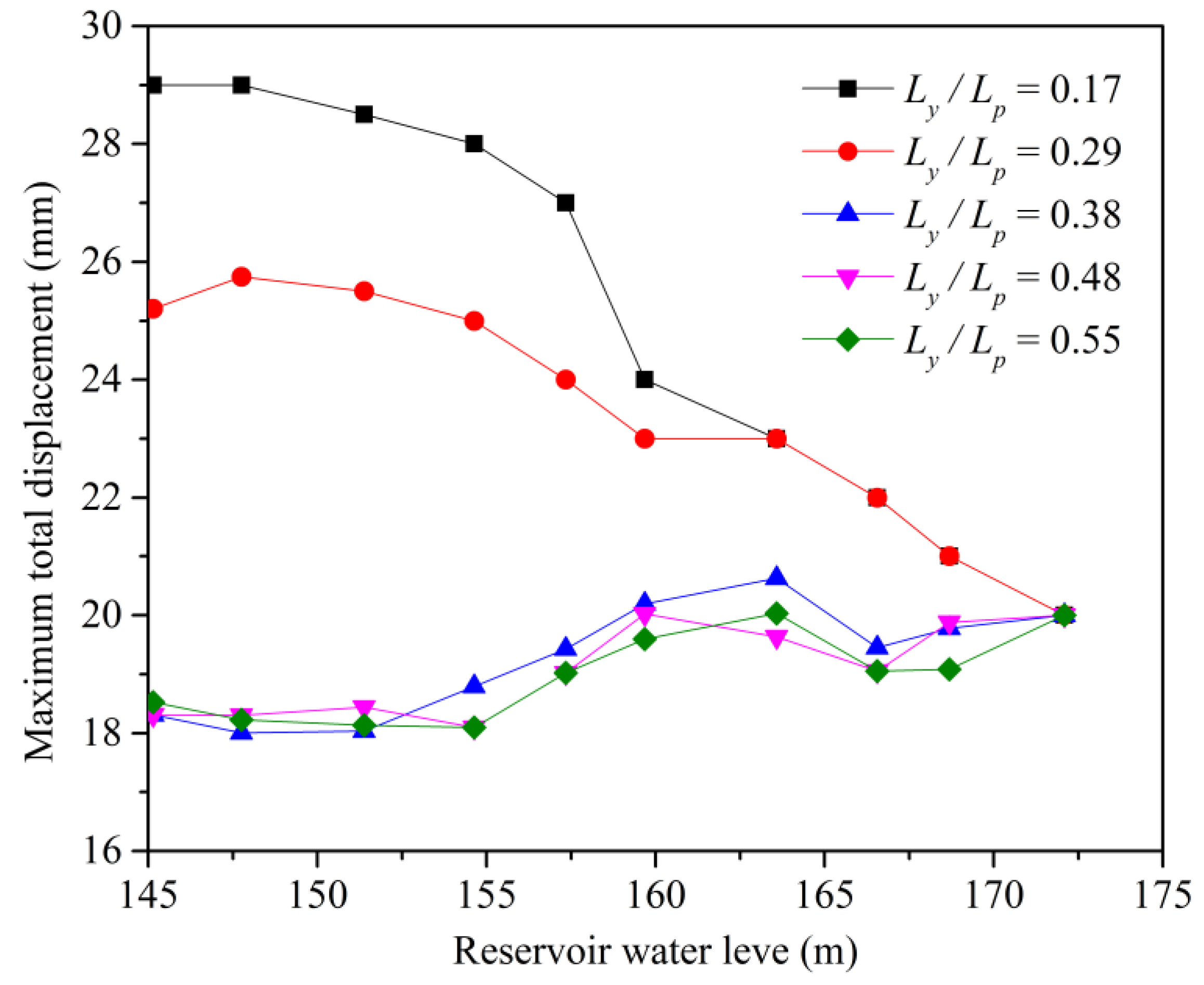
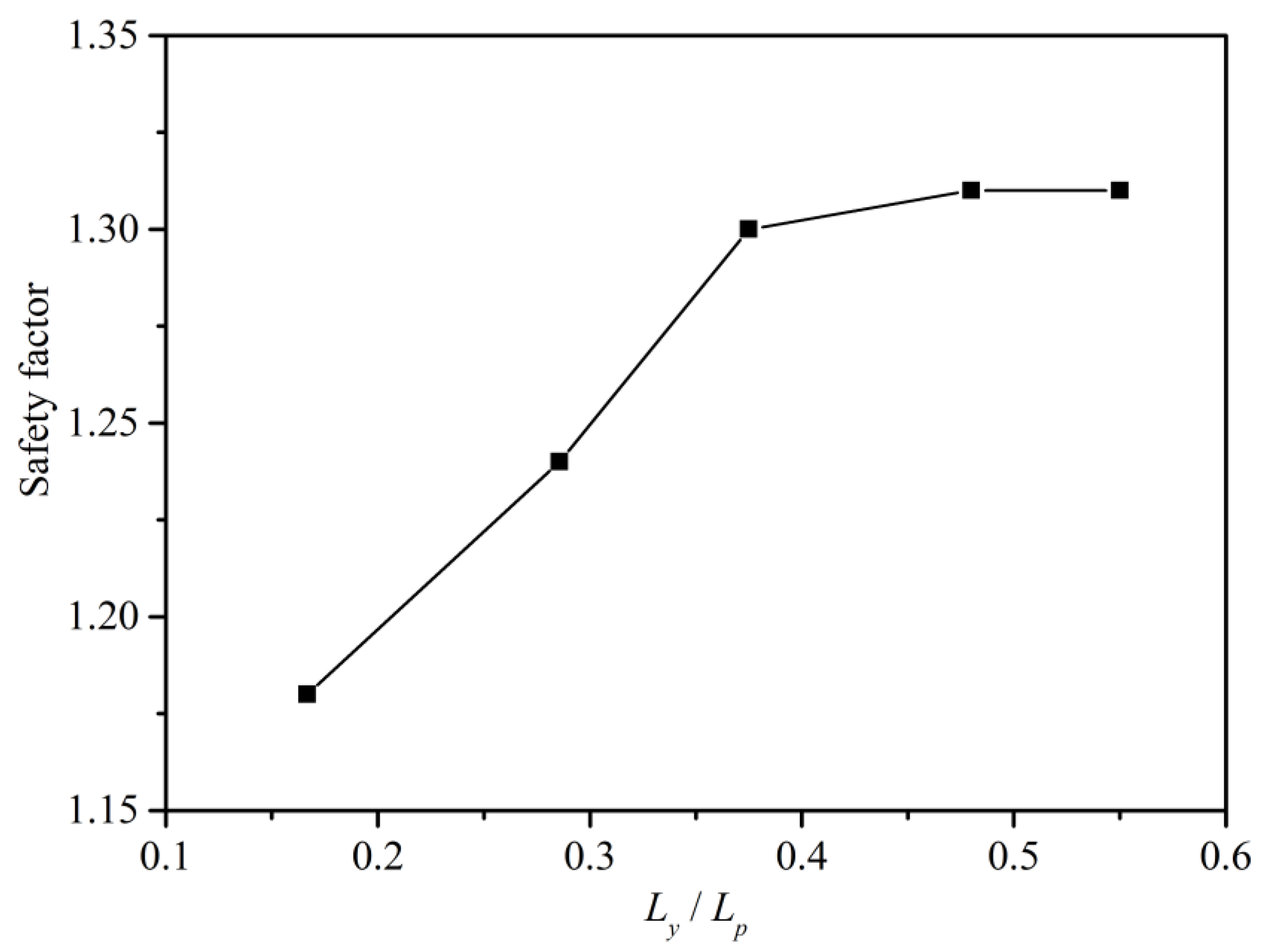
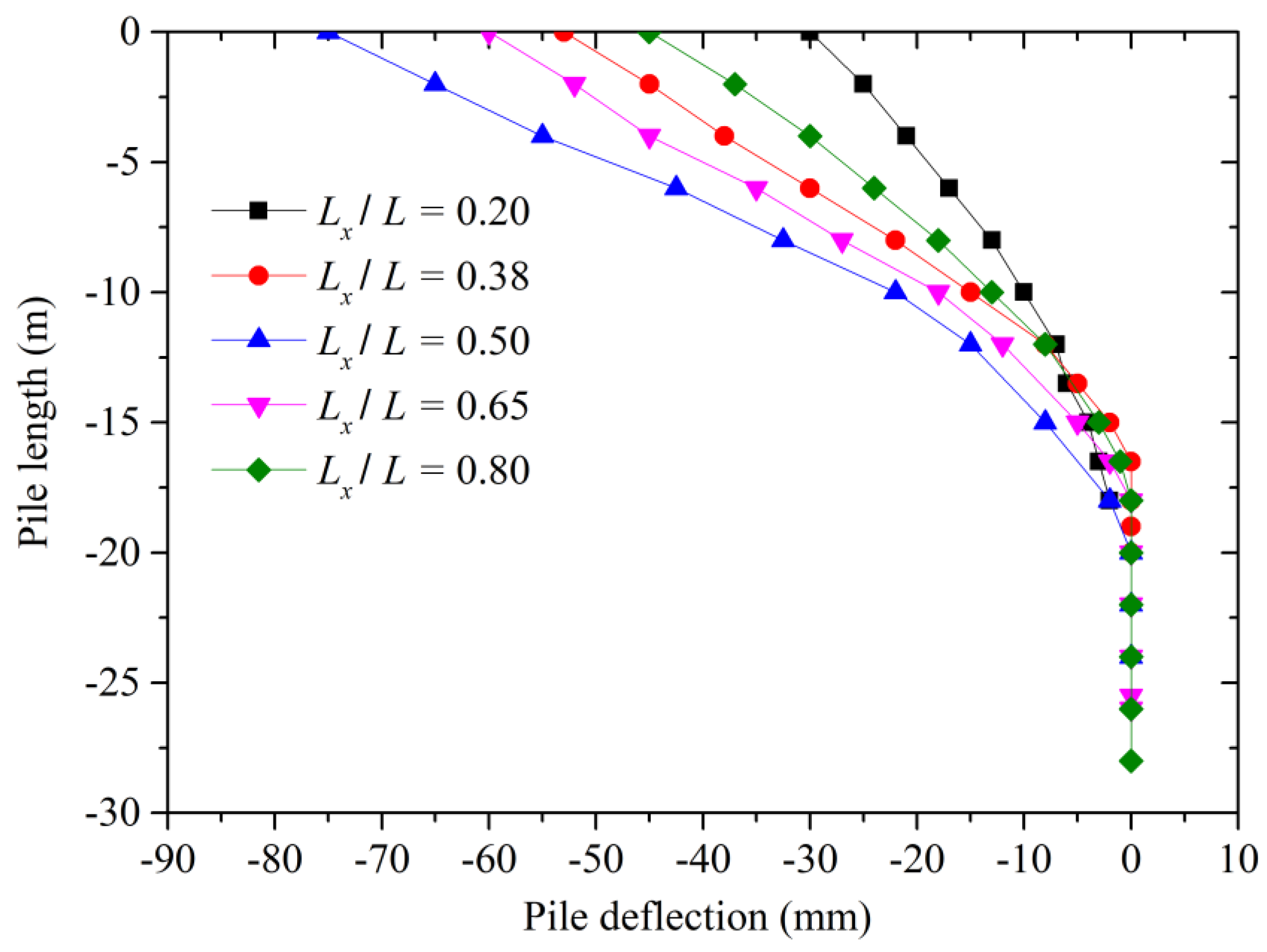
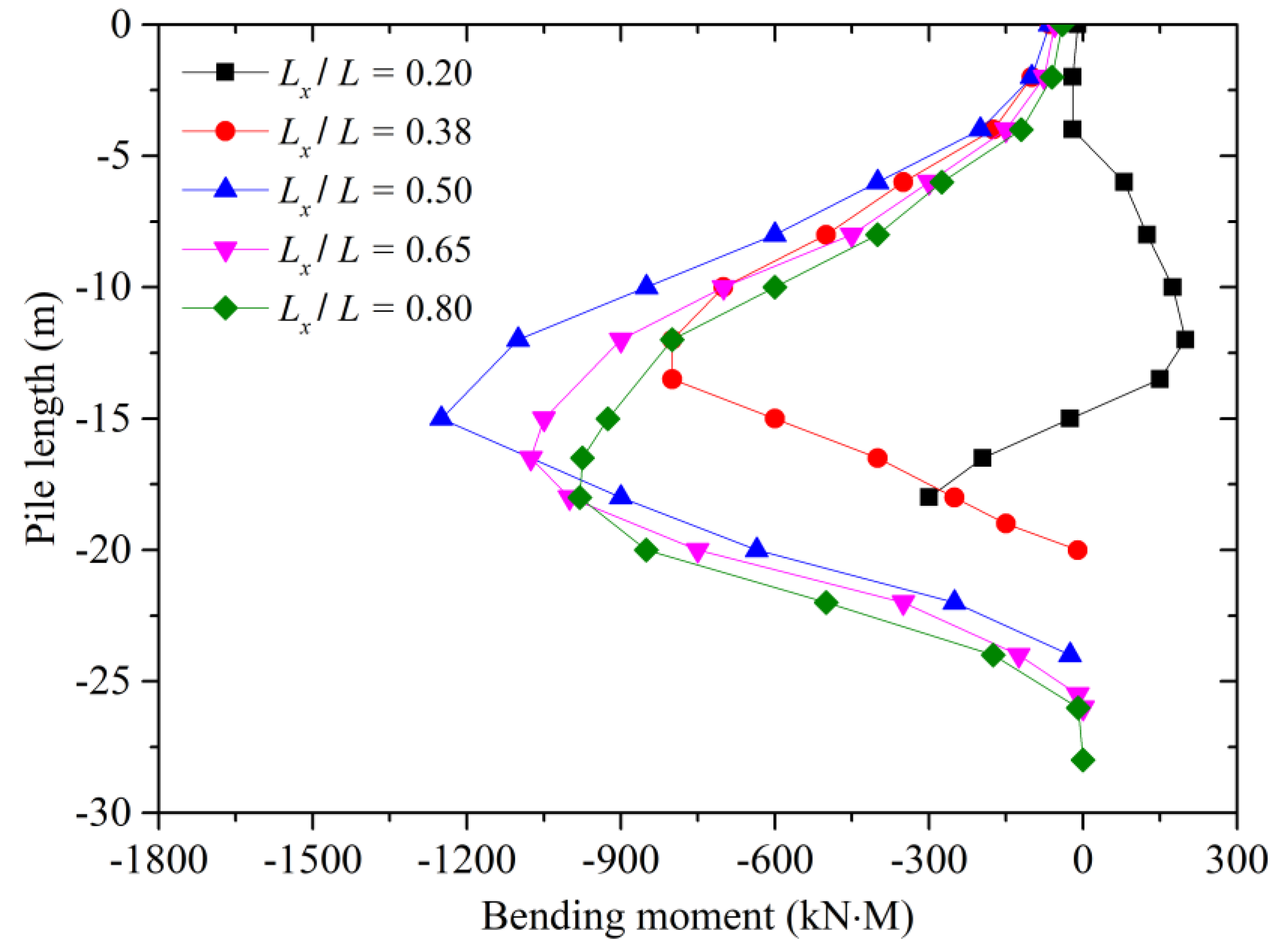
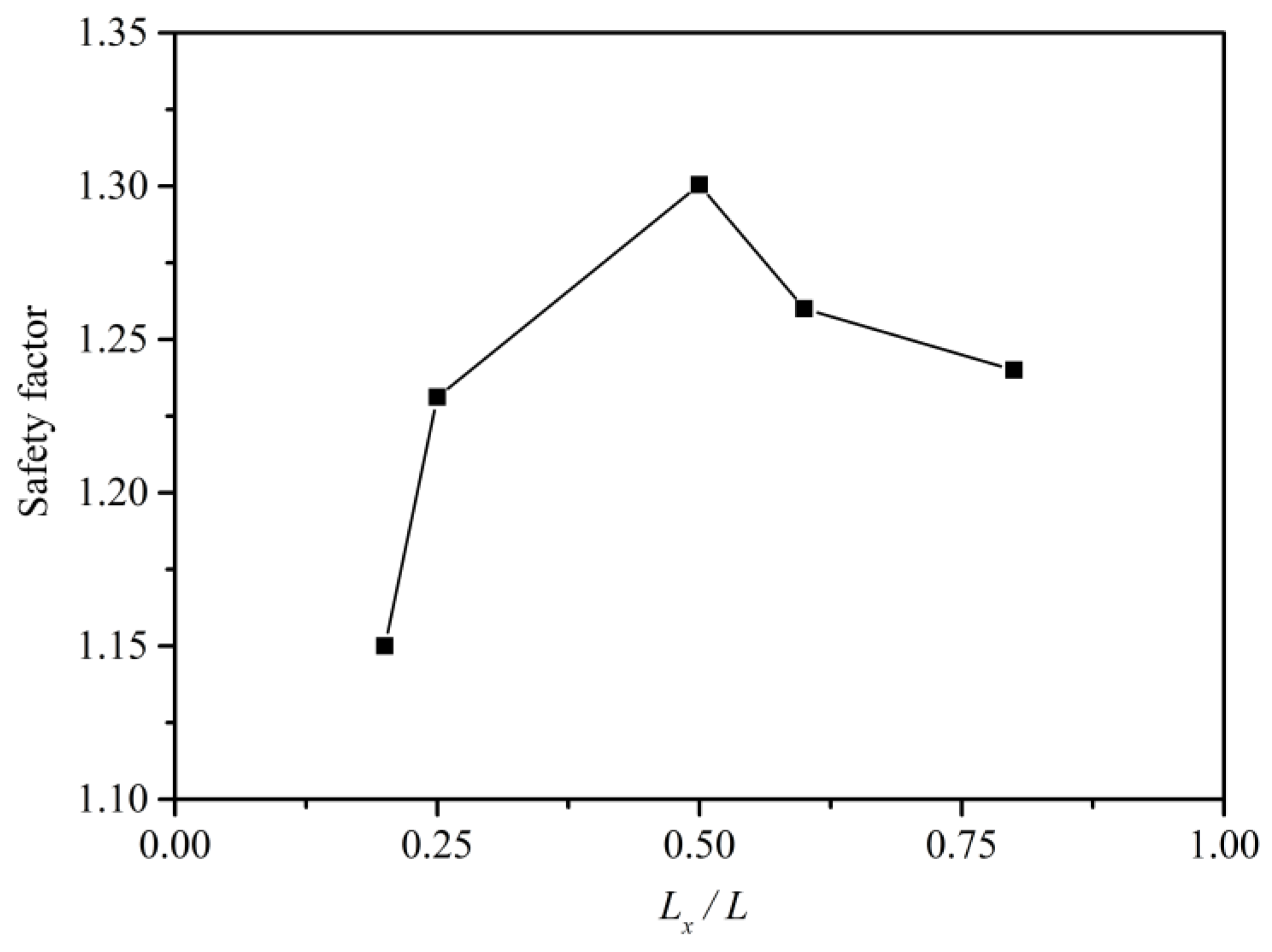
3.3. Parameter Analysis

The design parameters of anti-slide piles are directly related to the effectiveness and cost of landslide remediation. A significant challenge is how to optimize and determine these parameters reasonably, minimizing economic costs while ensuring that the remediation effects meet standards and are technically feasible. This is particularly complex for reservoir landslides that involve seepage–stress coupling. Therefore, in this section, numerical simulation methods will be employed to account for the effects of seepage-stress coupling, optimizing the design parameters of anti-slide piles, and proposing an improved design scheme for landslide remediation.

(a)

Pile spacing

The spacing between anti-slide piles is a critical design parameter. If the spacing is set too wide, the soil can easily slide out between the piles, causing them to behave similarly to single piles. Conversely, if the spacing is set too narrow, the economic costs will increase without a significant improvement in stabilization effectiveness. Therefore, studying the impact of pile spacing on landslide stability and designing an appropriate spacing is essential for enhancing the effectiveness of landslide remediation and reducing engineering costs.

Figure 9 shows the equivalent plastic strain and displacement field contour of the landslide for different $S$, respectively. It is evident from Figure 9a that when $S$ = 2$D$, the sliding surface of the landslide is effectively separated into upper and lower sections at the position of the anti-sliding piles. This indicates that the anti-sliding piles, due to the smaller spacing, act like a retaining wall, isolating the upper and lower soil masses and preventing the formation of a continuous sliding surface from top to bottom, resulting in a lower equivalent plastic strain for the entire landslide. When $S$ = 5$D$, as shown in Figure 9b, the sliding surface develops into a continuous curve extending from bottom to top, indicating that the piles have not mobilized the surrounding soil to resist sliding together, and each pile in the group piles plays the role of resisting sliding individually, and the effect of the anti-sliding pile group is not activated, resulting in a high equivalent plastic strain of the landslide.

Figure 10 and Figure 11, respectively, show the deformation and bending moment results of anti-slide piles corresponding to different pile spacings when the reservoir water level is 145 m. It can be seen from Figure 10 that the pile deflection first increases and then decreases as the pile spacing increases. When the S ≤ 4D, the pile spacing increases, and the pile deflection increases slightly. When the S ≥ 4D, the pile deflection decreases with the increase in pile spacing. The deflection of anti-slide piles is closely related to the effect of soil arch between anti-slide piles: when no soil arch can be formed between the anti-slide piles, the deflection of the anti-slide piles decreases. According to Figure 11, the larger the S, the larger the bending moment of the anti-slide piles. This is because, with the increase in the pile spacing, the landslide thrust borne by each anti-slip pile also increases gradually.

Figure 12 shows the calculation results of the maximum displacement of the landslide for different $S$ during the reservoir water level drops. It can be seen from Figure 12 that the maximum displacement increases from 15 mm to 26 mm as the pile spacing increases from 2$D$ to 4$D$ when the reservoir level drops to 145 m; the maximum displacement of the landslide is better controlled, and the change amplitude is also smaller. When the $S$ $>$ 4$D$, the maximum displacement of the landslide increases continuously, which indicates that the anti-slip piles have a poor anti-slip effect and the overall stability of the landslide is not well controlled.

Figure 13 presents the variation curve of the safety factor of the anti-sliding piles for different values of $S$. It can be seen that, as the $S$ increases, the safety factor of the landslide gradually decreases. When the $S$ is 5$D$ and 6$D$, the safety factor of the landslide is relatively low. When $S$ is 3$D$ and 4$D$, the difference in safety factors between the two is minimal. Therefore, considering economic factors and the ease of construction, an $S$ of 4$D$ is sufficient to achieve effective landslide remediation. Based on the comprehensive analysis, a pile spacing of 4$D$ is deemed reasonable for stabilizing the landslide in this paper.

(b)

Embedment depth

The embedment depth $L_y$ of the anti-slip piles also determines the effectiveness of landslide management and the economic cost, which is an important parameter for the design of anti-slip piles. In this section, the influence of the $L_y$ of anti-slip piles on the effect of landslide stabilization when the reservoir water level is reduced to 145 m elevation will be discussed, to comprehensively determine the more reasonable embedment depth of anti-slip piles.

Figure 14 shows the equivalent plastic strain contour map of the landslide when $L_y/L_p$ is 0.17 and 0.55, respectively. During the service life of the anti-slide piles, the portion of the piles above the embedded section transfers the load to the stable rock mass within the embedded section under the action of landslide thrust. This utilizes the embedded effect and passive resistance of the stable stratum to counterbalance the landslide thrust resulting from landslide deformation. When the embedment depth is shallow, as shown in Figure 14a, the portion of the anti-slide piles above the embedded section carries most of the load, resulting in the increased displacement of the piles. This makes it challenging to effectively counteract the landslide thrust, leading to the overall instability and deformation of the landslide. Conversely, when the embedment depth is deep, as depicted in Figure 14b, the anti-slide pile can transfer the landslide thrust to the stable rock layer beneath the sliding surface. By leveraging the embedded effect and passive resistance of the stable stratum, the landslide thrust resulting from slope deformation is counterbalanced, thereby improving the overall stability of the landslide.

Figure 15 and Figure 16 show the results of the deformation and bending moment of the anti-slide pile for different embedment depths, respectively. It can be seen from Figure 15 that the pile deflection shows an obvious decreasing trend with the growth of the embedment depth. When the $L_y/L_p$ = 0.17, the embedment depth of the anti-slide pile is shallow, and the displacement of the pile end also begins to appear, and the anti-slide pile slides with the landslide soil. This shows that the anti-slip pile reinforcement effect is poor when the embedding depth is insufficient. In addition, it can be seen from Figure 15 that when $L_y/L_p$ > 0.38, the pile displacements are nearly identical. This indicates that once the embedment depth reaches a certain threshold, further increases in depth do not significantly enhance the reinforcement effect of the anti-slide piles. From Figure 16, it is evident that as the embedment depth increases, the bending moment of the anti-slide pile exhibits an upward trend. However, this growth rate gradually slows with further increases in embedment depth. When the anti-slide pile crosses the slip surface, the maximum bending moment is generally reached at the same position along the pile’s cross-section.

Figure 17 illustrates the maximum landslide displacement for various embedment depths of the anti-slide piles during the drop in reservoir water level. The embedment depth significantly impacts landslide displacement. The maximum displacement of the landslide decreases from 18 mm to 29 mm when the $L_y/L_p$ is increased from 0.17 to 0.55. When the $L_y/L_p$ $\ge$ 0.38, the maximum displacement shows little variation during the decline of the reservoir water level, indicating that the anti-slide piles can effectively maintain the stability of the landslide in this range.

Figure 18 shows the variation curve of the safety factor of the anti-sliding piles for embedment depth ratio $L_y/L_p$. Clearly, as the $L_y/L_p$ increases, the safety factor of the landslide also increases. When the $L_y/L_p$ $\ge$ 0.48, the increase in the safety factor tends to level off. This is attributed to the presence of an effective embedment depth for the anti-slide piles. Once this effective depth is exceeded, the anti-slide effect does not continue to increase, and the overall remediation impact on the landslide is not significantly enhanced. Therefore, while ensuring safety reserves, it is advisable to minimize the materials used for the anti-slide piles to reduce remediation costs. Consequently, $L_y/L_p$ =0.48 can be used as the reasonable anchoring depth ratio of anti-slide piles in landslide restoration in this study.

(c)

Pile position

The selection of locations for anti-slide piles is crucial for the effectiveness of landslide remediation. Many researchers believe that different displacements of anti-slide piles result in varying failure modes of landslides, which subsequently impact the stability of the slope in different ways. Therefore, optimizing the placement of anti-slide piles is essential.

In this section, the $L_x$ was varied to investigate the effect of the choice of anti-slip pile location on the landslide stability at a reservoir level of 145 m, while maintaining the pile spacing S = 4$D$ and the embedment ratio $L_x/L$ = 0.38. Figure 19 shows the equivalent plastic strain contour map of the landslide when $L_x/L$ = 0.20 and 0.80, respectively. The sliding body slides along the bedrock interface regardless of where in the landslide the anti-slip piles are arranged. When the anti-sliding piles are positioned at the toe of the landslide (i.e., $L_x/L$ = 0.2), the equivalent plastic strain in the soil near the piles increases and extends toward the top of the landslide. The toe cannot withstand the weight of the upper soil, leading to the gradual failure of the entire landslide. This results in the formation of a continuous zone of soil movement from around the piles to the top of the landslide, causing sliding. At this point, the anti-sliding piles experience almost no horizontal displacement and cannot effectively perform their sliding resistance function. When the anti-sliding piles are positioned at the top of the landslide (i.e., $L_x/L$ = 0.8), the sliding zone area is significantly reduced, ensuring the stability of the lower part of the landslide. In this situation, the sliding resistance of the soil below the piles helps maintain the stability of the entire anti-sliding pile landslide.

Figure 20 and Figure 21 show the results of the displacement and bending moment of the anti-slip pile at different pile positions, respectively. From Figure 20 and Figure 21, it can be seen that the pile displacement and bending moment show a trend of increasing and then decreasing with the increase in $L_x/L$. When the anti-slip piles are arranged in the middle of the landslide (i.e., $L_x/L$ = 0.5), the pile displacement and bending moment reach the maximum value. This is because, on one hand, when the anti-slide pile is positioned near the foot of the landslide, its embedment depth is shallow, and the corresponding critical slip surface does not intersect with the anti-slide pile. On the other hand, when the anti-slide pile is located near the top of the landslide, the volume of the landslide body decreases, leading to a reduction in the landslide thrust acting on the anti-slide pile. Therefore, when $L_x/L$ = 0.5, the pile bending moment and displacement of the skid-resistant pile are both maximized. In addition, it is worth noting that when $L_x/L$ = 0.2, the displacement curve of the pile is approximately linear, which indicates that the anti-slip pile produces rotation and overturning damage may occur. This is because when the anti-slip pile is arranged at the foot of the landslide, the thickness of the landslide slip body is larger, and thus the embedment depth of the anti-slip pile is smaller and the anchorage is insufficient.

Figure 22 shows the calculation results of the maximum displacement of the landslide for different pile locations during the reservoir water level drops. When the anti-slip piles are arranged in the middle of the landslide (i.e., $L_x/L$ = 0.5), the maximum displacement of the landslide during the water level decline is small, and the landslide stability is effectively controlled. With the upward and downward movement of the pile position, the landslide displacement of the landslide gradually increases.

Figure 23 shows the variation curve of the safety factor of the anti-sliding piles for different pile locations. When the anti-slide pile is located in the middle of the landslide (i.e., $L_x/L$ = 0.5), the safety factor of the landslide is the largest. Therefore, from the point of view of the maximum displacement and safety factor, it is appropriate to set the anti-slide pile in the middle of the landslide in this paper.

4. Conclusions

In this study, numerical simulations were conducted using the finite element software Abaqus to investigate the deformation and failure mechanisms of reservoir bank landslides during water level drawdown. Additionally, the stabilizing effect of anti-slide piles on landslides was analyzed, with a particular focus on the influence of pile spacing, embedment depth, and arrangement on the maximum landslide displacement and safety factor. The key findings are summarized as follows:

1. The decline in the reservoir water level reduces the landslide safety coefficient and affects the distribution of the reservoir landslide displacement field and equivalent plastic strain field. In the process of reservoir landslide management and design, the influence of the decline in the reservoir water level should be considered.

2. The interactions between anti-slip piles and soil to form the soil arch effect, with anti-slip piles blocking the slide effect of reservoir landslides, leading to prevention and control, is obvious, and can effectively reduce the reservoir landslide deformation and improve the reservoir landslide safety coefficient.

3. The pile spacing, embedding depth, and location of anti-slip piles have a significant effect on the stability of stabilized reservoir landslides. The determination of a reasonable pile spacing requires a combination of factors such as reinforcement effectiveness and economics. The embedment depth of anti-slip piles should ensure that they can penetrate below the slip surface, but after reaching the critical embedment depth, the reinforcement effect of the anti-slip piles will not be enhanced with the increase in embedment depth. Anti-slip piles should be installed in the middle of the landslide to maximize their reinforcement effect.

It has to be recognized that this paper still has some limitations. For example, the anti-slip piles in this paper are conventional circular piles, and other shapes of anti-slip piles, such as H-shaped and rectangular, still need to be investigated for their effectiveness in stabilizing landslides during the period of declining reservoir water level. In addition, this paper only considers the case of reservoir water level decline; when considering the coupled effect of rainfall and reservoir water level changes, the landslide stability has to face a more complicated situation. These problems are to be studied in the future.