A Comparative Study of a Two-Dimensional Slope Hydrodynamic Model (TDSHM), Long Short-Term Memory (LSTM), and Convolutional Neural Network (CNN) Models for Runoff Prediction
Abstract
1. Introduction
2. Research Area and Data
2.1. Study Area Overview
2.2. Data
2.3. Data Preprocessing
- Missing value detection: temporal gaps in time series data may disrupt temporal dependency learning, necessitating systematic identification of incomplete records.
- Noise reduction: a moving average filter with a 3-point window was applied to smooth stochastic fluctuations in time series variables while preserving trend patterns [38].
2.4. Selection of Feature Parameters
- Runoff Coefficient (K) and H: 0.586
- Peak Discharge (Qmax) and H: 0.508
- Total Precipitation (P) and H: 0.488
- Maximum 30 min Rainfall Intensity (I30) and H: 0.452
- Total Rainfall Time (T) and H: 0.368
- Rainfall Erosivity (R) and H: 0.341
- Average Rainfall Intensity (I) and H: 0.322
2.5. Validation Set Samples
3. Methods
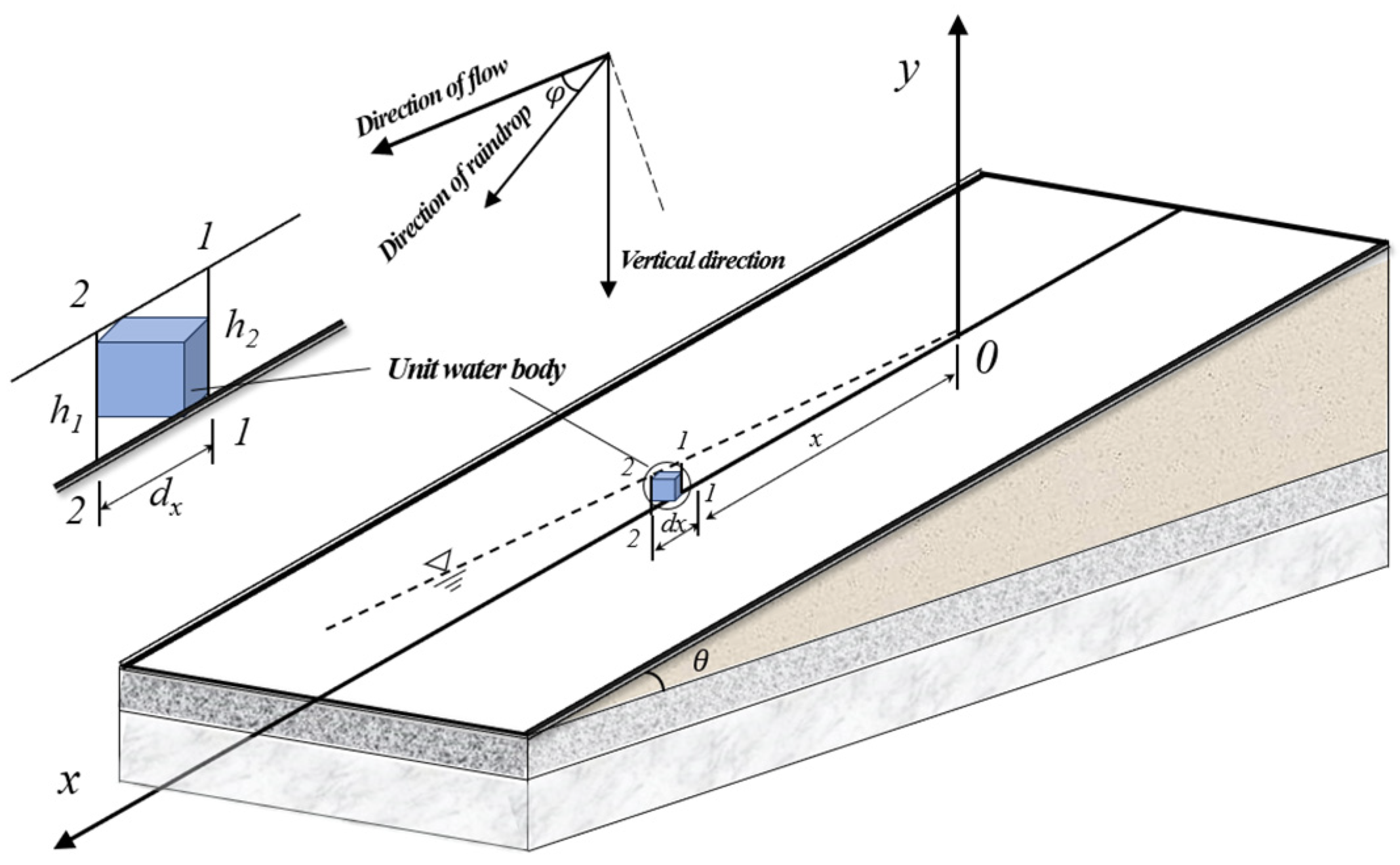
3.1. Two-Dimensional Slope Hydrodynamic Simulation Model (TDSHM)
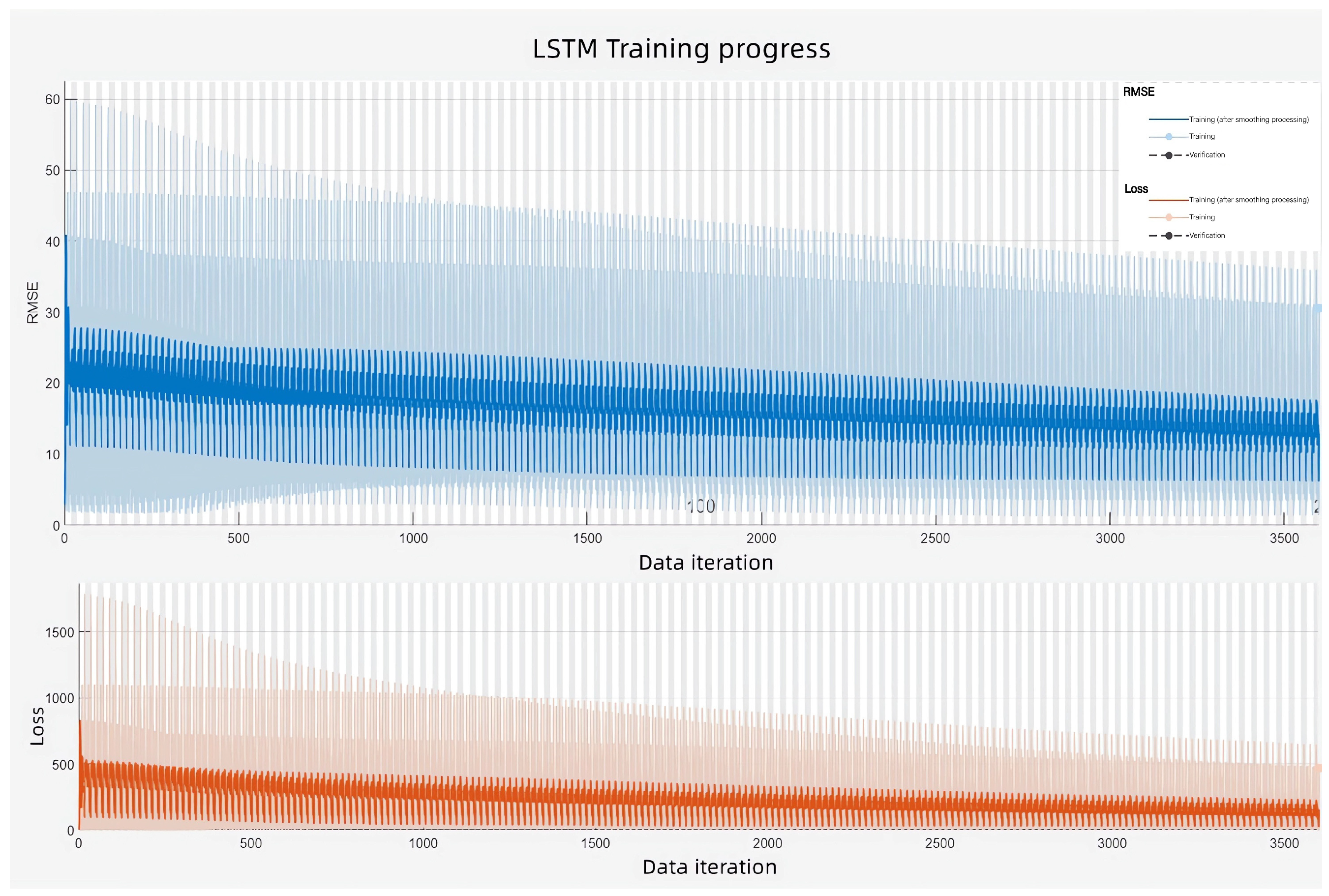
3.2. LSTM Neural Network Model
- (1)
- LSTM Structure
- (2)
- Learning Algorithm
- (3)
- Model Construction
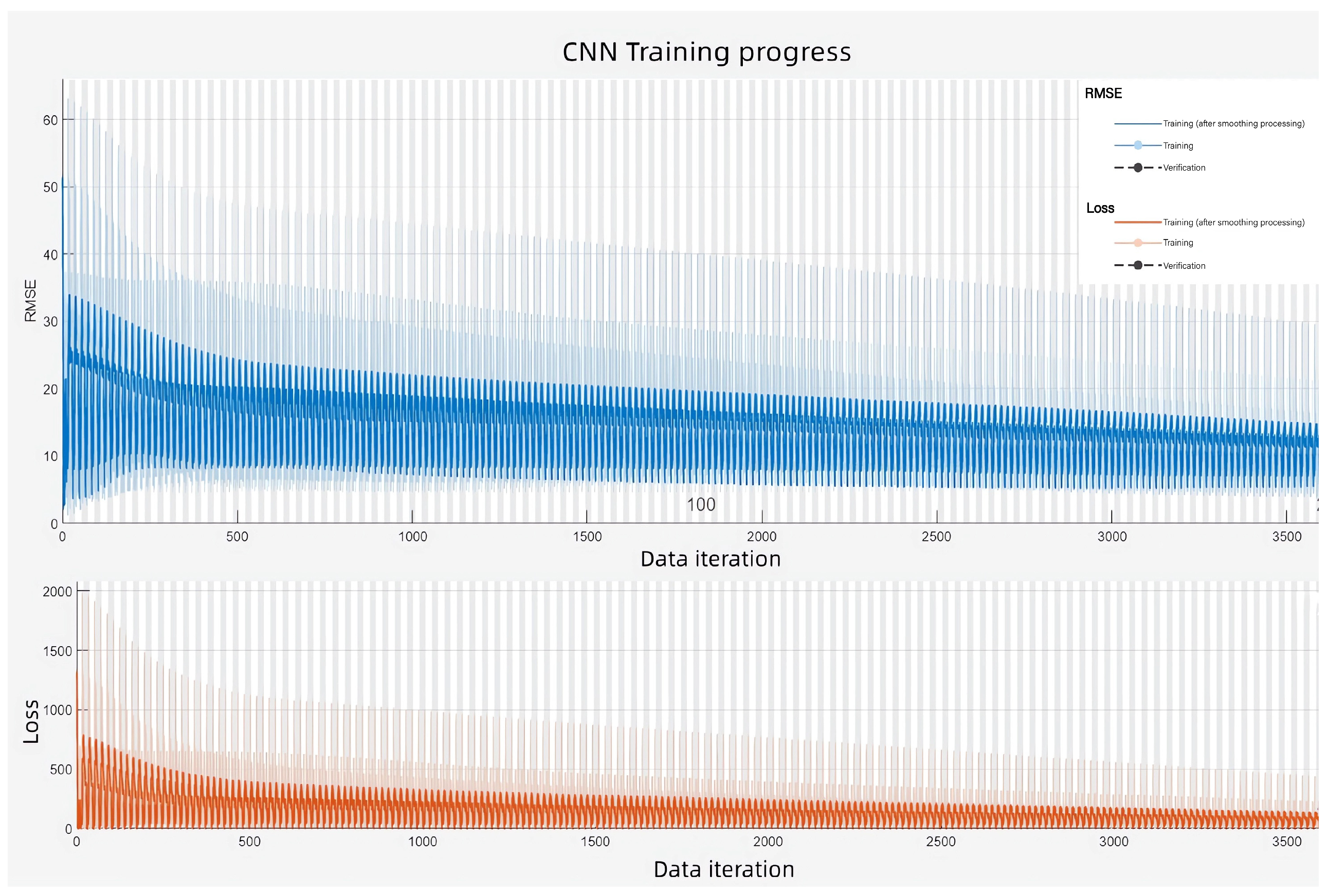
3.3. CNN Neural Network Model
- (1)
- CNN Structure
- (2)
- Learning Algorithm
- (3)
- Model Construction
3.4. Model Evaluation Indicators
4. Results
4.1. Two-Dimensional Slope Hydrodynamic Model (TDSHM) Results
4.1.1. Parameter Calibration
4.1.2. Model Calculation Results
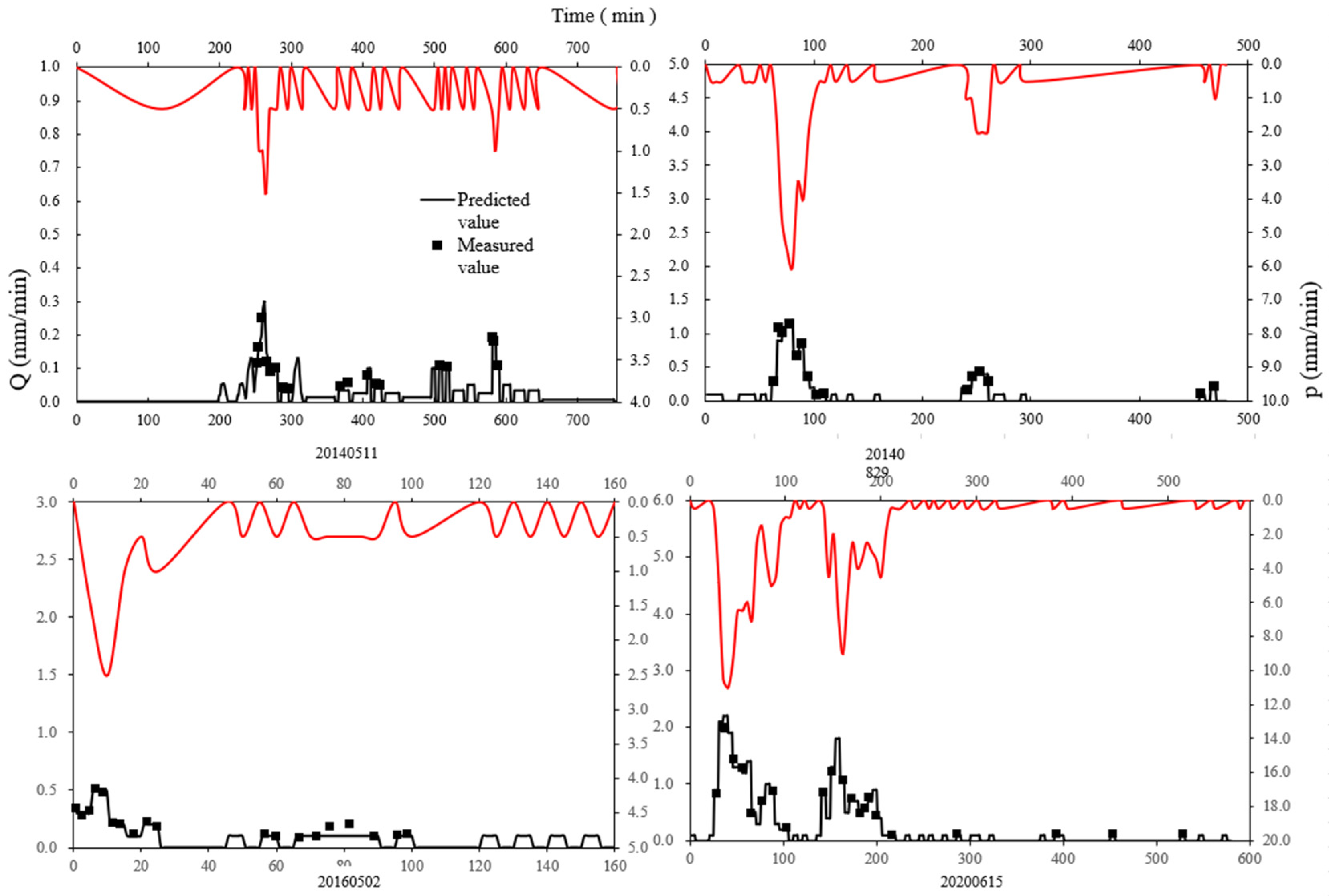
4.1.3. Model Process Verification
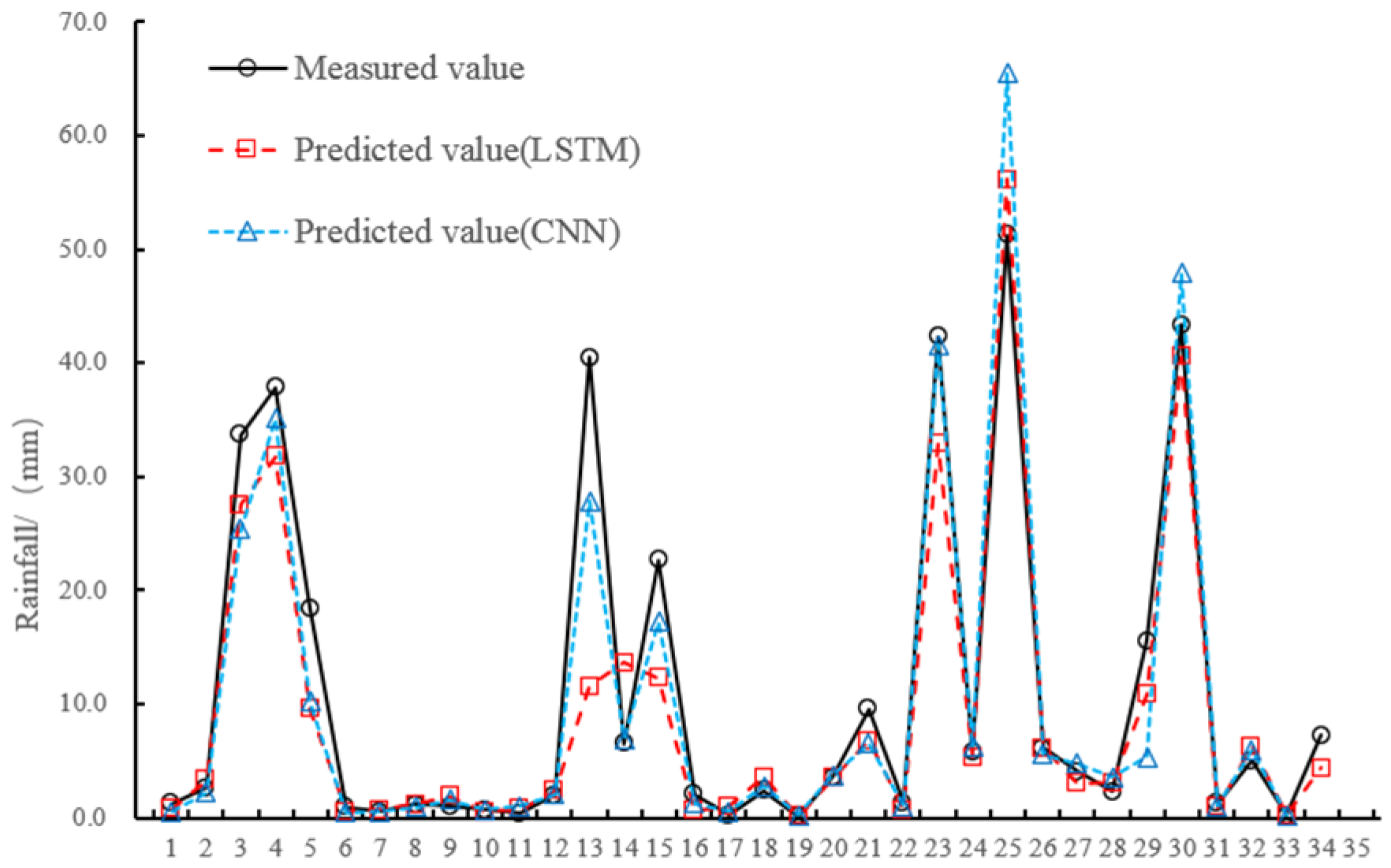
4.2. Neural Network Model Results
4.3. Model Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Wei, J.; Sun, Q.; Huang, C. Research on Coupling Knowledge Embedding and Data-Driven Deep Learning Models for Runoff Prediction. Water 2024, 16, 2130. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Ajmal, M.; Achite, M.; Kim, T.W. Comprehensive review: Advancements in rainfall-runoff modelling for flood mitigation. Climate 2022, 10, 147. [Google Scholar] [CrossRef]
- Wei, J.; Li, Y.; Sun, Q.; Huang, C. A Survey on Data-Driven Runoff Forecasting Models Based on Neural Networks. Water 2023, 15, 2613. [Google Scholar]
- Fan, Y.; Fu, X.; Kan, G.; Liang, K.; Yu, H. Combining Multiple Machine Learning Methods Based on CARS Algorithm to Implement Runoff Simulation. Water 2024, 16, 2397. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Liu, X.; Ren, Z.; Wu, S. Research on Runoff Prediction Based on Time2Vec-TCN-Transformer Driven by Multi-Source Data. Electronics 2024, 13, 2681. [Google Scholar] [CrossRef]
- Lu, D.; Yang, T.; Liu, X. Editorial: Data-driven machine learning for advancing hydrological and hydraulic predictability. Front. Water 2023, 5, 1215966. [Google Scholar] [CrossRef]
- Rozos, E.; Dimitriadis, P.; Bellos, V. Machine Learning in Assessing the Performance of Hydrological Models. Hydrology 2022, 9, 5. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine learning methods for empirical streamflow simulation: Acomparison of model accuracy, interpretability, and uncertainty in seasonal watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Su, H.; Jia, Y.; Ni, G.; Gong, J.; Cao, X.; Zhang, M.; Niu, C.; Zhang, D. Research on the Application of Machine Learning in Runoff Prediction. China Rural. Water Conserv. Hydropower 2018, 6, 40–43. [Google Scholar]
- Liang, H.; Huang, S.; Meng, E.; Huang, Q. Research on runoff prediction based on multiple mixed models. J. Hydraul. Eng. 2020, 51, 112–125. [Google Scholar]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a Long Short-Term Memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, Y.; Chen, H.; Yu, X. Runoff prediction of island reservoir based on multiple recurrent neural networks. J. Hydroelectr. Power 2021, 40, 14–26. [Google Scholar]
- Tian, Y.; Tan, W.; Wang, G.; Yuan, X. Performance and interpretability of LSTM variant model in runoff prediction. Water Resour. Conserv. 2019, 39, 188–194. [Google Scholar]
- Jiang, Z.; Lu, B.; Zhou, Z.; Zhao, Y. Comparison of Process-Driven SWAT Model and Data-Driven Machine Learning Techniques in Simulating Streamflow: A Case Study in the Fenhe River Basin. Sustainability 2024, 16, 6074. [Google Scholar] [CrossRef]
- Li, J.; Ai, P.; Xiong, C.; Song, Y. Coupled intelligent prediction model for medium- to long-term runoff based on teleconnection factors selection and spatial-temporal analysis. PLoS ONE 2024, 19, e0313871. [Google Scholar] [CrossRef]
- Bhusal, A.; Parajuli, U.; Regmi, S.; Kalra, A. Application of Machine Learning and Process-Based Models for Rainfall-Runoff Simulation in DuPage River Basin, Illinois. Hydrology 2022, 9, 117. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Tai, Y.C.; Bouchut, F.; Mangeney, A.; Pelanti, M.; Chen, R.F.; Chang, K.J. Simulation of Tsaoling landslide, Taiwan, based on Saint Venant equations over general topography. J. Eng. Geol. 2009, 104, 181–189. [Google Scholar] [CrossRef]
- Yu, C.-W.; Hodges, B.R.; Liu, F. Automated detection of instability-inducing channel geometry transitions in Saint-Venant simulations of large-scale river networks. Water 2021, 13, 2236. [Google Scholar] [CrossRef]
- Chen, T.-Y.K.; Capart, H. Kinematic wave solutions for dam-break floods in non-uniform valleys. J. Hydrol. 2020, 582, 124381. [Google Scholar] [CrossRef]
- Ponce, V.M. Modeling surface runoff with kinematic, diffusion, and dynamic waves. In Surface-Water Hydrology; Springer: Dordrecht, The Netherlands, 1996; pp. 121–132. [Google Scholar]
- Cai, Z.; Xie, J.; Chen, Y.; Yang, Y.; Wang, C.; Wang, J. Rigid Vegetation Affects Slope Flow Velocity. Water 2024, 16, 2240. [Google Scholar] [CrossRef]
- Shi, P.; Li, P.; Li, Z.; Sun, J.; Wang, D.; Min, Z. Effects of grass vegetation coverage and position on runoff and sediment yields on the slope of Loess Plateau, China. Agric. Water Manag. 2022, 259, 107231. [Google Scholar] [CrossRef]
- Lan, M.; Hu, H.; Tian, F.; Hu, H. A two-dimensional numerical model coupled with multiple hillslope hydrodynamic processes and its application to subsurface flow simulation. Sci. China Technol. Sci. 2013, 56, 2491–2500. [Google Scholar] [CrossRef]
- Yu, C.W.; Hodges, B.R.; Liu, F. A new form of the Saint-Venant equations for variable to pography. Hydrol. Earth Syst. Sci. 2020, 24, 4001–4024. [Google Scholar] [CrossRef]
- Pasculli, A.; Longo, R.; Sciarra, N.; Di Nucci, C. Surface Water Flow Balance of a River Basin Using a Shallow Water Approach and GPU Parallel Computing—Pescara River (Italy) as Test Case. Water 2022, 14, 234. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C. A 2D-SWEs framework for efficient catchment-scale simulations: Hydrodynamic scaling properties of river networks and implications for non-uniform grids generation. J. Hydrol. 2021, 599, 126306. [Google Scholar] [CrossRef]
- Roy, B.; Singh, M.P.; Kaloop, M.R.; Kumar, D.; Hu, J.-W.; Kumar, R.; Hwang, W. Data-driven approach for rainfall-runoff modelling using equilibrium optimizer coupled extreme learning machine and deep neural network. Appl. Sci. 2021, 11, 6238. [Google Scholar] [CrossRef]
- Kumar, V.; Kedam, N.; Sharma, K.V.; Mehta, D.J.; Caloiero, T. Advanced machine learning techniques to improve hydrological prediction: A comparative analysis of streamflow prediction models. Water 2023, 15, 2572. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Zou, Q.; Ye, L.; Zhu, S.; Zhang, H. Study on optimization and combination strategy of multiple daily runoff prediction models coupled with physical mechanism and LSTM. J. Hydrol. 2023, 624, 129969. [Google Scholar] [CrossRef]
- Mohammadi, B. A review on the applications of machine learning for runoff modeling. Sustain. Water Resour. Manag. 2021, 7, 98. [Google Scholar] [CrossRef]
- Ayzel, G. Openforecast v2: Development and benchmarking of the first national-scale operational runoff forecasting system in russia. Hydrology 2021, 8, 3. [Google Scholar] [CrossRef]
- Fan, C.; Chen, M.; Wang, X.; Wang, J.; Huang, B. A review on data preprocessing techniques toward efficient and reliable knowledge discovery from building operational data. Front. Energy Res. 2021, 9, 652801. [Google Scholar] [CrossRef]
- Zhan, X.; Xu, Q.; Zheng, Y.; Lu, G.; Gevaert, O. Reliability-based cleaning of noisy training labels with inductive conformal prediction in multi-modal biomedical data mining. arXiv 2023, arXiv:2309.07332. [Google Scholar]
- Kannan, K.S.; Manoj, K.; Arumugam, S. Labeling methods for identifying outliers. Int. J. Stat. Syst. 2015, 10, 231–238. [Google Scholar]
- Mowbray, F.I.; Fox-Wasylyshyn, S.M.; El-Masri, M.M. Univariate outliers: A conceptual overview for the nurse researcher. Can. J. Nurs. Res. 2019, 51, 31–37. [Google Scholar] [CrossRef]
- Chen, Z.; Xue, Q.; Xiao, R.; Liu, Y.; Shen, J. State of health estimation for lithium-ion batteries based on fusion of autoregressive moving average model and elman neural network. IEEE Access 2019, 7, 102662–102678. [Google Scholar] [CrossRef]
- Shantal, M.; Othman, Z.; Bakar, A.A. A novel approach for data feature weighting using correlation coefficients and min–max normalization. Symmetry 2023, 15, 2185. [Google Scholar] [CrossRef]
- Chu, S.T. Green-Ampt analysis of wetting patterns for surface emitters. J. Irrig. Drain. Eng. 1994, 120, 414–421. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C. Mechanism of Soil Conservation on Slope of Steep Hillside Forest Land. J. Beijing For. Univ. 1994, 4, 1–7. [Google Scholar]
- Mou, J.Z. Calculating formula of raindrop velocity. Soil Water Conserv. China 1983, 42–43. [Google Scholar] [CrossRef]
- Shamaa, M.T.E.I. A Comparative Study of Two Numerical Methods for Regulating Unsteady Flow in Open Channels. MEJ-Mansoura Eng. J. 2021, 27, 14–27. [Google Scholar] [CrossRef]
- Kaddi, Y.; Proust, S.; Faure, J.B.; Cierco, F.-X. Experimental and numerical study of unsteady flows in a compound open channel. Environ. Fluid Mech. 2024, 24, 335–365. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning (ICML-13), Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Afrin, N.; Ahamed, F.; Rahman, A. Development of a convolutional neural network based regional flood frequency analysis model for South-east Australia. Nat. Hazards 2024, 120, 11349–11376. [Google Scholar] [CrossRef]
- Vialatte, J.-C.; Vincent, G.; Gilles, C. Learning local receptive fields and their weight sharing scheme on graphs. In Proceedings of the 2017 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Montreal, QC, Canada, 14–16 November 2017; IEEE: New York, NY, USA, 2017. [Google Scholar]
- Wang, X.; Bao, A.; Cheng, Y.; Yu, Q. Weight-sharing multi-stage multi-scale ensemble convolutional neural network. Int. J. Mach. Learn. Cyber 2019, 10, 1631–1642. [Google Scholar] [CrossRef]
- Kumar, P.; Arora, H.C.; Bahrami, A.; Kumar, A.; Kumar, K. Development of a Reliable Machine Learning Model to Predict Compressive Strength of FRP-Confined Concrete Cylinders. Buildings 2023, 13, 931. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.; Liu, C.; Ren, L.; Cai, X.; Li, K. Hydrological Simulation and Parameter Optimization Based on the Distributed Xin’anjiang Model and the Particle Swarm Optimization Algorithm: A Case Study of Xunhe Watershed in Shandong, China. Water 2024, 16, 3168. [Google Scholar] [CrossRef]
- Lan, T.; Lin, K.; Xu, C.Y.; Tan, X.; Chen, X. Dynamics of hydrological-model parameters: Mechanisms, problems and solutions. Hydrol. Earth Syst. Sci. 2020, 24, 1347–1366. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef]
- Xu, Y.; Lin, K.; Hu, C.; Wang, S.; Wu, Q.; Zhang, L.; Ran, G. Deep transfer learning based on transformer for flood forecasting in data-sparse basins. J. Hydrol. 2023, 625, 129956. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Paki, R. Improving time series forecasting using LSTM and attention models. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 673–691. [Google Scholar] [CrossRef]
- Wen, X.; Li, W. Time series prediction based on LSTM-attention-LSTM model. IEEE Access 2023, 11, 48322–48331. [Google Scholar] [CrossRef]
- Al-Hussein, A.A.M.; Khan, S.; Ncibi, K.; Hamdi, N.; Hamed, Y. Flood analysis using HEC-RAS and HEC-HMS: A case study of Khazir River (Middle East—Northern Iraq). Water 2022, 14, 3779. [Google Scholar] [CrossRef]
- Symonds, A.M.; Vijverberg, T.; Post, S.; Van der Spek, B.-J.; Henrotte, J.; Sokolewicz, M. Comparison between Mike 21 FM, Delft3D and Delft3D FM flow models of western port bay, Australia. Coast. Eng. 2016, 2, 11. [Google Scholar] [CrossRef]
- Lu, D.; Konapala, G.; Painter, S.L.; Kao, S.-C.; Gangrade, S. Streamflow simulation in data-scarce basins using Bayesian and physics-informed machine learning models. J. Hydrometeorol. 2021, 22, 1421–1438. [Google Scholar] [CrossRef]
- Galety, M.; Al Mukthar, F.H.; Maaroof, R.J.; Rofoo, F. Deep neural network concepts for classification using convolutional neural network: A systematic review and evaluation. Tech. Rom. J. Appl. Sci. Technol. 2021, 3, 58–70. [Google Scholar] [CrossRef]
- Man, Y.; Yang, Q.; Shao, J.; Wang, G.; Bai, L.; Xue, Y. An enhanced LSTM model for daily runoff prediction in the upper reaches of the Huaihe River. Engineering 2023, 24, 230–239. [Google Scholar] [CrossRef]
- Hao, H.; Hao, Y.; Li, Z.; Qi, C.; Wang, Q.; Zhang, M.; Liu, Y.; Liu, Q.; Yeh, T.-C.J. Insight into glacio-hydrologicalprocesses using explainable machine-learning (XAI) models. J. Hydrol. 2024, 634, 131047. [Google Scholar] [CrossRef]









| Parameters | Minimum Value | Maximum Value | Mean | Standard Deviation |
|---|---|---|---|---|
| P | 0.50 | 286.00 | 40.55 | 40.02 |
| T | 5.00 | 4565.00 | 952.97 | 771.06 |
| I | 0.40 | 306.00 | 6.67 | 22.69 |
| I30 | 0.50 | 130.91 | 21.56 | 19.56 |
| R | 0.08 | 4661.18 | 312.35 | 568.95 |
| Qmax | 0.01 | 88.00 | 4.56 | 10.04 |
| K | 0.01 | 17.60 | 0.45 | 1.48 |
| H | 0.02 | 147.80 | 10.21 | 24.17 |
| No. | Rainfall Date | Rainfall (mm) | Rainfall Intensity (mm/h) | Rain Type |
|---|---|---|---|---|
| 1 | 2014.05.11 | 18.00 | 1.430 | Moderate rain |
| 2 | 2014.08.29 | 45.00 | 5.745 | Heavy rain |
| 3 | 2015.08.10 | 78.50 | 2.201 | Torrential rain |
| 4 | 2015.05.15 | 69.60 | 6.692 | Torrential rain |
| 5 | 2016.05.02 | 9.50 | 4.839 | Light rain |
| 6 | 2016.07.07 | 77.5 | 32.07 | Torrential rain |
| 7 | 2016.10.28 | 6.00 | 0.480 | Light rain |
| 8 | 2017.06.10 | 145.00 | 7.945 | Extraordinarily torrential rain |
| 9 | 2017.10.14 | 6.00 | 1.029 | Light rain |
| 10 | 2018.09.17 | 37.00 | 2.581 | Heavy rain |
| 11 | 2019.08.28 | 13.50 | 1.080 | Moderate rain |
| 12 | 2019.09.02 | 39.50 | 2.184 | Heavy rain |
| 13 | 2020.06.15 | 146.50 | 15.287 | Torrential rain |
| 14 | 2020.09.11 | 35.00 | 3.043 | Heavy rain |
| 15 | 2021.06.03 | 34.00 | 0.895 | Heavy rain |
| W | K (m/h) | Kd | Sm | D | H | n | det |
|---|---|---|---|---|---|---|---|
| 0.100 | 0.016 | 0.025 | 0.015 | 0.01 | 2.0 | 0.02 | 0.010 |
| NO. | Date of Rainfall | MRE (%) | NO. | Date of Rainfall | MRE (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| TDSHM | LSTM | CNN | TDSHM | LSTM | CNN | ||||
| 1 | 2014.05.11 | 7.82 | 5.46 | 0.71 | 9 | 2017.10.14 | 7.64 | 48.21 | 80.43 |
| 2 | 2014.08.29 | 19.53 | 50.61 | 41.72 | 10 | 2018.09.17 | 5.52 | 46.50 | 78.97 |
| 3 | 2015.08.10 | 6.55 | 2.36 | 1.39 | 11 | 2019.08.28 | 9.33 | 13.70 | 15.44 |
| 4 | 2015.05.15 | 8.67 | 21.63 | 11.25 | 12 | 2019.09.02 | 15.32 | 8.70 | 7.12 |
| 5 | 2016.05.02 | 13.54 | 86.34 | 61.22 | 13 | 2020.06.15 | 16.55 | 36.15 | 28.54 |
| 6 | 2016.07.07 | 8.98 | 6.94 | 25.78 | 14 | 2020.09.11 | 14.33 | 5.17 | 1.26 |
| 7 | 2016.10.28 | 6.55 | 12.55 | 1.92 | 15 | 2021.06.03 | 17.59 | 28.77 | 42.13 |
| 8 | 2017.06.10 | 3.67 | 0.57 | 23.87 | Mean average value | 10.77 | 24.38 | 28.10 | |
| NO. | Types | NSE | MAE (mm) | MAPE |
|---|---|---|---|---|
| 1 | TDSHM Model | 0.801 | 3.17 | 11.97 |
| 2 | LSTM Neural Networks | 0.751 | 4.61 | 24.36 |
| 3 | CNN Neural Networks | 0.506 | 6.82 | 37.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Pan, J.; Shao, G. A Comparative Study of a Two-Dimensional Slope Hydrodynamic Model (TDSHM), Long Short-Term Memory (LSTM), and Convolutional Neural Network (CNN) Models for Runoff Prediction. Water 2025, 17, 1380. https://doi.org/10.3390/w17091380
Zhou Y, Pan J, Shao G. A Comparative Study of a Two-Dimensional Slope Hydrodynamic Model (TDSHM), Long Short-Term Memory (LSTM), and Convolutional Neural Network (CNN) Models for Runoff Prediction. Water. 2025; 17(9):1380. https://doi.org/10.3390/w17091380
Chicago/Turabian StyleZhou, Yuhao, Jing Pan, and Guangcheng Shao. 2025. "A Comparative Study of a Two-Dimensional Slope Hydrodynamic Model (TDSHM), Long Short-Term Memory (LSTM), and Convolutional Neural Network (CNN) Models for Runoff Prediction" Water 17, no. 9: 1380. https://doi.org/10.3390/w17091380
APA StyleZhou, Y., Pan, J., & Shao, G. (2025). A Comparative Study of a Two-Dimensional Slope Hydrodynamic Model (TDSHM), Long Short-Term Memory (LSTM), and Convolutional Neural Network (CNN) Models for Runoff Prediction. Water, 17(9), 1380. https://doi.org/10.3390/w17091380





