Next Article in Journal
Comparative Analysis of Nonlinear Models from Different Domains: A Case Study on the Quality of Groundwater in an Alluvial Aquifer in Northwestern Croatia
Previous Article in Journal
Monthly Streamflow Forecasting for the Irtysh River Based on a Deep Learning Model Combined with Runoff Decomposition
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 9
10.3390/w17091377
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Experimental Study on the Influence of Rising Water Levels on the Buoyancy of Building Structure

by
Zhisong Fan
1,
Changjie Xu
2,
Kelang Yang
1,
Xiuli Xue
1 and
Chaofeng Zeng
1,*
1
Hunan Provincial Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring, School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China
2
State Key Laboratory of Performance Monitoring Protecting of Rail Transit Infrastructure, East China Jiaotong University, Nanchang 330013, China
*
Author to whom correspondence should be addressed.
Water 2025, 17(9), 1377; https://doi.org/10.3390/w17091377
Submission received: 31 March 2025 / Revised: 18 April 2025 / Accepted: 1 May 2025 / Published: 2 May 2025
(This article belongs to the Section Hydrology)
Browse Figures
Versions Notes

Abstract

:
This study investigates the complete process of water level elevation’s impact on structural buoyancy under varying environmental conditions (with/without surrounding barriers) using model testing. The experiments simulated the buoyancy response patterns in sandy soil layers under different hydraulic heads. Dynamic variations of structural buoyancy over time were systematically analyzed, revealing distinct differences across the working conditions. The key findings demonstrate: (1) in the presence of the barrier effect, the growth of structure buoyancy is significantly slower than that without a barrier, but the measured value of structure buoyancy in sand is basically consistent with the theoretical value of Archimedes’ law, and the reduction coefficient is between 0.78 and 0.96; (2) the influence rate of water level rise under high water head pressure on structure buoyancy is significantly higher than that under low water head pressure. Therefore, special attention should be paid to monitoring structure buoyancy when the water level rises under high water levels.

1. Introduction

In recent years, China’s accelerated urbanization has driven the rapid expansion of underground space development [1,2,3,4,5,6,7,8,9,10], which has emerged as a critical component of modern urban development strategies [11,12,13,14,15,16,17,18]. However, this progress has revealed significant engineering challenges [19,20,21,22,23,24,25], particularly the growing concerns within both engineering and academic communities regarding structural anti-floating issues [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Practical engineering scenarios demonstrate that abrupt groundwater level surges—caused by factors including inadequate design or construction practices [45,46,47,48,49,50,51,52,53], sudden torrential rainfall [54,55,56,57,58,59,60,61,62,63,64], and tidal influences [65,66,67,68,69]—can induce dramatic short-term increases in structural buoyancy, especially in the complex urban underground environment, where the mechanism of structural force change caused by the rise of water level has not yet been clarified. These phenomena pose substantial safety hazards to subsurface structures in high-water-table regions, necessitating urgent technical attention [70,71,72,73,74,75,76].
Current anti-floating design for underground structures primarily focuses on determining waterproofing levels, typically calculated by Archimedes’ principle [77,78,79,80]. However, actual engineering scenarios prove more complex, as geological conditions, surrounding environments, and water level fluctuations may yield varying outcomes [81,82,83,84,85,86,87,88,89,90]. Domestic and international scholars have, therefore, conducted multi-faceted research on how groundwater level changes affect structural buoyancy. Mei et al. [91,92,93,94] investigated buoyancy variation patterns under different groundwater levels in clay through laboratory model tests, concluding that while the variation patterns remained fundamentally consistent across water levels, measured values were consistently lower than theoretical values calculated by Archimedes’ principle. Zhou et al. [95] simulated the entire process of seepage-induced characteristic changes in sandy soil under varying water pressures using PFC software, revealing variation patterns of multiple parameters and demonstrating that soil–water interaction persists throughout the seepage process. Xu et al. [96,97] compared seepage conditions with/without underground barriers, establishing that barrier impact depends on both the barrier’s width within the aquifer and its burial depth, they believe that the existence of underground structures blocks the free flow of groundwater, causing the water level downstream to not be replenished in time. Zeng [25,76] also holds this view. He analyzed the impact of pumping on the surrounding environment through engineering examples, which also mentioned the barrier effect on groundwater. Mu et al. [98,99] conducted model tests to examine how vertical cross-flow seepage in confined aquifers affects pore pressure near underground structures and structural buoyancy. Tang et al. [100,101] analyzed pore pressure variations in clay foundations during water level fluctuations under different stress conditions, finding that moderate water level changes would not immediately reduce pore pressure thresholds to levels causing structural uplift. Zhang et al. [102] designed silo models with different diameters and tested them in pure water, sand and clay. They analyzed the effects of friction between soil and structure, negative pressure at the bottom and other factors on buoyancy. Liu et al. [103,104,105] studied the reduction coefficient of groundwater buoyancy in clayey soil by model test, finite element simulation and machine learning. In their study, they measured the buoyancy reduction coefficient of various clay soils and found that it was mainly affected by the permeability coefficient and saturation.
All the above studies have provided help for people to understand the law of the influence of groundwater level changes on structural buoyancy under different conditions but few people have studied the process of the influence of water head changes on the buoyancy of building structures when there are barriers. This paper will simulate the buoyancy change of the structure in the process of water level rise through the model test, and systematically analyze the change law of the structure buoyancy in this process.

2. Test Scheme

2.1. Test Equipment

The experimental equipment used in the whole test includes a self-made model box simulating soil layer environment (Figure 1c), the size of which is 2.4 m × 0.5 m × 1.2 m; A small steel model box (Figure 1a) used to simulate the building structure, with a size of 0.495 m × 0.4 m × 0.7 m and a mass of 10 kg; Counterweight iron block, total mass of 150 kg; Acrylic panels to simulate barriers around buildings(Figure 1b); PVC pipe observation well, LVDT displacement sensor, water and soil pressure box; The resistance strain gauge and computer data acquisition system are used to collect experimental data.

2.2. Soil Parameters and Test Conditions

In this study, medium fine sand was used as the model soil mass. The basic physical properties of the soil mass were obtained according to the Standard of Geotechnical Test Methods after the soil was saturated with water, as shown in Table 1, and the particle gradation curve was shown in Figure 2.
There are two working conditions in this test, one without barrier and the other with barrier. Details of working conditions are shown in Table 2, where H is the distance between the barrier and the structure, D is the depth of the barrier inserted into the soil, and H is the buried depth of the structure. The test arrangement with barrier is shown in Figure 3, where A is the target structure and B is the barrier structure.

2.3. Test Procedure

(1)
Test preparation. Before the experiment, the water and soil pressure box was put into pure water for calibration and repeated 4 times; the two sides of the barrier structure (acrylic plate) were installed with transparent water sealing film to achieve better water-blocking effect; the main structure (steel model box) was coated with vaseline and PVC film from the bottom up to 30 cm around, on the one hand to reduce the friction between the structure and the soil, on the other hand to prevent water from leaking out from the bottom corners of the structure.
(2)
Lay the soil and place the structure. The soil layer is laid and compacted in layers of 10cm each until the thickness reaches 70 cm. The quality of each layer of soil is controlled during the filling process, and the compacted soil density is tested with a micro-penetration instrument to ensure the similarity of the compacted soil inside the box. In addition, in the process of soil laying, they are buried and filled in strict accordance with the positions of the lower structures and measuring points in Figure 3. When the building structure is placed, the counterweight is added to it immediately and the data are recorded.
(3)
The soil is static and saturated. Slowly drain water from the tank until the water level reaches about 70 cm and maintain this water level all the time, waiting for 3d to saturate the soil. During this process, the L-shaped water level tube on the side of the model box is observed at regular intervals to confirm that the overall water level has reached the set state.
(4)
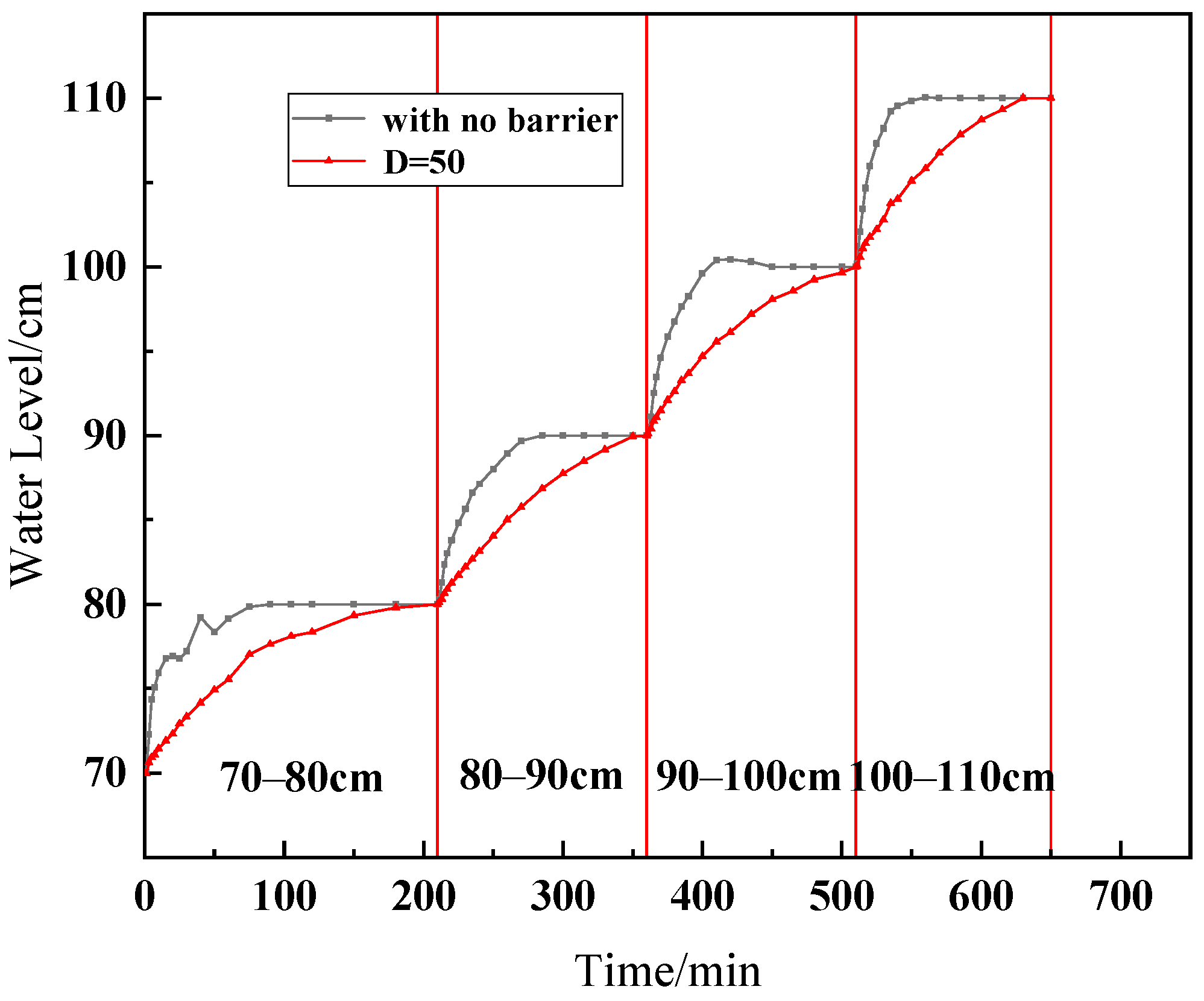
Rising water level. Start the experiment and put water into the tank. The water level starts from 70 cm and rises successively to 80 cm, 90 cm, 100 cm and 110 cm. The L-shaped water level tube, observation well and water and soil pressure box data are always observed during each water level raising process. Once the L-shaped water level gauge and soil-pressure sensors demonstrated consistent readings with less than 1% variation over a 20 min period, the system would proceed to the next stage of controlled water level elevation.

3. Results and Analysis

In this paper, four different water level elevations were carried out in both working conditions, namely 70–80 cm, 80–90 cm, 90–100 cm and 100–110 cm. Accordingly, the influence data of the rising water level on the structure under different head water level conditions were obtained, including two aspects of water level and buoyancy. Through these two aspects, the change process of water level and buoyancy at the structure with time is explored.

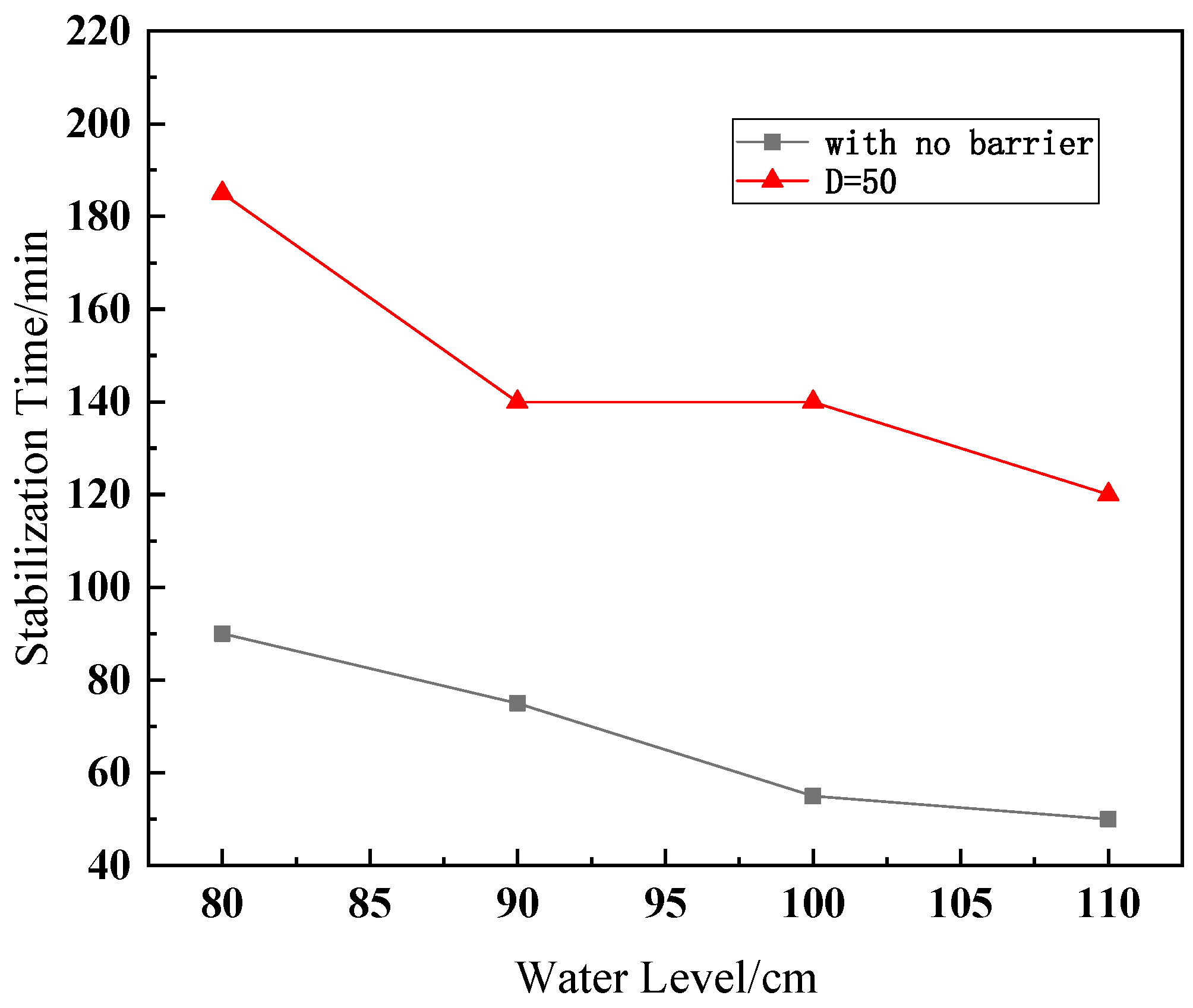
3.1. Water Level Change Process

Figure 4 reveals the dynamic effects of water level uplift on water level at the structure under different working conditions. Comparing the monitoring data of two typical working conditions (barrier/no barrier), it can be seen that the barrier structure has a significant regulation effect on the water level response rate under different hydraulic gradients. When there is a seepage barrier, the water level rise rate at the structure is reduced by about 42–57% compared with the condition without a barrier, and the typical time–history curve shows obvious slow change characteristics. In addition, the final stable head converges to the set value (ΔH = 10 cm) in all operating conditions, which is attributed to the stepped head maintenance mechanism adopted in the test design (each stage head retention time ≥ 1.4 h).
Figure 5 further verifies the hydraulic delay effect of the barrier system through quantitative analysis. Comparing the water level stabilization time parameters under the four groups of characteristic water heads (80 cm, 90 cm, 100 cm, 110 cm), it is found that the average water level response characteristic time at the structure under the non-barrier condition is about 1 ± 0.5 h, while it is extended to about 1.5 ± 0.5 h under the barrier condition, and the time delay rate is 50%. It is worth noting that although the total test duration remained constant at 6.5 h (including all levels of head stability periods), the effective response time of a single stage of water level rise under the barrier condition was about 50% shorter than that of the control group. The quantitative analysis results are mutually verified with the time–history curve of the figure, which jointly reveals the physical mechanism that the seepage barrier causes non-Darcy seepage zone to form around the structure by changing the permeability anisotropy of the medium, thus significantly delaying the pore water pressure transfer process.

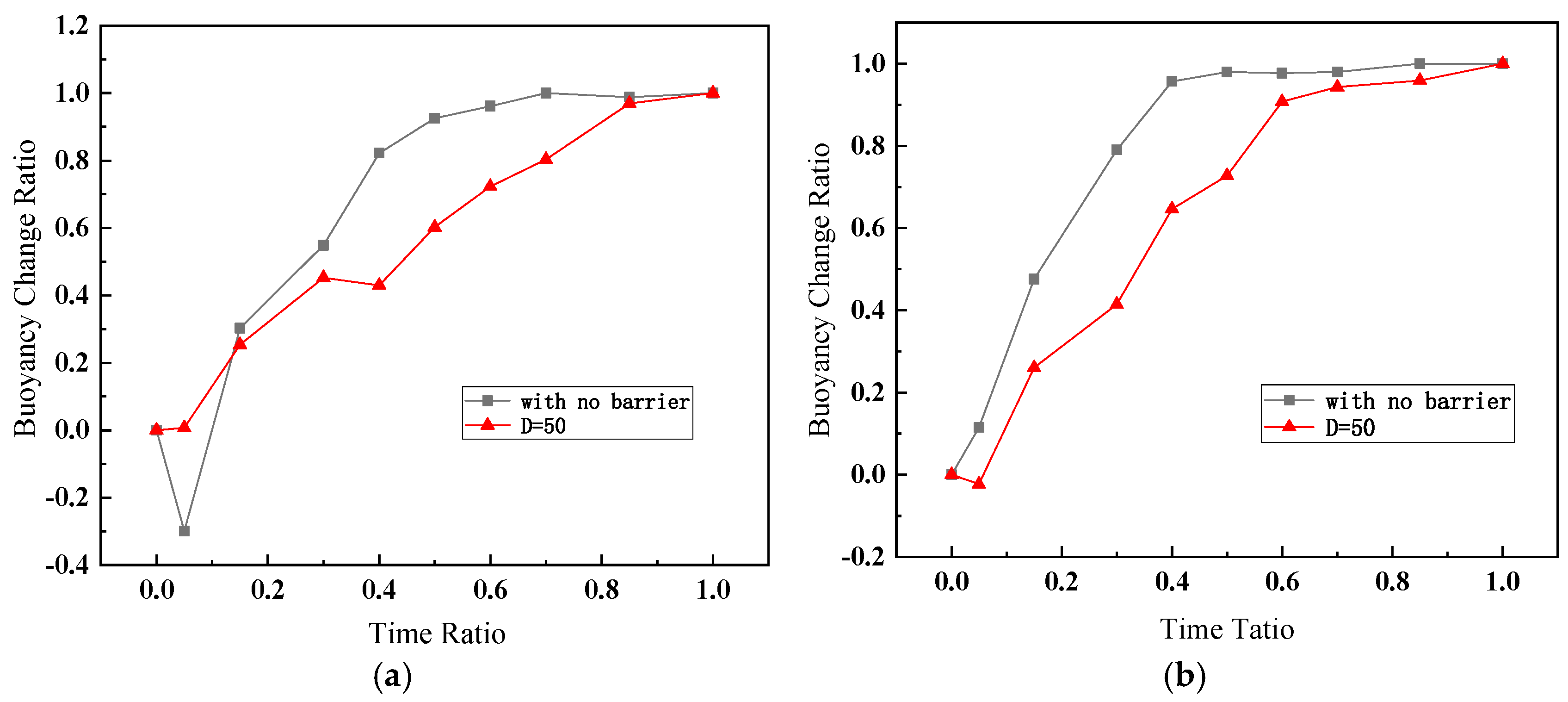
3.2. Buoyancy Change Process

Since the structural displacement is monitored by the LVDT displacement sensor during the whole test process, the reading change of the displacement sensor from the beginning to the end is less than 0.3 mm, which can be approximately regarded as the structure does not float up. Therefore, the forces on the structure include self-weight plus counterweight G, buoyancy F of groundwater on the structure, effective soil reaction P, and friction f around the structure and between the soil, as shown in Figure 6.
Measures to reduce the friction of the structure were been mentioned above. In order to simplify the calculation, the friction force f can be ignored in this study, and the following equation can be obtained:
G = F + P
In the formula, G remains constant throughout the experiment, equal to the self-weight plus the counterweight by calculation, a total of 1.6 KN; F is the buoyancy force on the structure; The effective soil reaction P can be converted from the test value of the earth pressure box. It should be noted that the value measured by the earth pressure box test is the total reaction force including pore water pressure, while the effective soil reaction P refers to the load of the model box, which can be calculated by the following formula, where K1 is the total reaction force obtained by the test of the earth pressure box. K2 is the water pressure obtained by the water pressure box (K1 = σ × a, σ is the stress obtained by the water pressure box, A is the bottom area of the structure):
P = K1 − K2
Take structural buoyancy changes in the process of water level rising from 90–100 cm to 100–110 cm as an example (Figure 7). It can be seen from both figures that when there is no barrier in front of the structure, buoyancy increases rapidly at the beginning of each stage of water level change, and then gradually slows down until it becomes stable. After the barrier is set up, the growth of buoyancy always maintains a slow and continuous state, and the time required to reach stability is significantly longer. This difference is basically the same in each stage of the water level. The reason is that the barrier acts as a “speed bump” in the path of groundwater. When the water level rises, the groundwater can rush directly to the structural area without a barrier; therefore, the buoyancy response is rapid. When there is a barrier, the groundwater needs to bypass the obstacle and percolate along a more tortuous path, which naturally takes more time.
Groundwater changes in the surrounding environment are also different due to head uplift under different hydraulic conditions. Taking the situation without a barrier as an example, in order to see the change process of buoyancy over time more clearly, the time and the buoyancy force subjected to the structure are normalized and expressed by the time ratio a (the total time of time/change to stability) and the buoyancy change ratio b (the change in buoyancy/absolute value of the final change in buoyancy), respectively.
As can be seen from Figure 8, when the water level changes from 100 cm to 110 cm, the time required for b to approach 1 is shorter than the time required for the water level to change from 70 cm to 80 cm, and the overall trend shows that with an increase in hydraulic gradient, the buoyancy change rate of the structure is getting faster and faster. At the same time, it can also be seen from the comparison of different working conditions that the dynamic response of water level and the evolution process of buoyancy present significant synchronization in time domain characteristics. Therefore, it can be considered that the change of water level under a high water level in a certain period of time has a greater impact on the structure than the change of water level under a low water level. The reason for this phenomenon is that the initial pore water pressure in the soil layer is greater under the high head water level, which causes the groundwater flow rate to become faster when the water level is raised than at the low head level. In practical projects, especially in high-water level areas (such as coastal areas), attention should be paid to the harm to the building when the water level rises caused by rainfall or other circumstances, and preventive or remedial measures should be taken more quickly.

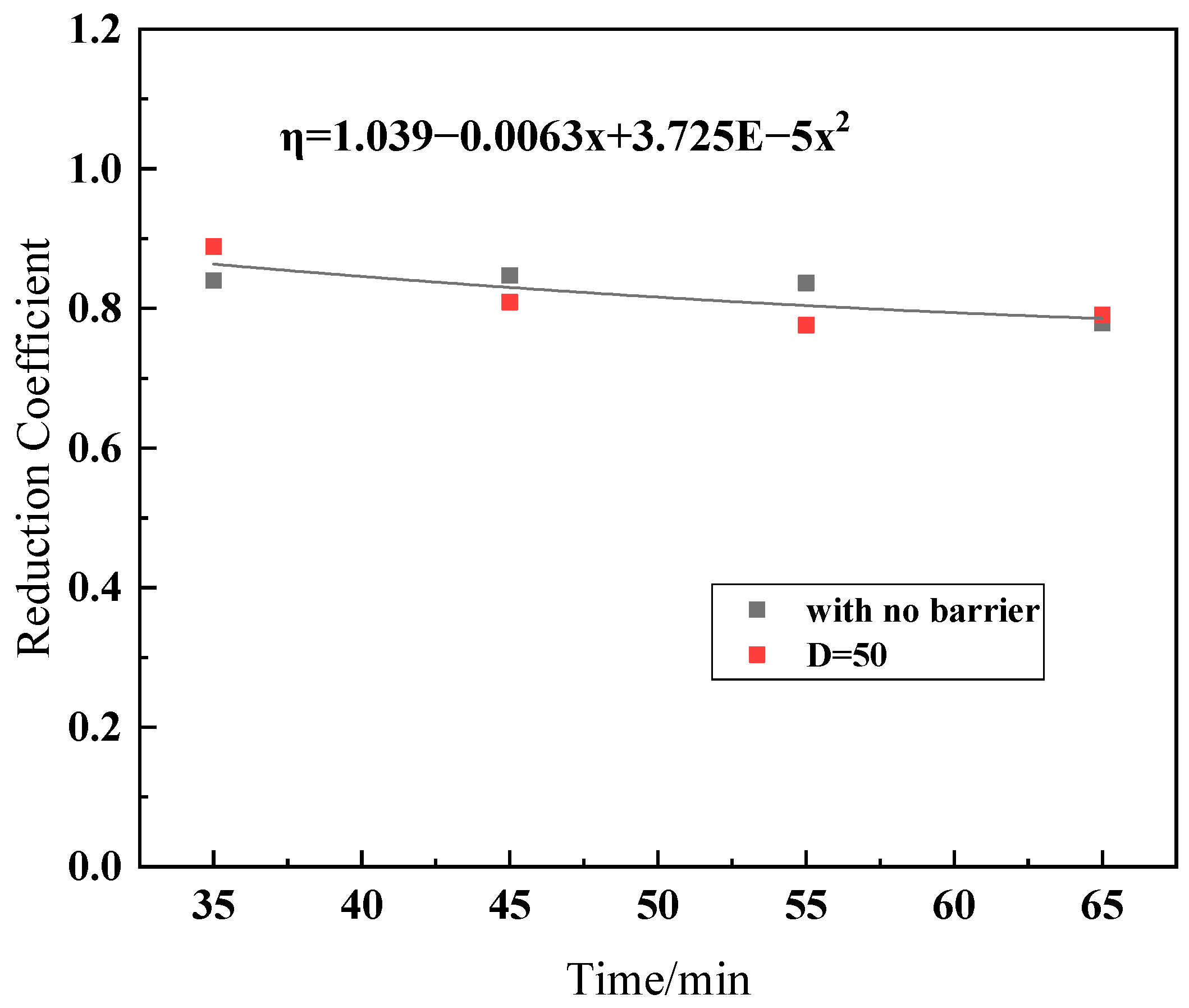
3.3. Buoyancy Attenuation Coefficient

Based on the test results, the final buoyancy force F and theoretical buoyancy force F at the bottom of the structure under different conditions can be obtained, as shown in Figure 9. In addition, by comparing the ultimate buoyancy force F of the structure obtained by the test with the theoretical value F of the structure subjected to buoyancy under the same conditions, the buoyancy reduction coefficient as shown in Figure 10 can be obtained. It is worth noting that the water level in both images is the distance below which the structure is submerged, not the water head level.
It can be seen from Figure 9 that the final buoyancy of the structure obtained by changing the head water pressure in the sandy soil layer is slightly smaller than the theoretical value obtained by Archimedes’ law, but the overall trend is basically consistent with the theory. In addition, the author obtained the predicted buoyancy value of the structure under different water level uplifts by fitting the measured data. As can be seen from the figure, the rule is basically linear, but the research results need to be further verified by more measured projects.
As can be seen from Figure 10, the reduction coefficient (η) obtained by the ratio of the measured and theoretical value of the final buoyancy of the structure at different water levels under two working conditions is roughly between 0.78 and 0.96, and the reduction amount of buoyancy is small. This result is also in good agreement with the final part of the conclusion in a previous study [86,87]. In this study, the authors observed that the reduction coefficient range under the sandy soil foundation is 0.85–0.95. The deviation may stem from different test conditions, such as soil density and soil saturation. From the above comprehensive results, it can be seen that when there is a barrier effect in sandy soil geological conditions, the change of the structure’s buoyancy force will have a certain difference, but the final buoyancy force of the structure will be consistent with the theoretical value under Archimedes’ law, and there is only a small amount of reduction. In practical engineering, the theoretical value obtained by Archimedes’ law can be basically calculated.

4. Discussion

This study mainly explains a common problem, that is, when adjacent underground structures produce a barrier effect, due to some reason, this influences the process of the rising groundwater level in the distance on the buoyancy of the structure behind the barrier. The purpose is to evaluate the timeliness of the changes in the force characteristics of the structure under the above circumstances, so as to take anti-buoyancy measures for the structure in a timely manner. However, in actual engineering, the stratum structure we encounter is often complex, and the soil layer is usually a multi-layer structure rather than a single sandy soil layer. In addition, in actual engineering, underground structures are diverse and could be subway stations or pile foundations, and groundwater also flows away from both sides around the structure. In order to study this issue better and more systematically, more numerical simulation studies and on-site engineering monitoring are still needed in the future. These are all the key points of future research.

5. Conclusions

(1)
Under the same change of head pressure, the buoyancy growth of the structure with the barrier effect is significantly slower than that without a barrier, which indicates that the situation with other structures around the building has more sufficient time to deal with the accident of water level surge.
(2)
Regardless of whether there is a barrier or not, the influence rate of water level change under high head water pressure on the structural stress is much higher than that under low head water pressure. Therefore, more attention should be paid to the detection of the water levels around the building structure in practical projects to avoid engineering accidents caused by sudden changes to water levels under high head water pressure.
(3)
No matter whether there is a barrier or not, the pore pressure and buoyancy of the structure are basically consistent with the theoretical values based on Archimedes’ law under sandy geological conditions, with only a small amount of reduction, and the reduction coefficient is between 0.78 and 0.96.

Author Contributions

Conceptualization, Z.F. and C.Z.; Methodology, Z.F. and C.Z.; Software, Z.F. and K.Y.; Validation, C.X.; Formal analysis, Z.F.; Investigation, X.X.; Writing—original draft, Z.F.; Writing—review & editing, K.Y. and C.Z.; Supervision, Z.F., C.X. and C.Z.; Project administration, C.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China [grant numbers 52478342 and 52238009], the Science and Technology Innovation Program of Hunan Province [grant number 2022RC1172], and the Natural Science Foundation of Jiangxi Province [grant number 20223BBG71018].

Data Availability Statement

Data is contained within the article.

Acknowledgments

The authors are grateful for the warm and efficient work of the editors and reviewers.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zheng, G.; Ha, D.; Zeng, C.; Cheng, X.; Zhou, H.; Cao, J. Influence of the opening timing of recharge wells on settlement caused by dewatering in excavations. J. Hydrol. 2019, 573, 534–545. [Google Scholar] [CrossRef]
  2. Zheng, G.; Ha, D.; Loaiciga, H.; Zhou, H.; Zeng, C.; Zhang, H. Estimation of the hydraulic parameters of leaky aquifers based on pumping tests and coupled simulation/optimization: Verification using a layered aquifer in Tianjin, China. Hydrogeol. J. 2019, 27, 3081–3095. [Google Scholar] [CrossRef]
  3. Zeng, C.-F.; Zheng, G.; Zhou, X.-F.; Xue, X.-L.; Zhou, H.-Z. Behaviours of wall and soil during pre-excavation dewatering under different foundation pit widths. Comput. Geotech. 2019, 115, 103169. [Google Scholar] [CrossRef]
  4. Ni, J.C.; Cheng, W.-C.; Ge, L. A case history of field pumping tests in a deep gravel formation in the Taipei Basin, Taiwan. Eng. Geol. 2011, 117, 17–28. [Google Scholar] [CrossRef]
  5. Gornitz, V.; Oppenheimer, M.; Kopp, R.; Horton, R.; Orton, P.; Rosenzweig, C.; Solecki, W.; Patrick, L. Enhancing New York City’s resilience to sea level rise and increased coastal flooding. Urban Clim. 2020, 33, 100654. [Google Scholar] [CrossRef]
  6. Zeng, C.-F.; Zheng, G.; Xue, X.-L.; Mei, G.-X. Combined recharge: A method to prevent ground settlement induced by redevelopment of recharge wells. J. Hydrol. 2019, 568, 1–11. [Google Scholar] [CrossRef]
  7. Zeng, C.-F.; Zheng, G.; Xue, X.-L. Responses of deep soil layers to combined recharge in a leaky aquifer. Eng. Geol. 2019, 260, 105263. [Google Scholar] [CrossRef]
  8. Zeng, C.-F.; Xue, X.-L.; Zheng, G.; Xue, T.-Y.; Mei, G.-X. Responses of retaining wall and surrounding ground to pre-excavation dewatering in an alternated multi-aquifer-aquitard system. J. Hydrol. 2018, 559, 609–626. [Google Scholar] [CrossRef]
  9. Zeng, C.-F.; Xue, X.-L.; Li, M.-K. Use of cross wall to restrict enclosure movement during dewatering inside a metro pit before soil excavation. Tunn. Undergr. Space Technol. 2021, 112, 103909. [Google Scholar] [CrossRef]
  10. Zeng, C.F.; Powrie, W.; Xu, C.J.; Xue, X.L. Wall movement during dewatering inside a diaphragm wall before soil excavation. Undergr. Space 2025, 22, 355–368. [Google Scholar] [CrossRef]
  11. Rice, J.D.; Duncan, J.M. Findings of case histories on the long-term performance of seepage barriers in dams. J. Geotech. Geoenviron. Eng. 2010, 136, 2–15. [Google Scholar] [CrossRef]
  12. Attard, G.; Winiarski, T.; Rossier, Y.; Eisenlohr, L. Impact of underground structures on the flow of urban groundwater. Hydrogeol. J. 2016, 24, 5–19. [Google Scholar] [CrossRef]
  13. Zeng, C.-F.; Wang, S.; Xue, X.-L.; Zheng, G.; Mei, G.-X. Characteristics of ground settlement due to combined actions of groundwater drawdown and enclosure wall movement. J. Hydrol. 2022, 17, 4095–4112. [Google Scholar] [CrossRef]
  14. Abu-Rizaiza, O.S. Threats from groundwater table rise in urban areas in developing countries. Water Int. 1999, 24, 46–52. [Google Scholar] [CrossRef]
  15. Guan, X.; Madabhushi, G.S.P. Effect of water table on the behaviour of retaining walls and adjacent structures during earthquake loading. Soil Dyn. Earthq. Eng. 2025, 191, 109273. [Google Scholar] [CrossRef]
  16. Feng, S.-J.; Li, Y.-C.; Chen, H.; Chen, Z.-L. Response of pavement and stratified ground due to vehicle loads considering rise of water table. Int. J. Pavement Eng. 2019, 20, 191–203. [Google Scholar] [CrossRef]
  17. Zeng, C.-F.; Wang, S.; Xue, X.-L.; Zheng, G.; Mei, G.-X. Evolution of deep ground settlement subject to groundwater drawdown during dewatering in a multi-layered aquifer-aquitard system: Insights from numerical modelling. J. Hydrol. 2021, 603, 127078. [Google Scholar] [CrossRef]
  18. Zeng, C.-F.; Song, W.-W.; Xue, X.-L.; Li, M.-K.; Bai, N.; Mei, G.-X. Construction dewatering in a metro station incorporating buttress retaining wall to limit ground settlement: Insights from experimental modelling. Tunn. Undergr. Space Technol. 2021, 116, 104124. [Google Scholar] [CrossRef]
  19. Ha, D.; Zheng, G.; Zhou, H.; Zeng, C.; Zhang, H. Estimation of hydraulic parameters from pumping tests in a multiaquifer system. Undergr. Space 2020, 5, 210–222. [Google Scholar] [CrossRef]
  20. Yang, K.; Xu, C.; Zeng, C.; Zhu, L.; Xue, X.; Han, L. Analysis of Recharge Efficiency Under Barrier Effects Incurred by Adjacent Underground Structures. Water 2025, 17, 257. [Google Scholar] [CrossRef]
  21. Shi, J.; Ng, C.W.W.; Chen, Y. Three-dimensional numerical parametric study of the influence of basement excavation on existing tunnel. Comput. Geotech. 2015, 63, 146–158. [Google Scholar] [CrossRef]
  22. Xue, X.-L.; Sun, H.-Y.; Zeng, C.-F.; Chen, H.-B.; Zheng, G.; Xu, C.-J.; Han, L. Why pile-supported building settled continuously after water level was stabilized during dewatering: Clues from interaction between pile and multi aquifers. J. Hydrol. 2024, 638, 131539. [Google Scholar] [CrossRef]
  23. He, D.; Zeng, C.; Xu, C.; Xue, X.; Zhao, Y.; Han, L.; Sun, H. Barrier Effect of Existing Building Pile on the Responses of Groundwater and Soil During Foundation Pit Dewatering. Water 2024, 16, 2977. [Google Scholar] [CrossRef]
  24. Xue, T.; Xue, X.; Long, S.; Chen, Q.; Lu, S.; Zeng, C. Effect of pre-existing underground structures on groundwater flow and strata movement induced by dewatering and excavation. Water 2023, 15, 814. [Google Scholar] [CrossRef]
  25. Zeng, C.-F.; Liao, H.; Xue, X.-L.; Long, S.-C.; Luo, G.-J.; Diao, Y.; Li, M.-G. Responses of groundwater and soil to dewatering considering the barrier effect of adjacent metro station on multi-aquifers. J. Hydrol. 2022, 612, 128117. [Google Scholar] [CrossRef]
  26. Chen, R.; Meng, F.; Li, Z.; Ye, Y.; Ye, J. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils. Tunn. Undergr. Space Technol. 2016, 58, 224–235. [Google Scholar] [CrossRef]
  27. Bikçe, M.; Örnek, M.; Cansız, Ö.F. The effect of buoyancy force on structural damage: A case study. Eng. Fail. Anal. 2018, 92, 553–565. [Google Scholar] [CrossRef]
  28. Acosta-Martinez, H.E.; Gourvenec, S.M.; Randolph, M.F. An experimental investigation of a shallow skirted foundation under compression and tension. Soils Found. 2008, 48, 247–254. [Google Scholar] [CrossRef]
  29. Chian, S.; Madabhushi, S. Effect of buried depth and diameter on uplift of underground structures in liquefied soils. Soil Dyn. Earthq. Eng. 2012, 41, 181–190. [Google Scholar] [CrossRef]
  30. Huang, Y.; Yu, M. Review of soil liquefaction characteristics during major earthquakes of the twenty-first century. Nat. Hazards 2013, 65, 2375–2384. [Google Scholar] [CrossRef]
  31. Kosekt, J.; Matsuo, O.; Koga, Y. Uplift behavior of underground structures caused by liquefaction of surrounding soil during earthquake. Soils Found. 1997, 37, 97–108. [Google Scholar] [CrossRef]
  32. Wong, I. Methods of resisting hydrostatic uplift in substructures. Tunn. Undergr. Space Technol. 2001, 16, 77–86. [Google Scholar] [CrossRef]
  33. Zhang, D. Experimental Study on Anti-Floating of Underground Structures. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2007. [Google Scholar]
  34. Li, G. Some problems about principle of effective stress. Chin. J. Geotech. Eng. 2011, 33, 315–320. [Google Scholar]
  35. Ni, P.; Mei, G.; Zhao, Y. Antiflotation design for water tank using pressure relief technique. Mar. Georesour. Geotechnol. 2018, 36, 471–483. [Google Scholar] [CrossRef]
  36. Jackson, D.C. It Is a Crime to Design a Dam without Considering upward Pressure: Engineers and Uplift, 1890–1930. In Henry PG Darcy and Other Pioneers in Hydraulics; ASCE Library: Reston, VA, USA, 2003; pp. 220–232. [Google Scholar]
  37. Liu, G.; Jia, P.; Sun, J.; Jiang, Z.; Yang, F.; Yang, G.; Shao, G. Research and application of new anti-floating anchor in anti-floating reinforcement of existing underground structures. Front. Earth Sci. 2024, 12, 1364752. [Google Scholar] [CrossRef]
  38. Kong, D.; Guan, Y.; Yuan, H. Study on the anti-floating water level of the underground structure’s comprehensive anti-floating. Structures 2023, 56, 104921. [Google Scholar] [CrossRef]
  39. Yibin, L.; Jibin, C.; Yuanyuan, W.; Pan, S. Anti-floating failure mechanism of underground structures in expansive soil area and application of active anti-floating measures. Hydrogeol. Eng. Geol. 2022, 49, 64–73. [Google Scholar]
  40. Luo, G.; Yang, F.; Li, H.; Pan, H.; Cao, H. Simplified Calculation Method for Active Anti-Floating of Elliptical Basements by Relief Wells. Appl. Sci. 2023, 13, 12647. [Google Scholar] [CrossRef]
  41. Sun, W.; Liu, H.; Zhang, W.; Liu, S.; Gao, X. Investigation on overburden thickness considering face and anti-floating stability of shallow shield tunnel. Comput. Geotech. Res. 2023, 160, 105562. [Google Scholar] [CrossRef]
  42. Kou, H.-l.; Guo, W.; Zhang, M.-Y. Pullout performance of GFRP anti-floating anchor in weathered soil. Tunn. Undergr. Space Technol. 2015, 49, 408–416. [Google Scholar] [CrossRef]
  43. Yang, M.; Wu, J.; Lu, Q.; Li, P. Optimization of Uplift Piles for a Base Plate Considering Local Anti-Floating Stability. Appl. Sci. 2024, 14, 5000. [Google Scholar] [CrossRef]
  44. Huang, Q.; Wang, J.; Li, M.; Fei, M.; Dong, J. Modeling the influence of urbanization on urban pluvial flooding: A scenario-based case study in Shanghai, China. Nat. Hazards 2017, 87, 1035–1055. [Google Scholar] [CrossRef]
  45. Boltton, M.; Stewart, D. The effect on propped diaphragm walls of rising groundwater in stiff clay. Géotechnique 1994, 44, 111–127. [Google Scholar] [CrossRef]
  46. Lee, F.; Juneja, A.; Tan, T. Stress and pore pressure changes due to sand compaction pile installation in soft clay. Géotechnique 2004, 54, 1–16. [Google Scholar] [CrossRef]
  47. Li, M.-G.; Chen, J.-J.; Xu, Y.-S.; Tong, D.-G.; Cao, W.-W.; Shi, Y.-J. Effects of groundwater exploitation and recharge on land subsidence and infrastructure settlement patterns in Shanghai. Eng. Geol. 2021, 282, 105995. [Google Scholar] [CrossRef]
  48. López-Fernández, C.; Prieto, D.A.; Fernández-Viejo, G.; Pando, L.; Fernández, E.C. Surface subsidence induced by groundwater drainage tunneling in granite residual soils (Burata Railway Tunnel, Spain). J. Geotech. Geoenviron. Eng. 2013, 139, 821–824. [Google Scholar] [CrossRef]
  49. Schwamb, T.; Elshafie, M.Z.; Soga, K.; Mair, R.J. Considerations for monitoring of deep circular excavations. Proc. Inst. Civ. Eng. Geotech. Eng. 2016, 169, 477–493. [Google Scholar] [CrossRef]
  50. Wang, J.; Wu, Y.; Liu, X.; Yang, T.; Wang, H.; Zhu, Y. Areal subsidence under pumping well–curtain interaction in subway foundation pit dewatering: Conceptual model and numerical simulations. Env. Earth Sci. 2016, 75, 198. [Google Scholar] [CrossRef]
  51. Figueroa-Miranda, S.; Tuxpan-Vargas, J.; Ramos-Leal, J.A.; Hernández-Madrigal, V.M.; Villaseñor-Reyes, C.I. Land subsidence by groundwater over-exploitation from aquifers in tectonic valleys of Central Mexico: A review. Eng. Geol. 2018, 246, 91–106. [Google Scholar] [CrossRef]
  52. Motagh, M.; Shamshiri, R.; Haghighi, M.H.; Wetzel, H.-U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
  53. Ou, C.-Y.; Liao, J.-T.; Cheng, W.-L. Building response and ground movements induced by a deep excavation. Geotechnique 2000, 50, 209–220. [Google Scholar] [CrossRef]
  54. Hu, W.; Wang, Y.; Li, H.; Huang, M.; Hou, M.; Li, Z.; She, D.; Si, B. Dominant role of climate in determining spatio-temporal distribution of potential groundwater recharge at a regional scale. J. Hydrol. 2019, 578, 124042. [Google Scholar] [CrossRef]
  55. Oo, K.T.; Haishan, C.; Jonah, K. Climate Change Impact on the Trigger of Natural Disasters over South-Eastern Himalayas Foothill Region of Myanmar: Extreme Rainfall Analysis. Int. J. Geophys. 2023, 2023, 2186857. [Google Scholar] [CrossRef]
  56. Walia, D. Rainfall Induced Landslide Hazards and Forecast under Changing Climatic Patterns and Associated Adaptations. In Climate Change in India; CRC Press: Boca Raton, FL, USA, 2024; pp. 144–173. [Google Scholar]
  57. Wang, Y.; Hu, Y.; Wang, H.; Luo, J.; Hou, D. Extreme rainfall effects on water table dynamics and surface water-groundwater interactions: Insights from a semiarid alluvial fan in Northern China. J. Hydrol. 2025, 657, 133157. [Google Scholar] [CrossRef]
  58. Wittenberg, H.; Aksoy, H.; Miegel, K. Fast response of groundwater to heavy rainfall. J. Hydrol. 2019, 571, 837–842. [Google Scholar] [CrossRef]
  59. Tsuchida, T.; Athapaththu, A.; Hanaoka, T.; Kawaguchi, M. Investigation of landslide calamity due to torrential rainfall in Shobara City, Japan. Soils Found. 2015, 55, 1305–1317. [Google Scholar] [CrossRef]
  60. Chowdhuri, I.; Pal, S.C.; Chakrabortty, R.; Malik, S.; Das, B.; Roy, P. Torrential rainfall-induced landslide susceptibility assessment using machine learning and statistical methods of eastern Himalaya. Nat. Hazards 2021, 107, 697–722. [Google Scholar] [CrossRef]
  61. Chen, L.; Wang, W.; Bu, A. Numerical Simulation Study of Basement Water Discharge Pressure Relief Method under Rainstorm Conditions. Buildings 2023, 13, 2772. [Google Scholar] [CrossRef]
  62. Fowler, H.J.; Lenderink, G.; Prein, A.F.; Westra, S.; Allan, R.P.; Ban, N.; Barbero, R.; Berg, P.; Blenkinsop, S.; Do, H.X. Anthropogenic intensification of short-duration rainfall extremes. Nat. Rev. Earth Environ. 2021, 2, 107–122. [Google Scholar] [CrossRef]
  63. Abancó, C.; Hürlimann, M.; Moya, J.; Berenguer, M. Critical rainfall conditions for the initiation of torrential flows. Results from the Rebaixader catchment (Central Pyrenees). J. Hydrol. 2016, 541, 218–229. [Google Scholar] [CrossRef]
  64. Wasko, C.; Nathan, R.; Stein, L.; O’Shea, D. Evidence of shorter more extreme rainfalls and increased flood variability under climate change. J. Hydrol. 2021, 603, 126994. [Google Scholar] [CrossRef]
  65. Mao, X.; Enot, P.; Barry, D.A.; Li, L.; Binley, A.; Jeng, D.-S. Tidal influence on behaviour of a coastal aquifer adjacent to a low-relief estuary. J. Hydrol. 2006, 327, 110–127. [Google Scholar] [CrossRef]
  66. Saucier, F.J.; Chassé, J. Tidal circulation and buoyancy effects in the St. Lawrence Estuary. Atmos. Ocean 2000, 38, 505–556. [Google Scholar] [CrossRef]
  67. Zheng, L.; Weisberg, R.H. Tide, buoyancy, and wind-driven circulation of the Charlotte Harbor estuary: A model study. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
  68. Münchow, A.; Garvine, R.W. Dynamical properties of a buoyancy-driven coastal current. J. Geophys. Res. Ocean. 1993, 98, 20063–20077. [Google Scholar] [CrossRef]
  69. Preusse, P.; Eckermann, S.; Oberheide, J.; Hagan, M.; Offermann, D. Modulation of gravity waves by tides as seen in CRISTA temperatures. Adv. Space Res. 2001, 27, 1773–1778. [Google Scholar] [CrossRef]
  70. Herman, J.P.; Tsegaye, S.; Missimer, T.M. Evaluating Stormwater Infiltration Systems in High Water Table Areas: Insights from Southwest Florida. Water 2024, 16, 3198. [Google Scholar] [CrossRef]
  71. Luo, C.-Y.; Shen, S.-L.; Han, J.; Ye, G.-L.; Horpibulsuk, S. Hydrogeochemical environment of aquifer groundwater in Shanghai and potential hazards to underground infrastructures. Nat. Hazards 2015, 78, 753–774. [Google Scholar] [CrossRef]
  72. Tariq Amin Chaudhary, M. Implications of rising groundwater level on structural integrity of underground structures–investigations and retrofit of a large building complex. Struct. Surv. 2012, 30, 111–129. [Google Scholar] [CrossRef]
  73. Liu, H.; Song, E. Working mechanism of cutoff walls in reducing uplift of large underground structures induced by soil liquefaction. Comput. Geotech. 2006, 33, 209–221. [Google Scholar] [CrossRef]
  74. Zeng, C.-F.; Powrie, W.; Xue, X.-L.; Li, M.-K.; Mei, G.-X. Effectiveness of a buttress wall in reducing retaining wall movement during dewatering before bulk excavation. Acta Geotech. 2021, 16, 3253–3267. [Google Scholar] [CrossRef]
  75. Zeng, C.-F.; Powrie, W.; Chen, H.-B.; Wang, S.; Diao, Y.; Xue, X.-L. Ground behavior due to dewatering inside a foundation pit considering the barrier effect of preexisting building piles on aquifer flow. J. Geotech. Geoenviron. Eng. 2024, 150, 05024004. [Google Scholar] [CrossRef]
  76. Zeng, C.-F.; Chen, H.-B.; Liao, H.; Xue, X.-L.; Chen, Q.-N.; Diao, Y. Behaviours of groundwater and strata during dewatering of large-scale excavations with a nearby underground barrier. J. Hydrol. 2023, 620, 129400. [Google Scholar] [CrossRef]
  77. Terzaghi, K. Theoretical Soil Mechanics; Wiley: Hoboken, NJ, USA, 1943. [Google Scholar]
  78. Kaul, K. Cut-and-Cover Metro Structures: Geo-Structural Design: An Integrated Approach; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
  79. Piazza, R.; Buzzaccaro, S.; Secchi, E.; Parola, A. What buoyancy really is. A generalized Archimedes’ principle for sedimentation and ultracentrifugation. Soft Matter 2012, 8, 7112–7115. [Google Scholar] [CrossRef]
  80. Bear, J. Hydraulics of Groundwater; Courier Corporation: New York, NY, USA, 1979. [Google Scholar]
  81. Eid, H.T. Bearing capacity and settlement of skirted shallow foundations on sand. Int. J. Geomech. 2013, 13, 645–652. [Google Scholar] [CrossRef]
  82. Guo, H.; Zhou, R.; Sun, C.; Lin, Y.; Xie, J. Buoyancy of underground structures and pore water pressure conduction law in silty clay strata. Heliyon 2024, 10, e24256. [Google Scholar] [CrossRef]
  83. Hu, Z.; Yang, Z.; Wilkinson, S.P. Analysis of passive earth pressure modification due to seepage flow effects. Can. Geotech. J. 2018, 55, 666–679. [Google Scholar] [CrossRef]
  84. Kolay, P.; Kumar, S.; Tiwari, D. Improvement of bearing capacity of shallow foundation on geogrid reinforced silty clay and sand. J. Constr. Eng. 2013, 2013, 293809. [Google Scholar] [CrossRef]
  85. Luke, A.M.; Rauch, A.F.; Olson, R.E.; Mecham, E.C. Components of suction caisson capacity measured in axial pullout tests. Ocean Eng. 2005, 32, 878–891. [Google Scholar] [CrossRef]
  86. Ni, P.; Kang, X.; Song, L.; Mei, G.; Zhao, Y. Model tests of buoyant force on underground structures. J. Test. Eval. 2019, 47, 1216–1235. [Google Scholar] [CrossRef]
  87. Ren, Z.; Lu, Q.; Liu, K.; Ni, P.; Mei, G. Model-scale tests to examine water pressures acting on potentially buoyant underground structures in clay strata. J. Rock Mech. Geotech. Eng. 2022, 14, 861–872. [Google Scholar] [CrossRef]
  88. Santos, P.J.; Barros, P.L. Active earth pressure due to soil mass partially subjected to water seepage. Can. Geotech. J. 2015, 52, 1886–1891. [Google Scholar] [CrossRef]
  89. Shen, S.-L.; Wu, Y.-X.; Misra, A. Calculation of head difference at two sides of a cut-off barrier during excavation dewatering. Comput. Geotech. 2017, 91, 192–202. [Google Scholar] [CrossRef]
  90. Taiebat, H.; Carter, J. Numerical studies of the bearing capacity of shallow foundations on cohesive soil subjected to combined loading. Géotechnique 2000, 50, 409–418. [Google Scholar] [CrossRef]
  91. Song, L.; Kang, X.; Mei, G. Buoyancy force on shallow foundations in clayey soil: An experimental investigation based on the “Half Interval Search”. Ocean Eng. 2017, 129, 637–641. [Google Scholar] [CrossRef]
  92. Ren, Z.; Ni, P.; Mei, G. Time effect of buoyant force reduction for underground structures in clays: Model test and case study. Int. J. Geomech. 2020, 20, 04020185. [Google Scholar] [CrossRef]
  93. Mei, G.; Song, L.; Zai, J. Experimental study on reduction of groundwater buoyancy. Chin. J. Geotech. Eng. 2009, 31, 1476–1480. [Google Scholar]
  94. Song, L.; Wang, X.; Wu, H.; Zhou, K.; Mei, G. Permeation process of clay under different stresses. Chin. J. Geotech. Eng. 2022, 44, 755–761. [Google Scholar]
  95. Zhou, J.; Yao, Z.; Gang, Z. Mesomechanical simulation of seepage flow in sandy soil. Chin. J. Geotech. Eng. 2007, 29, 977–981. [Google Scholar]
  96. Xu, Y.; Shen, S.; Ma, L. Cutoff effect of groundwater seepage due to existence of underground structure. J. Zhejiang Univ. Eng. Sci. 2010, 44, 1902–1906. [Google Scholar]
  97. Wang, X.; Xu, Y. Experimental investigation on the permeability of gap-graded soil due to horizontal suffusion considering boundary effect. J. Rock Mech. Geotech. Eng. 2024, 16, 1072–1084. [Google Scholar] [CrossRef]
  98. Li, Y.; Mu, L.; Cao, J. Impact of Seepage on the Underground Water Level in a Complex Soil-Water-Structure System. Adv. Civ. Eng. 2022, 2022, 7034778. [Google Scholar] [CrossRef]
  99. Zhang, J.-W.; Cao, J.; Mu, L.; Wang, L.; Li, J. Buoyancy force acting on underground structures considering seepage of confined water. Complexity 2019, 2019, 7672930. [Google Scholar] [CrossRef]
  100. Tang, Y.-F.; Cao, X.-W.; Li, M.; Cui, C.; Song, L.-H. Experimental Research on Pore Pressure and Transfer Mechanism in Clay. J. Chang. River Sci. Res. Inst. 2024, 41, 110. [Google Scholar]
  101. Tang, Y.-F.; Jiao, M.; Liu, X.-Y.; Qi, D.; Song, L. Experimental study on variation of pore pressure of clay foundation during groundwater level fluctuation. J. Nanjing Tech Univ. 2024, 46, 103–111. [Google Scholar]
  102. Zhang, Q.; Ouyang, L.; Wang, Z.; Liu, H.; Zhang, Y. Buoyancy reduction coefficients for underground silos in sand and clay. Indian Geotech. J. 2019, 49, 216–223. [Google Scholar] [CrossRef]
  103. Liu, H.; Sun, W.; Zhang, Y.; Zhang, W.; Han, F.; Su, W. Experimental analysis on the interaction between underground structures and sand layer under groundwater level change. Undergr. Space 2023, 10, 15–36. [Google Scholar] [CrossRef]
  104. Liu, H.-L.; Kong, G.-Q.; Sun, X.-J. Comparative test of effect of pore liquid on permeability characteristics of transparent soil. J. Hydraul. Eng. 2017, 48, 1303–1310. [Google Scholar]
  105. Sun, W.; Zhang, W.; Han, L. Determination of groundwater buoyancy reduction coefficient in clay: Model tests, numerical simulations and machine learning methods. Undergr. Space 2023, 13, 228–240. [Google Scholar] [CrossRef]
Water 17 01377 g001
Figure 1. The main structure used in the test: (a) steel model box diagram, (b) acrylic panels, (c) simulated soil layer environment model box.
Figure 1. The main structure used in the test: (a) steel model box diagram, (b) acrylic panels, (c) simulated soil layer environment model box.
Water 17 01377 g001
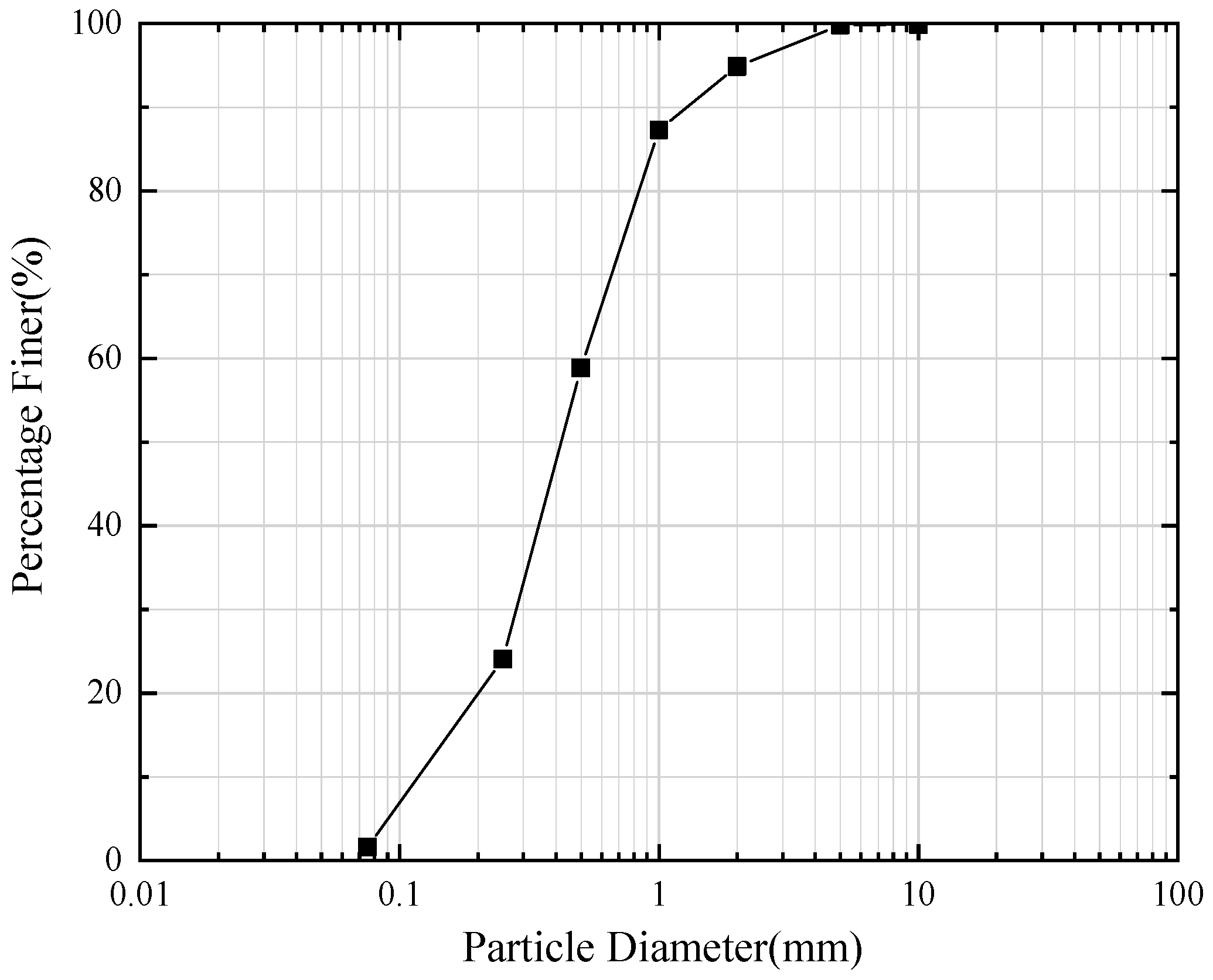
Water 17 01377 g002
Figure 2. Soil particle gradation.
Figure 2. Soil particle gradation.
Water 17 01377 g002
Water 17 01377 g003
Figure 3. Structure and monitoring site layout: (a) plan Layout, (b) side layout.
Figure 3. Structure and monitoring site layout: (a) plan Layout, (b) side layout.
Water 17 01377 g003
Water 17 01377 g004
Figure 4. Time–history of water level change at the contrast structure with or without barrier.
Figure 4. Time–history of water level change at the contrast structure with or without barrier.
Water 17 01377 g004
Water 17 01377 g005
Figure 5. Time required for water level stabilization under each water head.
Figure 5. Time required for water level stabilization under each water head.
Water 17 01377 g005
Water 17 01377 g006
Figure 6. Structural stress analysis.
Figure 6. Structural stress analysis.
Water 17 01377 g006
Water 17 01377 g007
Figure 7. Variation of structural buoyancy under different water levels with time: (a) 90–100 cm, (b) 100–110 cm.
Figure 7. Variation of structural buoyancy under different water levels with time: (a) 90–100 cm, (b) 100–110 cm.
Water 17 01377 g007
Water 17 01377 g008
Figure 8. Structural buoyancy changes during water level rise (without barrier).
Figure 8. Structural buoyancy changes during water level rise (without barrier).
Water 17 01377 g008
Water 17 01377 g009
Figure 9. Buoyancy force under different water levels of the structure with or without barriers (fitting analysis).
Figure 9. Buoyancy force under different water levels of the structure with or without barriers (fitting analysis).
Water 17 01377 g009
Water 17 01377 g010
Figure 10. Buoyancy reduction coefficient under each water level.
Figure 10. Buoyancy reduction coefficient under each water level.
Water 17 01377 g010
Table 1. Parameters of the model soil.
Table 1. Parameters of the model soil.
Soil TypeDry Density
(g/cm3)		Wet Density
(g/cm3)		Moisture
Content (%)		Void Ratio
(e)		Specific Gravity
(GS)		Permeability (m/d)
Sandy1.611.8514.660.72.657.65
Table 2. Test conditions.
Table 2. Test conditions.
ConditionsHDh
no barrier0025 cm
barrier50 cm50 cm25 cm
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Fan, Z.; Xu, C.; Yang, K.; Xue, X.; Zeng, C. Experimental Study on the Influence of Rising Water Levels on the Buoyancy of Building Structure. Water 2025, 17, 1377. https://doi.org/10.3390/w17091377

AMA Style

Fan Z, Xu C, Yang K, Xue X, Zeng C. Experimental Study on the Influence of Rising Water Levels on the Buoyancy of Building Structure. Water. 2025; 17(9):1377. https://doi.org/10.3390/w17091377

Chicago/Turabian Style

Fan, Zhisong, Changjie Xu, Kelang Yang, Xiuli Xue, and Chaofeng Zeng. 2025. "Experimental Study on the Influence of Rising Water Levels on the Buoyancy of Building Structure" Water 17, no. 9: 1377. https://doi.org/10.3390/w17091377

APA Style

Fan, Z., Xu, C., Yang, K., Xue, X., & Zeng, C. (2025). Experimental Study on the Influence of Rising Water Levels on the Buoyancy of Building Structure. Water, 17(9), 1377. https://doi.org/10.3390/w17091377

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop