Monthly Streamflow Forecasting for the Irtysh River Based on a Deep Learning Model Combined with Runoff Decomposition
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
3. Methodology
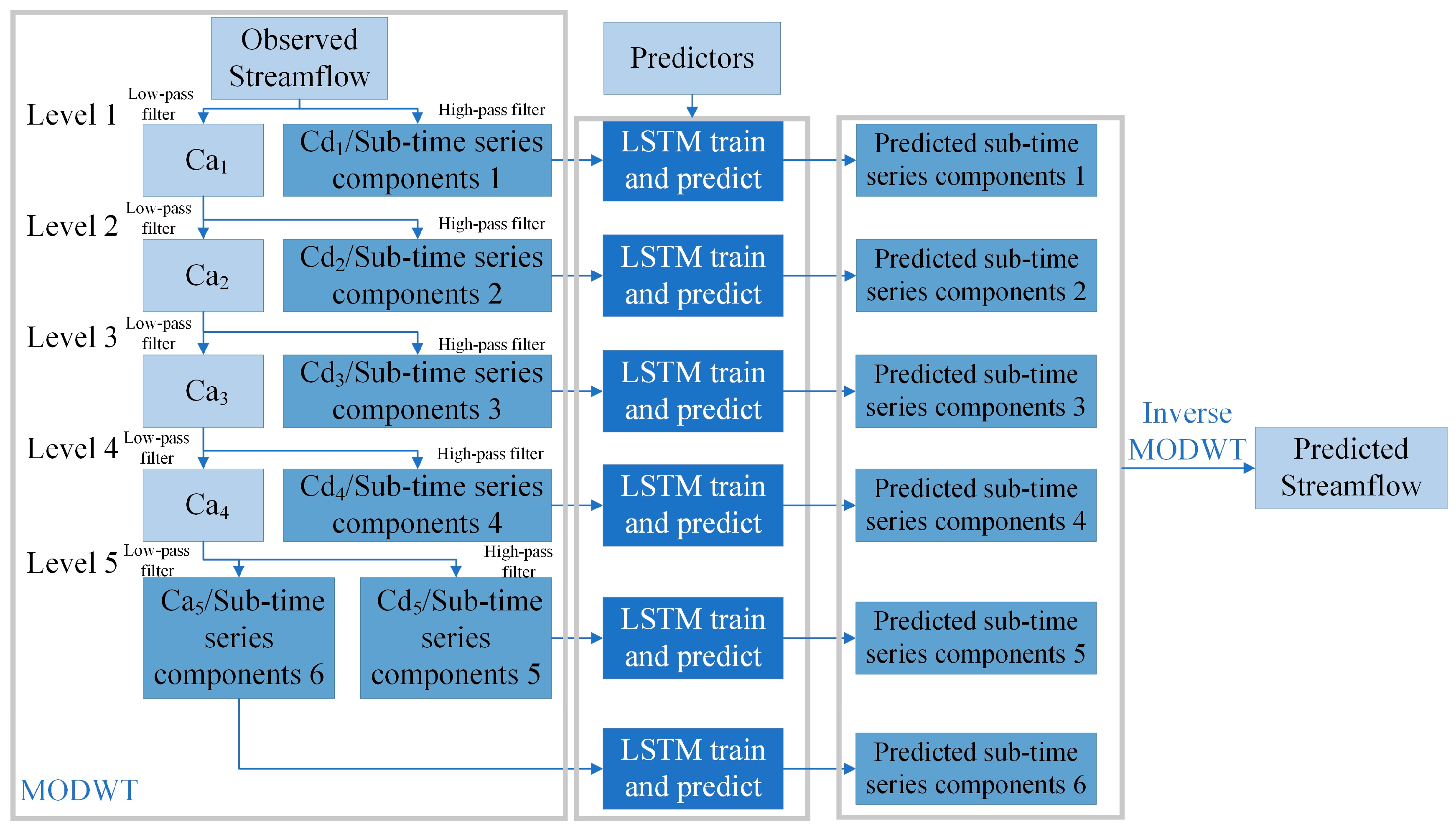
3.1. SSA-MODWT-LSTM Model
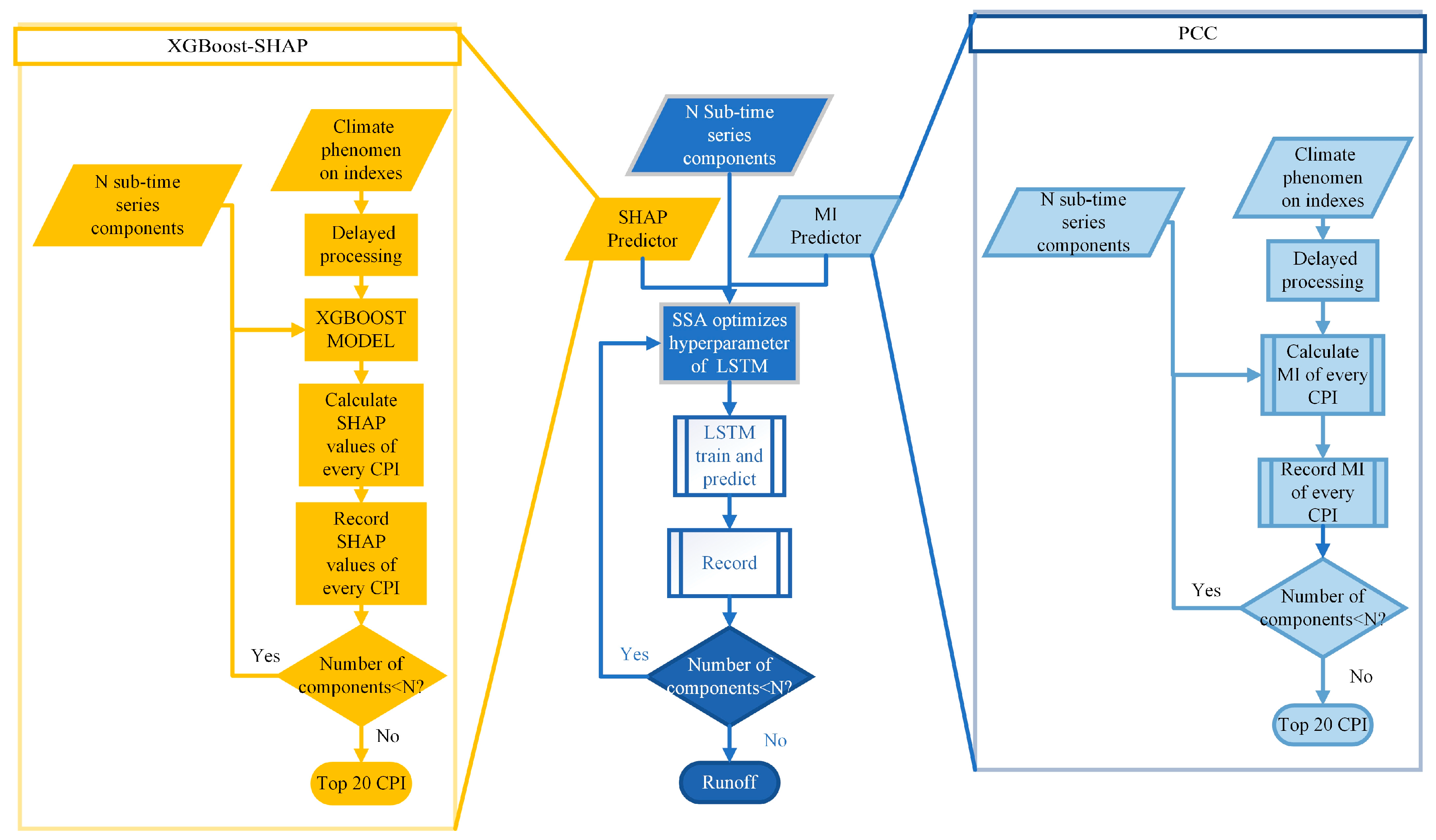
3.2. Selection of Predictors
3.3. Model Setup and Method of Model Performance Evaluation
4. Results
4.1. The Runoff Components Decomposed by MODWT
4.2. Performance of the SSA-MODWT-LSTM Model
4.2.1. Evaluation of SSA and MODWT
4.2.2. Comparison of the Performance Between SHAP and MI
4.2.3. Model Performance at Different Leading Time
4.3. Predictor Identified by XGBoost-SHAP Model in Data Limited Area
5. Discussion
5.1. Performance of the SHAP-SSA-MODWT-LSTM Model
5.2. Interpretation of the Predictor Identified by XGBoost-SHAP Model
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, W.; Chen, Y.; Fang, G.; Kaldybayev, A. Machine Learning Method Is an Alternative for the Hydrological Model in an Alpine Catchment in the Tianshan Region, Central Asia. J. Hydrol. Reg. Stud. 2023, 49, 101492. [Google Scholar] [CrossRef]
- Chen, S.; Ren, M.; Sun, W. Combining Two-Stage Decomposition Based Machine Learning Methods for Annual Runoff Forecasting. J. Hydrol. 2021, 603, 126945. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Santisirisomboon, J.; Lu, W.; Zhao, B. A Physical Process and Machine Learning Combined Hydrological Model for Daily Streamflow Simulations of Large Watersheds with Limited Observation Data. J. Hydrol. 2020, 590, 125206. [Google Scholar] [CrossRef]
- Jougla, R.; Leconte, R. Short-Term Hydrological Forecast Using Artificial Neural Network Models with Different Combinations and Spatial Representations of Hydrometeorological Inputs. Water 2022, 14, 552. [Google Scholar] [CrossRef]
- Wang, L.; Li, X.; Ma, C.; Bai, Y. Improving the Prediction Accuracy of Monthly Streamflow Using a Data-Driven Model Based on a Double-Processing Strategy. J. Hydrol. 2019, 573, 733–745. [Google Scholar] [CrossRef]
- Tegegne, G.; Park, D.K.; Kim, Y.O. Comparison of Hydrological Models for the Assessment of Water Resources in a Data-Scarce Region, the Upper Blue Nile River Basin. J. Hydrol. Reg. Stud. 2017, 14, 49–66. [Google Scholar] [CrossRef]
- Scaling Point-Scale (Pedo)Transfer Functions to Seamless Large-Domain Parameter Estimates for High-Resolution Distributed Hydrologic Modeling: An Example for the Rhine River-Imhoff-2020-Water Resources Research-Wiley Online Library. Available online: https://agupubs.onlinelibrary.wiley.com/doi/10.1029/2019WR026807 (accessed on 15 April 2025).
- Li, K.; Wang, Y.; Li, X.; Yuan, Z.; Xu, J. Simulation Effect Evaluation of Single-Outlet and Multi-Outlet Calibration of Soil and Water Assessment Tool Model Driven by Climate Forecast System Reanalysis Data and Ground-Based Meteorological Station Data—A Case Study in a Yellow River Source. Water Supply 2020, 21, 1061–1071. [Google Scholar] [CrossRef]
- Gu, P.; Wang, G.; Liu, G.; Wu, Y.; Liu, H.; Jiang, X.; Liu, T. Evaluation of Multisource Precipitation Input for Hydrological Modeling in an Alpine Basin: A Case Study from the Yellow River Source Region (China). Hydrol. Res. 2022, 53, 314–335. [Google Scholar] [CrossRef]
- Li, C.; Cai, Y.; Li, Z.; Zhang, Q.; Sun, L.; Li, X.; Zhou, P. Hydrological Response to Climate and Land Use Changes in the Dry–Warm Valley of the Upper Yangtze River. Engineering 2022, 19, 24–39. [Google Scholar] [CrossRef]
- Barbetta, S.; Sahoo, B.; Bonaccorsi, B.; Nanda, T.; Chatterjee, C.; Moramarco, T.; Todini, E. Addressing Effective Real-Time Forecasting Inflows to Dams through Predictive Uncertainty Estimate. J. Hydrol. 2023, 620, 129512. [Google Scholar] [CrossRef]
- Xi, Y.; Peng, S.; Ducharne, A.; Ciais, P.; Gumbricht, T.; Jimenez, C.; Poulter, B.; Prigent, C.; Qiu, C.; Saunois, M.; et al. Gridded Maps of Wetlands Dynamics over Mid-Low Latitudes for 1980–2020 Based on TOPMODEL. Sci. Data 2022, 9, 347. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 978-1-118-67492-5. [Google Scholar]
- Kwon, H.-H.; Brown, C.; Xu, K.; Lall, U. Seasonal and Annual Maximum Streamflow Forecasting Using Climate Information: Application to the Three Gorges Dam in the Yangtze River Basin, China. Hydrol. Sci. J. 2009, 54, 582–595. [Google Scholar] [CrossRef]
- Panahi, F.; Ehteram, M.; Ahmed, A.N.; Huang, Y.F.; Mosavi, A.; El-Shafie, A. Streamflow Prediction with Large Climate Indices Using Several Hybrid Multilayer Perceptrons and Copula Bayesian Model Averaging. Ecol. Indic. 2021, 133, 108285. [Google Scholar] [CrossRef]
- Aghaabbasi, M.; Chalermpong, S. Machine Learning Techniques for Evaluating the Nonlinear Link between Built-Environment Characteristics and Travel Behaviors: A Systematic Review. Travel Behav. Soc. 2023, 33, 100640. [Google Scholar] [CrossRef]
- Wang, S.; Peng, H.; Hu, Q.; Jiang, M. Analysis of Runoff Generation Driving Factors Based on Hydrological Model and Interpretable Machine Learning Method. J. Hydrol. Reg. Stud. 2022, 42, 101139. [Google Scholar] [CrossRef]
- Zhao, X.; Lv, H.; Lv, S.; Sang, Y.; Wei, Y.; Zhu, X. Enhancing Robustness of Monthly Streamflow Forecasting Model Using Gated Recurrent Unit Based on Improved Grey Wolf Optimizer. J. Hydrol. 2021, 601, 126607. [Google Scholar] [CrossRef]
- Xu, D.; Liao, A.; Wang, W.; Tian, W.; Zang, H. Improved Monthly Runoff Time Series Prediction Using the CABES-LSTM Mixture Model Based on CEEMDAN-VMD Decomposition. J. Hydroinform. 2023, 26, 255–283. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, R.; Wang, W.; Zheng, Q.; Ma, R.; Tang, R.; Wang, Y. Runoff Prediction Using Combined Machine Learning Models and Signal Decomposition. J. Water Clim. Change 2024, 16, 230–247. [Google Scholar] [CrossRef]
- Cai, X.; Li, D. M-EDEM: A MNN-Based Empirical Decomposition Ensemble Method for Improved Time Series Forecasting. Knowl.-Based Syst. 2024, 283, 111157. [Google Scholar] [CrossRef]
- Ji, Y.; Dong, H.-T.; Xing, Z.-X.; Sun, M.-X.; Fu, Q.; Liu, D. Application of the Decomposition-Prediction-Reconstruction Framework to Medium- and Long-Term Runoff Forecasting. Water Supply 2020, 21, 696–709. [Google Scholar] [CrossRef]
- Wrzesiński, D.; Sobkowiak, L.; Mares, I.; Dobrica, V.; Mares, C. Variability of River Runoff in Poland and Its Connection to Solar Variability. Atmosphere 2023, 14, 1184. [Google Scholar] [CrossRef]
- Russell, G.L.; Miller, J.R. Global River Runoff Calculated from a Global Atmospheric General Circulation Model. J. Hydrol. 1990, 117, 241–254. [Google Scholar] [CrossRef]
- Nguyen, T.-T.-H.; Li, M.-H.; Vu, T.M.; Chen, P.-Y. Multiple Drought Indices and Their Teleconnections with ENSO in Various Spatiotemporal Scales over the Mekong River Basin. Sci. Total Environ. 2023, 854, 158589. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Kahya, E.; Ghorbani, M.A. Spatial and Temporal Linkages between Large-Scale Atmospheric Oscillations and Hydrologic Drought Indices in Turkey. In Integrated Drought Management, Volume 2; CRC Press: Boca Raton, FL, USA, 2023; ISBN 978-1-003-27654-8. [Google Scholar]
- Chiew, F.H.S.; Piechota, T.C.; Dracup, J.A.; McMahon, T.A. El Nino/Southern Oscillation and Australian Rainfall, Streamflow and Drought: Links and Potential for Forecasting. J. Hydrol. 1998, 204, 138–149. [Google Scholar] [CrossRef]
- Yongchao, L.; Yongjian, D.; Ersi, K.; Jishi, Z. The Relationship between ENSO Cycle and Temperature, Precipitation and Runoff in the Qilian Mountain Area. J. Geogr. Sci. 2003, 13, 293–298. [Google Scholar] [CrossRef]
- Hernandez, D.; Mendoza, P.A.; Boisier, J.P.; Ricchetti, F. Hydrologic Sensitivities and ENSO Variability Across Hydrological Regimes in Central Chile (28°–41° S). Water Resour. Res. 2022, 58, e2021WR031860. [Google Scholar] [CrossRef]
- Zhou, Y.; Mu, Z.; Peng, L.; Gao, R.; Yin, Z.; Tang, R. Mid-Term and Long-Term Hydrological Forecasting of Snowmelt Runoff in Western Tianshan Mountains Based on Mutual Information and Neural Network. J. Chang. River Sci. Res. Inst. 2018, 35, 17–21. [Google Scholar] [CrossRef]
- Liao, S.; Liu, Z.; Liu, B.; Cheng, C.; Jin, X.; Zhao, Z. Multistep-Ahead Daily Inflow Forecasting Using the ERA-Interim Reanalysis Data Set Based on Gradient-Boosting Regression Trees. Hydrol. Earth Syst. Sci. 2020, 24, 2343–2363. [Google Scholar] [CrossRef]
- BfG-GRDC Data Download. Available online: https://www.bafg.de/GRDC/EN/02_srvcs/21_tmsrs/210_prtl/prtl_node.html (accessed on 6 November 2023).
- Yang, Y.; Li, W.; Liu, D. Monthly Runoff Prediction for Xijiang River via Gated Recurrent Unit, Discrete Wavelet Transform, and Variational Modal Decomposition. Water 2024, 16, 1552. [Google Scholar] [CrossRef]
- Jamei, M.; Ali, M.; Malik, A.; Karbasi, M.; Rai, P.; Yaseen, Z.M. Development of a TVF-EMD-Based Multi-Decomposition Technique Integrated with Encoder-Decoder-Bidirectional-LSTM for Monthly Rainfall Forecasting. J. Hydrol. 2023, 617, 129105. [Google Scholar] [CrossRef]
- Wang, W.; Du, Y.; Chau, K.; Xu, D.; Liu, C.; Ma, Q. An Ensemble Hybrid Forecasting Model for Annual Runoff Based on Sample Entropy, Secondary Decomposition, and Long Short-Term Memory Neural Network. Water Resour Manag. 2021, 35, 4695–4726. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly Streamflow Prediction Using Modified EMD-Based Support Vector Machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Difi, S.; Heddam, S.; Zerouali, B.; Kim, S.; Elmeddahi, Y.; Bailek, N.; Augusto Guimarães Santos, C.; Abida, H. Improved Daily Streamflow Forecasting for Semi-Arid Environments Using Hybrid Machine Learning and Multi-Scale Analysis Techniques. J. Hydroinform. 2024, 26, 3266–3286. [Google Scholar] [CrossRef]
- Frank, M.J., Jr. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar]
- Patnaik, B.; Mishra, M.; Bansal, R.C.; Jena, R.K. MODWT-XGBoost Based Smart Energy Solution for Fault Detection and Classification in a Smart Microgrid. Appl. Energy 2021, 285, 116457. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.; Beaufays, F. Long Short-Term Memory Based Recurrent Neural Network Architectures for Large Vocabulary Speech Recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- The Shapley Value: Essays in Honor of Lloyd S., Shapley; Roth, A.E., Ed.; Cambridge University Press: Cambridge, UK, 1988; ISBN 978-0-521-36177-4. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall/CRC: New York, NY, USA, 2017; ISBN 978-1-315-13947-0. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, Y. Relationships between North Africa Subtropical High and Summer Precipitation over Central Asia. Air Land Geogr. 2022, 45, 1050–1060. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning Forecasting Methods: Concerns and Ways Forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current Status and Future Directions. Int. J. Forecast. 2021, 37, 388–427. [Google Scholar] [CrossRef]
- Yang, H.; Xu, G.; Mao, H.; Wang, Y. Spatiotemporal Variation in Precipitation and Water Vapor Transport Over Central Asia in Winter and Summer Under Global Warming. Front. Earth Sci. 2020, 8, 297. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y.; Shen, Y.; Li, B. Tracking Climate Change in Central Asia through Temperature and Precipitation Extremes. J. Geogr. Sci. 2019, 29, 3–28. [Google Scholar] [CrossRef]
- Wei, W.; Zou, S.; Duan, W.; Chen, Y.; Li, S.; Zhou, Y. Spatiotemporal Variability in Extreme Precipitation and Associated Large-Scale Climate Mechanisms in Central Asia from 1950 to 2019. J. Hydrol. 2023, 620, 129417. [Google Scholar] [CrossRef]
- Huang, W.; Feng, S.; Chen, J.; Chen, F. Physical Mechanisms of Summer Precipitation Variations in the Tarim Basin in Northwestern China. J. Clim. 2015, 28, 3579–3591. [Google Scholar] [CrossRef]
- Botsyun, S.; Mutz, S.G.; Ehlers, T.A.; Koptev, A.; Wang, X.; Schmidt, B.; Appel, E.; Scherer, D.E. Influence of Large-Scale Atmospheric Dynamics on Precipitation Seasonality of the Tibetan Plateau and Central Asia in Cold and Warm Climates During the Late Cenozoic. JGR Atmos. 2022, 127, e2021JD035810. [Google Scholar] [CrossRef]









| Model Setting | Model with MODWT | Model Without MODWT |
|---|---|---|
| MODWT with SSA | SHAP-SSA-MODWT-LSTM | SHAP-SSA-LSTM |
| MI-SSA-MODWT-LSTM | MI-SSA-LSTM | |
| MODWT without SSA | SHAP-MODWT-LSTM | SHAP-LSTM |
| MI-MODWT-LSTM | MI-LSTM |
| IMFs | Period | Mean | Max | Min | Skewn | Stdev | Var | Entropy |
|---|---|---|---|---|---|---|---|---|
| IMF1 | Train Period | 0.00 | 2437.59 | −2579.58 | 0.01 | 558.26 | 311,658.00 | 2.38 |
| IMF1 | Test Period | 0.00 | 1621.74 | −1450.39 | 0.27 | 490.20 | 240,297.30 | 2.81 |
| IMF2 | Train Period | 0.00 | 2582.46 | −3579.18 | −0.61 | 957.03 | 915,909.50 | 2.83 |
| IMF2 | Test Period | 0.00 | 2014.88 | −3112.34 | −0.62 | 979.14 | 958,724.40 | 3.00 |
| IMF3 | Train Period | 0.00 | 2729.02 | −3023.41 | −0.15 | 1263.89 | 1,597,407.00 | 3.22 |
| IMF3 | Test Period | 0.00 | 2700.79 | −3197.62 | −0.25 | 1240.70 | 1,539,334.00 | 3.12 |
| IMF4 | Train Period | 0.00 | 994.08 | −1071.44 | −0.37 | 408.83 | 167,144.70 | 3.12 |
| IMF4 | Test Period | 0.00 | 745.83 | −1425.88 | −0.70 | 444.49 | 197,569.10 | 3.11 |
| IMF5 | Train Period | 0.00 | 549.76 | −671.03 | −0.19 | 242.26 | 58,689.93 | 3.15 |
| IMF5 | Test Period | 0.00 | 505.60 | −706.62 | −0.54 | 257.94 | 66,534.04 | 3.14 |
| IMF6 | Train Period | 2033.11 | 3082.00 | 1249.65 | 0.32 | 410.58 | 168,575.20 | 3.23 |
| IMF6 | Test Period | 2253.28 | 2869.28 | 1645.44 | −0.10 | 305.10 | 93,085.53 | 3.15 |
| Stations | Models | NSE | R | Bias (%) | MARE (%) |
|---|---|---|---|---|---|
| Omsk | SHAP-SSA-MODWT-LSTM | 0.851 | 0.927 | −0.640 | 14.743 |
| SHAP-MODWT-LSTM | 0.708 | 0.852 | −1.576 | 21.173 | |
| SHAP-SSA-LSTM | 0.725 | 0.861 | −2.086 | 18.429 | |
| SHAP-LSTM | 0.682 | 0.823 | −2.301 | 23.361 | |
| MI-SSA-MODWT-LSTM | 0.793 | 0.907 | −2.074 | 18.034 | |
| MI-MODWT-LSTM | 0.761 | 0.881 | −1.789 | 20.121 | |
| MI-SSA-LSTM | 0.738 | 0.870 | 3.094 | 15.410 | |
| MI-LSTM | 0.703 | 0.812 | −3.938 | 19.549 | |
| Tobolsk | SHAP-SSA-MODWT-LSTM | 0.941 | 0.971 | −1.732 | 16.977 |
| SHAP-MODWT-LSTM | 0.794 | 0.906 | −2.870 | 28.510 | |
| SHAP-SSA-LSTM | 0.757 | 0.884 | −7.325 | 22.310 | |
| SHAP-LSTM | 0.702 | 0.811 | −9.276 | 26.375 | |
| MI-SSA-MODWT-LSTM | 0.813 | 0.916 | −12.760 | 25.306 | |
| MI-MODWT-LSTM | 0.787 | 0.907 | −13.697 | 25.532 | |
| MI-SSA-LSTM | 0.797 | 0.897 | −14.302 | 16.818 | |
| MI-LSTM | 0.721 | 0.883 | −17.203 | 18.212 |
| Stations | Models | NSE | R | Bias (%) | MARE (%) |
|---|---|---|---|---|---|
| Omsk | MI-SSA-MODWT-LSTM | 0.600 | 0.742 | −2.353 | 7.627 |
| SHAP-SSA-MODWT-LSTM | 0.664 | 0.847 | −2.276 | 5.569 | |
| SSA-MODWT-LSTM | 0.374 | 0.706 | −2.998 | 7.752 | |
| Tobolsk | MI-SSA-MODWT-LSTM | 0.623 | 0.725 | −4.453 | 18.473 |
| SHAP-SSA-MODWT-LSTM | 0.846 | 0.946 | −0.847 | 10.015 | |
| SSA-MODWT-LSTM | 0.457 | 0.647 | −7.936 | 17.465 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yong, K.; Li, M.; Xiao, P.; Gao, B.; Zheng, C. Monthly Streamflow Forecasting for the Irtysh River Based on a Deep Learning Model Combined with Runoff Decomposition. Water 2025, 17, 1375. https://doi.org/10.3390/w17091375
Yong K, Li M, Xiao P, Gao B, Zheng C. Monthly Streamflow Forecasting for the Irtysh River Based on a Deep Learning Model Combined with Runoff Decomposition. Water. 2025; 17(9):1375. https://doi.org/10.3390/w17091375
Chicago/Turabian StyleYong, Kaiqiang, Mingliang Li, Peng Xiao, Bing Gao, and Chengxin Zheng. 2025. "Monthly Streamflow Forecasting for the Irtysh River Based on a Deep Learning Model Combined with Runoff Decomposition" Water 17, no. 9: 1375. https://doi.org/10.3390/w17091375
APA StyleYong, K., Li, M., Xiao, P., Gao, B., & Zheng, C. (2025). Monthly Streamflow Forecasting for the Irtysh River Based on a Deep Learning Model Combined with Runoff Decomposition. Water, 17(9), 1375. https://doi.org/10.3390/w17091375








