Comparing SWMM and HEC-RAS Hydrological Modeling Performance in Semi-Urbanized Watershed
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Work
2.2. SWMM Implementation
- The first of these modeling parameters was overland flow path length. When using WDT, PCSWMM automatically calculates flow width using the method by [46] and flow length by dividing the area by the flow width. This value is dependent on the subcatchment size and can vary broadly. It was decided to compare scenarios with the automatically calculated flow length to those with a manually designated maximum length of 150 m (500 ft) [47] to see if this adjustment was necessary for accurate results.
- The second modeling parameter was the representation of storage basins within the subcatchments. SWMM applications for urban watersheds consider storage basins in terms of artificial detention and retention ponds where geometry is known. This sub-watershed, in addition to detention ponds for Tiger Town, features several surface ponds of unknown depth and varying dimensions as part of the MMC stream network. This study compared models where these basins were and were not included as storage objects in the model. These basins utilized a simplified geometry, assuming a constant area with depth due to a lack of bathymetric data.
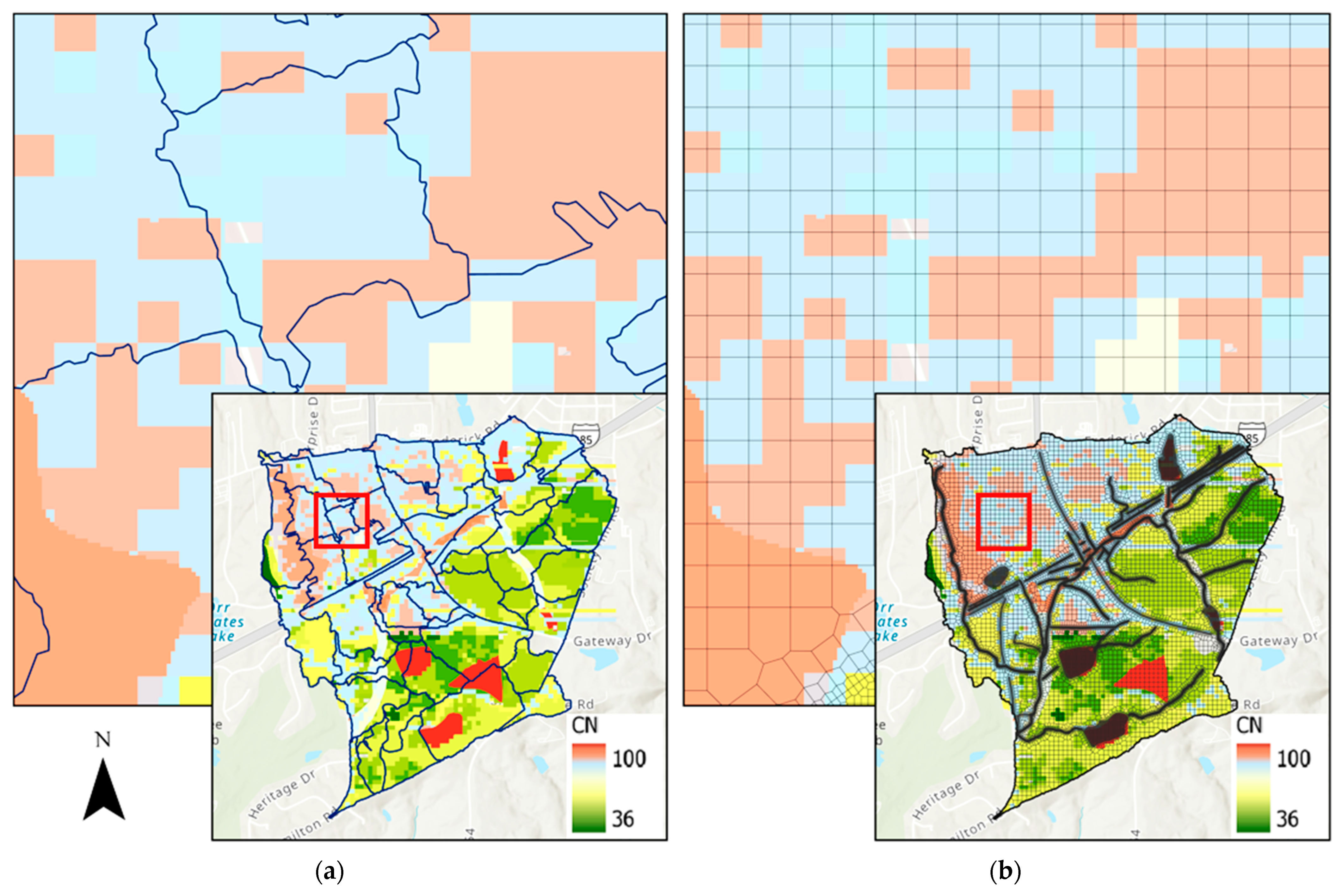
- The third modeling parameter was linked to the target discretization size of subcatchments in the SWMM simulation. Models such as HEC-RAS utilize a two-dimensional rain-on-grid approach for calculating runoff and overland flows. Initial comparisons of SWMM and HEC-RAS results for this watershed showed that HEC-RAS models had better representation of hydrograph drawdown. This was initially theorized to be due to the higher level of discretization possible with HEC-RAS. Two sizes of subcatchment discretization area were tested for this study to see the effects of increasing subcatchment density: 10 ha and 5 ha.
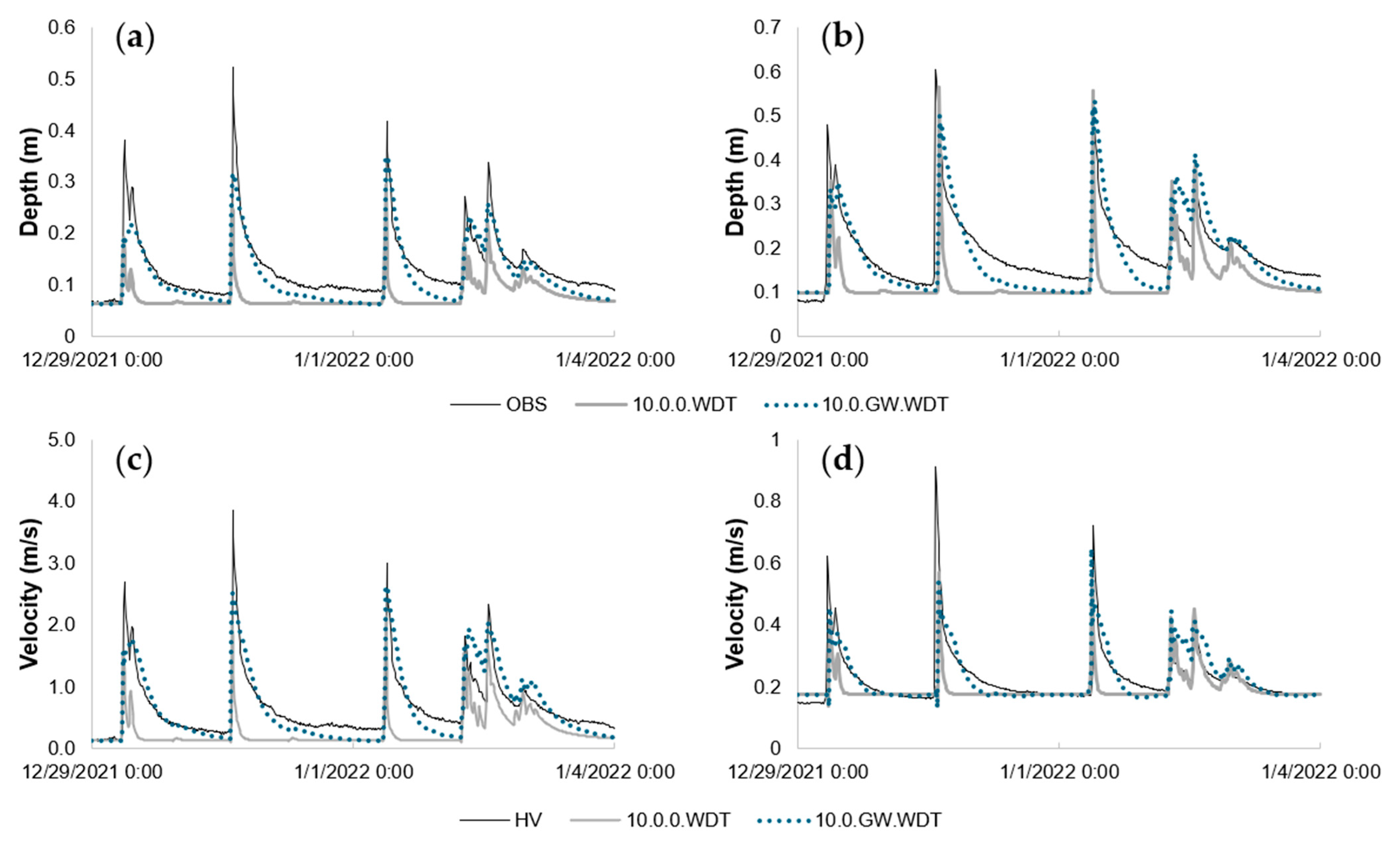
- The fourth and last modeling parameter for SWMM was the inclusion of aquifer components and groundwater–surface water interactions. It was previously observed [48] that accounting for groundwater did improve the overall accuracy of hydrograph drawdown curves compared to earlier results from [35] which neglected groundwater and that a single aquifer approach was valid for this scenario. This sensitivity analysis included groundwater as a parameter to investigate how it interacts with other physical characteristics of the watershed model. The representation of groundwater interflow is governed by Equation (1) [8]:
2.3. HEC-RAS Implementation
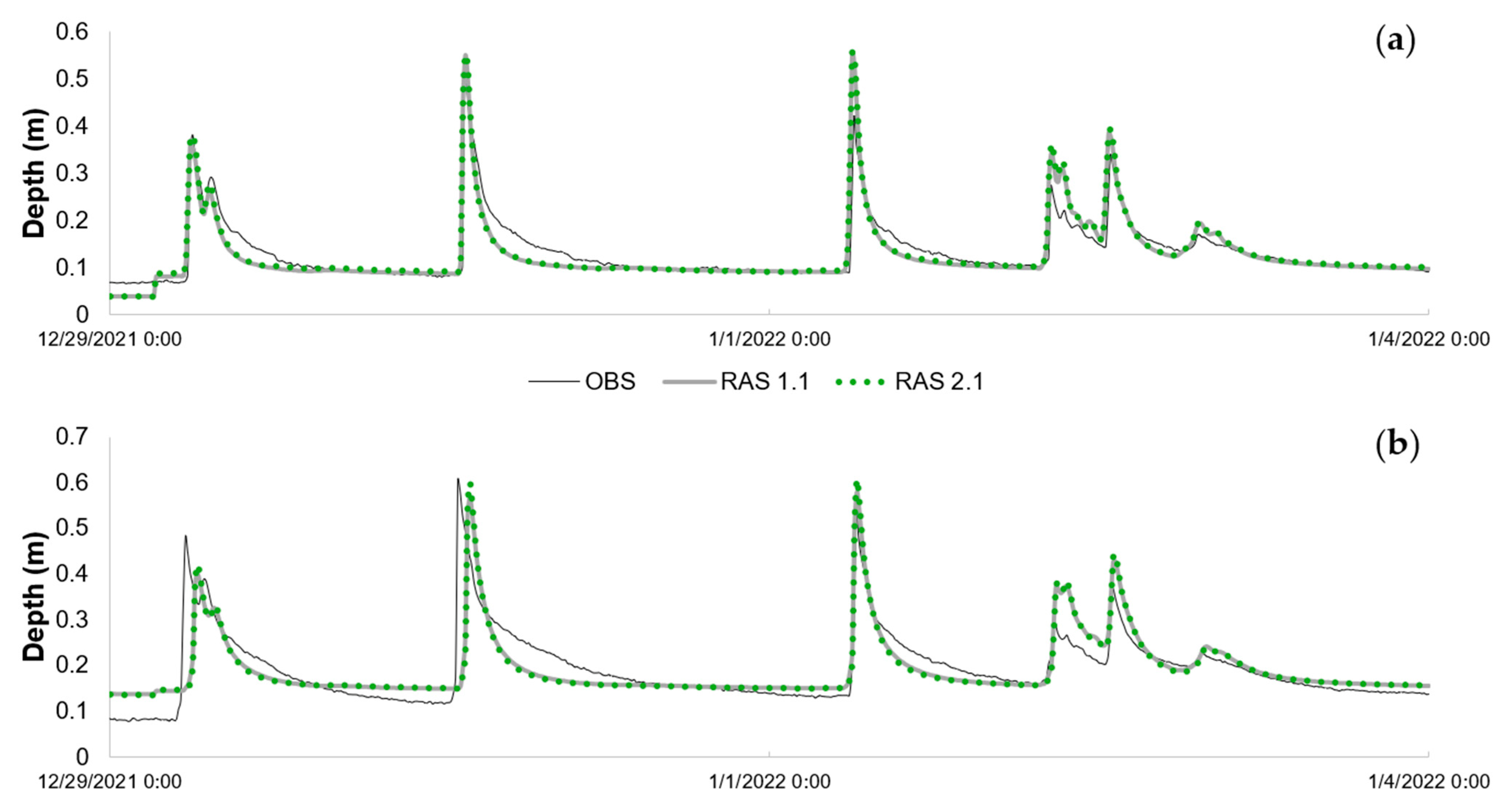
- The first was the effect of the average grid cell size for the overland flows, which was either 30 m or 60 m. These do not correspond to the cells that were refined to represent the stream channels, culverts, and other conveyance.
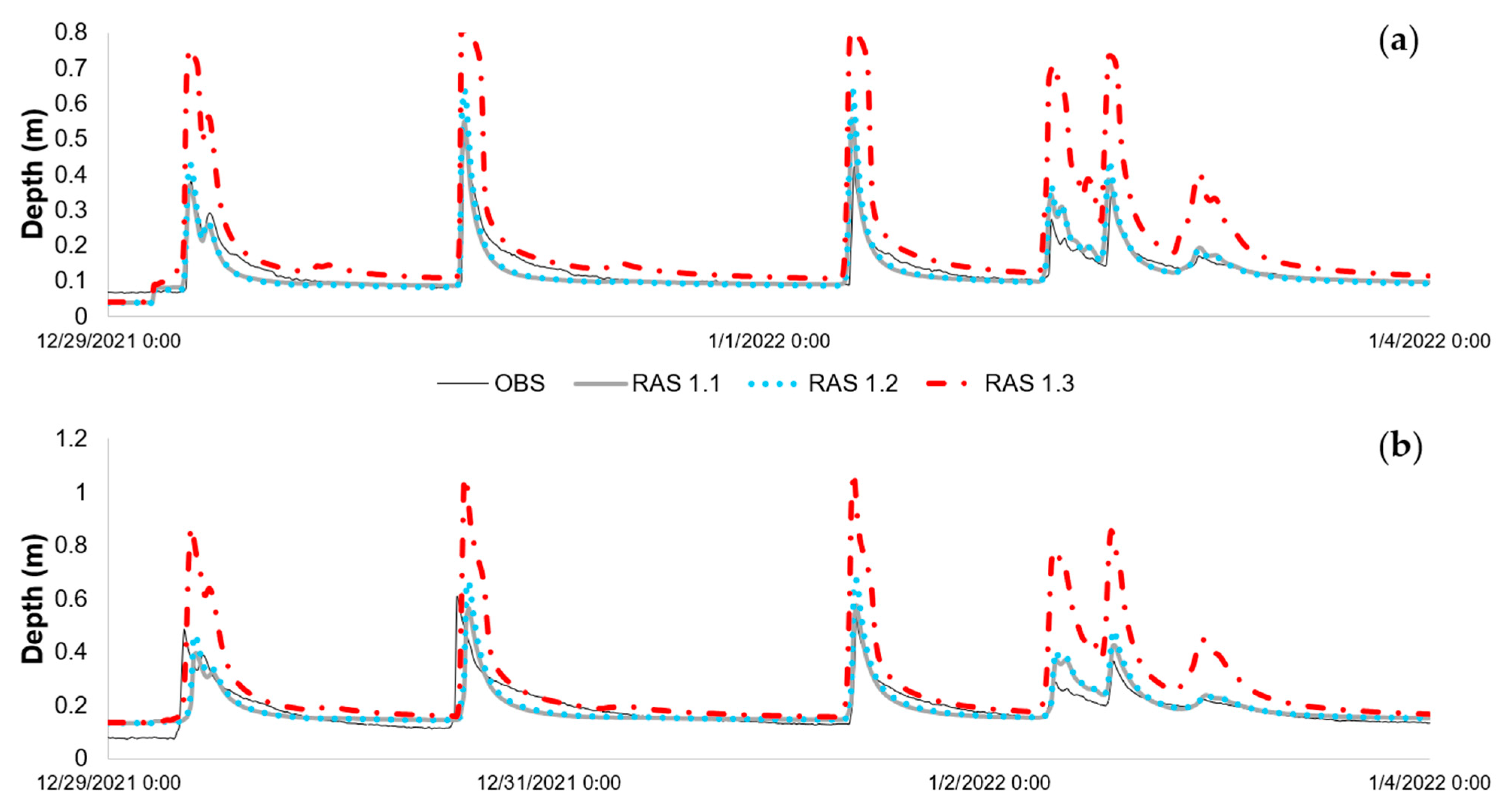
- The second was the effect of infiltration, with three conditions considered: (1) disabling infiltration, (2) normal antecedent moisture conditions (i.e., AMC CNII), and (3) wet antecedent moisture conditions (AMC CNIII), as shown in Table 5. For the wet soil condition scenario (AMC III), CN III was derived from CN II (Average Runoff Potential, AMC II) using Table 4.2 from [54].
2.4. Analysis
- Larger default subcatchment delineation area of 10 ha;
- No explicit representation of intermittent storage objects (SUs);
- No groundwater or aquifer object (GW);
- Overland flow width calculated by the WDT.
- For HEC-RAS, the baseline scenario corresponded to the conditions in which calibration was developed, using a computational mesh size of 30 m × 30 m and an infiltration layer with the CN corresponding to AMC II.
3. Results
3.1. Subcatchment Overland Flow Length
3.2. Representation of Surface Storage
3.3. Spatial Discretization of Subcatchments
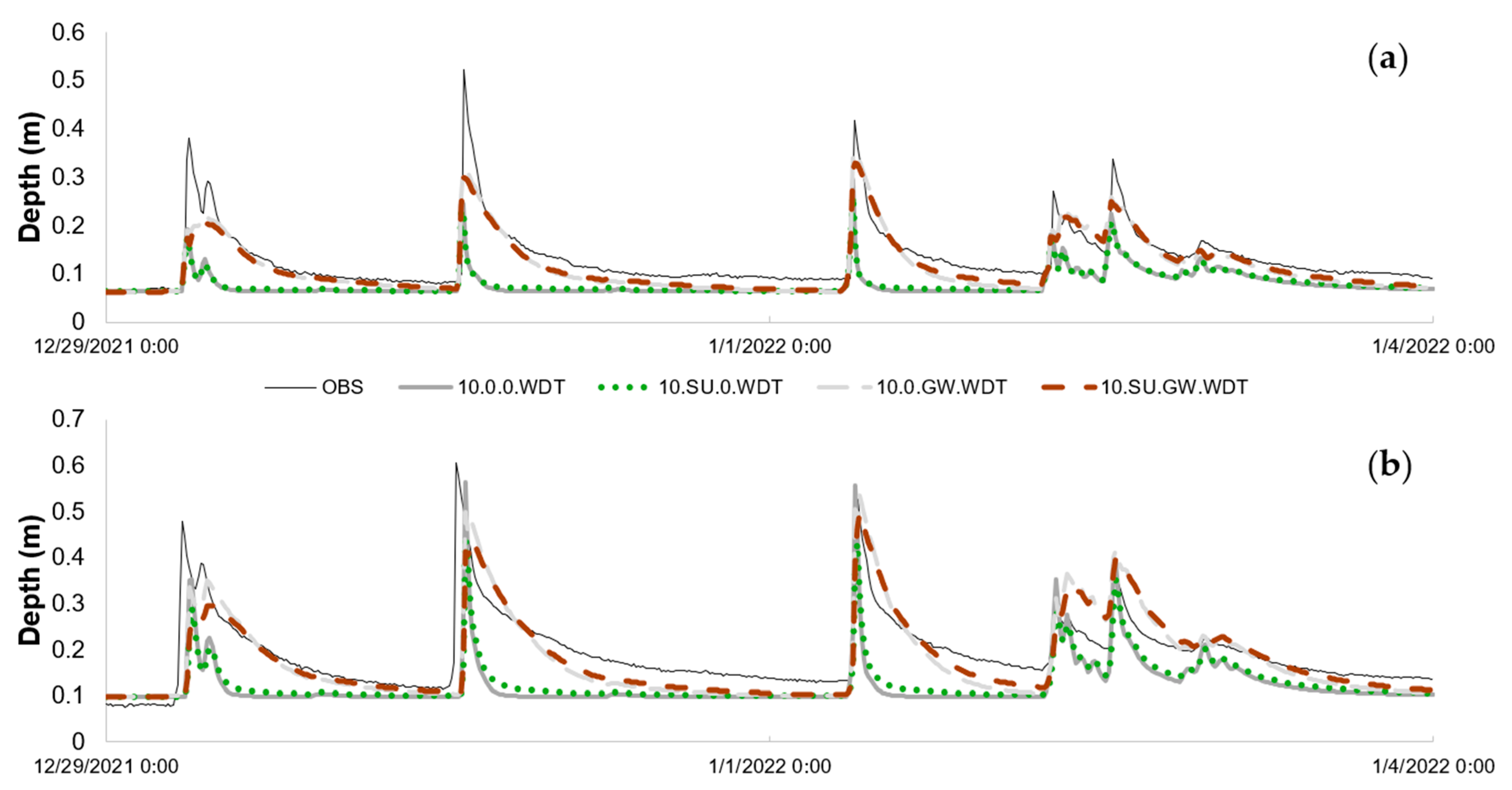
3.4. Aquifer and Groundwater
3.5. Comparison of HEC-RAS Scenarios
3.5.1. Infiltration
3.5.2. Spatial Discretization of Grid Cells
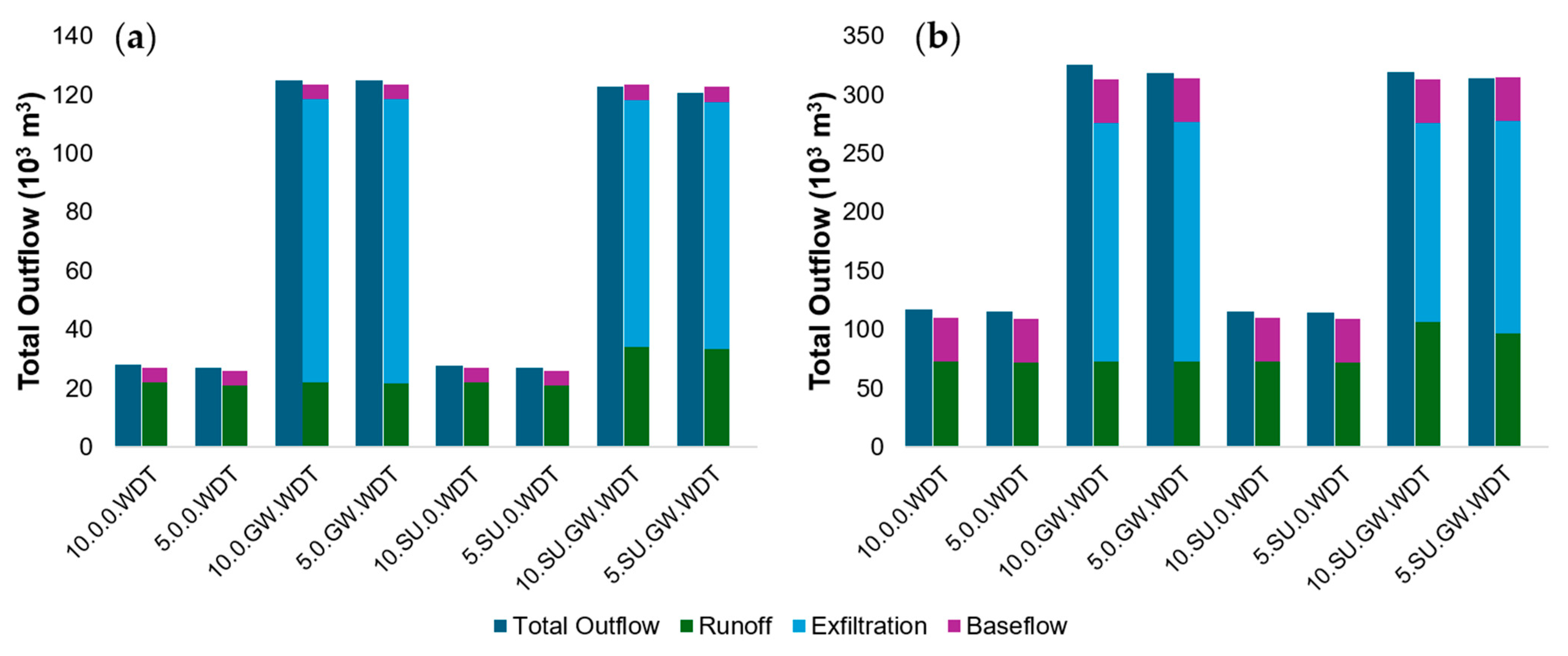
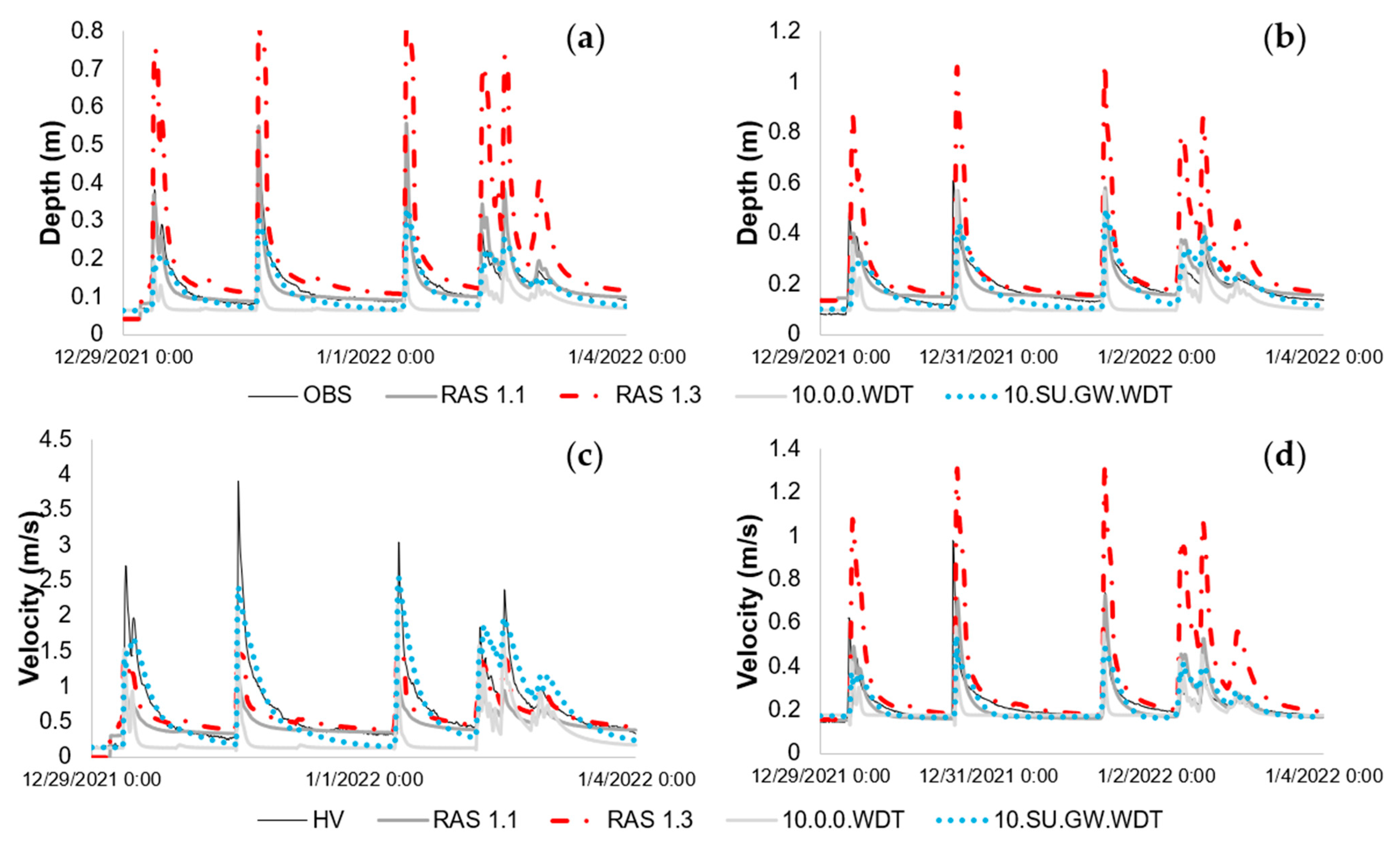
3.6. Comparison of Cumulative Junction Outflow
- The SWMM simulations that do not consider groundwater and aquifers, as well as RAS 1.1 and 1.2, will only consider infiltration for runoff calculations, after which it will no longer be considered.
- The HEC-RAS model that does not consider infiltration (i.e., RAS 1.3) will have most of the rainfall converted to surface runoff. The only abstraction will be depression storage, though there will be no infiltration. These models will generate the most runoff.
- The SWMM simulations that consider the aquifer component will also have an increased runoff, though not as large as RAS 1.3, as a portion of the infiltrated water will enter the subsurface compartment and exfiltrate back into surface junctions as the runoff recedes.
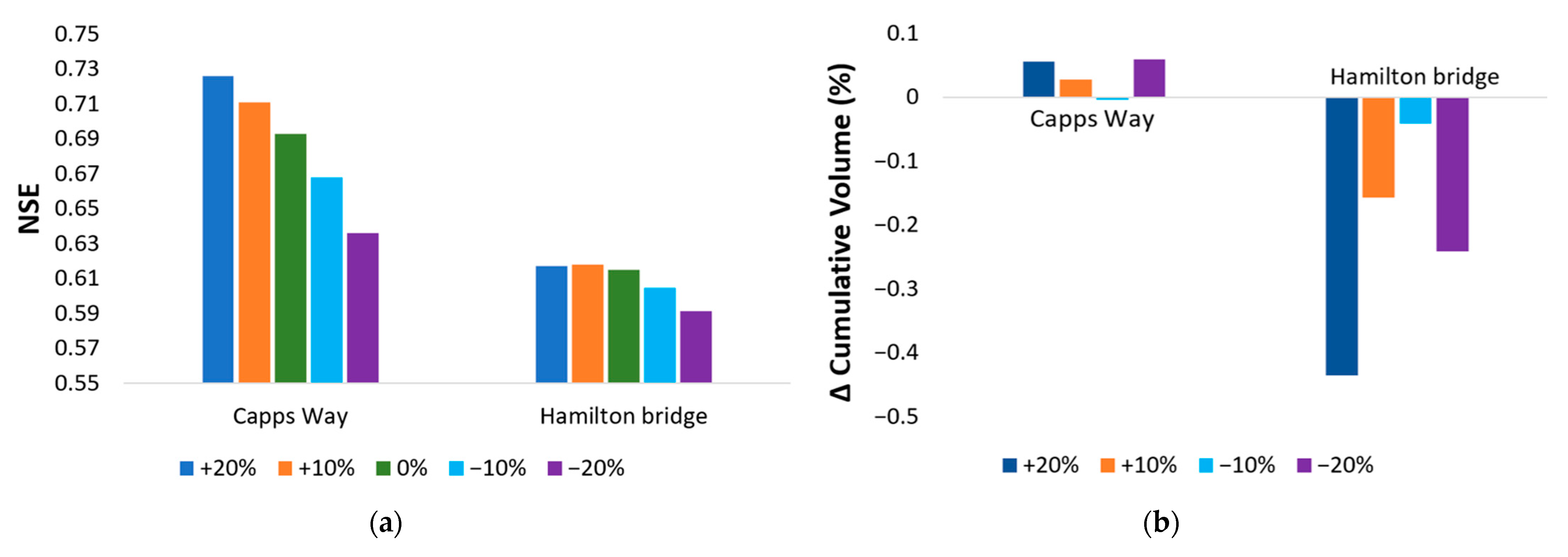
3.7. Sensitivity Analysis
4. Discussion and Research Limitations
4.1. Discussion
4.2. Limitations
5. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- USGS. Effects of Urban Development on Floods. Available online: https://pubs.usgs.gov/fs/fs07603/ (accessed on 10 February 2025).
- US EPA. Construction Site Runoff Control Minimum Control Measure. Available online: https://www.epa.gov/system/files/documents/2023-09/EPA-Stormwater-Phase-II-Final-Rule-Factsheet-2.6-Construction-Runoff.pdf (accessed on 10 February 2025).
- US EPA. Storm Water Management Model (SWMM). Available online: https://www.epa.gov/water-research/storm-water-management-model-swmm#capabilities (accessed on 10 February 2025).
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, M.M.B. An Overview of Rainfall-Runoff Model Types; National Exposure Research Laboratory Office of Research and Development U.S. Environmental Protection Agency: Athens, GA, USA, 2017; pp. 16–19. [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine. Resilient Design with Distributed Rainfall-Runoff Modeling; National Academies Press: Washington, DC, USA, 2023; pp. 8–17. [Google Scholar] [CrossRef]
- Rossman, L.A.; Simon, M.A. Appendix A: Useful Tables. In Storm Water Management Model User’s Manual Version 5.2; Center for Environmental Solutions and Emergency Response Office of Research and Development U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2022. [Google Scholar]
- Brunner, G.W. HEC-RAS 2D User’s Manual Version 6.4; Hydrologic Engineering Center U.S. Army Corps of Engineers: Davis, CA, USA, 2023. [Google Scholar]
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual; National Risk Management Laboratory Office of Research and Development U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2016; Volume 1—Hydrology (Revised). [Google Scholar]
- Niazi, M.; Nietch, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm Water Management Model: Performance Review and Gap Analysis. J. Sustain. Water Built Environ. 2017, 3, 04017002. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.; Cho, M.; Yoon, J.; Yoon, Y.; Kim, S.; Kim, G.; Kim, L.; Aksoy, H. Using SWMM as a tool for hydrologic impact assessment. Desalination 2007, 212, 344–356. [Google Scholar] [CrossRef]
- Jun, S.; Park, J.H.; Lee, W.; Park, C.; Lee, S.; Lee, K.S.; Jeong, G.C. The changes in potential usable water resources by increasing the amount of groundwater use: The case of Gapcheon watershed in Korea. Geosci. J. 2010, 14, 33–39. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. HEC Newsletter—Spring 2016: Advances in Hydrologic Engineering. Available online: https://www.hec.usace.army.mil/newsletters/HEC_Newsletter_Spring2016.pdf#:~:text=HEC,capability%20to%20handle%20large%20terrain (accessed on 24 March 2025).
- Bartles, M.; Brauer, T.; Ho, D.; Fleming, M.; Karlovits, G.; Pak, J.; Van, N.; Willis, J. Hydrological Modeling System HEC-HMS User’s Manual; Hydrologic Engineering Center Institute for Water Resources U.S. Army Corps of Engineers: Davis, CA, USA. Available online: https://www.hec.usace.army.mil/confluence/hmsdocs/hmsum/latest (accessed on 20 March 2025).
- James, W. Optimal Model Complexity. In Rules for Responsible Modeling, 4th ed.; Computational Hydraulics International: Guelph, ON, Canada, 2005; pp. 61–71. [Google Scholar]
- Warwick, J.J.; Tadepalli, T. Efficacy of SWMM Application. J. Water Resour. Plann. Manag. 1991, 117, 352–366. [Google Scholar] [CrossRef]
- Snikitha, S.; Kumar, G.P.; Dwarakish, G.S. A Comprehensive Review of Cutting-Edge Flood Modelling Approaches for Urban Flood Resilience Enhancement. Water Conserv. Sci. Eng. 2024, 10, 2. [Google Scholar] [CrossRef]
- Ghosh, I.; Hellweger, F.L. Effects of Spatial Resolution in Urban Hydrologic Simulations. J. Hydrol. Eng. 2011, 17, 129–137. [Google Scholar] [CrossRef]
- Zarriello, P.J.; Barlow, L.K. Measured and Simulated Runoff to the Lower Charles River, Massachusetts, October 1999–September 2000; U.S. Geological Survey: Northborough, MA, USA, 2002. [Google Scholar]
- Goldstein, A.; Foti, R.; Montalta, F. Effects of Spatial Resolution in Modeling Stormwater Runoff for an Urban Block. J. Hydrol. Eng. 2016, 21, 06016009. [Google Scholar] [CrossRef]
- Shaneyfelt, K.M.; Johnson, J.P.; Hunt, W.F. Hydrologic Modeling of Distributed Stormwater Control Measure Retrofit and Examination of Impact on Subcatchment Discretization in PCSWMM. J. Sustain. Water Built Environ. 2021, 7, 04021008. [Google Scholar] [CrossRef]
- Kim, B.; Sanders, B.F.; Schubert, J.E.; Famiglietti, J.S. Mesh type tradeoffs in 2D hydrodynamic modeling of flooding with a Godunov-based flow solver. Adv. Water. Resour. 2014, 68, 42–61. [Google Scholar] [CrossRef]
- David, A.; Schmalz, B. A Systematic Analysis of the Interaction between Rain-on-Grid-Simulations and Spatial Resolution in 2D Hydrodynamic Modeling. Water 2021, 13, 2346. [Google Scholar] [CrossRef]
- Godara, N.; Bruland, O.; Alfredsen, K. Comparison of two hydrodynamic models for their rain-on-grid technique to simulate flash floods in steep catchment. Front. Water 2024, 6, 1384205. [Google Scholar] [CrossRef]
- Ongdas, N.; Akiyanova, F.; Karakulov, Y.; Muratbayeva, A.; Zinabdin, N. Application of HEC-RAS (2D) for Flood Hazard Maps Gen-eration for Yesil (Ishim) River in Kazakhstan. Water 2020, 12, 2672. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Ferraro, D.; Macchione, F.; Petaccia, G. Performances of the New HEC-RAS Version 5 for 2-D Hydrodynamic-Based Rainfall-Runoff Simulations at Basin Scale: Comparison with a State-of-the Art Model. Water 2020, 12, 2326. [Google Scholar] [CrossRef]
- Wanniarachchi, S.S.; Wijesekera, N.T.S. Challenges in field approximations of regional scale hydrology. J. Hydrol. Reg. Stud. 2020, 27, 100647. [Google Scholar] [CrossRef]
- Ali, S.E. Assessing the Performance of 2D HEC-RAS Rain-on-Grid Model: A Case Study in the Rainbow Creek Subwatershed. Master’s Thesis, The University of Guelph, Guelph, ON, Canada, 2024. Available online: https://hdl.handle.net/10214/28047 (accessed on 20 March 2025).
- Ennouini, W.; Fenocchi, A.; Petaccia, G.; Persi, E.; Sibilla, S. A complete methodology to assess hydraulic risk in small ungauged catchments based on HEC-RAS 2D Rain-On-Grid simulations. Nat. Hazard. 2024, 120, 7381–7409. [Google Scholar] [CrossRef]
- James, W.R.C.; Finney, K.; James, W. Auto-Integrating Multiple HEC-RAS Flood-line Models into Catchment-wide SWMM Flood Forecasting Models. AWRA Hydrol. Watershed Manag. Tech. Comm. 2012, 7, 1–15. [Google Scholar]
- Khalaj, M.R.; Noor, H.; Dastranj, A. Investigation and simulation of flood inundation hazard in urban areas in Iran. Geoenviron. Disasters 2021, 8, 18. [Google Scholar] [CrossRef]
- Khatooni, K.; Hooshyaripor, F.; Malekmohammadi, B.; Noori, R. A new approach for urban flood risk assessment using coupled SWMM-HEC-RAS-2D model. J. Environ. Manage. 2025, 374, 123849. [Google Scholar] [CrossRef]
- Barszcz, M.; Bartosik, Z.; Rukść, S.; Batory, J. Comparison of maximum flows calculated in urban catchment using HEC-RAS and SWMM models. Sci. Rev. Eng. Environ. Stud. 2016, 25, 410–424. [Google Scholar]
- Sun, P.; Wang, S.; Gan, H.; Liu, B.; Jia, L. Application of HEC-RAS for flood forecasting in perched river—A case study of hilly region, China. IOP Conf. Ser. Earth Environ. Sci. 2017, 61, 012067. [Google Scholar] [CrossRef]
- Bagheri, K.; Requieron, W.; Tavakol, H. A Comparative Study of 2-Dimensional Hydraulic Modeling Software, Case Study: Sorrento Valley, San Diego, California. J. Water Manag. Model. 2020, 28, C471. [Google Scholar] [CrossRef]
- Xiao, H. Evaluating Alternatives for the implementation of Curve Number in SWMM for an urbanized watershed. Master’s Thesis, Auburn University, Auburn, AL, USA, 2022. [Google Scholar]
- Onset Computer Corporation. HOBO U20L Water Level Logger (U20L-0x) Manual; Onset Computer Corporation: Bourne, MA, USA, 2024. [Google Scholar]
- Onset Computer Corporation. HOBO Data Logging Rain Gauge (RG3 and RG3-M) Manual; Onset Computer Corporation: Bourne, MA, USA, 2018. [Google Scholar]
- Teledyne Isco. 2150 Area Velocity Flow Module and Sensor Installation and Operation Guide; Teledyne Instruments, Inc.: Lincoln, NE, USA, 2024. [Google Scholar]
- USDA. USDA Geospatial Data Gateway (GDG). Available online: https://datagateway.nrcs.usda.gov/ (accessed on 2 June 2023).
- USGS. StreamStats. Available online: https://streamstats.usgs.gov/ss/ (accessed on 7 June 2023).
- City of Auburn. City of Auburn (COA) Map. Available online: https://webgis.auburnalabama.org/coamap/ (accessed on 6 January 2025).
- Moore, M. Measuring and Modeling Stormwater Runoff from an Interstate in a Rural/Forested Watershed. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 2016. [Google Scholar]
- Siddiqui, A.R. Curve Number Generator: A QGIS Plugin to Generate Curve Number Layer from Land Use and Soil. 2020. Available online: https://github.com/ar-siddiqui/curve_number_generator (accessed on 2 June 2023).
- USGS. Annual National Land Cover Database. 2024. Available online: https://www.usgs.gov/centers/eros/science/annual-national-land-cover-database (accessed on 28 February 2025).
- USDA. Soil Survey Geographic Database (SSURGO). 2024. Available online: https://doi.org/10.15482/USDA.ADC/1242479 (accessed on 28 February 2025).
- Guo, J.C.; Urbonas, B. Conversion of Natural Watershed to Kinematic Wave Cascading Plane. J. Hydrol. Eng. 2009, 14, 839–846. [Google Scholar] [CrossRef]
- UDFCD. Chapter 5—Runoff. In Drainage Criteria Manual; Urban Drainage and Flood Control District: Dever, CO, USA, 2007. [Google Scholar]
- Bragg, M.; Vasconcelos, J. Evaluating the Effects of Groundwater on Runoff Modelling Using PCSWMM. J. Water Manag. Model. 2025; in review. [Google Scholar]
- USGS. Soil Properties Dataset in the United States. Available online: https://www.sciencebase.gov/catalog/item/5fd7c19cd34e30b9123cb51f (accessed on 9 June 2023).
- USDA. Web Soil Survey. Available online: https://websoilsurvey.nrcs.usda.gov/app/WebSoilSurvey.aspx (accessed on 9 June 2023).
- USGS. National Ground-Water Monitoring Network. Available online: https://cida.usgs.gov/ngwmn/index.jsp (accessed on 9 June 2023).
- NWS. Evaporation Climatology (mm). Available online: https://www.cpc.ncep.noaa.gov/products/Soilmst_Monitoring/US/Evap/Evap_clim.shtml (accessed on 13 February 2025).
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- USDA. Section 4: Hydrology. In SCS National Engineering Handbook; Soil Conservation Service, U.S. Department of Agriculture: Washington, DC, USA, 1972; p. 10.7. [Google Scholar]
- Saghafian, B.; Julien, P.Y. Introduction. In Resistance to Sheet Flow; Hydrological Modeling Group Center for Geosciences Colorado State University: Fort Collins, CO, USA, 1989; pp. 1–2. [Google Scholar]
- Kim, J.; Johnson, L.; Cifelli, R.; Thorstensen, A.; Chandrasekar, V. Assessment of antecedent moisture condition on flood frequency: An experimental study in Napa River Basin. CA J. Hydrol. Reg. Stud. 2019, 26, 100629. [Google Scholar] [CrossRef]
- Tu, M.C.; Wadzuk, B.; Traver, R. Methodology to simulate unsaturated zone hydrology in Storm Water Management Model (SWMM) for green infrastructure design and evaluation. PLoS ONE 2020, 15, e0235528. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. Water Quality. Available online: https://www.hec.usace.army.mil/software/waterquality/ (accessed on 27 March 2025).
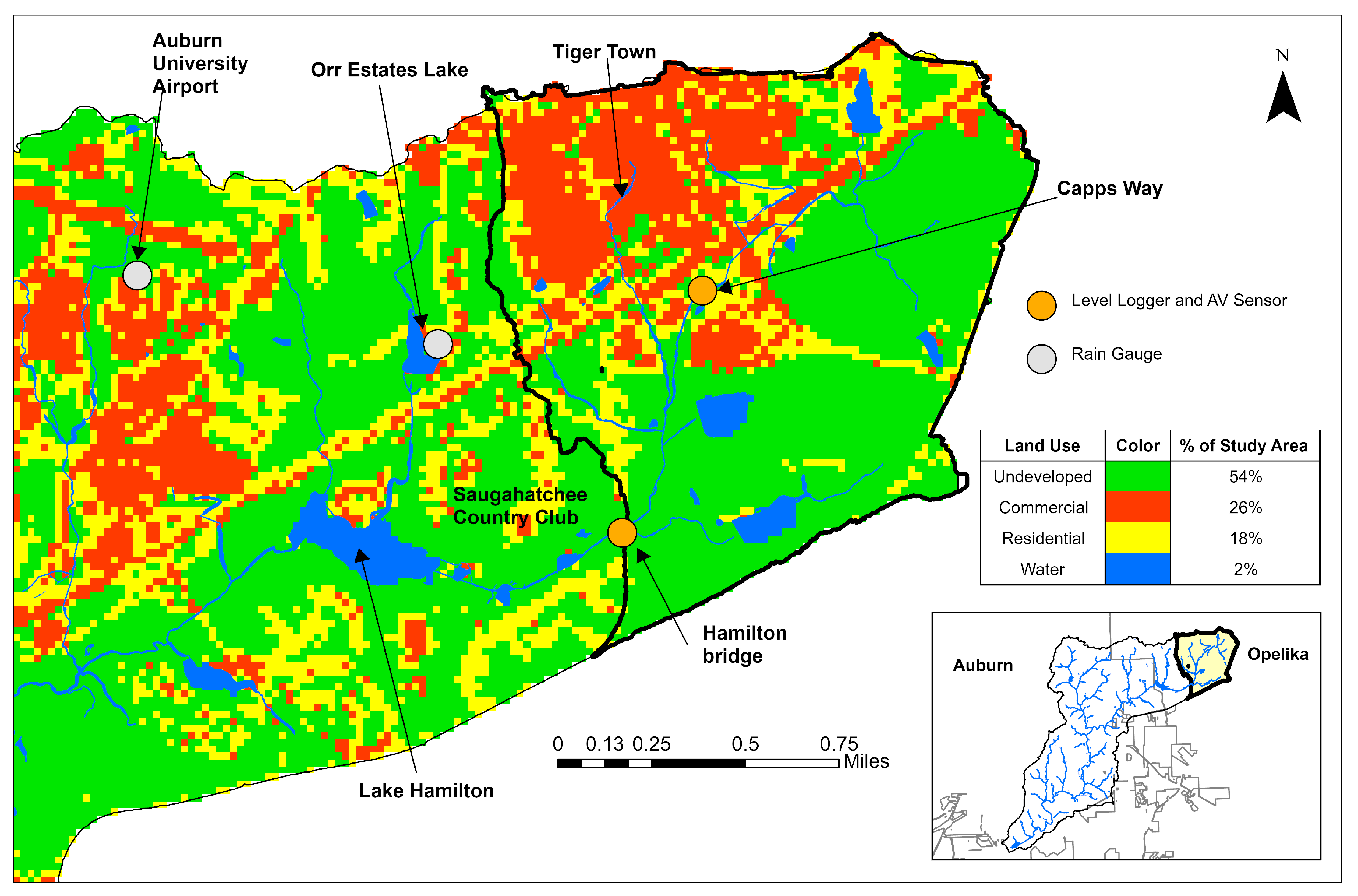







| Location | Data Collected |
|---|---|
| Capps Way | Stream depth, stream velocity |
| Hamilton bridge | Stream depth, stream velocity |
| Auburn University Airport | Rainfall |
| Orr Estates Lake | Rainfall |
| Surface | Manning’s Roughness (n) | Depression Storage (Dstor) | ||
|---|---|---|---|---|
| n | Range | Dstor | Range | |
| Overland pervious | 0.30 | 0.20–0.40 | 4 mm | 2.5–8.0 mm |
| Overland impervious | 0.011 | 0.010–0.019 | 2 mm | 1.0–2.5 mm |
| Natural channel | 0.30 | 0.20–0.40 | - | - |
| Culvert and sewer | 0.011 | 0.010–0.019 | - | - |
| Aquifer Component | Units | Value | Range |
|---|---|---|---|
| Porosity [49] | - | 0.473 | 0.396–0.487 |
| Wilting point [50] | - | 0.167 | 0.063–0.198 |
| Field capacity [50] | - | 0.253 | 0.160–0.280 |
| Conductivity [50] | mm/h | 56.4 | 33–236 |
| Conductivity slope [8] | - | 40.2 | 40–44 |
| Tension slope | - | 15 | - |
| Upper evaporation fraction | - | 0.4 | - |
| Lower evaporation depth | m | 2 | - |
| Lower groundwater loss rate [51] | mm/h | 0.014 | - |
| Initial unsaturated zone moisture content | - | 0.3 | - |
| Subcatchment Groundwater Components | Value | ||
| A1 | 0.368 | ||
| B1 | 0.976 | ||
| A2 | 0.862 | ||
| B2 | 3.22 | ||
| A3 | 0 | ||
| Scenario Name | Subcatchment Delineation Area | Storage (SU) | Groundwater (GW) | Flow Length |
|---|---|---|---|---|
| 10.0.0.WDT | 10 ha | Off | Off | WDT |
| 10.0.0.150 | 10 ha | Off | Off | Max 150 m |
| 10.0.GW.WDT | 10 ha | Off | On | WDT |
| 10.0.GW.150 | 10 ha | Off | On | Max 150 m |
| 10.SU.0.WDT | 10 ha | On | Off | WDT |
| 10.SU.0.150 | 10 ha | On | Off | Max 150 m |
| 10.SU.GW.WDT | 10 ha | On | On | WDT |
| 10.SU.GW.150 | 10 ha | On | On | Max 150 m |
| 5.0.0.WDT | 5 ha | Off | Off | WDT |
| 5.0.0.150 | 5 ha | Off | Off | Max 150 m |
| 5.0.GW.WDT | 5 ha | Off | On | WDT |
| 5.0.GW.150 | 5 ha | Off | On | Max 150 m |
| 5.SU.0.WDT | 5 ha | On | Off | WDT |
| 5.SU.0.150 | 5 ha | On | Off | Max 150 m |
| 5.SU.GW.WDT | 5 ha | On | On | WDT |
| 5.SU.GW.150 | 5 ha | On | On | Max 150 m |
| Scenario Name | Mesh Size | Infiltration Layer | Antecedent Moisture Condition |
|---|---|---|---|
| RAS 1.1 | 30 m | On | AMC II |
| RAS 1.2 | 30 m | On | AMC III |
| RAS 1.3 | 30 m | Off | - |
| RAS 2.1 | 60 m | On | AMC II |
| RAS 2.2 | 60 m | On | AMC III |
| RAS 2.3 | 60 m | Off | - |
| Scenario | NSE | R2 | RMSE | |||
|---|---|---|---|---|---|---|
| CAP | HAM | CAP | HAM | CAP | HAM | |
| 10.0.0.WDT | −0.37 | −0.50 | 0.39 | 0.29 | 1.30 | 1.77 |
| 10.0.0.150 | −0.38 | −0.55 | 0.37 | 0.27 | 1.31 | 1.80 |
| 10.0.GW.WDT | 0.74 | 0.46 | 0.82 | 0.65 | 0.54 | 0.88 |
| 10.0.GW.150 | 0.73 | 0.45 | 0.81 | 0.65 | 0.55 | 0.91 |
| 10.SU.0.WDT | −0.32 | −0.29 | 0.41 | 0.38 | 1.24 | 1.62 |
| 10.SU.0.150 | −0.31 | −0.32 | 0.39 | 0.36 | 1.25 | 1.64 |
| 10.SU.GW.WDT | 0.75 | 0.51 | 0.82 | 0.62 | 0.48 | 0.77 |
| 10.SU.GW.150 | 0.74 | 0.49 | 0.81 | 0.63 | 0.51 | 0.81 |
| Scenario | NSE | R2 | RMSE | |||
|---|---|---|---|---|---|---|
| CAP | HAM | CAP | HAM | CAP | HAM | |
| 10.0.0.WDT | −0.19 | 0.12 | 0.38 | 0.23 | 9.58 | 0.95 |
| 5.0.0.WDT | −0.25 | 0.06 | 0.40 | 0.23 | 10.00 | 1.08 |
| 10.0.GW.WDT | 0.72 | 0.32 | 0.80 | 0.40 | 4.47 | 0.77 |
| 5.0.GW.WDT | 0.75 | 0.33 | 0.78 | 0.46 | 4.02 | 0.86 |
| 10.SU.0.WDT | −0.11 | 0.09 | 0.40 | 0.27 | 8.96 | 1.09 |
| 5.SU.0.WDT | −0.21 | −0.02 | 0.39 | 0.23 | 9.54 | 1.23 |
| 10.SU.GW.WDT | 0.76 | 0.39 | 0.80 | 0.44 | 3.88 | 0.77 |
| 5.SU.GW.WDT | 0.76 | 0.34 | 0.78 | 0.46 | 3.54 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bragg, M.A.; Poudel, A.; Vasconcelos, J.G. Comparing SWMM and HEC-RAS Hydrological Modeling Performance in Semi-Urbanized Watershed. Water 2025, 17, 1331. https://doi.org/10.3390/w17091331
Bragg MA, Poudel A, Vasconcelos JG. Comparing SWMM and HEC-RAS Hydrological Modeling Performance in Semi-Urbanized Watershed. Water. 2025; 17(9):1331. https://doi.org/10.3390/w17091331
Chicago/Turabian StyleBragg, Michael A., Ashmita Poudel, and Jose G. Vasconcelos. 2025. "Comparing SWMM and HEC-RAS Hydrological Modeling Performance in Semi-Urbanized Watershed" Water 17, no. 9: 1331. https://doi.org/10.3390/w17091331
APA StyleBragg, M. A., Poudel, A., & Vasconcelos, J. G. (2025). Comparing SWMM and HEC-RAS Hydrological Modeling Performance in Semi-Urbanized Watershed. Water, 17(9), 1331. https://doi.org/10.3390/w17091331







