Prediction of the Water-Conducting Fracture Zone Height Across the Entire Mining Area Based on the Multiple Nonlinear Coordinated Regression Model
Abstract
1. Introduction
2. Analysis of the Factors for the HWCFZ and Research Methods
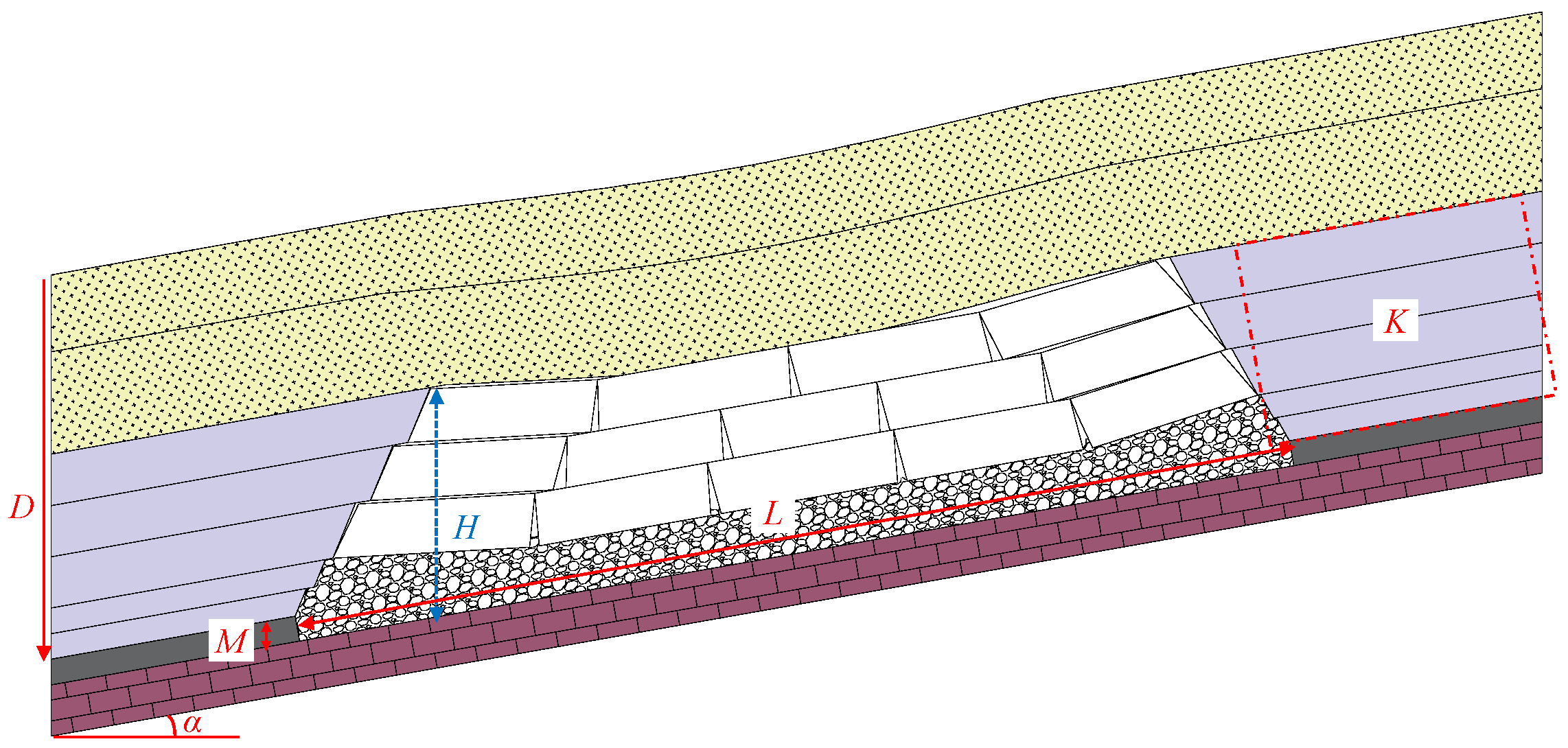
2.1. Analysis of Influencing Factors of the HWCFZ
- (1)
- Mining Thickness M
- (2)
- Mining Depth D
- (3)
- Length of Panel L
- (4)
- Coal Seam Dip α
- (5)
- Proportion Coefficient of Hard Rock K
2.2. Specific Lines of Research
3. Results and Discussion
3.1. Measured Data of the WCFZ
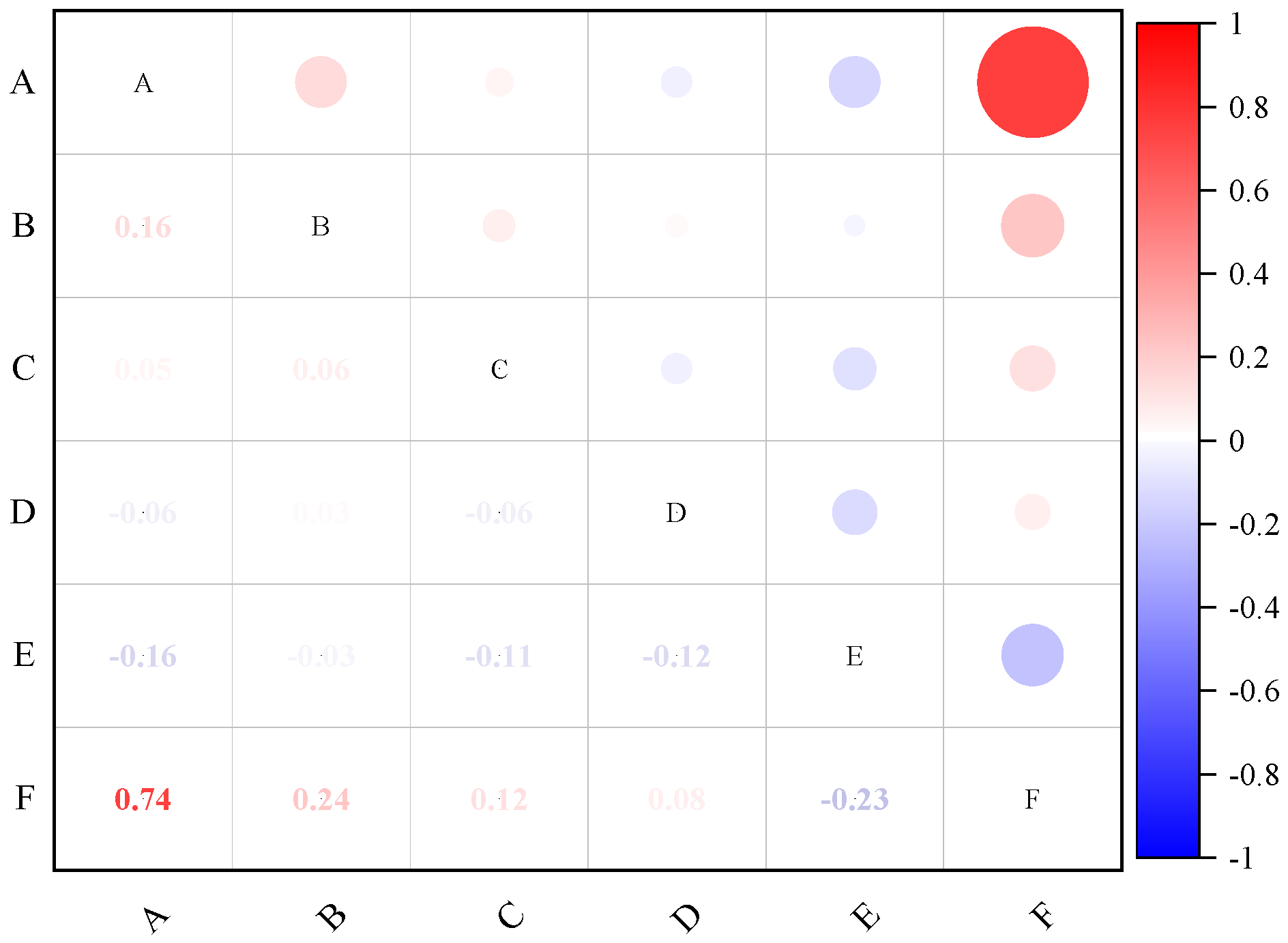
3.1.1. Correlation Analysis
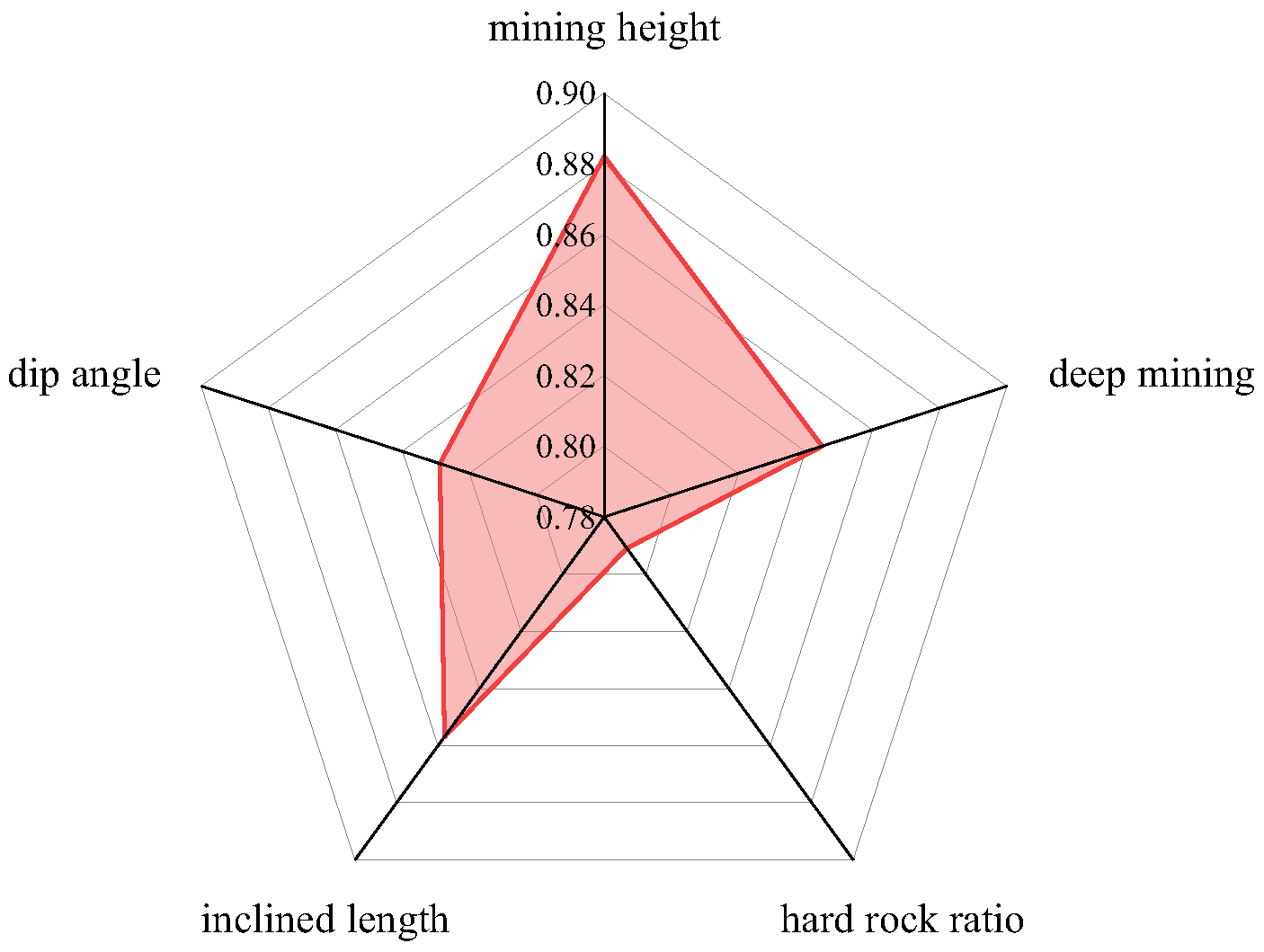
3.1.2. Principal Component Analysis
3.2. Prediction Models for the HWCFZ
3.2.1. Nonlinear Additive Regression Model
3.2.2. Multivariate Nonlinear Coordinated Regression Model
3.2.3. Neural Network Model
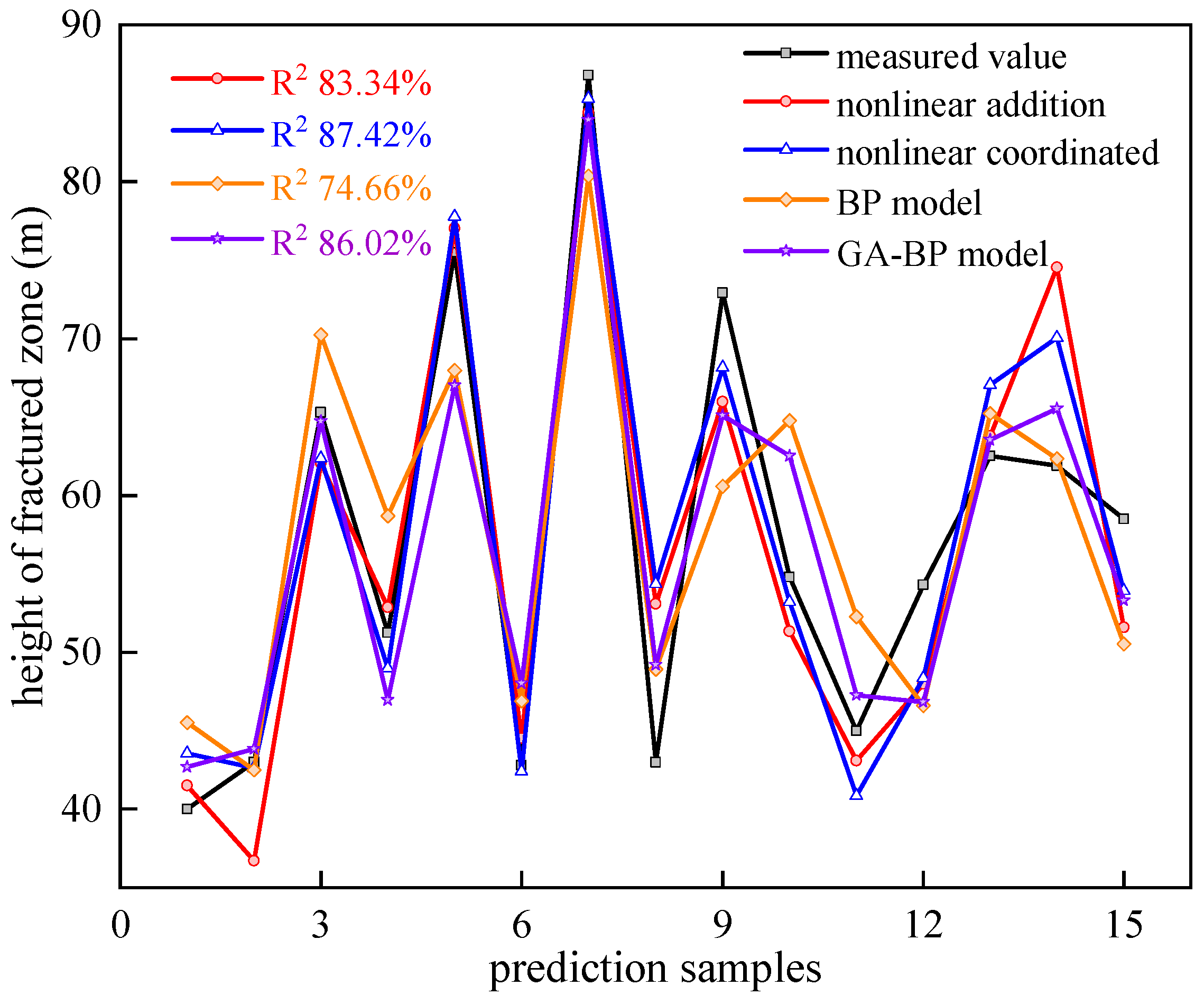
3.2.4. Comparison of Prediction Models
3.3. Analysis of Safe Water Break Distance of Panel Based on Hydraulic Fracture Zone Modeling
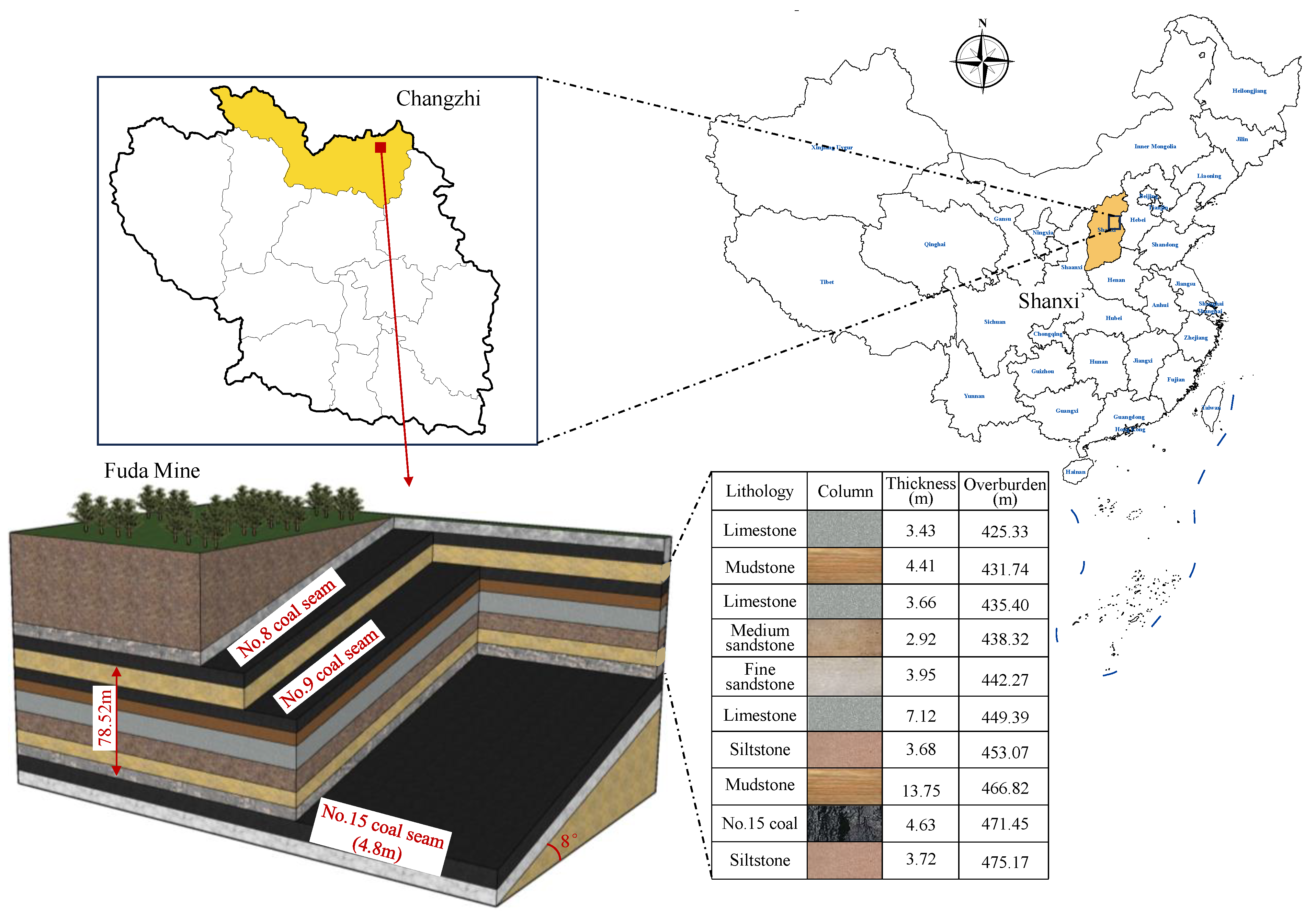
3.3.1. Geological Overview
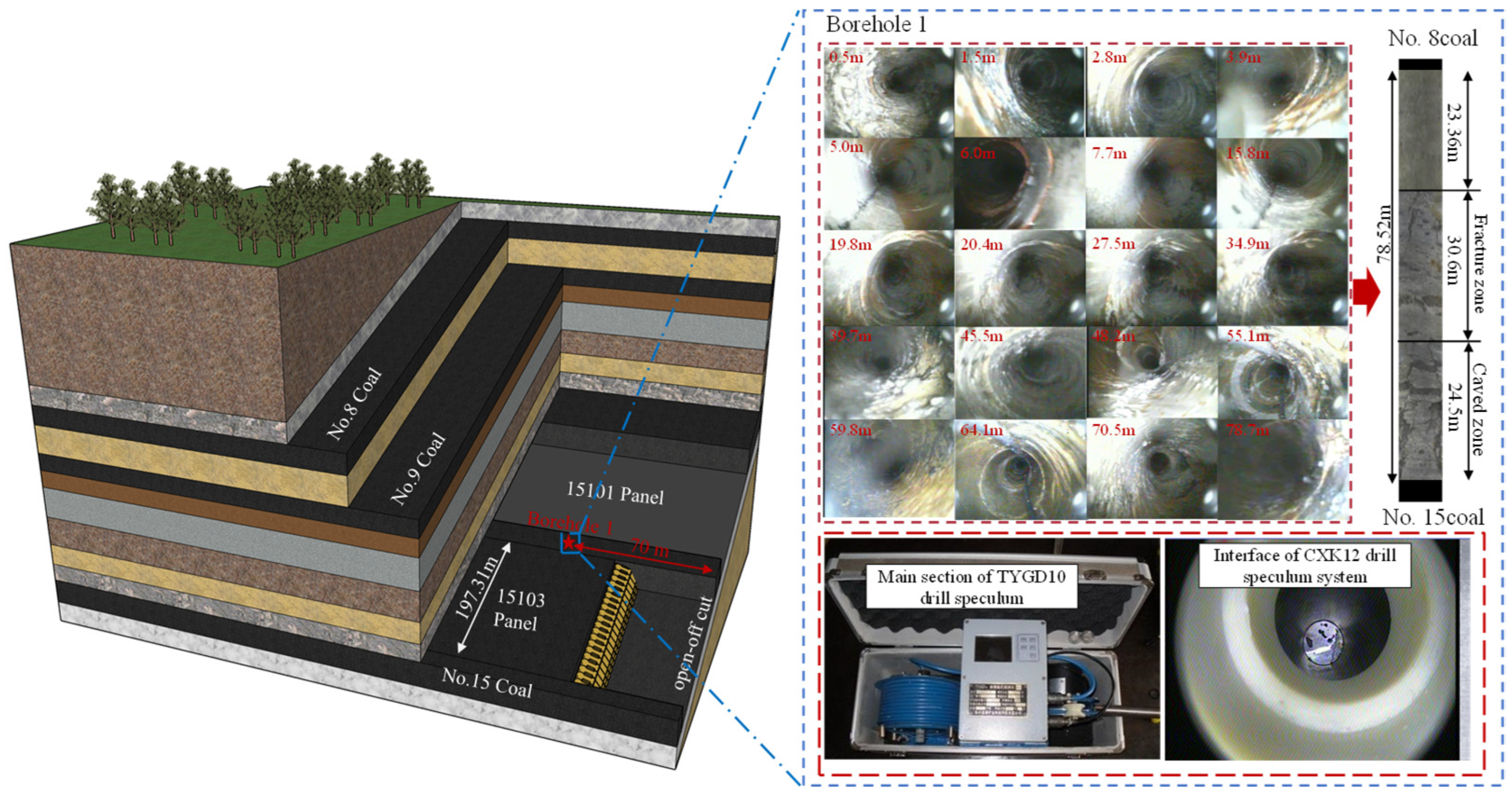
3.3.2. Model Verification and Comparison
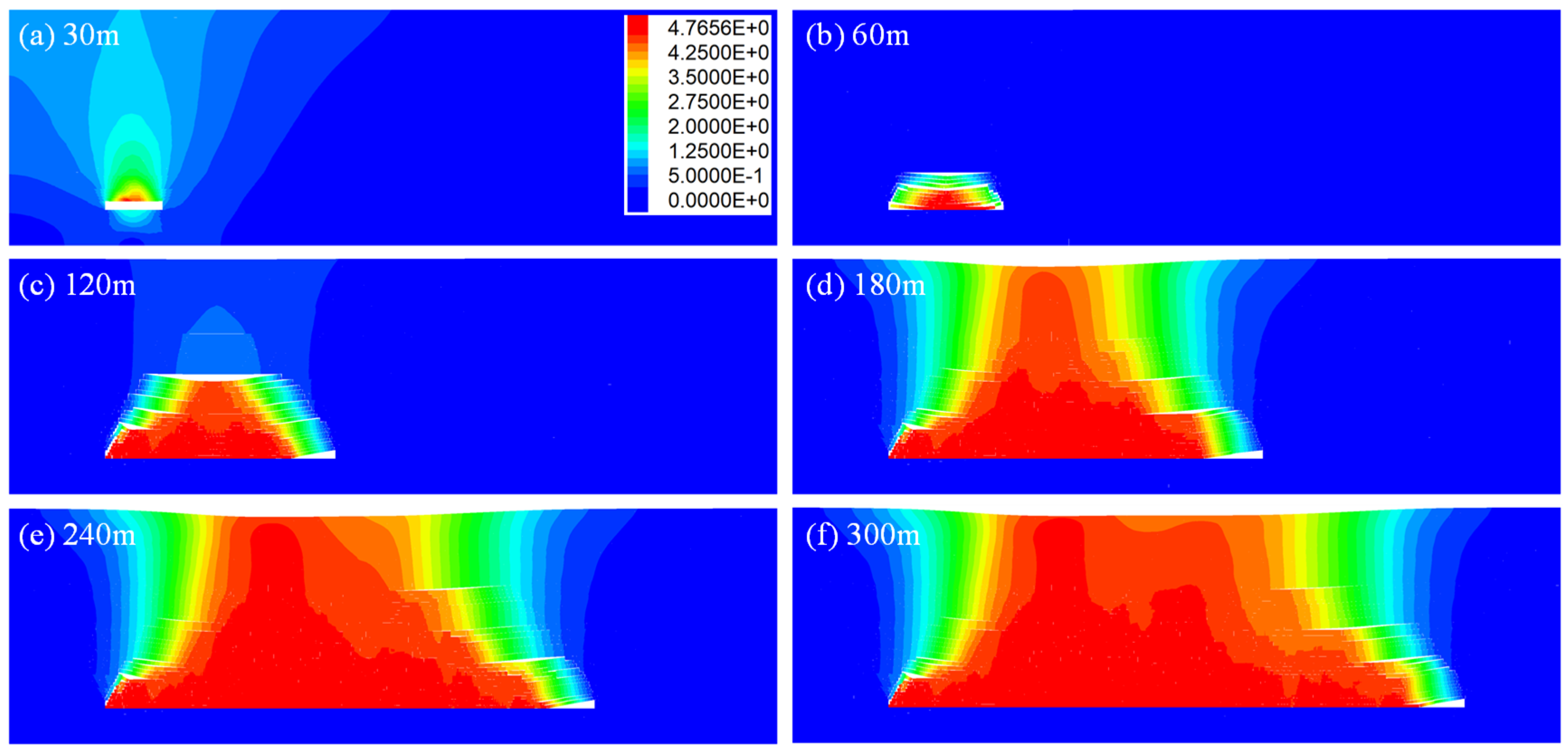
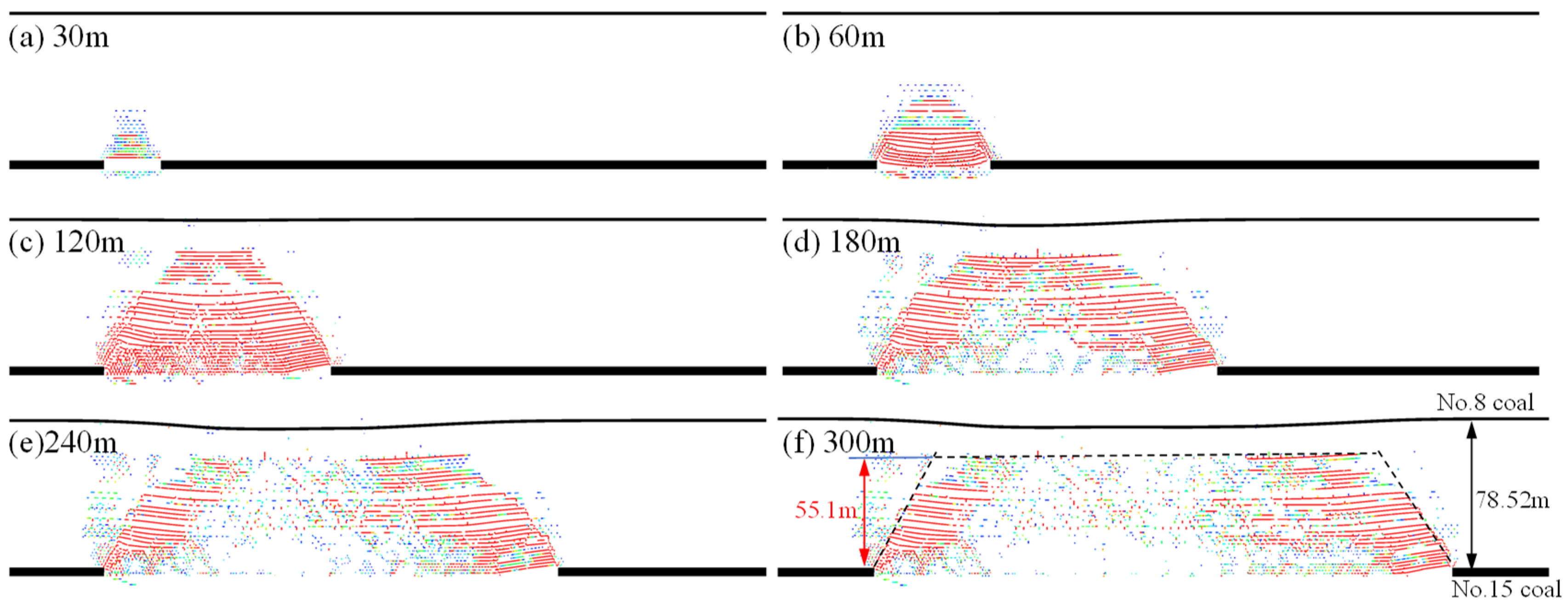
3.3.3. Developmental Pattern of Water-Conducting Fissure Zones
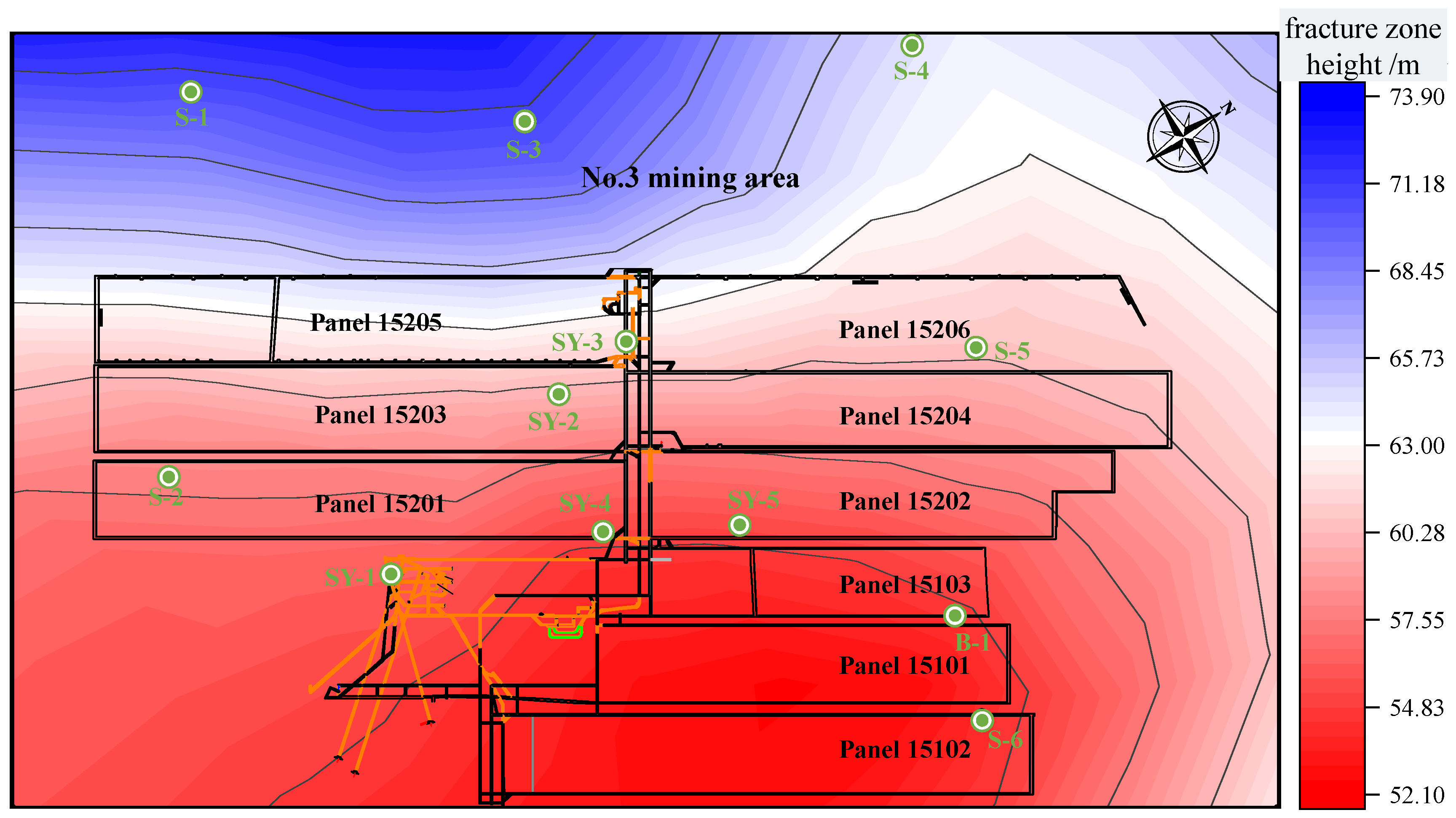
3.3.4. Prediction of the Water-Conducting Fracture Zone Height Across the Entire Mining Area of the Fuda Coal Mine
4. Conclusions
- (1)
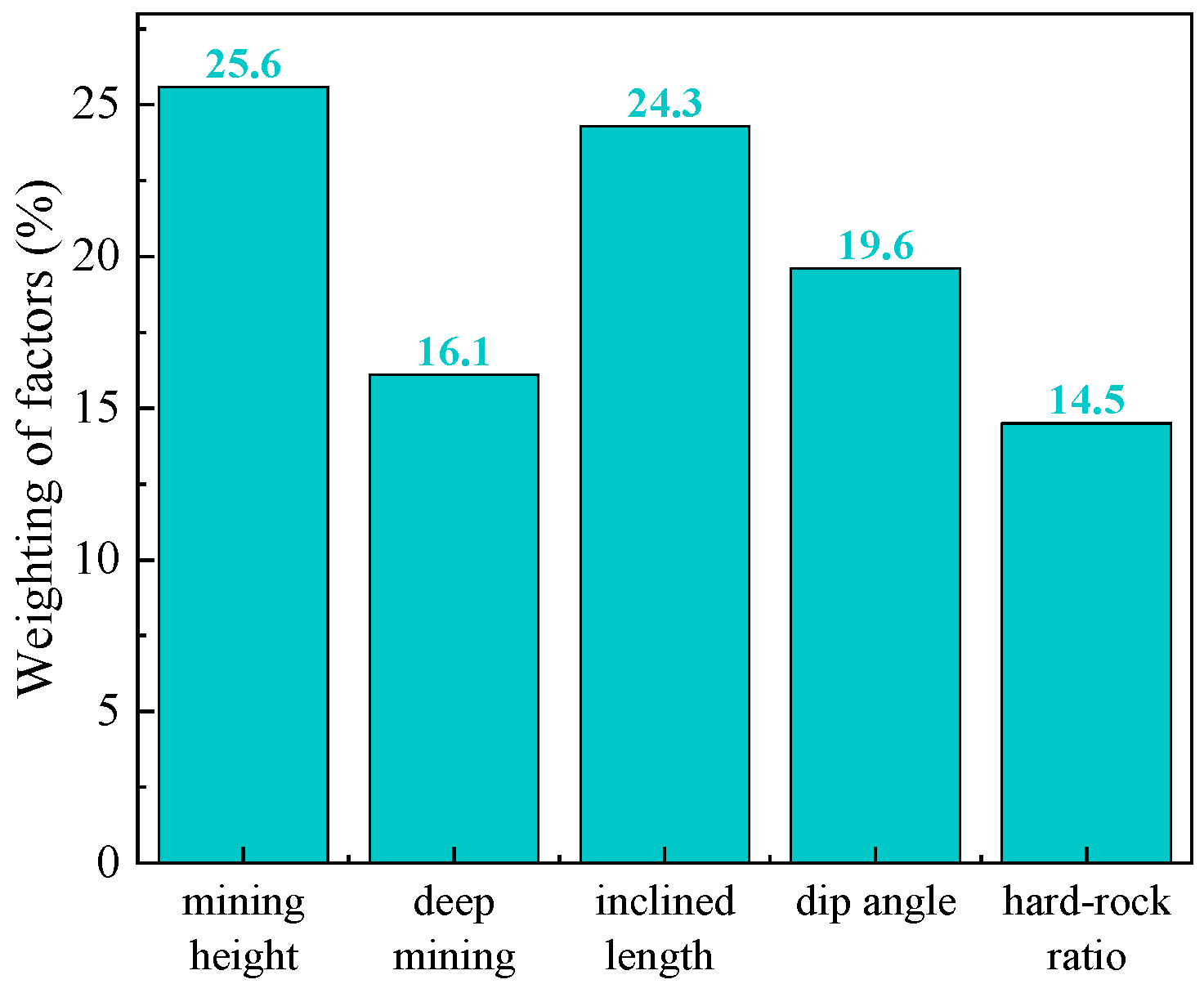
- The five influencing factors—mining thickness, burial depth, length of the panel, coal seam dip, and proportion coefficient of hard rock—were identified through an analysis of their impact on the development of the HWCFZ. Using grey relational analysis and principal component analysis methods, the correlation and weight of the HWCFZ were studied. The correlation coefficients for all five factors exceeded 0.79, showing a positive relationship between correlation and weight. Mining thickness had the highest weight at 0.256, followed by the length of the panel at 0.243. Burial depth and coal seam dip had moderate influences, while the proportion coefficient of hard rock had a relatively smaller impact.
- (2)
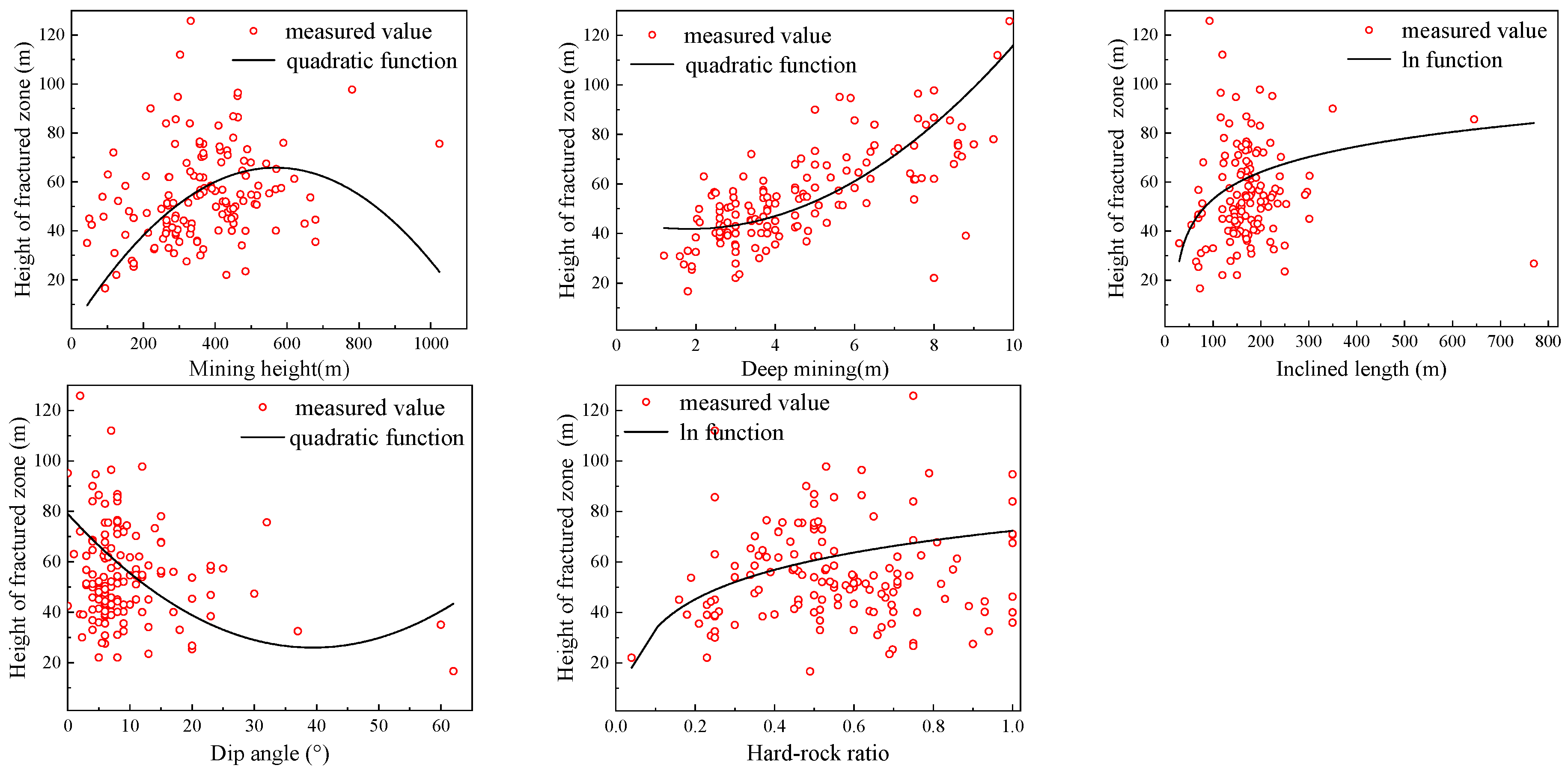
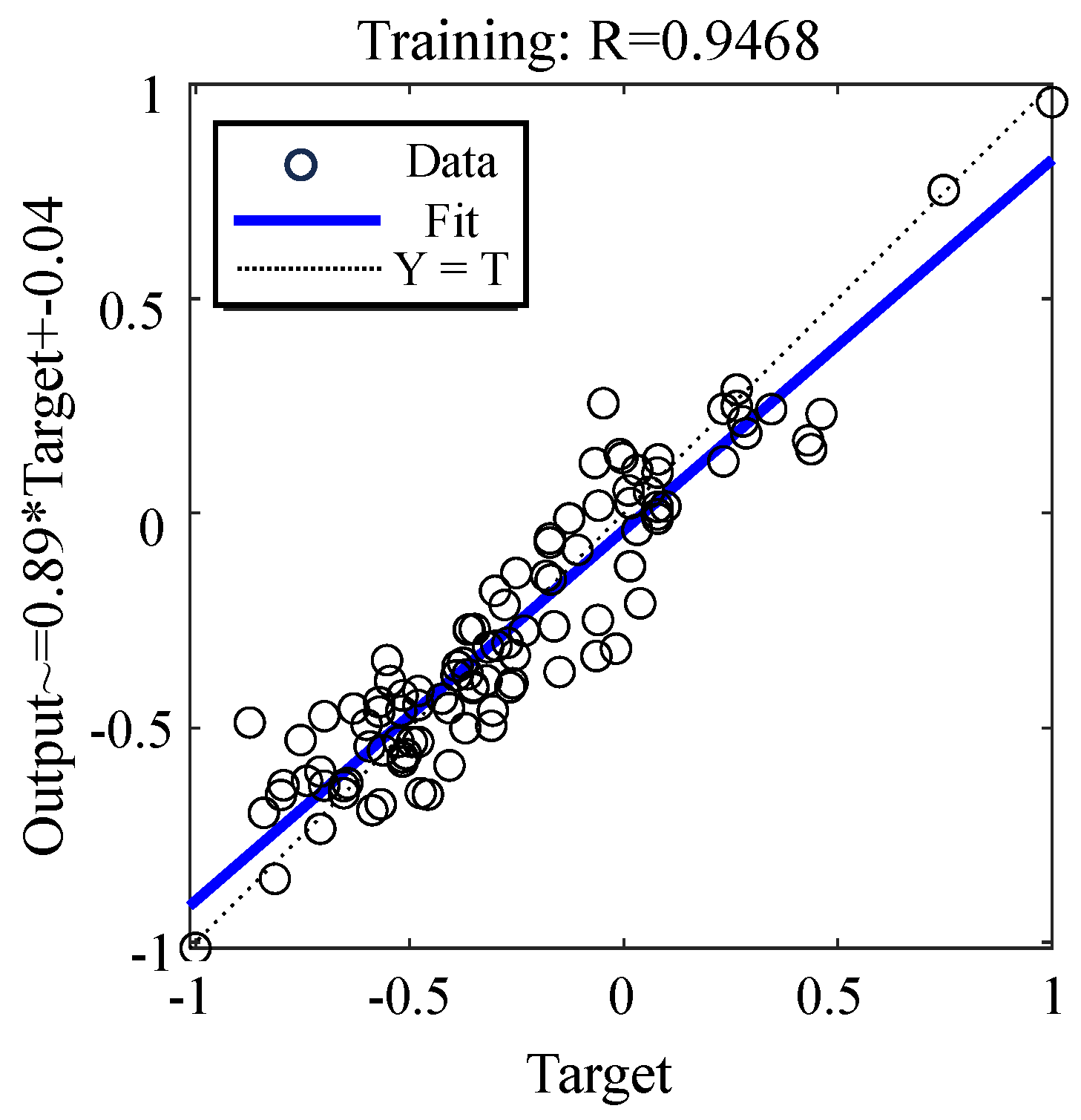
- The nonlinear relationships between each influencing factor and the HWCFZ were identified by nonlinear fitting on the measured data for individual factors. On account of the deviations between the prediction results of the nonlinear additive regression model and the measured values, a multivariate nonlinear coordinated regression model was proposed. A comparison of the absolute errors and R2 values among the nonlinear additive regression model, nonlinear coordinated regression model, BP neural network model, and GA-BP neural network model revealed that the nonlinear coordinated regression model had an error rate of 7.23% and the highest R2 fitting value of 87.42%, confirming its accuracy.
- (3)
- Borehole B-1 at the Fuda Coal Mine and numerical simulation results were used to validate the multivariate nonlinear coordinated regression model. The accuracy rates of 97.5%, respectively, demonstrate that the predicted results closely align with the measured values. Therefore, these models can be effectively applied to predict the HWCFZ at the Fuda Coal Mine.
- (4)
- Based on the borehole data and mining conditions, the distribution of the WCFZ development height across the entire Fuda Coal Mine area was fitted using the multivariate nonlinear coordinated regression prediction model. As the No. 15 coal seam extends to the north, the development of the HWCFZ in the entire mining area gradually increases from 52.1 m to 73.9 m.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, D.D.; Hou, X.A.; Yang, T.H.; Zhao, Y.; Zhang, P.H.; Yang, B.; Liu, Y.L.; Ma, K. Calibration of Water Inrush Channel and Numerical Simulation of Water Inrush Process in Coal Mine Roof. Front. Earth Sci. 2022, 10, 931508. [Google Scholar] [CrossRef]
- Li, Y.; Lei, X.H.; Wang, N.; Ren, Y.Q.; Jin, X.Y.; Li, G.S.; Li, T.Z.; Ou, X.J. Study on the Failure Characteristics of Overburden and the Evolution Law of Seepage Field in Deep Buried Thick Coal Seam under Aquifers. Nat. Hazards 2023, 118, 1035–1064. [Google Scholar] [CrossRef]
- Lu, C.J.; Xu, J.P.; Li, Q.; Zhao, H.; He, Y. Research on the Development Law of Water-Conducting Fracture Zone in the Combined Mining of Jurassic and Carboniferous Coal Seams. Appl. Sci. 2022, 12, 11178. [Google Scholar] [CrossRef]
- Wang, X.; Yin, S.; Xu, B.; Cao, M.; Zhang, R.; Tang, Z.; Huang, W.; Li, W. Study on Height Optimization Prediction Model of Overburden Water-Conducting Fracture Zone under Fully Mechanized Mining. Coal Sci. Technol. 2023, 51 (Suppl. S1), 284–297. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, S.; Yu, H.; Liu, Y. Comprehensive Analysis Control Effect of Faults on the Height of Fractured Water-Conducting Zone in Longwall Mining. Nat. Hazards 2021, 108, 2143–2165. [Google Scholar] [CrossRef]
- Feng, D.; Hou, E.; Xie, X.; Hou, P.; Chen, M.T. Research on Water-Conducting Fractured Zone Height under the Condition of Large Mining Height in Yushen Mining Area, China. Lithosphere 2023, 2023, 8918348. [Google Scholar] [CrossRef]
- Han, Y.; Wang, Q.; Li, W.; Yang, Z.; Gu, T.; Wang, Z. Predicting the Height of the Water-Conducting Fractured Zone in Fully Mechanized Top Coal Caving Longwall Mining of Very Thick Jurassic Coal Seams in Western China Based on the NNBR Model. Mine Water Environ. 2023, 42, 121–133. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Wang, K.; Tan, X.; Zhang, L.; Zhang, T. Development and Height Prediction of Fractured Water-Conducting Zone in Weakly Cemented Overburden: A Case Study of Tashidian Erjingtian Mine. Sustainability 2023, 15, 13899. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Wang, K.; Tan, X.; Zhang, T.; Zhang, L. Characteristic Developments of the Water-Conducting Fracture Zones in Weakly Cemented Overlying Strata of Jurassic Coal Mines in Western China. Water 2023, 15, 1097. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, S.; Liao, J.; Li, L.; Jia, J.; Tang, Q.; Li, X.; Gao, C. Reasonable Working-Face Size Based on Full Mining of Overburden Failure. Sustainability 2023, 15, 3351. [Google Scholar] [CrossRef]
- Li, X.; Li, Q.; Xu, X.; Zhao, Y.; Li, P.; Wang, Q. Multiple Influence Factor Sensitivity Analysis and Height Prediction of Water-Conducting Fracture Zone. Geofluids 2021, 2021, 8825906. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, S.; Yang, B.; Liu, J.; Ye, Z. Predicting the Height of the Water-Conducting Fractured Zone Using Multiple Regression Analysis and GIS. Environ. Earth Sci. 2019, 78, 422. [Google Scholar] [CrossRef]
- Yang, P.; Yang, W.; Nie, Y.; Saleem, F.; Lu, F.; Ma, R.; Li, R. Predicting the Height of the Water-Conducting Fractured Zone Based on a Multiple Regression Model and Information Entropy in the Northern Ordos Basin, China. Mine Water Environ. 2021, 41, 225–236. [Google Scholar] [CrossRef]
- Yin, H.; Dong, F.; Zhang, Y.; Cheng, W.; Zhai, P.; Ren, X.; Liu, Z.; Zhai, Y.; Li, X. Height Prediction and 3D Visualization of Mining-Induced Water-Conducting Fracture Zone in Western Ordos Basin Based on a Multi-Factor Regression Analysis. Energies 2022, 15, 3850. [Google Scholar] [CrossRef]
- Ajayi, K.M.; Shahbazi, K.; Tukkaraja, P.; Katzenstein, K. Estimation of Radon Diffusivity Tensor for Fractured Rocks in Cave Mines Using a Discrete Fracture Network Model. J. Environ. Radioact. 2019, 196, 104–112. [Google Scholar] [CrossRef] [PubMed]
- Suner, M.C.; Tulu, I.B. Examining the Effect of Natural Fractures on Stone Mine Pillar Strength Through Synthetic Rock Mass Approach. Min. Metall. Explor. 2022, 39, 1863–1871. [Google Scholar] [CrossRef]
- Gao, Z.; Jin, L.; Liu, P.; Wei, J. Height Prediction of Water-Conducting Fracture Zone in Jurassic Coalfield of Ordos Basin Based on Improved Radial Movement Optimization Algorithm Back-Propagation Neural Network. Mathematics 2024, 12, 1602. [Google Scholar] [CrossRef]
- Gu, L.; Shen, Y.; Wang, N.; Kou, H.; Song, S. Prediction of the Height of Fractured Water-Conducting Zone: Significant Factors and Model Optimization. Water 2023, 15, 2720. [Google Scholar] [CrossRef]
- Guo, C.; Yang, Z.; Li, S.; Lou, J. Predicting the Water-Conducting Fracture Zone (WCFZ) Height Using an MPGA-SVR Approach. Sustainability 2020, 12, 1809. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, C.; Liu, W.; Pang, L. Evaluation on Development Height of Water-Conducted Fractures on Overburden Roof Based on Nonlinear Algorithm. Water 2022, 14, 3853. [Google Scholar] [CrossRef]
- Iraji, S.; Soltanmohammadi, R.; Matheus, G.F.; Basso, M.; Vidal, A.C. Application of Unsupervised Learning and Deep Learning for Rock Type Prediction and Petrophysical Characterization Using Multi-Scale Data. Geoenergy Sci. Eng. 2023, 230, 221241. [Google Scholar] [CrossRef]
- Zhai, P.; Li, N. Predicting the Height of the Hydraulic Fracture Zone Using a Convolutional Neural Network. Mine Water Environ. 2023, 42, 500–512. [Google Scholar] [CrossRef]
- Fernández, A.; Sanchidrián, J.A.; Segarra, P.; Gómez, S.; Li, E.M.; Navarro, R. Rock Mass Structural Recognition from Drill Monitoring Technology in Underground Mining Using Discontinuity Index and Machine Learning Techniques. Int. J. Min. Sci. Technol. 2023, 33, 555–571. [Google Scholar] [CrossRef]
- Zhao, D.; Li, Z.; Feng, G.; Wang, F.; Hao, C.; He, Y.; Dong, S. Using Swarm Intelligence Optimization Algorithms to Predict the Height of Fractured Water-Conducting Zone. Energy Explor. Exploit. 2023, 41, 1603–1627. [Google Scholar] [CrossRef]
- Zhao, B.; He, S.; Bai, K.; Lu, X.; Wang, W. Elastic Wave Prospecting of Water-Conducting Fractured Zones in Coal Mining. Sci. Rep. 2024, 14, 7036. [Google Scholar] [CrossRef]
- Lee, S.C.H.; Noh, K.A.M.; Zakariah, M.N.A. High-Resolution Electrical Resistivity Tomography and Seismic Refraction for Groundwater Exploration in Fractured Hard Rocks: A Case Study in Kanthan, Perak, Malaysia. J. Asian Earth Sci. 2021, 218, 104880. [Google Scholar] [CrossRef]
- Xu, C.; Zhou, K.; Xiong, X.; Gao, F.; Zhou, J. Research on Height Prediction of Water-Conducting Fracture Zone in Coal Mining Based on Intelligent Algorithm Combined with Extreme Boosting Machine. Expert Syst. Appl. 2024, 249, 123669. [Google Scholar] [CrossRef]
- Gao, W.; Li, Y.; He, Q. Determination of Fractured Water-Conducting Zone Height Based on Microseismic Monitoring: A Case Study in Weiqiang Coalmine, Shaanxi, China. Sustainability 2022, 14, 8385. [Google Scholar] [CrossRef]
- Zhao, D.; Wu, Q. An Approach to Predict the Height of Fractured Water-Conducting Zone of Coal Roof Strata Using Random Forest Regression. Sci. Rep. 2018, 8, 10986. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Mishra, S. Applications of Machine Learning for Facies and Fracture Prediction Using Bayesian Network Theory and Random Forest: Case Studies from the Appalachian Basin, USA. J. Pet. Sci. Eng. 2018, 170, 1005–1017. [Google Scholar] [CrossRef]
- Li, B.; Wu, H.; Li, T. Height Prediction of Water-Conducting Fractured Zone under Fully Mechanized Mining Based on Weighted Multivariate Nonlinear Regression. J. Min. Saf. Eng. 2022, 39, 536–545. [Google Scholar]
- Duarte, B.P.M.; Atkinson, A.C.; Oliveira, N.M.C. Optimum design for ill-conditioned models: K-optimality and stable parameterizations. Chemom. Intell. Lab. Syst. 2023, 239, 104874. [Google Scholar] [CrossRef]
- Chu, E.Y.; Stull, K.E. An investigation of the relationship between long bone measurements and stature: Implications for estimating skeletal stature in subadults. Int. J. Leg. Med. 2025, 139, 441–453. [Google Scholar] [CrossRef] [PubMed]
- Mikolajczyk, A.P.; Fortela, D.L.B.; Berry, J.C.; Chirdon, W.M.; Hernandez, R.A.; Gang, D.D.; Zappi, M.E. Evaluating the Suitability of Linear and Nonlinear Regression Approaches for the Langmuir Adsorption Model as Applied toward Biomass-Based Adsorbents: Testing Residuals and Assessing Model Validity. Langmuir 2024, 40, 20428–20442. [Google Scholar] [CrossRef]
- Biswal, A.; Jwo, D.-J. Maximum Correntropy Extended Kalman Filtering with Nonlinear Regression Technique for GPS Navigation. Appl. Sci. 2024, 14, 7657. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Z.; Zhang, D.; Huang, X. Biomass allometric models for Larix rupprechtii based on Kosak’s taper curve equations and nonlinear seemingly unrelated regression. Front. Plant Sci. 2023, 13, 1056837. [Google Scholar] [CrossRef]



| Number | Mining Thickness/m | Mining Depth/m | Length of Panel/m | Proportion Coefficient of Hard Rock | Coal Seam Dip/° | Height of the Fractured Water-Conducting Zone/m |
|---|---|---|---|---|---|---|
| 1 | 1.2 | 120 | 75 | 0.66 | 8 | 31 |
| 2 | 1.6 | 285 | 180 | 0.24 | 6 | 30.8 |
| 3 | 1.7 | 320 | 65 | 0.9 | 6 | 27.5 |
| 4 | 1.8 | 270 | 100 | 0.6 | 18 | 33 |
| 5 | 1.8 | 93 | 73 | 0.49 | 62 | 16.6 |
| … | … | … | … | … | … | … |
| 146 | 8.7 | 409 | 198 | 0.5 | 6 | 83 |
| 147 | 9 | 590 | 220 | 0.51 | 8 | 76 |
| 148 | 9.5 | 450 | 123 | 0.65 | 15 | 78 |
| 149 | 9.6 | 302 | 120 | 0.25 | 7 | 112 |
| 150 | 9.9 | 332 | 93 | 0.75 | 2 | 125.8 |
| Model | Parameter | Estimation | Standard Error | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower Limit | Upper Limit | ||||
| Mining thickness | a1 | 1.095 | 0.150 | 0.799 | 1.391 |
| b1 | −4.44 | 2.029 | −8.449 | −0.431 | |
| Mining depth | a2 | 0.01 | 0.000 | −0.01 | 0.01 |
| b2 | 0.005 | 0.028 | −0.050 | 0.060 | |
| Length of panel | a3 | 9.037 | 3.749 | 1.629 | 16.445 |
| Coal seam dip | a4 | 8.34 | 3.034 | 2.345 | 14.335 |
| b4 | 0.011 | 0.008 | −0.005 | 0.028 | |
| Proportion coefficient of hard rock | a5 | −0.739 | 0.426 | −1.580 | 0.102 |
| a6 | 7.575 | 19.610 | −31.179 | 46.329 | |
| Model | Parameter | Estimation | Standard Error | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower Limit | Upper Limit | ||||
| Mining thickness | a1 | 1.336 | 17.31 | −35.48 | 33.16 |
| b1 | 10.276 | 16.09 | −20.07 | 27.63 | |
| c1 | −35.216 | 18.08 | −29.92 | 29.48 | |
| Mining depth | a2 | −1.260 | 9.72 | −33.336 | 31.82 |
| b2 | 1783.82 | 11.84 | −28.75 | 36.38 | |
| c2 | −1279.85 | 0.47 | −38.11 | 48.41 | |
| Length of panel | a3 | 0.008 | 6.457 | −29.851 | 29.87 |
| b3 | −0.025 | 14.207 | −34.145 | 38.10 | |
| Coal seam dip | a4 | 0.123 | 5.209 | −18.161 | 12.41 |
| b4 | 0.258 | 2.175 | −3.023 | 2.54 | |
| C4 | 0.001 | 2.065 | −4.082 | 4.082 | |
| Proportion coefficient of hard rock | a5 | −0.001 | 1.789 | −1.936 | 1.936 |
| b5 | 0.000 | 1.817 | −2.591 | 2.592 | |
| a6 | 41.850 | 2.638 | 36.634 | 47.066 | |
| Model | Measurement | Nonlinear Additive Regression Model | Nonlinear Coordinated Regression Model | BP | GA-BP |
|---|---|---|---|---|---|
| 1 | 40.00 m | 41.51 m | 43.56 m | 45.51 m | 42.69 m |
| 2 | 42.99 m | 36.70 m | 42.62 m | 42.49 m | 43.85 m |
| 3 | 65.30 m | 62.05 m | 62.36 m | 70.24 m | 64.71 m |
| 4 | 51.25 m | 52.86 m | 48.96 m | 58.69 m | 46.96 m |
| 5 | 75.50 m | 77.01 m | 77.75 m | 67.97 m | 66.99 m |
| 6 | 42.81 m | 44.53 m | 42.41 m | 46.88 m | 48.00 m |
| 7 | 86.80 m | 84.39 m | 85.29 m | 80.34 m | 83.94 m |
| 8 | 43.00 m | 53.08 m | 54.35 m | 48.93 m | 49.19 m |
| 9 | 72.90 m | 65.98 m | 68.15 m | 60.58 m | 65.11 m |
| 10 | 54.79 m | 51.35 m | 53.20 m | 64.75 m | 62.52 m |
| 11 | 45.00 m | 43.09 m | 40.84 m | 52.28 m | 47.26 m |
| 12 | 54.30 m | 47.97 m | 48.35 m | 46.60 m | 46.84 m |
| 13 | 62.53 m | 63.80 m | 67.07 m | 65.23 m | 63.55 m |
| 14 | 61.90 m | 74.54 m | 70.06 m | 62.33 m | 65.53 m |
| 15 | 58.50 m | 51.59 m | 53.93 m | 50.55 m | 53.30 m |
| Mean absolute error rate | 8.31% | 7.23% | 10.78% | 7.94% |
| Serial No. | Lithology | Thickness (m) | Density (kg/m3) | Bulk Modulus (GPa) | Shear Modulus (GPa) | Cohesion (MPa) | Tensile Strength (MPa) | Friction Angle (°) |
|---|---|---|---|---|---|---|---|---|
| 1 | Fine Sandstone | 17.4 | 2500 | 4.8 | 3.5 | 3.4 | 1.1 | 38 |
| 2 | Mudstone | 4 | 2200 | 2.38 | 1.62 | 3.5 | 1.8 | 33 |
| 3 | No. 8 Coal | 1.6 | 1560 | 1.8 | 1.2 | 1.7 | 1.3 | 32 |
| 4 | Siltstone | 31.95 | 2400 | 3.4 | 2.2 | 4.1 | 2.0 | 36 |
| 5 | Limestone | 3.43 | 2550 | 11.2 | 10.7 | 20 | 8.2 | 48 |
| 6 | Sandy Mudstone | 6.41 | 2200 | 2.3 | 1.6 | 1.8 | 1.2 | 34 |
| 7 | Limestone | 3.66 | 2550 | 11.2 | 10.7 | 20 | 8.2 | 48 |
| 8 | Medium Sandstone | 2.92 | 2640 | 5.8 | 4.7 | 2.8 | 0.9 | 40 |
| 9 | Fine Sandstone | 3.95 | 2500 | 4.8 | 3.5 | 3.4 | 1.1 | 38 |
| 10 | Limestone | 7.12 | 2550 | 11.2 | 10.7 | 20 | 8.2 | 48 |
| 11 | Siltstone | 3.68 | 2400 | 3.4 | 2.2 | 4.1 | 2.0 | 36 |
| 12 | Sandy Mudstone | 13.75 | 2200 | 2.3 | 1.6 | 1.8 | 1.2 | 34 |
| 13 | No. 15 Coal | 4.63 | 1560 | 1.8 | 1.2 | 1.7 | 1.3 | 32 |
| 14 | Siltstone | 3.72 | 2400 | 3.4 | 2.2 | 4.1 | 2.0 | 36 |
| 15 | Fine Sandstone | 14.78 | 2500 | 4.8 | 3.5 | 3.4 | 1.1 | 38 |
| Number | Thickness of Coal Seam/m | Mining Depth/m | Length of Panel/m | Coal Seam Dip/° | Proportion Coefficient of Hard Rock | Prediction Value/m |
|---|---|---|---|---|---|---|
| S1 | 4.88 | 662.33 | 220.00 | 8.00 | 0.48 | 69.57 |
| S2 | 4.75 | 432.03 | 194.58 | 8.00 | 0.27 | 56.21 |
| S3 | 5.16 | 703.49 | 220.00 | 8.00 | 0.48 | 73.88 |
| S4 | 4.74 | 709.21 | 220.00 | 8.00 | 0.32 | 62.44 |
| S5 | 4.63 | 471.44 | 241.41 | 8.00 | 0.37 | 60.70 |
| S6 | 4.35 | 314.38 | 200.11 | 8.00 | 0.35 | 52.13 |
| SY-1 | 4.81 | 357.12 | 215.00 | 8.00 | 0.38 | 58.01 |
| SY-2 | 4.80 | 519.15 | 215.75 | 8.00 | 0.30 | 60.27 |
| SY-3 | 4.89 | 485.98 | 215.00 | 8.00 | 0.34 | 61.88 |
| SY-4 | 4.46 | 339.74 | 194.57 | 8.00 | 0.32 | 52.86 |
| SY-5 | 4.60 | 374.30 | 219.67 | 8.00 | 0.55 | 56.46 |
| B-1 | 4.42 | 326.3 | 197.31 | 8.00 | 0.46 | 56.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Shi, X.; Chen, J.; Wang, K. Prediction of the Water-Conducting Fracture Zone Height Across the Entire Mining Area Based on the Multiple Nonlinear Coordinated Regression Model. Water 2025, 17, 1303. https://doi.org/10.3390/w17091303
Feng J, Shi X, Chen J, Wang K. Prediction of the Water-Conducting Fracture Zone Height Across the Entire Mining Area Based on the Multiple Nonlinear Coordinated Regression Model. Water. 2025; 17(9):1303. https://doi.org/10.3390/w17091303
Chicago/Turabian StyleFeng, Jianye, Xiaoming Shi, Jiasen Chen, and Kang Wang. 2025. "Prediction of the Water-Conducting Fracture Zone Height Across the Entire Mining Area Based on the Multiple Nonlinear Coordinated Regression Model" Water 17, no. 9: 1303. https://doi.org/10.3390/w17091303
APA StyleFeng, J., Shi, X., Chen, J., & Wang, K. (2025). Prediction of the Water-Conducting Fracture Zone Height Across the Entire Mining Area Based on the Multiple Nonlinear Coordinated Regression Model. Water, 17(9), 1303. https://doi.org/10.3390/w17091303






