Turbulent and Subcritical Flows over Macro-Roughness Elements †
Abstract
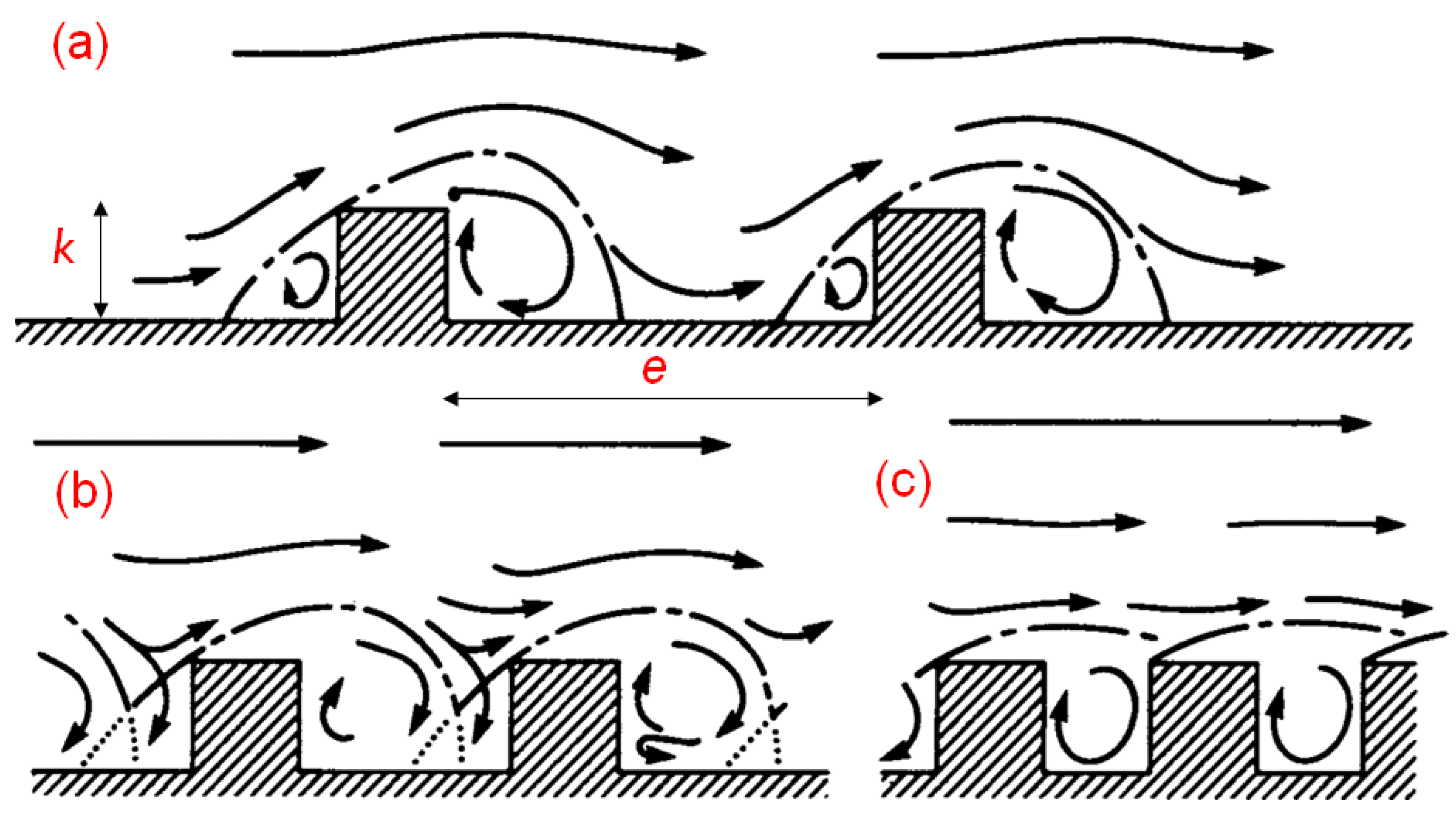
1. Introduction
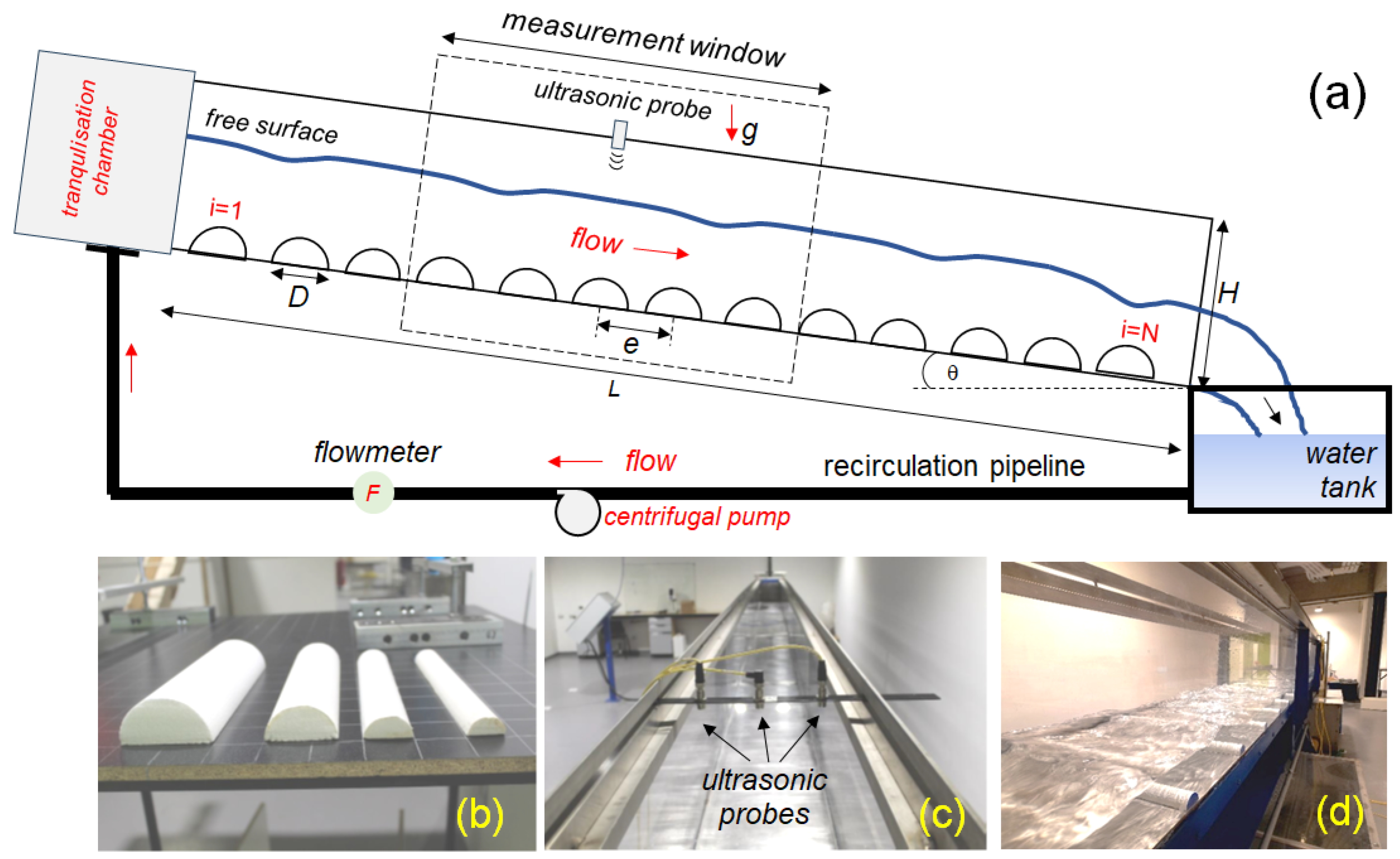
2. Experimental Setup
2.1. Materials
2.2. Methodology
2.3. Estimation of the Normal Depth of the Flow and Froude and Reynolds Numbers
3. Results and Discussion
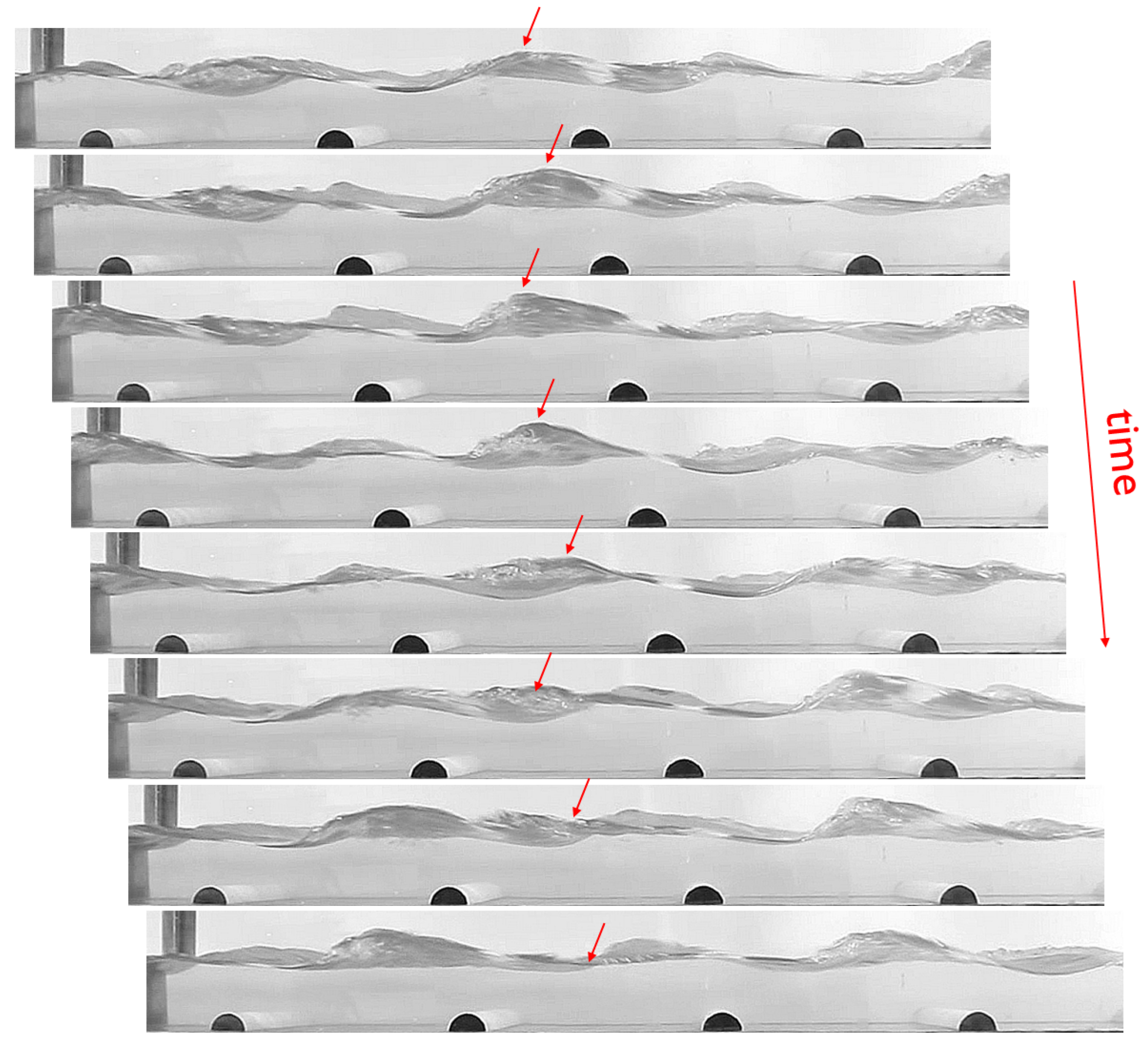
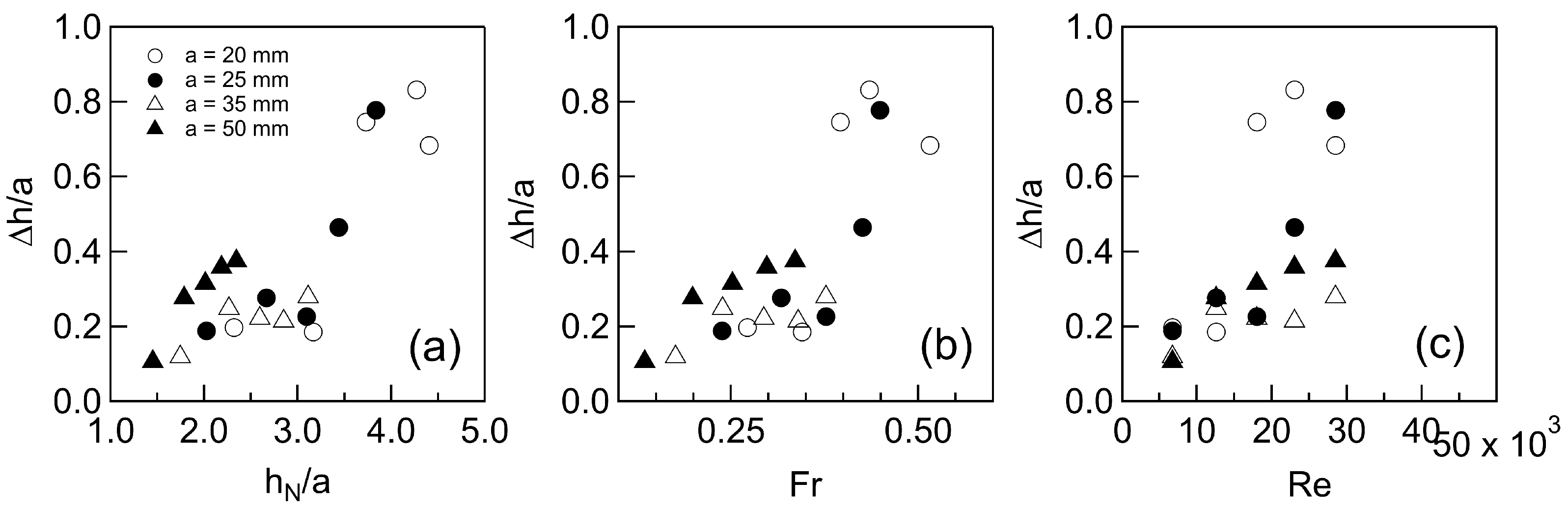
3.1. Deformation of the Free Surface and Backwater Profiles
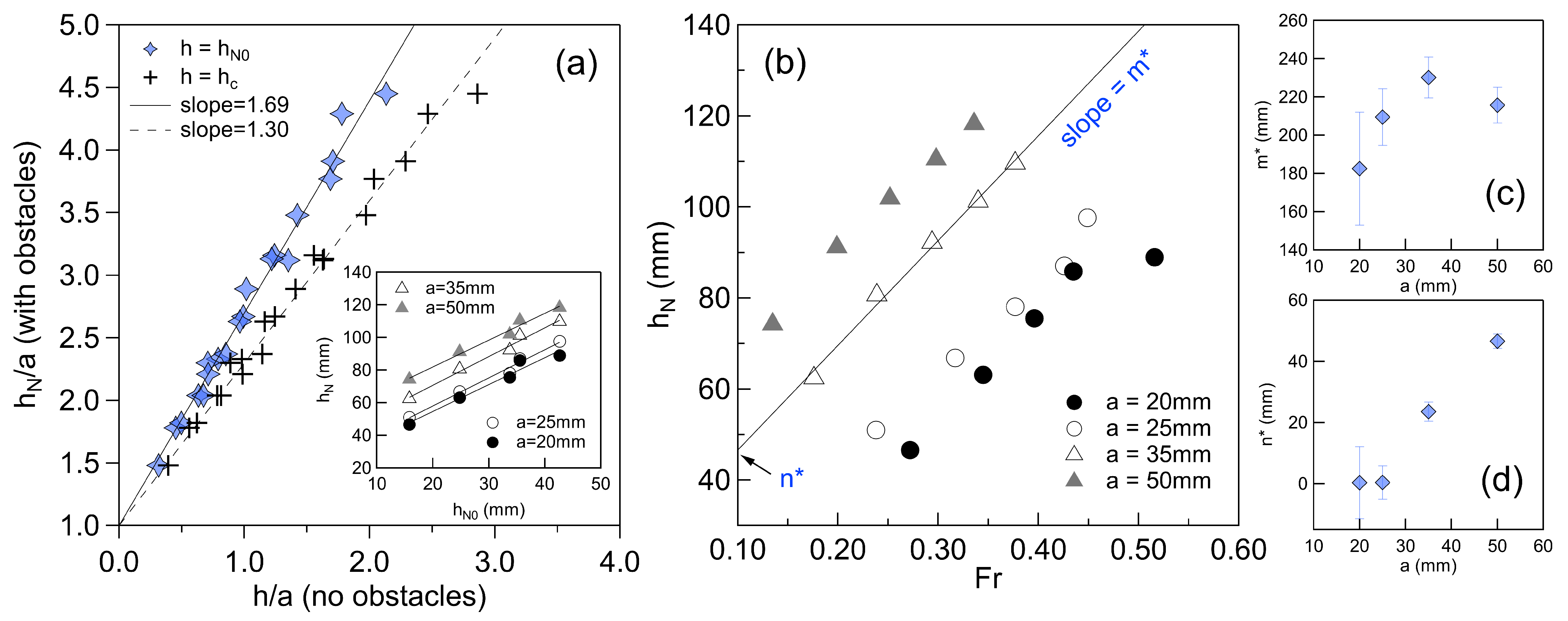
3.2. Distribution of the Normal Depth
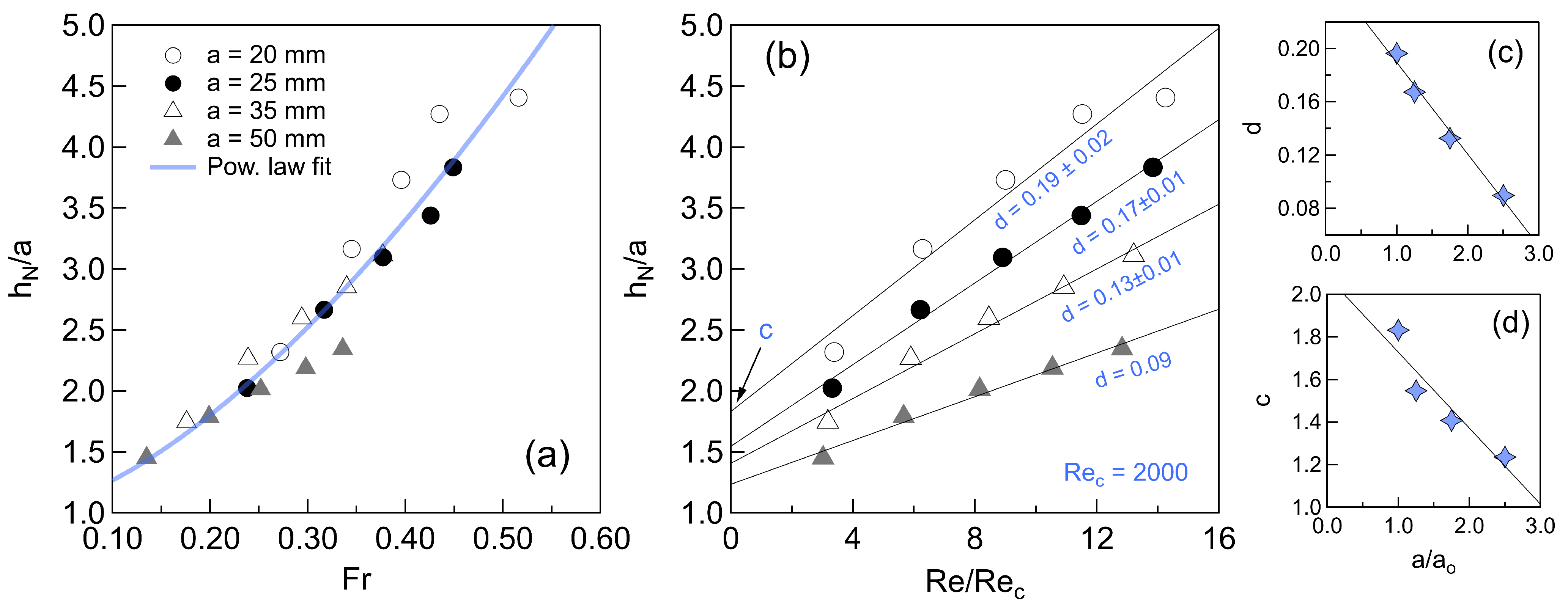
3.3. About the Darcy Friction Coefficient
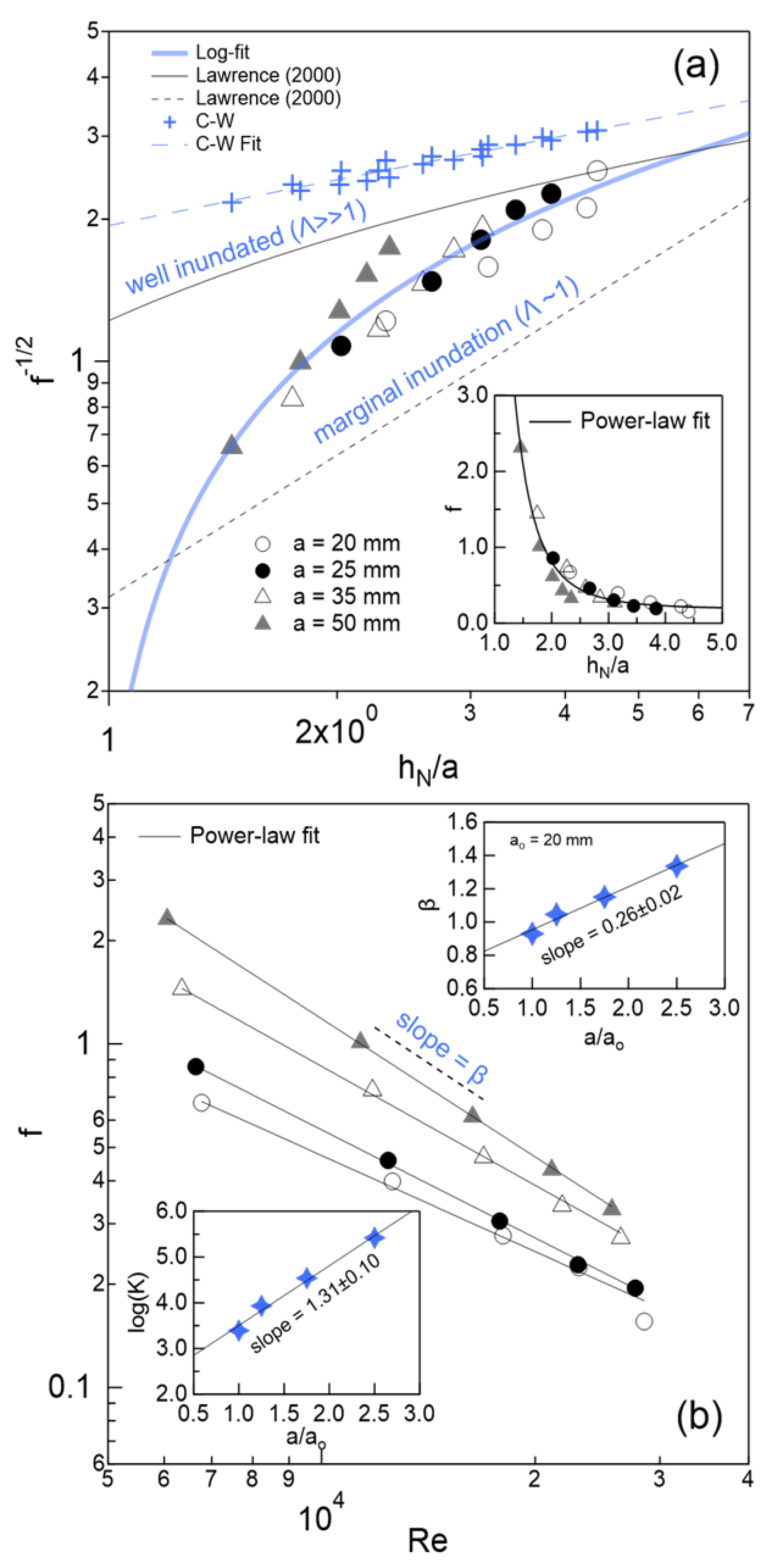
3.4. Comparison to Bazin’s Dataset
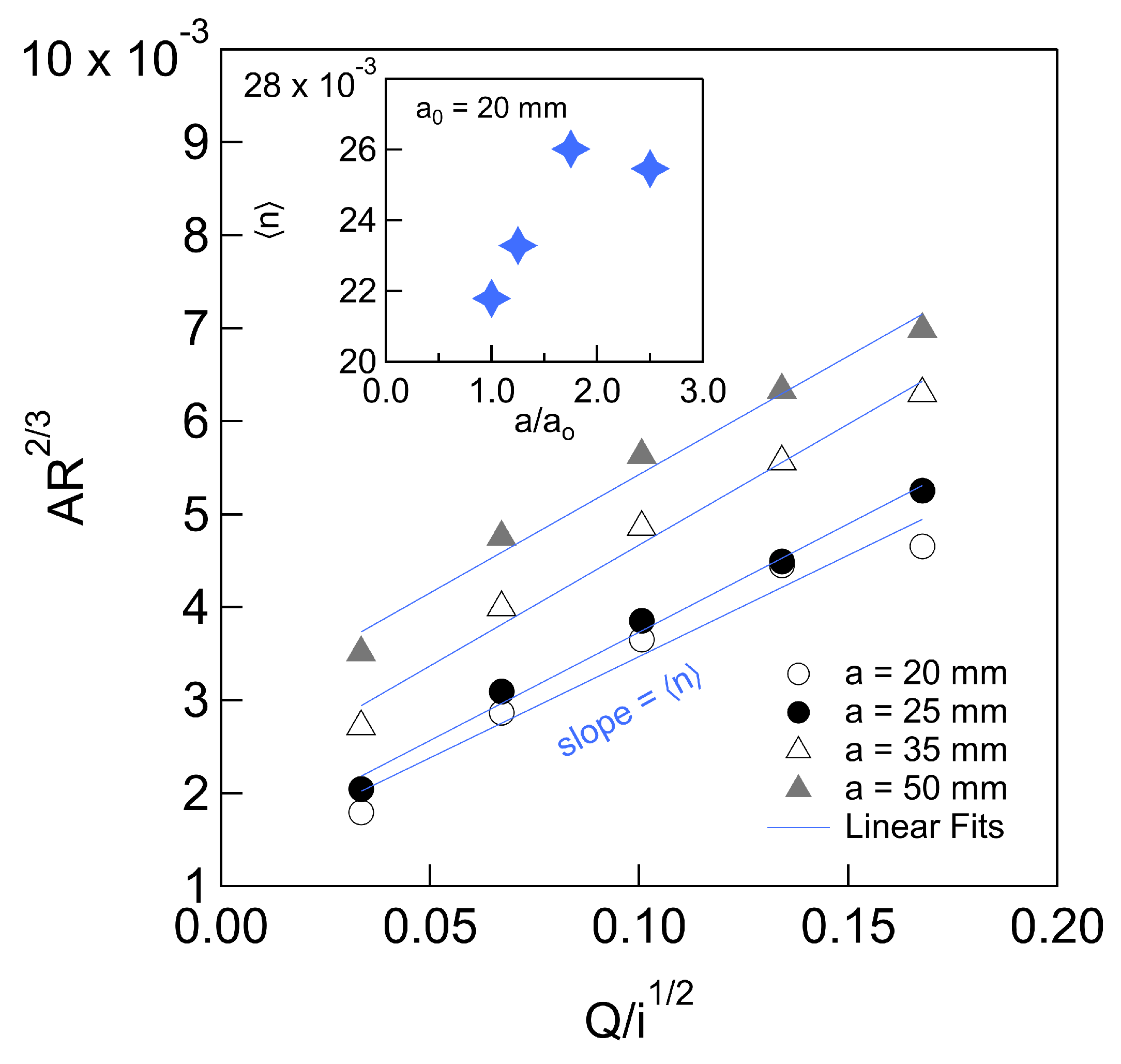
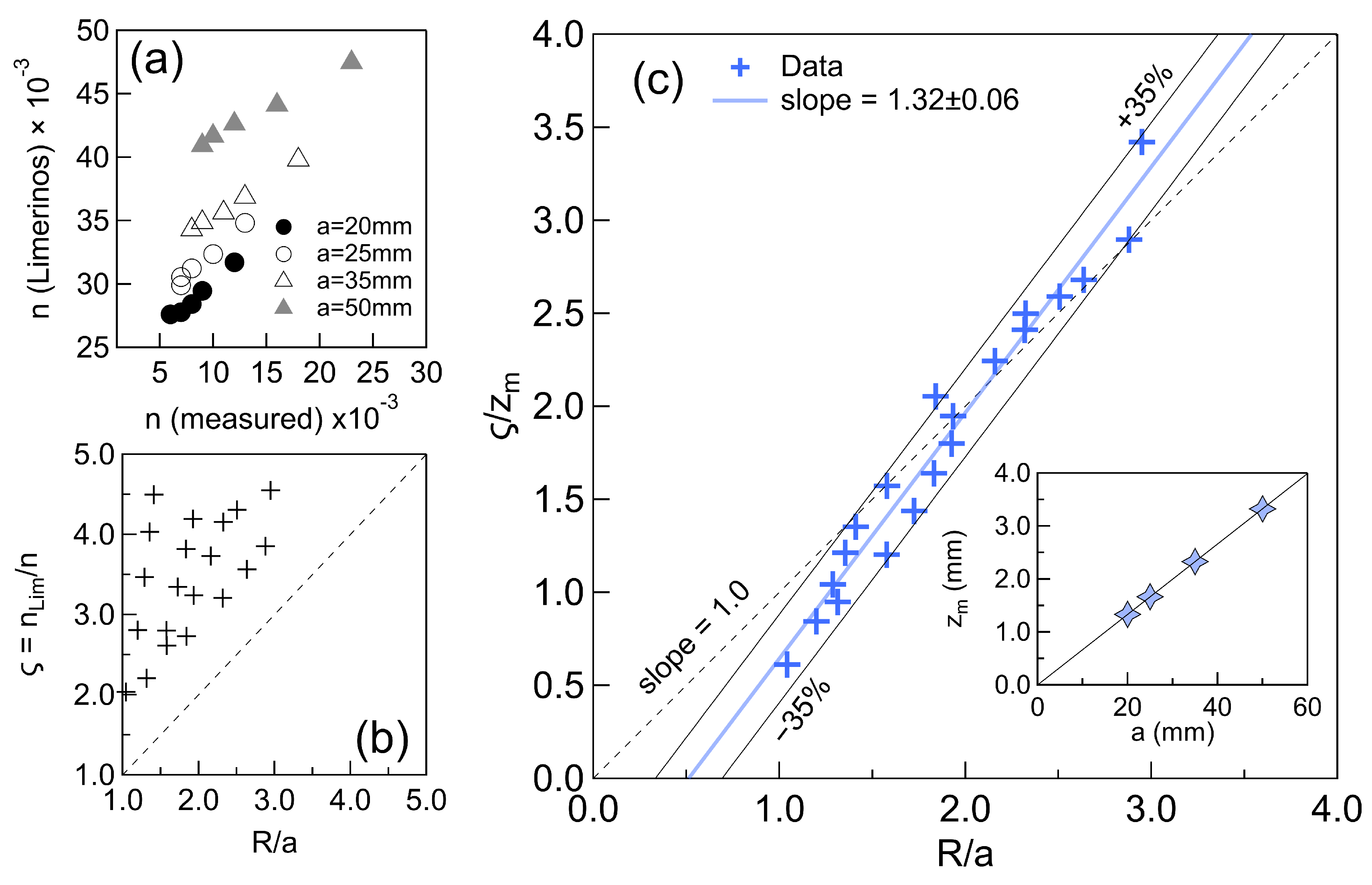
3.5. Determination of the Manning Roughness Coefficient
4. Conclusions
- The free surface deformation is strongly influenced by the size of the cylinders, producing patterns whose amplitudes correlate with the normal flow depth () and the Froude () and Reynold numbers ().
- The Darcy friction factor (f) exhibits a strong inverse relationship with the submergence ratio , and this trend is similarly observed with . These relationships yield robust scaling laws consistent with the early observations of Bazin and Darcy, despite their use of rectangular rather than cylindrical roughness elements.
- The coefficient f follows a Nikuradse-type logarithmic law, with empirical fitting parameters dependent on cylinder size, spacing, and flow regime (as captured by ). The friction factor reaches notably high values, in some instances exceeding 2, reflecting the pronounced energy dissipation in this flow regime.
- An unexpected yet important finding is that Manning’s resistance law is also recoverable from the experimental data. The Manning coefficient (n) shows a clear dependence on the cylinder radius. A detailed analysis reveals new scaling relationships for n as functions of , reaffirming that submergence ratios—expressed either as or —play a central role in controlling flow resistance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PUCV | Pontificia Universidad Catolica de Valparaíso |
Nomenclature
| Fluid kinematic viscosity | |
| Fluid density | |
| Boundary layer thickness | |
| Shear velocity | |
| U | Velocity of the approximating flow |
| a | Radius of the cylinders |
| Time average of flow depth at a given position x | |
| Normal depth of the flow | |
| Amplitude of the surface waves | |
| R | Hydraulic depth |
| Q | Flow rate |
| W | Width of the flume |
| A | Wetted area |
| V | Cross-section average velocity of the flow |
| Froude number | |
| Reynolds number | |
| f | Darcy’s hydrodynamic friction factor |
| Colebrook–White friction factor | |
| Wall roughness size | |
| n | Manning roughness coefficient |
| Limerinos roughness coefficient | |
| J | Friction or energy slope |
| i | Bottom slope of the flume |
References
- Parker, G. 1D Sediment Transport Morphodynamics with Applications to Rivers and Turbidity Currents; CSDMS: Boulder, CO, USA, 2004; Volume 13, p. 2006. [Google Scholar]
- Bathurst, J.C. Flow resistance estimation in mountain rivers. J. Hydraul. Eng. 1985, 111, 625–643. [Google Scholar] [CrossRef]
- Aguirre-Pe, J.; Fuentes, R. Resistance to flow in steep rough streams. J. Hydraul. Eng. 1990, 116, 1374–1387. [Google Scholar] [CrossRef]
- Nicosia, A.; Carollo, F.G.; Ferro, V. Effects of boulder arrangement on flow resistance due to macro-scale bed roughness. Water 2023, 15, 349. [Google Scholar] [CrossRef]
- Abulnaga, B. Slurry Systems Handbook; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Aberle, J.; Smart, G. The influence of roughness structure on flow resistance on steep slopes. J. Hydraul. Res. 2003, 41, 259–269. [Google Scholar] [CrossRef]
- Bathurst, J.C. Flow resistance of large-scale roughness. J. Hydraul. Div. 1978, 104, 1587–1603. [Google Scholar] [CrossRef]
- Bathurst, J.C.; Simons, D.B.; Li, R.M. Resistance equation for large-scale roughness. J. Hydraul. Div. 1981, 107, 1593–1613. [Google Scholar] [CrossRef]
- Cassan, L.; Tien, T.D.; Courret, D.; Laurens, P.; Dartus, D. Hydraulic resistance of emergent macroroughness at large Froude numbers: Design of nature-like fishpasses. J. Hydraul. Eng. 2014, 140, 04014043. [Google Scholar] [CrossRef]
- Coleman, S.; Nikora, V.I.; McLean, S.; Schlicke, E. Spatially averaged turbulent flow over square ribs. J. Eng. Mech. 2007, 133, 194–204. [Google Scholar] [CrossRef]
- Djenidi, L.; Elavarasan, R.; Antonia, R. The turbulent boundary layer over transverse square cavities. J. Fluid Mech. 1999, 395, 271–294. [Google Scholar] [CrossRef]
- Hey, R.D. Flow resistance in gravel-bed rivers. J. Hydraul. Div. 1979, 105, 365–379. [Google Scholar] [CrossRef]
- Thappeta, S.K.; Bhallamudi, S.M.; Fiener, P.; Narasimhan, B. Resistance in steep open channels due to randomly distributed macroroughness elements at large Froude numbers. J. Hydrol. Eng. 2017, 22, 04017052. [Google Scholar] [CrossRef]
- Stoesser, T.; Nikora, V.I. Flow structure over square bars at intermediate submergence: Large Eddy Simulation study of bar spacing effect. Acta Geophys. 2008, 56, 876–893. [Google Scholar] [CrossRef]
- Colosimo, C.; Copertino, V.A.; Veltri, M. Friction factor evaluation in gravel-bed rivers. J. Hydraul. Eng. 1988, 114, 861–876. [Google Scholar] [CrossRef]
- Ferguson, R. Flow resistance equations for gravel-and boulder-bed streams. Water Resour. Res. 2007, 43, 1–12. [Google Scholar] [CrossRef]
- Kumar, B. Flow resistance in alluvial channel. Water Resour. 2011, 38, 745–754. [Google Scholar] [CrossRef]
- Pagliara, S.; Chiavaccini, P. Flow resistance of rock chutes with protruding boulders. J. Hydraul. Eng. 2006, 132, 545–552. [Google Scholar] [CrossRef]
- Pagliara, S.; Das, R.; Carnacina, I. Flow resistance in large-scale roughness condition. Can. J. Civ. Eng. 2008, 35, 1285–1293. [Google Scholar] [CrossRef]
- Darcy, H. Recherches Hydrauliques Entreprises par M. Henry Darcy Continuées par M. Henri Bazin. Rapport fait à l’Académie des Sciences sur un Mémoire de M. Bazin sur le Mouvement de l’eau dans les Canaux déCouverts; Imprenta Impériale de París, Dunod: Paris, France, 1865; Volume 1. [Google Scholar]
- Perry, A.E.; Schofield, W.H.; Joubert, P.N. Rough wall turbulent boundary layers. J. Fluid Mech. 1969, 37, 383–413. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; MC Graw Hill: Seattle, WA, USA, 1988. [Google Scholar]
- Lim, H.S. Open channel flow friction factor: Logarithmic law. J. Coast. Res. 2018, 34, 229–237. [Google Scholar] [CrossRef]
- Davis, J.; Barmuta, L. An ecologically useful classification of mean and near-bed flows in streams and rivers. Freshw. Biol. 1989, 21, 271–282. [Google Scholar] [CrossRef]
- Morris, H.M., Jr. Flow in rough conduits. Trans. Am. Soc. Civ. Eng. 1955, 120, 373–398. [Google Scholar] [CrossRef]
- Morris, H.N. A new concept of flow in rough conduits. In Proceedings of the American Society of Civil Engineers; ASCE: Reston, VA, USA, 1955; Volume 80, pp. 1–31. [Google Scholar]
- Oke, T.R. Boundary Layer Climates; Routledge: London, UK, 2002. [Google Scholar]
- Nikora, V.; McEwan, I.; McLean, S.; Coleman, S.; Pokrajac, D.; Walters, R. Double-averaging concept for rough-bed open-channel and overland flows: Theoretical background. J. Hydraul. Eng. 2007, 133, 873–883. [Google Scholar] [CrossRef]
- Lawrence, D. Macroscale surface roughness and frictional resistance in overland flow. Earth Surf. Process. Landforms J. Br. Geomorphol. Group 1997, 22, 365–382. [Google Scholar] [CrossRef]
- Lawrence, D. Hydraulic resistance in overland flow during partial and marginal surface inundation: Experimental observations and modeling. Water Resour. Res. 2000, 36, 2381–2393. [Google Scholar] [CrossRef]
- Nikuradse, J. Laws of Flow in Rough Pipes; NACA TN 1292; NASA: Washington, DC, USA, 1950.
- Bayazit, M. Free surface flow in a channel of large relative roughness. J. Hydraul. Res. 1976, 14, 115–126. [Google Scholar] [CrossRef]
- McSherry, R.; Chua, K.; Stoesser, T.; Mulahasan, S. Free surface flow over square bars at intermediate relative submergence. J. Hydraul. Res. 2018, 56, 825–843. [Google Scholar] [CrossRef]
- Schindler, R.J.; Ackerman, J.D. The environmental hydraulics of turbulent boundary layers. In Advances in Environmental Fluid Mechanics; World Scientific: Singapore, 2010; pp. 87–125. [Google Scholar]
- Martinez, F.; Farias, J. Friction factor and surface deformation of subcritical flows on a train of cylindrical ribs. In Proceedings of the 12th International Conference on Fluvial Hydraulics, River Flow, Liverpool, UK, 2–6 September 2024; CRC Press: Boca Raton, FL, USA, 2025; pp. 359–367. [Google Scholar]
- Forbes, L.K.; Schwartz, L.W. Free-surface flow over a semicircular obstruction. J. Fluid Mech. 1982, 114, 299–314. [Google Scholar] [CrossRef]
- Vigié, F. Etude Expérimentale d’un écoulement à surface Libre Au-Dessus d’un Obstacle. Ph.D. Thesis, Institut National Polytechnique, Toulouse, France, 2005. [Google Scholar]
- Ryu, D.; Choi, D.H.; Patel, V. Analysis of turbulent flow in channels roughened by two-dimensional ribs and three-dimensional blocks. Part I: Resistance. Int. J. Heat Fluid Flow 2007, 28, 1098–1111. [Google Scholar] [CrossRef]
- Monin, A.; Yaglom, A. Statistical Fluid Mechanics: Mechanics of Turbulence; MIT Press: Cambridge, MA, USA, 1975; Volume 1, 874p. [Google Scholar]
- Pokrajac, D.; Campbell, L.J.; Nikora, V.; Manes, C.; McEwan, I. Quadrant analysis of persistent spatial velocity perturbations over square-bar roughness. Exp. Fluids 2007, 42, 413–423. [Google Scholar] [CrossRef]
- Choo, Y.M.; Kim, J.G.; Park, S.H. A Study on the friction factor and Reynolds number relationship for flow in smooth and rough channels. Water 2021, 13, 1714. [Google Scholar] [CrossRef]
- Blasius, H. Das aehnlichkeitsgesetz bei reibungsvorgängen in flüssigkeiten. In Mitteilungen über Forschungsarbeiten auf dem Gebiete des Ingenieurwesens: Insbesondere aus den Laboratorien der Technischen Hochschulen; Springer: Berlin/Heidelberg, Germany, 1913; pp. 1–41. [Google Scholar]
- Colebrook, C.F. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. Journal of the Institution of Civil Engineers 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Limerinos, J.T. Determination of the Manning Coefficient from Measured Bed Roughness in Natural Channels; US Government Printing Office: Washington, DC, USA, 1970.
- HEC-RAS 2D Sediment Technical Reference Manual. Available online: https://www.hec.usace.army.mil/confluence/rasdocs/d2sd/ras2dsedtr/latest/model-description/bedform-geometry-and-hydraulic-roughness/bottom-roughness (accessed on 21 March 2024).




| Array | a (mm) | e (mm) | N - | (mm) |
|---|---|---|---|---|
| 1 | 20.0 | 255.3 | 39 | 46.4–88.1 |
| 2 | 25.0 | 319.1 | 31 | 50.6–95.9 |
| 3 | 35.0 | 446.7 | 22 | 61.1–108.9 |
| 4 | 50.0 | 638.2 | 16 | 72.6–117.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez, F.; Farías, J. Turbulent and Subcritical Flows over Macro-Roughness Elements. Water 2025, 17, 1301. https://doi.org/10.3390/w17091301
Martínez F, Farías J. Turbulent and Subcritical Flows over Macro-Roughness Elements. Water. 2025; 17(9):1301. https://doi.org/10.3390/w17091301
Chicago/Turabian StyleMartínez, Francisco, and Javier Farías. 2025. "Turbulent and Subcritical Flows over Macro-Roughness Elements" Water 17, no. 9: 1301. https://doi.org/10.3390/w17091301
APA StyleMartínez, F., & Farías, J. (2025). Turbulent and Subcritical Flows over Macro-Roughness Elements. Water, 17(9), 1301. https://doi.org/10.3390/w17091301







