Waterway Regulation Effects on River Hydrodynamics and Hydrological Regimes: A Numerical Investigation
Abstract
1. Introduction
2. Materials and Methods
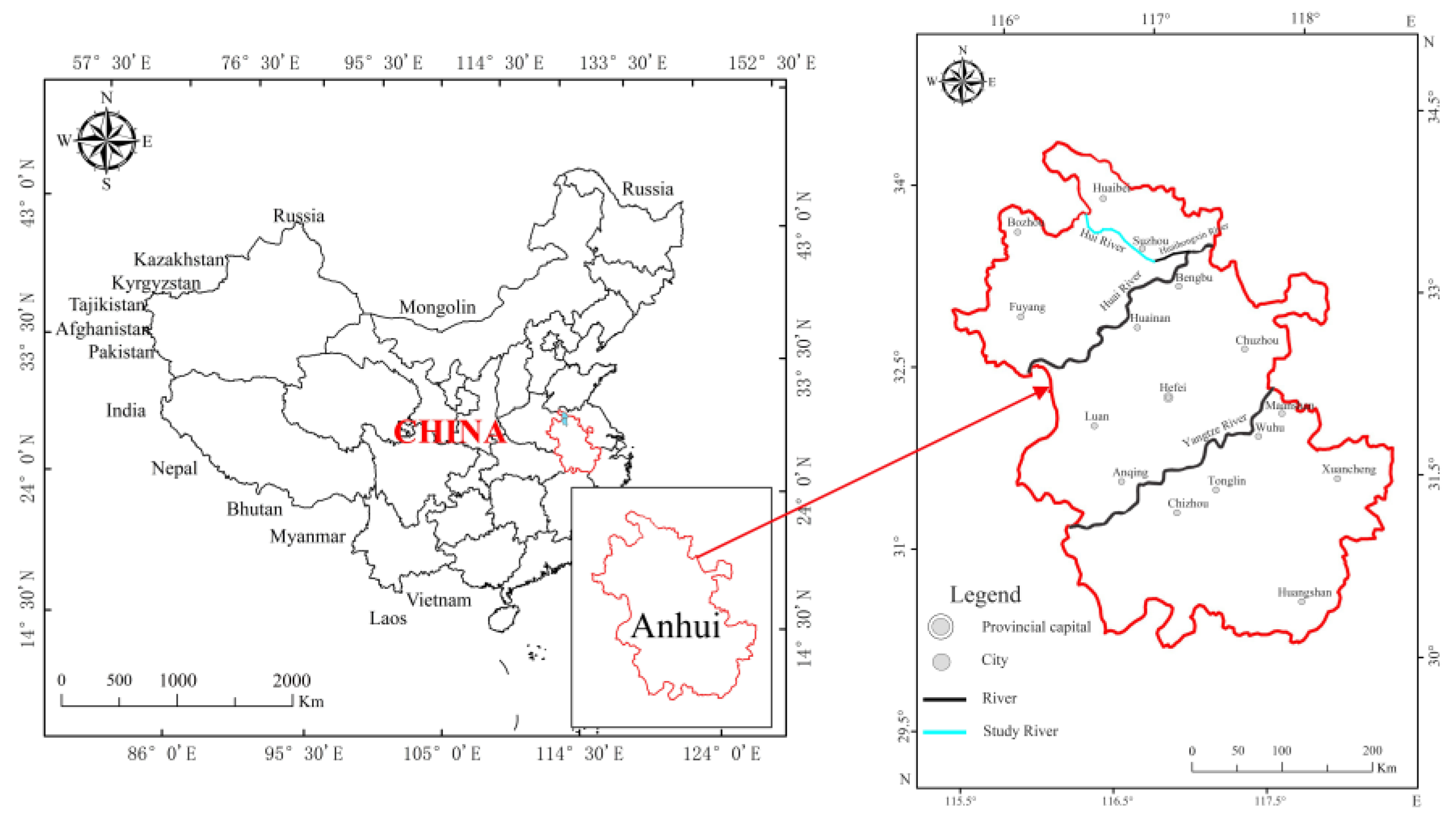
2.1. Study Area
2.2. Modeling of River Flow Dynamics
2.2.1. Mathematical Model of River Flow Dynamics
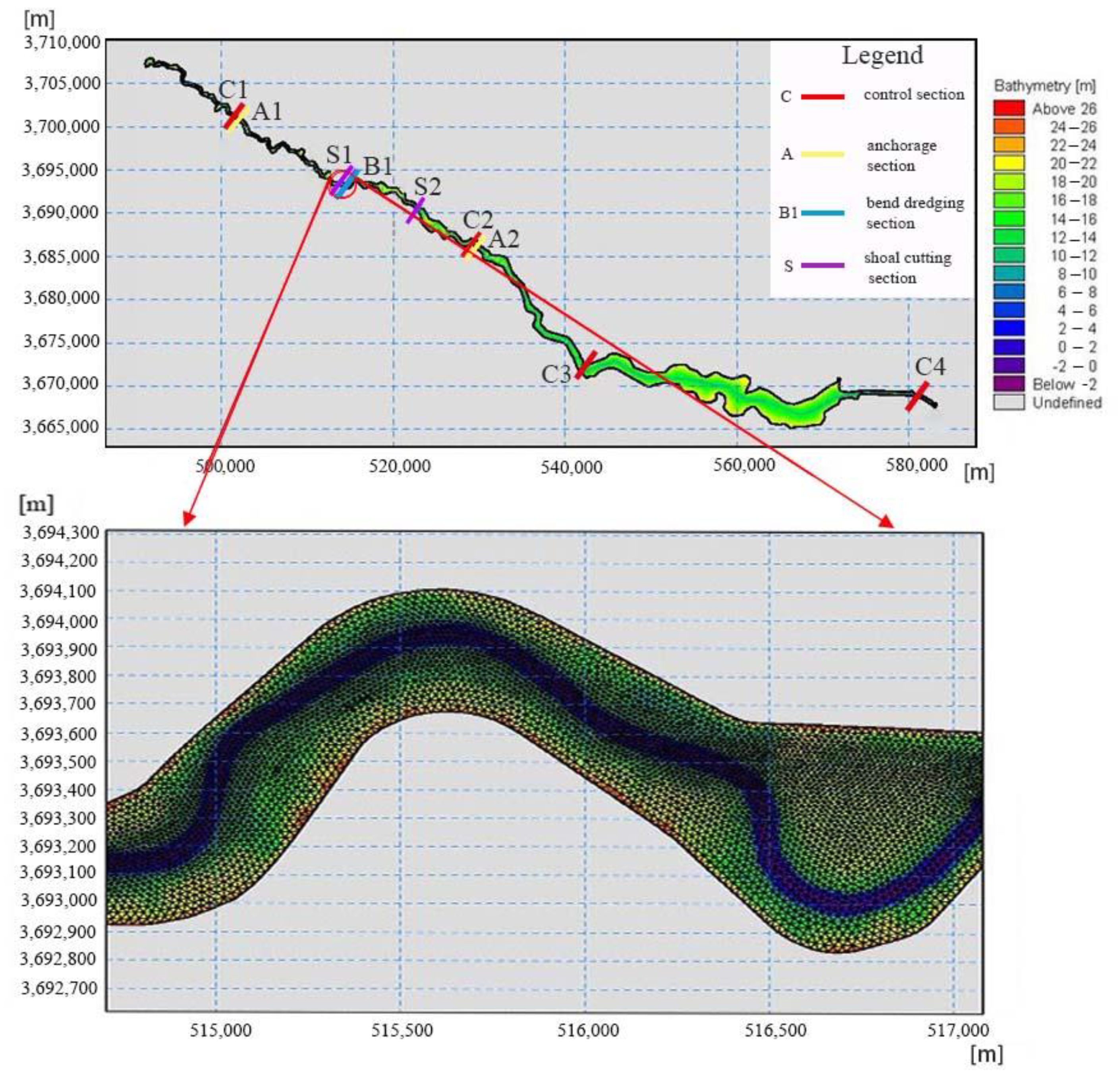
2.2.2. Establishment of a Two-Dimensional Numerical Model of River Flow
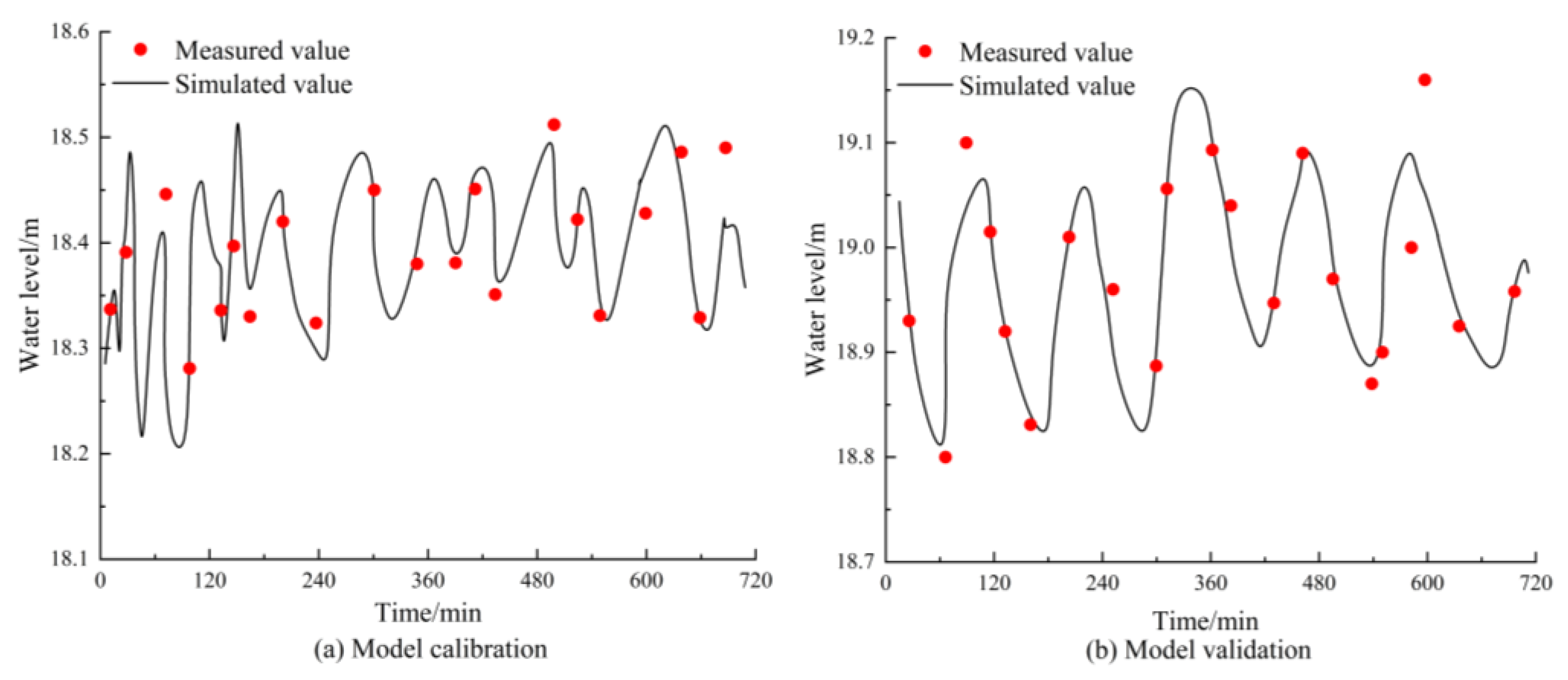
2.2.3. Calibration and Validation of Parameters
3. Results and Analysis
3.1. Analysis of the Impacts of the Waterway Project on River Water Levels
3.2. Analysis of Flow Velocity Impacts Pre- and Post-Implementation of the Navigation Channel Project
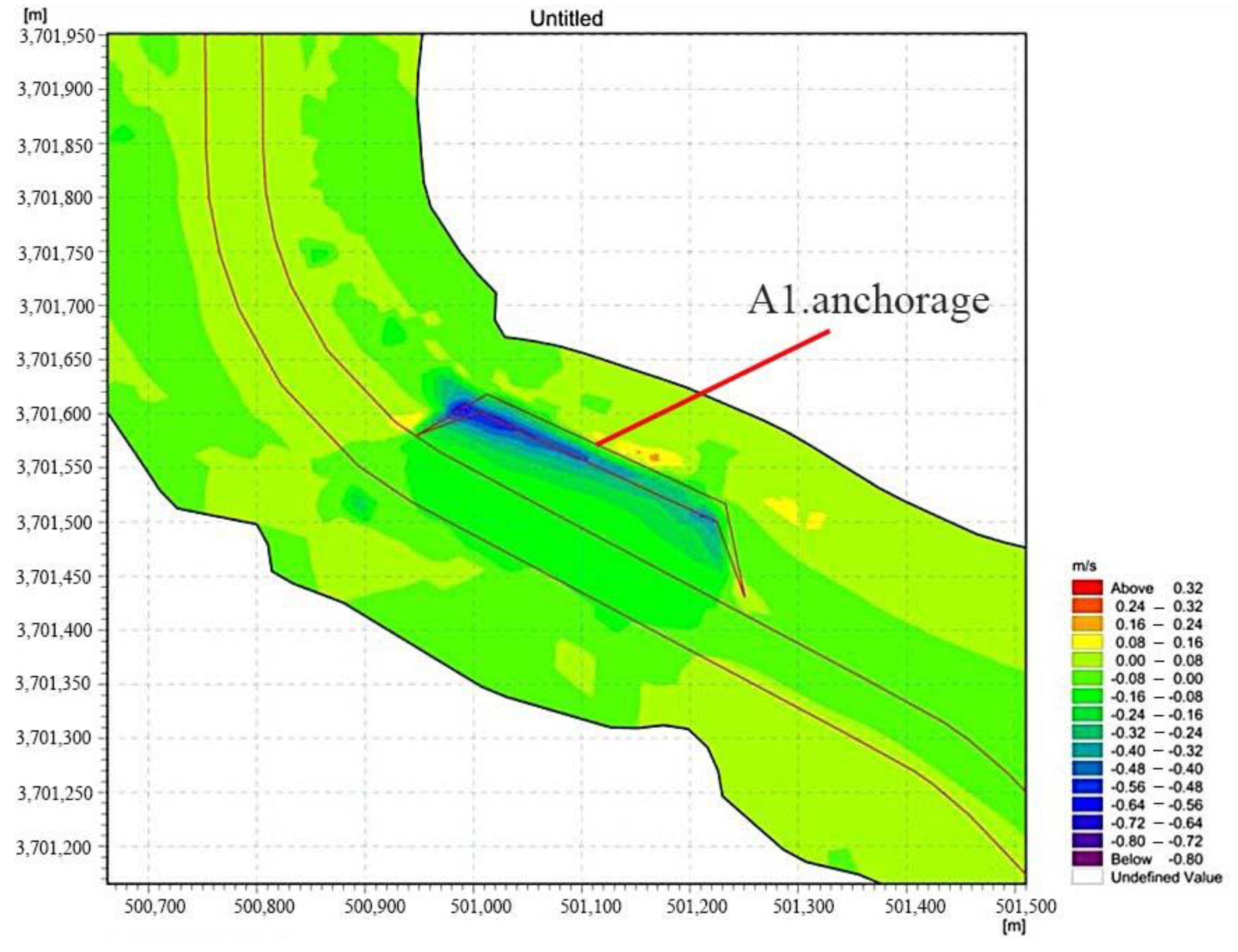
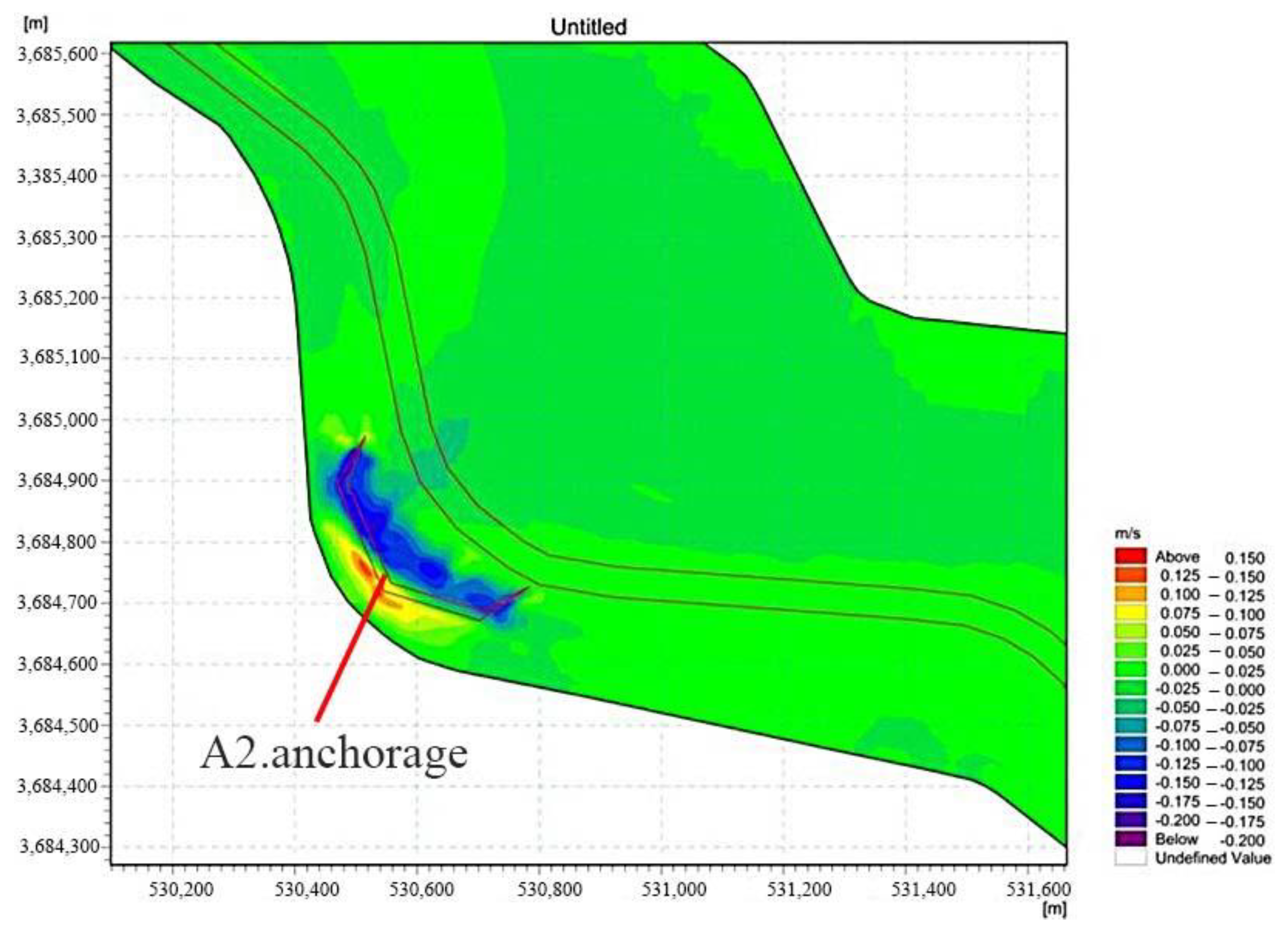
3.2.1. Impact Analysis of Anchorage Projects on River Hydrological Characteristics
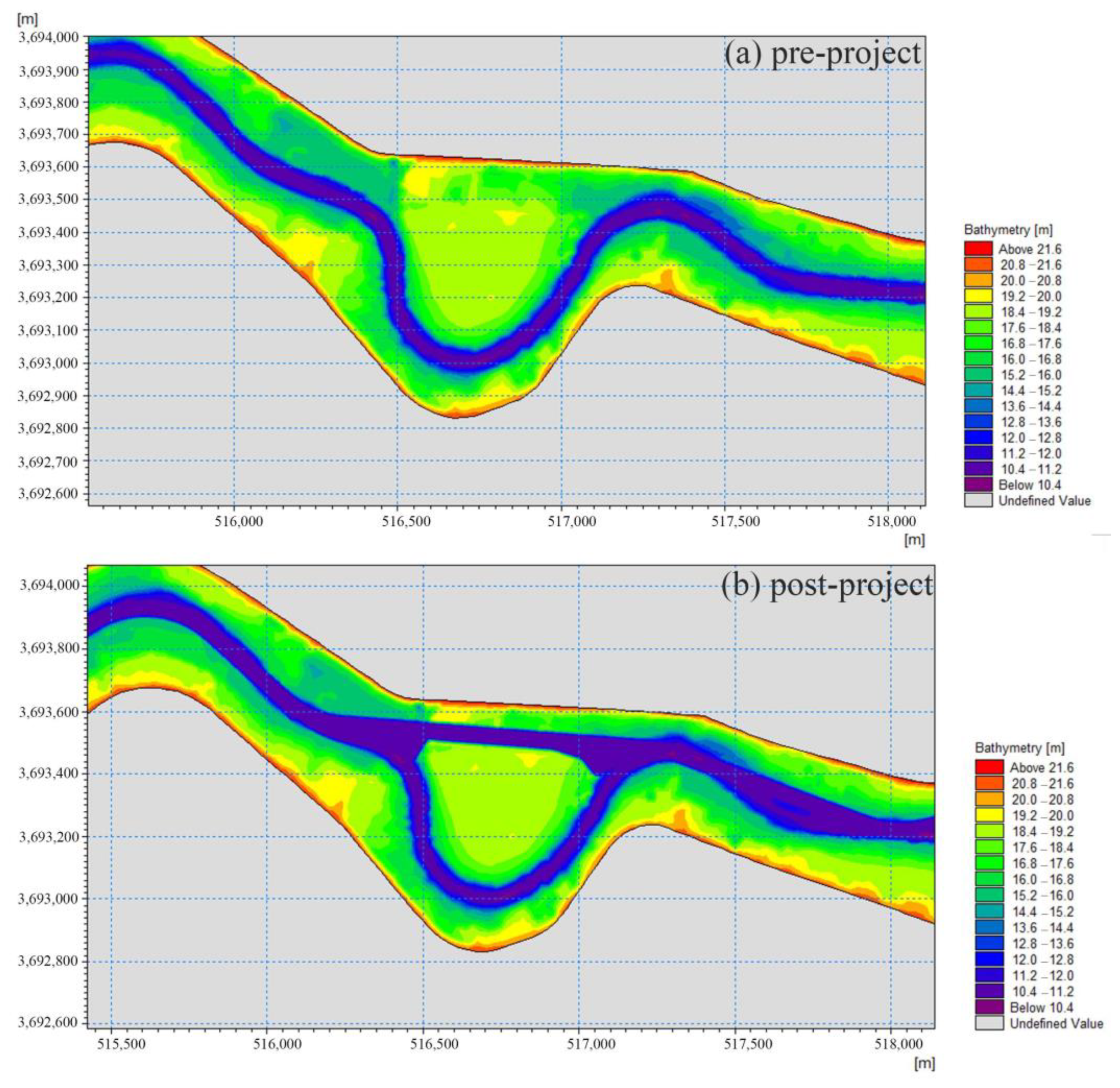
3.2.2. Impact Analysis of Left Branch Dredging in a Curved River Section on the Hydrological Characteristics
3.2.3. Impact Analysis of the Shoal Cutting Project on the Hydrological Characteristics
4. Discussion
- (1)
- Impact on the river water level
- (2)
- Impact on river water flow velocity
- (3)
- Impact on river regime
- (4)
- Influence on sediment movement
- (5)
- Impact on the river ecological environment
- (1)
- Optimizing engineering design
- (2)
- Improving hydrological dynamic monitoring conditions
- (3)
- Ecological protection and restoration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Geoffrey, E.P.; Angela, M.G. Dams and geomorphology: Research progress and future directions. Geomorphology 2004, 71, 27–47. [Google Scholar]
- Ibisate, A.; Díaz, E.; Ollero, A.; Acín, V.; Granado, D. Channel response to multiple damming in a meandering river, middle and lower Aragón River (Spain). Hydrobiologia 2013, 712, 5–23. [Google Scholar] [CrossRef]
- Yuan, W.H.; Yin, D.W.; Finlayson, B.; Chen, Z.Y. Assessing the potential for change in the middle Yangtze River channel following impoundment of the Three Gorges Dam. Geomorphology 2012, 147, 27–34. [Google Scholar] [CrossRef]
- Lee, J.S.; Julien, P.Y. Downstream Hydraulic Geometry of Alluvial Channels. J. Hydraul. Eng. 2006, 132, 1347–1352. [Google Scholar] [CrossRef]
- Zhou, R.S.; Huang, Z.X.; Wang, T. Comparison of Channel Improvement Schemes for the Mangniushao Shoal Reach of the Songhua River. Port Waterw. Eng. 2024, 4, 119–125+182. [Google Scholar]
- Liang, W.; Wang, J.; Leung, C.; Goh, S.; Sang, S. Opportunities and challenges for gas coproduction from coal measure gas reservoirs with coal-shale-tight sandstone layers: A review. Deep Undergr. Sci. Eng. 2025, 4, 83–104. [Google Scholar] [CrossRef]
- Pannone, M.; De Vincenzo, A. On the Prediction of the Characteristic Times of River Meander Cutoff Sequence: Theoretical Model and Comparison with Laboratory and Field Observations. Water Resour. Res. 2022, 58, e2021WR031661. [Google Scholar] [CrossRef]
- Yang, Y.P.; Li, M.; Liu, W.L. Relationship between the Evolution of Bars and Channels in the Jingjiang Reach of the Yangtze River and the Improvement of Navigation Depth Resources. Adv. Water Sci. 2022, 33, 240–252. [Google Scholar]
- Korpak, J. Assessment of Changes in Channel Morphology in a Mountain River Regulated Using Grade Control Structures. J. Ecol. Eng. 2020, 21, 163–176. [Google Scholar] [CrossRef]
- Han, Z.; Xie, H.; Li, H.; Li, W.; Wen, X.; Xie, M. Morphological Evolution of the Lingding Channel in the Pearl River Estuary over the Last Decades. J. Coast. Res. 2020, 37, 104–112. [Google Scholar] [CrossRef]
- Shiono, K.; Chan, T.L.; Spooner, J.; Rameshwaran, P.; Chandler, J.H. The effect of floodplain roughness on flow structures, bedforms and sediment transport rates in meandering channels with overbank flows: Part II. J. Hydraul. Res. 2009, 47, 20–28. [Google Scholar] [CrossRef]
- Rui, S.; Zhang, H.; Xu, H.; Zha, X.; Xu, M.; Shen, K. Seabed structures and foundations related to deep-sea resource development: A review based on design and research. Deep Undergr. Sci. Eng. 2024, 3, 131–148. [Google Scholar] [CrossRef]
- Li, S.X. Channel regulation engineering plan for Reach in Xijiang River. IOP Conf. Ser. Earth Environ. Sci. 2021, 643, 012119. [Google Scholar] [CrossRef]
- Czajka, A.; Nádudvari, Á. Anthropogenic influences on the morphodynamics of the upper Odra channel. Environ. Socio-Econ. Stud. 2016, 4, 43–52. [Google Scholar] [CrossRef][Green Version]
- Xia, J.Q.; Zong, Q.L.; Deng, S.S.; Xu, Q.X.; Lu, J.Y. Seasonal variations in composite riverbank stability in the Lower Jingjiang Reach, China. J. Hydrol. 2014, 519, 3664–3673. [Google Scholar] [CrossRef]
- Zhong, Y.Z.; Tong, R. Research on the Construction of a Three-Dimensional Hydrodynamic Model for Complex Mountainous River Channels and Estimation of Flash Flood Discharge. Water Resour. Hydropower Eng. 2024, 55, 497–501. [Google Scholar]
- Millar, R.G. Theoretical regime equations for mobile gravel-bed rivers with stable banks. Geomorphology 2004, 64, 207–220. [Google Scholar] [CrossRef]
- Xu, F. Research on Waterway Regulation Technology—Taking the Channel Regulation of the Downstream Section of Baishi kiln in Beijiang River as an Example. Master’s Thesis, Hubei University of Technology, Wuhan, China, 2017. [Google Scholar]
- Huang, Y.; Zhang, J.B.; Zhou, Q.; Hou, J. Effect of newly-developed channel on water and sediment transport in curved and branched rivers in mountainous areas. Port Waterw. Eng. 2021, 9, 93–100. [Google Scholar]
- Wang, H.F. Gabion Riprap Technology for Bank Protection Construction of Important Flood Storage Area in Huai River Basin. Henan Water Conserv. S.-N. Water Divers. 2024, 53, 32–33. [Google Scholar]
- Chen, K.F.; Lu, P.D.; Wang, N.R. Characteristics and Causes of Re-siltation of Estuarine Bar Channels Under the Influence of Channel Improvement Projects: A Case Study of the Sheyang Port Channel. Adv. Water Sci. 2017, 28, 240–248. [Google Scholar]
- Banasiak, R. Large-Scale Two-Dimensional Cascade Modeling of the Odra River for Flood Hazard Management. Water 2024, 16, 20. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Sawczynski, S.Z.; Biegowski, J. An Equilibrium Transport Formula for Modeling Sedimenta-tion of Dredged Channels. Coast. Eng. J. 2017, 59, 1–35. [Google Scholar] [CrossRef]
- Leedertse, J.J.; Gritton, E.C.; Liu, S.K. A water-quality simulation model for well-mixed estuaries and coastal seas. In The Rand Corporation Technical Report R-708-NYC; RAND: Santa Monica, CA, USA, 1971; Volume 2, p. 43. [Google Scholar]
- Syed, Z.H.; Choi, G.; Byeon, S. A Numerical Approach to Predict Water Levels in Ungauged Regions—Case Study of the Meghna River Estuary, Bangladesh. Water 2018, 10, 110. [Google Scholar] [CrossRef]
- Salman, S.; Abolfazl, S.; Bahram, S.; Sayed, M.B. Modeling Spatial Pattern of Salinity Using MIKE21 and Prin-cipal Component Analysis Technique in Urmia Lake. Curr. World Environ. 2015, 10, 626–633. [Google Scholar]
- De, S.G.; Therrien, R.; Refsgaard, J.C. Simulating seasonal variations of tile drainage discharge in an agricultural catchment. Water Resour. Res. 2017, 53, 3896–3920. [Google Scholar]
- Gao, Y.; Li, F.P.; Mao, L.C.; Yan, N.X.; Peng, C.K.; Tao, H. Simulation on water quality of reservoir at con-struction phase by pollutant release from oxidation of waste rocks rich S and Fe. Environ. Technol. Innov. 2022, 28, 102860. [Google Scholar] [CrossRef]
- Li, G.; Zhu, H.J.; Hong, F.Z.; Wei, W.; Jiang, S.; Zhang, K.Y.; Si, Y.H.; Hui, M. A combined hydrodynamic model and deep learning method to predict water level in ungauged rivers. J. Hydrol. 2023, 625, 130025. [Google Scholar] [CrossRef]
- Zhang, K.C.; Li, Q.J.; Zhang, J.; Shi, H.Y.; Yu, J.; Guo, X.C.; Du, Y.G. Simulation and Analysis of Back Siltation in a Navigation Channel Using MIKE 21. J. Ocean. Univ. China 2022, 21, 893–902. [Google Scholar] [CrossRef]
- Ramos, H.C.; Besharat, M.C. Urban flood risk and economic viability analyses of a smart sustainable drainage system. Sustainability 2021, 13, 13889. [Google Scholar] [CrossRef]
- Wang, M. Research on Remediation Technology of Hekuantan Rapids Group in Lancang River. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2019. [Google Scholar]
- Ni, Z.H.; Kong, X.Y.; Zhang, X.J. Calculation and analysis of channel improvement scheme in Zhushitan reservoir area of Minjiang river. Port Waterw. Eng. 2015, 9, 112–116+137. [Google Scholar]
- Surendra, K.M.; Vijay, P.S. Role of dimensionless numbers in wave analysis. Hydrol. Process. 2003, 17, 651–669. [Google Scholar]
- Dong, X.J.; Liu, X.; Dong, Z. Numerical Simulation of Rainfall Runoff in the Tai-Dong River Basin. Yangtze River 2021, 52, 77–80. [Google Scholar]
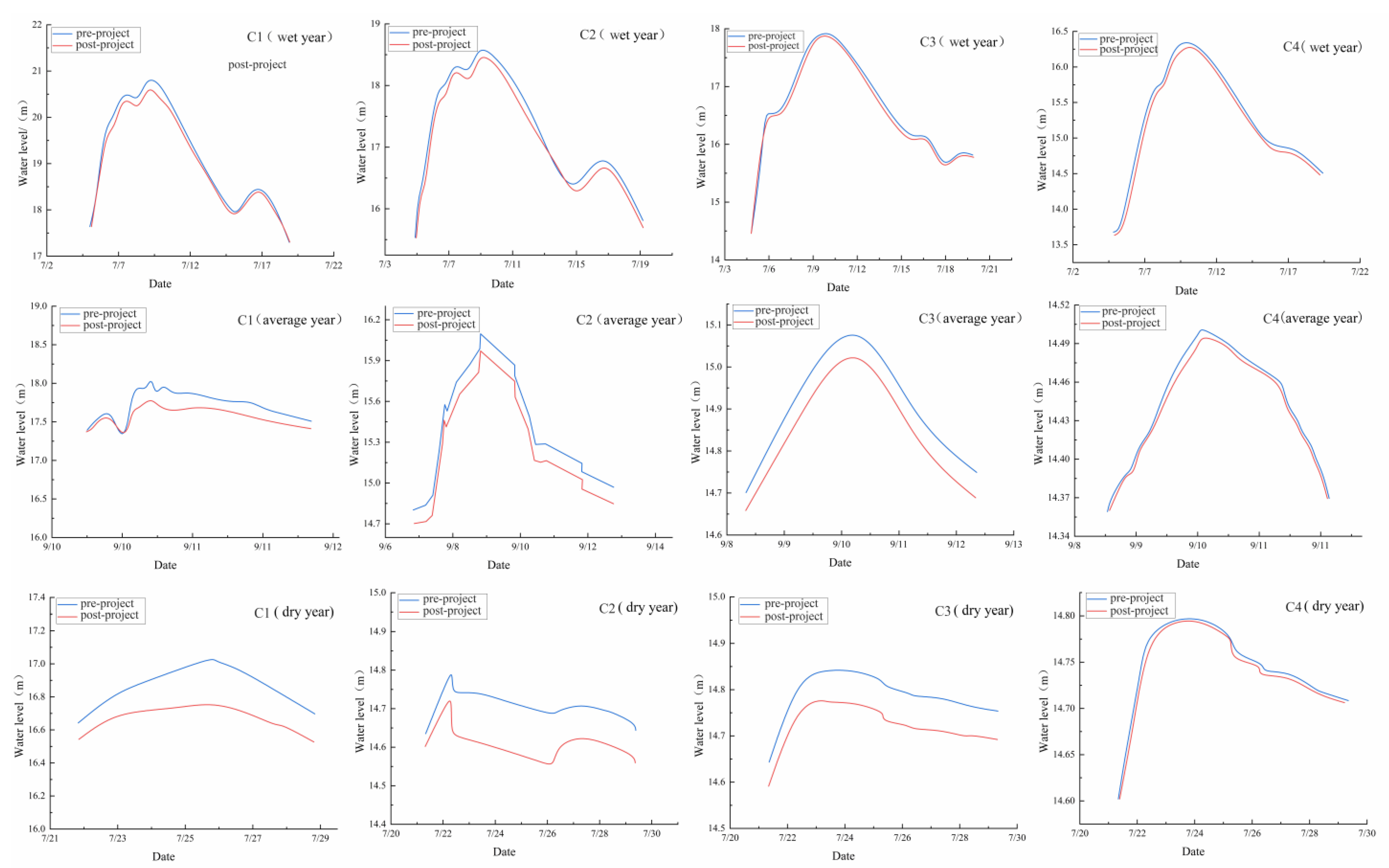
| Control Sections | The Maximum Water Level Drawdown Before and After the Project in a Wet Year (m) | The Maximum Water Level Drawdown Before and After the Project in a Normal Water Year (m) | The Maximum Water Level Drawdown Before and After the Project in a Dry Year (m) |
|---|---|---|---|
| C1 | 0.21 | 0.23 | 0.26 |
| C2 | 0.11 | 0.12 | 0.13 |
| C3 | 0.05 | 0.06 | 0.07 |
| C4 | 0.001 | 0.002 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, C.; Wang, D.; Li, X.; Yao, Z.; Guo, P.; Jiang, C.; Xing, H.; Ren, J.; Tong, F.; Wang, Y. Waterway Regulation Effects on River Hydrodynamics and Hydrological Regimes: A Numerical Investigation. Water 2025, 17, 1261. https://doi.org/10.3390/w17091261
Quan C, Wang D, Li X, Yao Z, Guo P, Jiang C, Xing H, Ren J, Tong F, Wang Y. Waterway Regulation Effects on River Hydrodynamics and Hydrological Regimes: A Numerical Investigation. Water. 2025; 17(9):1261. https://doi.org/10.3390/w17091261
Chicago/Turabian StyleQuan, Chuanjie, Dasheng Wang, Xian Li, Zhenxing Yao, Panpan Guo, Chen Jiang, Haodong Xing, Jianyang Ren, Fang Tong, and Yixian Wang. 2025. "Waterway Regulation Effects on River Hydrodynamics and Hydrological Regimes: A Numerical Investigation" Water 17, no. 9: 1261. https://doi.org/10.3390/w17091261
APA StyleQuan, C., Wang, D., Li, X., Yao, Z., Guo, P., Jiang, C., Xing, H., Ren, J., Tong, F., & Wang, Y. (2025). Waterway Regulation Effects on River Hydrodynamics and Hydrological Regimes: A Numerical Investigation. Water, 17(9), 1261. https://doi.org/10.3390/w17091261








