Study on Characteristics of the Water Diversion Ratio and Impact of the Diversion Dyke at South and North Ports of the Minjiang River During Wet Season
Abstract
:1. Introduction
2. Study Area and Methodology
2.1. Study Area
2.2. Model Establishment
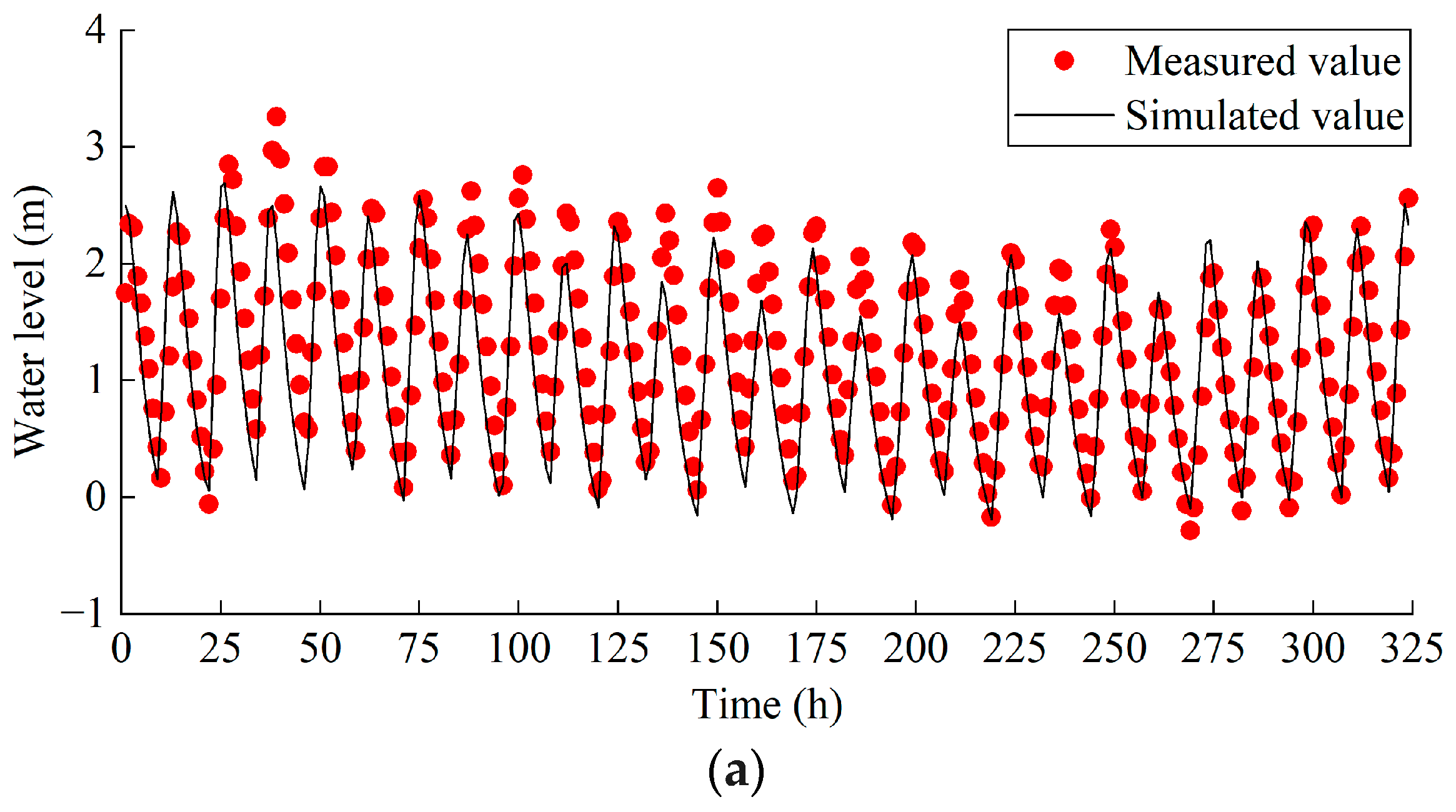
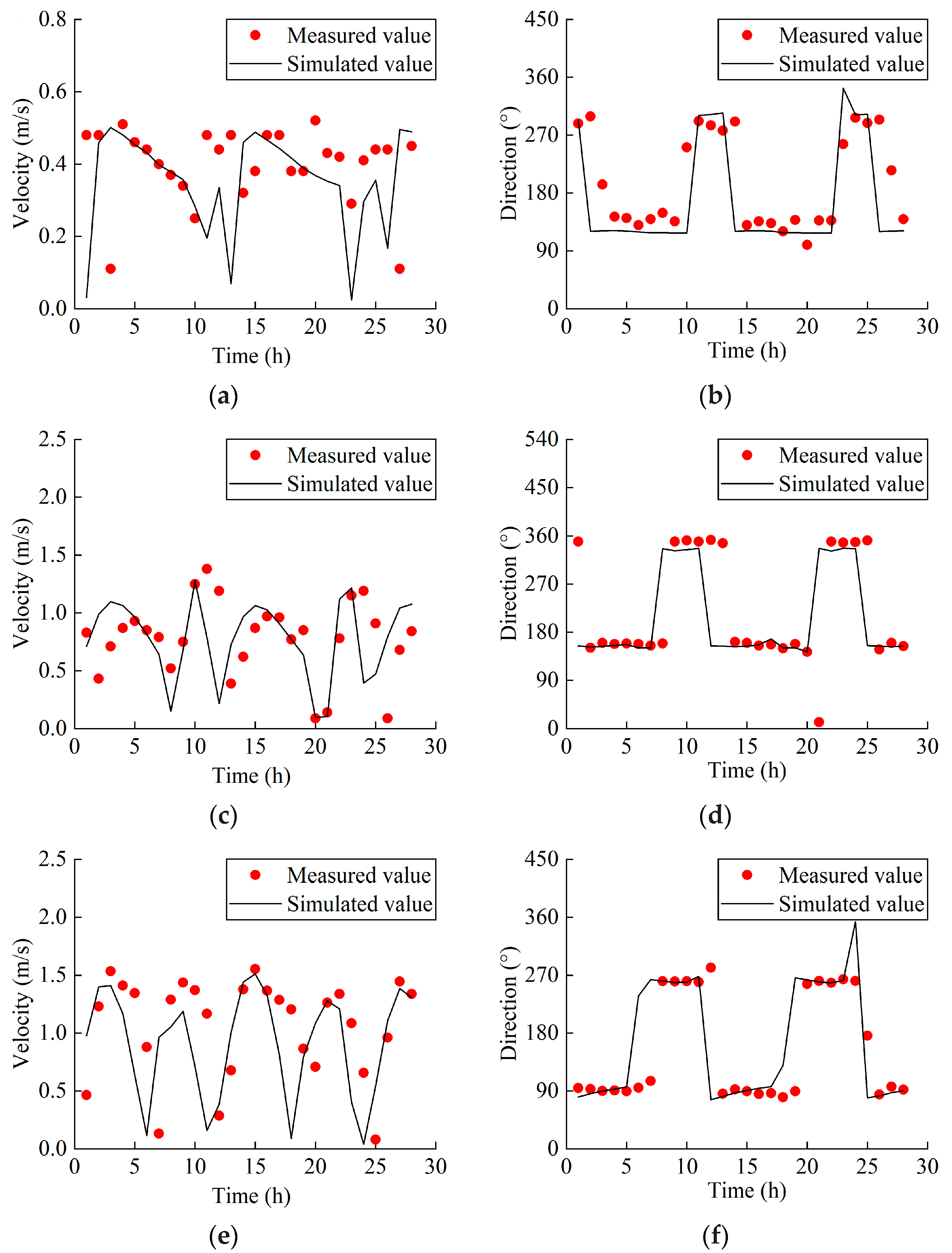
2.3. Model Validation
2.4. Calculation Method of the WDR
3. Results and Discussion
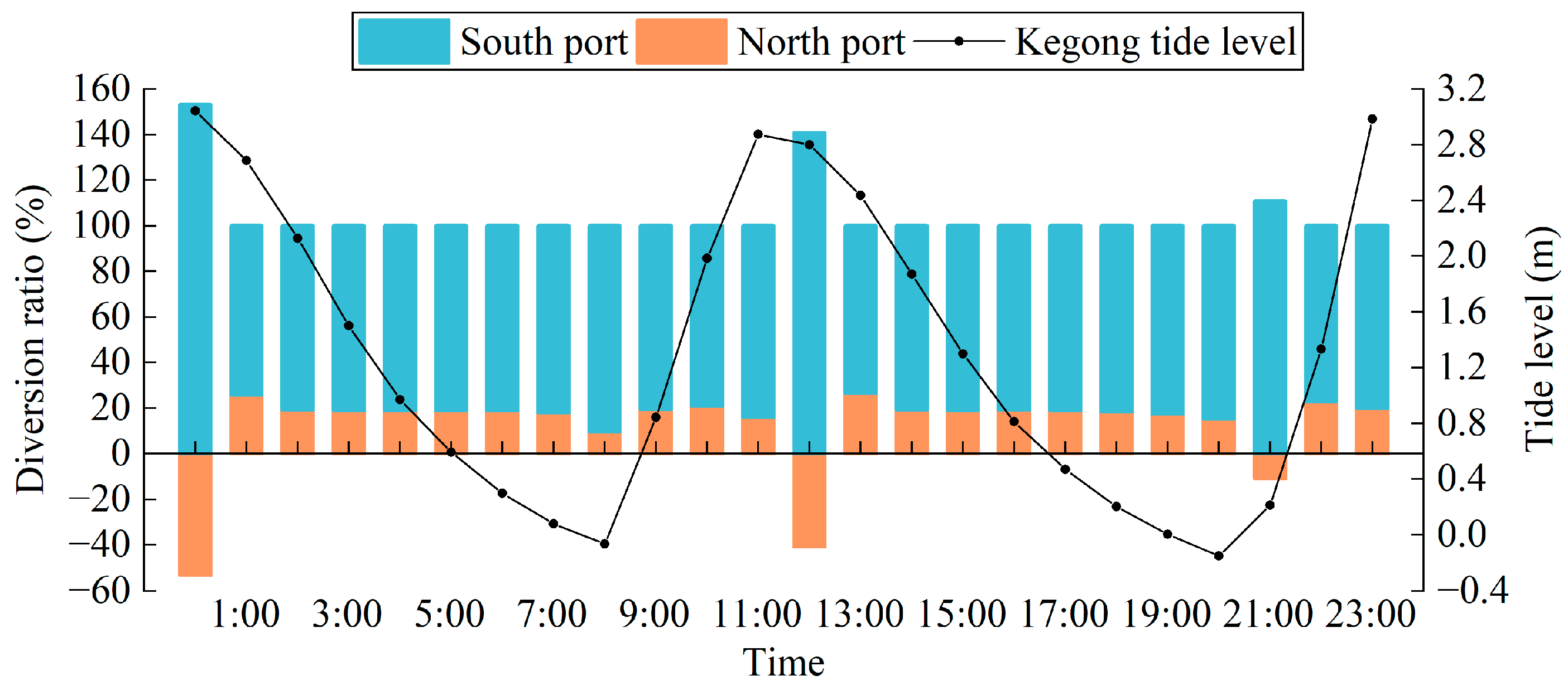
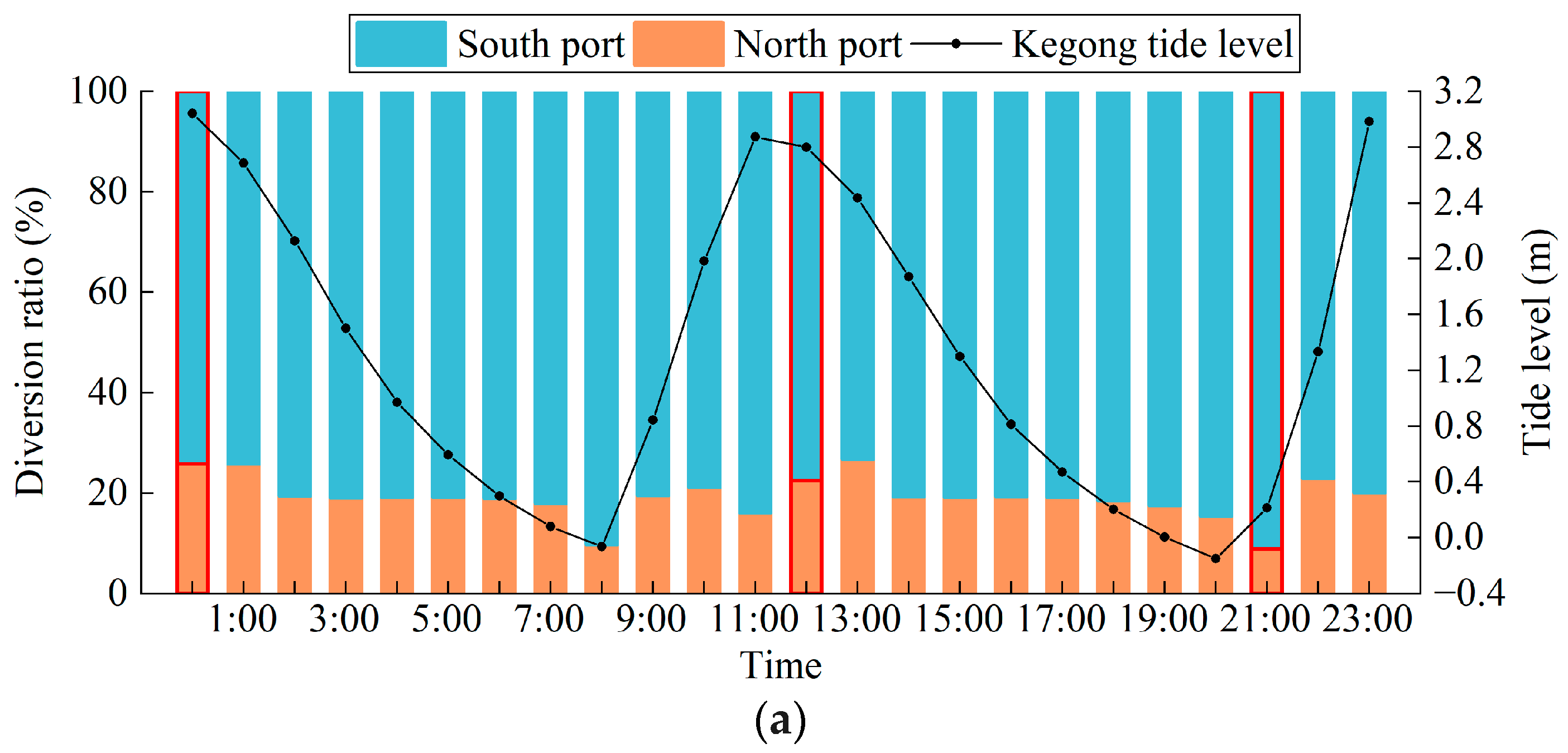
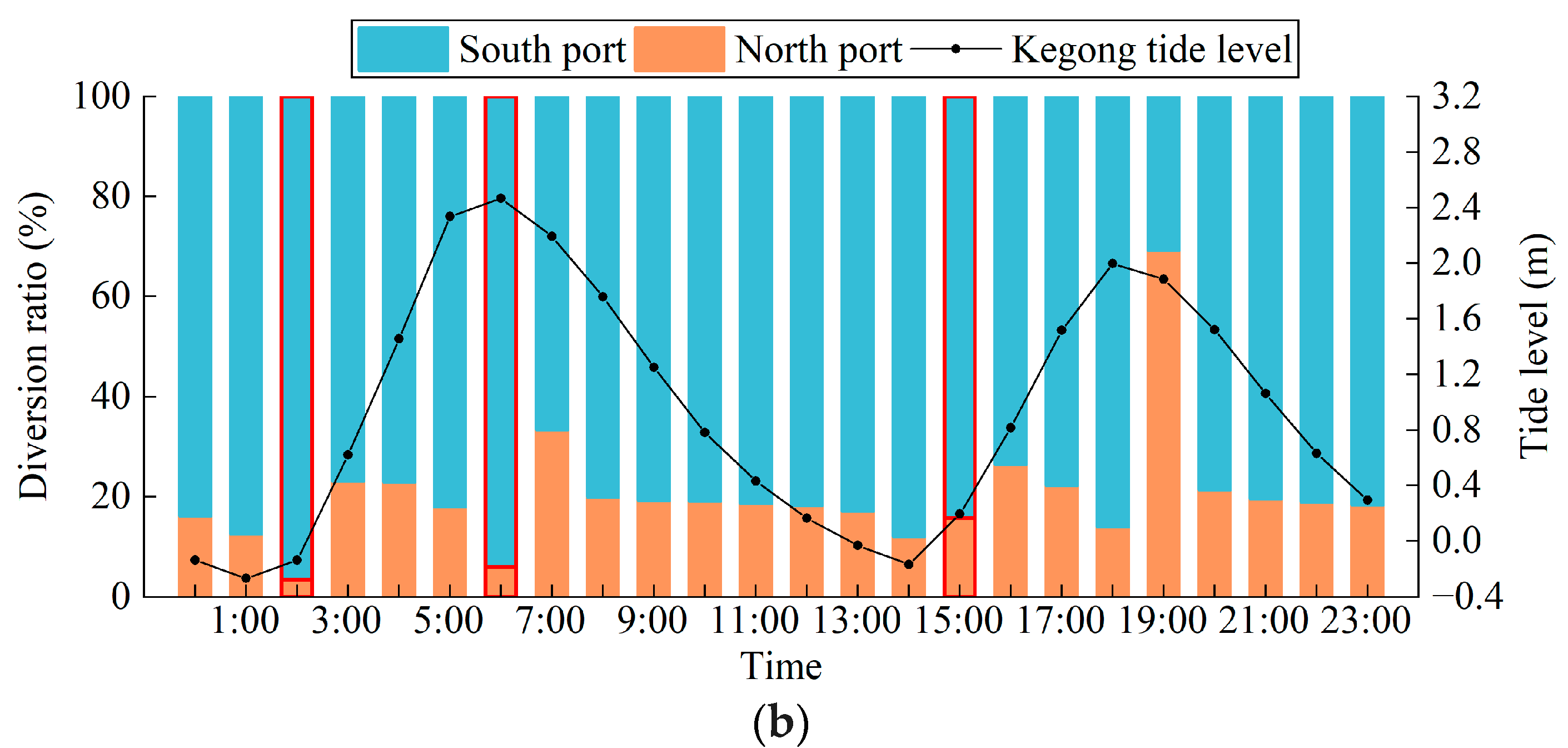
3.1. Spatiotemporal Dynamic Characteristics of the WDR Changes in the South and North Ports
3.2. The Impact of a Diversion Dyke on the WDR
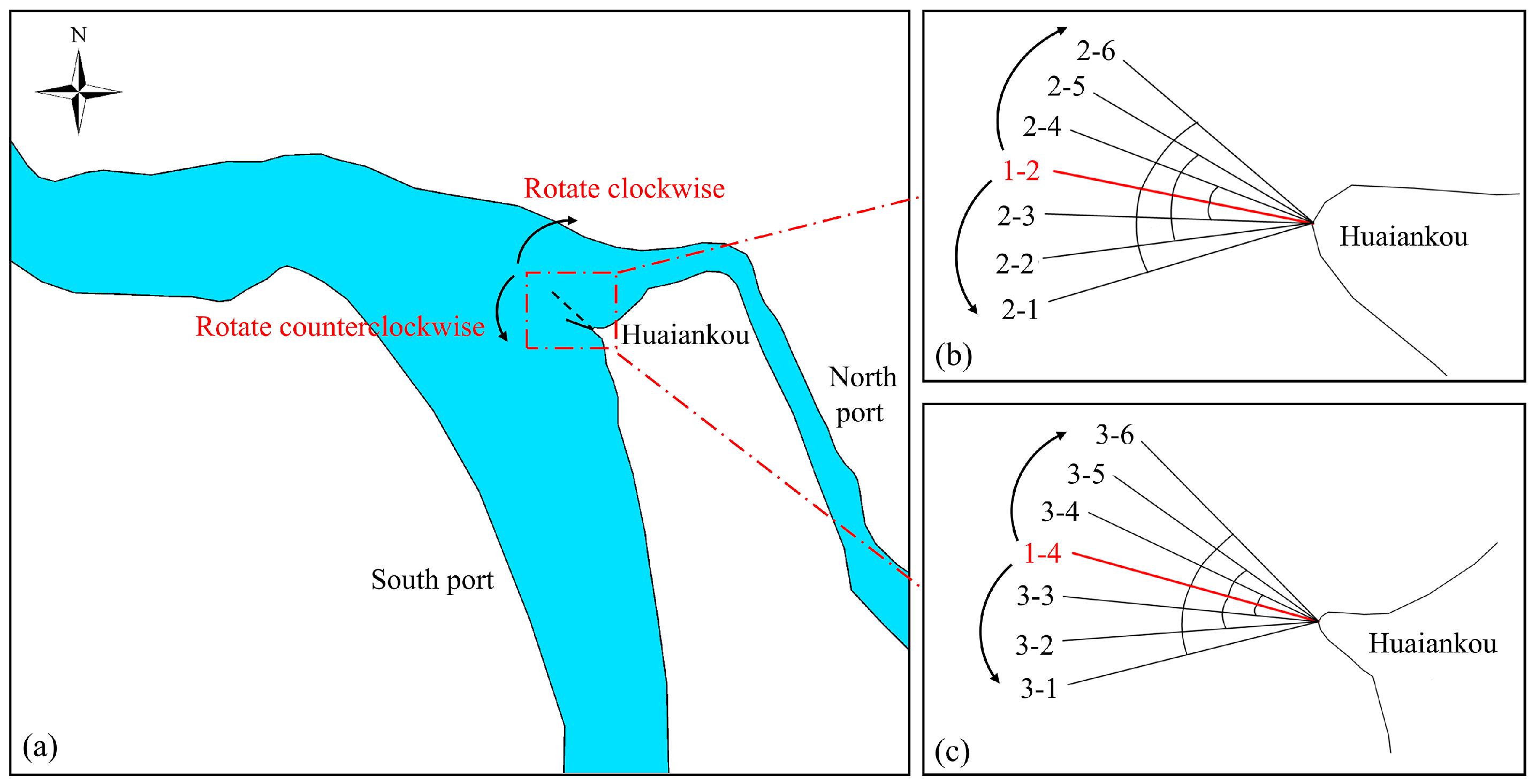
3.2.1. The Variation in Diversion Dyke Length
3.2.2. The Variation in Diversion Dyke Angle
4. Conclusions
- (1)
- During the wet season, the WDR of the North Port is approximately 20%. The WDR is higher during the ebb phase of the neap tide, but lower during its flood phase compared to the spring tide. Regardless of tidal conditions, the WDR of the North Port is consistently higher during the ebb phase than during the flood phase. Furthermore, the WDR during the flooding and ebbing surge periods is higher than during the slack tide moments. During the flood and ebb phases, the WDR of the North Port generally shows a trend of first increasing and then decreasing as the tide level rises and falls.
- (2)
- The WDR of the North Port increases as the length of the existing dyke increases. Once the dyke length exceeds approximately 450 m, the WDR begins to increase significantly. Within the range of 450 m to 600 m, the dyke lengths of 500 m and 550 m are the critical values influencing the variation in the WDR for both the South and North Ports.
- (3)
- The existing diversion dyke with a length of 110 m has little effect on regulating the water flow between the South and North Port, and changes in the angle of the dyke do not significantly affect the WDR. However, the original diversion dyke with a length of 450 m is more sensitive to angle changes. When the rotation angle reaches 30°, the WDR shows a significant change. The larger the counterclockwise rotation angle of the dyke, the more pronounced the increase in the WDR of the North Port.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Q.; Zhu, J.R.; Lyu, H.H.; Pan, S.Q.; Chen, S.L. Impacts of topography change on saltwater intrusion over the past decade in the Changjiang. Estuar. Coast. Shelf Sci. 2018, 231, 106469. [Google Scholar] [CrossRef]
- Hu, P.; Lei, Y.L.; Deng, S.Y.; Cao, Z.X.; Liu, H.H.; He, Z.G. Role of bar-channel interactions in a dominant branch shift: The Taipingkou waterway, Yangtze River, China. River Res. Appl. 2021, 37, 494–508. [Google Scholar] [CrossRef]
- Prandle, D.; Lane, A. Sensitivity of estuaries to sea level rise: Vulnerability indices. Estuar. Coast. Shelf Sci. 2015, 160, 60–68. [Google Scholar] [CrossRef]
- Ankita, P.; Mery, B. Changes in river bed terrain and its impact on flood propagation—A case study of River Jayanti, West Bengal, India. Geomat. Nat. Hazards Risk 2019, 10, 1928–1947. [Google Scholar] [CrossRef]
- Kleinhans, M.G. Sorting out river channel patterns. Prog. Phys. Geogr.-Earth Environ. 2010, 34, 287–326. [Google Scholar] [CrossRef]
- Carling, P.; Jansen, J.; Meshkova, L. Multichannel rivers: Their definition and classification. Earth Surf. Process. Landf. 2014, 39, 26–37. [Google Scholar] [CrossRef]
- Best, J. Anthropogenic stresses on the world’s big rivers. Nat. Geosci. 2019, 12, 7–21. [Google Scholar] [CrossRef]
- Luchi, R.; Zolezzi, G.; Tubino, M. Modelling mid-channel bars in meandering channels. Earth Surf. Process. Landf. 2010, 35, 902–917. [Google Scholar] [CrossRef]
- Wang, D.W.; Ma, Y.X.; Liu, X.F.; Huang, H.Q.; Huang, L.; Deng, C.Y. Meandering-anabranching river channel change in response to flow-sediment regulation: Data analysis and model validation. J. Hydrol. 2019, 579, 124209. [Google Scholar] [CrossRef]
- Lyu, B.; Li, J.; Hu, P.; Cao, Z.; Liu, H. High-resolution hydro-sediment-morphodynamic modelling of a meandering river reach with mid-channel bars on multiyear timescales: A case study of Shashi Reach in Middle Yangtze River. J. Hydrol. 2024, 635, 131167. [Google Scholar] [CrossRef]
- Song, W.W.; Pang, Y. Research on the influence of diversion flow ratio on the water environment in Nanjing. Water Supply 2019, 19, 2367–2378. [Google Scholar] [CrossRef]
- Alomari, N.K.; Yusuf, B.; Mohammad, T.A.; Ghazali, A.H. Experimental investigation of scour at a channel junctions of different diversion angles and bed width ratios. Catena 2018, 166, 10–20. [Google Scholar] [CrossRef]
- Abdulhafedh, A.Y.; Alomari, N.K.; Al-Janabi, A.M.S. Scour hole reduction at a diversion channel junction using different entrance edge shapes. Int. J. Sediment Res. 2023, 38, 811–820. [Google Scholar] [CrossRef]
- Xu, X.S.; Zhou, C.; Tan, Y.S.; Chen, D.B.; Fu, J.; Chai, C.; Liang, L.F. Analyzing the diversion effect of debris flow in cross channels utilizing two-phase flow theory and the principle of energy conservation. Water 2024, 16, 2134. [Google Scholar] [CrossRef]
- Zhang, J.H.; Yu, M.H. Experimental study of flood diversion in the middle and lower Han River, China. Can. J. Civ. Eng. 2014, 41, 381–388. [Google Scholar] [CrossRef]
- Wang, C.L.; Zhao, Y.; Ning, L.; Bi, J. Permeability Evolution of Coal Subjected to Triaxial Compression Based on In-Situ Nuclear Magnetic Resonance. Int. J. Rock Mech. Min. Sci. 2022, 158, 105213. [Google Scholar] [CrossRef]
- Wang, C.L.; Pan, L.H.; Zhao, Y.; Zhang, Y.F.; Shen, W.K. Analysis of the Pressure-Pulse Propagation in Rock: A New Approach to Simultaneously Determine Permeability, Porosity, and Adsorption Capacity. Rock Mech. Rock Eng. 2019, 52, 4301–4317. [Google Scholar] [CrossRef]
- Gao, Y.Y.; Yang, H.J.; Wang, L.Z.; Zhao, M. Three-dimensional numerical investigation on flow behaviors around a diversion dike. Phys. Fluids 2022, 34, 125119. [Google Scholar] [CrossRef]
- Ranjbar-Zahedani, M.; Keshavarzi, A.; Khabbaz, H.; Ball, J.E. Optimizing flow diversion structure as an effective pier-scour countermeasure. J. Hydraul. Res. 2021, 59, 963–976. [Google Scholar] [CrossRef]
- Iqbal, S.; Tanaka, N. An experimental investigation on Dike stabilization against floods. Geosciences 2023, 13, 307. [Google Scholar] [CrossRef]
- Nandhini, D.; Murali, K.; Harish, S.; Schüttrumpf, H.; Heins, K.; Gries, T. A state-of-the-art review of normal and extreme flow interaction with spur dikes and its failure mechanism. Phys. Fluids 2024, 36, 051301. [Google Scholar] [CrossRef]
- Xie, R.R.; Rao, P.Y.; Pang, Y.; Shi, C.C.; Li, J.B.; Shen, D.D. Salt intrusion alters nitrogen cycling in tidal reaches as determined in field and laboratory investigations. Sci. Total Environ. 2020, 729, 138803. [Google Scholar] [CrossRef] [PubMed]
- Xie, R.R.; Pang, Y.; Luo, B.R.; Li, J.B.; Wu, C.S.; Zheng, Y.Y.; Sun, Q.Y.; Zhang, P.; Wang, F.F. Spatiotemporal variability in salinity and hydraulic relationship with salt intrusion in the tidal reaches of the Minjiang River, Fujian province, China. Environ. Sci. Pollut. Res. 2017, 24, 11847–11855. [Google Scholar] [CrossRef]
- Dai, W.H.; Wu, S.X.; Zhang, Y.; Tang, H.W. Preliminary studies on improvement measures to the diversion ratio of Nanjing Baguazhou branch. Hydro-Sci. Eng. 2013, 1–7. [Google Scholar] [CrossRef]
- Yu, Z.M.; Zou, Q.S.; Chen, Y.Q.; Xu, P.; Wang, L.H. Analysis of the variation characteristics of diversion ratios between the South and North Ports of the Minjiang River during flood and ebb tides. In Proceedings of the 2022 Chinese Hydraulic Engineering Society Academic Conference (Volume 5), Beijing, China, 8 November 2022; Yellow River Water Conservancy Press: Beijing, China, 2022; pp. 224–230. [Google Scholar]
- Wu, J. Analysis of the variation characteristics and causes of the diversion ratio of North and South Ports in the Mingjiang River. Hydraul. Sci. Technol. 2024, 16–21. [Google Scholar]
- Chen, B.Y. Application of the Delft3D 2D hydrodynamic model in the study of tidal range, water levels, and diversion ratio of North and South Ports in the lower reaches of the Mingjiang River. Hydraul. Sci. Technol. 2020, 28–33. [Google Scholar]
- Yu, P.P.; Tang, H.W.; Xiao, Y.; Fu, H.; Chen, J.M.; Liang, D.F. Effects of a diversion dyke on river flow: A case study. Proc. Inst. Civ. Eng.-Water Manag. 2015, 168, 210–219. [Google Scholar] [CrossRef]
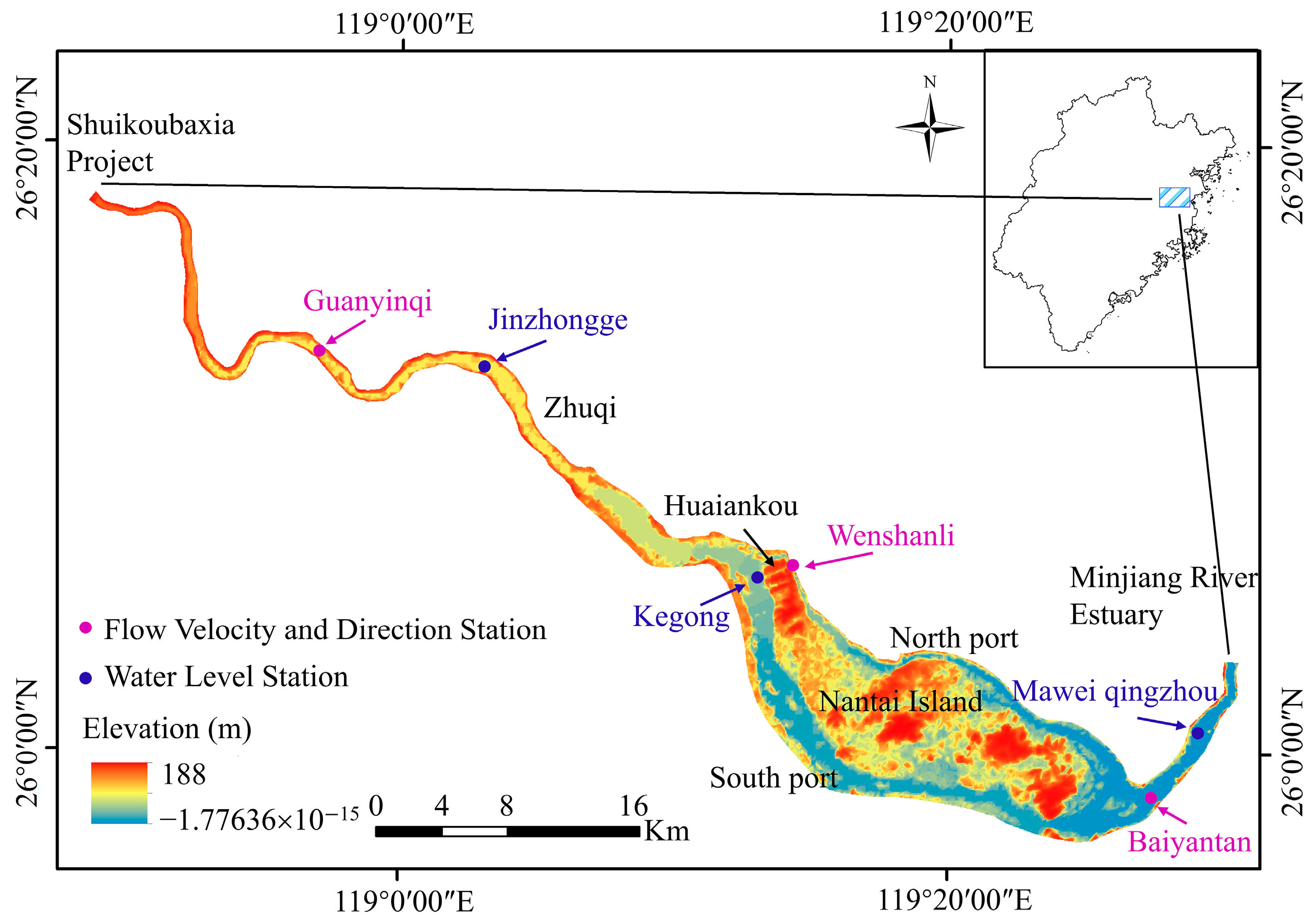

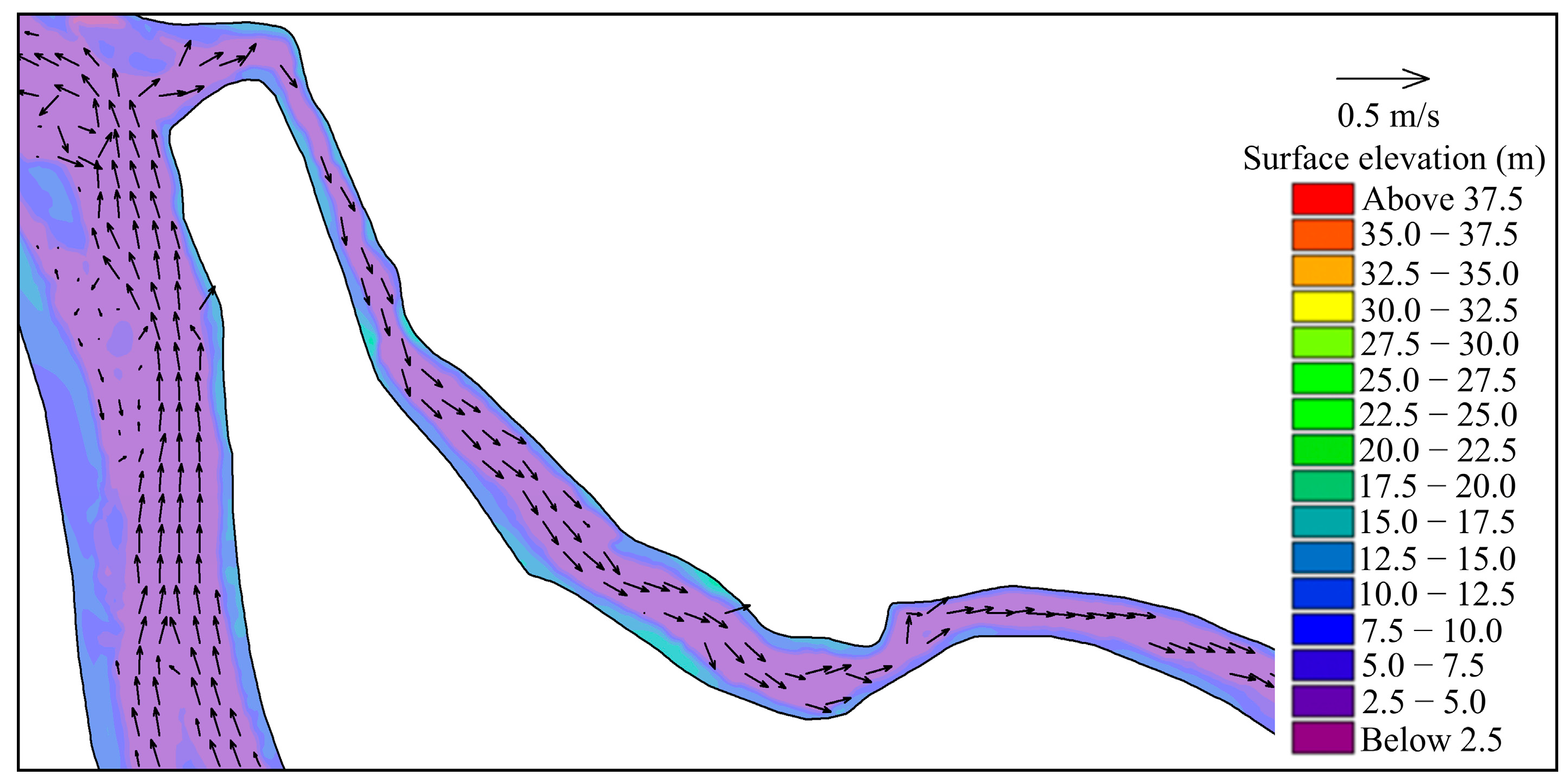


| Boundary Type | Location Description | Parameter Settings |
|---|---|---|
| Upstream Boundary | Shuikoubaxia project | Discharge of 1108.92 m3/s, measured at Zhuqi Station during the 2017 wet season. |
| Downstream Boundary | Minjiang River estuary | Defined by hourly tidal levels at the Minjiang River estuary, simulated using the MIKE 21 tidal prediction function. |
| Closed Boundaries | Levees on both sides and land boundaries of river islets | Impermeable boundary. |
| Dynamic Boundary | Wetting and drying boundaries across the entire domain | Drying depth = 0.005 m; flooding depth = 0.05 m; wetting depth = 0.1 m. |
| Monitoring Stations | Mean Absolute Error (MAE) | Mean Squared Error (MSE) |
|---|---|---|
| Jinzhongge | 0.37 m | 0.20 |
| Kegong | 0.44 m | 0.26 |
| Maweiqingzhou | 0.61 m | 0.57 |
| Spring Tide | Neap Tide | ||
|---|---|---|---|
| Over the entire day | 19.13% | Over the entire day | 20.17% |
| Ebb tide stage | 19.32% | Ebb tide stage | 20.76% |
| Flood tide stage | 16.63% | Flood tide stage | 16.00% |
| Ebbing tide (4:00, 15:00) | 19.00% | Ebbing tide (10:00, 21:00) | 19.50% |
| Low slack tide (8:00, 20:00) | 12.50% | Low slack tide (1:00, 14:00) | 12.50% |
| Flooding tide (9:00, 22:00) | 21.00% | Flooding tide (4:00, 16:00) | 24.50% |
| High slack tide (0:00, 11:00) | 21.00% | High slack tide (6:00, 18:00) | 10.00% |
| Operational Condition Number | 1-1 | 1-2 | 1-3 | 1-4 | 1-5 | 1-6 | 1-7 |
| Diversion dyke length/m | 50 | 110 | 300 | 450 | 500 | 550 | 600 |
| Simulation Time | Diversion Dyke Length/m | ||||||
|---|---|---|---|---|---|---|---|
| 50 | 110 | 300 | 450 | 500 | 550 | 600 | |
| Spring tide | 19.10% | 19.10% | 19.16% | 19.67% | 19.68% | 20.72% | 20.76% |
| Neap tide | 18.74% | 18.74% | 18.71% | 18.99% | 19.01% | 19.40% | 19.41% |
| Operating Condition Number for the Dyke Length of 110 m | Operating Condition Number for the Dyke Length of 450 m | Operating Condition Description |
|---|---|---|
| 2-1 | 3-1 | −30° |
| 2-2 | 3-2 | −20° |
| 2-3 | 3-3 | −10° |
| 1-2 | 1-4 | 0° |
| 2-4 | 3-4 | +10° |
| 2-5 | 3-5 | +20° |
| 2-6 | 3-6 | +30° |
| Diversion Dyke Length/m | Simulation Time | Rotation Angle of the Diversion Dyke | ||||||
|---|---|---|---|---|---|---|---|---|
| −30° | −20° | −10° | 0° | +10° | +20° | +30° | ||
| 110 | Spring tide | 19.10% | 19.09% | 19.09% | 19.10% | 19.09% | 19.09% | 19.09% |
| Neap tide | 18.74% | 18.74% | 18.74% | 18.74% | 18.74% | 18.74% | 18.74% | |
| 450 | Spring tide | 24.98% | 21.52% | 20.42% | 19.67% | 19.25% | 17.55% | 14.18% |
| Neap tide | 23.60% | 19.58% | 19.26% | 18.99% | 18.76% | 17.35% | 13.98% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Yang, W.; Wang, Z.; Huangfu, K.; Cai, F.; Chen, H.; Chen, Y. Study on Characteristics of the Water Diversion Ratio and Impact of the Diversion Dyke at South and North Ports of the Minjiang River During Wet Season. Water 2025, 17, 1183. https://doi.org/10.3390/w17081183
Chen C, Yang W, Wang Z, Huangfu K, Cai F, Chen H, Chen Y. Study on Characteristics of the Water Diversion Ratio and Impact of the Diversion Dyke at South and North Ports of the Minjiang River During Wet Season. Water. 2025; 17(8):1183. https://doi.org/10.3390/w17081183
Chicago/Turabian StyleChen, Cheng, Weijia Yang, Zhihui Wang, Kailong Huangfu, Feng Cai, Haoyan Chen, and Youlin Chen. 2025. "Study on Characteristics of the Water Diversion Ratio and Impact of the Diversion Dyke at South and North Ports of the Minjiang River During Wet Season" Water 17, no. 8: 1183. https://doi.org/10.3390/w17081183
APA StyleChen, C., Yang, W., Wang, Z., Huangfu, K., Cai, F., Chen, H., & Chen, Y. (2025). Study on Characteristics of the Water Diversion Ratio and Impact of the Diversion Dyke at South and North Ports of the Minjiang River During Wet Season. Water, 17(8), 1183. https://doi.org/10.3390/w17081183





