Estimation of Solöz River Water Balance Components and Rainfall Runoff Pattern with WEAP Model 1
Abstract
1. Introduction
2. Materials and Methods
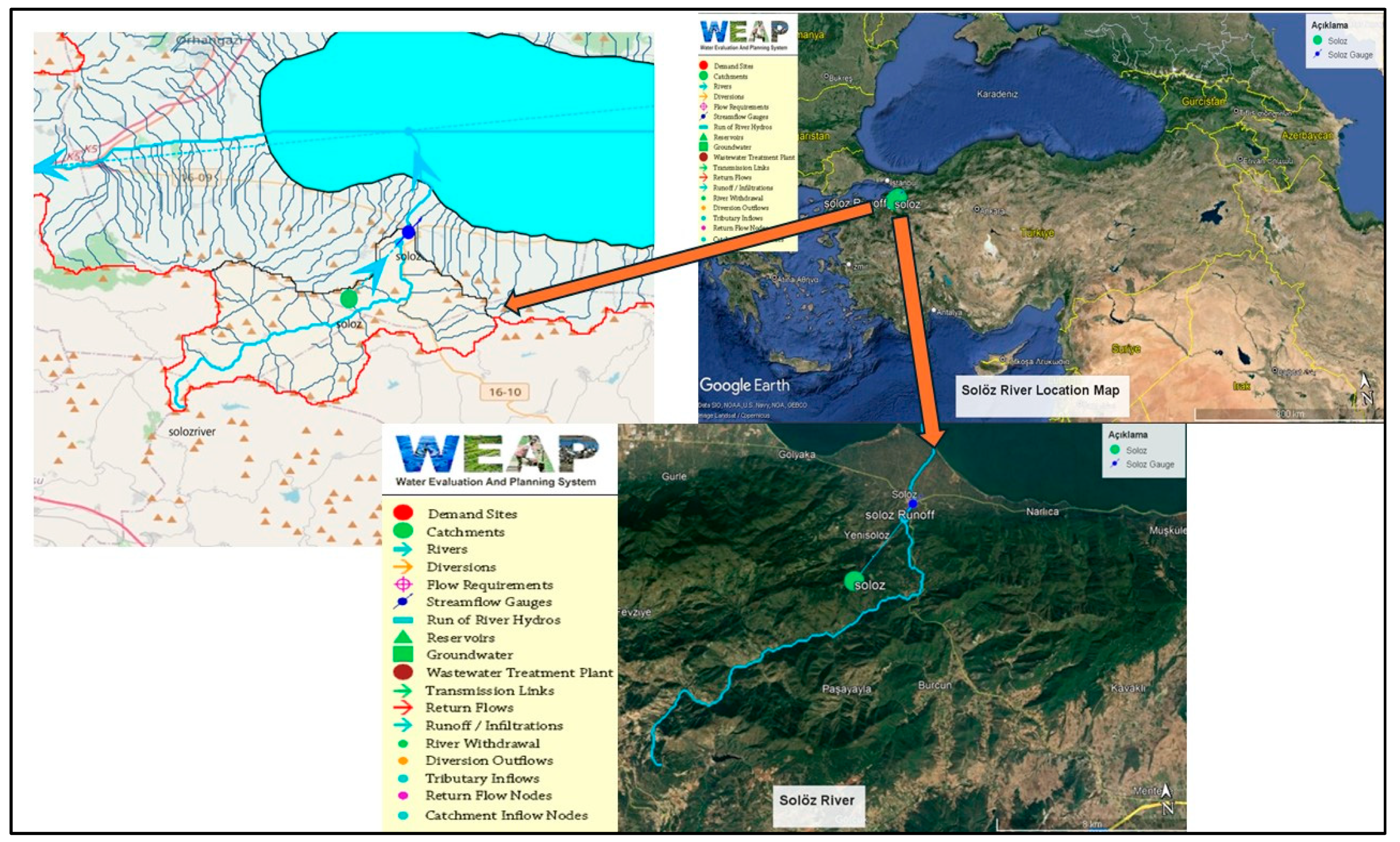
2.1. Study Site
2.2. Modeling and Data with Weap Model
3. Results and Discussion
3.1. Rainfall Runoff Method (Soil Moisture Method)
3.2. Soloz Basin Water Budget and Calibration Values
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, T.; Song, C.; Ke, L.; Wang, J.; Liu, K.; Wu, Q. Estimating seasonal water budgets in global lakes by using multi-source remote sensing measurements. J. Hydrol. 2021, 593, 125781. [Google Scholar]
- Johnston, B.R.; Hiwasaki, L.; Klaver, I.J.; Castillo, A.R.; Strang, V. Water, Cultural Diversity, and Global Environmental Change: Emerging Trends, Sustainable Futures? Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Wada, Y.; Wisser, D.; Bierkens, M.F. Global modeling of withdrawal, allocation and consumptive use of surface water and groundwater resources. Earth Syst. Dyn. Discuss 2014, 5, 15–40. [Google Scholar]
- Zarfl, C.; Lumsdon, A.E.; Berlekamp, J.; Tydecks, L.; Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 2015, 77, 161–170. [Google Scholar]
- Williamson, C.E.; Saros, J.E.; Vincent, W.F.; Smol, J.P. Lakes and reservoirs as sentinels, integrators, and regulators of climate change. Limnol. Oceanogr. 2009, 54, 2273–2282. [Google Scholar]
- Zhang, B.; Wu, Y.; Zhu, L.; Wang, J.; Li, J.; Chen, D. Estimation and trend detection of water storage at Nam Co Lake, central Tibetan Plateau. J. Hydrol. 2011, 405, 161–170. [Google Scholar]
- Sterling, S.M.; Ducharne, A.; Polcher, J. The impact of global land-cover change on the terrestrial water cycle. Nat. Clim. Change 2013, 3, 385–390. [Google Scholar]
- Wang, J.; Song, C.; Reager, J.T.; Yao, F.; Famiglietti, J.S.; Sheng, Y.; MacDonald, G.M.; Brun, F.; Schmied, H.M.; Marston, R.A.; et al. Recent global decline in endorheic basin water storages. Nat. Geosci. 2018, 11, 926–932. [Google Scholar]
- Erler, A.R.; Frey, S.K.; Khader, O.; D’Orgeville, M.; Park, Y.; Hwang, H.; Lapen, D.R.; Peltier, W.R.; Sudicky, E.A. Simulating climate change impacts on surface water resources within a lake-affected region using regional climate projections. Water Resour. Res. 2019, 55, 130–155. [Google Scholar]
- Cr’etaux, J.-F.; Abarca-Del-Río, R.; Bergé-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake volume monitoring from space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar]
- Hirschi, M.; Seneviratne, S.I.; Schär, C. Seasonal variations in terrestrial water storage for major midlatitude river basins. J. Hydrometeorol. 2006, 7, 39–60. [Google Scholar]
- Yeh, P.J.F.; Famiglietti, J. Regional terrestrial water storage change and evapotranspiration from terrestrial and atmospheric water balance computations. J. Geophys. Res. Atmos. 2008, 113, D09108. [Google Scholar] [CrossRef]
- Sheffield, J.; Ferguson, C.R.; Troy, T.J.; Wood, E.F.; McCabe, M.F. Closing the terrestrial water budget from satellite remote sensing. Geophys. Res. Lett. 2009, 36, L07403. [Google Scholar] [CrossRef]
- Pan, M.; Sahoo, A.K.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, E.F. Multisource estimation of long term terrestrial water budget for major global river basins. J. Clim. 2012, 25, 3191–3206. [Google Scholar] [CrossRef]
- Hamlington, B.; Reager, J.; Chandanpurkar, H.; Kim, K.Y. Amplitude modulation of seasonal variability in terrestrial water storage. Geophys. Res. Lett. 2019, 46, 4404–4412. [Google Scholar] [CrossRef]
- Borja, S.; Kalantari, Z.; Destouni, G. Global Wetting by Seasonal Surface Water Over the Last Decades. Earth’s Future 2020, 8, e2019EF001449. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Selek, Z.; Aslan, C. Utilization of WEAP Model in Integrated Water Resources Management: The Case of Lake Burdur Basin. Gazi J. Eng. Sci. 2019, 5, 54–64. [Google Scholar]
- Goshime, D.W.; Haile, A.T.; Rientjes, T.; Absi, R.; Ledesert, B.; Siegfried, T. Implications of Water Abstraction on the Interconnected Central Rift Valley Lakes sub-basin of Ethiopia Using WEAP. J. Hydrol. Reg. Stud. 2021, 38, 100969. [Google Scholar] [CrossRef]
- Weap. Available online: https://www.weap21.org (accessed on 25 August 2024).
- Alemayehu, T.; McCartney, M.; Kebede, S. Modelling to evaluate the water resource implications of planned infrastructure development in the Lake Tana subbasin, Ethiopia. Ecohydrol. Hydrobiol. 2010, 10, 211–221. [Google Scholar]
- Adgolign, T.B.; Srinivasa-Rao, G.V.R.; Abbulu, Y. WEAP modelling of surface water resources allocation in Didessa sub-basin, West Ethiopia. Sustain. Water Resour. Manag. 2015, 2, 55–70. [Google Scholar] [CrossRef]
- Gedefaw, M.; Hao, W.; Denghua, Y.; Qin, T.; Wang, K.; Girma, A.; Batsuren, D.; Abiyu, A. Water resources allocation systems under irrigation expansion and climate change scenario in Awash River Basin of Ethiopia. Water 2019, 11, 1966. [Google Scholar] [CrossRef]
- McCartney, M.P.; Girma, M.M. Evaluating the downstream implications of planned water resource development in the Ethiopian portion of the Blue Nile River. Water Int. 2012, 37, 362–379. [Google Scholar] [CrossRef]
- Arranz, R.; McCartney, M. Application of the Water Evaluation and Planning (WEAP) Model to Assess Future Water Demands and Resources in the Olifants Catchment, South Africa; IWMI Working Paper 116; IWMI: Colombo, Sri Lanka, 2007. [Google Scholar]
- Mounir, Z.M.; Ma, C.M.; Amadou, I. Application of water evaluation and planning (WEAP): A model to assess future water demands in the Niger River (In Niger Republic). Mod. Appl. Sci. 2011, 5, 38–49. [Google Scholar] [CrossRef][Green Version]
- Hassan, D.; Rais, M.N.; Ahmed, W.; Bano, R.; Burian, S.J.; Ijaz, M.W.; Bhatti, F.A. Future water demand modeling using water evaluation and planning: A case study of the Indus Basin in Pakistan. Water Resour. Manag. 2019, 5, 637–643. [Google Scholar] [CrossRef]
- Meşeli, A. Environmental Problems in Iznik Lake Basin. J. Dicle Univ. Ziya Gökalp Fac. Educ. 2010, 14, 134–148. [Google Scholar]
- Cebe, K.; Inan, A. Estimation of Runoff into Havran Dam Lake with SWMM. Eur. J. Sci. Technol. 2020, 152–160. [Google Scholar] [CrossRef]
- Paudel, S.; Benjankar, R. Integrated Hydrological Modeling to Analyze the Effects of Precipitation on Surface Water and Groundwater Hydrologic Processes in a Small Watershed. Hydrology 2022, 9, 37. [Google Scholar] [CrossRef]
- Pasculli, A.; Longo, R.; Sciarra, N.; Di Nucci, C. Surface Water Flow Balance of a River Basin Using a Shallow Water Approach and GPU Parallel Computing—Pescara River (Italy) as Test Case. Water 2022, 14, 234. [Google Scholar] [CrossRef]
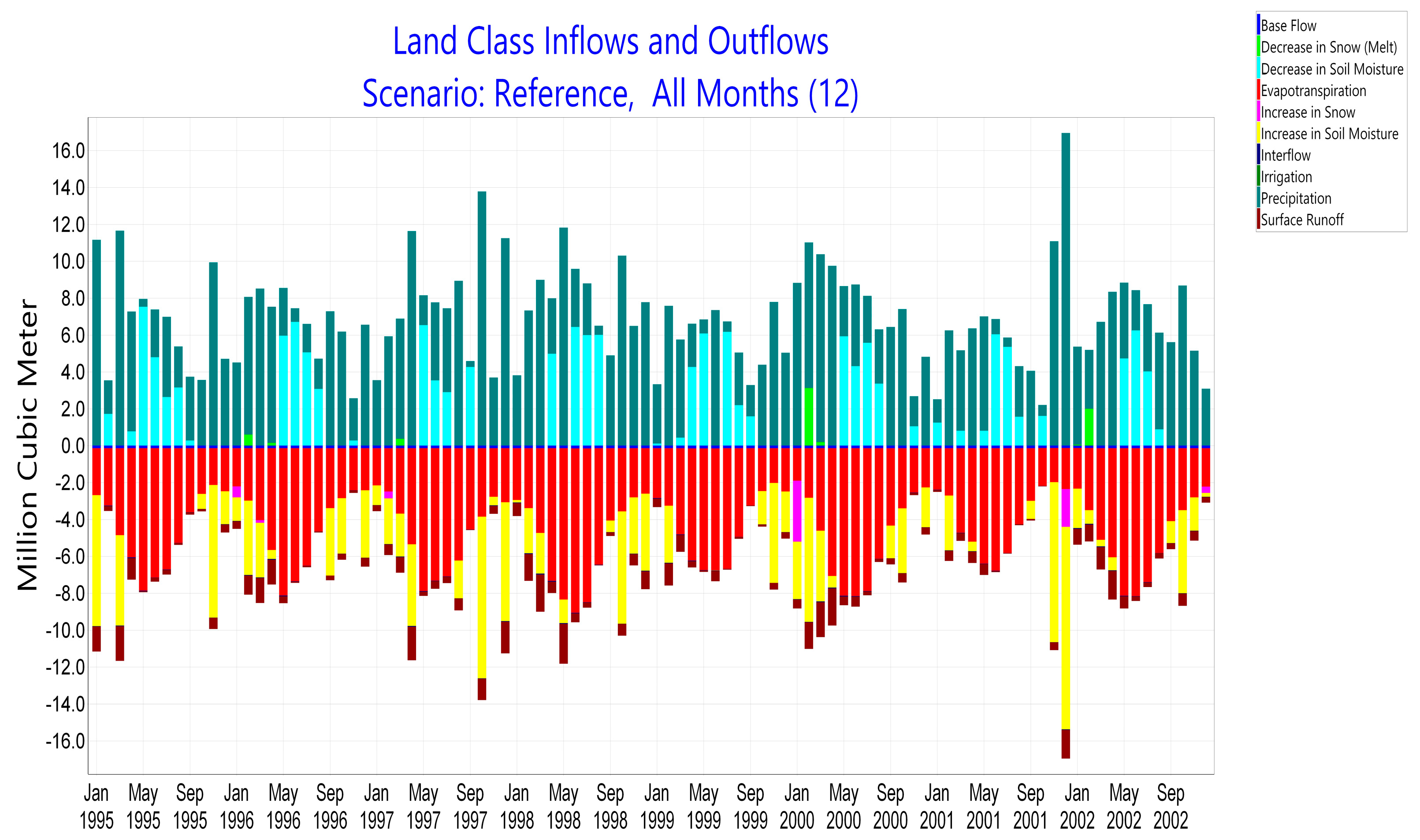
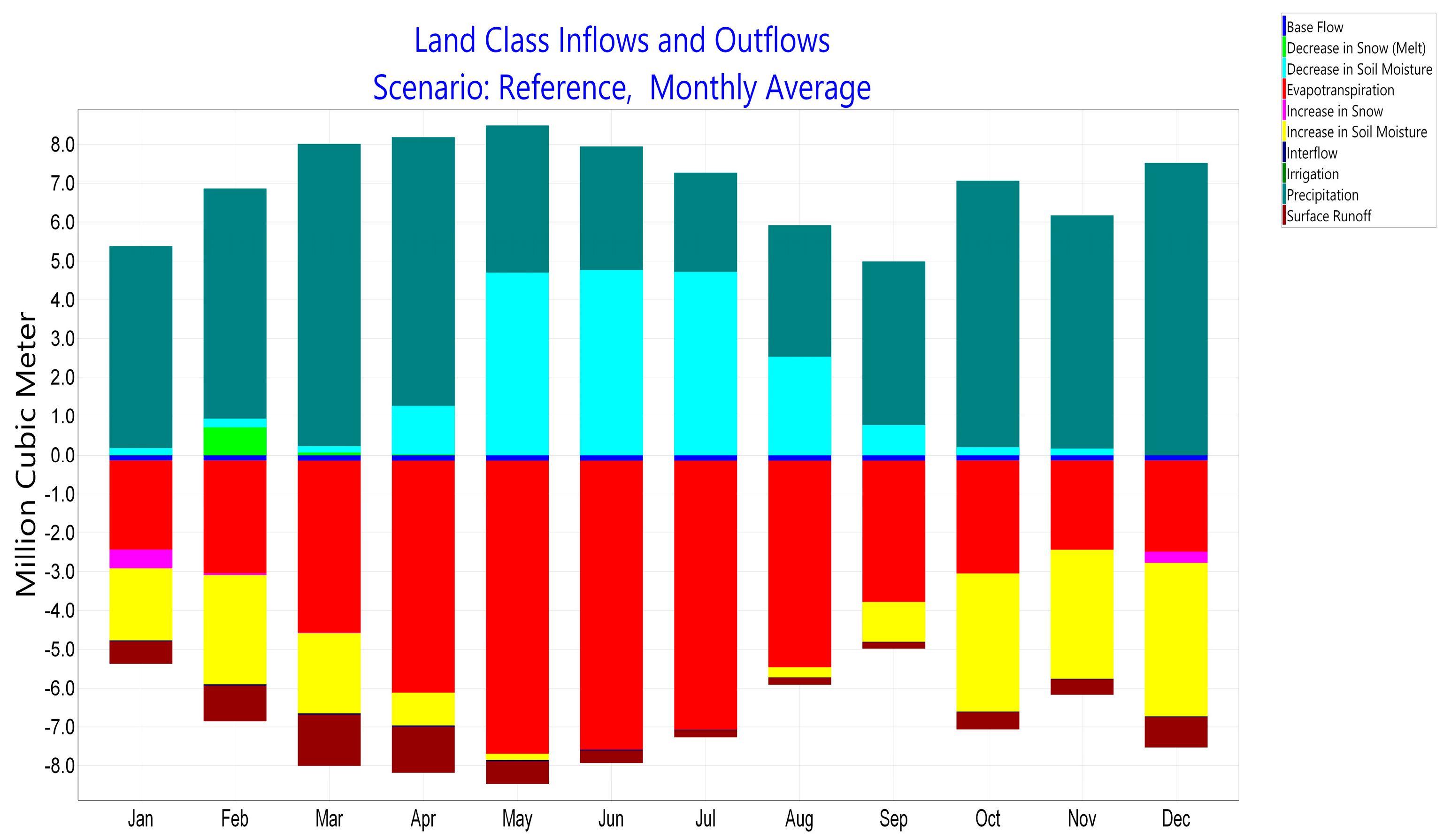
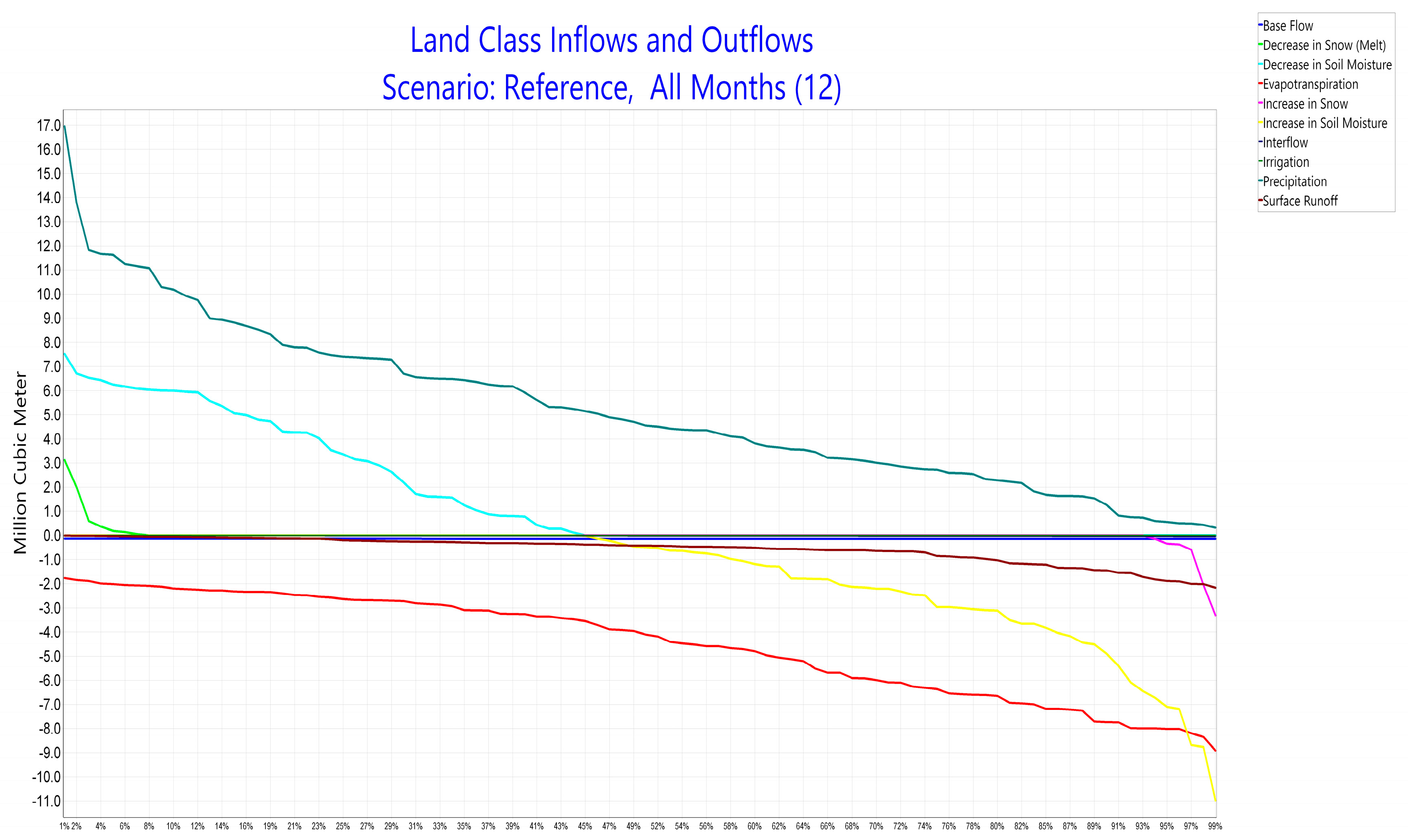
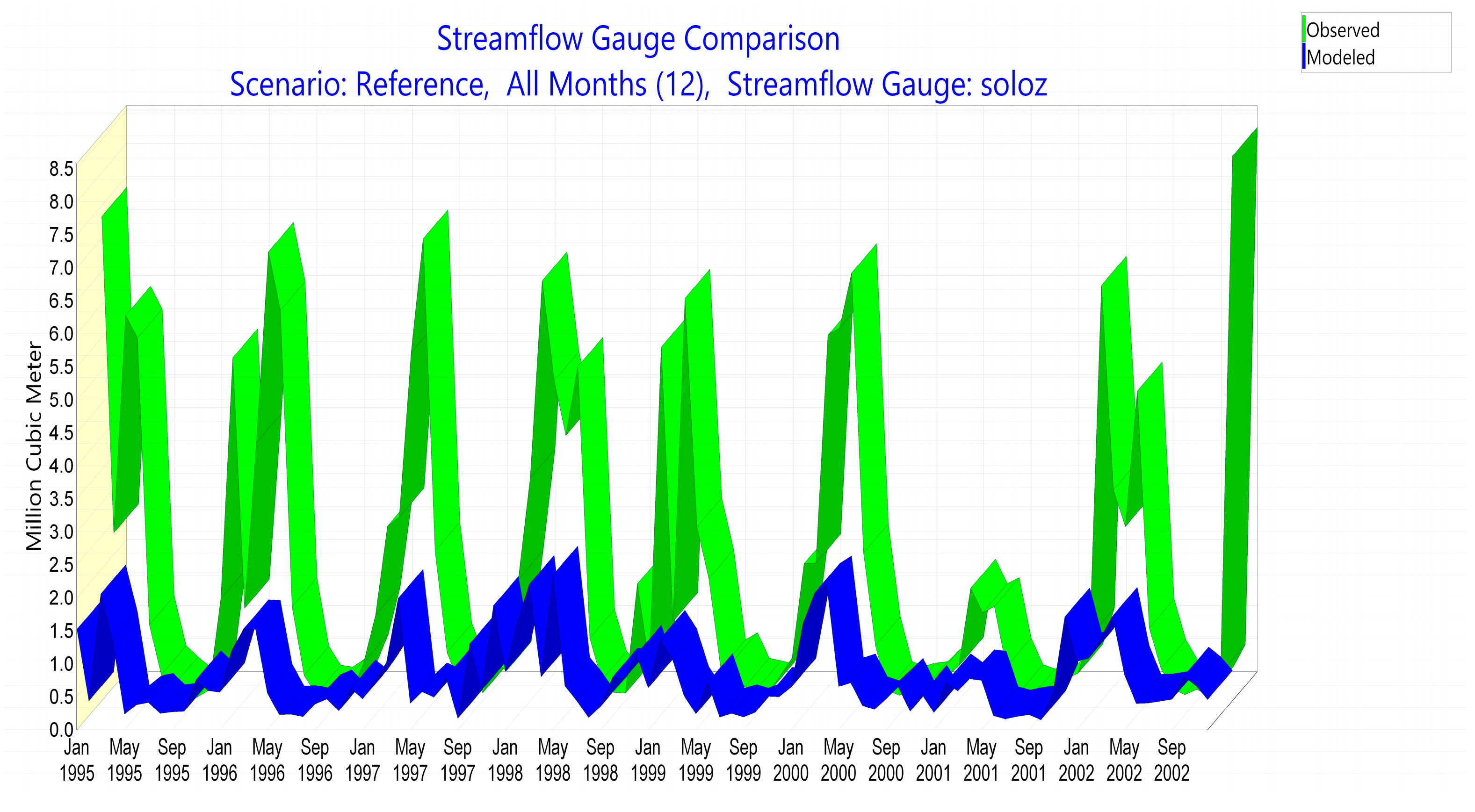
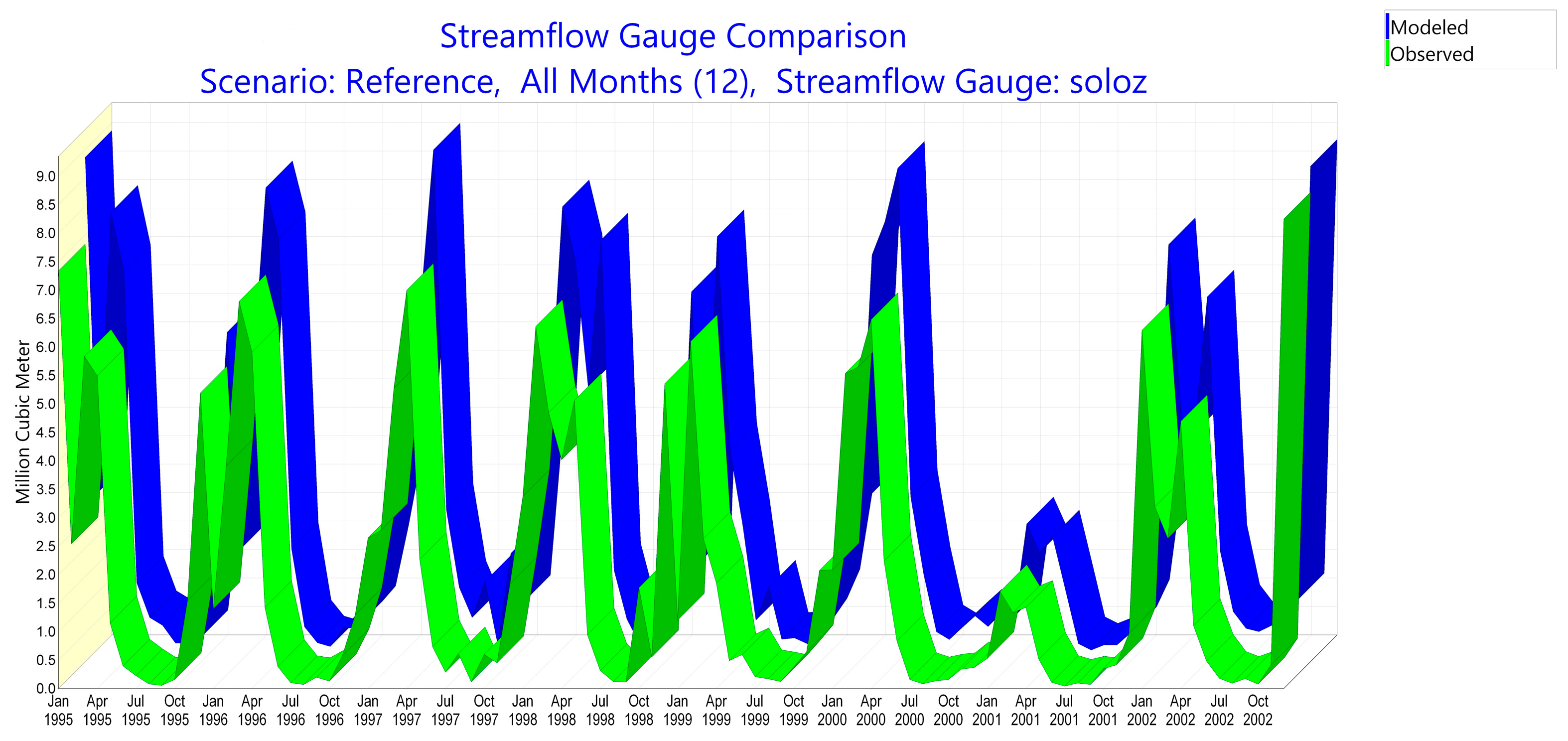
| Variable | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
|---|---|---|---|---|---|---|---|---|
| Base Flow | −1,684,720 | −1,657,600 | −1,626,500 | −1,693,010 | −1,697,580 | −1,670,610 | −1,620,100 | −1,611,610 |
| Decrease in Snow (Melt) | 0 | 739,160 | 373,269 | 0 | 0 | 3,307,173 | 0 | 2,045,918 |
| Decrease in Soil Moisture | 20,876,820 | 21,090,415 | 17,230,849 | 23,419,481 | 20,880,383 | 20,216,329 | 17,445,973 | 15,894,642 |
| Evapotranspiration | −52,940,200 | −50,919,900 | −54,780,100 | −62,046,400 | −50,741,400 | −57,560,400 | −46,151,300 | −57,480,200 |
| Increase in Snow | 0 | −739,160 | −373,269 | 0 | 0 | −3,307,170 | −2,045,920 | −337,797 |
| Increase in Soil Moisture | −21,788,800 | −19,061,300 | −28,015,600 | −20,009,600 | −12,530,200 | −21,734,900 | −24,119,500 | −11,644,700 |
| Interflow | −268,206 | −257,589 | −296,958 | −376,246 | −242,836 | −303,659 | −179,500 | −334,258 |
| Precipitation | 62,402,162 | 56,694,560 | 75,988,619 | 70,860,802 | 48,866,217 | 69,578,906 | 61,175,115 | 61,246,232 |
| Surface Runoff | −6,590,210 | −5,875,680 | −8,509,720 | −10,141,100 | −4,516,880 | −8,517,580 | −4,503,140 | −7,764,760 |
| Sum | 6804.87 | 12,891.5 | −9431.27 | 14,030.6 | 17,790.4 | 8039.09 | 1669.59 | 13,456 |
| Variable | 90% |
|---|---|
| Base Flow | −142,621 |
| Decrease in Snow (Melt) | 0 |
| Decrease in Soil Moisture | 0 |
| Evapotranspiration | −7,737,900 |
| Increase in Snow | 0 |
| Increase in Soil Moisture | −4,899,010 |
| Interflow | −41,940.4 |
| Precipitation | 1,263,536 |
| Surface Runoff | −1,449,120 |
| Calibration Metrics | Value Obtained by Comparing Model Results and Observed Values | Reasonable Range |
|---|---|---|
| NSE | 0.028 | >0.5 weak 0.75–1 very good 1 perfect |
| R2 | 0.56 | >0.5 weak 0.7–0.9 very good 1 perfect |
| NRMSE (%) | 114 | 100–80 weak >50 very good 50–80 acceptable |
| Calibration Metrics | Value Obtained by Comparing Model Results and Observed Values | Reasonable Range |
|---|---|---|
| NSE | 0.83 | >0.5 weak 0.75–1 very good 1 perfect |
| R2 | 0.98 | > 0.5 weak 0.7–0.9 very good 1 perfect |
| NRMSE (%) | 48 | 100–80 weak >50 very good 50–80 acceptable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sezer Güney, B.; Karaer, F. Estimation of Solöz River Water Balance Components and Rainfall Runoff Pattern with WEAP Model 1. Water 2025, 17, 1129. https://doi.org/10.3390/w17081129
Sezer Güney B, Karaer F. Estimation of Solöz River Water Balance Components and Rainfall Runoff Pattern with WEAP Model 1. Water. 2025; 17(8):1129. https://doi.org/10.3390/w17081129
Chicago/Turabian StyleSezer Güney, Bihter, and Feza Karaer. 2025. "Estimation of Solöz River Water Balance Components and Rainfall Runoff Pattern with WEAP Model 1" Water 17, no. 8: 1129. https://doi.org/10.3390/w17081129
APA StyleSezer Güney, B., & Karaer, F. (2025). Estimation of Solöz River Water Balance Components and Rainfall Runoff Pattern with WEAP Model 1. Water, 17(8), 1129. https://doi.org/10.3390/w17081129






