Kinetic Modeling of Volatile Fatty Acids Production Using Cassava Wastewater as Low-Cost Substrate
Abstract
1. Introduction
2. Materials and Methods
2.1. Substrate and Inoculum
2.2. Experimental Setup
2.3. Analytical Methods
2.4. Kinetic Model Fitting
3. Results and Discussion
3.1. Physicochemical Characterization of Substrate and Inoculum Solids Concentration
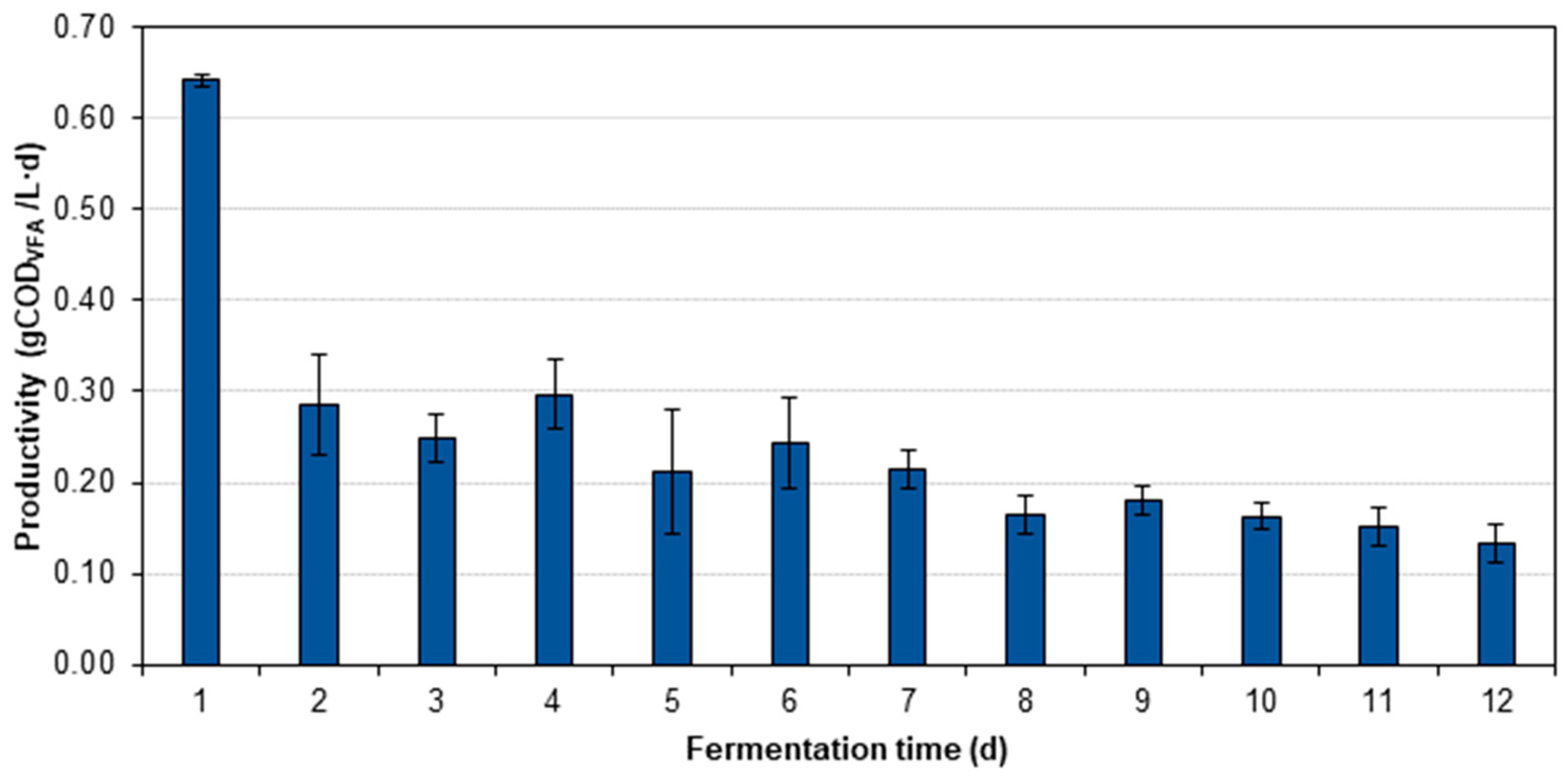
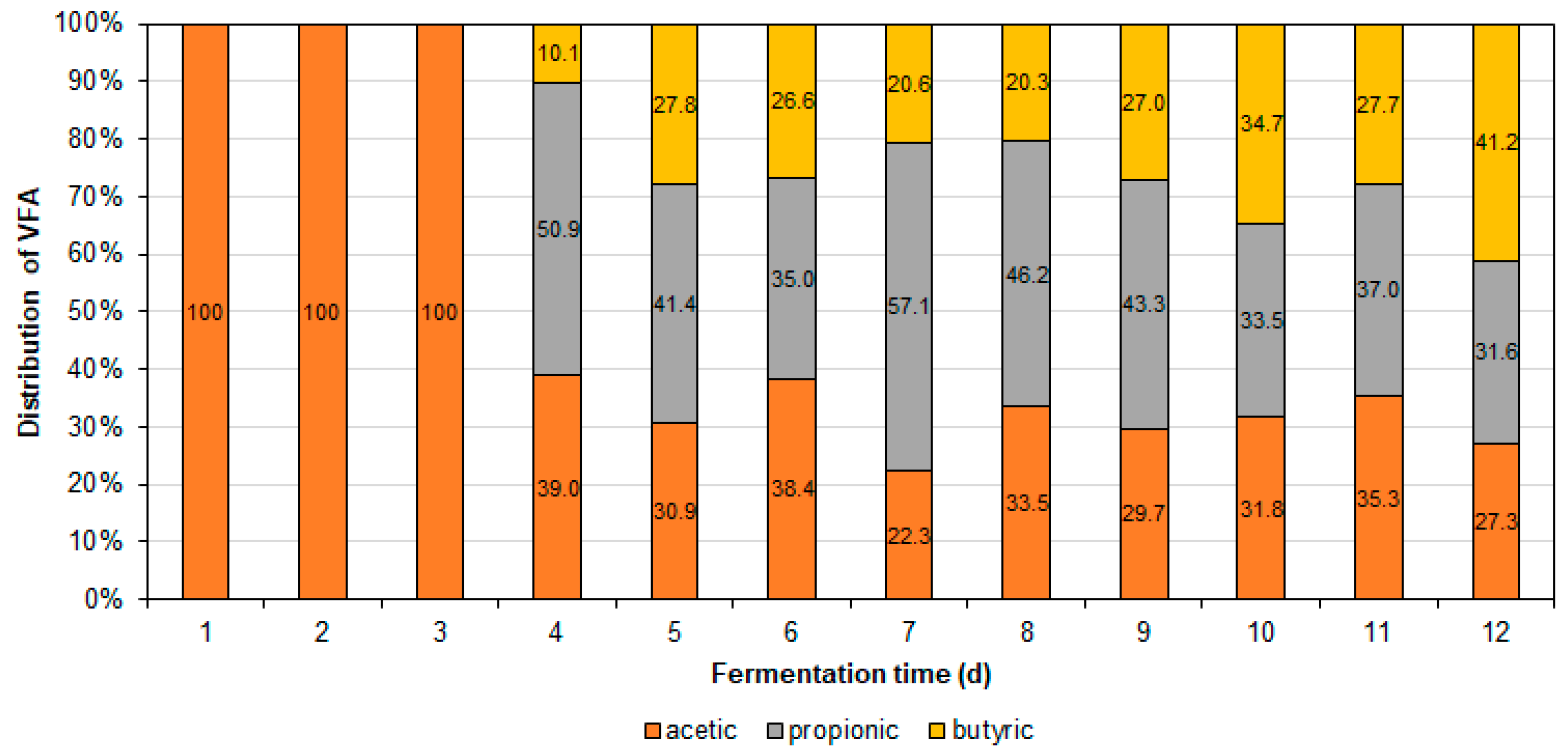
3.2. Yield, Productivity, and VFA Distribution
3.3. Kinetic Model Fitting of AF
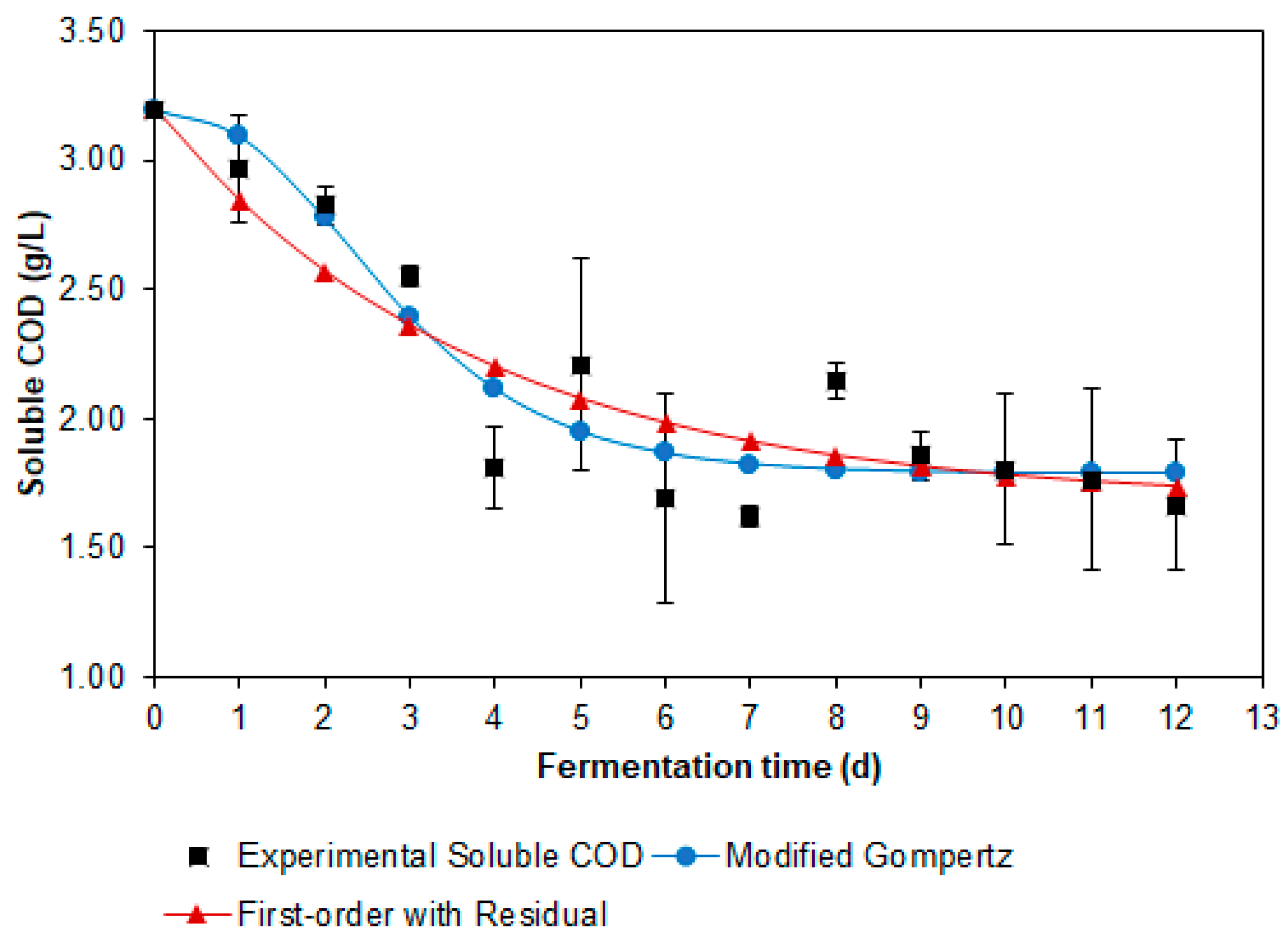
3.3.1. Modeling of Soluble Organic Matter Consumption
3.3.2. Modeling of VFA Production from CWW
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Howeler, R.H.; Oates, C.G.; Costa Allem, A. Strategic Environmental Assessment. An Assessment of the Impact of Cassava Production and Processing on the Environment and Biodiversity. 2001. Volume 5. Available online: http://ciat-library.ciat.cgiar.org/Articulos_Ciat/biblioteca/Strategic_environmental_assessment.pdf (accessed on 25 March 2025).
- Torres, P.; Rodríguez, J.A.; Uribe, I.E. Tratamiento de Aguas Residuales Del Proceso de Extracción de Almidón de Yuca En Filtro Anaerobio: Influencia Del Medio de Soporte. Sci. Et Tech. Año IX 2003, 3, 75–80. [Google Scholar]
- Pérez Vidal, A.; Torres Lozada, P.; Silva Leal, J. Tratamiento Anaerobio de Las Aguas Residuales Del Proceso de Extracción de Almidón de Yuca. Optimización de Variables Ambientales y Operacionales. Dyna 2009, 76, 139–148. [Google Scholar]
- Sarria Núñez, H. Contaminación y Toxicidad de Las Aguas Residuales de Las Rallanderías Del Norte Del Cauca, Colombia. Ph.D. Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2011. [Google Scholar]
- Torres, P.; Rodríguez, J.; Rojas, O. Extracción de Almidón de Yuca. Manejo Integral y Control de La Contaminación Hídrica. Livest. Res. Rural. Dev. 2005, 17, 1–11. [Google Scholar]
- Hasan, S.D.M.; Giongo, C.; Fiorese, M.L.; Gomes, S.D.; Ferrari, T.C.; Savoldi, T.E. Volatile Fatty Acids Production from Anaerobic Treatment of Cassava Waste Water: Effect of Temperature and Alkalinity. Environ. Technol. 2015, 36, 2637–2646. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, A.H.; Ren, Z.; Tao, L. Value Proposition of Untapped Wet Wastes: Carboxylic Acid Production through Anaerobic Digestion. iScience 2020, 23, 101221. [Google Scholar] [CrossRef]
- de Sousa e Silva, A.; Morais, N.W.S.; Coelho, M.M.H.; Pereira, E.L.; dos Santos, A.B. Potentialities of Biotechnological Recovery of Methane, Hydrogen and Carboxylic Acids from Agro-Industrial Wastewaters. Bioresour. Technol. Rep. 2020, 10, 100406. [Google Scholar] [CrossRef]
- Li, W.W.; Yu, H.Q. From Wastewater to Bioenergy and Biochemicals via Two-Stage Bioconversion Processes: A Future Paradigm. Biotechnol. Adv. 2011, 29, 972–982. [Google Scholar] [CrossRef]
- Atasoy, M.; Owusu-Agyeman, I.; Plaza, E.; Cetecioglu, Z. Bio-Based Volatile Fatty Acid Production and Recovery from Waste Streams: Current Status and Future Challenges. Bioresour. Technol. 2018, 268, 773–786. [Google Scholar] [CrossRef]
- Trancone, G.; Policastro, G.; Spasiano, D.; Race, M.; Parrino, F.; Fratino, U.; Fabbricino, M.; Pirozzi, F. Treatment of Concrete Waste from Construction and Demolition Activities: Application of Organic Acids from Continuous Dark Fermentation in Moving Bed Biofilm Reactors. Chem. Eng. J. 2025, 505, 159536. [Google Scholar] [CrossRef]
- Trancone, G.; Spasiano, D.; Race, M.; Luongo, V.; Petrella, A.; Pirozzi, F.; Fratino, U.; Piccinni, A.F. A Combined System for Asbestos-Cement Waste Degradation by Dark Fermentation and Resulting Supernatant Valorization in Anaerobic Digestion. Chemosphere 2022, 300, 134500. [Google Scholar] [CrossRef]
- Li, W.; Huang, J.; Shi, Z.; Han, W.; Lü, T.; Lin, Y.; Meng, J.; Xu, X.; Hou, P. Machine Learning Enabled Prediction and Process Optimization of VFA Production from Riboflavin-Mediated Sludge Fermentation. Front. Environ. Sci. Eng. 2023, 17, 135. [Google Scholar] [CrossRef]
- Amorim, N.C.S.; Amorim, E.L.C.; Kato, M.T.; Florencio, L.; Gavazza, S. The Effect of Methanogenesis Inhibition, Inoculum and Substrate Concentration on Hydrogen and Carboxylic Acids Production from Cassava Wastewater. Biodegradation 2018, 29, 41–58. [Google Scholar] [CrossRef] [PubMed]
- Morais, N.W.S.; Coelho, M.M.H.; Ferreira, T.J.T.; Pereira, E.L.; Leitão, R.C.; dos Santos, A.B. A Kinetic Study on Carboxylic Acids Production Using Bovine Slaughterhouse Wastewater: A Promising Substrate for Resource Recovery in Biotechnological Processes. Bioprocess Biosyst. Eng. 2021, 44, 271–282. [Google Scholar] [CrossRef]
- Morais, N.W.S.; Coelho, M.M.H.; Silva, A.d.S.e.; Pereira, E.L.; Leitão, R.C.; dos Santos, A.B. Kinetic Modeling of Anaerobic Carboxylic Acid Production from Swine Wastewater. Bioresour. Technol. 2020, 297, 122520. [Google Scholar] [CrossRef]
- Atasoy, M.; Scott, W.T.; Regueira, A.; Mauricio-Iglesias, M.; Schaap, P.J.; Smidt, H. Biobased Short Chain Fatty Acid Production—Exploring Microbial Community Dynamics and Metabolic Networks through Kinetic and Microbial Modeling Approaches. Biotechnol. Adv. 2024, 73, 108363. [Google Scholar] [CrossRef]
- Coelho, M.M.H.; Morais, N.W.S.; Pereira, E.L.; Leitão, R.C.; dos Santos, A.B. Potential Assessment and Kinetic Modeling of Carboxylic Acids Production Using Dairy Wastewater as Substrate. Biochem. Eng. J. 2020, 156, 107502. [Google Scholar] [CrossRef]
- Coelho, M.M.H.; Morais, N.W.S.; Ferreira, T.J.T.; Silva, F.S.S.; Pereira, E.L.; dos Santos, A.B. Carboxylic Acids Production Using Residual Glycerol as a Substrate in Anaerobic Fermentation: A Kinetic Modeling Study. Biomass Bioenergy 2020, 143, 105874. [Google Scholar] [CrossRef]
- de Sousa e Silva, A.; Tavares Ferreira, T.J.; Sales Morais, N.W.; Lopes Pereira, E.; Bezerra dos Santos, A. S/X Ratio Impacts the Profile and Kinetics of Carboxylic Acids Production from the Acidogenic Fermentation of Dairy Wastewater. Environ. Pollut. 2021, 287, 117605. [Google Scholar] [CrossRef]
- Morais, N.W.S. Recuperacao de Subprodutos (Metano e Ácidos Carboxílicos) Em Sistemas Anaeróbios Tratando Residuos Agroindustriais. Master’s Thesis, Universidade Federal do Ceará, Fortaleza, Brazil, 2019. [Google Scholar]
- Policastro, G.; Luongo, V.; Frunzo, L.; Fabbricino, M. A Comprehensive Review of Mathematical Models of Photo Fermentation. Crit. Rev. Biotechnol. 2021, 41, 628–648. [Google Scholar] [CrossRef]
- Boshagh, F.; Rostami, K.; van Niel, E.W.J. Application of Kinetic Models in Dark Fermentative Hydrogen Production–A Critical Review. Int. J. Hydrogen Energy 2022, 47, 21952–21968. [Google Scholar] [CrossRef]
- Mu, Y.; Wang, G.; Yu, H.Q. Kinetic Modeling of Batch Hydrogen Production Process by Mixed Anaerobic Cultures. Bioresour. Technol. 2006, 97, 1302–1307. [Google Scholar] [CrossRef] [PubMed]
- Membere, E.; Sallis, P. Effect of Temperature on Kinetics of Biogas Production from Macroalgae. Bioresour. Technol. 2018, 263, 410–417. [Google Scholar] [CrossRef]
- Ramos, R.E.; Márquez, M.C. Volatile Fatty Acids from Household Food Waste: Production and Kinetics. ChemEngineering 2024, 8, 84. [Google Scholar] [CrossRef]
- Infantes, D.; Gonzáles del Campo, A.; Villaseñor, J.; Fernández, F.J. Kinetic Model and Study of the Influence of PH, Temperature and Undissociated Acids on Acidogenic Fermentation. Biochem. Eng. J. 2012, 66, 66–72. [Google Scholar] [CrossRef]
- Trisakti, B.; Turmuzi, M.; Taslim, T.; Irvan, I. Determination of Kinetic Models in Acidogenesis Process of Palm Oil Mill Effluent. Ecol. Eng. Environ. Technol. 2024, 25, 118–125. [Google Scholar] [CrossRef]
- Undiandeye, J.; Kiman, S.; Abubakar, A.M.; Dahunsi, S.O. Medium Chain Carboxylate Production from Cassava Wastes Pretreated by Ensiling. Biofuels Bioprod. Biorefin. 2023, 17, 933–943. [Google Scholar] [CrossRef]
- Mañunga, T. Acople Entre Un Reactor Anaerobio de Medio Suspendido y Un Reactor Anaerobio de Crecimiento Adherido Para La Producción de Hidrógeno y Metano a Partir de Agua Residual Del Proceso de Extracción de Almidón de Yuca. Ph.D. Thesis, Universidad del Valle, Cali, Colombia, 2019. [Google Scholar]
- Sanchez-Ledesma, L.M.; Rodríguez-Victoria, J.A.; Ramírez-Malule, H. Effect of Fermentation Time, PH, and Their Interaction on the Production of Volatile Fatty Acids from Cassava Wastewater. Water 2024, 16, 1514. [Google Scholar] [CrossRef]
- Sanchez-Ledesma, L.M.; Rodríguez-Victoria, J.A.; Ramírez-Malule, H. Acidogenic Fermentation of Cassava Wastewater: Effect of the Substrate-to-Microorganism Ratio and Temperature on Volatile Fatty Acids Production. Water 2024, 16, 3344. [Google Scholar] [CrossRef]
- Bolaji, I.O.; Dionisi, D. Acidogenic Fermentation of Vegetable and Salad Waste for Chemicals Production: Effect of PH Buffer and Retention Time. J. Environ. Chem. Eng. 2017, 5, 5933–5943. [Google Scholar] [CrossRef]
- APHA; AWWA; WEF. Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2005. [Google Scholar]
- Dubois, M.; Gilles, K.; Hamilton, J.K.; Rebers, P.A.; Smith, F. A Colorimetric Method for the Determination of Sugars. Anal. Chem. 1956, 28, 350–356. [Google Scholar] [CrossRef]
- DiLallo, R.; Albertson, O. Volatile Acids by Direct Titration. Water Pollut. Control. Fed. 1961, 33, 356–365. [Google Scholar]
- Karne, H.; Bendre, A.; Singh, A. Mathematical Modelling of a Pilot Scale Biogas Plant. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Pererva, Y.; Miller, C.D.; Sims, R.C. Existing Empirical Kinetic Models in Biochemical Methane Potential (BMP) Testing, Their Selection and Numerical Solution. Water 2020, 12, 1831. [Google Scholar] [CrossRef]
- Cheah, Y.K.; Vidal-Antich, C.; Dosta, J.; Mata-Álvarez, J. Volatile Fatty Acid Production from Mesophilic Acidogenic Fermentation of Organic Fraction of Municipal Solid Waste and Food Waste under Acidic and Alkaline PH. Environ. Sci. Pollut. Res. 2019, 26, 35509–35522. [Google Scholar] [CrossRef] [PubMed]
- Niz, M.Y.K.; Formagini, E.L.; Boncz, M.À.; Paulo, P.L. Acidogenic Fermentation of Cassava Wastewater for Volatile Fatty Acids Production. Int. J. Environ. Waste Manag. 2020, 25, 245–261. [Google Scholar] [CrossRef]
- Simonetti, S.; Saptoro, A.; Martín, C.F.; Dionisi, D. Product Concentration, Yield and Productivity in Anaerobic Digestion to Produce Short Chain Organic Acids: A Critical Analysis of Literature Data. Processes 2020, 8, 1538. [Google Scholar] [CrossRef]
- Liu, H.; Xie, L.; Chen, Y.G.; Zhou, Q. VFAs Production Potential of Brewery Industry Wastewater and Starch Wastewater. Adv. Mat. Res. 2013, 777, 225–231. [Google Scholar] [CrossRef]
- Lucas, S.D.M.; Peixoto, G.; Mockaitis, G.; Zaiat, M.; Gomes, S.D. Energy Recovery from Agro-Industrial Wastewaters through Biohydrogen Production: Kinetic Evaluation and Technological Feasibility. Renew. Energy 2015, 75, 496–504. [Google Scholar] [CrossRef]
- Wang, L.; Hao, J.; Wang, C.; Li, Y.; Yang, Q. Carbohydrate-to-Protein Ratio Regulates Hydrolysis and Acidogenesis Processes during Volatile Fatty Acids Production. Bioresour. Technol. 2022, 355, 127266. [Google Scholar] [CrossRef]
- Amorim, N.C. dos S. Produção de Ácido Capróico Associado á Produção de Hidrogênio Utilizando a Manipueira. Ph.D. Thesis, Universidade Federal de Pernambuco, Recife, Brazil, 2018. [Google Scholar]
- Sarkar, O.; Rova, U.; Christakopoulos, P.; Matsakas, L. Ethanol Addition Promotes Elongation of Short-Chain Fatty Acids to Medium-Chain Fatty Acids Using Brewery Spent Grains as Substrate. J. Environ. Chem. Eng. 2021, 9, 105990. [Google Scholar] [CrossRef]
- Mu, Y.; Yu, H.Q.; Wang, G. A Kinetic Approach to Anaerobic Hydrogen-Producing Process. Water Res. 2007, 41, 1152–1160. [Google Scholar] [CrossRef] [PubMed]
- Fang, F.; Ni, B.J.; Yu, H.Q. Estimating the Kinetic Parameters of Activated Sludge Storage Using Weighted Non-Linear Least-Squares and Accelerating Genetic Algorithm. Water Res. 2009, 43, 2595–2604. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Liu, H.; Yin, B.; Ma, H. Modeling of Enhanced VFAs Production from Waste Activated Sludge by Modified ADM1 with Improved Particle Swarm Optimization for Parameters Estimation. Biochem. Eng. J. 2015, 103, 22–31. [Google Scholar] [CrossRef]
- Labatut, R.A.; Angenent, L.T.; Scott, N.R. Biochemical Methane Potential and Biodegradability of Complex Organic Substrates. Bioresour. Technol. 2011, 102, 2255–2264. [Google Scholar] [CrossRef]


| Kinetic Model | Kinetic Model Equation | Description of Variables |
|---|---|---|
| First-order | St: concentration of soluble organic matter over time (gCOD/L) S0: initial soluble organic matter concentration (gCOD/L) KB: soluble substrate degradation rate constant (d−1) t: fermentation time (d) Sr: residual soluble organic matter concentration (gCOD/L) X0: initial biomass concentration (gVSS/L) KL: Logistic model constant (L/gCOD·d) µmax: maximum microbial growth rate (d−1) Ks: saturation constant/Monod constant (gCOD/L) X: final biomass concentration (gVSS/L) Rmax: maximum substrate conversion rate (gCOD/L·d) Smax: maximum substrate conversion (gCOD/L) λ: lag phase time (d) | |
| First-order with residual | ||
| Logistic | ||
| Monod with growth | ||
| Logarithmic | ||
| Modified Gompertz |
| Kinetic Model | Kinetic Model Equation | Description of Variables |
|---|---|---|
| First-order | VFAt: VFA concentration over time (gCOD/L) VFAf: final concentration of VFAs (gCOD/L) KVFA: first-order VFA production rate constant (d−1) t: fermentation time (d) K”VFA: second-order VFA production rate constant (L/gCOD·d) n: shape constant λ: lag phase time (d) µm: maximum VFA productivity (gCOD/L·d) e: Euler number v: constant of the Richards model m: constant of the BPK model t0: time when VFA production rate is maximum (d) | |
| Second-order | ||
| Fitzhugh | ||
| Cone | ||
| Monomolecular | ||
| Modified Gompertz | ||
| Logistic | ||
| Transference | ||
| Richards | ||
| BPK |
| Parameter | Units | Value |
|---|---|---|
| pH | --- | 4.21 |
| TCOD | mg/L | 4975.00 |
| SCOD | mg/L | 4470.00 |
| Total VFAs | mgHAc/L | 1187.58 |
| Carbohydrates | mg/L | 1906.00 |
| Total alkalinity | mgCaCO3/L | 0 |
| Bicarbonate alkalinity | mgCaCO3/L | 0 |
| Total acidity | mgCaCO3/L | 759.54 |
| TS | mg/L | 4705.00 |
| VS | mg/L | 3450.00 |
| Ammonia nitrogen | mgNH4+/L | 66.25 |
| Orthophosphates | mgPO43−/L | 1.55 |
| Parameter | Units | Value |
|---|---|---|
| TS | g/L | 54.11 |
| VS | g/L | 38.98 |
| VS/TS | --- | 0.72 |
| Kinetic Model | Parameters and Fitting Criteria | Value |
|---|---|---|
| First-order | (d−1) | 0.068 |
| 0.724 | ||
| 0.276 | ||
| −31.152 | ||
| First-order with residual | (d−1) | 0.267 |
| 0.847 | ||
| 0.204 | ||
| −38.915 | ||
| Logistic | (L/gCOD·d) | 0.011 |
| (d−1) | 0.060 | |
| 0.681 | ||
| 0.296 | ||
| −29.281 | ||
| Monod with Growth | (gCOD/L) | 2.805 |
| X (gVSS/L) | 5.423 | |
| (d−1) | 0.019 | |
| 0.753 | ||
| 0.260 | ||
| −26.322 | ||
| Logarithmic | (gCOD/L·d) | 0.025 |
| 0.509 | ||
| 0.367 | ||
| −23.683 | ||
| Modified Gompertz | (gCOD/L) | 1.412 |
| (gCOD/L·d) | 0.396 | |
| λ (d) | 0.929 | |
| 0.885 | ||
| 0.177 | ||
| −36.291 |
| Kinetic Model | Parameters and Fitting Criteria | Value |
|---|---|---|
| First-order | (d−1) | 0.297 |
| 0.925 | ||
| 0.137 | ||
| −49.315 | ||
| Second-order | (L/g·d) | 0.402 |
| 0.836 | ||
| 0.202 | ||
| −39.229 | ||
| Fitzhugh | (d−1) | 0.240 |
| n | 1.239 | |
| 0.925 | ||
| 0.137 | ||
| −47.479 | ||
| Cone | (d−1) | 0.432 |
| n | 1.713 | |
| 0.892 | ||
| 0.164 | ||
| −41.826 | ||
| Monomolecular | (d−1) | 0.297 |
| λ (d) | 0 | |
| 0.925 | ||
| 0.137 | ||
| −46.479 | ||
| Modified Gompertz | (g/L·d) | 0.284 |
| λ (d) | 0 | |
| 0.922 | ||
| 0.140 | ||
| −45.966 | ||
| Logistic | (g/L·d) | 0.263 |
| λ (d) | 0 | |
| 0.920 | ||
| 0.141 | ||
| −45.648 | ||
| Transference | (g/L·d) | 0.474 |
| λ (d) | 0 | |
| 0.925 | ||
| 0.137 | ||
| −46.479 | ||
| Richards | (g/L·d) | 0.028 |
| λ (d) | 0 | |
| v | 0.039 | |
| 0.922 | ||
| 0.140 | ||
| −42.489 | ||
| BPK | m | 0.924 |
| (d) | 0.319 | |
| (g/L·d) | 0.382 | |
| (d−1) | 0.239 | |
| 0.926 | ||
| 0.136 | ||
| −46.718 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez-Ledesma, L.M.; Rodríguez-Victoria, J.A.; Ramírez-Malule, H. Kinetic Modeling of Volatile Fatty Acids Production Using Cassava Wastewater as Low-Cost Substrate. Water 2025, 17, 991. https://doi.org/10.3390/w17070991
Sanchez-Ledesma LM, Rodríguez-Victoria JA, Ramírez-Malule H. Kinetic Modeling of Volatile Fatty Acids Production Using Cassava Wastewater as Low-Cost Substrate. Water. 2025; 17(7):991. https://doi.org/10.3390/w17070991
Chicago/Turabian StyleSanchez-Ledesma, Lina Marcela, Jenny Alexandra Rodríguez-Victoria, and Howard Ramírez-Malule. 2025. "Kinetic Modeling of Volatile Fatty Acids Production Using Cassava Wastewater as Low-Cost Substrate" Water 17, no. 7: 991. https://doi.org/10.3390/w17070991
APA StyleSanchez-Ledesma, L. M., Rodríguez-Victoria, J. A., & Ramírez-Malule, H. (2025). Kinetic Modeling of Volatile Fatty Acids Production Using Cassava Wastewater as Low-Cost Substrate. Water, 17(7), 991. https://doi.org/10.3390/w17070991






