Preliminary Multi-Objective Optimization of Mobile Drip Irrigation System Design and Deficit Irrigation Schedule: A Full Growth Cycle Simulation for Alfalfa Using HYDRUS-2D
Abstract
1. Introduction
2. Materials and Methods
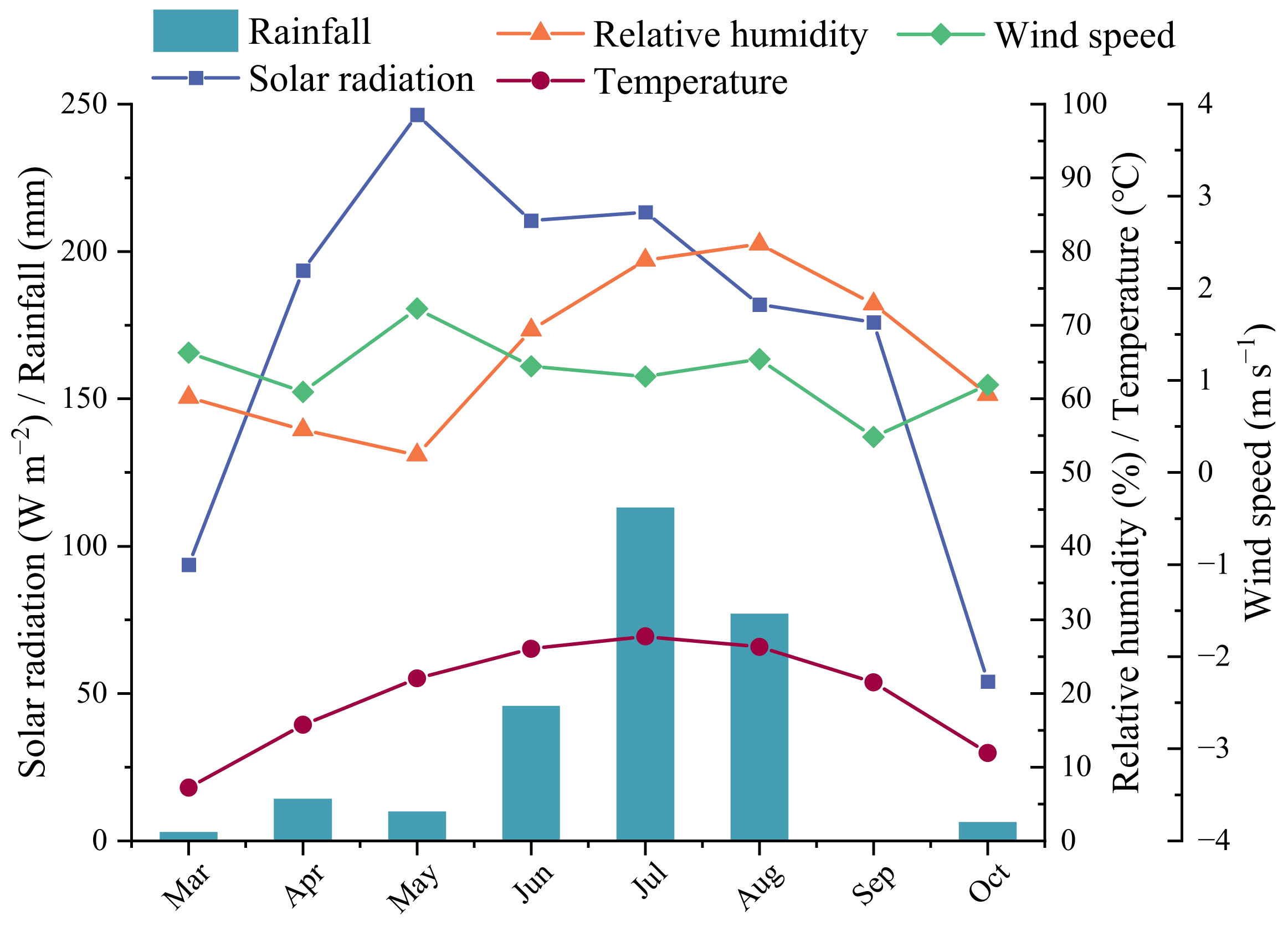
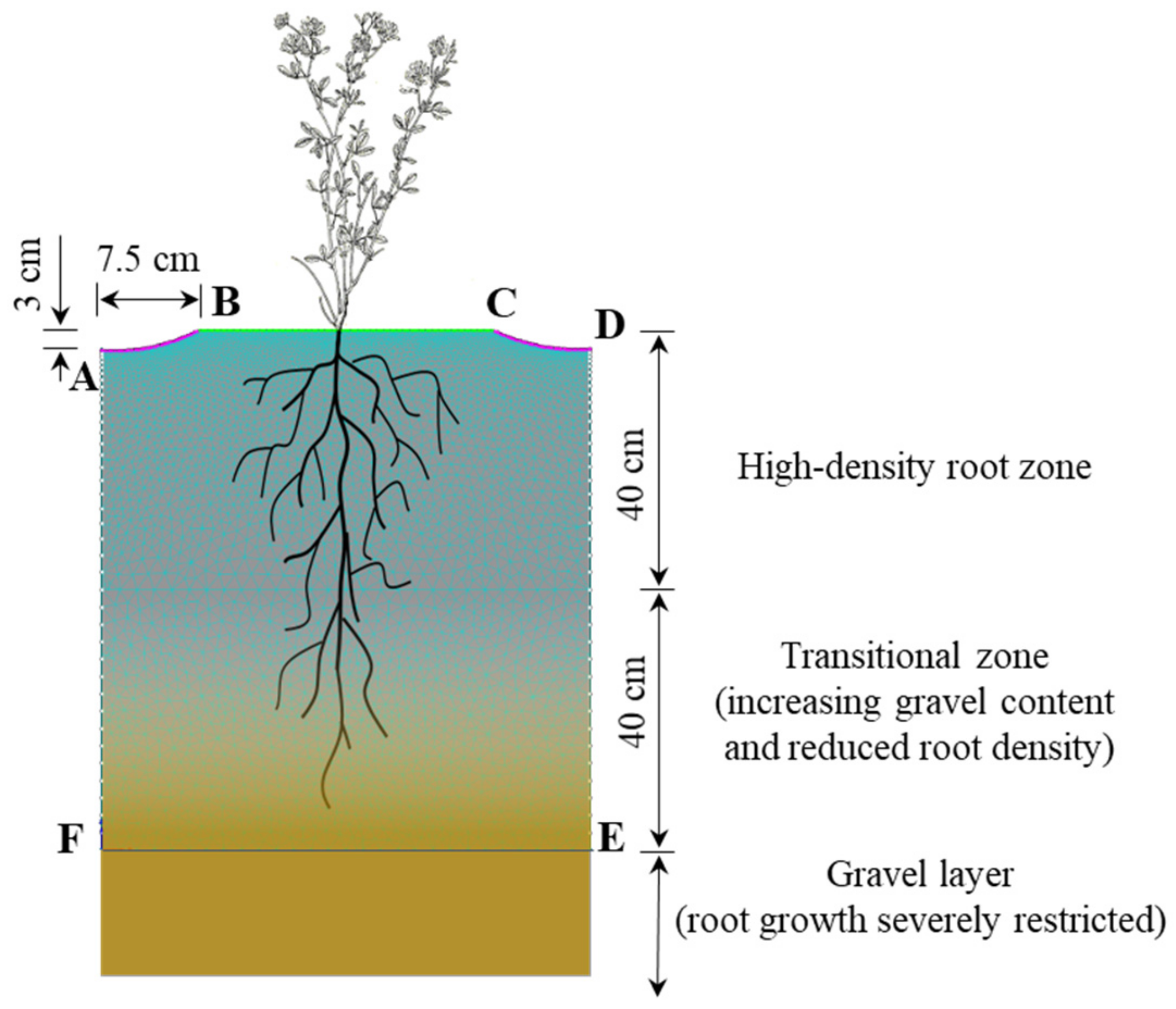
2.1. Field Experiment
2.2. HYDRUS-2D Numerical Model
2.2.1. Soil Water Movement Simulation
2.2.2. Crop Evapotranspiration
2.2.3. Crop Root Water Uptake
2.2.4. Initial and Boundary Conditions
2.2.5. Model Validation
2.3. Multi-Objective Optimization Method
2.4. Data Processing
3. Results and Analysis
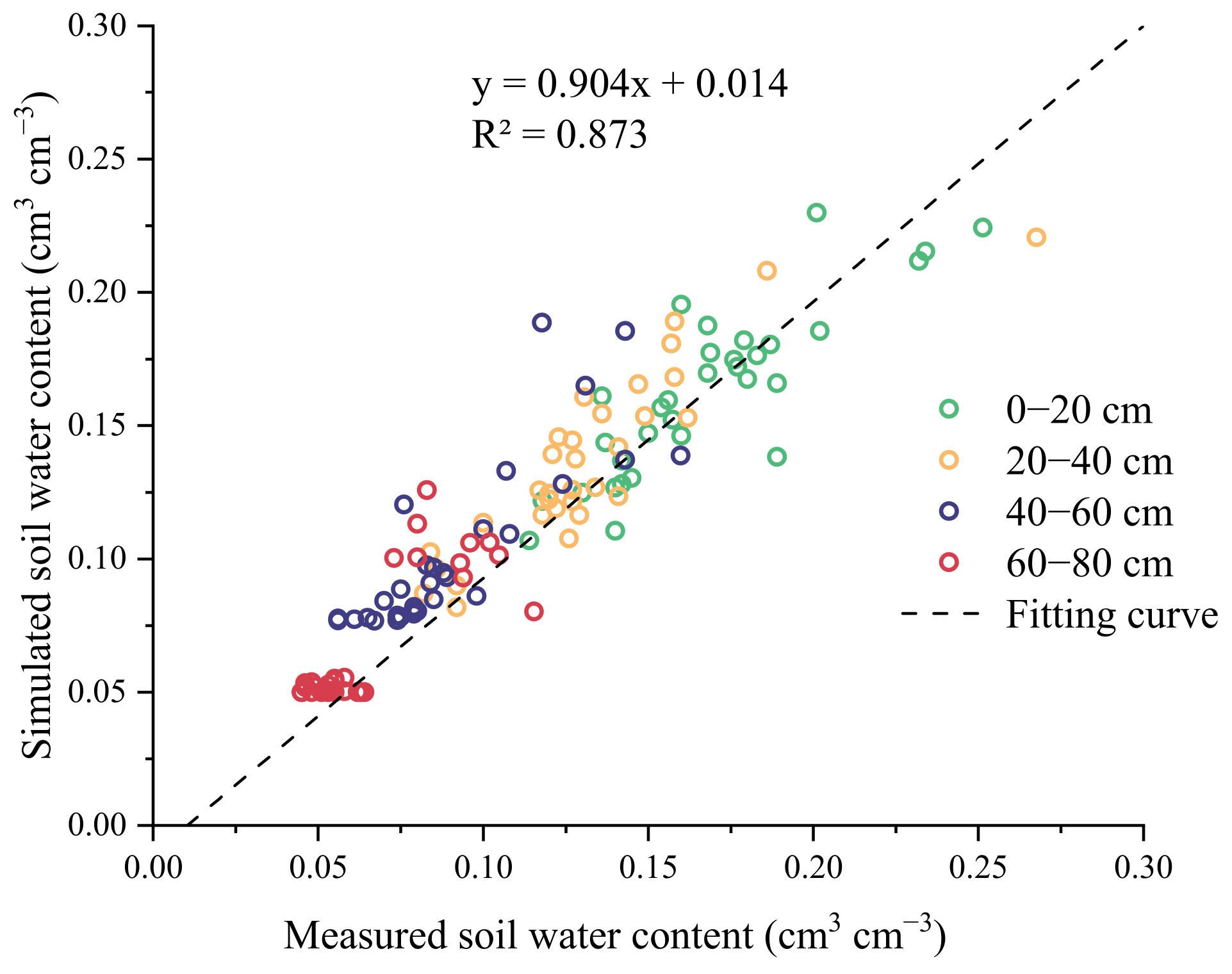
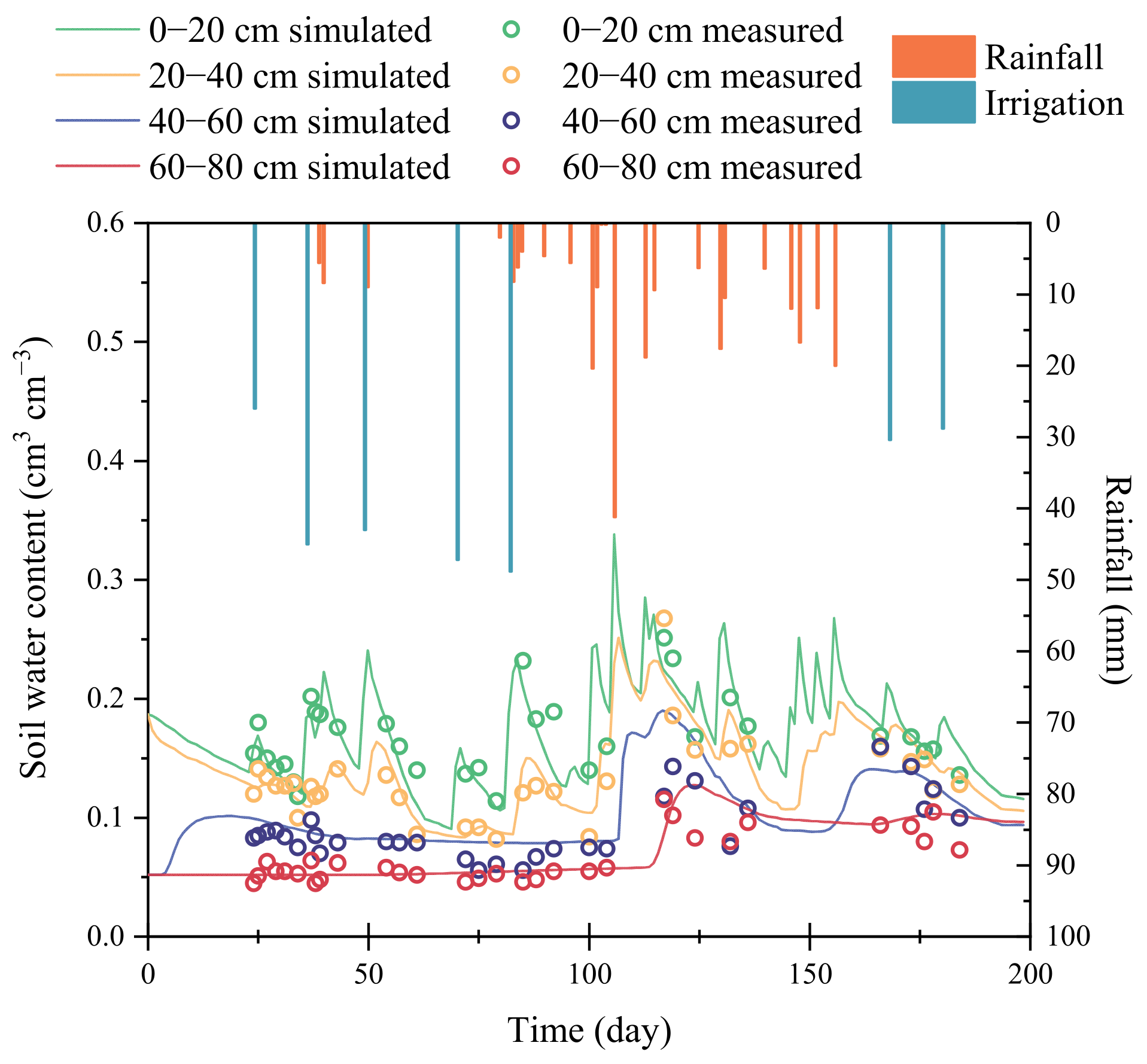
3.1. Model Validation
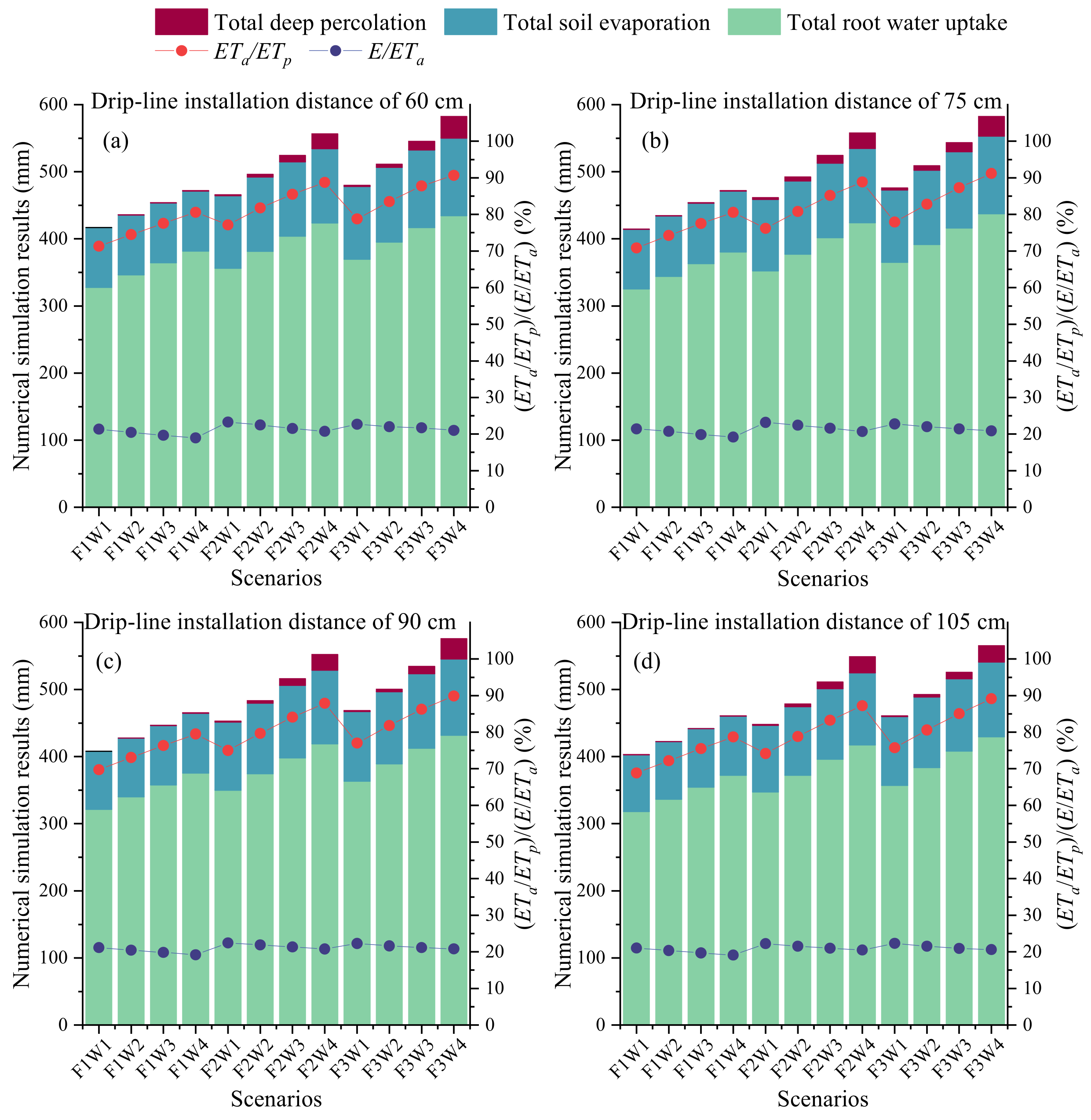
3.2. Soil Water Movement
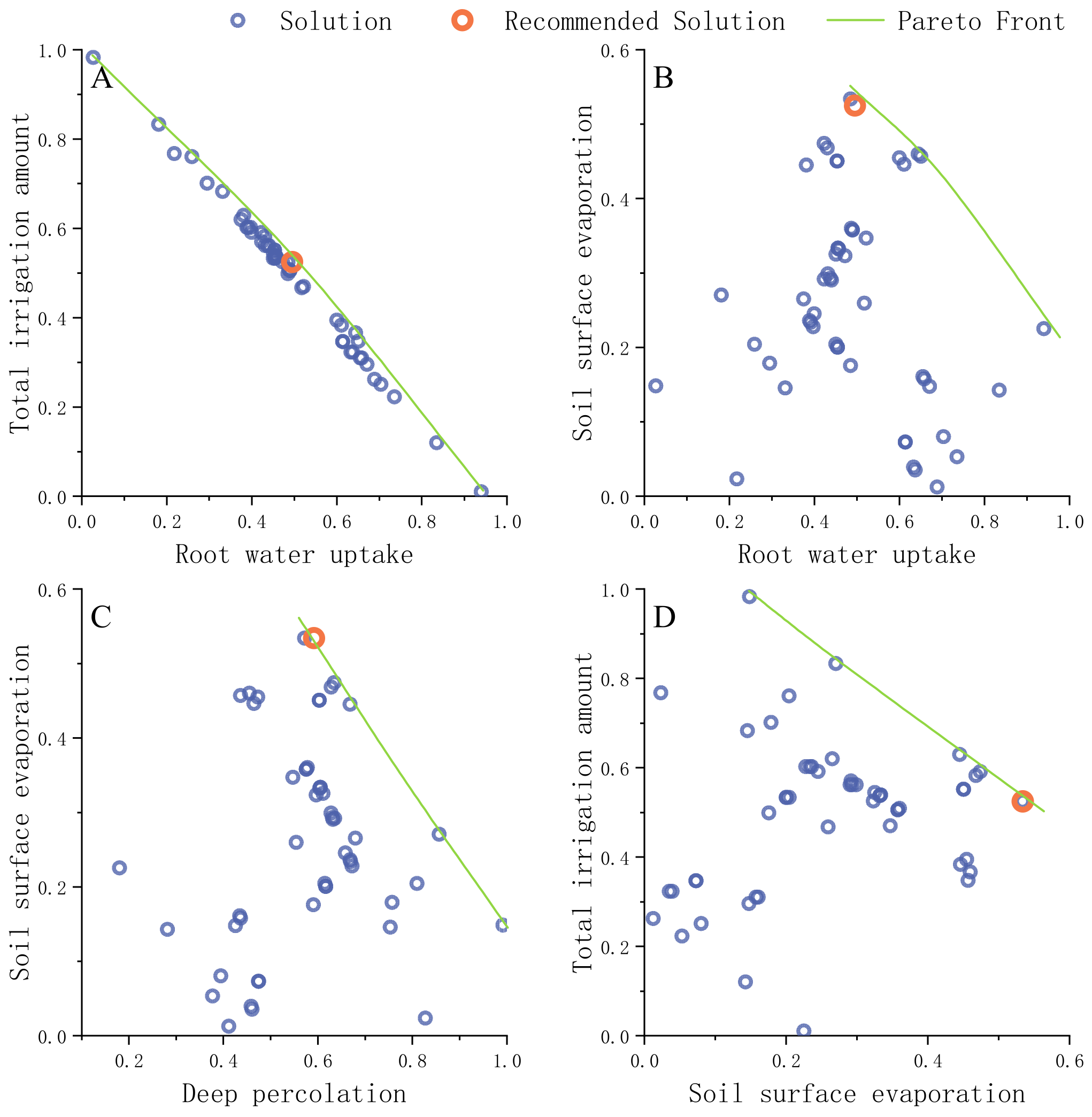
3.3. Multi-Objective Optimization Results
4. Discussion
5. Conclusions
- (1)
- The field experiment demonstrated that HYDRUS-2D can accurately simulate soil water movement using MDI systems, with the simulated values closely matching the measured values throughout the alfalfa growing season. The RMSE values of soil water content at all measured depths were all less than 0.021 cm3/cm3, with NRMSE values below 23.3%, and MAE values below 0.014 cm3/cm3.
- (2)
- Under the current soil texture and crop conditions, the drip-line installation distance did not significantly affect the irrigation performance. However, increasing the deficit irrigation threshold from F1 to F3 enhanced alfalfa root water uptake by 12.24–15.34%, but this also increased the annual total irrigation amount, soil surface evaporation (by up to 29.58%), and the risk of deep percolation. Similar trends were observed with increasing irrigation depth. Thus, formulating irrigation schedules requires balancing these competing objectives.
- (3)
- The NSGA-II multi-objective algorithm conducted Pareto optimization among multiple conflicting objectives, and the Pareto front in the results represents the trade-offs and compromises among the optimization objectives. For this case study, a drip-line installation distance of 105 cm, a deficit irrigation threshold of 50–55% FC, and an irrigation depth of 112% W are recommended to achieve a balance among the optimization objectives.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Salehi, M. Global water shortage and potable water safety; Today’s concern and tomorrow’s crisis. Environ. Int. 2022, 158, 106936. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Wu, X.; Zhang, M.; Wang, X.; Zuo, Q.; Wu, X.; Zhang, H.; Ben-Gal, A. Numerically scheduling plant water deficit index-based smart irrigation to optimize crop yield and water use efficiency. Agric. Water Manag. 2021, 248, 106774. [Google Scholar] [CrossRef]
- Li, M.; Zhou, S.; Shen, S.; Wang, J.; Yang, Y.; Wu, Y.; Chen, F.; Lei, Y. Climate-smart irrigation strategy can mitigate agricultural water consumption while ensuring food security under a changing climate. Agric. Water Manag. 2024, 292, 108663. [Google Scholar] [CrossRef]
- Fereres, E.; Soriano, M.A. Deficit irrigation for reducing agricultural water use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Y.; Sun, S.; Zhu, M.; Xue, J.; Gao, Z.; Zhao, J.; Tang, Y. Research on crop irrigation schedules under deficit irrigation-a meta-analysis. Water Resour. Manag. 2022, 36, 4799–4817. [Google Scholar] [CrossRef]
- Wu, W.; Liu, M.; Wu, X.; Wang, Z.; Yang, H. Effects of deficit irrigation on nitrogen uptake and soil mineral nitrogen in alfalfa grasslands of the inland arid area of China. Agric. Water Manag. 2022, 269, 107724. [Google Scholar] [CrossRef]
- Bali, K.M.; Putnam, D.; Wang, D.; Begna, S.; Holder, B.; Mohamed, A.Z.; Paloutzian, L.; Dahlke, H.E.; Eltarabily, M.G. Midsummer deficit irrigation of alfalfa for water conservation in the San Joaquin Valley of California. J. Irrig. Drain. Eng. 2024, 150, 04024029. [Google Scholar] [CrossRef]
- Wagle, P.; Gowda, P.H.; Northup, B.K. Dynamics of evapotranspiration over a non-irrigated alfalfa field in the Southern Great Plains of the United States. Agric. Water Manag. 2019, 223, 105727. [Google Scholar] [CrossRef]
- Ismail, S.M.; Almarshadi, M.H. Maximizing productivity and water use efficiency of alfalfa under precise subsurface drip irrigation in arid regions. Irrig. Drain. 2013, 62, 57–66. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Z.; Mu, L.; Xu, R.; Yang, H. Effect of regulated deficit irrigation on alfalfa performance under two irrigation systems in the inland arid area of midwestern China. Agric. Water Manag. 2021, 248, 106764. [Google Scholar] [CrossRef]
- Zhang, H.; Yan, H.; Hui, X.; Zhao, H.; Wang, W.; Guo, H. Experiments and numerical simulations of soil water movement under mobile drip irrigation system. Trans. Chin. Soc. Agric. Eng. 2023, 39, 158–168. (In Chinese) [Google Scholar]
- Koudahe, K.; Aguilar, J.; Djaman, K.; Sheshukov, A.Y. Evapotranspiration, fiber yield and quality, and water productivity of cotton (Gossypium hirsutum L.) under different irrigation technologies in a semiarid climate. Irrig. Sci. 2024, 42, 575–594. [Google Scholar] [CrossRef]
- Kisekka, I.; Oker, T.; Nguyen, G.; Aguilar, J.; Rogers, D. Revisiting precision mobile drip irrigation under limited water. Irrig. Sci. 2017, 35, 483–500. [Google Scholar] [CrossRef]
- Oker, T.E.; Kisekka, I.; Sheshukov, A.Y.; Aguilar, J.; Rogers, D. Evaluation of dynamic uniformity and application efficiency of mobile drip irrigation. Irrig. Sci. 2020, 38, 17–35. [Google Scholar] [CrossRef]
- Soto, A.L.; Shrestha, R.; Xue, Q.; Colaizzi, P.; O’Shaughnessy, S.; Workneh, F.; Adhikari, R.; Rush, C. Evaluation of three irrigation application systems for watermelon production in the Texas High Plains. Agron. J. 2024, 116, 2535–2550. [Google Scholar] [CrossRef]
- O’Shaughnessy, S.A.; Colaizzi, P.D. Performance of precision mobile drip irrigation in the Texas High Plains Region. Agronomy 2017, 7, 68. [Google Scholar] [CrossRef]
- Holt, J.; Yost, M.; Creech, E.; Winward, D.; Barker, B. On-farm evaluations of overhead irrigation sprinkler packages at full and reduced rates. Soil Sci. Soc. Am. J. 2024, 88, 152–165. [Google Scholar] [CrossRef]
- Dabach, S.; Shani, U.; Lazarovitch, N. Optimal tensiometer placement for high-frequency subsurface drip irrigation management in heterogeneous soils. Agric. Water Manag. 2015, 152, 91–98. [Google Scholar] [CrossRef]
- Kandelous, M.M.; Kamai, T.; Vrugt, J.A.; Simunek, J.; Hanson, B.; Hopmans, J.W. Evaluation of subsurface drip irrigation design and management parameters for alfalfa. Agric. Water Manag. 2012, 109, 81–93. [Google Scholar] [CrossRef]
- Azad, N.; Behmanesh, J.; Rezaverdinejad, V.; Abbasi, F.; Navabian, M. Developing an optimization model in drip fertigation management to consider environmental issues and supply plant requirements. Agric. Water Manag. 2018, 208, 344–356. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.I.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Wiley & Sons: New York, NY, USA, 1978. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. In Irrigation and Drainage Paper No. 56; United Nations FAO: Rome, Italy, 1998; pp. 24–28. [Google Scholar]
- Taylor, S.A.; Ashcroft, G.M. Physical Edaphology; Freeman and Co.: San Francisco, CA, USA, 1972; pp. 434–435. [Google Scholar]
- Vrugt, J.A.; Hopmans, J.W.; Šimùnek, J. Calibration of a two-dimensional root water uptake model. Soil Sci. Soc. Am. J. 2001, 65, 1027–1037. [Google Scholar]
- Jiang, R.; He, W.; He, L.; Yang, J.Y.; Qian, B.; Zhou, W.; He, P. Modelling adaptation strategies to reduce adverse impacts of climate change on maize cropping system in Northeast China. Sci. Rep. 2021, 11, 810. [Google Scholar]
- Zhao, W.; Ma, F.; Cao, W.; Ma, F.; Han, L. Effects of water and fertilizer coupling on the yield and quality of tomatoes. Trans. Chin. Soc. Agric. Eng. 2022, 38, 95–101. (In Chinese) [Google Scholar]
- Reynolds, S.; Guerrero, B.; Golden, B.; Amosson, S.; Marek, T.; Bell, J.M. Economic feasibility of conversion to mobile drip irrigation in the Central Ogallala region. Irrig. Sci. 2020, 38, 569–575. [Google Scholar] [CrossRef]
- Oker, T.E.; Kisekka, I.; Sheshukov, A.Y.; Aguilar, J.; Rogers, D.H. Evaluation of maize production under mobile drip irrigation. Agric. Water Manag. 2018, 210, 11–21. [Google Scholar] [CrossRef]
- Oker, T.E.; Sheshukov, A.Y.; Aguilar, J.; Rogers, D.H.; Kisekka, I. Evaluating soil water redistribution under mobile drip irrigation, low-elevation spray application, and low-energy precision application using HYDRUS. J. Irrig. Drain. Eng. 2021, 147, 04021016. [Google Scholar] [CrossRef]
- Bristow, K.L.; Simunek, J.; Helalia, S.A.; Siyal, A.A. Numerical simulations of the effects furrow surface conditions and fertilizer locations have on plant nitrogen and water use in furrow irrigated systems. Agric. Water Manag. 2020, 232, 106044. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Guo, J.; Yan, H. Alfalfa (Medicago sativa L.) Nitrogen utilization, yield and quality respond to nitrogen application level with center pivot fertigation system. Agronomy 2024, 14, 48. [Google Scholar] [CrossRef]
- Undersander, D.; Cosgrove, D.; Cullen, E.; Grau, C.; Rice, M.E.; Renz, M.; Sheaffer, C.; Shewmaker, G.; Sulc, M. Alfalfa Management Guide; American Society of Agronomy; Crop Science Society of America; Soil Science Society of America: Madison, WI, USA, 2011. [Google Scholar]
- Clement, C.; Sleiderink, J.; Svane, S.F.; Smith, A.G.; Diamantopoulos, E.; Desbroll, D.B.; Thorup-Kristensen, K. Comparing the deep root growth and water uptake of intermediate wheatgrass (Kernza) to alfalfa. Plant Soil 2022, 472, 369–390. [Google Scholar] [CrossRef]
- McCallum, M.H.; Connor, D.J.; O’Leary, G.J. Water Use by Lucerne and Effect on Crops in the Victorian Wimmera. Aust. J. Agric. Res. 2001, 52, 193–201. [Google Scholar] [CrossRef]
- Ward, P.R.; Dunin, F.X.; Micin, S.F. Water use and root growth by annual and perennial pastures and subsequent crops in a phase rotation. Agric. Water Manag. 2002, 53, 83–97. [Google Scholar] [CrossRef]
- Hanson, B.; Bali, K.; Orloff, S.; Carlson, H.; Sanden, B.; Putnam, D. Midsummer deficit irrigation of alfalfa as a strategy for providing water for water—Short areas. Sustain. Irrig. Manag. Technol. Policies II 2008, 112, 115. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y.; Ma, C.; Sun, H.; Ren, W.; Wang, X. Maximizing the water productivity and economic returns of alfalfa by deficit irrigation in China: A meta-analysis. Agric. Water Manag. 2023, 287, 108454. [Google Scholar] [CrossRef]

| θr/ (cm3 cm−3) | θs/ (m3 cm−3) | α/ (cm−1) | n | Ks/ (cm h−1) | l |
|---|---|---|---|---|---|
| 0.010 | 0.573 | 0.003 | 1.441 | 2.193 | 2.734 |
| Soil Depth/ cm | RMSE/ (cm3 cm−3) | NRMSE/ % | MAE/ (cm3 cm−3) | R2 |
|---|---|---|---|---|
| 0–20 | 0.018 | 10.6 | 0.014 | 0.731 |
| 20–40 | 0.017 | 12.8 | 0.013 | 0.783 |
| 40–60 | 0.021 | 23.2 | 0.014 | 0.697 |
| 60–80 | 0.014 | 21.8 | 0.009 | 0.675 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ma, F.; Wang, W.; Ding, F.; Hui, X.; Yan, H. Preliminary Multi-Objective Optimization of Mobile Drip Irrigation System Design and Deficit Irrigation Schedule: A Full Growth Cycle Simulation for Alfalfa Using HYDRUS-2D. Water 2025, 17, 966. https://doi.org/10.3390/w17070966
Zhang H, Ma F, Wang W, Ding F, Hui X, Yan H. Preliminary Multi-Objective Optimization of Mobile Drip Irrigation System Design and Deficit Irrigation Schedule: A Full Growth Cycle Simulation for Alfalfa Using HYDRUS-2D. Water. 2025; 17(7):966. https://doi.org/10.3390/w17070966
Chicago/Turabian StyleZhang, Haohui, Feng Ma, Wentao Wang, Feng Ding, Xin Hui, and Haijun Yan. 2025. "Preliminary Multi-Objective Optimization of Mobile Drip Irrigation System Design and Deficit Irrigation Schedule: A Full Growth Cycle Simulation for Alfalfa Using HYDRUS-2D" Water 17, no. 7: 966. https://doi.org/10.3390/w17070966
APA StyleZhang, H., Ma, F., Wang, W., Ding, F., Hui, X., & Yan, H. (2025). Preliminary Multi-Objective Optimization of Mobile Drip Irrigation System Design and Deficit Irrigation Schedule: A Full Growth Cycle Simulation for Alfalfa Using HYDRUS-2D. Water, 17(7), 966. https://doi.org/10.3390/w17070966







