Main Methods of Regionalization of Minimum Flows, Advantages and Disadvantages and Their Limitations: A Review

Abstract

Estimating surface runoff in ungauged basins is important for planning and managing water resources, as well as for developing civil and environmental projects. Within the estimation of surface runoff are the minimum flows, which are important for assessing water availability and the possibility of granting water resources. To estimate surface runoff in ungauged basins, regionalization is a technique that has been used and consists of transferring variables, functions and/or parameters from gauged basins to the ungauged basin. This study reviews the minimum flow regionalization methods used in studies published between 2015 and 2023 in the CAPES, Scielo, Scopus and Web of Science databases. The regionalization methods were grouped according to their approach, namely the regionalization of hydrological signatures and the regionalization of hydrological model parameters. Most studies focused on regionalizing hydrological signatures, particularly minimum flows and flow duration curves. For regionalizing hydrological model parameters, common approaches included spatial proximity, physical similarity and regression techniques. Some methods can estimate the flow time series at the location of interest, which can be an advantage for estimating different statistics from the data; other methods focus on estimating a specific flow statistic. Most methods require several gauged basins in their study area to obtain reliable estimates of minimum flows in ungauged basins. The study discusses the advantages, disadvantages and limitations of each method.

1. Introduction

Surface runoff is the main source of water for agricultural, industrial and urban use, and therefore has direct impacts on human lives. Its estimation is not only important for understanding the relationships between various hydrological processes but is also crucial for the design of various civil and environmental projects, as well as for water resource planning and management [1].

Three major groups can be defined within flow estimation: maximum, average and minimum flows. Maximum flows are primarily associated with flood risks in a watershed and the design of flood control hydraulic structures, as well as in the design of dam spillways, stormwater galleries, bridge spans, among others. The long-term average flow represents the highest flow that can be regularized. Its estimation is used in the calculation of the volume when planning the construction of a reservoir. The estimation of minimum flows is crucial for assessing the availability of watercourses for irrigation and hydroelectric projects, to decide whether it is necessary to artificially regulate a watercourse or not and to evaluate the possibility of granting the use of water resources for a specific purpose [2]. In this way, minimum flows serve as a reference for the allocation of surface water use and thus provide important data to assist management agencies in decision-making [3].

In this context, the National Water and Basic Sanitation Agency (ANA), the agency responsible for water resource management in Brazil, adopts the flow that is equaled or exceeded 95% of the time, referred to as Q₉₅, as a criterion to evaluate the balance between the demand for multiple uses and the available water supply [4]. Various flow rates are used as reference in Brazil, according to the surface water allocation criteria of each state: Goiás (GO/Brazil) and Mato Grosso do Sul (MS/Brazil) have adopted the minimum flow Q₉₅ as a reference [5], while the state of Minas Gerais (MG/Brazil) adopted the minimum flow Q_7,10 (the minimum flow over 7 consecutive days with a return period of 10 years). The state of Bahia (BA/Brazil) adopted the minimum flow Q₉₀ (flow equaled and/or exceeded 90% of the time) and states such as Ceará (CE/Brazil) and Rio Grande do Norte (RN/Brazil) adopted the minimum flow Q_90reg, which is the regulated flow with 90% reliability [6]. Thus, the most adopted reference flows for the allocation of surface water withdrawals by water resource management agencies in Brazil are Q₉₀, Q₉₅, Q_7,10 and Q_90reg [6,7]. On the other hand, in Chile, the available flow to grant a permanent water use right must have a maximum exceedance probability of 85% [8]. In Colombia, the estimation of the minimum flow with a 10-year return period is included in the procedure for estimating environmental flow, which incorporates hydrological, geomorphological, hydraulic, water quality, ecological and ecosystem service aspects [9]. Additionally, various hydrological methods are used to estimate environmental flows, where, for example, some criteria consider the 75% and 95% exceedance percentiles of the flow duration curve [10]. This highlights the importance of estimating minimum flows for the proper management and planning of water resources.

The estimation of surface runoff in a basin depends on accurate input data such as precipitation and streamflow. However, in many developing countries, there are limitations in the number of hydrological and meteorological stations providing sufficient information for flow forecasting due to financial constraints [1]. For instance, in countries like Brazil, which has continental dimensions, the monitoring of basins is often inadequate, making surface runoff estimation a significant challenge [11,12]. Consequently, the scarcity of hydrological information, which serves as a basis for decision-making related to water resource management, is one of the main factors hindering the proper planning of these resources and, simultaneously, the granting of water use rights [13].

The determination of minimum flows is based on the data availability. When a significant historical flow series is available at the site of interest, a statistical probability analysis can be conducted. However, since such information is not always available, regionalization techniques are commonly used [5]. Regionalization is a technique used to estimate flows in regions with limited or no hydrological information by transferring variables, functions, and/or parameters from a gauged basin [14,15].

Thus, the objective of this paper is to identify the main methods for obtaining minimum flows in basins, highlighting their advantages, disadvantages and limitations. The structure of the paper is as follows: first, the research and its objective are contextualized. Next, the methodology used and the main methods of regionalization of minimum flows found in the literature review are presented. In the fourth section, the advantages, disadvantages and limitations of each method are discussed. Subsequently, in the fifth section, the conclusions are presented, followed by the references.

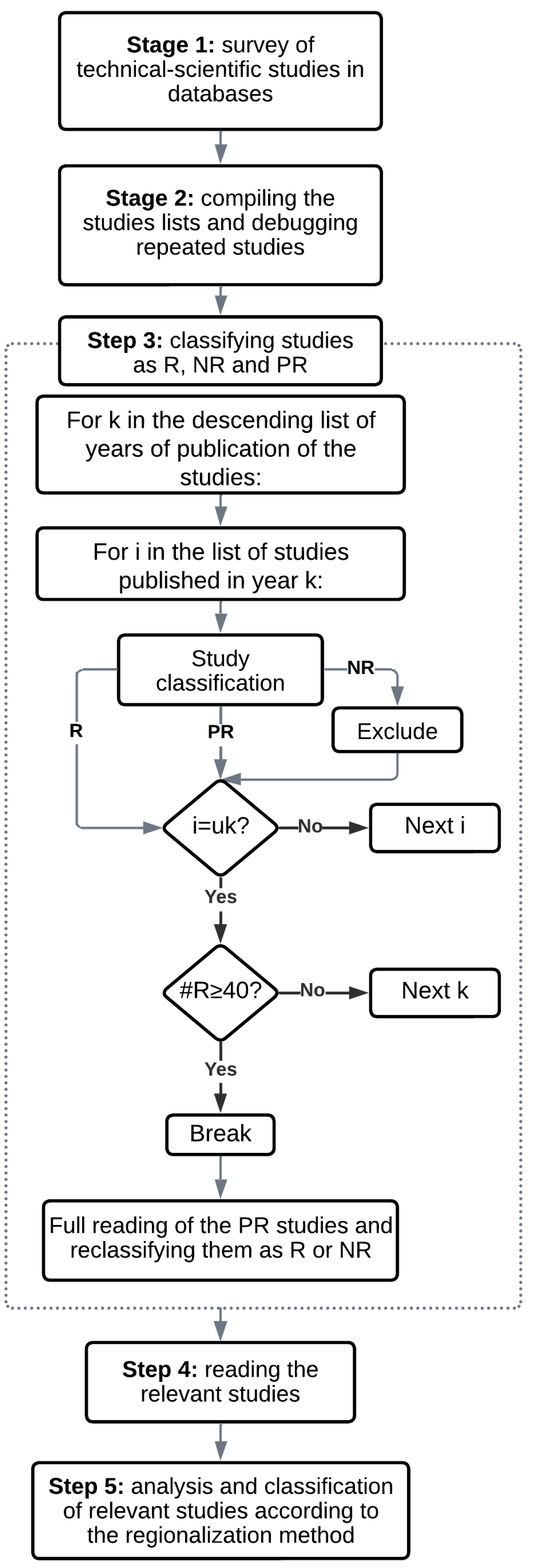
2. Materials and Methods

This research can be classified as qualitative in terms of approach, as basic research in terms of nature, as exploratory and descriptive in terms of objectives, and as bibliographic and documentary in terms of procedures [16].

The scientific publications available in the CAPES, Scielo, Scopus and Web of Science databases were analyzed.

The research consists of five stages, as shown in Figure 1.

The first stage involved gathering technical-scientific studies from the databases. In general, the research context used the following keywords: regionalization, minimum flows, watershed. Specifically, the search expression used in the mentioned databases was: (TITLE-ABS-KEY(regionalization) AND TITLE-ABS-KEY((low* OR minimal* OR minimum) AND (flow* OR discharge* OR streamflow*)) AND TITLE-ABS-KEY(watershed* OR basin*)). As the search formula illustrates, the keyword search was conducted to obtain studies containing the string in the title, abstract and keywords of the article. The search was performed without restrictions on aspects such as language, geographic region of production, search period or type of production (e.g., limited to articles or book chapters). Thus, for each database, a list of studies containing the search expressions was obtained.

The second stage was dedicated to compiling the lists obtained in the first stage. To achieve this, a code was developed in the R programming language, aiming to generate a single list with non-redundant references.

The third stage consisted of classifying the list of articles generated in the second stage regarding their relevance to the research objective. To this end, the criterion of adherence to the topic in question (minimum flow regionalization methods) was applied to the title, keywords and abstract. Based on this criterion, the articles were classified as relevant (R), not relevant (NR) and pending review (PR) (articles that could not be classified as relevant or not relevant based solely on the title, keywords and abstract). The classification process began with the most recent articles and proceeded to older ones, filtering by year of publication and classifying all articles published in the given year. The goal was to identify at least 40 relevant articles. The “pending review” articles were fully read after reaching the target of 40 relevant articles and subsequently reclassified as either relevant or not relevant.

In the fourth stage, the selected articles were read with the primary objective of identifying the regionalization methods used by the authors and subsequently proposing a classification structure. Based on this classification structure, the fifth stage involved grouping the studies into two major categories. The first category refers to those presenting regionalization methods for hydrological model parameters, while the second refers to those presenting regionalization of hydrological signatures. Additionally, the main advantages, disadvantages and limitations identified by the authors of the articles were noted.

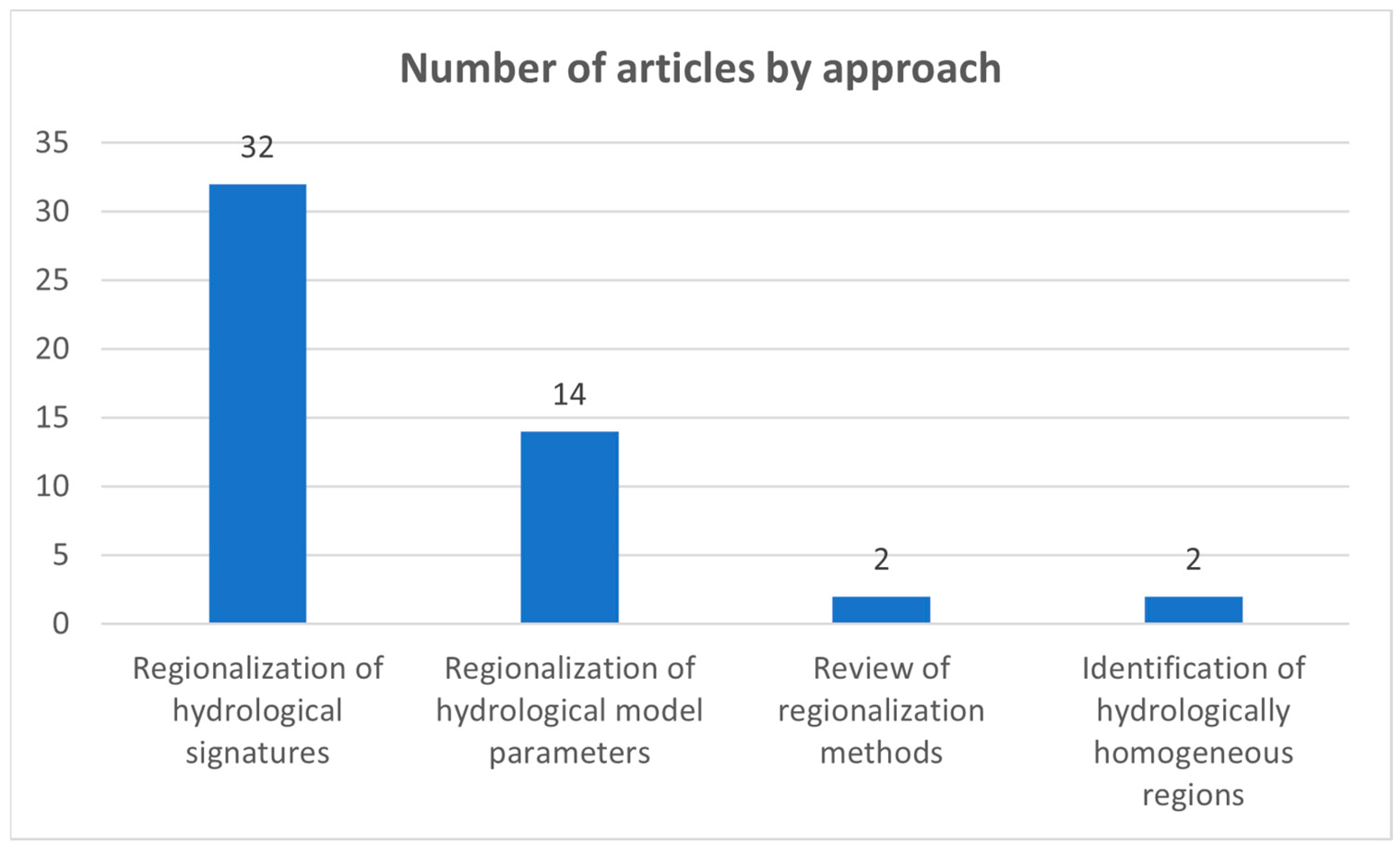
3. Results

In the first stage, a total of 905 publications were found. Subsequently, duplicate studies were removed (433 publications), resulting in a list of 472 publications. The target of 40 relevant articles was reached for the period 2015–2023 after reviewing approximately 230 articles. After fully reading and reclassifying the articles categorized as “pending review” (20 articles), a final total of 50 articles were classified as relevant. The list of articles can be found in Supplementary Materials Table S1.

It was identified that most of the articles (32) focused primarily on the regionalization of hydrological signatures, followed by studies related to the regionalization of hydrological model parameters (14). Additionally, two review articles were found, as well as two articles in which the main topic was the identification of hydrologically homogeneous regions. Figure 2 presents a summary of the number of articles found according to each regionalization approach.

According to Cupak [17], two approaches for estimating flows at ungauged locations are presented in the literature: the deterministic approach and the stochastic approach. In the first, a rainfall-runoff model is used to generate a continuous flow time series, allowing for the estimation of the desired flow statistic. In the stochastic approach, these flow statistics of interest are estimated from flow statistics at a gauged location, using basin descriptors or spatial distance as a measure of similarity.

In this regard, it should be noted that not all articles related to the deterministic approach, i.e., those presenting methods for the regionalization of hydrological model parameters, focused on the estimation of minimum flows. However, these flows can be estimated from the flow series generated through regionalization. Articles related to the regionalization of hydrological signatures enable the estimation of minimum flows either through explicit equations or flow duration curves.

3.1. Regionalization of Hydrological Model Parameters

The regionalization of hydrological model parameters is considered a deterministic approach. The concept behind this regionalization is to use the calibrated parameters of the hydrological model from the gauged basin(s) (referred to as donor basins) to estimate the hydrological model parameters for an ungauged target basin, thereby predicting its flow time series [1].

The main methods of regionalization of hydrological model parameters found in the literature review are presented below.

3.1.1. Methods Based on Similarity

In similarity-based regionalization, the hydrological model parameters are transferred by considering different measures of similarity in terms of physical similarity and/or spatial proximity [1,18].

• Physical similarity

This method is based on the premise that basins with similar conditions (climate, land use, geological conditions), even if geographically distant, should exhibit similar hydrological responses. Thus, gauged basins can transfer parameter sets to an ungauged basin with similar conditions [1,19].

To apply this method, it is necessary to define the similarity between basins. For this purpose, the similarity index or cluster analysis are two approaches used to identify similar basins, thereby generating a set of hydrological model parameters that can be transferred from donor basins to ungauged basins [1].

For example, Ditthakit et al. [20] and Qi et al. [21] used the similarity index presented in Equation (1):

$${SI}_{ud}={\sum }_{i=1}^k{\displaystyle \frac{|{CD}_{d,i}-{CD}_{u,i}|}{∆{CD}_i}},$$

(1)

where ${SI}_{ud}$ is the similarity index, $CD$ represents the basin descriptor, $u$ and $d$ represent the ungauged and donor basin, respectively, $k$ is the total number of basin descriptors, and $∆C{D}_i$ represents the range of the basin descriptor.

Other similarity indices can be found in the work of Guo et al. [1].

Within cluster analysis, one of the methods used is cluster analysis. Cluster analysis is a process in which a set of feature vectors is divided into groups such that the vectors within a group are as similar as possible, while the vectors from different groups are as distinct as possible [17]. A summary of cluster analysis methods can be found in Cupak [17].

Other approaches beyond cluster analysis that allow for the grouping of basins are presented by Cupak [17], such as the classification and regression tree (CART), the residual pattern approach (RPA) used by Cupak et al. [22] and seasonality methods employed by Beskow et al. [23] and Cupak et al. [24]. In the latter approach, it was observed that seasonality indices were calculated in both studies, followed by the use of cluster analysis.

It is important to emphasize that physical similarity regionalization is not limited to the regionalization of hydrological model parameters, but also encompasses flow regimes, observed flow and hydrological signatures [1]. In this regard, although several basin clustering techniques have already been mentioned in this section, it is worth noting that none of the analyzed articles defined hydrologically homogeneous regions. Instead, they justified some measure of similarity between donor and recipient basins. However, most of the articles focusing on hydrological signature regionalization used basin clustering approaches, thereby simultaneously adopting a physical similarity approach.

2.

Spatial proximity

This approach follows the logic that basins located close to each other should exhibit similar hydrological behavior, as climatic and basin conditions are expected to vary uniformly across space [25]. Thus, gauged donor basins for hydrological model parameters are selected based on their spatial proximity to the ungauged basin, without considering any information regarding the basin’s attributes [19].

In the regionalization methods based on similarity, several techniques were identified for transferring parameters from donor basins to recipient basins, such as IDW interpolation [20,21,26], the arithmetic mean of each parameter from the donor basins [21,27,28] or direct transfer when only one basin is defined as the donor [28,29,30]. Another transfer approach found was the catchment runoff response similarity (CRRS) [31]. For example, Qi et al. [21] found in their study that the IDW approach outperformed the arithmetic mean approach for all regionalization methods based on spatial proximity and physical similarity, as well as for all hydrological models analyzed. They further noted that this finding is consistent with previous studies cited in their work.

It is important to emphasize that not only can a set of parameters for the ungauged basin be obtained from the parameter sets of donor basins, but also the flow response of the receiving basin can be derived from the flow responses generated for that same basin using each parameter set from the donor basins. This latter approach is known as output averaging and was employed by Farfán et al. [26] and Qi et al. [21].

In similarity-based regionalization methods, the selection of the number of donor basins is crucial, as it directly affects the simulation results of the receiving basin [1]. Thus, some studies have adopted different approaches: some used a single donor basin based on the smallest geographic distance or attribute-based distance [28,30], while others tested multiple donors to optimize prediction. Golian et al. [32] found the best results for 2 to 9 donors, whereas Farfán et al. [26] defined 10 donors as the most reliable number. Qi et al. [21] found that the optimal number of donor basins for the parameter averaging transfer option always varies between one and five, while for the output averaging option, it ranges between four and six. In their study, the output averaging option outperformed the parameter averaging option globally and they argued that it is consistent with previous regional studies. Farfán et al. [26] reached the same conclusion. Thus, the use of five to six donor basins is recommended for more accurate predictions [1,21].

The integration of physical similarity methods with spatial proximity was considered by Qi et al. [21] to enhance regionalization capacity. In this study, the distance between basin outlets was used as one of the descriptors and a similarity index based on this distance was calculated.

3.1.2. Regression-Based Methods

Regression-based methods aim to relate a dependent variable (in this case, each hydrological model parameter) with a set of independent variables (in this case, physical or climatic characteristics of the basin) [26]. Unlike physical similarity-based regionalization, this type of regionalization does not require the definition of a similarity measure between basins [1].

The selection criteria for basin descriptors and multiple linear regression equations varied among the analyzed studies. Farfán et al. [26] conducted a preliminary correlation analysis among the descriptors and grouped those that were strongly correlated, selecting only one from each group to avoid redundancies, in addition to establishing a minimum correlation threshold of 0.25 between the hydrological model parameter and the descriptor. The verification of multicollinearity among explanatory variables using the variance inflation factor (VIF) was performed by Golian et al. [32] and Sheikh Goodarzi et al. [33] to ensure variable independence. Different criteria were employed for selecting the best regressions: Mekonnen et al. [27] and Golian et al. [32] used the coefficient of determination (R²); Sheikh Goodarzi et al. [33], Soni et al. [28] and Chang et al. [34] applied stepwise regression analysis to identify the most suitable equations; and Cenobio-Cruz et al. [35] optimized the regression equation coefficients using a genetic algorithm.

A Random Forest regression approach was applied by Prieto et al. [36] not specifically to regionalize hydrological model parameters, but rather the principal components of flow index. In this way, these components were regionalized and used to condition hydrological model parameters through a Bayesian framework, enabling the prediction of streamflow time series in ungauged basins. Additionally, the authors developed new statistical tests to evaluate the performance of both the hydrological model and the regionalization method in estimating flow indices in the space of principal components.

Approximate Bayesian computation was employed by Dal Molin et al. [37] as a novel approach to calibrate a rainfall-runoff hydrological model for regionalized flow signatures. These signatures were derived from a seasonal flow duration curve generated by a cumulative distribution function with parameters dependent on daily precipitation series and the morphometric properties of the basin. The authors concluded that the main application of this approach is forecasting streamflow time series in ungauged basins. Although this study does not focus on the regionalization of hydrological model parameters, it is included in this section due to its use of hydrological signatures for model calibration.

Table 1. Approaches for regionalization of hydrological model parameters: similarity criteria and regression techniques.

Method	Article	Similarity Criteria/Regression Technique
Physical similarity	Ditthakit et al. [20]	Similarity index (Equation (1))
	Qi et al. [21]	Similarity index (Equation (1))
	Soni et al. [28]	Distance between attributes of the hydrographic basins
	Golian et al. [32]	Euclidean distance between attributes of the hydrographic basins
	Farfán et al. [26]	Euclidean distance between attributes of the hydrographic basins
	Garna et al. [29]	Comparison between physical attributes of the hydrographic basins, arguing strong Pearson correlation coefficients for variables such as precipitation and temperature
	Tegegne et al. [31]	Extension of the catchment runoff response similarity (CRRS) approach
	Mekonnen et al. [27]	Comparable areas
Spatial proximity	Ditthakit et al. [20]	-
	Farfán et al. [26]	-
	Jahanshahi et al. [30]	-
	Mekonnen et al. [27]	-
	Qi et al. [21]	-
	Soni et al. [28]	-
Regression-based methods	Cenobio-Cruz et al. [35]	Multiple linear regression
	Chang et al. [34]	Multiple linear regression
	Ditthakit et al. [20]	Multiple linear regression, Random Forest, M5 model tree
	Farfán et al. [26]	Multiple linear regression, artificial neural networks
	Golian et al. [32]	Multiple linear regression, Random Forest
	Mekonnen et al. [27]	Multiple linear regression
	Qi et al. [21]	Multiple linear regression
	Sheikh Goodarzi et al. [33]	Multiple linear regression
	Soni et al. [28]	Multiple linear regression, artificial neural networks

presents the approaches for the regionalization of hydrological model parameters, as well as the articles found for each approach and their characteristics.

3.2. Regionalization of Hydrological Signatures

Hydrological signatures are values derived from observed or modeled hydrological data series, such as precipitation, streamflow or soil moisture. These signatures are estimated to extract relevant information regarding hydrological behavior, such as the speed and spatiotemporal variability of the rainfall-runoff response [38]. Common examples of hydrological signatures include mean flow, flow percentiles, flood frequency, baseflow index or the slope of the flow duration curve [1,38].

In recent years, the study of hydrological signatures has gained increased attention due to their various important applications, such as basin characterization and classification, streamflow prediction in ungauged basins, insights of hydrological processes, hydrological similarity over time or space, water resource planning and management, and assessing ecological and environmental flow [1,38].

Hydrological model parameters can also be calibrated based on hydrological signatures, where the core of this approach is not to directly calibrate the model on the observed streamflow series, but rather to identify hydrologically significant patterns within all available data regarding the system’s behavior and calibrate the model on these signatures [39].

However, Guo et al. [1] emphasize that in regionalization, studying the relationship between hydrological signatures and basin attributes appears to be more straightforward than studying the relationship between hydrological model parameters and basin attributes. Considering that the articles classified in this category present regional equations for estimating hydrological signatures (specifically low flows) based on basin attributes, or methods for estimating flow duration curves that also use these attributes, Figure 2 shows that most of the reviewed articles focus on this approach, thus agreeing with Guo et al. [1].

In this regionalization approach, it was observed that most studies defined hydrologically homogeneous regions prior to obtaining regional equations that describe hydrological signatures as a function of basin attributes. Other articles either did not consider or did not clearly present a procedure for defining hydrologically homogeneous regions. As highlighted in the methods based on similarity section, utilizing basin clustering prior to the regionalization of hydrological signatures simultaneously adopts a physical similarity approach.

To define such regions, it was noted that cluster analysis was the most commonly used technique, with the Ward method [22,40,41,42,43,44,45,46] and K-means [23,24,40,42,47,48,49] being the most frequently applied. To a lesser extent, the single linkage and complete linkage methods were also used [42,50]. Other clustering methods employed included Partitioning Around Medoids (PAM), K-harmonic means (KHM), Fuzzy C-means (FCM) and the Genetic K-means algorithm (GKA) [23]. Studies focused on the identification of hydrologically homogeneous regions were presented by Basso et al. [51] and Coelho et al. [52].

To conduct cluster analysis, it is necessary to define a dissimilarity measure to quantify the similarity between two objects or clusters [42]. The most used dissimilarity measure was the Euclidean distance [24,40,44,46,47], followed by the Mahalanobis distance [23,42,50] and the Manhattan distance [23,42].

In addition to cluster analysis, other techniques were used to define hydrologically homogeneous regions. Rodrigues et al. [53] and Amorim et al. [54] made the flow series dimensionless and analyzed their frequency of occurrence, assuming that the curves of dimensionless flow versus frequency are similar within the same hydrologically homogeneous region. Matos et al. [55] applied the procedure described by Lisboa et al. [56], based on the verification of statistical regression criteria, such as the coefficient of determination and percentage error. Euclydes et al. [57] proposed two criteria, which were employed by Cecilio et al. [58] and Lopes et al. [13,59], considering the frequency distribution of dimensionless flows and the fit of multiple regression models with the physical and climatic characteristics of the sub-basins. It is thus noted that the methods described by Euclydes et al. [57] and Lisboa et al. [56] are similar.

In addition to cluster analysis, Cupak et al. [22] employed the residual pattern approach to group similar basins in terms of low flow and basin attributes. By applying this approach, the authors developed a regression model for all the analyzed basins and grouped them according to the residues extracted from the model. Ouarda et al. [45], in addition to the hierarchical cluster analysis, used canonical correlation analysis (CCA) and region of influence (ROI) approach to delineate homogeneous regions. Tormam et al. [46] used discriminant analysis, a technique employed to classify objects into exhaustive and mutually exclusive groups based on a set of independent variables, to test the results of homogeneous regions generated by cluster analysis. Boscarello et al. [43] refined the basin clustering conducted with the unsupervised learning algorithm self-organizing map (SOM) using Ward’s hierarchical clustering. Bazzo et al. [11] considered regions hydrologically homogeneous when the regressions for the flow of interest achieved coefficients of determination greater than 0.90 and standard error values below 1. To achieve this, the authors iteratively combined areas until these parameters were met. On the other hand, Pruski et al. [60] developed their work on a pre-defined sub-basin considered homogeneous based on a previous study. Costa et al. [61] defined their homogeneous region based on average daily flows but did not provide details of the procedure.

Defining hydrologically homogeneous regions and subsequently obtaining equations that associate streamflows with physical or climatic variables of the basins is a procedure commonly known in Brazil as the Eletrobrás method or traditional method. This method is described in a methodological guide outlining procedures for streamflow regionalization, which was published by Eletrobrás [58,62]. Some studies found in the review explicitly used this method [11,41,48,55,58,62,63]. The mass conservation method was applied by Bazzo et al. [11]. As they describe, the difference from the traditional method is that it forces the equations to pass through both the origin and the flow value at the point where tributaries discharge into the main river.

To minimize the risk associated with the extrapolation of minimum streamflow regionalization equations, Pruski et al. [60] proposed a method in which a threshold value is defined as the maximum specific minimum flow found at the streamflow stations used in the regionalization process. Thus, specific minimum flows estimated from the regionalization equation that exceed the threshold value are adjusted to assume that value. Subsequently, the corresponding minimum flows must be updated according to this criterion. According to the authors, this restriction establishes a physical limit for minimum flows, which simultaneously mitigates the risk of overestimating flows in extrapolated regions.

Some hydrological signatures require a frequency analysis prior to regionalization. This is the case with the minimum flow Q_7,10, which was present in all articles that used this analysis to estimate minimum flows and subsequently regionalize them [13,41,45,53,54,59,62,64]. In general, it was observed that this statistic is obtained for each gauged basin in each hydrologically homogeneous region. Probabilistic models are then tested, followed by an analysis of the adequacy of the observed data to the applied probability models, using goodness-of-fit tests to assist in selecting the best-fitted probability model. Subsequently, the target hydrological signature is estimated, and finally, its regionalization is performed.

Some articles utilized the traditional method, linear interpolation, modified linear interpolation, Chaves and modified Chaves for estimating hydrological signatures related to minimum flows [48,58,62]. The first method has already been discussed earlier. The other four methods are based on the location of gauged stations, watershed areas, mean precipitation, and distances measured along the channel between the section of interest and the gauged stations. Details regarding the application of these methods can be found in Cecilio et al. [58]. In addition to the aforementioned methods, Ferreira et al. [48] employed a geostatistical approach for estimating hydrological signatures related to minimum flows, using simple Kriging and ordinary Kriging methods, presenting a less common approach for hydrological signature estimation. Other less common approaches are presented below.

Ouarda et al. [45], in addition to using multiple linear regression and spatial interpolation, applied generalized additive models (GAMs) for the regional estimation of low-flow hydrological signatures. According to the authors, these models extend generalized linear models (GLMs) by replacing the linear predictor with a set of smooth functions of the independent or explanatory variables. Ferreira et al. [65] evaluated several machine learning approaches to regionalize three types of minimum flows (Q_7,10, Q₉₀ and Q₉₅) and long-term average flow. The authors employed the Random Forest, Earth and linear model algorithms. The predictor variables were related to morphometry, topography, climate, land use and cover, and surface conditions, with elimination performed through Pearson correlation analysis and recursive feature elimination (RFE). Konrad et al. [44] developed a method for estimating seasonal and annual minimum flows based on a single flow measurement and regional similarity in deviations between daily flow and minimum flow for a period of interest, defining six regions through hierarchical clustering. Piol et al. [66] used regional indicators, a simpler and faster approach than conventional methods, to estimate minimum, mean and maximum flows. Ahn et al. [67] applied a time-varying spatial hierarchical Bayesian model, using a two-parameter lognormal distribution, considered appropriate for modeling the minimum flow of interest, with parameters conditioned on factors such as sea surface temperature and basin conditions.

Regarding the regionalization of flow duration curves, Gaviria et al. [49] regionalized flow duration curves in Colombia by defining hydrologically homogeneous regions and applying multiple linear regressions to estimate characteristic flow percentages in a dimensionless manner based on the attributes of each basin. On the other hand, Waseem et al. [68] proposed an extended version of the IDW method, incorporating weights based on both geographic and physiographic spaces to estimate percentiles of the flow duration curve at ungauged sites. Requena et al. [69] evaluated the regional streamflow based frequency analysis (RSBFA) approach to estimate low flow quantiles by transferring daily series from gauged locations to ungauged sites and applying local frequency analysis. Boscarello et al. [43] classified river basins using the unsupervised learning algorithm self-organizing map (SOM), followed by hierarchical clustering and estimated flow duration curves using a lognormal distribution, whose parameters were regionalized through stepwise multiple linear regression, with the physical indices of the basins as independent variables.

In some cases, the classification of an article could be directed both towards the section on regionalization of hydrological model parameters and the section on regionalization of hydrological signatures. This is the case for the study by Costa et al. [61], who employed the flow-index model, a stochastic daily streamflow model [61,70], to generate flow duration curves for long-term flows and annual flow duration curves in their study area. Their work explored the evolutionary polynomial regression (EPR) technique to identify regional equations for model parameters over a homogeneous region and to assess the reliability of information transfer. This article was included in this section because, although model parameters were regionalized, the outcome was a hydrological signature.

Finally, three regionalization methodologies were used by Basso et al. [71] to estimate the minimum reference flow in several basins in the state of Goiás (Brazil) and to compare the results with on-site flow measurements. Their results showed significant variation between the measured and estimated flows across the three methodologies. Consequently, they concluded that regionalization is a viable approach for estimating reference flows in rural basins, but the results should be compared with field measurements, as underestimations or overestimations may occur.

Table 2. Approaches for regionalization of hydrological signatures: dissimilarity measures, basin clustering techniques and regression techniques.

Regionalization Approach	Dissimilarity Measure Between Basins	Basin Clustering Technique	Regression Technique
Minimum flow	Euclidean distance [24,40,44,46,47] Mahalanobis distance [23,42,50] Manhattan distance [23,42]	Cluster analysis [23,40,42,50] Dimensionless flows and analysis of their frequency of occurrence [53,54] Procedure described by Lisboa et al. [56] Criteria proposed by Euclydes et al. [57] Residual pattern approach [22]	Multiple linear regression [22,24,40] Power regression [23,62,63] Linear interpolation, modified linear interpolation, Chaves and modified Chaves methods [48,58,62] Geostatistical approach [48] Generalized additive models (GAMs) [45] Machine learning [65]
Flow duration curve	Euclidean distance [43,49]	Cluster analysis [49] Self organizing map (SOM) [43]	Regionalized quantiles via multiple linear regression or logarithmic regression [49,69] Parameters of a lognormal distribution regionalized via stepwise multiple linear regression [43] Quantiles regionalized via IDW interpolation and its extension [68] Parameters of a model regionalized via evolutionary polynomial regression (EPR) [61]

presents the two main approaches for the regionalization of hydrological signatures identified, including the main dissimilarity measures, clustering techniques and regression techniques, as well as the studies that applied them.

4. Discussion

4.1. Advantages and Disadvantages

According to Qi et al. [21], several regionalization methods have already been proposed and numerous comparative studies on these methods have been conducted in different regions over the past decades. However, no definitive conclusion has yet been reached regarding which method is most successful for use in ungauged basins. Nonetheless, from the perspective of flow estimation in ungauged locations, whether using deterministic or stochastic approaches, the former would be preferred if the study aims to estimate multiple types of flow quantiles or signatures, while the latter would be more suitable if only a few flow quantiles are of interest [69].

Table 3. Advantages and disadvantages of minimum flow regionalization methods.

Method	Advantages	Disadvantages
Regionalization of hydrological model parameters
Physical similarity	The main advantage of the physical similarity method over the linear regression method is that it uses physical and climatic attributes of the basins without requiring the assumption of linearity between them [72].	This method requires a detailed selection of the most relevant attributes of the basins [26].
Spatial proximity	This method does not require basin attribute definition because the hydrological model parameters are transferred from nearby donor basins [26].	Assuming that the gauged basins exhibit similar hydrological behavior is often inaccurate, potentially leading to significant errors in estimates [65].
Regression-based methods	The main appeal of this approach is its ability to interpolate the hydrological model parameter values among the basin attributes [34]. Comment: it is recommended to use the largest possible number of donor basins to generate a robust regression [26].	This method requires a detailed selection of the most relevant attributes of the basins [26]. The interdependencies of the hydrological model parameters, inherent to the calibration process results, are overly simplified, thereby increasing the uncertainty in the regression and reducing performance [34]. The “black box” nature of these methods does not allow for a detailed analysis of the processes involved between input and output variables [26].
Regionalization of hydrological signatures
Traditional method	Regression equations are easy to apply and cover a larger area compared to the mass conservation method [11]. This method stands out compared to methods such as linear interpolation or modified linear interpolation due to its simple and straightforward implementation, ease of use and reliable performance [41,55].	Its application in small drainage areas needs a detailed analysis due to its greater heterogeneity [71]. Its implementation faces limitations when data availability for a given basin is limited [58].
IL, ILM, C, CM methods *	Methods aimed at overcoming the scarcity of available information, offering an advantage over the traditional method when the existing databases in the basin are limited [58].	Results from some studies show that the estimation of minimum flows has low accuracy when the section of interest is located in a tributary river reach [48,58].
RSBFA	It allows to estimate the complete daily flow series at ungauged sites [69]. It does not require a dense measurement network or flow measurements at the point of interest and is independent of complex statistical models [69].	Preferred approach if the objective is to estimate a large number and/or different types of minimum flow quantiles [69].

Notes: * IL: Linear interpolation; ILM: linear interpolation modified; C: Chaves; CM: Chaves modified.

presents advantages and disadvantages found in the research according to regionalization approaches.

4.2. Limitations

Regarding the limitations of regionalization methods, it can be highlighted that the results of similarity-based methods (spatial proximity or physical similarity) are directly influenced by the number of donor basins, which may depend on the hydrological model, the research region, the density of measurement stations and the regionalization method used [1]. However, the use of multiple donor basins can reduce random errors compared to relying on a single one [1].

When analyzing the spatial proximity method specifically, its main limitation is its high dependence on many calibrated basins surrounding the basin of interest, which may not yield satisfactory regionalization results in areas with low density of flow gauges [1,26,65]. Additionally, this method assumes that adjacent basins have similar meteorological conditions and underlying surfaces, implying it cannot be applied in regions with drastic and complex spatial changes in these conditions [1]. Regarding the physical similarity method, its primary limitation may be the accessibility of certain geo-environmental data, especially when rainfall-runoff models are used to estimate flows in ungauged basins [54]. Similar to the spatial proximity method, this approach is less appealing in regions with a low number of gauged basins [54].

Methods based on the estimation of hydrological signatures, such as quantiles through regional regression equations, are limited by the need for a minimum quantity of flow data in the study area to develop the regressions effectively [48]. Another key point is that gauging stations typically cover large drainage areas and extrapolating regression equations using inputs beyond the limits for which the models were calibrated is not recommended [53,60,71]. In the specific case of the linear regression model, Naghettini et al. [73] identify two reasons for this: first, as the values of the independent variable deviate from its mean, the confidence interval around the regression line widens; second, the relationship between the independent and dependent variables may not remain linear for values that exceed the input range used in the regression. Due to the nature of the mass conservation method, which forces the regression to pass through the confluence of tributaries with the main river, it is impossible to generate regionalization equations for tributaries without gauging stations, thereby limiting the method’s applicability [11].

4.3. Recent Advances

Ouarda et al. [45] introduced GAMs, one of the most recent methods in regional flood frequency analysis, for the regional estimation of minimum flow signatures, comparing their results with classical approaches such as multiple linear regression, which is widely used in regionalization studies. The authors highlight that GAMs offer greater flexibility in the relationships between the response variable and explanatory variables compared to classical models like multiple linear regression, allowing the incorporation of variables whose relationship with the response variable is not necessarily linear, something that can be an advantage over multiple linear regression. Lastly, they emphasize that the main advantage of GAMs is their ability to provide explicit expressions for the functions between the response variable and explanatory variables.

Ferreira et al. [65] evaluated various machine learning approaches for streamflow regionalization, including multiple linear regression. The authors report that the field of hydrology has increasingly focused on certain machine learning models due to their broad applicability and high capacity for relating multiple variables, in addition to generally demonstrating good predictive performance. Key features of these approaches are presented: one benefit of the linear model is its simplicity, making it more practical in various situations. However, its results are generally less accurate than the Random Forest approach, which, in contrast, makes generating easily interpretable equations infeasible. The Earth approach is considered an advancement of linear regression, allowing the generation of interpretable equations, which enhances its applicability, and it has been shown to deliver comparable or superior performance to Random Forest.

Another advance in flow regionalization, specifically in flow duration curves, was presented by Waseem et al. [68], who proposed an extended version of the inverse distance weighting (IDW) method to provide “alternative weights” based on a combination of geographic and physiographic spaces rather than just geographic space, as assumed by the traditional IDW method. According to their results, the proposed method can be considered an approach that provides more accurate and consistent results compared to the traditional IDW method.

5. Conclusions and Future Outlook

The estimation of minimum flows is essential for the sustainable management of water resources, directly influencing the planning of multiple water uses, water rights allocation and water availability assessment, among others. However, many regions face limitations in the availability of hydrological data for this estimation. Thus, regionalization emerges as a key technique to overcome this limitation, allowing the transfer of information from gauged basins to ungauged basins, thereby enabling the estimation of minimum flows in data-scarce regions. In this context, this study presented the frequently used approaches for the regionalization of minimum flows, namely the regionalization of hydrological model parameters and the regionalization of hydrological signatures. Regarding the first approach, the main methods used were similarity-based methods, including physical similarity and spatial proximity, as well as regression-based methods. Regarding the second regionalization approach, it was common to find the regionalization of minimum flows, followed by the regionalization of flow duration curves.

In spatial proximity and physical similarity methods, using multiple donor basins can reduce random errors compared to a single donor basin, making these approaches less attractive for regions with a low number of gauged basins. Regression-based methods are also affected by the number of gauged basins, as it is recommended to use as many donor basins as possible to generate robust regressions.

In the hydrological signature regionalization approach, hydrologically homogeneous regions were commonly defined prior to obtaining signature regressions, thus adopting a physical similarity approach. In this approach, minimum flows were generally expressed as a dependent variable in regressions, where the independent variables were climatological and physical basin attributes. Traditional regressions such as multiple linear regression or non-linear regressions such as power regression and machine learning techniques were found. Flow duration curves were estimated by either regionalizing multiple quantiles or regionalizing probability distribution parameters or mathematical models.

It can be inferred that, for both model parameter regressions and hydrological signature regressions such as low flows, multiple linear regression presents disadvantages compared to more flexible regression models, such as generalized additive models (GAMs) or machine learning approaches like Random Forest and Earth. This approach not only allows for better regression results but is also part of new tools, such as big data, used to identify large-scale regional hydrological characteristics. This, in turn, enables a better representation of hydrological similarity and consequently leads to improved classification of watersheds, which is crucial for the regionalization approach based on physical similarity [1].

Moreover, given the conditions of global climate change, it is important to discuss whether parameter regionalization is still applicable in this context and how runoff simulations in an ungauged basin under climate change should be improved [1].