Research on Data-Driven Prediction of Inrush Probability in Coal Mines Under the Mechanism of Feature Reconstruction in Information Interconnectivity
Abstract
1. Introduction
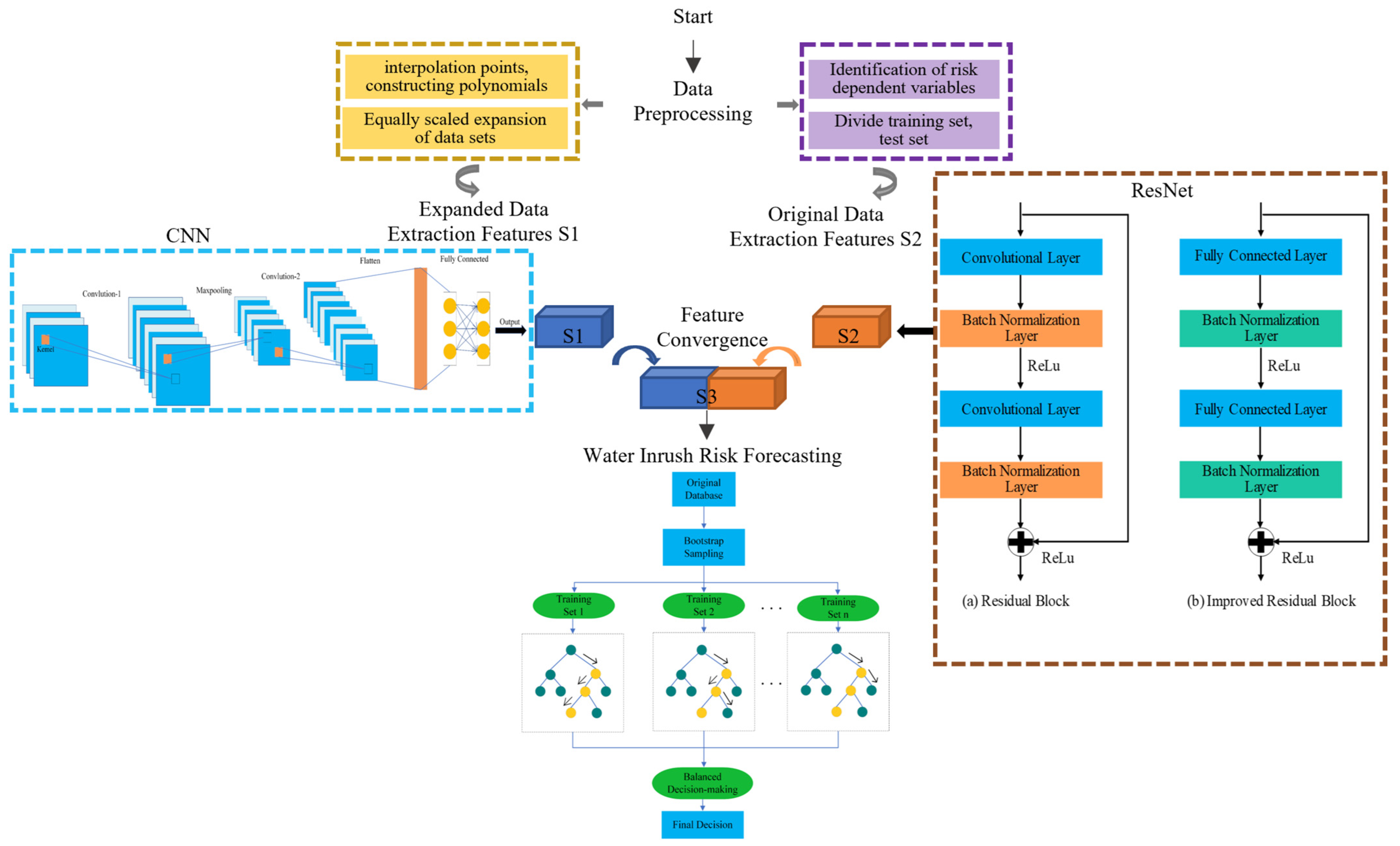
2. Data Processing for Research
3. Model Principles
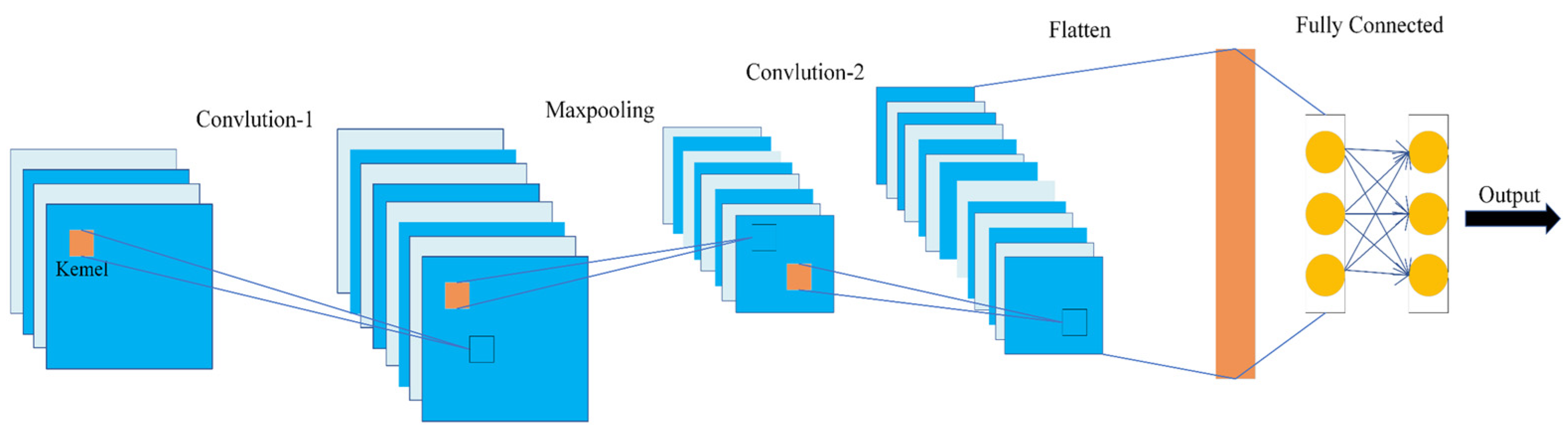
3.1. Principles of CNN
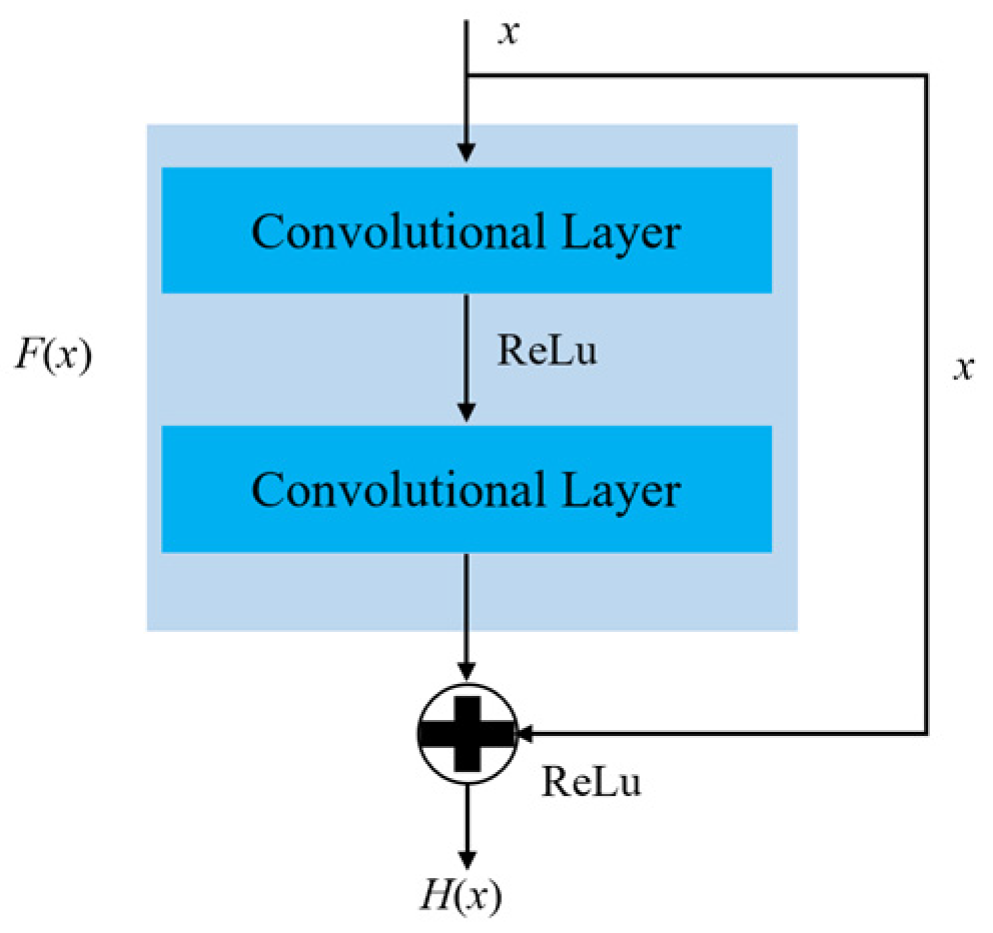
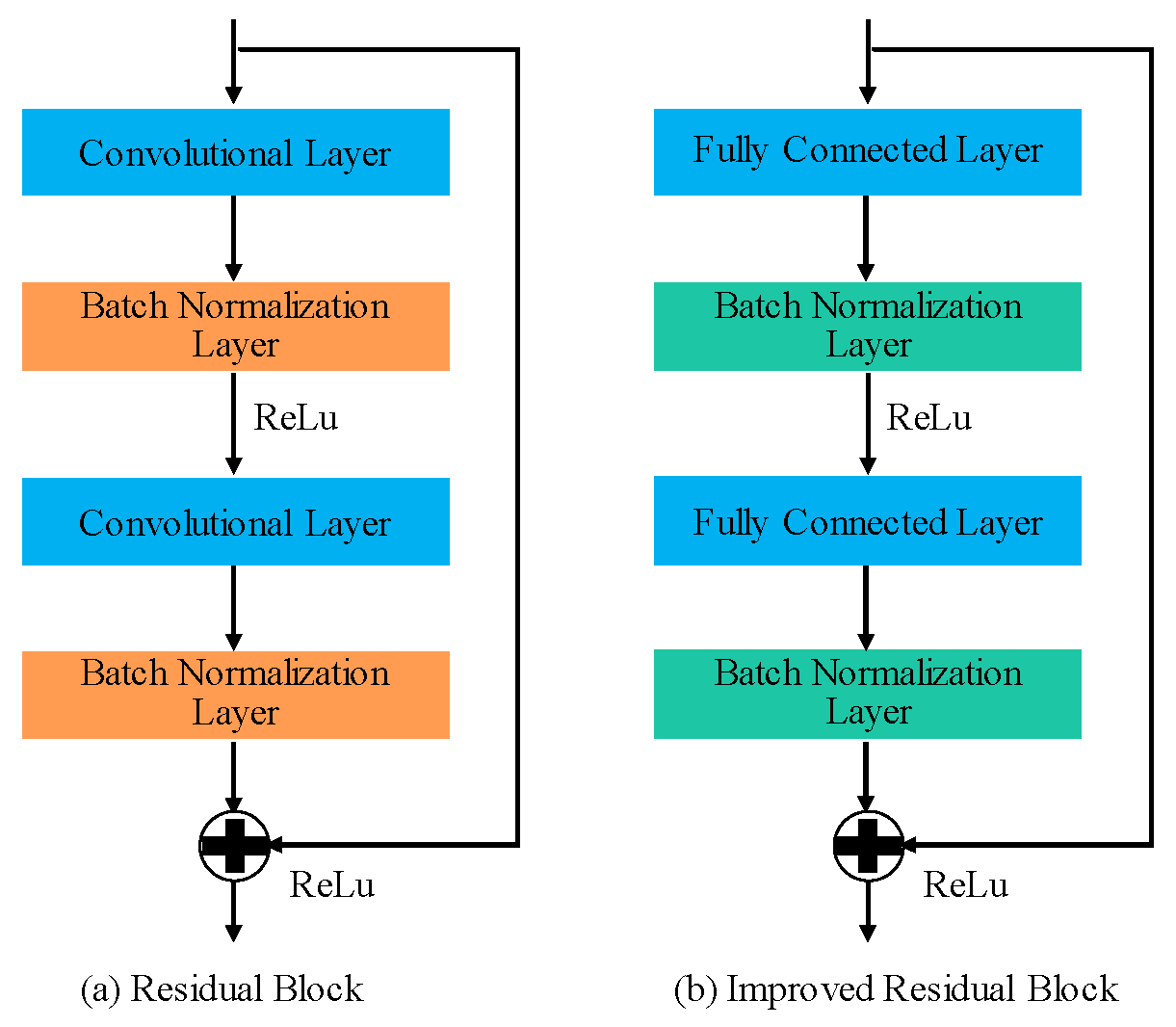
3.2. Principles of ResNet (Residual Networks)
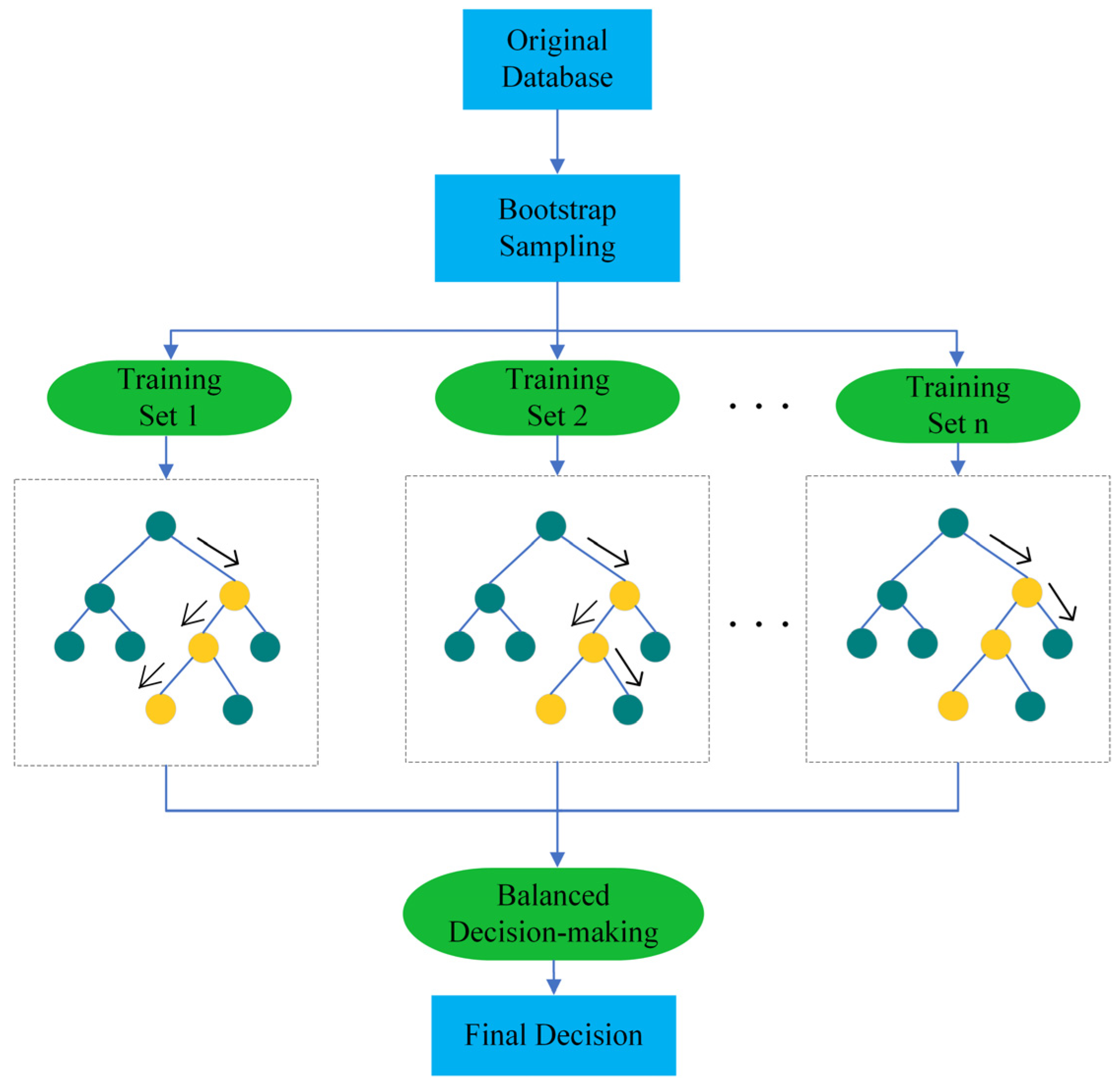
3.3. Principles of Random Forest (RF)
3.4. Model Construction
4. Case Study
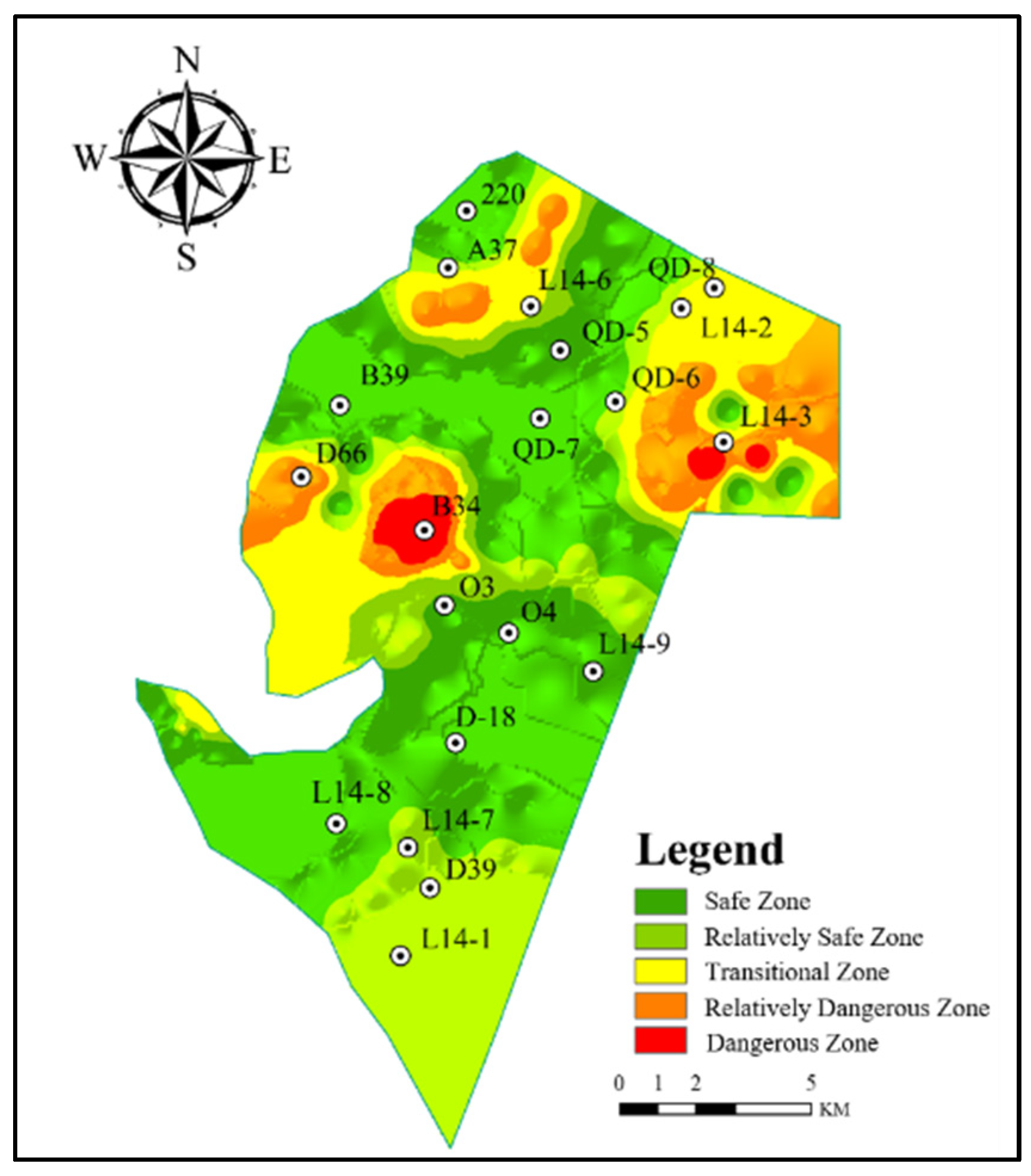
4.1. Research Background
4.2. Model Configuration and Evaluation Metrics
4.2.1. Model Parameters
4.2.2. Evaluation Metrics
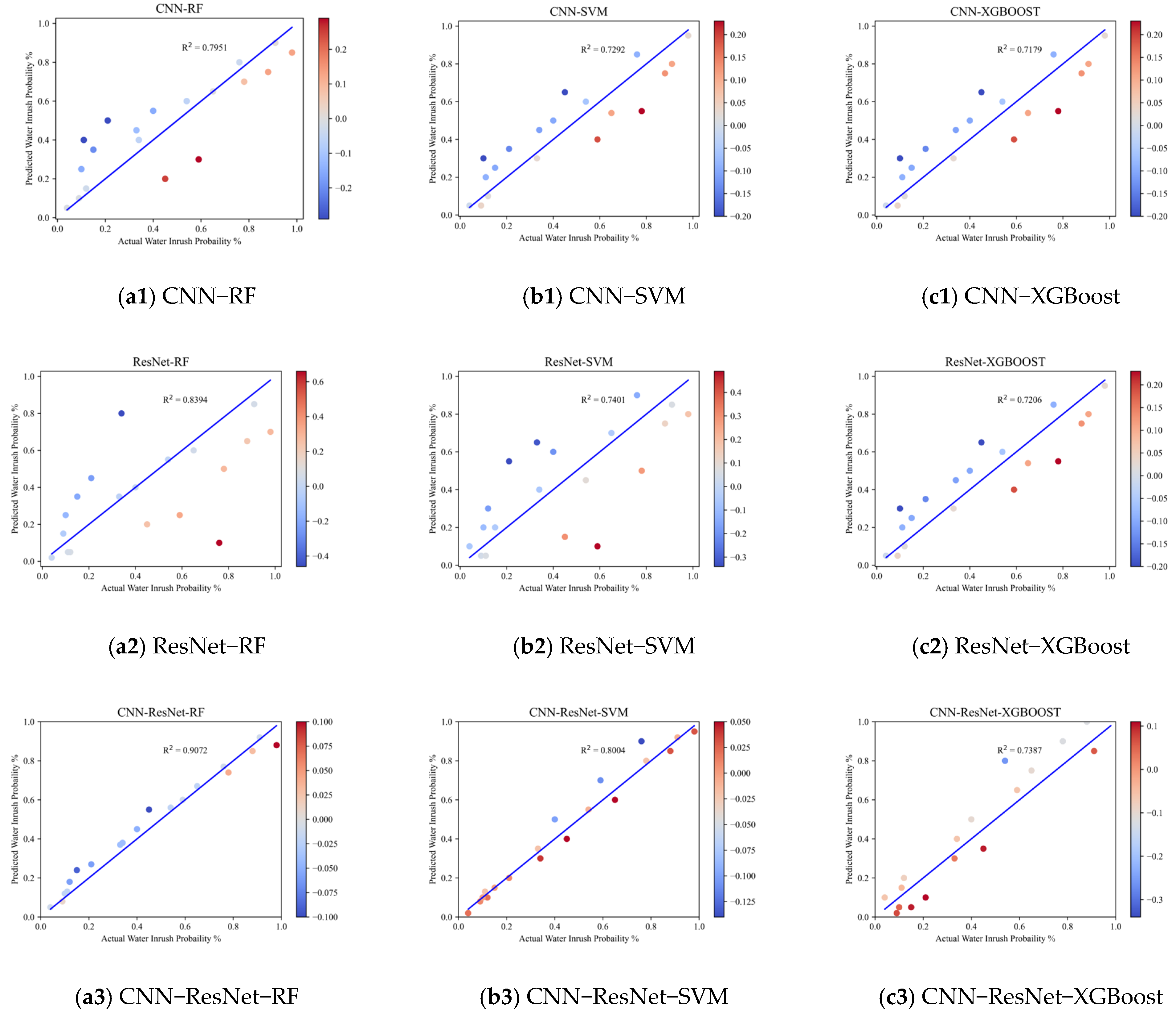
4.3. Comparative Analysis
4.4. Case Validation
5. Conclusions
- A data augmentation method based on bilinear interpolation was introduced, enhancing the training set of the model. By leveraging the augmented dataset, the model effectively harnessed the information contained within the training samples, addressing the issue of insufficient sample size associated with water inrush data. The augmented dataset exhibited characteristics in terms of extrema, mean, and standard deviation that were similar to those of the original samples, ensuring the reliability of data augmentation and establishing a solid foundation for subsequent model training.
- The features extracted from the augmented data using a CNN were seamlessly integrated with the original data features obtained through ResNet. This fusion capitalizes on the strengths of both architectures: a CNN excels at capturing local features, while ResNet, with its residual connections, effectively captures deep features. The combination produces a richer representation of features, which demonstrates a distinct advantage over employing either a CNN or ResNet in isolation for feature extraction.
- Compared to XGBoost and SVM predictive algorithms, the proposed model based on data augmentation and CNN-ResNet-RF represents an effective and viable approach for predicting water inrush risks in mines. The R2 value is nearly 1, indicating strong explanatory power regarding data variability. The model achieved reductions in MAE of 36.54% and 50.11% compared to SVM and XGBoost, respectively; reductions in MAPE of 45.49% and 44.18%; and reductions in RMSE of 37.10% and 71.24%. Following optimization and adaptability adjustments, this methodology can also be applied for forecasting other monitoring metrics, such as maximum water inflow and the development height of water-conducting fractures, showcasing its substantial potential for broader application.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Acharya, B.S.; Kharel, G. Acid mine drainage from coal mining in the United States—An overview. J. Hydrol. 2020, 588, 125061. [Google Scholar] [CrossRef]
- Naidu, G.; Ryu, S.; Thiruvenkatachari, R.; Choi, Y.; Jeong, S.; Vigneswaran, S. A critical review on remediation, reuse, and resource recovery from acid mine drainage. Environ. Pollut. 2019, 247, 1110–1124. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, Q.; Han, P. A review of water rock interaction in underground coal mining: Problems and analysis. Bull. Eng. Geol. Environ. 2023, 82, 157. [Google Scholar] [CrossRef]
- Zhang, C.; Jia, S.; Ren, Z.P.; Bai, Q.S.; Wang, L.; Han, P.H. Strength Evolution Characteristics of Coal with Different Pore Structures and Mineral Inclusions Based on CT Scanning Reconstruction. Nat. Resour. Res. 2024, 33, 2725–2742. [Google Scholar] [CrossRef]
- An, P.; Li, M.; Ma, S.; Zhang, J.; Huang, Z. Analysis of the thickness of the outburst prevention layer in karst tunnels under the control of compressive faults. Tunn. Undergr. Space Technol. 2024, 147, 105710. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, C.; Pang, L. Overburden and surface subsidence with slicing paste filling mining in thick coal seams. Front. Earth Sci. 2023, 10, 1027816. [Google Scholar] [CrossRef]
- Li, M.; Jiang, Z.; Liu, S.; Tong, X.; Chen, S.; Gao, Z.; Dai, Q. Research and application of response characteristics of mine transient electromagnetic perspective detection technology. J. China Coal Soc. 2024, 49, 1976–1988. [Google Scholar]
- Li, N.; Du, W. Enhanced Methods for Evaluating Water-inrush Risk from Underlying Aquifers: Incorporating Dynamic Weight Theory and Uncertainty Analysis Model. Water Resour. Manag. 2024, 38, 4615–4631. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, C.; Liu, W.; Pang, L. Evaluation on Development Height of Water-Conduted Fractures on Overburden Roof Based on Nonlinear Algorithm. Water 2022, 14, 3853. [Google Scholar] [CrossRef]
- Kong, H.-Q.; Zhang, N. Risk assessment of water inrush accident during tunnel construction based on FAHP-I-TOPSIS. J. Clean. Prod. 2024, 449, 141744. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, C.; Yang, Y.; Liu, W.; Zhu, Y. Identification of mine water sources using a multi-dimensional ion-causative nonlinear algorithmic model. Sci. Rep. 2024, 14, 3305. [Google Scholar] [CrossRef] [PubMed]
- Gai, Q.; He, M.; Gao, Y.; Lu, C. A two-dimensional model test system for floor failure during automatic roadway formation mining without pillars above confined water. Eng. Fail. Anal. 2024, 162, 108369. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, Q.; Zhang, W. Evolution of mining-induced water inrush disaster from a hidden fault in coal seam floor based on a coupled stress-seepage-damage model. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 78. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, Z.; Gu, Q.; Lin, Y.; Moyo, D.; Wu, Y.; Zou, C.; Zhao, K. Experimental investigation on the pore structure and Water Inrush Evolution Law of weakly cemented fault fracture zone with different filling gradations. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 162. [Google Scholar] [CrossRef]
- Zhang, J.; Song, Z.; Zhang, L.; Wu, S.; Wang, S.; Zhang, Y.; Dong, X.; Wang, J.; Han, Y.; Kan, B. Mechanical behaviours of bedded sandstone under hydromechanical coupling. J. Rock Mech. Geotech. Eng. 2024, 16, 1245–1261. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Peng, Z.; Zhang, M.; Hu, Y.; Oua, Q.; Zhang, J.; Tian, Y.; Shi, X. An improved model to predict the water-inrush risk under an unconsolidated confined aquifer based on analytic hierarchy process and information value method. Geomat. Nat. Hazards Risk 2023, 14, 2236277. [Google Scholar] [CrossRef]
- Gai, Q.; Gao, Y.; Zhang, X.; He, M. A New Method for Evaluating Floor Spatial Failure Characteristics and Water Inrush Risk Based on Microseismic Monitoring. Rock Mech. Rock Eng. 2024, 57, 2847–2875. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Ye, Z.; Liu, Y.; Wang, Y. A dynamic combination algorithm based scenario construction theory for mine water-inrush accident multi-objective optimization. Expert Syst. Appl. 2024, 238, 121871. [Google Scholar] [CrossRef]
- Dong, S.; Fan, M.; Guo, X.; Liu, Y.; Guo, K.; Ji, Z.; Li, C.; Xue, X. Characteristics and prevention and control techniques of typical water hazards in coal mines in Shaanxi Province. J. China Coal Soc. 2024, 49, 902–916. [Google Scholar]
- Liu, Y.; Ji, M.; Wang, Y.; Liu, G.; Gu, P.; Wang, Q. Fractal mechanical model of variable mass seepage in karst collapse column of mine. Phys. Fluids 2024, 36, 022031. [Google Scholar] [CrossRef]
- Li, B.; Wu, Q.; Yang, Y.; Wu, H.; Li, T. Characteristics of roof rock failure during coal seam mining and prediction techniques for mine water inflow in exposed karst areas. Bull. Eng. Geol. Environ. 2024, 83, 388. [Google Scholar] [CrossRef]
- Niu, C.; Tian, Q.; Xiao, L.; Xue, X.; Zhang, R.; Xu, D.; Luo, S. Principal causes of water damage in mining roofs under giant thick topsoil-lilou coal mine. Appl. Water Sci. 2024, 14, 146. [Google Scholar] [CrossRef]
- Qu, X.; Qiu, M.; Shi, L.; Han, J. The characteristics of rare earth elements in the main water filling sources of Sunan mining area. J. Clean. Prod. 2023, 428, 139472. [Google Scholar] [CrossRef]
- Wu, G.; Yu, W.; Guo, H.; Pan, B.; Liu, X. Investigation on water inrush fracture mechanics model based on fracture mechanics and microseismic monitoring. Ain Shams Eng. J. 2024, 15, 102587. [Google Scholar] [CrossRef]
- Amiri, A.F.; Kichou, S.; Oudira, H.; Chouder, A.; Silvestre, S. Fault Detection and Diagnosis of a Photovoltaic System Based on Deep Learning Using the Combination of a Convolutional Neural Network (CNN) and Bidirectional Gated Recurrent Unit (Bi-GRU). Sustainability 2024, 16, 1012. [Google Scholar] [CrossRef]
- Guo, Y.; Sun, H.; Liu, H.; Deng, Z. Radar Signal Recognition Based on CNN With a Hybrid Attention Mechanism and Skip Feature Aggregation. IEEE Trans. Instrum. Meas. 2024, 73, 2518913. [Google Scholar] [CrossRef]
- Wu, Z.; Shen, C.; van den Hengel, A. Wider or Deeper: Revisiting the ResNet Model for Visual Recognition. Pattern Recognit. 2019, 90, 119–133. [Google Scholar] [CrossRef]
- Gia Nhu, N.; Nin Ho Le, V.; Elhoseny, M.; Shankar, K.; Gupta, B.B.; Abd El-Latif, A.A. Secure blockchain enabled Cyber-physical systems in healthcare using deep belief network with ResNet model. J. Parallel Distrib. Comput. 2021, 153, 150–160. [Google Scholar] [CrossRef]
- Roy, S.K.; Manna, S.; Song, T.; Bruzzone, L. Attention-Based Adaptive SpectralSpatial Kernel ResNet for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7831–7843. [Google Scholar] [CrossRef]
- Ji, Z.; Zhou, M.; Wang, Q.; Huang, J. Predicting the International Roughness Index of JPCP and CRCP Rigid Pavement: A Random Forest (RF) Model Hybridized with Modified Beetle Antennae Search (MBAS) for Higher Accuracy. Cmes-Comput. Model. Eng. Sci. 2024, 139, 1557–1582. [Google Scholar] [CrossRef]
- Khajavi, H.; Rastgoo, A. Predicting the carbon dioxide emission caused by road transport using a Random Forest (RF) model combined by Meta-Heuristic Algorithms. Sustain. Cities Soc. 2023, 93, 104503. [Google Scholar] [CrossRef]

| No. | Key Indicator | Data Type | Unit | Evaluation Criteria |
|---|---|---|---|---|
| X1 | Development degree of Water-Conducting Structures | Float | None | Not Developed (0.1), Slightly Developed (0.3), Moderately Developed (0.5), Developed (0.8), Well Developed (1.0) |
| X2 | Fracture Permeability Characteristics | Float | None | Water-Blocking (0.1), Non-Water (0.3), Water Storage (0.5), Water-Conducting (0.8), Water-Rich (1.0) |
| X3 | Inclined Length of Working Face | Float | m | Actual width of the working face |
| X4 | Aquifer Water Pressure | Float | MPa | Actual water pressure value |
| X5 | Monthly Advancement Distance of Working Face | Float | m | Actual advancement distance of the working face |
| X6 | Aquitard Thickness | Float | m | Actual thickness of the aquitard |
| X7 | Depth of Floor Damage | Float | m | Actual depth of floor damage |
| X8 | Effective Thickness of Floor Aquitard | Float | m | Actual effective thickness of the aquitard |
| X9 | Percentage of Sandstone in the Aquitard | Float | None | Actual percentage of sandstone in the aquitard |
| X10 | Percentage of Mudstone in the Aquitard | Float | None | Actual percentage of mudstone in the aquitard |
| X11 | Percentage of Limestone in the Aquitard | Float | None | Actual percentage of limestone in the aquitard |
| X12 | Mining Height of Working Face | Float | m | Actual mining height of the working face |
| X13 | Structural Water Retention | Float | None | Low (0.1), Slightly Low (0.3), Moderate (0.5), Rich (0.8), Very Rich (1.0) |
| X14 | Collapse Pillar | Logical | None | Presence of collapse pillar (1 if present, 0 if absent) |
| X15 | Fault | Logical | None | Presence of fault (1 if present, 0 if absent) |
| X16 | Fracture Zone | Logical | None | Presence of fracture zone (1 if present, 0 if absent) |
| X17 | Fault Displacement | Float | m | Actual displacement value |
| X18 | Mining Depth of Working Face | Float | m | Actual coal seam mining depth |
| X19 | Water Source | Logical | None | Main aquifer classified as Ordovician gray water (1 if yes, 0 if no) |
| X20 | Water Quality | Logical | None | Change in water quality (1 if changed, 0 if unchanged) |
| X21 | Water Temperature | Float | °C | Actual water temperature value |
| X22 | Strike Length of Working Face | Float | m | Actual strike length of the working face |
| X23 | Coal Seam Dip Angle | Float | ° | Actual coal seam dip angle |
| X24 | Coal Seam Thickness | Float | m | Actual thickness of the coal seam |
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | … | X24 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.000 | 0.500 | 142.000 | 1.520 | 50.000 | 28.000 | 16.030 | 11.970 | … | 0.800 |
| 2 | 0.978 | 0.505 | 142.896 | 1.524 | 50.805 | 28.841 | 16.062 | 11.879 | … | 0.785 |
| … | … | … | … | … | … | … | … | … | … | … |
| 158 | 0.864 | 0.922 | 115.581 | 3.101 | 90.215 | 43.910 | 13.172 | 30.808 | … | 2.672 |
| 159 | 0.845 | 0.941 | 115.513 | 3.120 | 90.243 | 44.026 | 13.197 | 31.019 | … | 2.704 |
| 160 | 0.869 | 0.940 | 115.587 | 3.103 | 90.202 | 43.934 | 13.183 | 30.901 | … | 2.653 |
| No. | Xmin | Xmax | Xmean | Xstd |
|---|---|---|---|---|
| X1 | 0.1 | 1 | 0.552 | 0.186 |
| X2 | 0.1 | 1 | 0.562 | 0.162 |
| X3 | 28 | 220 | 121.96 | 43.805 |
| X4 | 0.85 | 12 | 3.212 | 2.260 |
| X5 | 25.8 | 180 | 63.236 | 40.114 |
| X6 | 10.96 | 181 | 46.293 | 34.227 |
| X7 | 3.73 | 24.45 | 14.127 | 4.902 |
| X8 | 0 | 161.95 | 32.042 | 31.729 |
| X9 | 0.05 | 0.97 | 0.507 | 0.210 |
| X10 | 0.01 | 0.8 | 0.37 | 0.175 |
| X11 | 0 | 0.67 | 0.123 | 0.139 |
| X12 | 0.8 | 9.8 | 2.19 | 1.924 |
| X13 | 0.3 | 1 | 0.522 | 0.119 |
| X14 | 0 | 1 | 0.24 | 0.427 |
| X15 | 0 | 1 | 0.98 | 0.14 |
| X16 | 1 | 1 | 1 | 0 |
| X17 | 0 | 23 | 3.041 | 4.365 |
| X18 | 10.6 | 120 | 36.63 | 26.770 |
| X19 | 0 | 1 | 0.92 | 0.271 |
| X20 | 0 | 1 | 0.18 | 0.384 |
| X21 | 18.71 | 55.72 | 26.777 | 8.211 |
| X22 | 50 | 290 | 58.6 | 61.151 |
| X23 | 3 | 34 | 14.8 | 7.365 |
| X24 | 0.8 | 9.8 | 2.314 | 2.102 |
| Layer Type | Output | Convolution Kernel | Activation Function | Instructions |
|---|---|---|---|---|
| Input Layer | (None, 24, 1, 1) | - | - | Input 24-dimensional features, total of 160 |
| Conv2D | (None, 24, 1, 32) | (1, 3) | relu | 32 filters, padding = ‘same’ |
| Batch Normalization | (None, 24, 1, 32) | - | - | Normalized output |
| Max Pooling | (None, 12, 1, 32) | (1, 2) | - | Downsampling, selecting every two units |
| Conv2D | (None, 12, 1, 64) | (1, 3) | relu | 64 filters, padding = ‘same’ |
| Batch Normalization | (None, 12, 1, 64) | - | - | Normalized output |
| Max Pooling | (None, 6, 1, 64) | (1, 2) | - | Downsampling, selecting every two units |
| Flatten | (None, 384) | - | - | Flattening the output |
| Dense | (None, 64) | 64 | relu | Hidden layer with 64 neurons |
| Dense | (None, 8) | 8 | linear | Output layer with 8 neurons |
| Layer Type | Output | Convolution Kernel | Activation Function | Instructions |
| Input Layer | (None, 24) | - | - | Input 24-dimensional features, total of 160 sets |
| Dense | (None, 64) | 64 | relu | First fully connected layer with 64 neurons |
| Batch Normalization | (None, 64) | - | - | Normalized output |
| Dense | (None, 64) | 64 | relu | Second fully connected layer with 64 neurons |
| Batch Normalization | (None, 64) | - | - | Normalized output |
| Add | (None, 64) | - | - | Skip connection, summing input with previous layer output |
| Dense | (None, 8) | 8 | linear | Output layer with 8 neurons |
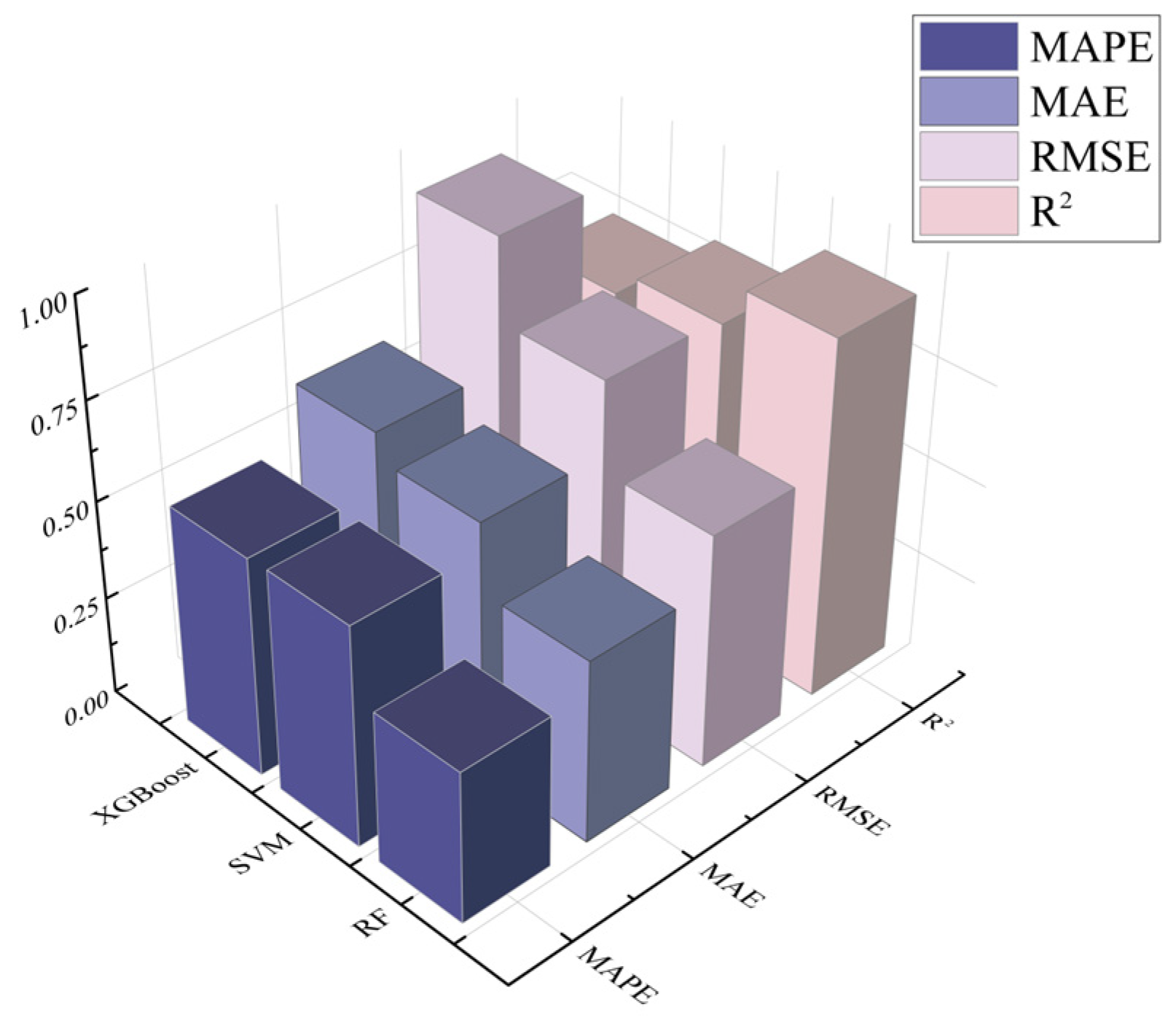
| RF | SVM | XgBoost | ||
|---|---|---|---|---|
| S1 | MAE | 0.6271 | 0.7261 | 0.7540 |
| MAPE | 0.6164 | 0.6250 | 0.5975 | |
| RMSE | 0.8920 | 1.0653 | 1.0749 | |
| R2 | 0.7951 | 0.7292 | 0.7179 | |
| S2 | MAE | 0.9238 | 0.6917 | 0.7684 |
| MAPE | 0.7092 | 0.6267 | 0.6394 | |
| RMSE | 1.3614 | 1.0011 | 1.1979 | |
| R2 | 0.8394 | 0.7401 | 0.7206 | |
| S3 | MAE | 0.4666 | 0.6371 | 0.7004 |
| MAPE | 0.3880 | 0.5645 | 0.5594 | |
| RMSE | 0.5946 | 0.8162 | 1.0182 | |
| R2 | 0.9072 | 0.8004 | 0.7387 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Peng, Z.; Zheng, Q. Research on Data-Driven Prediction of Inrush Probability in Coal Mines Under the Mechanism of Feature Reconstruction in Information Interconnectivity. Water 2025, 17, 843. https://doi.org/10.3390/w17060843
Xu S, Peng Z, Zheng Q. Research on Data-Driven Prediction of Inrush Probability in Coal Mines Under the Mechanism of Feature Reconstruction in Information Interconnectivity. Water. 2025; 17(6):843. https://doi.org/10.3390/w17060843
Chicago/Turabian StyleXu, Shuyu, Zhiwen Peng, and Qiushuang Zheng. 2025. "Research on Data-Driven Prediction of Inrush Probability in Coal Mines Under the Mechanism of Feature Reconstruction in Information Interconnectivity" Water 17, no. 6: 843. https://doi.org/10.3390/w17060843
APA StyleXu, S., Peng, Z., & Zheng, Q. (2025). Research on Data-Driven Prediction of Inrush Probability in Coal Mines Under the Mechanism of Feature Reconstruction in Information Interconnectivity. Water, 17(6), 843. https://doi.org/10.3390/w17060843






