Compound Flood Risk Assessment of Extreme Rainfall and High River Water Level
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Datasets
2.2. Copula-Based Joint Distribution Model
2.2.1. Marginal Distribution Function and Joint Distribution Function
2.2.2. Goodness-of-Fit Criterion
2.2.3. Flood Risk Probability Calculation
2.3. Urban Inundation Model
2.3.1. InfoWorks ICM
2.3.2. Model Setup
2.4. Compound Impact of Rainfall and River Water Level
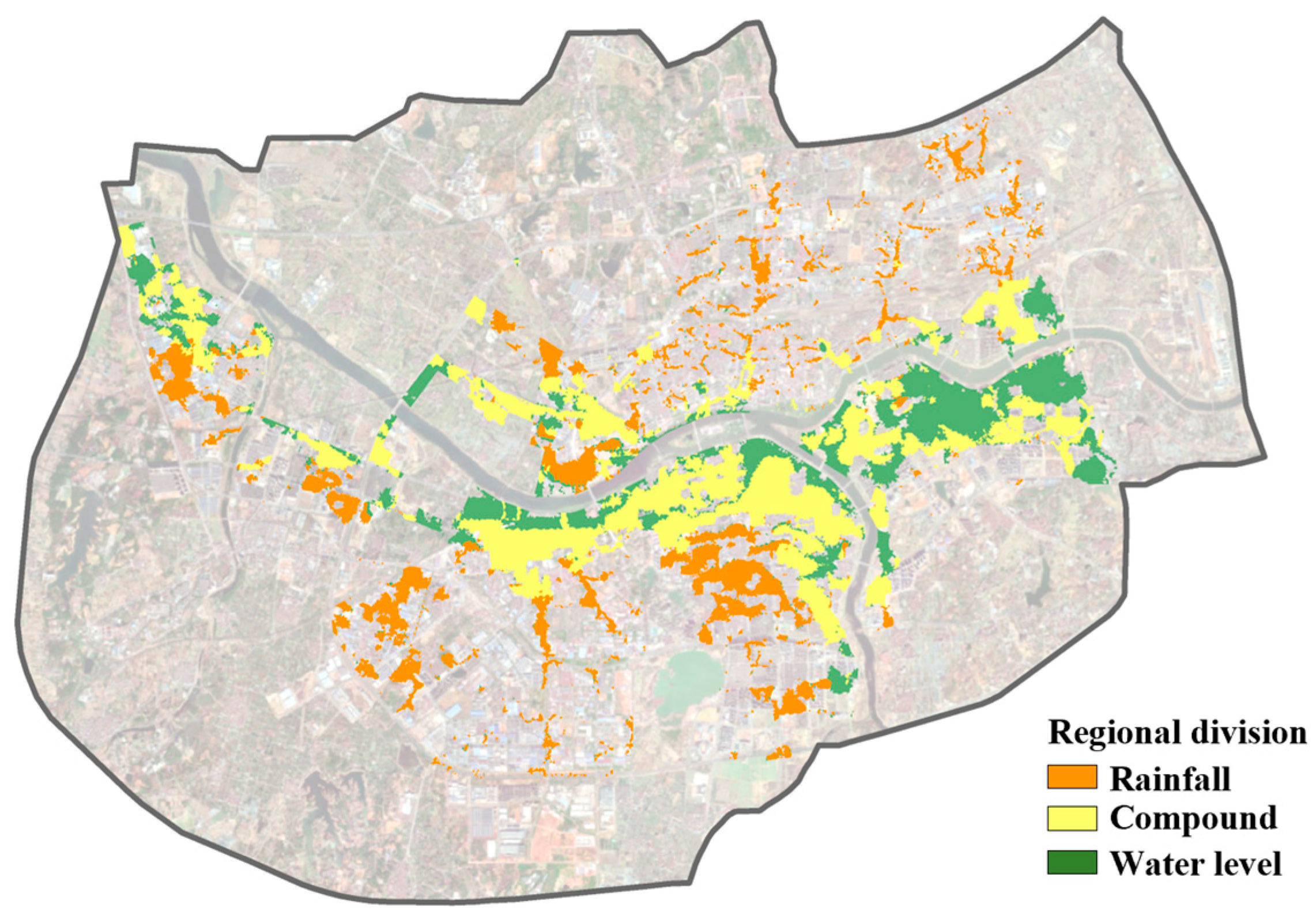
2.4.1. Regional Division of Disaster Factors
2.4.2. Amplification Factor
3. Results and Discussion
3.1. Joint Probability Distribution Model Fitting
3.1.1. Marginal Probabilities
3.1.2. Best-Fit Copula Selection
3.2. Joint Flood Risk Probability Analysis
3.3. Simulations of the Compound Impact of Rainfall and Water Level
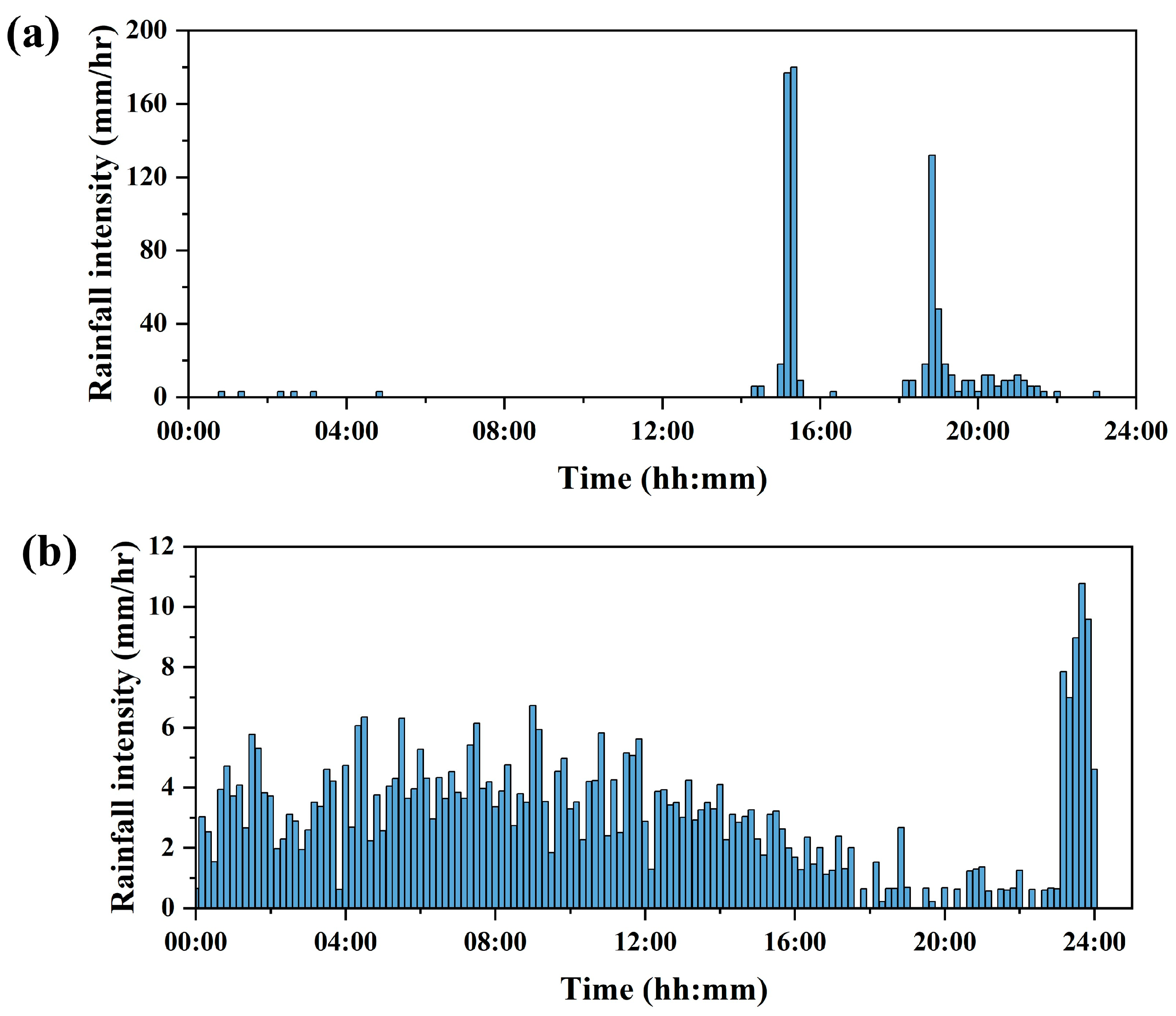
3.3.1. Model Calibration and Validation
3.3.2. Compound Flood Risk Assessment
3.4. Limitations and the Future Work
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IPCC. Climate Change 2021: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Escobar Carias, M.S.; Johnston, D.W.; Knott, R.; Sweeney, R. Flood disasters and health among the urban poor. Health Econ. 2022, 31, 2072–2089. [Google Scholar] [CrossRef] [PubMed]
- Ding, W.; Wu, J.; Tang, R.; Chen, X.; Xu, Y. A review of flood risk in China during 1950–2019: Urbanization, socioeconomic impact trends and flood risk management. Water 2022, 14, 3246. [Google Scholar] [CrossRef]
- Fang, J.; Wahl, T.; Fang, J.; Sun, X.; Kong, F.; Liu, M. Compound flood potential from storm surge and heavy precipitation in coastal China: Dependence, drivers, and impacts. Hydrol. Earth Syst. Sci. 2021, 25, 4403–4416. [Google Scholar] [CrossRef]
- Zhao, Z.; Huo, A.; Liu, Q.; Yang, L.; Luo, C.; Ahmed, A.; Elbeltagi, A. Assessment of urban inundation and prediction of combined flood disaster in the middle reaches of Yellow river basin under extreme precipitation. J. Hydrol. 2024, 640, 131707. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; Van Den Hurk, B.J.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T. Future climate risk from compound events. Nat. Clim. Change 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Chan, F.; Wang, Z.; Chen, J.; Lu, X.; Nafea, T.; Montz, B.; Adekola, O.; Pezzoli, A.; Griffiths, J.; Peng, Y. Selected global flood preparation and response lessons: Implications for more resilient Chinese Cities. Nat. Hazards 2023, 118, 1767–1796. [Google Scholar] [CrossRef]
- Tanaka, T.; Tachikawa, Y.; Ichikawa, Y.; Yorozu, K. Impact assessment of upstream flooding on extreme flood frequency analysis by incorporating a flood-inundation model for flood risk assessment. J. Hydrol. 2017, 554, 370–382. [Google Scholar] [CrossRef]
- Wang, X.; Xia, J.; Zhou, S.L.; Deng, S.; Li, Q. Assessment of the joint impact of rainfall and river water level on urban flooding in Wuhan City, China. J. Hydrol. 2022, 613, 128419. [Google Scholar] [CrossRef]
- Huang, W.; Ye, F.; Zhang, Y.J.; Park, K.; Du, J.; Moghimi, S.; Myers, E.; Pe’eri, S.; Calzada, J.R.; Yu, H. Compounding factors for extreme flooding around Galveston Bay during Hurricane Harvey. Ocean Model. 2021, 158, 101735. [Google Scholar] [CrossRef]
- Hsiao, S.-C.; Chiang, W.-S.; Jang, J.-H.; Wu, H.-L.; Lu, W.-S.; Chen, W.-B.; Wu, Y.-T. Flood risk influenced by the compound effect of storm surge and rainfall under climate change for low-lying coastal areas. Sci. Total Environ. 2021, 764, 144439. [Google Scholar] [CrossRef]
- Shi, P.; Ye, T.; Wang, Y.; Zhou, T.; Xu, W.; Du, J.; Wang, J.A.; Li, N.; Huang, C.; Liu, L. Disaster risk science: A geographical perspective and a research framework. Int. J. Disaster Risk Sci. 2020, 11, 426–440. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.; Zeng, Z.; Li, R.; Li, Z.; Li, X.; Lai, C. Compound effects in complex estuary-ocean interaction region under various combination patterns of storm surge and fluvial floods. Urban Clim. 2024, 58, 102186. [Google Scholar] [CrossRef]
- Zeng, Z.; Lai, C.; Wang, Z.; Chen, Y.; Chen, X. Future sea level rise exacerbates compound floods induced by rainstorm and storm tide during super typhoon events: A case study from Zhuhai, China. Sci. Total Environ. 2024, 911, 168799. [Google Scholar] [CrossRef]
- Sadegh, M.; Moftakhari, H.; Gupta, H.V.; Ragno, E.; Mazdiyasni, O.; Sanders, B.; Matthew, R.; AghaKouchak, A. Multihazard scenarios for analysis of compound extreme events. Geophys. Res. Lett. 2018, 45, 5470–5480. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P.; Xia, Y.; Shi, C.; Zhang, X. A multivariate approach for statistical assessments of compound extremes. J. Hydrol. 2018, 565, 87–94. [Google Scholar] [CrossRef]
- Ghanbari, M.; Arabi, M.; Kao, S.C.; Obeysekera, J.; Sweet, W. Climate change and changes in compound coastal-riverine flooding hazard along the US coasts. Earth’s Future 2021, 9, e2021EF002055. [Google Scholar] [CrossRef]
- Lin, M.Y.; Sun, M.H.; Sun, W.Y.; Fu, H.S.; Chen, W.B.; Chang, C.H. Formulating a warning threshold for coastal compound flooding: A copula-based approach. Ecol. Indic. 2024, 162, 111994. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, W.; Shen, P. Flood risk assessment of loss of life for a coastal city under the compound effect of storm surge and rainfall. Urban Clim. 2023, 47, 101396. [Google Scholar] [CrossRef]
- Chen, W.; Huang, G.; Zhang, H. Urban stormwater inundation simulation based on SWMM and diffusive overland-flow model. Water Sci. Technol. 2017, 76, 3392–3403. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.; Guo, S.; Liao, W.; Zeng, Z.; Chen, X. Scenario-based projections of future urban inundation within a coupled hydrodynamic model framework: A case study in Dongguan City, China. J. Hydrol. 2017, 547, 428–442. [Google Scholar] [CrossRef]
- Löwe, R.; Urich, C.; Domingo, N.S.; Mark, O.; Deletic, A.; Arnbjerg-Nielsen, K. Assessment of urban pluvial flood risk and efficiency of adaptation options through simulations—A new generation of urban planning tools. J. Hydrol. 2017, 550, 355–367. [Google Scholar] [CrossRef]
- Tang, B.; Nederhoff, K.; Gallien, T. Quantifying compound coastal flooding effects in urban regions using a tightly coupled 1D-2D model explicitly resolving flood defense infrastructure. Coast. Eng. 2025, 199, 104728. [Google Scholar] [CrossRef]
- Kumbier, K.; Carvalho, R.C.; Vafeidis, A.T.; Woodroffe, C.D. Investigating compound flooding in an estuary using hydrodynamic modelling: A case study from the Shoalhaven River, Australia. Nat. Hazards Earth Syst. Sci. 2018, 18, 463–477. [Google Scholar] [CrossRef]
- Wei, H.; Wu, H.; Zhang, L.; Liu, J. Urban flooding simulation and flood risk assessment based on the InfoWorks ICM model: A case study of the urban inland rivers in Zhengzhou, China. Water Sci. Technol. 2024, 90, 1338–1358. [Google Scholar] [CrossRef]
- Zhu, W.; Cao, Z.; Kawaike, K.; Luo, P.; Yamanoi, K.; Koshiba, T. A novel urban flood risk assessment framework based on refined numerical simulation technology. J. Hydrol. 2024, 645, 132152. [Google Scholar] [CrossRef]
- Zhong, M.; Xiao, L.; Li, X.; Mei, Y.; Jiang, T.; Song, L.; Chen, X. A study on compound flood prediction and inundation simulation under future scenarios in a coastal city. J. Hydrol. 2024, 628, 130475. [Google Scholar] [CrossRef]
- Xue, W.; Wu, Z.; Xu, H.; Wang, H.; Ma, C.; Zhou, Y. A framework for amplification flood risk assessment and threshold determination of combined rainfall and river level in an inland city. J. Hydrol. 2024, 640, 131725. [Google Scholar] [CrossRef]
- Moradian, S.; AghaKouchak, A.; Gharbia, S.; Broderick, C.; Olbert, A.I. Forecasting of compound ocean-fluvial floods using machine learning. J. Environ. Manag. 2024, 364, 121295. [Google Scholar] [CrossRef]
- Di Bacco, M.; Contento, A.; Scorzini, A.R. Exploring the compound nature of coastal flooding by tropical cyclones: A machine learning framework. J. Hydrol. 2024, 645, 132262. [Google Scholar] [CrossRef]
- Chen, J.; Tian, Y.; Zhang, S.; Li, Y.; Guo, Z. Study of Urban Flooding Response under Superstandard Conditions. Water 2023, 15, 1492. [Google Scholar] [CrossRef]
- Ding, J.; He, W.; Wu, S.; Fan, L.; Zhang, G.; Yang, L.; Feng, Q. Effects of heavy rainfall and outer river level on urban waterlogging in hilly areas of South China: A case study of Nanhu Port, Changsha City. Desalination Water Treat. 2023, 302, 121–128. [Google Scholar] [CrossRef]
- Dodangeh, E.; Shahedi, K.; Solaimani, K.; Shiau, J.-T.; Abraham, J. Data-based bivariate uncertainty assessment of extreme rainfall-runoff using copulas: Comparison between annual maximum series (AMS) and peaks over threshold (POT). Environ. Monit. Assess. 2019, 191, 67. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Xiong, L.; Xu, C.Y.; Guo, S. Bivariate frequency analysis of nonstationary low-flow series based on the time-varying copula. Hydrol. Process. 2015, 29, 1521–1534. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. In Annales de l’ISUP; L’institut de Statistique de l’Université de Paris: Paris, France, 1959; pp. 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Wit, E.; Heuvel, E.v.d.; Romeijn, J.W. ‘All models are wrong…’: An introduction to model uncertainty. Stat. Neerl. 2012, 66, 217–236. [Google Scholar] [CrossRef]
- Reddy, M.J.; Ganguli, P. Bivariate flood frequency analysis of upper Godavari River flows using Archimedean copulas. Water Resour. Manag. 2012, 26, 3995–4018. [Google Scholar] [CrossRef]
- Lian, J.; Xu, K.; Ma, C. Joint impact of rainfall and tidal level on flood risk in a coastal city with a complex river network: A case study of Fuzhou City, China. Hydrol. Earth Syst. Sci. 2013, 17, 679–689. [Google Scholar] [CrossRef]
- Zang, W.; Zhao, X.; Li, M.; Xue, X. Research progress and development trend of urban flood simulation technology. China Flood Drought Manag. 2020, 30, 1–13. [Google Scholar]
- Gao, L.; Du, H.; Huang, H.; Zhang, L.; Zhang, P. Modelling the compound floods upon combined rainfall and storm surge events in a low-lying coastal city. J. Hydrol. 2023, 627, 130476. [Google Scholar] [CrossRef]
- Bilskie, M.V.; Hagen, S.C. Defining Flood Zone Transitions in Low-Gradient Coastal Regions. Geophys. Res. Lett. 2018, 45, 2761–2770. [Google Scholar] [CrossRef]
- Han, S.; Tahvildari, N. Compound flooding hazards due to storm surge and pluvial flow in a low-gradient coastal region. Water Resour. Res. 2024, 60, e2023WR037014. [Google Scholar] [CrossRef]
- Shi, S.; Yang, B.; Jiang, W. Numerical simulations of compound flooding caused by storm surge and heavy rain with the presence of urban drainage system, coastal dam and tide gates: A case study of Xiangshan, China. Coast. Eng. 2022, 172, 104064. [Google Scholar] [CrossRef]
- Liang, H.; Zhou, X. Impact of tides and surges on fluvial floods in coastal regions. Remote Sens. 2022, 14, 5779. [Google Scholar] [CrossRef]
- Gao, L.; Mei, J.; Li, J.; Zhang, W.; Lai, C. Effect of intense rainfall and high riverine water level on compound flood hazards in a river-valley city: A case study of Yingde, China. J. Hydrol. 2023, 625, 130044. [Google Scholar] [CrossRef]
- Zellou, B.; Rahali, H. Assessment of the joint impact of extreme rainfall and storm surge on the risk of flooding in a coastal area. J. Hydrol. 2019, 569, 647–665. [Google Scholar] [CrossRef]
- Song, M.; Zhang, J.; Liu, Y.; Liu, C.; Bao, Z.; Jin, J.; He, R.; Bian, G.; Wang, G. Time-varying copula-based compound flood risk assessment of extreme rainfall and high water level under a non-stationary environment. J. Flood Risk Manag. 2024, 17, e13032. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, L.; Hao, Z.; Li, J.; Thorstensen, A.; Gao, H. A Framework for Exploring Joint Effects of Conditional Factors on Compound Floods. Water Resour. Res. 2018, 54, 2681–2696. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, H.; Liu, Y.; Chai, B.; Bin, C. The spatial overlay effect of urban waterlogging risk and land use value. Sci. Total Environ. 2024, 947, 174290. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Gou, L.; Liu, S.; Peng, D. Effect of urban neighbourhood layout on the flood intrusion rate of residential buildings and associated risk for pedestrians. Sustain. Cities Soc. 2023, 92, 104485. [Google Scholar] [CrossRef]
- Machineni, N.; Sinha, V.S.; Singh, P.; Reddy, N. The impact of distributed landuse information in hydrodynamic model application in storm surge inundation. Estuar. Coast. Shelf Sci. 2019, 231, 106466. [Google Scholar] [CrossRef]

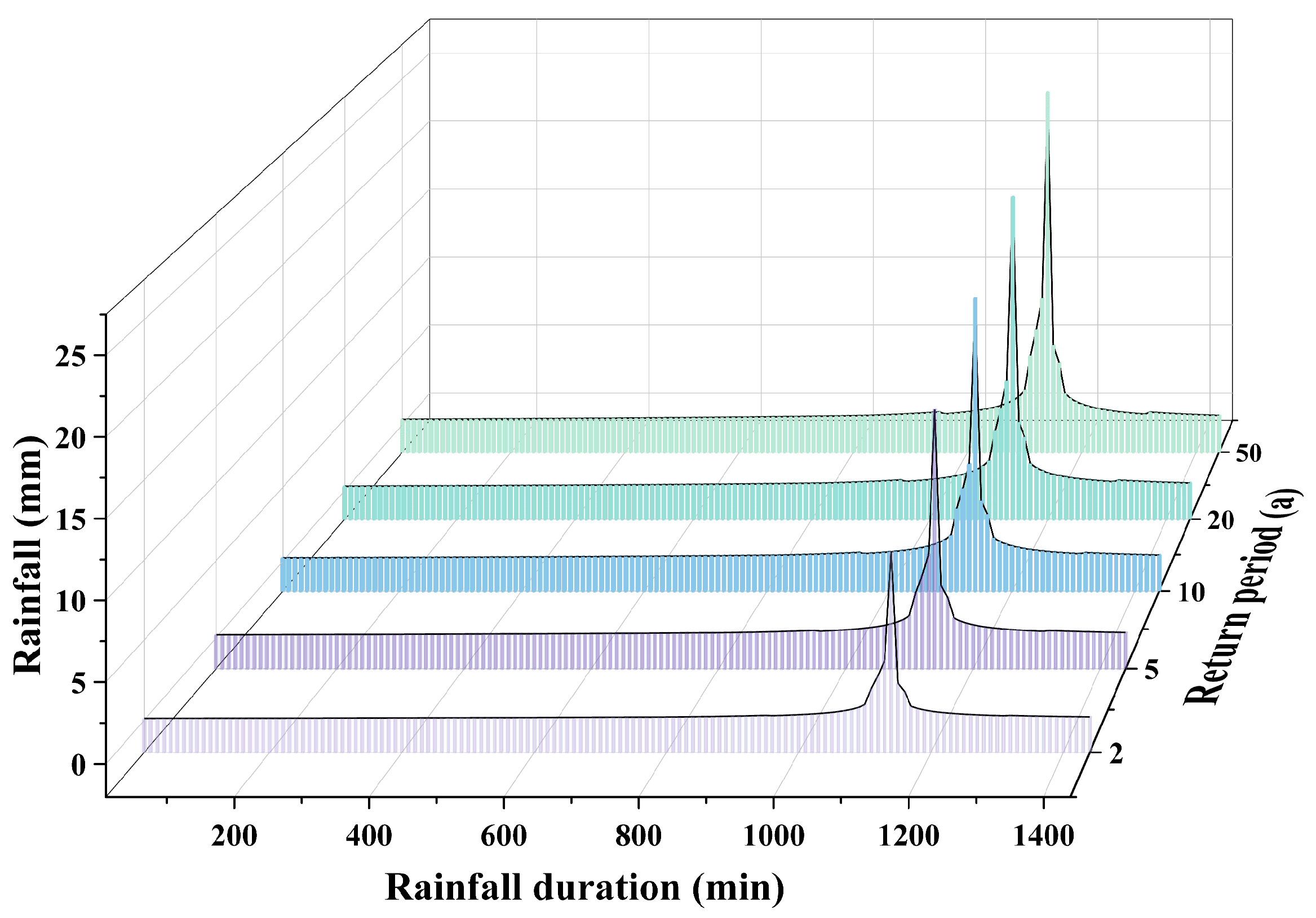

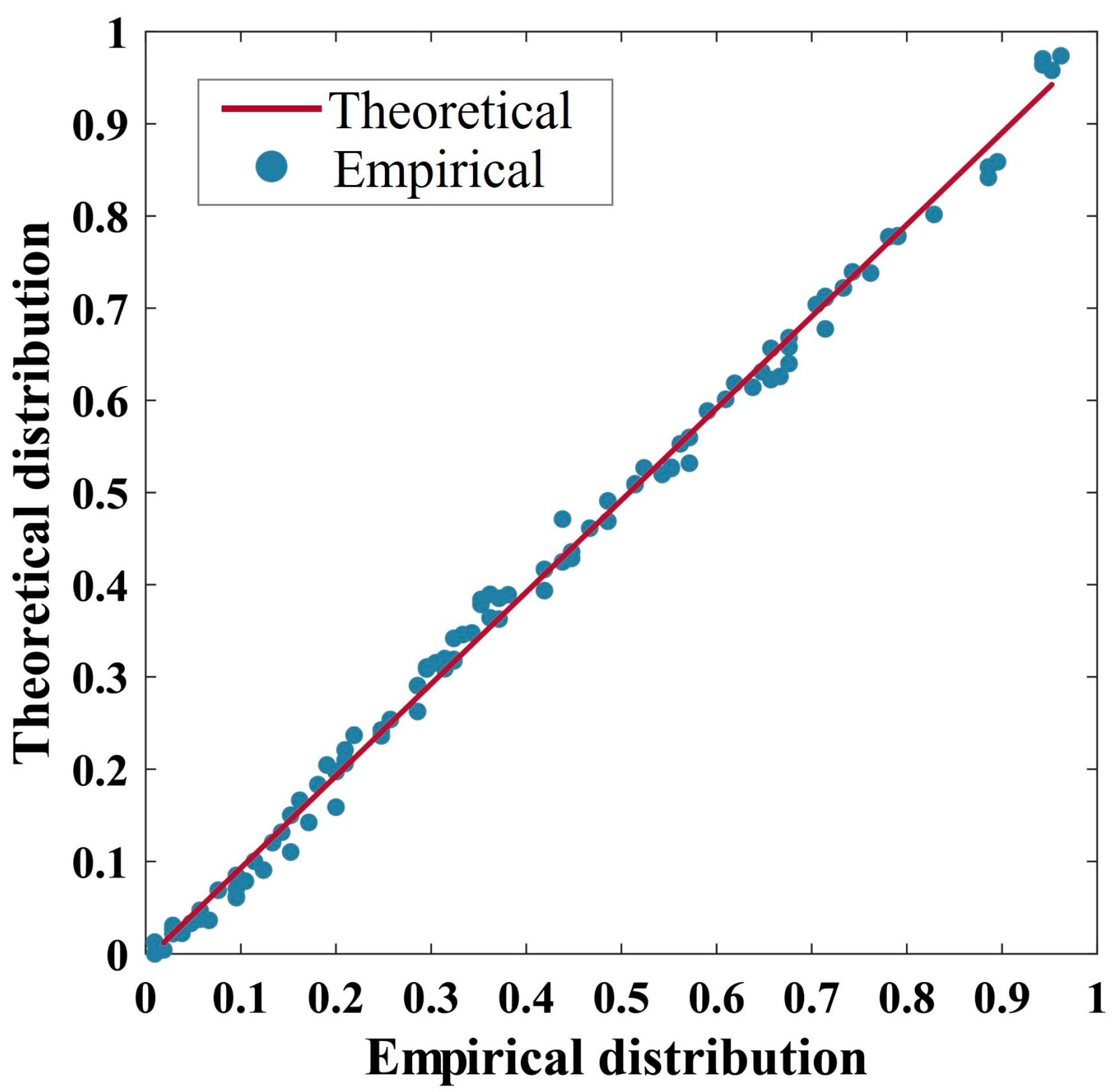
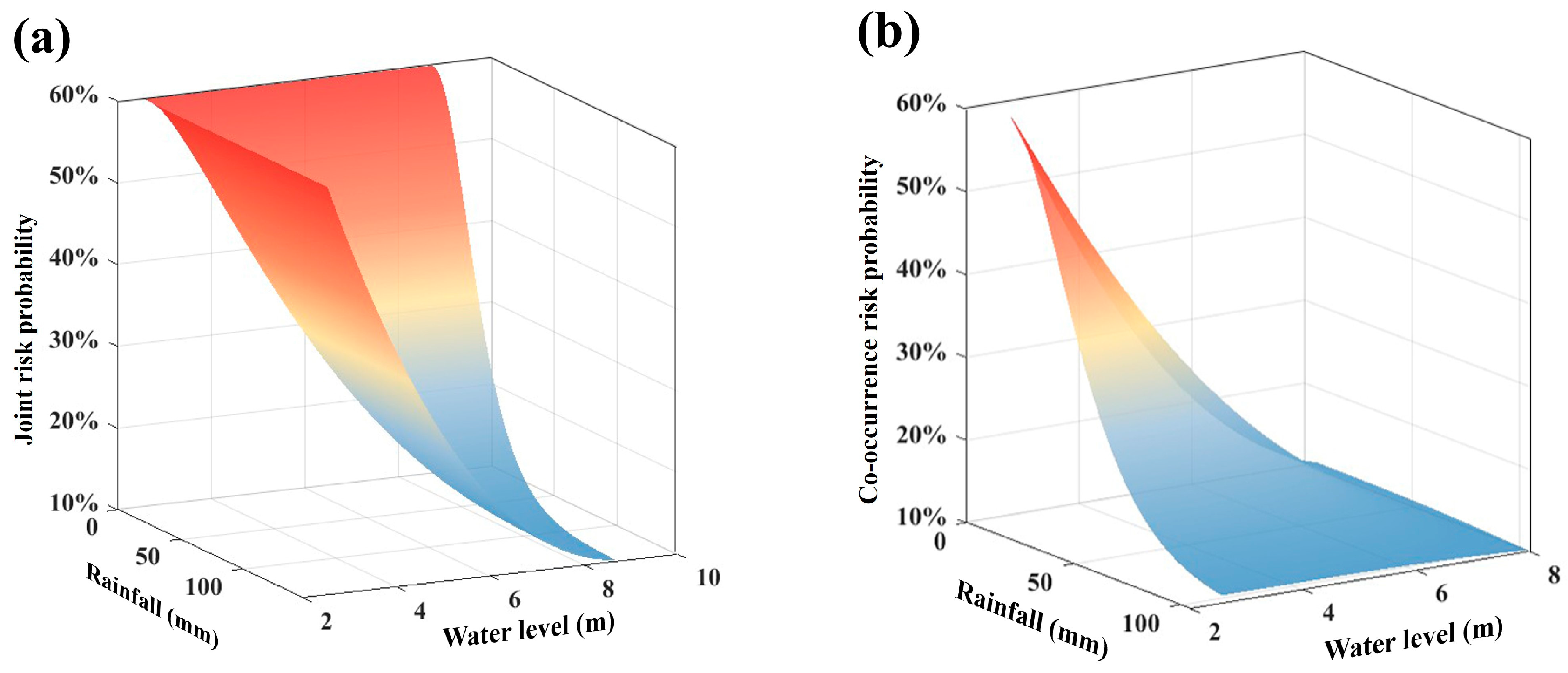
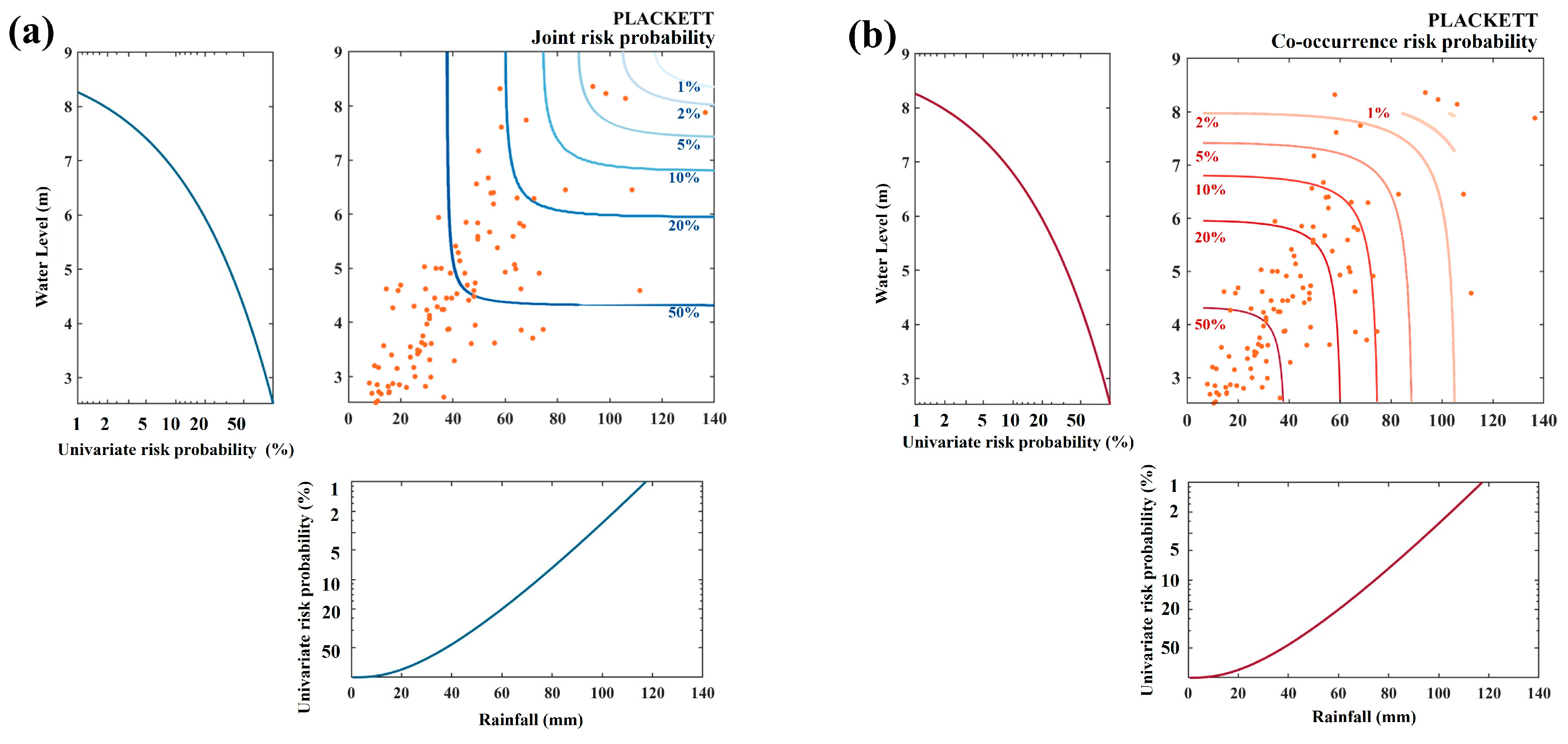




| Scenario | Return Period of Rainfall | Return Period of Water Level |
|---|---|---|
| 1 | 50a | none |
| 2 | none | 50a |
| 3 | 50a | 50a |
| Distribution Type | Rainfall | Water Level | ||||
|---|---|---|---|---|---|---|
| AIC | BIC | K-S Test | AIC | BIC | K-S Test | |
| Gamma | 945.6234 | 950.9313 | 0.0437 | 367.7278 | 373.0357 | 0.0650 |
| Normal | 972.7642 | 978.0721 | 0.0929 | 381.1816 | 386.4895 | 0.0882 |
| Logistic | 966.5638 | 971.8717 | 0.0773 | 382.1771 | 387.4850 | 0.0842 |
| Lognormal | 948.6829 | 953.9908 | 0.0660 | 364.8406 | 370.1485 | 0.0567 |
| Generalized Pareto | 947.7451 | 955.7070 | 0.0545 | 350.9790 | 358.9408 | 0.0510 |
| Generalized Extreme Value | 950.2942 | 958.2560 | 0.0508 | 366.6013 | 374.5632 | 0.0581 |
| Weibull | 949.6653 | 954.9732 | 0.0538 | 381.1705 | 386.4785 | 0.0929 |
| Copula | AIC | BIC | RMSE | NSE |
|---|---|---|---|---|
| Plackett | −96.7726 | −94.1187 | 0.2141 | 0.9940 |
| Frank | −94.4306 | −91.7767 | 0.2181 | 0.9938 |
| Gumbel | −78.4587 | −75.8047 | 0.2473 | 0.9920 |
| t | −75.4061 | −70.0982 | 0.2050 | 0.9945 |
| AMH | −63.1409 | −60.4869 | 0.4846 | 0.9692 |
| Gaussian | −61.0861 | −58.4321 | 0.2045 | 0.9945 |
| Joe | −57.7902 | −55.1363 | 0.3211 | 0.9865 |
| FGM | −39.0723 | −36.4183 | 0.6551 | 0.9437 |
| Clayton | −14.7418 | −12.0879 | 0.1894 | 0.9953 |
| Surface Type | Loss Model | Fixed Runoff Coefficient | Routing Model | Routing Parameter |
|---|---|---|---|---|
| Road | FIXED | 0.80 | SWMM | 0.013 |
| Green | 0.15 | 0.050 | ||
| Water | 1.00 | 0.050 | ||
| Building | 0.85 | 0.012 | ||
| Other | 0.45 | 0.030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Wang, C.; Mo, J.; Hou, S.; Dang, X.; Shi, H.; Gong, Y. Compound Flood Risk Assessment of Extreme Rainfall and High River Water Level. Water 2025, 17, 841. https://doi.org/10.3390/w17060841
Li W, Wang C, Mo J, Hou S, Dang X, Shi H, Gong Y. Compound Flood Risk Assessment of Extreme Rainfall and High River Water Level. Water. 2025; 17(6):841. https://doi.org/10.3390/w17060841
Chicago/Turabian StyleLi, Wanchun, Chengbo Wang, Junfeng Mo, Shaoxuan Hou, Xin Dang, Honghong Shi, and Yongwei Gong. 2025. "Compound Flood Risk Assessment of Extreme Rainfall and High River Water Level" Water 17, no. 6: 841. https://doi.org/10.3390/w17060841
APA StyleLi, W., Wang, C., Mo, J., Hou, S., Dang, X., Shi, H., & Gong, Y. (2025). Compound Flood Risk Assessment of Extreme Rainfall and High River Water Level. Water, 17(6), 841. https://doi.org/10.3390/w17060841







