Estimation of the Rainfall Erosivity Factor (R-Factor) for Application in Soil Loss Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Rainfall Data Collection and Analysis
2.3. R-Factor Determination and Mapping
3. Results
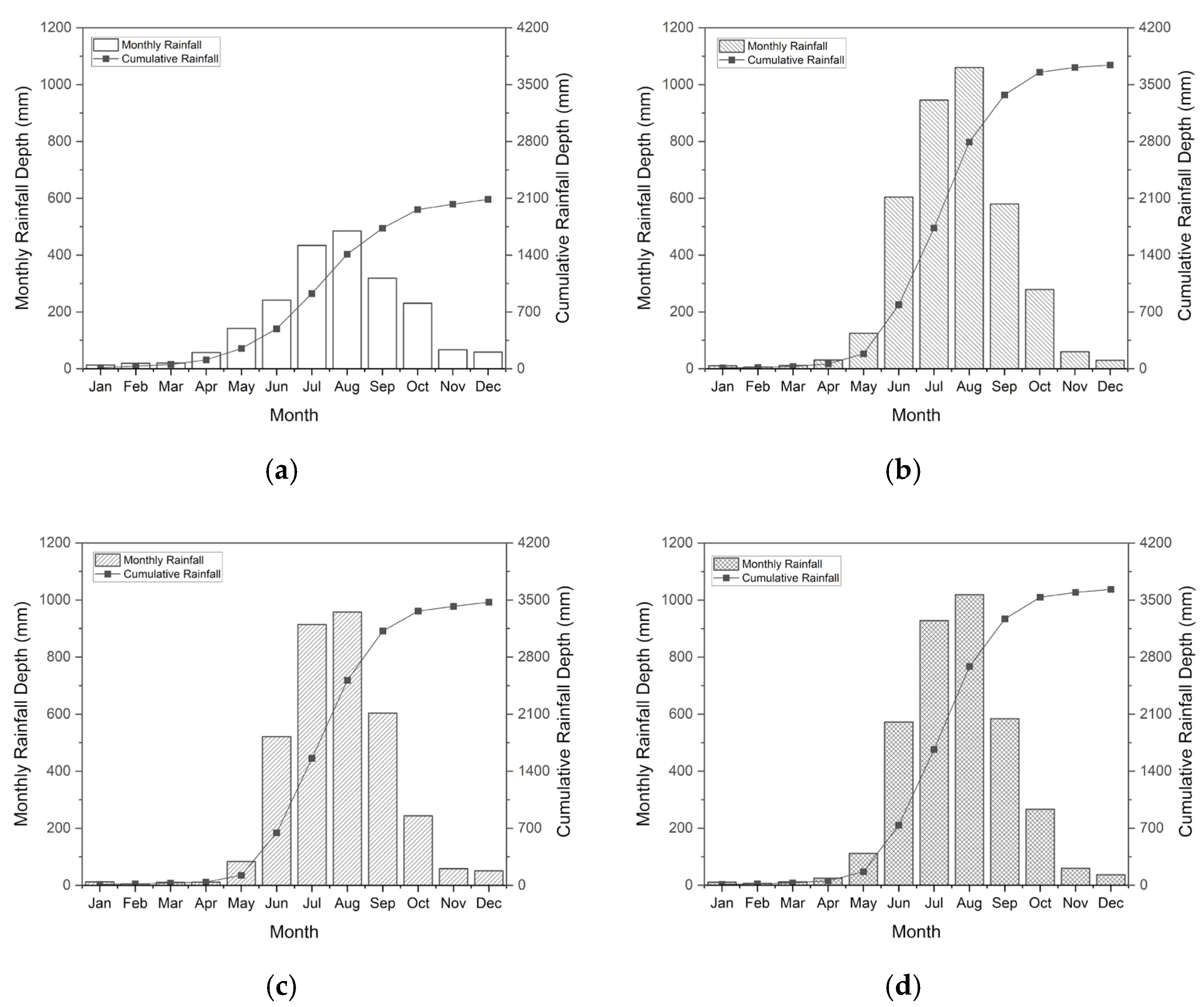
3.1. Rainfall Characteristics
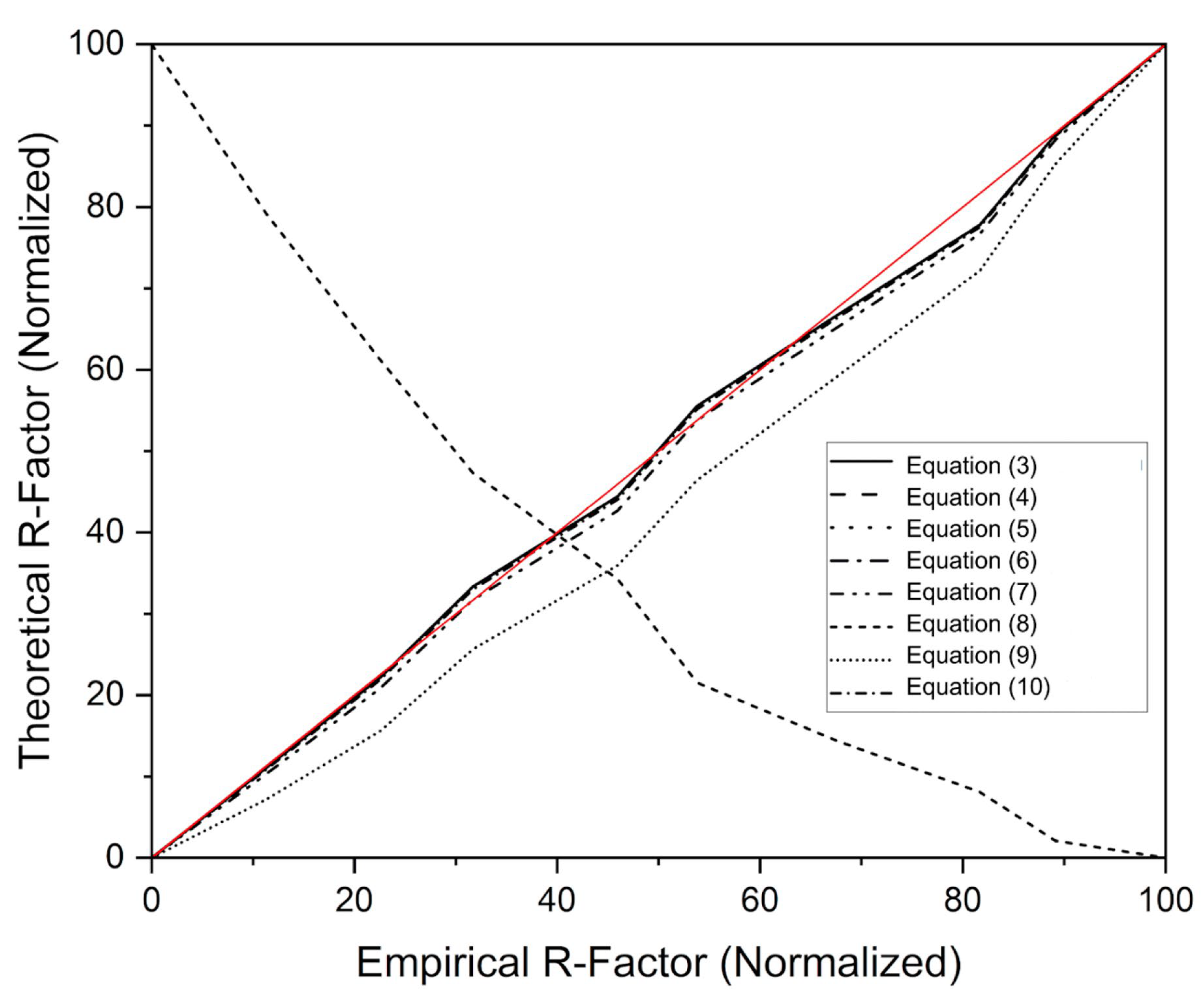
3.2. R-Factor Equations
4. Discussion
4.1. Developed Rainfall Erosivity Factor Equation
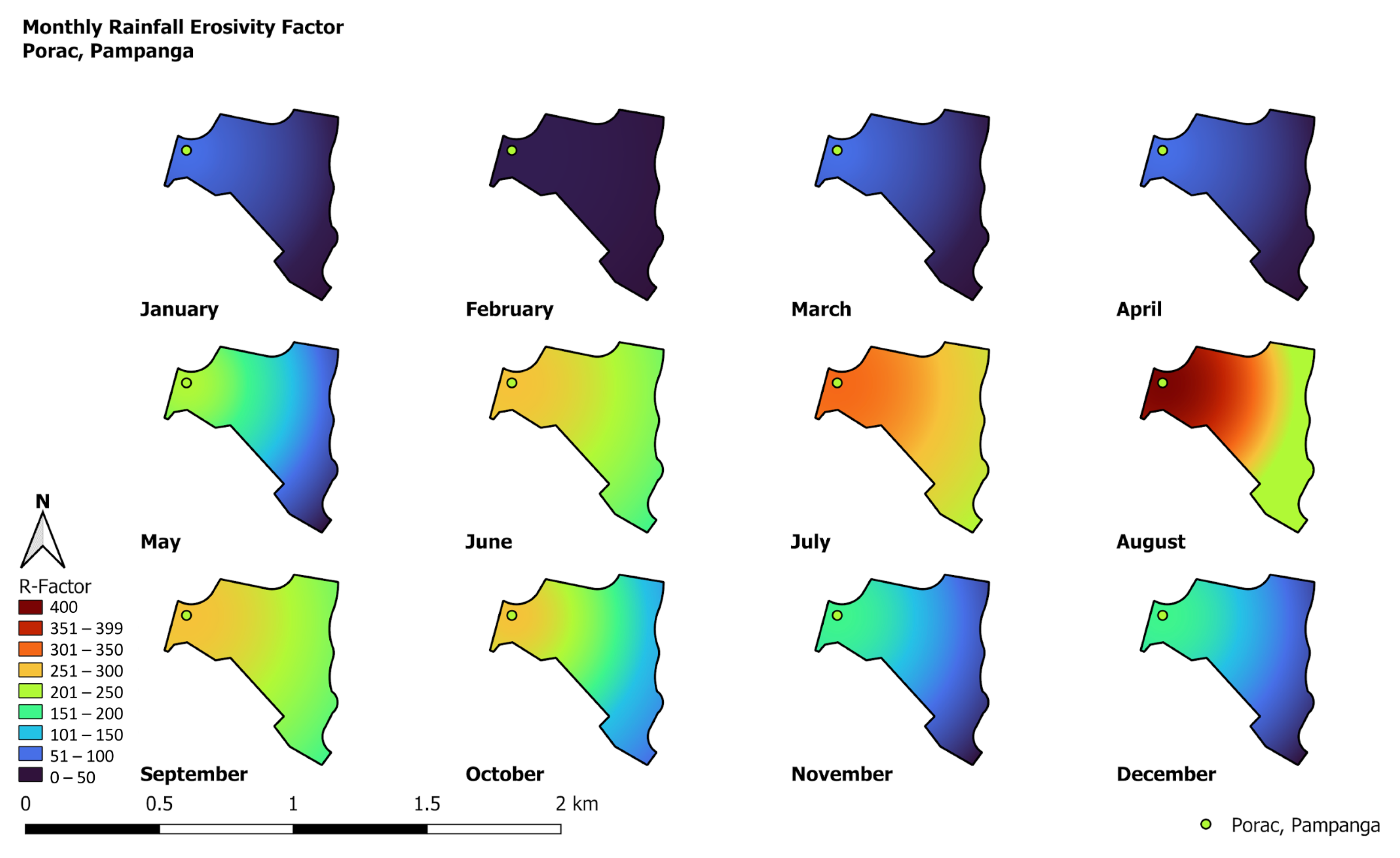
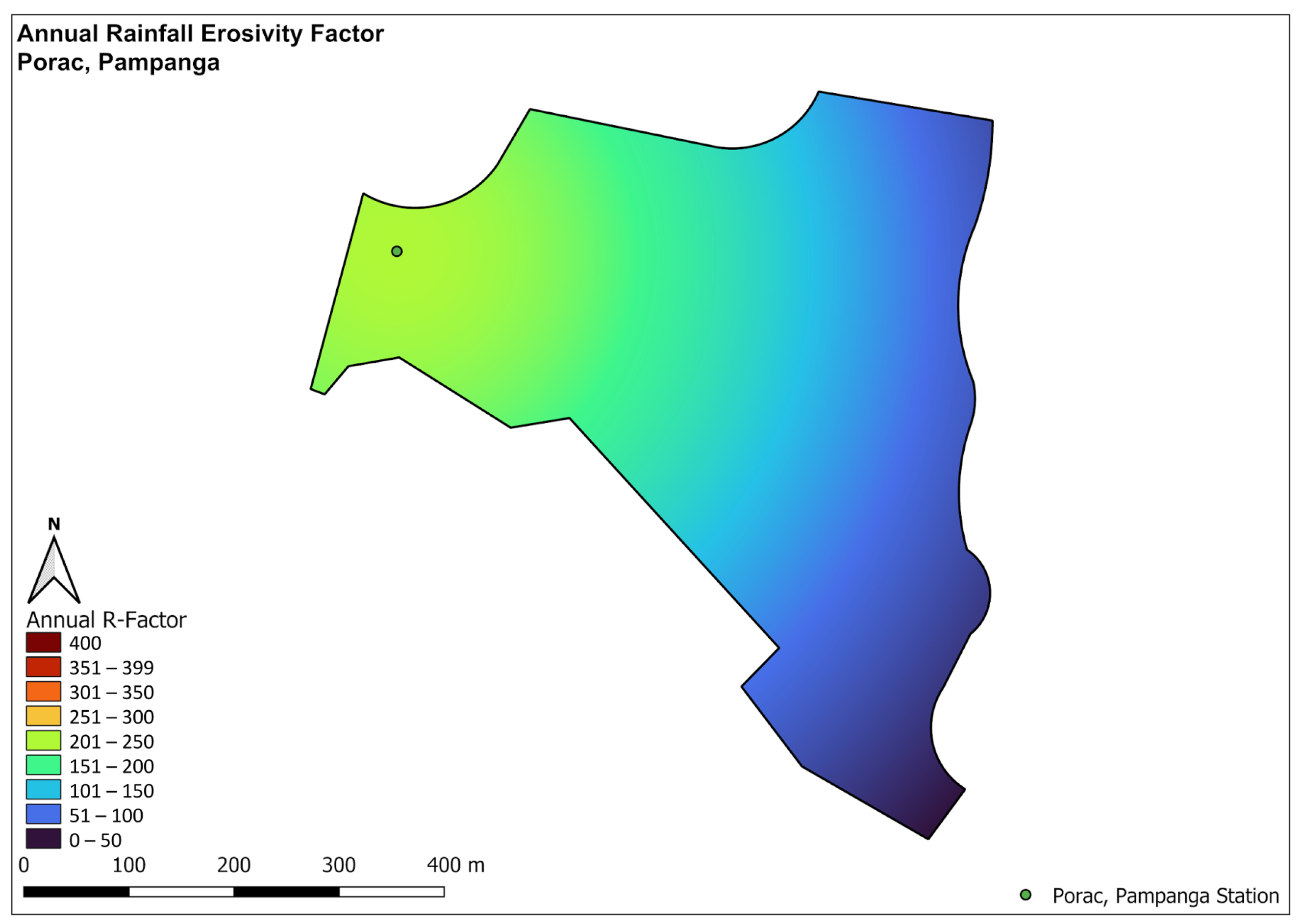
4.2. GIS Rainfall Erosivity Analysis
5. Conclusions
- (1)
- Rainfall depth estimates obtained from global resource platforms did not properly represent the peak rainfall events within the year.
- (2)
- The accuracy of the estimates obtained from different R-factor equations varied depending on the specific climatic and topographic conditions of the location where the equation originated.
- (3)
- Multiple R-factor equations tend to use similar parameters, such as variations of rainfall data with other variables and constants, to estimate the erosivity of rainfall in a specific area.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Admas, B.F.; Gashaw, T.; Adem, A.A.; Worqlul, A.W.; Dile, Y.T.; Molla, E. Identification of soil erosion hot-spot areas for prioritization of conservation measures using the SWAT model in Ribb watershed, Ethiopia. Resour. Environ. Sustain. 2022, 8, 100059. [Google Scholar] [CrossRef]
- García-Ruiz, J.M.; Beguería, S.; Lana-Renault, N.; Nadal-Romero, E.; Cerdà, A. Ongoing and emerging questions in water erosion studies. Land Degrad. Amp. Dev. 2016, 28, 5–21. [Google Scholar] [CrossRef]
- Benchettouh, A.; Kouri, L.; Jebari, S. Spatial estimation of soil erosion risk using RUSLE/GIS techniques and practices conservation suggested for reducing soil erosion in Wadi Mina watershed (northwest, Algeria). Arab. J. Geosci. 2017, 10, 79. [Google Scholar] [CrossRef]
- Meng, X.; Zhu, Y.; Yin, M.; Liu, D. The impact of land use and rainfall patterns on the soil loss of the hillslope. Sci. Rep. 2021, 11, 16341. [Google Scholar] [CrossRef] [PubMed]
- Igwe, P.U.; Onuigbo, A.A.; Chinedu, O.C.; Ezeaku, I.I.; Muoneke, M.M. Soil Erosion: A Review of Models and Applications. Int. J. Adv. Eng. Res. Sci. 2017, 4, 138–150. [Google Scholar] [CrossRef]
- Borrelli, P.; Alewell, C.; Alvarez, P.J.M.; Anache, J.A.A.; Baartman, J.; Ballabio, C.; Bezak, N.; Biddoccu, M.; Cerdà, A.; Chalise, D.; et al. Soil erosion modelling: A global review and statistical analysis. Sci. Total Environ. 2021, 780, 146494. [Google Scholar] [CrossRef] [PubMed]
- Kinnell, P. Event soil loss, runoff and the Universal Soil Loss Equation family of models: A review. J. Hydrol. 2010, 385, 384–397. [Google Scholar] [CrossRef]
- Delgado, M.E.M.; Canters, F. Modeling the impacts of agroforestry systems on the spatial patterns of soil erosion risk in three catchments of Claveria, the Philippines. Agrofor. Syst. 2011, 85, 411–423. [Google Scholar] [CrossRef]
- Schmitt, L.K. Developing and applying a soil erosion model in a data-poor context to an island in the rural Philippines. Environ. Dev. Sustain. 2007, 11, 19–42. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Handbook; Science and Education Administration, US Department of Agriculture: Washington, DC, USA, 1978; p. 537.
- Wischmeier, W.H.; Smith, D.D. Factors affecting sheet and rill erosion. Transactions 1957, 38, 889. [Google Scholar] [CrossRef]
- Khouni, I.; Louhichi, G.; Ghrabi, A. Use of GIS based Inverse Distance Weighted interpolation to assess sur-face water quality: Case of Wadi El Bey, Tunisia. Environ. Technol. Innov. 2021, 24, 101892. [Google Scholar] [CrossRef]
- Loureiro, N.; Coutinho, M.S.S. A new procedure to estimate the RUSLE EI30 index, based on monthly rainfall data and applied to the Algarve region, Portugal. J. Hydrol. 2001, 250, 12–18. [Google Scholar] [CrossRef]
- Roose, E.; Lal, R. Introduction to the Conservation Management of Water, Biomass and Soil Fertility (GCES) [FAO Corporate Document Repository]. 1994. Available online: https://horizon.documentation.ird.fr/exl-doc/pleins_textes/divers15-05/010012051.pdf (accessed on 15 June 2023).
- Kassam, A.; Velthuizen, H.; Mitchell, A.; Fischer, G.; Shah, M. A Case Study of Kenya Resources Data Base and Land Productivity Technical Annex 2 Soil Erosion and Productivity. Agro-Ecological Land Resources Assessment for Agricultural Development Planning; Food and Agriculture Organization (FAO): Rome, Italy, 1991. [Google Scholar]
- Arnoldus, H.M.J. An Approximation of the Rainfall Factor in the Universal Soil Loss Equation. An Approximation of the Rainfall Factor in the Universal Soil Loss Equation; John Wiley and Sons: Hoboken, NJ, USA, 1980; pp. 127–132. [Google Scholar]
- Hurni, H. Soil Conservation Manual for Ethiopia: A Field Guide for Conservation Implementation; Community Forests and Soil Conservation Development Department: Addis Abeba, Ethiopia, 1985. [Google Scholar]
- Morgan, R.P.C. Soil Erosion and Conservation; John Wiley Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Singh, G. Soil Loss Prediction Research in India; Central Soil & Water Conservation Research & Training Institute: Kota, India, 1981. [Google Scholar]
- Macalalad, R.V.; Badilla, R.A.; Cabrera, O.C.; Bagtasa, G. Hydrological response of the Pampanga River basin in the Philippines to intense tropical cyclone rainfall. J. Hydrometeorol. 2021, 22, 781–794. [Google Scholar] [CrossRef]
- PAGASA. Climate of the Philippines. Department of Science and Technology Philippines. Available online: https://www.pagasa.dost.gov.ph/information/climate-philippines (accessed on 25 April 2023).
- PAGASA. Climate and Agrometeorological Data Section. Rainfall Amount Data Set for Clark Airport, Pampanga Station [Data Set]; Philippine Atmospheric, Geophysical and Astronomical Services Administration: Quezon City, Philippines, 2021.
- PAGASA. Hydrometeorological Data Application Section. Rainfall Intensity-Duration-Frequency for Zambales and Olon-Gapo Stations [Data Set]; Philippine Atmospheric, Geophysical and Astronomical Services Administration: Quezon City, Philippines, 2021.
- National Aeronautics and Space Administration. Point Daily Humidity/Precipitation Data [Data Set]; NASA: Washington, DC, USA, 2021.
- National Centers for Environmental Information. Daily Rainfall Data for Porac, Pampanga [Data Set]; American National Oceanic and Atmospheric Administration: Washington, DC, USA, 2020.
- Ranzi, R.; Le, T.H.; Rulli, M.C. A RUSLE approach to model suspended sediment load in the Lo river (Vietnam): Effects of reservoirs and land use changes. J. Hydrol. 2012, 422–423, 17–29. [Google Scholar] [CrossRef]
- Adediji, A. Assessment of Revised Universal Soil Loss Equation (RUSLE) in Katsina Area, Katsina State of Nigeria using Remote Sensing (RS) and Geographic Information System (GIS). Iran. J. Energy Environ. 2010, 1, 255–264. [Google Scholar]
- Vinay, M.; Mahalingam, B. Quantification of soil erosion by water using GIS and remote sensing techniques. J. Earth Sci. 2015, 4, 103–110. [Google Scholar]
- Joshi, V.; Susware, N.; Sinha, D. Estimating soil loss from a watershed in Western Deccan, India, using Revised Universal Soil Loss Equation. Acta Geogr. Debrecin 2016, 10, 13–25. [Google Scholar] [CrossRef]

| Station Number | Location | Latitude (o) | Longitude (o) | Elevation (m) | Distance (km) |
|---|---|---|---|---|---|
| 1 | Clark, Pampanga | 15.1717 | 120.5617 | 151.6 | 9.19 |
| 2 | Iba, Zambales | 15.3284 | 119.9657 | 5.538 | 63.13 |
| 3 | Cubi Pt., Olongapo | 14.7877 | 120.2666 | 19.09 | 43.99 |
| 4 | Porac, Pampanga | 15.1074 | 120.5076 | 79.02 | - |
| Reference | Equation | Variables | Equation Number | Remarks |
|---|---|---|---|---|
| 1957 [10] | E = total kinetic energy I30 = maximum 30 min rainfall intensity | (3) | ||
| 2001 [13] | N = number of years of analysis rainn = monthly rainfall amount when rainfall ≥ 10 mm daysn = number of days when rainfall ≥ 10 mm m = month index i = year index | (4) | ||
| 1996 [14] | r = mean annual rainfall a = constant variable | (5) | Tested a = 0.5445 | |
| 1992 [15] | AAP = average annual precipitation | (6) | Tested a = 0.7824 | |
| 1980 [16] | P = average annual rainfall amount Pi = average monthly rainfall amount | (7) | Tested a = 0.1345 | |
| 1985 [17] | P = average annual rainfall amount | (8) | ||
| 1986 [18] | P = average annual rainfall amount | (9) | Tested a = 0.1701 | |
| 1981 [19] | AAP = average annual precipitation | (10) | Tested a = 0.1868 |
| Month | Rainfall Depth (mm) | Ratio Relative to PAGASA | |||
|---|---|---|---|---|---|
| PAGASA | NASA | GWC | NASA | GWC | |
| January | 11.01 ± 17.1 | 36.36 ± 27.0 | 24.29 ± 24.4 | 3.4 ± 1.2 | 2.3 ± 1.2 |
| February | 6.176 ± 5.21 | 37.06 ± 28.9 | 21.78 ± 19.2 | 6.1 ± 2.6 | 3.6 ± 2.6 |
| March | 11.43 ± 12.0 | 38.06 ± 32.3 | 34.40 ± 33.2 | 3.4 ± 1.3 | 3.1 ± 1.3 |
| April | 24.88 ± 13.8 | 53.86 ± 53.1 | 79.01 ± 51.5 | 2.2 ± 1.1 | 3.2 ± 1.1 |
| May | 111.8 ± 63.9 | 131.1 ± 57.4 | 132.2 ± 60.2 | 1.2 ± 0.1 | 1.2 ± 0.1 |
| June | 572.3 ± 307 | 384.3 ± 169 | 109.7 ± 95.9 | 0.7 ± 0.4 | 0.2 ± 0.4 |
| July | 928.0 ± 408 | 551.9 ± 191 | 154.4 ± 115 | 0.6 ± 0.4 | 0.2 ± 0.4 |
| August | 1019 ± 510 | 637.4 ± 327 | 131.1 ± 117 | 0.7 ± 0.4 | 0.2 ± 0.4 |
| September | 583.9 ± 300 | 441.7 ± 160 | 142.7 ± 145 | 0.8 ± 0.4 | 0.3 ± 0.4 |
| October | 266.8 ± 170 | 283.5 ± 175 | 113.9 ± 119 | 1.1 ± 0.3 | 0.5 ± 0.3 |
| November | 59.27 ± 61.9 | 125.2 ± 162 | 79.23 ± 77.2 | 2.2 ± 0.6 | 1.4 ± 0.6 |
| December | 36.76 ± 47.4 | 120.5 ± 100 | 77.32 ± 65.1 | 3.3 ± 1.2 | 2.2 ± 1.2 |
| Annual | 302.6 ± 75.7 | 236.7 ± 46.8 | 91.66 ± 53.4 | 2.1 ± 1.7 | 1.5 ± 1.3 |
| Reference | Eqn No. | R-Factor (MJ/ha mm/h) | ||
|---|---|---|---|---|
| PAGASA | NASA | GWC | ||
| 1957 [10] | (3) | 88.75 | - | - |
| 2001 [13] | (4) | 19,254 | 13,055 | 5161 |
| 1996 [14] | (5) | 108.9 | 85.23 | 33.00 |
| 1992 [15] | (6) | 118.4–119.3 | 118.4–118.9 | 117.7–118.4 |
| 1980 [16] | (7) | 23.68–28.78 | 20.07–25.28 | 18.69–23.42 |
| 1985 [17] | (8) | −4.533–−0.433 | −0.4707–−2.180 | −7.446–−4.497 |
| 1986 [18] | (9) | 3.191–6.839 | 3.037–5.285 | 0.599–3.223 |
| 1981 [19] | (10) | 81.32–83.97 | 81.20–82.84 | 79.44–81.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz, A.M.D.; Maniquiz-Redillas, M.C.; Tanhueco, R.M.; De Leon, M.P. Estimation of the Rainfall Erosivity Factor (R-Factor) for Application in Soil Loss Models. Water 2025, 17, 837. https://doi.org/10.3390/w17060837
Cruz AMD, Maniquiz-Redillas MC, Tanhueco RM, De Leon MP. Estimation of the Rainfall Erosivity Factor (R-Factor) for Application in Soil Loss Models. Water. 2025; 17(6):837. https://doi.org/10.3390/w17060837
Chicago/Turabian StyleCruz, Andre Miguel Dela, Marla C. Maniquiz-Redillas, Renan M. Tanhueco, and Mario P. De Leon. 2025. "Estimation of the Rainfall Erosivity Factor (R-Factor) for Application in Soil Loss Models" Water 17, no. 6: 837. https://doi.org/10.3390/w17060837
APA StyleCruz, A. M. D., Maniquiz-Redillas, M. C., Tanhueco, R. M., & De Leon, M. P. (2025). Estimation of the Rainfall Erosivity Factor (R-Factor) for Application in Soil Loss Models. Water, 17(6), 837. https://doi.org/10.3390/w17060837








