Probabilistic Risk Assessment (PRA) for Sustainable Water Resource Management: A Future Flood Inundation Example
Abstract
1. Introduction
2. Data and Methods
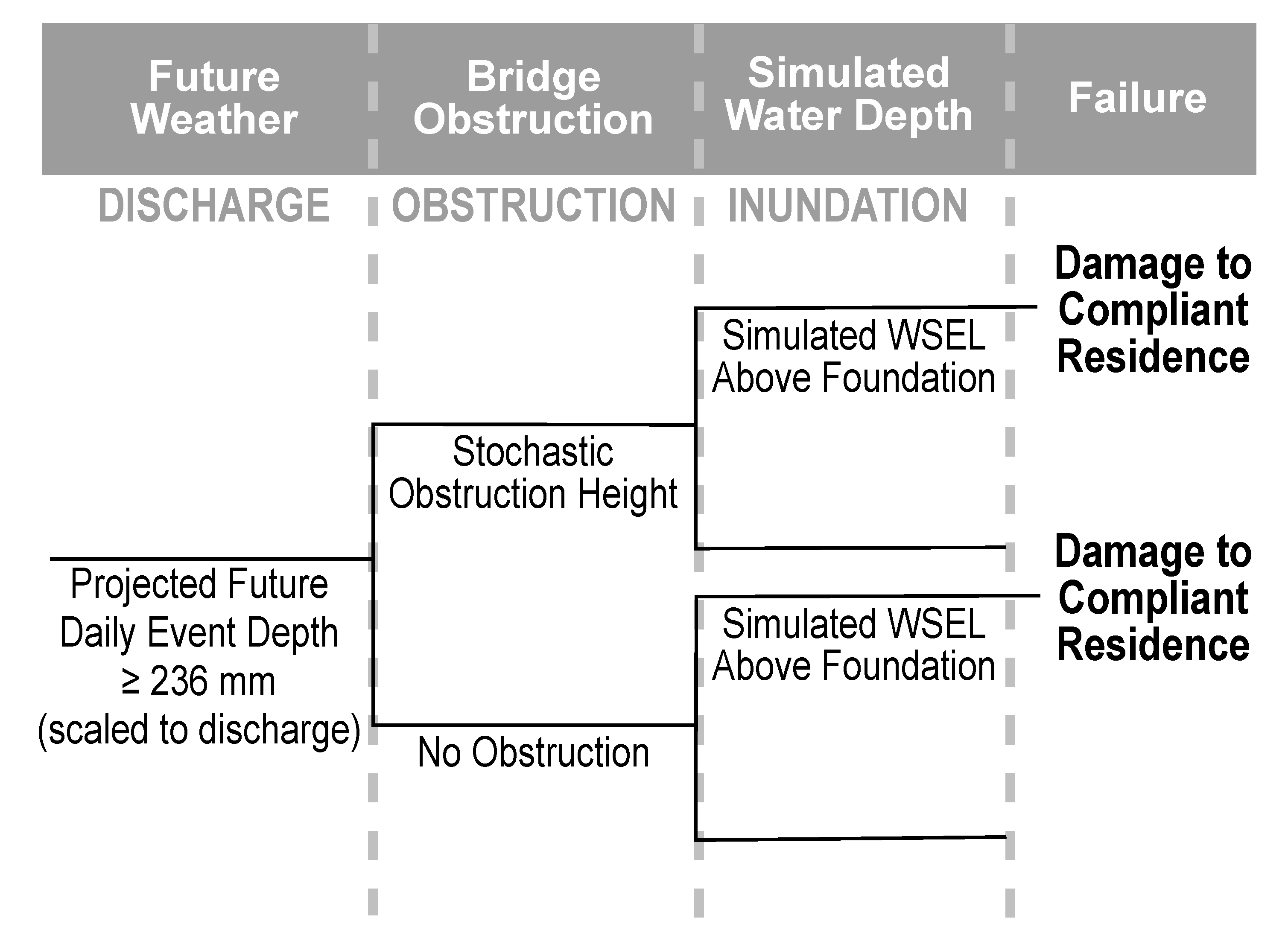
2.1. Probabilistic Risk Assessment (PRA)
Event Tree and Initiating Event
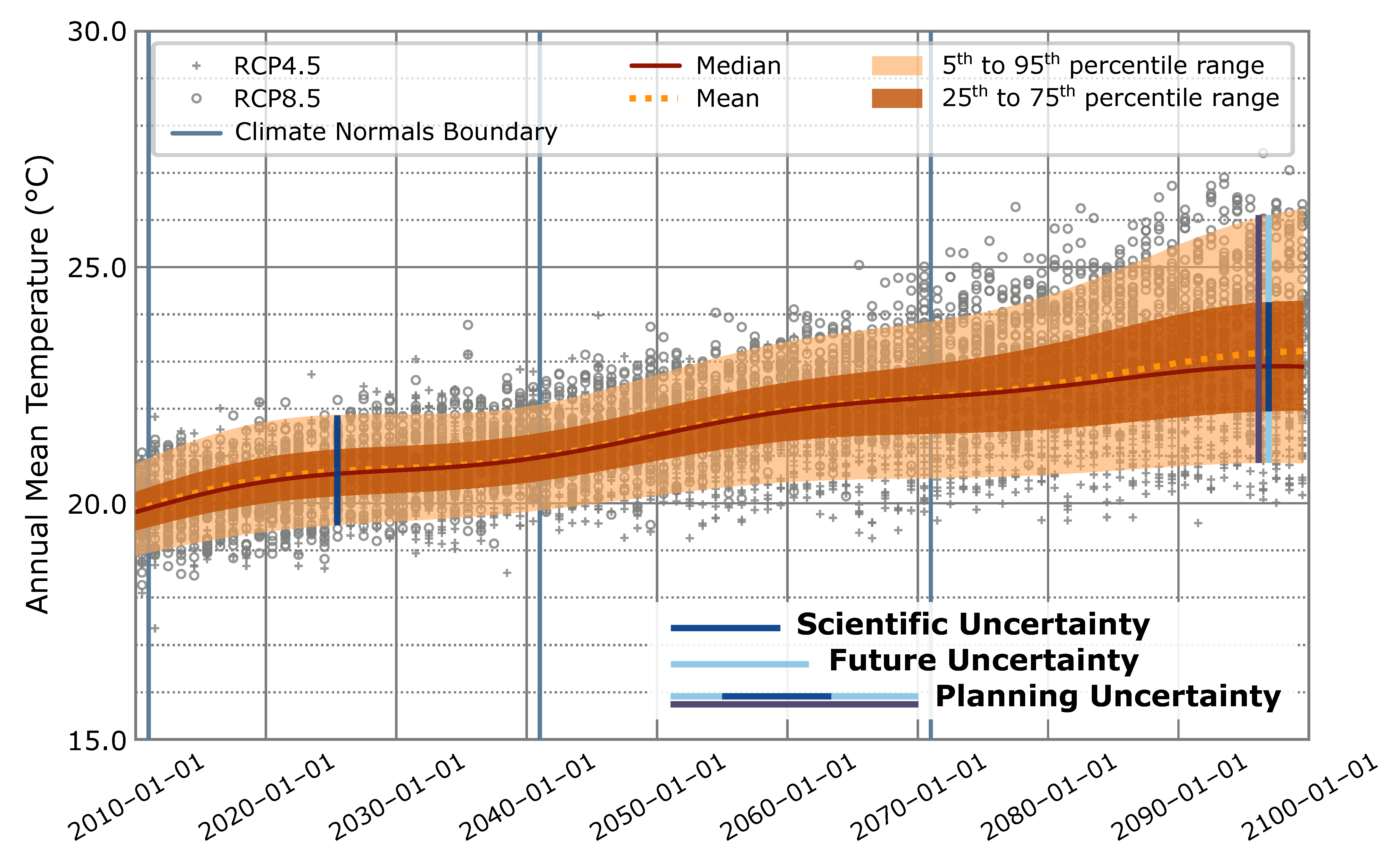
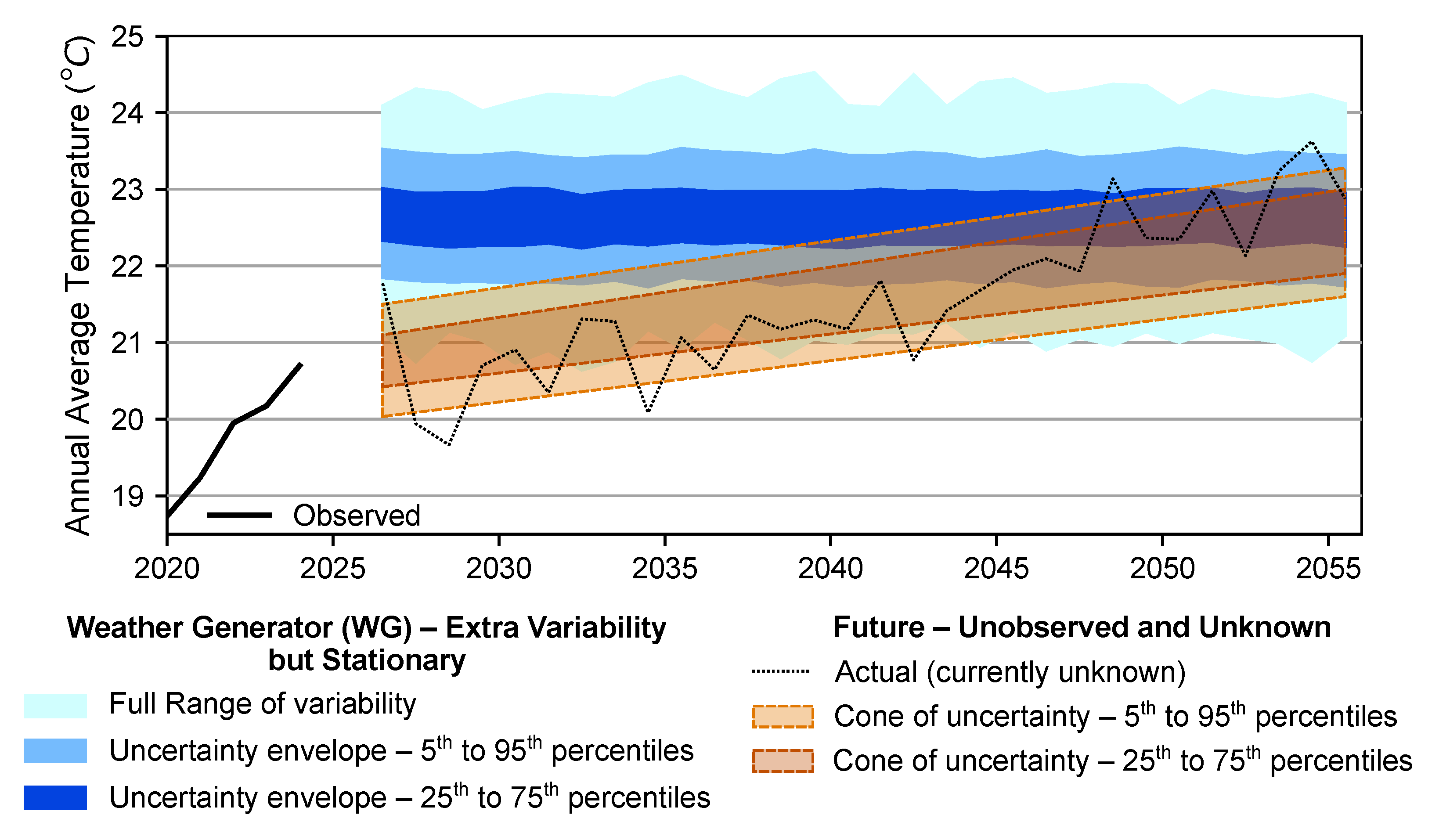
2.2. Future Weather and Climate Inputs
Stationarity
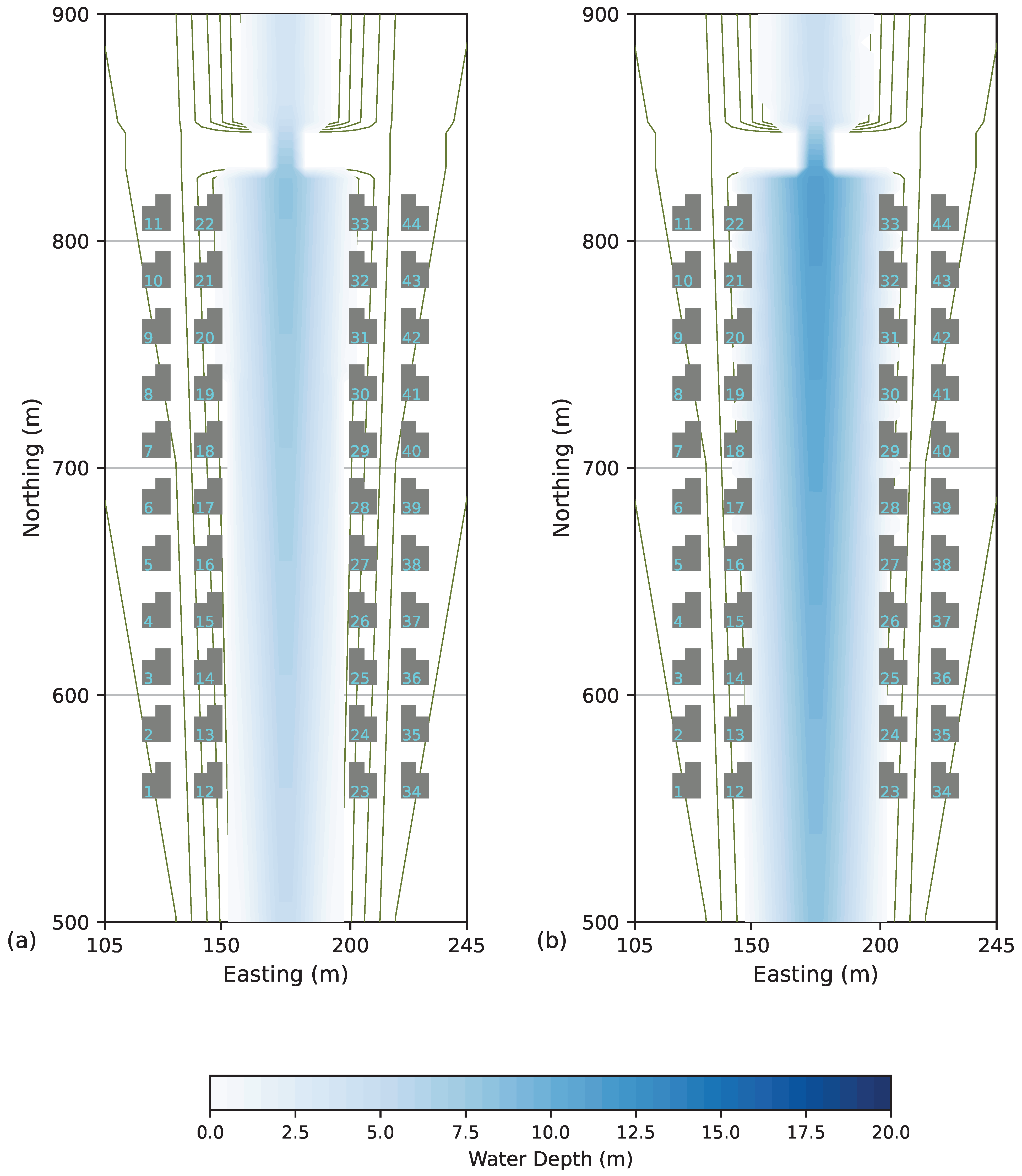
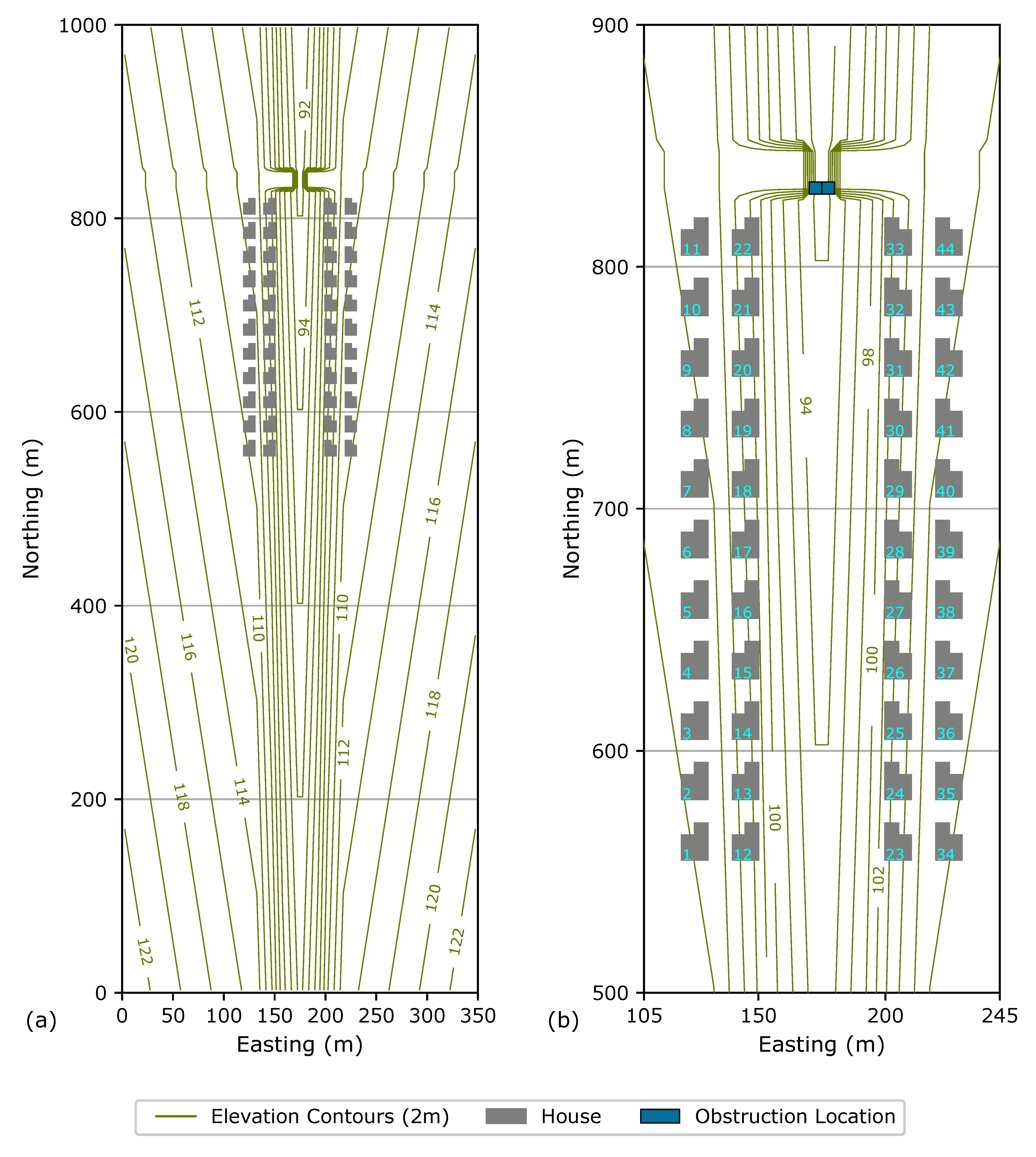
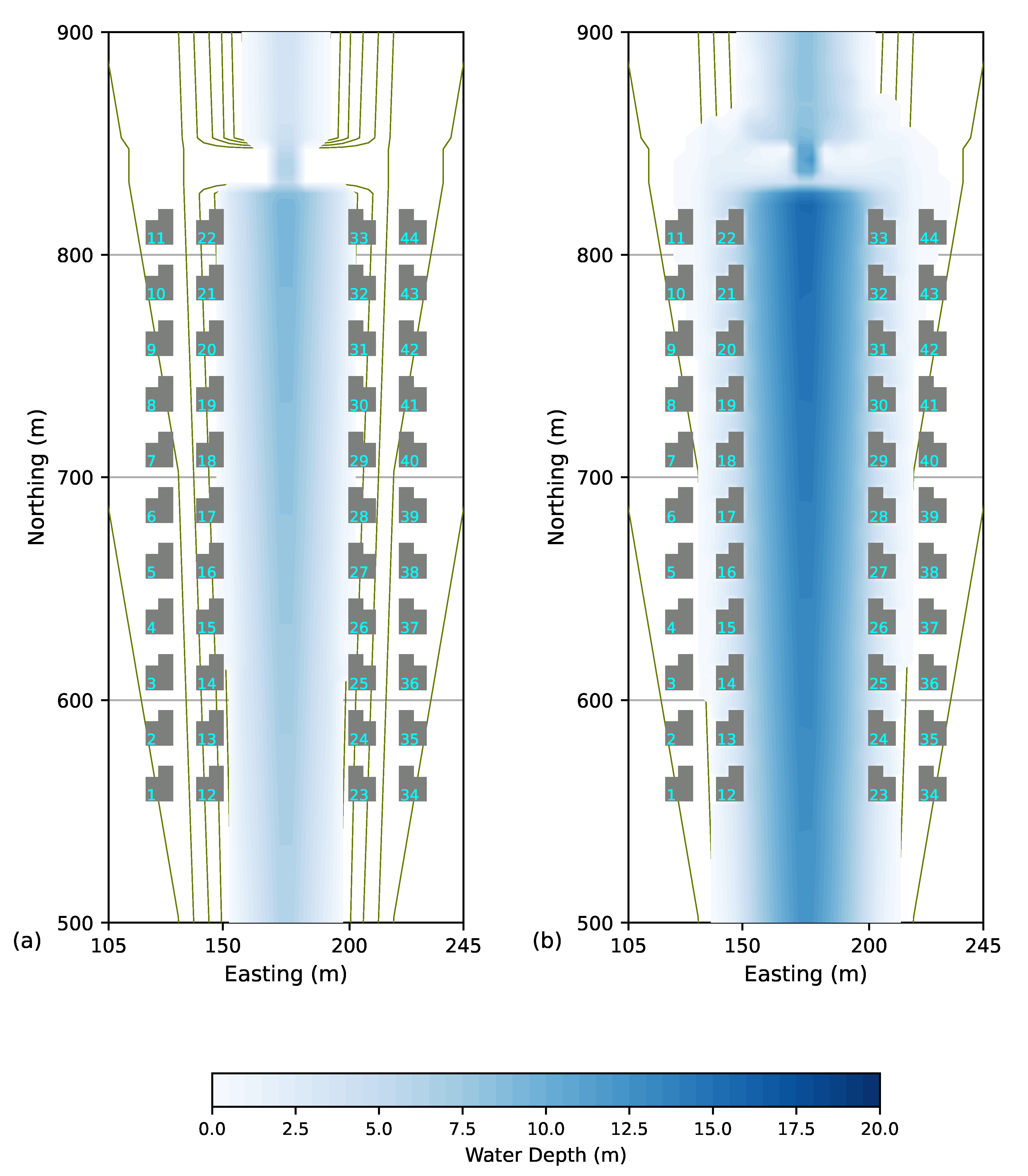
2.3. Inundation Simulation
MOD_FreeSurf2D Implementation
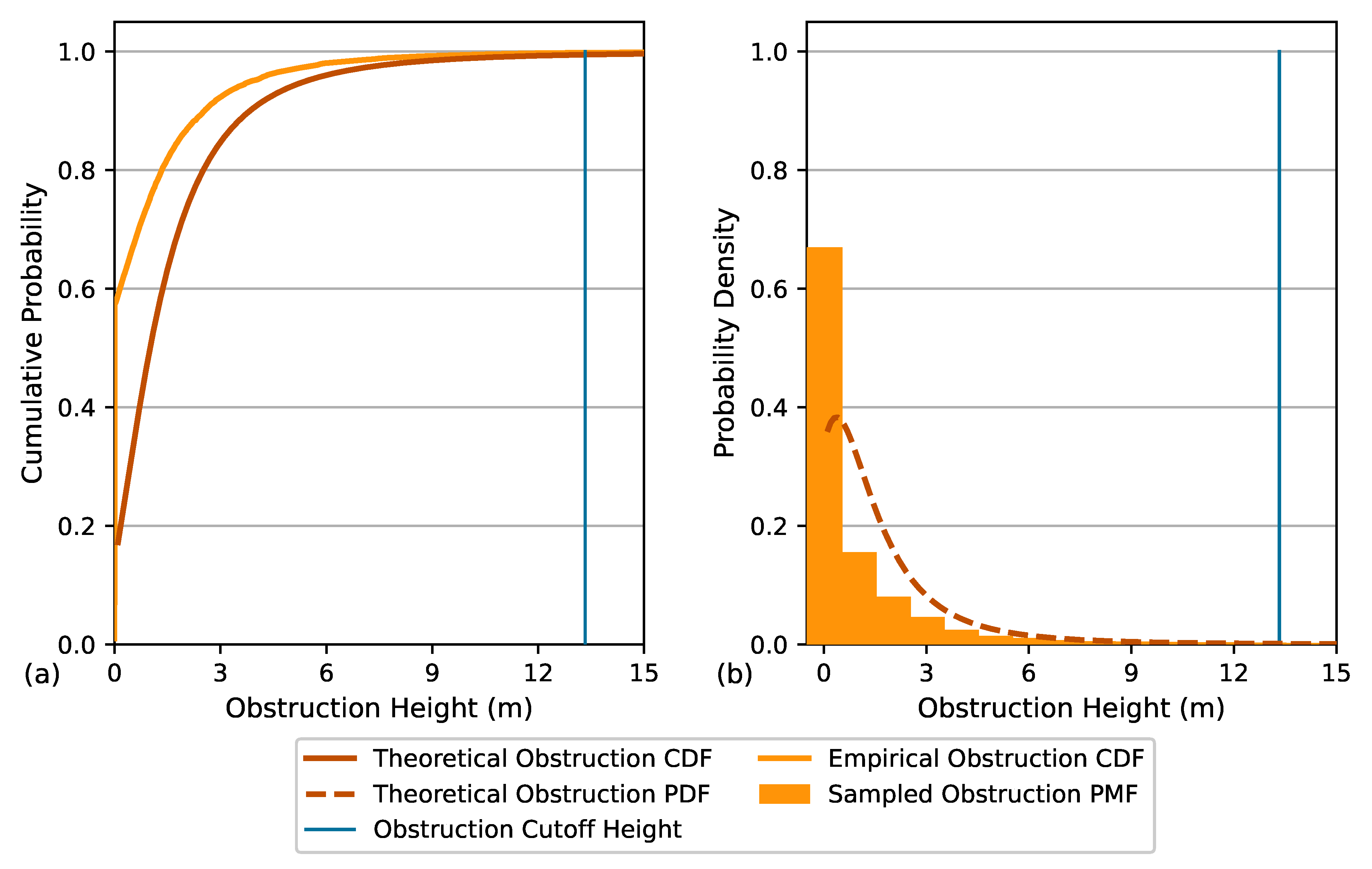
2.4. Obstruction Representation
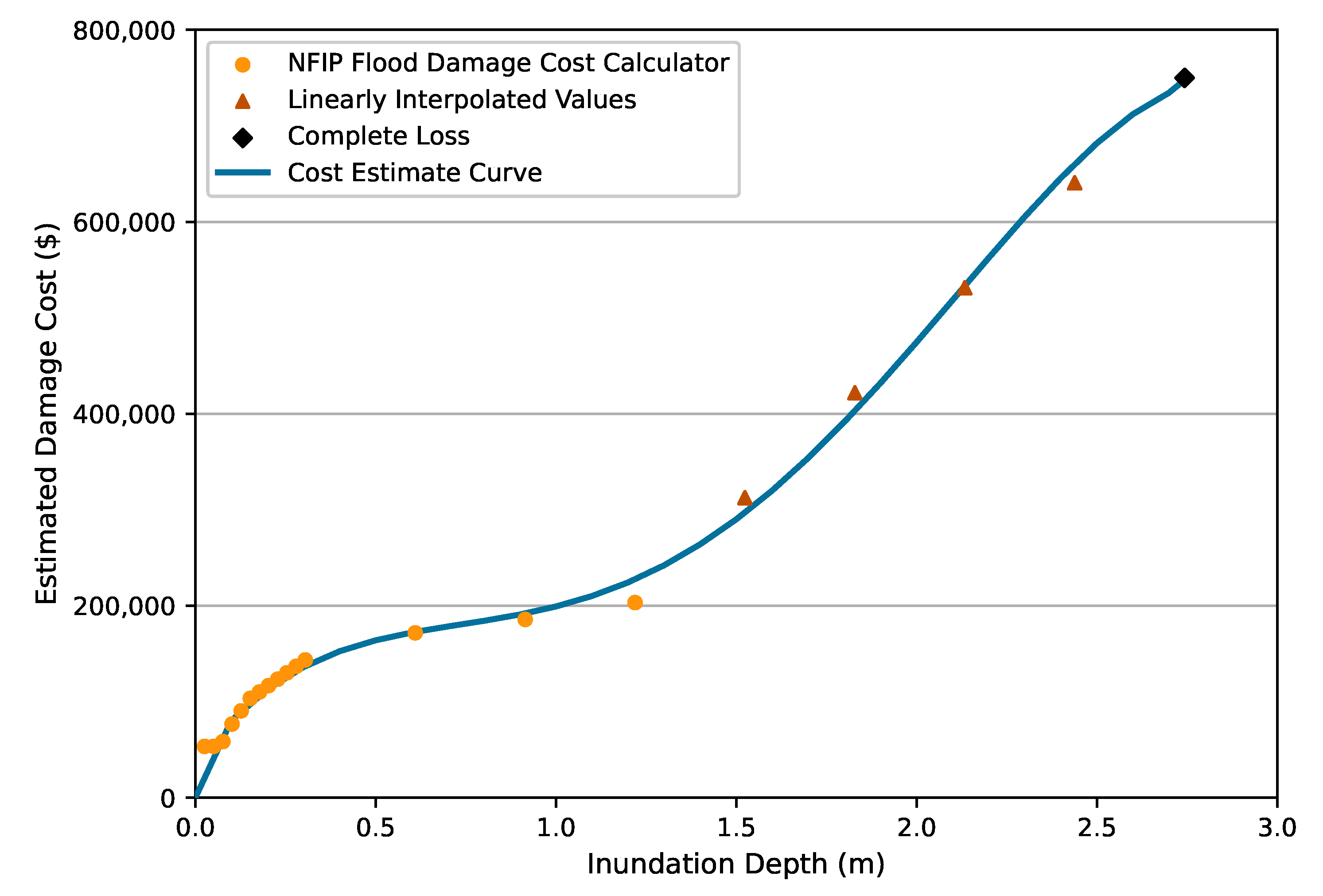
2.5. Damage Cost Estimation
3. Results
4. Discussion
4.1. Limitations
4.2. Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMIP5 | Coupled model intercomparison project phase 5 |
| CMIP6 | Coupled model intercomparison project phase 6 |
| CDF | Cumulative distribution function |
| FEMA | Federal emergency management administration |
| GEV | Generalized extreme value |
| LOCA | Localized constructed analogs downscaling |
| LOCA2 | Localized constructed analogs downscaling, Version 2 |
| LULC | Land use and land cover |
| NFIP | National flood insurance program |
| PDE | Partial differential equation |
| Probability density function | |
| PMF | Probability mass function |
| PR | Probability ratio |
| PRA | Probabilistic risk assessment |
| RCP | Representative concentration pathway |
| SPEI | Standardized precipitation evapotranspiration index |
| Degree of implicitness for semi-implicit numerical methods | |
| WG | Stochastic weather generator |
| WSEL | Water surface elevation |
Appendix A
Appendix A.1
| House Index | Row | Col | Topo. El. (m) | Foundation El (m) | House Index | Row | Col | Topo. El. (m) | Foundation El. (m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 114 | 27 | 109.35 | 109.63 | 23 | 114 | 40 | 101.85 | 104.30 |
| 2 | 119 | 27 | 109.10 | 109.38 | 24 | 119 | 40 | 101.60 | 104.05 |
| 3 | 124 | 27 | 108.85 | 109.13 | 25 | 124 | 40 | 101.35 | 103.80 |
| 4 | 129 | 27 | 108.60 | 108.88 | 26 | 129 | 40 | 101.10 | 103.55 |
| 5 | 134 | 27 | 108.35 | 108.63 | 27 | 134 | 40 | 100.85 | 103.30 |
| 6 | 139 | 27 | 108.10 | 108.38 | 28 | 139 | 40 | 100.60 | 103.05 |
| 7 | 144 | 27 | 107.85 | 108.13 | 29 | 144 | 40 | 100.35 | 102.80 |
| 8 | 149 | 27 | 107.60 | 107.88 | 30 | 149 | 40 | 100.10 | 102.55 |
| 9 | 154 | 27 | 107.35 | 107.63 | 31 | 154 | 40 | 99.85 | 102.30 |
| 10 | 159 | 27 | 107.10 | 107.38 | 32 | 159 | 40 | 99.60 | 102.05 |
| 11 | 164 | 27 | 106.85 | 107.13 | 33 | 164 | 40 | 99.35 | 101.80 |
| 12 | 114 | 31 | 101.85 | 104.30 | 34 | 114 | 44 | 109.35 | 109.63 |
| 13 | 119 | 31 | 101.60 | 104.05 | 35 | 119 | 44 | 109.10 | 109.38 |
| 14 | 124 | 31 | 101.35 | 103.80 | 36 | 124 | 44 | 108.85 | 109.13 |
| 15 | 129 | 31 | 101.10 | 103.55 | 37 | 129 | 44 | 108.60 | 108.88 |
| 16 | 134 | 31 | 100.85 | 103.30 | 38 | 134 | 44 | 108.35 | 108.63 |
| 17 | 139 | 31 | 100.60 | 103.05 | 39 | 139 | 44 | 108.10 | 108.38 |
| 18 | 144 | 31 | 100.35 | 102.80 | 40 | 144 | 44 | 107.85 | 108.13 |
| 19 | 149 | 31 | 100.10 | 102.55 | 41 | 149 | 44 | 107.60 | 107.88 |
| 20 | 154 | 31 | 99.85 | 102.30 | 42 | 154 | 44 | 107.35 | 107.63 |
| 21 | 159 | 31 | 99.60 | 102.05 | 43 | 159 | 44 | 107.10 | 107.38 |
| 22 | 164 | 31 | 99.35 | 101.80 | 44 | 164 | 44 | 106.85 | 107.13 |
| Depth (in) | Depth (m) | Damage Cost (USD) | Source |
|---|---|---|---|
| 1 | 0.0254 | USD 53,454 | NFIP Cost Calculator 1 |
| 2 | 0.0508 | USD 53,564 | NFIP Cost Calculator 1 |
| 3 | 0.0762 | USD 58,448 | NFIP Cost Calculator 1 |
| 4 | 0.1016 | USD 76,707 | NFIP Cost Calculator 1 |
| 5 | 0.1270 | USD 90,496 | NFIP Cost Calculator 1 |
| 6 | 0.1524 | USD 103,505 | NFIP Cost Calculator 1 |
| 7 | 0.1778 | USD 110,174 | NFIP Cost Calculator 1 |
| 8 | 0.2032 | USD 116,843 | NFIP Cost Calculator 1 |
| 9 | 0.2286 | USD 123,512 | NFIP Cost Calculator 1 |
| 10 | 0.2540 | USD 130,181 | NFIP Cost Calculator 1 |
| 11 | 0.2794 | USD 136,850 | NFIP Cost Calculator 1 |
| 12 | 0.3048 | USD 143,519 | NFIP Cost Calculator 1 |
| 24 | 0.6096 | USD 171,775 | NFIP Cost Calculator 1 |
| 36 | 0.9144 | USD 185,704 | NFIP Cost Calculator 1 |
| 48 | 1.2192 | USD 203,280 | NFIP Cost Calculator 1 |
| 60 | 1.5240 | USD 312,624 | Linear interpolation |
| 72 | 1.8288 | USD 421,968 | Linear interpolation |
| 84 | 2.1336 | USD 531,312 | Linear interpolation |
| 96 | 2.4384 | USD 640,656 | Linear interpolation |
| 108 | 2.7432 | USD 750,000 | Complete loss cost, assumed |
Appendix A.2
References
- Browne, A. Explainer: What Is Sustainability and Why Is It Important? 2022. Available online: https://earth.org/what-is-sustainability/ (accessed on 25 October 2024).
- United Nations. Sustainability; United Nations: New York, NY, USA, 2024. [Google Scholar]
- U.S. Chamber of Commerce Foundation. Circularity vs. Sustainability. 2016. Available online: https://www.uschamberfoundation.org/disasters/circularity-vs-sustainability (accessed on 25 October 2024).
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Otto, F.; Giguere, J.; Clarke, B.; Barnes, C.; Zachariah, M.; Merz, N.; Philip, S.; Kew, S.; Pinto, I.; Vahlberg, M. When Risks Become Reality: Extreme Weather in 2024; World Weather Attribution Annual Report; Imperial College London, Royal Netherlands Meteorological Institute, Red Cross Red Crescent Climate Centre, Imperial College: London, UK, 2024. [Google Scholar]
- World Weather Attribution (WWA). When Risks Become Reality: Extreme Weather in 2024. 2024. Available online: https://www.worldweatherattribution.org/when-risks-become-reality-extreme-weather-in-2024/ (accessed on 29 January 2025).
- Vodanube LLC. Uncertainty; Vodanube LLC: Fort Collins, CO, USA, 2024; Available online: https://www.vodanube.com/uncertainty/ (accessed on 28 October 2024).
- Martin, N.; White, J. Water Resources’ AI–ML Data Uncertainty Risk and Mitigation Using Data Assimilation. Water 2024, 16, 2758. [Google Scholar] [CrossRef]
- Clarke, B.; Otto, F. Reporting Extreme Weather and Climate Change: A Guide for Journalists; Technical Report; World Weather Attribution (WWA), Imperial College: London, UK, 2023; Available online: https://www.worldweatherattribution.org/wp-content/uploads/ENG_WWA-Reporting-extreme-weather-and-climate-change.pdf (accessed on 3 December 2024).
- World Weather Attribution (WWA). Exploring the Contribution of Climate Change to Extreme Weather Events. 2024. Available online: https://www.worldweatherattribution.org/ (accessed on 10 October 2024).
- van Oldenborgh, G.J.; van der Wiel, K.; Kew, S.; Philip, S.; Otto, F.; Vautard, R.; King, A.; Lott, F.; Arrighi, J.; Singh, R.; et al. Pathways and pitfalls in extreme event attribution. Clim. Chang. 2021, 166, 13. [Google Scholar] [CrossRef]
- Philip, S.; Kew, S.; van Oldenborgh, G.J.; Otto, F.; Vautard, R.; van der Wiel, K.; King, A.; Lott, F.; Arrighi, J.; Singh, R.; et al. A protocol for probabilistic extreme event attribution analyses. Adv. Stat. Climatol. Meteorol. Oceanogr. 2020, 6, 177–203. [Google Scholar] [CrossRef]
- Hsu, F.; Railsback, J. The Space Shuttle Probabilistic Risk Assessment Framework. In Proceedings of the Probabilistic Safety Assessment and Management, Berlin, Germany, 14–18 June 2004; Spitzer, C., Schmocker, U., Dang, V.N., Eds.; Springer: London, UK, 2004; pp. 1466–1473. [Google Scholar] [CrossRef]
- Stamatelatos, M.; Dezfuli, H.; Apostolakis, G.; Everline, C.; Guarro, S.; Mathias, D.; Mosleh, A.; Paulos, T.; Riha, D.; Smith, C.; et al. Probabilistic Risk Assessment Procedures Guide for NASA Managers and Practitioners, 2nd ed.; NASA: Hanover, MD, USA, 2011. [Google Scholar]
- Pan, X.; Ding, S.; Zhang, W.; Liu, T.; Wang, L.; Wang, L. Probabilistic Risk Assessment in Space Launches Using Bayesian Network with Fuzzy Method. Aerospace 2022, 9, 311. [Google Scholar] [CrossRef]
- Alkhatib, S.; Sakurahara, T.; Reihani, S.; Kee, E.; Ratte, B.; Kaspar, K.; Hunt, S.; Mohaghegh, Z. Phenomenological Nondimensional Parameter Decomposition to Enhance the Use of Simulation Modeling in Fire Probabilistic Risk Assessment of Nuclear Power Plants. J. Nucl. Eng. 2024, 5, 226–245. [Google Scholar] [CrossRef]
- Lee, J.; Tayfur, H.; Hamza, M.M.; Alzahrani, Y.A.; Diaconeasa, M.A. A Limited-Scope Probabilistic Risk Assessment Study to Risk-Inform the Design of a Fuel Storage System for Spent Pebble-Filled Dry Casks. Eng 2023, 4, 1655–1683. [Google Scholar] [CrossRef]
- Kubo, K. Accident Sequence Precursor Analysis of an Incident in a Japanese Nuclear Power Plant Based on Dynamic Probabilistic Risk Assessment—Kubo—2023—Science and Technology of Nuclear Installations—Wiley Online Library. Sci. Technol. Nucl. Install. 2023, 2023, 7402217. [Google Scholar] [CrossRef]
- Han, L.; Fan, Y.; Chen, R.; Zhai, Y.; Liu, Z.; Zhao, Y.; Li, R.; Xia, L. Probabilistic Risk Assessment of Heavy Metals in Mining Soils Based on Fractions: A Case Study in Southern Shaanxi, China. Toxics 2023, 11, 997. [Google Scholar] [CrossRef]
- Guadalupe, G.A.; Grandez-Yoplac, D.E.; Arellanos, E.; Doménech, E. Probabilistic Risk Assessment of Metals, Acrylamide and Ochratoxin A in Instant Coffee from Brazil, Colombia, Mexico and Peru. Foods 2024, 13, 726. [Google Scholar] [CrossRef]
- Ololade, I.A.; Alabi, B.A.; Oladoja, N.A.; Ololade, O.O.; Apata, A.O. Occurrence and probabilistic risk assessment of polycyclic aromatic hydrocarbons in blood and urine of auto-mechanics in Akure Metro, Nigeria. Environ. Monit. Assess. 2023, 195, 727. [Google Scholar] [CrossRef]
- Landquist, H.; Rosén, L.; Lindhe, A.; Hassellöv, I.M. VRAKA—A Probabilistic Risk Assessment Method for Potentially Polluting Shipwrecks. Front. Environ. Sci. 2016, 4, 49. [Google Scholar] [CrossRef]
- Sawe, S.F.; Shilla, D.A.; Machiwa, J.F. Assessment of Ecological Risk of Heavy Metals Using Probabilistic Risk Assessment Model (AQUARISK) in Surface Sediments from Wami Estuary, Tanzania. Biomed Res. Int. 2021, 2021, 6635903. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.T.; Pan, X.D.; Han, J.L. Distribution and Probabilistic Risk Assessment of Antibiotics, Illegal Drugs, and Toxic Elements in Gastropods from Southeast China. Foods 2024, 13, 1166. [Google Scholar] [CrossRef] [PubMed]
- Sheng, D.; Wen, X.; Wu, J.; Wu, M.; Yu, H.; Zhang, C. Comprehensive Probabilistic Health Risk Assessment for Exposure to Arsenic and Cadmium in Groundwater. Environ. Manag. 2021, 67, 779–792. [Google Scholar] [CrossRef]
- Stehle, S.; Knäbel, A.; Schulz, R. Probabilistic risk assessment of insecticide concentrations in agricultural surface waters: A critical appraisal. Environ. Monit. Assess. 2013, 185, 6295–6310. [Google Scholar] [CrossRef]
- Zhou, H.; Yue, X.; Chen, Y.; Liu, Y.; Gong, G. Comprehensive Environmental and Health Risk Assessment of Soil Heavy Metal(loid)s Considering Uncertainties: The Case of a Typical Metal Mining Area in Daye City, China. Minerals 2023, 13, 1389. [Google Scholar] [CrossRef]
- Martin, N.; Nicholaides, K.; Southard, P. Enhanced Water Resources Risk from Collocation of Disposal Wells and Legacy Oil and Gas Exploration and Production Regions in Texas. Jawra J. Am. Water Resour. Assoc. 2022, 58, 1433–1453. [Google Scholar] [CrossRef]
- Rish, W.R. A probabilistic risk assessment of class I hazardous waste injection wells. In Developments in Water Science, 1st ed.; Underground Injection Science and Technology; Tsang, C.F., Apps, J.A., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2005; Volume 52, pp. 93–135. [Google Scholar] [CrossRef]
- Bernal, G.A.; Salgado-Galvez, M.A.; Zuloaga, D.; Tristancho, J.; Gonzalez, D.; Cardona, O.D. Integration of Probabilistic and Multi-Hazard Risk Assessment Within Urban Development Planning and Emergency Preparedness and Response: Application to Manizales, Colombia. Int. J. Disaster Risk Sci. 2017, 8, 270–283. [Google Scholar] [CrossRef]
- Salgado-Gálvez, M.A.; Bernal, G.A.; Zuloaga, D.; Marulanda, M.C.; Cardona, O.D.; Henao, S. Probabilistic Seismic Risk Assessment in Manizales, Colombia: Quantifying Losses for Insurance Purposes. Int. J. Disaster Risk Sci. 2017, 8, 296–307. [Google Scholar] [CrossRef]
- García-Montiel, E.; Zepeda-Mondragón, F.; Morones-Esquivel, M.M.; Ramírez-Aldaba, H.; López-Serrano, P.M.; Briseño-Reyes, J.; Montiel-Antuna, E. Probabilistic Risk Assessment of Exposure to Fluoride in Drinking Water in Victoria de Durango, Mexico. Sustainability 2023, 15, 14630. [Google Scholar] [CrossRef]
- Shahsavani, S.; Mohammadpour, A.; Shooshtarian, M.R.; Soleimani, H.; Ghalhari, M.R.; Badeenezhad, A.; Baboli, Z.; Morovati, R.; Javanmardi, P. An ontology-based study on water quality: Probabilistic risk assessment of exposure to fluoride and nitrate in Shiraz drinking water, Iran using fuzzy multi-criteria group decision-making models. Environ. Monit. Assess. 2022, 195, 35. [Google Scholar] [CrossRef] [PubMed]
- Masoudvaziri, N.; Elhami-Khorasani, N.; Sun, K. Toward Probabilistic Risk Assessment of Wildland–Urban Interface Communities for Wildfires. Fire Technol. 2023, 59, 1379–1403. [Google Scholar] [CrossRef]
- Monge, J.J.; Dowling, L.J.; Wegner, S.; Melia, N.; Cheon, P.E.S.; Schou, W.; McDonald, G.W.; Journeaux, P.; Wakelin, S.J.; McDonald, N. Probabilistic Risk Assessment of the Economy-Wide Impacts From a Changing Wildfire Climate on a Regional Rural Landscape. Earth’s Future 2023, 11, e2022EF003446. [Google Scholar] [CrossRef]
- Zhao, H.; Cheng, Y.; Zhang, X.; Yu, S.; Chen, M.; Zhang, C. A Probabilistic Statistical Risk Assessment Method for Soil Erosion Using Remote Sensing Data: A Case Study of the Dali River Basin. Remote Sens. 2024, 16, 3491. [Google Scholar] [CrossRef]
- Wang, X.; Xia, X.; Zhang, X.; Gu, X.; Zhang, Q. Probabilistic Risk Assessment of Soil Slope Stability Subjected to Water Drawdown by Finite Element Limit Analysis. Appl. Sci. 2022, 12, 10282. [Google Scholar] [CrossRef]
- Martin, N. Watershed-Scale, Probabilistic Risk Assessment of Water Resources Impacts from Climate Change. Water 2021, 13, 40. [Google Scholar] [CrossRef]
- Martin, N. Risk Assessment of Future Climate and Land Use/Land Cover Change Impacts on Water Resources. Hydrology 2021, 8, 38. [Google Scholar] [CrossRef]
- Martin, N. Incorporating Weather Attribution to Future Water Budget Projections. Hydrology 2023, 10, 219. [Google Scholar] [CrossRef]
- Perica, S.; Pavlovic, S.; St. Laurent, M.; Trypaluk, C.; Unruh, D.; Wilhite, O. NOAA Atlas 14: Precipitation-Frequency Atlas of the United States, Volume 11 Version 2.0: Texas; Technical Report; NOAA: Silver Spring, MD, USA, 2018. [Google Scholar]
- Hershfield, D.M. Rainfall Frequency Atlas of the United States for Durations from 30 Minutes to 24 Hours and Return Periods from I to 100 Years; Technical Report 40; U.S. Department of Commerce, Weather Bureau: Washington, DC, USA, 1963. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology, TATA McGRAW-HILL ed.; McGraw-Hill Education: Gautam Buddha Nagar, India, 1988. [Google Scholar]
- Schumacher, D.L.; Zachariah, M.; Otto, F.; Barnes, C.; Philip, S.; Kew, S.; Vahlberg, M.; Singh, R.; Heinrich, D.; Arrighi, J.; et al. High Temperatures Exacerbated by Climate Change Made 2022 Northern Hemisphere Soil Moisture Droughts More Likely; Technical Report; World Weather Attribution (WWA), Imperial College: London, UK, 2022. [Google Scholar]
- Cryer, J.D.; Chan, K.S. Time Series Analysis with Applications in R, 2nd ed.; Springer Texts in Statistics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples, 4th ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- World Meteorological Organization. Guide to Hydrological Practices, Volume II: Management of Water Resources and Application of Hydrological Practices; World Meteorological Organization (WMO): Geneva, Switzerland, 2009; Volume II. [Google Scholar] [CrossRef]
- Kyojo, E.A.; Osima, S.E.; Mirau, S.S.; Masanja, V.G. Applying Stationary and Nonstationary Generalized Extreme Value Distributions in Modeling Annual Extreme Temperature Patterns. Adv. Meteorol. 2024, 2024, 9652134. [Google Scholar] [CrossRef]
- De Paola, F.; Giugni, M.; Pugliese, F.; Annis, A.; Nardi, F. GEV Parameter Estimation and Stationary vs. Non-Stationary Analysis of Extreme Rainfall in African Test Cities. Hydrology 2018, 5, 28. [Google Scholar] [CrossRef]
- Martin, N. Climate Change and Water Budgets: Accounting for Increased Drought Risk Based on Recent Observations. 2024. Available online: https://sciencefeatured.com/2024/08/21/climate-change-and-water-budgets-accounting-for-increased-drought-risk-based-on-recent-observations/ (accessed on 25 September 2024).
- Fowler, H.J.; Davies, P.; Lee, S.H. The Climate Is Changing So Fast That We Haven’t Seen How Bad Extreme Weather Could Get. 2024. Available online: http://theconversation.com/the-climate-is-changing-so-fast-that-we-havent-seen-how-bad-extreme-weather-could-get-235726 (accessed on 25 September 2024).
- National Academies of Sciences, Engineering, and Medicine. Modernizing Probable Maximum Precipitation Estimation; National Academies Press: Washington, DC, USA, 2024. [Google Scholar] [CrossRef]
- Martin, N.; Gorelick, S.M. MOD_FreeSurf2D: A MATLAB surface fluid flow model for rivers and streams. Comput. Geosci. 2005, 31, 929–946. [Google Scholar] [CrossRef]
- Casulli, V.; Cheng, R.T. Semi-implicit finite difference methods for three-dimensional shallow water flow. Int. J. Numer. Methods Fluids 1992, 15, 629–648. [Google Scholar] [CrossRef]
- Casulli, V. Semi-implicit finite difference methods for the two-dimensional shallow water equations. J. Comput. Phys. 1990, 86, 56–74. [Google Scholar] [CrossRef]
- Casulli, V.; Cattani, E. Stability, accuracy and efficiency of a semi-implicit method for three-dimensional shallow water flow. Comput. Math. Appl. 1994, 27, 99–112. [Google Scholar] [CrossRef]
- Casulli, V. Numerical simulation of three-dimensional free surface flow in isopycnal co-ordinates. Int. J. Numer. Methods Fluids 1998, 25, 645–658. [Google Scholar] [CrossRef]
- Casulli, V. A semi-implicit finite difference method for non-hydrostatic, free-surface flows. Int. J. Numer. Methods Fluids 1999, 30, 425–440. [Google Scholar] [CrossRef]
- Cheng, R.T.; Casulli, V.; Gartner, J.W. Tidal, Residual, Intertidal Mudflat (TRIM) Model and its Applications to San Francisco Bay, California. Estuar. Coast. Shelf Sci. 1993, 36, 235–280. [Google Scholar] [CrossRef]
- Orlanski, I. A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys. 1976, 21, 251–269. [Google Scholar] [CrossRef]
- Paulik, R.; Wild, A.; Zorn, C.; Wotherspoon, L. Residential building flood damage: Insights on processes and implications for risk assessments. J. Flood Risk Manag. 2022, 15, e12832. [Google Scholar] [CrossRef]
- Peña, F.; Obeysekera, J.; Jane, R.; Nardi, F.; Maran, C.; Cadogan, A.; de Groen, F.; Melesse, A. Investigating compound flooding in a low elevation coastal karst environment using multivariate statistical and 2D hydrodynamic modeling. Weather Clim. Extrem. 2023, 39, 100534. [Google Scholar] [CrossRef]
- Slager, K.; Burzel, A.; Bos, E.; De Bruikn, K.; Wagenaar, D.; Winsemius, H.; Bouwer, L.; Van der Doef, M. User Guide—Delft FIAT. 2016. Available online: https://deltares.github.io/Delft-FIAT/stable/user_guide/ (accessed on 26 November 2024).
- National Association of Realtors. Homes for Sale, Apartments & Houses for Rent. 2024. Available online: https://www.realtor.com/ (accessed on 26 November 2024).
- Ellen Macarthur Foundation. Circular Economy Introduction. 2024. Available online: https://www.ellenmacarthurfoundation.org/topics/circular-economy-introduction/overview (accessed on 25 October 2024).
- Natural Resources Defense Council (NRDC). Regenerative Agriculture 101. 2021. Available online: https://www.nrdc.org/stories/regenerative-agriculture-101 (accessed on 25 October 2024).
- Hamidi, A.; Ramavandi, B.; Sorial, G.A. Sponge City—An emerging concept in sustainable water resource management: A scientometric analysis. Resour. Environ. Sustain. 2021, 5, 100028. [Google Scholar] [CrossRef]
- Harrisberg, K. What Are ’Sponge Cities’ and How Can They Prevent Floods? 2022. Available online: https://climatechampions.unfccc.int/what-are-sponge-cities-and-how-can-they-prevent-floods/ (accessed on 25 October 2024).
- Mossop, E. Not ‘If’, but ‘When’: City Planners Need to Design for Flooding. These Examples Show the Way. 2021. Available online: http://theconversation.com/not-if-but-when-city-planners-need-to-design-for-flooding-these-examples-show-the-way-157578 (accessed on 18 October 2024).
- Kelman, I. Disaster by Choice: How Our Actions Turn Natural Hazard…; Oxford University Press: New York, NY, USA, 2020. [Google Scholar]
- Kelman, I. Floods Are Going to Get Worse: We Need to Start Preparing for Them Now. 2021. Available online: http://theconversation.com/floods-are-going-to-get-worse-we-need-to-start-preparing-for-them-now-172902 (accessed on 18 October 2024).






| Recurrence Interval | 24-h Event 1 | WG Event Magnitude Range 2 | |
|---|---|---|---|
| (Year) | (mm) | Lower Bound (mm) | Upper Bound (mm) |
| 2 | 96 | 96 | 153.7 |
| 5 | 141 | 141 | 247.6 |
| 10 | 179 | 179 | 255.7 |
| 25 | 236 | 236 | 290.9 |
| 50 | 285 | 285 | 415.5 |
| 100 | 343 | 343 | 498.1 |
| 200 | 408 | NA 3 | NA 3 |
| 500 | 506 | NA 3 | NA 3 |
| 1000 | 589 | NA 3 | NA 3 |
| Scenario | Future Mitigation Cost | Current Adaptation Cost 2 | |||||
|---|---|---|---|---|---|---|---|
| 250th Percentile | 50th Percentile | Mean | 750th Percentile | 900th Percentile | Max. | ||
| All Failures | 0.224 | 2.461 | 6.725 | 11.607 | 17.099 | 55.656 | NA 3 |
| No Obstruction | 0.000 | 1.272 | 5.940 | 10.430 | 16.193 | 53.687 | NA 3 |
| Obstruction Only | 0.325 | 3.183 | 7.510 | 13.590 | 18.639 | 57.625 | NA 3 |
| Drop 2 Houses | 0.025 | 1.753 | 5.688 | 9.818 | 14.960 | 48.877 | 1.5 |
| Drop 4 Houses | 0.000 | 1.104 | 4.761 | 8.041 | 13.054 | 42.520 | 3.0 |
| Drop 6 Houses | 0.000 | 0.713 | 3.944 | 6.477 | 11.428 | 36.705 | 4.5 |
| Drop 8 Houses | 0.000 | 0.421 | 3.211 | 5.030 | 9.850 | 31.188 | 6.0 |
| Drop 10 Houses | 0.000 | 0.173 | 2.555 | 3.885 | 8.251 | 25.965 | 7.5 |
| Drop 12 Houses | 0.000 | 0.000 | 1.964 | 2.950 | 6.638 | 20.972 | 9.0 |
| Drop 14 Houses | 0.000 | 0.000 | 1.438 | 2.038 | 5.040 | 16.182 | 10.5 |
| Drop 16 Houses | 0.000 | 0.000 | 0.979 | 1.314 | 3.504 | 11.574 | 12.0 |
| Drop 18 Houses | 0.000 | 0.000 | 0.588 | 0.795 | 2.113 | 7.251 | 13.5 |
| Adaptation Scenario | Mitigation Savings Relative to “All Failures” 1 (+Is Savings and −Is Extra Cost, M USD 2) | |||||
|---|---|---|---|---|---|---|
| 25th Percentile | 50th Percentile | Mean | 75th Percentile | 90th Percentile | Max | |
| Drop 2 Houses | —1.301 | —0.792 | —0.463 | 0.289 | 0.639 | 5.279 |
| Drop 4 Houses | —2.776 | —1.643 | —1.035 | 0.566 | 1.045 | 10.136 |
| Drop 6 Houses | —4.276 | —2.752 | —1.718 | 0.630 | 1.171 | 14.451 |
| Drop 8 Houses | —5.776 | —3.960 | —2.486 | 0.577 | 1.248 | 18.468 |
| Drop 10 Houses | —7.276 | —5.213 | —3.329 | 0.222 | 1.347 | 22.191 |
| Drop 12 Houses | —8.776 | —6.539 | —4.239 | —0.343 | 1.461 | 25.684 |
| Drop 14 Houses | —10.276 | —8.039 | —5.213 | —0.931 | 1.558 | 28.974 |
| Drop 16 Houses | —11.776 | —9.539 | —6.253 | —1.707 | 1.595 | 32.082 |
| Drop 18 Houses | —13.276 | —11.039 | —7.363 | —2.688 | 1.485 | 34.905 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martin, N.; Peña, F.; Powers, D. Probabilistic Risk Assessment (PRA) for Sustainable Water Resource Management: A Future Flood Inundation Example. Water 2025, 17, 816. https://doi.org/10.3390/w17060816
Martin N, Peña F, Powers D. Probabilistic Risk Assessment (PRA) for Sustainable Water Resource Management: A Future Flood Inundation Example. Water. 2025; 17(6):816. https://doi.org/10.3390/w17060816
Chicago/Turabian StyleMartin, Nick, Francisco Peña, and David Powers. 2025. "Probabilistic Risk Assessment (PRA) for Sustainable Water Resource Management: A Future Flood Inundation Example" Water 17, no. 6: 816. https://doi.org/10.3390/w17060816
APA StyleMartin, N., Peña, F., & Powers, D. (2025). Probabilistic Risk Assessment (PRA) for Sustainable Water Resource Management: A Future Flood Inundation Example. Water, 17(6), 816. https://doi.org/10.3390/w17060816








