Evaluating Modeling Approaches for Phytoplankton Productivity in Estuaries
Abstract
1. Introduction
2. Materials and Methods
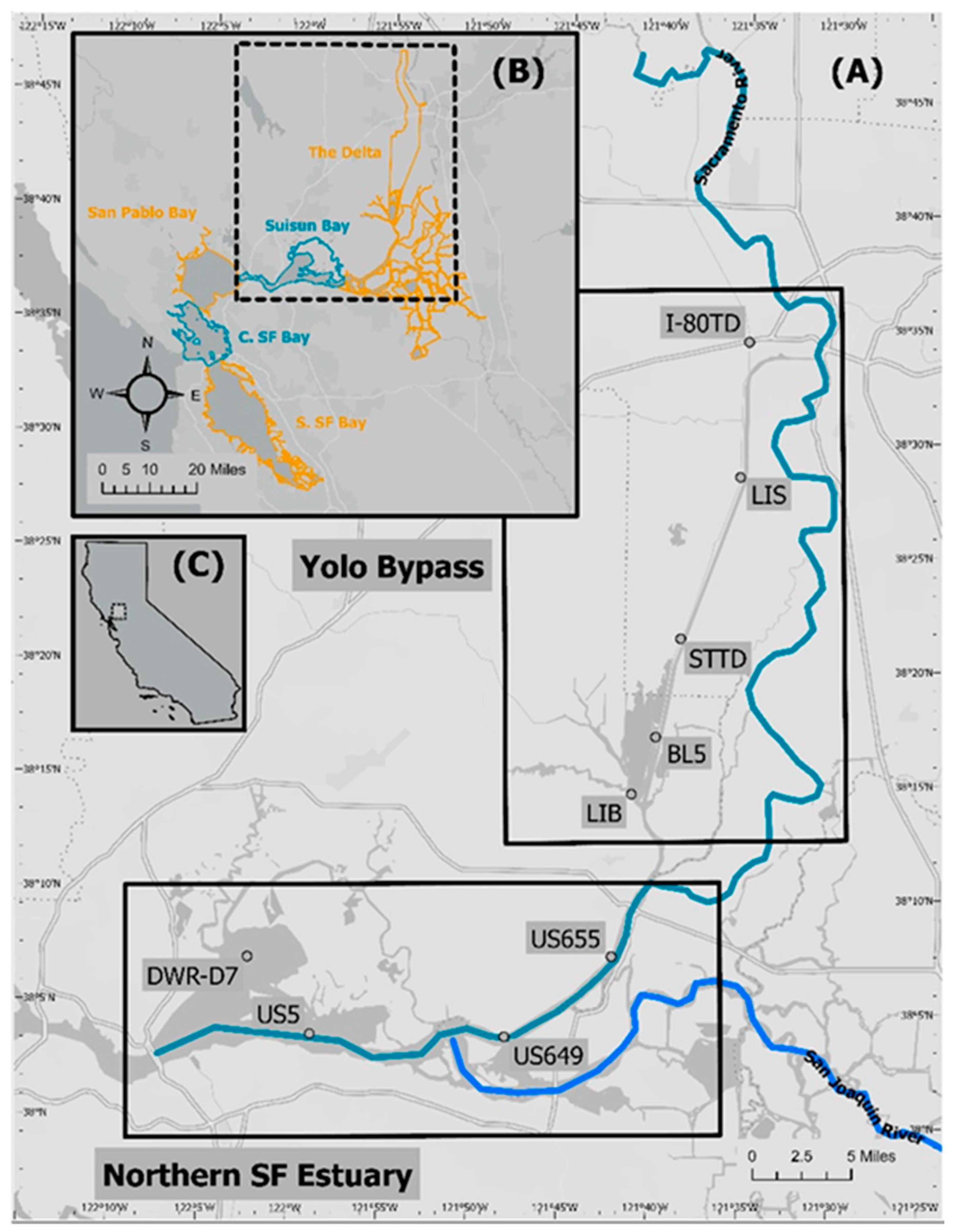
2.1. Study Region Description
2.2. Sampling and Laboratory Methods
2.3. Modeling Approaches
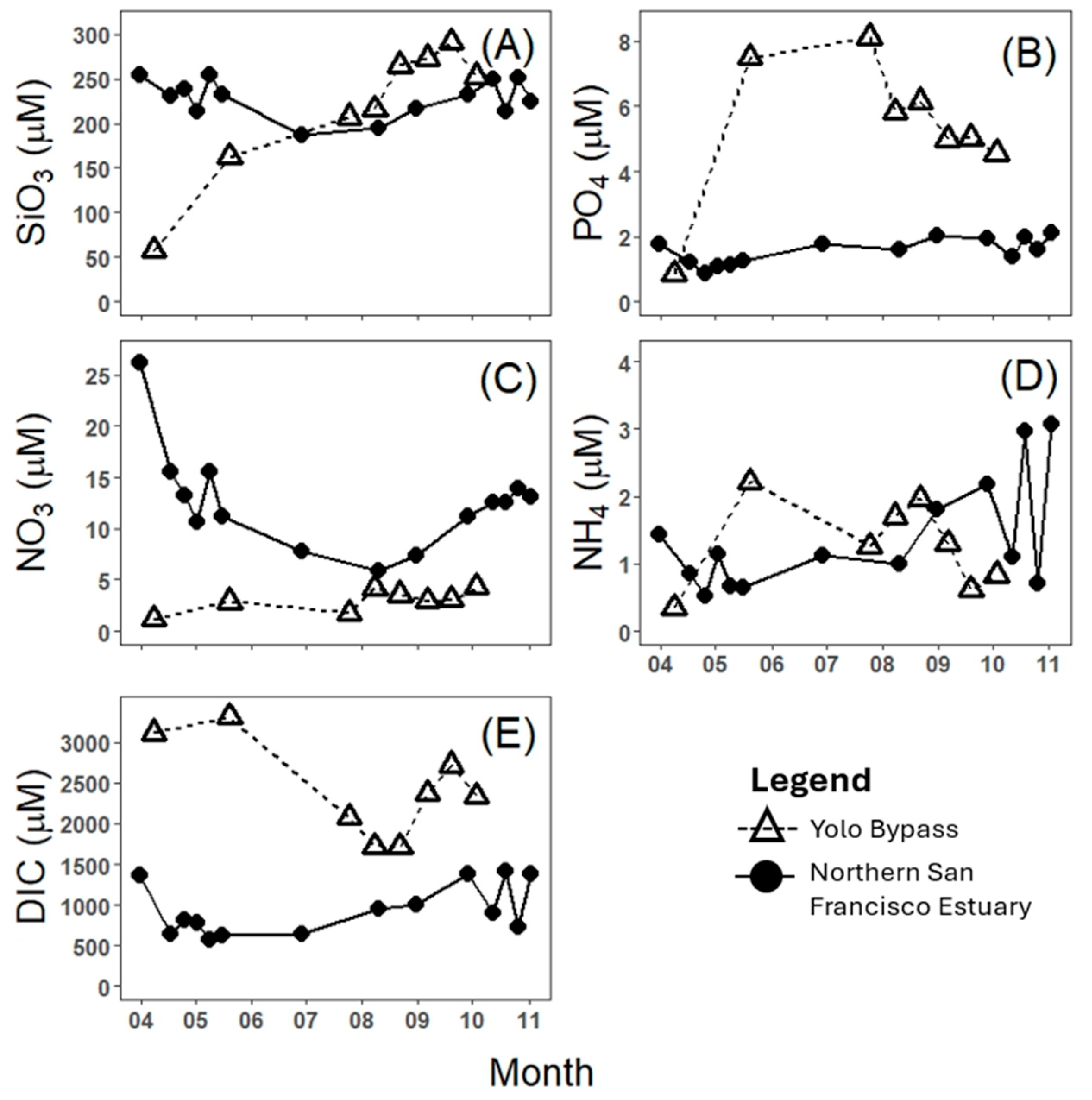
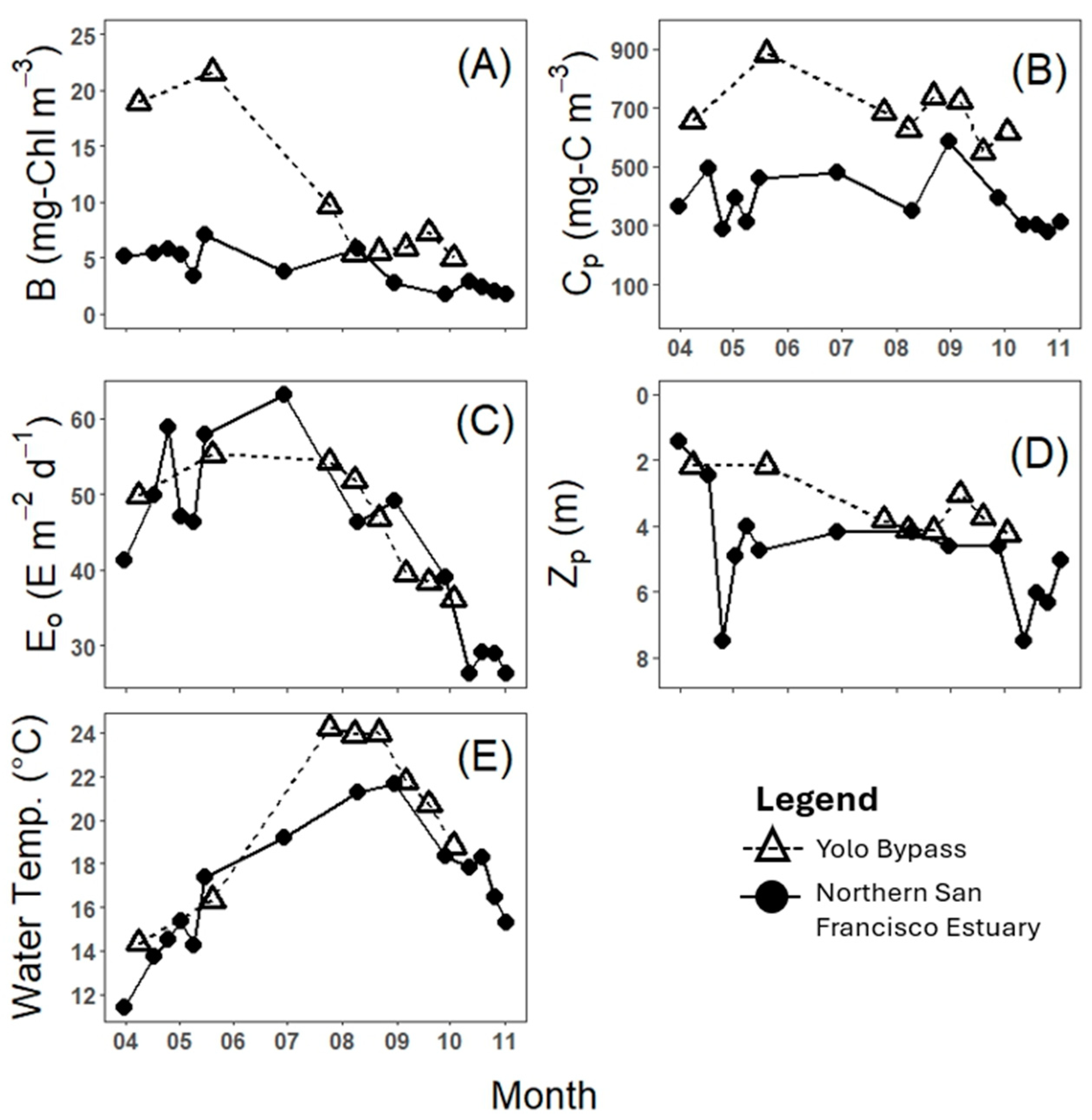
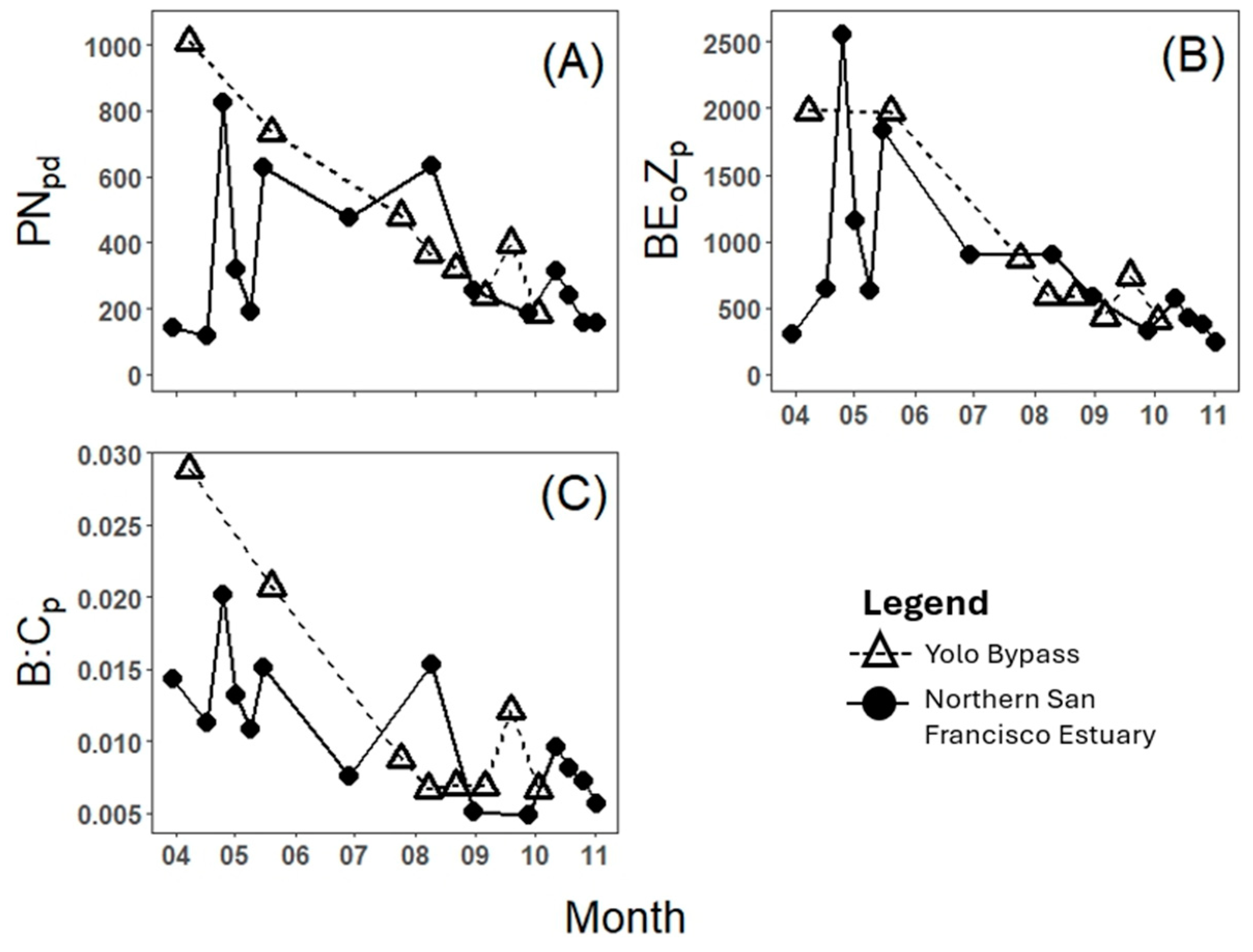
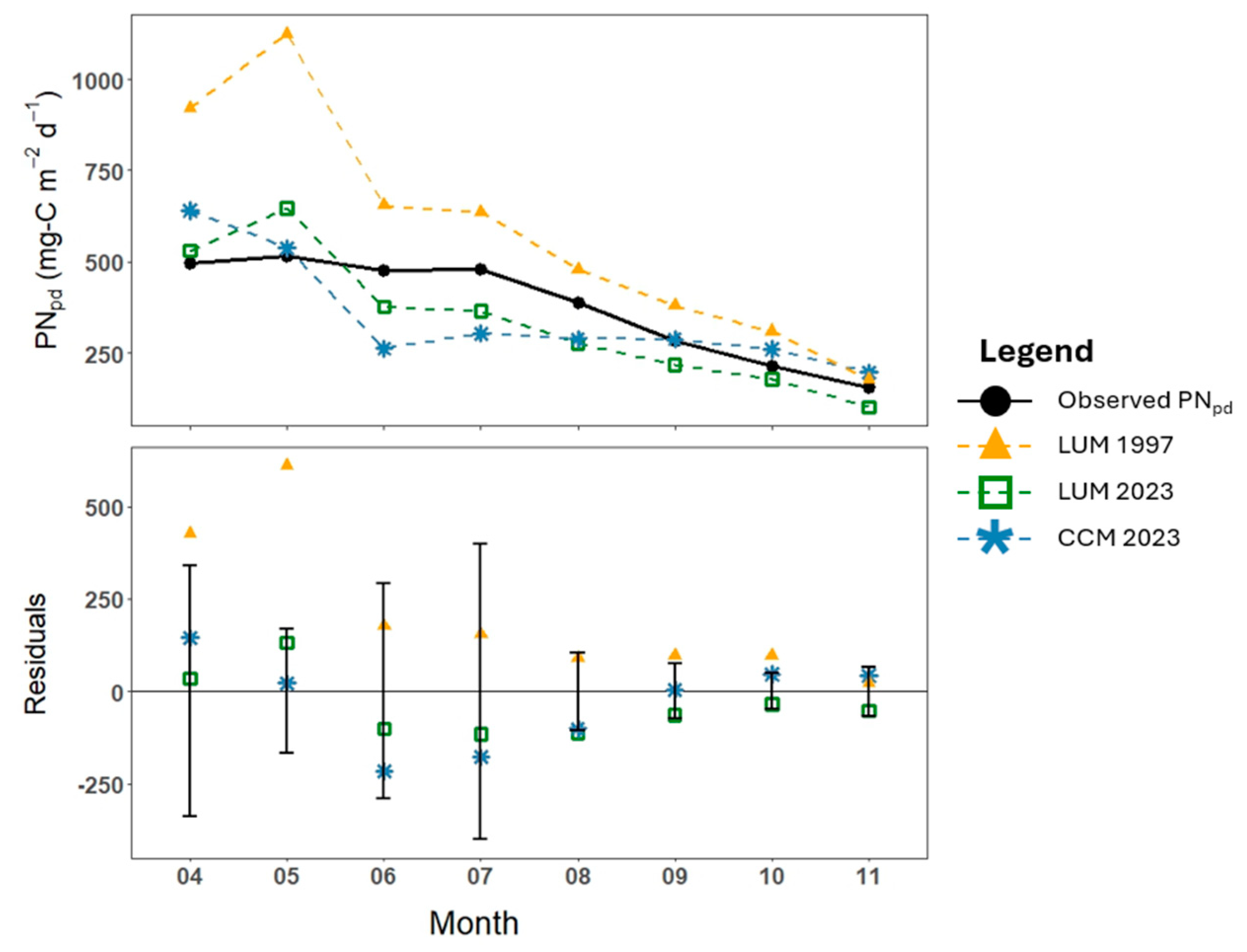
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davidson, N.C. How much wetland has the world lost? Long-term and recent trends in global wetland area. Mar. Freshw. Res. 2014, 65, 934. [Google Scholar] [CrossRef]
- Milligan, B.; Kraus-Polk, A. Evolving the Evolving: Territory, Place and Rewilding in the California Delta. Urban Plan. 2017, 2, 93–114. [Google Scholar] [CrossRef]
- Cloern, J.E.; Safran, S.M.; Smith Vaughn, L.; Robinson, A.; Whipple, A.A.; Boyer, K.E.; Drexler, J.Z.; Naiman, R.J.; Pinckney, J.L.; Howe, E.R.; et al. On the human appropriation of wetland primary production. Sci. Total Environ. 2021, 785, 147097. [Google Scholar] [CrossRef]
- Sommer, T.; Armor, C.; Baxter, R.; Breuer, R.; Brown, L.; Chotkowski, M.; Culberson, S.; Feyrer, F.; Gingras, M.; Herbold, B.; et al. The Collapse of Pelagic Fishes in the Upper San Francisco Estuary. Fisheries 2007, 32, 270–277. [Google Scholar] [CrossRef]
- Jassby, A.; Cloern, J.; Cole, B. Annual primary production: Patterns and mechanisms of change in a nutrient-rich tidal ecosystem. Limnol. Oceanogr. 2002, 47, 698–712. [Google Scholar] [CrossRef]
- Gross, E.; Holleman, R.; Kimmerer, W.; Munger, S.; Burdick, S.; Durand, J. Using Age Tracers to Estimate Ecological Rates in a Phytoplankton Model. Water 2023, 15, 2097. [Google Scholar] [CrossRef]
- Cloern, J. Tidal stirring and phytoplankton bloom dynamics in an estuary. J. Mar. Res. 1991, 49, 203–221. [Google Scholar] [CrossRef]
- Slawyk, G.; Collos, Y.; Auclair, J. The use of the 13C and 15N isotopes for the simultaneous measurement of carbon and nitrogen turnover rates in marine phytoplankton. Limnol. Oceanogr. 1977, 22, 925–932. [Google Scholar] [CrossRef]
- Dugdale, R.C.; Wilkerson, F.P. The use of 15N to measure nitrogen uptake in eutrophic oceans; experimental considerations. Limnol. Oceanogr. 1986, 31, 673–689. [Google Scholar] [CrossRef]
- Cole, B.; Cloern, J. Significance of biomass and light availability to phytoplankton productiivty in San Francisco Bay. Mar. Ecol. Prog. Ser. 1984, 17, 15–24. [Google Scholar] [CrossRef]
- Kimmerer, W.; Parker, A.; Lidström, U.; Carpenter, E. Short-Term and Interannual Variability in Primary Production in the Low-Salinity Zone of the San Francisco Estuary. Estuaries Coasts 2012, 35, 913–929. [Google Scholar] [CrossRef][Green Version]
- Parker, A.; Kimmerer, W.; Lidström, U. Reevaluating the Generality of an Empirical Model for Light-Limited Primary Production in the San Francisco Estuary. Estuaries Coasts 2012, 35, 930–942. [Google Scholar] [CrossRef]
- Jassby, A. Phytoplankton in the Upper San Francisco Estuary: Recent Biomass Trends, Their Causes, and Their Trophic Significance. San Franc. Estuary Watershed Sci. 2008, 6. [Google Scholar] [CrossRef]
- Cloern, J.E.; Jassby, A.D.; Thompson, J.K.; Hieb, K.A. A cold phase of the East Pacific triggers new phytoplankton blooms in San Francisco Bay. Proc. Natl. Acad. Sci. USA 2007, 104, 18561–18565. [Google Scholar] [CrossRef] [PubMed]
- Harding, L.W.; Mallonee, M.E.; Perry, E.S. Toward a Predictive Understanding of Primary Productivity in a Temperate, Partially Stratified Estuary. Estuar. Coast. Shelf Sci. 2002, 55, 437–463. [Google Scholar] [CrossRef]
- Kromkamp, J.; Peene, J.; Van Rijswijk, P.; Sandee, A.; Goosen, N. Nutrients, light and primary production by phytoplankton and microphytobenthos in the eutrophic, turbid Westerschelde estuary (The Netherlands). Hydrobiologia 1995, 311, 9–19. [Google Scholar] [CrossRef]
- Burt, W.J.; Westberry, T.K.; Behrenfeld, M.J.; Zeng, C.; Izett, R.W.; Tortell, P.D. Carbon: Chlorophyll Ratios and Net Primary Productivity of Subarctic Pacific Surface Waters Derived From Autonomous Shipboard Sensors. Glob. Biogeochem. Cycles 2018, 32, 267–288. [Google Scholar] [CrossRef]
- Cloern, J.E.; Grenz, C.; Vidergar-Lucas, L. An empirical model of the phytoplankton chlorophyll: Carbon ratio—The conversion factor between productivity and growth rate. Limnol. Oceanogr. 1995, 40, 1313–1321. [Google Scholar] [CrossRef]
- Parker, A.; Fuller, J.; Dugdale, R. Estimating dissolved inorganic carbon concentrations from salinity in San Francisco Bay for use in 14C-primary production studies. Interag. Ecol. Program San Franc. Estuary 2006, 19, 17–22. [Google Scholar]
- Arar, E.; Collins, G. Method 445.0: In Vitro Determination of Chlorophyll a and Pheophytin a in Marine and Freshwater Algae by Fluorescence; National Exposure Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 1997.
- Solórzano, L. Determination of Ammonia in Natural Waters by the Phenolhypochlorite Method. Limnol. Oceanogr. 1969, 14, 799–801. [Google Scholar] [CrossRef]
- Bran Luebbe Inc. Bran Luebbe Autoanalyzer Applications: Autoanalyzer Method No. G-177-96 Silicate in Water and Seawater; Bran Luebbe Inc.: Buffalo Grove, IL, USA, 1999. [Google Scholar]
- Bran Luebbe Inc. Bran Luebbe Autoanalyzer Applications: Autoanalyzer Method No. G-175-96 Phosphate in Water and Seawater; Bran Luebbe Inc.: Buffalo Grove, IL, USA, 1999. [Google Scholar]
- Bran Luebbe Inc. Bran Luebbe Autoanalyzer Applications: Autoanalyzer Method No. G-172-96 Nitrate and Nitrite in Water and Seawater; Bran Luebbe Inc.: Buffalo Grove, IL, USA, 1999. [Google Scholar]
- Wilkerson, F.; Dugdale, R.; Parker, A.; Blaser, S.; Pimenta, A. Nutrient uptake and primary productivity in an urban estuary: Using rate measurements to evaluate phytoplankton response to different hydrological and nutrient conditions. Aquat. Ecol. 2015, 49, 211–233. [Google Scholar] [CrossRef]
- Parker, A.E. Differential supply of autochthonous organic carbon and nitrogen to the microbial loop in the Delaware Estuary. Estuaries 2005, 28, 856–867. [Google Scholar] [CrossRef]
- Legendre, L.; Gosselin, M. Estimation of N or C uptake rates by phytoplankton using 15N or 13C: Revisiting the usual computation formulae. J. Plankton Res. 1997, 19, 263–271. [Google Scholar] [CrossRef][Green Version]
- Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-based ocean productivity and phytoplankton physiology from space. Glob. Biogeochem. Cycles 2005, 19, GB1006. [Google Scholar] [CrossRef]
- Jakobsen, H.H.; Markager, S. Carbon-to-chlorophyll ratio for phytoplankton in temperate coastal waters: Seasonal patterns and relationship to nutrients: C:Chl for phytoplankton in temperate coastal waters. Limnol. Oceanogr. 2016, 61, 1853–1868. [Google Scholar] [CrossRef]
- Franklin, J. Plant Growth Chamber Handbook. New Phytol. 1998, 138, 743–750. [Google Scholar] [CrossRef]
- Zeileis, A.; Hothorn, T. Diagnostic Checking in Regression Relationships. R News 2002, 2, 7–10. [Google Scholar]
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024.
- Willmott, C.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- López-Sandoval, D.C.; Delgado-Huertas, A.; Agustí, S. The 13C method as a robust alternative to 14C-based measurements of primary productivity in the Mediterranean Sea. J. Plankton Res. 2018, 40, 544–554. [Google Scholar] [CrossRef]
- Cole, B.; Cloern, J. An empirical model for estimating phytoplankton productivity in estuaries. Mar. Ecol. Prog. Ser. 1987, 35, 299–305. [Google Scholar] [CrossRef]
- Cloern, J.E.; Foster, S.Q.; Kleckner, A.E. Phytoplankton primary production in the world’s estuarine-coastal ecosystems. Biogeosciences 2014, 11, 2477–2501. [Google Scholar] [CrossRef]
- Nixon, S.W. Coastal marine eutrophication: A definition, social causes, and future concerns. Ophelia 1995, 41, 199–219. [Google Scholar] [CrossRef]
- Cloern, J. Our evolving conceptual model of the coastal eutrophication problem. Mar. Ecol. Prog. Ser. 2001, 210, 223–253. [Google Scholar] [CrossRef]
- Sharp, J.H. Marine and Aquatic Communities, Stress from Eutrophication. In Encyclopedia of Biodiversity; Elsevier: Amsterdam, The Netherlands, 2001; pp. 1–11. ISBN 978-0-12-226865-6. [Google Scholar]
- Wilkerson, F.P.; Dugdale, R.C.; Hogue, V.E.; Marchi, A. Phytoplankton blooms and nitrogen productivity in San Francisco Bay. Estuaries Coasts 2006, 29, 401–416. [Google Scholar] [CrossRef]
- Gazeau, F.; Gattuso, J.-P.; Middelburg, J.J.; Brion, N.; Schiettecatte, L.-S.; Frankignoulle, M.; Borges, A.V. Planktonic and whole system metabolism in a nutrient-rich estuary (the Scheldt estuary). Estuaries 2005, 28, 868–883. [Google Scholar] [CrossRef]
- Joint, I.R.; Pomroy, A.J. Primary production in a turbid estuary. Estuar. Coast. Shelf Sci. 1981, 13, 303–316. [Google Scholar] [CrossRef]
- Raine, R.C.T.; Patching, J.W. Aspects of carbon and nitrogen cycling in a shallow marine environment. J. Exp. Mar. Biol. Ecol. 1980, 47, 127–139. [Google Scholar] [CrossRef]
- Kocum, E.; Underwood, G.; Nedwell, D. Simultaneous measurement of phytoplanktonic primary production, nutrient and light availability along a turbid, eutrophic UK east coast estuary (the Colne Estuary). Mar. Ecol. Prog. Ser. 2002, 231, 1–12. [Google Scholar] [CrossRef]
- Alpine, A.; Cloern, J. Trophic interactions and direct physical effects control phytoplankton biomass and production in an estuary. Limnol. Oceanogr. 1992, 37, 946–955. [Google Scholar] [CrossRef]
- Lorenzi, A. Primary Productivity and rbcL Gene Expression in Central San Francisco Bay; San Francisco State University: San Francisco, CA, USA, 2005. [Google Scholar]
- Harding, L.W.; Meeson, B.W.; Fisher, T.R. Phytoplankton production in two east coast estuaries: Photosynthesis-light functions and patterns of carbon assimilation in Chesapeake and Delaware Bays. Estuar. Coast. Shelf Sci. 1986, 23, 773–806. [Google Scholar] [CrossRef]
- Campbell, J.W.; O’Reilly, J.E. Role of satellites in estimating primary productivity on the northwest Atlantic continental shelf. Cont. Shelf Res. 1988, 8, 179–204. [Google Scholar] [CrossRef]
- Balch, W.; Evans, R.; Brown, J.; Feldman, G.; McClain, C.; Esaias, W. The remote sensing of ocean primary productivity: Use of a new data compilation to test satellite algorithms. J. Geophys. Res. Oceans 1992, 97, 2279–2293. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Falkowski, P.G. Photosynthetic rates derived from satellite-based chlorophyll concentration. Limnol. Oceanogr. 1997, 42, 1–20. [Google Scholar] [CrossRef]
- Stumpner, E.B.; Bergamaschi, B.A.; Kraus, T.E.C.; Parker, A.E.; Wilkerson, F.P.; Downing, B.D.; Dugdale, R.C.; Murrell, M.C.; Carpenter, K.D.; Orlando, J.L.; et al. Spatial variability of phytoplankton in a shallow tidal freshwater system reveals complex controls on abundance and community structure. Sci. Total Environ. 2020, 700, 134392. [Google Scholar] [CrossRef] [PubMed]
- Graff, J.R.; Westberry, T.K.; Milligan, A.J.; Brown, M.B.; Dall’Olmo, G.; Dongen-Vogels, V.V.; Reifel, K.M.; Behrenfeld, M.J. Analytical phytoplankton carbon measurements spanning diverse ecosystems. Deep Sea Res. Part I Oceanogr. Res. Pap. 2015, 102, 16–25. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Weather Forecasting with Ensemble Methods. Science 2005, 310, 248–249. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Stuart, V.; Nair, A.; Oka, K.; Nakane, T.; Bouman, H.; Forget, M.; Maass, H.; Platt, T. Carbon-to-chlorophyll ratio and growth rate of phytoplankton in the sea. Mar. Ecol. Prog. Ser. 2009, 383, 73–84. [Google Scholar] [CrossRef]

| Symbol | Parameter | Units |
|---|---|---|
| SFED | San Francisco Estuary and Delta | |
| LUM | light utilization model | |
| CCM | chlorophyll-a to carbon model | |
| ρC | transport (uptake) rate of carbon | mg-C m−3 d−1 |
| PNpd | depth-integrated daily net phytoplankton productivity | mg-C m−2 d−1 |
| PNpy | depth-integrated annual net phytoplankton productivity | g-C m−2 yr−1 |
| B | chlorophyll-a concentration | mg-Chl m−3 |
| Eo | ambient photosynthetically active radiation | Einsteins m−2 d−1 |
| Zp | photic zone depth | m |
| Cp | phytoplankton carbon concentration | mg-C m−3 |
| BEoZp | composite parameter | Einsteins mg-Chl m−4 d−1 |
| B:Cp | chlorophyll-a to phytoplankton carbon ratio | mg-Chl mg-C−1 |
| ψ | light utilization model regression slope | mg-C m2 mg-Chl−1 Einsteins−1 |
| Ω | chlorophyll-a to carbon model regression slope | mgC2 mgChl−1 m−2 d−1 |
| MAE | mean absolute error |
| Estimate Source | Regression Slope | PNpy Estimate (g-C m−2 yr−1) | Within CI95 | MAE | Percent Error |
|---|---|---|---|---|---|
| Observed | - | 137 | ±24 | - | - |
| LUM 2023 | Ψ = 0.42 | 125 | Yes | 31% | −9% |
| LUM 1997 | Ψ = 0.73 | 217 | No | 61% | 58% |
| CCM 2023 | Ω = 3.47 × 104 | 131 | Yes | 36% | −4% |
| Year(s) | Location(s) | Season | Photoperiod | ψ | Reference |
|---|---|---|---|---|---|
| 2023 | nSFE + YB | March–November | 24 h | 0.42 ± 0.02 | This study |
| nSFE | data | 0.38 ± 0.02 | |||
| YB | data | 0.45 ± 0.02 | |||
| 1980 | South SF Bay | Annual | 24 h | 0.99 ± 0.09 | [10] Cole & Cloern (1984), refit data |
| San Pablo Bay | data | 1.22 ± 0.15 | |||
| 1988 | Suisun Bay | May–October | 24 h | 0.81 ± 0.10 | [45] Alpine & Cloern (1992), calculated from data in Table 2 |
| 1997 | Delta | May–November | 30 m | 0.73 ± 0.05 | [5] Jassby et al. (2002), as reported |
| 2004–2005 | Central SF Bay | Annual | 6 h | 0.37 ± 0.04 | [46] Lorenzi 2006, as reported |
| 2006 | San Pablo—Suisun Bay | March–August | 6 h | 0.29 ± 0.03 | [12] Parker et al. (2012), as reported |
| 2007 | Suisun Bay | 24 h | 0.56 ± 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoshovsky, R.; Wilkerson, F.; Parker, A.; Dugdale, R. Evaluating Modeling Approaches for Phytoplankton Productivity in Estuaries. Water 2025, 17, 747. https://doi.org/10.3390/w17050747
Hoshovsky R, Wilkerson F, Parker A, Dugdale R. Evaluating Modeling Approaches for Phytoplankton Productivity in Estuaries. Water. 2025; 17(5):747. https://doi.org/10.3390/w17050747
Chicago/Turabian StyleHoshovsky, Reed, Frances Wilkerson, Alexander Parker, and Richard Dugdale. 2025. "Evaluating Modeling Approaches for Phytoplankton Productivity in Estuaries" Water 17, no. 5: 747. https://doi.org/10.3390/w17050747
APA StyleHoshovsky, R., Wilkerson, F., Parker, A., & Dugdale, R. (2025). Evaluating Modeling Approaches for Phytoplankton Productivity in Estuaries. Water, 17(5), 747. https://doi.org/10.3390/w17050747






