A Study of the Scale Dependency and Anisotropy of the Permeability of Fractured Rock Masses
Abstract
1. Introduction
- Geometric parameters, such as joint spacing, trace length, etc. [19,22,23]. For example, Schultz [24] suggested that the REV size of a rock mass is five to ten times the average joint spacing. Zhang and Xu [25] considered that the REV size to be three to four times the maximum expected value of the joint trace length.
- Mechanical parameters, such as the shear stress, elastic modulus, and uniaxial compressive strength [19,26,27,28]. For example, Wang et al. [29] used the two-dimensional particle flow code (PFC2D) to study the size effect and directionality of the shear strength of stratified rocks and determined the REV size based on shear strength. Li et al. [28] conducted a series of uniaxial compression numerical simulation tests using PFC3D based on a synthetic rock model and estimated the REV dimensions using the elastic modulus and uniaxial compressive strength.
- Hydraulic parameters, including connectivity and permeability. For example, Min et al. [1] determined the REV size based on rock permeability and found that the permeability values calculated at the REV size have tensor characteristics. Bang et al. [30] estimated the REV size with respect to the hydraulic behavior based on a three-dimensional (3D) discrete fracture network model. Rong et al. [6] discussed the effects of fracture geometric parameters such as the trace length, spacing, aperture, orientation, and the number of fracture groups on the REV size. Wang et al. [31] studied the hydraulic properties of fractured rock masses related to the fracture length and aperture under both radial and unidirectional flow conditions and estimated the REV size.
2. Discrete Fracture Network Model
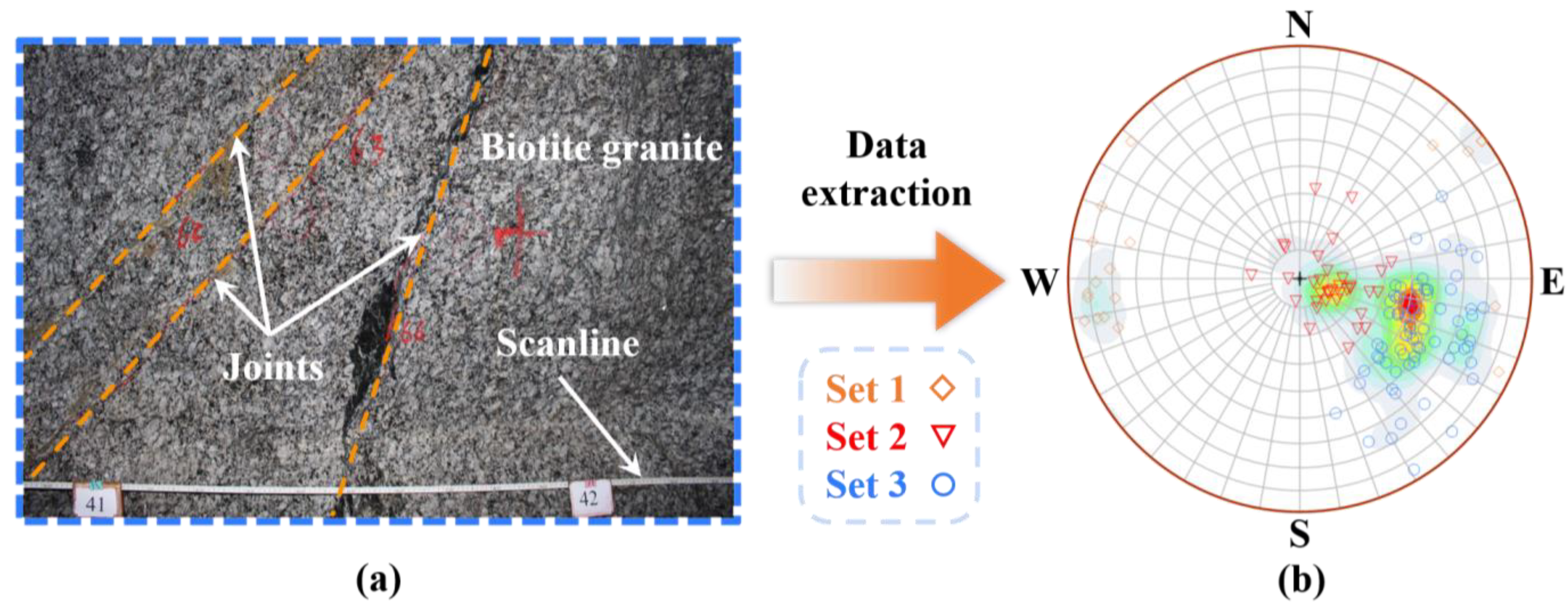
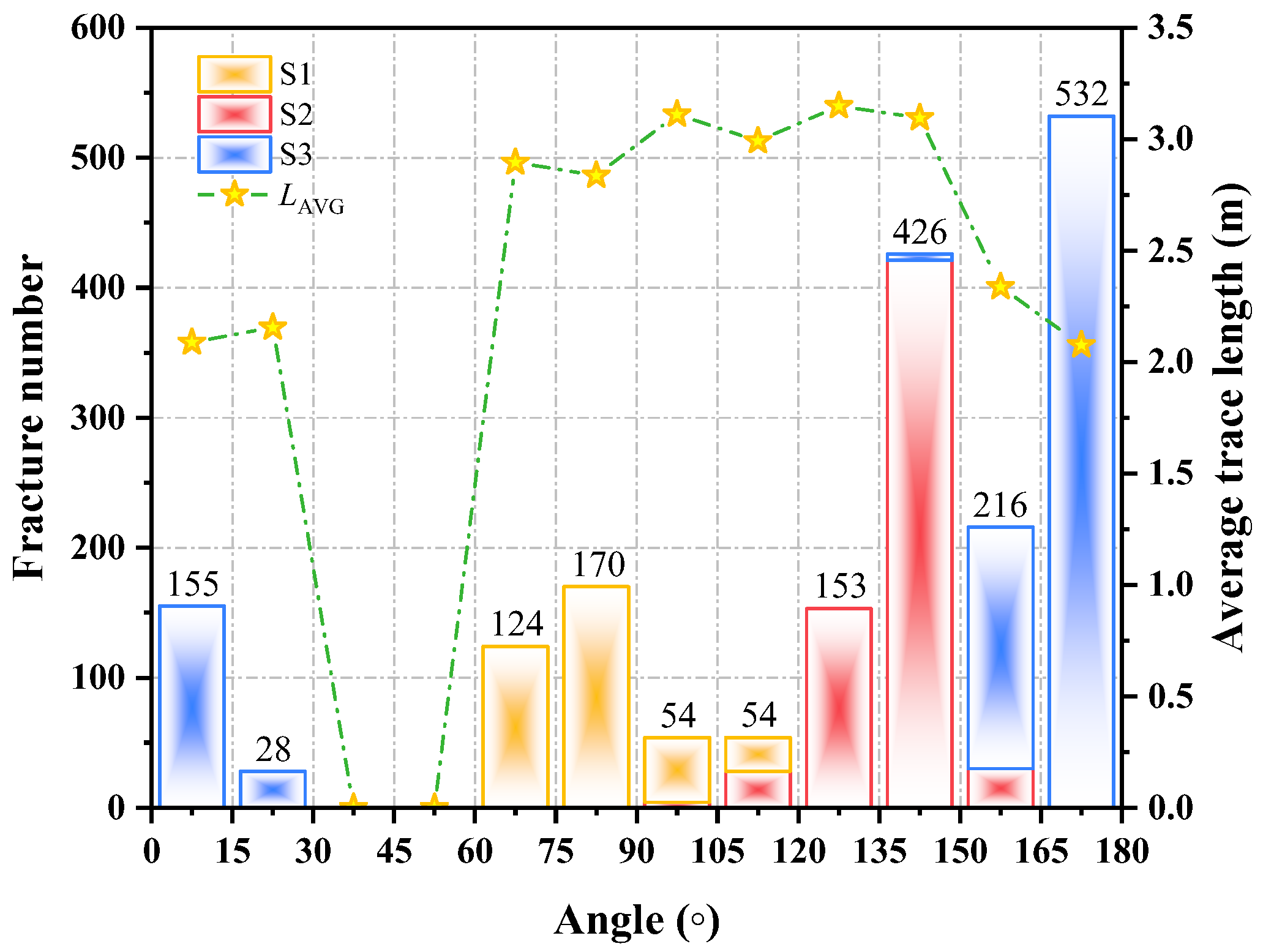
2.1. Joint Mapping
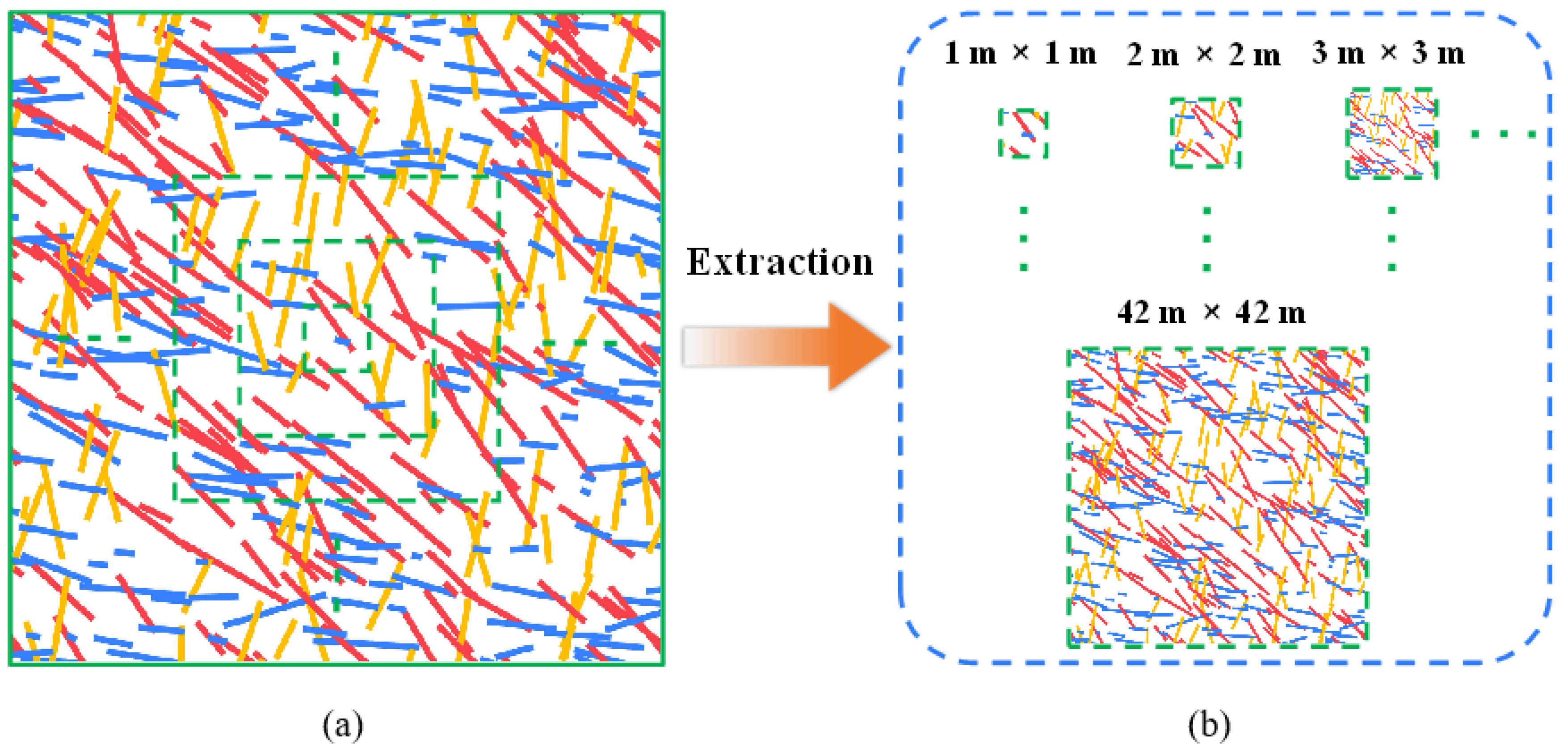
2.2. Generation of the 3D DFN Model
3. Calculation Method for Fluid Flow in Rock Masses
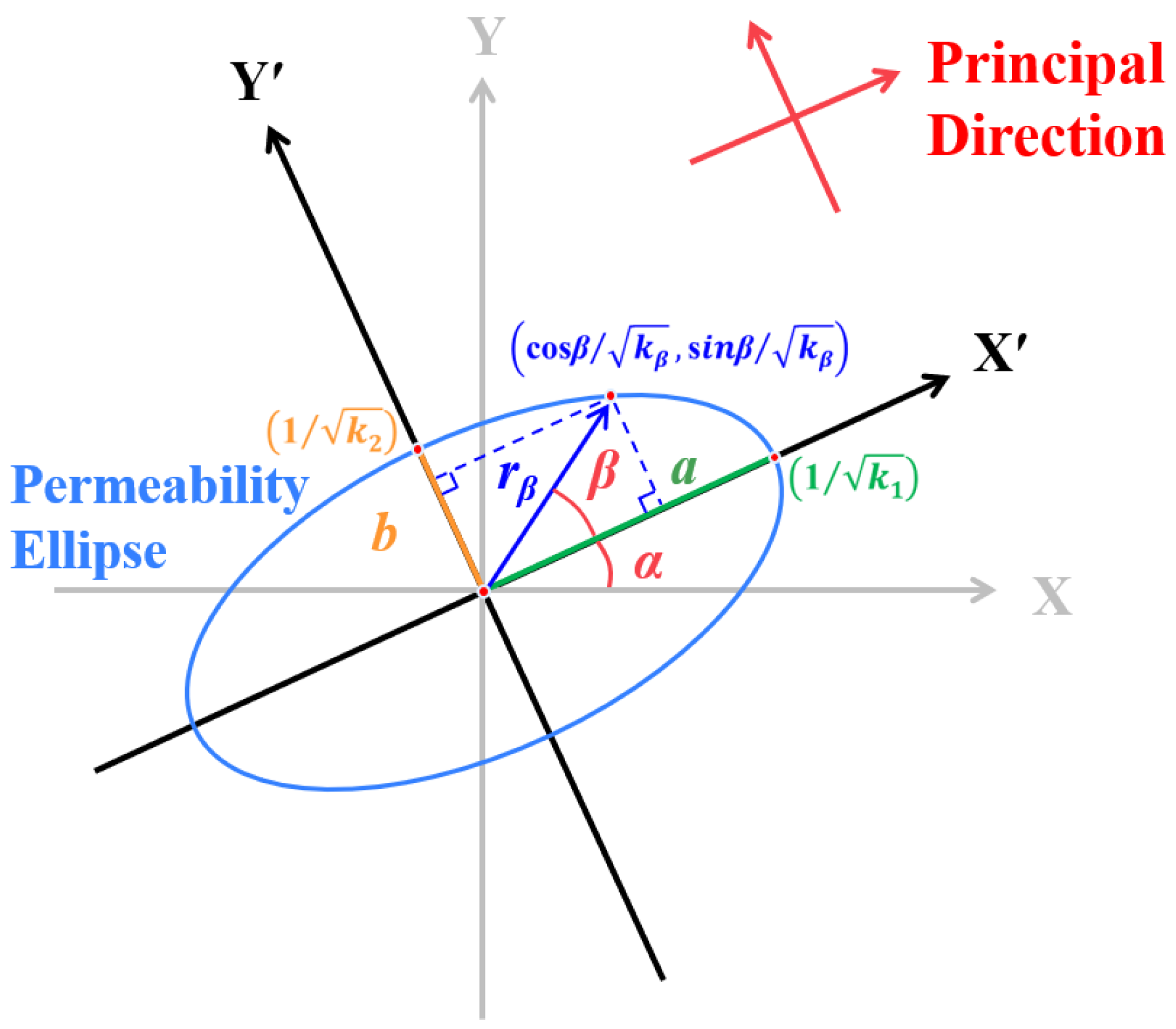
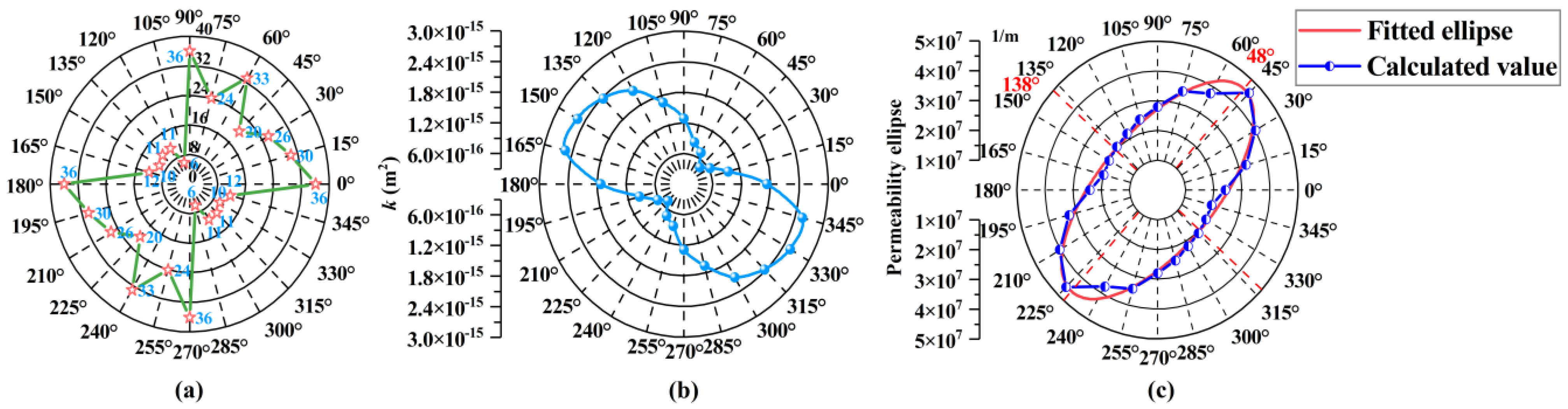
3.1. Permeability Tensor
3.2. Fluid Flow Simulation Method
3.3. Verification
4. Numerical Simulation
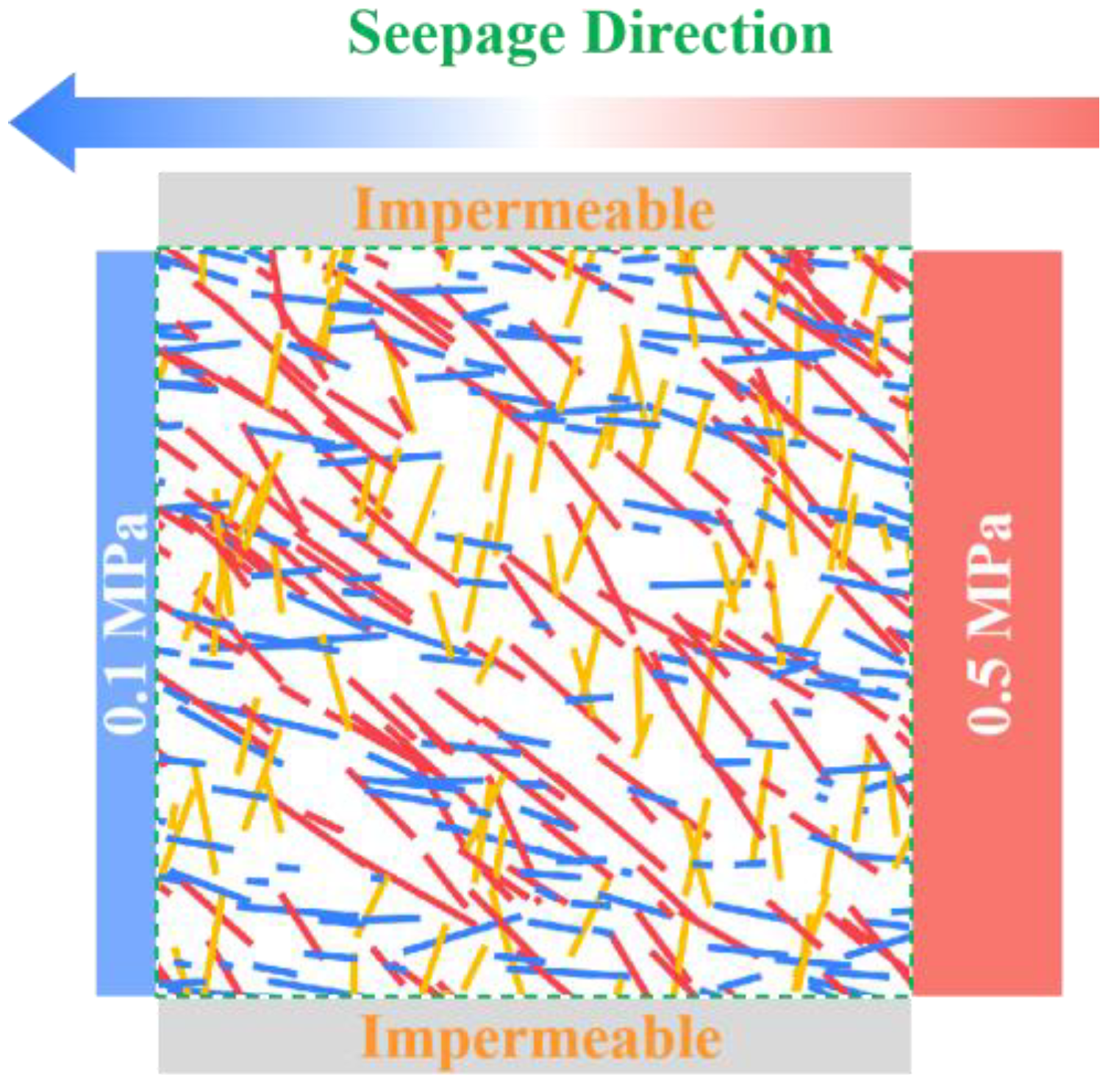
4.1. Model Generation and Boundary Conditions
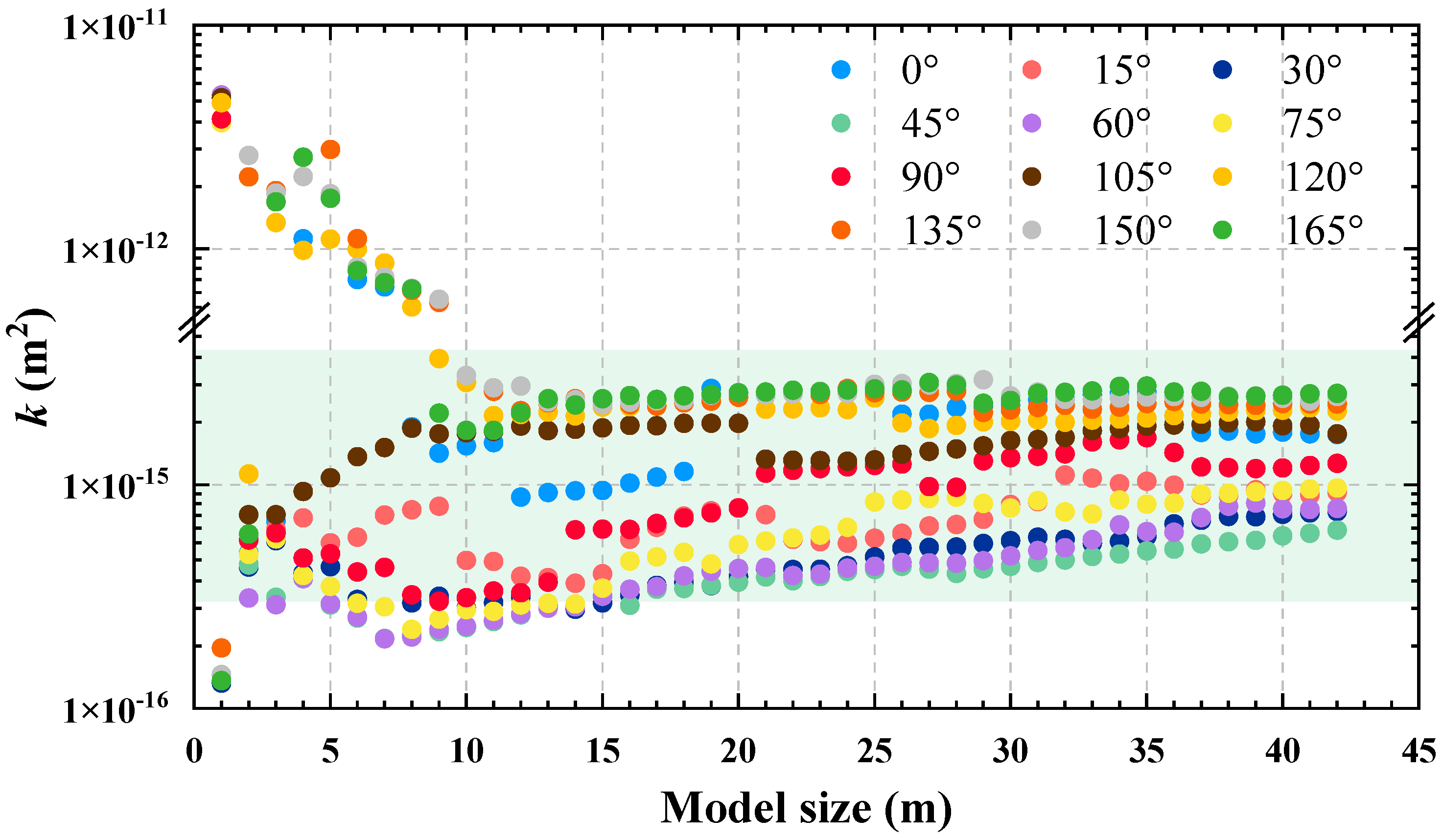
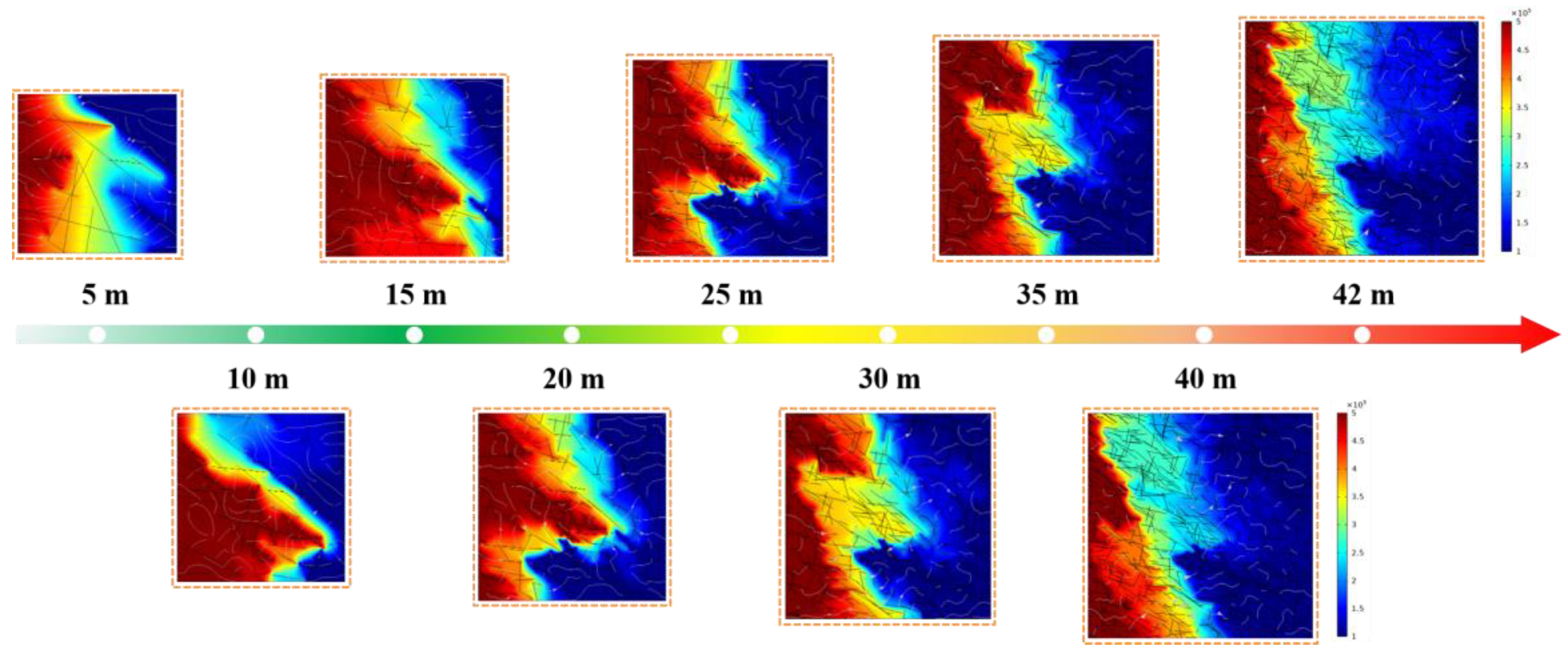
4.2. Simulation Results
5. Estimation of the REV Size
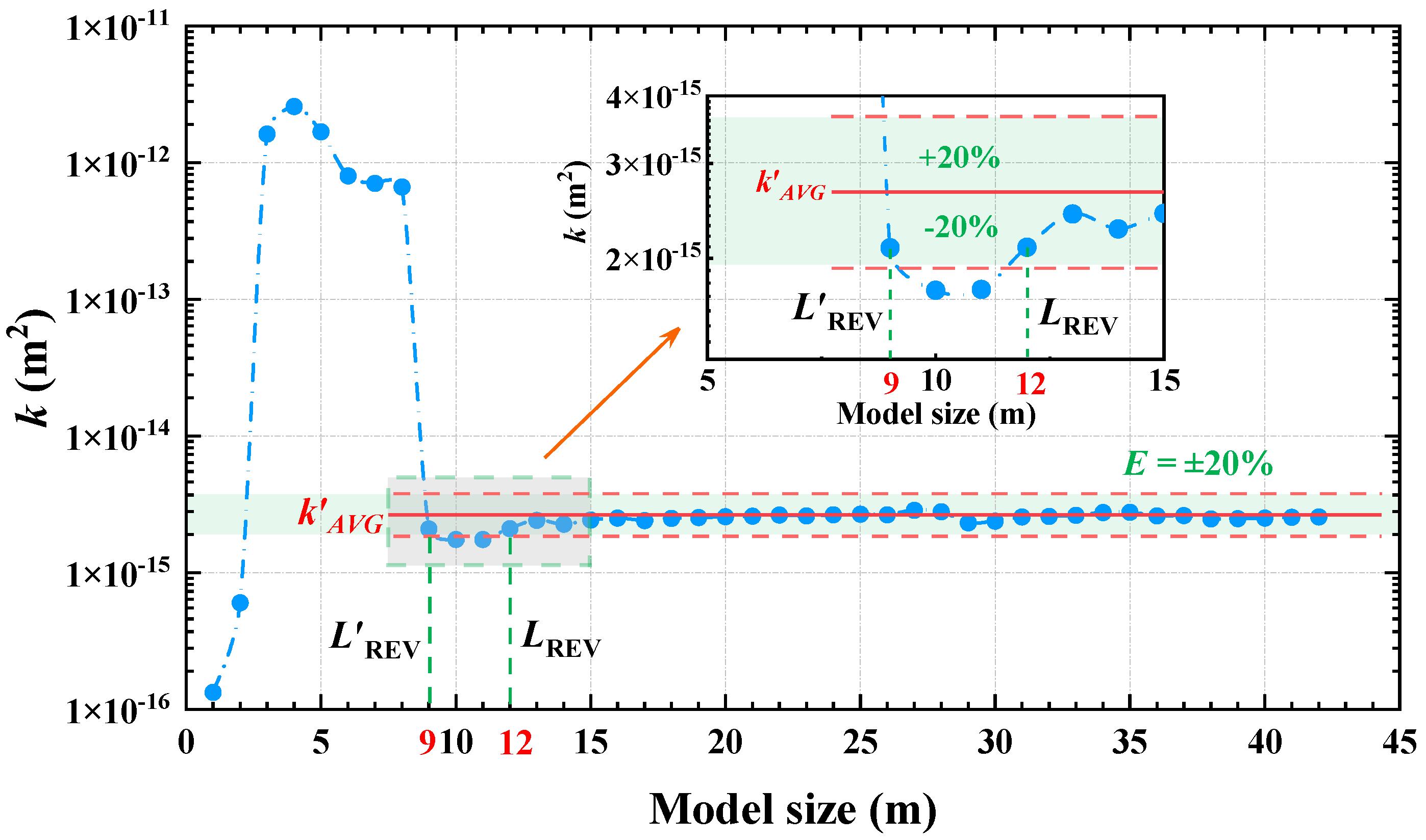
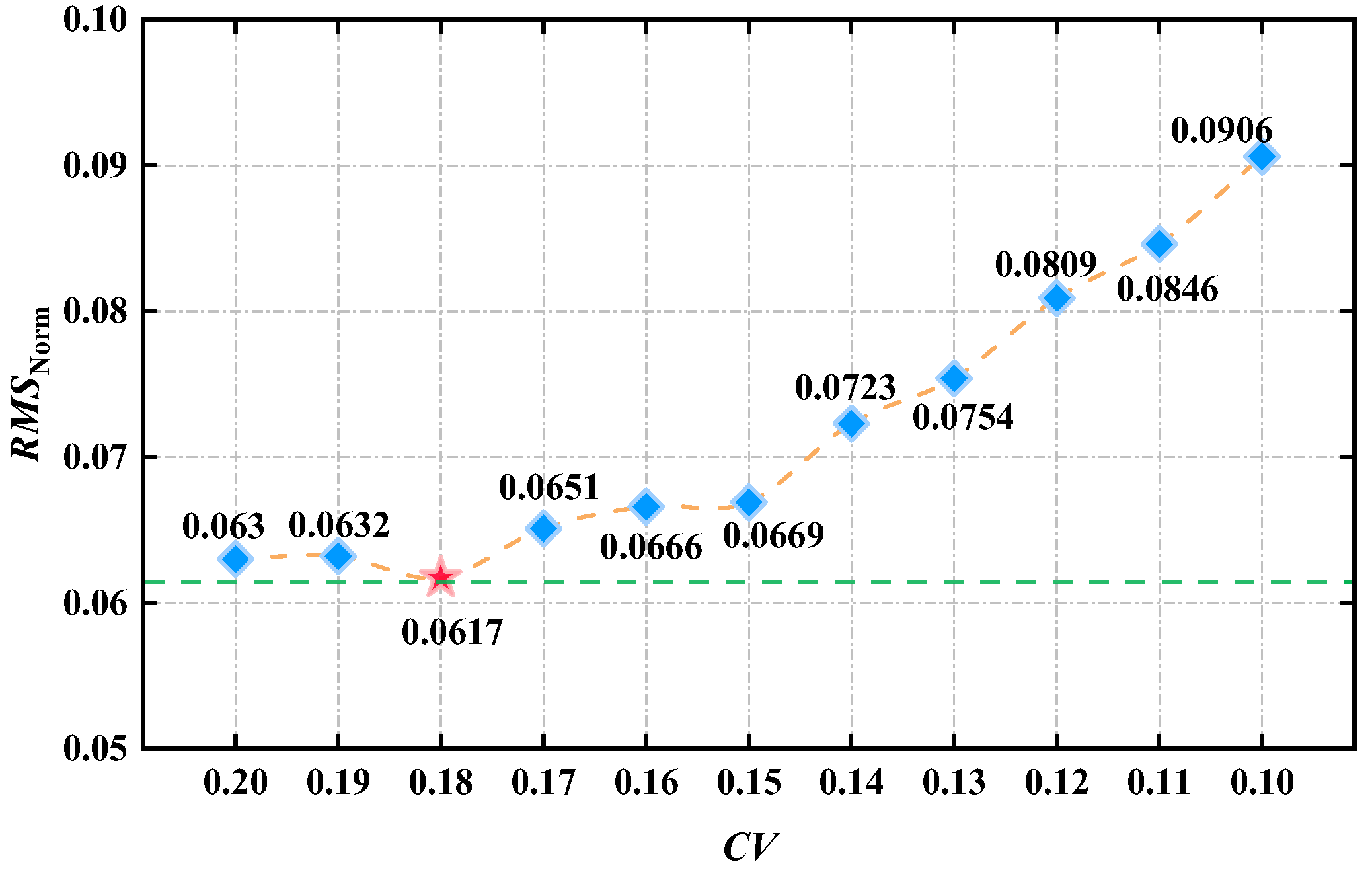
5.1. Estimation of the REV Size Based on Permeability
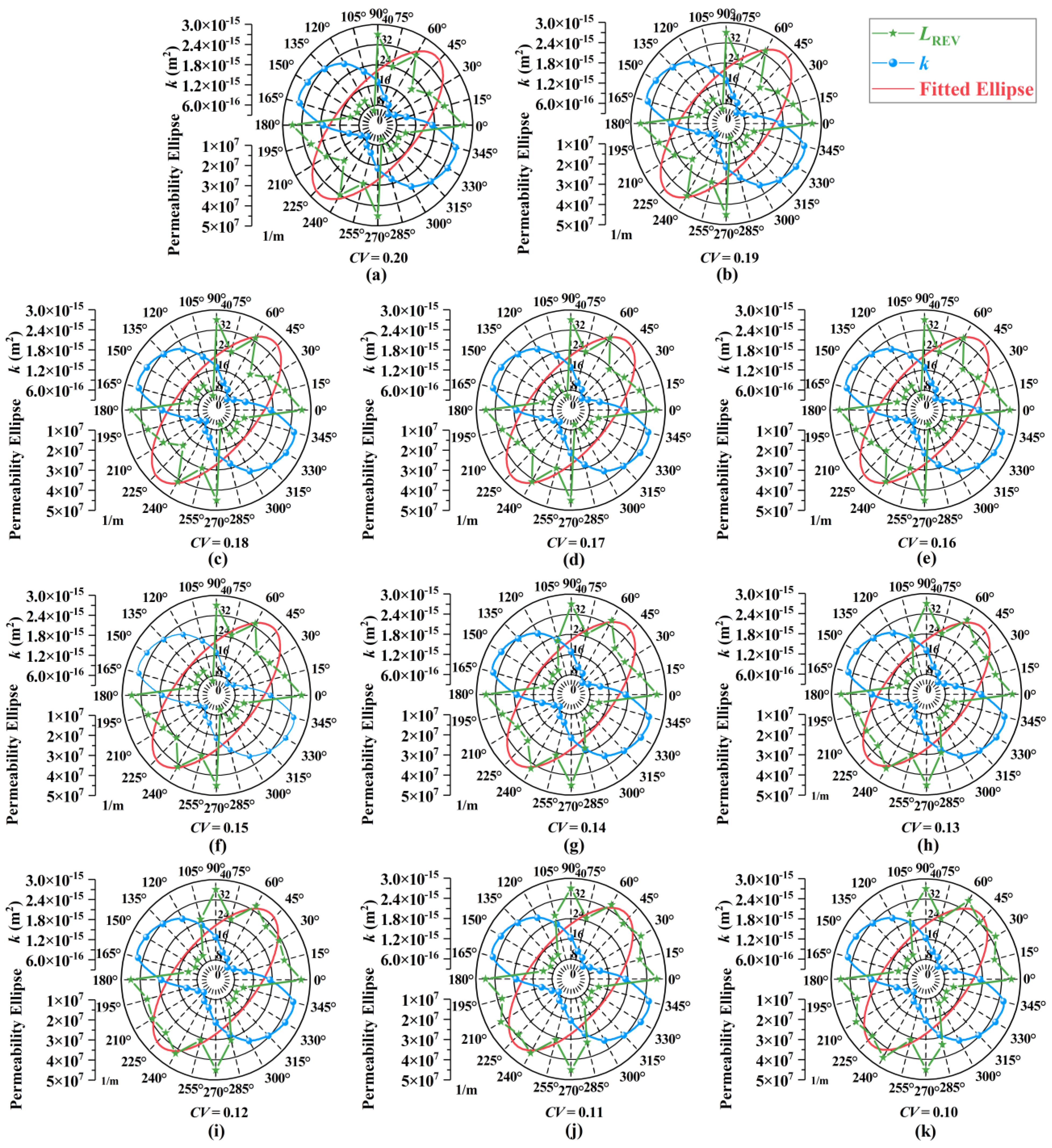
5.2. Estimation of the REV Size Based on the Anisotropy Index
6. Discussion
6.1. Influence of the Joint Geometry on the Permeability and REV Size
6.2. Comparison Between the Geometric and Hydraulic REV Sizes
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Min, K.-B.; Jing, L.; Stephansson, O. Determining the Equivalent Permeability Tensor for Fractured Rock Masses Using a Stochastic REV Approach: Method and Application to the Field Data from Sellafield, UK. Hydrogeol. J. 2004, 12, 497–510. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Hydraulic Properties of Fractured Rock Masses with Correlated Fracture Length and Aperture. Int. J. Rock Mech. Min. Sci. 2007, 44, 704–719. [Google Scholar] [CrossRef]
- Cui, Z.; Zhang, Y.; Sheng, Q.; Cui, L. Investigating the Scale Effect of Rock Mass in the Yangfanggou Hydropower Plant with the Discrete Fracture Network Engineering Approach. Int. J. Geomech. 2020, 20, 04020033. [Google Scholar] [CrossRef]
- Luo, L.; Liang, X.; Ma, B.; Zhou, H. A Karst Networks Generation Model Based on the Anisotropic Fast Marching Algorithm. J. Hydrol. 2021, 600, 126507. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, J.; Liu, R.; Li, S.; Liu, D.; Wang, X. Estimation of the Representative Elementary Volume of Three-Dimensional Fracture Networks Based on Permeability and Trace Map Analysis: A Case Study. Eng. Geol. 2022, 309, 106848. [Google Scholar] [CrossRef]
- Rong, G.; Peng, J.; Wang, X.; Liu, G.; Hou, D. Permeability Tensor and Representative Elementary Volume of Fractured Rock Masses. Hydrogeol. J. 2013, 21, 1655–1671. [Google Scholar] [CrossRef]
- Liu, R.; Zhu, T.; Jiang, Y.; Li, B.; Yu, L.; Du, Y.; Wang, Y. A Predictive Model Correlating Permeability to Two-Dimensional Fracture Network Parameters. Bull. Eng. Geol. Environ. 2019, 78, 1589–1605. [Google Scholar] [CrossRef]
- Oda, M. A Method for Evaluating the Effect of Crack Geometry on the Mechanical Behavior of Cracked Rock Masses. Mech. Mater. 1983, 2, 163–171. [Google Scholar] [CrossRef]
- Park, B.; Min, K.-B. Bonded-Particle Discrete Element Modeling of Mechanical Behavior of Transversely Isotropic Rock. Int. J. Rock Mech. Min. Sci. 2015, 76, 243–255. [Google Scholar] [CrossRef]
- Wu, Q.; Jiang, Y.; Tang, H.; Luo, H.; Wang, X.; Kang, J.; Zhang, S.; Yi, X.; Fan, L. Experimental and Numerical Studies on the Evolution of Shear Behaviour and Damage of Natural Discontinuities at the Interface Between Different Rock Types. Rock Mech. Rock Eng. 2020, 53, 3721–3744. [Google Scholar] [CrossRef]
- Wu, Q.; Kulatilake, P.H.S.W. REV and Its Properties on Fracture System and Mechanical Properties, and an Orthotropic Constitutive Model for a Jointed Rock Mass in a Dam Site in China. Comput. Geotech. 2012, 43, 124–142. [Google Scholar] [CrossRef]
- Khani, A.; Baghbanan, A.; Hashemolhosseini, H. Numerical Investigation of the Effect of Fracture Intensity on Deformability and REV of Fractured Rock Masses. Int. J. Rock Mech. Min. Sci. 2013, 63, 104–112. [Google Scholar] [CrossRef]
- He, J.; Chen, S.; Shahrour, I. Numerical Estimation and Prediction of Stress-Dependent Permeability Tensor for Fractured Rock Masses. Int. J. Rock Mech. Min. Sci. 2013, 59, 70–79. [Google Scholar] [CrossRef]
- Li, Z.-W.; Feng, X.-T.; Zhang, Y.-J.; Xu, T.-F. Effect of Hydrological Spatial Variability on the Heat Production Performance of a Naturally Fractured Geothermal Reservoir. Environ. Earth Sci. 2018, 77, 496. [Google Scholar] [CrossRef]
- Mahboubi Niazmandi, M.; Binesh, S.M. A DFN–DEM Approach to Study the Influence of Confinement on the REV Size of Fractured Rock Masses. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 587–601. [Google Scholar] [CrossRef]
- Long, J.C.S.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous Media Equivalents for Networks of Discontinuous Fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Oda, M. A Method for Evaluating the Representative Elementary Volume Based on Joint Survey of Rock Masses. Can. Geotech. J. 1988, 25, 440–447. [Google Scholar] [CrossRef]
- Esmaieli, K.; Hadjigeorgiou, J.; Grenon, M. Estimating Geometrical and Mechanical REV Based on Synthetic Rock Mass Models at Brunswick Mine. Int. J. Rock Mech. Min. Sci. 2010, 47, 915–926. [Google Scholar] [CrossRef]
- Wei, L.; Hudson, J.A. A Coupled Discrete-Continuum Approach for Modelling of Water Flow in Jointed Rocks. Géotechnique 1993, 43, 21–36. [Google Scholar] [CrossRef]
- Gutierrez, M.; Youn, D.-J. Effects of Fracture Distribution and Length Scale on the Equivalent Continuum Elastic Compliance of Fractured Rock Masses. J. Rock Mech. Geotech. Eng. 2015, 7, 626–637. [Google Scholar] [CrossRef]
- Ni, P.; Wang, S.; Wang, C.; Zhang, S. Estimation of REV Size for Fractured Rock Mass Based on Damage Coefficient. Rock Mech. Rock Eng. 2017, 50, 555–570. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Shang, Y. Determination of the Geometrical REV Based on Fracture Connectivity: A Case Study of an Underground Excavation at the Songta Dam Site, China. Bull. Eng. Geol. Environ. 2018, 77, 1599–1606. [Google Scholar] [CrossRef]
- Schultz, R.A. Relative Scale and the Strength and Deformability of Rock Masses. J. Struct. Geol. 1996, 18, 1139–1149. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, W. Analysis of Joint Network Simulation Method and REV Scale. Rock Soil. Mech. 2008, 29, 1675–1680. [Google Scholar]
- Min, K.-B.; Jing, L. Numerical Determination of the Equivalent Elastic Compliance Tensor for Fractured Rock Masses Using the Distinct Element Method. Int. J. Rock Mech. Min. Sci. 2003, 40, 795–816. [Google Scholar] [CrossRef]
- Huang, H.; Shen, J.; Chen, Q.; Karakus, M. Estimation of REV for Fractured Rock Masses Based on Geological Strength Index. Int. J. Rock Mech. Min. Sci. 2020, 126, 104179. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Chen, J.; Zhang, Z.; Li, K.; Han, X. Scale Dependency and Anisotropy of Mechanical Properties of Jointed Rock Masses: Insights from a Numerical Study. Bull. Eng. Geol. Environ. 2023, 82, 114. [Google Scholar] [CrossRef]
- Wang, P.; Ren, F.; Miao, S.; Cai, M.; Yang, T. Evaluation of the Anisotropy and Directionality of a Jointed Rock Mass under Numerical Direct Shear Tests. Eng. Geol. 2017, 225, 29–41. [Google Scholar] [CrossRef]
- Bang, S.-H.; Jeon, S.-W.; Kwon, S.-K. Modeling the Hydraulic Characteristics of a Fractured Rock Mass with Correlated Fracture Length and Aperture: Application in the Underground Research Tunnel at Kaeri. Nucl. Eng. Technol. 2012, 44, 639–652. [Google Scholar] [CrossRef]
- Wang, Z.; Li, W.; Qiao, L.; Liu, J.; Yang, J. Hydraulic Properties of Fractured Rock Mass with Correlated Fracture Length and Aperture in Both Radial and Unidirectional Flow Configurations. Comput. Geotech. 2018, 104, 167–184. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q.; Chen, J.; Han, L.; Song, S. Identification of Structural Domain Boundaries at the Songta Dam Site Based on Nonparametric Tests. Int. J. Rock Mech. Min. Sci. 2014, 70, 177–184. [Google Scholar] [CrossRef]
- Mauldon, M.; Dunne, W.M.; Rohrbaugh, M.B. Circular Scanlines and Circular Windows: New Tools for Characterizing the Geometry of Fracture Traces. J. Struct. Geol. 2001, 23, 247–258. [Google Scholar] [CrossRef]
- Wu, Q.; Kulatilake, P.H.S.W.; Tang, H. Comparison of Rock Discontinuity Mean Trace Length and Density Estimation Methods Using Discontinuity Data from an Outcrop in Wenchuan Area, China. Comput. Geotech. 2011, 38, 258–268. [Google Scholar] [CrossRef]
- Han, X.; Chen, J.; Wang, Q.; Li, Y.; Zhang, W.; Yu, T. A 3D Fracture Network Model for the Undisturbed Rock Mass at the Songta Dam Site Based on Small Samples. Rock Mech. Rock Eng. 2016, 49, 611–619. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, Y.; Li, X.; Wang, X.; Ma, F.; Zhao, J.; Zhang, Y. Extraction and Statistics of Discontinuity Orientation and Trace Length from Typical Fractured Rock Mass: A Case Study of the Xinchang Underground Research Laboratory Site, China. Eng. Geol. 2020, 269, 105553. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Shang, Y. Connectivity of Three-Dimensional Fracture Networks: A Case Study from a Dam Site in Southwest China. Rock Mech. Rock Eng. 2017, 50, 241–249. [Google Scholar] [CrossRef]
- Hammah, R.E.; Curran, J.H. On Distance Measures for the Fuzzy K-Means Algorithm for Joint Data. Rock Mech. Rock Eng. 1999, 32, 1–27. [Google Scholar] [CrossRef]
- Qiu, J.; Zhou, C.; Wang, Z.; Feng, F. Dynamic Responses and Failure Behavior of Jointed Rock Masses Considering Pre-Existing Joints Using a Hybrid BPM-DFN Approach. Comput. Geotech. 2023, 155, 105237. [Google Scholar] [CrossRef]
- Zhou, C.; Xie, H.; Zhu, J. Revealing Size Effect and Associated Variability of Rocks Based on BPM–μDFN Modelling: Significance of Internal Microstructure and Strain Rate. Rock Mech. Rock Eng. 2024, 57, 2983–2996. [Google Scholar] [CrossRef]
- Warburton, P.M. A Stereological Interpretation of Joint Trace Data. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1980, 17, 181–190. [Google Scholar] [CrossRef]
- Oda, M. Fabric Tensor for Discontinuous Geological Materials. Soils Found. 1982, 22, 96–108. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Wathugala, D.N.; Stephansson, O. Stochastic Three Dimensional Joint Size, Intensity and System Modelling and a Validation to an Area in Stripa Mine, Sweden. Soils Found. 1993, 33, 55–70. [Google Scholar] [CrossRef]
- Snow, D.T. Anisotropic Permeability of Fractured Media. Water Resour. Res. 1969, 5, 1273–1289. [Google Scholar] [CrossRef]
- Öhman, J.; Niemi, A. Upscaling of Fracture Hydraulics by Means of an Oriented Correlated Stochastic Continuum Model. Water Resour. Res. 2003, 39, 1277. [Google Scholar] [CrossRef]
- Wang, Z.; Rutqvist, J.; Zuo, J.; Dai, Y. A Modified Equivalent Permeability Model of Fracture Element and its Verification. Chin. J. Rock Mech. Eng. 2013, 32, 728–733. [Google Scholar]
- Einstein, H.H.; Locsin, J.-L.Z. Modeling Rock Fracture Intersections and Application to the Boston Area. J. Geotech. Geoenviron. Eng. 2012, 138, 1415–1421. [Google Scholar] [CrossRef]
- Lang, P.S.; Paluszny, A.; Zimmerman, R.W. Permeability Tensor of Three-dimensional Fractured Porous Rock and a Comparison to Trace Map Predictions. J. Geophys. Res. Solid Earth 2014, 119, 6288–6307. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.; Liu, R.; Li, B. Estimation of Permeability of 3-D Discrete Fracture Networks: An Alternative Possibility Based on Trace Map Analysis. Eng. Geol. 2017, 226, 12–19. [Google Scholar] [CrossRef]
- Zhu, W.; Khirevich, S.; Patzek, T.W. Impact of Fracture Geometry and Topology on the Connectivity and Flow Properties of Stochastic Fracture Networks. Water Resour. Res. 2021, 57, e2020WR028652. [Google Scholar] [CrossRef]






| Joint Set | Joint Number | Dip Direction (°) | Dip (°) | Fisher Constant | Spherical Std. (°) | Measured Trace Length | Joint Density (m−3) | ||
|---|---|---|---|---|---|---|---|---|---|
| Mean (m) | Std. (m) | Distribution | |||||||
| 1 | 19 | 265.0 | 82.2 | 10.87 | 14.43 | 1.48 | 0.57 | Log-normal | 0.030 |
| 2 | 35 | 100.6 | 11.8 | 28.40 | 8.75 | 2.19 | 1.57 | Gamma | 0.160 |
| 3 | 74 | 113.3 | 48.3 | 17.11 | 10.01 | 1.35 | 0.79 | Log-normal | 0.062 |
| Joint Set | Joint Number | Dip Direction (°) | Dip (°) | Spherical Std. (°) | Measured Trace Length | ||
|---|---|---|---|---|---|---|---|
| Mean (m) | Std. (m) | ||||||
| 1 | Field | 19 | 265.0 | 82.2 | 14.43 | 1.48 | 0.57 |
| Generated | 20 | 272.5 | 79.0 | 13.08 | 1.26 | 0.51 | |
| 2 | Field | 35 | 100.6 | 11.8 | 8.75 | 2.19 | 1.57 |
| Generated | 34 | 89.8 | 8.0 | 9.88 | 2.47 | 1.76 | |
| 3 | Field | 74 | 113.3 | 48.3 | 10.01 | 1.35 | 0.79 |
| Generated | 73 | 112.1 | 45.3 | 9.85 | 1.65 | 0.75 | |
| Fracture Model | Outlet Flow (m3/s) | Relative Difference | ||||
|---|---|---|---|---|---|---|
| Solution of Wang et al. [46] | Solution of This Work | Theoretical Solution | Wang et al. [46] | Theoretical Solution | ||
| Single-fracture model | α = 50° | 0.0811 | 0.0777 | 0.0793 | 4.19% | 2.02% |
| α = 55° | 0.0868 | 0.0831 | 0.0848 | 4.26% | 2.00% | |
| α = 60° | 0.0919 | 0.0879 | 0.0896 | 4.35% | 1.90% | |
| α = 65° | 0.0964 | 0.0920 | 0.0938 | 4.56% | 1.92% | |
| α = 70° | 0.1000 | 0.0954 | 0.0972 | 4.60% | 1.85% | |
| α = 75° | 0.0984 | 0.0980 | 0.0999 | 0.41% | 1.90% | |
| α = 80° | 0.1002 | 0.0999 | 0.1019 | 0.30% | 1.96% | |
| α = 85° | 0.1011 | 0.1011 | 0.1031 | 0.00% | 1.94% | |
| α = 90° | 0.1040 | 0.1015 | 0.1035 | 2.40% | 1.93% | |
| Double-fracture model | 0.1424 | 0.1399 | 0.1424 | 1.78% | 1.78% | |
| CV | L′REV (m) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ = 0° | θ = 15° | θ = 30° | θ = 45° | θ = 60° | θ = 75° | θ = 90° | θ = 105° | θ = 120° | θ = 135° | θ = 150° | θ = 165° | |
| 0.20 | 34 | 25 | 21 | 15 | 29 | 18 | 17 | 2 | 9 | 11 | 10 | 9 |
| 0.19 | 35 | 25 | 21 | 17 | 30 | 19 | 18 | 3 | 9 | 11 | 10 | 9 |
| 0.18 | 35 | 26 | 23 | 17 | 30 | 20 | 18 | 3 | 9 | 11 | 10 | 9 |
| 0.17 | 35 | 26 | 24 | 19 | 31 | 20 | 19 | 4 | 9 | 11 | 10 | 9 |
| 0.16 | 36 | 27 | 24 | 21 | 32 | 20 | 19 | 4 | 9 | 11 | 10 | 9 |
| 0.15 | 36 | 27 | 25 | 23 | 32 | 21 | 20 | 5 | 10 | 11 | 10 | 9 |
| 0.14 | 36 | 28 | 26 | 26 | 33 | 22 | 20 | 22 | 10 | 11 | 10 | 9 |
| 0.13 | 36 | 29 | 29 | 29 | 33 | 22 | 34 | 24 | 10 | 11 | 10 | 9 |
| 0.12 | 36 | 29 | 31 | 30 | 34 | 23 | 35 | 25 | 10 | 11 | 10 | 9 |
| 0.11 | 36 | 30 | 34 | 31 | 34 | 24 | 36 | 26 | 10 | 11 | 10 | 9 |
| 0.10 | 36 | 30 | 34 | 32 | 36 | 24 | 36 | 27 | 10 | 11 | 10 | 9 |
| CV | LREV (m) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ = 0° | θ = 15° | θ = 30° | θ = 45° | θ = 60° | θ = 75° | θ = 90° | θ = 105° | θ = 120° | θ = 135° | θ = 150° | θ = 165° | |
| 0.20 | 36 | 29 | 25 | 20 | 32 | 24 | 36 | 6 | 11 | 11 | 10 | 12 |
| 0.19 | 36 | 29 | 25 | 20 | 33 | 24 | 36 | 6 | 11 | 11 | 10 | 12 |
| 0.18 | 36 | 30 | 26 | 20 | 33 | 24 | 36 | 6 | 11 | 11 | 10 | 12 |
| 0.17 | 36 | 30 | 26 | 23 | 33 | 24 | 36 | 6 | 11 | 11 | 10 | 12 |
| 0.16 | 36 | 30 | 26 | 23 | 33 | 24 | 36 | 6 | 11 | 11 | 10 | 12 |
| 0.15 | 36 | 30 | 26 | 24 | 33 | 25 | 36 | 6 | 11 | 11 | 10 | 12 |
| 0.14 | 36 | 30 | 26 | 26 | 34 | 25 | 36 | 22 | 11 | 11 | 10 | 12 |
| 0.13 | 36 | 30 | 29 | 29 | 34 | 25 | 36 | 24 | 11 | 11 | 10 | 12 |
| 0.12 | 36 | 30 | 31 | 30 | 34 | 25 | 36 | 25 | 11 | 11 | 10 | 12 |
| 0.11 | 36 | 30 | 34 | 31 | 34 | 25 | 36 | 26 | 11 | 11 | 10 | 12 |
| 0.10 | 36 | 30 | 34 | 32 | 36 | 25 | 36 | 27 | 11 | 11 | 10 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, H.; Li, Y. A Study of the Scale Dependency and Anisotropy of the Permeability of Fractured Rock Masses. Water 2025, 17, 697. https://doi.org/10.3390/w17050697
Qian H, Li Y. A Study of the Scale Dependency and Anisotropy of the Permeability of Fractured Rock Masses. Water. 2025; 17(5):697. https://doi.org/10.3390/w17050697
Chicago/Turabian StyleQian, Honglue, and Yanyan Li. 2025. "A Study of the Scale Dependency and Anisotropy of the Permeability of Fractured Rock Masses" Water 17, no. 5: 697. https://doi.org/10.3390/w17050697
APA StyleQian, H., & Li, Y. (2025). A Study of the Scale Dependency and Anisotropy of the Permeability of Fractured Rock Masses. Water, 17(5), 697. https://doi.org/10.3390/w17050697







