Research on the Spatiotemporal Evolution Patterns of Landslide-Induced Surge Waves Based on Physical Model Experiments

Abstract

The impact generated by landslide-induced surge waves in large reservoirs poses significant threats to the safety of coastal residents and their property. It is essential to further elucidate the characteristics of these surge waves and enhance the capabilities of surge wave prediction and emergency warning systems. This research takes the Wangjiashan landslide in the Baihetan Hydropower Station reservoir area as a prototype, constructing a three-dimensional landslide model at a 1:150 scale. Through experiments designed under varying water levels and slope friction coefficients, the spatiotemporal evolution patterns of the landslide-induced surge waves along the riverbank were analyzed. The research results indicate that through the use of the zero-crossing method, fundamental characteristics of landslide-induced surge waves such as the maximum wave height, maximum period, significant wave height, and significant wave period could be obtained. Based on the statistical analysis of significant wave heights, the surge waves were categorized into three levels—small waves, moderate waves, and large waves—accounting for 15.79%, 78.95%, and 5.26% of the total waves, respectively. The height of surge waves decreases with an increase in the slope friction coefficient and river channel water depth. Additionally, the interaction between the landslide’s entry velocity into the water and the water level determines the effectiveness of wave propagation. This research provides crucial data support and theoretical foundations for the prediction and emergency warning of landslide-induced surge waves, offering significant implications for the prevention and mitigation of reservoir and landslide disasters.

1. Introduction

The complex hydrogeological and physical environment in Southwest China, coupled with intensive engineering activities, has made the prevention and control of landslide geological disasters a critical research focus in ensuring the safety of high dams and large reservoirs, as well as in disaster prevention and mitigation [1]. Landslide-induced surge waves in reservoirs represent a highly destructive secondary hazard. Following the instability of reservoir slopes and their high-speed entry into water, landslide masses can block river channels. The generated surge waves propagate, overlap, and climb along reservoir banks, posing threats to navigating vessels and dam structures. Large surge waves, in particular, carry the risk of overtopping and dam breach floods, posing severe threats to downstream communities [2].

The complete process of landslide-induced surge waves includes wave generation, propagation, climbing, and submersion. Among these, wave generation (from the landslide’s impact with the water to when the landslide mass comes to rest) is the most critical phase. It represents the endpoint of landslide energy transfer and the starting point of wave propagation, directly influencing the intensity and hazard potential of surge waves [3]. Numerous researchers have utilized physical experiments, including 2D simplified landslide surge wave flume experiments, 3D simplified surge wave experiments, and 3D prototype-scaled model tests, to investigate the characteristics of landslide-induced surge waves [4,5,6]. A comprehensive landslide surge wave experimental system typically includes a water body model, a landslide mass model, and a monitoring system. The primary objectives of these experiments are as follows: (1) To identify the key parameters influencing the generation and propagation characteristics of landslide-induced surge waves and propose empirical formulas for describing wave characteristics (e.g., maximum wave height, wave climbing, and propagation) based on experimental data [7]. (2) To validate the effectiveness and accuracy of various empirical and theoretical formulas [8]. (3) To adjust and optimize numerical model parameters based on experimental data and validate their effectiveness [9].

The wave characteristics of landslide-induced surge waves depend on landslide motion parameters, geometric parameters, and water body characteristics [10]. However, due to the limitations of physical experiments, not all influencing factors can be comprehensively considered. Thus, most physical model experiments of landslide-induced surge waves involve varying degrees of simplification [11]. For instance, many experiments assume a constant still water depth, neglecting the impact of underwater topography on wave characteristics. Simplified physical model experiments also abstract landslide mass and water body models into regular shapes or singular conditions. Landslide mass models are generally simplified into block models, granular models, or other forms. Previous studies have often treated landslides as rigid blocks with simple structures, while granular models account for internal deformation during water entry [12]. Other models include high-speed fluid-like landslides and viscous landslide masses. However, these simplifications may result in discrepancies between experimental conditions and real-world scenarios. Comparative studies show that granular and finite-deformation landslide masses generate surge waves that are approximately 65% and 84%, respectively, of those generated by rigid bodies under the same conditions [13]. Considering the potential block-sliding mechanism of the Wangjiashan landslide, this study adopts block-type physical model experiments to investigate its sliding mechanism and surge wave characteristics.

Current research on landslide-induced surge waves primarily focuses on the initial wave height, establishing correlations between propagated and climbing waves and maximum wave height to predict wave propagation range and hazard magnitude [14,15]. However, wave trains with the same initial wave height may carry vastly different energy levels. Using the mean period as the wave period does not necessarily capture the maximum wave effects on structures, as waves with periods larger or smaller than the mean period may induce greater impacts on structures [16]. Yi et al. [17] conducted experiments by simplifying landslide shapes, considering factors such as relative width and relative length, and performed tests using rigid blocks and granular masses, deriving empirical formulas for landslide-induced surge waves. Miller et al. [18] found through large-scale flume experiments that compared to landslide volume, the magnitude of surge waves is more dependent on water depth. However, the surge wave characteristics of block-sliding landslide models remain underexplored, with a lack of in-depth targeted studies.

To address these gaps, this study investigates the characteristics of surge waves triggered by different landslide velocities and water levels based on block-type physical model experiments of the Wangjiashan landslide in the Baihetan reservoir. With the use of a 1:150-scaled 3D rock landslide model, nine groups of experiments were conducted under varying water levels and slope friction coefficients. Surge wave characteristics were analyzed using wave characteristic methods, defining the wave height and period as key descriptive parameters and extracting these parameters using the zero-crossing method to research the spatiotemporal distribution of landslide-induced surge waves along the riverbank. Effective wave heights were extracted and categorized into three levels: small, moderate, and large waves. The Wangjiashan landslide area was divided into corresponding wave zones based on wave levels. Representative points (10 for small waves, 8 for moderate waves, and 9 for large waves) were selected for analyzing surge wave characteristics under different water depths and slope friction coefficients. This research enhances the understanding of the spatiotemporal evolution patterns of real-world landslide-induced surge waves, providing critical data and theoretical support for disaster prediction and the mitigation of landslide-induced surge waves.

2. The Experimental Design of the Physical Model

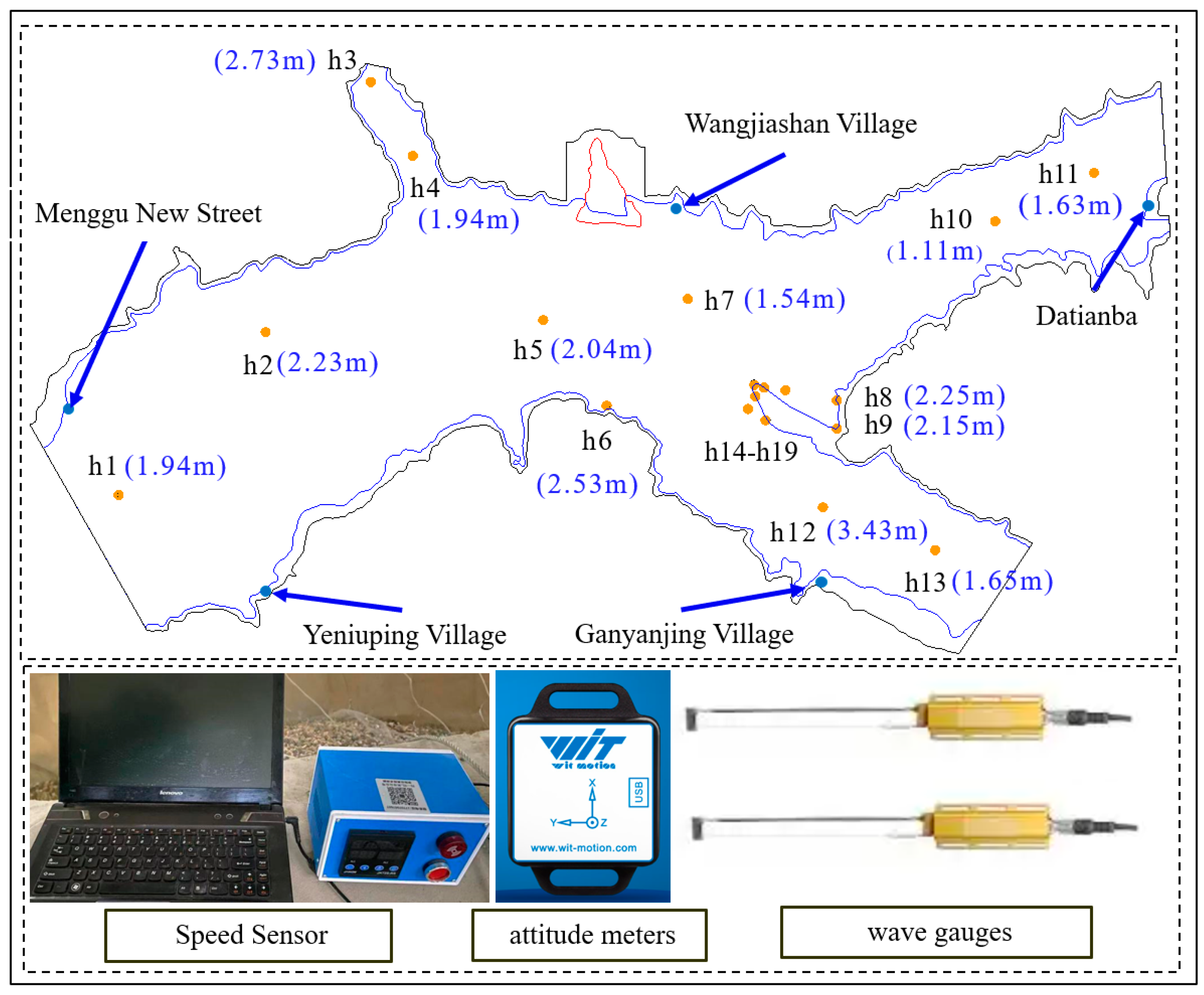
The landslide model features an approximately triangular plan shape, with a downslope length of 5.3 m, a width ranging from 0.6 to 3.33 m, a post-landslide crest elevation of approximately 7.5 m, and slopes between 35° and 45°. The centerline of the river channel is 60 m. Based on the fissure structure and degree of development of the rocky landslide mass, the rigid-block rock landslide model used in the experiments was constructed by assembling plastic cylinders with diameters of 16 cm and heights of 30 cm and 60 cm, filled with natural gravel to simulate rigid-block combinations. The physical model of the experiment is shown in Figure 1. The symbol wjs represents Wangjiashan.

As shown in Figure 2, the instrumentation for the experiments included high-definition cameras, wave gauges, attitude meters, landslide velocity meters, and flow meters. Thirteen camera lenses provided comprehensive coverage of the physical model’s flow field, facilitating image recording throughout the experimental process. The cameras possess a resolution of 48 megapixels with an accuracy of approximately 2 mm. Nineteen wave gauges were deployed to monitor water level variations at various points along the river channel, operating at a sampling frequency of 50 Hz and an accuracy of 0.1 mm. The layout of the measuring instruments is shown in Figure 2.

The model is based on the Wangjiashan landslide, located on the northern side of Wangjiashan in the Xiaojiang branch reservoir on the right bank of the Baihetan Hydropower Station reservoir area. According to Froude similarity theory, to ensure consistency between the experimental phenomena and those of the prototype, the model was designed based on geometric and kinematic similarity [19]. A scale of 1:150 was selected, considering factors such as the experimental site, instrumentation, and testing techniques. A large-scale physical model was constructed at the Key Laboratory of Geotechnical Mechanics and Dam Engineering, Ministry of Education, China University of Water Resources and Electric Power. The model dimensions are as follows: a total length of 65 m, a width of 40 m, and a river channel height ranging from 1.3 to 3 m. Control panels were installed on the landslide mass, as shown in Figure 1, to regulate the sliding time of the landslide, ensuring that the landslide fulfills various design requirements.

Based on the engineering geological data and monitoring information of the Wangjiashan landslide [20], when the water storage elevation reaches 800 m, the Wangjiashan landslide enters a stage of rapid accelerated deformation, ultimately stabilizing at an elevation of 825 m. To achieve the objectives of this research, nine experimental schemes, as listed in

Table 1. Physical experimental parameters of Wangjiashan landslide-induced surge waves.

Test ID	Landslide Volume/(m3)	Water Level (m)	Experimental Landslide Entry Velocity (m·s−1)	Actual Landslide Entry Velocity (m·s−1)	Landslide Surface Friction Coefficient (ƒ)
wjs1	1.23	825	0.63	7.72	0.4
wjs2	1.23	815	0.79	9.68	0.4
wjs3	1.23	800	0.85	10.41	0.4
wjs4	1.23	825	0.45	5.51	0.45
wjs5	1.23	815	0.65	7.96	0.45
wjs6	1.23	800	0.75	9.19	0.45
wjs7	1.23	825	0.41	5.02	0.5
wjs8	1.23	815	0.53	6.49	0.5
wjs9	1.23	800	0.58	7.10	0.5

, were designed. Different water levels were selected as variables for the analysis of landslide-induced surge waves, specifically actual water levels of 800 m, 815 m, and 825 m. Additionally, to analyze the effect of landslide-induced surge waves by altering the landslide friction, different substrate materials were employed, as illustrated in Figure 1. Green oil-based material with a friction coefficient of 0.45 is laid on the left slope, and transparent plastic material with a friction coefficient of 0.50 is laid on the right slope. The friction coefficient of the landslide surface is measured by the attitude meters sliding down different material bottoms on the same slope surface.

3. Analysis of Landslide-Induced Surge Waves

3.1. Analysis of Spatiotemporal Distribution Characteristics of Landslide-Induced Surge Waves

To analyze the surge wave characteristics in this study, the characteristic wave method from wave theory was employed, using the wave height and period as the primary parameters to describe wave characteristics. Landslide-induced surge waves are extremely complex, possessing nonlinear three-dimensional features and significant randomness, categorizing them as a type of random wave. Due to their irregular waveforms, the zero-crossing method [21] is typically used to extract wave heights and periods.

Based on the definition of characteristic waves, the maximum wave height, maximum period, effective wave height, and effective period of the initial surge wave were selected as the characteristic values. A statistical analysis of the wave height and period characteristics of the initial surge wave for wjs1 was conducted, with the results presented in

Table 2. Actual data of characteristic values of initial surge waves.

Wave Gauge Number	Volume (m3)	Initial Wave Height H (m)	Effective Wave Height (m)	Wave Period T (s)	Effective Period (s)	Initial Wave Length (m)	Wave Steepness H/L
1	1.23	1.94	1.65	32.82	30.94	145.06	0.01
2	1.23	2.23	1.74	32.82	30.94	145.06	0.02
3	1.23	2.73	2.01	32.60	31.53	144.09	0.02
4	1.23	1.94	1.65	30.47	28.56	134.68	0.01
5	1.23	2.04	1.47	33.42	30.15	147.72	0.02
6	1.23	2.53	1.91	30.60	34.53	135.25	0.02
7	1.23	1.54	0.81	37.48	32.49	165.66	0.01
8	1.23	2.25	2.25	30.88	30.29	136.49	0.02
9	1.23	2.15	2.62	29.76	34.59	131.54	0.02
10	1.23	1.11	1.04	31.11	33.70	137.51	0.01
11	1.23	1.63	1.62	37.96	33.48	167.78	0.01
12	1.23	3.43	1.90	22.78	23.68	100.69	0.03
13	1.23	1.65	1.04	20.03	25.05	88.53	0.02
14	1.23	1.92	1.44	39.68	31.12	175.39	0.01
15	1.23	2.93	2.10	27.67	21.55	122.30	0.02
16	1.23	2.64	1.73	25.24	21.23	111.56	0.02
17	1.23	1.99	1.42	38.45	32.74	169.95	0.01
18	1.23	2.27	1.87	26.7	28.66	118.01	0.02
19	1.23	1.46	1.68	24.98	28.33	110.41	0.01

.

• Maximum Wave Height and Maximum Period.

The maximum wave height and period of the initial surge wave are determined by identifying the highest wave height and period within the surge wave series generated by landslide-induced surge waves. The maximum wave height of the initial surge wave also corresponds to the maximum surge wave height of the first wave column at the landslide entry point, referred to as the initial wave height. As presented in Table 2, the maximum wave height measured in the rigid-block rock landslide-induced surge wave model experiments ranges from 7.40 × 10⁻³ to 22.86 × 10⁻³ m. Based on a model scale of 1:150, the prototype’s maximum initial wave height ranges from 1.11 to 3.43 m. The average wave height of the model is 14.31 × 10⁻³ m, corresponding to an average wave height of 2.15 m in the prototype. The maximum wave height measured at the monitoring point in the wjs1 experiment corresponds to the wave period of the prototype, which is 20.03 to 39.68 s.

• Effective Wave Height and Effective Period.

The effective wave height and effective period are determined by ranking the wave heights in the surge wave series from largest to smallest and calculating the average wave height and period of the top one-third of the waves [22]. According to the statistical results of the initial surge wave’s effective wave height and effective period presented in Table 2, the model’s effective wave height ranges from 5.40 × 10⁻³ to 17.47 × 10⁻³ m, and the calculated effective period ranges from 21.23 to 34.59 s. For the prototype, the calculated effective wave height ranges from 0.81 to 2.62 m.

The difference between the effective wave height and maximum wave height reflects the extremity of the waves and the potential impact on coastal areas. The effective wave height represents the average height of the larger waves within a wave group, while the maximum wave height denotes the height of the single highest wave. Together, these metrics describe the statistical characteristics and potential impacts of the waves [23]. As shown in

Table 3. Characteristic extreme values of initial surge waves.

Characteristic Extreme Value	Maximum Wave Height (m)	Effective Wave Height (m)	Period (s)	Effective Period (s)
Maximum value	3.43	2.62	39.68	34.59
Minimum value	1.11	0.81	20.03	21.23
Mean value	2.15	1.68	30.81	29.66

, the average values are 2.15 m for wave height and 30.81 s for period, representing the typical characteristics of the waves.

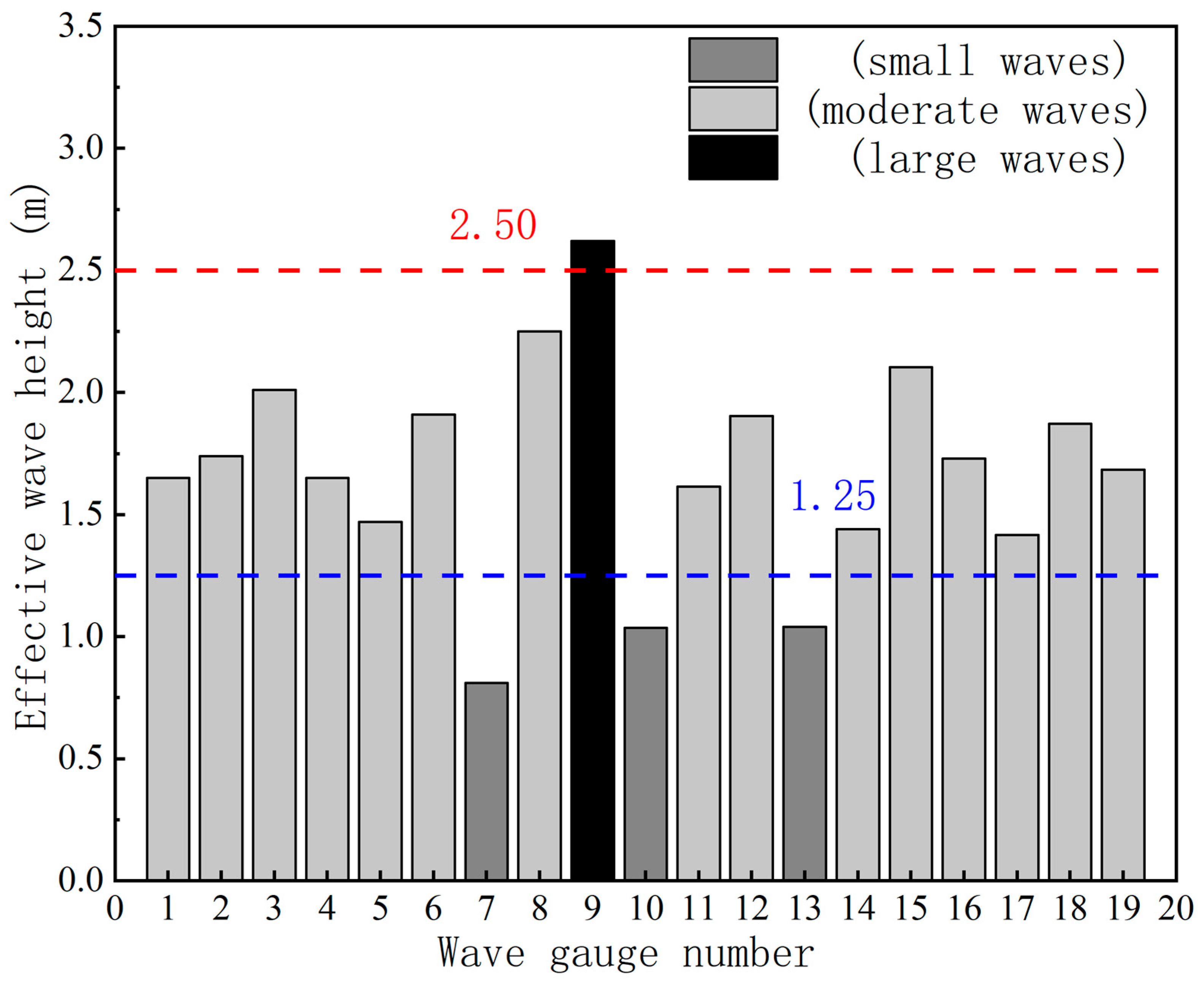
According to the International Wave Scale, waves are classified into ten levels based on effective wave height. However, considering practical application scenarios, this study categorizes waves into three levels for analysis: small waves (wave level ≤ 3; effective wave height < 1.25 m), moderate waves (wave level 4; 1.25 m ≤ effective wave height < 2.50 m), and large waves (wave level 5; 2.50 m ≤ effective wave height < 4.00 m). Figure 3 illustrates the wave classifications at various monitoring points in the wjs1 experiment based on the aforementioned criteria.

Based on wave classification, the Wangjiashan landslide area was divided into three categories: small waves, moderate waves, and large waves. Most of Ganyanjing Village and Datianba falls within the small-wave category, indicating relatively favorable conditions. Similarly, 74.83% of Yeniu Ping Village and Menggu New Street is classified as small-wave regions. In contrast, 87.50% of Xiangbinling’s area falls under moderate-wave conditions, necessitating special attention.

Wave steepness is defined as the ratio of wave height (H) to wave length (L) [24], with the critical wave steepness value being 0.142. The wave steepness calculations for the rigid-block rock landslide-induced surge wave experiments are summarized in Table 2. As shown in Table 2, the initial surge waves under various experimental conditions exhibit wave steepness values ranging from 0.01 to 0.03, all below the critical wave steepness value, indicating that once formed, the initial surge waves are unlikely to undergo breaking. Therefore, the surge caused by the Wangjiashan landslide will not experience wave breaking. But in real-world scenarios, steep waves tend to carry higher energy and can lead to increased erosion, structural damage, and flooding along shorelines and in reservoirs. The steepness of a wave can also influence the effectiveness of early warning systems, as it affects the wave’s speed and propagation distance. Future research should further investigate the relationship between wave steepness and the impact on built environments, particularly in areas with complex topographies and variable sediment structures. This would help refine hazard assessment models and improve disaster preparedness strategies in landslide-prone regions.

This analysis strengthens the credibility of the experimental outcomes, confirming that the observed trends in surge wave behavior reflect real physical phenomena rather than artifacts of the experimental conditions.

3.2. The Effect of Water Levels

Representative points were selected from each wave classification category—10 points for small waves, 8 points for moderate waves, and 9 points for large waves—to conduct detailed analyses. The height and propagation characteristics of the waves are influenced by multiple factors, with the water level and friction coefficient being critical variables affecting wave propagation. This research analyzes the experimental data and images from monitoring points 8, 9, and 10 to compare wave behaviors under different water levels and friction coefficients, focusing on their impacts on the maximum wave height and effective wave height. Through quantitative analysis and data comparison, the regulatory effects of the water level and friction coefficient on wave energy propagation and dissipation are elucidated.

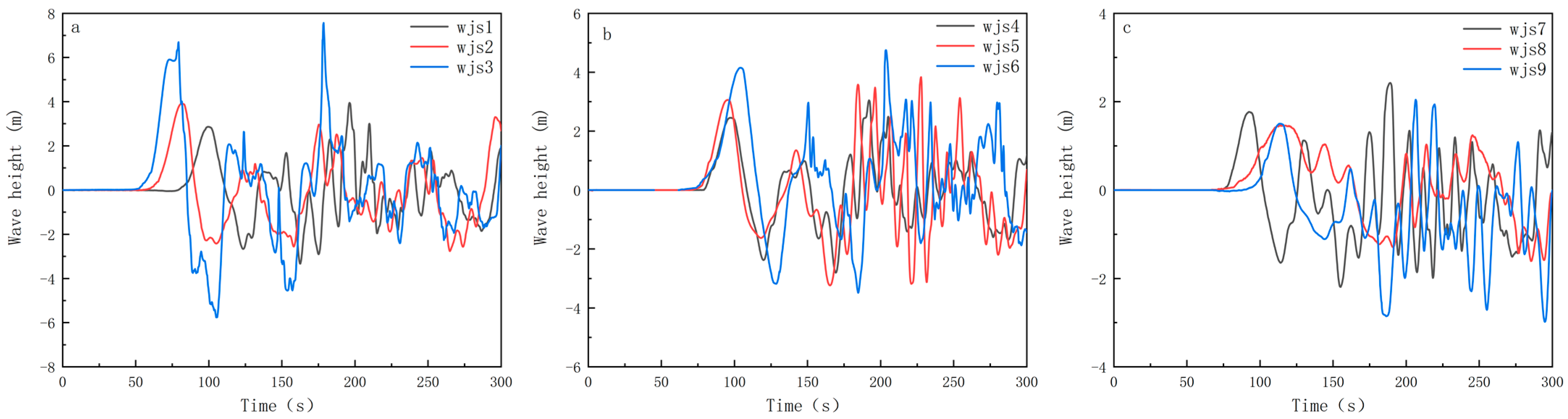
As illustrated in Figure 4, all monitoring points exhibit significant wave heights and larger amplitude fluctuations under a water level of 800 m. When the landslide mass is closer to the water surface, the kinetic energy generated upon water entry is more rapidly transferred to the water body, resulting in higher surge waves. The proximity of the landslide mass to the water surface enhances the efficiency of kinetic energy conversion, concentrating wave energy to a greater extent. Experimental data indicate that under an 800 m water level, surge wave heights at the monitoring points are notably significant under the same conditions, showing larger amplitudes in the initial stages and maintaining high energy states over longer periods. Specifically, monitoring point 8 demonstrates wave peaks significantly higher than those at points 9 and 10, consistent with the data showing higher wave heights and longer oscillation times.

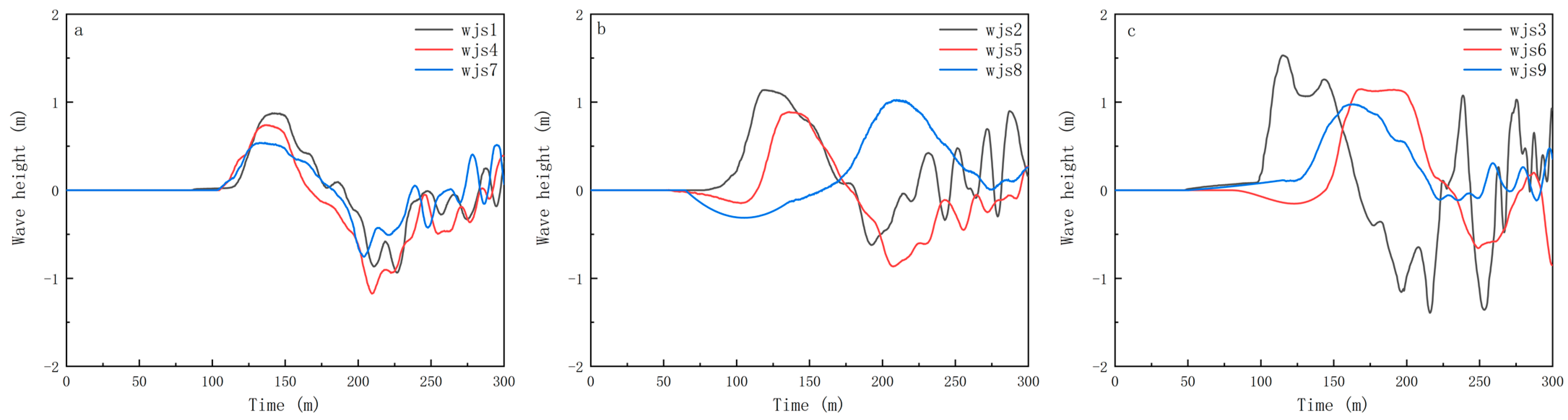
When the distance between the landslide mass and the water surface increases (e.g., at a water level of 825 m), the kinetic energy from the landslide’s water entry is rapidly converted into wave energy. Under these conditions, waves typically exhibit rapid initial excitation and a swift increase in wave height. However, due to the shorter propagation path, wave energy is concentrated and released quickly, resulting in relatively smaller wave heights that decay rapidly over time. For example, in Figure 5, wjs1, wjs4, and wjs7 show waves that quickly reach peak values and then rapidly attenuate, demonstrating the restrictive effect of high water levels on wave propagation paths.

Conversely, when the distance between the landslide mass and the water surface is larger (e.g., at an 800 m water level), wave energy gradually accumulates along the propagation path, forming higher surge wave heights. Although the initial kinetic energy conversion efficiency may be lower, the longer propagation path provides ample space for wave energy accumulation and sustained propagation. Experiments wjs3, wjs6, and wjs9 exhibit higher wave amplitudes and longer propagation durations under low-water-level conditions, indicating significant energy accumulation effects.

Differences among monitoring points reflect the influence of spatial distribution, topographical conditions, and surrounding water body characteristics on surge wave behavior. During wave propagation, factors such as topographical reflection and boundary effects can cause varying surge wave responses at different monitoring points. Overall, the three monitoring points demonstrate the significant regulatory effects of the water level and friction coefficient on wave behavior, revealing the complexity and multifactorial coupling of wave height variations.

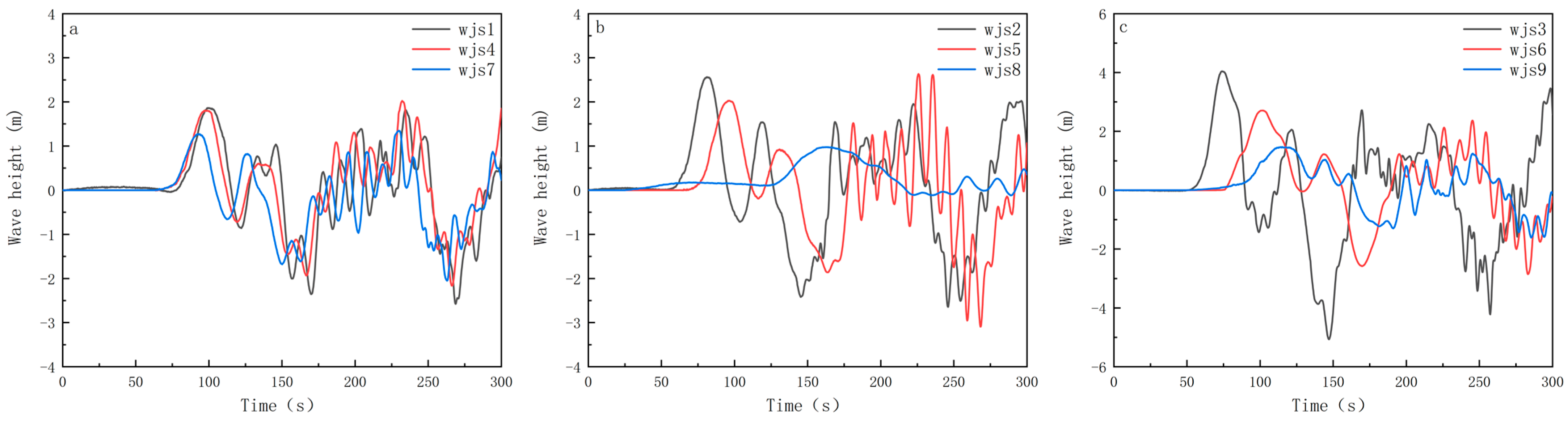
In a comparison of Figure 5 and Figure 6, effective wave heights are generally higher under lower water levels, as longer propagation paths facilitate continuous wave energy accumulation and propagation. Wave energy can accumulate and be maintained more effectively under lower-water-level conditions, resulting in higher effective wave heights. For example, in Figure 6a, wjs3 (800 m water level, friction coefficient of 0.40) exhibits a larger effective wave height, indicating that energy is maintained during propagation. Under higher-water-level conditions, effective wave heights are relatively lower, primarily due to rapid energy conversion and limited accumulation.

Shorter propagation paths cause faster energy release in the initial stages, leading to lower subsequent wave energy. For instance, in Figure 6a, although the initial wave amplitude in experiment wjs1 (825 m water level, friction coefficient of 0.40) is higher, the overall energy dissipates quickly, resulting in a lower effective wave height. This causes the effective wave height at monitoring point 8 in the wjs1 experiment to be lower than at point 9, whereas in the wjs3 experiment, monitoring point 8 has a higher effective wave height than point 9.

Specifically, the wave height increases significantly as the water level rises. For point 8, the wave height increased by 37.32% from wjs1 to wjs2, by 71.54% from wjs2 to wjs3, and by 135.21% from wjs1 to wjs3. For point 9, the wave height increased by 38.89% from wjs1 to wjs2, and by 60% from wjs2 to wjs3. The total increase from wjs1 to wjs3 was 122.22%, indicating a substantial growth in wave height with higher water levels. As the water level increases, the wave height exhibits a significant rise. For point 10, the wave height increased by 29.89% from wjs1 to wjs2, by 35.40% from wjs2 to wjs3, and by 75.86% from wjs1 to wjs3. These results highlight the significant impact of water level changes on wave height, with the change in wave height becoming more pronounced as the water level increases.

3.3. The Effect of the Landslide’s Entry Speed

The friction coefficient will affect the moving speed of an object. The surge generated by a landslide should be directly related to the landslide’s entry speed. Therefore, it is crucial to analyze the surge wave heights caused by different inflow velocities under different landslide slope friction coefficient conditions.

Quantitative analysis reveals that, as shown in Figure 7, under identical water level conditions, experiment wjs1 (friction coefficient: 0.40) has a significantly higher maximum wave height compared to wjs4 (friction coefficient: 0.45), with wjs1’s maximum wave height exceeding wjs4’s by 0.90 m, an increase of 29.5%. This indicates that the friction coefficient significantly affects wave energy dissipation and suppresses wave height. An increased friction coefficient introduces greater resistance during wave propagation, causing rapid energy dissipation and thereby inhibiting the formation of maximum wave heights. For instance, in experiment wjs7 (825 m water level, friction coefficient of 0.50), as shown in Figure 7, the maximum wave height is lower, indicating that high friction coefficients substantially suppress wave propagation capabilities.

The synergistic effect of a high water level and low friction coefficient is illustrated in Figure 8 (wjs1: 825 m water level, friction coefficient of 0.40), where a high water level facilitates rapid kinetic energy transfer, while a low friction coefficient reduces energy dissipation, resulting in higher initial wave amplitudes. However, the high water level restricts the propagation path, limiting wave energy accumulation and causing rapid attenuation over time.

The enhancing effect of a low water level and low friction coefficient is demonstrated in Figure 9 (wjs3: 800 m water level, friction coefficient of 0.40), where the greater distance between the landslide mass and the water surface allows wave energy to accumulate and propagate over a longer path. The low friction coefficient reduces energy dissipation, significantly increasing surge wave height and amplitude. The images show higher wave amplitudes and longer durations.

The suppressive effect of a high water level and high friction coefficient is shown in Figure 9 (wjs9: 800 m water level, friction coefficient of 0.50), where the large distance between the landslide mass and the water surface combined with the high friction coefficient causes rapid energy dissipation during wave propagation, resulting in lower surge wave heights and shorter propagation durations.

As landslide entry speed decreases, the wave height shows a consistent decline. For point 8, the wave height decreased by 13.99% from wjs1 to wjs4, by 30.49% from wjs4 to wjs7, and by 40.49% from wjs1 to wjs7. For point 9, the wave height decreased by 4.84% from wjs1 to wjs4, by 29.32% from wjs4 to wjs7, and by 32.26% from wjs1 to wjs7. For point 10, the wave height decreased by 16.09% from wjs1 to wjs4, by 27.40% from wjs4 to wjs7, and by 39.08% from wjs1 to wjs7. These results indicate a significant decline in wave height as landslide entry speed decreases.

The water level and friction coefficient jointly determine the variation patterns of surge wave heights. The combination of lower water levels and lower friction coefficients facilitates wave energy accumulation and propagation, whereas higher water levels and higher friction coefficients suppress wave propagation capabilities. Wave behavior and energy accumulation are influenced by multiple factors in a complex dynamic interplay, exhibiting intricate dynamic characteristics.

4. Discussion

This study investigates the spatiotemporal evolution of landslide-induced surge waves, focusing on the Wangjiashan landslide in the Baihetan Hydropower Station reservoir. The key findings reveal the significant influence of the water level and friction coefficient on wave propagation. Specifically, lower water levels promote higher surge waves by allowing more energy accumulation, while higher friction coefficients lead to increased wave dissipation. These results align with previous studies, such as Yi et al. (2022) [17], but extend them by incorporating the effects of both slope friction and water depth on wave behavior.

The results are consistent with earlier studies on the influence of landslide velocity and wave propagation, such as those by Peng et al. (2017) [3] and Xiao et al. (2014) [11]. However, the present study offers a more realistic model with block-type landslide simulation, which better represents the sliding mechanism of natural landslides compared to traditional rigid-block models.

Our study highlights the critical role of factors such as water level, slope friction, and landslide entry velocity in determining wave characteristics. By incorporating these parameters into early warning systems, engineers can improve the predictive accuracy of surge waves, allowing for the timely evacuation of at-risk populations and protection of infrastructure. Additionally, these findings can aid in designing more resilient structures such as dams and coastal defenses, ensuring that they can withstand the impact of landslide-generated waves. Future research should focus on integrating these parameters into real-time monitoring systems to provide dynamic hazard assessments and preventive measures.

In addition to advancing theoretical knowledge, this study also provides valuable insights for real-world applications, particularly for the Wangjiashan area. The results from the physical model experiments offer a basis for developing an early warning system tailored to the surge waves generated by the Wangjiashan landslide. By understanding how factors like the water depth and friction coefficient affect wave intensity, authorities can better predict potential hazards and issue timely warnings to protect downstream communities and infrastructure.

Despite valuable insights, this study has limitations, particularly related to the scale of the physical models and the lack of consideration of complex topographies. Future studies should incorporate real-world topographical features and investigate additional factors such as varying landslide shapes and velocities. Moreover, while the zero-crossing method provided useful results, exploring advanced signal processing techniques may offer more detailed wave characteristics.

While the findings of this study provide valuable insights into landslide-induced surge waves, there are several limitations to consider.

Scale Effects: The study uses a 1:150-scale model to simulate the landslide and wave dynamics. While this scale was chosen for its balance between experimental accuracy and practical feasibility, scaling effects may influence the precision of wave characteristics, particularly the wave height and period. Future studies could explore the use of larger-scale models to more closely replicate real-world conditions and assess how scale effects impact the accuracy of results.

Simplified Assumptions: The model assumes a rigid-block landslide with uniform material properties and friction coefficients. In reality, landslides may involve more complex dynamics, including granular materials, non-uniform friction, and variable landslide entry speeds. Incorporating granular materials or realistic friction models could offer a more accurate representation of landslide behavior and its effect on wave generation.

Given the findings and limitations of this study, several promising avenues for future research can be identified:

Complex Topography and Heterogeneous Media: Future studies should incorporate complex topographies and geological conditions (e.g., river meanders, obstacles, and varying sediments) using 3D simulations and large-scale models for more accurate surge wave predictions in natural reservoirs. Regarding the limitations of the current study, future research should analyze the impact of landslide dimensions, soil characteristics, including cohesion, and the slope of the terrain on landslide velocity and wave dynamics. While these parameters are closely related to landslide input velocities, they are distinct and can independently influence the landslide’s behavior.

Advanced Wave Modeling and Prediction: This study lays the groundwork for improving surge wave prediction models. Machine learning, especially deep learning, could analyze large datasets and real-time monitoring data to enhance prediction accuracy and early warning systems.

Study of Large-Scale Real-World Events: Field studies in large reservoirs are crucial for validating experimental and simulation results. Research should also explore how surge waves interact with infrastructure, helping to develop effective risk mitigation strategies.

This study contributes to the understanding of landslide-induced surge waves by examining the combined effects of water level and friction. It also highlights practical implications for developing early warning systems for landslide-induced surge waves in the Wangjiashan area. Although this study has limitations, it provides a foundation for future research into more accurate predictive models and better disaster management strategies.

5. Conclusions

Based on the operational water depth, slope friction coefficient, and other conditions of the Wangjiashan landslide located on the northern side of Wangjiashan in the Xiaojian branch reservoir on the right bank of the Baihetan Hydropower Station reservoir area in the Jinsha River, a three-dimensional physical model system was designed to simulate landslide-induced surge waves using rigid-block rock landslides. With a focus on key influencing factors such as landslide mass volume, slope inclination angle, landslide entry velocity, and river channel depth, a total of nine experimental runs were conducted. From the results, the conclusions described below can be drawn:

With observational data from physical model experiments, the zero-crossing method was employed to extract wave heights and periods, and statistical calculations provided the maximum wave height, maximum period, effective wave height, effective period, and wave steepness characteristics of the initial surge waves. The wave steepness of the initial surge waves obtained under various experimental conditions ranged from 0.01 to 0.03, all below the critical wave steepness value, indicating that the initial surge waves are unlikely to undergo breaking once formed.

Based on the classification of effective wave heights, the model area was categorized into three levels: small waves, moderate waves, and large waves. The small-wave region accounted for 15.79% of the entire river channel, the moderate-wave region accounted for 78.95%, and the large-wave region accounted for 5.26%. Most of Ganyanjing Village and Datianba fell within the small-wave category, indicating relatively favorable conditions. Similarly, 74.83% of Yaniu Ping Village and Menggu Xinjie was classified as small-wave regions. In contrast, 87.50% of Xiangbinling’s area fell under moderate-wave conditions, necessitating special attention.

This study demonstrates the significant impact of both water level and landslide entry speed on wave height. As the water level decreased, the wave height showed a marked increase, with a total rise of 122.22% from wjs1 to wjs3. Similarly, a decrease in landslide entry speed led to a consistent decline in wave height. Specifically, the wave height decreased by 40.49% from wjs1 to wjs7 as the entry speed decreased, demonstrating a clear direct relationship between entry speed and wave height. These findings highlight the importance of water level and landslide entry speed in controlling surge wave dynamics, which can be crucial for designing engineering structures and improving hazard mitigation strategies in landslide-prone areas.

An analysis of the influence of the slope friction coefficient and river channel water depth on the initial wave height revealed that the maximum wave height in the series of experiments is typically influenced by the combined effects of the water level and friction coefficient. Lower water levels and lower friction coefficients facilitate the formation of higher maximum wave heights, whereas higher water levels and higher friction coefficients inhibit the accumulation of wave energy. The maximum wave height increased with the increase in landslide entry velocity and decreased with the increase in river channel water depth. The effective wave height reflects the overall energy propagation and maintenance capability of the waves. Low friction coefficients and longer propagation paths aid in preserving wave energy, thereby increasing the effective wave height. Conversely, high friction coefficients accelerate the dissipation of wave energy, reducing the effective wave height. The interaction between the water level and friction coefficient determines the final outcome of wave propagation. Typically, the combination of lower water levels and lower friction coefficients results in higher maximum and effective wave heights, while the combination of higher water levels and higher friction coefficients significantly suppresses wave propagation capabilities.

This research provides theoretical support for a deeper understanding of wave propagation mechanisms and regulatory strategies. The destructive power of surge waves arises both from instantaneous maximum wave heights and from the effective propagation energy of the waves. To address maximum wave heights, rapid response measures should be implemented to mitigate the sudden impact of landslide events. For effective wave heights, strengthening coastal embankments, improving slope conditions, and other measures should be undertaken to enhance coastal resilience against sustained wave actions.