Three-Dimensional Finite Element Modeling of Thermal Stratification in the Riba-Roja Reservoir Confluence: A Fluid–Thermal Multiphysics Approach

Abstract

This study presents a numerical investigation of the hydrodynamic and thermal interactions at the confluence of the Ebro and Segre Rivers in the Riba-roja Reservoir, using the Finite Element Method (FEM) within the Kratos Multiphysics framework. The coupled Navier–Stokes and energy equations were solved, employing the variational multi-scale (VMS) method for stabilization. Field data from thermal imaging and in situ measurements in March and October 2011 were used for model validation. The results revealed complex mixing and stratification dynamics influenced by regulated and unregulated flows, seasonal temperature variations, and reservoir geometry. Despite some discrepancies in temperature predictions due to the decoupled energy equation, the model effectively captured the system’s thermal behavior. This work represents a first step toward incorporating a fully coupled energy equation and exploring the effects of thermal mixing and stratification on suspended sediment transport. This study enhances understanding of fluid–thermal interactions in reservoir systems, with implications for water quality management and ecological conservation.

1. Introduction

Thermal stratification, characterized by the formation of temperature layers in water bodies, plays a critical role in influencing reservoir and river ecosystems. It affects nutrient cycling, dissolved oxygen distribution, and microbial dynamics, which impacts water quality and ecological health [1,2,3,4]. Seasonal variations in climate drive stratification patterns, creating hypolimnetic layers with reduced oxygen levels that alter sediment interactions and nutrient mobility [5,6,7]. Studies on reservoirs, such as Cannonsville and Liuxihe, demonstrate that climate change intensifies the duration and stability of stratification, necessitating innovative strategies such as selective withdrawal to manage water quality under these evolving conditions [1,8]. Furthermore, the regulation of downstream temperatures by reservoir operations, as observed in the Sacramento and Yangtze rivers, highlights the need for advanced modeling frameworks to address thermal and hydrological impacts on riverine habitats [3,6].

Modeling approaches have been extensively employed to analyze stratification dynamics. A concise summary of various approaches used to model thermal stratification in rivers, lakes, or reservoirs is shown in Table 1. One-dimensional models, such as DYRESM, effectively simulate vertical thermal structures but are limited in capturing lateral and horizontal dynamics, as demonstrated in Lake Ammersee and Cannonsville Reservoir [1,9,10,11]. Two-dimensional models, such as CE-QUAL-W2, have been widely applied to reservoirs like Aguamilpa and Riba-roja, providing an improved representation of longitudinal and vertical thermal profiles. However, as width-integrated models, they share limitations with tools like DYRESM, particularly in their inability to accurately resolve lateral dynamics [12,13]. Hybrid modeling techniques, including reduced-order models such as the ThSSim model and the multilayer river basin model (RBM), were coupled with different thermal stratification methodologies, such as CE-QUAL-W2 and a semi-Lagrangian thermal stratification model, to efficiently simulate long-term thermal trends, addressing computational limitations while maintaining accuracy [14,15]. Furthermore, integrating selective withdrawal strategies with temperature control curtains (TCCs) has proven effective in stabilizing downstream temperatures, as evidenced in deep stratified reservoirs [16].

Recent advances in three-dimensional models have provided more profound insights into hydrodynamic and thermal mixing processes, effectively capturing inflow density differences, wind forces, and reservoir morphology in systems such as Mequinenza [17,18,19,20,21]. These models, coupled with high-resolution thermal imaging, have revealed critical patterns in stratification and mixing under varying climatic and hydrological conditions [22,23]. Although three-dimensional models offer comprehensive simulations, their high computational demand underscores the need for pseudo-three-dimensional models, which balance computational efficiency with spatial resolution [19]. The inherent limitations of one- and two-dimensional models in capturing localized dynamics and the resource-intensive nature of three-dimensional models highlight the importance of adaptive frameworks tailored to the unique dynamics of individual water bodies. While previous two-dimensional models, such as those by Arbat-Bofill et al. (2014) [13] and Ramon et al. (2013) [18], have provided valuable insights into thermal stratification, they often fail to resolve the vertical mixing processes and localized hydrodynamic effects that significantly influence heat transport. Furthermore, a critical gap remains—a lack of consideration for coupling multiple physics, such as fluid dynamics, multi-phase flow, thermal interaction, sediment transport, and particle tracking, either collectively or selectively, without incurring significant computational costs. This study aims to address these limitations by leveraging a fully three-dimensional model that explicitly captures these complex interactions, providing a more comprehensive representation of thermal and hydrodynamic processes in reservoir confluences. The proposed framework integrates these complex processes within a robust and computationally efficient approach, offering an improved predictive capability for reservoir thermal behavior under varying environmental conditions.

This study fills the research gaps identified in the previous literature by demonstrating how the 3D Two-Fluid Finite Element Method (FEM) model, available in Kratos Multiphysics [24,25,26], effectively captures intricate thermal stratification in a real-world environment [27,28]. The case study centers on the Ebro–Segre confluence of the Riba-roja Reservoir, known for its dynamic ecology. In contrast to earlier research, which typically utilized simplified or one-dimensional models, this work leverages a comprehensive three-dimensional multiphysics framework built on the FEM. Unlike commercial software, Kratos provides a modular and extensible architecture that allows seamless integration of hydrodynamics, multi-phase flow, and thermal interactions while maintaining computational efficiency. The framework’s variational multi-scale (VMS) stabilization further enhances accuracy in convection-dominated flows, making it particularly effective in resolving thermal stratification and localized mixing. This sophisticated modeling approach accurately depicts the reservoir’s hydrodynamics, thermal gradients, and related processes. By incorporating these features, this study aims to enhance understanding of the factors influencing thermal stratification, serving as a valuable resource for reservoir management and ecological evaluations in varied environmental contexts.

Table 1. Summary of previous thermal stratification studies on rivers and reservoirs.

Study Area and Reference	Modeling Approach, Validation, and Thermal Coupling
Carpathian mountain rivers, Europe (Fuks et al., 2024 [29])	XGBoost and wavelet analysis for climate impact on thermal regimes; validated with hydrological and climatological data; separates climate from reservoir effects.
Wujiang River Basin, China (Shi et al., 2023 [8])	Nitrogen transformation model with isotopic data; validated using in situ nitrogen sampling across depths; focuses on stratification-induced nitrogen cycling.
Southeastern United States, USA (Cheng et al., 2020 [7])	Thermal stratification and cooling potential model; validated with climate models; optimizes temperature release strategies.
Various reservoirs and lakes (Wells, 2020 [5])	Hydrodynamic and water quality equations; validated with observed vs. simulated temperature dynamics; models temperature stratification.
1400 U.S. Reservoirs (Yigzaw et al., 2019 [10])	Multilayer stratification model for Earth systems; validated using Nash–Sutcliffe efficiency metrics; addresses vertical gradient modeling.
Karkheh Reservoir, Iran (Noori et al., 2019 [14])	ThSSim reduced-order thermal model; validated through observed temperature profile comparison; integrates a reduced-order model.
Tennessee River Basin, USA (Smith et al., 2018 [15])	Two-layer temperature model; validated against historical temperature data; simulates surface and bottom layer coupling.
Ebro-Segre Confluence, Spain (Arbat-Bofill et al., 2016 [20])	3D hydrodynamic and thermal modeling at the Ebro–Segre confluence using FreeFlow 3D; validated with in situ measurements and thermal imaging.
Ebro River, Spain (Martí-Cardona et al., 2016 [17])	ASTER and Landsat images used for mapping water surface temperatures; validated high-resolution thermal patterns supporting 3D model calibration.
Riba-roja Reservoir, Spain (Arbat-Bofill et al., 2014 [13])	Hydrodynamic simulations of the Riba-roja Reservoir; assessed impacts of inflow characteristics on stratification and water age.
Riba-roja Reservoir, Spain (Ramon et al., 2013 [18])	Characterized mixing and circulation at the Ebro–Segre confluence; analyzed density- and wind-driven mixing processes.

Table 1. Summary of previous thermal stratification studies on rivers and reservoirs.

Study Area and Reference	Modeling Approach, Validation, and Thermal Coupling
Carpathian mountain rivers, Europe (Fuks et al., 2024 [29])	XGBoost and wavelet analysis for climate impact on thermal regimes; validated with hydrological and climatological data; separates climate from reservoir effects.
Wujiang River Basin, China (Shi et al., 2023 [8])	Nitrogen transformation model with isotopic data; validated using in situ nitrogen sampling across depths; focuses on stratification-induced nitrogen cycling.
Southeastern United States, USA (Cheng et al., 2020 [7])	Thermal stratification and cooling potential model; validated with climate models; optimizes temperature release strategies.
Various reservoirs and lakes (Wells, 2020 [5])	Hydrodynamic and water quality equations; validated with observed vs. simulated temperature dynamics; models temperature stratification.
1400 U.S. Reservoirs (Yigzaw et al., 2019 [10])	Multilayer stratification model for Earth systems; validated using Nash–Sutcliffe efficiency metrics; addresses vertical gradient modeling.
Karkheh Reservoir, Iran (Noori et al., 2019 [14])	ThSSim reduced-order thermal model; validated through observed temperature profile comparison; integrates a reduced-order model.
Tennessee River Basin, USA (Smith et al., 2018 [15])	Two-layer temperature model; validated against historical temperature data; simulates surface and bottom layer coupling.
Ebro-Segre Confluence, Spain (Arbat-Bofill et al., 2016 [20])	3D hydrodynamic and thermal modeling at the Ebro–Segre confluence using FreeFlow 3D; validated with in situ measurements and thermal imaging.
Ebro River, Spain (Martí-Cardona et al., 2016 [17])	ASTER and Landsat images used for mapping water surface temperatures; validated high-resolution thermal patterns supporting 3D model calibration.
Riba-roja Reservoir, Spain (Arbat-Bofill et al., 2014 [13])	Hydrodynamic simulations of the Riba-roja Reservoir; assessed impacts of inflow characteristics on stratification and water age.
Riba-roja Reservoir, Spain (Ramon et al., 2013 [18])	Characterized mixing and circulation at the Ebro–Segre confluence; analyzed density- and wind-driven mixing processes.

2. Models and Methods

2.1. Kratos Multiphysics Framework

Kratos Multiphysics [30] is an open-source framework developed to solve multi-disciplinary problems [24,25,31]. Designed at the International Center for Numerical Methods in Engineering (CIMNE) in collaboration with other institutes, it provides a versatile platform for tackling complex physics scenarios where multiple interacting fields need to be modeled simultaneously. The framework adopts an object-oriented design to enhance flexibility, extensibility, and research collaboration. By breaking down problems into modular objects, Kratos allows seamless integration of different physics formulations [32,33,34,35,36,37,38]. Its layered architecture facilitates application interaction while isolating dependencies to enhance code maintenance and scalability. The kernel of Kratos implements the data structures and the routines required across all the applications, including fluid dynamics, structural mechanics, and thermal simulations, ensuring a cohesive computational environment. Moreover, Python scripting interfaces enhance Kratos’s adaptability for custom simulations, facilitating straightforward pre-processing, execution, and post-processing. In this work, we use and further enhance the application for simulating two-fluid flow models, incorporating the capability to account for thermal effects.

2.2. Governing Equations

2.2.1. Fluid Dynamics Governing Equations

Navier–Stokes Equations

The governing equations for the fluid flow derive from the Navier–Stokes equations, describing the conservation of momentum and mass. The momentum conservation equation is

$$\rho \left({\displaystyle \frac{\partial \mathbf{u}}{\partial t}}+\mathbf{u}·\nabla \mathbf{u}\right)=\rho \mathbf{b}+\nabla ·\sigma ,\mathrm{in}\Omega ,$$

(1)

where $\rho$ is the density, u is the velocity field, and $\mathbf{b}$ represents the body force per unit volume, typically accounting for gravitational effects. The total stress tensor $\sigma$ governs the internal forces acting on the fluid and is given by

$$\sigma =-p\mathbf{I}+\mu \left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^{\top }\right),$$

(2)

where p is the pressure, $\mu$ is the dynamic viscosity, and $\mathbf{I}$ denotes the identity tensor. The term $\nabla {\mathbf{u}}^{\top }$ represents the transpose of the velocity gradient.

The conservation of mass for incompressible flows simplifies to

$$\nabla ·\mathbf{u}=0,\mathrm{in}\Omega .$$

(3)

A discontinuous pressure gradient is imposed at the free surface to account for the interface discontinuity. This is handled through a local enrichment pressure space combined with static condensation, as described in [39], which allows accurate interface representation without introducing additional degrees of freedom. The energy equation, which is presented in the section ’Thermal Governing Equations’, is also considered to capture the thermal effects in the fluid flow.

Two-Fluid Domain and Interface Conditions

The computational domain $\Omega$ consists of two immiscible fluid regions, ${\Omega }_1\left(t\right)$ and ${\Omega }_2\left(t\right)$, each characterized by distinct material properties. The density $\rho (\mathbf{x},t)$ and dynamic viscosity $\mu (\mathbf{x},t)$ vary spatially and temporally according to the region they belong to:

$$\rho (\mathbf{x},t)=\left\{\begin{array}{cc}{\rho }_1,\hfill & \mathbf{x}\in {\Omega }_1\left(t\right),\hfill \\ {\rho }_2,\hfill & \mathbf{x}\in {\Omega }_2\left(t\right),\hfill \end{array}\right.\mu (\mathbf{x},t)=\left\{\begin{array}{cc}{\mu }_1,\hfill & \mathbf{x}\in {\Omega }_1\left(t\right),\hfill \\ {\mu }_2,\hfill & \mathbf{x}\in {\Omega }_2\left(t\right).\hfill \end{array}\right.$$

(4)

Here, ${\rho }_1$ and ${\rho }_2$ are the densities of the two fluids occupying ${\Omega }_1\left(t\right)$ and ${\Omega }_2\left(t\right)$, respectively, while ${\mu }_1$ and ${\mu }_2$ denote their corresponding dynamic viscosities. The time-dependent nature of ${\Omega }_1\left(t\right)$ and ${\Omega }_2\left(t\right)$ indicates the movement of the interface.

The interface $\Gamma \left(t\right)$ is defined as the moving boundary between the two fluid regions, $\Gamma \left(t\right)=\partial {\Omega }_1\left(t\right)\cap \partial {\Omega }_2\left(t\right)$. At this interface, continuity and equilibrium conditions must be enforced.

The velocity continuity condition is given by

$${\mathbf{u}}_1(\mathbf{x},t)={\mathbf{u}}_2(\mathbf{x},t)\mathrm{on}\Gamma \left(t\right),$$

(5)

which ensures that there is no velocity jump across the interface. Alternatively, this can be written as

$$\mathbf{u}(\mathbf{x},t)=0\mathrm{on}\Gamma \left(t\right).$$

(6)

The equilibrium condition for the interface, neglecting surface tension, is determined by the balance of normal stresses. This can be expressed as

$$({\sigma }_1(\mathbf{x},t)-{\sigma }_2(\mathbf{x},t))·\mathbf{n}=0\mathrm{on}\Gamma \left(t\right),$$

(7)

where ${\sigma }_1$ and ${\sigma }_2$ are the stress tensors in ${\Omega }_1\left(t\right)$ and ${\Omega }_2\left(t\right)$, respectively, and $\mathbf{n}$ is the outward unit normal vector on $\partial {\Omega }_1\left(t\right)$. Alternatively, this can be represented as

$$\sigma (\mathbf{x},t)·\mathbf{n}=0\mathrm{on}\Gamma \left(t\right),$$

(8)

where $\sigma ={\sigma }_1-{\sigma }_2$.

These interface conditions ensure proper interaction between the two fluids, allowing the model to capture realistic interfacial dynamics.

Level-Set Formulation

To track the interface $\Gamma$ during time evolution, the level-set method is employed—an Eulerian interface-capturing technique known for its ability to handle large interface deformations and topological changes. A scalar function $\varphi$ is introduced, which implicitly defines the interface as the zero level set:

$$\Gamma =\{\mathbf{x}\mid \varphi (\mathbf{x},t)=0\}\mathrm{for}\mathbf{x}\in \Omega ,$$

(9)

and it distinguishes the fluid domains as follows [28,40]:

$$\varphi (\mathbf{x},t)=\left\{\begin{array}{cc}<0\hfill & \mathrm{if}\mathbf{x}\in {\Omega }_1,\hfill \\ 0\hfill & \mathrm{if}\mathbf{x}\in \Gamma ,\hfill \\ >0\hfill & \mathrm{if}\mathbf{x}\in {\Omega }_2.\hfill \end{array}\right.$$

The evolution of $\varphi$ is governed by the purely hyperbolic transport equation

$${\displaystyle \frac{\partial \varphi }{\partial t}}+\mathbf{u}·\nabla \varphi =0\mathrm{in}\Omega ,$$

(10)

subject to the initial condition

$$\varphi (\mathbf{x},0)={\varphi }_0\left(\mathbf{x}\right)\mathrm{in}\Omega ,$$

(11)

and the inflow boundary condition

$$\varphi (\mathbf{x},t)={\varphi }_{\mathrm{in}}\mathrm{on}\partial {\Omega }_{\mathrm{in}}.$$

(12)

The level-set method in this study utilizes an Eulerian scheme with error compensation steps to ensure accurate interface tracking. Specifically, the back-and-forth error compensation (BFEC) method is employed to maintain the accuracy of the level-set function $\varphi$ [27]. To maintain the signed-distance property of the level-set function [41], ensuring $\parallel \nabla \varphi \parallel \approx 1$, the following eikonal equation is considered:

$$|\nabla \varphi |=1.$$

(13)

A re-initialization procedure, often performed at each time step, solves this equation to restore the signed-distance property, which is crucial for accurate curvature and normal vector computation:

$$\kappa =-\nabla ·\mathbf{n},\mathbf{n}={\displaystyle \frac{\nabla \varphi }{|\nabla \varphi |}}.$$

(14)

Furthermore, to enhance numerical stability and accuracy during the solution of the level-set equation, a Streamline Upwind Petrov–Galerkin (SUPG) stabilization scheme is employed. Inaccuracies in the conservation of mass are a known challenge with the level-set approach. The frequent re-initialization, combined with the BFEC and SUPG stabilization, aims to mitigate these issues, ensuring robust and accurate interface tracking.

Boundary Conditions

Boundary conditions ensure the compatibility of the solution with the physical problem [42]:

• Inlet Boundary Condition: This specifies the velocity distribution or the total pressure

  $$p_{\mathrm{total}}=p_{\mathrm{static}}+{\displaystyle \frac{1}{2}}\rho v^2,$$

  (15)

  where $p_{\mathrm{static}}$ is the static pressure and v is the flow velocity.
• No-Slip Wall Boundary Condition: This enforces $\mathbf{u}={\mathbf{u}}_{\mathrm{wall}}$ for viscous flows, where tangential velocity is zero relative to the wall.
• Slip Wall Boundary Condition: This allows tangential velocity but sets $\mathbf{u}·\mathbf{n}=0$, with $\mathbf{n}$ being the normal vector.
• Outlet Boundary Condition: This often uses zero-pressure conditions to ensure free outflow:

  $$p=0\mathrm{on}\mathrm{the}\mathrm{outlet}\mathrm{surface}.$$

  (16)

Stabilization Techniques

The variational multi-scale (VMS) framework is used to address numerical instabilities [43], decomposing the velocity field into resolved and subscale components. Stabilization techniques derived from the Subgrid-Scale (SGS) method are crucial for ensuring numerical stability and accuracy, particularly in convection-dominated flows and two-fluid problems characterized by sharp gradients and significant density/viscosity contrasts.

Specifically, the Algebraic Subgrid-Scale Stabilization (ASGS) method is used, which stabilizes the numerical solution by approximating unresolved subscales using the residual of the governing equations. This method incorporates these subscales directly into the element-based formulation, enhancing the robustness of the momentum and continuity equations. It is particularly effective in convection-dominated flows, where numerical instabilities are prevalent.

The stabilization terms are added element-wise to the weak form of the equations, contributing components proportional to an intrinsic time parameter $\tau$. This parameter depends on factors such as the element size h, the velocity magnitude $|{\mathbf{u}}_h|$, and material properties like viscosity $\nu$. By adjusting these terms, ASGS effectively controls numerical oscillations without altering the original physical behavior of the solution. This approach is well suited for complex flow scenarios, including multi-phase and thermal interactions, as demonstrated in the present study.

2.2.2. Thermal Governing Equations

Energy Equation

In thermally coupled incompressible flow problems, the energy equation is coupled to the fluid flow through temperature-dependent effects. The governing equation for the temperature field is [44,45]

$$\rho C\left({\displaystyle \frac{\partial T}{\partial t}}+\mathbf{v}·\nabla T\right)=\kappa \Delta T,\mathrm{in}\Omega .$$

(17)

Here, T is the temperature field, $\mathbf{v}$ is the velocity field, C is the specific heat capacity, $\kappa$ is the thermal conductivity, and $\rho$ is the density.

Boussinesq Approximation

The Boussinesq approximation is employed to model buoyancy-driven flows, where temperature variations induce changes in fluid density, thereby affecting the body force. Specifically, the temperature field obtained from the solution of the energy equation is used to update the body force term in the Navier–Stokes equations for the subsequent time step. This coupling is represented by the following expression for the body force term, $\mathbf{b}$:

$$\mathbf{b}=\rho \mathbf{g}\left[1-\beta (T-T_0)\right],$$

(18)

where g is the gravitational acceleration, $\beta$ is the thermal expansion coefficient, T is the temperature field, $T_0$ is the reference temperature, and $\rho$ is the fluid density.

This approximation simplifies the treatment of thermal buoyancy by assuming that density variations are significant only in the buoyancy term while other fluid properties remain constant.

2.3. Coupling Strategy

The coupling strategy ensures numerical stability and flexibility through a staggered approach. The solution procedure is as follows:

• **Initialization:**

  -

  Initialize velocity $\mathbf{v}$, pressure p, and temperature T fields.

• **Fluid Solver:**

  -

  Solve the Navier–Stokes and continuity equations to compute ${\mathbf{v}}^n$ and $p^n$.

  -

  Include the buoyancy force $\rho \mathbf{g}[1-\beta (T^{n-1}-T_0)]$ from the previous temperature field.

  -

  Solve the level-set convection equation to update the interface $\Gamma$ location.

• **Thermal Solver:**

  -

  Solve the energy equation for $T^n$ using the velocity field ${\mathbf{v}}^n$.

  -

  Update the buoyancy term for the next time step based on $T^n$.

• **Iterative Update:**

  -

  Advance to the next time step and repeat until convergence.

This staggered approach effectively captures the interaction between the thermal and fluid fields while maintaining computational efficiency.

3. Study Area and Field Data

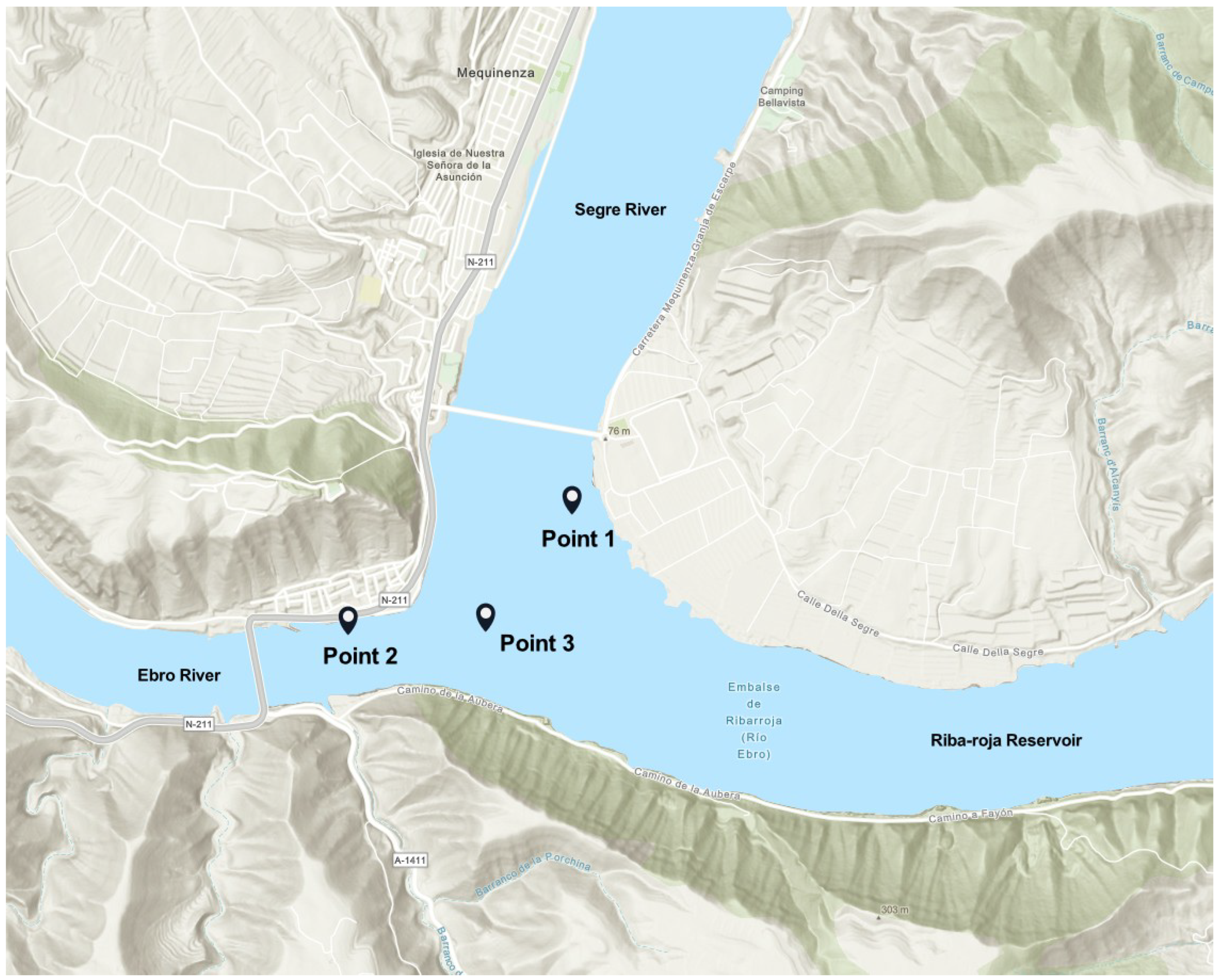
This study focuses on the confluence of the Ebro and Segre Rivers, located at the tail end of the Riba-roja Reservoir in northeastern Spain (41°18′ N, 0°21′ E), as shown in Figure 1. This reservoir, part of the Mequinenza–Riba-roja–Flix system, serves multiple purposes, including hydroelectric power generation, irrigation, urban water supply, navigation, and flood control. The elongated reservoir has a nominal capacity of 210 hm³, with an average residence time of 8 days, varying from 3 days during high flows to nearly a month under reduced inflow conditions. The Ebro River contributes approximately 58.8 percent of the reservoir inflow, with its regulated discharge characterized by consistent hypolimnetic temperatures due to the upstream Mequinenza Dam. In contrast, the Segre River contributes 41.1 percent of the inflow and exhibits significant seasonal variability in discharge, temperature, and suspended sediment concentrations. This dynamic interplay of regulated and unregulated flows, coupled with the complex reservoir geometry, results in highly variable hydrodynamic and thermal patterns.

Thermal stratification is a defining characteristic of the reservoir, with the most substantial stratification observed during summer when solar radiation heats the surface water, creating a thermocline at a depth of 5–10 m. The colder, denser hypolimnetic water released from the Mequinenza Dam submerges beneath the warmer surface waters, forming an anoxic hypolimnion. In autumn and winter, surface cooling promotes vertical mixing, breaking the stratification. Differences in water temperatures between the rivers can exceed 10 °C depending on the season, further complicating the mixing processes at the confluence. Suspended sediment transport also varies significantly, with the Segre River responding more to meteorological conditions and storm events, while the Ebro River’s sediment load is regulated by the upstream reservoir. These mixing and stratification dynamics directly influence the reservoir’s water quality and ecological conditions.

Field data collected during campaigns in March and October 2011 provided critical insights into the thermal and hydrodynamic behavior of the Ebro–Segre confluence (as presented in [20]). Thermal imaging of the confluence area, captured using a hyperspectral thermo-airborne spectrographic imager (TASI) sensor during aerial surveys conducted by the Cartographic Institute of Catalonia (ICC), revealed detailed surface temperature patterns. These observations were complemented by in situ measurements of surface water temperatures using thermometers and spectral radiometers for sensor calibration. Vertical temperature profiles were taken at three different points across the confluence, as shown in Figure 1, to assess the model’s performance in various regions. The boundary conditions for the simulations included constant inflow rates and temperatures: on 31 March 2011, the Segre River discharged 91.2 m³/s at 15 °C, and the Ebro River contributed 492.9 m³/s at 10.7 °C. Combined with the reservoir’s complex hydrodynamics, these datasets offer a comprehensive foundation for studying mixing and stratification phenomena at the Ebro–Segre confluence.

3.1. Computational Model for Fluid–Thermal Interaction

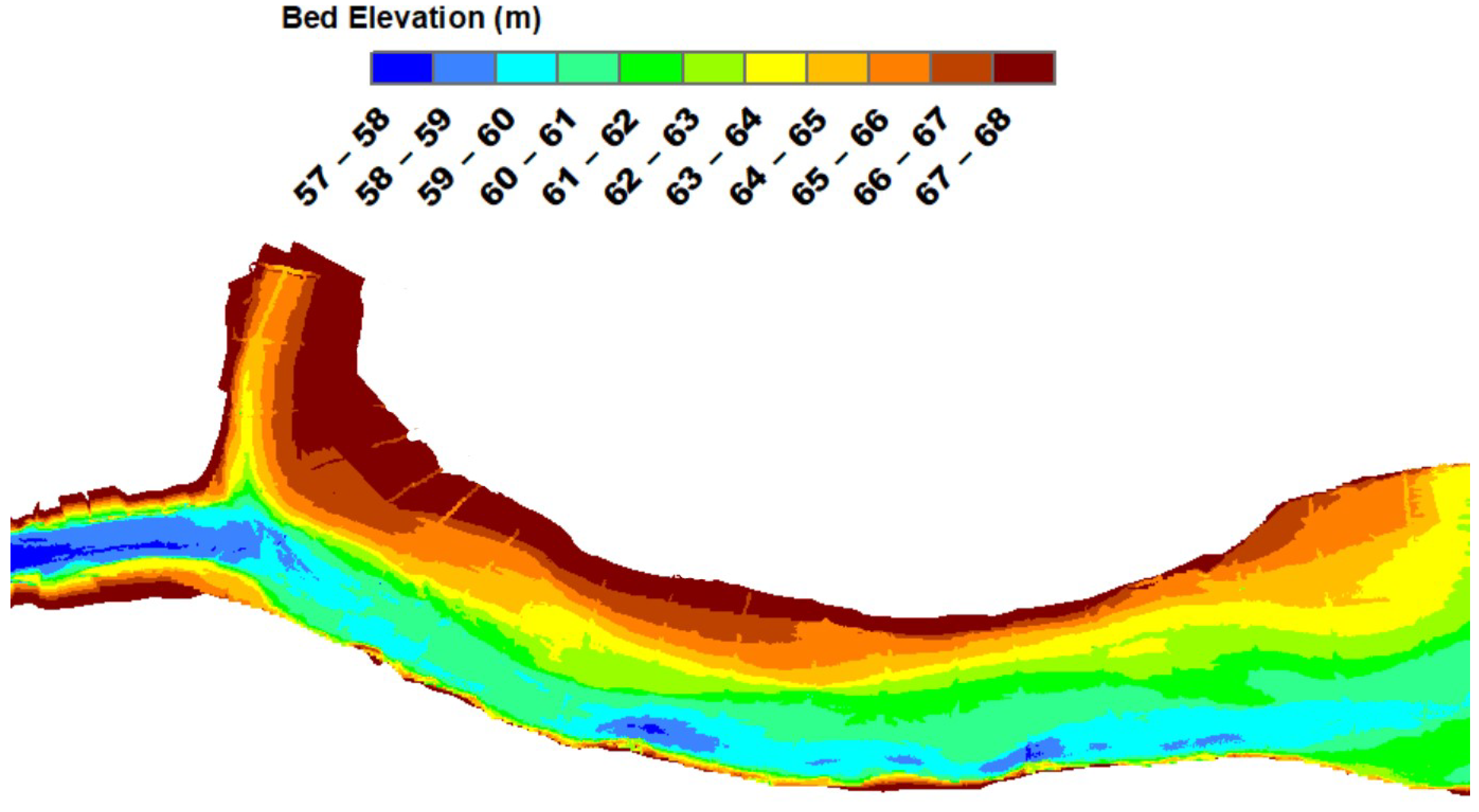
A comprehensive computational model was developed for the fluid–thermal interaction in the Ebro–Segre confluence. The bed topology was generated using raster data from the 2020 bathymetric survey (Figure 2) that were adapted from the previous study [46]. These data were used to create a three-dimensional finite element mesh of roughly 1,400,000 elements with an average element size of 15 m, as shown in Figure 3, providing the resolution required for accurate numerical simulations.

3.2. Fluid Boundary Conditions

At the Ebro and Segre Rivers’ inlets, constant volumetric discharge boundary conditions were imposed. A constant hydrostatic pressure boundary condition was applied at the outlet to simulate realistic flow behavior. A no-slip wall boundary condition was enforced for the domain’s bottom surface, while the top surface was treated as an outlet boundary to represent open-channel conditions.

3.3. Thermal Boundary Conditions

For the thermal modeling, constant temperature boundary conditions were assigned to the inlets to capture the thermal inflows from the rivers. A zero heat flux condition was applied to all other boundaries, ensuring no heat exchange occurred.

This computational model allowed the simulation of hydrodynamic and thermal processes within the study area, accounting for complex interactions between fluid flow and temperature variations in the confluence region.

4. Results

This section presents the computational model’s results. The model was developed to simulate the fluid–thermal interactions in the Ebro–Segre river system. The primary focus of this study is to compare the model’s predictions for surface water temperature with measurements obtained during a field campaign in 2011 using a TASI sensor. This comparison highlights the model’s ability to replicate the thermal stratification and surface temperature distribution observed in the study area.

4.1. Temporal Evolution and Mixing of Water Surface Temperature Within the Confluence

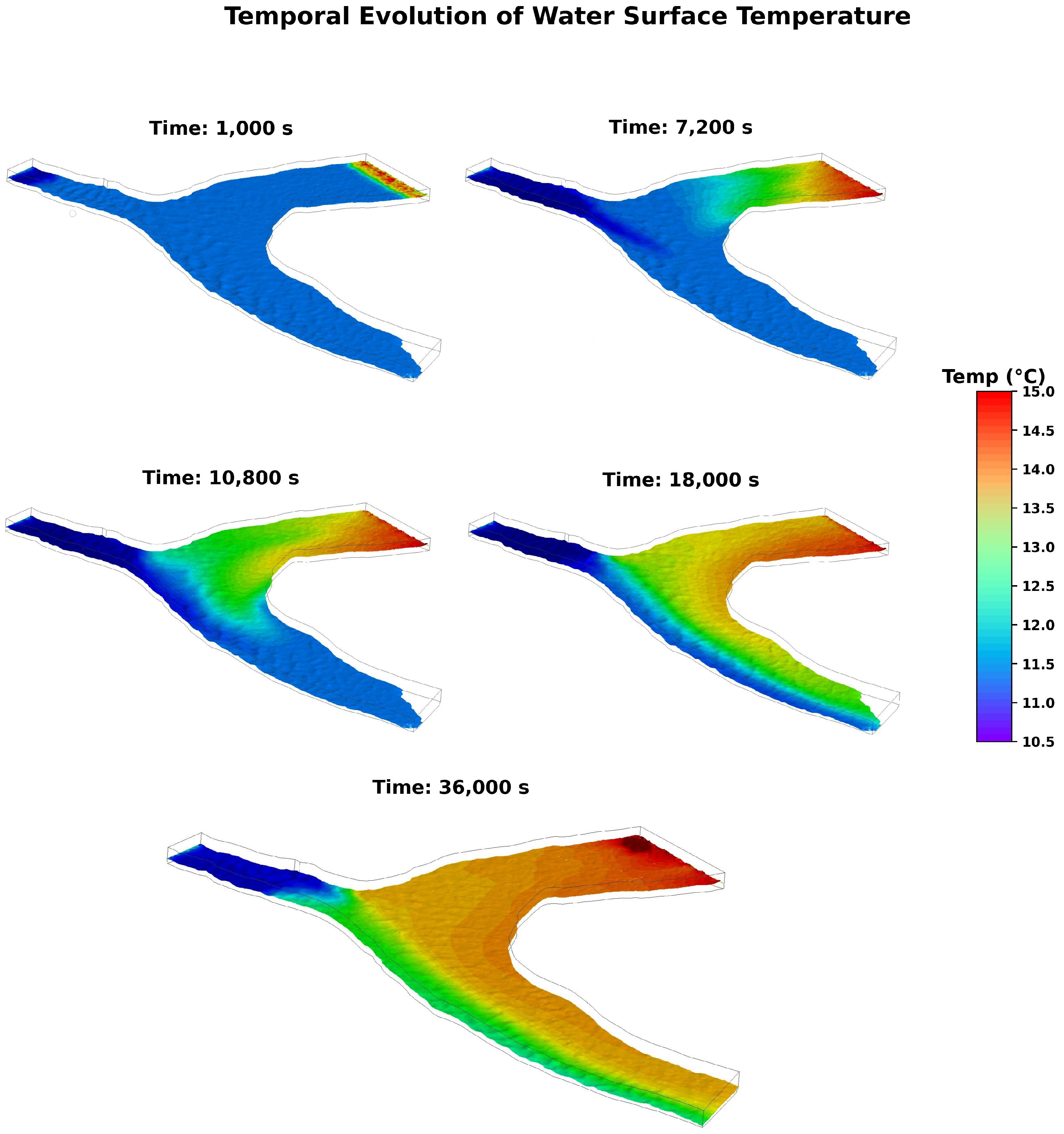
The temporal evolution of water surface temperature within the confluence is depicted in Figure 4, which presents a series of contour plots at distinct simulation times: 1000 s, 7200 s, 10,800 s, 18,000 s, and 36,000 s. These plots illustrate the dynamic mixing and stratification processes driven by the studied domain’s thermal gradient and flow conditions. At 1000 s, the temperature distribution showed initial stratification patterns with relatively sharp thermal boundaries between the inflowing streams. The upstream colder water mass was distinctly visible, with limited mixing observed in the central confluence region. This initial state provides insight into the temperature gradients that govern the early mixing stages. The simulation captured the gradual diffusion of thermal energy and advection throughout the confluence as time progressed. By 7200 s, significant thermal mixing was evident as the temperature boundaries blurred, and warmer water from one stream dispersed into the adjacent cooler region. The mixing intensified at 10,800 s, where broader temperature gradients appeared across the domain, indicating the effective dispersion mechanisms modeled by the simulation. At this stage, the results reveal the model’s capability to replicate complex mixing processes driven by both hydrodynamic forces and thermal energy transport. By 18,000 s and 36,000 s, the confluence exhibited a near-homogenized thermal field, with only subtle temperature variations persisting in localized regions. The evolution toward equilibrium was distinctly captured, highlighting the robustness of the model in resolving the interplay of advection and diffusion processes over time. The subplot format in Figure 4 enables a comprehensive assessment of temporal transitions in the thermal field, emphasizing the accuracy of the simulation in representing both transient and steady-state dynamics.

Overall, the detailed visualization of temporal evolution confirms the model’s performance in capturing the key physical processes governing thermal mixing in natural water bodies. The distinct time steps illustrate how the interplay of hydrodynamic forces and thermal gradients drives the transition from initial stratification to eventual thermal homogenization, underscoring the reliability of the numerical framework employed in this study.

4.2. Surface Temperature Comparison

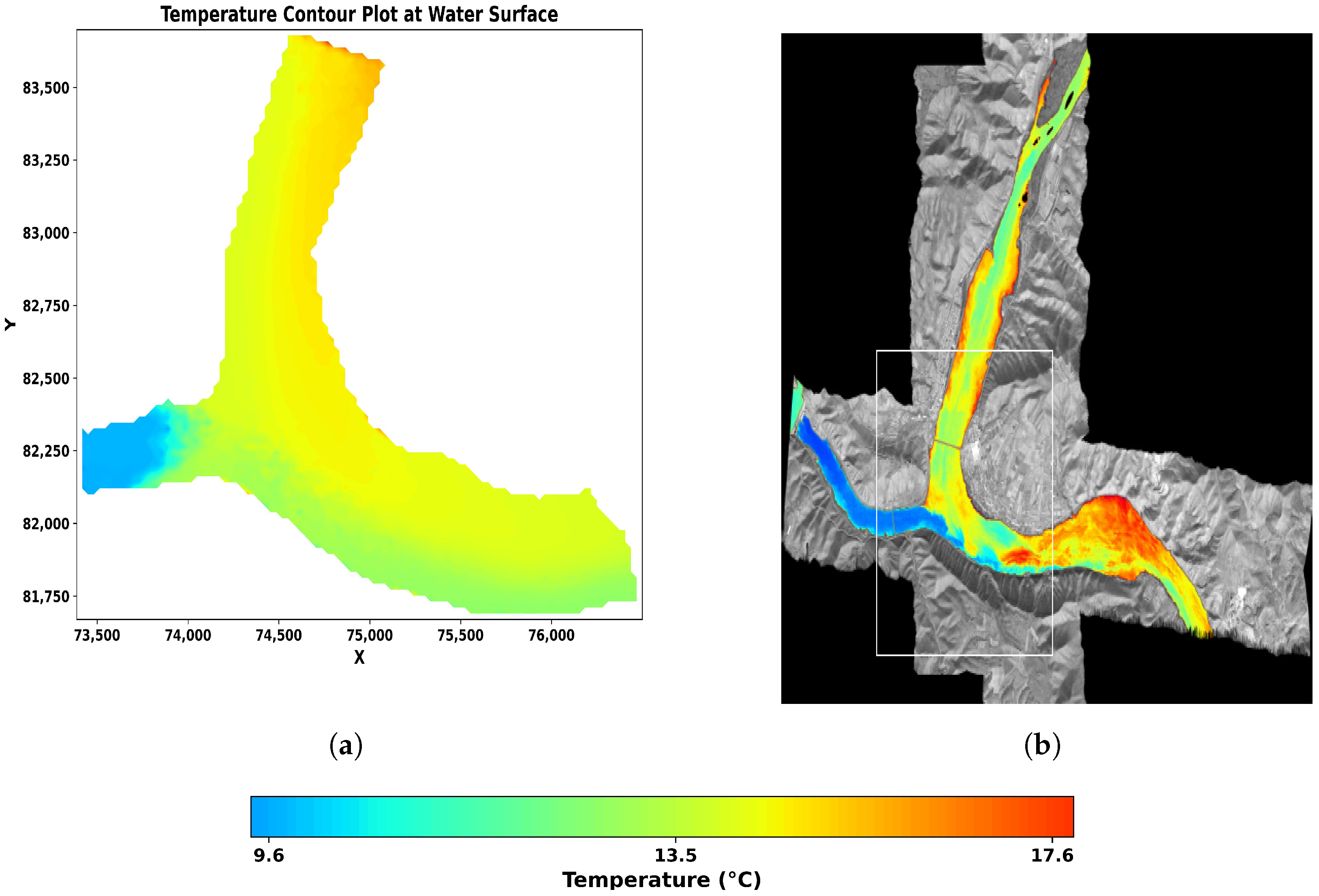
Figure 5 presents the surface temperature distribution obtained from the computational model (left) after 10 h of simulation time and the measurements recorded by the TASI sensor (right) on 31 January 2011, at midday. The model results demonstrate a clear thermal gradient along the river system, with warmer temperatures concentrated near regions of reduced flow velocity. However, the TASI measurements show higher surface temperatures, particularly downstream, with values exceeding 19.85 °C in some areas, compared with the Segre River inflow temperature of approximately 15 °C. This increment is likely influenced by solar radiation, which affects surface water layers during the daytime, a process not included in the current thermal boundary condition setup.

The boundary conditions applied in the simulation, as outlined in the sections “Study Area and Field Data” and “Fluid Boundary Conditions”, included constant inflow rates of 91.2 m³/s at 15 °C for the Segre River and 492.9 m³/s at 10.7 °C for the Ebro River. These were combined with a constant hydrostatic pressure at the outlet, no-slip conditions at the bottom, and zero heat flux at other boundaries. These conditions were crucial for modeling the thermal gradients and flow dynamics at the Ebro–Segre confluence.

The model effectively captured the general thermal distribution pattern, aligning well with the observed data in regions where hydrodynamic and thermal processes dominate. However, deviations were observed in downstream areas where prolonged residence times and solar exposure appear to amplify surface temperatures. These discrepancies highlight the importance of incorporating solar radiation effects in future modeling efforts to improve accuracy. Despite these limitations, the computational results demonstrate robustness in resolving large-scale thermal dynamics and provide a valuable framework for studying similar river reservoir systems.

4.3. Analysis of Temperature Profiles

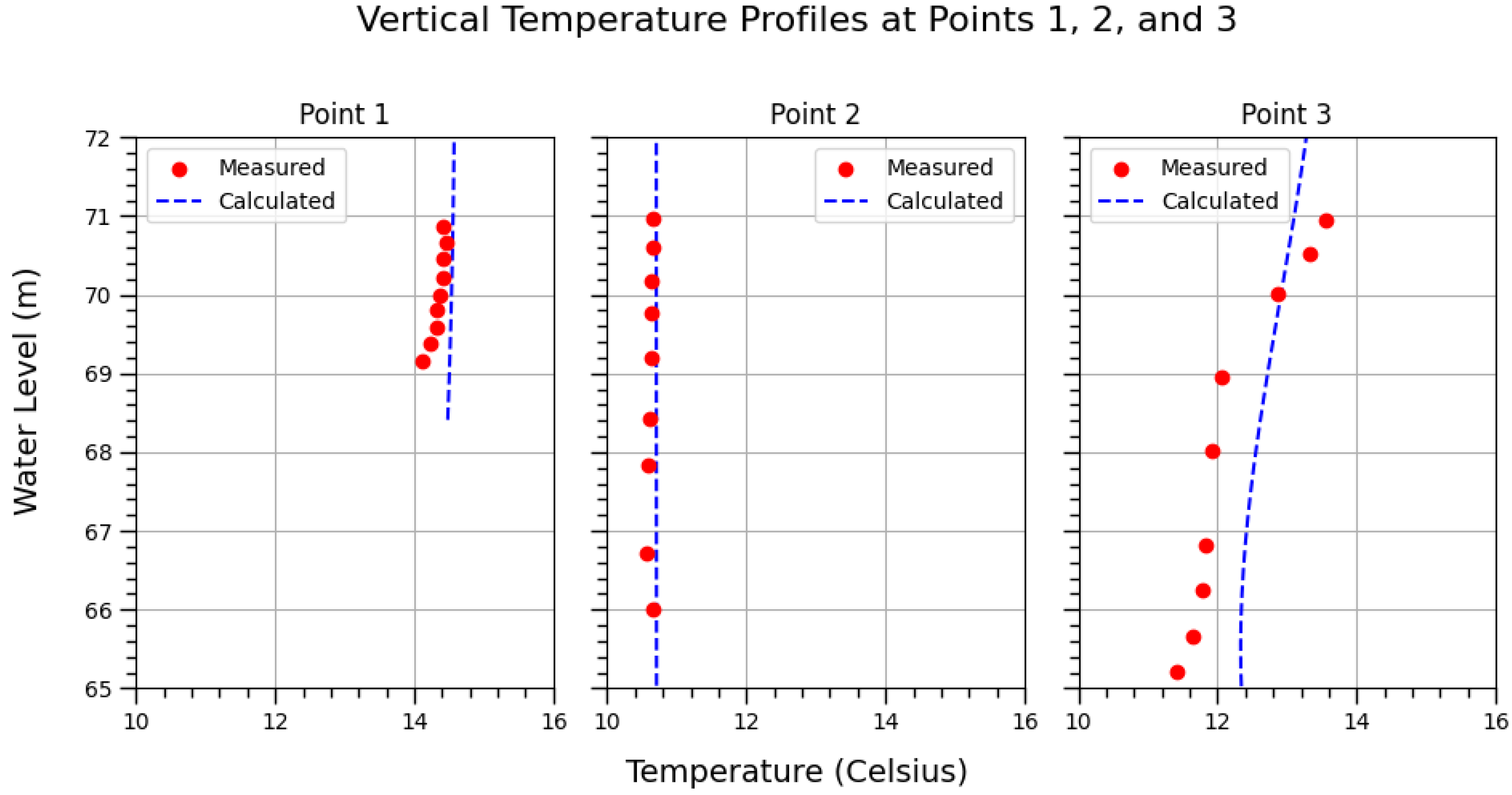
The vertical temperature profiles at three strategic locations within the confluence of the Ebro and Segre rivers are analyzed in Figure 6. Point 1 is situated near the confluence on the side of the Segre River, while Point 2 is located on the opposite side, near the Ebro River. Point 3 is positioned directly in the confluence zone where the rivers merge, as shown in Figure 1. These locations are critical for comparing the thermal vertical profiles, as they represent different flow dynamics and thermal behavior across the confluence area. The measured profiles were compared with the model’s predictions to assess the accuracy of the simulation in capturing thermal stratification and mixing processes at each point.

• Point 1:

This location near the side of the Segre River is characterized by relatively high flow velocities and lower thermal stratification. The measured temperature profile shows a steep gradient near the surface, indicating significant thermal mixing. The computational model accurately captured the general trend of the observed profile, highlighting its effectiveness in simulating the temperature distribution. However, a slight overestimation of surface temperature suggests that refining the turbulence parameterization could improve the resolution of mixing processes in this region.

• Point 2:

Near the Ebro River side, Point 2 experiences complex flow interactions and mixing due to the merging of the two rivers. The measured temperature profile exhibits pronounced thermal stratification, with colder water near the bottom. The model successfully reproduced this stratification pattern, demonstrating its robustness in capturing such complex interactions. Minor discrepancies at mid-depth levels may arise from the simplified treatment of local turbulence and secondary flow structures in the numerical simulation. Enhancing the model’s representation of these processes could further improve accuracy.

• Point 3:

Positioned at the confluence where the rivers merge, Point 3 is influenced by the combined flow dynamics of the two rivers. The measured profile reveals a more uniform temperature distribution with a moderate thermal gradient near the bottom. The model’s prediction aligned closely with the observed profile in capturing the stratification trend, indicating strong performance in capturing downstream mixing and stratification effects. However, a slight overestimation of bottom temperatures suggests that potential enhancements in boundary-layer modeling could be beneficial.

Overall, the model demonstrated considerable success in capturing the general trends and value assessments of temperature profiles across different zones. The identified discrepancies point to areas for further refinement. Addressing these limitations will enhance the model’s accuracy and reliability in simulating complex thermal dynamics.

4.4. Evaluating the Model’s Convergence Performance and Mesh Sensitivity Analysis

Following the analysis of the temperature profiles, this subsection presents a detailed examination of the temporal evolution of the relative residuals and the sensitivity of the model to mesh refinement to ensure the reliability and robustness of the numerical solutions.

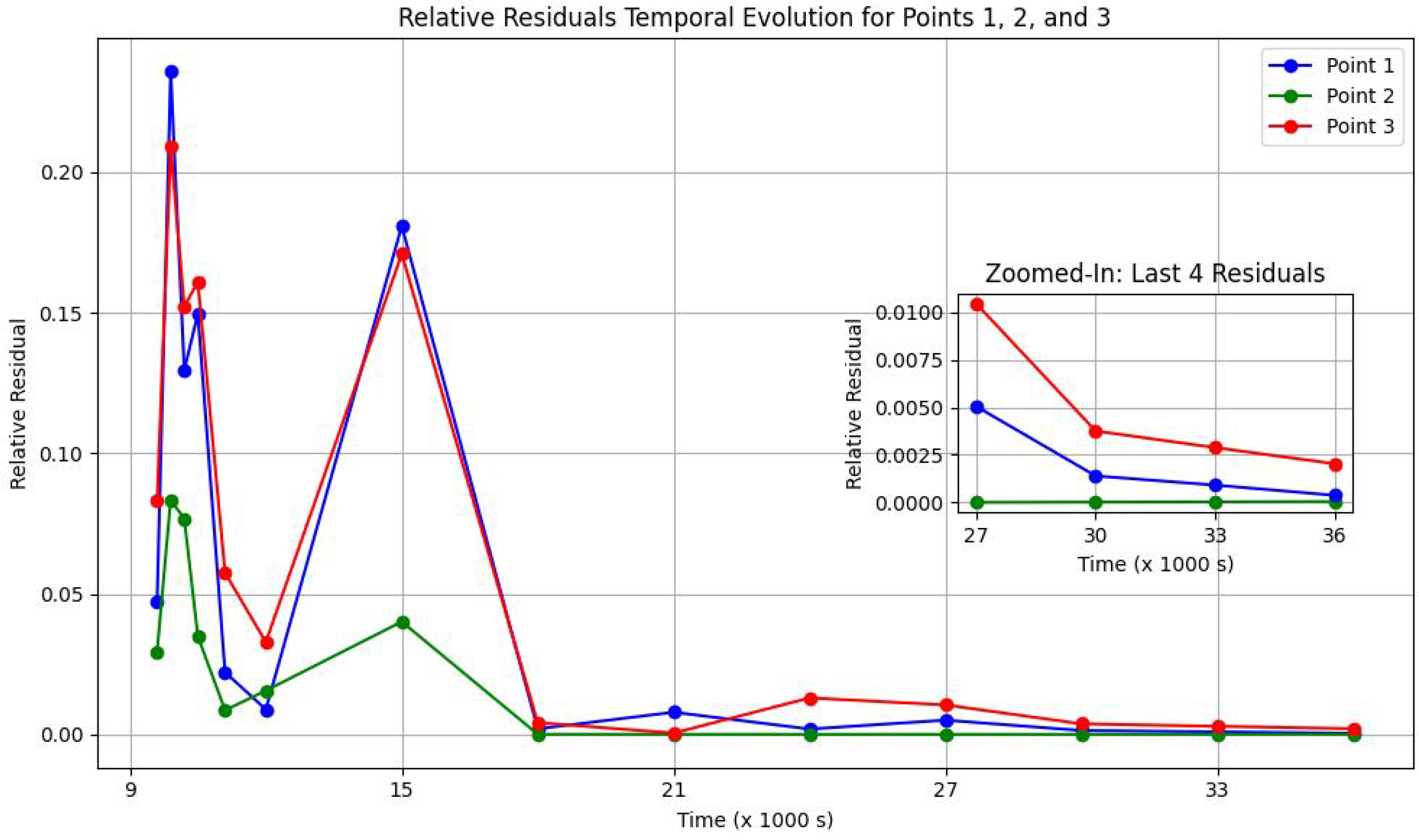
4.4.1. Temporal Convergence Analysis

Figure 7 illustrates the temporal evolution of the relative residuals for the vertical temperature profiles at the three strategic points analyzed in the previous subsection. Initially, all points exhibited high relative residuals due to the model’s rapid adjustment to the initial and boundary conditions. This was particularly evident during the first 15,000 s, when significant fluctuations reflected the transient nature of flow and thermal mixing processes at the confluence. The spikes observed were linked to dynamic interactions between the warmer Ebro and cooler Segre inflows.

The relative residual is a key indicator of numerical convergence, measuring how much the solution changes between consecutive time steps. It is defined as

$$\mathrm{RelRes}={\displaystyle \frac{{\sum }_{i=1}^N|T_{\mathrm{sim},i}^n-T_{\mathrm{sim},i}^{n-1}|}{{\sum }_{i=1}^N\left|T_{\mathrm{sim},i}^n\right|}},$$

(19)

where $T_{\mathrm{sim},i}^n$ and $T_{\mathrm{sim},i}^{n-1}$ are the simulated temperature values at point i in the current and previous time steps, respectively, and N is the total number of observations. A decreasing relative residual over time indicates numerical stability and convergence of the simulation.

As the simulation progressed, the residuals for all points decreased markedly, stabilizing below the 0.0025 threshold set as the convergence criterion. The inset clearly demonstrates this convergence trend during the last four time steps, confirming that the model reached a numerically steady state. The rapid decline in residuals followed by stabilization suggests that the thermal stratification was well captured by the model. This temporal pattern ensures that the numerical solutions are accurate and not influenced by ongoing transients, validating the chosen convergence tolerance as both rigorous and suitable for the complex hydrodynamic and thermal interactions present at the rivers’ confluence.

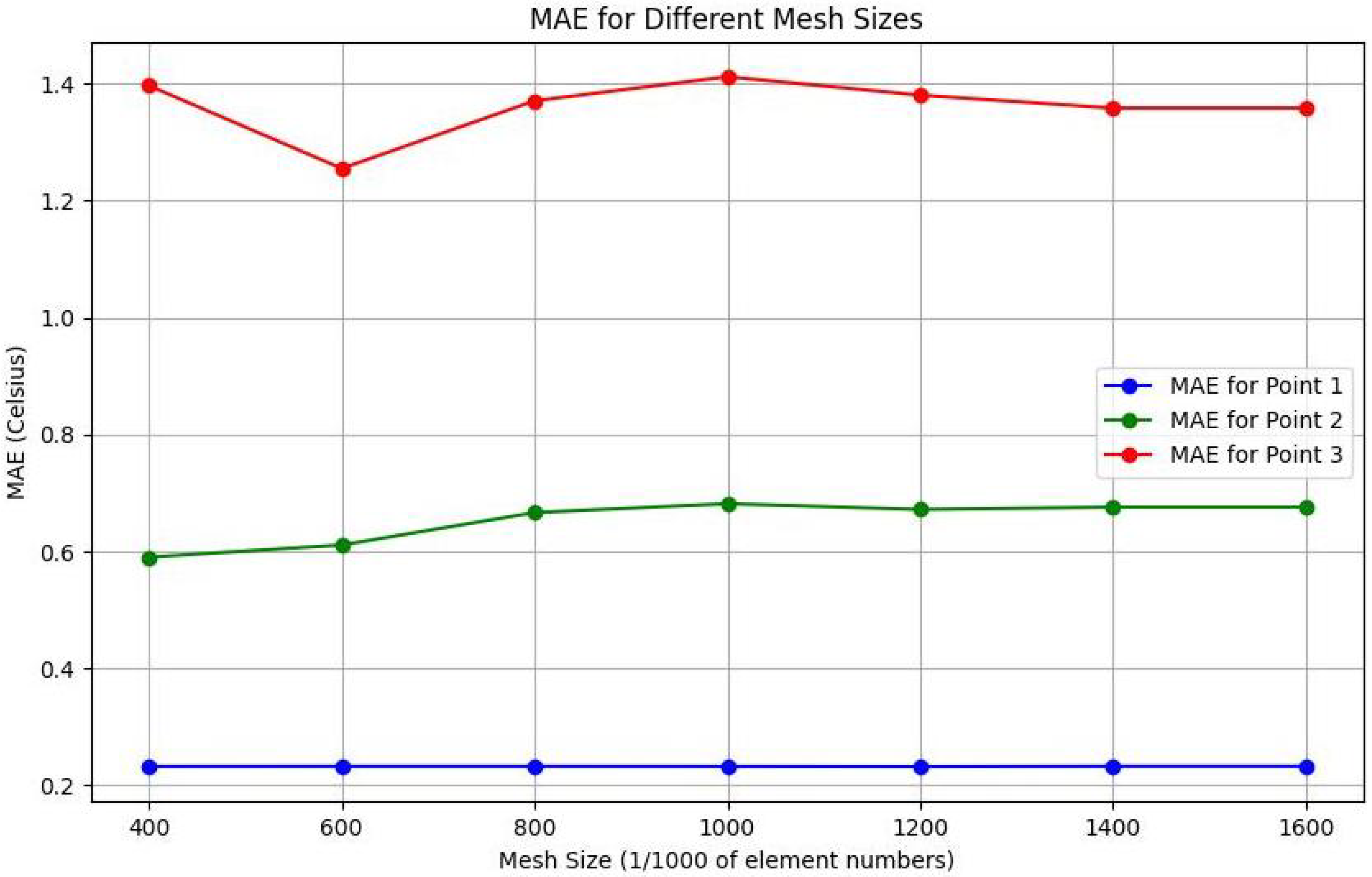
4.4.2. Mesh Sensitivity Analysis

To further validate the model, a mesh sensitivity analysis was conducted, as shown in Figure 8. This analysis examined the mean absolute error (MAE) of the vertical temperature profiles at the same points across different mesh sizes. The MAE quantifies the average magnitude of errors between the simulated and measured temperature values and is given by

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N|T_{\mathrm{sim},i}-T_{\mathrm{obs},i}|,$$

(20)

where $T_{\mathrm{sim},i}$ and $T_{\mathrm{obs},i}$ are the simulated and observed temperature values at point i and N is the total number of observations. A lower MAE indicates better agreement between the model’s predictions and experimental data.

Point 1 consistently exhibited the lowest MAE, maintaining values close to 0.2 °C regardless of mesh refinement. This indicates that Point 1 is located in a region of minimal thermal gradient or a more homogeneous flow field. Conversely, Point 3 exhibited the highest MAE values, fluctuating between 1.2 °C and 1.4 °C, suggesting its location in a zone with complex flow dynamics or stronger thermal gradients, possibly influenced by the mixing layers at the confluence. Point 2 exhibited intermediate behavior, with MAE values around 0.6 °C.

The minor variations in MAE across the mesh sizes indicate that the model is relatively insensitive to further refinement beyond 1,400,000 elements, confirming mesh independence. This consistency across mesh sizes validates the selected mesh as a balanced choice that ensures numerical accuracy without unnecessary computational costs.

The combined analysis of temporal residuals and mesh sensitivity provides robust evidence of the model’s reliability and numerical stability. By confirming convergence and mesh independence, this analysis effectively supports the accuracy and validity of the simulation results presented in the previous subsection.

5. Discussion

The computational model effectively replicates the observed temperature profiles at the three selected points, demonstrating its ability to capture the thermal stratification and mixing processes under complex hydrodynamic conditions. The well-captured patterns at Points 2 and 3 reflect the model’s strength in resolving the large-scale thermal gradients and mixing zones. However, the discrepancies observed at Point 1, particularly compared with thermal imaging, highlight specific limitations in the current study.

A potential reason for these discrepancies is the influence of localized and subscale phenomena, which may originate from small-scale turbulence or water surface radiation effects. In the main flow, as the Reynolds number falls below the threshold for fully developed turbulence, no significant turbulent patterns are expected. The observed discrepancies are primarily due to highly localized and natural phenomena, such as flow separation, recirculation, and enhanced mixing in complex geometric areas, which occur in real-world measurements but are not fully captured by the model. These localized effects are central to the mixing processes and can lead to temperature variations.

The VMS method used in the simulation, analogous to the LES (Large Eddy Simulation) approach [47], decomposes flow variables into resolved and subgrid-scale components. While this approach effectively captures large-scale flow features, limitations arise from the boundary-layer mesh resolution, especially in large-scale simulations. Due to computational resource constraints, achieving the necessary mesh refinement near the bed and top surfaces becomes challenging. This limitation leads to unresolved flow details in these regions, contributing to the discrepancies observed in the model’s results.

Additionally, the absence of a thermal boundary condition that accounts for radiation at the water–air interface limits the model’s ability to replicate the heating effects observed in the thermal images, particularly downstream. This suggests that localized phenomena, possibly due to thermal radiation or small-scale turbulence, influence the temperature distribution. Future studies will incorporate these effects into the model to enhance predictive accuracy.

The thermal surface interface condition could benefit from the integration of level-set technology to dynamically track the free surface. While the model successfully captured many thermal and hydrodynamic processes, discrepancies were observed, especially in areas with rapid temperature changes. These deviations suggest a need for more robust thermal modeling, potentially incorporating surface thermal radiation effects. The one-way coupling between the energy and Navier–Stokes equations, where temperature influences flow but not vice versa within the same iteration, likely contributes to these inaccuracies, particularly where strong thermal feedback exists. Refining mesh resolution and improving boundary condition handling are also crucial for accurately representing complex thermal and hydrodynamic behaviors in natural water bodies.

6. Conclusions

In this study, we developed and applied a detailed computational model to investigate the hydrodynamic and thermal interactions at the confluence of the Ebro and Segre Rivers in the Riba-roja Reservoir. The use of the Finite Element Method (FEM) and the variational multi-scale (VMS) stabilization technique within the Kratos Multiphysics framework allowed us to accurately simulate the complex fluid–thermal dynamics. The model was validated using field data from thermal imaging and in situ measurements, demonstrating its capability to capture the intricate mixing and stratification patterns observed in the reservoir.

The results of our model highlight its effectiveness in capturing the thermal stratification and mixing dynamics driven by the interplay of regulated and unregulated flows, seasonal temperature variations, and reservoir geometry. The VMS stabilization technique ensures numerical stability, particularly in convection-dominated flows, preventing spurious oscillations and enhancing the robustness of the solution. The staggered coupling approach provides numerical stability and flexibility, allowing for the efficient solution of the coupled fluid–thermal problem.

However, limitations were observed. Discrepancies between simulated and observed temperatures, especially in sharp gradient regions, are attributed to the one-way coupled energy equation and insufficient boundary-layer mesh resolution due to computational constraints. The lack of a radiative thermal boundary condition further impacted accuracy. To address these limitations, future work will focus on fully coupling the energy and Navier–Stokes equations; incorporating radiative effects; refining mesh resolution, particularly near boundaries; and integrating level-set free surface tracking.

Future studies will also investigate the impact of thermal mixing and stratification on suspended sediment transport. Understanding these interactions is crucial for effective water quality management and ecological conservation in reservoir environments. The methodologies and findings presented in this study can be applied to other reservoir systems, contributing to a broader understanding of fluid–thermal interactions in natural and engineered water bodies.