Abstract
Estuarine areas have experienced varying levels of pollution globally due to increased industrial and social development. Water diversion projects can mitigate water pollution in estuaries, but it is necessary to consider freshwater runoff and tidal variations and their effects on water resource scheduling in the tidal reaches. In this study, a multi-objective optimal scheduling model of a tidal-sluice pump based on this flexible freshwater reservoir was established with the aim of mean water level of diversion port, water diversion quantity, and ecological flow. The tidal reach was generalized as a flexible freshwater reservoir, and a hydrodynamic model was used to construct the water level and discharge capacity curves. The advantage of this model is that it transforms complex multidimensional hydrodynamic problems into hydrological problems for water resource scheduling and reduces the complexity of model coupling. In the decision-making application example of the Hanjiang–Rongjiang–Lianjiang Water Transfer Project, the model’s average annual diversions under typical rich, average, and low-flow day schemes all satisfied the minimum diversion requirement of 5.50 × 108 m3. In addition, the average ecological discharge flows all met the ecological discharge requirements of 112 m3/s for the Rongjiang River, and electricity costs were reduced by at least 6.8568 million CNY. This model simplifies the calculation process, improves scheduling efficiency, and maximizes the benefits of the project, providing a new approach for solving water resource scheduling problems in tidal reaches.
1. Introduction
River estuaries [1] are generally flat, densely populated areas that have become economically developed [2]. However, with such rapid economic and social development, water resource development and associated pollutants are increasing, which has resulted in a sharp decline in the self-purification capacity of rivers and a deterioration of the ecological environment [3,4]. Such degradation seriously restricts the productivity and living standards of residents, such as those within the Lianjiang River area within the Pearl River Delta region of China. The construction of water diversion projects [5,6,7] and the transfer of water from external basins [8] can effectively improve the self-purification capacity of river water bodies and their environmental capacity, which is essential for restoring and improving the ecological environment of estuarine areas. However, under the dual influence of river runoff and ocean tides, the hydrodynamic conditions of estuarine river sections [9,10,11] entering the sea are complex [12,13,14,15,16], and this increases the difficulty in scheduling water resources in tidal reaches. Inappropriate scheduling schemes result in freshwater resource wastage or the influx of salty water and other unfavorable situations, which further deteriorate the quality of water in the receiving area.
Current studies on water resource dispatching in tidal reaches have mainly focused on two aspects. The first involves analyses and observations of the mechanism impacting the estuarine water environment relating to water project dispatching in the upstream area of tidal reaches. For example, Zhou et al. [17] analyzed the impact of upstream reservoir flood controls and power generation schedules on the change in the tidal level in the estuary of the Qiantang River. Additionally, Kong [6] studied the impact of inter-river water diversions on water pollution controls in the Liaohe River estuary. Yi et al. [18] studied the impact of water and sand transfer from the Xiaolangdi Reservoir on the environment and plankton in the Yellow River estuary, and Xiao and Ji [19] analyzed the impact of freshwater and environmental factors on the change in estuarine salinity in several estuaries of the Pearl River estuary in China. Lu et al. [20] analyzed the law of saltwater intrusion in the Yangtze River estuary and the water supply energy of the Three Gorges Reservoir. The second aspect involves exploring the use of water engineering scheduling schemes for tidal reaches oriented to various types of scheduling objectives. For example, based on the established mathematical model of water quantity and quality of the tidal river network, Jiang et al. [21] used COD (Chemical Oxygen Demand) as the water quality simulation factor to simulate and analyze the water quality improvement effect of the Foshan river course under the joint dispatching of a sluice and pumping station in dry seasons. Aiming at the demand of water resources dispatching in typical river network areas, He et al. [22] proposed the joint dispatching strategy of gate pump-river reservoir to improve water environment and ensure water supply safety. The case study of the Pearl River Delta [22] proves that it can effectively shorten the water replacement time in the dry season and improve the degree of water supply security. Similarly, in the Pearl River Estuary, Ye et al. [23] used a combination of macro and micro methods to construct a water resources scheduling model that couples the salt tide forecasting model and the water resources system pipe network model. The simulation results [23] show that the model can reasonably describe the multi-source water quantity and water quality joint scheduling process in the Pearl River Estuary. Wang et al. [24] coupled the hydrodynamic module (HD) and advection-dispersion module (AD) in MIKE11 to simulate and evaluate a complex river network diversion and drainage scheduling scheme. Qin et al. [25] simulated the water level and flow changes caused by the action surface of various forces based on the hydrodynamic module of the planar two-dimensional hydrodynamic model MIKE21 and proposed a feasible ecological water replenishment scheme. Rahman and Ali [26] modeled a river based on the HEC-RAS one-dimensional unsteady flow to analyze the effects of flow and tide level variations and calibrated the model by comparing the simulated flow and water level with measured data from an intermediate station. He et al. [27] established a comprehensive hydrodynamic fitness (CHF) model of a basin based on water exchanges, saltwater intrusions, and sediment decomposition to study the effect of water diversion projects, reflect the local environmental conditions, and elucidate the effects of water allocation and water transfer projects. Furthermore, Iglesias et al. [2] utilized a 2DH version of openTELEMAC-MASCARET to build an estuarine hydrodynamic model aimed at establishing the location of estuaries with the highest development potential.
However, there are two main limitations associated with existing studies. First, most have been based on coupled hydrodynamic simulations and water resource scheduling models [28]. Such models are highly complex, involve long computation times, and it is generally difficult for them to meet the real-time scheduling requirements of water resource systems. Second, most existing studies have also considered changes in water quality in the receiving area or the amount of water supplied by the water transfer project as the primary goal in assessing the advantages, disadvantages, and feasibility of the dispatch program. In contrast, fewer studies have focused on reducing the cost of projects that divert and transfer water. For example, when evaluating the water resource dispatching scheme for the river network of the Pearl River estuary, Wang et al. [24] evaluated the advantages and disadvantages of the original dispatching scheme, the landscape dispatching scheme, and the emergency dispatching scheme using the exchange capacity of the water body as an evaluation index, that is, from the perspective of the half-exchange cycle and the water-exchange rate, whereas Qin et al. [25] analyzed the changes that occurred in the receiving area after receiving water by considering the amount of replenishment required for three rich, average, and dry years.
In the Hanjiang–Rongjiang–Lianjiang Water Transfer Project in Guangdong Province, firstly, the Rongjiang River has a typical tidal river section, and secondly, the project is an inter-basin water transfer project, which meets the requirements of this paper, that is, the inter-basin water transfer project of the tidal river section. Therefore, we focused on the Hanjiang–Rongjiang–Lianjiang Water Transfer Project in the coastal area of Guangdong, China, to introduce the traditional concept of a “freshwater reservoir” into scheduling the water resources of the tidal reach of the river with the main goal of reducing the cost of water diversion and ensuring the ecological flow. In this respect, we considered the freshwater area of the tidal reach of the river as a “freshwater reservoir”, and through considering the tidal water jacking characteristics, we propose the concept of a “Flexible Fresh Water Reservoir”.
2. Study Area
2.1. Overview of Study Area
This paper focuses on the adjacent Hanjiang River, Rongjiang River, and Lianjiang River located on the Chaoshan Plain in eastern Guangdong Province, China. All three rivers flow into the sea. The estuaries of the Hanjiang and Lianjiang Rivers are equipped with tidal gates; however, the estuary of the Rongjiang River is not. Therefore, the Rongjiang River Estuary is representative of a typical tidal reach. The distribution and development of water resources among the three rivers are uneven. From north to south, the Hanjiang River has the largest water resources, followed by the Rongjiang River, and then the Lianjiang River. However, the utilization rates of these resources are inversely related to their availability: the Hanjiang River has the lowest utilization rate, the Rongjiang River is in the middle, and the Lianjiang River has the highest rate. The Lianjiang River Basin faces significant pollution issues, with severe over-extraction of ecological flows, necessitating urgent ecological water supply. In response, Guangdong Province initiated the Hanjiang–Rongjiang–Lianjiang Water Transfer Project. This project uses the Hanjiang River as the main water source and connects with the Rongjiang River as a secondary water source. It aims to replenish the Lianjiang River through rivers, tunnels, and pipelines while simultaneously addressing the water needs of the downstream areas of the Hanjiang and Rongjiang Rivers. The project’s objectives are to enhance the carrying capacity of the Lianjiang River’s water environment, optimize the allocation of water resources in the Three Rivers Basin, and promote the restoration and improvement of the aquatic ecosystem in the ChaoShan Plain.
The Hanjiang–Rongjiang–Lianjiang Water Transfer Project utilizes the Luhu Tunnel Water Diversion Project to redirect water from the Hanjiang River to the Fengjiang River, which is a tributary of the Rongjiang River. Additionally, the project involves the Chaoshui River Dredging Project and the Guanbu Water Pumping Project, which transport water from the Fengjiang River estuary of the Rongjiang River to the Lianjiang River. Among these, the Chaoshui River Dredging Project operates as an artesian diversion, while the Guanbu Water Pumping Project functions as a pumping station. Because there is no tidal gate at the estuary of the Rongjiang River, the lower reaches of the river are influenced by tidal fluctuations, impacting areas up to the Sanzhou Barrage on the main stream and the Beihe Barrage Gate on the tributary Beihe. Both the water diversion outlets of the Chaoshui River Dredging Project and the Guanbu Water Pumping Project are located in the tidal section of the river, complicating the management of water resources for the Hanjiang–Rongjiang–Lianjiang Water Transfer Project. This paper focuses on the tidal zone of the Rongjiang River from the Sanzhou Barrage in the main stream down to the tributary Beihe Barrage Gate, extending to the sea. The geographic distribution of the river, along with engineering and hydrological stations, is illustrated in Figure 1, which includes the Mayu Tide Station as the tidal monitoring station.
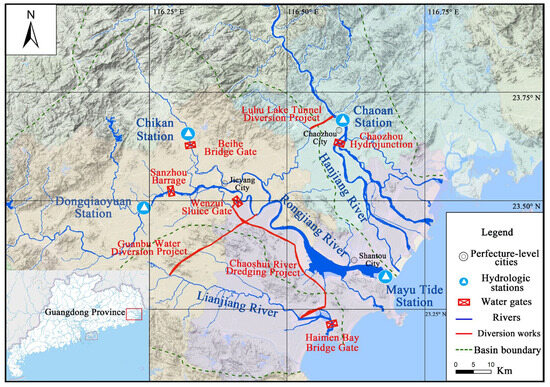
Figure 1.
Map showing distribution map of Hanjiang–Rongjiang–Lianjiang Water Transfer Project.
2.2. System Generalization
The study area selected was the tidal-sensitive area below the Sanzhou Barrage of the main stream of the Rongjiang River and the Beiheqiao Barrage of the tributary up to the mouth of the estuary. The Hanjiang–Rongjiang–Lianjiang Water Transfer Project was generalized based on the relative positions of the Hanjiang, Rongjiang, and Lianjiang Rivers, as well as the hydraulic connections and topological relationships among the sub-projects (Figure 2).
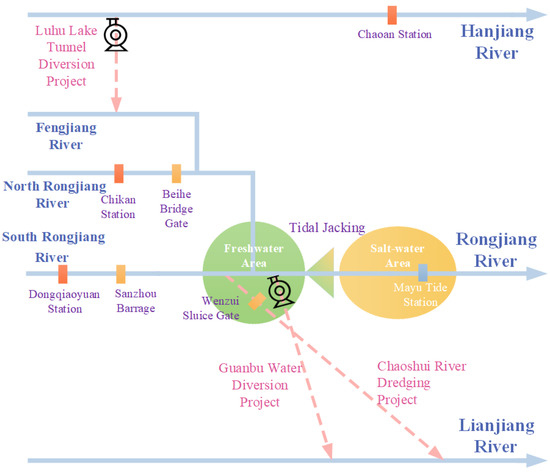
Figure 2.
Generalization of the Hanjiang–Rongjiang–Lianjiang Water Transfer Project.
2.3. Data
The inputs to the system are the diversions from the Luhu Lake Tunnel Diversion Project and the incoming water from the South and North Rongjiang River, and the outputs are the withdrawals from the Rongjiang River’s Guanbu Pumping Station, the Chaoshui River Dredging Project, and the Rongjiang River’s river channel discharges (Figure 2). The data utilized include the annual water flow from 1967 to 2017 at Dongqiaoyuan Station on the South Rongjiang River and Chikan Station on the North Rongjiang River; the diversion flow from Luhu Lake on the Hanjiang River; the ecological, domestic, industrial, and agricultural water demand of the Rongjiang River; the topography of 96 measured river cross-sections from the Sanzhou Barrage on the South Rongjiang River and Beiheqiao Barrage on the Beihe River to the sea mouth; and tidal information from 1954 to 2017 from the Mayu Tide Station at the mouth of the Rongjiang River.
3. Methods and Principles
3.1. Flexible Freshwater Reservoir Conceptualization
Owing to differences in density, the upstream water of the river entering the sea is blocked by tidal water in the tidal reach, forming a freshwater area similar to a freshwater reservoir. The tidal water is therefore considered to be a reservoir dam. The dam height and site changed with fluctuations in the tidal water level; therefore, the freshwater area is regarded as a flexible freshwater reservoir, and a schematic diagram is shown in Figure 3.
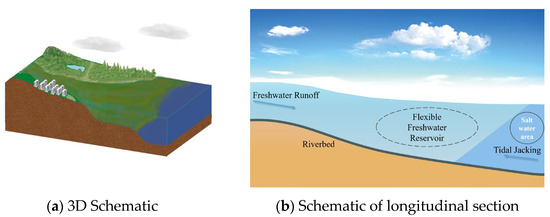
Figure 3.
Diagram of flexible freshwater reservoir.
3.2. Flexible Freshwater Reservoir Characterization Curve
3.2.1. Calculation of Stage-Capacity Curve
The water level and capacity curves of the flexible freshwater reservoir differ during various tide levels. Based on the use of a combination of different tidal levels and upstream water inflows, a one-dimensional hydrodynamic model was employed to calculate the water surface line of the tidal reach, and the water storage capacity of the reach was calculated using a cross-sectional method [29]. In the tidal reach, the water level of the flexible freshwater reservoir is elevated due to the intrusion of the salty tide, and the water from the upstream cannot be discharged and is stored in the reservoir; after the tide recedes, the water level of the reservoir decreases, and the freshwater is discharged. The water surface line of the flexible freshwater reservoir is calculated based on a one-dimensional constant flow. The one-dimensional constant flow calculation formula is as follows:
where and are the water levels of the upstream and downstream sections of the study area, respectively; and are the kinetic energy correction coefficients of the upstream and downstream sections, respectively; and are the average velocity of the upper and lower reaches of the river section, respectively; is the acceleration of gravity; and are the frictional head loss and local head loss, respectively; is the calculated river flow; is the length of the river; is the average flow modulus of the upstream and downstream sections; is the loss coefficient; is the average velocity of the section; is the river roughness; is the cross-sectional area of water; and is the hydraulic radius.
3.2.2. Calculation of Discharge Capacity Curve
The discharge capacity of the flexible freshwater reservoir is calculated based on the reservoir’s water level and capacity curves, as follows:
where is the discharge volume of the reservoir at time ; and represent the storage volume of the reservoir at times and , respectively, which are obtained by querying the water level and storage capacity curves; and is the length of a single time period.
3.3. Tidal-Sluice-Pump Optimal Operation Model Based on Flexible Freshwater Reservoir Concept
The aim of optimal water resource scheduling is to meet the temporal and spatial demands for water resources with respect to both quantity and quality, thereby ensuring the coordinated development of the economy, society, and ecological environment, and fully utilizing the limited water resources to obtain the best comprehensive benefits. The aim of such optimal scheduling is generally related to meeting economic, social, and ecological goals. In the water transfer process, the energy consumption of pumping stations is an important factor that needs to be considered to ensure that water transfer projects provide comprehensive benefits. The amount of water diverted and the ecological water demand are also important indicators of whether comprehensive benefits are being provided. In this study, an optimal scheduling model of a tidal-sluice pump based on a flexible freshwater reservoir was constructed based on the following: the highest average weighted water level of the pumping stations at all levels during the scheduling period, the maximum amount of water transferred from the receiving area during the scheduling period, the maximum amount of ecological discharge during the scheduling period, and the scheduling objectives associated with energy consumption, the water supply, and the ecological water demand.
3.3.1. Objective Functions
This paper examines the objective function from three perspectives: economic benefits, social benefits, and ecological benefits. The operating electricity cost of the pumping station represents the economic benefits; thus, a lower electricity cost for the same volume of water diverted indicates better economic benefits. Social benefits are reflected in the amount of water diverted; therefore, a larger quantity of water diverted for the same electricity charge signifies improved social benefits. Lastly, ecological benefits are represented by the amount of ecological discharge, where a greater volume of ecological discharge corresponds to enhanced ecological benefits.
(1) Economic efficiency target, . This function is mainly reflected in the energy consumption of the pump station and is related to the pump’s head, which represents the work of the pump per unit weight of fluid and is commonly used to measure the pump’s ability to lift fluids. It is affected by the water level of the intake; when the water level is too low, the head increases, the operating efficiency of the pumping station is reduced, and the energy consumption increases. Therefore, it is expressed by the highest average weighted water level of the pumping station during the scheduling period. The use of a tidal river reach in which a high amount of water is diverted reduces the energy consumption of the pumping station. The specific formula used to calculate this is as follows:
where is the average water level at the intake during the start-up period of the pumping station; is the total number of scheduling periods; is the start-up state of the pumping station at time , with a value of 1 indicating start-up and 0 indicating shutdown; and is the water level at the intake of the Guanbu Water Diversion Project at time . The pumping station can be turned on at any time.
(2) Social benefits target, . This function is mainly embodied in the water transfer project diversion through the Rongjiang Guanbu Water Diversion Project and the Chaoshui River Dredging Project to solve the problem of diverting water from the Lianjiang River, maximizing social benefits, and using the maximum amount of water transferred from the receiving area during the scheduling period to approximate the social benefits. The social benefit target can be expressed as follows:
where is the total amount of water transferred during the scheduling period, is the lifting flow rate of the Guanbu Water Diversion Project at time , is the diversion flow rate of the water sluice on the farms at time , and is the length of a single period.
(3) Eco-efficiency target, . This function is mainly reflected in the ecological discharge of water; specifically, during water transfer, the ecological flow of the lower reaches of the Rongjiang River must not be destroyed. If excessive water is diverted, river flow will decrease, disrupting downstream ecology and degrading water quality. The flexible freshwater ecological discharge of the reservoir is evaluated to measure the ecological benefits. Regarding discharge capacity limits, the higher the ecological discharge, the stronger the ecological benefits. The eco-efficiency target can be expressed as follows:
where is the ecological discharge of water from the river downstream of the flexible freshwater reservoir, and is the discharge flow of the reservoir at time .
3.3.2. Constraint Conditions
(1) The water balance constraints are as follows:
where and are the inlet and outlet flows, respectively, of the flexible freshwater reservoir at time ; , , and are the water transfer flows of the South, North, and Han branches of the Rongjiang River, respectively; and , , , , and are the total water consumption of the Rongjiang River, the domestic, industrial, and agricultural water consumption rates, and the water demand for loss at time , respectively.
(2) Water demand constraints are reflected in five aspects: ecological, domestic, industrial, agricultural, and water losses during water transfers, of which the ecological downstream water constraint is calculated as follows:
The domestic water demand constraints are calculated as follows:
The industrial water demand constraints are calculated as follows:
The agricultural water demand constraints are calculated as follows:
And the water loss constraint during a water transfer is calculated as follows:
where , , , , and are the appropriate ecological water demand, domestic water demand, industrial water demand, agricultural water demand, and water loss demand for the Rongjiang River during the scheduling period, respectively.
(3) Water transfer project constraints. The specific expressions are as follows:
where and are the overcurrent capacities of the Guanbu and Wenzui Sluice Gates, respectively.
3.3.3. NSGA-III Algorithm
The main tenet of the NSGA-III algorithm is to introduce a reference point mechanism based on NSGA-II and to retain individuals of the population that are non-dominated and close to the reference point. The NSGA-III and NSGA-II algorithms have similar frameworks, and the difference between the two mainly stems from changes in the selection mechanism. NSGA-II is mainly sorted by the crowding degree, which obviously does not play a consequential role in high-dimensional target spaces, whereas NSGA-III drastically adapts crowding degree sorting, thereby maintaining population diversity by introducing widely distributed reference points. Based on the Pymoo (version 0.6.1.1) library in Python(version 3.9), an optimal scheduling model was established, and the NSGA-III algorithm was selected to solve the construction model. Pymoo is an open-source multi-objective optimization library that focuses on solving multi-objective optimization problems. The design concept of Pymoo is easy to use and highly scalable; the library contains a series of classical optimization algorithms that have been implemented, such as NSGA-II and MOEA/D, and supports new custom optimization algorithms. Pymoo provides a set of flexible and efficient tools to help researchers and developers solve complex problems, such as engineering design and machine learning hyperparameter tuning, and users can customize the objective functions and constraints. In addition, Pymoo provides a rich set of evaluation metrics for measuring the quality of optimization results, the core feature of which is its modular architecture. This feature allows users to easily adapt or replace algorithmic components such as population generators, crossover operations, and mutation operations.
The proposed model selected three typical days obtained by wiring according to Pearson’s type III curve, namely October 9, 1982 (p = 25%), April 1, 1994 (p = 50%), and February 8, 1969 (p = 75%), and it set the population number as Np = 200, the number of evolutionary generations as N = 5000, and initial water levels as 1.84, 0.79, and 1.69 m, respectively, for the scheduling periods.
3.4. Multi-Objective Collaborative Decision-Making Theory
A multi-objective decision problem is formulated as follows:
where is the feasible domain, and ; is the -dimensional decision variable, and are the objective functions.
We used the degree of system coordination to express the optimal degree of each goal. Introducing a system coordination degree can promote collaboration among parties and improve the efficiency and quality of multi-objective optimization problems. In practice, it is necessary to balance the interests and goals of all parties, maximize synergistic effects, fully consider the interests and goals of all parties, and produce a “win-win” outcome situation. In this study, the independent variables constituted pumping station opening and closing, and the objectives were pumping station operation costs, the water supply for the water transfer project, and the ecological underflow. Logically, these three objectives cannot be optimized simultaneously. For example, giving priority to the water supply quantity of the water transfer project may lead to higher pumping station operating costs and insufficient ecological underdrainage flow, which will deteriorate the ecology and water quality downstream of the Rongjiang River. In contrast, although prioritizing ecological discharge volume may reduce the operating cost of the pumping station, it will also result in an insufficient volume of water for the water transfer project, which will affect moderation of the water quality of the Lianjiang River.
To unify the metrics, the synergistic contribution function between and the decision variable pump station start/stop was defined using the following:
(1) The larger the indicator, the more desirable the type of objective function
where is the tolerance limit of the decision maker of , that is, the minimum acceptable target value; and is the ideal value of , that is, the maximum value.
(2) The smaller the indicator, the more desirable the type of objective function
where is the tolerance limit of the decision maker, that is, the highest acceptable target value; and is the ideal value of , that is, the minimum value.
The synergistic contribution function defined in Equations (14) and (15) satisfies 0 < < 1, and the larger it is, the higher the degree of synergy between the objective function and decision variable.
The synergistic contribution displacement rate function between objective functions and is defined as follows:
A replacement rate analysis was performed to facilitate the solution of the multi-objective decision problems.
Using the defined synergistic contribution function , the multi-objective decision problem (13) was transformed into a multi-objective synergistic decision model as follows:
The system coordination degree function for the multi-objective decision problem (13) is defined as follows:
where ; ; .
The system coordination function satisfies , where the closer is to 1, the higher the system coordination is. Therefore, solving the multi-objective decision model (17) can be transformed into solving the single-objective optimization problem with maximum system coordination as follows:
4. Results
4.1. Flexible Freshwater Characteristic Curve
4.1.1. Stage-Capacity Curve
Based on the tidal reaches of the Rongjiang River and different upstream water inflows, a cross-section between the water intakes at the Guanbu and the Mayu Tide Stations was selected as the virtual dam site for the flexible freshwater reservoir. The water level and reservoir capacity curves of the flexible freshwater reservoir in the Rongjiang River were constructed using the one-dimensional constant flow in Hec-Ras (version 5.0.7, developed by United States Army Corps of Engineers, Vicksburg, MS, USA) and the cross-sectional method (Figure 4), with the coordinate system of the Zhujiang River as the base plane. The capacity curves of the flexible freshwater reservoir are a cluster of smooth curves that change with the upstream water inflow (Figure 4). Each curve represents the change in the reservoir capacity caused by the change in the tidal level when the upstream water inflow is certain. When the upstream inflow increases, the curvature of the water level storage capacity curve obviously becomes larger; that is, the curve becomes steeper. When the upstream inflow is constant, the higher the tidal level of the virtual dam site and the greater the storage capacity of the reservoir. The higher the water level of the reservoir, the closer the curves are.
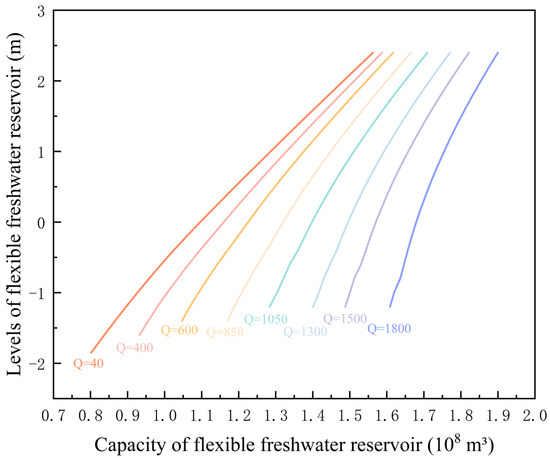
Figure 4.
Stage-capacity curve of flexible freshwater reservoir.
The reservoir capacity curve is not only a form of expression; Figure 4 shows a curved cluster drawn from the change in flow. The curved cluster was drawn from the starting water level of the water intake of the Guanbu Pumping Station, which also displays a smooth curved cluster.
4.1.2. Discharge Capacity Curve
The discharge capacity curve of the flexible freshwater reservoir of the Rongjiang River was studied. Combined with the discharge frequency calculation, three typical days representing high-flow days (p = 25%), normal-flow days (p = 50%), and typical low-flow days (p = 75%) were obtained using the Pearson type III curve to calculate and analyze the discharge capacity. The process results are shown in Figure 5.
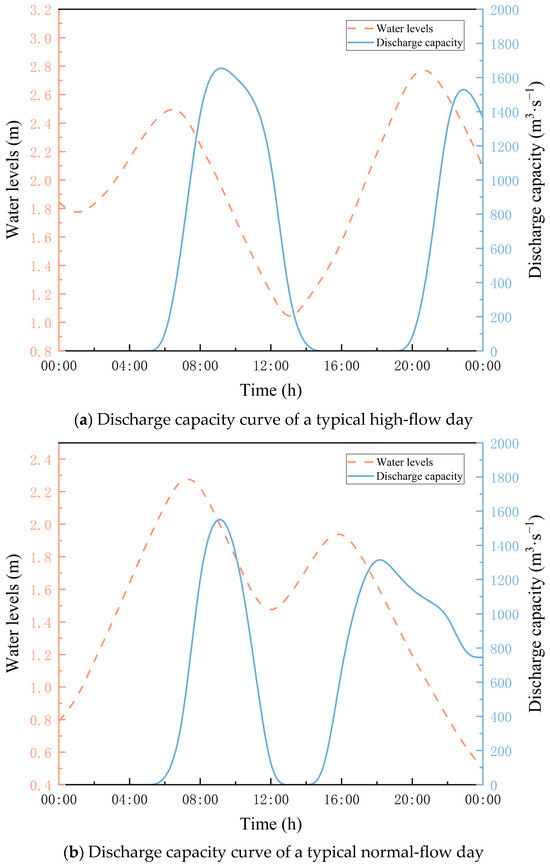
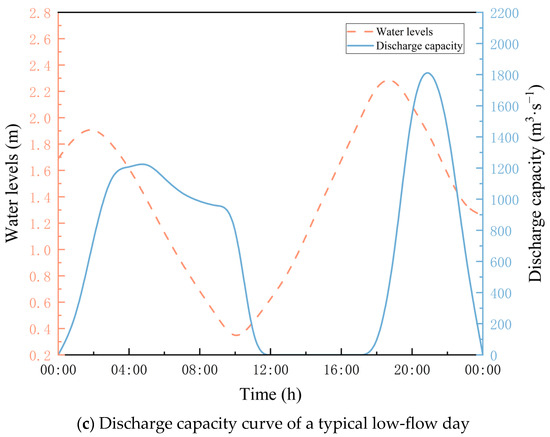
Figure 5.
Typical daily discharge capacity curve.
Regardless of the typical day scenario, the water level of the reservoir varied with high and low tides during the day, and the water level process conformed to the tidal level rise and fall process (Figure 5). During the rising tide period of the reservoir water level, the incoming water from upstream was stored in the flexible freshwater reservoir and could not be discharged; during the falling tide period of the reservoir water level, the reservoir was discharged. The water-level change process, which reflects the characteristics of high and low tides, was chosen for graphical presentation. The discharge capacity curves for the three typical days show that the discharge capacity of the flexible freshwater reservoir is related to the amount of water stored in the reservoir during rising tide. If more water is stored in the reservoir during the rising tide period, the peak discharge during the falling tide period is also higher. This characteristic also determines that the discharge capacity curve of the reservoir cannot be plotted as a standard discharge capacity graph and can only be shown in the form of a typical day’s discharge process.
4.2. Multi-Objective Collaborative Decision-Making
According to the synergistic decision theory described in Section 3.4 and Equations (16) and (18), the Euclidean distance minimization formula was used to calculate the degree of coordination by considering , and the weights of the two objective functions of water diversion and ecological discharge were 0.5. The partial synergistic contribution, synergistic replacement rate, and degree of system coordination on different typical days are shown in Table 1, Table 2 and Table 3.

Table 1.
Results of synergistic decision-making calculations for high-flow day.

Table 2.
Results of synergistic decision-making calculations for normal-flow day.

Table 3.
Results of synergistic decision-making calculations for low-flow day.
Based on the system coordination degree, the optimal programs for abundant, flat, and dry water days were determined as Program 5, Program 1, and Program 1, respectively. When the contribution of water diversion increases, the contribution of ecological drainage decreases, and the two are in a competitive relationship.
4.3. Multi-Objective Optimal Scheduling Results
Three typical day-optimal scheduling processes were obtained based on the multi-objective collaborative decision-making method for non-inferior solution frontiers. The typical daily scheduling process of the flexible freshwater reservoir in the Rongjiang River is shown in Figure 6, where (i), (ii), and (iii) are the optimized scheduling results for high-flow, normal-flow, and low-flow days, respectively. According to the results of typical daily scheduling, some basic rules can be summarized: when the tide rises, the Guanbu Water Pumping Station should be operated, and the pool sluice should be closed simultaneously. This approach maintains the flexible freshwater reservoir’s high water level, reduces the pump head of the Guanbu Water Pumping Station, and reduces the operating costs of the pumping station. In the ebb tide, and when the water level remains high, the Wenzui Sluice Gate should be opened to provide a self-flow water diversion. During an ebb tide, when the water level is low, the Guanbu Water Pumping Station should be closed, and only the Wenzui Sluice Gate should be opened to provide a self-flow water diversion; the upstream water should be naturally discharged to meet the downstream ecological water demand.
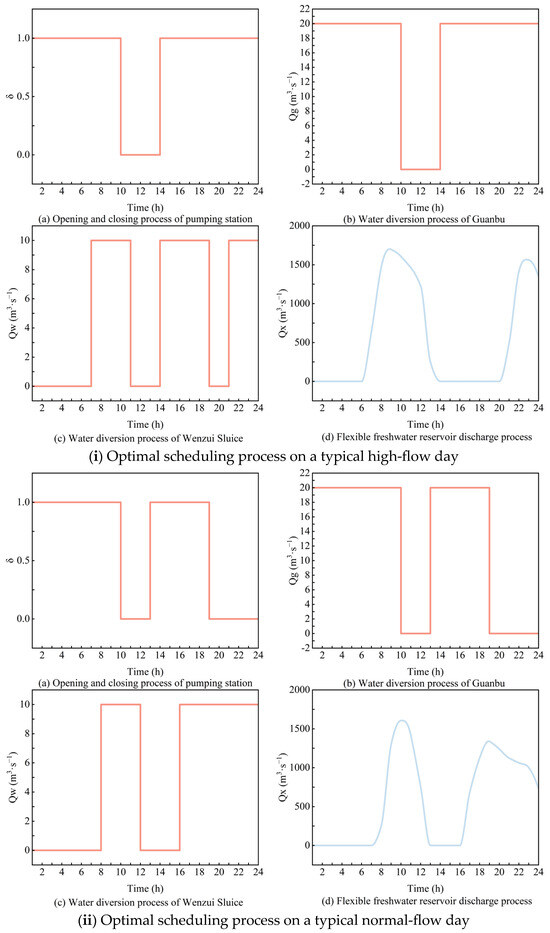
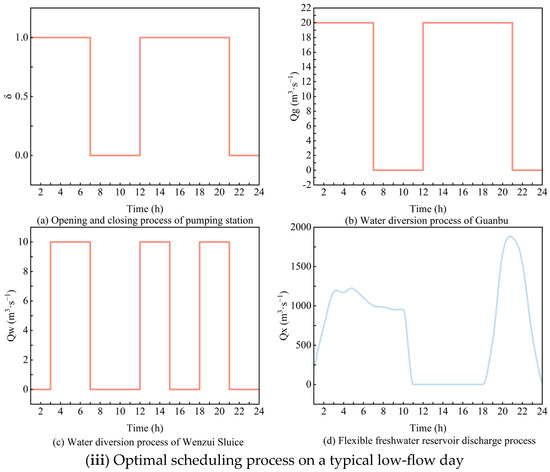
Figure 6.
Typical daily optimal scheduling process of “Flexible Fresh Water Reservoir”.
The conventional scheme and the three typical daily scheduling schemes were calculated according to the corresponding annual indicators (Table 4). The three indicators are the annual total cost of pumping electricity, the average annual amount of water diversion, and the annual amount of ecological water discharged.

Table 4.
Comparison between a typical day optimization scheme and a conventional scheme.
In terms of economic benefits, the total installed capacity of the pressurized pumping station of the Rongjiang River Guanbu Diversion Project was 10,800 kW. The electricity cost of pumping was calculated according to the actual electricity consumption during pumping within the project. After consulting with the Shantou Municipal Electricity Supply Bureau, the price of purchased electricity was determined as 0.65 CNY/(kW·h), there were 242 annual pumping days on average, and the average annual pumping electricity cost before optimization was 40.8336 million CNY. The optimized high-flow day scheme of the Guanbu Water Pumping Station is as follows: operating for 20 h per day with an average annual pumping electricity cost of 33.9768 million CNY. The optimized normal-flow and low-flow day schemes are as follows: operating for 16 h per day, with an average annual pumping electricity cost of 27.1814 million CNY. Compared with before optimization, the average annual pumping electricity cost of the high-flow day scheme is reduced by 6.8568 million CNY, and the associated cost reductions for normal- and low-flow day schemes are both 13.6522 million CNY.
The average annual amount of water diverted was calculated as a quantitative indicator based on the typical daily average water diversion. Before optimization, the average annual amount diverted under the conventional scheme was 5.70 × 108 m3, and it was necessary to divert an average annual amount of 5.50 × 108 m3 in the Lianjiang River basin. After optimization, the average annual water amount diverted was 6.33 × 108 m3 for the high-flow day scheme, with 5.76 × 108 m3 and 5.66 × 108 m3 for the normal-flow and low-flow day schemes, respectively. Compared with the average annual amount of water diverted under the conventional scheme before optimization, the average annual amount diverted increased by 0.63 × 103 m3 and 0.06 × 108 m3 for the high-flow and normal-flow day schemes and decreased by 0.04 × 108 m3 for the low-flow day scheme. Compared with the average annual amount that needs to be diverted in the Lianjiang River Basin, the average annual amount diverted increased by 0.83 × 108 m3, 0.26 × 108, and 0.16 × 108 m3 for the high-flow day, normal-flow, and low-flow day schemes, respectively. The average annual amount of water diverted under the high-flow and normal-flow day schemes was greater than that of the conventional scheme before optimization. The average annual amount of water diverted under the low-flow day scheme was slightly less than that of the conventional scheme, but it nonetheless matched that of the Lianjiang River Basin. Combined with the economic benefits, the cost per m3 of diverted water decreased for each of the typical day-optimized dispatch schemes.
To quantify the ecological benefits, the annual amount of ecological water discharged was calculated as an auxiliary comparative indicator. Before optimization, the annual ecological discharge of the conventional scheme was 35.70 × 108 m3, and the average ecological discharge flow rate was 112 m3/s. After optimization, the annual ecological discharge of the high-flow day scheme was 114.64 × 108 m3, and the average ecological discharge flow rate was 363.52 m3/s; for the normal-flow day scheme, these values were 118.71 × 108 m3, and 376.43 m3/s, respectively, and those for the low-flow day scheme were 137.24 × 108 m3 and 435.19 m3/s, respectively. The ecological water demand flow in the wet season in Rongjiang was 113.20 m3/s, and the ecological water demand flow rate in the dry season was 14.8 m3/s. The results of the three typical daily scheduling schemes are clearly in accordance with the ecological discharge flow requirements. When the annual average water diversion increased, the annual ecological discharge decreased, demonstrating a clear competition between the two.
Before optimization, the pumping station in the conventional scheme was operated 24 h a day during the diversion period, which wastes electricity. In the optimized typical day scheme, the pumping station is open during high-tide periods and closed during low-tide periods, which reduces the operational cost of the pumping station, ensures water diversion and ecological water discharge, and maximizes the benefits of the water pumping project.
5. Discussion
Under the premise that the hydrodynamic conditions of the tidal river are complex and the cost of water transfer is one of the important factors considered with respect to inter-basin water transfer, the method proposed in this study considers the tidal jacking characteristics of the tidal river and employs these. While ensuring the amount of ecological discharge, its main goal is to optimize the cost of water project scheduling and the amount of water diverted, reduce the coupling degree between the hydrodynamic model and the water resource scheduling model, and improve the calculation efficiency. As the optimized pump operational time is linked to the high water level section, the pump head and operating costs are reduced, the operating efficiency is increased, and water diversion is guaranteed. In addition, as the pumps and gates are not continuously open for 24 h, the ecological discharge flow is also guaranteed.
The timing of water diversion, the amount of water diversion, and the change in water quality after drinking water in the receiving area are the main objectives of water resources regulation in the estuary area. Jiang et al. [21] studied the joint operation of sluice and pump in the dry season in the Foshan waterway, He et al. [22] proposed the joint operation strategy of sluice and pump-river reservoir in the Pearl River Delta. Ye et al. [23] proposed the coupling water resources scheduling model of the salt tide prediction model and the water resources system pipe network model in the Pearl River Estuary, Kong [6] studied the influence mechanism of upstream water conservancy project scheduling on the water environment of Liaohe Estuary, and Wang et al. [24] established the model based on MIKE11, which all improved the water diversion amount, shortened the water replacement time and improved the water quality of the estuary. Although there is currently no water quality model in this paper, the proposed model optimizes the timing of water diversion so that the ecological discharge flow in the diversion area and the amount of water diversion in the receiving area can be guaranteed, and at least the water quality in the diversion area will not deteriorate. If the water quality model of the study area can be increased to study the change in water quality in the water-receiving area after the implementation of the water diversion scheme, it will undoubtedly make this paper more perfect. The problem of water diversion cost, which is easy to ignore, is also regarded as one of the goals. Under the premise of ensuring the ecological discharge flow of the water diversion area, the benefits of the water diversion project are brought into play as much as possible.
The model proposed in this paper relies on the hydrodynamic model to construct the characteristic curve and converts the water resources scheduling problem in the estuary area into a multi-objective optimization problem. Different from the general practice, that is, using the hydrodynamic model to establish the water resources scheduling model in the study area, such as Wang et al. [24], coupled MIKE11’s hydrodynamic module (HD) and advection-dispersion module (AD) to simulate the water diversion and drainage scheduling scheme of complex river networks; Qin et al. [25] proposed a feasible ecological water replenishment scheme based on the hydrodynamic module of the planar two-dimensional hydrodynamic model MIKE21.
This study has room for improvement. Through studying inter-basin water transfer, we aimed to improve the water environment carrying capacity of the Lianjiang River Basin and promote the restoration and improvement of the water ecological environment. The optimization model of this paper stays at the level of improving the discharged ecological flow and fails to quantify the improvement of the water quality of Lianjiang River by the water transfer project due to the limitation of the Lianjiang River’s water quality data. Future studies should target the enhancement of the Lianjiang River’s water quality and incorporate it into a multi-objective optimization framework. The tidal conditions used in the model are based on historical data and do not take into account the future potential tidal changes caused by climate change. In the future, the tidal prediction model will be considered to improve the model. In order to understand the robustness and flexibility of the model, a sensitivity analysis model needs to be added in the subsequent research to test the influence of input parameters on the performance of the model. The potential role of stakeholders (such as local communities) in the decision-making process should also be taken into account. Increasing the corresponding potential role analysis model can make the model closer to real life. At the same time, in order to improve the universality of the model and enable the model to be applied in areas with limited computing resources, the model should be further simplified, or user-friendly tools should be developed to make the model easier to access. In addition, to ensure that the optimized scheduling scheme is universal and able to cope with different situations, rules should be extracted from the optimization scheme to obtain common scheduling rules and reduce the difficulty of daily management of sluices.
6. Conclusions
This study focused on the Rongjiang River Basin to generalize the tidal reach of the basin, construct a flexible freshwater reservoir model, and evaluate the joint optimal operation of the proposed reservoir from economic, social, and ecological perspectives. A tidal-sluice-pump multi-objective collaborative optimization scheduling model was established by analyzing the economic, social, and ecological requirements of the basin. Based on the proposed model, the NSGA-III algorithm was used to optimize this scheduling model. Three typical day-optimal scheduling processes were obtained based on a multi-objective collaborative decision-making method for non-inferior solution frontiers. The quantitative analysis of the typical schemes provides a theoretical basis for the optimal usage of flexible freshwater reservoirs in the Rongjiang River Basin. The main conclusions are as follows:
- (1)
- A flexible freshwater reservoir was constructed below the Guanbu diversion and above the Mayu Tide Station based on the Hec-Ras one-dimensional steady flow. The reservoir dam site and height change dynamically with the tides, and the reservoir capacity is thus dynamic.
- (2)
- The discharge capacity of the proposed reservoir is related to the degree of change in the reservoir storage. During the flood tide, the upstream inflow accumulates in the reservoir and cannot be discharged; the reservoir discharges water during ebb tides, and the discharge capacity at this time is related to the amount of storage accumulated in the flood tide section.
- (3)
- The optimized scheduling scheme reduces the cost of electricity, meets the requirements of water diversion and ecological drainage, simplifies the calculation process, and dramatically improves the scheduling efficiency. These results can provide an important reference for developing water resource scheduling schemes in tidal reaches.
In subsequent research, the scheduling rules of different typical days can be extracted according to the optimal scheduling results of typical days and water level changes at the diversion gates. Therefore, daily scheduling can be based on such information to reduce the scheduling workload. In addition, tidal sluice pump scheduling can be implemented to improve the river water environment.
Author Contributions
Conceptualization, X.W. and Y.W.; methodology, X.W., Y.W. and C.S.; software, C.S. and Y.X.; validation, K.Z. and X.P.; formal analysis, F.Z.; investigation, X.W.; resources, X.W.; data curation, X.W.; writing—original draft, C.S.; writing—review and editing, X.W.; visualization, K.Z. and C.S.; supervision, X.W.; administration, X.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Water Resources Science and Technology Program of Hunan Province. P.R.C (Grant No. XSKJ2024064-3), and the Key Scientific and Technological Project of the Ministry of Water Resources. P.R.C (Grant No. SKR-2022075).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Yan Wu was employed by the company China Three Gorges Renewables (Group) Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Liang, C.Z.; Yip, L.S. Tidal flats as a significant carbon reservoir in global coastal ecosystems. Front. Mar. Sci. 2022, 9, 900896. [Google Scholar] [CrossRef]
- Iglesias, I.; Bio, A.; Bastos, L.; Avilez-Valente, P. Estuarine hydrodynamic patterns and hydrokinetic energy production: The Douro estuary case study. Energy 2021, 222, 119972. [Google Scholar] [CrossRef]
- Nordhaus, I.; Roelke, D.L.; Vaquer-Sunyer, R.; Winter, C. Coastal systems in transition from a ‘natural’ to an ‘anthropogenically-modified’ state. Estuar. Coast. Shelf Sci. 2018, 211, 1–5. [Google Scholar] [CrossRef]
- Liu, X.Q.; Li, M.T.; Chen, J.; Jun, X.Y.; Zhang, W.G.; Chen, Z.Y.; Ai, W.; Hou, L.J.; Pan, Z.H. Natural and reservoir-induced channel changes in the Yangtze River tidal reach. J. Hydrol. 2022, 605, 127398. [Google Scholar] [CrossRef]
- Lian, J.J.; Yan, L.L.; Yao, Y.; Chen, Y.L. Hydrodynamic and water quality impacts of water transfer project on regulating reservoir: A case study of Dongzhang reservoir. J. Hydrol. 2022, 614, 128494. [Google Scholar] [CrossRef]
- Kong, X. Influence of inter-river water diversion on estuary pollution control: A case study of Liaodong Bay. Reg. Stud. Mar. Sci. 2024, 70, 103362. [Google Scholar] [CrossRef]
- Xing, M.; Qu, S.; Xu, H.; Shi, P.; Chen, X.; Ji, F.; Liu, M. A continuation-dynamic constitution analysis approach based on digital stable marker tracing and study on simulation of ecological tidal water diversion. Sci. Rep. 2023, 13, 23096. [Google Scholar] [CrossRef]
- Xi, H.; Xie, Y.; Liu, S.; Mao, Q.; Shen, T.; Zhang, Q. Multi-objective optimal scheduling of generalized water resources based on an inter-basin water transfer project. Water 2023, 15, 3195. [Google Scholar] [CrossRef]
- Pan, H.D.; Xu, T.F.; Wei, Z.X. A modified tidal harmonic analysis model for short-term water level observations. Ocean. Modell. 2023, 186, 102251. [Google Scholar] [CrossRef]
- Huang, H.; Wang, Y.; Wang, S.; Lan, Y.; Huang, X. Saltwater intrusion in the Changjiang River estuary in response to the east route of the south-to-north water transfer project in the new period after 2003. Sustainability 2024, 16, 683. [Google Scholar] [CrossRef]
- Kim, J.W.; Woo, S.-B. A numerical approach to the treatment of submerged water exchange processes through the sluice gates of a tidal power plant. Renew. Energy 2023, 219, 119408. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, X.; Dong, C.; Ren, J.; Zhang, Q.; Huang, Y. Characteristics and influencing factors of storm surge-induced salinity augmentation in the Pearl River estuary, South China. Sustainability 2024, 16, 2254. [Google Scholar] [CrossRef]
- Giannini, G.; Ramos, V.; Rosa-Santos, P.; Calheiros-Cabral, T.; Taveira-Pinto, F. Hydrokinetic power resource assessment in a combined estuarine and river region. Sustainability 2022, 14, 2606. [Google Scholar] [CrossRef]
- Li, M.; Chen, Z.; Finlayson, B.; Wei, T.; Chen, J.; Wu, X.; Xu, H.; Webber, M.; Barnett, J.; Wang, M. Water diversion and sea-level rise: Potential threats to freshwater supplies in the Changjiang River estuary. Estuar. Coast. Shelf Sci. 2015, 156, 52–60. [Google Scholar] [CrossRef]
- Geyer, W.R.; Ralston, D.K.; Haller, M.C.; Bassett, C.; Honegger, D. The structure and dynamics of an estuarine tidal intrusion front. J. Geophys. Res. Ocean. 2024, 129, e2023JC020371. [Google Scholar] [CrossRef]
- Guo, Y. Hydrodynamics in estuaries and coast: Analysis and modeling. Water 2022, 14, 1478. [Google Scholar] [CrossRef]
- Zhou, H.; Pan, H.; Gan, M.; Zhang, G.; Wang, S.; Ying, C. Study on the tidal variability related to flooding and hydroelectric operations in the Qiantang River estuary. Estuar. Coast. Shelf Sci. 2024, 305, 108845. [Google Scholar] [CrossRef]
- Yi, Y.J.; Gao, Y.N.; Wu, X.F.; Jia, W.F.; Liu, Q. Modeling the effect of artificial flow and sediment flux on the environment and plankton of an estuary. Int. J. Sediment. Res. 2023, 38, 335–348. [Google Scholar] [CrossRef]
- Xiao, F.; Ji, C. Impacts of environmental factors and freshwater discharges from multiple river outlets on estuarine salinity variation in rainy season: A case study of the Pearl River Estuary in China. J. Hydrol. 2023, 623, 129784. [Google Scholar] [CrossRef]
- Lu, J.; Chen, J.H.; Chen, S.L.; Fu, Q.P. Feasibility analysis on control of saline tide of Yangtze River estuary by co-regulation of reservoir group in upper Yangtze River. Yangtze River 2015, 46, 6–9+23. [Google Scholar]
- Jiang, T.; Zhu, S.L.; Zhang, Q.; Chen, X.H. Numerical simulation on effects of gate-pump joint operation on water environment in tidal river network. J. Hydraul. Eng. 2011, 42, 388–395. [Google Scholar]
- He, X.C.; Huang, F.F.; Ru, X.W.; Wan, D.H.; Zheng, J.L.; Wu, Q.; Zhang, L. Study on Water Resources Dispatching Strategy and Technology in Typical River Network Area of the Pearl River. J. North China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2016, 37, 55–60. [Google Scholar]
- Ye, R.H.; Zhang, W.M.; Shen, Z.; Zou, H.Z.; Gong, X.L. Water Supply Operation Model of Pearl River Estuary in Period of Dry Season Saltwater Tide. Water Resour. Power 2016, 34, 23–27. [Google Scholar]
- Wang, H.; Xu, W.; Wu, X. Study on water environmental dispatch scheme for complex river network in Pearl River Estuary. MATEC Web Conf. 2018, 246, 02031. [Google Scholar] [CrossRef]
- Qin, L.J.; Gao, Z.W.; Xie, Y. A simulation of ecological water replenishment for Liaohe estuary wetland based on the MIKE21 model. Wetl. Sci. Manag. 2024, 20, 25–30. [Google Scholar]
- Rahman, M.; Ali, M.S. Drivers of tidal flow variability in the Pussur fluvial estuary: A numerical study by HEC-RAS. Heliyon 2024, 10, e25662. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Jiang, A.; Zhang, J.; Xu, H.; Xiao, Y.; Chen, S.; Yu, X. Comprehensive hydrodynamic fitness of an estuary channel and the effects of a water diversion inflow. Estuaries Coasts 2021, 45, 382–392. [Google Scholar] [CrossRef]
- Kai, F.; Haoxuan, D.; Liang, G. Accurate water level predictions in a tidal reach: Integration of physics-based and machine learning approaches. J. Hydrol. 2023, 622, 129705. [Google Scholar] [CrossRef]
- Wei, L.; Zhan, N.; Tao, C. Geometric analysis of reservoir capacity calculation model based on cross-section method. Yellow River 2006, 10, 72–73 + 77. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).