Effects of Climate Change on the Estimation of Extreme Sea Levels in the Ayeyarwady Sea of Myanmar by Monte Carlo
Abstract
1. Introduction
2. Study Area
3. Numerical Methods
3.1. Description of Hydrodynamic Model
3.2. Description of Cyclone Model
3.3. Hydrodynamic Model Configuration
3.4. Hydrodynamic Model Validation
3.4.1. Tidal Level Validation
3.4.2. Storm Surge Validation
4. Implementation of the Monte Carlo Approach
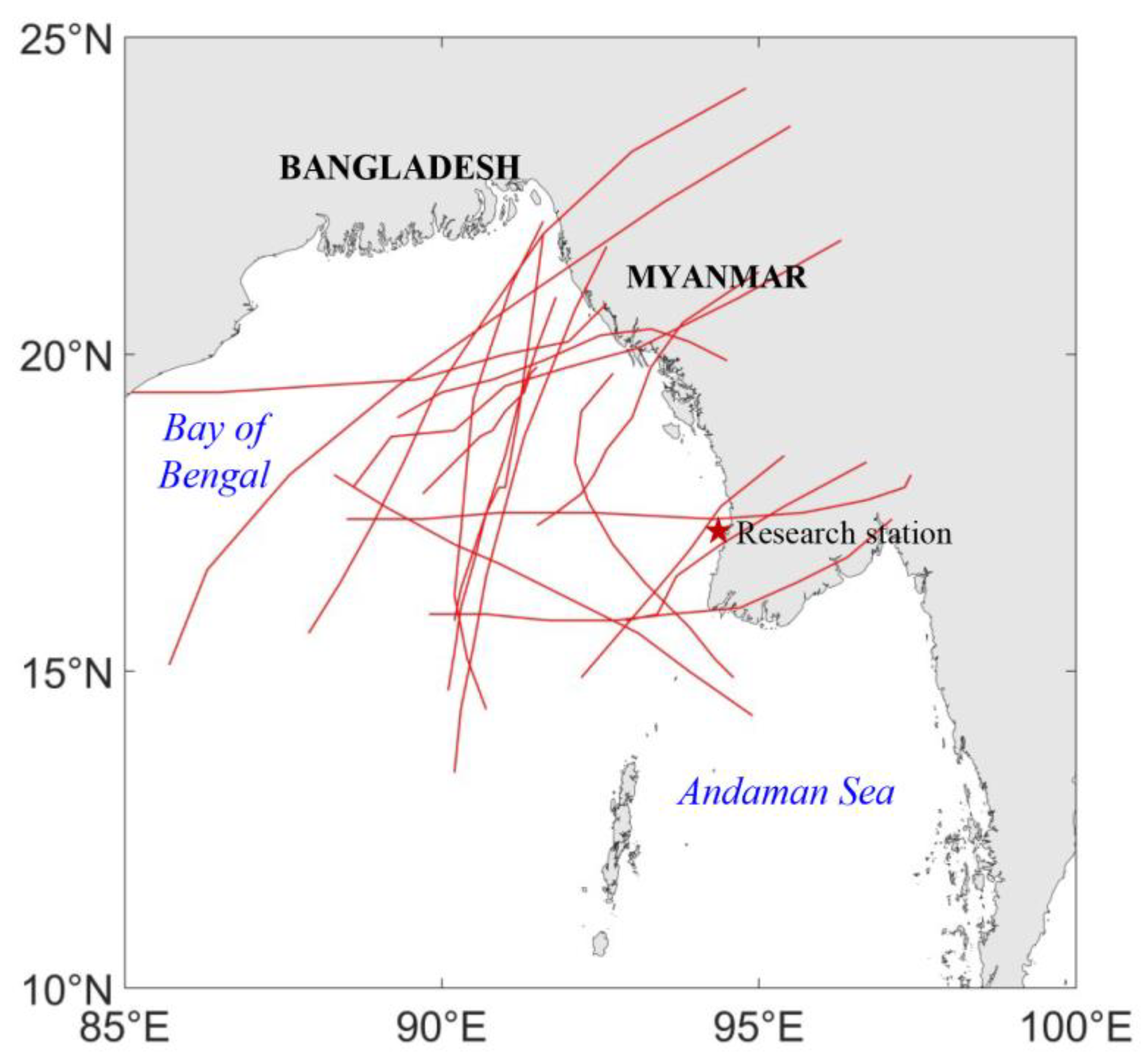
4.1. Selection of Historical Typical Cyclones
4.2. Generation of Synthetic Cyclone Tracks
5. Extreme Sea Levels in Myanmar’s Ayeyarwady Seas
5.1. Extreme Sea Level Estimation Under No Climate Change Influence
5.2. Extreme Sea Level Estimation Under Climate Change Influence
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, A.B.; Katz, R.W. US billion-dollar weather and climate disasters: Data sources, trends, accuracy and biases. Nat. Hazards 2013, 67, 387–410. [Google Scholar] [CrossRef]
- Dube, S.K.; Jain, I.; Rao, A.D.; Murty, T.S. Storm surge modelling for the Bay of Bengal and Arabian Sea. Nat. Hazards 2009, 51, 3–27. [Google Scholar] [CrossRef]
- Karim, M.F.; Mimura, N. Impacts of climate change and sea-level rise on cyclonic storm surge floods in Bangladesh. Glob. Environ. Change 2008, 18, 490–500. [Google Scholar] [CrossRef]
- Nicholls, R. Storm Surges in Coastal Areas; World Bank: Washington, DC, USA, 2006. [Google Scholar]
- Frank, N.L.; Husain, S.A. The deadliest tropical cyclone in history? Bull. Am. Meteorol. Soc. 1971, 52, 438–445. [Google Scholar] [CrossRef]
- Dasgupta, S.; Laplante, B.; Murray, S.; Wheeler, D. Climate Change and the Future Impacts of Storm-Surge Disasters in Developing Countries. SSRN Electron. J. 2009, 1–22. [Google Scholar] [CrossRef]
- Feng, A.Q.; Gao, J.B.; Wu, S.H.; Liu, Y.H.; He, X.J. A review of storm surge disaster risk research and adaptation in China under climate change. Prog. Geogr. 2016, 35, 1411–1419. [Google Scholar] [CrossRef]
- Bevacqua, E.; Maraun, D.; Vousdoukas, M.I.; Voukouvalas, E.; Vrac, M.; Mentaschi, L.; Widmann, M. Higher probability of compound flooding from precipitation and storm surge in Europe under anthropogenic climate change. Sci. Adv. 2019, 5, eaaw5531. [Google Scholar] [CrossRef]
- Zheng, F.; Westra, S.; Sisson, S.A. Quantifying the dependence between extreme rainfall and storm surge in the coastal zone. J. Hydrol. 2013, 505, 172–187. [Google Scholar] [CrossRef]
- Wu, W.; Leonard, M. Impact of ENSO on dependence between extreme rainfall and storm surge. Environ. Res. Lett. 2019, 14, 124043. [Google Scholar] [CrossRef]
- Rehana, S.; Dhanya, C.T. Modeling of extreme risk in river water quality under climate change. J. Water Clim. Change 2018, 9, jwc2018024. [Google Scholar] [CrossRef]
- Roy, K.; Gain, A.K.; Mallick, B.; Vogt, J. Social, hydro-ecological and climatic change in the southwest coastal region of Bangladesh. Reg. Environ. Change 2017, 17, 1895–1906. [Google Scholar] [CrossRef]
- Wallace, E.E.; MacArthur, R.C.; Chowdhury, S.; Sakumoto, L.K. FEMA Coastal Flood Hazard Analysis and Mapping Guidelines for the Pacific Coast; ASCE Library: Reston, VR, USA, 2012; pp. 247–256. [Google Scholar] [CrossRef]
- Xu, S.; Huang, W. Frequency analysis for predicting 1% annual maximum water levels along Florida coast, US. Hydrol. Process. 2008, 22, 4507–4518. [Google Scholar] [CrossRef]
- Xu, S.; Huang, W. Estimating extreme water levels with long-term data by GEV distribution at Wusong station near Shanghai city in Yangtze Estuary. Ocean Eng. 2011, 38, 468–478. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Li, Y.; Yu, H.; Wen, M.; Hu, Y. Risk assessment of coastal flooding disaster by storm surge based on Elevation-Area method and hydrodynamic models: Taking Bohai Bay as an example. China Geol. 2024, 7, 494–504. [Google Scholar] [CrossRef]
- Xu, S.; Huang, W.; Zhang, G.; Gao, F.; Li, X. Integrating Monte Carlo and hydrodynamic models for estimating extreme water levels by storm surge in Colombo, Sri Lanka. Nat. Hazards 2014, 71, 703–721. [Google Scholar] [CrossRef]
- Scheffner, N.W.; Borgman, L.E.; Mark, D.J. Empirical simulation technique based storm surge frequency analyses. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 93–101. [Google Scholar] [CrossRef]
- Myers, V.A. Joint Probability Method of tide Frequency Analysis Applied to Atlantic City and Long Beach Island, N.J.; Rutgers University Libraries: New Brunswick, NJ, USA, 1970. [Google Scholar]
- Wang, S.; Manausa, M.E.; Dean, R.; Walton, T. Combined Total Storm Tide Frequency Restudy for Gulf County, Florida; Florida State University: Tallahassee, FL, USA, 2007. [Google Scholar]
- Toro, G.R.; Resio, D.T.; Divoky, D.; Niedoroda, A.W.; Reed, C. Efficient joint-probability methods for hurricane surge frequency analysis. Ocean Eng. 2010, 37, 125–134. [Google Scholar] [CrossRef]
- Yu, S.; Wu, W.; Naess, A. Extreme value prediction with modified Enhanced Monte Carlo method based on tail index correction. J. Sea Res. 2023, 192, 102354. [Google Scholar] [CrossRef]
- Hussain, M.; Tajima, Y. Numerical investigation of surge–tide interactions in the Bay of Bengal along the Bangladesh coast. Nat. Hazards 2017, 86, 669–694. [Google Scholar] [CrossRef]
- Seeger, K.; Peffeköver, A.; Minderhoud, P.S.J.; Vogel, A.; Brückner, H.; Kraas, F.; Oo, N.W.; Brill, D. Evaluating flood hazards in data-sparse coastal lowlands: Highlighting the Ayeyarwady Delta (Myanmar). Environ. Res. Lett. 2024, 19, 084007. [Google Scholar] [CrossRef]
- Gayathri, R.; Bhaskaran, P.K.; Sen, D. Numerical Study on Storm Surge and Associated Coastal Inundation for 2009 AILA Cyclone in the Head Bay of Bengal. Aquat. Procedia 2015, 4, 404–411. [Google Scholar] [CrossRef]
- Russell, L.R. Probability Distributions for Hurricane Effects. ASCE Waterw. 1971, 97, 139–154. [Google Scholar] [CrossRef]
- Sheppard, D.; Slinn, D.; Hagen, S. Design Hurricane Storm Surge Pilot Study; ACM: New York, NY, USA, 2006. [Google Scholar]
- Symonds, A.M.; Vijverberg, T.; Post, S.; Van Der Spek, B.-J.; Henrotte, J.; Sokolewicz, M. Comparison between mike 21 fm, delft3d and delft3d fm flow models of western port bay, australia. Coast. Eng. Proc. 2017, 11, 1–12. [Google Scholar] [CrossRef]
- Putzu, S.; Enrile, F.; Besio, G.; Cucco, A.; Cutroneo, L.; Capello, M.; Stocchino, A. A Reasoned Comparison between Two Hydrodynamic Models: Delft3D-Flow and ROMS (Regional Oceanic Modelling System). J. Mar. Sci. Eng. 2019, 7, 464. [Google Scholar] [CrossRef]
- Kulikov, M.E.; Arkhipkin, V.S.; Medvedev, I.P.; Kovachev, S.A.; Krylov, A.A. Numerical Modeling of Extreme Sea Levels on the Laptev Sea Coast. Geosciences 2024, 14, 245. [Google Scholar] [CrossRef]
- Narulita, N.A.; Wiyono, R.U.A.; Halik, G.; Pratama, M. Tsunami—Tides Interaction of the South Coast of Jember Using Delft3D-Flow. J. Tek. Pengair. 2023, 14, 143–152. [Google Scholar] [CrossRef]
- Panigrahi, J.K.; Umesh, P.A.; Padhy, C.P.; Swain, J. Nearshore propagation of cyclonic waves. Nat. Hazards 2012, 60, 605–622. [Google Scholar] [CrossRef]
- Panigrahi, J.K.; Tripathy, J.K.; Murty, A.S.N. Extremity analysis of storm surge for fixing safe design water level. Nat. Hazards 2011, 56, 347–358. [Google Scholar] [CrossRef]
- Jelesnianski, C.P. A numerical calculation of storm tides induced by a tropical storm impinging on a continental shelf. Mon. Weather Rev. 1965, 93, 343–358. [Google Scholar] [CrossRef]
- Yasui, H.; Ohkuma, T.; Marukawa, H.; Katagiri, J. Study on evaluation time in typhoon simulation based on Monte Carlo method. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1529–1540. [Google Scholar] [CrossRef]






| Cyclone | Specific Site | Maximum Surge | Value |
|---|---|---|---|
| 1992 Sandoway Cyclone | Sandoway | Measured | 1.4 m |
| Simulated | 1.48 m | ||
| Gwa | Measured | 0.7 m | |
| Simulated | 0.73 m | ||
| 1994 Sittwe Cyclone | Sittwe | Measured | 3.7 m |
| Simulated | 3.76 m | ||
| Sandoway | Measured | 0.8 m | |
| Simulated | 0.83 m |
| Return Period (Year) | Extremely High Sea Level (m) | Extremely Low Sea Level (m) |
|---|---|---|
| 50 | 4.43 | −0.24 |
| 100 | 4.83 | −0.52 |
| 200 | 6.06 | −1.23 |
| 1000 | 7.24 | −2.19 |
| Return Period (Year) | Storm Surge (m) | Storm Surge with Cyclone Intensification (m) |
|---|---|---|
| 50 | 1.85 | 2.14 |
| 100 | 2.25 | 2.59 |
| 200 | 3.48 | 4.06 |
| 1000 | 4.66 | 5.54 |
| Return Period (Year) | Extremely High Sea Level with Cyclone Intensification (m) | Extremely High Sea Level with Cyclone Intensification and Sea Level Rise (m) |
|---|---|---|
| 50 | 4.72 | 5.03 |
| 100 | 5.17 | 5.48 |
| 200 | 6.64 | 6.95 |
| 1000 | 8.12 | 8.43 |
| Return Period (Year) | Extremely Low Sea Level with Cyclone Intensification (m) |
|---|---|
| 50 | −0.49 |
| 100 | −0.72 |
| 200 | −1.59 |
| 1000 | −2.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, K.; He, L.; Liu, S.; Xu, S. Effects of Climate Change on the Estimation of Extreme Sea Levels in the Ayeyarwady Sea of Myanmar by Monte Carlo. Water 2025, 17, 429. https://doi.org/10.3390/w17030429
Yin K, He L, Liu S, Xu S. Effects of Climate Change on the Estimation of Extreme Sea Levels in the Ayeyarwady Sea of Myanmar by Monte Carlo. Water. 2025; 17(3):429. https://doi.org/10.3390/w17030429
Chicago/Turabian StyleYin, Kai, Liye He, Shuo Liu, and Sudong Xu. 2025. "Effects of Climate Change on the Estimation of Extreme Sea Levels in the Ayeyarwady Sea of Myanmar by Monte Carlo" Water 17, no. 3: 429. https://doi.org/10.3390/w17030429
APA StyleYin, K., He, L., Liu, S., & Xu, S. (2025). Effects of Climate Change on the Estimation of Extreme Sea Levels in the Ayeyarwady Sea of Myanmar by Monte Carlo. Water, 17(3), 429. https://doi.org/10.3390/w17030429




