Wave–Structure Interaction Modeling of Transient Flow Around Channel Obstacles and Contractions
Abstract
1. Introduction
2. Materials and Methods
2.1. Turbulence Modeling Using Large Eddy Simulation (LES)
2.2. Air Entrainment Modeling
2.3. Stability of Numerical Solution and Selecting the Numerical Method
2.4. Initial and Boundary Conditions
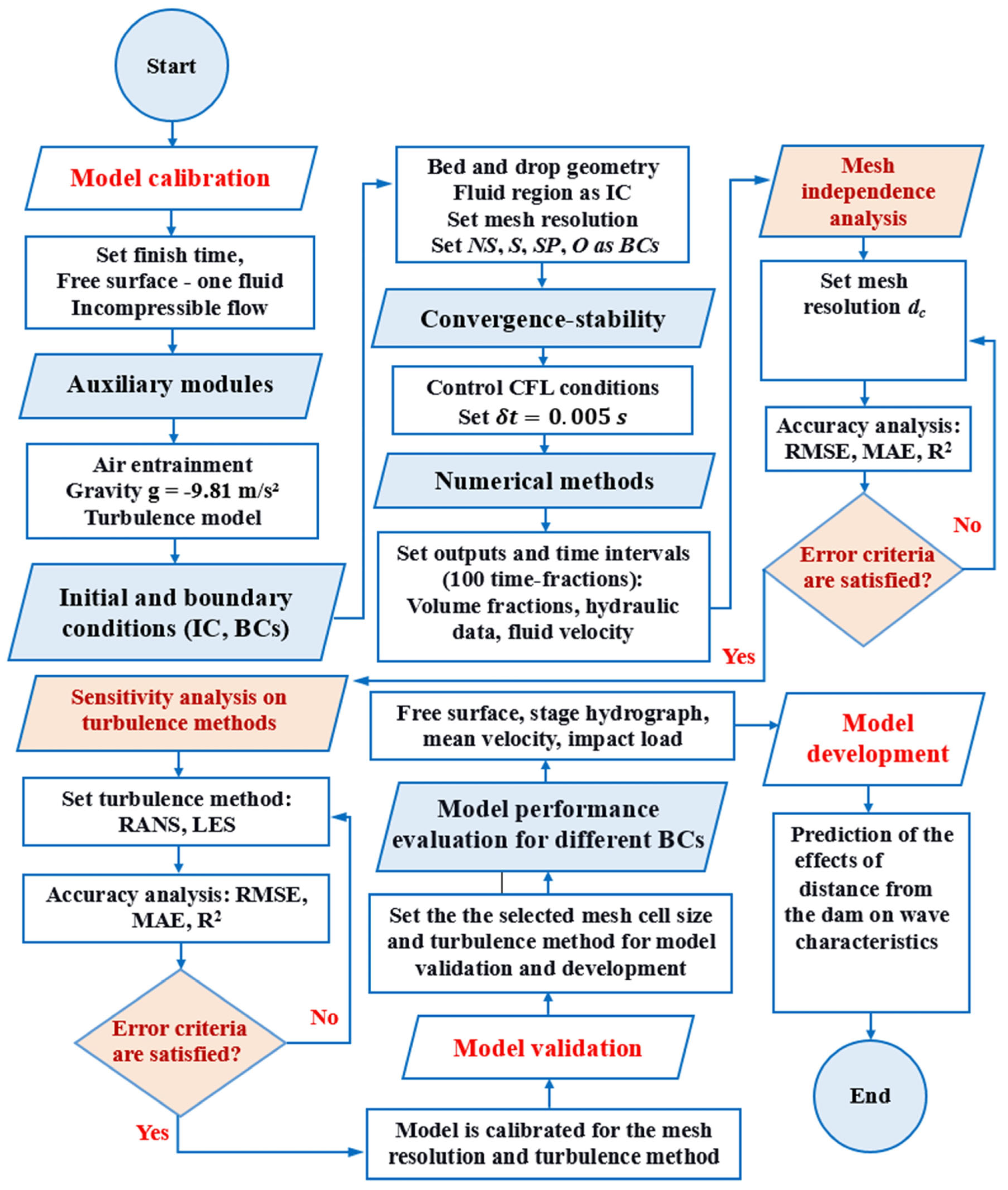
2.5. Model Calibration and Validation
2.5.1. Model Calibration Against Mesh Resolution
2.5.2. Model Validation
3. Results
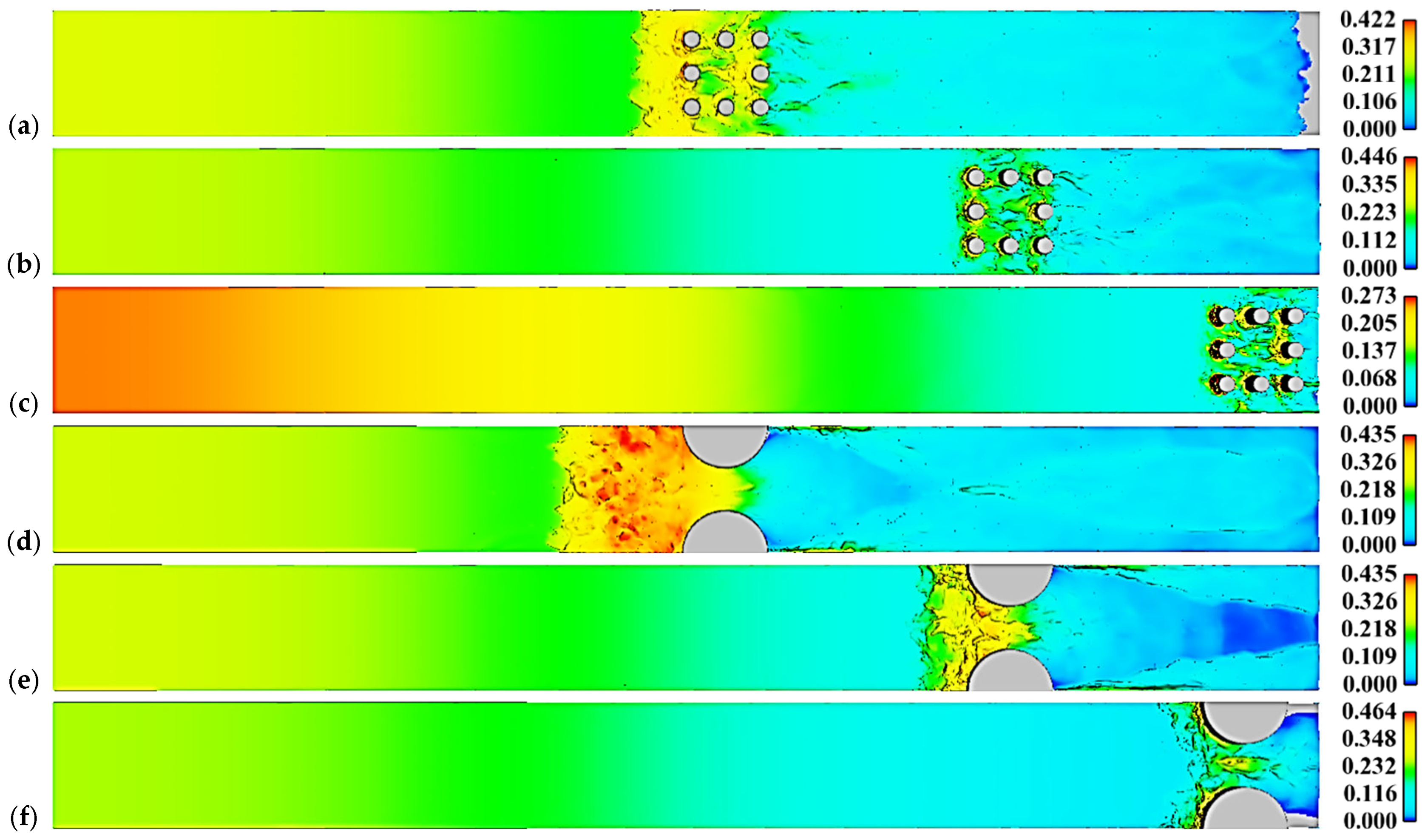
3.1. Modeling the Dam-Break Flow Around the Obstacles and Contractions
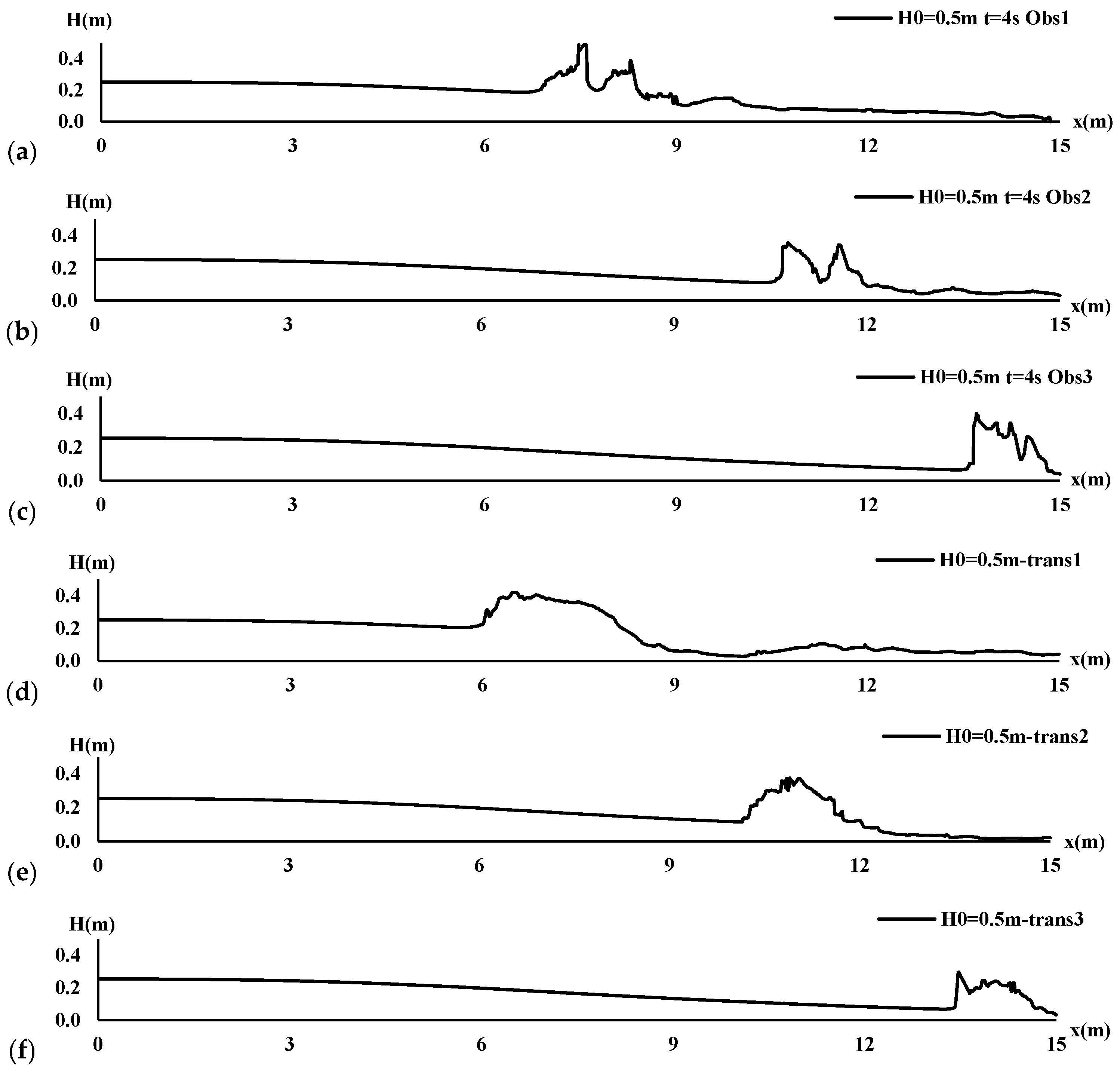
3.2. Free Surface Profile
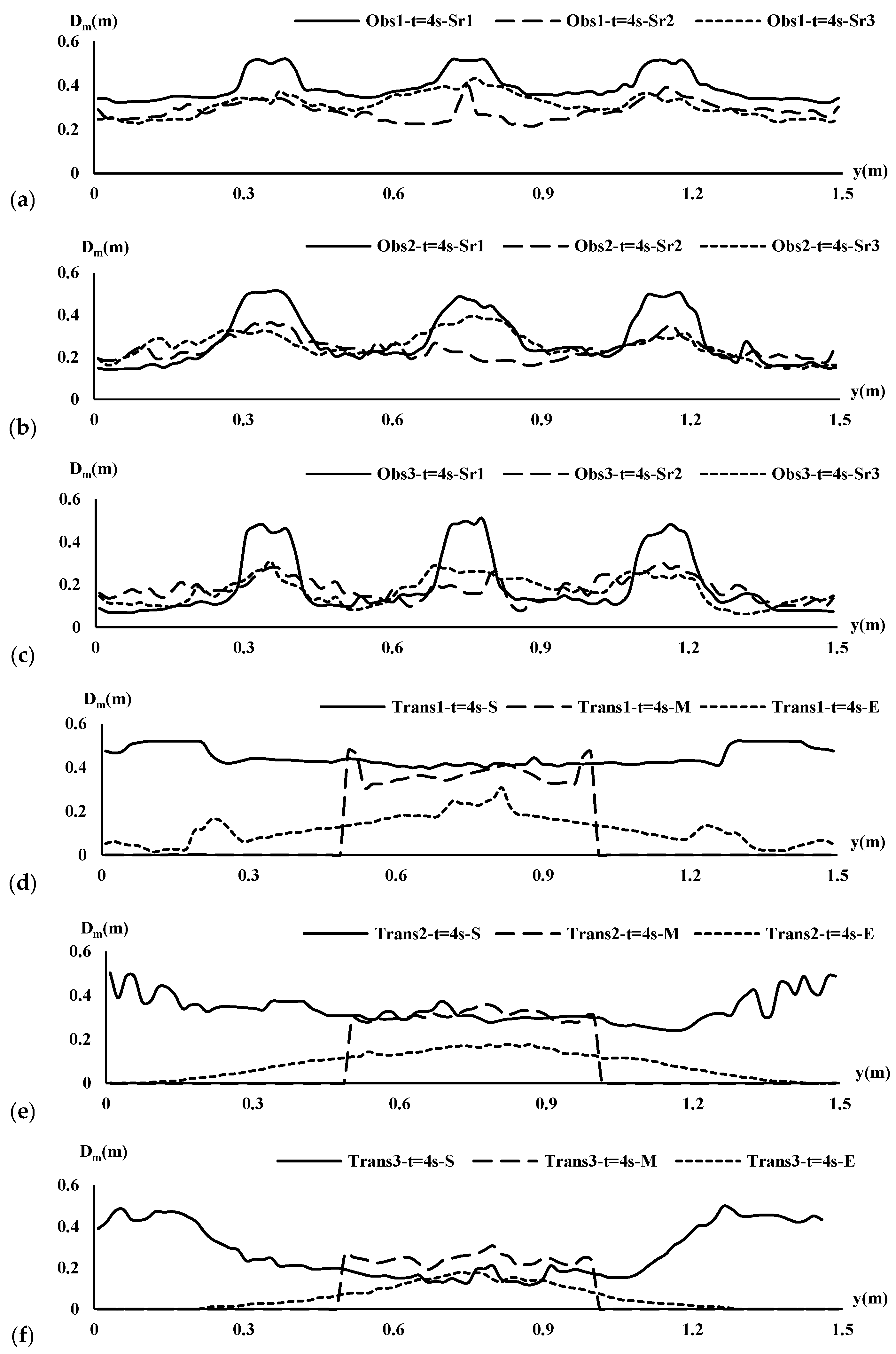
3.3. Flow Depth Fluctuations
3.4. Turbulence Structures and Air Entrainment
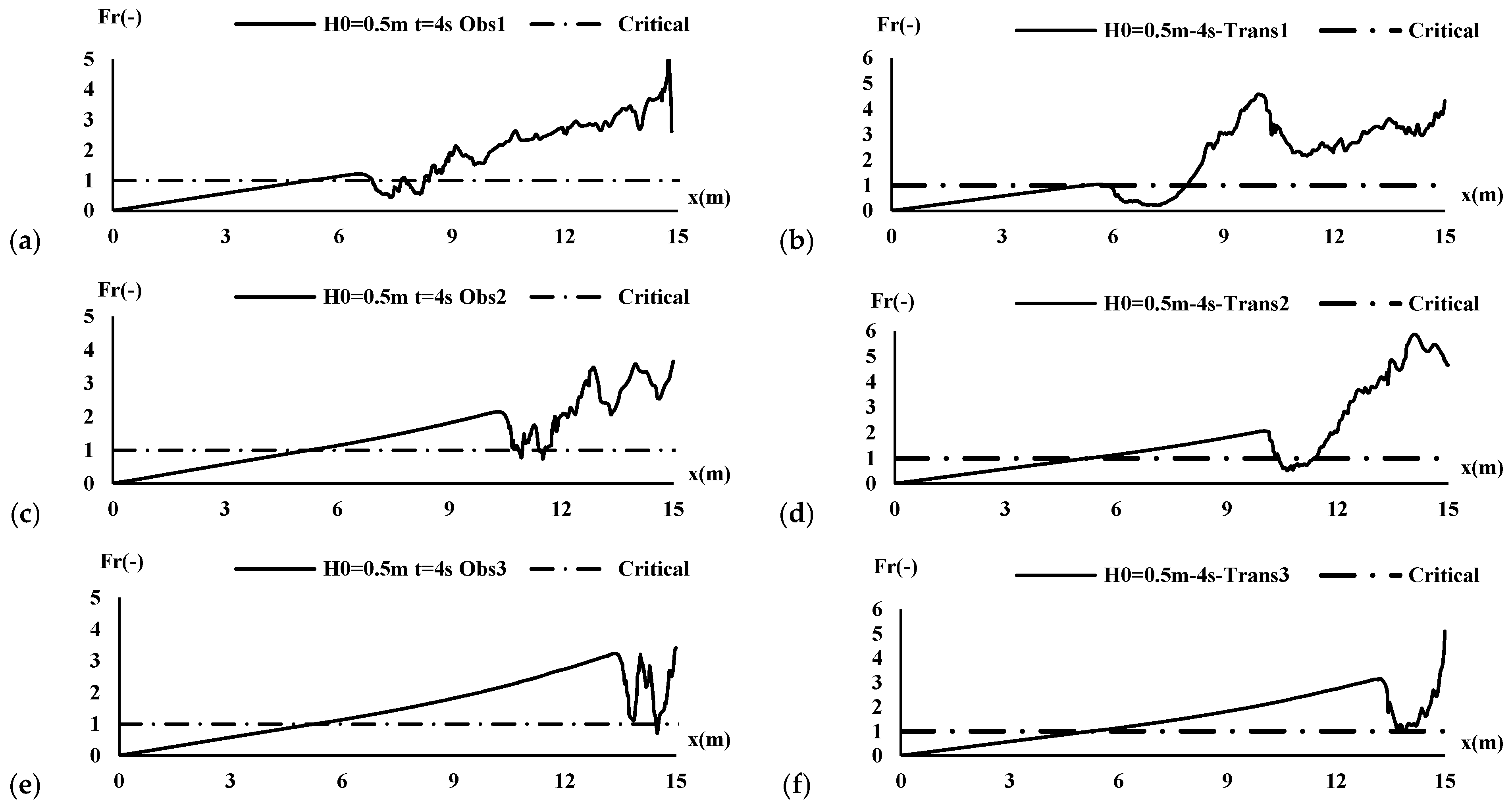
3.5. Dam-Break Flow Regime Variations
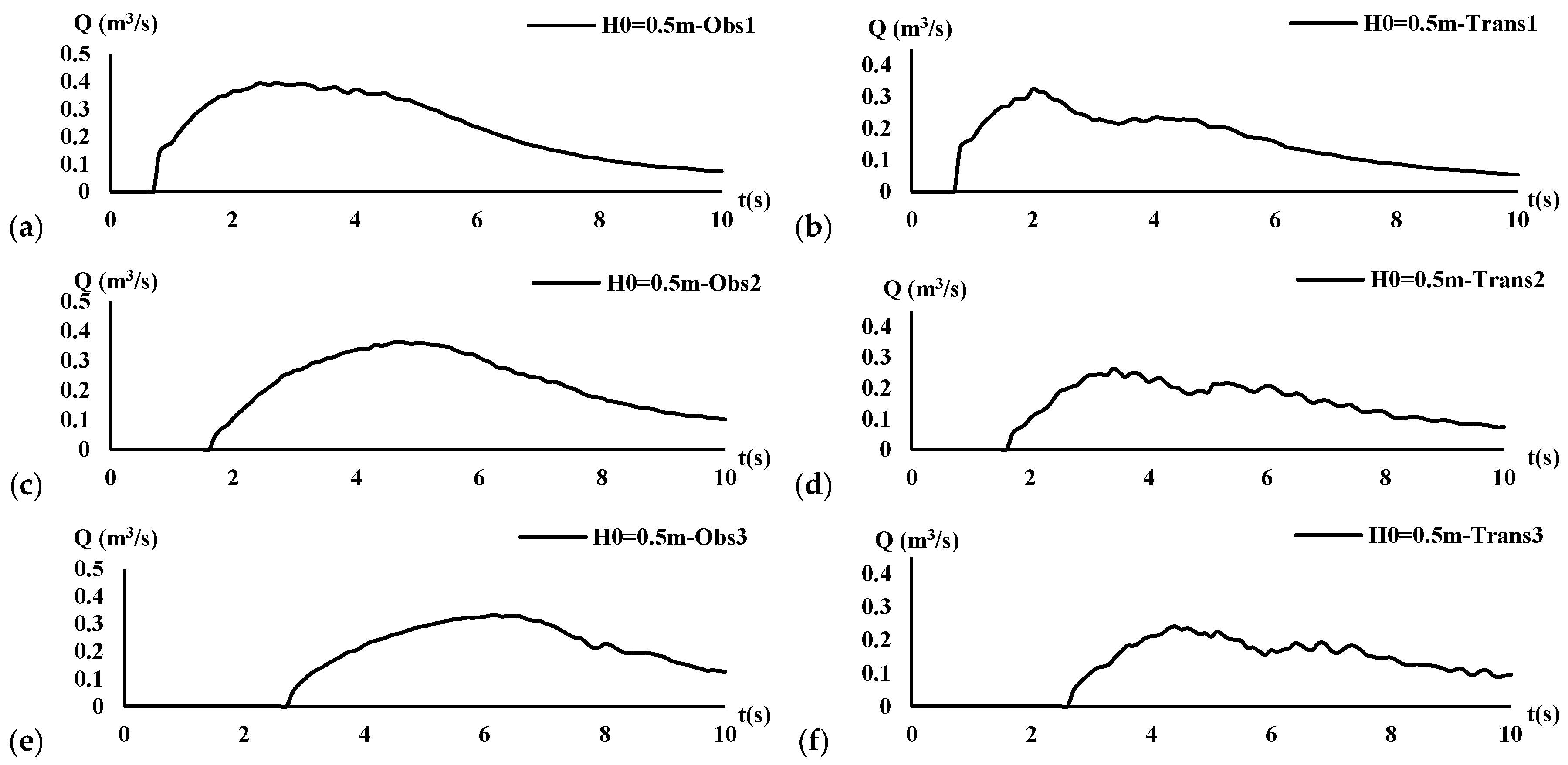
3.6. Inflow Hydrograph in the Downstream Channel
4. Discussion
5. Conclusions
- (1)
- The numerical model successfully predicted the evolution of dam-break waves around downstream structures with high accuracy.
- (2)
- Reducing the distance of obstacles to the dam significantly decreased wave height, kinetic energy, and turbulence intensity, particularly at the early stages of the dam break.
- (3)
- Hydraulic jumps and transcritical flow regimes were more pronounced around obstacles near the dam.
- (4)
- The study captured critical phenomena such as air entrainment, vortex shedding, and flow field variations near obstacles, emphasizing their dependency on the proximity of the downstream structures to the dam.
- (5)
- The inflow hydrograph and peak discharge decreased as the distance of obstacles and contractions from the dam increased, showing the structures’ retentive effects on wave dynamics.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haile, T.; Goitom, H.; Degu, A.M.; Grum, B.; Abebe, B.A. Simulation of urban environment flood inundation from potential dam break: Case of Midimar Embankment Dam, Tigray, Northern Ethiopia. Sustain. Water Resour. Manag. 2024, 10, 46. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, Z.; Cheng, Z.; Xiang, Y.; Chen, J.; Zhang, P.; Yang, X. Uncertainty analysis of dam-break flood risk consequences under the influence of non-structural measures. Int. J. Disaster Risk Reduct. 2024, 102, 104265. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Sadeghi, S.; Gohari, S.H.; Oodi, S.; Karimpour, S.; Di Francesco, S. Dam-break flow dynamics over a vegetated channel with and without a drop. Water Resour. Manag. 2023, 613, 128395. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Asim, T.; Mishra, R.; Ahmadi Dehrashid, F.; Heidarian, P.; Nsom, B. Study the effect of obstacle arrangements on the dam-break flow. Int. J. Comadem. 2022, 25, 41–50. [Google Scholar]
- Nazari, R.; Karimi, M. High-resolution hydrodynamic modeling and flood damage assessment in complex urban systems. In XXVIII General Assembly of the International Union of Geodesy and Geophysics (IUGG); German Research Centre for Geosciences: Berlin, Germany, 2023. [Google Scholar]
- Di Cristo, C.; Greco, M.; Iervolino, M.; Vacca, A. Impact Force of a Geomorphic Dam-Break Wave against an Obstacle: Effects of Sediment Inertia. Water 2021, 13, 232. [Google Scholar] [CrossRef]
- Giglou, A.N.; Nazari, R.R.; Jazaei, F.; Karimi, M. Numerical analysis of surface hydrogeological water budget to estimate unconfined aquifers recharge. J. Environ. Manag. 2023, 346, 118892. [Google Scholar] [CrossRef]
- Nazari, R.; Fahad, M.G.R.; Karimi, M.; Eslamian, S. Continuous large-scale simulation models in flood studies. In Flood Handbook; CRC Press: Boca Raton, FL, USA, 2022; pp. 335–350. [Google Scholar]
- Liu, J.; Song, T.; Mei, C.; Wang, H.; Zhang, D.; Nazli, S. Flood risk zoning of cascade reservoir dam break based on a 1D-2D coupled hydrodynamic model: A case study on the Jinsha-Yalong River. J. Hydrol. 2024, 639, 131555. [Google Scholar] [CrossRef]
- Qiu, W.; Li, Y.; Zhang, Y.; Wen, L.; Wang, T.; Wang, J.; Sun, X. Numerical investigation on the evolution process of cascade dam-break flood in the downstream earth-rock dam reservoir area based on coupled CFD-DEM. J. Hydrol. 2024, 635, 131162. [Google Scholar] [CrossRef]
- Zhou, X.; Su, L.; He, X.; Hu, R.; Yuan, H. Experimental investigations of propagation characteristics and wave energy of dam-break waves on wet bed. Ocean Eng. 2024, 301, 117566. [Google Scholar] [CrossRef]
- Han, Z.; Xie, W.; Yang, F.; Li, Y.; Huang, J.; Li, C.; Chen, G. 3D-SPH-DEM coupling simulation for the large deformation failure process of check dams under debris flow impact incorporating the nonlinear collision-constraint bond model. Eng. Anal. Bound. Elem. 2024, 167, 105877. [Google Scholar] [CrossRef]
- Biscarini, C.; Di Francesco, S.; Ridolfi, E.; Manciola, P. On the Simulation of Floods in a Narrow Bending Valley: The Malpasset Dam Break Case Study. Water 2016, 8, 545. [Google Scholar] [CrossRef]
- Akgün, C.; Nas, S.S.; Uslu, A. 2D and 3D Numerical Simulation of Dam-Break Flooding: A Case Study of the Tuzluca Dam, Turkey. Water 2023, 15, 3622. [Google Scholar] [CrossRef]
- Hien, L.T.T.; Van Chien, N. Investigate Impact Force of Dam-Break Flow against Structures by Both 2D and 3D Numerical Simulations. Water 2021, 13, 344. [Google Scholar] [CrossRef]
- Biscarini, C.; Di Francesco, S.; Manciola, P. CFD modelling approach for dam break flow studies. Hydrol. Earth Syst. Sci. 2010, 14, 705–718. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Nsom, B.; Gohari, S.; Banejad, H. A comprehensive study on dam-break flow over dry and wet beds. Ocean Eng. 2019, 188, 106279. [Google Scholar] [CrossRef]
- Del Gaudio, A.; La Forgia, G.; Constantinescu, G.; De Paola, F.; Di Cristo, C.; Iervolino, M.; Leopardi, A.; Vacca, A. Modelling the impact of a dam-break wave on a vertical wall. Earth Surf. Process. Landf. 2024, 49, 2080–2095. [Google Scholar] [CrossRef]
- Kocaman, S.; Özmen-Çagatay, H. The effect of lateral channel contraction on dam break flows: Laboratory experiment. J. Hydrol. 2012, 432, 145–153. [Google Scholar] [CrossRef]
- Cozzolino, L.; Pepe, V.; Morlando, F.; Cimorelli, L.; D’Aniello, A.; Della Morte, R.; Pianese, D. Exact solution of the dam-break problem for constrictions and obstructions in constant width rectangular channels. J. Hydraul. Eng. 2017, 143, 04017047. [Google Scholar] [CrossRef]
- Hogg, A.J.; Skevington, E.W. Dam-break reflection. Q. J. Mech. Appl. Math. 2021, 74, 441–465. [Google Scholar] [CrossRef]
- Valiani, A.; Caleffi, V. Dam break in rectangular channels with different upstream-downstream widths. Adv. Water Resour. 2019, 132, 103389. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, J.; Vetsch, D.F.; Boes, R.M.; Tan, G. Numerical simulation of air entrainment on stepped spillways. In Proceedings of the E-Proceedings of the 38th IAHR World Congress, Panama City, PA, USA, 1–6 September 2019; p. 1494. [Google Scholar] [CrossRef]
- Saghi, H.; Lakzian, E. Effects of using obstacles on the dam-break flow based on entropy generation analysis. Eur. Phys. J. Plus 2019, 134, 237. [Google Scholar] [CrossRef]
- Issakhov, A.; Zhandaulet, Y.; Nogaeva, A. Numerical simulation of dam break flow for various forms of the obstacle by VOF method. Int. J. Multiph. Flow 2018, 109, 191–206. [Google Scholar] [CrossRef]
- Elong, A.J.; Zhou, L.; Karney, B.; Xue, Z.; Lu, Y. A Comprehensive Numerical Overview of the Performance of Godunov Solutions Using Roe and Rusanov Schemes Applied to Dam-Break Flow. Water 2024, 16, 950. [Google Scholar] [CrossRef]
- Van Dang, H.; Park, H.; Shin, S.; Ha, T.; Cox, D.T. Numerical modeling and assessment of flood mitigation structures in idealized coastal communities: OpenFOAM simulations for hydrodynamics and pressures on the buildings. Ocean Eng. 2024, 307, 118147. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; He, X. Modeling transient flow dynamics around a bluff body using deep learning techniques. Ocean Eng. 2024, 295, 116880. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Nsom, B.; Okhravi, S.; Dehrashid, F.A.; Heidarian, P.; DiFrancesco, S. Numerical investigation of dam break flow over erodible beds with diverse substrate level variations. J. Hydrol. Hydromech. 2024, 72, 80–94. [Google Scholar] [CrossRef]
- Garoosi, F. Numerical Study of Natural Convection Heat Transfer in a Square Cavity with a Cold Obstacle Inside Using the Lagrangian Particle Method. SSRN 2024. [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Lee, H.C.; Wahab, A.K.A. Performance of different turbulence models in predicting flow kinematics around an open offshore intake. SN Appl. Sci. 2019, 1, 1266. [Google Scholar] [CrossRef]
- Heidarian, P.; Neyshabouri SA, A.S.; Khoshkonesh, A.; Bahmanpouri, F.; Nsom, B.; Eidi, A. Numerical study of flow characteristics and energy dissipation over the slotted roller bucket system. Model. Earth Syst. Environ. 2022, 8, 5337–5351. [Google Scholar] [CrossRef]
- Boudjelal, S.; Fourar, A.; Massouh, F. Experimental and numerical simulation of free surface flow over an obstacle on a sloped channel. Model. Earth Syst. Environ. 2022, 8, 1025–1033. [Google Scholar] [CrossRef]
- Lobovský, L.; Botia-Vera, E.; Castellana, F.; Mas-Soler, J.; Souto-Iglesias, A. Experimental investigation of dynamic pressure loads during dam break. J. Fluid Struct. 2014, 48, 407–434. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Toro, E.F. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J. Hydraul. Res. 1995, 33, 843–864. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Nazari, R.; Nikoo, M.R.; Karimi, M. Enhancing flood risk assessment in urban areas by integrating hydrodynamic models and machine learning techniques. Sci. Total Environ. 2024, 952, 175859. [Google Scholar] [CrossRef]
- Pasculli, A. Viscosity Variability Impact on 2D Laminar and Turbulent Poiseuille Velocity Profiles; Characteristic-Based Split (CBS) Stabilization. In Proceedings of the 2018 5th International Conference on Mathematics and Computers in Sciences and Industry (MCSI), Corfù, Greece, 25–27 August 2018. [Google Scholar] [CrossRef]
- Pasculli, A. CFD-FEM 2D Modelling of a Local Water Flow. Some Numerical Results. Alp. Mediterr. Quat. 2008, 21B, 215–228, ISSN: 2279-7327; SCOPUS: 2-s2.0-84983037047. [Google Scholar]
- Chung, T.J. Computational Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Sun, J.; Lu, L.; Lin, B.; Liu, L. Processes of dike-break induced flows: A combined experimental and numerical model study. Int. J. Sediment Res. 2017, 32, 465–471. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, W.; Zhang, F.; Zhang, W.; Wei, W.; Zhang, X. Improved general unit hydrograph model for dam-break flood hydrograph. J. Hydrol. 2024, 635, 131216. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, F.; Xu, W.; Bo, H.; Zhang, X. An innovative method for measuring the three-dimensional water surface morphology of unsteady flow using light detection and ranging technology. Ocean Eng. 2023, 276, 114079. [Google Scholar] [CrossRef]
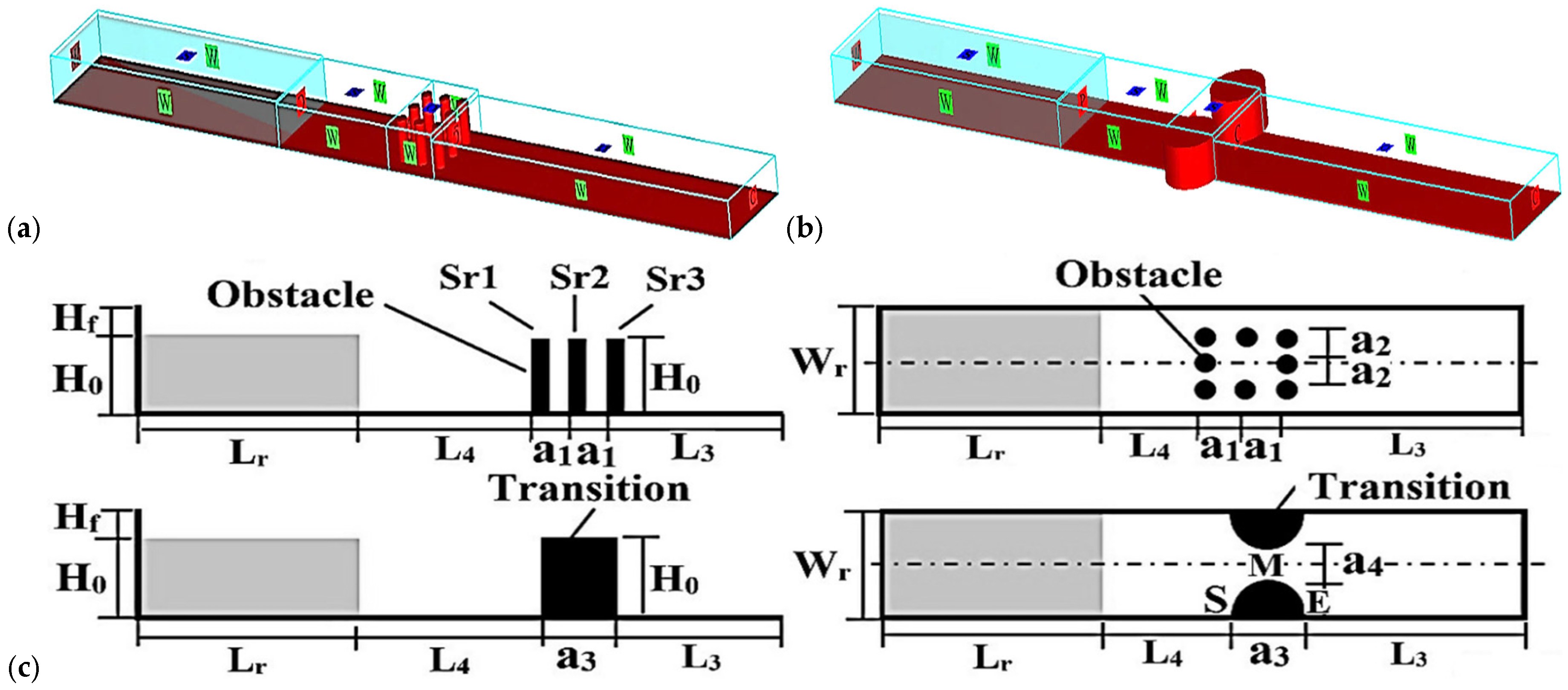

| Model | H0 (m) | a1 (m) | a2 (m) | a3 (m) | a4 (m) | Wr (m) | L4 (m) | L3 (m) | Lr (m) | Description |
|---|---|---|---|---|---|---|---|---|---|---|
| S1,1 | 0.5 | 0.5 | 0.4 | - | - | 1.5 | 2.43 | 6.57 | 5 | Obstacles near the dam |
| S1,2 | 0.5 | 0.5 | 0.4 | - | - | 1.5 | 5.76 | 3.24 | 5 | Obstacles in the middle of the channel |
| S1,3 | 0.5 | 0.5 | 0.4 | - | - | 1.5 | 8.7 | 0.3 | 5 | Obstacles at the end of the channel |
| S1,3 | - | - | - | 0.5 | 0.5 | 1.5 | 2.43 | 6.57 | 5 | Contractions near the dam |
| S1,5 | - | - | - | 0.5 | 0.5 | 1.5 | 5.76 | 3.24 | 5 | Contractions in the middle of the channel |
| S1,6 | - | - | - | 0.5 | 0.5 | 1.5 | 8.7 | 0.3 | 5 | Contractions at the end of the channel |
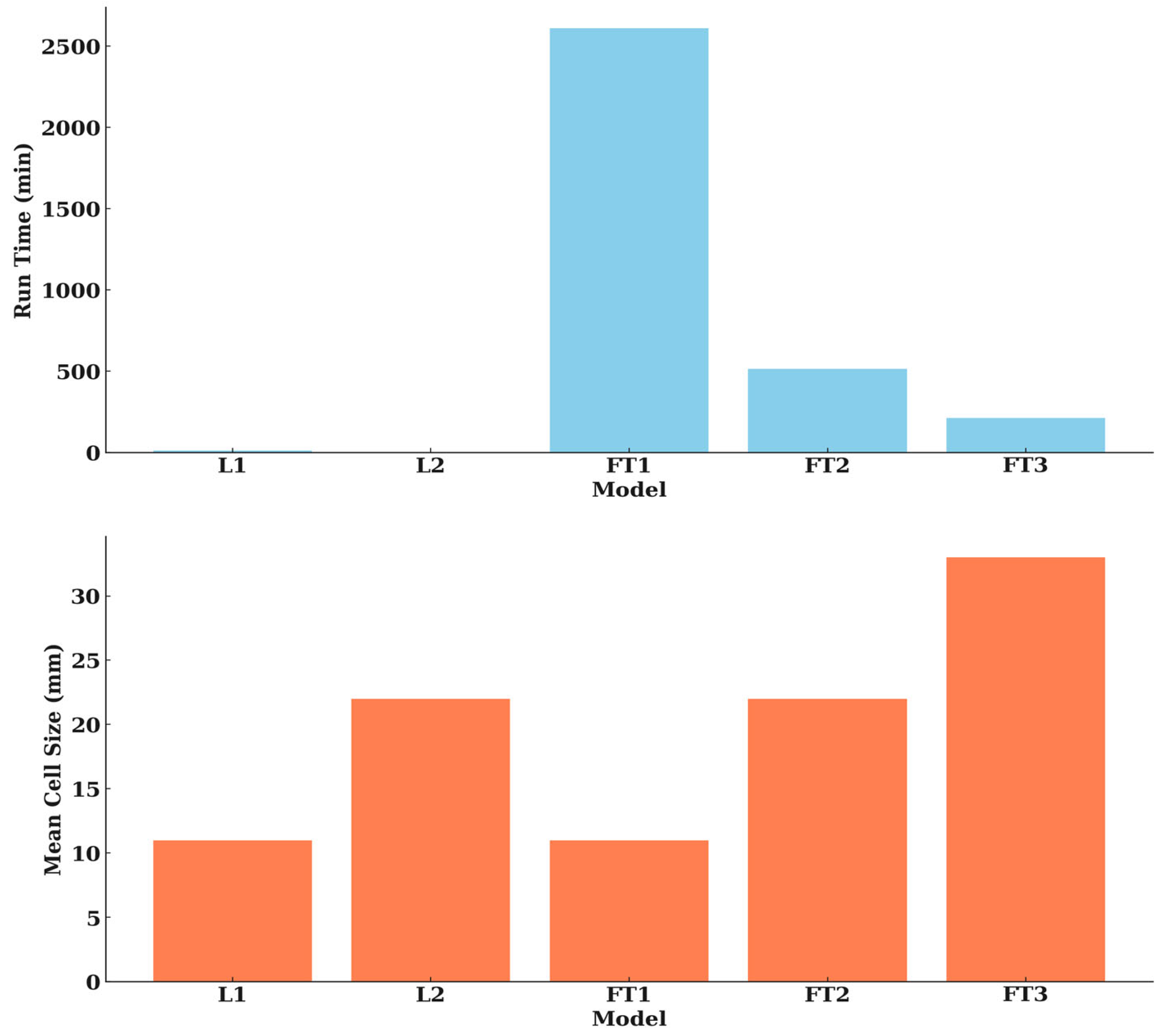
| Model for Validation | Number of Cells in Mesh-Block 1 | Number of Cells in Mesh-Block 2 | Number of Cells in Mesh-Block 3 | Mean Cell Size (mm) | Run Time (min) |
|---|---|---|---|---|---|
| L1 | 12,960 | 51,510 | - | 11 | 12.6 |
| L2 | 2160 | 6936 | - | 22 | 1.8 |
| FT1 | 979,294 | 1,280,000 | 1,140,000 | 11 | 2610 |
| FT2 | 86,400 | 160,000 | 145,000 | 22 | 514 |
| FT3 | 21,250 | 234,360 | 35,154 | 33 | 212 |
| Validation Cases | MAE Values |
|---|---|
| L1 | 0.0165 |
| L2 | 0.0132 |
| FT1 | 0.0532 |
| FT2 | 0.0666 |
| FT3 | 0.081 |
| Model | Number of Cells | Run Time (min) |
|---|---|---|
| S1,1 | 1,606,169 | 2178 |
| S1,2 | 1,823,595 | 2388 |
| S1,3 | 2,036,470 | 2400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oodi, S.; Gohari, S.; Di Francesco, S.; Nazari, R.; Nikoo, M.R.; Heidarian, P.; Eidi, A.; Khoshkonesh, A. Wave–Structure Interaction Modeling of Transient Flow Around Channel Obstacles and Contractions. Water 2025, 17, 424. https://doi.org/10.3390/w17030424
Oodi S, Gohari S, Di Francesco S, Nazari R, Nikoo MR, Heidarian P, Eidi A, Khoshkonesh A. Wave–Structure Interaction Modeling of Transient Flow Around Channel Obstacles and Contractions. Water. 2025; 17(3):424. https://doi.org/10.3390/w17030424
Chicago/Turabian StyleOodi, Shahin, Saeed Gohari, Silvia Di Francesco, Rouzbeh Nazari, Mohammad Reza Nikoo, Payam Heidarian, Ali Eidi, and Alireza Khoshkonesh. 2025. "Wave–Structure Interaction Modeling of Transient Flow Around Channel Obstacles and Contractions" Water 17, no. 3: 424. https://doi.org/10.3390/w17030424
APA StyleOodi, S., Gohari, S., Di Francesco, S., Nazari, R., Nikoo, M. R., Heidarian, P., Eidi, A., & Khoshkonesh, A. (2025). Wave–Structure Interaction Modeling of Transient Flow Around Channel Obstacles and Contractions. Water, 17(3), 424. https://doi.org/10.3390/w17030424











