Efficient Naval Surveillance: Addressing Label Noise with Rockafellian Risk Minimization for Water Security
Abstract
1. Introduction
2. Materials and Methods
2.1. Background
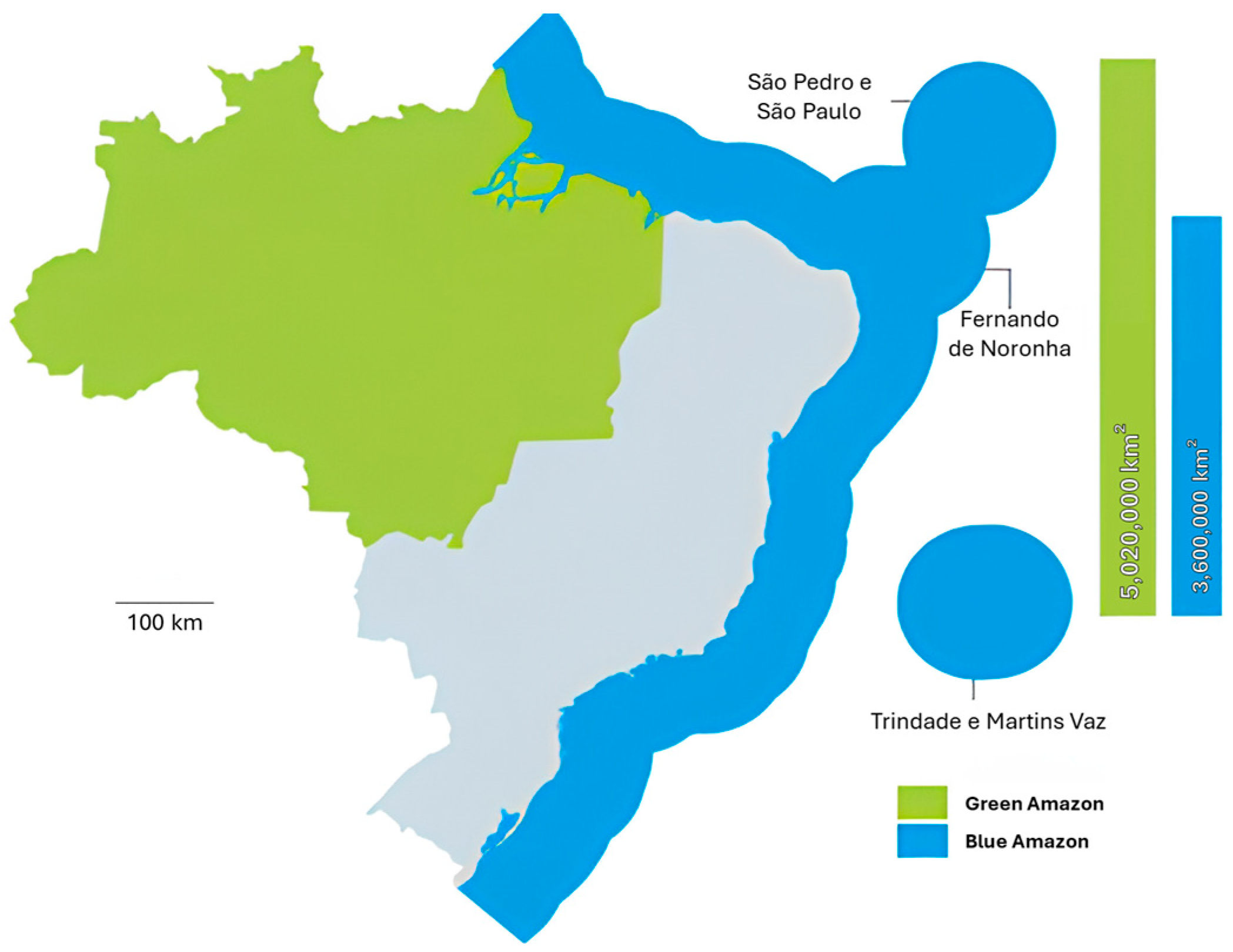
2.1.1. The Blue Amazon
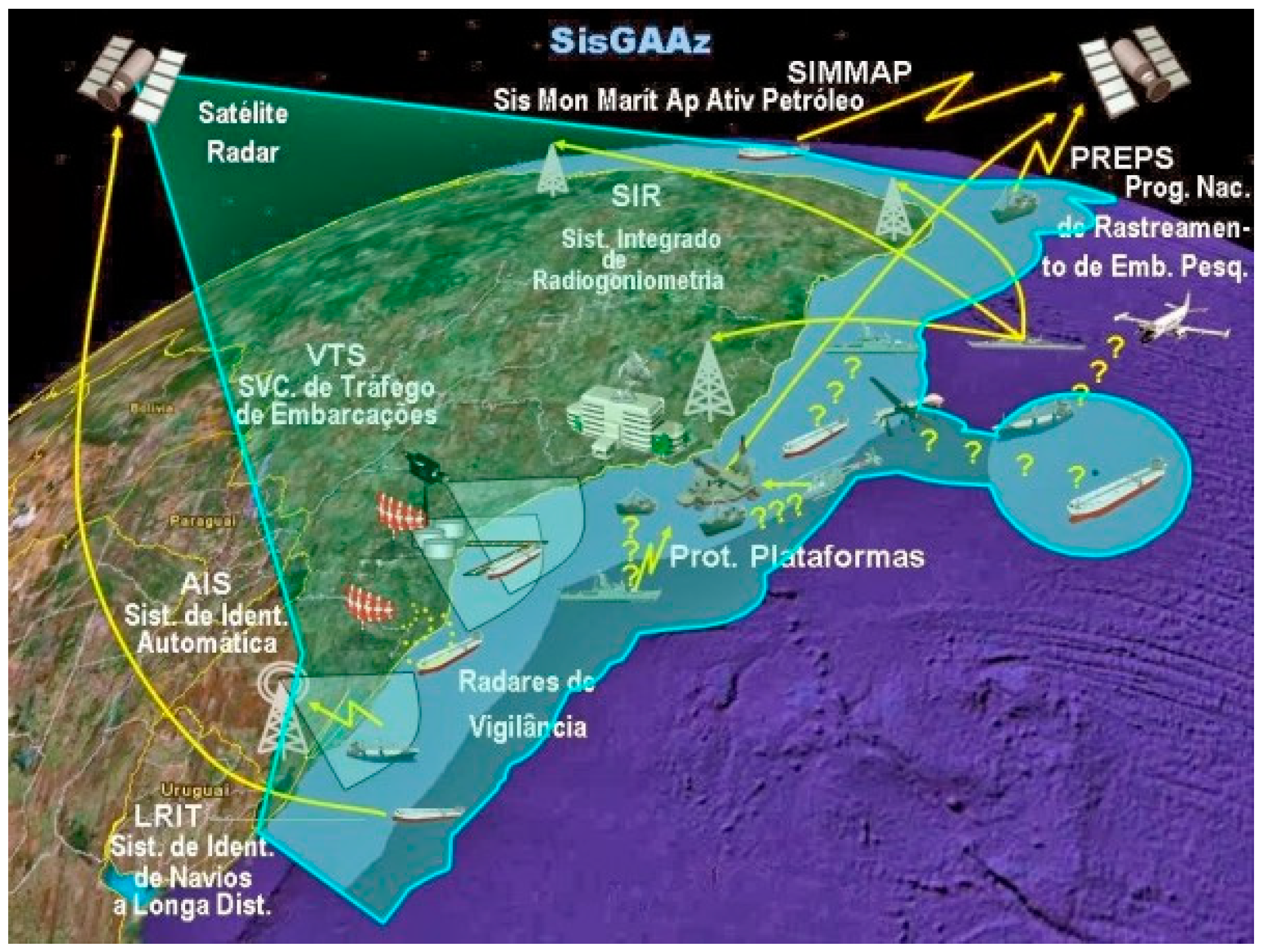
2.1.2. Surveillance System
2.2. Concepts
2.2.1. Classification
2.2.2. Learning and Optimization
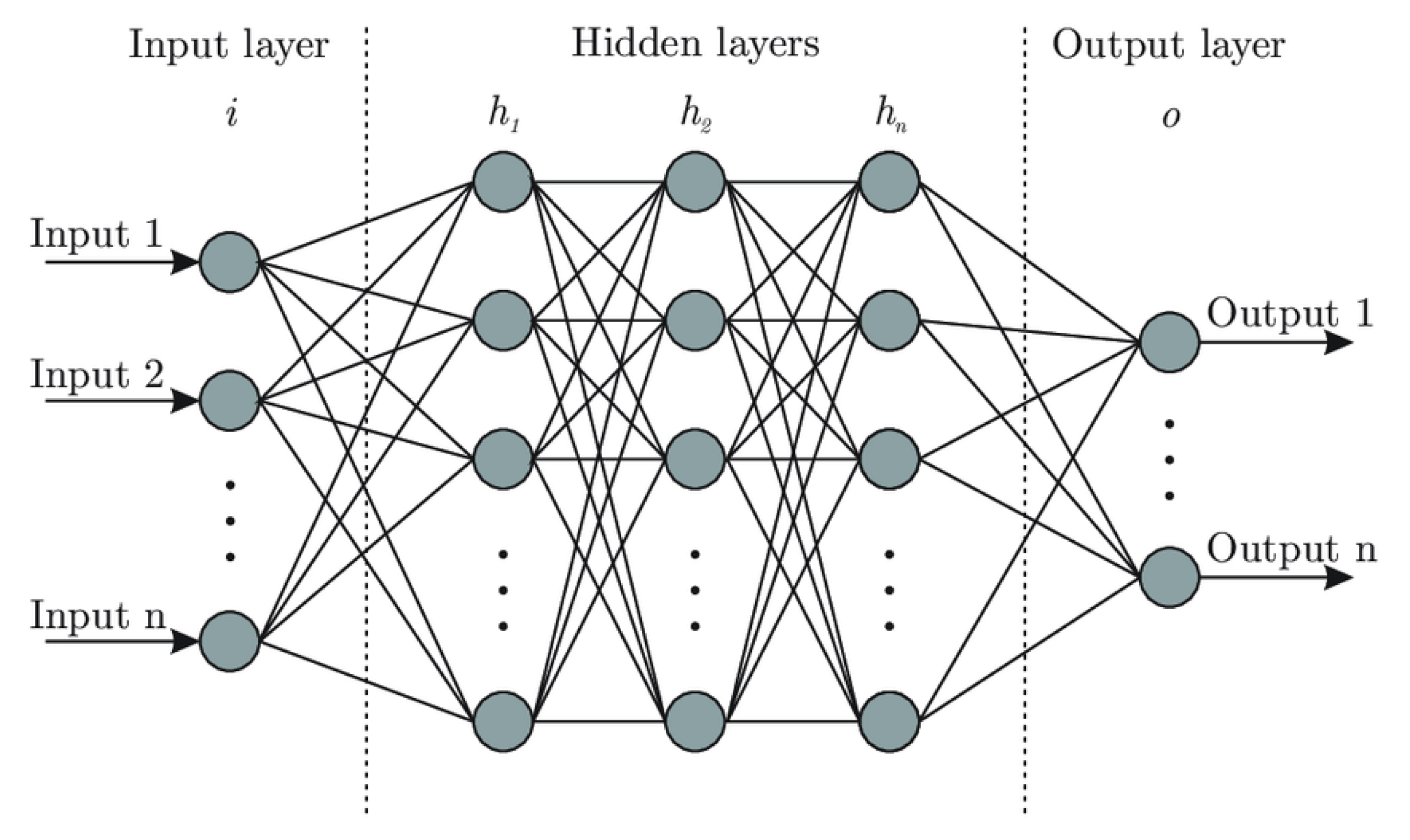
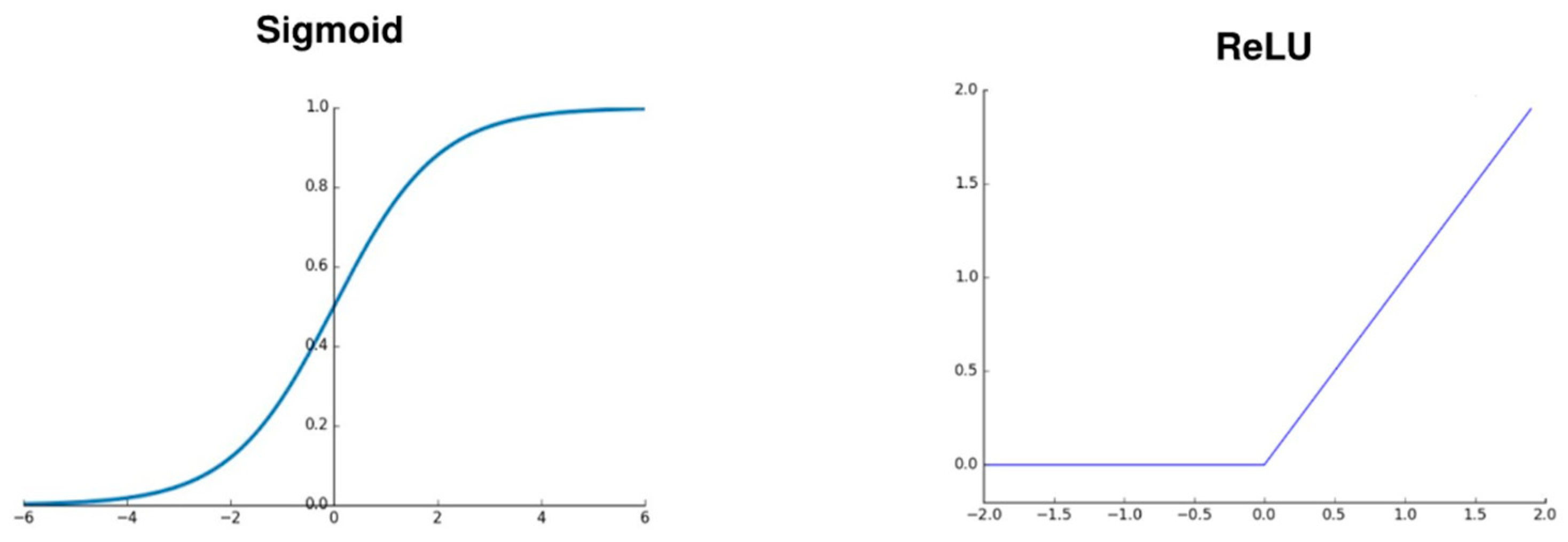
2.2.3. Neural Networks
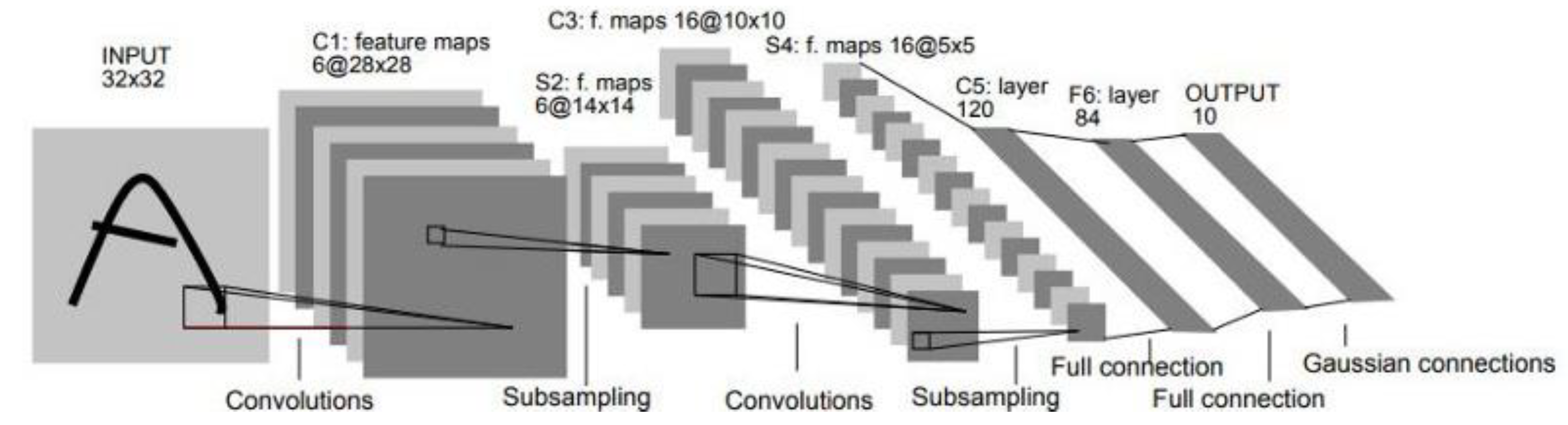
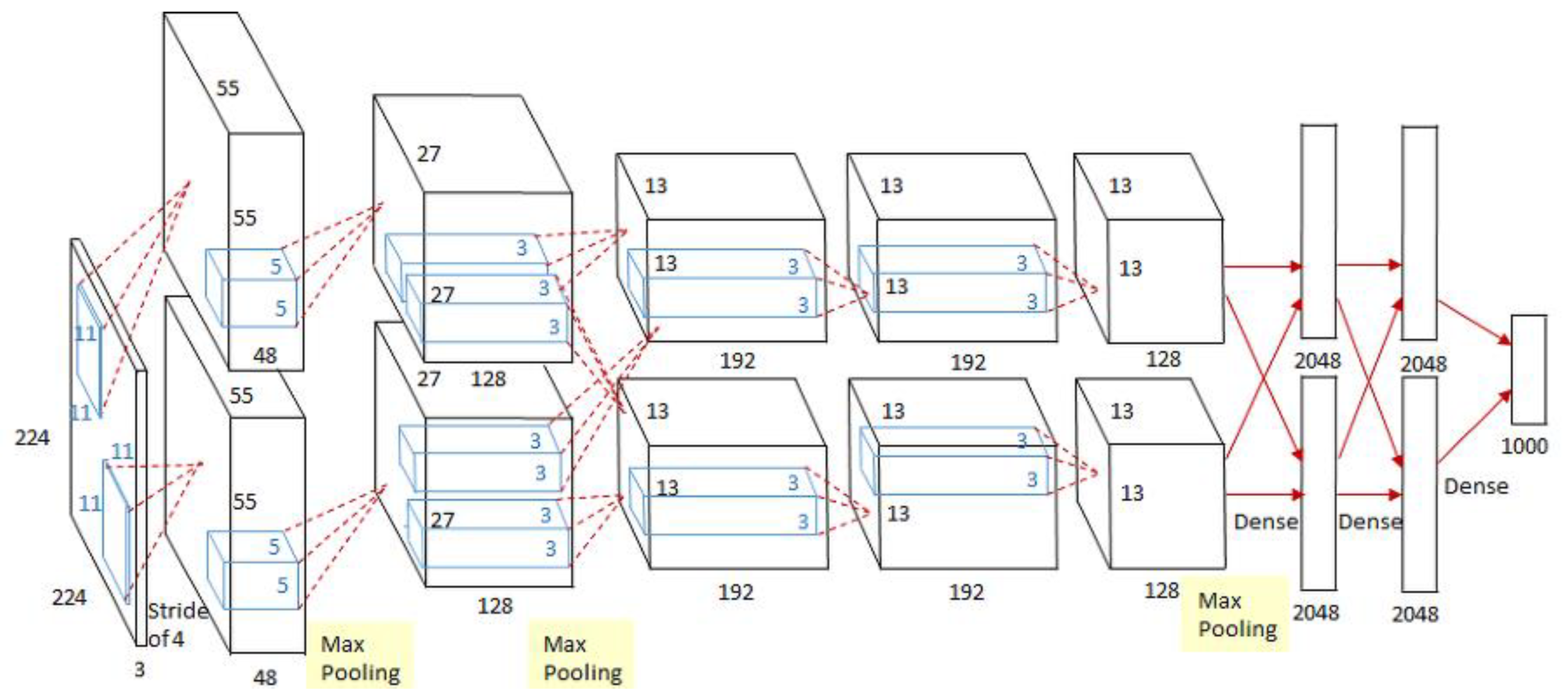
2.2.4. Computer Vision and Convolutional Neural Networks
2.3. Literature Review
2.3.1. Classification Problem
2.3.2. Neural Networks Structures
2.3.3. Maritime Computer Vision
2.3.4. Label Noise
2.4. Rockafellian Risk Minimization
2.4.1. Formulation
2.4.2. Training Algorithm
3. Results
3.1. MASATI Dataset
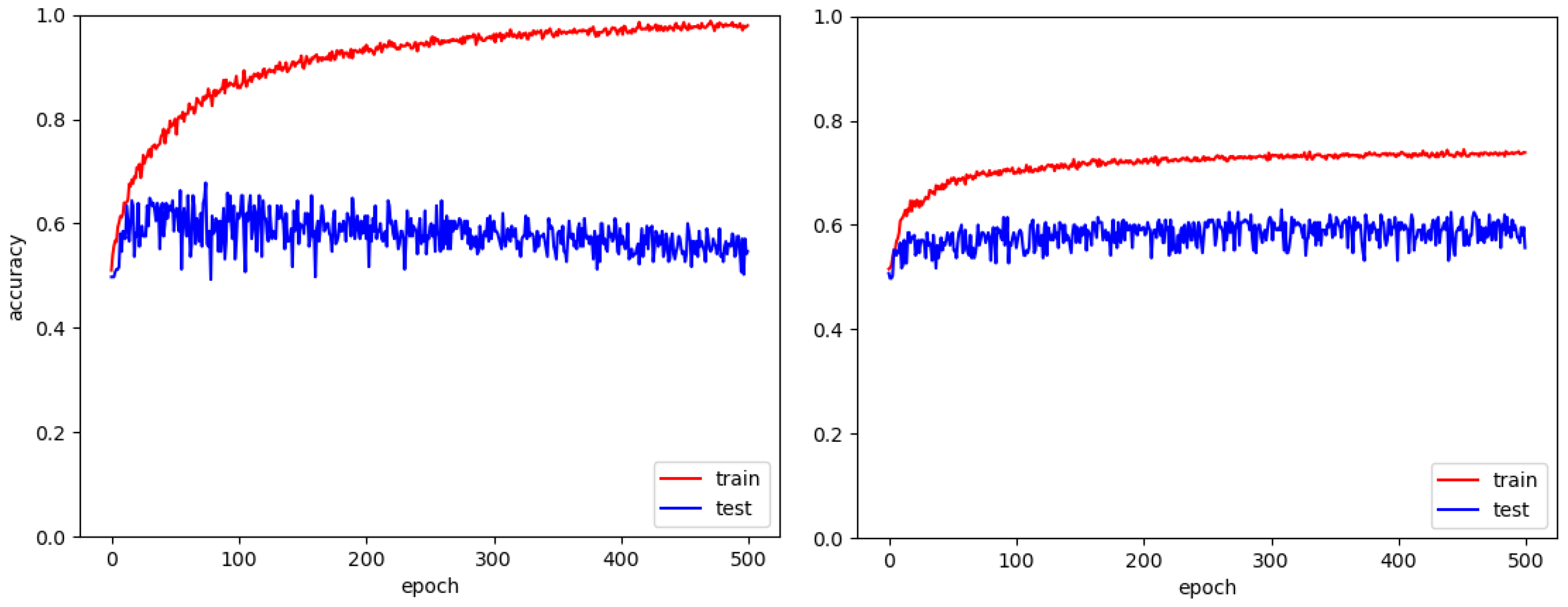
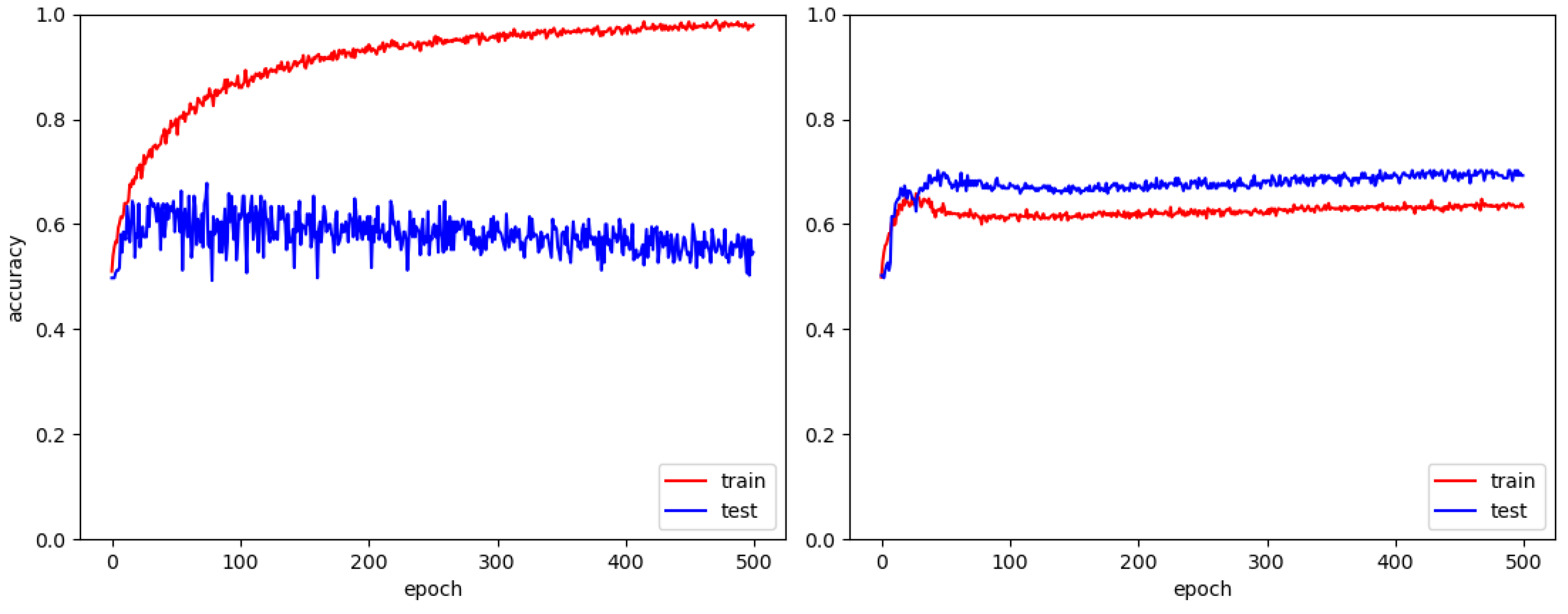
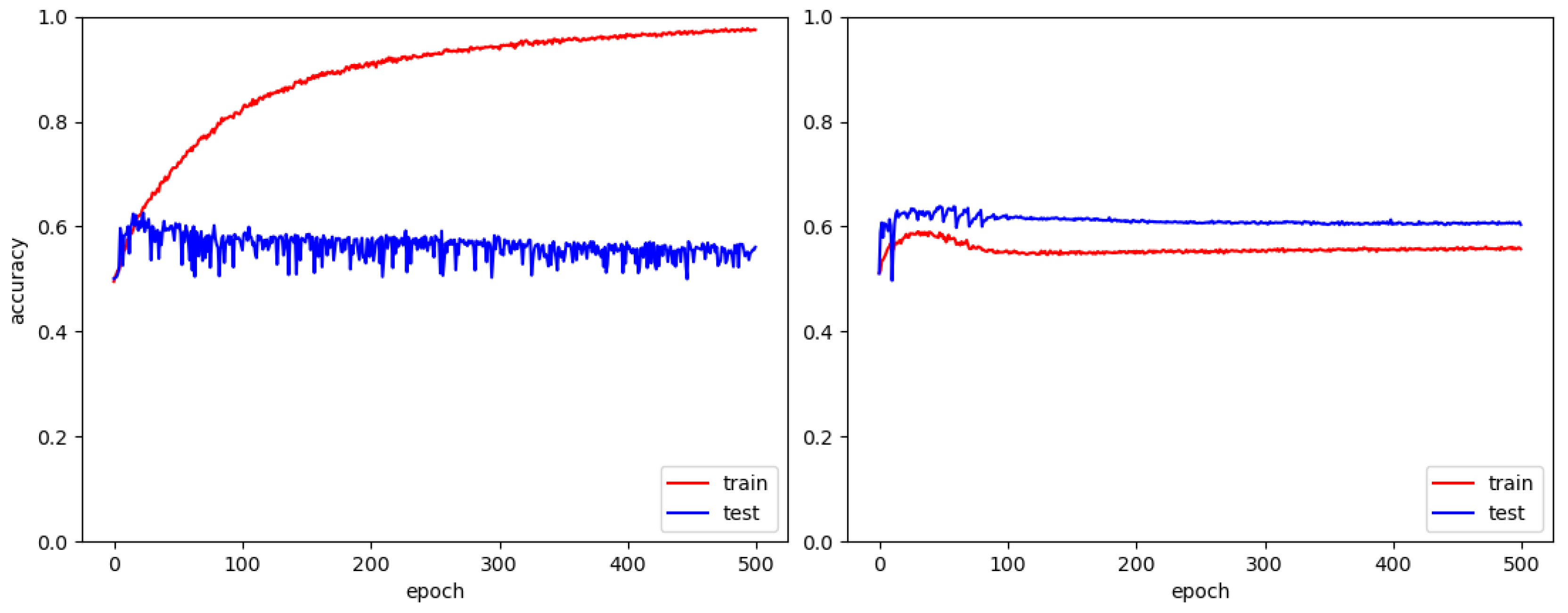
3.1.1. Accuracy Results with MASATI
3.1.2. U-Optimization Analysis with MASATI
3.2. AIRBUS Dataset
3.2.1. Accuracy Results with AIRBUS
3.2.2. U-Optimization Analysis with AIRBUS
4. Conclusions and Future Work
4.1. Conclusions
4.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wiesebron, M. Blue Amazon: Thinking the Defense of Brazilian Maritime Territory. Austral Braz. J. Strategy Int. Relat. 2013, 2, 101–124. Available online: https://www.files.ethz.ch/isn/166009/37107-147326-1-PB.pdf#page=102 (accessed on 12 June 2023).
- Brazilian Navy Command. Brazilian Navy Naval Policy. Available online: https://www.naval.com.br/blog/wp-content/uploads/2019/04/PoliticaNavalMB.pdf (accessed on 9 April 2023).
- Interdisciplinary Observatory on Climate Change. Last Frontier at Sea. Available online: https://obsinterclima.eco.br/mapas/ultima-fronteira-no-mar/ (accessed on 7 April 2023).
- Brazilian Navy Social Communication Center. Blue Amazon—The Heritage Brazilian at Sea. Villegagnon Journal Supplement—VII Academic Congress on National Defense. Available online: http://www.redebim.dphdm.mar.mil.br/vinculos/000006/00000600.pdf (accessed on 9 April 2023).
- de Oliveira Andrade, I.; da Rocha, A.J.R.; Franco, L.G.A. DP 0261—Blue Amazon Management System (SisGAAz): Sovereignty, Surveillance and Defense of the Brazilian Jurisdictional Waters; Discussion Paper; Instituto de Pesquisa Economica Aplicada—IPEA: Brasília, Brazil, 2021; 35p. [Google Scholar] [CrossRef]
- de Oliveira Andrade, I.; Franco, L.G.A.; Hillebrand, G.R.L. DP 2471—Science, Technology and Innovation in The Brazilian Navy’s Strategic Programs; Discussion Paper; Instituto de Pesquisa Economica Aplicada—IPEA: Brasília, Brazil, 2019; Available online: https://www.researchgate.net/publication/335925079_Ciencia_Tecnologia_e_Inovacao_nos_Programas_Estrategicos_da_Marinha_do_Brasil (accessed on 12 June 2023).
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Gewalt, R. Supervised vs. Unsupervised vs. Reinforcement Learning—The Fundamental Differences, Fly Spaceships with Your Mind. Available online: https://www.opit.com/magazine/supervised-vs-unsupervised-learning/ (accessed on 10 April 2023).
- Sohil, F.; Sohali, M.U.; Shabbir, J. An Introduction to Statistical Learning with Applications in R, Statistical Theory and Related Fields; Informa UK Limited: London, UK, 2021; Volume 6. [Google Scholar] [CrossRef]
- Petercour, Machine Learning Classification vs. Regression, DEV Community. Available online: https://dev.to/petercour/machine-learning-classification-vs-regression-1gn (accessed on 10 April 2023).
- Gunjal, S. Logistic Regression from Scratch with Python, Quality Tech Tutorials. Available online: https://satishgunjal.com/binary_lr/ (accessed on 24 April 2023).
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 17 June 2023).
- Burkov, A. The Hundred-Page Machine Learning Book. 2019. Available online: http://ema.cri-info.cm/wp-content/uploads/2019/07/2019BurkovTheHundred-pageMachineLearning.pdf (accessed on 22 June 2023).
- Haykin, S.S. Neural Networks and Learning Machines, 3rd ed.; Prentice-Hall: New York, NY, USA, 2009. [Google Scholar]
- Banoula, M. What is Perceptron? A Beginner’s Guide [updated]: Simplilearn. Available online: https://www.simplilearn.com/tutorials/deep-learning-tutorial/perceptron (accessed on 24 April 2023).
- Shanmugamani, R. Deep Learning for Computer Vision: Expert Techniques to Train Advanced Neural Networks Using TensorFlow and Keras; Packt Publishing: Birmingham, UK, 2018. [Google Scholar]
- Activation Function—AI Wiki. Available online: https://machine-learning.paperspace.com/wiki/activation-function (accessed on 24 April 2023).
- Szeliski, R. Computer Vision: Algorithms and Applications, 2nd ed.; Springer Ltd.: London, UK, 2022. [Google Scholar]
- Varghese, L.J.; Jacob, S.S.; Sundar, C.; Raglend, J. Design and Implementation of a Machine Learning Assisted Smart Wheelchair in an IoT Environment. Research Square Platform LLC: Durham, NC, USA, 2021. [Google Scholar] [CrossRef]
- Khan, S.; Rahmani, H.; Shah, S.A.A.; Bennamoun, M. A Guide to Convolutional Neural Networks for Computer Vision; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Chen, L.; Li, S.; Bai, Q.; Yang, J.; Jiang, S.; Miao, Y. Review of Image Classification Algorithms Based on Convolutional Neural Networks. Remote Sens. 2021, 13, 4712. [Google Scholar] [CrossRef]
- Torén, R. Comparing CNN Methods for Detection and Tracking of Ships in Satellite Images. Master’s Thesis, Department of Computer and Information Science, Linköping University, Linköping, Sweden, 2020. [Google Scholar]
- TensorFlow Core. Introduction to Automatic Encoders. Available online: https://www.tensorflow.org/tutorials/generative/autoencoder?hl=pt-br (accessed on 28 April 2023).
- CS 230—Convolutional Neural Networks Cheatsheet. Available online: https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-convolutional-neural-networks (accessed on 28 April 2023).
- Royset, J.O.; Chen, L.L.; Eckstrand, E. Rockafellian Relaxation in Optimization under Uncertainty: Asymptotically Exact Formulations. arXiv 2022, arXiv:2204.04762. Available online: https://arxiv.org/abs/2204.04762 (accessed on 27 June 2023).
- Maron, M.E. Automatic Indexing: An Experimental Inquiry. J. ACM 1961, 8, 404–417. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of Decision Trees. Mach. Lang. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Lang. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hinton, G.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 49–50. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain; American Psychological Association (APA). Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Steinbuch, K.; Widrow, B. A Critical Comparison of Two Kinds of Adaptive Classification Networks. IEEE Trans. Electron. Comput. 1965, EC-14, 737–740. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 6088. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics; JMLR Workshop and Conference Proceedings, Sardinia, Italy, 13–15 May 2010; pp. 249–256. Available online: https://proceedings.mlr.press/v9/glorot10a.html (accessed on 8 May 2023).
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2012; Available online: https://papers.nips.cc/paper_files/paper/2012/hash/c399862d3b9d6b76c8436e924a68c45b-Abstract.html (accessed on 8 May 2023).
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. Available online: http://arxiv.org/abs/1409.4842 (accessed on 8 May 2023).
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. Available online: http://arxiv.org/abs/1409.1556 (accessed on 8 May 2023).
- Shadeed, G.A.; Tawfeeq, M.A.; Mahmoud, S.M. Automatic Medical Images Segmentation Based on Deep Learning Networks. IOP Conf. Ser. Mater. Sci. Eng. 2020, 870, 012117. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Fortunati, V. Deep Learning Applications in Radiology: A Deep Dive on Classification. Available online: https://www.quantib.com/blog/deep-learning-applications-in-radiology/classification (accessed on 9 May 2023).
- Veit, A.; Wilber, M.J.; Belongie, S. Residual Networks Behave Like Ensembles of Relatively Shallow Networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2016; Available online: https://proceedings.neurips.cc/paper_files/paper/2016/hash/37bc2f75bf1bcfe8450a1a41c200364c-Abstract.html (accessed on 7 June 2023).
- Hanin, B. Which Neural Net Architectures Give Rise to Exploding and Vanishing Gradients? arXiv 2018, arXiv:1801.03744. Available online: http://arxiv.org/abs/1801.03744 (accessed on 7 June 2023).
- Tetreault, B.J. Use of the Automatic Identification System (AIS) for maritime domain awareness (MDA). In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA 17–23 September 2005; Volume 2, pp. 1590–1594. [Google Scholar] [CrossRef]
- Zardoua, Y.; Astito, A.; Boulaala, M. A Comparison of AIS, X-Band Marine Radar Systems and Camera Surveillance Systems in the Collection of Tracking Data. arXiv 2020, arXiv:2206.12809. [Google Scholar]
- Ma, M.; Chen, J.; Liu, W.; Yang, W. Ship Classification and Detection Based on CNN Using GF-3 SAR Images. Remote Sens. 2018, 10, 2043. [Google Scholar] [CrossRef]
- Ødegaard, N.; Knapskog, A.O.; Cochin, C.; Louvigne, J.-C. Classification of ships using real and simulated data in a convolutional neural network. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Bentes, C.; Velotto, D.; Tings, B. Ship Classification in TerraSAR-X Images with Convolutional Neural Networks. IEEE J. Ocean. Eng. 2018, 43, 258–266. [Google Scholar] [CrossRef]
- Gallego, A.-J.; Pertusa, A.; Gil, P. Automatic Ship Classification from Optical Aerial Images with Convolutional Neural Networks. Remote Sens. 2018, 10, 511. [Google Scholar] [CrossRef]
- Fang, H.; Chen, M.; Liu, X.; Yao, S. Infrared Small Target Detection with Total Variation and Reweighted ℓ 1 Regularization. Math. Probl. Eng. 2020, 2020, 1529704. [Google Scholar] [CrossRef]
- Kanellakis, C.; Nikolakopoulos, G. Survey on Computer Vision for UAVs: Current Developments and Trends. J. Intell. Robot. Syst. 2017, 87, 141–168. [Google Scholar] [CrossRef]
- Cruz, G.; Bernardino, A. Aerial Detection in Maritime Scenarios Using Convolutional Neural Networks. In Advanced Concepts for Intelligent Vision Systems; Lecture Notes in Computer Science; Blanc-Talon, J., Distante, C., Philips, W., Popescu, D., Scheunders, P., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Volume 10016, pp. 373–384. [Google Scholar] [CrossRef]
- Lo, L.-Y.; Yiu, C.H.; Tang, Y.; Yang, A.-S.; Li, B.; Wen, C.-Y. Dynamic Object Tracking on Autonomous UAV System for Surveillance Applications. Sensors 2021, 21, 7888. [Google Scholar] [CrossRef]
- Lygouras, E.; Santavas, N.; Taitzoglou, A.; Tarchanidis, K.; Mitropoulos, A.; Gasteratos, A. Unsupervised Human Detection with an Embedded Vision System on a Fully Autonomous UAV for Search and Rescue Operations. Sensors 2019, 19, 3542. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2016, arXiv:1506.02640. Available online: http://arxiv.org/abs/1506.02640 (accessed on 10 May 2023).
- WACV 2023—Maritime Workshop. Available online: https://seadronessee.cs.uni-tuebingen.de/wacv23 (accessed on 20 May 2023).
- Hickey, R.J. Noise modelling and evaluating learning from examples. Artif. Intell. 1996, 82, 157–179. [Google Scholar] [CrossRef]
- Song, H.; Kim, M.; Park, D.; Shin, Y.; Lee, J.-G. Learning from Noisy Labels with Deep Neural Networks: A Survey. arXiv 2022, arXiv:2007.08199. Available online: http://arxiv.org/abs/2007.08199 (accessed on 21 May 2023). [CrossRef] [PubMed]
- Liu, T.; Tao, D. Classification with Noisy Labels by Importance Reweighting. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 447–461. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Wu, Q.; Li, H.; Chen, Y. Generative Poisoning Attack Method Against Neural Networks. arXiv 2017, arXiv:1703.01340. Available online: http://arxiv.org/abs/1703.01340 (accessed on 22 May 2023).
- Ren, M.; Zeng, W.; Yang, B.; Urtasun, R. Learning to Reweight Examples for Robust Deep Learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Thulasidasan, S.; Bhattacharya, T.; Bilmes, J.; Chennupati, G.; Mohd-Yusof, J. Combating Label Noise in Deep Learning Using Abstention. arXiv 2019, arXiv:1905.10964. Available online: http://arxiv.org/abs/1905.10964 (accessed on 21 May 2023).
- Chen, L.; Huang, N.; Mu, C.; Helm, H.S.; Lytvynets, K.; Yang, W.; Priebe, C.E. Deep Learning with Label Noise: A Hierarchical Approach. arXiv 2022, arXiv:2205.14299. Available online: http://arxiv.org/abs/2205.14299 (accessed on 21 May 2023).
- Narasimhan, H.; Menon, A.K.; Jitkrittum, W.; Kumar, S. Learning to reject meets OOD detection: Are all abstentions created equal? arXiv 2023, arXiv:2301.12386. Available online: http://arxiv.org/abs/2301.12386 (accessed on 21 May 2023).
- Ni, C.; Charoenphakdee, N.; Honda, J.; Sugiyama, M. On the Calibration of Multiclass Classification with Rejection. arXiv 2019, arXiv:1901.10655. Available online: http://arxiv.org/abs/1901.10655 (accessed on 22 May 2023).
- Ramaswamy, H.G.; Tewari, A.; Agarwal, S. Consistent algorithms for multiclass classification with an abstain option. Electron. J. Stat. 2018, 12, 530–554. [Google Scholar] [CrossRef]
- Katz-Samuels, J.; Nakhleh, J.; Nowak, R.; Li, Y. Training OOD Detectors in their Natural Habitats. arXiv 2022, arXiv:2202.03299. Available online: http://arxiv.org/abs/2202.03299 (accessed on 22 May 2023).
- Royset, J.O.; Wets, R.J.-B. An Optimization Primer. In Springer Series in Operations Research and Financial Engineering; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Wang, W.; Carreira-Perpiñán, M.Á. Projection onto the probability simplex: An efficient algorithm with a simple proof, and an application. arXiv 2013, arXiv:1309.1541. Available online: http://arxiv.org/abs/1309.1541 (accessed on 22 April 2023).
- Airbus Ship Detection Challenge. Available online: https://kaggle.com/competitions/airbus-ship-detection (accessed on 30 May 2023).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. Available online: http://arxiv.org/abs/1412.6980 (accessed on 8 May 2023).
- Bishop, C.M. Neural Networks: A Pattern Recognition Perspective. In Handbook of Neural Computation; CRC Press: Boca Raton, FL, USA, 2020; pp. 1–6. [Google Scholar]






| # | Layer | Filters | Kernel Size | Output Size | # Parameters |
|---|---|---|---|---|---|
| 1 | Convolution | 16 | 3 × 3 | 128 × 128 × 16 | 448 |
| Max-Pooling | 2 × 2 | 64 × 64 × 16 | |||
| 2 | Convolution | 32 | 3 × 3 | 64 × 64 × 32 | 4640 |
| Max-Pooling | 2 × 2 | 32 × 32 × 32 | |||
| 3 | Convolution | 64 | 3 × 3 | 32 × 32 × 64 | 18,496 |
| Max-Pooling | 2 × 2 | 16 × 16 × 64 | |||
| 4 | Convolution | 128 | 3 × 3 | 16 × 16 × 128 | 73,856 |
| Max-Pooling | 2 × 2 | 8 × 8 × 128 | |||
| 5 | Fully connected | 256 | 1 × 256 | 2,097,408 | |
| 6 | Fully connected | 128 | 1 × 128 | 32,896 | |
| 7 | Softmax (Output) | 2 | 1 × 2 | 258 |
| # | Layer | Filters | Kernel Size | Output Size | # Parameters |
|---|---|---|---|---|---|
| 1 | Convolution | 32 | 3 × 3 | 128 × 128 × 32 | 896 |
| 2 | Batch Normalization Activation | 128 | |||
| 3 | Max-Pooling | 2 × 2 | 64 × 64 × 32 | - | |
| 4 | Convolution Activation | 64 | 3 × 3 | 64 × 64 × 64 | 18,496 |
| Max-Pooling | 2 × 2 | 32 × 32 × 64 | |||
| 5 | Fully-connected | 128 | 1 × 128 | 8,388,736 | |
| 6 | Batch Normalization Activation | 512 | |||
| 7 | Softmax (Output) | 2 | 1 × 2 | 258 |
| Parameters | ||||
|---|---|---|---|---|
| Algorithm | Epochs (κ) | Iterations (τ) | Stepsize (µ) | Penalty (θ) |
| ERM | 500 | 1 | - | - |
| RRM(ADH-LP) | 10 | 50 | 0.5 | 0.15, 0.20, 0.25, 0.30, 0.35 |
| Dataset | ||||||||
|---|---|---|---|---|---|---|---|---|
| MASATI | AIRBUS | |||||||
| CNN Optimizer | CNN Optimizer | |||||||
| Adam | SGD | Adam | SGD | |||||
| Optimization phase | w | u | w | u | w | u | w | u |
| Algorithm | Total runtime in seconds over optimization phases | |||||||
| ERM | 500 | - | 1400 | - | 22,500 | - | 68,500 | - |
| RRM (ADH-LP) | 500 | 600 | 1400 | 600 | 22,500 | 1000 | 68,500 | 1000 |
| Corrupted Training Data Percentage | |||||
|---|---|---|---|---|---|
| Method | 40% | 30% | 20% | 10% | 0% |
| ERM | 0.624 | 0.653 | 0.785 | 0.858 | 0.941 |
| RRM (μ = 0.5) | |||||
| θ = 0.15 | 0.624 | 0.668 | 0.800 | 0.863 | 0.951 |
| θ = 0.20 | 0.609 | 0.726 | 0.848 | 0.878 | 0.931 |
| θ = 0.25 | 0.668 | 0.682 | 0.814 | 0.863 | 0.941 |
| θ = 0.30 | 0.604 | 0.702 | 0.804 | 0.843 | 0.926 |
| θ = 0.35 | 0.614 | 0.692 | 0.756 | 0.834 | 0.921 |
| Corrupted Training Data Percentage | |||||
|---|---|---|---|---|---|
| Method | 40% | 30% | 20% | 10% | 0% |
| ERM | 0.556 | 0.546 | 0.581 | 0.663 | 0.648 |
| RRM (μ = 0.5) | |||||
| θ = 0.15 | 0.604 | 0.648 | 0.648 | 0.639 | 0.634 |
| θ = 0.20 | 0.663 | 0.692 | 0.648 | 0.648 | 0.609 |
| θ = 0.25 | 0.639 | 0.687 | 0.658 | 0.629 | 0.614 |
| θ = 0.30 | 0.668 | 0.585 | 0.600 | 0.643 | 0.634 |
| θ = 0.35 | 0.624 | 0.556 | 0.639 | 0.648 | 0.653 |
| ADH-LP/SGD RRM (μ = 0.5) | Contamination Levels | |||||||
|---|---|---|---|---|---|---|---|---|
| 40% (737 Mislabeled Images) | 30% (553 Mislabeled Images) | 20% (368 Mislabeled Images) | 10% (184 Mislabeled Images) | |||||
| Value of Penalty θ | Model Accuracy | # of Mislabeled Images Excluded | Model Accuracy | # of Mislabeled Images Excluded | Model Accuracy | # of Mislabeled Images Excluded | Model Accuracy | # of Mislabeled Images Excluded |
| 0.15 | 0.604 | 327 | 0.648 | 286 | 0.648 | 211 | 0.639 | 99 |
| 0.20 | 0.663 | 338 | 0.692 | 290 | 0.648 | 197 | 0.648 | 91 |
| 0.25 | 0.639 | 318 | 0.687 | 263 | 0.658 | 163 | 0.629 | 94 |
| 0.30 | 0.668 | 295 | 0.585 | 230 | 0.600 | 159 | 0.643 | 87 |
| 0.35 | 0.624 | 253 | 0.556 | 213 | 0.639 | 140 | 0.648 | 71 |
| Nominal Probability (1/N) | Iteration Number | |||||
|---|---|---|---|---|---|---|
| i = 1 | i = 2 | i = 49 | ||||
| -Values | Mislabeled Images | Correct Labeled Images | Mislabeled Images | Correct Labeled Images | Mislabeled Images | Correct Labeled Images |
| >>0 | 0 | 1 | 0 | 1 | 1 | 1 |
| ≈0 | 304 | 813 | 266 | 782 | 338 | 1005 |
| −1.5 · | 0 | 0 | 37 | 92 | 1 | 5 |
| −2.7 · | 249 | 477 | 38 | 41 | 0 | 1 |
| −4.0 · | 0 | 0 | 212 | 375 | 0 | 1 |
| −5.4 · | 0 | 0 | 0 | 0 | 213 | 278 |
| Total of images | 553 | 1291 | 553 | 1291 | 553 | 1291 |
| Nominal Probability (1/N) | Iteration Number | |||||
|---|---|---|---|---|---|---|
| i = 1 | i = 2 | i = 49 | ||||
| -Values | Mislabeled Images | Correct Labeled Images | Mislabeled Images | Correct Labeled Images | Mislabeled Images | Correct Labeled Images |
| >>0 | 0 | 1 | 0 | 1 | 0 | 1 |
| ≈0 | 133 | 453 | 93 | 370 | 260 | 863 |
| −1.5 · | 0 | 0 | 39 | 105 | 3 | 1 |
| −2.7 · | 420 | 837 | 40 | 83 | 0 | 0 |
| −4.0 · | 0 | 0 | 381 | 732 | 0 | 0 |
| −5.4 · | 0 | 0 | 0 | 0 | 290 | 426 |
| Total of labels | 553 | 1291 | 553 | 1291 | 553 | 1291 |
| Corrupted Training Data Percentage | |||||
|---|---|---|---|---|---|
| Method | 40% | 30% | 20% | 10% | 0% |
| ERM | 0.588 | 0.657 | 0.729 | 0.797 | 0.867 |
| RRM (μ = 0.5) | |||||
| θ = 0.15 | 0.602 | 0.692 | 0.758 | 0.831 | 0.868 |
| θ = 0.20 | 0.607 | 0.668 | 0.751 | 0.819 | 0.875 |
| θ = 0.25 | 0.616 | 0.690 | 0.763 | 0.823 | 0.867 |
| θ = 0.30 | 0.619 | 0.686 | 0.783 | 0.824 | 0.872 |
| θ = 0.35 | 0.602 | 0.695 | 0.767 | 0.819 | 0.872 |
| Corrupted Training Data Percentage | |||||
|---|---|---|---|---|---|
| Method | 40% | 30% | 20% | 10% | 0% |
| ERM | 0.560 | 0.629 | 0.681 | 0.735 | 0.769 |
| RRM (μ = 0.5) | |||||
| θ = 0.15 | 0.603 | 0.739 | 0.745 | 0.774 | 0.764 |
| θ = 0.20 | 0.671 | 0.755 | 0.753 | 0.775 | 0.769 |
| θ = 0.25 | 0.687 | 0.733 | 0.757 | 0.769 | 0.767 |
| θ = 0.30 | 0.684 | 0.744 | 0.764 | 0.765 | 0.774 |
| θ = 0.35 | 0.661 | 0.747 | 0.764 | 0.770 | 0.779 |
| ADH-LP/SGD | Contamination Levels in AIRBUS | |||||||
|---|---|---|---|---|---|---|---|---|
| 40% (3336 Mislabeled Images) | 30% (2502 Mislabeled Images) | 20% (1668 Mislabeled Images) | 10% (834 Mislabeled Images) | |||||
| Value of Penalty θ | Model Accuracy | # of Mislabeled Images Excluded | Model Accuracy | # of Mislabeled Images Excluded | Model Accuracy | # of Mislabeled Images Excluded | Model Accuracy | # of Mislabeled Images Excluded |
| 0.15 | 0.603 | 1985 | 0.739 | 1812 | 0.745 | 1210 | 0.774 | 621 |
| 0.20 | 0.671 | 2108 | 0.755 | 1767 | 0.753 | 1200 | 0.775 | 587 |
| 0.25 | 0.687 | 2127 | 0.733 | 1701 | 0.757 | 1158 | 0.769 | 573 |
| 0.30 | 0.684 | 2019 | 0.744 | 1636 | 0.764 | 1154 | 0.765 | 564 |
| 0.35 | 0.661 | 1737 | 0.747 | 1635 | 0.764 | 1109 | 0.770 | 538 |
| Nominal Probability (1/N) | Iteration Number | |||||
|---|---|---|---|---|---|---|
| i = 1 | i = 2 | i = 49 | ||||
| -Values | Mislabeled Images | Correct Labeled Images | Mislabeled Images | Correct Labeled Images | Mislabeled Images | Correct Labeled Images |
| >>0 | 0 | 1 | 0 | 1 | 0 | 2 |
| ≈0 | 131 | 264 | 64 | 194 | 1346 | 3135 |
| −3.0 · | 0 | 0 | 24 | 63 | 2 | 1 |
| −6.0 · | 3205 | 4739 | 67 | 153 | 3 | 6 |
| −9.0 · | 0 | 0 | 3181 | 4593 | 0 | 0 |
| −12.0 · | 0 | 0 | 0 | 0 | 1985 | 1860 |
| Total of images | 3336 | 5004 | 3336 | 5004 | 3336 | 5004 |
| Nominal Probability (1/N) | Iteration Number | |||||
|---|---|---|---|---|---|---|
| i = 1 | i = 2 | i = 49 | ||||
| -Values | Mislabeled Images | Correct Labeled Images | Mislabeled Images | Correct Labeled Images | Mislabeled Images | Correct Labeled Images |
| >>0 | 1 | 0 | 1 | 0 | 1 | 0 |
| ≈0 | 418 | 1257 | 312 | 1117 | 1192 | 3591 |
| −3.0 · | 0 | 0 | 142 | 590 | 7 | 1 |
| −6.0 · | 2917 | 3747 | 106 | 140 | 2 | 2 |
| −9.0 · | 0 | 0 | 2775 | 3157 | 5 | 6 |
| −12.0 · | 0 | 0 | 0 | 0 | 2129 | 1404 |
| Total of images | 3336 | 5004 | 3336 | 5004 | 3336 | 5004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rangel, G.C.; Alves, V.B.A.d.S.; Costa, I.P.d.A.; Moreira, M.Â.L.; Costa, A.P.d.A.; Santos, M.d.; Eckstrand, E.C. Efficient Naval Surveillance: Addressing Label Noise with Rockafellian Risk Minimization for Water Security. Water 2025, 17, 401. https://doi.org/10.3390/w17030401
Rangel GC, Alves VBAdS, Costa IPdA, Moreira MÂL, Costa APdA, Santos Md, Eckstrand EC. Efficient Naval Surveillance: Addressing Label Noise with Rockafellian Risk Minimization for Water Security. Water. 2025; 17(3):401. https://doi.org/10.3390/w17030401
Chicago/Turabian StyleRangel, Gabriel Custódio, Victor Benicio Ardilha da Silva Alves, Igor Pinheiro de Araújo Costa, Miguel Ângelo Lellis Moreira, Arthur Pinheiro de Araújo Costa, Marcos dos Santos, and Eric Charles Eckstrand. 2025. "Efficient Naval Surveillance: Addressing Label Noise with Rockafellian Risk Minimization for Water Security" Water 17, no. 3: 401. https://doi.org/10.3390/w17030401
APA StyleRangel, G. C., Alves, V. B. A. d. S., Costa, I. P. d. A., Moreira, M. Â. L., Costa, A. P. d. A., Santos, M. d., & Eckstrand, E. C. (2025). Efficient Naval Surveillance: Addressing Label Noise with Rockafellian Risk Minimization for Water Security. Water, 17(3), 401. https://doi.org/10.3390/w17030401








