Effect of the Shear Band on Water Migration in the Interface Between Lean Clay and an Engineering Structure: A Case Study of Loess-like Soil in Changchun Area, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Experimental Grouping and Design
2.2.1. Experimental Grouping
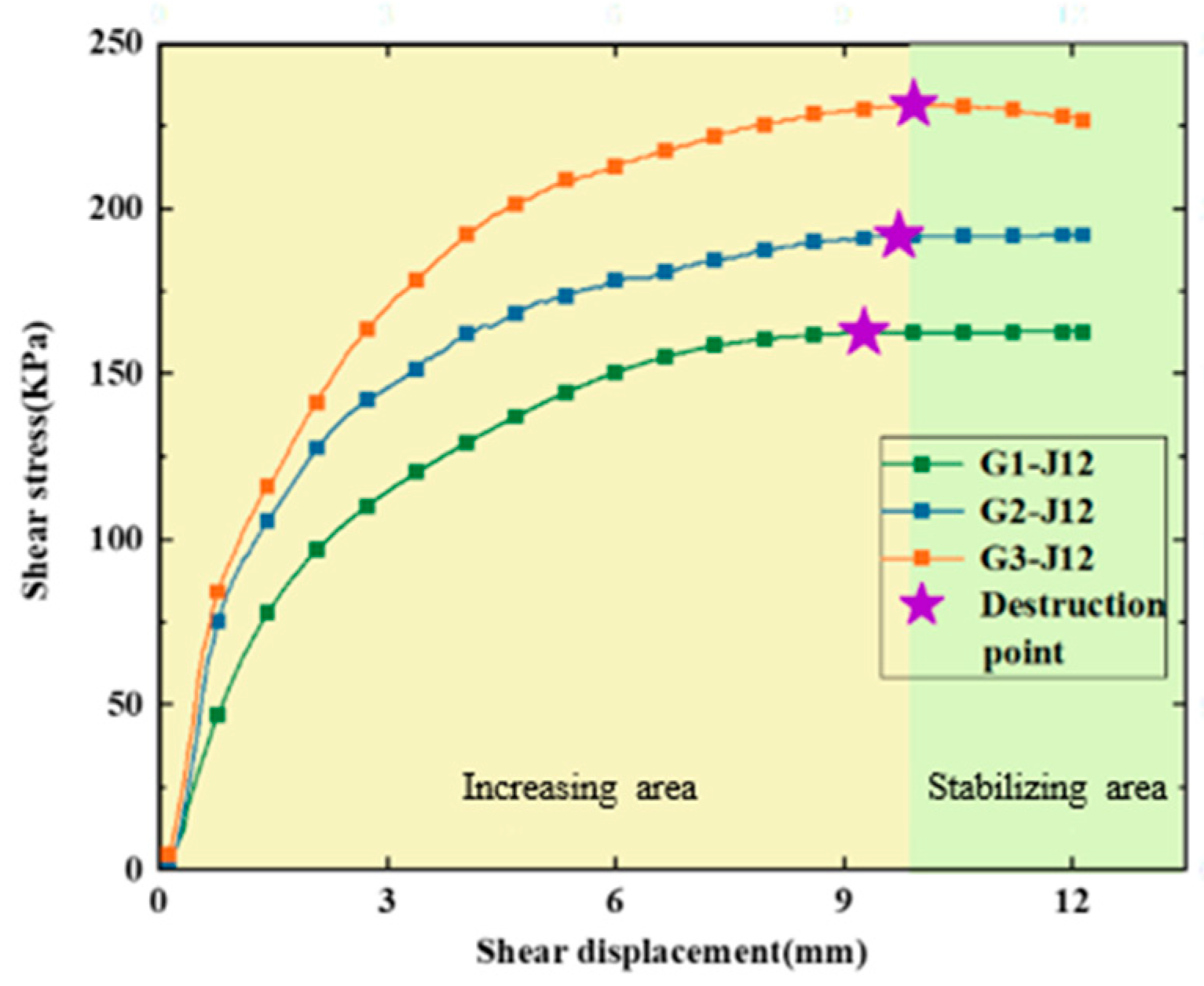
2.2.2. Direct Shear Test
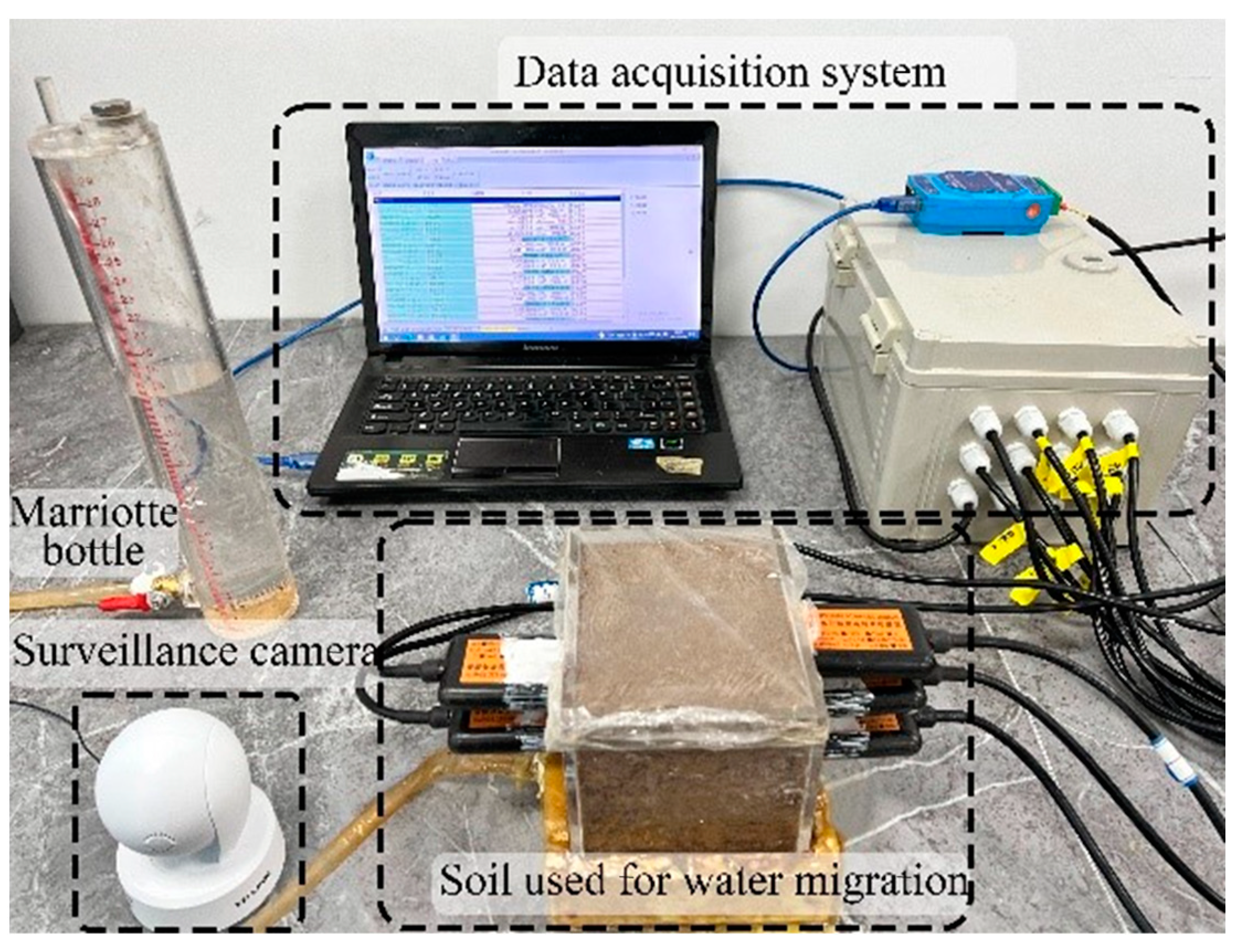
2.2.3. Soil Water Migration Test with the Shear Band
3. Results and Discussion
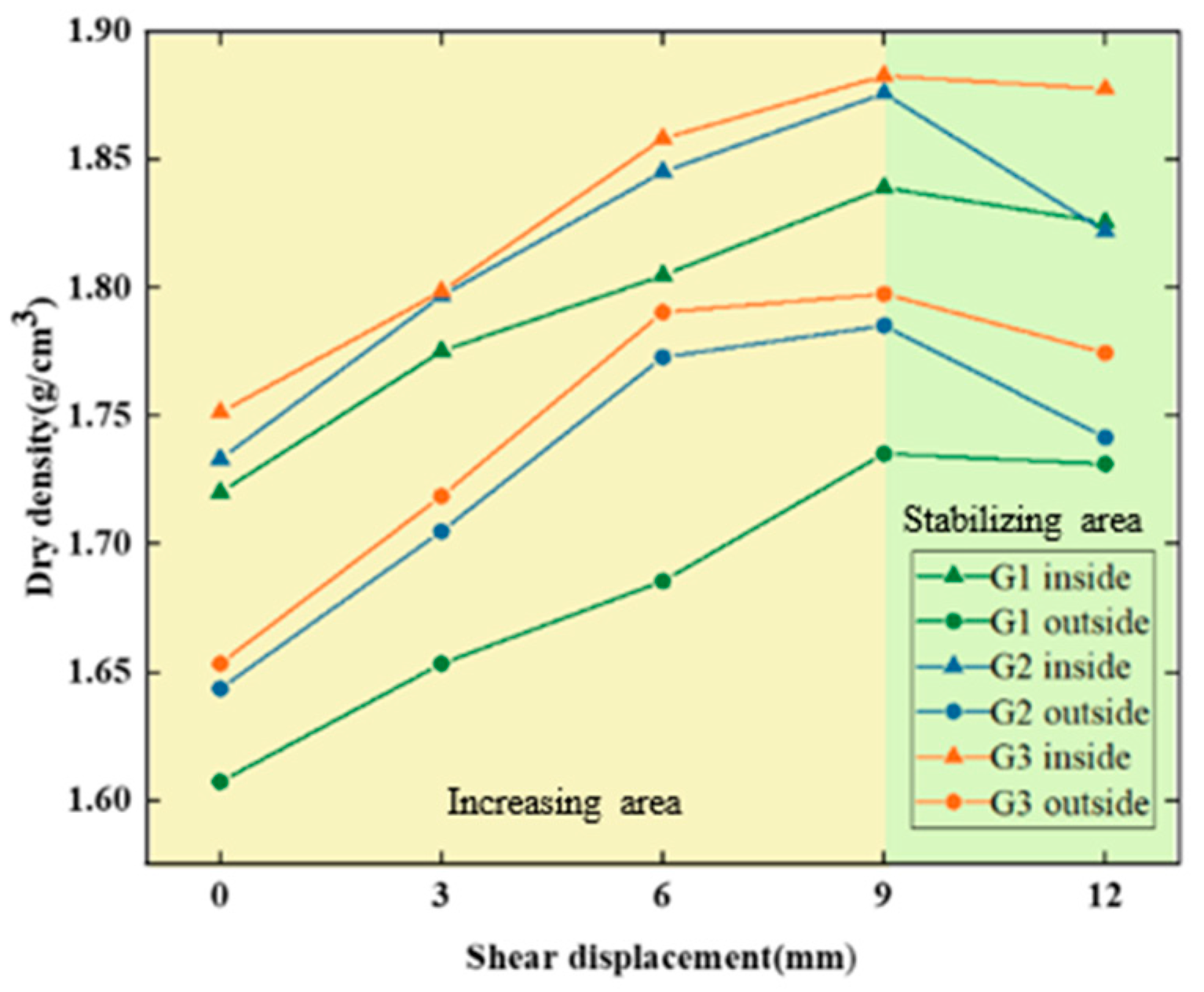
3.1. Analysis of the Dry Density of Soil in the Lean Clay–Concrete Shear Band
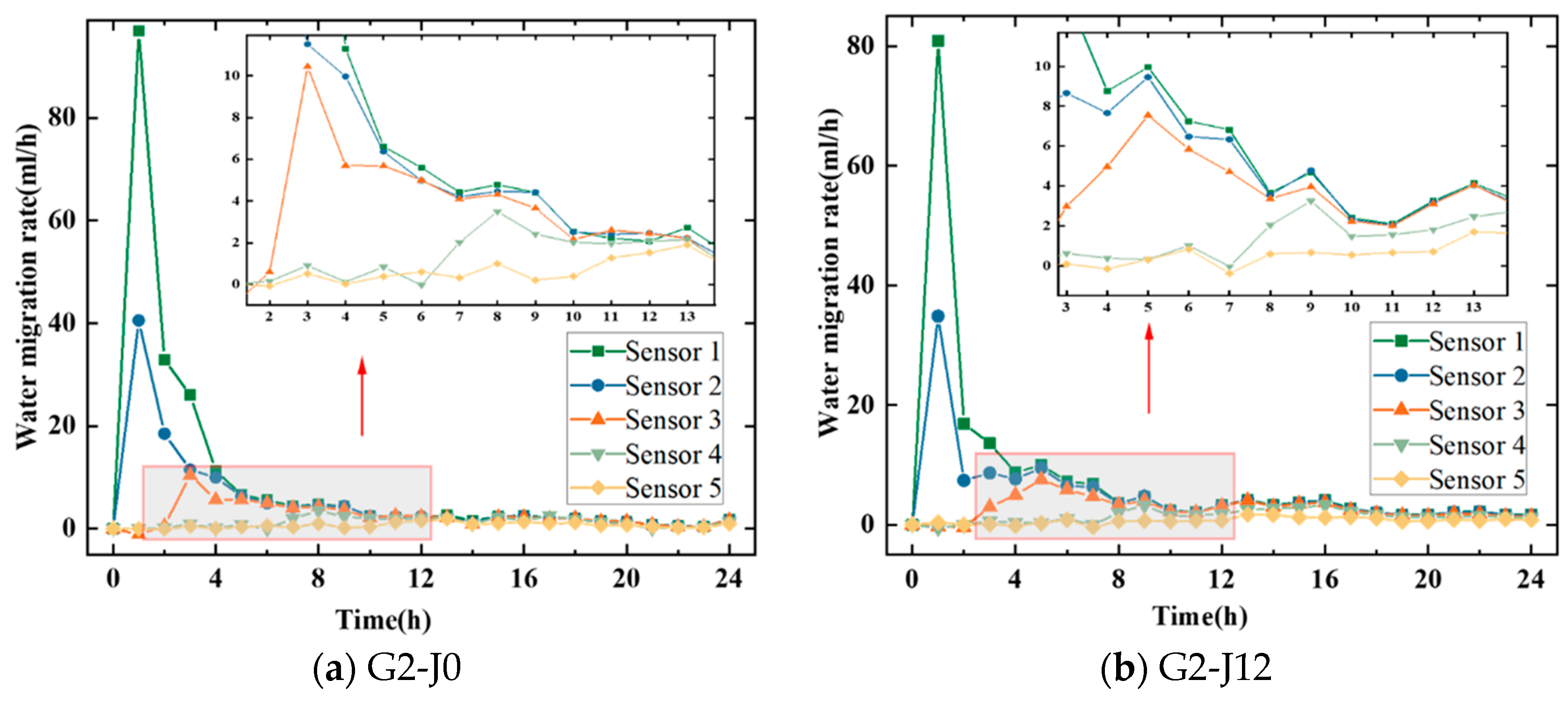
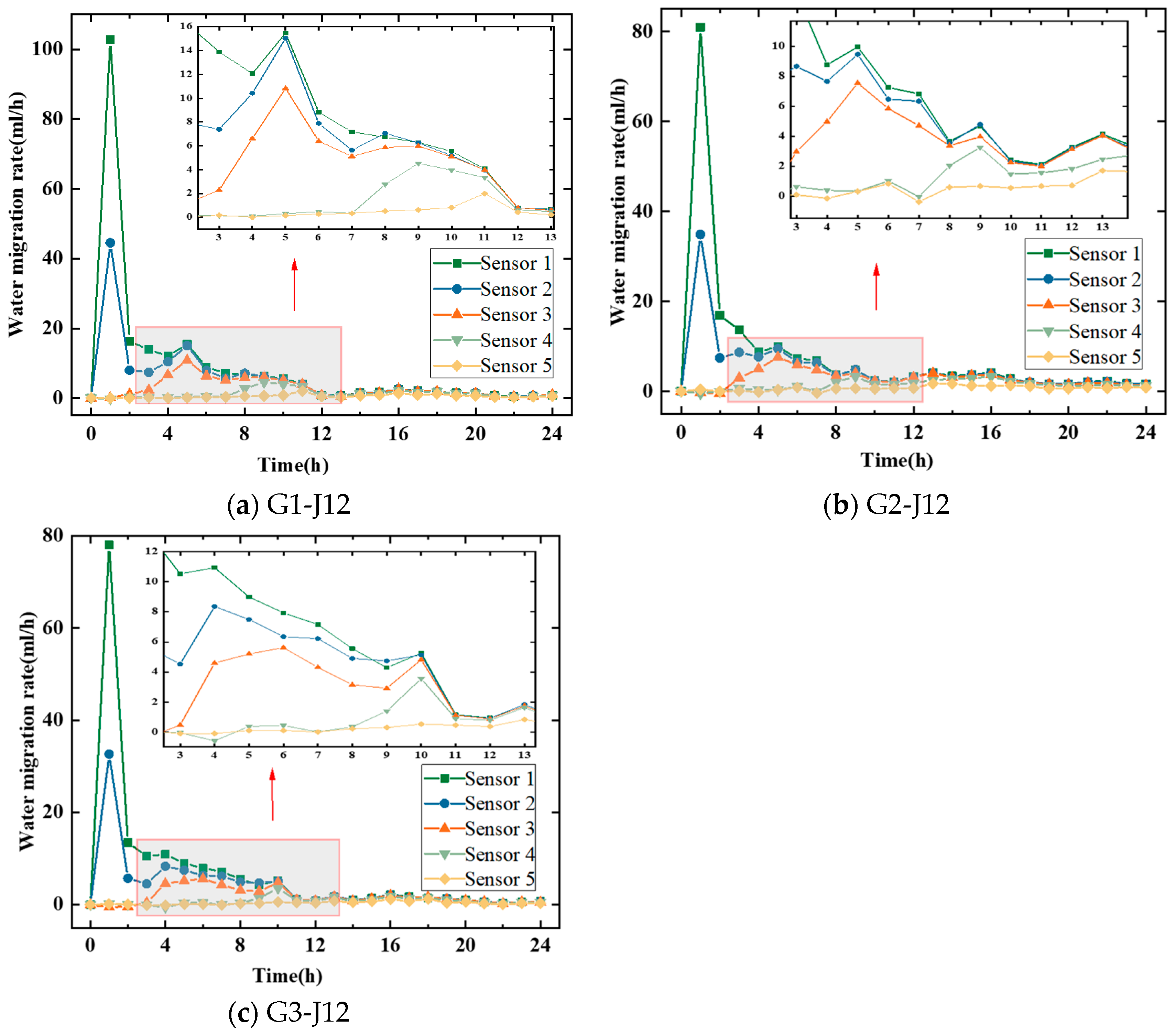
3.2. Changes in the Rate of Water Migration in Soil Under Different Influencing Factors
- (1)
- Shear Displacement
- (2)
- Normal stress
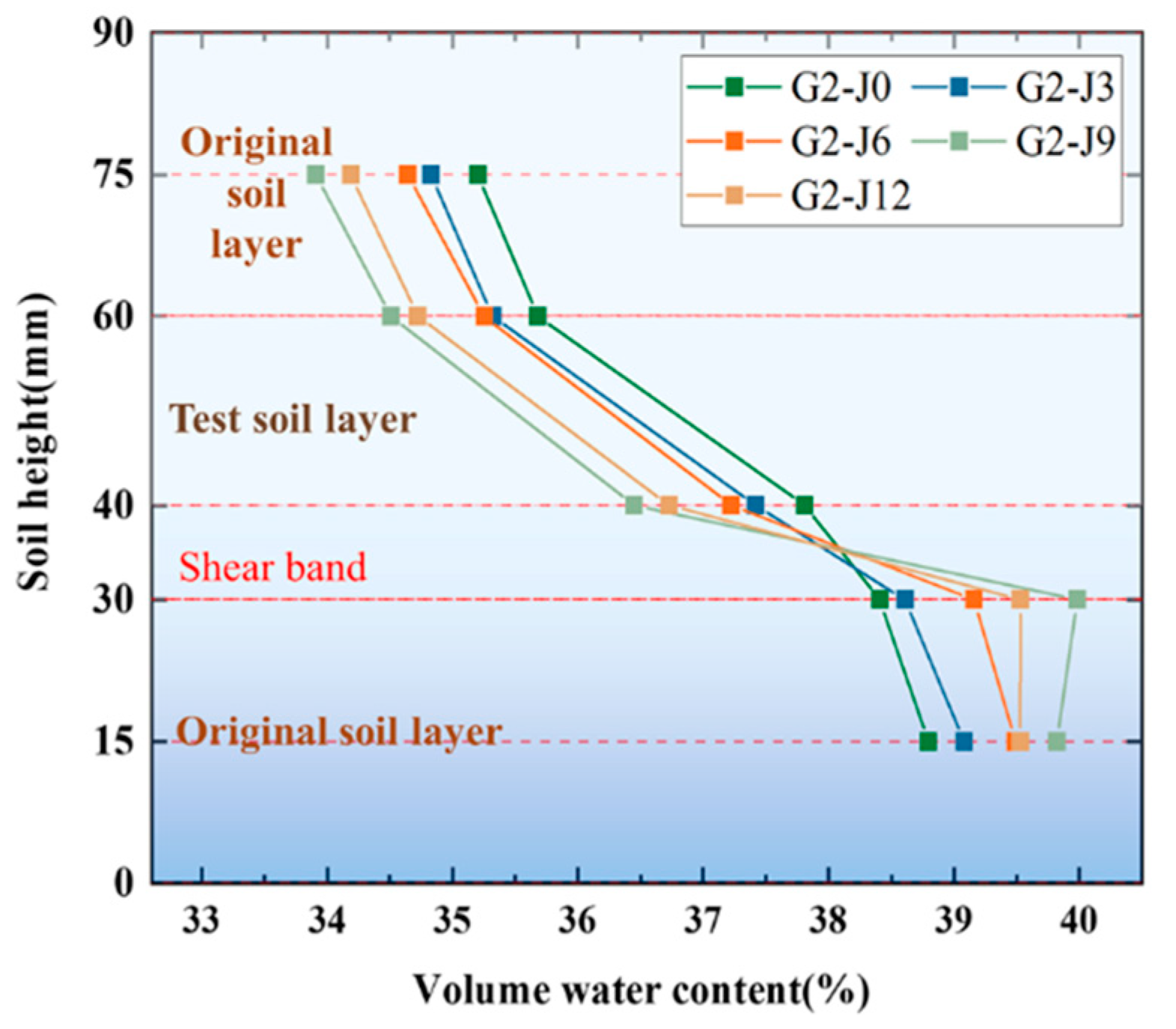
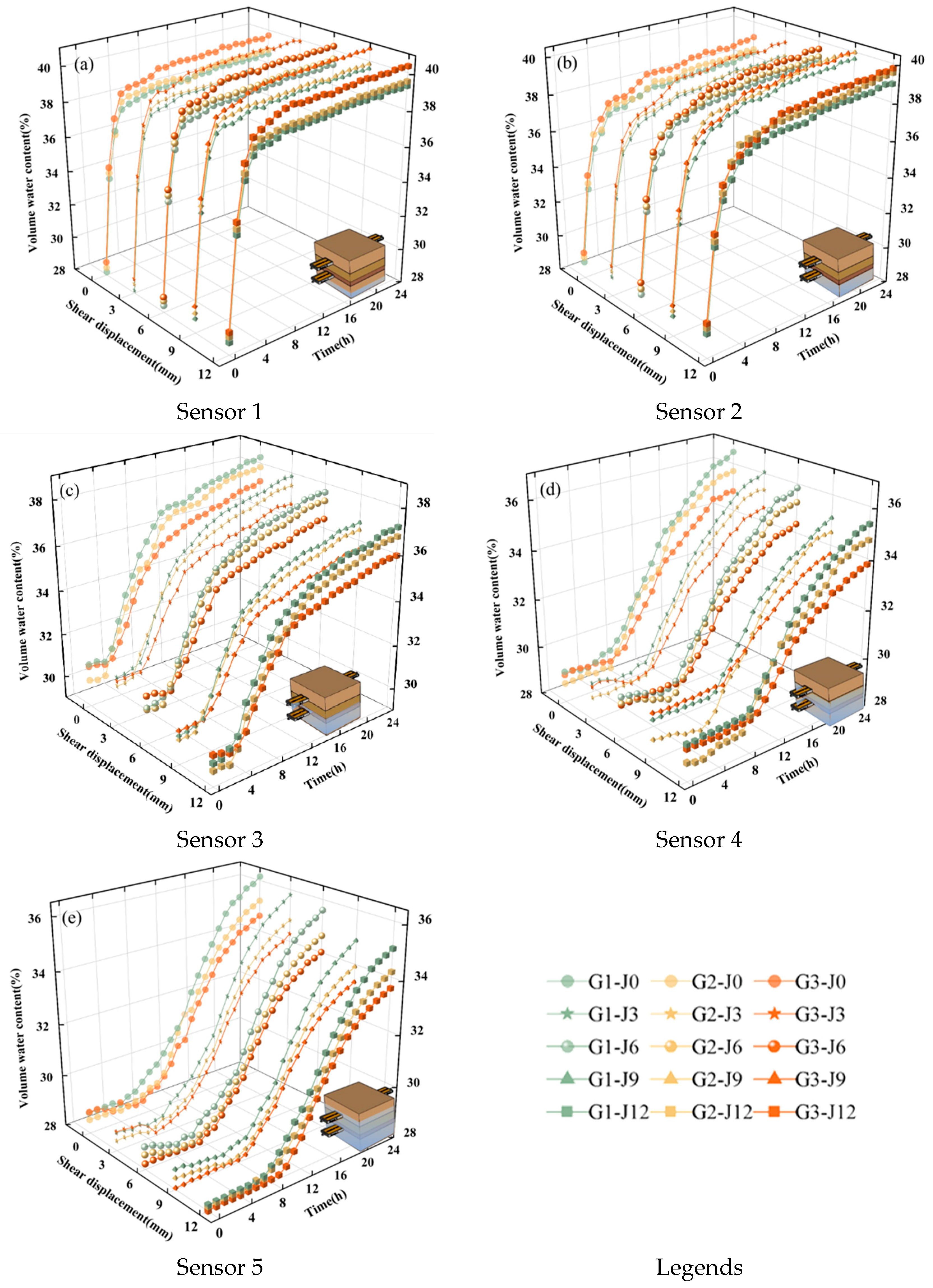
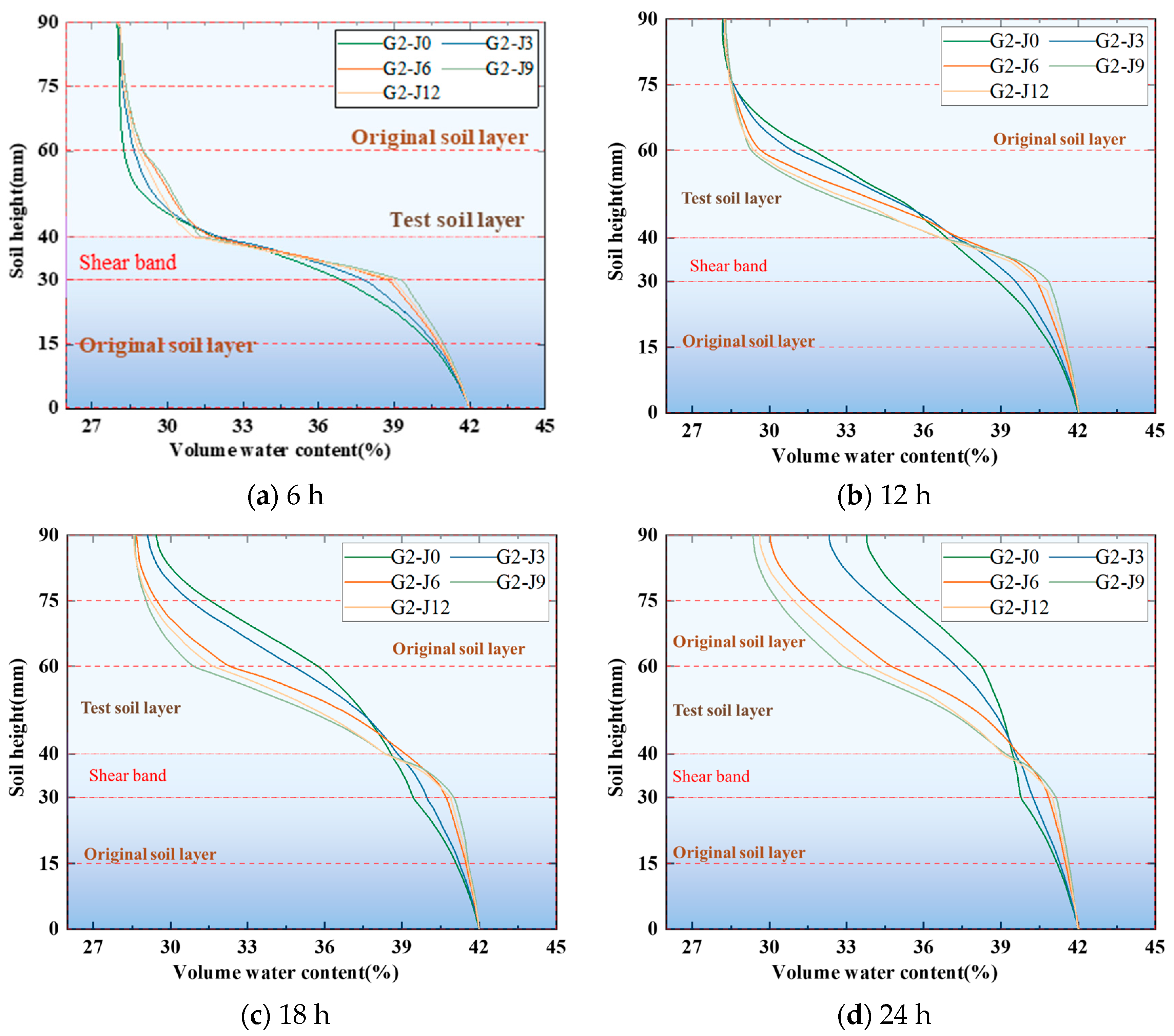
3.3. Changes in Soil Volume Water Content Under Different Influencing Factors
- (1)
- Shear Displacement
- (2)
- Normal stress
4. Numerical Simulation
4.1. Model Principle
4.2. Parameter Values
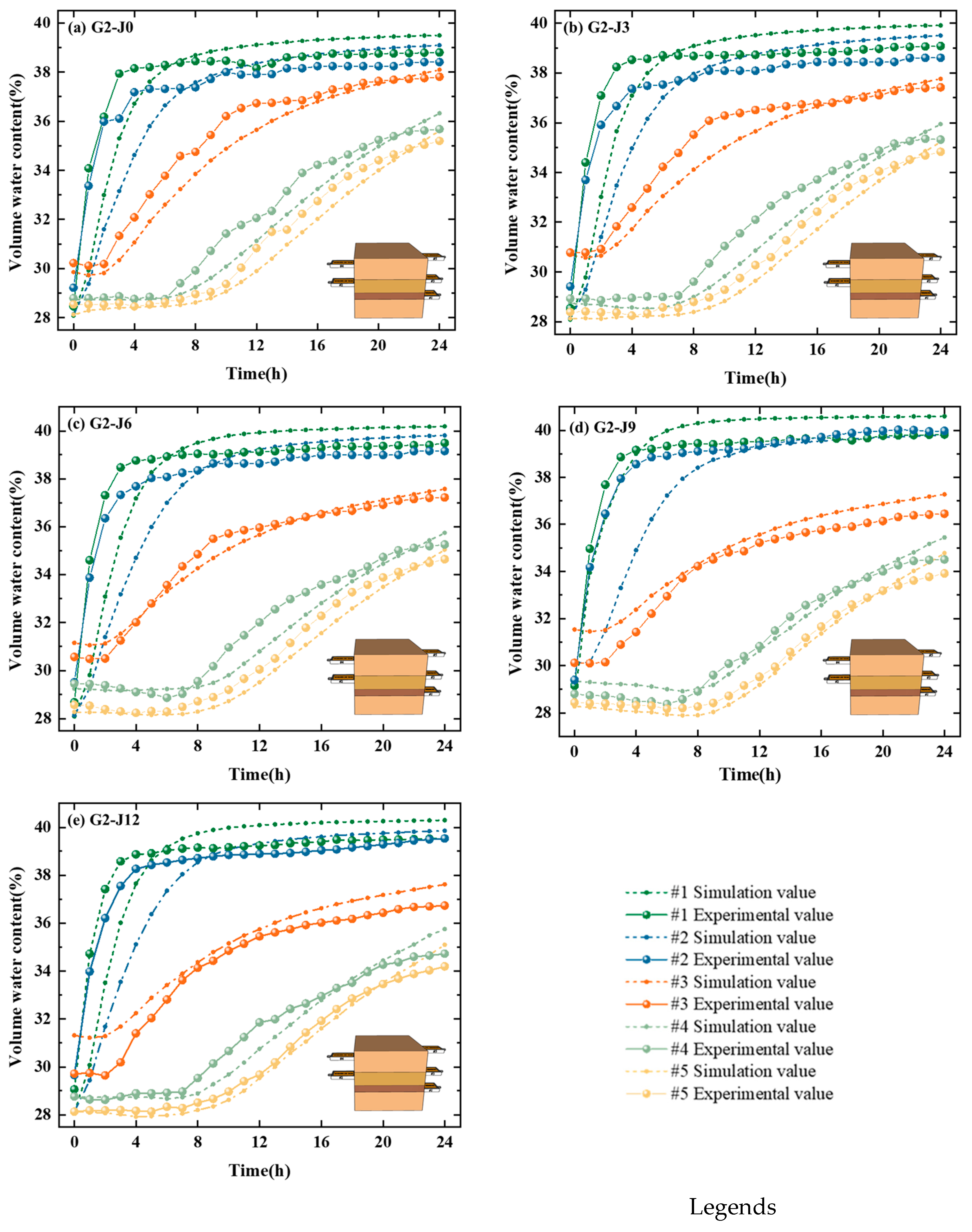
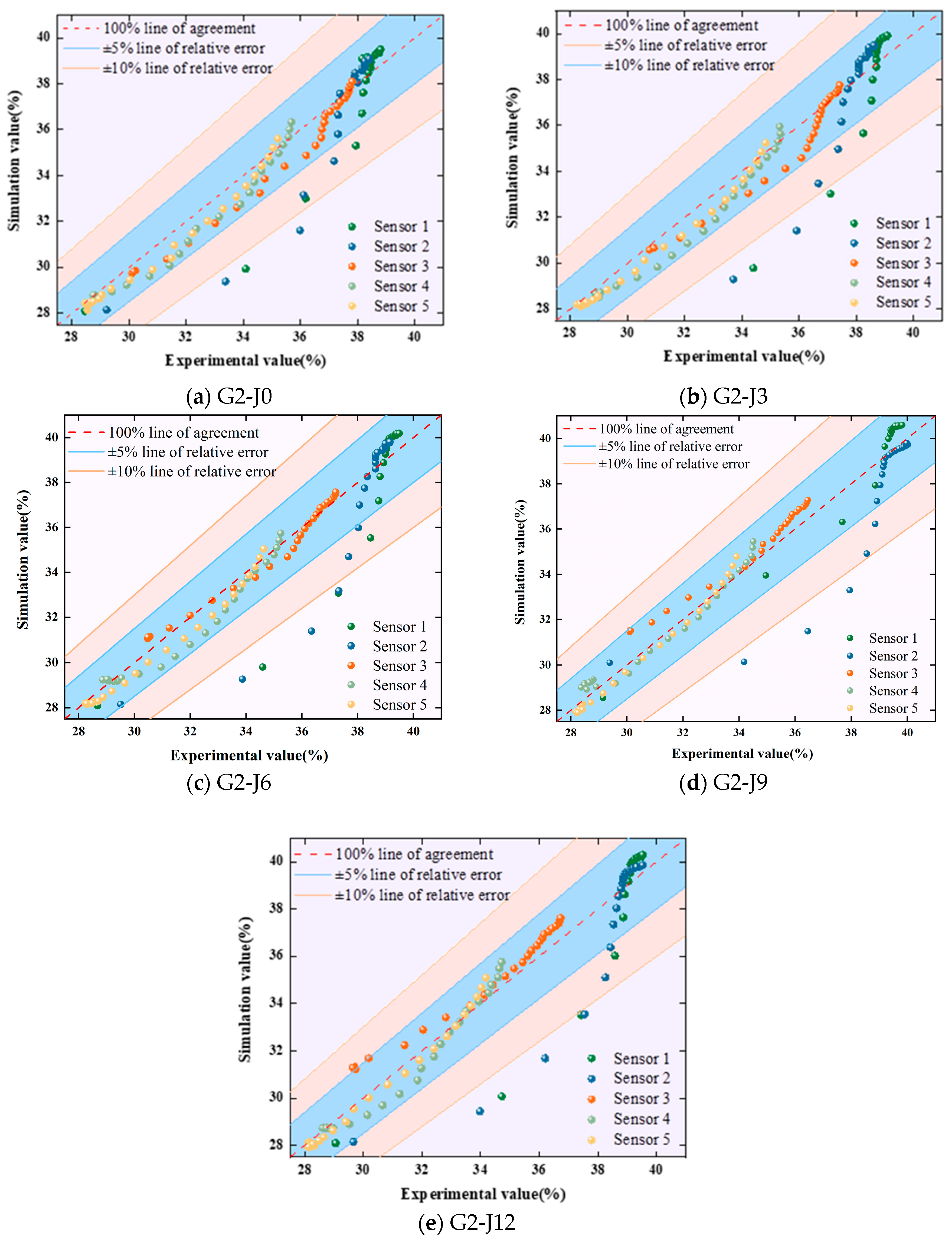
4.3. Model Verification and Prediction
5. Conclusions
- (1)
- The water migration rate of the soil containing the shear band in the interface area decreased. A substantial amount of moisture accumulated within the shear band, and the water content was positively correlated with the shear strength of the interface.
- (2)
- The shear displacement and normal stress significantly affect moisture migration within the interface region. With the increase in shear displacement, the volume water content of the soil in the shear band decreased initially and then increased, and the inflection point corresponded to the displacement at which the interface failed. The volume water content of the soil in the shear band exhibited a negative correlation with normal stress.
- (3)
- A numerical model of water migration within the lean clay–structure interface region with a shear band was established. The model effectively simulates the process of water migration in the lean clay–structure interface region.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, M.P.; Sen, S.; Pathak, H.; Dogra, A.B. Early age cracking relevant to mass concrete dam structures during the construction schedule. Constr. Build. Mater. 2024, 411, 134739. [Google Scholar] [CrossRef]
- Hashemi, A.; Sutman, M.; Abuel-Naga, H. Thermomechanical response of kaolin clay–concrete interface in the context of energy geostructures. Can. Geotech. J. 2022, 60, 380–396. [Google Scholar] [CrossRef]
- Brown, E. Reducing risks in the investigation, design and construction of large concrete dams. J. Rock Mech. Geotech. Eng. 2017, 9, 197–209. [Google Scholar] [CrossRef]
- Lv, Y.; Shen, Y.; An, L.; Wei, X.; Chen, X.; He, R.; Shi, B.; Zhou, Z. A novel cement-based interface functional material for application onto shotcrete-rock interface of tunnel in cold regions. Constr. Build. Mater. 2024, 438, 136923. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, B.; Wang, H.; Cheng, J.; Cai, C.; Wang, X.; Lv, C. Large-scale field test on the shear behavior of concrete pipe-silty soil interfaces in pipe jacking: A case study. Construct. Build. Mater. 2024, 419, 135470. [Google Scholar] [CrossRef]
- Zhang, D.; Lu, T. Establishment and application of an interface model between soil and structure. Chin. J. Geotech. Eng. 1998, 20, 65–69. [Google Scholar]
- Qin, Y.; Shang, C.; Li, X.; Lai, J.; Shi, X.; Liu, T. Failure mechanism and countermeasures of rainfall-induced collapsed shallow loess tunnels under bad terrain: A case study. Fail. Anal. 2023, 152, 107477. [Google Scholar] [CrossRef]
- Zhou, S.; Tian, Z.; Di, H.; Guo, P.; Fu, L. Investigation of a loess-mudstone landslide and the induced structural damage in a high-speed railway tunnel. Bull. Geol. Environ. 2020, 79, 2201–2212. [Google Scholar] [CrossRef]
- Shen, Y.; Tang, T.; Wang, D.; Chen, M.; Liu, Y.; Wang, Y. Nonzero angle between the directions of matric suction and gravity during horizontal freezing. Acta Geotech. 2024, 19, 821–831. [Google Scholar] [CrossRef]
- Li, H.; Yan, C.; Shi, Y.; Sun, W.; Bao, H.; Li, C. A statistical damage model for the soil-structure interface considering interface roughness and soil shear area. Constr. Build. Mater. 2024, 431, 136606. [Google Scholar] [CrossRef]
- Campos, A.; Lopez, C.M.; Blanco, A.; Aguado, A. Effects of an internal sulfate attack and an alkali-aggregate reaction in a concrete dam. Constr. Build. Mater. 2018, 166, 668–683. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T. A model for the mechanics of jointed rock. J. Soil. Mech. Found. Div. 1968, 94, 637–659. [Google Scholar] [CrossRef]
- Uesugi, M.; Kishida, H.; Tsubakihara, Y. Behavior of sand particles in sand-steel friction. Soils Found. 1988, 28, 107–118. [Google Scholar] [CrossRef]
- Uesugi, M.; Kishida, H.; Uchikawa, Y. Friction between dry sand and concrete under monotonic and repeated loading. Soils Found. 1990, 30, 115–128. [Google Scholar] [CrossRef]
- Zhang, G.; Liang, D.; Zhang, J. Image analysis measurement of soil particle movement during a soil–structure interface test. Comput. Geotech. 2006, 33, 248–259. [Google Scholar] [CrossRef]
- Wang, J.; Gutierrez, M.S.; Dove, J.E. Numerical studies of shear banding in interface shear tests using a new strain calculation method. Int. J. Numer. Anal. Met. 2007, 31, 1349–1366. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Xiao, Y.; Li, J. Effect of roughness on shear behavior of red clay– concrete interface in large-scale direct shear tests. Can. Geotech. J. 2015, 52, 1122–1135. [Google Scholar] [CrossRef]
- Pan, J.; Wang, B.; Wang, Q.; Ling, X.; Fang, R.; Liu, J.; Wang, Z. An adhesion-ploughing friction model of the interface between concrete and silty clay. Constr. Build. Mater. 2023, 376, 131039. [Google Scholar] [CrossRef]
- Wang, G.; Wei, X.; Zou, T. A hollow cylinder radial-seepage apparatus for evaluating permeability of sheared compacted clay. Geotech. Test. J. 2018, 42, 1133–1149. [Google Scholar] [CrossRef]
- Alnmr, A.; Ray, R. Numerical simulation of replacement method to improve unsaturated expansive soil. Pollack Period. 2023, 18, 41–47. [Google Scholar] [CrossRef]
- Alnmr, A.; Alzawi, M.O.; Ray, R.; Abdullah, S.; Ibraheem, J. Experimental Investigation of the Soil-Water Characteristic Curves (SWCC) of Expansive Soil: Effects of Sand Content, Initial Saturation, and Initial Dry Unit Weight. Water 2024, 16, 627. [Google Scholar] [CrossRef]
- Pham, T.A.; Sutman, M.; Medero, G.M. Density-dependent model of soil–water characteristic curves and application in predicting unsaturated soil–structure bearing resistance. Int. J. Geomech. 2023, 23, 04023017. [Google Scholar] [CrossRef]
- Lei, H.; Wu, Y.; Yu, Y.; Zhang, B.; Lv, H. Influence of Shear on Permeability of Clayey Soil. Int. J. Geomech. 2016, 16, 04016010. [Google Scholar] [CrossRef]
- Liu, Q.; Yu, Y.; Zhang, B.; Wang, X.; Lv, H.; Zhan, Z. A new apparatus for shear-seepage testing at the clayey soil-structure interface. Geotech. Test. J. 2022, 45, 281–299. [Google Scholar] [CrossRef]
- Zeng, Z.; Tang, C.; Cheng, Q.; An, N.; Yang, Z.; Gong, X.; Chen, X.Y. Field and numerical investigation of soil hydro-thermal response to the climatic conditions in southern China considering soil heterogeneity. Eng. Geol. 2024, 329, 107401. [Google Scholar] [CrossRef]
- ASTMD2487-17; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2017.
- Fang, R.; Wang, B.; Pan, J.; Liu, J.; Wang, Z.; Wang, Q.; Ling, X. Effect of concrete surface roughness on shear strength of frozen soil–concrete interface based on 3D printing technology. Constr. Build. Mater. 2023, 366, 130158. [Google Scholar] [CrossRef]
- Pan, J.; Wang, B.; Wang, Q.; Ling, X.; Fang, R.; Liu, J.; Wang, Z. Thickness of the shear band of silty clay–concrete interface based on the particle image velocimetry technique. Constr. Build. Mater. 2023, 388, 131712. [Google Scholar] [CrossRef]
- GB/T50123-2019; Standard for Geotechnical Test Methods. China Planning Press: Beijing, China, 2019.
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Van Genuchten, M. A Closed-Form Equation for Predict in the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Zhuang, X.; Peng, W. A simplified method for determining the model parameters of soil-water characteristic curve under different dry densities. J. Chang. River Sci. Res. Inst. 2019, 36, 64–67. [Google Scholar]

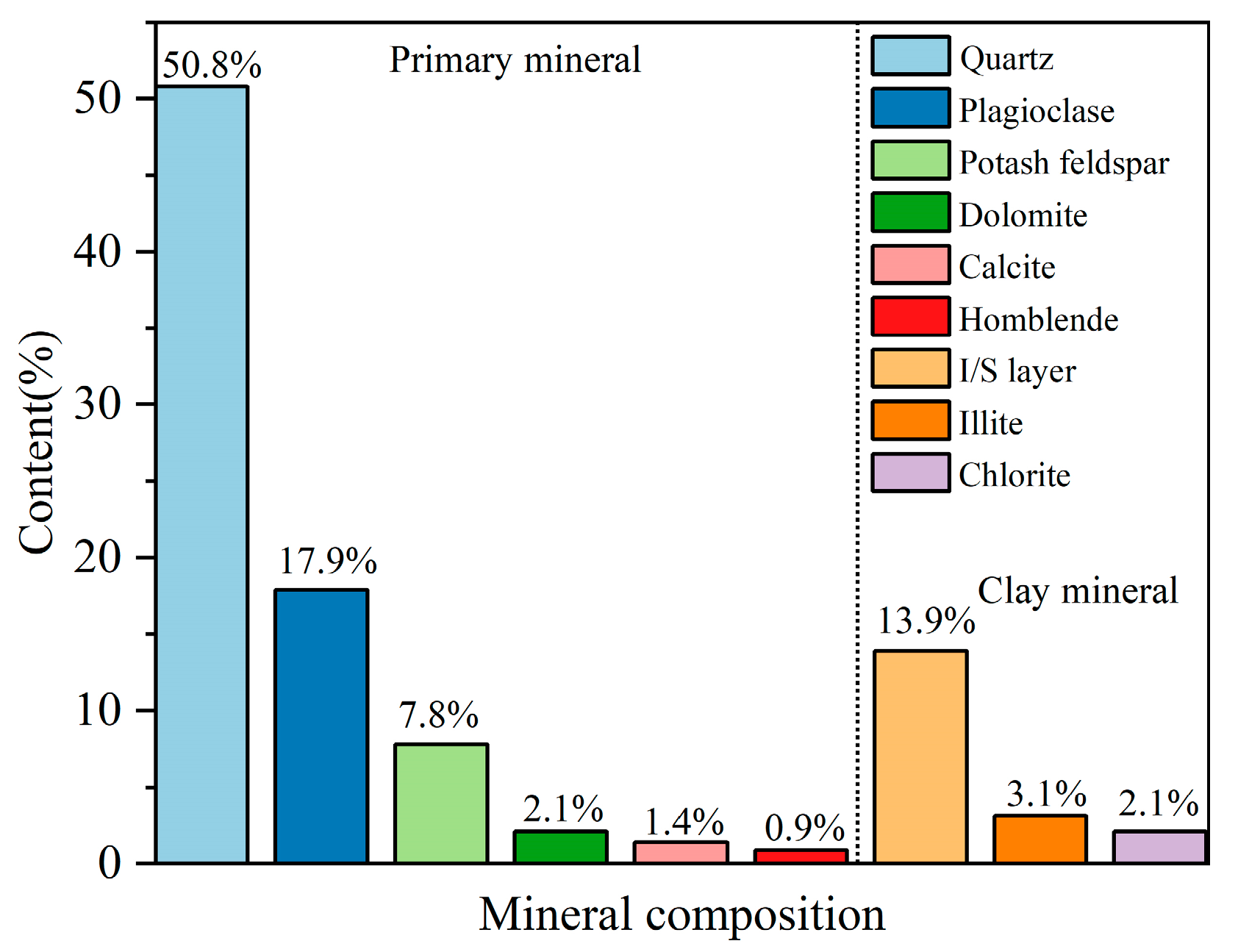

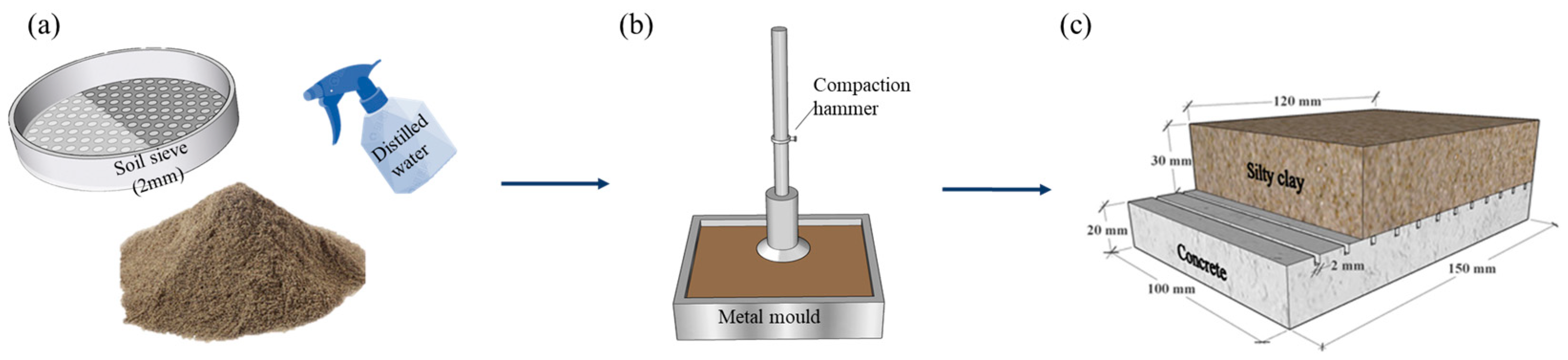
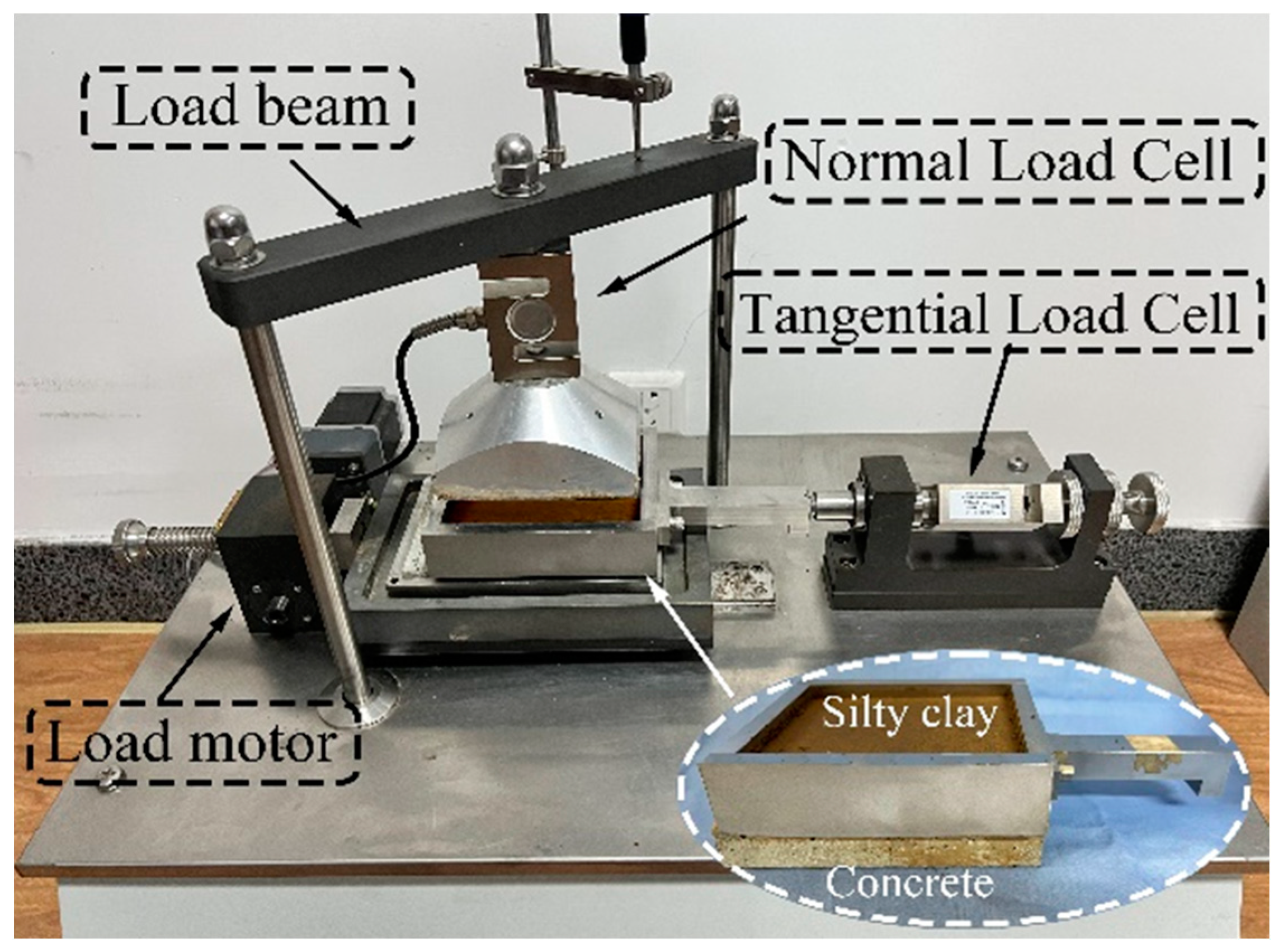
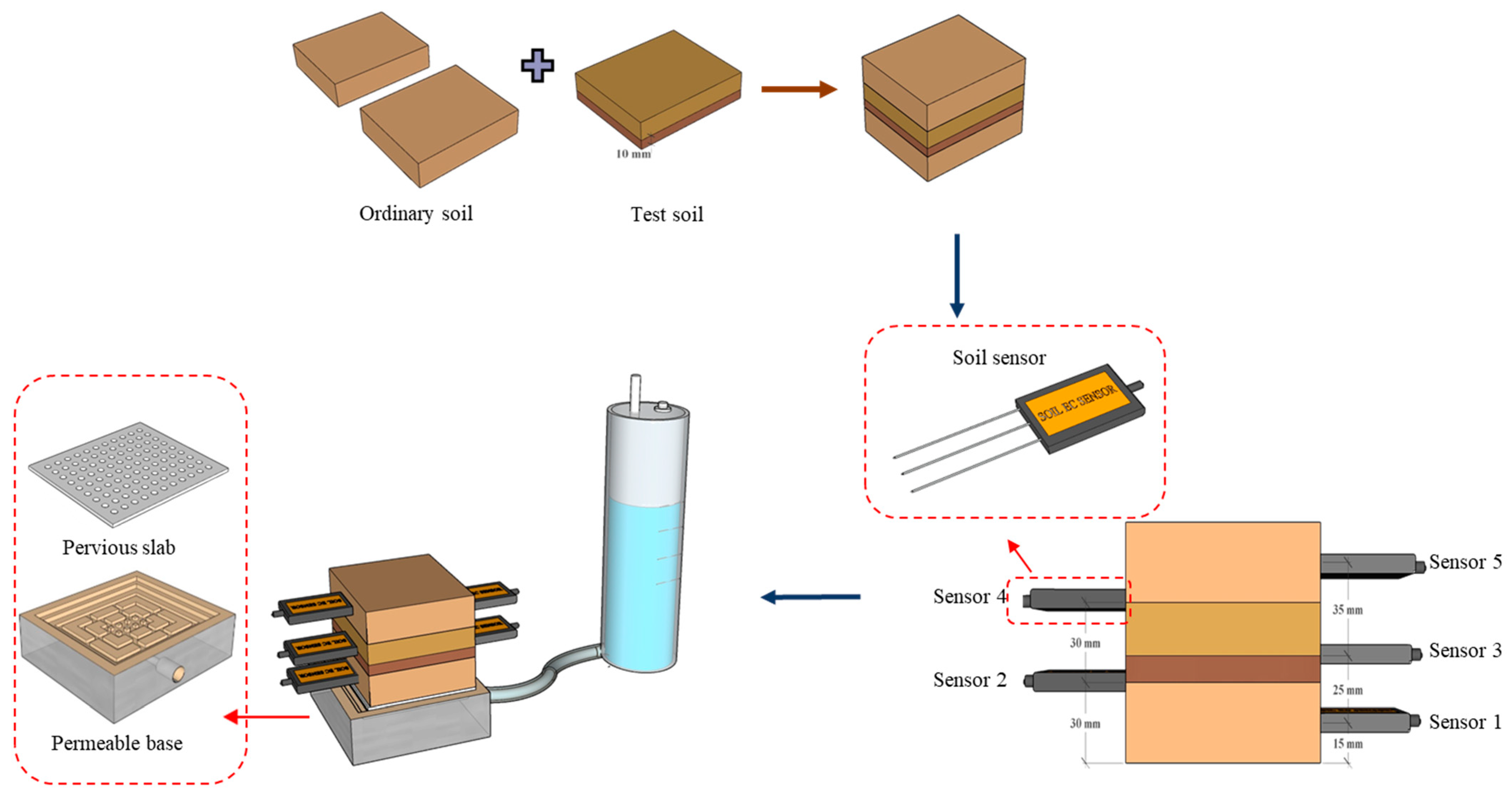

| Particle Diameter (%) | Optimum Water Content (%) | Maximum Dry Density (g/cm3) | Liquid Limit (%) | Plastic Limit (%) | ||
|---|---|---|---|---|---|---|
| 2–0.075 mm | 0.075–0.005 mm | <0.005 mm | ||||
| 1.4 | 66.06 | 32.54 | 20.7 | 1.64 | 34.39 | 19.04 |
| Water | Cement | Sand | Gravel | Superplasticizer |
|---|---|---|---|---|
| 180 | 360 | 705 | 1155 | 1.44 |
| Groups | Number | Initial Water Content/% | Normal Stress/kPa | Shear Displacement/mm | Number of Samples |
|---|---|---|---|---|---|
| G1 | G1-JX | 20.7 | 300 | 0, 3, 6, 9, 12 | 25 |
| G2 | G2-JX | 20.7 | 400 | 0, 3, 6, 9, 12 | 25 |
| G3 | G3-JX | 20.7 | 500 | 0, 3, 6, 9, 12 | 25 |
| Shear Displacement (mm)/Position | Group | ||
|---|---|---|---|
| G1 | G2 | G3 | |
| 0/Inside the shear band | 1.7000 | 1.7331 | 1.7512 |
| 3/Inside the shear band | 1.7752 | 1.7968 | 1.7985 |
| 6/Inside the shear band | 1.8048 | 1.8452 | 1.8582 |
| 9/Inside the shear band | 1.8390 | 1.8758 | 1.8827 |
| 12/Inside the shear band | 1.8255 | 1.8519 | 1.8776 |
| 0/Outside the shear band | 1.6071 | 1.6434 | 1.6533 |
| 3/Outside the shear band | 1.6533 | 1.7049 | 1.7186 |
| 6/Outside the shear band | 1.6854 | 1.7729 | 1.7904 |
| 9/Outside the shear band | 1.7352 | 1.7852 | 1.7976 |
| 12/Outside the shear band | 1.7311 | 1.7415 | 1.7745 |
| Group | Sensor 1 | Sensor 2 | Sensor 3 | Sensor 4 | Sensor 5 |
|---|---|---|---|---|---|
| G2-J0 | 34.7652 | 17.3788 | 4.6260 | 2.3013 | 1.2683 |
| G2-J3 | 28.6589 | 14.9105 | 4.5971 | 2.1800 | 1.1526 |
| G2-J6 | 28.4000 | 14.4722 | 4.0581 | 2.0035 | 1.0656 |
| G2-J9 | 26.1043 | 13.7580 | 3.7796 | 1.5002 | 0.7284 |
| G2-J12 | 26.0233 | 13.6081 | 3.9069 | 1.9900 | 0.9814 |
| Position | Inside/Outside Shear Band | Ordinary Soil | |||||
|---|---|---|---|---|---|---|---|
| Shear Displacement | 0 mm | 3 mm | 6 mm | 9 mm | 12 mm | ||
| Parameters | |||||||
| a (^10−3 kPa−1) | 5.043/9.951 | 3.177/6.221 | 2.260/3.769 | 1.830/3.450 | 2.157/4.474 | 6.404 | |
| m | 0.400/0.368 | 0.300/0.352 | 0.255/0.317 | 0.217/0.309 | 0.247/0.336 | 0.354 | |
| n | 1.515/1.583 | 1.429/1.543 | 1.342/1.465 | 1.277/1.447 | 1.328/1.505 | 1.547 | |
| (%) | 0.42 | ||||||
| (%) | 0.045 | ||||||
| ks (^10−10 m/s) | 2.772/3.680 | 2.250/3.034 | 1.911/2.435 | 1.719/2.338 | 1.867/2.697 | 6.165 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Fu, L.; Wang, Q.; Chen, H.; Feng, X.; Pan, J. Effect of the Shear Band on Water Migration in the Interface Between Lean Clay and an Engineering Structure: A Case Study of Loess-like Soil in Changchun Area, China. Water 2025, 17, 350. https://doi.org/10.3390/w17030350
Wang B, Fu L, Wang Q, Chen H, Feng X, Pan J. Effect of the Shear Band on Water Migration in the Interface Between Lean Clay and an Engineering Structure: A Case Study of Loess-like Soil in Changchun Area, China. Water. 2025; 17(3):350. https://doi.org/10.3390/w17030350
Chicago/Turabian StyleWang, Boxin, Lanting Fu, Qing Wang, Huie Chen, Xue Feng, and Jingjing Pan. 2025. "Effect of the Shear Band on Water Migration in the Interface Between Lean Clay and an Engineering Structure: A Case Study of Loess-like Soil in Changchun Area, China" Water 17, no. 3: 350. https://doi.org/10.3390/w17030350
APA StyleWang, B., Fu, L., Wang, Q., Chen, H., Feng, X., & Pan, J. (2025). Effect of the Shear Band on Water Migration in the Interface Between Lean Clay and an Engineering Structure: A Case Study of Loess-like Soil in Changchun Area, China. Water, 17(3), 350. https://doi.org/10.3390/w17030350







