Research on the Disaster-Causing Factors of Water and Sand Inrush and the Evolution of Surface Collapse Funnel

Abstract

Water and sand inrush is frequently accompanied by surface subsidence, which severely constrains the sustainable development of coordinated coal mining and ecological environment. This study investigated four key influencing factors based on a water and sand inrush test system: fracture width, aquifer thickness, sand particle size composition and stratigraphic sedimentary structure. It obtained the morphological evolution characteristics of collapse funnels and revealed the evolution mechanism of collapse funnels induced by water and sand inrush. The results indicate that fracture width and aquifer thickness mainly affect the range of collapse funnel, and both show a positive correlation with the radius of collapse funnels. Sandy particle size composition plays a dominant role in the morphology of collapse funnels induced by disasters: as the size of the soil skeleton particles increases, the morphology of collapse funnels changes sequentially from a bowl shape to an inverted cone shape and then to a funnel shape with a sunken center and raised slopes. The stratigraphic sedimentary structure has a significant impact on the morphology and damage induced by disasters in collapse funnels. The upper clay layer of the underlying aquifer inhibits the water and sand inrush processes to some extent. An increase in the thickness and number of clay layers effectively prevents the water and sand mixture from flowing into the fracture channel from the lateral direction. This reduces the damage range of collapse funnels and decreases the rate of water and sand inrush. This study clarifies the formation mechanism of surface collapse funnels under the influence of the disaster-causing factors of water and sand inrush, and provides theoretical guidance for the prevention and control of such disasters.

1. Introduction

Western China is rich in coal resources. Its main stratigraphic sedimentary structures are shallowly buried coal seams (with a burial depth of less than 100 m in some mining areas), thin bedrock and an overlying thin unconsolidated layer [1]. These features make large-scale underground mining with full-seam mining in one pass or open-pit mining possible. However, the region has a dry and infertile climate with fragile ecological environment. Under the combined effect of intense mining activities and special engineering geological conditions, it is highly prone to sudden water and sand inrush disasters. The water and sand would inundate the workers and equipment, and often accompany surface subsidence accidents [2,3,4,5]. A notable example is the water and sand inrush caused by boreholes at the Longde Coal Mine in Shaanxi Province [6], where the total surface subsidence volume was approximately 16,354.2 m³, with an average collapse flow rate of 3270.8 m³/h (see Figure 1). Coal seam roof collapse accidents and surface subsidence caused by coal seam disturbance exacerbate the imbalance of the regional water and soil environment, severely hindering the development of regional coal resources and the sustainable development of the ecological environment [7,8,9].

Due to the concealed nature of underground engineering, it is difficult to study the mechanisms by which water and sand inrush cause disasters through on-site observations. Therefore, many scholars have analyzed the evolution of these disasters via methods such as similar model tests, laboratory tests and numerical simulations. Zeng et al. [10] conducted a similar modeling experiment, dividing the process of disaster caused by the water and sand inrush into three stages: overlying rock fracture development, water-sand channel formation and evolution of the channels. Liu et al. [11] have clarified that the degree of compaction, water pressure and confining pressure all regulate the duration and intensity. Wang et al. [12] proposed that there is a positive correlation between the thickness of the sand layer and the particle size of the sand and the critical hydraulic gradient.

Yang et al. [13] proposed that, in the Neogene Pliocene Series N₂ red soil stratum, there are two types of water and sand inrush. The type of inrush depends on the relationship between the initial fracture width and the thickness of the soil layer. Shen et al. [14] investigated the localization characteristics of strain rate, dissipated energy, and particle spin rate during ground disturbance propagation in the context of tunnel water and sand inrush under dual-stratum conditions. Jiang et al. [15] analyzed water-sandy dolomite tunnels and, through fluid-solid coupling model experiments, revealed three types of water inrush mechanism.

The evolution process of water and sand inrush is synergistically regulated by multiple factors, and scholars have conducted studies on factors such as clay content, water pressure conditions, sand particle size, and porous media channels. Regarding the influence of clay content: Chen et al. [16] clarified the differences in the evolution paths of water and sand inrush and the characteristics of collapse pits under different clay contents by controlling the clay content of the unconsolidated layer and combining it with the morphological analysis of collapse pits; Yuan et al. [17] pointed out that the initial rate of water and sand inrush is mainly determined by water pressure, and classified settlement funnels into two types based on clay content.

Regarding sand particle size and porous media channels, the migration characteristics of water and sand inside porous media channels have been obtained by controlling the particle size of fractured rock, porosity, and sand particle size [18,19,20]. Liang et al. [21] found that there are two migration modes—“seepage-driven” and “force-driven”—for the flow of sand-mud-water mixtures in porous media; Xu et al. [22] pointed out that the porosity and skeleton structure of fractured rock mass are key disaster-causing factors; Zhang et al. [23] indicated that fractured rock mass has a certain sand-filtering capacity, and when its load-bearing limit is exceeded, the sand gushing volume shows a significant increasing trend with the initial sand mass; Liang et al. [24] clarified the quantitative relationship between sand flow velocity and caving zone height. PU et al. [25] pointed out that, before entering the fissure, the sand grains formed a funnel shape with a gradually increasing radius, which eventually stabilized. Zhang et al. [26,27] pointed out the morphological characteristics of mining-induced fractures in different stratigraphic sedimentary structures, and indicated that the ratio of fracture width to sand particle size is the initiating condition that determines the occurrence of water and sand inrush disasters.

Regarding the flow characteristics of water and sand: Sui et al. [28] pointed out that the sand flow velocity first decreases with the increase in the height of the glass bead pore bed, and tends to stabilize once the pore bed height approaches a certain critical value. Zhao et al. [29] established critical criteria for water and sand inrush and obtained the characteristics of water and sand inrush under different water pressure changes through laboratory tests. Qiu et al. [30] indicated that the larger the fracture dip angle and width, the higher the probability of water and sand inrush, the shorter the disaster duration, and the more intense the disaster process. Li et al. [31] established a correlation model between flow rate, fracture inlet pressure, pore inlet pressure, and water-sand mass through correlation analysis, realizing the quantitative prediction of water-sand outflow. Yuan et al. [32] found that water pressure has the greatest impact on the intensity of sudden water gushing and sand discharge.

Current research has conducted in-depth discussions on three aspects of water and sand inrush: disaster stage; influencing factors; and the flow characteristics. However, although the existing results focus on key factors such as clay content and water pressure, there are two limitations. First, the range of key disaster-causing factors selected is insufficient. Second, the specific mechanism by which they trigger surface subsidence still needs to be studied further. Based on a water and sand inrush test system, this study conducts water and sand inrush experiments by controlling factors including fracture width, aquifer thickness, sand particle size composition and stratigraphic sedimentary structure. It reveals the mechanism of surface collapse funnels induced by water and sand inrush, providing a reference for the coordinated development of coal resource development and ecological environmental protection in Western China.

2. Test Equipment and Scheme Design

2.1. Testing System

The test for collapse funnels induced by water and sand inrush is primarily conducted using the “water and sand inrush test system,” as shown in Figure 2. This system consists of three main components: a water and sand inrush test bench, an energy storage tank, and a servo control system.

The water and sand inrush test bench comprises a load-bearing frame, a test chamber, a confined water chamber (loading head), and a base of the test chamber, as shown in Figure 2a. The upper surface of the confined water chamber is designed with a water inlet, and 34 water outlet holes are arranged at its bottom. Connected to the loading cylinder via a piston rod, this pressure head can simultaneously provide water pressure and vertical load. The test chamber is cylindrical, with a wall thickness of 15 mm, an inner diameter of 400 mm, and a height of 380 mm. It is connected to the base of the test chamber via a connector fitted with a circular seal ring. The base of the test chamber mainly consists of a chassis, upright columns, and a vertically adjustable specimen loading slot. The chassis has an outer diameter of 460 mm, with a threaded hole of 120 mm in diameter at its center for installing the specimen loading slot. Twelve sensor wire holes (each with a diameter of 2.5 mm) are evenly distributed 150 mm away from the center, enabling an increase in the type and number of stress monitoring points. The vertically adjustable specimen bearing slot is composed of a bearing slot body, an adjustable specimen bearing tray, and a channel bottom cover, all connected via threaded joints. Among these components, the loading slot body can accommodate fracture channels of different configurations.

To improve the stability of water pressure and flow rate in the experiment, an energy storage tank is installed between the control system and the water and sand inrush test bench, as shown in Figure 2b. The cylindrical energy storage tank has a wall thickness of 10 mm, an inner diameter of 300 mm and a height of 1000 mm. To improve monitoring accuracy of water pressure and flow rate, a flow meter and water pressure sensor have been installed at the tank’s water outlet, located at the back of the tank.

The servo control system is composed of a control console and a servo system, as shown in Figure 2c. The control console has a maximum sampling frequency of 10 Hz and can automatically record parameters in real time, including time, displacement, load, water pressure and water flow rate. The servo system comprises two subsystems: a servo control system for the water pressure and water yield, and a servo control system for displacement and loading. The servo control system for water pressure and water yield provides dual control of both pressure and flow rate, ensuring a stable supply and constant pressure. It can provide a maximum water pressure of 2.0 MPa, a maximum water supply rate of 150 L/h, and features a water pressure control accuracy of 0.01 MPa. The servo control system for displacement and loading provides dual control of both displacement and stress. It has a maximum indenter stroke of 400 mm (with a stroke accuracy of 0.01 mm) and can apply a maximum load of 600 kN (with a load accuracy of 0.01 kN). This subsystem supports continuous and stepwise loading and unloading, enabling it to meet the requirements of various simulation scenarios.

2.2. Sample Preparation

2.2.1. Sand Sample Preparation

To simulate the influence of different particle size compositions on the structural evolution of collapse funnels, clean river sand with four particle size ranges—<0.25 mm, 0.25–0.5 mm, 0.5–1.0 mm, and 1.0–2.0 mm—was obtained using sieves. Three types of sand sample (coarse, medium and fine-grained) were then prepared according to specific particle size composition ratios. The particle size composition of each sample, along with details of the sieve-based preparation and sampling process, are presented in

Table 1. Statistical table of various sand particle size compositions.

Serial Number	Sandy Type	Particle Size of Sand Grains/mm				Cu	d60
		2~1	1~0.5	0.5~0.25	<0.075
1	Coarse sand	20	50	20	10	3.2	0.7
2	Medium sand	10	25	40	25	6	0.45
3	Fine-grained sand	/	5	15	80	20	0.22

and Figure 3, respectively.

2.2.2. Preparation of Fracture Channels

For the experiment, concrete was used to prepare specimens with fracture channels, which were employed to simulate bedrock containing mining-induced fractures. The key advantages of this method are as follows:

Diverse fracture channel morphologies, which can be custom designed;

Low cost and a relatively simple preparation process;

Material properties that closely resemble real-world geological conditions.

The materials required are rapid-setting, high-strength cement; coarse sand; hydraulic oil; and water. The main tools required are specimen preparation molds; prefabricated fracture molds; a vibrator; a rubber hammer; and sandpaper, as shown in Figure 4a,b.

The steps below were followed to prepare concrete specimens with fracture channels: First, rapid-setting cement and coarse sand were weighed in a 1:1 ratio, mixed together and stirred until uniform. Then, water was added to form cement mortar. This mortar was poured into molds for the specimens, with hydraulic oil applied to the inner walls of the molds. The molds were then placed on a vibrator to achieve compaction through uniform vibration. Prefabricated fracture molds (with hydraulic oil applied to their surfaces) were then inserted into the preset fracture positions. After standing for 15–20 min, the outer molds were removed. Finally, the specimens were placed in a dry, well-ventilated area. After 20 min, the prefabricated fracture molds were removed and the specimen surfaces smoothed with sandpaper, completing the preparation process. The finished specimens are shown in Figure 4c.

2.3. Test Plan and Procedures

The steps of the test for collapse funnels induced by water and sand inrush are as follows:

• In accordance with the test requirements, the pore water pressure and soil stress transducers were arranged and fixed in place with glass glue. They were then connected to the sensors and data acquisition system for debugging purposes. Taking into account the influence of temperature and experimental errors, the sensors are calibrated to meet the accuracy requirements before conducting the tests. The BWK-type pore water pressure transducers have a maximum range of 0.5 MPa and an accuracy of 0.1 kPa, and the micro BWT-type soil stress transducers have the same maximum range and accuracy. Prior to use, the pore water pressure transducers should be immersed in water for 20–30 min to saturate them.
• Install the specimen bearing slot and adjust the specimen bearing tray to the topmost position. Secure the bottom cover of the inrush port and place the test specimen into the bearing slot. To improve the sealing performance of the test system, apply petroleum jelly to the threaded joints and the inner wall of the bearing slot.
• Secure the test base, place a sealing rubber gasket on the base, then mount the test chamber and tighten the connecting bolts.
• In accordance with the test design, place sand (or soil) samples into the test chamber and tamp them to achieve compaction. Next, set the servo control system to apply constant pressure loading and allow it to stabilize for 1 min. Then, use the water pressure control system to inject water into the chamber, while opening the air vent on the top of the pressure head. Once the chamber is fully filled with water, close the air vent; maintain the water pressure at the preset test value and leave the system to stand for 2 min.
• Adjust the adjustable specimen bearing tray to the preset test position and leave it to stand for 0.5 min.
• Open the bottom cover of the water and sand inrush hole quickly, then monitor and record any changes in pressure and the inrush rate of water and sand during the test.
• Replace the test conditions, repeat Steps 1–6, and conduct statistical analysis on the test results.

Considering the influencing factors of water and sand inrush disasters, separate tests were conducted to investigate the effects of four factors: fracture width, aquifer thickness, sand particle size composition, and stratigraphic sedimentary structure. The test design is presented in

Table 2. Experimental protocol design.

Experimental Variable	Serial Number	Sandy Type	Fracture Width	Water Pressure	Aquifer Thickness	Stratigraphic Sedimentary Structure
Fracture width	A1	Medium sand	6	0.03	150	Single sand layer
	A2		8
	A3		10
	A4		12
	A5		14
	A6		16
Aquifer thickness	B1	Medium sand	6	0.03	70	Single sand layer
	B2				150
	B3				250
	B4		8		70
	B5				150
	B6				250
	B7		16		70
	B8				150
	B9				250
Sand particle size composition	C1	Fine-grained sand	8	0.03	150	Single sand layer
	C2	Medium sand
	C3	Coarse sand
Stratigraphic sedimentary structure	D1	Fine-grained sand, Medium sand, Clay	16	0.03	110	Fine-grained sand 40/Clay 35/Fine-grained sand 35
	D2			0.035~0.13	110	Fine-grained sand 40/Clay 35/Fine-grained sand 35
	D3			0.03	140	Fine-grained sand 70/Clay 35/Fine-grained sand 35
	D4			0.03	205	Fine-grained sand 70/Clay 35/Medium sand 50/Clay 30/Medium sand 20

.

2.4. Experimental Data Processing

This study was conducted using the water and sand inrush test system. Due to limitations in model size, when the top of the funnel reached the inner wall of the test chamber, its lateral development was restricted. This resulted in differences compared to the natural expansion of the actual stratum. However, in both the test chamber and the actual stratum, the sand would stop sliding once it reached the natural angle of repose. After the sand collapsed, a stable accumulation body formed around the entrance of the channel. The volume of the sand collapse was calculated based on the angle of repose to avoid the influence of scale differences. Based on this, the study assumes that the collapse funnel is ‘inverted conical’ and calculates the collapse volume accordingly.

The morphology of the collapse funnel in water and sand inrush is characterized by three parameters: the funnel central depth (h), the funnel top radius (r), and the average measured funnel slope angle (α) (see Figure 5). Nevertheless, there are two limitations in the test: first, due to the size of the chamber, the top radius of the funnel cannot continue to expand once it reaches the chamber wall; second, the heterogeneity of the sand interferes with observations.

To simplify the analysis, it is necessary to exclude the limiting effect of boundary size. Since the morphology of an inverted cone can be determined by the central drawdown and the average measured funnel slope angle α, the funnel can be assumed as an inverted cone based on the test measurement results. On this basis, the radius of the upper segment of the funnel under theoretical conditions can be derived, and finally the theoretical volume of the funnel can be calculated.

$$r=h/\tan \alpha$$

(1)

$$V={\displaystyle \frac{1}{3}}\pi r^{3}h$$

(2)

where h is funnel central depth, mm; r is funnel top radius, mm; α is average measured funnel slope angle (°).

3. Analysis of Collapse Funnel Destruction Forms and Influencing Factors

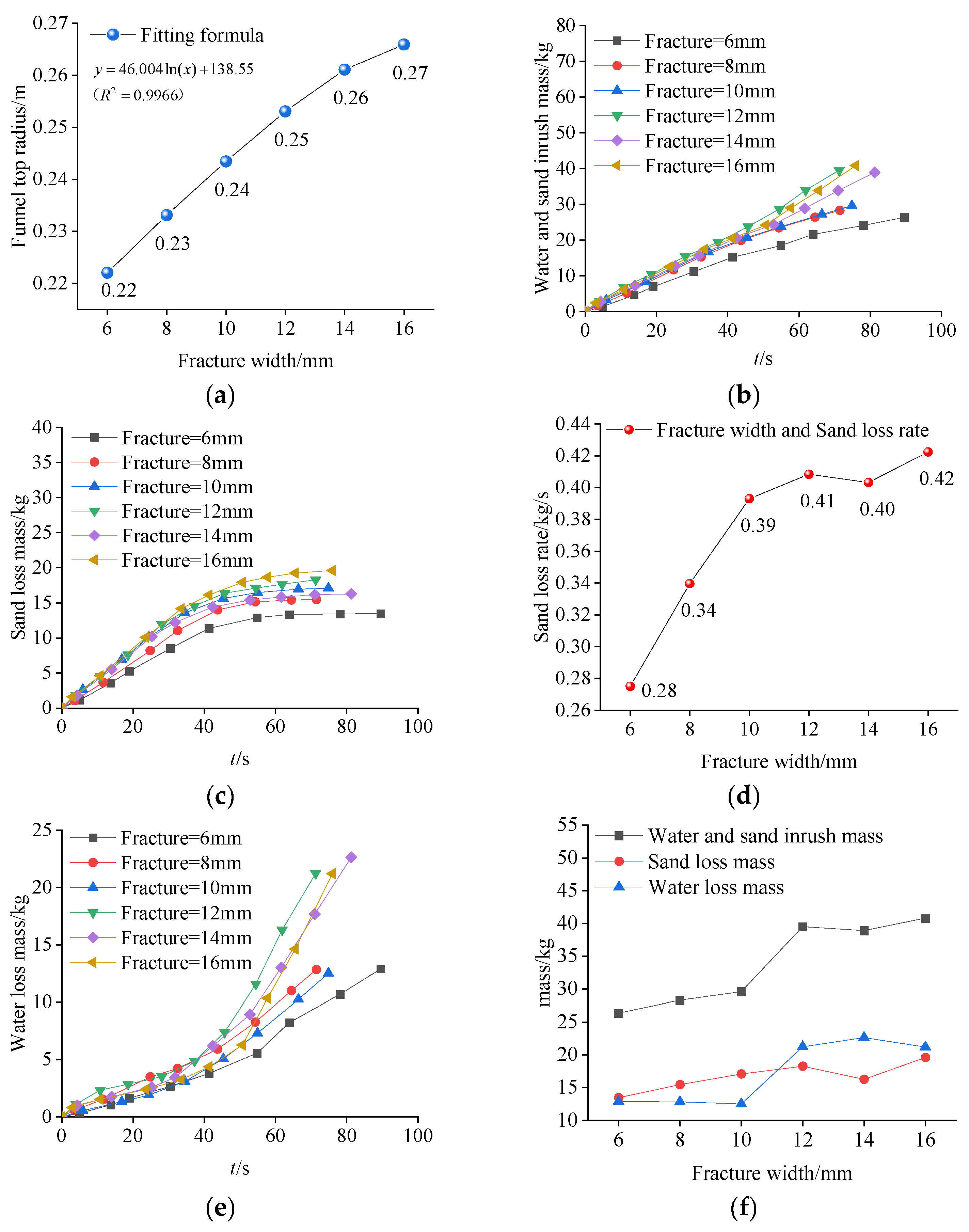
3.1. Fracture Width

Medium sand samples were used for the tests, and water and sand inrush tests with different fracture widths were conducted under the conditions of an aquifer thickness of 150 mm and a water pressure of 0.03 MPa. The test results are presented in Table 3. Based on the average measured funnel slope angle, the funnel top radius was estimated. Regression fitting showed that the fracture width had a positive logarithmic correlation with the funnel top radius, as shown in Figure 6a.

Table 3. Test results of collapse funnels under different fracture widths.

Serial Number	Fracture Width/mm	Average Measured Funnel Slope Angle/°	Funnel Top Radius/mm	Collapse Funnel Volume/m3
A1	6	34.04	222.05	7.745 × 10−3
A2	8	32.76	233.11	8.536 × 10−3
A3	10	31.64	243.44	9.309 × 10−3
A4	12	30.66	253.03	1.006 × 10−2
A5	14	29.88	261.07	1.071 × 10−2
A6	16	29.43	265.88	1.111 × 10−2

Table 3. Test results of collapse funnels under different fracture widths.

Serial Number	Fracture Width/mm	Average Measured Funnel Slope Angle/°	Funnel Top Radius/mm	Collapse Funnel Volume/m3
A1	6	34.04	222.05	7.745 × 10−3
A2	8	32.76	233.11	8.536 × 10−3
A3	10	31.64	243.44	9.309 × 10−3
A4	12	30.66	253.03	1.006 × 10−2
A5	14	29.88	261.07	1.071 × 10−2
A6	16	29.43	265.88	1.111 × 10−2

$$r=46.004\ln (x)+138.55$$

(3)

In the formula, where x is fracture width, mm; r is funnel top radius, mm.

The collapse funnel volume was calculated based on the funnel top radius, as presented in Table 3. Data indicate that as the fracture width increases, the funnel top radius gradually increases—resulting in a larger collapse funnel volume and consequently a greater degree of hazard. However, the magnitude of this increase (in both radius and volume) gradually diminishes as the fracture width increases further.

Figure 6. The relationship between fracture width and various parameters: (a) Fracture width and funnel top radius; (b) Different fracture width and water and sand inrush mass; (c) Different fracture width and sand loss mass; (d) Fracture width and sand loss rate; (e) Different fracture width and water loss mass; (f) Fracture width and content.

Figure 6. The relationship between fracture width and various parameters: (a) Fracture width and funnel top radius; (b) Different fracture width and water and sand inrush mass; (c) Different fracture width and sand loss mass; (d) Fracture width and sand loss rate; (e) Different fracture width and water loss mass; (f) Fracture width and content.

To investigate the influence of fracture width on the morphological evolution mechanism of collapse funnels and the water-sand migration characteristics during their formation process, the formation process of the collapse funnel is presented in

Table 4. Analysis of the Formation Process of Different Types of Fractures Width Collapse Funnel.

Fracture Width	Water and Sand Inrush Mode	Sand Loss Parameter Changes	Characteristics of Water-Sand Migration	The Influence of the Funnel Shape
6–10 mm	The water and sand inrush mass exhibits logarithmic growth, as shown in Figure 6b.	The sand loss mass consistently exhibits a trend of rapid increase followed by gradual deceleration. This description is consistent with the literature [26] as shown in Figure 6c; the fracture width has a positive logarithmic correlation with the sand loss rate, as shown in Figure 6d.	The water loss mass exhibits a stable increase, while the water loss rate increases slowly; with a small water flow drag force, the lateral expansion of the sand proceeds at a low speed, as shown in Figure 6e.	The collapse funnel exhibits shallow lateral development, with a slope angle ranging from 31.64° to 34.04°, and a small funnel top radius.
12–16 mm	The water and sand inrush mass exhibits nearly linear rapid growth, as shown in Figure 6b.		The water loss mass exhibits two distinct phases. Before approximately 40 s, it shows a stable increase with a slight increase in the water loss rate; after approximately 40 s, the water loss rate increases abruptly, the water flow drag force rises instantaneously, and the lateral expansion of the sand proceeds rapidly, as shown in Figure 6e.	The collapse funnel exhibits deep lateral development, with a slope angle ranging from 29.43° to 30.66°, and a large funnel top radius.

and Figure 6.

An increase in fracture width facilitates water flow, significantly enhancing the drag force of the water. Once the drag force exceeds the shear strength of the sand, it can no longer maintain stability and continuously collapses towards the center of the funnel. During this process, the drag force of the water remains greater than the shear strength of the sand, causing it to expand both vertically (into deeper layers) and laterally. Ultimately, this leads to a gradual decrease in the funnel’s slope angle.

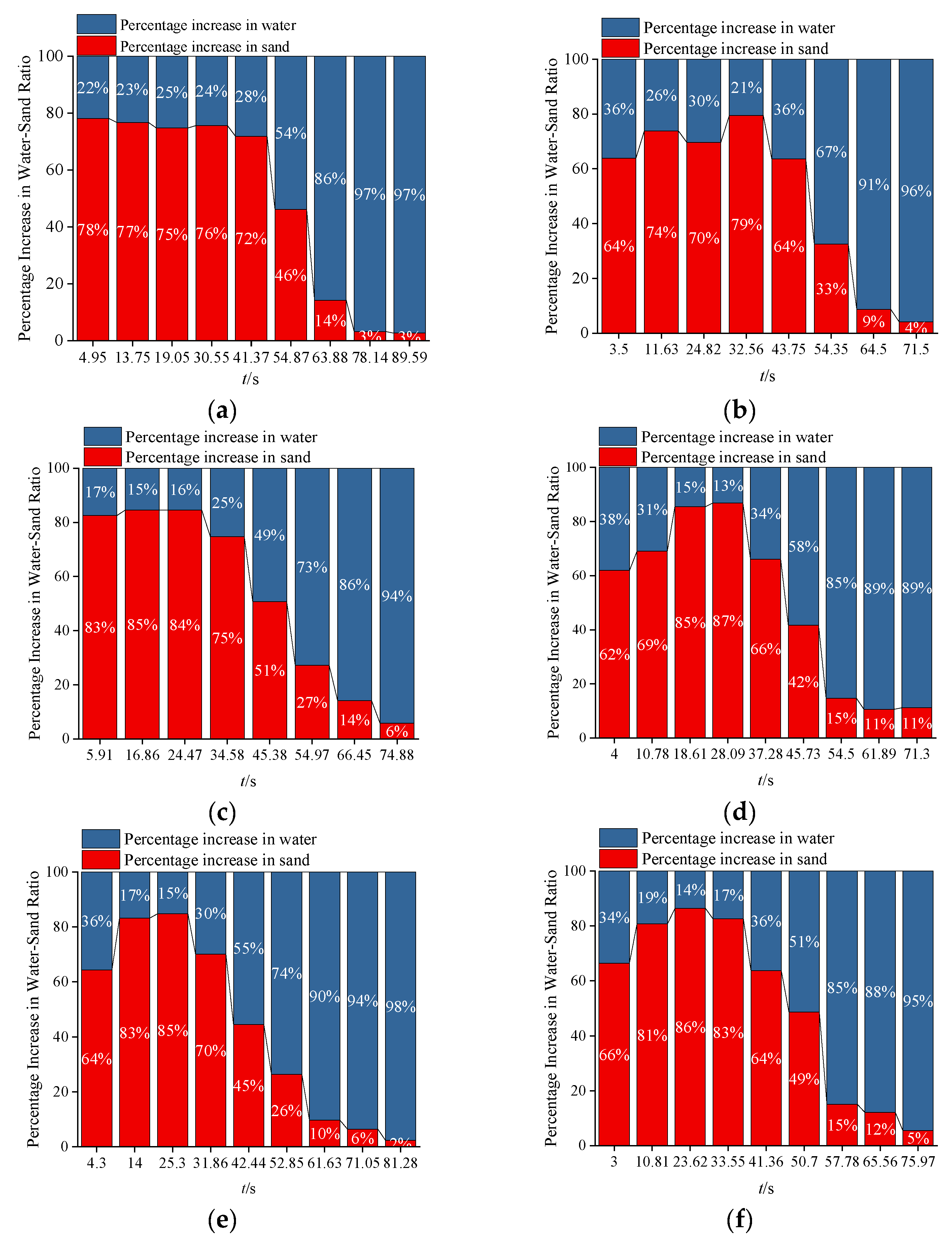
Based on the fracture width range, water and sand inrush is classified into two types: the slow-increase type and the stable-increase type. Their water-sand migration mechanisms are analyzed with reference to Figure 6f and Figure 7. When the fracture width ranges from 6 mm to 10 mm (see Figure 7a–c), in the initial stage, the increment of sand loss is higher than that of water loss (with sand accounting for 64–85%). The ratio of water mass increment to sand mass increment is relatively stable, and the promoting effect of water on sand movement is weak. Sand occupy the channel space, restricting water flow to only “local scouring” and resulting in a small water loss mass. As time progresses until the sand loss mass reaches an inflection point, the supply of sand decreases, and the proportion of water mass increment rises rapidly. At this stage, the space of the fracture channel is limited, the change in water loss rate is not significant, the water flow drag force is weak, and the lateral expansion of the collapse funnel is restricted.

When the fracture width ranges from 12 mm to 16 mm (see Figure 7d–f), at the initial stage of water and sand inrush, the sand is rapidly flushed out under the combined action of water flow and gravity. This causes the proportion of sand in the water-sand mixture to increase continuously until it reaches a peak (sand accounting for 85–87%), which corresponds to the inflection point of the sand loss mass. After this point, the proportion of the water mass increment rises. Meanwhile, the decrease in sand loss mass increases the available space for water flow in the fracture channel. At this stage, the water loss rate surges sharply; the sufficient water flow carries the sand, causing the sand to collapse both laterally and vertically. This ultimately results in a decrease in the funnel slope angle and an increase in the funnel top radius.

3.2. Aquifer Thickness

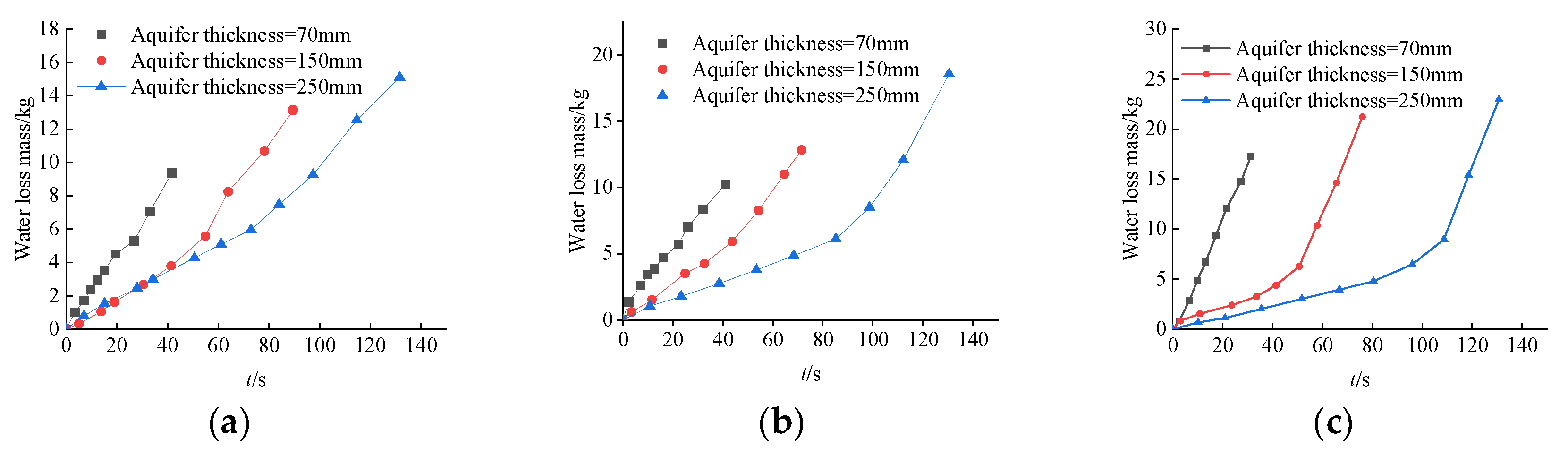
Water and sand inrush tests were conducted using sand samples and under a water pressure of 0.03 MPa, with the aquifer thicknesses set to 70 mm, 150 mm, and 250 mm, respectively.

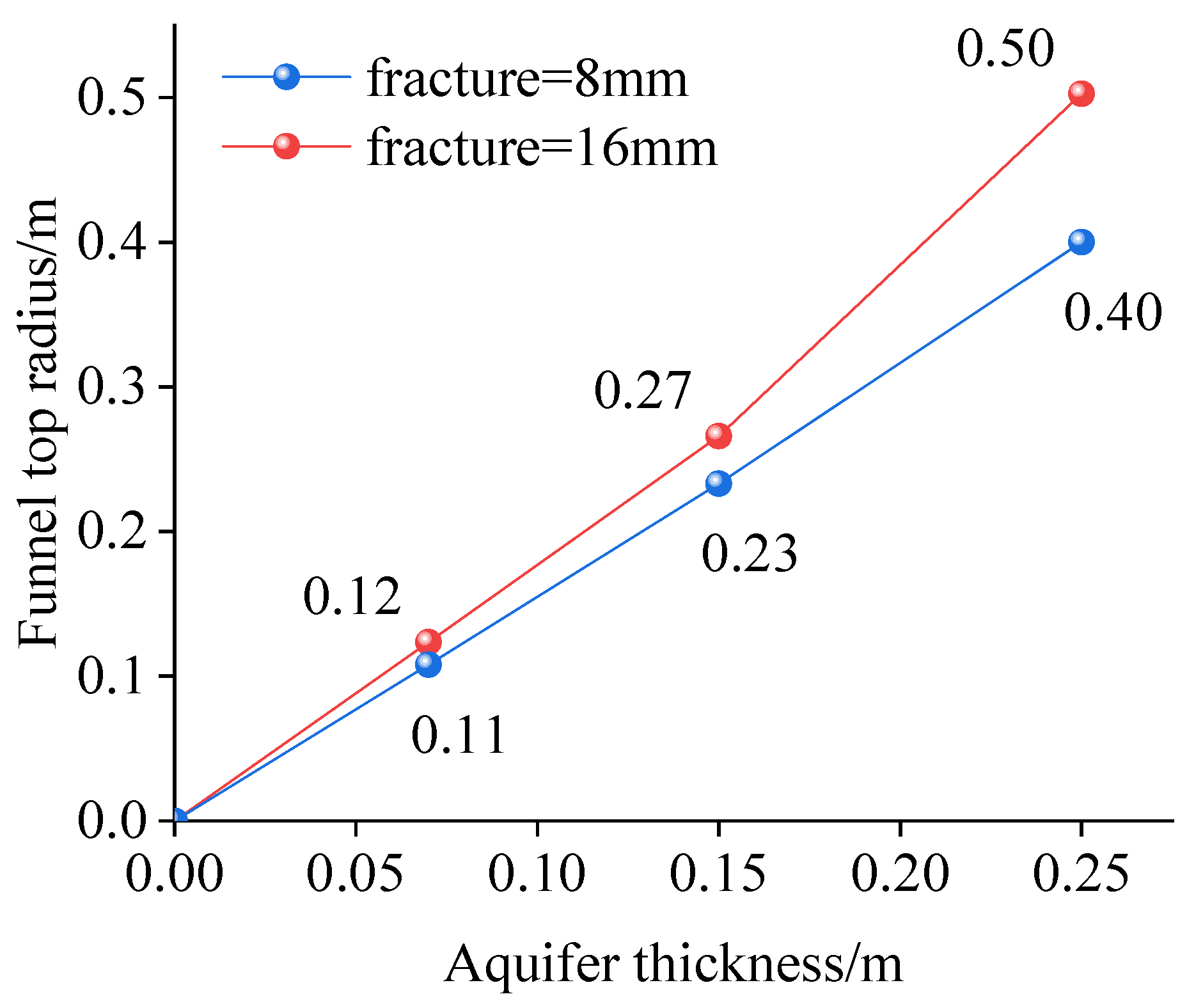
As shown in

Table 5. Parameters of collapse funnels formed under different conditions.

Serial Number	Fracture Width/mm	Aquifer Thickness/mm	Average Measured Funnel Slope Angle/°	Funnel top RADIUS r/mm	Collapse Funnel Volume/m3	Regression Formula for the Aquifer Thickness and the Water and Sand Inrush Mass	Coefficient of Determination (R2)	Water And Sand Inrush Rate kg/s
B1	6	70	28.9	126.8	1.179 × 10−3	Y = 0.2914t + 0.5936	0.9900	0.2914
B2		150	37.4	196.19	6.046 × 10−3	Y = 0.3058t + 0.906	0.9854	0.3058
B3		250	35.2	354.40	3.288 × 10−2	Y = 0.4189t + 0.1124	0.9886	0.4189
B4	8	70	33.36	108	8.55× 10−4	Y = 0.3285t + 1.2532	0.9787	0.3285
B5		150	32.76	233.11	8.536 × 10−3	Y = 0.4047t + 0.87	0.9898	0.4047
B6		250	31.96	400.08	4.19 × 10−2	Y = 0.4572t − 0.7227	0.9969	0.4572
B7	16	70	29.55	123.5	1.112 × 10−3	Y = 0.691t + 0.0475	0.9973	0.6910
B8		150	29.43	265.94	1.111 × 10−2	Y = 0.5123t + 0.1549	0.9934	0.5123
B9		250	26.45	502.63	6.614 × 10−2	Y = 0.5118t − 1.4659	0.9939	0.5118

, with the increase in aquifer thickness, the funnel slope angle decreases. This expands the affected range of the collapse funnel and increases the hazard degree of water and sand inrush.

The funnel top radius was estimated based on its average measured funnel slope angle. A nearly linear positive correlation was observed between the aquifer thickness and the funnel top radius, as shown in Figure 8. The reason for this correlation requires further analysis of changes in water-sand migration.

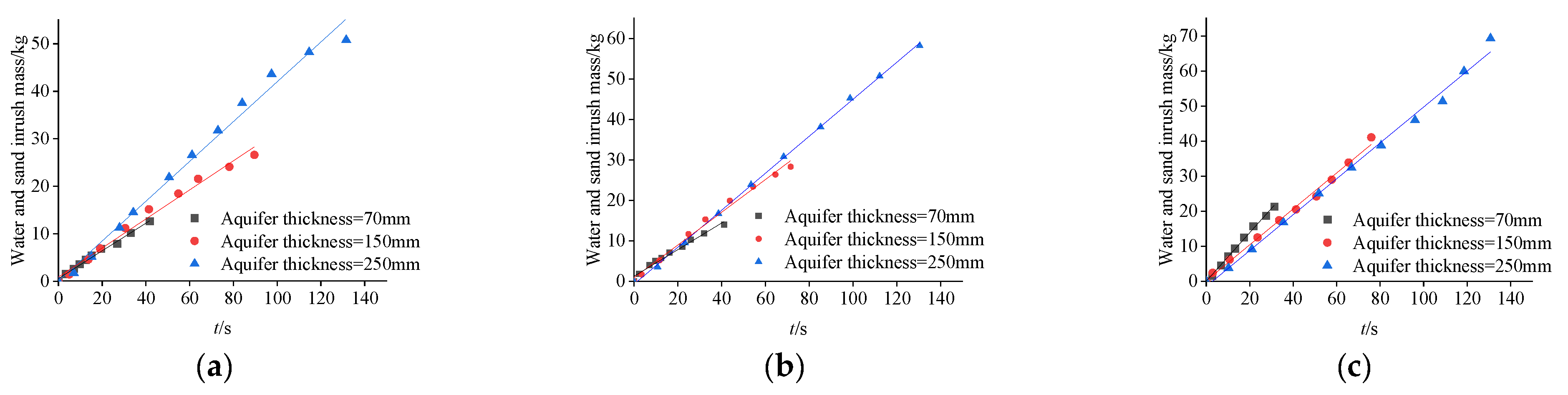
Through statistical analysis of the test results, relationship diagrams between different aquifer thicknesses and water and sand inrush mass were obtained under three fracture width conditions.

As can be seen from Figure 9, the aquifer thickness has a significant impact on the water and sand inrush mass—that is, the greater the aquifer thickness, the larger the water and sand inrush mass. Under different aquifer thicknesses, the water and sand inrush mass all exhibit a nearly linear increase with increasing time, as shown in Table 5. In such cases, each regression formula has a high degree of fitting, and the coefficients of determination (R²) are all greater than 0.98.

Reference [27] states that the flow velocity of dry sand is independent of the sand layer thickness, whereas the water-sand inrush rate varies depending on the aquifer thickness, with differences relating to fracture width and pore water pressure. The influence of pore water pressure can be reflected by changes in water loss mass over time.

As can be seen from Figure 10a,b, at fracture widths of 6 mm and 8 mm, the water and sand inrush rate is low. In the thick aquifer (250 mm), the seepage path of water in the sand layer is longer, the sand supply is sufficient, and the pore water pressure can continuously drive the sand to inrush at a higher rate. In the thin aquifers (70 mm and 150 mm), the water and sand inrush rate is similar to that in the thick aquifer (250 mm) in the initial stage; however, due to insufficient sand supply, the water and sand inrush mass decreases, ultimately leading to a decline in the water and sand inrush rate.

As can be seen from Figure 10c, at a fracture width of 16 mm, a large amount of sand loss from the thick aquifer (250 mm), occupying the space of the fracture channel. The water flow drag force is small, resulting in a poor promotion effect on the water and sand inrush rate. In contrast, the sand supply in the thin aquifers (70 mm and 150 mm) is small, making it difficult to form a large accumulation of sand that blocks the fracture channel space. The water flow drag force is large here, which plays a promoting role in increasing the water and sand inrush rate.

Thus, it can be concluded that when water and sand inrush flows unimpeded, the water and sand inrush mass is significantly affected by the aquifer thickness, while the water and sand inrush rate is jointly affected by both the fracture width and the aquifer thickness.

3.3. Sandy Particle Size Composition

Basic sand samples with three grain size compositions—coarse sand, medium sand, and fine-grained sand—were prepared. Constant test conditions were set, including a fracture opening of 8 mm, an aquifer thickness of 150 mm, a water pressure of 0.03 MPa, and a single vertical fracture.

The collapse funnel morphologies and their parameters formed by sand of the three grain size compositions under the same test conditions are detailed in Figure 11a–f and

Table 6. Test results of different sand particle size compositions.

Serial Number	Sand Particle Size Composition	Average Measured Funnel Slope Angle/°	D60/mm	Funnel Top Radius r/mm
C1	Fine-grained sand	30.915	0.7	180~196
C2	Medium sand	32.76	0.45	180~196
C3	Coarse sand	33.315	0.22	180~196

.

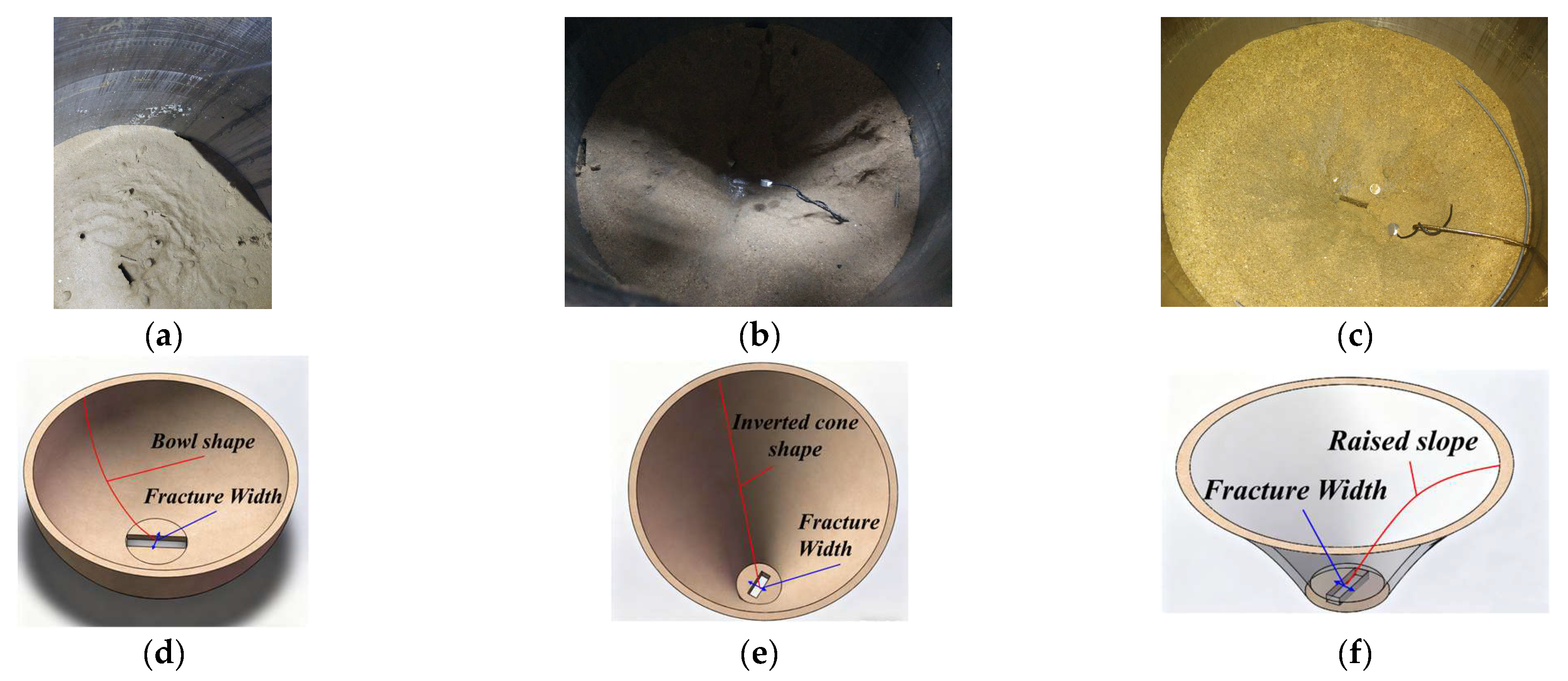
Regarding morphological characteristics: For medium sand, during funnel collapse, sand is gradually flushed out from the center to the edges, with no obvious local accumulation or retention. Its morphology is most similar to an inverted cone. For fine-grained sand, due to its fine particles and high fluidity, the central area first settles under the combined action of water pressure and gravity during collapse. Additionally, the edge sand has strong accumulation properties; coupled with its poor permeability (which prevents water in the central area from draining easily), the pore water pressure offsets part of the sand’s self-weight. Thus, a bowl-shaped funnel is formed, featuring a “deep center and shallow, gentle edges,” with the smallest central depth (Figure 11d). For coarse sand, its large particles interlock and provide mutual support, forming a well-structured soil skeleton with good permeability. During collapse, water in the central area can drain quickly; under its own gravity, the sand is more likely to settle downward, creating a relatively deep central depression. In contrast, the coarse particles in the slope area are less prone to sliding downward with the central settlement due to the supporting force of the soil skeleton. Instead, local accumulation occurs, forming slope protrusions (Figure 11f).

With the increase in coarse sand particle content, the collapse funnel slope angle gradually increases, and its central depth increases with the increase in skeleton particle size, as shown in Table 6.

From the above, it can be inferred that under the same conditions, the collapse funnel formed by silty-fine sand has the largest size, followed by that formed by medium sand, and the smallest by coarse sand. This pattern also indicates that the smaller the sand particle size, the more prone the sand is to movement, and the larger the sand inrush volume.

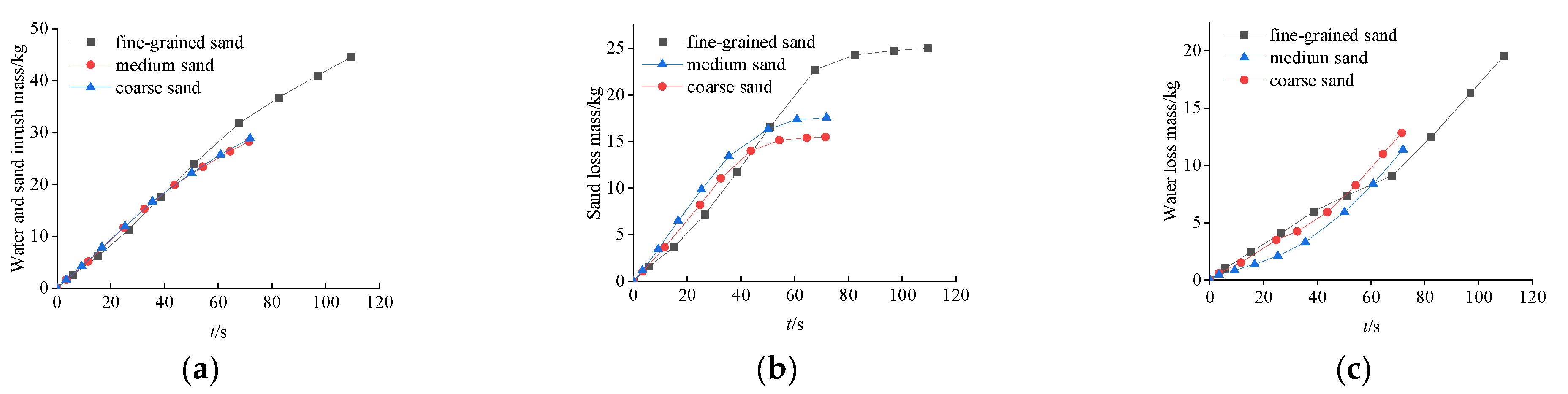
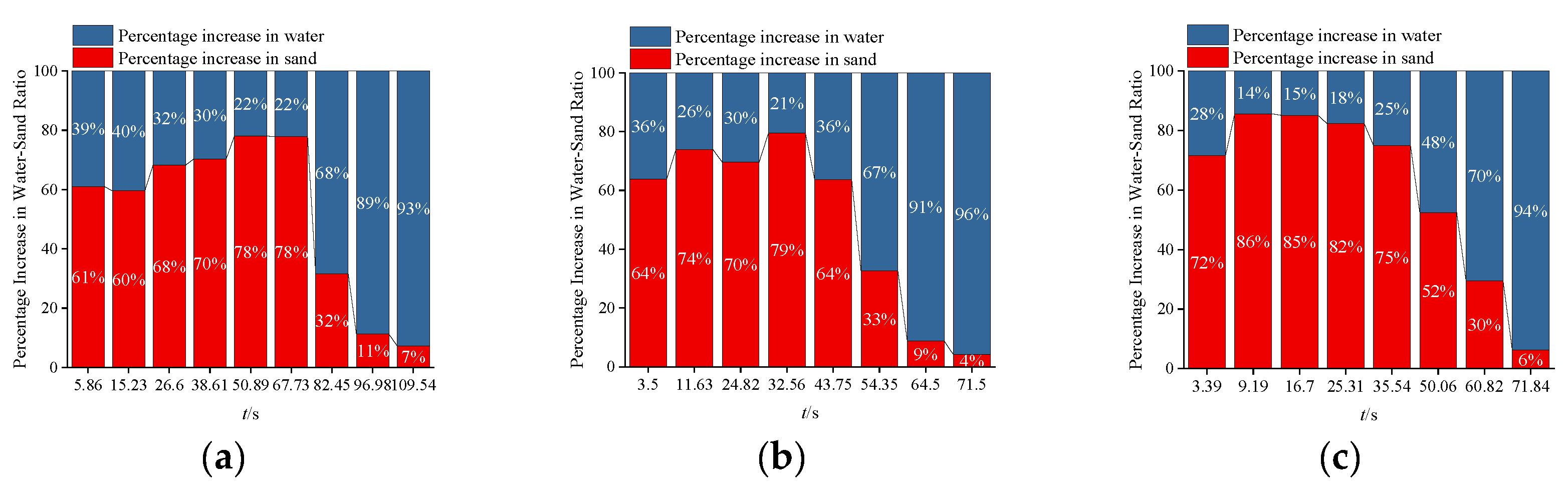
The water and sand inrush characteristics of the three sand samples with different grain size compositions exhibit a similar overall variation pattern, but with certain differences, as shown in Figure 12a.

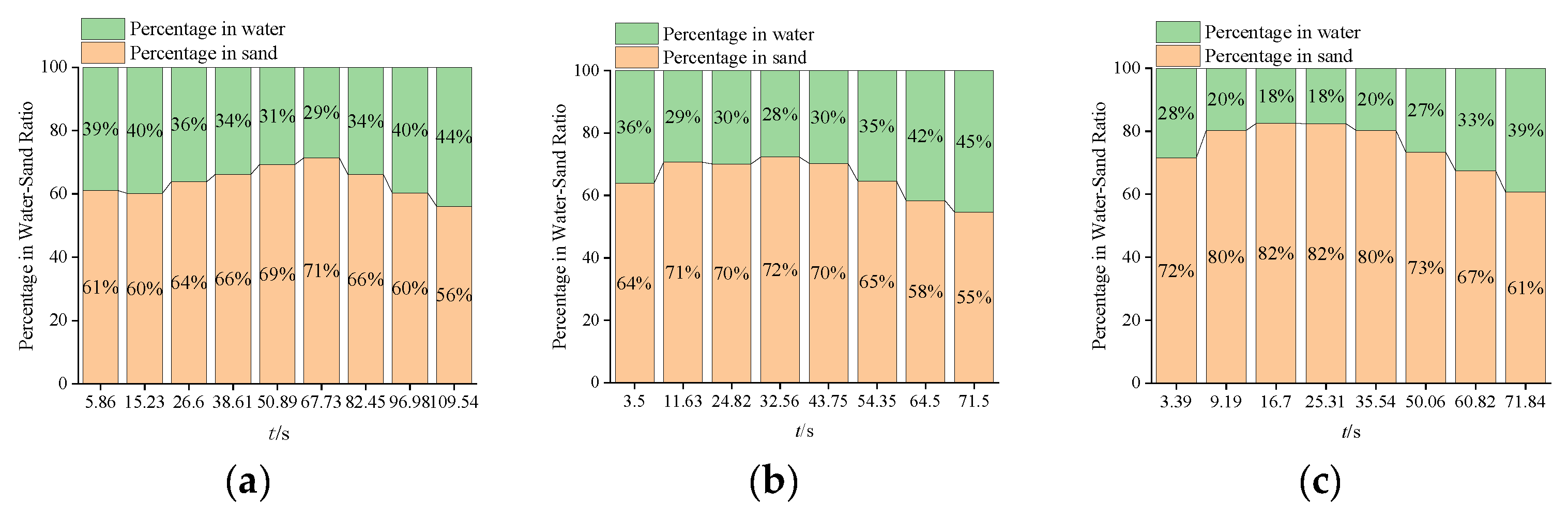
The common characteristics are as follows: during the stable sand loss stage, the water and sand inrush rates of the three sand types are basically the same; moreover, in this stage, the sand content in the inrush mixture is high, with sand loss as the dominant process, as shown in Figure 13.

The differences are mainly reflected in: (1) The stable sand loss duration of fine-grained sand (approximately 53 s) is longer than that of medium sand and coarse sand (approximately 28 s), and the sand loss mass of fine-grained sand is significantly greater than that of coarse sand and medium sand, as shown in Figure 12b.

(2) During the stable sand loss stage, the data show that the coarse sand has the highest sand content percentage (82%), followed by the medium sand (72%), with the fine sand having the lowest proportion (71%). In terms of loss performance, the fine sand has the largest loss mass and the longest stable sand loss time (67.73 s), while the medium sand (43.75 s) and coarse sand (35.54 s) decrease successively. See Figure 13 and Figure 14.

(3) The water loss mass of fine-grained sand is significantly greater than that of medium sand and coarse sand. Its water loss rate first decreases slowly and then maintains a stable state; while the water loss rates of medium sand and coarse sand first increase slowly and then stabilize after reaching a certain level, as shown in Figure 12c.

The causes of the above phenomena can be analyzed from the differences in sand particle properties and force-bearing laws: Compared with coarse-grained sand, fine-grained sand has lower weight, larger specific surface area, greater contact area with water, stronger water buoyancy and drag force acting on it, and smaller interparticle friction force; thus, it is more likely to be driven by water flow. In the initial stage of water inrush, the rapid migration of fine-grained sand leads to the sudden expansion of local pores and a sharp increase in water permeability, causing the water loss mass to significantly exceed that of medium-coarse sand in a short period. This is accompanied by the expansion of the collapse funnel and an increase in sand loss mass. Therefore, under the same water environment, fine-grained sand is more prone to movement with water flow.

Under otherwise identical conditions, the higher the proportion of fine-grained components in the aquifer, the greater the risk of water and sand inrush. Its water and sand inrush rate, sand loss mass, and scale of the collapse funnel are all greater than those of aquifers with a high proportion of coarse-grained components. If a water and sand inrush disaster occurs under the same conditions, the hazard degree of fine-grained sand aquifers is significantly higher.

3.4. Stratigraphic Sedimentary Structure

Different from previous methods that analyze surface subsidence induced by water and sand inrush by adjusting clay particle content, due to the complex and variable stratigraphic sedimentary structure of unconsolidated strata, establishing a composite stratigraphic sedimentary structure can more realistically reproduce the morphological evolution characteristics of the collapse funnel during mining. The experimental design and results are shown in

Table 7. Statistical table of the test results of water and sand inrush for different stratigraphic sedimentary structures.

Serial Number	Stratigraphic Sedimentary Structure					Water Pressure/MPa	Form a Continuous funnel	Average Measured Funnel Slope Angle/°	Sand Loss Mass/kg
D1	Fine-grained sand 40		Clay 35		Fine-grained sand 35	0.03	No	11.3	0.20
D2	Fine-grained sand 40		Clay 35		Fine-grained sand 35	0.035~0.13	No	43.5	0.24
D3	Fine-grained sand 70		Clay 35		Fine-grained sand 35	0.03	Yes	60.26	4.02
D4	Fine-grained sand 70	Clay 35	Medium sand 50	Clay 30	Medium sand 20	0.03	Yes	57.26	3.84

.

During the test, the water in the test chamber was supplied by the upper water head. Considering the hydraulic recharge issue of the aquifer at the bottom of the uncemented strata (which has a multi-layered composite structure with interbedded layers), when laying the clay layers between the aquifers, a certain space was reserved between the boundary of the clay layers and the inner wall of the test chamber (a 30 mm gap was reserved in this test). This space served as a natural hydraulic recharge channel connecting the upper aquifer and the bottom aquifer. Subsequently, the upper aquifer with the corresponding thickness was laid in accordance with the test design requirements. The specific laying process is shown in Figure 15.

Test Phenomenon Description:

Scheme D1: After the channel was opened, a small amount of sand flowed out, and basically no further sand inrush phenomenon occurred—only a small amount of clear water seeped out. A sand pit with a diameter of 130 mm and a depth of 13 mm was formed on the surface of the sand layer inside the chamber, as shown in Figure 16a.

Scheme D2: The phenomena in the early stage of the test were basically the same as those in Scheme D1. When only clear water seeped out, the water pressure was gradually increased from 0.035 MPa to 0.13 MPa, but no water and sand inrush phenomenon was induced. A sand pit with a depth of approximately 15 mm and a diameter of 190 mm was formed inside the chamber.

Scheme D3: A penetrating funnel appeared in the center of the test chamber, with a top diameter of 140 mm. The clay layer was damaged, and vertical water-sand recharge occurred between the upper and lower aquifers, as shown in Figure 16b.

Scheme D4: A penetrating funnel appeared in the center of the test chamber, with a top diameter of approximately 100 mm. Cavities of different sizes formed between the two clay layers. Vertical water-sand recharge occurred between the upper and lower aquifers, and the boundary thickness of the bottom aquifer remained unchanged.

Since the bottom aquifer in Schemes D1 and D2 had a small thickness, the downward movement space for the upper clay layer was limited after water and sand inrush occurred in the bottom aquifer. Fracture channels were blocked by the downward-moving clay, preventing sand from entering the channels—only a small amount of water seeped out. Additionally, the critical seepage hydraulic gradient for the seepage deformation and failure of clay is extremely high; under such conditions, even increasing water pressure is difficult to induce water and sand inrush disasters. Moreover, due to the high plasticity of clay, it rapidly undergoes corresponding downward deformation as the space for sand gushing from the bottom aquifer forms, hindering the lateral recharge of water and sand. This inhibits the expansion of the funnel in the bottom aquifer, resulting in the sand pit shown in Figure 16a.

In contrast, a larger thickness of the bottom aquifer provides greater downward movement space for the clay layer. When the downward movement exceeds the clay’s own ultimate strength, the clay layer is damaged; and as the downward displacement increases, the degree of clay damage intensifies. This leads to the connection between the upper aquifer and the bottom aquifer, allowing water and sand to inrush along the fracture channels—thus forming the penetrating funnel shown in Figure 16b.

The difference between Scheme 4 and Scheme 3 in terms of stratigraphic combination structure lies in that Scheme 4 consists of 5 sets of strata (3 aquifers and 2 clay layers). Since water can only enter the test chamber through the upper water head, the vertical recharge between aquifers is achieved via the hydraulic recharge channels reserved between the clay layers and the test chamber wall.

As can be seen from Figure 16e, the funnel slope of the top aquifer is relatively small. Due to the large thickness of the bottom aquifer, the upper clay layer at the mining-induced fractures in the bedrock is severely damaged under the combined action of hydrodynamic force and its own gravity, with a penetrating cavity forming in the center. Fractures can be clearly observed around this cavity. From Figure 16f, it can be seen that a large amount of clay accumulates above the fractures. After removing the strata above the bottom aquifer inside the chamber, it is found that the funnel formed in the bottom aquifer has a small size (the collapse funnel has an upper diameter of 130 mm and a depth of 70 mm) and a steep slope.

As shown in Figure 17, both the sand loss mass and the sand loss mass rate of Scheme D3 are higher than those of Scheme D4. Scheme D4 (0.22 kg/s) has a slightly higher water mass loss rate than Scheme D3 (0.17 kg/s). This indicates that an increase in the number of clay layers makes the bottom containing the upper clay layer more prone to clogging due to water flow. This increases the resistance to sand movement, resulting in a slower recharge sand rate for the bottom aquifer. At the same time, if the fracture channels are partially clogged by the clay, the flow passage area is reduced and the local flow velocity increases. Ultimately, the water loss mass rate of Scheme D4 is slightly higher than that of Scheme D3.

At the moment the fracture widths, the sand in the bottom aquifer above the fracture inrush from the fracture driven by the power source. As the inrush space expands, the upper clay layer undergoes tensile and shear failure under the action of water pressure and gravity. At this point, the upper and lower aquifers are directly connected. Due to the limited water supply in the test, the water and sand from the upper aquifer inrush directly along the vertical channel, and the recharge mass at the test chamber wall decreases instantaneously—this further leads to a reduction in sand recharge into the bottom aquifer, which is also one of the reasons for the small size of the bottom aquifer’s funnel.

The clay layer above the bottom aquifer exerts a certain inhibitory effect on water and sand inrush. Moreover, the greater the thickness and number of such clay layers, the more significant the effect—whether in blocking the fracture channels or hindering the lateral inflow of water and sand into the fractures. In addition, the water recharge conditions of the aquifer or its own water richness have a certain impact on the characteristics of water and sand inrush.

4. Discussion

4.1. Prevention Measures for Water and Sand Inrush

By analyzing how each of the above factors influences surface subsidence, we can conclude that sand particle size composition is the primary factor affecting underground subsidence. The ‘safest condition’ for preventing subsidence is when the clay layer above the underlying aquifer fully blocks fractures and maintains its structural integrity. The specific reasons are as follows:

The sand particle size composition is the dominant factor determining the form and severity of the collapse funnel, and therefore directly determines its morphological characteristics and hazard level.

The width of the fractures is a key controlling factor. Fractures serve as the main channels for the flow of water and sand. An increase in fracture width means an expansion of the channels’ cross-sectional area, which directly enhances the flow capacity of water and sand. This intensifies the occurrence and scale of water and sand inrush.

An increase in the thickness of the aquifer will directly exacerbate the collapse disaster. However, the thickness of the bottom aquifer and the upper clay layer jointly determine the development of the collapse funnel and the severity of the disaster. On the one hand, the thickness of the bottom aquifer directly affects the stability of the upper clay layer. If the bottom aquifer is thin, the clay layer cannot sink sufficiently to block the rock fractures effectively. On the other hand, if the bottom aquifer is too thick, the clay layer will lose stability and collapse due to insufficient strength, thereby triggering severe subsidence.

Taking into account the geological characteristics of shallow-buried coal seams, thin bedrock and a simple stratum structure in the western region, as well as the action mechanisms of the various influencing factors, preventive techniques for surface subsidence caused by water and sand inrush can be developed in two ways:

Artificial grouting creates a protective layer. By injecting a cementitious slurry into the stratum, the slurry solidifies and enhances the stratum’s mechanical properties, thereby achieving anti-seepage and reinforcement effects.

Pre-mining shotcrete reinforcement. Combining anchor rod support with grouting reinforces the base rock, controlling the width of fractures and reducing disturbance to the coal seam roof during mining. This prevents fractures from extending to the water-bearing layer, reducing the risk of subsidence.

4.2. Limitations

The research provides theoretical guidance on how to prevent and control surface subsidence disasters caused by water and sand inrush. However, the study is limited by the experimental conditions and has the following main limitations: Firstly, this study is based on the theory of natural cessation angle of sand subsidence, using an inverted conical funnel model to calculate the collapse volume and correcting the deviations caused by size effects. However, this method still requires further verification. In addition, the collapse radius and volume in the paper were calculated based on the inverted conical funnel model under medium sand conditions. However, in actual engineering, the shape of the collapse funnel is significantly affected by the composition of sand particles. Moreover, the study only analyzed the dominant role of a single factor and lacked multi-factor interaction analysis. In the future, the inverted conical funnel formula will be corrected through numerical simulation, and a multi-factor interaction analysis will be conducted using random forests.

5. Conclusions

Given the limited quantitative research on surface subsidence induced by water and sand inrush at present, this study focuses on the morphology and mechanism of collapse funnels induced by water and sand inrush hazards. Through the analysis of the morphological evolution of collapse funnels, the following conclusions are drawn:

(1)

An increase in fracture width promotes water and sand inrush, resulting in nearly linear growth of the top radius of the collapse funnel and water and sand loss mass. As the fracture width increases, the volume of water in the fracture channel increases, causing a sharp rise in water loss and a significant increase in the drag force of the water. This expansion also increases the influence range of the collapse funnel.

(2)

The thickness of the aquifer is almost linearly and positively correlated with the radius of the collapse pit’s top and the mass of water and sand inrush. An increase in aquifer thickness will expand the collapse pit’s influence range and intensify the severity of the water and sand inrush disaster. The rate of water and sand inrush is affected by both the width of the fractures and the thickness of the aquifer. As the width of the aquifer thickness increases, so does the rate of water and sand inrush. However, once the width of the fractures increases a certain value, the rate of water and sand inrush decreases as the thickness of the aquifer increases.

(3)

The composition of the sand particles plays a dominant role in the degree to which water and sand cause disasters, as well as in the morphology of the collapse funnel. As the proportion of fine particles in the aquifer increases, the collapse funnel’s morphology changes from a “central depression and slope bulge” to an inverted cone and then a bowl. At the same time, the degree to which the inrush of water and sand causes disasters and the range of damage caused by the collapse funnel also gradually increase.

(4)

When the clay layer above the bottom aquifer is taken into account, the size of the collapse funnel, the amount of sand lost and the rate of sand loss are all significantly smaller. Furthermore, as the thickness and quantity of the bottom aquifer increase, the effect of either blocking the fracture channel or preventing lateral inflow of water and sand into the fracture becomes more pronounced.