Validation of Sea Level Anomalies from the SWOT Altimetry Mission Around the Coastal Regions of East Asia and the US West Coast

The validation of altimeter data in the coastal zones is of great importance for monitoring coastal sea level changes. Therefore, this study focuses on the validation of sea level anomaly (SLA) estimates from three altimetry missions (i.e., SWOT, ICESat-2 and Sentinel-3A) within the distance band of 50 km to the coast in two study areas: the coastal region of East Asia (0° N–40° N, 100° E–140° E) and the US West Coast (30° N–60° N, 145° W–115° W). The selection of these three missions is because they carry the advanced radar and laser altimeters. 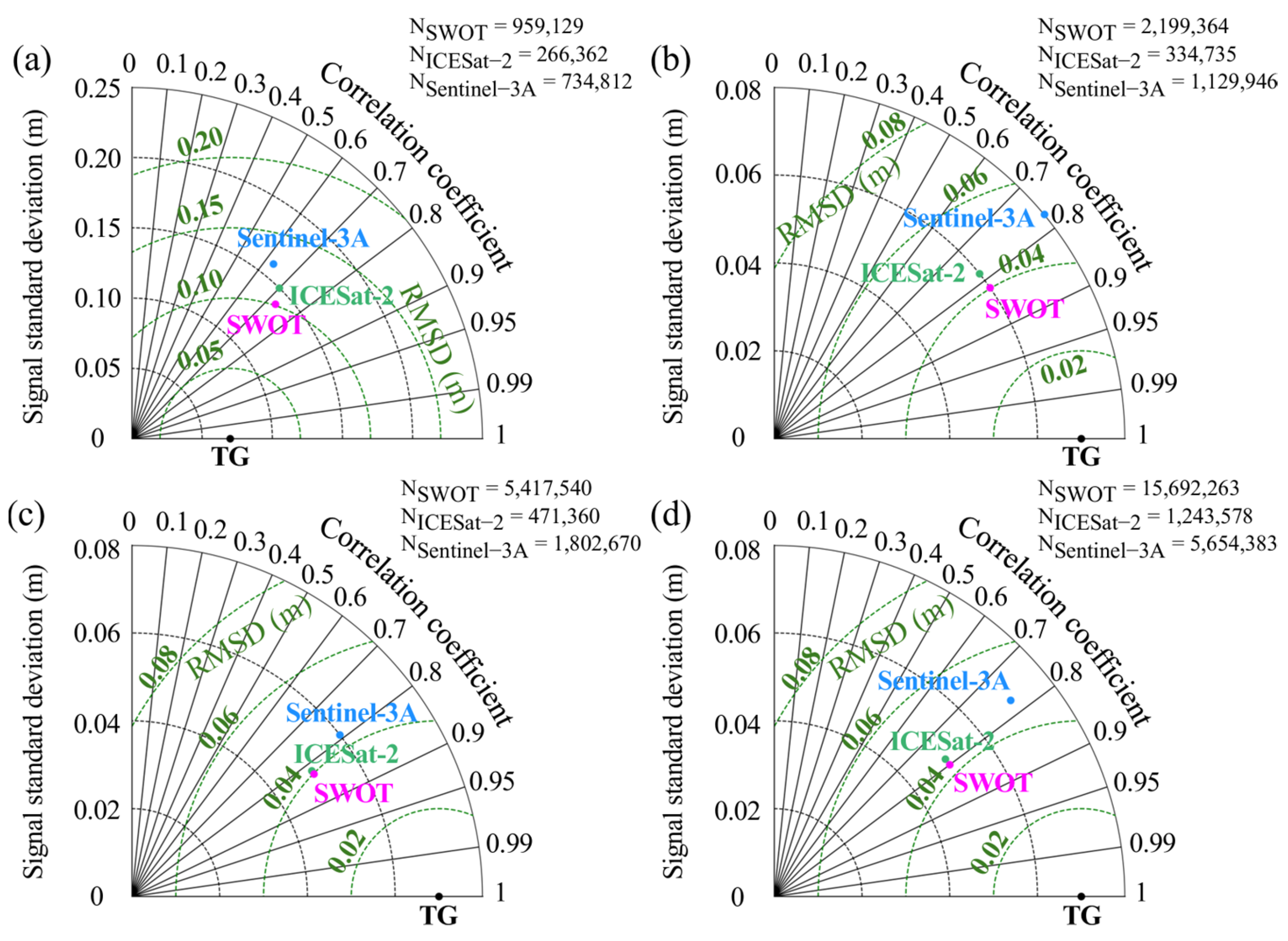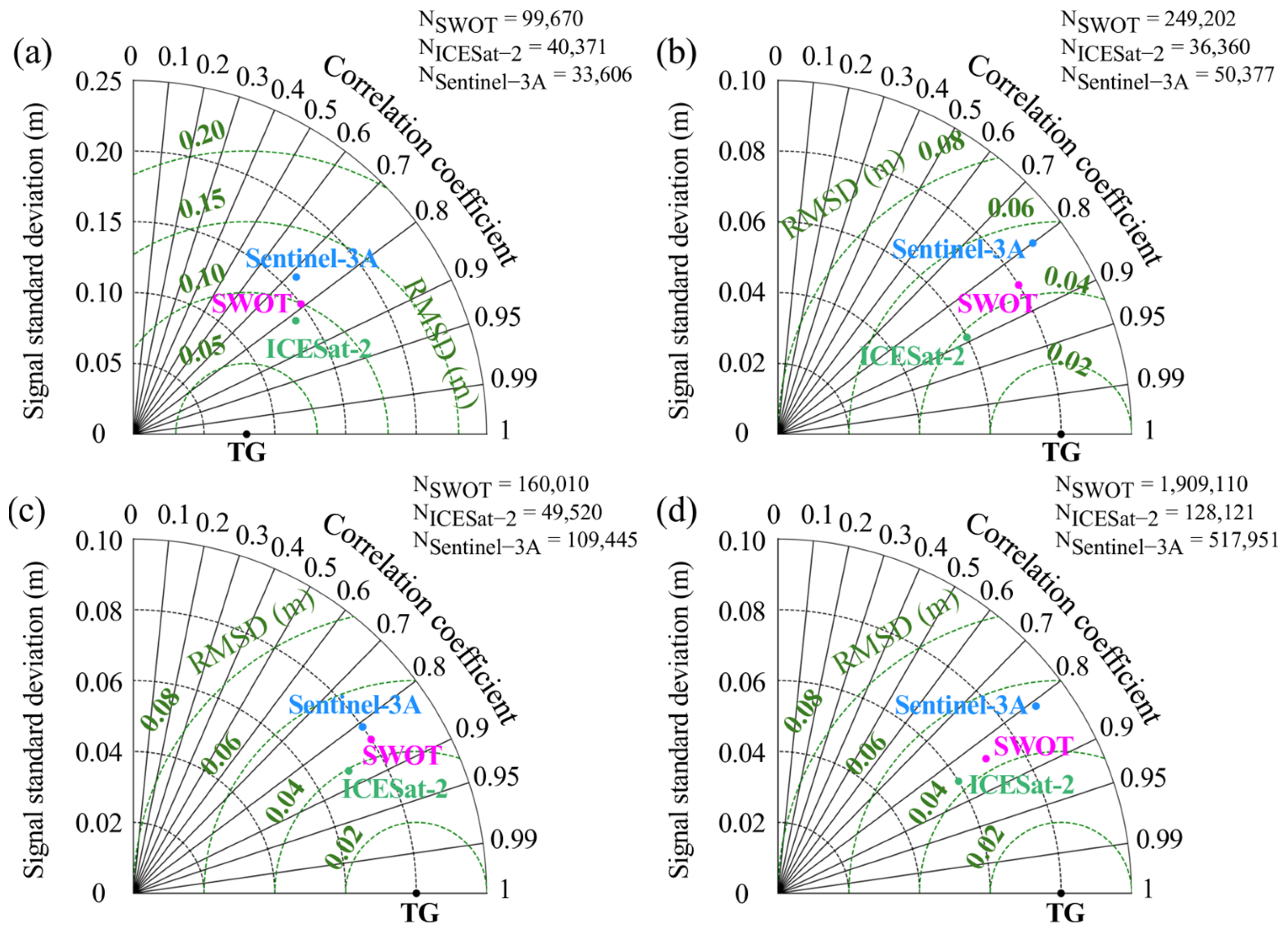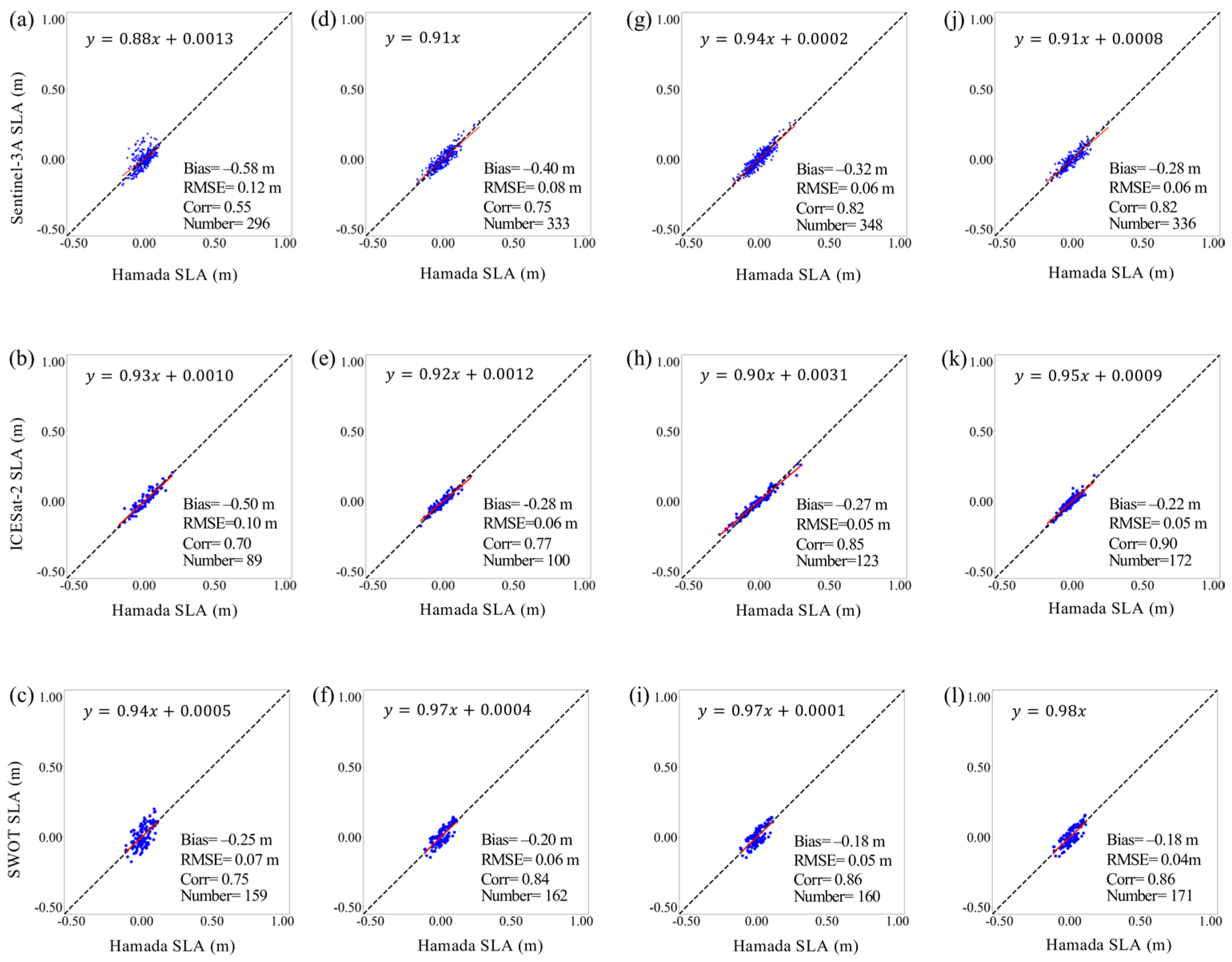Although the validation of any single altimeter is not new, the comparison of their performance together in the coastal zones is the first time to our knowledge. Because the spatial resolutions of these three altimeters are different, the spatially averaged altimeter measurements are used for the validation against tide gauges. Moreover, the validation is conducted over four coastal strips (0–5 km, 5–10 km, 10–20 km, and 20–50 km) to better reveal their performance when approaching towards the coastlines. The results show that these three missions achieve similar performance in terms of correlation coefficient and Root Mean Square Error (RMSE) in the 5–50 km coastal strip. The superior performance of the SWOT mission to the ICESat-2 and Sentinel-3A is observed in the last 5 km to coasts (0.06 m/0.73 against 0.09 m/0.70 and 0.12 m/0.63 for coastal regions of East Asia, 0.11 m/0.79 against 0.10 m/0.82 and 0.14 m/0.72 for the US West Coast), where the land contamination is the most significant. The ICESat-2 achieves the best performance (0.10 m) in the US West Coast due to the reduced range bias in higher latitudes, and the SWOT outperforms in the lower-latitude East Asia coastal region (0.06 m). To further investigate the data quality of the SWOT mission, a triple collocation model is applied to quantify the errors. The results reveal that the SWOT obtains similar error variance relative to the tide gauges in both study areas (i.e., 0.010 m² vs. 0.005 m² for the coastal region of East Asia, and 0.010 m² vs. 0.007 m² for the US West Coast). The above findings highlight the SWOT’s advantages in monitoring the coastal sea level changes.