A Data-Driven Framework for Flood Mitigation: Transformer-Based Damage Prediction and Reinforcement Learning for Reservoir Operations
Abstract
1. Introduction
2. Materials and Methods
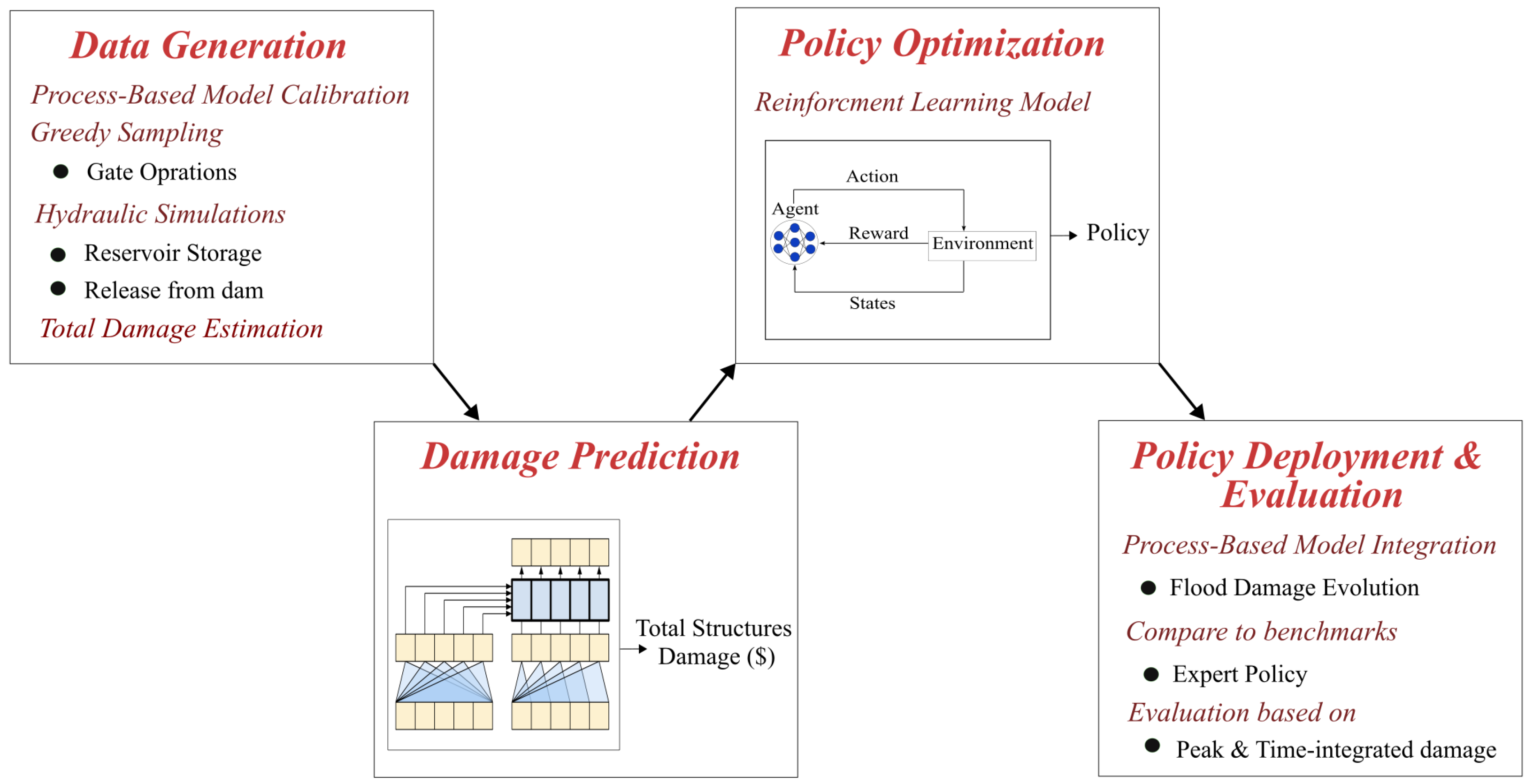
2.1. A Data-Driven Framework for Flood Mitigation
- Data Generation: The first phase of our framework focuses on process-based data generation. Advanced hydraulic models, such as HEC-RAS, after calibration can be employed to simulate reservoir water levels, releases, and downstream inundation under alternative gate operation strategies. To ensure sufficient coverage of operational scenarios, A Greedy Sampling scheme is employed to systematically generate a diverse set of gate operation strategies. The resulting hydraulic outputs (e.g., flood depth and extent) are merged with geospatial and socio-economic datasets in consequence models (e.g., HEC-FIA) to estimate economic losses. This component provides the critical input data for subsequent stages of the framework, including machine learning-driven optimization and decision support, enabling end-to-end evaluation of mitigation strategies.
- Damage Prediction: Process-based hydraulic simulations are computationally expensive, hindering flood mitigation strategy optimization. To overcome this, a machine learning (e.g., Transformers or recurrent neural networks) model is developed in this phase as a surrogate to predict flood damages using pre-generated simulation data. The model shall process time-series inputs, such as reservoir storage, release rates, and gate operations, capturing long-range dependencies efficiently. This component enables rapid and accurate estimation of downstream flood impacts, especially economic losses, which serves as feedback for optimizing reservoir gate operation strategies in the next phase. By replacing iterative process-based simulations, the damage predictive model reduces computational costs without sacrificing fidelity.
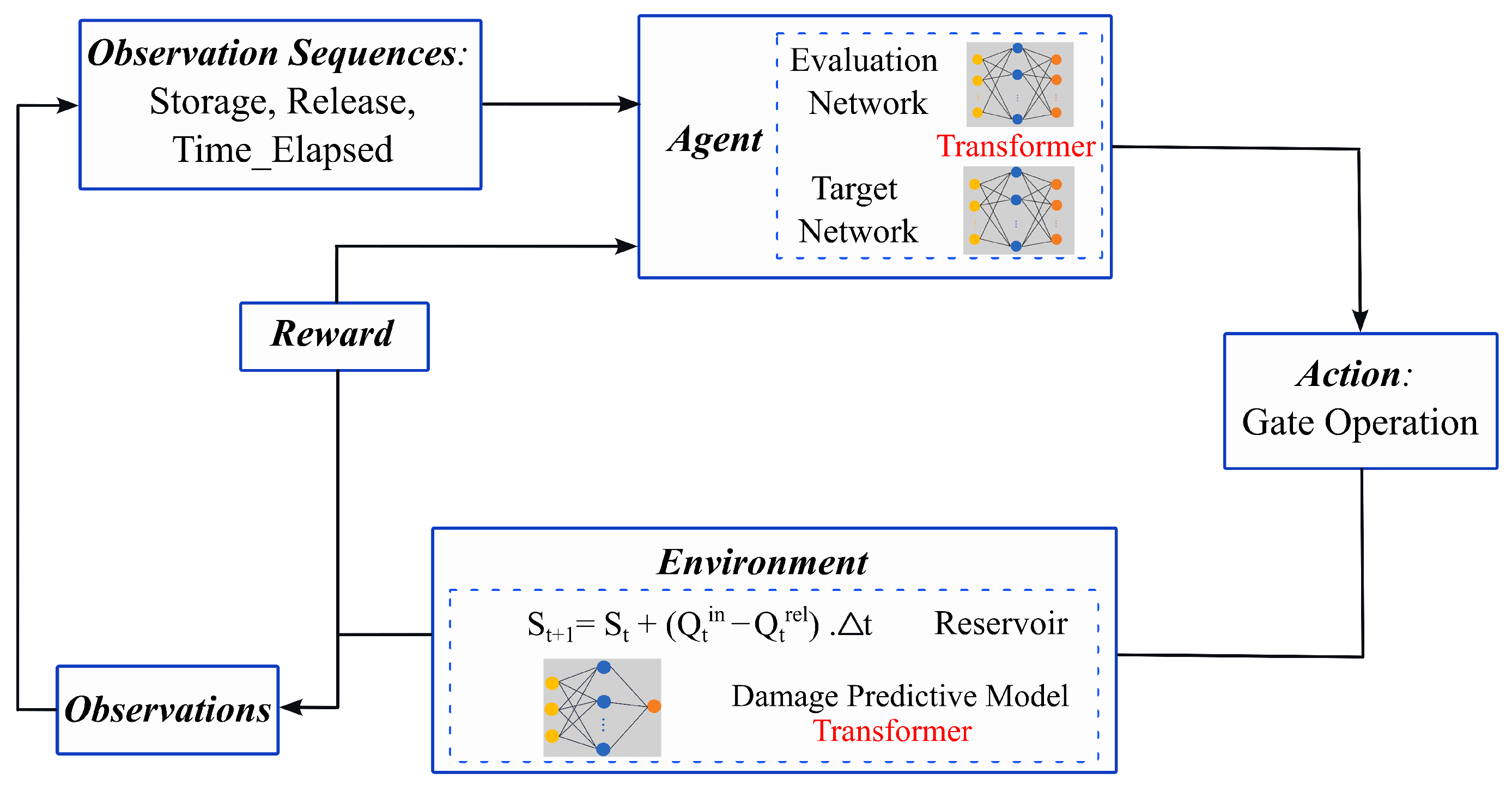
- Policy Optimization: Model-free control and optimization methods, such as reinforcement learning (RL) or genetic algorithms (GAs), can be employed to train an AI agent (i.e., the computer program) to discover optimal flood mitigation strategies, i.e., the reservoir gate operation policy in this phase. The agent learns through iterative interactions with a virtual environment, specifically, the damage-prediction surrogate model developed earlier. The problem needs to be formulated as a partially observable Markov decision process (POMDP), where the agent observes historical hydrologic states (e.g., reservoir storage and water release), takes actions (gate adjustments), and receives a penalty or negative reward based on predicted flood damage. The learning objective is to maximize cumulative reward, ultimately deriving an optimal control policy that minimizes flood damage during extreme events.
- Policy Deployment and Evaluation: The optimized flood mitigation policy from the previous component is deployed by integrating it with the process-based hydraulic model, where it autonomously generates a sequence of gate operations during simulated flood events. Simultaneously, the system calculates the evolution of flood damage, enabling direct performance comparisons against conventional baseline operations (e.g., human operator decisions and a zero-open alternative). Rigorous validation using historical and synthetic flood scenarios can quantify improvements in damage reduction, evaluated through both peak damage (the maximum instantaneous impact) and time-integrated damage (the cumulative losses over the event duration). The deployment component also allows fine-tuning recommendations, ensuring practical implementation in real-world reservoir management systems.
2.2. Process-Based Hydraulic Model
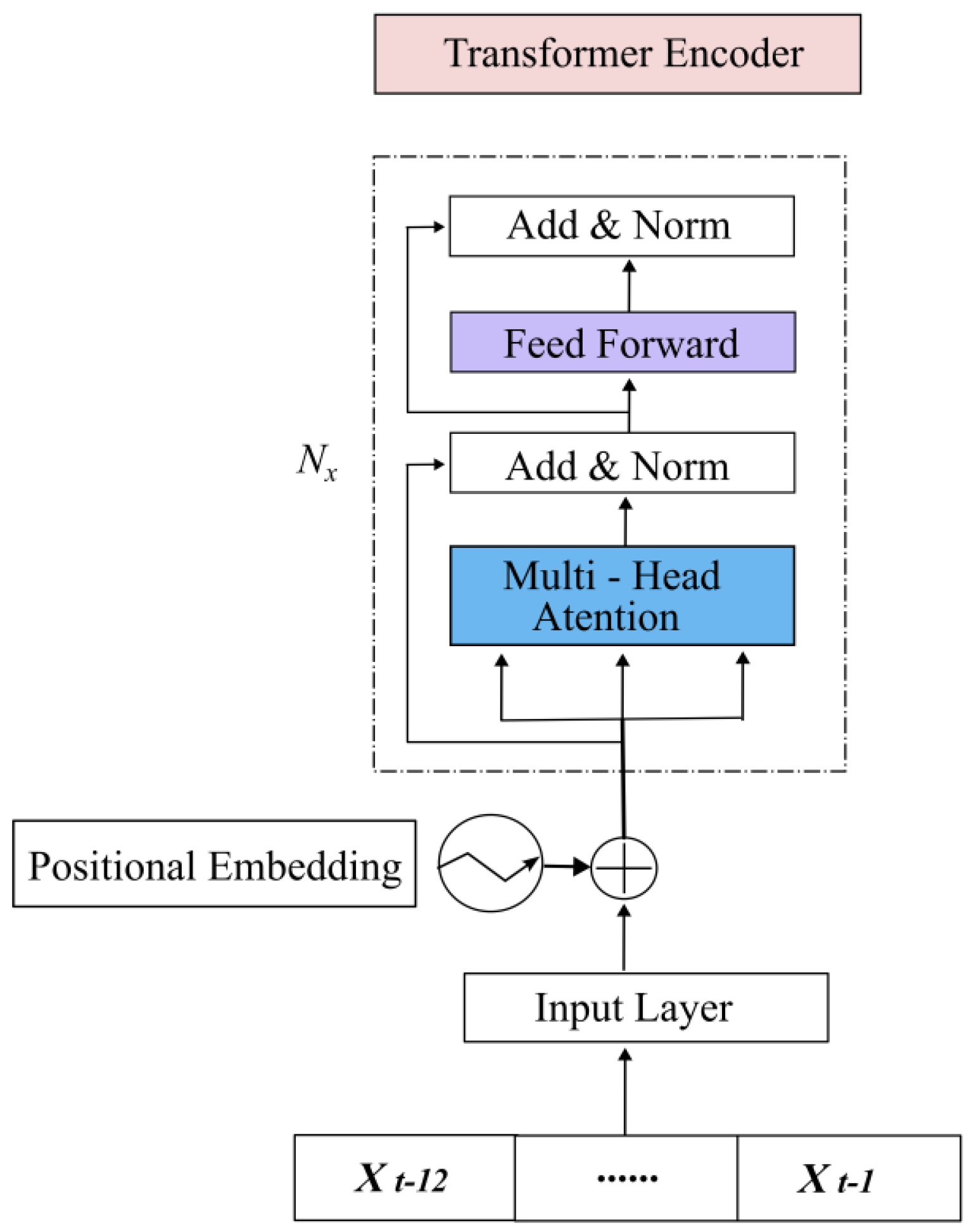
2.3. Transformers
2.4. Reinforcement Learning
2.4.1. MDP and POMDP
- is the finite set of environment states,
- is the finite set of possible actions,
- is the state transition probability function, satisfying ,
- is the initial state,
- is the reward function.
- is the set of possible observations,
- is the observation function, defining the probability of receiving observation o after taking action a and arriving at state , satisfying .
2.4.2. Transformer-Based Deep Q-Learning
3. Data Generation
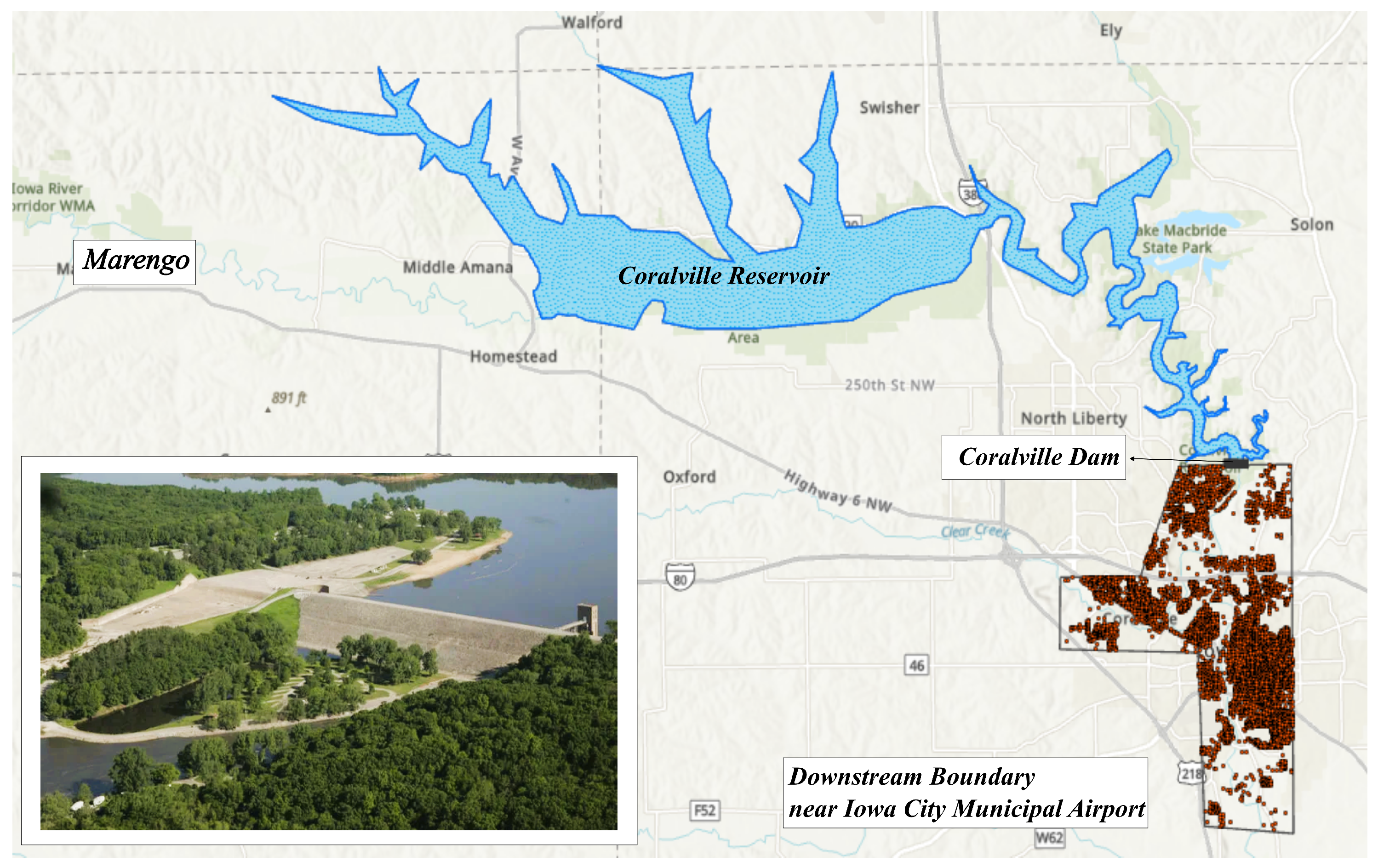
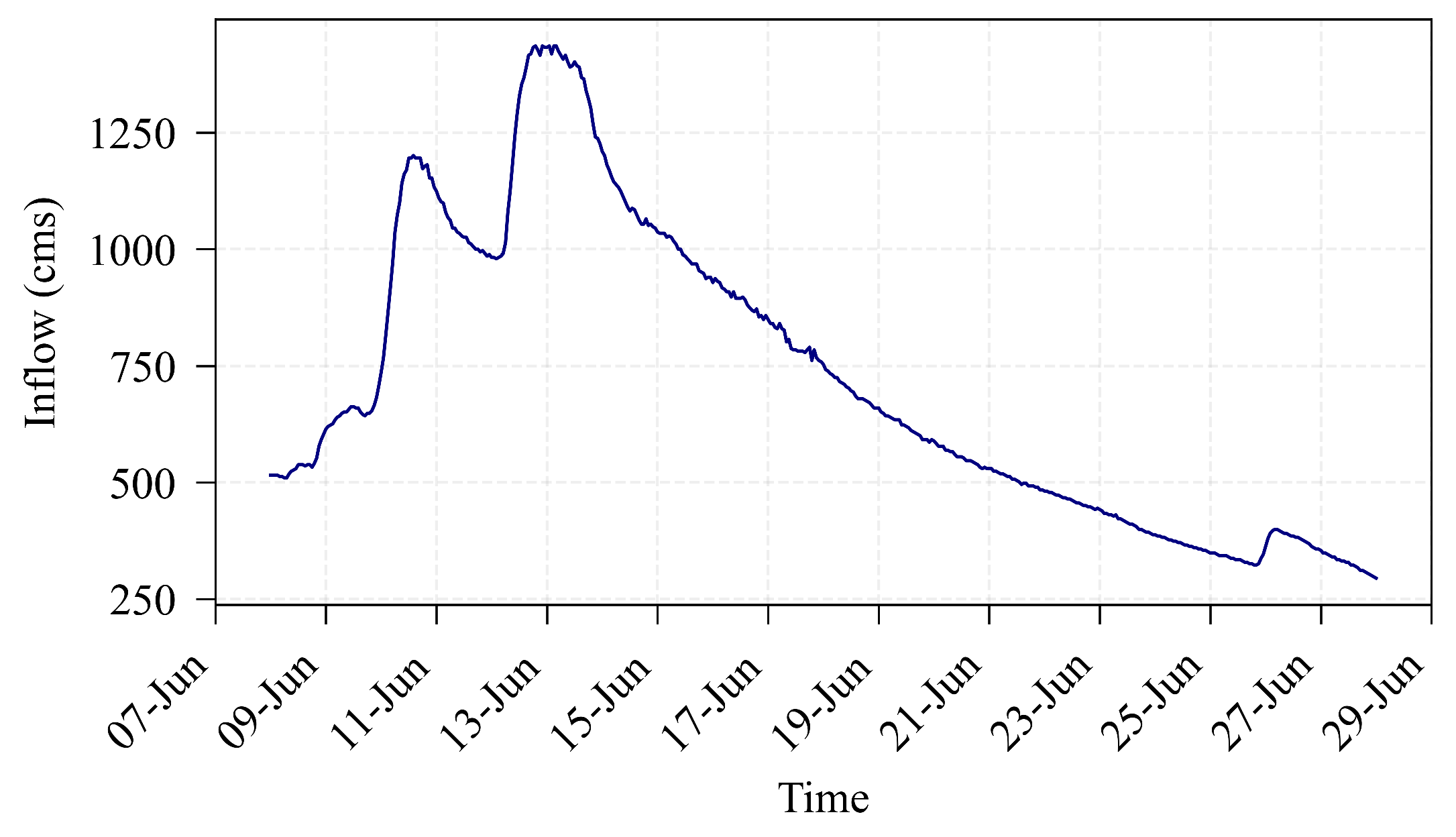
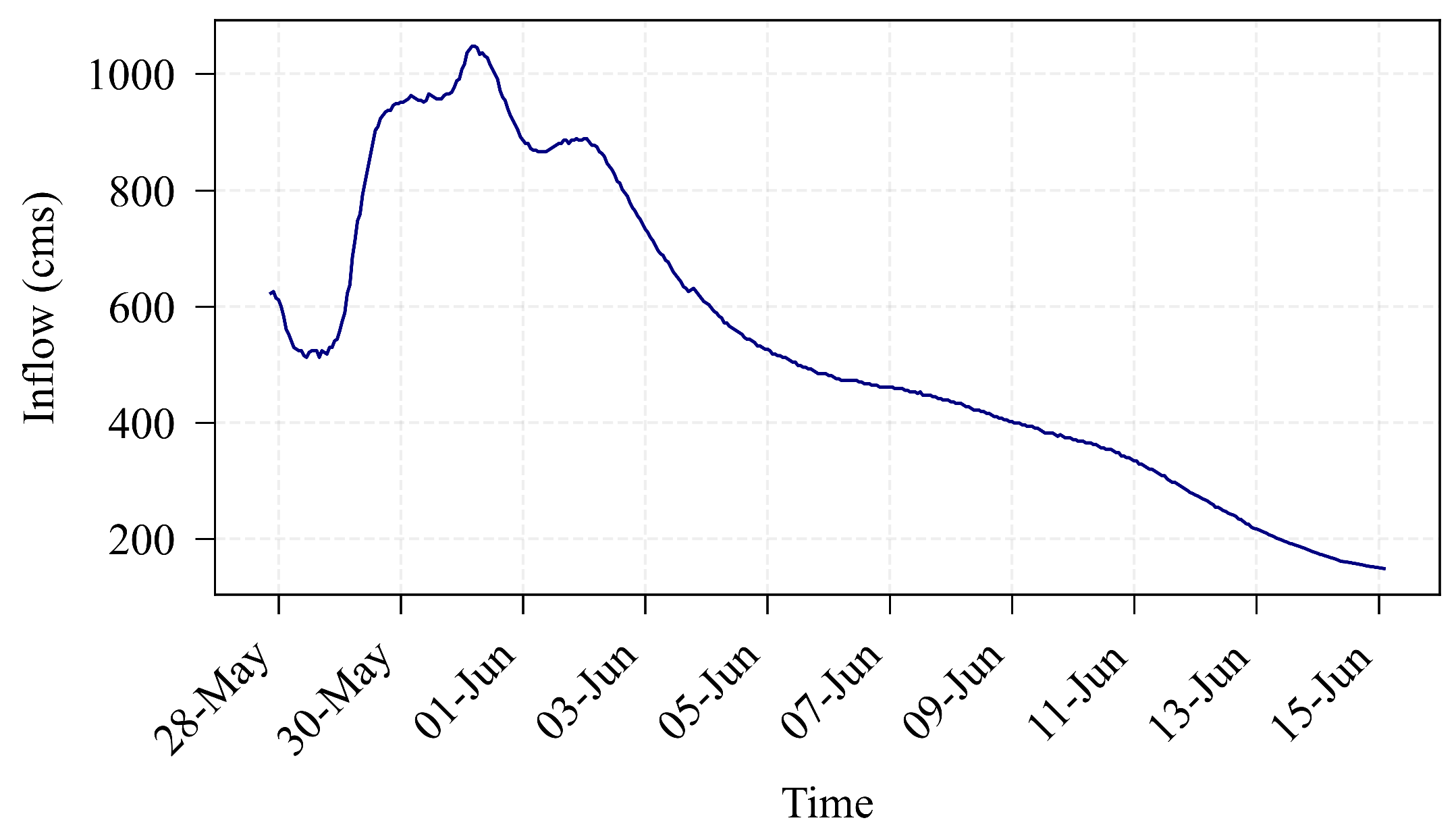
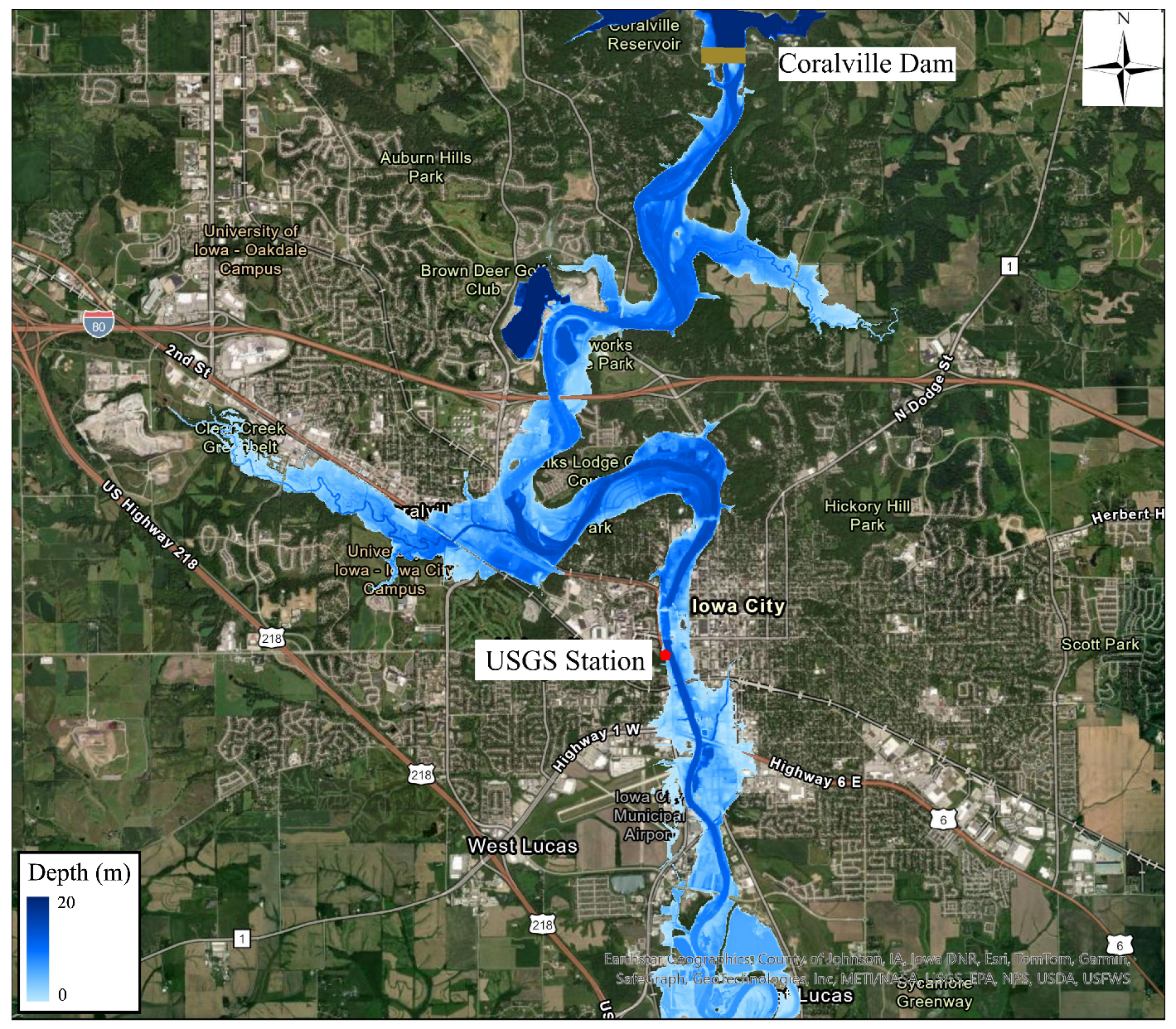
3.1. 2008 Iowa Flood Event
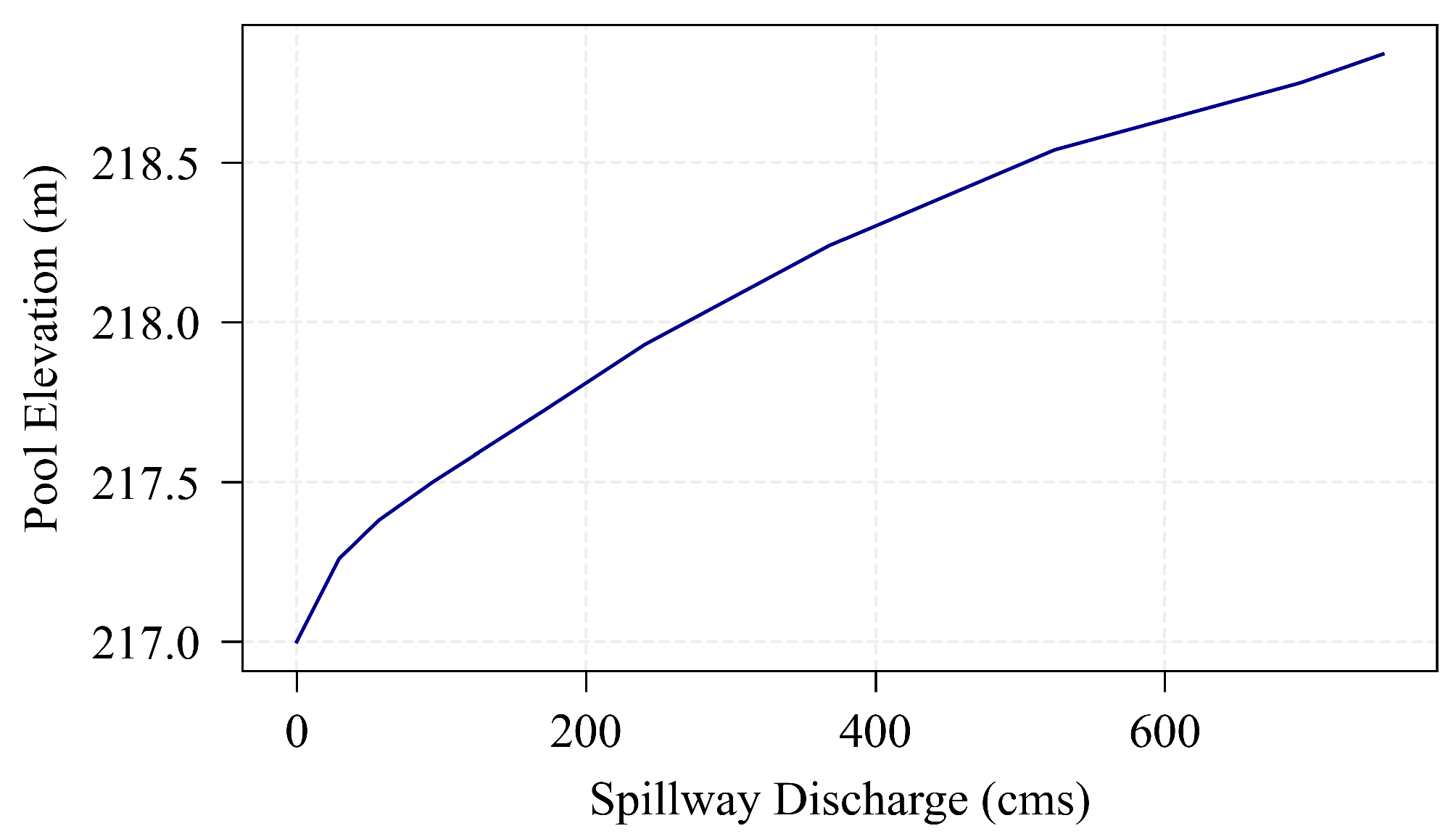
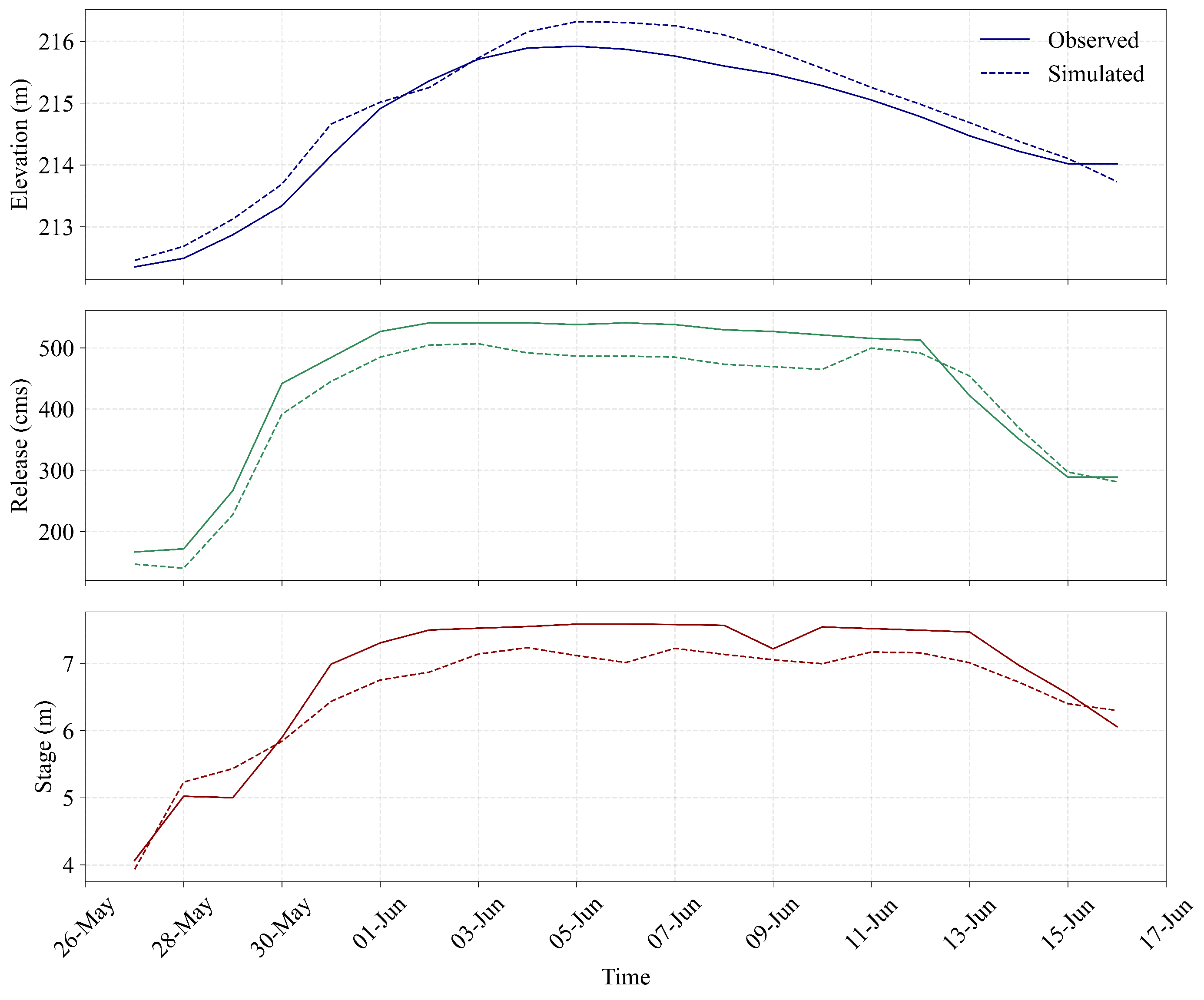
3.2. Model Calibration
- Reservoir pool-elevation time series,
- Release hydrographs from the reservoir,
- Stage hydrographs at downstream USGS stations, particularly the Iowa City station.
3.3. Hydraulic Simulations and Damage Estimation
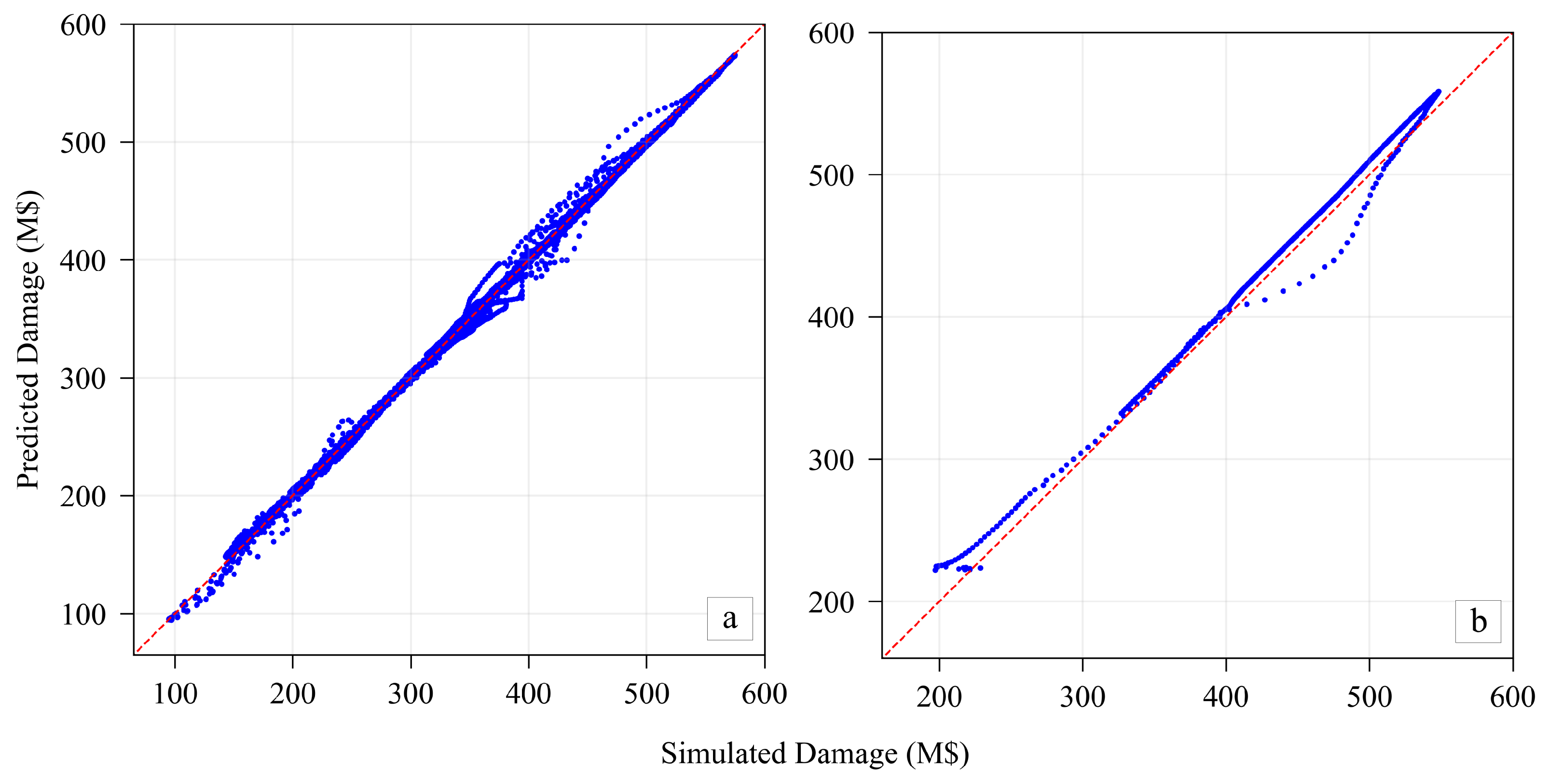
4. Data-Driven Flood Damage Prediction
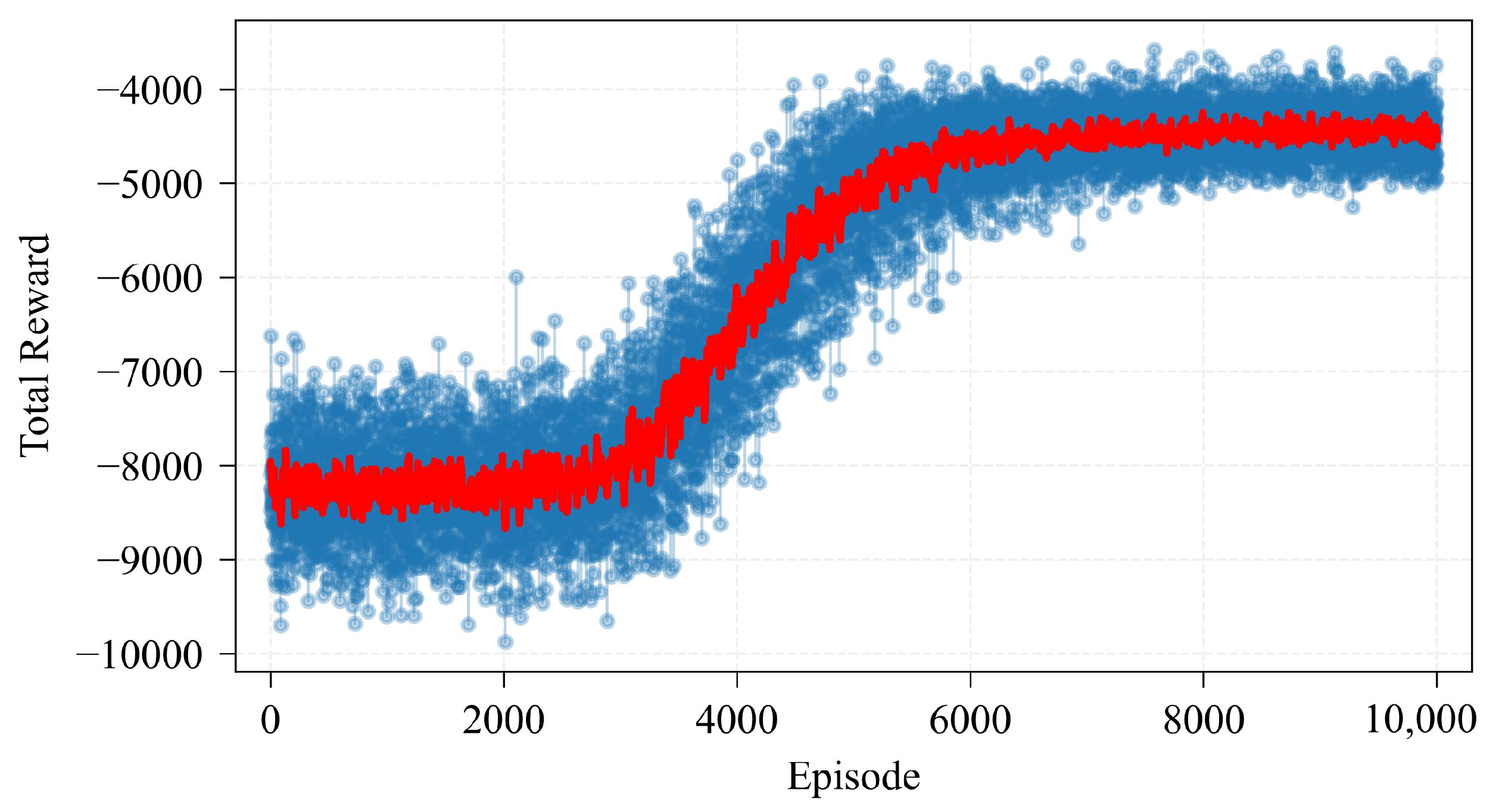
5. Policy Optimization
5.1. Flood Mitigation as an RL Problem
- is the predicted downstream damage (M$) at the current decision step, obtained as the maximum of the hourly damage predictions within the current 12-h action interval,
- is the damage at the previous decision step,
- and are the gate openings at the current and previous decision steps, respectively,
- is the mean inflow during the current decision step,
- is the 75th percentile inflow threshold computed from the inflow series,
- is an indicator function equal to 1 if the gate is opened during interval , and 0 otherwise,
- , , , and are weighting coefficients reflecting the trade-offs among objectives.
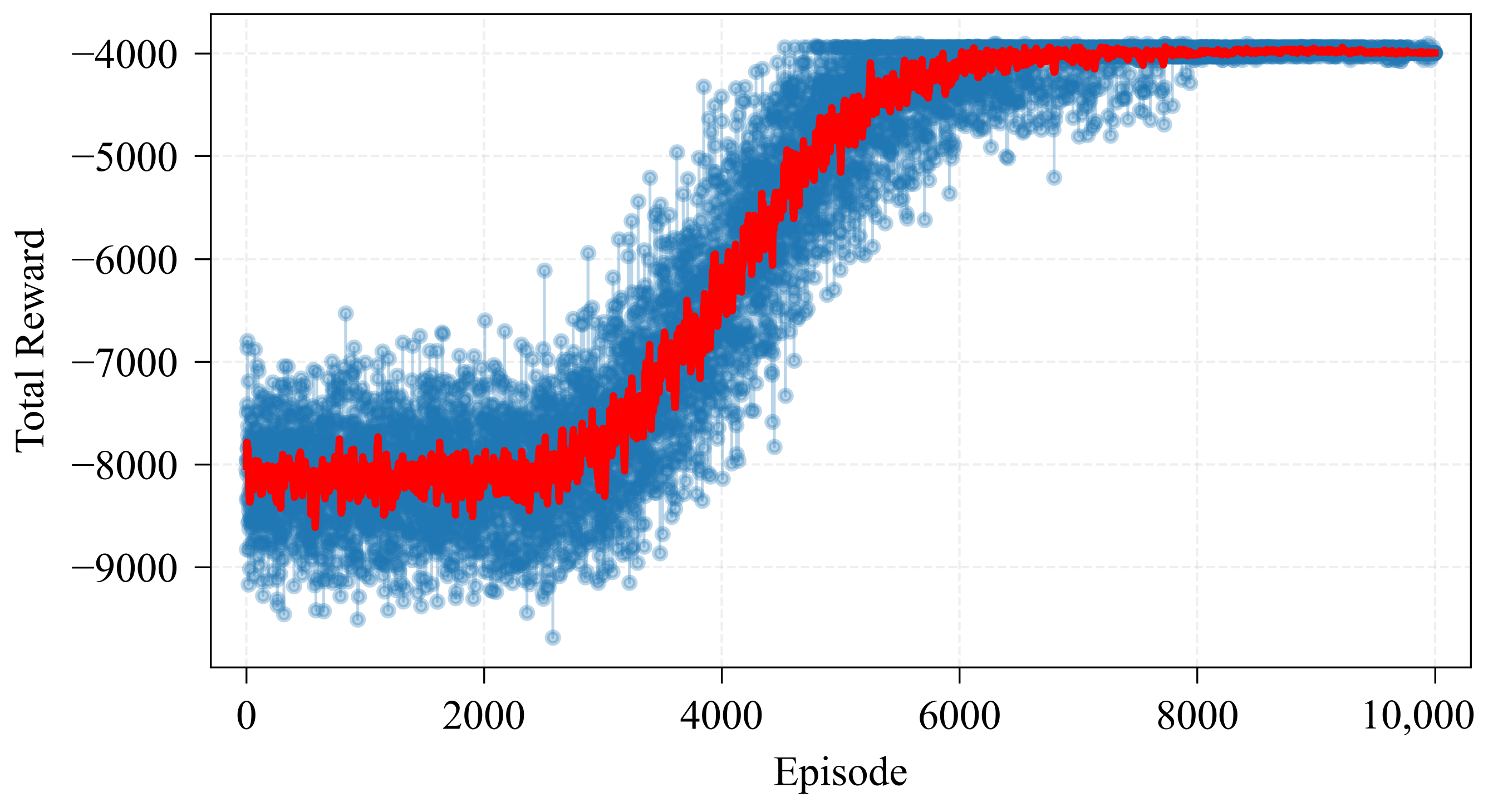
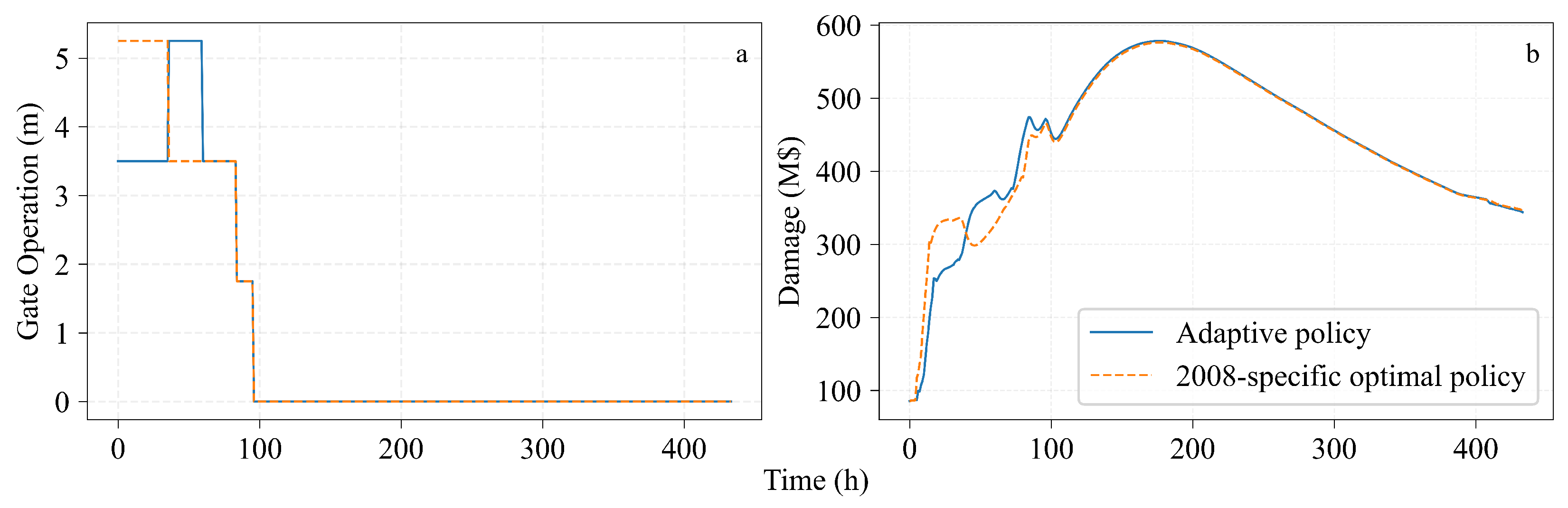
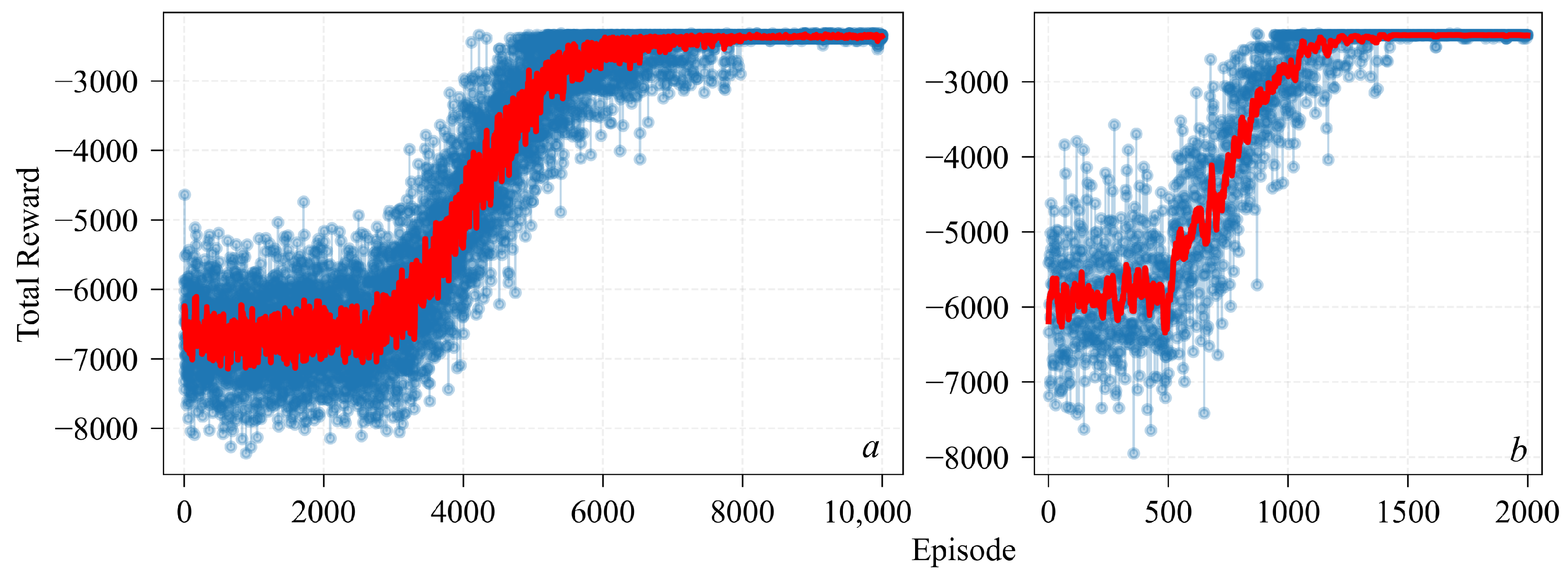
5.2. Learning for Optimal Policy
6. Policy Deployment and Evaluation
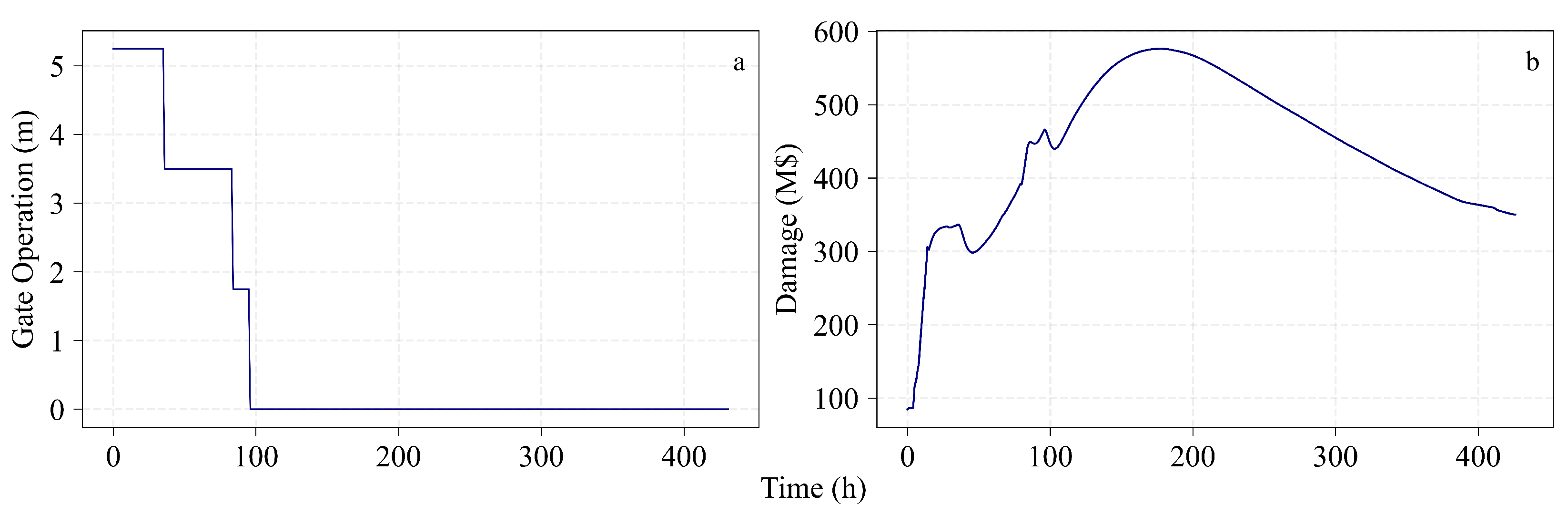
6.1. Policy Deployment
6.2. Policy Evaluation
6.3. GA Optimization
7. Adaptive Policies
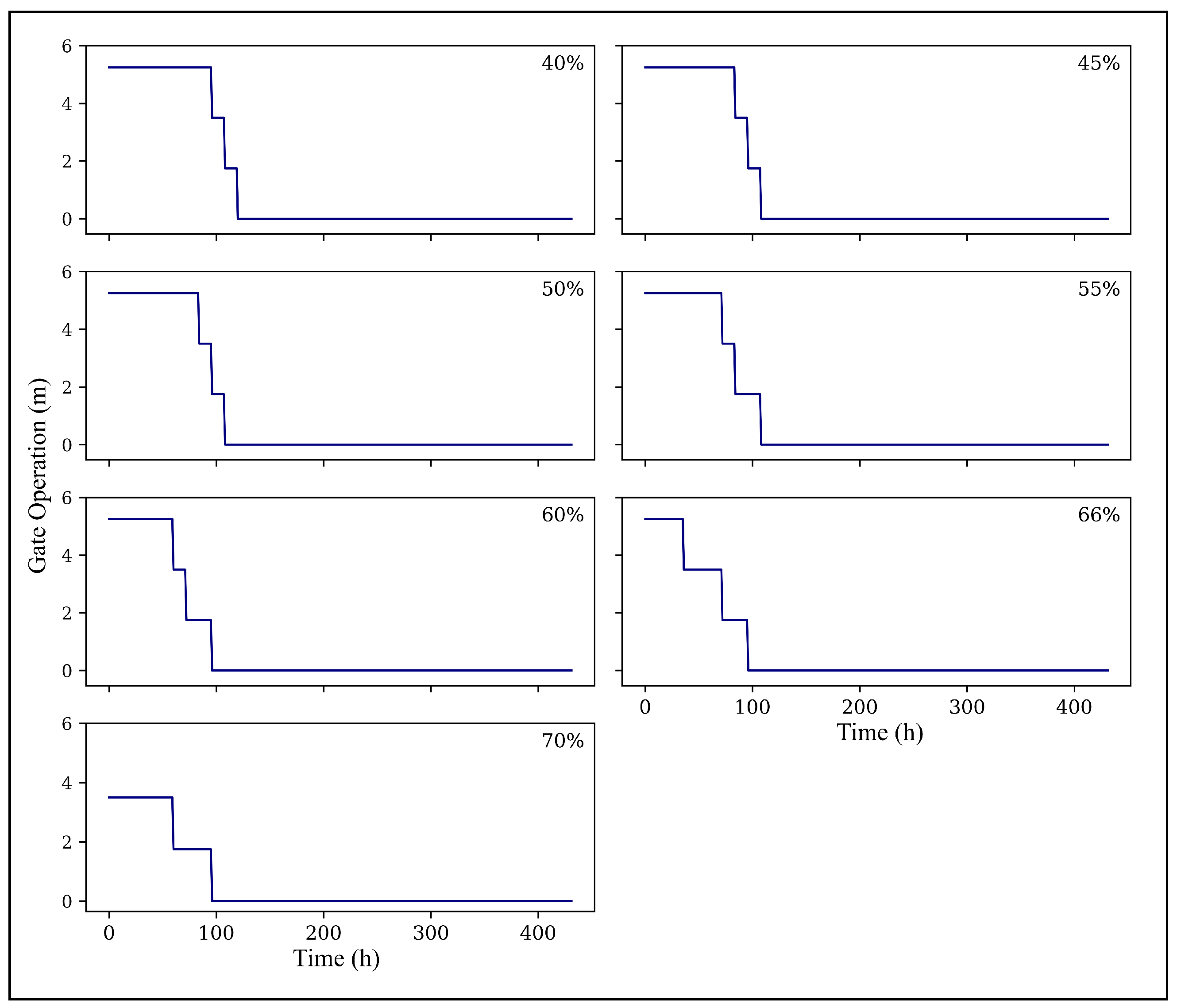
7.1. Initial Reservoir Storage Variation
- At 0.40–0.50 storage, the policy maintained higher gate openings for longer durations, taking advantage of surplus capacity to reduce downstream risk aggressively.
- At 0.65–0.70 storage, the agent initiated gate closures earlier to preserve control, yet still outperformed benchmark policies by carefully modulating releases before peak inflow.
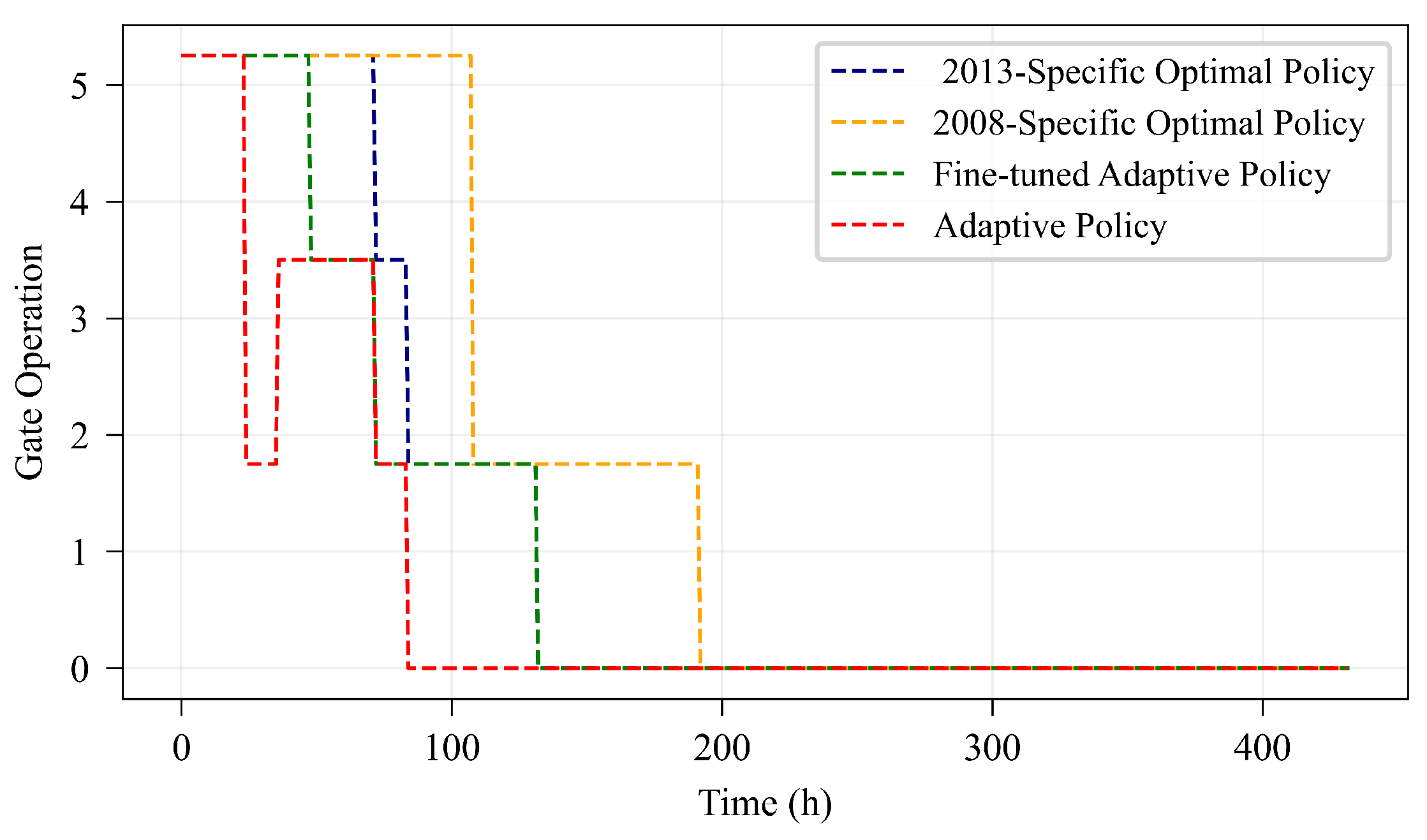
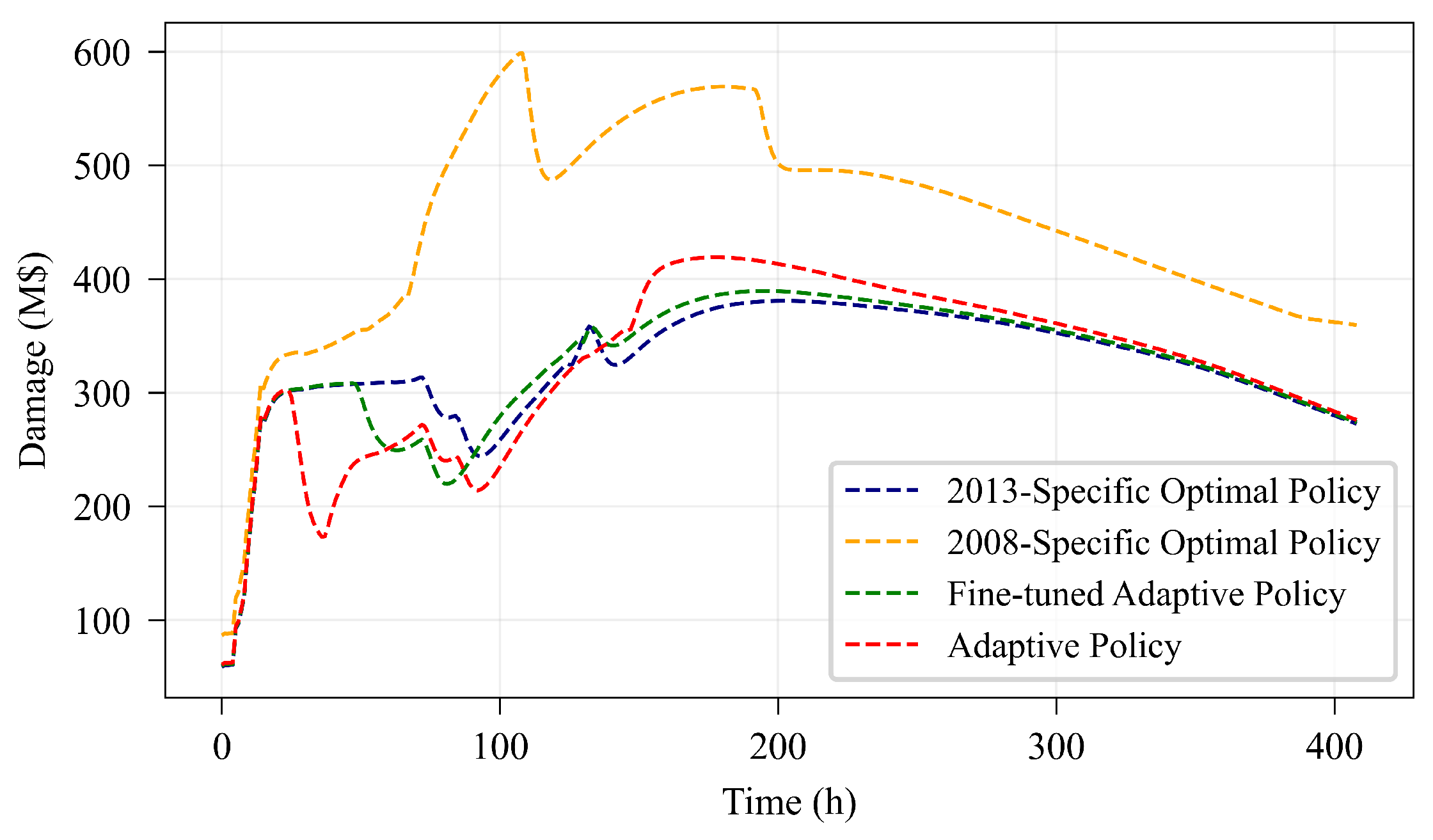
7.2. Adaptive Policy
7.3. Mitigation of the 2013 Iowa Flood
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rentschler, J.; Salhab, M.; Jafino, B.A. Flood Exposure and Poverty in 188 Countries. Nat. Commun. 2022, 13, 3527. [Google Scholar] [CrossRef]
- Tellman, B.; Sullivan, J.A.; Kuhn, C.; Kettner, A.J.; Doyle, C.S.; Brakenridge, G.R.; Erickson, T.A.; Slayback, D.A. Satellite Imaging Reveals Increased Proportion of Population Exposed to Floods. Nature 2021, 596, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future Flood Losses in Major Coastal Cities. Nat. Clim. Change 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, P.; Liu, D.; Zhang, X.; Xu, W.; Xiang, D. An analytical two-stage risk analysis model in the real-time reservoir operation. J. Hydrol. 2024, 645, 132256. [Google Scholar] [CrossRef]
- Li, H.; Liu, P.; Guo, S.; Cheng, L.; Yin, J. Climatic Control of Upper Yangtze River Flood Hazard Diminished by Reservoir Groups. Environ. Res. Lett. 2020, 15, 124013. [Google Scholar] [CrossRef]
- Mishra, V.; Aaadhar, S.; Shah, H.; Kumar, R.; Pattanaik, D.R.; Tiwari, A.D. The Kerala Flood of 2018: Combined Impact of Extreme Rainfall and Reservoir Storage. Hydrol. Earth Syst. Sci. Discuss. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Mahootchi, M.; Tizhoosh, H.R.; Ponnambalam, K.P. Reservoir Operation Optimization by Reinforcement Learning. J. Water Manag. Model. 2007, 15, R227-08. [Google Scholar] [CrossRef]
- Watts, R.J.; Richter, B.D.; Opperman, J.J.; Bowmer, K.H. Dam reoperation in an era of climate change. Mar. Freshw. Res. 2011, 62, 321–327. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.a.; Liu, W.; Wan, X.Y.; Yeh, W.W.G. A Multi-objective Risk Management Model for Real-time Flood Control Optimal Operation of a Parallel Reservoir System. J. Hydrol. 2020, 590, 125264. [Google Scholar] [CrossRef]
- Shenava, N.; Shourian, M. Optimal Reservoir Operation with Water Supply Enhancement and Flood Mitigation Objectives Using an Optimization–Simulation Approach. Water Resour. Manag. 2018, 32, 4393–4407. [Google Scholar] [CrossRef]
- Lai, V.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. A Review of Reservoir Operation Optimisations: From Traditional Models to Metaheuristic Algorithms. Arch. Comput. Methods Eng. 2022, 29, 3435–3457. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Ye, L.; Chen, L.; Wang, Q.; Dai, L.; Zhou, J.; Singh, V.P.; Huang, M.; Zhang, J. Risk Analysis of Flood Control Reservoir Operation Considering Multiple Uncertainties. J. Hydrol. 2018, 565, 672–684. [Google Scholar] [CrossRef]
- Wan, W.; Zhao, J.; Lund, J.R.; Zhao, T.; Lei, X.; Wang, H. Optimal Hedging Rule for Reservoir Refill. J. Water Resour. Plan. Manag. 2016, 142, 04016051. [Google Scholar] [CrossRef]
- Ming, B.; Liu, P.; Chang, J.; Wang, Y.; Huang, Q. Deriving Operating Rules of Pumped Water Storage Using Multiobjective Optimization: Case Study of the Han to Wei Interbasin Water Transfer Project, China. J. Water Resour. Plan. Manag. 2017, 143, 05017012. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Sule, B.F.; Loucks, D.P. Stochastic dynamic programming models for reservoir operation optimization. Water Resour. Res. 1984, 20, 1499–1505. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, C.; Peng, Y.; Fu, G.; Zhou, H. A Two-Stage Bayesian Stochastic Optimization Model for Cascaded Hydropower Systems Considering Varying Uncertainty of Flow Forecasts. Water Resour. Res. 2014, 50, 9267–9286. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Xu, W.; Wang, B. An Optimal Operation Model for Hydropower Stations Considering Inflow Forecasts with Different Lead-Times. Water Resour. Manag. 2019, 33, 173–188. [Google Scholar] [CrossRef]
- Xi, S.; Wang, B.; Liang, G.; Li, X.; Lou, L. Inter-basin Water Transfer-supply Model and Risk Analysis with Consideration of Rainfall Forecast Information. Sci. China Technol. Sci. 2010, 53, 3316–3323. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, X.; Niu, R.; Yang, K.; Zhao, L. The Assessment of Landslide Susceptibility Mapping Using Random Forest and Decision Tree Methods in the Three Gorges Reservoir Area, China. Environ. Earth Sci. 2017, 76, 405. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chang, J.X.; Huang, Q. Simulation with RBF Neural Network Model for Reservoir Operation Rules. Water Resour. Manag. 2010, 24, 2597–2610. [Google Scholar] [CrossRef]
- Quinn, J.D.; Reed, P.M.; Giuliani, M.; Castelletti, A. What Is Controlling Our Control Rules? Opening the Black Box of Multireservoir Operating Policies Using Time-Varying Sensitivity Analysis. Water Resour. Res. 2019, 55, 5962–5984. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal Operation of Multireservoir Systems: State-of-the-Art Review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Giuliani, M.; Lamontagne, J.R.; Reed, P.M.; Castelletti, A. A state-of-the-art review of optimal reservoir control for managing conflicting demands in a changing world. Water Resour. Res. 2021, 57, e2021WR029927. [Google Scholar] [CrossRef]
- Xu, J.; Qiao, J.; Sun, Q.; Shen, K. A Deep Reinforcement Learning Framework for Cascade Reservoir Operations Under Runoff Uncertainty. Water 2025, 17, 2324. [Google Scholar] [CrossRef]
- Saikai, Y.; Peake, A.; Chenu, K. Deep reinforcement learning for irrigation scheduling using high-dimensional sensor feedback. PLoS Water 2023, 2, e0000169. [Google Scholar] [CrossRef]
- Castelletti, A.; Corani, G.; Rizzoli, A.; Soncini-Sessa, R.; Weber, E. Reinforcement learning in the operational management of a water system. In IFAC Workshop on Modeling and Control in Environmental Issues; Keio University: Yokohama, Japan, 2002; pp. 325–330. [Google Scholar]
- Lee, J.H.; Labadie, J.W. Stochastic Optimization of Multireservoir Systems via Reinforcement Learning. Water Resour. Res. 2007, 43, W11408. [Google Scholar] [CrossRef]
- Riemer-Sørensen, S.; Rosenlund, G.H. Deep reinforcement learning for long term hydropower production scheduling. In Proceedings of the 2020 International Conference on SMART Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020; pp. 1–6. [Google Scholar]
- Wang, X.; Nair, T.; Li, H.; Wong, Y.S.R.; Kelkar, N.; Vaidyanathan, S.; Nayak, R.; An, B.; Krishnaswamy, J.; Tambe, M. Efficient reservoir management through deep reinforcement learning. arXiv 2020, arXiv:2012.03822. [Google Scholar] [CrossRef]
- Xu, W.; Meng, F.; Guo, W.; Li, X.; Fu, G. Deep reinforcement learning for optimal hydropower reservoir operation. J. Water Resour. Plan. Manag. 2021, 147, 04021045. [Google Scholar] [CrossRef]
- Tian, W.; Liao, Z.; Zhang, Z.; Wu, H.; Xin, K. Flooding and overflow mitigation using deep reinforcement learning based on Koopman operator of urban drainage systems. Water Resour. Res. 2022, 58, e2021WR030939. [Google Scholar] [CrossRef]
- Wu, R.; Wang, R.; Hao, J.; Wu, Q.; Wang, P. Multiobjective multihydropower reservoir operation optimization with transformer-based deep reinforcement learning. J. Hydrol. 2024, 632, 130904. [Google Scholar] [CrossRef]
- Tabas, S.S.; Samadi, V. Fill-and-spill: Deep reinforcement learning policy gradient methods for reservoir operation decision and control. J. Water Resour. Plan. Manag. 2024, 150, 04024022. [Google Scholar] [CrossRef]
- Luo, W.; Wang, C.; Zhang, Y.; Zhao, J.; Huang, Z.; Wang, J.; Zhang, C. A deep reinforcement learning approach for joint scheduling of cascade reservoir system. J. Hydrol. 2025, 651, 132515. [Google Scholar] [CrossRef]
- Castro-Freibott, R.; García-Sánchez, Á.; Espiga-Fernández, F.; González-Santander de la Cruz, G. Deep Reinforcement Learning for Intraday Multireservoir Hydropower Management. Mathematics 2025, 13, 151. [Google Scholar] [CrossRef]
- Phankamolsil, Y.; Rittima, A.; Sawangphol, W.; Kraisangka, J.; Tabucanon, A.S.; Talaluxmana, Y.; Vudhivanich, V. Deep Reinforcement Learning for Multiple Reservoir Operation Planning in the Chao Phraya River Basin. Model. Earth Syst. Environ. 2025, 11, 102. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers, Hydrologic Engineering Center (HEC). HEC-RAS River Analysis System: Hydraulic Reference Manual; Technical Report; U.S. Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2021. [Google Scholar]
- Wing, O.E.J.; Pinter, N.; Bates, P.D.; Kousky, C. New insights into US flood vulnerability revealed from flood insurance big data. Nat. Commun. 2020, 11, 1444. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers, Hydrologic Engineering Center (HEC). HEC-FIA Flood Impact Analysis User’s Manual, Version 3.3 ed.; U.S. Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2020. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the EMNLP, Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A Transformer-Based Framework for Multivariate Time Series Representation Learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 2114–2124. [Google Scholar] [CrossRef]
- Grigsby, J.; Wang, Z.; Nguyen, N.; Qi, Y. Long-Range Transformers for Dynamic Spatiotemporal Forecasting. arXiv 2021, arXiv:2109.12218. [Google Scholar]
- Wang, S.; Lin, Y.; Jia, Y.; Sun, J.; Yang, Z. Unveiling the Multi-Dimensional Spatio-Temporal Fusion Transformer (MDSTFT): A Revolutionary Deep Learning Framework for Enhanced Multi-Variate Time Series Forecasting. IEEE Access 2024, 12, 115895–115904. [Google Scholar] [CrossRef]
- Keles, F.D.; Wijewardena, P.M.; Hegde, C. On the computational complexity of self-attention. In Proceedings of the International Conference on Algorithmic Learning Theory, Singapore, 20–23 February 2023; pp. 597–619. [Google Scholar]
- Liu, Y.; Xin, Y.; Yin, C. A Transformer-based Method to Simulate Multi-scale Soil Moisture. J. Hydrol. 2025, 655, 132900. [Google Scholar] [CrossRef]
- Jiang, M.; Weng, B.; Chen, J.; Huang, T.; Ye, F.; You, L. Transformer-enhanced Spatiotemporal Neural Network for Post-processing of Precipitation Forecasts. J. Hydrol. 2024, 630, 130720. [Google Scholar] [CrossRef]
- Jin, H.; Lu, H.; Zhao, Y.; Zhu, Z.; Yan, W.; Yang, Q.; Zhang, S. Integration of an Improved Transformer with Physical Models for the Spatiotemporal Simulation of Urban Flooding Depths. J. Hydrol. Reg. Stud. 2024, 51, 101627. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; The MIT Press: London, UK, 2018. [Google Scholar]
- Howard, R.A. Dynamic Programming and Markov Processes; Technology Press and Wiley: New York, NY, USA, 1960. [Google Scholar]
- Li, J.; Cai, M.; Kan, Z.; Xiao, S. Model-free reinforcement learning for motion planning of autonomous agents with complex tasks in partially observable environments. Auton. Agents Multi-Agent Syst. 2024, 38, 14. [Google Scholar] [CrossRef]
- Wang, Z.; Jha, K.; Xiao, S. Continual reinforcement learning for intelligent agricultural management under climate changes. Comput. Mater. Contin. 2024, 81, 1319–1336. [Google Scholar] [CrossRef]
- Kurniawati, H. Partially Observable Markov Decision Processes and robotics. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 253–277. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Cai, M.; Xiao, S. Reinforcement learning-based motion planning in partially observable environments under ethical constraints. AI Ethics 2025, 5, 1047–1067. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, S.; Wang, J.; Parab, A.; Patel, S. Reinforcement Learning-Based Agricultural Fertilization and Irrigation Considering N2O Emissions and Uncertain Climate Variability. AgriEngineering 2025, 7, 252. [Google Scholar] [CrossRef]
- Alabbad, Y.; Demir, I. Comprehensive flood vulnerability analysis in urban communities: Iowa case study. Int. J. Disaster Risk Reduct. 2022, 74, 102955. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. Coralville Lake Water Control Update Report with Integrated Environmental Assessment; Technical Report; US Army Corps of Engineers: Davis, CA, USA, 2022. [Google Scholar]
- U.S. Army Corps of Engineers. RiverGages.com: USACE Water Control Data. 2024. Available online: https://rivergages.mvr.usace.army.mil/WaterControl/shefgraph-historic.cfm?sid=IOWI4 (accessed on 3 August 2025).
- Tofighi, S.; Gurbuz, F.; Mantilla, R.; Xiao, S. Advancing Machine Learning-Based Streamflow Prediction Through Event Greedy Sampling, Asymmetric Loss Function, and Rainfall Forecasting Uncertainty; SSRN: Rochester, NY, USA, 2024. [Google Scholar] [CrossRef]
- Chen, Y.; Deierling, P.; Xiao, S. Exploring active learning strategies for predictive models in mechanics of materials. Appl. Phys. A Mater. Sci. Process. 2024, 130, 588. [Google Scholar] [CrossRef]






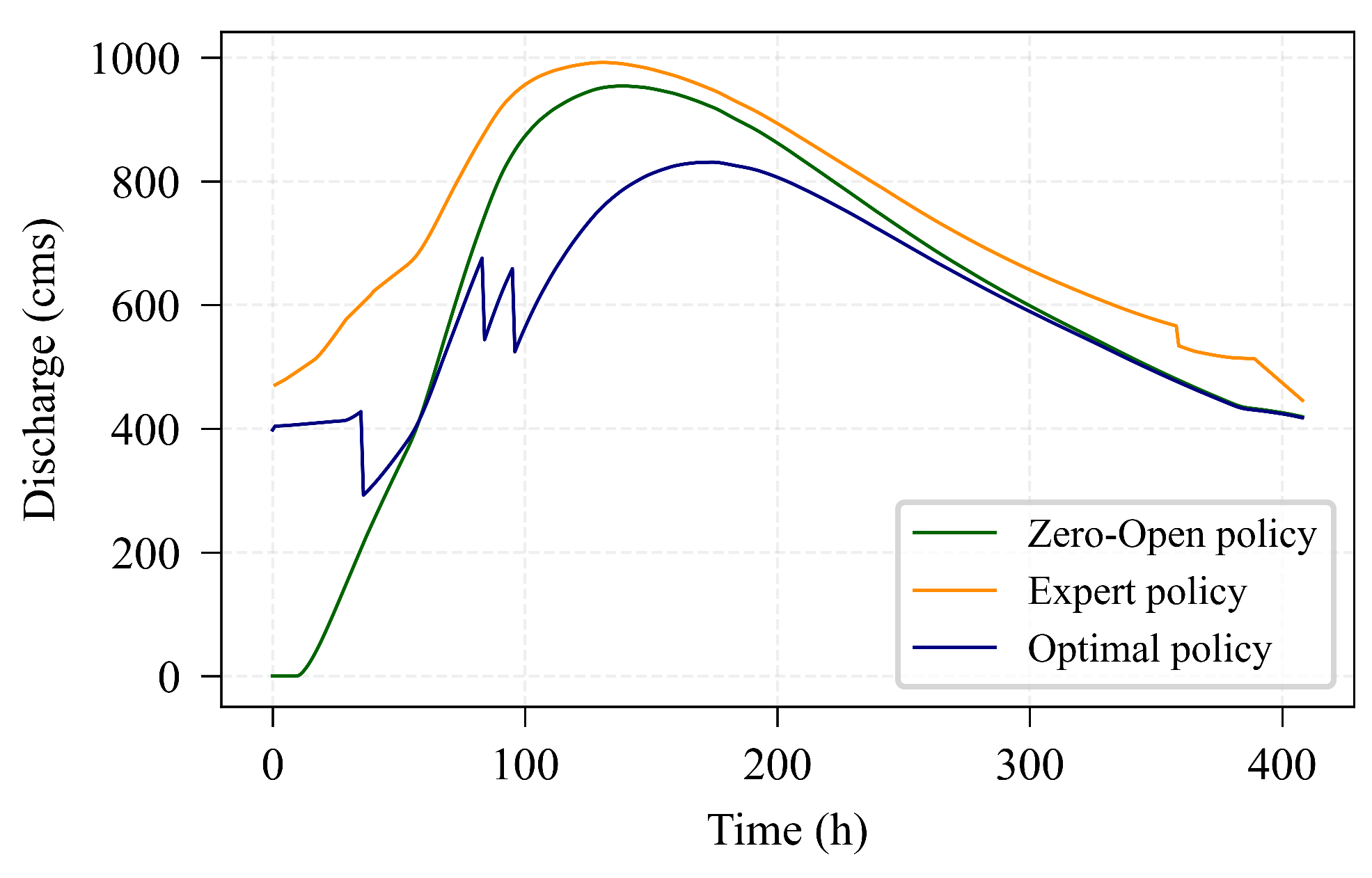
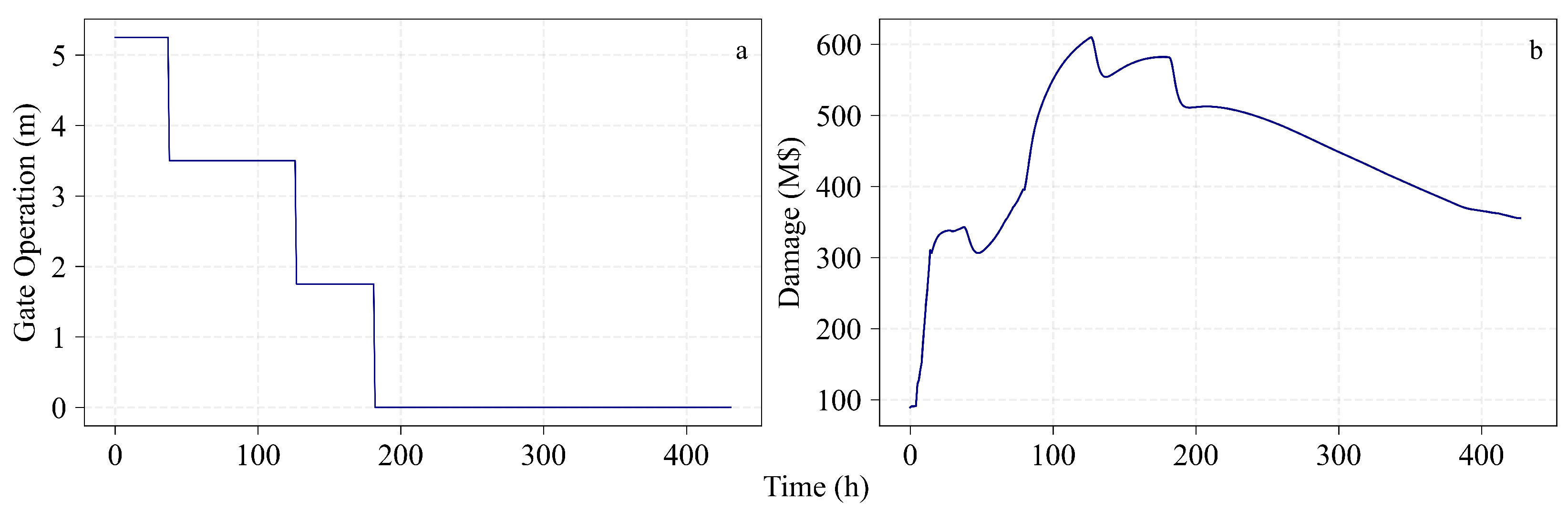
| Metric | Optimal Policy | Expert Policy | Zero-Open Policy |
|---|---|---|---|
| Peak damage (M$) | 576 (0.8936) | 644 (1.0) | 649 (1.0078) |
| Time-integrated damage (M$·h) | 181,330 (0.8100) | 223,853 (1.0) | 196,798 (0.8791) |
| Metric | Optimal Policy | Expert Policy | Zero-Open Policy |
|---|---|---|---|
| (cms) | 825 | 992 | 950 |
| (h) | 176 | 138 | 145 |
| Gate Operation | Peak Damage Ratio | Time-Integrated Damage Ratio |
|---|---|---|
| Expert policy | 1.00 | 1.00 |
| Learning-based optimal policy | 0.8936 | 0.8100 |
| GA-optimized strategy | 0.9410 | 0.8180 |
| Initial Reservoir Storage | Optimal Policy | |
|---|---|---|
| (% of the Max) | Peak Damage Ratio | Time-Integrated Damage Ratio |
| 40 | 0.8744 | 0.8097 |
| 45 | 0.8621 | 0.8093 |
| 50 | 0.8621 | 0.8093 |
| 55 | 0.8736 | 0.8096 |
| 60 | 0.8912 | 0.8101 |
| 66 | 0.8936 | 0.8100 |
| 70 | 0.9154 | 0.8099 |
| Policy | Peak Damage Ratio | Time-Integrated Damage Ratio |
|---|---|---|
| Expert policy | 1.00 | 1.00 |
| Adaptive | 0.8974 | 0.8109 |
| 2008-specific | 0.8936 | 0.8100 |
| Policy | Peak Damage Ratio | Time-Integrated Damage Ratio |
|---|---|---|
| Expert policy | 1.0 | 1.0 |
| 2013-specific optimal policy | 0.7265 | 0.7987 |
| Adaptive policy | 0.8020 | 0.7989 |
| Fine-tuned Adaptive policy | 0.7451 | 0.7994 |
| 2008-specific optimal policy | 1.0998 | 1.1457 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tofighi, S.; Gurbuz, F.; Mantilla, R.; Xiao, S. A Data-Driven Framework for Flood Mitigation: Transformer-Based Damage Prediction and Reinforcement Learning for Reservoir Operations. Water 2025, 17, 3024. https://doi.org/10.3390/w17203024
Tofighi S, Gurbuz F, Mantilla R, Xiao S. A Data-Driven Framework for Flood Mitigation: Transformer-Based Damage Prediction and Reinforcement Learning for Reservoir Operations. Water. 2025; 17(20):3024. https://doi.org/10.3390/w17203024
Chicago/Turabian StyleTofighi, Soheyla, Faruk Gurbuz, Ricardo Mantilla, and Shaoping Xiao. 2025. "A Data-Driven Framework for Flood Mitigation: Transformer-Based Damage Prediction and Reinforcement Learning for Reservoir Operations" Water 17, no. 20: 3024. https://doi.org/10.3390/w17203024
APA StyleTofighi, S., Gurbuz, F., Mantilla, R., & Xiao, S. (2025). A Data-Driven Framework for Flood Mitigation: Transformer-Based Damage Prediction and Reinforcement Learning for Reservoir Operations. Water, 17(20), 3024. https://doi.org/10.3390/w17203024









