Research on the Influence of Groundwater Level Dynamic Rising Process on Buildings Based on Numerical Simulation

Abstract

In the North China region, measures such as restricting groundwater extraction and promoting cross-basin water diversion have effectively alleviated the problem of excessive groundwater exploitation. Nevertheless, the continuous rise in groundwater levels may alter the mechanical properties of foundation soil layers, potentially leading to geotechnical hazards such as foundation instability and the uneven settlement of structures. This study employs FLAC3D software to simulate the displacement, deformation, and stress–strain behavior of buildings and their surrounding strata during the dynamic recovery of groundwater levels, aiming to assess the impact of this process on structural integrity. Research findings indicate that the maximum building settlement within the study area reaches 54.8 mm, with a maximum inter-column differential settlement of 8.9 mm and a peak settlement rate of 0.16 mm/day. In regions where differential settlement aligns with the interface between the floor slab and walls, tensile stress concentrations are observed. The maximum tensile stress in these zones increases progressively from 1.8 MPa to 2.19 MPa, suggesting a potential risk of tensile cracking in the concrete structures. The influence of groundwater level recovery on buildings exhibits distinct phase characteristics, and the response mechanisms of different lithological strata vary significantly. Therefore, particular attention should be given to the physical properties and mechanical behavior of strata that are highly sensitive to variations in moisture content. These findings hold significant reference value for the sustainable development and utilization of underground space in the North China region.

1. Introduction

In China, especially in the cities in the North China region, the acceleration of urbanization has driven the development of underground engineering towards larger scales and deeper excavation. This has given rise to a series of engineering problems related to groundwater, which have become significant challenges, restricting the safe development of urban underground space. In recent years, with the Chinese government’s increasing emphasis on groundwater resources, the groundwater levels in many regions of China have witnessed a notable rebound [1,2,3]. Although the rebound of groundwater levels effectively improves the regional hydrological cycle and promotes ecological restoration, due to variations in the rebound speed, amplitude, and driving factors, it poses potential risks to the safety of buildings [4,5,6]. For example, the rising groundwater level may increase the saturation of the stratum, thereby softening the soil structure and triggering the building settlement. Simultaneously, it may also enhance the buoyant force, leading to damage to the building structure [7,8]. Consequently, establishing a theory for the coordinated control of groundwater dynamic regulation and the safety of underground building structures has become a crucial scientific issue for ensuring the safe operation and maintenance of underground engineering.

Current research lacks in-depth investigations into how the rebound of groundwater levels specifically impacts buildings, and thus, fails to offer sufficient theoretical support for resolving specific engineering problems. As a result, analyzing the influence of groundwater level rebound on buildings using numerical simulation methods has emerged as a new research focus at present. For instance, Chang [9], Chen [10], Nguyen [11], and Lai [12], have, respectively, employed numerical simulation methods to analyze the impacts of groundwater level rise on tunnel structures, caused by factors such as blocked drainage blind pipes, sea-level rise, and construction activities. Zou has utilized numerical simulation methods to analyze the influence of high-water-head pressure on hydropower station tunnel projects [13]. However, in the current stage of research, static groundwater level boundary conditions are mostly adopted, which only simulate the transient response under a single water level condition. These studies lack dynamic tracking of periodic groundwater level fluctuations and thus fail to explain the cumulative damage effect on buildings caused by repeated deformations that are induced by such periodic fluctuations. Furthermore, the special geological structure of silty soil and sandy clay layers in the North China Plain is inherently different from that in other regions; the direct application of theories developed for other regions will inevitably lead to misjudgments in engineering practice.

For many years, the groundwater levels in Hebei Province have been on a long-term downward trend. During many engineering investigation and design phases, the potential future rebound of groundwater levels was not fully taken into account, leaving latent hazards in engineering structure and protection designs. Particularly under extreme weather conditions, such as the heavy rainfall events in Hebei Province in 2016 and 2021, seepage problems caused by rising groundwater levels have occurred in some areas. These problems include water infiltration in some garages, flooding, and cracking of the floor slab and walls. This paper takes the dynamic recovery of groundwater levels in the North China Plain as the research background, breaks through the limitations of the traditional static water level assumption, focuses on the sensitive stratum medium of the silt layer under long-term dewatering conditions, sets the water level boundary conditions, based on the accumulated groundwater level monitoring data in this area for many years, and uses the FLAC3D three-dimensional explicit finite difference software to construct a multi-field coupling numerical model of groundwater and building structures. It systematically studies the influential law of the entire process of dynamic water level recovery on buildings, and reveals the cumulative damage mechanism of building structures under unsteady water level conditions. It clarifies the evolution characteristics of the stress concentration area of underground structures, providing targeted theoretical basis and engineering practice reference for the safety prevention and control of buildings in the groundwater level recovery area of the North China Plain.

2. Study Area

Shijiazhuang is located on the western edge of the North China Plain. The per capita water resources in this area are approximately 157 m³, making it an extremely water-scarce region. Previously, the economic model of this area was mainly agricultural production. However, due to the severe shortage of water resources, agricultural irrigation has long relied on the exploitation of groundwater, leading to a continuous decline in the groundwater level. In recent years, with the acceleration of urbanization and the transformation and upgrading of the industrial structure, the demand for agricultural water has decreased year by year. At the same time, the successive commissioning of major water conservancy projects such as the South-to-North Water Diversion Project has effectively reduced the exploitation of groundwater, promoting a gradual rise in the groundwater level. In 2021, the annual precipitation in this area reached its highest level since 1996, with the maximum annual precipitation recorded at the Luquan District rainfall station being 1028 mm. According to the water resources bulletin released by Hebei Province in 2024, the shallow groundwater levels in 129 counties across the province generally showed an upward trend.

2.1. Hydrogeological Conditions

In the study area, groundwater is primarily categorized into two types: Quaternary loose rock pore water and carbonate rock karst fissure water. Pore water is predominantly found within the coarse sand and gravel strata of the Quaternary gravel-bearing pebbles. In contrast, the karst water is primarily located within the Cambrian oolitic limestone and the formation chert-bearing dolomite, as illustrated in Figure 1. Given that the karst aquifer is situated at a depth exceeding 100 m and is subject to regional structural influences, it exhibits minimal direct hydraulic connectivity with the pore water. Consequently, it does not significantly affect the shallow groundwater level variations examined in this study, rendering further discussion unnecessary. Precipitation infiltration serves as the principal source of pore water recharge, contributing approximately 56% of the total recharge, while lateral recharge constitutes about 38%. The groundwater flow in the region progresses from west to east, characterized by a gradient of approximately 6.1‰ and a gentle flow rate.

2.2. Engineering Geological Conditions

Through systematic drilling investigations, this study obtained the spatial distribution characteristics of the strata in the study area. Based on the vertical sequence of the strata from top to bottom, they can be classified into five distinct engineering geological layer units: the fill layer, the loess-like silt layer, the silt layer, the silty clay layer, and the gravel layer. The detailed stratigraphic profile is presented in Figure 2, while the engineering geological properties of each layer are summarized in

Table 1. Engineering geological characteristics of each soil layer.

Serial Number	Layer	Thickness (m)	Characterization
①	Miscellaneous fill	0.60–3.90	The soil is uneven, loose, slightly wet, containing a large amount of bricks and ash, and has poor engineering properties.
②	Loess-like silt	2.10–4.70	Mainly composed of powder particles, containing clay and sand particles, with low strength and toughness.
③	Silt	2.00–5.30	Mainly composed of powder particles, with low strength and toughness, slightly wet, moderately dense.
④	Silty clay	1.50–8.20	Mainly composed of clay and powder particles, locally containing a small amount of sand and gravel, soft plastic, moderate strength and toughness.
⑤	Gravel	-	The original rock composition is mainly composed of limestone and sandstone, accounting for about 50%. The particle size is generally between 2 cm and 6 cm, with a maximum particle size of 8 cm.

.

2.3. Groundwater Level Rise

Based on the dynamic groundwater level data obtained from monitoring points within the study area, it is observed that the groundwater level exhibits a general upward trend. The annual fluctuations in water level are minimal, indicating a relatively stable increase. Notably, in 2021, there was a marked rise in groundwater levels, with an increase exceeding 6 m. Despite this significant change, the burial depth of the water level remained relatively stable at approximately −5 m, as illustrated in Figure 3.

3. Methods

This study primarily addresses the challenge of determining whether the proposed numerical simulation method can accurately capture the effects of long-term dynamic changes in groundwater levels on buildings, thereby ensuring that the simulation results possess both reference value and theoretical significance. Consequently, an in-depth analysis of the numerical simulation method was conducted, taking into account the specific conditions of the research area. This led to the development of a theoretical framework for numerical simulation that is tailored to assess the impact of rising groundwater levels on buildings within the study region.

3.1. Selection of Numerical Simulation Software

This article employs the FLAC3D numerical simulation method to analyze the impact of groundwater level rise on buildings, due to several compelling reasons. Firstly, the FLAC3D method is highly regarded in geotechnical engineering applications, significantly contributing to analyses and research related to foundation deformation, building structure deformation, slope excavation stability, and anchor support stability, among other areas [14,15,16,17,18]. Furthermore, in engineering challenges involving fluid–structure interaction, FLAC3D 6.0 software is based on the explicit finite difference method and can simulate the interaction between fluids and solids by coupling algorithms that combine fluid motion equations with solid mechanics equations, thereby providing valuable insights into issues such as the effects of groundwater seepage on the stability of rock and soil, as well as structural stability [19,20,21,22,23,24]. Consequently, this study employs the FLAC3D numerical simulation technique to investigate the mechanisms by which rising groundwater levels affect buildings. Relevant research findings are referenced to enhance the credibility of the results, while this study also represents an innovative effort to broaden the application scope of FLAC3D. This approach aims to develop a novel theoretical framework for future analyses and research concerning the impact of groundwater level increases on engineering construction.

3.2. Numerical Simulation Scheme Analysis

The potential impact of rising groundwater levels on buildings can be categorized into three primary aspects [25]. First, an increase in groundwater levels can create a significant hydraulic head difference, resulting in pore water undergoing pressured seepage flow. This dynamic water pressure can exceed the gravitational or cohesive forces of soil particles, leading to piping and subsequent seepage damage. Second, as groundwater levels rise, previously unsaturated soil above the water table becomes saturated, altering its physical and mechanical properties. This transformation results in a reduction in the soil’s bearing capacity and strength, potentially causing deformation and structural damage to buildings. Thirdly, when the groundwater level rises above the bottom plate of a building’s foundation, the buoyant force acting on the foundation increases. This buoyancy is equivalent to the weight of the foundation displacing the groundwater. Concurrently, the soil surrounding the building’s underground structure transitions from an unsaturated to a saturated state. As a result, the pore water pressure progressively increases, and this static water pressure exerts lateral forces on the walls of the building’s underground structure.

In the study area, the minimal water gradient and slow runoff velocity, combined with the fact that groundwater level fluctuations are primarily influenced by precipitation, result in a consistent and gradual upward trend. Additionally, typical civil structures in the area have relatively small spans and shallow foundation depths, exerting minimal influence on the seepage field. Consequently, significant differences in hydraulic head or dynamic water pressure around these structures are unlikely. Thus, when evaluating the impact of rising groundwater levels on buildings within the study area, the effects of dynamic water pressure can be disregarded. However, soil saturation emerges as a critical variable in assessing the potential impacts of groundwater level rise on buildings. On a macro scale, the incremental rise in groundwater level affects buildings, while on a micro scale, the soil transitions from an unsaturated to a saturated state. This transition alters the mechanical properties of the soil, including pore water pressure, effective stress, soil structure, and hydrostatic pressure, thereby influencing the structural integrity and stability of buildings [26,27]. Therefore, in this numerical simulation study, the dynamic elevation process of the groundwater level is analogous to modeling the transition of a specific soil layer thickness from an unsaturated to a saturated state. The change in water level height corresponds to the thickness of the soil layer that undergoes this “unsaturated to saturated” transformation.

This study primarily investigates the impact of groundwater level fluctuations on the bearing capacity and strength variations in foundation soils: specifically, silt and silty clay. Additionally, it examines the plastic deformation of subterranean building structures, including concrete engineering, and the surrounding rock and soil. To this end, the Mohr–Coulomb constitutive model has been employed to analyze and assess potential deformation and failure in buildings, due to rising groundwater levels. This analysis is grounded in the Mohr–Coulomb criterion and the maximum tensile stress criterion.

3.3. Construction of 3D Numerical Simulation Model

The subject of this study is an eight-story high-rise residential building, located within the designated research area. Based on the construction specifications, the building employs a raft foundation composed of a uniformly thick reinforced concrete slab, measuring 500 mm in thickness, with foundation dimensions of 42 m × 18 m, a burial depth of 8 m, and a foundation-bearing layer consisting of the ③ silt layer. The underground wall is constructed from cast-in-place concrete, featuring a thickness of 400 mm, an anti-seepage grade of P6, and a permeability coefficient of ≤10⁻⁹ cm/s. The utilization of a raft foundation facilitates an even distribution of the building load, which is approximately 200 kPa. Detailed data are presented in

Table 2. Construction information of the researched building.

Material	Foundation Thickness (mm)	Wall Thickness (mm)	Foundation Size (m)	Foundation Depth (m)	Concrete Strength (MPa)	Anti Leakage Grade (MPa)	Permeability Coefficient (cm/s)	Building Load (Kpa)
Concrete	500	400	42 × 18	8	30	0.6	10−9	200

.

The physical and mechanical parameters, including Poisson’s ratio, density, porosity, elastic modulus, cohesion, and internal friction angle for each stratum, necessary for numerical simulation methods, were derived from in situ experiments and geotechnical tests. The original in situ soil samples were obtained by drilling, sealed promptly, and sent to the laboratory for the determination of soil-layer physical parameters. During the sampling process, disturbance was strictly controlled to ensure the representativeness of the samples. The initial saturation was determined by the drying weighing method. Poisson’s ratio and elastic modulus were calculated based on indoor triaxial compression test data, combined with Hooke’s law. Cohesion and the internal friction angle were determined through indoor direct shear tests and according to the Coulomb strength criterion. The permeability coefficient (k) was mainly determined by on-site unstable flow pumping tests, and the permeability coefficients of each soil layer were quantitatively calculated using the linear graphical method. Furthermore, since this study primarily simulates the process of groundwater level rise by equivalently modeling the transition from an unsaturated to a saturated state of the strata, it is essential to acquire additional “initial saturation” parameters for each stratum. The detailed data are presented in

Table 3. Physical and mechanical parameters of each soil layer.

Layer	Initial Saturation	Poisson’s Ratio	Density	Void Ratio	Elastic Modulus	Cohesion	Internal Friction	Permeability Coefficient
	%	-	g/cm3	-	MPa	kPa	°	cm/s
② Loess-like silt	67.8	0.31	1.86	0.92	12.2	23.3	25.5	3.8 × 10−4
③ Silt	50.5	0.30	1.88	0.88	13.3	20.19	24.9	8.8 × 10−5
④ Silty clay	82.4	0.32	2.04	0.82	18.2	22.5	19.7	3.2 × 10−5
⑤ Gravels	Saturated	0.35	2.20	0.5	30.0	40	35	1 × 10−3

.

Drawing upon comprehensive data on engineering geological conditions, geological physical and mechanical properties, and construction details from the study area, a three-dimensional geological model has been developed. The numerical model of the underground structure of the building is constructed, based on the information of the foundation size and burial depth. It mainly consists of two parts: the wall and the base plate. The wall part adopts a grid unit of 1 m × 0.4 m × 0.5 m, and the base plate part adopts a grid unit of 1 m × 1 m × 0.5 m. The numerical model size of the stratum area is 126 m × 72 m × 40 m, and the overall grid unit is 2 m × 2 m × 2 m. Due to the difference in grid scale between the stratum and the underground structure, the grid of the stratum around the building was locally encrypted, and the geometric shape of the model was optimized. Sharp corners were rounded to avoid stress concentration or stress singularity. The entire numerical model contains 97,875 zones and 104,156 grid points.

This numerical simulation adopts the fluid–solid coupling method and comprehensively considers the seepage effect of groundwater. Therefore, both mechanical boundary conditions and seepage boundary conditions need to be applied simultaneously in the model. The mechanical boundary conditions are achieved through velocity constraints: the bottom boundary of the model has a velocity of 0 in the X, Y, and Z directions; the left and right boundaries have velocity constraints in the horizontal X direction (velocity = 0); the front and back boundaries have velocity constraints in the horizontal Y direction (velocity = 0); and the top boundary is set as a free boundary, allowing free deformation. The seepage boundary conditions are set as follows: the top of the model is a permeable boundary, allowing free fluid exchange between nodes and the outside; the front, back, and bottom boundaries are impermeable boundaries with no fluid exchange; the left and right boundaries are set as constant head inflow boundaries to simulate the continuous water-injection process, thereby causing the groundwater level to rise.

This model is bifurcated into two principal components: the geological strata and the subterranean structural elements of the building. Given the significant influence of groundwater level fluctuations on the foundations and walls of these underground structures, this paper primarily focuses on examining the direct impacts of rising groundwater levels on these components. The potential transmission effects of deformation in the walls and foundations on other structural elements of the buildings have not been explored in this study. Consequently, the building structure has been simplified, as depicted in Figure 4.

3.4. Simulation Method for the Dynamic Rise in Groundwater Level

To investigate the effects of the long-term dynamic rise in groundwater levels on buildings, this study encompasses a period spanning nearly a decade, from June 2015 to December 2024. Given the seasonal variations, with the wet season occurring from June to December and the dry season from December to June of the subsequent year, the trend in water level changes during this timeframe remains relatively consistent. Consequently, a segmented simulation approach is employed, utilizing six-month intervals as the fundamental unit of analysis.

4. Results and Discussion

Drawing on the dynamic characteristics of the groundwater level rise process within the study area, and integrating findings from numerical simulations, this paper categorizes the entire cycle of groundwater level rise into four distinct stages. The detailed categorization is presented in

Table 4. Stage division of groundwater level dynamic rise process.

Stage	Period	Water Level	Description
First Stage	June 2015 to June 2019	−17.18 m to −13.09 m	The first stage is characterized by gradual fluctuations and a rising trend in groundwater levels. During this stage, there is a general upward trajectory in groundwater levels, with noticeable increases occurring in the wet season and minor declines observed during the dry season. The rebound in groundwater levels is predominantly concentrated within the silty clay layer (Layer ④).
Second Stage	June 2019 to August 2021	−13.09 m to −8.00 m	In the second stage, the groundwater level ascends above the bottom plate of the bearing layer (12.3 m) within the silt layer (③), and continues to rise until it reaches the bottom plate of the building’s underground structure, which is buried at a depth of −8 m. At this stage, the groundwater does not exert a buoyant force on the building, as it does not surpass the bottom plate.
Third Stage	August 2021 to June 2022	−8.00 m to −4.24 m	The third stage occurs when the groundwater level exceeds the building floor, thereby generating a buoyant force on the structure. During this phase, the water level progressively rises from the building floor, ultimately reaching a peak that surpasses the floor by approximately 4 m.
Fourth Stage	June 2022 to December 2024	−4.24 m to −6.20 m	The fourth stage is characterized by a stabilization of the water level, which remains relatively constant within the range of −4 m to −6 m and shows a tendency to stabilize.

, while Figure 5 illustrates the variations in water levels across these stages. Notably, each stage exhibits significant differences in the effects of groundwater recovery speed, amplitude, and distribution area on buildings and the surrounding strata.

4.1. Displacement of Geological Strata

Analyzing the overall trends depicted in Figure 6a–d, it is evident that as the groundwater level incrementally rises, the lower strata of the building undergo settlement deformation, due to the influence of building loads. This results in a gradual expansion of both the magnitude and extent of the settlement. Concurrently, a minor rebound is observed around the building and within the deeper strata, aligning with the findings of Tian [28] regarding ground deformation being induced by rising groundwater levels. The local strata predominantly consist of cohesive soil layers, which exhibit a minimal or delayed response to the rising groundwater level. During the initial phase of groundwater level increase, as illustrated in Figure 6a, the deformation range of the strata is notably limited, primarily occurring in the lower right corner of the building. A comparison with Figure 6a’ reveals that the deformation range closely corresponds with the stratigraphic distribution. The thickness of the silty clay layer in the lower right corner of the building exhibits a gradual increase. Enhanced plasticity of the silty clay upon water absorption results in more pronounced deformation at the lower right corner of the building, although the overall deformation remains relatively minor, with a maximum deformation of only 4 mm. As the groundwater level rises to the second stage, illustrated in Figure 6b,b’, and reaches the foundation bearing layer of silt (layer ③), the settlement range of the stratum expands from a localized area to encompass the entire lower section of the building, leading to a significant increase in stratum deformation. The deformation pattern continues to be influenced by the stratum distribution, with the settlement deformation of the lower left stratum of the building being less than that of the lower right stratum. As the groundwater level rises further, the deformation of the strata increases; however, the range and trend of deformation remain largely unchanged (as depicted in Figure 6c,d).

4.2. Displacement of Underground Structures of Buildings

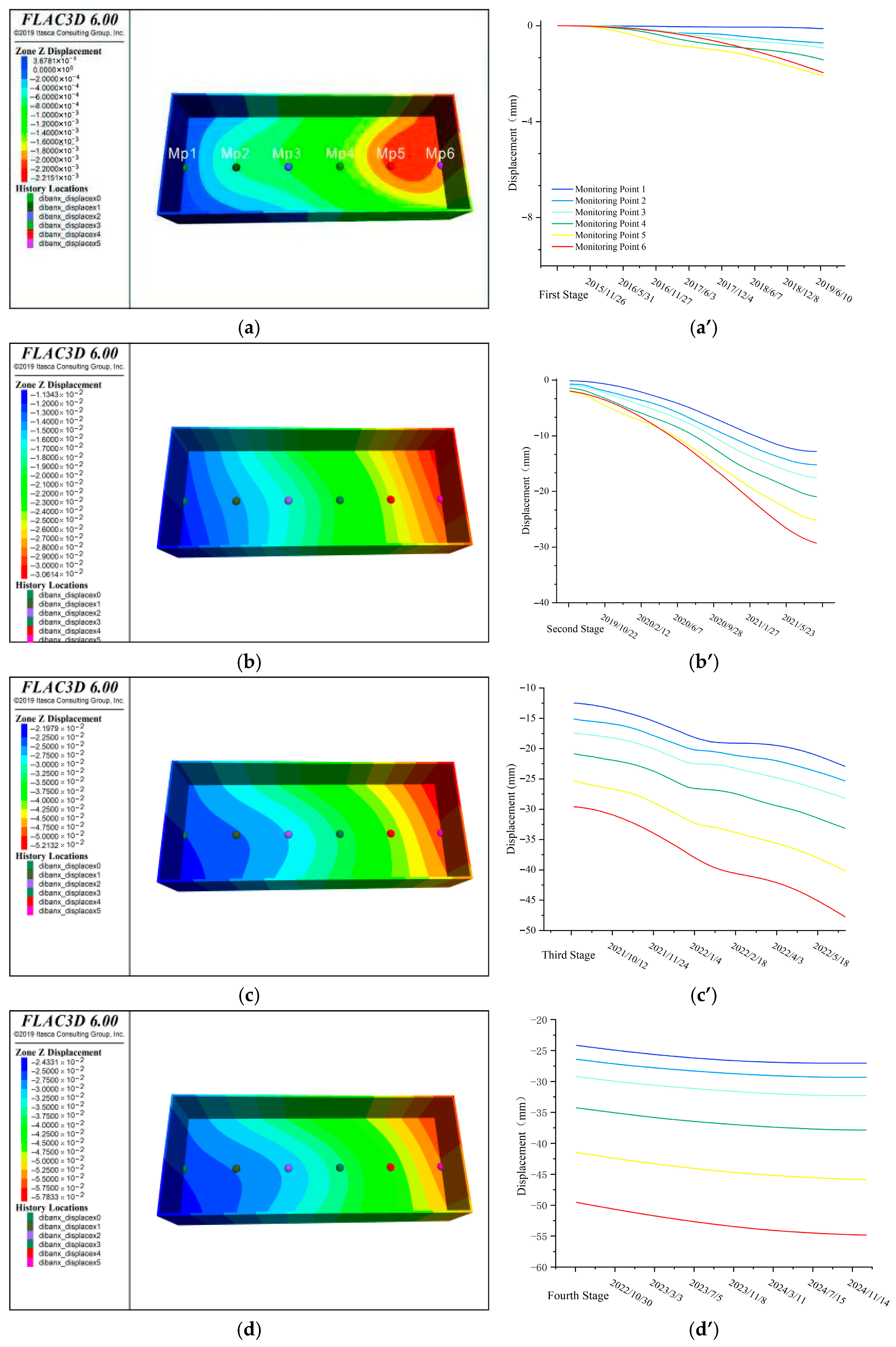
Influenced by the elevation of the groundwater level, the building demonstrates displacement deformation, as illustrated in Figure 7, indicating an overall settlement deformation. The deformation pattern aligns with that of the geological strata, exhibiting a progressively increasing deformation trend from left to right. The extent of settlement deformation escalates in conjunction with the rise in the groundwater level. Based on the distribution of load-bearing columns within the building, which have an approximate spacing of 8 m, monitoring points have been established on the foundation slab to observe deformation and displacement at various locations, as depicted in Figure 6a. During the initial phase (Figure 6a’), the maximum settlement deformation of the building’s underground structure is recorded at 2.2 mm, with both the magnitude and rate of settlement deformation being minimal. During the second stage (Figure 6b,b’), the settlement deformation of the building intensified considerably, reaching a maximum settlement deformation of 30.6 mm and a maximum settlement rate of approximately 0.034 mm/day. The greatest settlement difference was observed between monitoring points five and six, with a differential settlement of 4.13 mm. In the third stage (Figure 6c,c’), the building experienced a maximum settlement of 49.54 mm, with a peak settlement rate of approximately 0.16 mm/day and a maximum differential settlement of 8.05 mm. In the fourth stage (Figure 6d,d’), the settlement rate of the building decreased markedly, with a rate of 0.005 mm/day, while the maximum differential settlement remained within 9 mm. In accordance with the stipulations outlined in the Chinese “Code for Design of Building Foundation” GB50007-2011 [29], the total deformation of raft foundations for high-rise buildings must not exceed 200 mm, and the settlement rate during the stabilization phase should remain between 0.01 and 0.03 mm/d. Furthermore, the differential settlement limit, calculated for a column spacing of 8 m, is set at 16 mm. The total settlement deformation and differential settlement of the subject under investigation, observed during the dynamic rise in the groundwater level, fall within the permissible range specified by the code. However, the settlement rate, which is excessively rapid, poses potential risks.

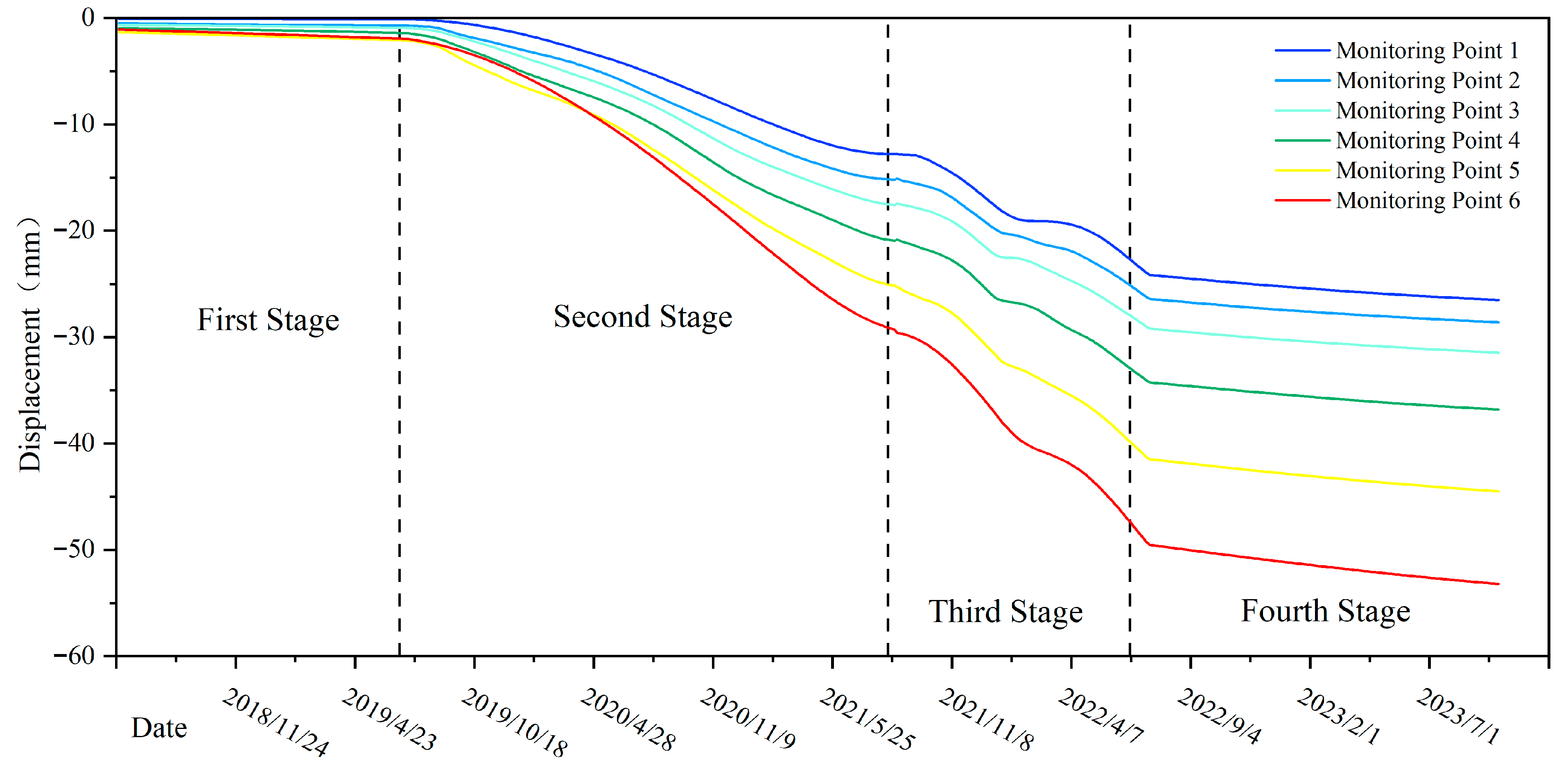
By analyzing the deformation and displacement of buildings in the first and second stages depicted in Figure 8, it is evident that, despite the similar magnitudes of groundwater level rise in both stages (4.09 m and 5.09 m, respectively), there is a notable disparity in the settlement deformation rate and the overall deformation of the buildings. This discrepancy can be attributed primarily to the differing response mechanisms of silty clay and silt in the study area to the rise in groundwater level, which results in the transition of the soil from an unsaturated to a saturated state. In the unsaturated state, silt exhibits high shear strength and low compressibility, due to matrix suction. However, as saturation progresses and the water film thickens, the matrix suction dissipates, leading to a significant reduction in the shear strength of the silt and a potential exponential increase in its compressibility. Over the past few decades, the research area has experienced a sustained decline in groundwater levels, leading to prolonged dewatering of the silty soil layer. This condition may have heightened the sensitivity of the soil’s physical properties to variations in moisture content, thereby causing significant displacement and deformation of the silty soil layer as groundwater levels rise. Consequently, buildings in the area are likely to undergo rapid settlement and deformation. In contrast, the silty clay layer, due to its proximity to the groundwater level and high saturation, exhibits relatively less sensitivity to groundwater level fluctuations, resulting in a comparatively smaller degree of displacement and deformation.

An analysis of the second and third stages depicted in Figure 8 reveals that, for the building under investigation, the buoyancy force generated when the groundwater level surpasses the building’s floor is insufficient to counteract the settlement trend or induce uplift. The building’s own load continues to predominantly drive the overall displacement deformation towards settlement.

In the fourth stage of Figure 8, it is evident that as the groundwater level stabilizes, there is a marked reduction in the rate of displacement and deformation, which gradually reaches a state of equilibrium.

4.3. Stress and Strain of Underground Structures of Buildings

An analysis of Figure 9a–d reveals that, as the groundwater level incrementally rises, the building floor experiences a notable stress concentration, indicated by a color transition from light blue to deep blue. Concurrently, the maximum principal stress exhibits a negative increase. The compressive stress on the floor progressively intensifies, reaching a peak value of approximately 0.31 MPa. Throughout the elevation of the groundwater level, the stress variation in the walls remains relatively insignificant; however, there is a discernible concentration of compressive stress at the four corners of the wall. The remaining sections of the wall sustain a relatively uniform distribution of compressive stress: approximately 0.25 MPa. According to the Chinese “Code for Design of Concrete Structures” GB50010-2010 [30], the standard compressive strength of C30 concrete is specified as 20.1 MPa. This standard indicates that the compressive stress exerted on the walls and bottom plates of buildings due to rising groundwater levels is unlikely to significantly affect the integrity of underground structures. However, an analysis of Figure 9a’–d’ reveals a concentration of tensile stress at the junction between the bottom plate and the wall, aligning with the direction of differential settlement. As the groundwater level increases, the area of stress concentration expands, and the tensile stress intensifies, with the maximum tensile stress rising from 1.8 MPa to 2.19 MPa. In accordance with the “Code for Design of Concrete Structures” GB50010-2010, which specifies a standard tensile strength value of 2.01 MPa for C30 concrete, it is observed that as the groundwater level rises, the tensile stress in affected regions progressively increases. Consequently, the concrete structure may transition from elastic to plastic deformation, potentially resulting in the formation of tensile cracks. Such structural changes could contribute to water seepage and leakage issues in buildings.

5. Conclusions

(1) The impact of the entire process of dynamic groundwater level rebound on buildings exhibits distinct phased characteristics. During the dynamic groundwater level rebound process, the maximum settlement of the building and the maximum differential settlement between columns both occur at the end of the fourth stage, and both remain within the specified range. Nevertheless, the maximum settlement rate of the building is observed in the third stage, reaching 0.16 mm/d, which exceeds the code standard. This situation may potentially pose a certain influence on the structural safety of the building.

(2) There are substantial differences in the response mechanisms of different strata lithologies to the rebound of the groundwater level. Thus, it is necessary to pay particular attention to strata whose physical properties and behaviors are sensitive to changes in the moisture content. In this study, the displacement and deformation induced by the impact of the groundwater level rebound on the silt layer that has been in a drained state for an extended period have exerted a notable impact on the building.

(3) During the groundwater level rebound process, tensile stress concentration zones emerge at the connection between the floor slab and the wall, in the direction consistent with the differential settlement. The maximum tensile stress has exceeded the standard value of the tensile strength of C30 concrete. This might be one of the crucial factors contributing to the leakage problem in the underground structure of the building.

Based on the research conclusions regarding the impact of dynamic groundwater level recovery on buildings, the following core suggestions should be given priority in engineering construction: Firstly, additional dynamic groundwater level monitoring wells should be set up in potential areas of water level recovery, and the stage characteristics and development trends of water level recovery should be accurately identified, based on the measured monitoring data. Secondly, during the investigation stage, the physical and mechanical properties of water-content-sensitive strata (especially the silt layer in a long-term drained state) should be analyzed more intensively, and the foundation design scheme should be optimized accordingly. Thirdly, during the construction and operation periods, the settlement deformation of buildings (with particular attention to the critical stages where the settlement rate exceeds the limit) and the stress state of underground structures (especially the tensile stress concentration at the connection between the bottom plate and the wall, to prevent concrete cracking and water seepage risks) should be monitored in real time. At the same time, it is necessary to avoid applying the experience theories of other regions or misjudging the structural deformation trend, due to the neglect of the buoyancy force effect. Moreover, the engineering countermeasures should be dynamically adjusted according to the different stage characteristics of water level recovery, to ensure the safety of the building structures and the rationality of the engineering construction.