Aquaculture Water Quality Classification Using XGBoost Classifier Model Optimized by the Honey Badger Algorithm with SHAP and DiCE-Based Explanations
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Custom Cross-Validation
2.3. Classifier Model
2.4. Metaheuristic-Based HBA
2.5. Custom-Defined Problem
2.6. Performance Analysis
- TP: Correctly predicted positive samples;
- TN: Correctly predicted negative samples;
- FP: Predicted positive but actually negative;
- FN: Predicted negative but actually positive.
2.7. SHAP
2.8. DiCE
3. Results
3.1. Custom k-Fold Validation-Based Evaluation of the HBA_GB Classifier
3.2. Performance of HBA_XGB Model
3.3. Confusion Matrix Analysis
3.4. Misclassification Output
3.5. ROC Curve Analysis
3.6. Controlling the Overfitting
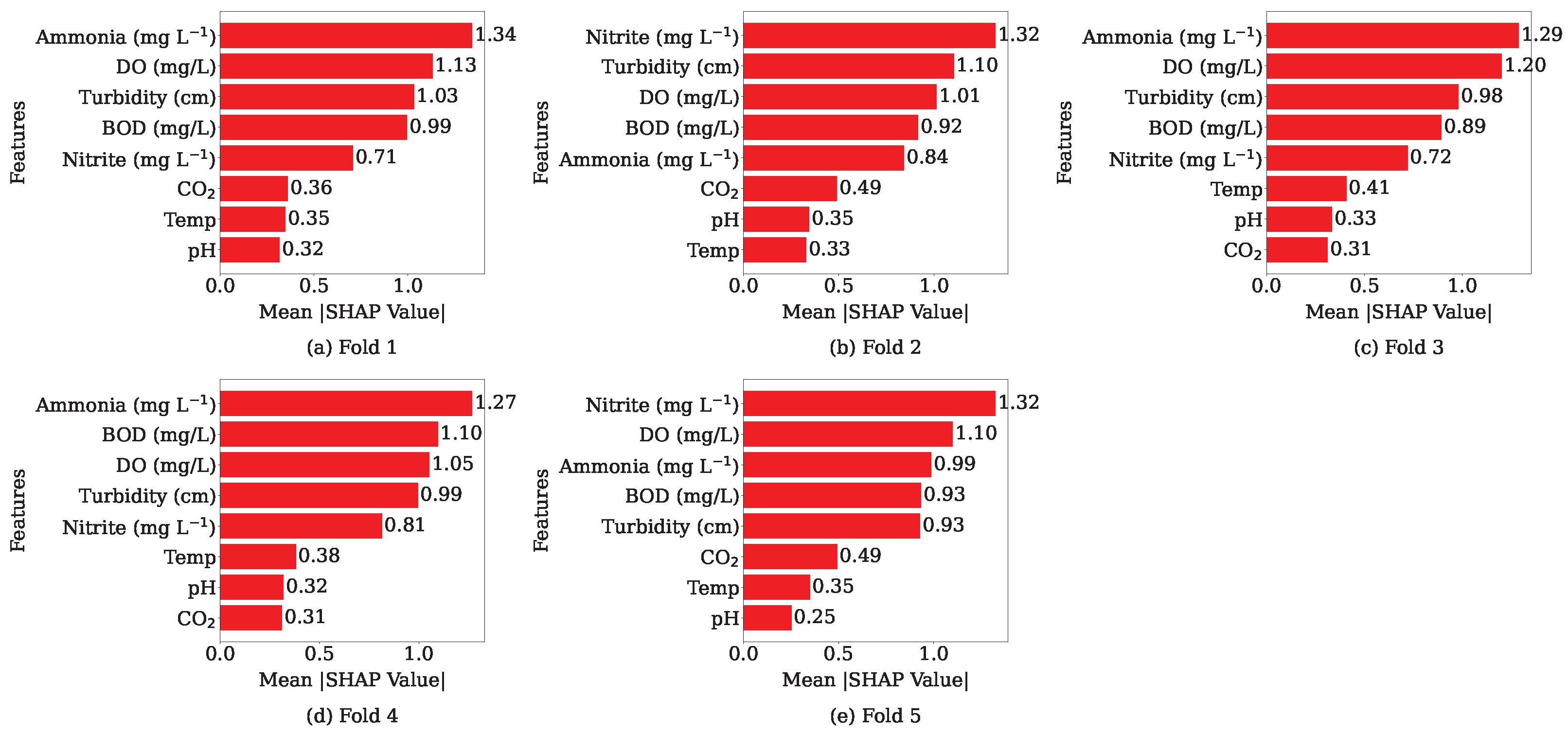
3.7. SHAP Analysis
3.8. DiCE Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eruola, A.O.; Ufoegbune, G.C.; Awomeso, J.A.; Abhulimen, S.A. Assessment of cadmium, lead and iron in hand dug wells of Ilaro and Aiyetoro, Ogun State, South-Western Nigeria. Res. J. Chem. Sci. 2011, 2231, 606X. [Google Scholar]
- Matta, G.; Kumar, P.; Uniyal, D.P.; Joshi, D.U. Communicating water, sanitation, and hygiene under sustainable development goals 3, 4, and 6 as the panacea for epidemics and pandemics referencing the succession of COVID-19 surges. ACS ES&T Water 2022, 2, 667–689. [Google Scholar] [CrossRef] [PubMed]
- FAO. The State of World Fisheries and Aquaculture 2018: Meeting the Sustainable Development Goals; Food and Agriculture Organization of the United Nations: Rome, Italy, 2018. [Google Scholar]
- MAAIF. Essentials of Aquaculture Production, Management and Development in Uganda; Ministry of Agriculture, Animal Industry and Fisheries (MAAIF): Entebbe, Uganda, 2018.
- Abd El-Hamed, N. Environmental studies of water quality and its effect on fish of some farms in Sharkia and Kafr El-Sheikh Governorates. 2014. Available online: https://research.asu.edu.eg/handle/12345678/26260 (accessed on 8 September 2025).
- Cline, D. Water Quality in Aquaculture; Alabama Cooperative Extension System, Auburn University: Auburn, AL, USA, 2019; Available online: https://freshwater-aquaculture.extension.org/water-quality-in-aquaculture/ (accessed on 26 August 2019).
- Palma, J.; Correia, M.; Leitão, F.; Andrade, J.P. Temperature effects on growth performance, fecundity and survival of Hippocampus guttulatus. Diversity 2024, 16, 719. [Google Scholar] [CrossRef]
- Devi, P.A.; Padmavathy, P.; Aanand, S.; Aruljothi, K. Review on water quality parameters in freshwater cage fish culture. Int. J. Appl. Res. 2017, 3, 114–120. [Google Scholar]
- Boyd, C.E. Water Quality Management for Pond Fish Culture; Elsevier Scientific Publishing Co.: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Bolorunduro, P.I.; Abdullah, A.Y. Water quality management in fish culture, national agricultural extension and research liaison services, Zaria. Ext. Bull. 1996, 98. [Google Scholar]
- Siti-Zahrah, A.; Misri, S.; Padilah, B.; Zulkafli, R.; Kua, B.C.; Azila, A.; Rimatulhana, R. Pre-disposing factors associated with outbreak of Streptococcal infection in floating cage-cultured red tilapia in reservoirs. In Proceedings of the 7th Asian Fisheries Forum, Penang, Malaysia, 1–2 December 2004; Volume 4, p. 129. [Google Scholar]
- Siti-Zahrah, A.; Padilah, B.; Azila, A.; Rimatulhana, R.; Shahidan, H. Multiple streptococcal species infection in cage-cultured red tilapia but showing similar clinical signs. In Diseases in Asian Aquaculture VI; Fish Health Section, Asian Fisheries Society: Manila, Philippines, 2008; pp. 313–320. [Google Scholar]
- Hepher, B.; Pruginin, Y. Commercial Fish Farming. A Wiley-Interscience Publication; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Nsonga, A. Indigenous fish species a panacea for cage aquaculture in Zambia: A case for Oreochromis macrochir at Kambashi out grower scheme. Int. J. Fish. Aquat. Stud. 2014, 2, 102–105. [Google Scholar]
- Daniel, S.; Larry, W.D.; Joseph, H.S. Comparative oxygen consumption and metabolism of striped bass (Morone saxatilis) and its hybrid. J. World Aquac. Soc. 2005, 36, 521–529. [Google Scholar] [CrossRef]
- Praveen, T.; Mishra, R. Somdutt. Water quality monitoring of Halali reservoir with reference to Cage aquaculture as a modern tool for obtaining enhanced fish production. Proc. Taal 2007, 318–324. [Google Scholar]
- Razali, R.M. Predictive Water Quality Monitoring in Aquaculture Using Machine Learning and IoT Automation. Adv. Comput. Intell. Syst. 2025, 1, 10–17. [Google Scholar]
- Nayan, A.A.; Kibria, M.G.; Rahman, M.O.; Saha, J. River water quality analysis and prediction using GBM. In Proceedings of the 2020 2nd International Conference on Advanced Information and Communication Technology (ICAICT), Dhaka, Bangladesh, 28–29 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 219–224. [Google Scholar]
- Nayan, A.A.; Mozumder, A.N.; Saha, J.; Mahmud, K.R.; Al Azad, A.K. Early detection of fish diseases by analyzing water quality using machine learning algorithm. Walailak J. Sci. Technol. 2020, 18, 351. [Google Scholar]
- Sen, S.; Maiti, S.; Manna, S.; Roy, B.; Ghosh, A. Smart Prediction of Water Quality System for Aquaculture using Machine Learning Algorithms. TechRxiv 2023. [Google Scholar] [CrossRef]
- Shams, M.Y.; Elshewey, A.M.; El-Kenawy, E.-S.M.; Ibrahim, A.; Talaat, F.M.; Tarek, Z. Water quality prediction using machine learning models based on grid search method. Multimed. Tools Appl. 2024, 83, 35307–35334. [Google Scholar] [CrossRef]
- Nasir, N.; Kansal, A.; Alshaltone, O.; Barneih, F.; Sameer, M.; Shanableh, A.; Al-Shamma’a, A. Water quality classification using machine learning algorithms. J. Water Process Eng. 2022, 48, 102920. [Google Scholar] [CrossRef]
- Malek, N.H.A.; Yaacob, W.F.W.; Nasir, S.A.M.; Shaadan, N. Prediction of water quality classification of the Kelantan River Basin, Malaysia, using machine learning techniques. Water 2022, 14, 1067. [Google Scholar] [CrossRef]
- Khan, M.S.I.; Islam, N.; Uddin, J.; Islam, S.; Nasir, M.K. Water quality prediction and classification based on principal component regression and gradient boosting classifier approach. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 4773–4781. [Google Scholar] [CrossRef]
- Ho, J.Y.; Afan, H.A.; El-Shafie, A.H.; Koting, S.B.; Mohd, N.S.; Jaafar, W.Z.; Sai, H.L.; Malek, M.A.; Ahmed, A.N.; Mohtar, W.H.M.; et al. Towards a time and cost effective approach to water quality index class prediction. J. Hydrol. 2019, 575, 148–165. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Rahman, A.; Olbert, A.I. Performance analysis of the water quality index model for predicting water state using machine learning techniques. Process Saf. Environ. Prot. 2023, 169, 808–828. [Google Scholar] [CrossRef]
- Reddy, A.P.; Sophia, P.E.; Kirubakaran, S.S. Automated Cardiovascular Disease Diagnosis using Honey Badger Optimization with Modified Deep Learning Model. Biomed. Mater. Devices 2025, 1–8. [Google Scholar] [CrossRef]
- Li, W.; Deng, M.; Liu, C.; Cao, Q. Analysis of Key Influencing Factors of Water Quality in Tai Lake Basin Based on XGBoost-SHAP. Water 2025, 17, 1619. [Google Scholar] [CrossRef]
- Oprea, S.-V.; Bâra, A. Diverse Counterfactual Explanations (DiCE) Role in Improving Sales and e-Commerce Strategies. J. Theor. Appl. Electron. Commer. Res. 2025, 20, 96. [Google Scholar] [CrossRef]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost algorithm-based prediction of concrete electrical resistivity for structural health monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the KDD’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Abualdenien, J.; Borrmann, A. Ensemble-learning approach for the classification of Levels Of Geometry (LOG) of building elements. Adv. Eng. Inform. 2022, 51, 101497. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Mothilal, R.K.; Sharma, A.; Tan, C. Explaining machine learning classifiers through diverse counterfactual explanations. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 607–617. [Google Scholar]







| Author | Dataset Information | Classification Model | Accuracy (%) |
|---|---|---|---|
| Mahmoud et al. [21] | Indian Water Quality Dataset | GB | 99.50 |
| Nasir et al. [22] | Indian Water Quality Dataset | CB | 94.51 |
| Nur et al. [23] | Department of Environment, Malaysia | GB | 94.90 |
| Khan et al. [24] | Gulshan Lake Water Quality Dataset | GB | 100 |
| Ho et al. [25] | Klang River Water Quality Dataset | DT | 81 |
| Uddin et al. [26] | Lee, Cork Harbor, and Youghal Bay | XGB | 100 |
| Feature | Index | Excellent (0) | Good (1) | Poor (2) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | Mean | Max | Min | ||
| Temp (°C) (F1) | 0 | 24.92 | 29.99 | 20.00 | 25.02 | 34.99 | 15.00 | 27.04 | 84.25 | 0.19 |
| Turbidity (cm) (F2) | 1 | 54.46 | 79.98 | 30.02 | 22.53 | 29.99 | 15.00 | 40.08 | 99.79 | 0.05 |
| DO (mg/L) (F3) | 2 | 4.01 | 5.00 | 3.00 | 6.46 | 7.99 | 5.00 | 5.43 | 14.97 | 0.13 |
| BOD (mg/L) (F4) | 3 | 1.50 | 2.00 | 1.00 | 4.02 | 5.99 | 2.01 | 3.81 | 14.94 | 1.00 |
| CO2 (mg/L) (F5) | 4 | 6.48 | 7.99 | 5.00 | 5.72 | 9.99 | 0.01 | 6.90 | 14.98 | 0.00 |
| pH (F6) | 5 | 7.79 | 8.99 | 6.50 | 7.75 | 9.49 | 6.00 | 7.61 | 14.85 | 0.00 |
| Alkalinity (mg/L) (F7) | 6 | 63.02 | 99.99 | 25.03 | 93.19 | 199.90 | 25.03 | 122.86 | 299.91 | 25.01 |
| Hardness (mg/L) (F8) | 7 | 112.78 | 149.92 | 75.25 | 135.45 | 299.75 | 20.01 | 132.54 | 398.80 | 0.26 |
| Calcium (mg/L) (F9) | 8 | 62.69 | 99.99 | 25.08 | 96.93 | 249.94 | 10.08 | 94.32 | 399.32 | 0.02 |
| Ammonia (mg/L) (F10) | 9 | 0.012 | 0.025 | 0.000 | 0.037 | 0.050 | 0.025 | 0.092 | 0.999 | 0.000 |
| Nitrite (mg/L) (F11) | 10 | 0.010 | 0.020 | 0.000 | 1.012 | 2.000 | 0.020 | 0.889 | 4.990 | 0.000 |
| Phosphorus (mg/L) (F12) | 11 | 0.998 | 1.999 | 0.031 | 1.264 | 2.999 | 0.010 | 1.251 | 4.974 | 0.000 |
| H2S (mg/L) (F13) | 12 | 0.019 | 0.020 | 0.019 | 0.010 | 0.019 | 0.000 | 0.020 | 0.099 | 0.000 |
| Plankton (No./L) (F14) | 13 | 3728.80 | 4498.68 | 3002.30 | 3888.95 | 5999.20 | 2002.15 | 3799.23 | 7460.42 | 78.60 |
| Hyperparameter | Type | Range |
|---|---|---|
| Number of Estimators (n_estimators) | Integer | 100 to 300 |
| Learning Rate (learning_rate) | Float | 0.001 to 0.2 |
| Max Depth (max_depth) | Integer | 3 to 7 |
| Minimum Child Weight (min_child_weight) | Integer | 1 to 10 |
| Fold No. | n_Estimators | Learning_Rate | Max_Depth | Min_Child_Weight | SFI |
|---|---|---|---|---|---|
| 1 | 300 | 0.2 | 7 | 10 | 0, 1, 2, 3, 4, 5, 9, 10 |
| 2 | 300 | 0.2 | 7 | 10 | 0, 1, 2, 3, 4, 5, 9, 10 |
| 3 | 300 | 0.2 | 7 | 10 | 0, 1, 2, 3, 4, 5, 9, 10 |
| 4 | 300 | 0.2 | 7 | 10 | 0, 1, 2, 3, 4, 5, 9, 10 |
| 5 | 300 | 0.2 | 7 | 10 | 0, 1, 2, 3, 4, 5, 9, 10 |
| Fold | Train | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| Acc. (%) | F1-Score. (%) | Pre. (%) | Rec. (%) | Acc. (%) | F1-Score (%) | Pre. (%) | Rec. (%) | |
| Fold-1 | 100 | 100 | 100 | 100 | 97.67 | 97.71 | 97.62 | 97.89 |
| Fold-2 | 100 | 100 | 100 | 100 | 98.45 | 98.46 | 98.49 | 98.46 |
| Fold-3 | 100 | 100 | 100 | 100 | 98.22 | 98.22 | 98.23 | 98.26 |
| Fold-4 | 100 | 100 | 100 | 100 | 97.52 | 97.56 | 97.50 | 97.68 |
| Fold-5 | 100 | 100 | 100 | 100 | 98.37 | 98.37 | 98.38 | 98.38 |
| Mean | 100 | 100 | 100 | 100 | 98.05 | 98.07 | 98.04 | 98.13 |
| Fold No. | Number of Misclassified | Misclassified Instances |
|---|---|---|
| 1 | 30 | 103, 203, 205, 227, 238, 257, 258, 263, 278, 283, 287, 290, 299, 309, 318, 321, 325, 331, 342, 386, 505, 618, 712, 761, 785, 790, 1180, 1374, 2801, 3028 |
| 2 | 20 | 208, 230, 237, 243, 323, 344, 347, 365, 374, 382, 383, 917, 1249, 1364, 1446, 1452, 1459, 1826, 2648, 2718 |
| 3 | 23 | 117, 148, 248, 267, 302, 317, 333, 339, 363, 373, 384, 385, 388, 395, 396, 398, 730, 777, 824, 943, 1013, 1821, 3068 |
| 4 | 32 | 103, 134, 149, 200, 205, 206, 227, 238, 240, 245, 301, 309, 318, 321, 325, 397, 505, 618, 656, 761, 790, 971, 1180, 1210, 1267, 1374, 2250, 2524, 2565, 3537, 3777, 4145 |
| 5 | 21 | 221, 230, 237, 243, 257, 258, 283, 347, 382, 386, 547, 1132, 1249, 1446, 1452, 1459, 1826, 2648, 2748, 2949, 4168 |
| Max Depth | Train | Test | Gap (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Acc. (%) | F1 (%) | Pre. (%) | Rec. (%) | Acc. (%) | F1 (%) | Pre. (%) | Rec. (%) | ||
| 1 | 99.00 | 99.01 | 99.01 | 99.02 | 98.14 | 98.17 | 98.09 | 98.31 | 0.86 |
| 2 | 99.63 | 99.64 | 99.64 | 99.64 | 97.91 | 97.95 | 97.86 | 98.09 | 1.72 |
| 3 | 99.97 | 99.97 | 99.97 | 99.97 | 98.14 | 98.17 | 98.09 | 98.31 | 1.83 |
| 4 | 100.00 | 100.00 | 100.00 | 100.00 | 97.75 | 97.79 | 97.70 | 97.95 | 2.25 |
| 5 | 100.00 | 100.00 | 100.00 | 100.00 | 97.75 | 97.79 | 97.70 | 97.96 | 2.25 |
| 6 | 100.00 | 100.00 | 100.00 | 100.00 | 97.67 | 97.71 | 97.62 | 97.89 | 2.33 |
| 7 | 100.00 | 100.00 | 100.00 | 100.00 | 97.67 | 97.71 | 97.62 | 97.89 | 2.33 |
| 8 | 100.00 | 100.00 | 100.00 | 100.00 | 97.67 | 97.71 | 97.62 | 97.88 | 2.33 |
| 9 | 100.00 | 100.00 | 100.00 | 100.00 | 97.91 | 97.94 | 97.86 | 98.09 | 2.09 |
| 10 | 100.00 | 100.00 | 100.00 | 100.00 | 98.06 | 98.10 | 98.01 | 98.22 | 1.94 |
| Index | Class (Actual→Pred) | Feature | Original | CF1 | CF2 | CF3 |
|---|---|---|---|---|---|---|
| 57 | 2→1 | F2 | 17.85 | 89.51 | N/A | N/A |
| 57 | 2→1 | F4 | 3.11 | 13.60 | 14.09 | N/A |
| 57 | 2→1 | F6 | 9.38 | N/A | N/A | 13.95 |
| 299 | 1→2 | F4 | 2.39 | 4.37 | N/A | N/A |
| 299 | 1→2 | F5 | 8.31 | N/A | 3.16 | N/A |
| 299 | 1→2 | F6 | 6.46 | N/A | 5.92 | N/A |
| 927 | 0→2 | F3 | 3.00 | 4.88 | 3.78 | 3.57 |
| 927 | 0→2 | F5 | 6.63 | 4.79 | N/A | 3.48 |
| Index | Class (Actual→Pred→Desired) | Feature | Original | CF1 | CF2 | CF3 |
|---|---|---|---|---|---|---|
| 0 | 1→1→2 | F4 | 2.47 | 8.76 | N/A | N/A |
| 0 | 1→1→2 | F5 | 4.32 | N/A | 10.42 | N/A |
| 0 | 1→1→2 | F1 | 30.33 | N/A | N/A | 9.73 |
| 1 | 0→0→2 | F3 | 4.39 | 12.66 | N/A | N/A |
| 1 | 0→0→2 | F5 | 6.68 | N/A | N/A | 9.62 |
| 1 | 0→0→2 | F6 | 6.75 | 12.54 | N/A | N/A |
| 1 | 0→0→2 | F10 | 0.002 | N/A | 0.60 | N/A |
| 3 | 2→2→1 | F1 | 28.30 | 32.69 | 32.24 | 30.60 |
| 3 | 2→2→1 | F3 | 4.08 | 5.84 | 5.76 | 5.47 |
| 3 | 2→2→1 | F5 | 3.09 | N/A | N/A | 5.39 |
| 3 | 2→2→1 | F6 | 6.71 | 5.72 | 5.64 | 5.35 |
| 3 | 2→2→1 | F10 | 0.02 | 0.38 | 0.37 | 0.35 |
| 3 | 2→2→1 | F11 | 4.92 | N/A | N/A | 1.79 |
| Author | Dataset Information | Classification Model | Accuracy (%) |
|---|---|---|---|
| Mahmoud et al. [21] | Indian Water Quality Dataset | GB | 99.50 |
| Nasir et al. [22] | Indian Water Quality Dataset | CB | 94.51 |
| Nur et al. [23] | Department of Environment, Malaysia | GB | 94.90 |
| Khan et al. [24] | Gulshan Lake Water Quality Dataset | GB | 100 |
| Ho et al. [25] | Klang River Water Quality Dataset | DT | 81 |
| Uddin et al. [26] | Lee, Cork Harbour, and Youghal Bay | XGB | 100 |
| Our method-1 | Aquaculture Water Quality Dataset | HBA_XGB (Fold 2) | 98.45 (highest accuracy among 5 folds) |
| Our method-2 | Aquaculture Water Quality Dataset | HBA_XGB (5-fold) | 98.05 (mean accuracy of custom 5 folds) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naim, S.M.; Das, P.; Tiang, J.-J.; Nahid, A.-A. Aquaculture Water Quality Classification Using XGBoost Classifier Model Optimized by the Honey Badger Algorithm with SHAP and DiCE-Based Explanations. Water 2025, 17, 2993. https://doi.org/10.3390/w17202993
Naim SM, Das P, Tiang J-J, Nahid A-A. Aquaculture Water Quality Classification Using XGBoost Classifier Model Optimized by the Honey Badger Algorithm with SHAP and DiCE-Based Explanations. Water. 2025; 17(20):2993. https://doi.org/10.3390/w17202993
Chicago/Turabian StyleNaim, S M, Prosenjit Das, Jun-Jiat Tiang, and Abdullah-Al Nahid. 2025. "Aquaculture Water Quality Classification Using XGBoost Classifier Model Optimized by the Honey Badger Algorithm with SHAP and DiCE-Based Explanations" Water 17, no. 20: 2993. https://doi.org/10.3390/w17202993
APA StyleNaim, S. M., Das, P., Tiang, J.-J., & Nahid, A.-A. (2025). Aquaculture Water Quality Classification Using XGBoost Classifier Model Optimized by the Honey Badger Algorithm with SHAP and DiCE-Based Explanations. Water, 17(20), 2993. https://doi.org/10.3390/w17202993








