Integrating Eco-Index and Hydropower Optimization for Cascade Reservoir Operations in the Lancang–Mekong River Basin
Abstract
1. Introduction
2. Study Area and Data
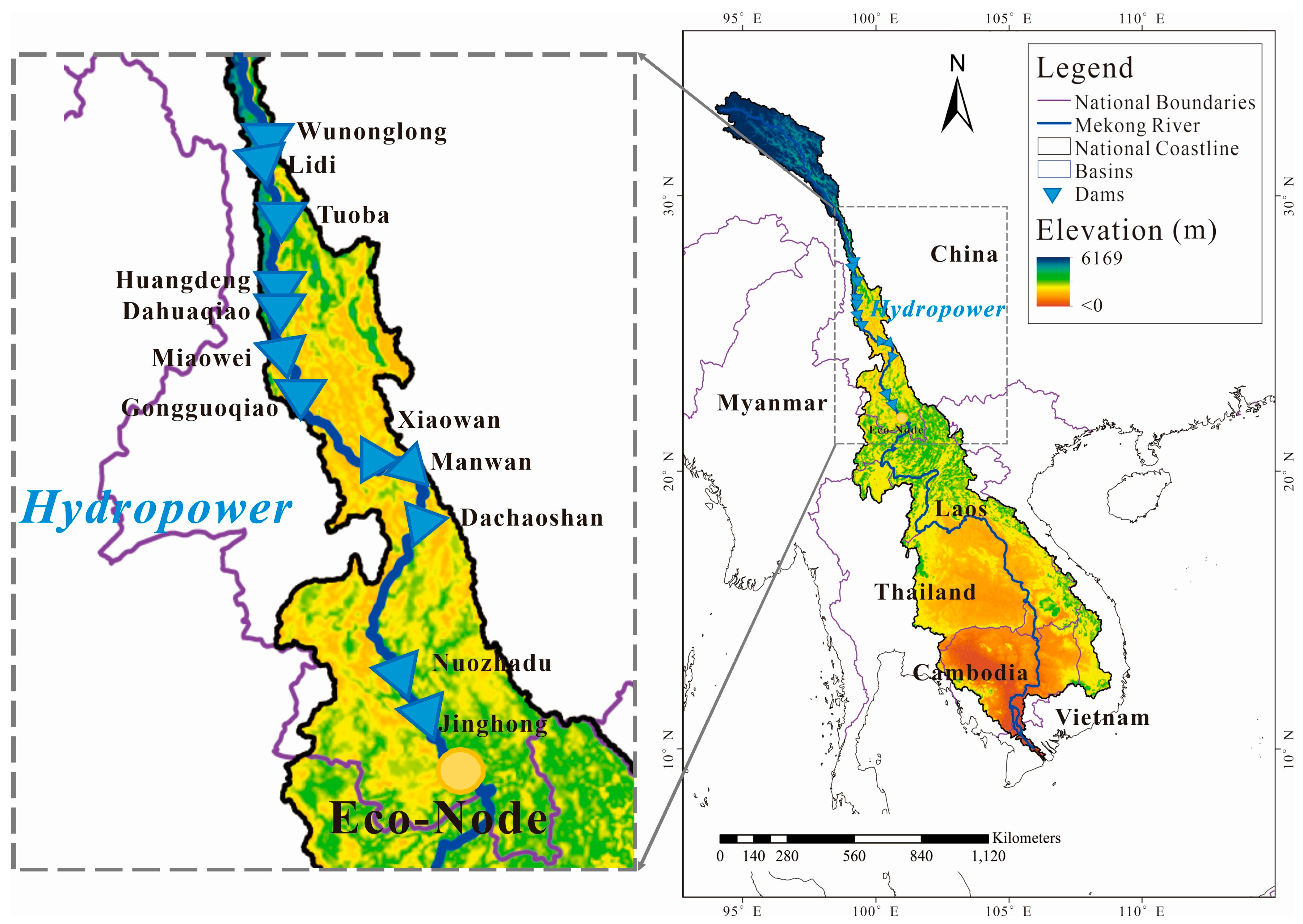
2.1. Overview of the Basin and Cascade Reservoir System
2.2. Data Sources and Processing
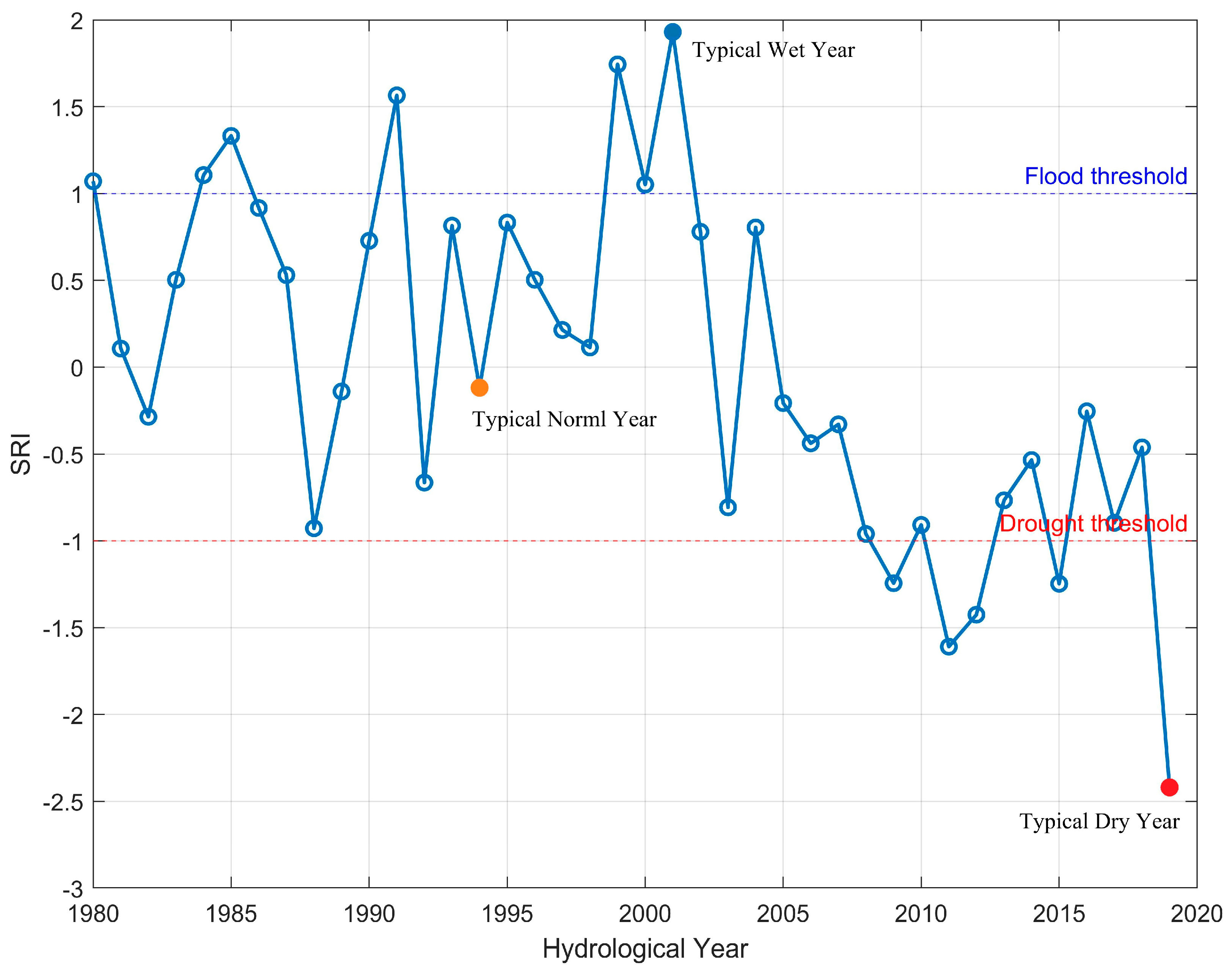
2.2.1. Hydrological Data and Year Classification
2.2.2. Ecological Indicator (EI)
2.2.3. Hydropower System Parameters
3. Methodology
3.1. Eco-Index Construction Method
3.2. Multi-Objective Coupled Optimization Model
3.3. Resilience and Robustness Analysis Framework
4. Results and Discussions
4.1. Eco-Index Based on IHA Metrics
4.2. Typical Years Identified with SRI Index
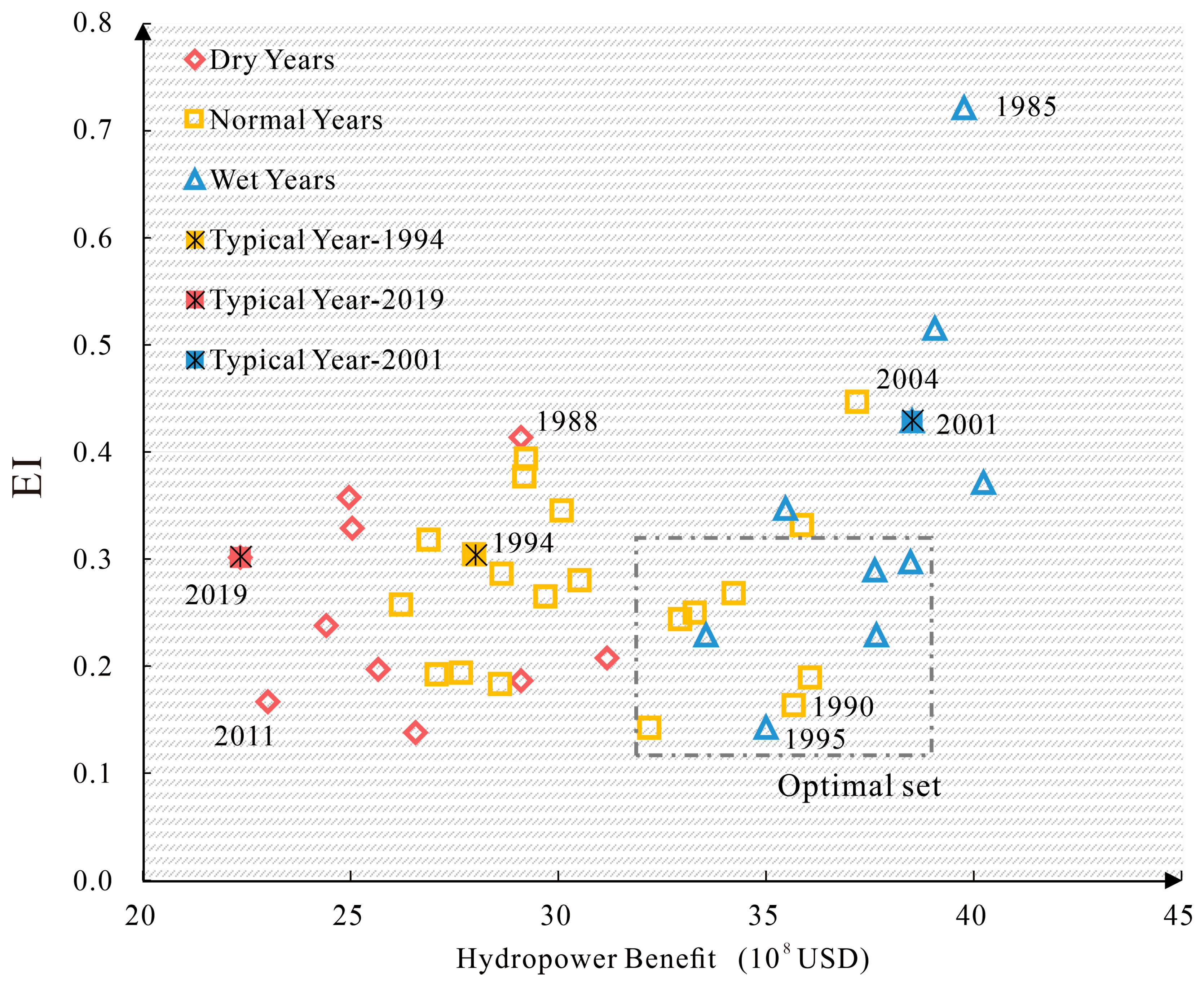
4.3. Analysis of Optimization Scheduling Results over the Entire Period
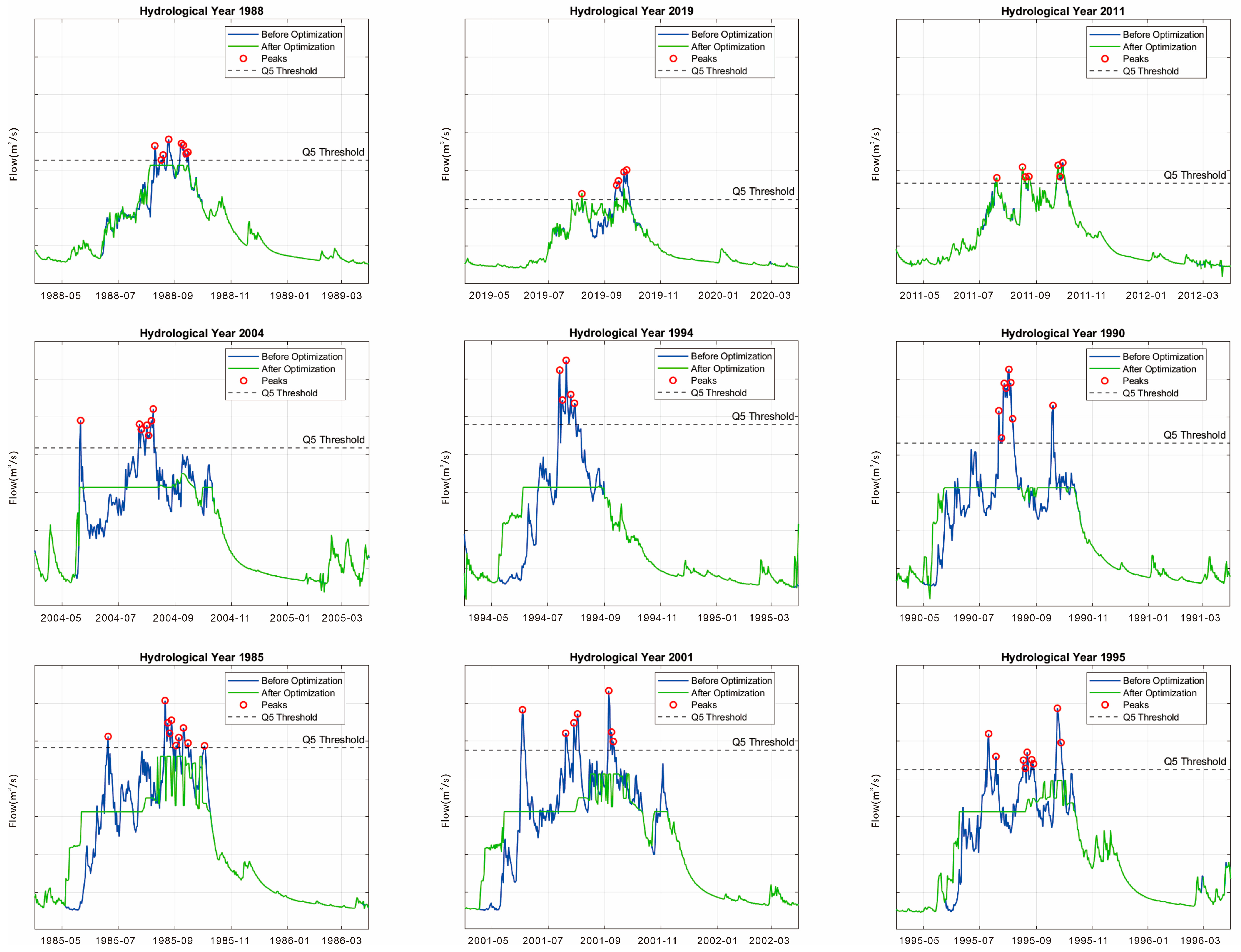
4.4. Response Characteristics of Hydropower Scheduling on EI Under Different Hydrological Year Types
4.5. Spatial Distribution Characteristics of Cascade Hydropower Generation and Key Control Station Analysis Under Different Hydrological Year Types
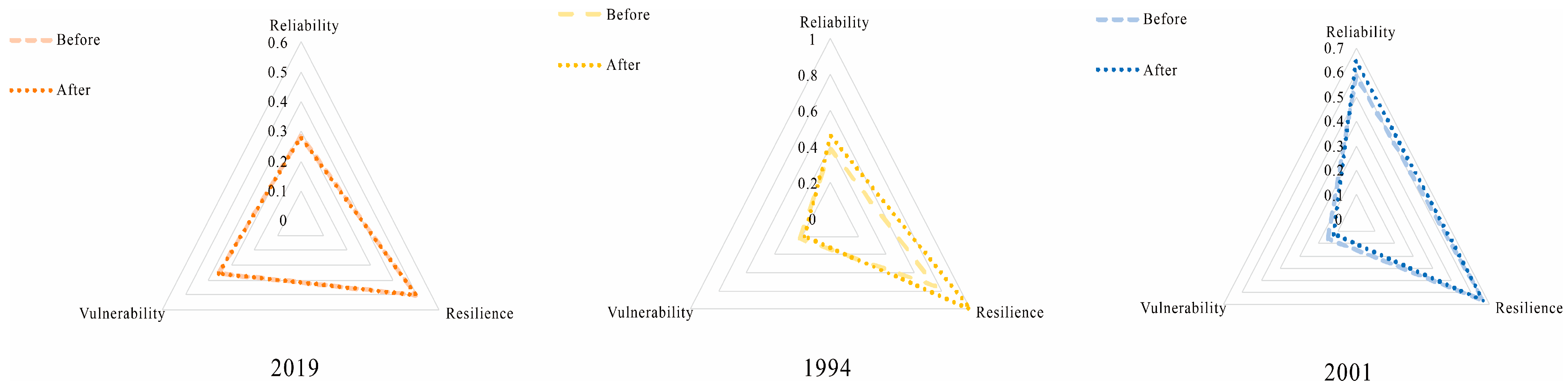
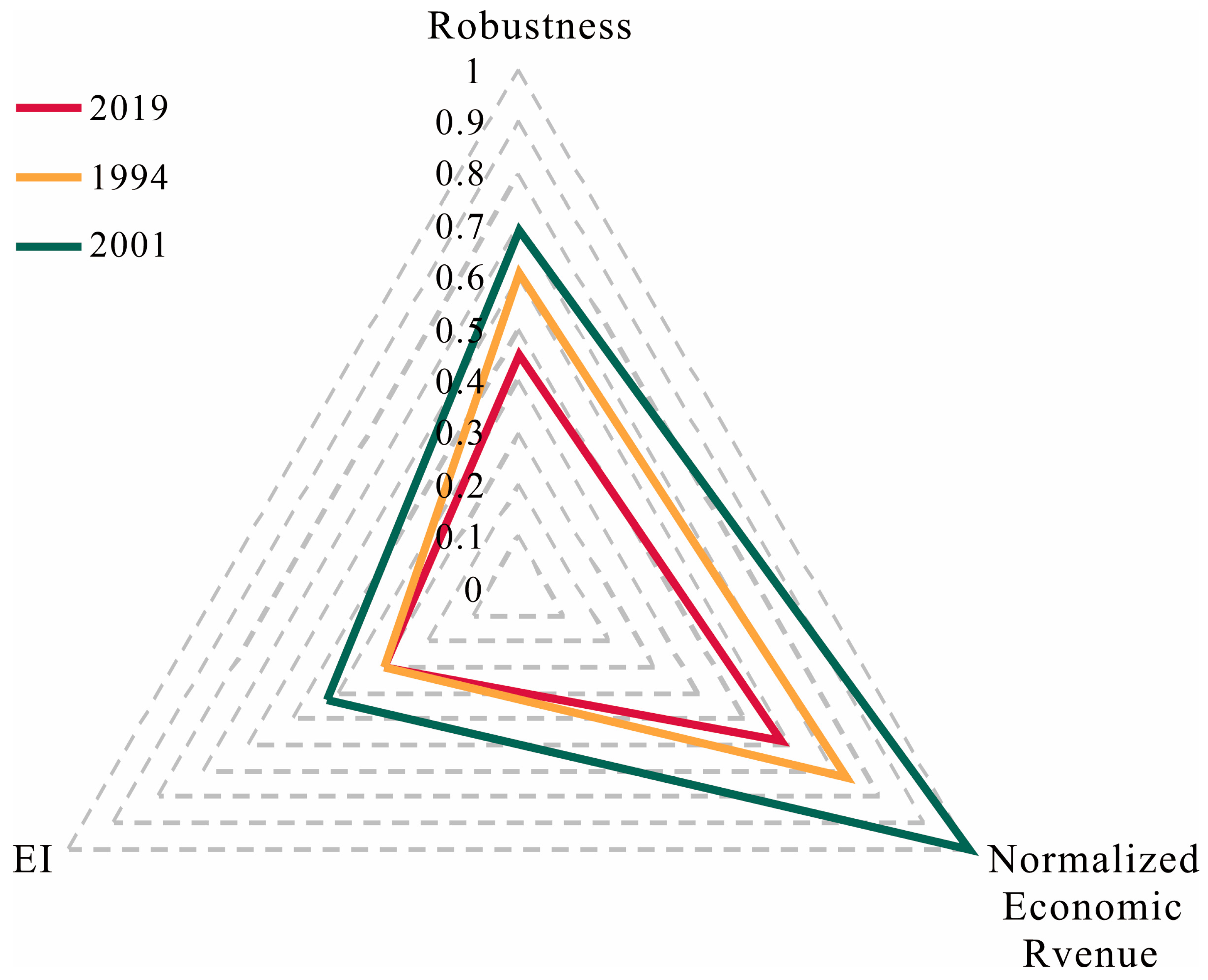
4.6. Resilience and Robustness Analysis of the System in a Typical Extreme Year
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grill, G.; Lehner, B.; Thieme, M.; Geenen, B.; Tickner, D.; Antonelli, F.; Babu, S.; Borrelli, P.; Cheng, L.; Crochetiere, H.; et al. Mapping the world’s free-flowing rivers. Nature 2019, 569, 215–221. [Google Scholar] [CrossRef]
- Ziv, G.; Baran, E.; Nam, S.; Rodriguez-Iturbe, I.; Levin, S.A. Trading-off fish biodiversity, food security, and hydropower in the Mekong River Basin. Proc. Natl. Acad. Sci. USA 2012, 109, 5609–5614. [Google Scholar] [CrossRef]
- De Stefano, L.; Duncan, J.; Dinar, S.; Stahl, K.; Strzepek, K.M.; Wolf, A.T. Climate change and the institutional resilience of international river basins. J. Peace Res. 2012, 49, 193–209. [Google Scholar] [CrossRef]
- de Bruin, S.P.; Schmeier, S.; van Beek, R.; Gulpen, M. Projecting conflict risk in transboundary river basins by 2050 following different ambition scenarios. Int. J. Water Resour Dev. 2024, 40, 7–32. [Google Scholar] [CrossRef]
- Soukhaphon, A.; Baird, I.G.; Hogan, Z.S. The impacts of hydropower dams in the mekong river basin: A review. Water 2020, 13, 265. [Google Scholar] [CrossRef]
- Mlambo, V.H.; Masuku, M.M. Trouble in the Nile Basin: Ethiopia, Egypt, and Sudan and the Nile stalemate. Cogent Soc. Sci. 2025, 11, 2491851. [Google Scholar] [CrossRef]
- Räsänen, T.A.; Someth, P.; Lauri, H.; Koponen, J.; Sarkkula, J.; Kummu, M. Observed river discharge changes due to hydropower operations in the Upper Mekong Basin. J. Hydrol. 2017, 545, 28–41. [Google Scholar] [CrossRef]
- Fan, H.; He, D.; Wang, H. Environmental consequences of damming the mainstream lancang-mekong river: A review. Earth-Sci. Rev. 2015, 146, 77–91. [Google Scholar] [CrossRef]
- Liu, Z.; He, X. Balancing-oriented hydropower operation makes the clean energy transition more affordable and simultaneously boosts water security. Nature Water 2023, 1, 778–789. [Google Scholar] [CrossRef]
- Ma, Y.; Zhong, P.-A.; Xu, B.; Bing, J.; Zhang, Y. Multiobjective and Joint Operation Model for Multistakeholder Cascade Hydropower System. J. Water Resour. Plan. Manag. 2020, 146, 04020083. [Google Scholar] [CrossRef]
- Ortiz-Partida, J.P.; Kahil, T.; Ermolieva, T.; Ermoliev, Y.; Lane, B.; Sandoval-Solis, S.; Wada, Y. A Two-Stage Stochastic Optimization for Robust Operation of Multipurpose Reservoirs. Water Resour. Manag. 2019, 33, 3815–3830. [Google Scholar] [CrossRef]
- Lin, N.M.; Rutten, M. Optimal Operation of a Network of Multi-purpose Reservoir: A Review. Procedia Eng. 2016, 154, 1376–1384. [Google Scholar] [CrossRef]
- Arthington, A.H.; Bunn, S.E.; Poff, N.L.; Naiman, R.J. The challenge of providing environmental flow rules to sustain river ecosystems. Ecol. Appl. 2006, 16, 1311–1318. [Google Scholar] [CrossRef] [PubMed]
- Ficklin, D.L.; Null, S.E.; Abatzoglou, J.T.; Novick, K.A.; Myers, D.T. Myers. Hydrological Intensification Will Increase the Complexity of Water Resource Management. Earth’s Future 2022, 10, e2021EF002487. [Google Scholar] [CrossRef]
- Asadieh, B.; Krakauer, N.Y. Global change in streamflow extremes under climate change over the 21st century. Hydrol. Earth Syst. Sci. 2017, 21, 5863–5874. [Google Scholar] [CrossRef]
- Slater, L.J.; Anderson, B.; Buechel, M.; Dadson, S.; Han, S.; Harrigan, S.; Kelder, T.; Kowal, K.; Lees, T.; Matthews, T.; et al. Nonstationary weather and water extremes: A review of methods for their detection, attribution, and management. Hydrol. Earth Syst. Sci. 2021, 25, 3897–3935. [Google Scholar] [CrossRef]
- Xie, Y.; Guo, S.; Xiong, L.; Tian, J.; Xiong, F. Nonstationary design flood estimation in response to climate change, population growth and cascade reservoir regulation. Water 2021, 13, 2687. [Google Scholar] [CrossRef]
- Olden, J.D.; Poff, N.L. Redundancy and the choice of hydrologic indices for characterizing streamflow regimes. River Res. Appl. 2003, 19, 101–121. [Google Scholar] [CrossRef]
- Wang, C.-H.; Blackmore, J.M. Resilience Concepts for Water Resource Systems. J. Water Resour. Plan. Manag. 2009, 135, 528–536. [Google Scholar] [CrossRef]
- Sommerwerk, N.; Bloesch, J.; Paunović, M.; Baumgartner, C.; Venohr, M.; Schneider-Jacoby, M.; Hein, T.; Tockner, K. Managing the world’s most international river: The Danube River Basin. Mar. Freshw. Res. 2010, 61, 736–748. [Google Scholar] [CrossRef]
- Winemiller, K.O.; McIntyre, P.B.; Castello, L.; Fluet-Chouinard, E.; Giarrizzo, T.; Nam, S.; Baird, I.G.; Darwall, W.; Lujan, N.K.; Harrison, I.; et al. Balancing hy-dropower and biodiversity in the Amazon, Congo, and Mekong. Science 2016, 351, 128–129. [Google Scholar] [CrossRef] [PubMed]
- Castello, L.; Macedo, M.N. Reducing adverse impacts of Amazon hydropower expansion. Environ. Conserv. 2016, 43, 107–117. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, X.; Zhao, H.; Ma, K. Development of a revised method for indicators of hydrologic alteration for analyzing the cumulative impacts of cascading reservoirs on flow regime. Hydrol. Earth Syst. Sci. 2020, 24, 4091–4107. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 2065. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, L.; Liu, T.; Li, J.; Feng, P. A Non-stationary Standardized Streamflow Index for hydrological drought using climate and human-induced indices as covariates. Sci. Total Environ. 2020, 699, 134278. [Google Scholar] [CrossRef]
- Sediqi, M.N.; Komori, D. Assessing Water Resource Sustainability in the Kabul River Basin: A Standardized Runoff Index and Reliability, Resilience, and Vulnerability Framework Approach. Sustainability 2023, 16, 246. [Google Scholar] [CrossRef]
- Asefa, T.; Clayton, J.; Adams, A.; Anderson, D. Performance evaluation of a water resources system under varying climatic conditions: Reliability, Resilience, Vulnerability and beyond. J. Hydrol. 2014, 508, 53–65. [Google Scholar] [CrossRef]
- Tangi, M.; Schmitt, R.; Almeida, R.; Bossi, S.; Flecker, A.; Sala, F.; Castelletti, A. Robust Hydropower Planning Balances Energy Generation, Carbon Emissions and Sediment Connectivity in the Mekong River Basin. Earth’s Future 2024, 12, e2023EF003647. [Google Scholar] [CrossRef]
- Sabo, J.L.; Ruhi, A.; Holtgrieve, G.W.; Elliott, V.; Arias, M.E.; Ngor, P.B.; Räsänen, T.A.; Nam, S. Designing river flows to improve food security futures in the Lower Mekong Basin. Science 2017, 358, 6368. [Google Scholar] [CrossRef]
- Adamson, P.T.; Rutherfurd, I.D.; Peel, M.C.; Conlan, I.A. The Hydrology of the Mekong River, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Sun, Q.; Song, W.; Han, Z.; Song, W.; Wang, Z. Assessment of Flood Disaster Risk in the Lancang–Mekong Region. Water 2024, 16, 3112. [Google Scholar] [CrossRef]
- Chen, D.; Liu, J.; Tang, Q. Water Resources in the Lancang-Mekong River Basin: Impact of Climate Change and Human Interventions; Springer: Singapore, 2024. [Google Scholar] [CrossRef]
- Hecht, J.S.; Lacombe, G.; Arias, M.E.; Dang, T.D.; Piman, T. Hydropower dams of the Mekong River basin: A review of their hydrological impacts. J. Hydrol. 2019, 568, 285–300. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Rubin, Z.K.; Minear, J.T. Dams on the Mekong: Cumulative sediment starvation. Water Resour. Res. 2014, 50, 5375–5377. [Google Scholar] [CrossRef]
- Ang, W.J.; Park, E.; Pokhrel, Y.; Tran, D.D.; Loc, H.H. Dams in the Mekong: A comprehensive database, spatiotemporal distribution, and hydropower potentials. Earth Syst. Sci. Data 2024, 16, 1209–1228. [Google Scholar] [CrossRef]
- Vu, D.T.; Dang, T.D.; Galelli, S.; Hossain, F. Satellite observations reveal 13 years of reservoir filling strategies, operating rules, and hydrological alterations in the Upper Mekong River basin. Hydrol. Earth Syst. Sci. 2022, 26, 2345–2364. [Google Scholar] [CrossRef]
- Chen, Q.; Shi, W.; Huisman, J.; Maberly, S.C.; Zhang, J.; Yu, J.; Chen, Y.; Tonina, D.; Yi, Q. Hydropower reservoirs on the upper Mekong River modify nutrient bioavailability downstream Qiuwen. Natl. Sci. Rev. 2020, 7, 1449–1457. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Luo, X. Precipitation and flow variations in the Lancang-Mekong River Basin and the implications of monsoon fluctuation and regional topography. Water 2019, 11, 2086. [Google Scholar] [CrossRef]
- Ngor, P.B.; McCann, K.S.; Grenouillet, G.; So, N.; McMeans, B.C.; Fraser, E.; Lek, S. Evidence of indiscriminate fishing effects in one of the world’s largest inland fisheries. Sci. Rep. 2018, 8, 8947. [Google Scholar] [CrossRef] [PubMed]
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The natural flow regime: A paradigm for river conservation and restoration. Bioscience 1997, 47, 769–784. [Google Scholar] [CrossRef]
- Poff, N.L.; Zimmerman, J.K.H. Ecological responses to altered flow regimes: A literature review to inform the science and management of environmental flows. Freshw. Biol. 2010, 55, 194–205. [Google Scholar] [CrossRef]
- Zhang, K.; Morovati, K.; Tian, F.; Yu, L.; Liu, B.; Olivares, M.A. Regional contributions of climate change and human activities to altered flow of the Lancang-mekong river. J. Hydrol. Reg. Stud. 2023, 50, 101535. [Google Scholar] [CrossRef]
- Pardo-Loaiza, J.; Solera, A.; Bergillos, R.J.; Paredes-Arquiola, J.; Andreu, J. Improving indicators of hydrological alteration in regulated and complex water resources systems: A case study in the duero river basin. Water 2021, 13, 2676. [Google Scholar] [CrossRef]
- Timpe, K.; Kaplan, D. The changing hydrology of a dammed Amazon. Sci. Adv. 2017, 3, e1700611. [Google Scholar] [CrossRef]
- DeGasperi, C.L.; Berge, H.B.; Whiting, K.R.; Burkey, J.J.; Cassin, J.L.; Fuerstenberg, R.R. Linking Hydrologic Alteration to Biological Impairment in Urbanizing Streams of the Puget Lowland, Washington, USA. J. Am. Water Resour. Assoc. 2009, 45, 512–533. [Google Scholar] [CrossRef]
- Vishwakarma, D.K.; Ali, R.; Bhat, S.A.; Elbeltagi, A.; Kushwaha, N.L.; Kumar, R.; Rajput, J.; Heddam, S.; Kuriqi, A. Pre- and post-dam river water temperature alteration prediction using advanced machine learning models. Environ. Sci. Pollut. Res. 2022, 29, 83321–83346. [Google Scholar] [CrossRef]
- Van Binh, D.; Kantoush, S.A.; Saber, M.; Mai, N.P.; Maskey, S.; Phong, D.T.; Sumi, T. Long-term alterations of flow regimes of the Mekong River and adaptation strategies for the Vietnamese Mekong Delta. J. Hydrol. Reg. Stud. 2020, 32, 100742. [Google Scholar] [CrossRef]
- Richter, B.D.; Baumgartner, J.V.; Powell, J.; Braun, D.P. A method for assessing hydrologic alteration within ecosystems. Conserv. Biol. 1996, 10, 1163–1174. [Google Scholar] [CrossRef]
- Ringnér, M. What is principal component analysis? Nat. Biotechnol. 2008, 26, 303–304. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D.A. Stopping Rules in Principal Components Analysis: A Comparison of Heuristical and Statistical Approaches. Ecology 1993, 74, 2204–2214. [Google Scholar] [CrossRef]
- He, W.; Ma, C.; Zhang, J.; Lian, J.; Wang, S.; Zhao, W. Multi-objective optimal operation of a large deep reservoir during storage period considering the outflow-temperature demand based on NSGA-II. J. Hydrol. 2020, 586, 124919. [Google Scholar] [CrossRef]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Loucks. Reliability, Resiliency, and Vulnerability Criteria. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Zeng, P.; Sun, F.; Liu, Y.; Che, Y. Future river basin health assessment through reliability-resilience-vulnerability: Thresholds of multiple dryness conditions. Sci. Total Environ. 2020, 741, 140395. [Google Scholar] [CrossRef]
- Zou, L.; Xia, J.; She, D. Analysis of Impacts of Climate Change and Human Activities on Hydrological Drought: A Case Study in the Wei River Basin, China. Water Resour. Manag. 2018, 32, 1421–1438. [Google Scholar] [CrossRef]
- GB/T 20481-2017; Meteorological Drought Classification. Chinese Standardization Administration; Standards Press of China: Beijing, China, 2017.

| Component | Representative Parameter | λ | Original Contribution (%) | Corrected Contribution () |
|---|---|---|---|---|
| PC 1 | 90-day Maximum (A17) | 13.93 | 43.5 | 49 |
| PC 2 | Mean flow in April (A4) | 4.09 | 12.8 | 14 |
| PC 3 | Mean flow in November (A11) | 2.95 | 9.2 | 10 |
| PC 4 | Date of maximum (A24) | 2.85 | 8.9 | 10 |
| PC 5 | Low pulse duration (A29) | 1.83 | 5.7 | 6 |
| PC 6 | Number of reversals (A32) | 1.31 | 4.1 | 5 |
| PC 7 | High pulse count(A26) | 1.25 | 3.9 | 4 |
| Total | 88.2 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhu, T. Integrating Eco-Index and Hydropower Optimization for Cascade Reservoir Operations in the Lancang–Mekong River Basin. Water 2025, 17, 2966. https://doi.org/10.3390/w17202966
Li C, Zhu T. Integrating Eco-Index and Hydropower Optimization for Cascade Reservoir Operations in the Lancang–Mekong River Basin. Water. 2025; 17(20):2966. https://doi.org/10.3390/w17202966
Chicago/Turabian StyleLi, Ci, and Tingju Zhu. 2025. "Integrating Eco-Index and Hydropower Optimization for Cascade Reservoir Operations in the Lancang–Mekong River Basin" Water 17, no. 20: 2966. https://doi.org/10.3390/w17202966
APA StyleLi, C., & Zhu, T. (2025). Integrating Eco-Index and Hydropower Optimization for Cascade Reservoir Operations in the Lancang–Mekong River Basin. Water, 17(20), 2966. https://doi.org/10.3390/w17202966





