Construction and Comparative Analysis of a Water Quality Simulation and Prediction Model for Plain River Networks
Abstract
1. Introduction
2. Numerical Simulation Methods and Application Analysis
2.1. Study Area and Data Sources
2.1.1. Overview of the Study Area
2.1.2. Data Sources and Processing
2.2. Numerical Model Construction
2.2.1. Development of the MIKE Hydrodynamic—Water Quality Model
2.2.2. Development of the CNN-LSTM-Attention Model
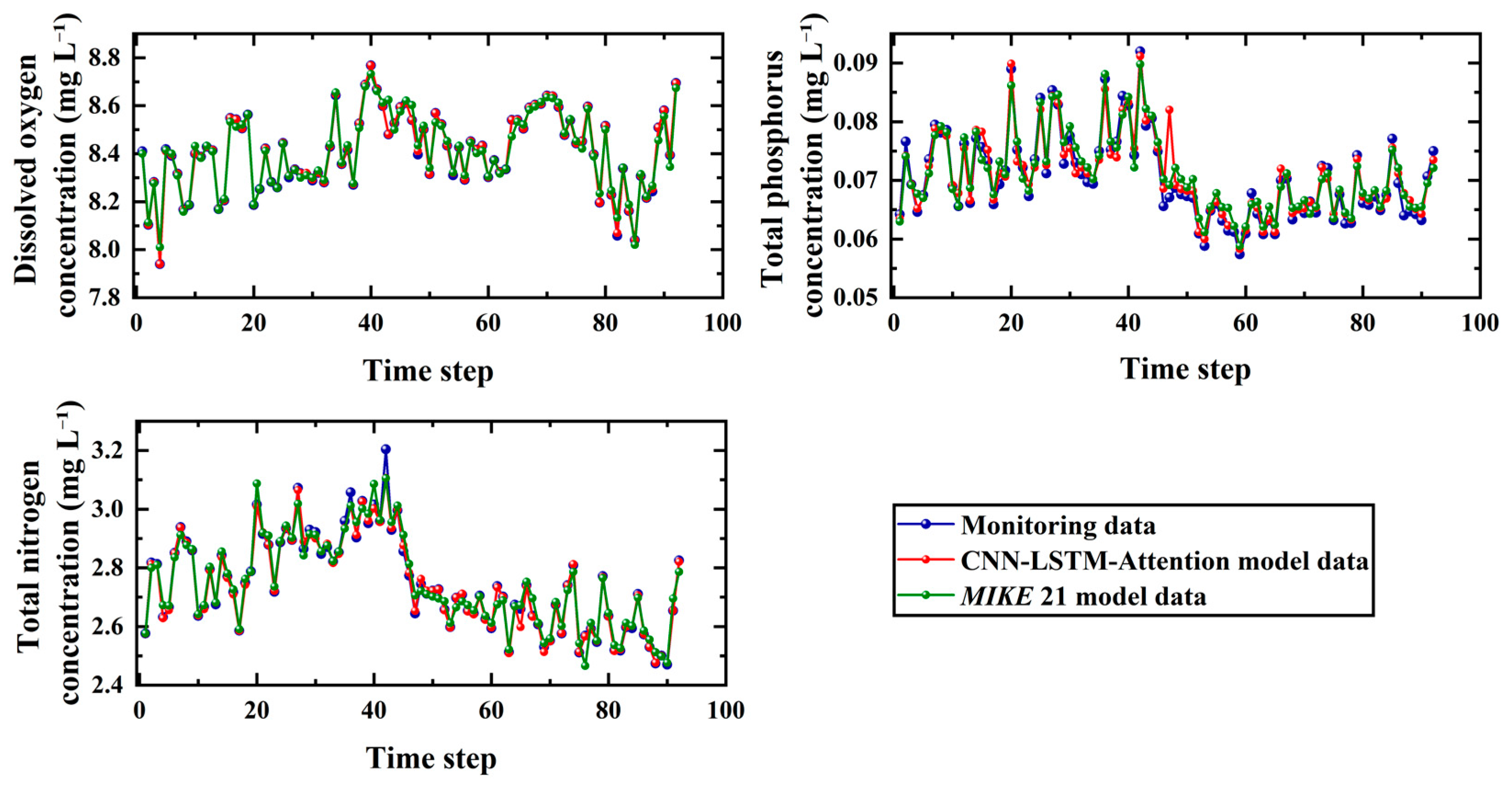
2.3. Model Validation and Results Analysis
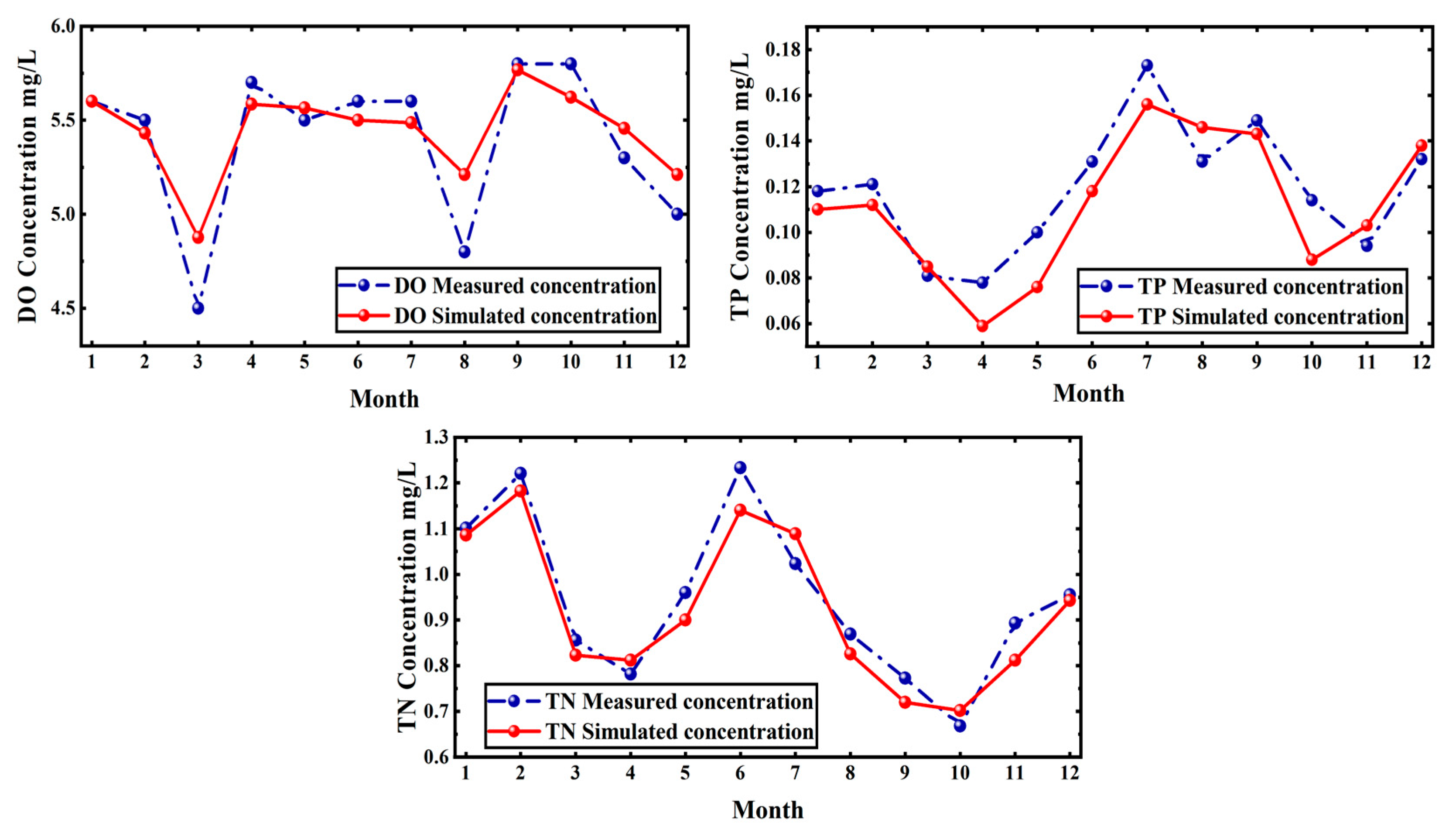
2.3.1. MIKE Model Validation Results
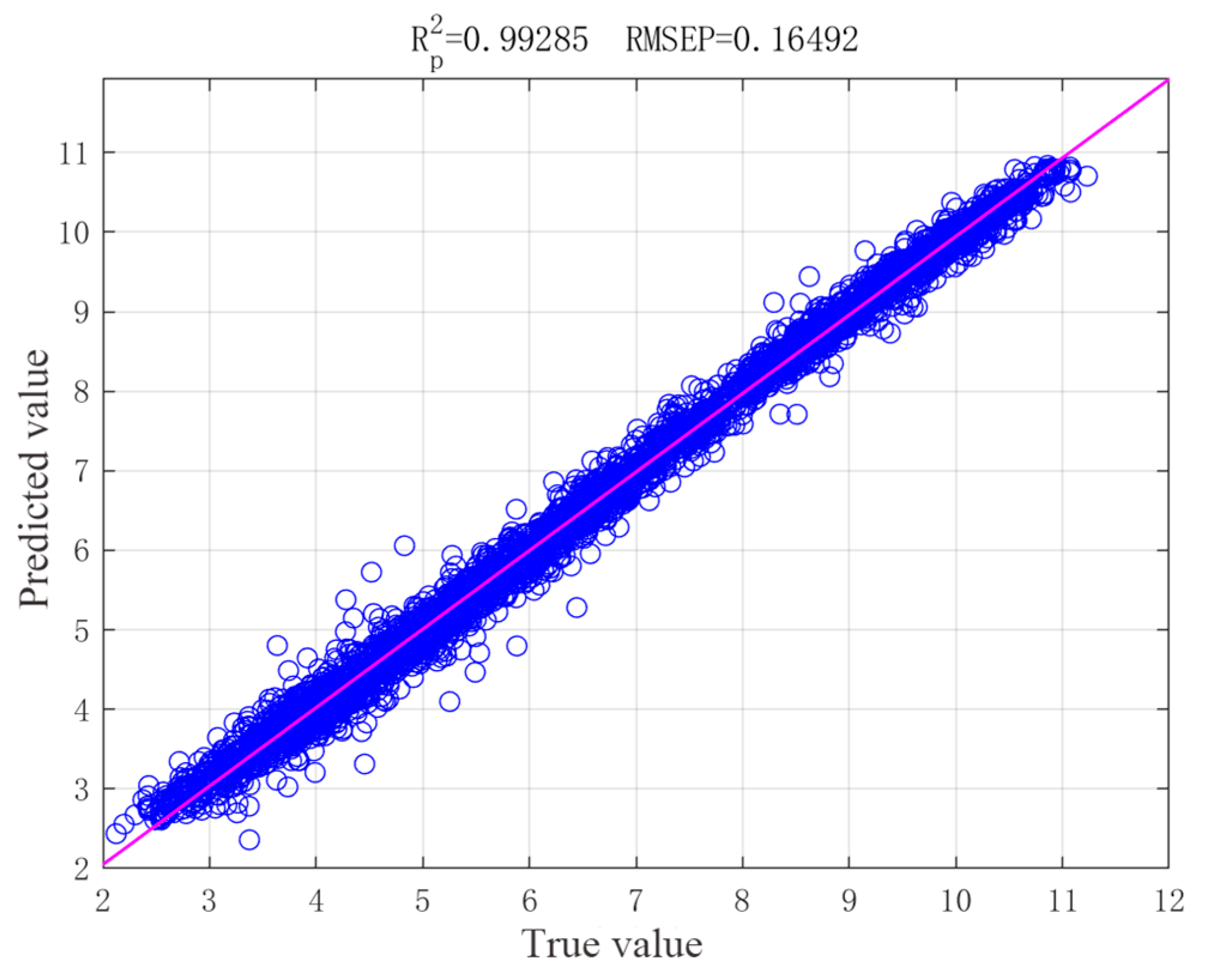
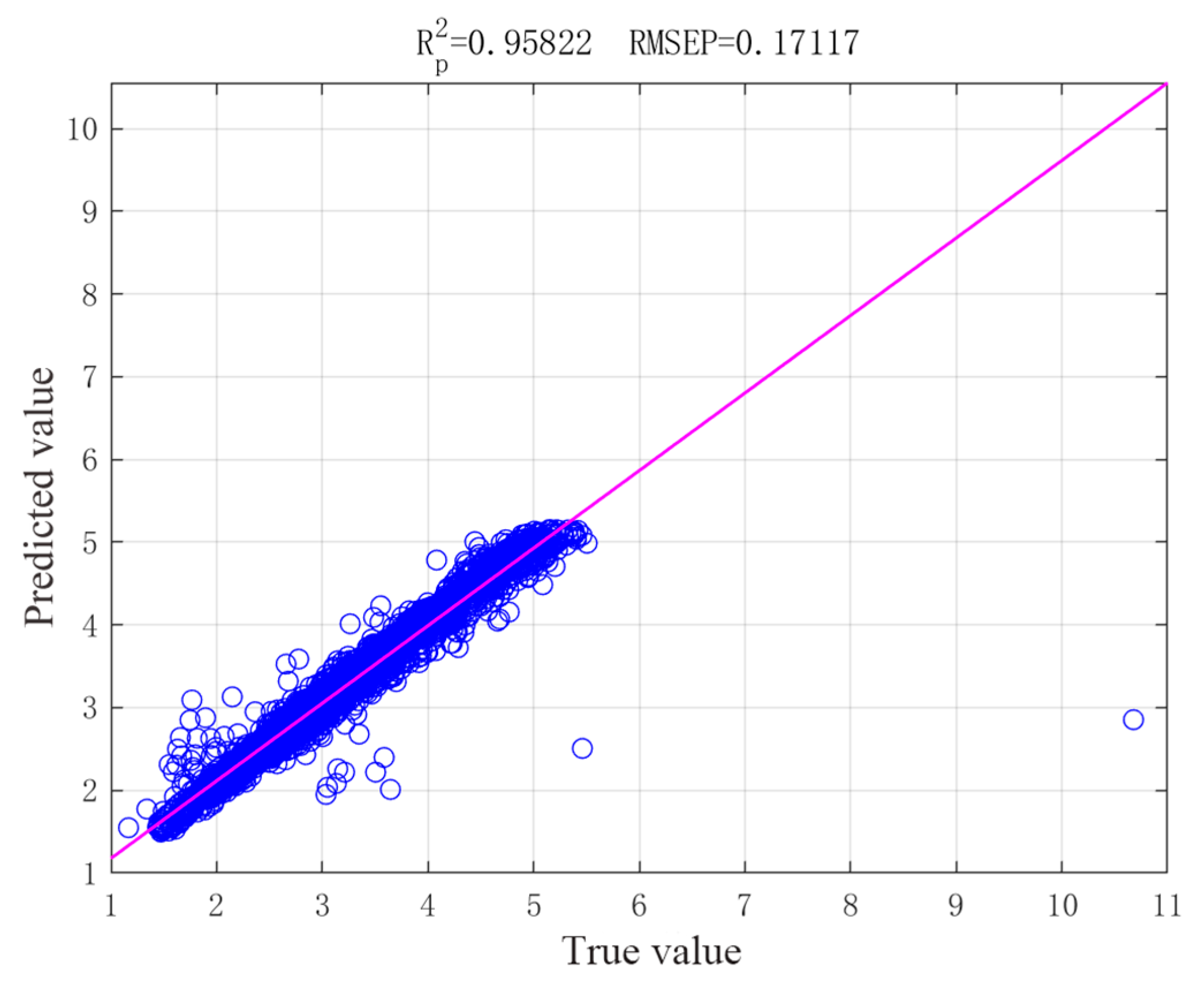
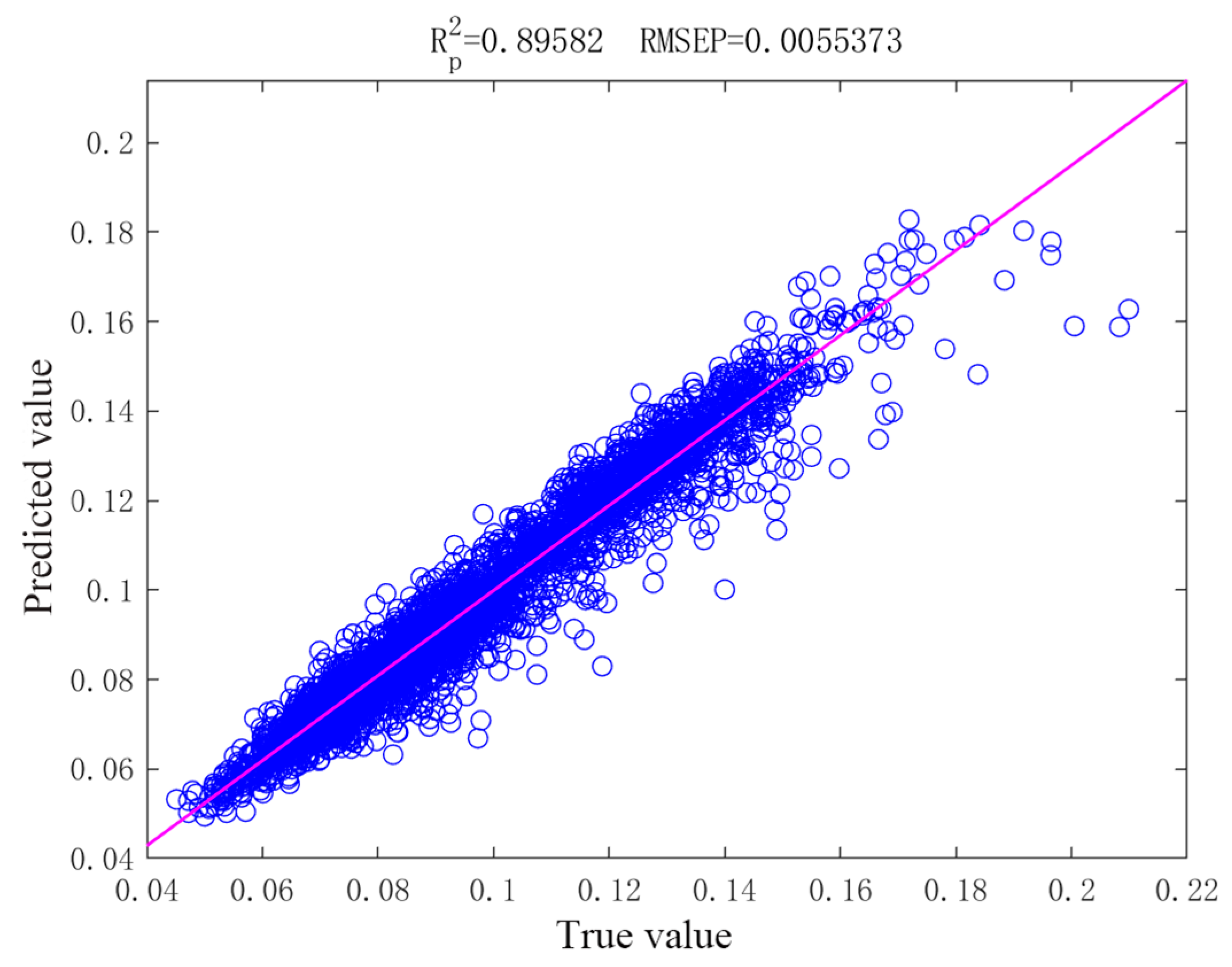
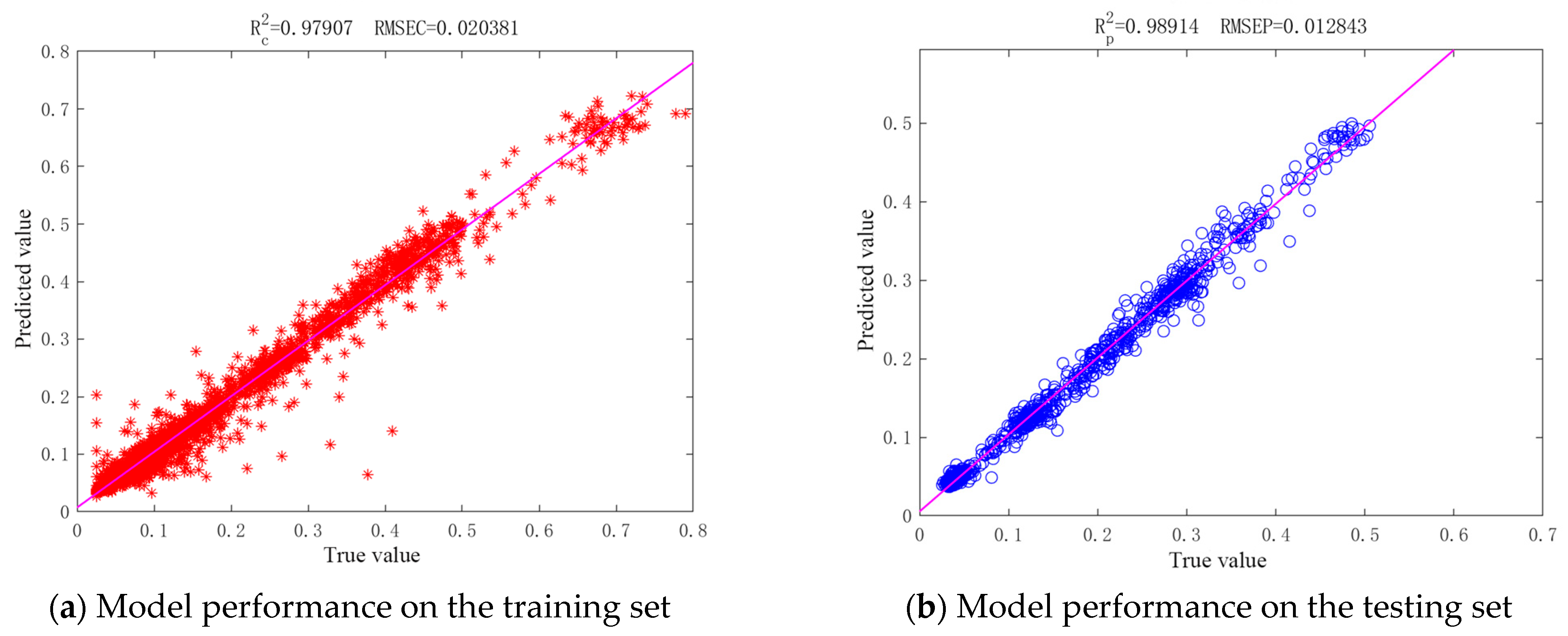
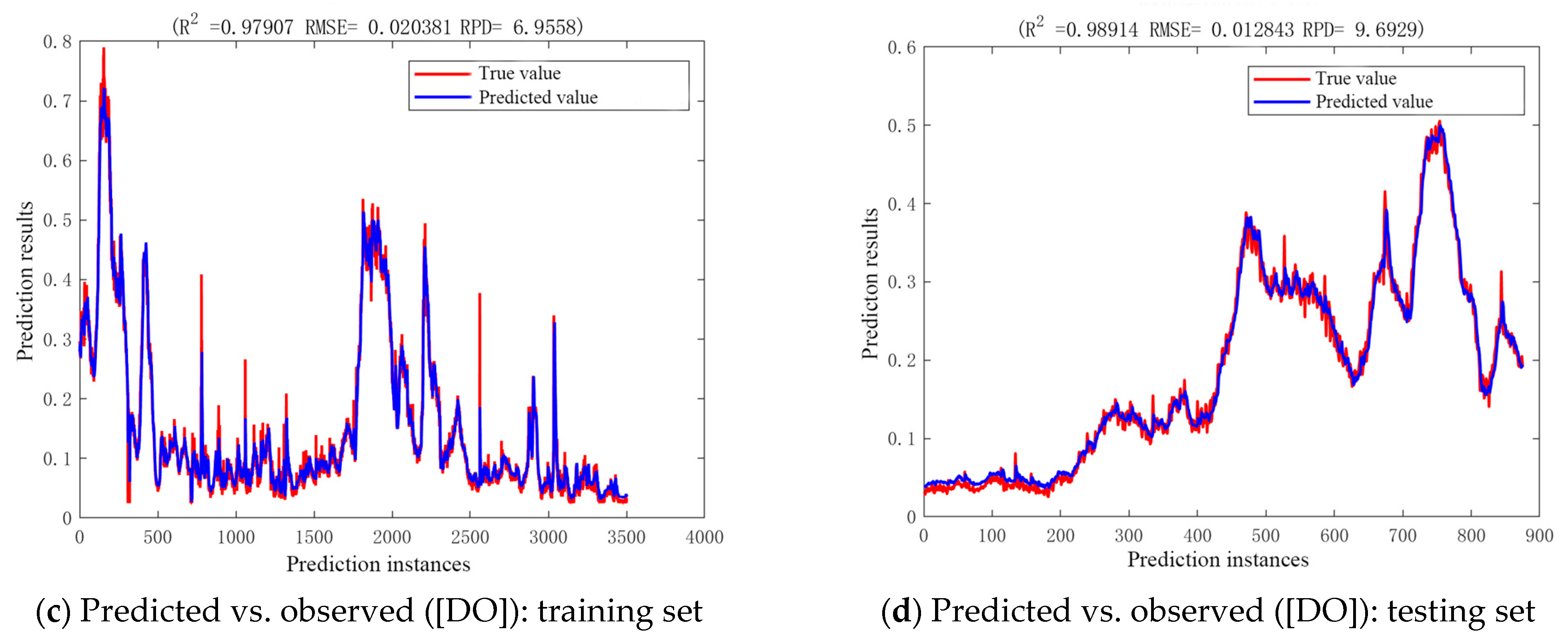
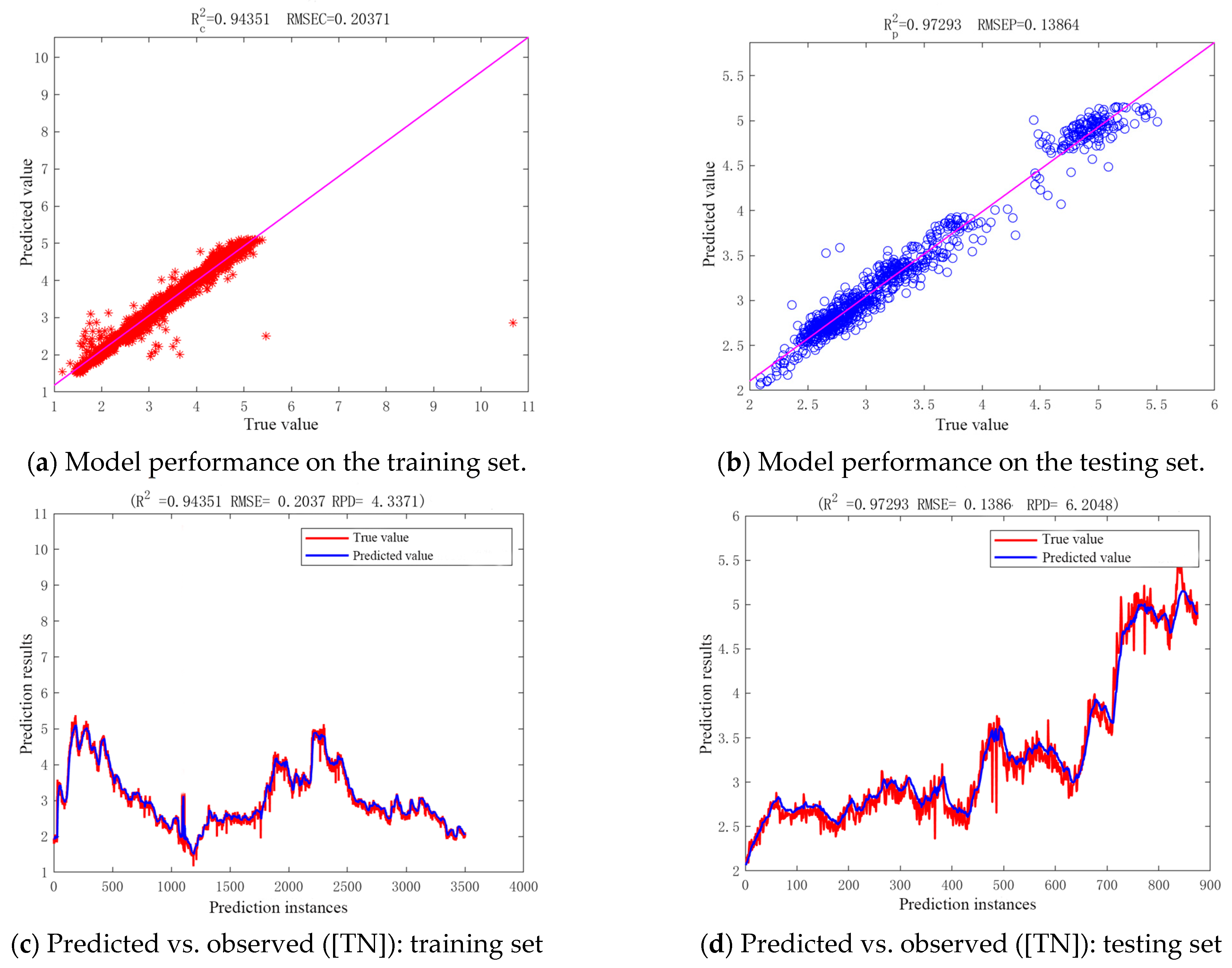
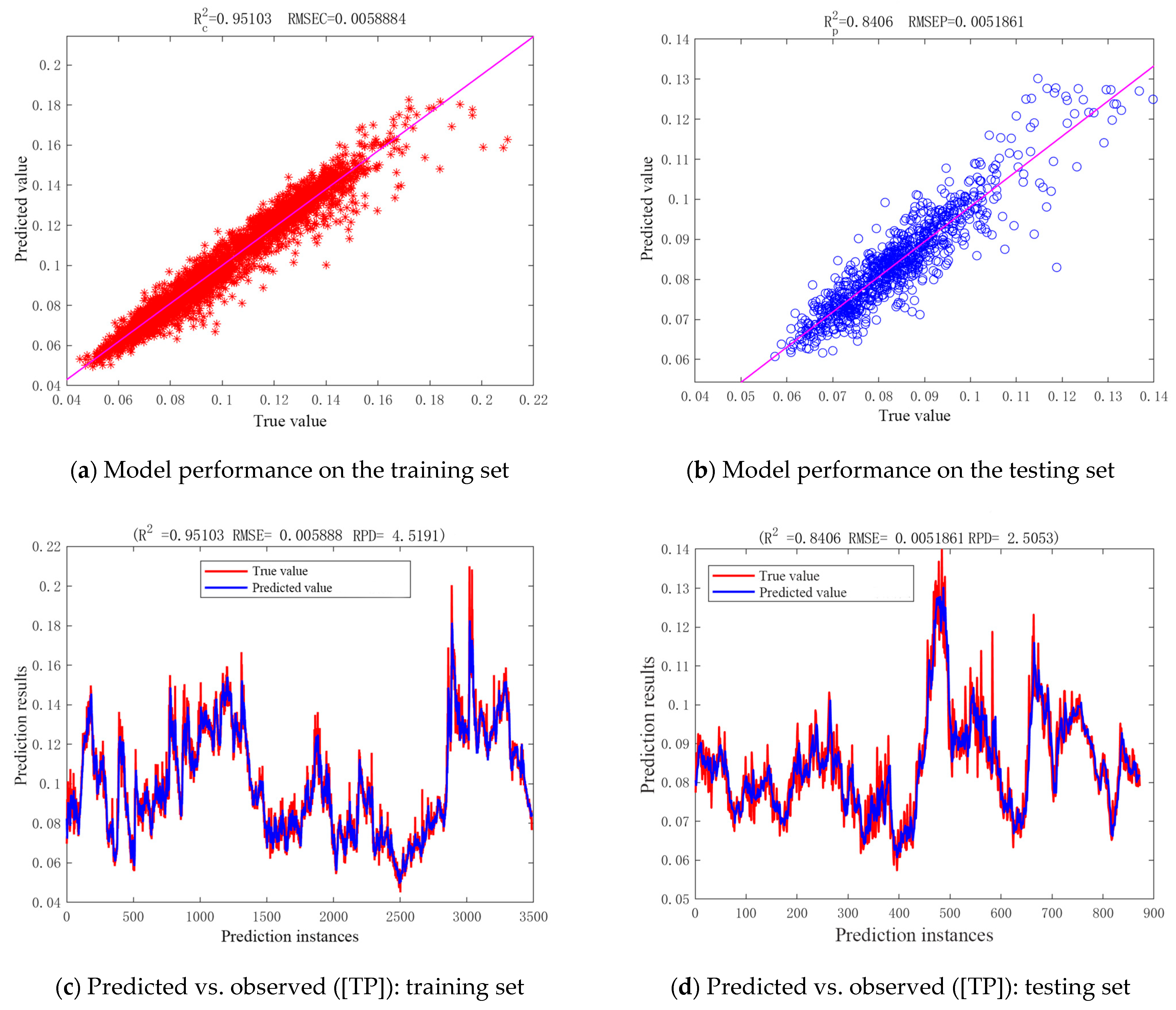
2.3.2. CNN-LSTM-Attention Model Validation Results
3. Discussion
4. Conclusions
- (1)
- The physics-based MIKE 21 model excels in simulating spatiotemporal distributions of hydrodynamics and water quality parameters across the river network (R2 > 0.88 for all three indicators), quantitatively capturing the impacts of sluice gates and the causal relationships between hydrodynamics and water quality. Its strengths in spatial resolution and physical interpretability cannot be replicated by deep learning approaches.
- (2)
- The CNN-LSTM-Attention model integrates spatial feature extraction and temporal modeling, and focuses on critical events, significantly enhancing point-scale prediction accuracy (DO R2 = 0.9934; TN R2 = 0.9435) for complex nonlinear dynamics and high-frequency fluctuations. However, its lower TP prediction accuracy (R2 = 0.8406) indicates limitations in simulating processes involving interfacial exchanges and complex biochemical reactions like phosphorus cycling.
- (3)
- Practical applications require model–target alignment: the CNN-LSTM-Attention is preferred for high-precision short-term forecasting or real-time alerts with sufficient data, while MIKE 21 is better suited for identifying the spatial mechanisms of pollutants, evaluating engineering measures, or simulating complex hydrological scenarios.
- (4)
- Future work should develop physics-informed hybrid models by integrating MIKE 21’s hydrodynamic fields as feature inputs and enhancing reliability through physical constraints to synergize both paradigms, ultimately strengthening the precision management of river network water environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, T.Y.; Liu, K.Q.; Shan, Y.S.; He, S. Flood control situation analysis and countermeasure research for river network areas in the Hangjiahu Plain. China Rural Water Hydropower 2019, 2019, 123–125. [Google Scholar]
- Zou, S.W.; Wang, H.Z.; Yuan, S.J. Key technologies and case analysis for water quality enhancement in plain river networks: A case study of Hongkou waterways. Water Purif. Technol. 2022, 41, 116–121. [Google Scholar]
- Li, X.; Tang, H.W.; Wang, L.L.; Hu, Z.J.; Jiao, C. Hydro-environmental simulation of integrated regulation of sluice-pump systems in plain river network regions. J. Hohai Univ. (Nat. Sci.) 2016, 44, 393–399. [Google Scholar]
- Huang, Z.R.; Miao, Y.; Zhang, Z.L. Development of flood control decision support system for plain river network cities in Taihu Basin. People's Yangtze 2023, 54, 16–19. [Google Scholar]
- Xu, C.D.; Zi, Y.H.; Huang, S.; Zhao, Z.H.; Ren, Z.H.; Hu, X.M.; Wang, H.R. Hydrodynamic regulation method for polder river networks based on MIKE 21. Water Resour. Hydropower Eng. 2023, 54, 161–170. [Google Scholar]
- Zainescu, F.; Vespremeanu-Stroe, A.; Anthony, E.; Tatui, F.; Preoteasa, L.; Mateescu, R. Flood deposition and storm removal of sediments in front of a deltaic wave-influenced river mouth. Mar. Geol. 2019, 417, 106015. [Google Scholar] [CrossRef]
- Khatib, M.; Kahil, M.; Soliman, M.R. Restoration of Qaraoun Lake aquatic life based on wetland treatment concept. Heliyon 2023, 9, e18169. [Google Scholar] [CrossRef]
- Ahmed, A.; Aidi, H.; Liu, Q.; Zhao, X.T.; Zhao, S.M. Tracing heavy metal migration in stone coal mining watersheds: Insights from coupled SWAT-MIKE21-ECO lab simulations. Chemosphere 2025, 385, 144588. [Google Scholar] [CrossRef]
- Elshemy, M.; Khadr, M.; Atta, Y.; Ahmed, A. Hydrodynamic and water quality modeling of Lake Manzala (Egypt) under data scarcity. Environ. Earth Sci. 2016, 75, 1329. [Google Scholar] [CrossRef]
- Hosseini-Sadabadi, S.A.; Rousseau, N.A.; Laurion, I.; Behmel, S.; Sadeghian, A.; Foulon, E.; Wauthy, M.; Cantin, A.-M. Spatiotemporal insights of phytoplankton dynamics in a northern, rural-urban lake using a 3D water quality model. J. Environ. Manag. 2024, 370, 122687. [Google Scholar] [CrossRef]
- Al-Rikab, W.J.; Abed Basim, S. Hydraulic behaviour and improving of water quality of the Chibayish Marshes. Mater. Today Proc. 2022, 60, 1459–1467. [Google Scholar] [CrossRef]
- Qin, Z.; He, Z.; Wu, G.; Tang, G.; Wang, Q. Developing Water-Quality Model for Jingpo Lake Based on EFDC. Water 2022, 14, 2596. [Google Scholar] [CrossRef]
- Maruthamuthu, R.; Balamurugan, S.; Kumar, N.N.; Kumar, K.D. Enhanced Water Quality Index Prediction using a Dual-Key Convolutional Transformer Autoencoder Network Integrating with Poplar Optimization. Franklin Open 2025, 100370. [Google Scholar] [CrossRef]
- Wai, K.P.; Koo, C.H.; Huang, Y.F.; Chong, W.C.; El-Shafie, A.; Sherif, M.; Ahmed, A.N. A practical temporal transfer learning model for multi-step water quality index forecasting using A CNN-coupled dual-path LSTM network. J. Hydrol. Reg. Stud. 2025, 60, 102553. [Google Scholar] [CrossRef]
- Meysam, A.; Salim, H.; Sungwon, K. A robust and explainable deep learning model based on an LSTM-CNN framework for reliable FDOM prediction in water quality monitoring: Incorporating SHAP analysis for enhanced interpretability. Process Saf. Environ. Prot. 2025, 107594. [Google Scholar] [CrossRef]
- Wang, Y.F.; Xie, L.Z.; Zhang, J.J.; Tian, Y.Z.; Li, S.S.; Wang, Y.G. Performance Evaluation of Water Quality Prediction for Different Durations Based on the ED-LSTM Model. South-North Water Transf. Water Sci. Technol. (Chin. Engl.), 2025; in press. [Google Scholar]
- Liu, K.; Liu, F.; Peng, Y.X.; Zhang, S.N.; Fan, J.; Du, X.N.; Wang, Z.R. Evaluation and Prediction of Watershed Water Quality Based on Machine Learning Models. Environ. Pollut. Control 2025, 47, 1–10. [Google Scholar]
- Xiao, F.; Zhang, R.; Jian, Z.; Liu, W.; Sun, T.; Pang, W.; Han, L.; Qin, H. Using ensemble machine learning to predict and understand spatiotemporal water quality variations across diverse watersheds in coastal urbanized areas. Ecol. Indic. 2025, 178, 113976. [Google Scholar] [CrossRef]
- Melikoglu, M. Predictive hybrid modelling for municipal water and wastewater: A global framework demonstrated in Türkiye. Cleaner Water 2025, 4, 100117. [Google Scholar] [CrossRef]
- GB 3838-2002; Environmental Quality Standards for Surface Water. Ministry of Environmental Protection of the People’s Republic of China: Beijing, China, 2002.
- Zhao, Y.H. Economic benefit analysis of flood control projects in polder areas: Case study of Yaozhuang Polder in Jiashan County. Zhejiang Hydrotech. 2010, 38–42. [Google Scholar] [CrossRef]
- Li, W.X.; Jiang, M.L.; Xu, L.G.; Hu, S.P.; You, H.L.; Zhou, Q.P.; Chen, Z.; Zhang, L. Spatiotemporal variation of phytoplankton in Poyang Lake and its response to extreme flood and drought events. J. Lake Sci. 2024, 1–15. [Google Scholar]
- Ju, J.Y.; Liu, J.G.; Zhang, X.L.; Hu, D.D.; Li, Z.Y. Study on Urban Flood Simulation in Zhengdong New District Based on MIKE Coupled Model. Water Resour. Power 2025, 16–20. [Google Scholar]
- Suriya, S.; Mudgal, B.V. Impact of urbanization on flooding: The Thirusoolam sub watershed-A case study. J. Hydrol. 2012, 412–413, 210–219. [Google Scholar] [CrossRef]
- Wahyudi, W.; Martono, D.; Utomo, S.; Sutjiningsih, D. Investigating Impact of Sea Sand Mining in Tunda Island Waters, Indonesia Based in Mike 21 Modelling. Croat. J. Fish. 2023, 81, 73–81. [Google Scholar] [CrossRef]
- Quinteros-Cartaya, C.; Köhler, J.; Li, W.; Faber, J.; Srivastava, N. Exploring a CNN model for earthquake magnitude estimation using HR-GNSS data. J. South Am. Earth Sci. 2024, 136, 136104815. [Google Scholar] [CrossRef]
- Cheng, Y.; Yin, H.L. A water quality prediction model for municipal pumping stations based on feature extraction optimization and CNN-LSTM. Acta Sci. Circumstantiae 2025, 1–9. [Google Scholar] [CrossRef]
- Salem, M.S.; Hassan, N.M.H.; Aly, M.M.; Soliman, Y.; Peters, R.W.; Mostafa, M.K. Integrating Deep Learning and Process-Based Modeling for Water Quality Prediction in Canals: CNN-LSTM and QUAL2K Analysis of Ismailia Canal. Sustainability 2025, 17, 7743. [Google Scholar] [CrossRef]
- Hassan, N.; Miah, M.S.A.; Shin, J. A Deep Bidirectional LSTM Model Enhanced by Transfer-Learning-Based Feature Extraction for Dynamic Human Activity Recognition. Appl. Sci. 2024, 14, 603. [Google Scholar] [CrossRef]
- Jin, C.; Li, B.; Yang, L.F.; Zhou, X.Z. Open channel flow velocity prediction model based on machine learning-CFD. People's Yangtze 2023, 54, 166–174. [Google Scholar]
- Ren, P.; Chen, M.X.; Cao, W.H.; Wang, Z.; Han, L.; Song, L.; Yang, L. Error analysis and correction of short-term numerical weather prediction under complex terrain based on machine learning. Acta Meteorol. Sin. 2020, 78, 1002–1020. [Google Scholar]
- Li, W.L. Research on Sequence Recommendation Algorithm Integrating Attention Mechanism and Multimodal Information. Master’s Thesis, Tianjin University of Technology, Tianjin, China, 2023. [Google Scholar]
- Tasnim, B.; Fang, X.; Hayworth, J.S. Hayworth. One- and Three-Dimensional Hydrodynamic, Water Temperature, and Dissolved Oxygen Modeling Comparison. Water 2024, 16, 317. [Google Scholar] [CrossRef]
- Quaghebeur, W.; Torfs, E.; De Baets, B.; Nopens, I. Hybrid differential equations: Integrating mechanistic and data-driven techniques for modellingof water systems. Water Res. 2022, 213, 118166. [Google Scholar] [CrossRef]
- Boris, V.; Divinsky, Y.; Saprykina, V. Quasi-homogeneous regions of climatic distributions of wind wave parameters in the Black Sea. Dyn. Atmos. Ocean. 2025, 110, 101535. [Google Scholar] [CrossRef]
- Baste, S.; Klotz, D.; Acuña Espinoza, E.; Bardossy, A.; Loritz, R. Unveiling the Limits of Deep Learning Models in Hydrological Extrapolation Tasks. EGUsphere, 2025; preprint. [Google Scholar]
- Sheikholeslami, R.; Hall, J.W. Global patterns and key drivers of stream nitrogen concentration: A machine learning approach. Sci. Total Environ. 2023, 868, 161623. [Google Scholar] [CrossRef]
- Kim, S.; Lee, E.; Hwang, H.-T.; Pyo, J.; Yun, D.; Baek, S.-S.; Cho, K.H. Spatiotemporal estimation of groundwater and surface water conditions by integrating deep learning and physics-based watershed models. Water Res. 2024, 23, 100228. [Google Scholar] [CrossRef]
- Zhong, M.; Zhang, H.R.; Wang, Y.F.; Geng, H. Runoff prediction using a hybrid physical mechanism and deep learning approach. Yunnan Electr. Power Technol. 2023, 51, 2–6+12. [Google Scholar]
- Erge, O.; van Oort, E. Combining physics-based and data-driven modeling in well construction: Hybrid fluid dynamics modeling. J. Nat. Gas Sci. Eng. 2022, 97, 104348. [Google Scholar] [CrossRef]


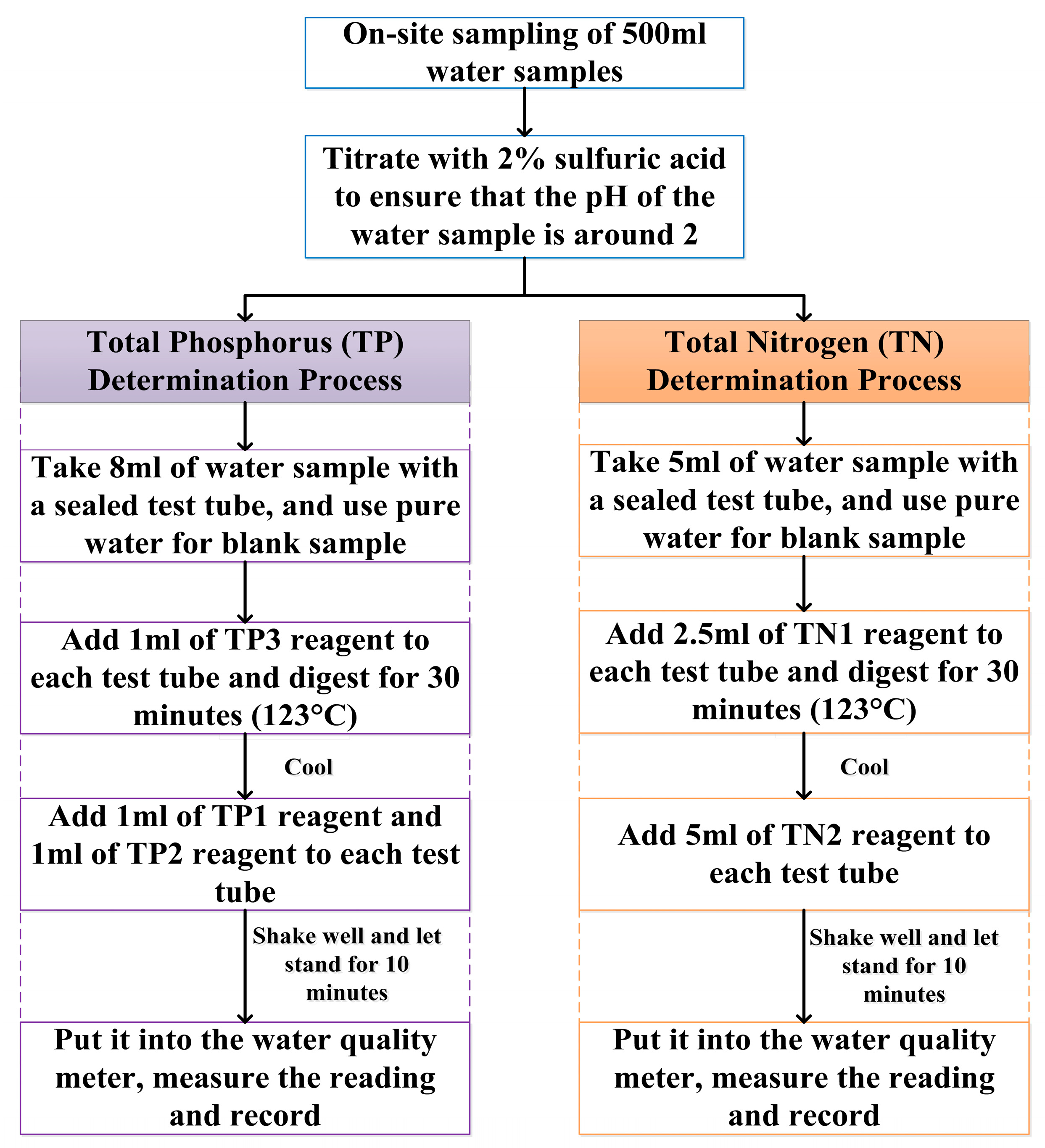
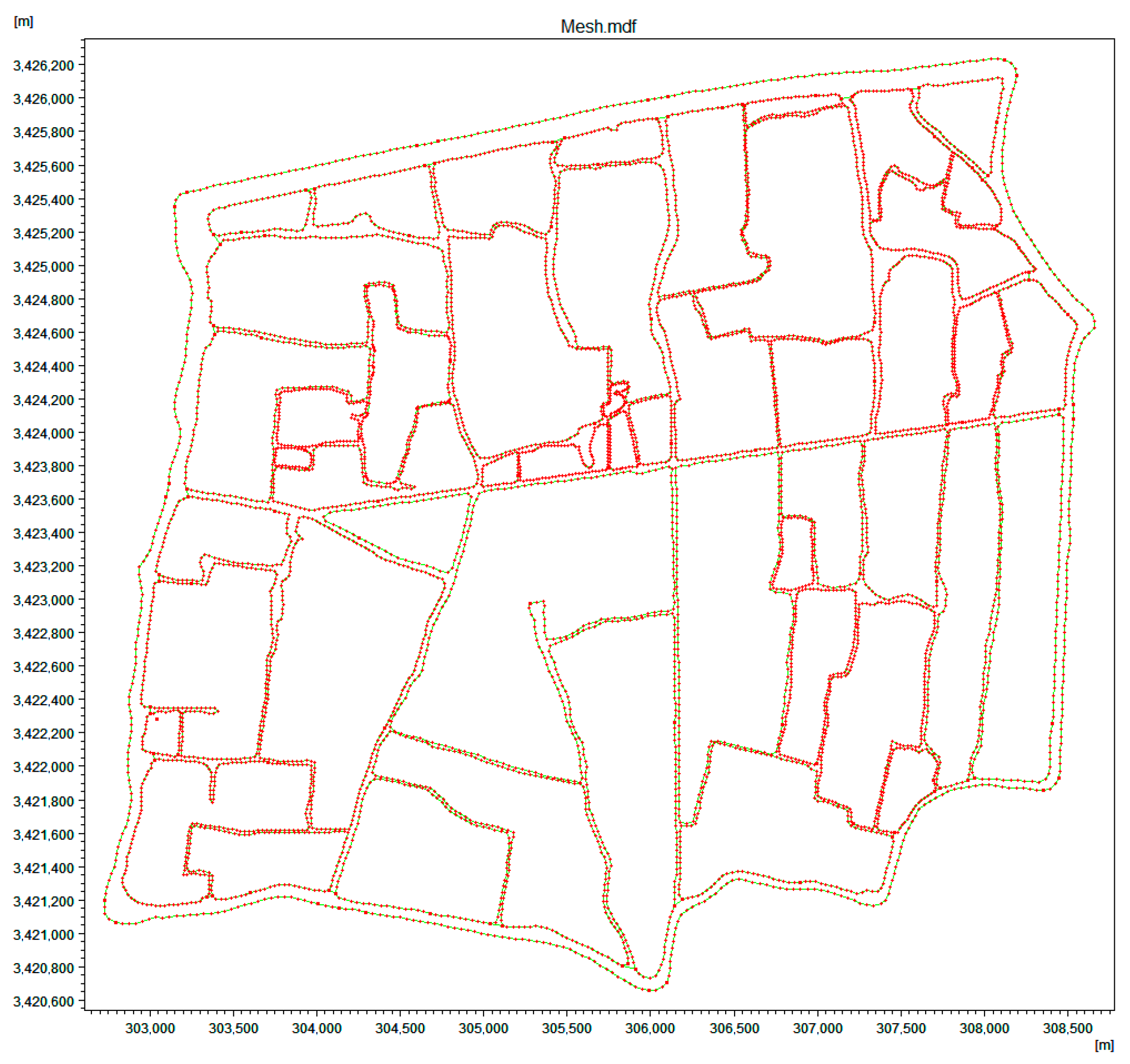

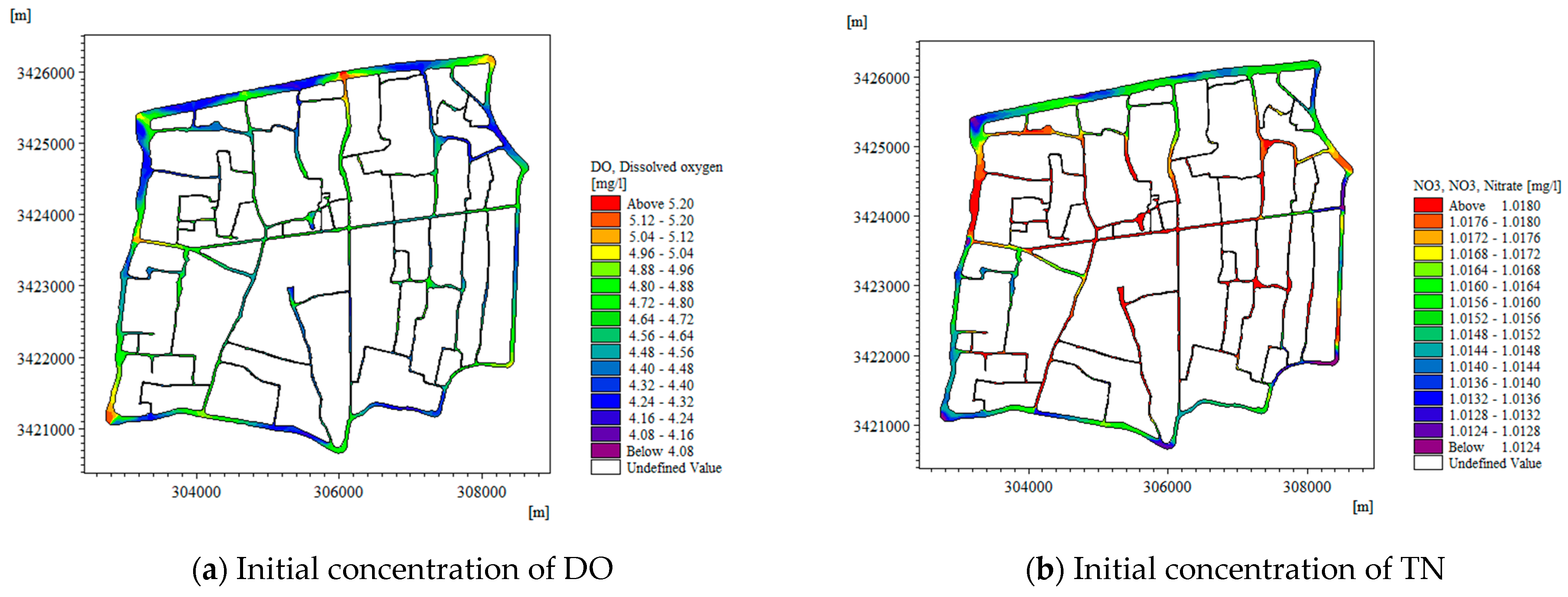


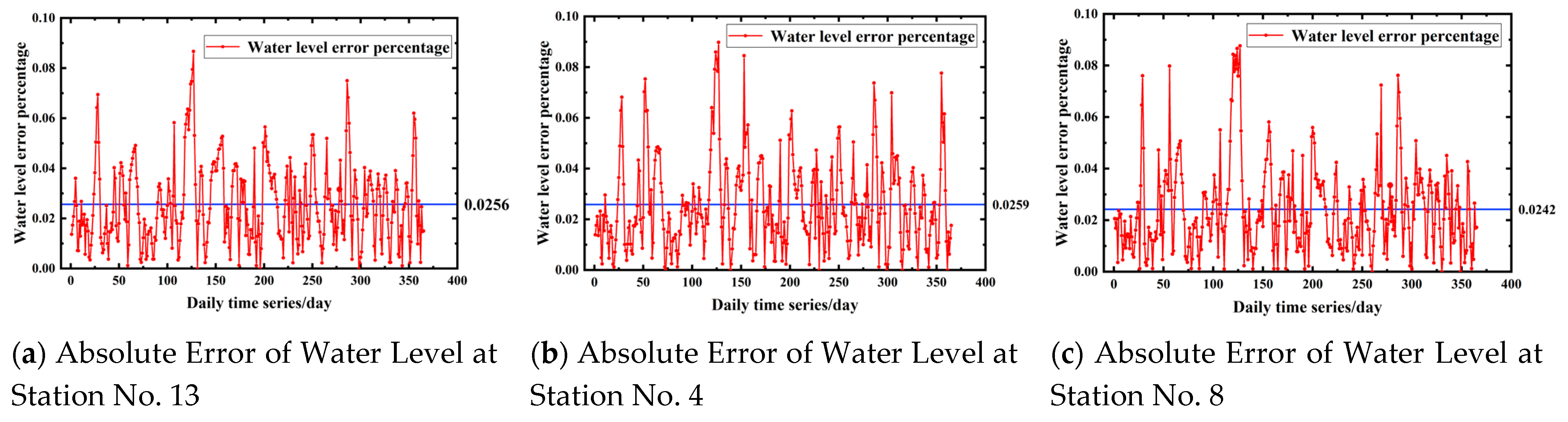
| Data Purpose | Data Source | Data Type | Time Period | Model/Analysis Applied |
|---|---|---|---|---|
| Hydrodynamic model calibration and validation | Polder Meteorological Station | Water Level | Year 2022 | MIKE 21 HD Module |
| Water quality model calibration and validation | Jiashan Hydrological Bureau | Monthly Water Quality (DO, TN, TP) | Year 2022–Year 2023 | MIKE 21 ECO Lab Module |
| Deep learning model training and testing | Hongqitang Dam Station Long-term Monitoring | High-frequency Water Quality (DO, TN, TP) | January 2022–February 2024 | CNN-LSTM-Attention Model |
| Comparative analysis of both models | Field Monitoring data | Daily Water Quality (DO, TN, TP) | October–December 2023 | MIKE 21 and CNN-LSTM-Attention Models |
| Parameter Symbol | Parameter Description | Value | Unit |
|---|---|---|---|
| DO | Maximum oxygen concentration at noon | 2 | per day |
| Half-saturation constant for respiration | 2 | mg/L | |
| Plant respiration rate | 0.125 | per day | |
| Respiration temperature coefficient | 1.08 | dimensionless | |
| Oxygen demand for nitrification (NH4-NO2) | 3.44 | gO2/g NH3-N | |
| Oxygen demand for nitrification (NO2-NO3) | 1.12 | gO2/g NO2-N | |
| Half-saturation constant for sediment oxygen demand | 2 | mg/L | |
| Sediment oxygen demand (per m2) | 0.5 | per day | |
| SOD temperature coefficient | 1.05 | dimensionless | |
| TP | Phosphorus fraction in dissolved COD | 1.088 | -- |
| Phosphorus uptake by plants | 0.092 | g P/g DO | |
| Phosphorus uptake by bacteria | 0.015 | g P/g DO | |
| Half-saturation constant for P uptake | 0.005 | mg/L | |
| TN | Half-saturation constant for nitrogen uptake | 0.05 | mg/L |
| Nitrogen uptake by bacteria | 0.108 | g N/g DO | |
| First-order decay rate for nitrification | 0.05 | per day | |
| Half-saturation constant for oxygen in nitrification | 2 | mg/L |
| Layer Type | Parameter | Setting Value | Design Purpose |
|---|---|---|---|
| CNN | Kernel Size | (3, 3) | Capturing local spatial features and patterns. |
| Number of Kernels | 64 | Extracting high-dimensional spatial representations. | |
| Activation Function | ReLU | Introducing nonlinearity. | |
| LSTM | Hidden Units | 128 | Modeling temporal dependencies and long-term dynamics. |
| Timesteps | 100 | Providing sufficient historical contexts for prediction. | |
| Dropout Rate | 0.2 | Mitigating overfitting for better generalization. | |
| Attention | Attention Mechanism | Bahdanau Attention | Focusing adaptively on critical time steps for decoding. |
| Attention Dimensionality | 32 | Balancing representational capacity and computational cost. | |
| Others | Optimizer | Adam | Efficient optimization of complex nonlinear models. |
| Learning Rate | 0.001 | Ensuring stable convergence. | |
| Batch Size | 32 | Balancing training efficiency and gradient stability. | |
| Epochs | 8100 | Sufficient for model convergence. | |
| Loss Function | Cross-Entropy Loss | Suitable for classification tasks. |
| Water Quality Indicators | DO | TN | TP |
|---|---|---|---|
| R2 | 0.889 | 0.942 | 0.880 |
| δ | 6.57% | 4.82% | 7.12% |
| Performance Index | Full Dataset (Training + Test) | CNN | LSTM | CNN-LSTM-Attention |
|---|---|---|---|---|
| RMSE | DO | 0.2532 | 0.2260 | 0.1649 |
| TN | 0.3446 | 0.3026 | 0.1712 | |
| TP | 0.0077 | 0.0075 | 0.0055 | |
| R2 | DO | 0.9167 | 0.9613 | 0.9929 |
| TN | 0.9092 | 0.9270 | 0.9582 | |
| TP | 0.8459 | 0.8574 | 0.8958 | |
| RPD | DO | 7.7619 | 8.5595 | 12.0074 |
| TN | 3.5813 | 3.8501 | 5.2709 | |
| TP | 2.4902 | 2.6147 | 3.5122 |
| Prediction Model | DO | TN | TP |
|---|---|---|---|
| MIKE 21 Model | 0.912 | 0.921 | 0.877 |
| CNN-LSTM-Attention Model | 0.977 | 0.982 | 0.834 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, Y.; Xu, C.; Ding, L.; Wang, M.; Ren, Z.; Wang, Z. Construction and Comparative Analysis of a Water Quality Simulation and Prediction Model for Plain River Networks. Water 2025, 17, 2948. https://doi.org/10.3390/w17202948
Lan Y, Xu C, Ding L, Wang M, Ren Z, Wang Z. Construction and Comparative Analysis of a Water Quality Simulation and Prediction Model for Plain River Networks. Water. 2025; 17(20):2948. https://doi.org/10.3390/w17202948
Chicago/Turabian StyleLan, Yue, Cundong Xu, Lianying Ding, Mingyan Wang, Zihao Ren, and Zhihang Wang. 2025. "Construction and Comparative Analysis of a Water Quality Simulation and Prediction Model for Plain River Networks" Water 17, no. 20: 2948. https://doi.org/10.3390/w17202948
APA StyleLan, Y., Xu, C., Ding, L., Wang, M., Ren, Z., & Wang, Z. (2025). Construction and Comparative Analysis of a Water Quality Simulation and Prediction Model for Plain River Networks. Water, 17(20), 2948. https://doi.org/10.3390/w17202948






