Spatial Regularities of Changes in the Duration of Low River Flows in Poland Under Climate Warming Conditions
Abstract
1. Introduction
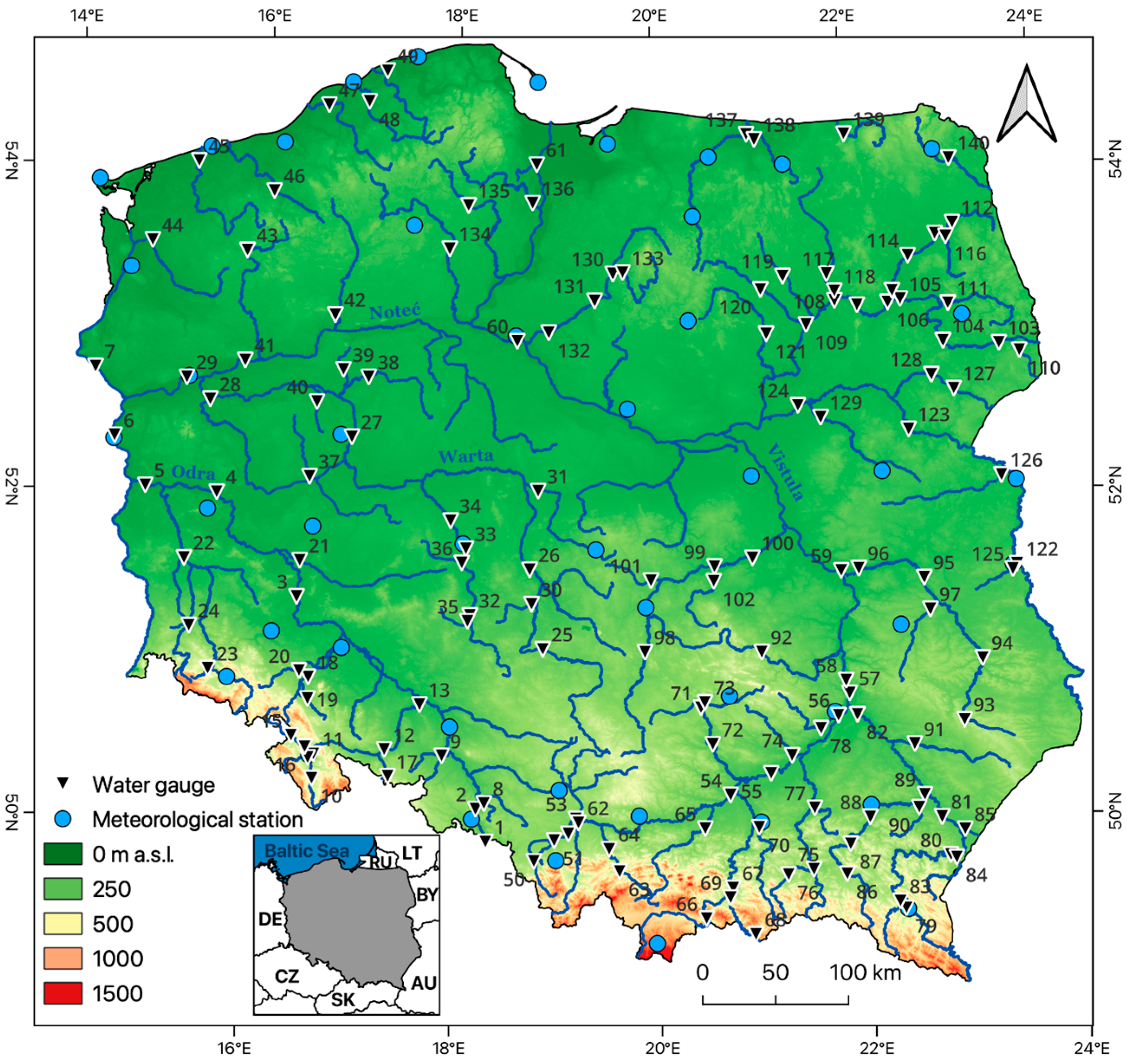
2. Materials and Methods
3. Results
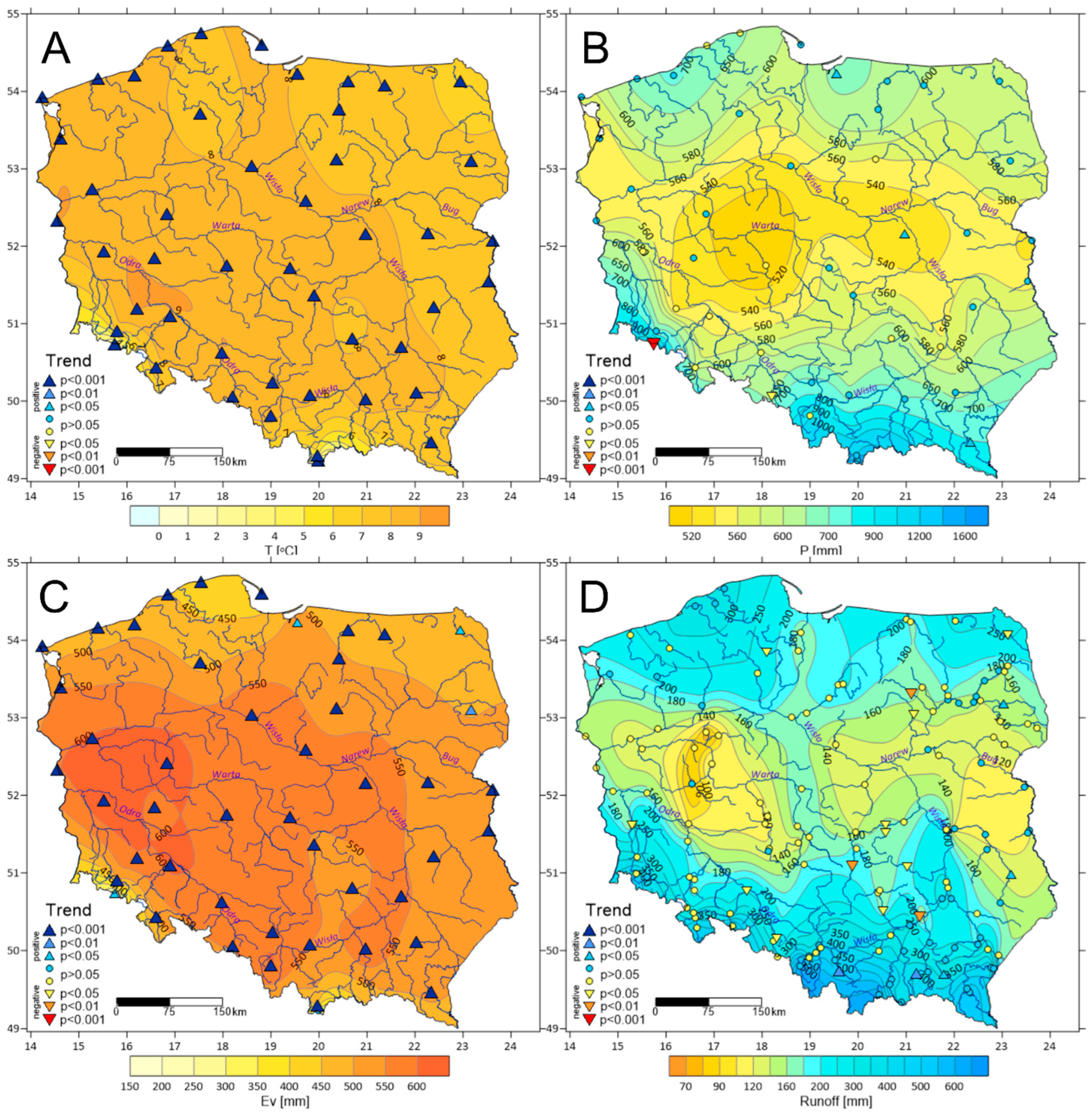
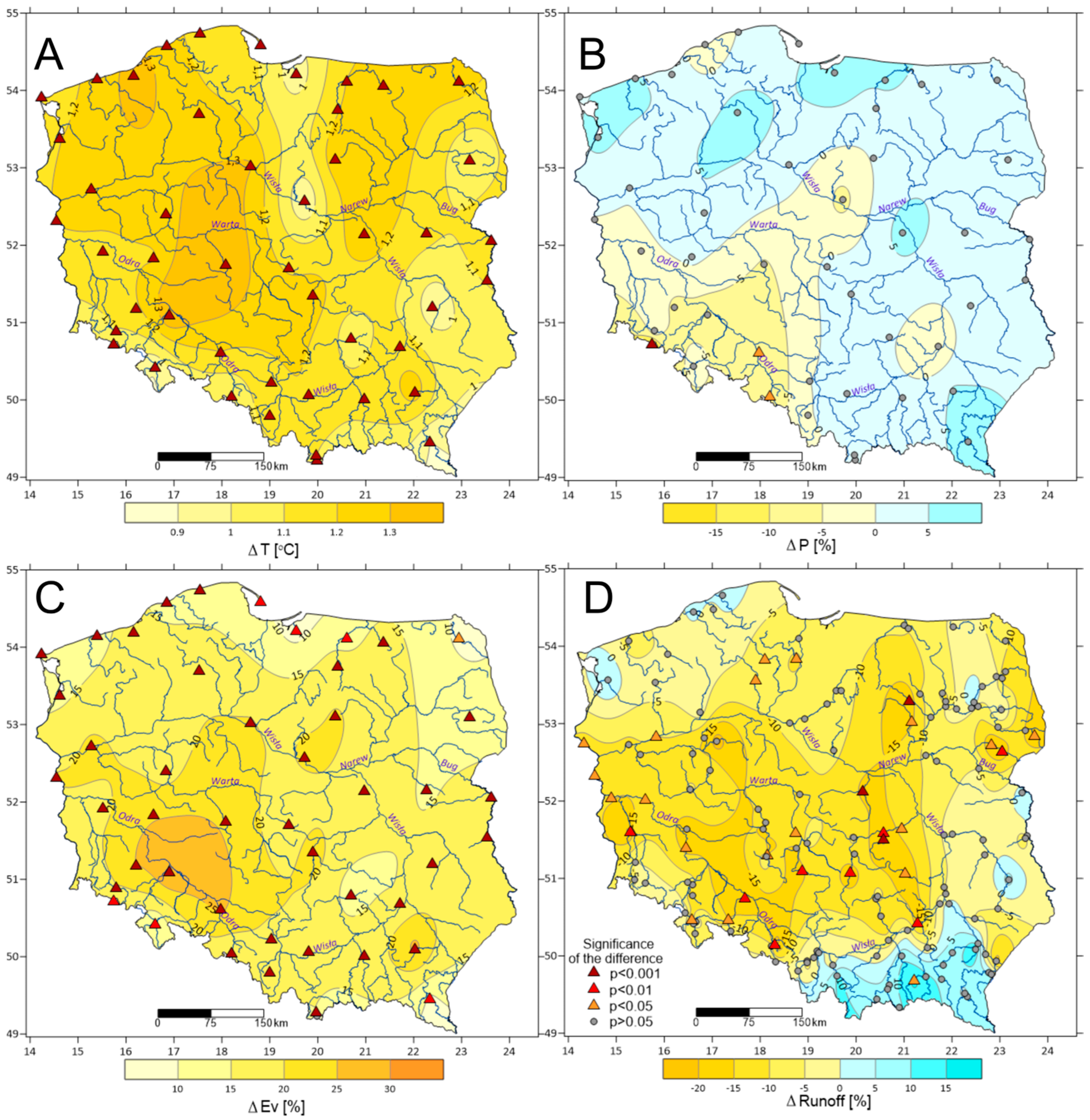
3.1. Changes in the Average Values of Hydro-Meteorological Elements in Poland in 1951–2020
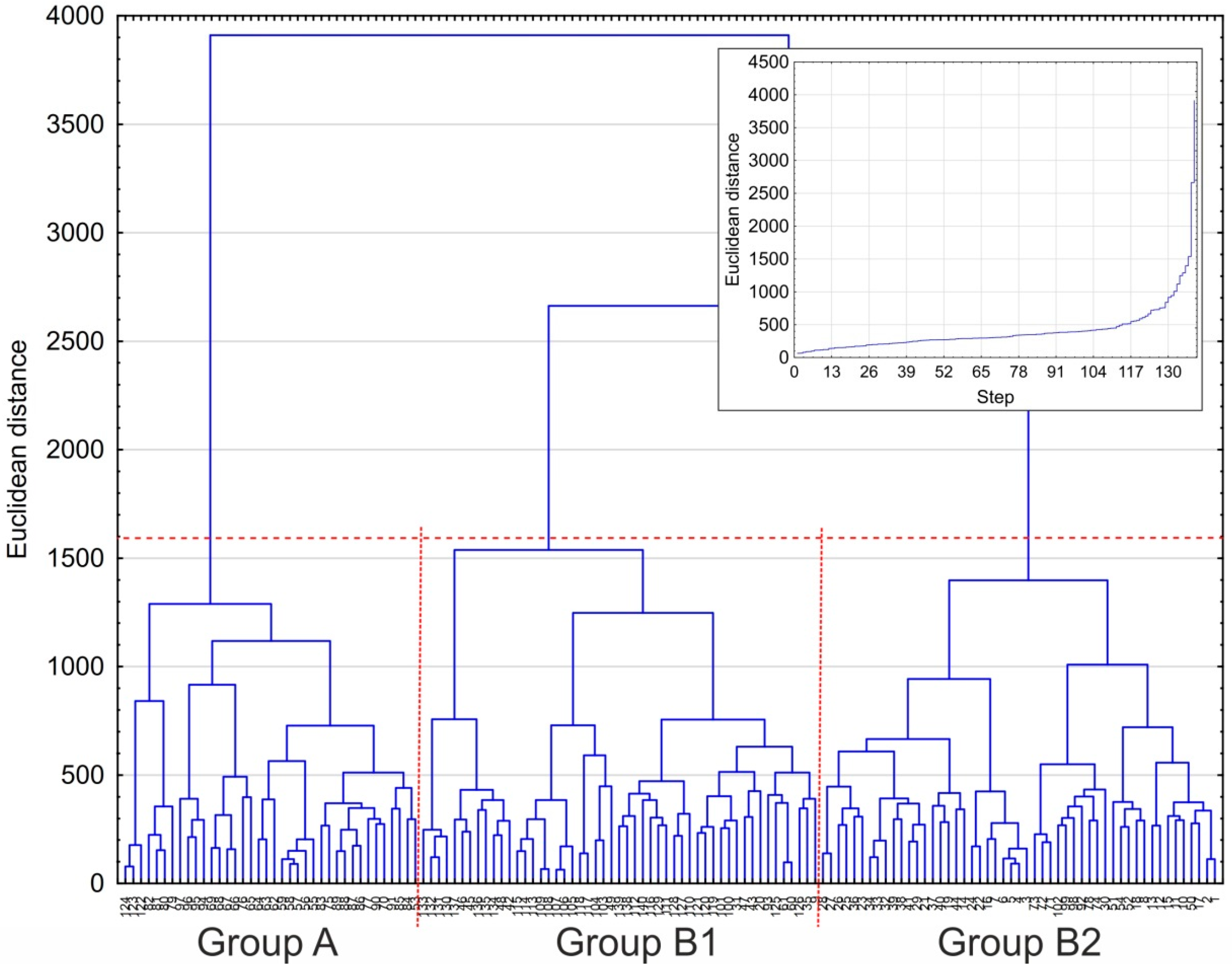
3.2. Results of the Procedure for Grouping Water Gauges Based on the Number of Days with Low Flows
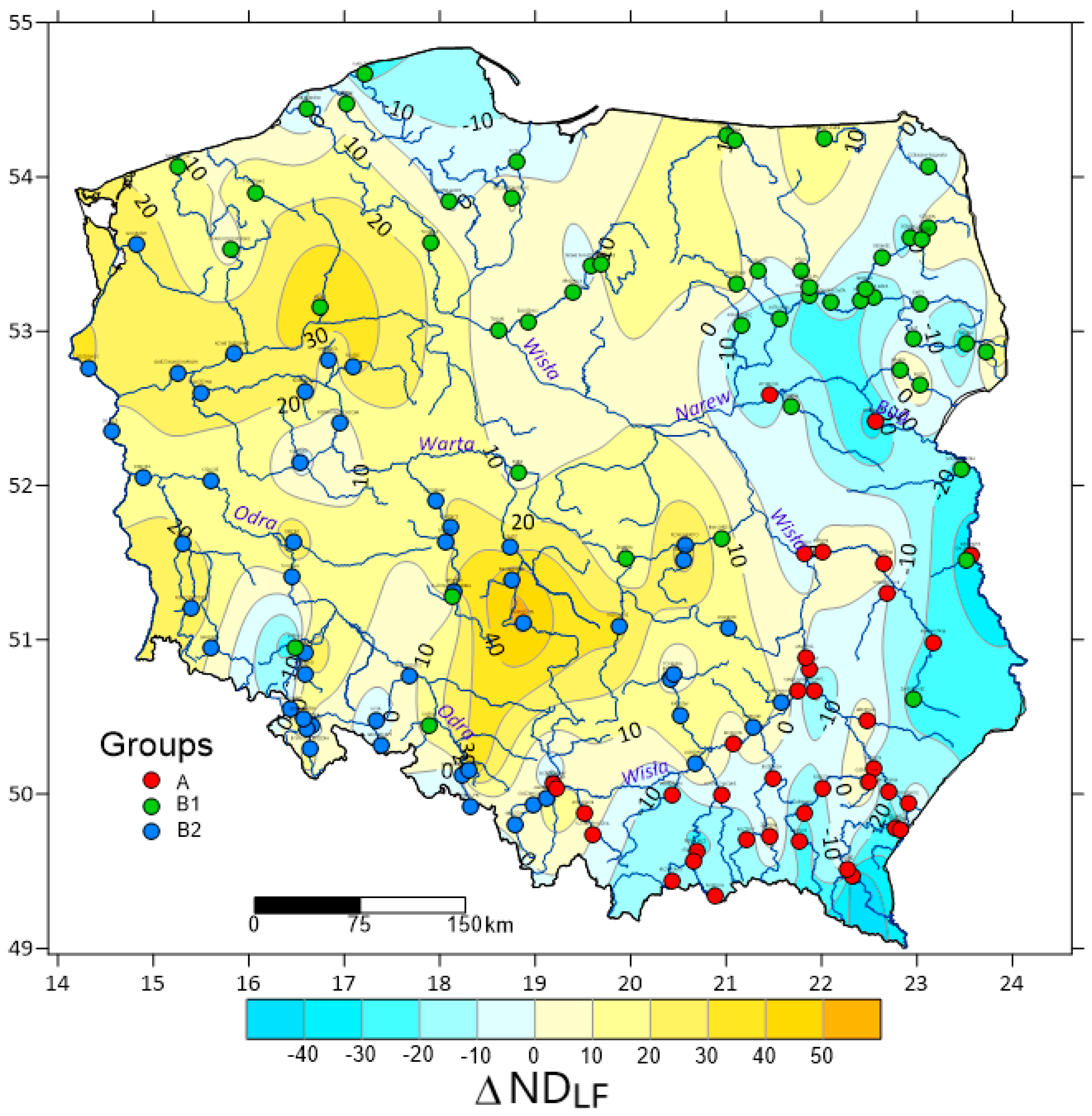
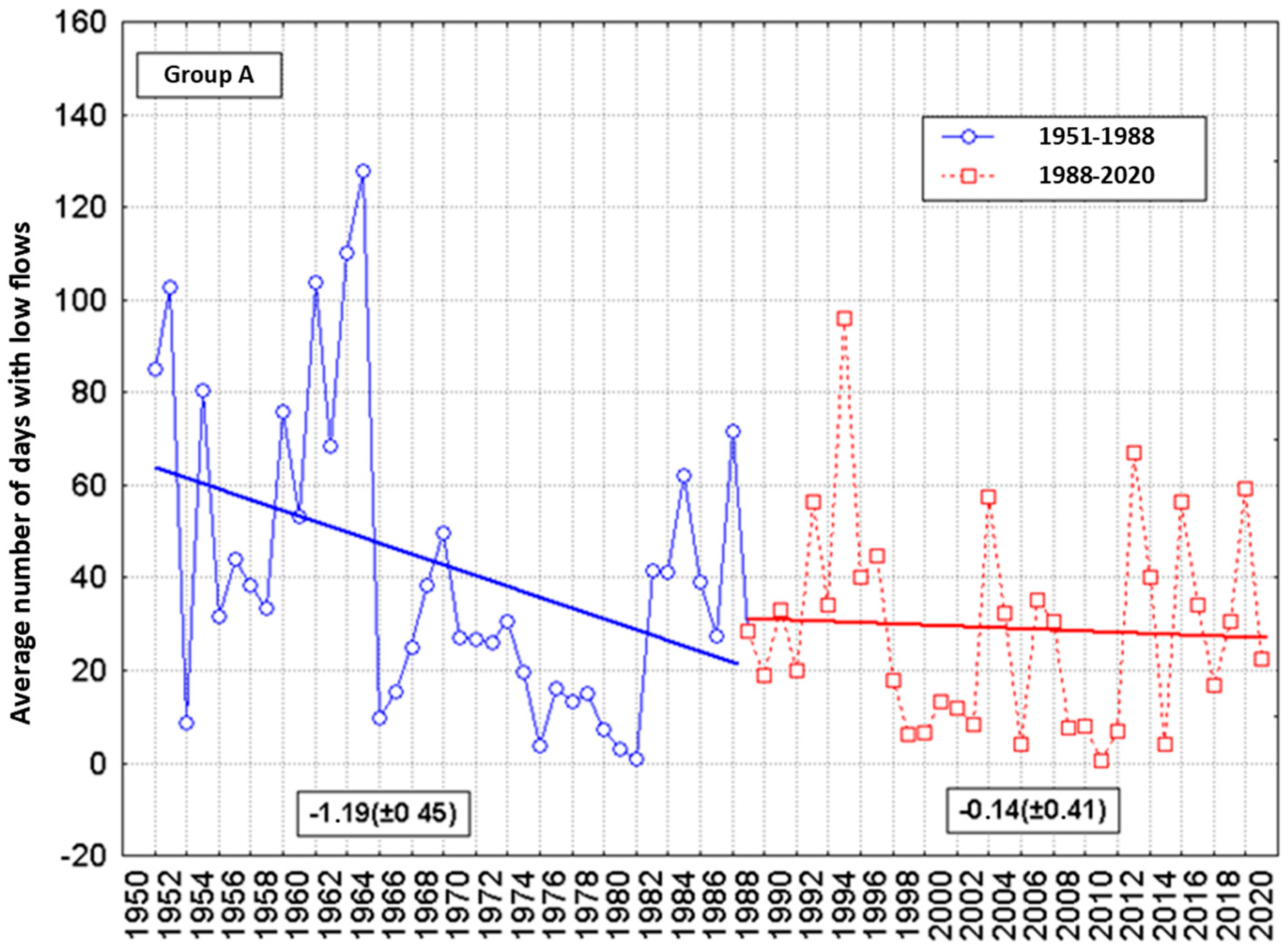
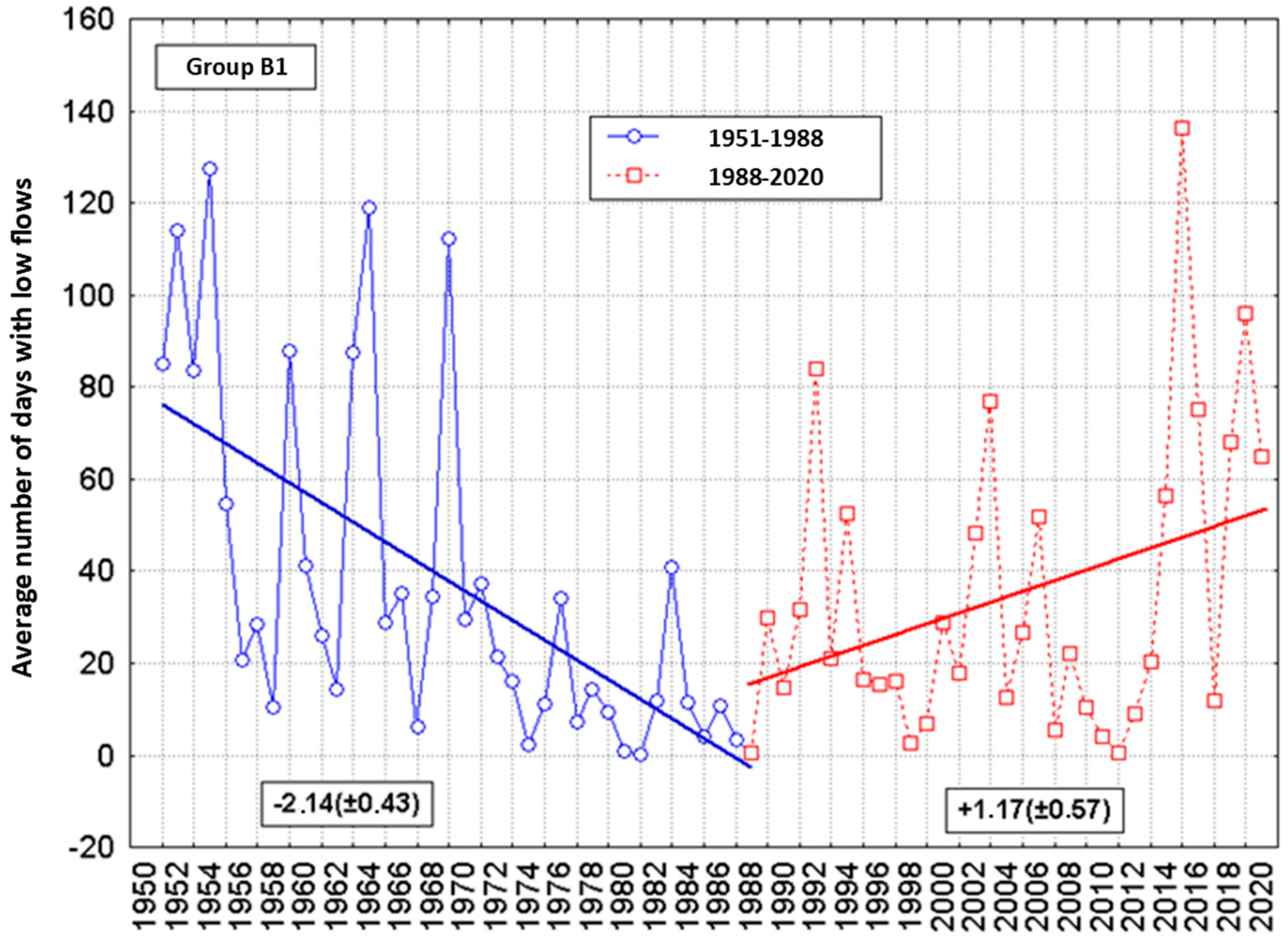
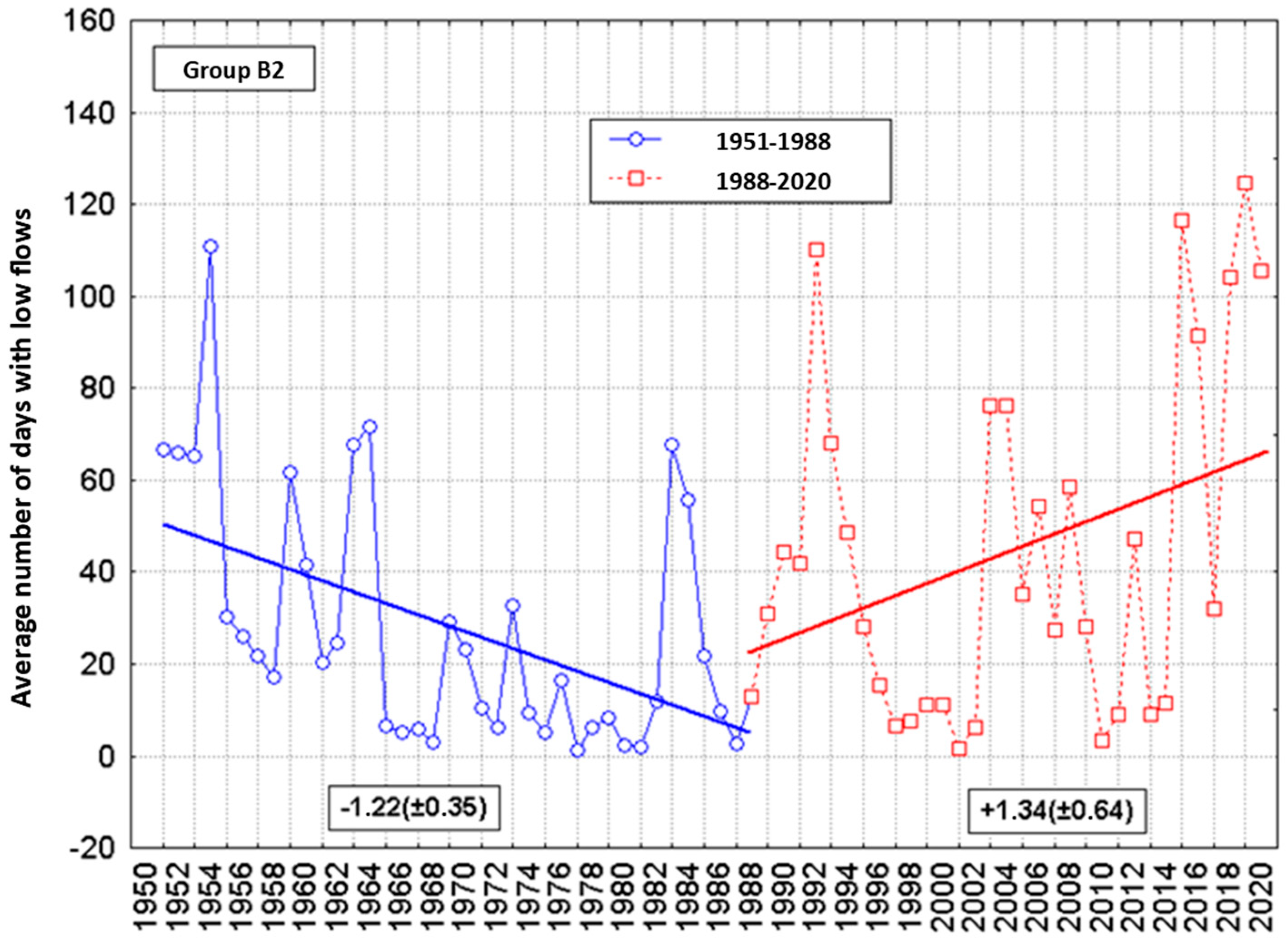
3.3. Regional Differentiation in the Number of Days with Low Flows in Poland
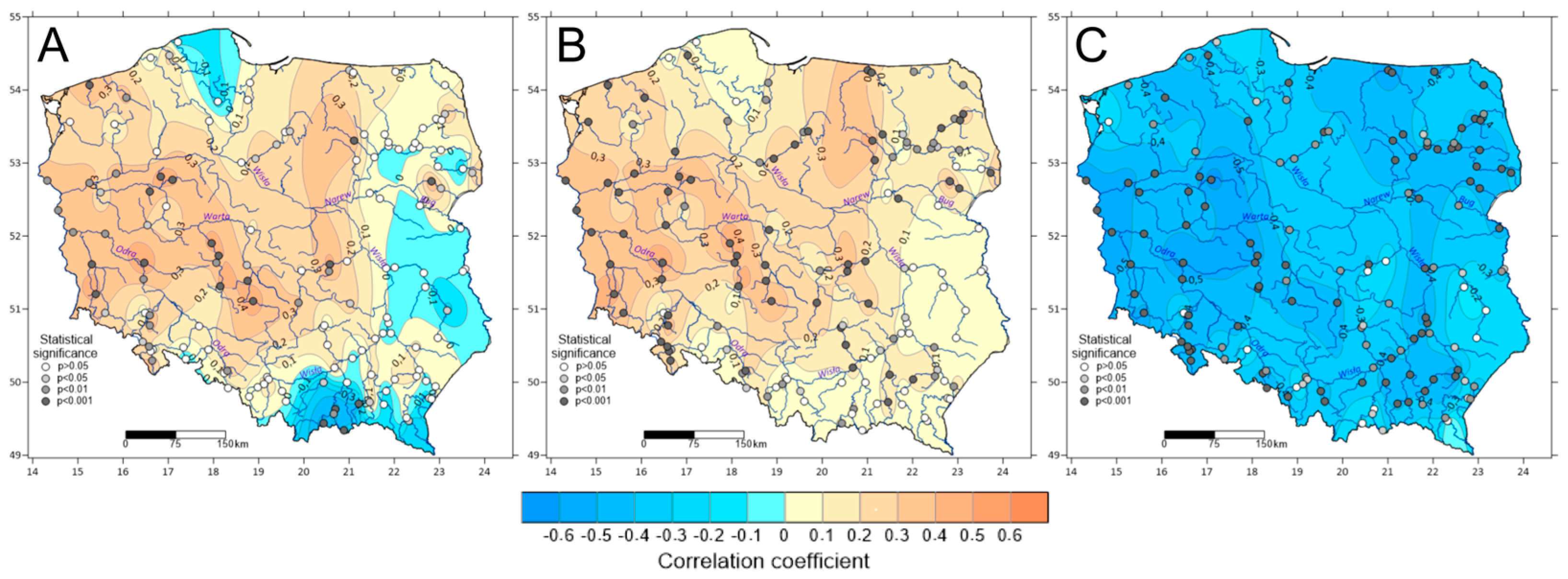
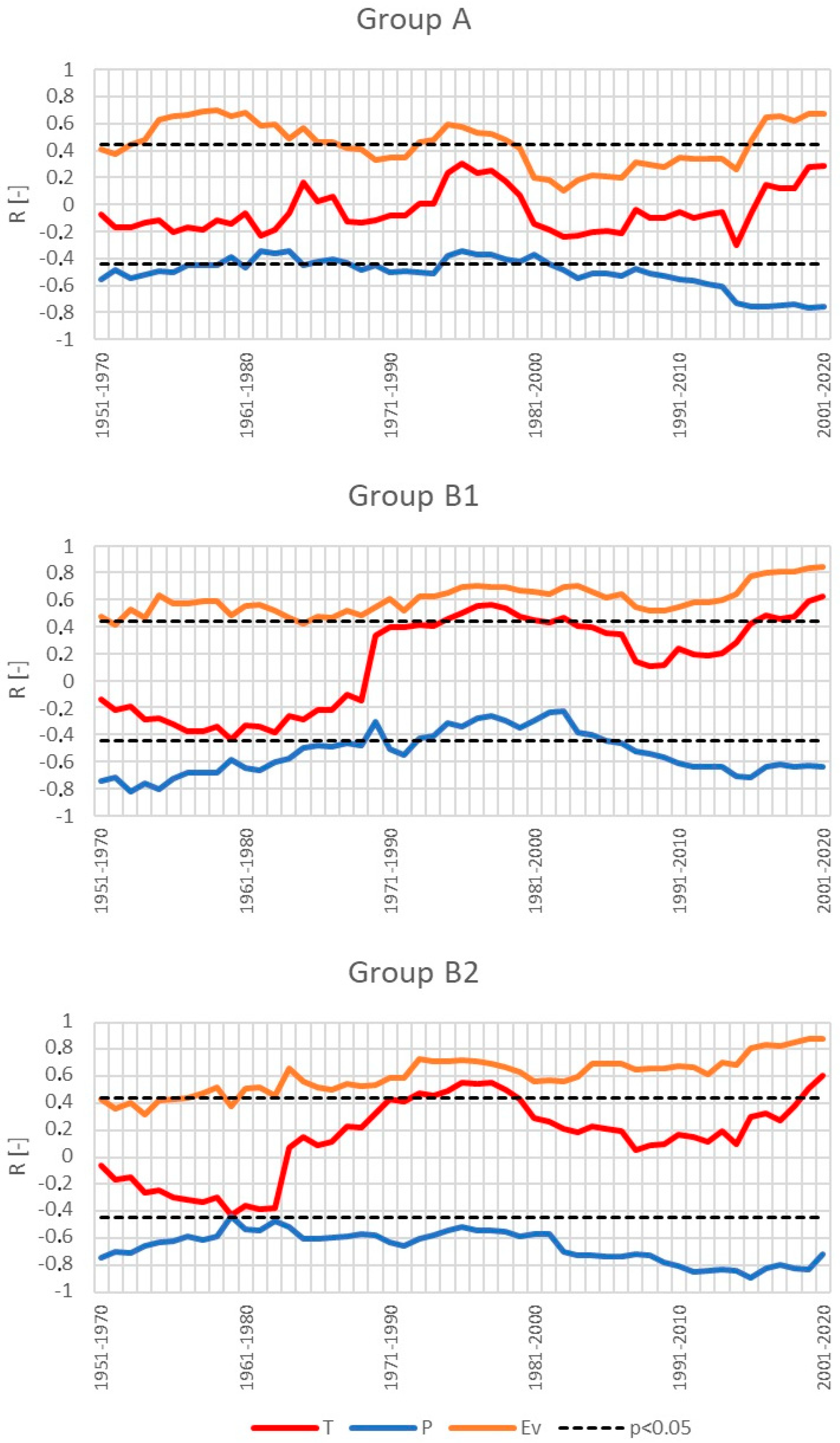
3.4. Formal Reasons for Spatial Differentiation of the Number of Days with Low Flows in Poland
4. Discussion and Conclusions
- In the multi-annual period 1951–2020, the average annual air temperature and evaporation showed strong increasing trends in Poland, in most cases statistically significant at the level of p < 0.001. In the case of precipitation totals and river runoff, the situation was different: in most locations, the trends were statistically insignificant (p > 0.05); however, increasing trends of runoff (p < 0.01) were concluded in south-western Poland.
- After 1988, the average air temperature increased throughout Poland from 0.9 to over 1.3 °C. Similar changes were determined for evaporation, which increased by about 10–25%. For both air temperature and evaporation, the statistical significance of the changes was very high, mostly at p < 0.001. In turn, such changes were not detected in the case of precipitation, with a statistically significant decrease by over 5% recorded only in the southern part of the Odra River basin. In most stations, statistically insignificant increases in precipitation totals were recorded. The most complex changes spatially occurred in the case of river runoff, with most of Poland characterized by a decrease in runoff after 1988 by about 5–15%, of which some changes were statistically significant. In the south-eastern part of the country, an increase in runoff by about 5–10% was recorded, but only in the case of one gauge, these changes were statistically significant.
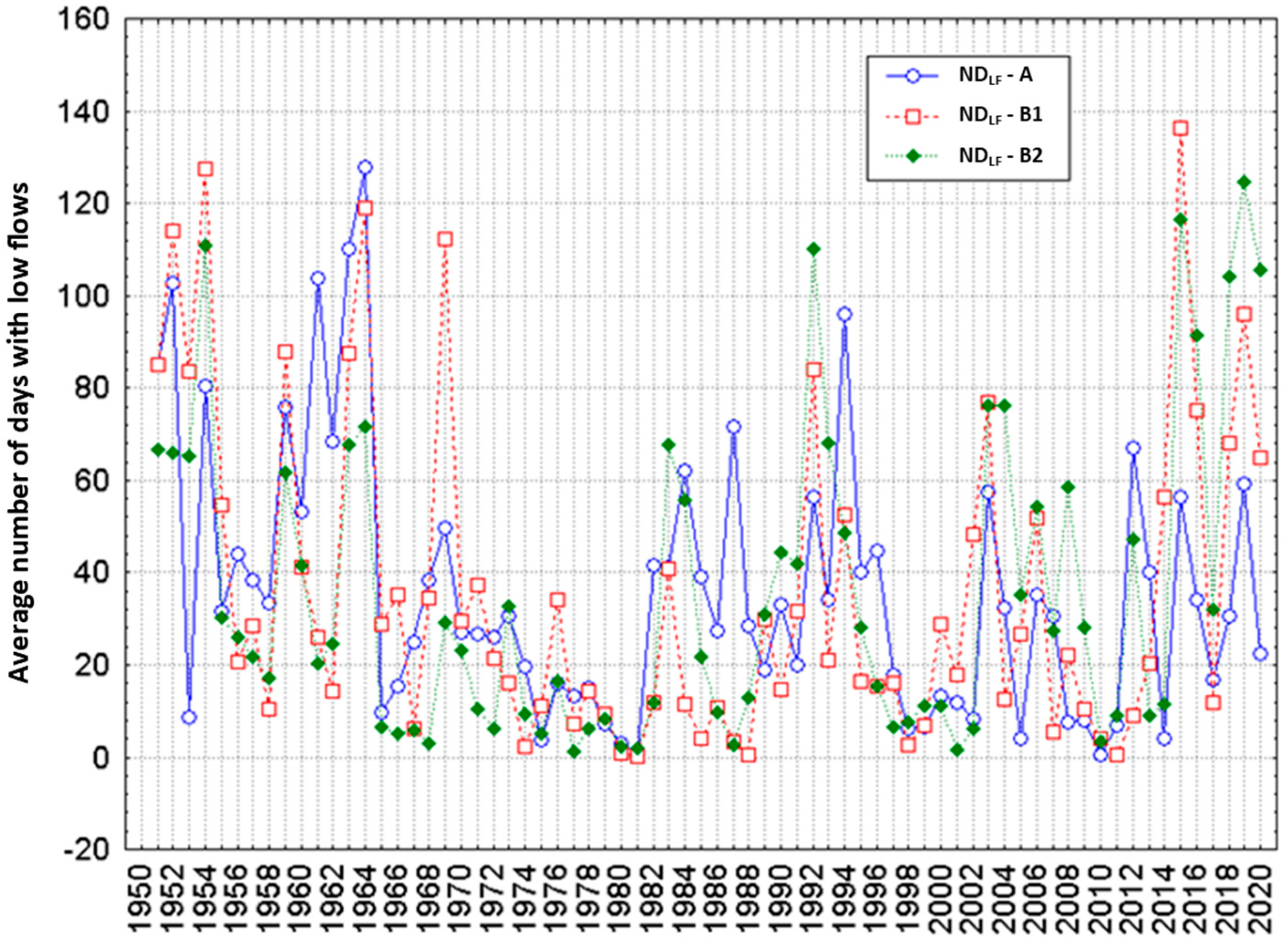
- Statistically significant decreasing trends of NDLF in the eastern and southern parts of the Vistula River basin were concluded, and such trends were characteristic of the whole Poland in the first separated sub-period (1951–1988). After 1988, a statistically significant increase in NDLF was observed in most stations along selected rivers, with some exceptions, including rivers in Southern Poland, where statistically significant decreasing trends of NDLF were detected.
- Annual NDLF was correlated with average annual air temperature, evaporation, and precipitation. In the case of air temperature, both positive (for most of the study area) and negative correlations (mainly for the right part of the Vistula River basin) were determined. Correlations with evaporation were positive and statistically significant over most of Poland; the southern and eastern parts of the Vistula River basin was an exception. The correlation of annual NDLF with precipitation totals was negative over the entire Poland and in many cases statistically significant (p < 0.001).
- The grouping of water gauges based on the NDLF revealed its regional differentiation. This led to a separation of two groups of gauges forming relatively homogenous territorial groups spatially. The distinguished group A included the south-eastern part of Poland, while group B covered the remaining part of the country. Group B was additionally split into sub-group B1 covering Northern and North-eastern Poland and sub-group B2 covering the south-western part of the country. The most important reason for the formation of these separate types in the NDLF set was differences in the nature of the variability of the course of the NDLF. The analysis of linear trends in each of the areas, carried out in each area separately for the years 1951–1988 and for the years 1988–2020, i.e., in the sub-periods before and after climate change, revealed the basic difference in their course between group A and sub-groups B1 and B2.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| No. | River | Gauge | Catchment Area [km2] | Runoff Depth [mm] | NDLF | Trend NDLF R * | River Regime ** |
|---|---|---|---|---|---|---|---|
| 1 | Odra | Chałupki | 4666 | 282.4 | 48.8 | −0.218 | 4 |
| 2 | Odra | Racibórz-Miedonia | 6744 | 300.8 | 47.6 | −0.154 | 4 |
| 3 | Odra | Ścinawa | 29,584 | 188.9 | 52.1 | 0.168 | 4 |
| 4 | Odra | Cigacice | 40,106 | 170.6 | 56.6 | 0.182 | 2 |
| 5 | Odra | Połęcko | 47,370 | 167.1 | 57.8 | 0.175 | 2 |
| 6 | Odra | Słubice | 53,600 | 174.2 | 59.8 | 0.187 | 2 |
| 7 | Odra | Gozdowice | 109,729 | 146.9 | 66.2 | 0.161 | 2 |
| 8 | Sumina | Nędza | 94.4 | 191.3 | 56.5 | 0.280 * | 4 |
| 9 | Biała | Dobra | 353 | 99.4 | 59.7 | 0.016 | 4 |
| 10 | Nysa Kłodzka | Bystrzyca Kłodzka | 260 | 466.7 | 45.6 | 0.224 | 4 |
| 11 | Nysa Kłodzka | Kłodzko | 1084 | 364.9 | 51.0 | −0.150 | 4 |
| 12 | Nysa Kłodzka | Nysa | 3276 | 278.6 | 43.6 | −0.115 | 4 |
| 13 | Nysa Kłodzka | Skorogoszcz | 4514 | 249.8 | 52.0 | 0.130 | 4 |
| 14 | Bystrzyca Dusznicka | Szalejów Dolny | 175 | 378.1 | 54.7 | 0.002 | 2 |
| 15 | Ścinawka | Tłumaczów | 256 | 279.8 | 57.8 | −0.023 | 2 |
| 16 | Ścinawka | Gorzuchów | 511 | 274.8 | 50.5 | 0.191 | 4 |
| 17 | Biała Głuchołaska | Głuchołazy | 283 | 542.0 | 57.3 | −0.108 | 4 |
| 18 | Bystrzyca | Krasków | 683 | 205.9 | 46.9 | 0.213 | 4 |
| 19 | Piława | Mościsko | 291 | 172.6 | 57.1 | 0.253 * | 4 |
| 20 | Strzegomka | Łażany | 356 | 198.0 | 58.0 | −0.324 * | 4 |
| 21 | Barycz | Osetno | 4579 | 101.6 | 48.9 | 0.336 * | 3 |
| 22 | Bóbr | Żagań | 4254 | 275.8 | 54.5 | 0.255 * | 4 |
| 23 | Kamienica | Barcinek | 97.2 | 389.7 | 55.0 | 0.065 | 2 |
| 24 | Kwisa | Nowogrodziec | 736 | 306.9 | 52.7 | 0.261 * | 4 |
| 25 | Warta | Działoszyn | 4088 | 185.8 | 64.6 | 0.293 * | 2 |
| 26 | Warta | Sieradz | 8140 | 171.3 | 65.2 | 0.037 | 2 |
| 27 | Warta | Poznań | 25,126 | 124.5 | 68.3 | −0.140 | 2 |
| 28 | Warta | Skwierzyna | 31,268 | 123.4 | 70.7 | −0.066 | 2 |
| 29 | Warta | Gorzów Wielkopolski | 52,186 | 124.4 | 59.9 | 0.119 | 2 |
| 30 | Oleśnica | Niechmirów | 592 | 126.7 | 60.9 | 0.321 * | 3 |
| 31 | Ner | Dąbie | 1712 | 181.6 | 44.5 | −0.012 | 2 |
| 32 | Prosna | Mirków | 1255 | 126.0 | 46.4 | 0.296 * | 2 |
| 33 | Prosna | Piwonice | 2938 | 119.2 | 55.4 | 0.091 | 2 |
| 34 | Prosna | Bogusław | 4304 | 114.3 | 48.2 | 0.142 | 2 |
| 35 | Niesób | Kuźnica Skakawska | 246 | 123.8 | 62.8 | −0.238 * | 3 |
| 36 | Ołobok | Ołobok | 447 | 110.7 | 60.0 | 0.093 | 3 |
| 37 | Mogilnica | Konojad | 663 | 77.3 | 52.8 | 0.109 | 3 |
| 38 | Wełna | Pruśce | 1130 | 92.5 | 65.2 | 0.187 | 3 |
| 39 | Flinta | Ryczywół | 276 | 74.1 | 53.4 | 0.222 | 3 |
| 40 | Sama | Szamotuły | 395 | 83.4 | 58.0 | 0.277 * | 3 |
| 41 | Noteć | Nowe Drezdenko | 15,970 | 143.2 | 53.7 | 0.219 | 2 |
| 42 | Gwda | Piła | 4704 | 180.0 | 49.4 | 0.181 | 1 |
| 43 | Drawa | Drawsko Pomorskie | 609 | 209.2 | 76.5 | −0.132 | 2 |
| 44 | Ina | Goleniów | 2163 | 185.5 | 66.6 | 0.174 | 2 |
| 45 | Rega | Trzebiatów | 2628 | 239.4 | 42.4 | 0.215 | 2 |
| 46 | Parsęta | Tychówko | 896 | 289.1 | 48.0 | 0.245 * | 2 |
| 47 | Wieprza | Stary Kraków | 1519 | 327.0 | 53.5 | −0.283 * | 1 |
| 48 | Słupia | Słupsk | 1450 | 338.5 | 35.1 | −0.002 | 1 |
| 49 | Łupawa | Smołdzino | 805 | 325.7 | 44.8 | −0.333 * | 1 |
| 50 | Wisła | Skoczów | 297 | 641.0 | 39.3 | −0.049 | 4 |
| 51 | Wisła | Goczałkowice | 738 | 381.0 | 44.7 | −0.066 | 5 |
| 52 | Wisła | Jawiszowice | 971 | 426.1 | 44.0 | 0.113 | 5 |
| 53 | Wisła | Bieruń Nowy | 1748 | 381.8 | 49.9 | −0.351 * | 4 |
| 54 | Wisła | Jagodniki | 12,058 | 334.4 | 51.4 | 0.135 | 4 |
| 55 | Wisła | Szczucin | 23,901 | 307.4 | 44.6 | −0.185 | 4 |
| 56 | Wisła | Sandomierz | 31,846 | 284.8 | 49.8 | −0.184 | 4 |
| 57 | Wisła | Zawichost | 50,732 | 261.9 | 45.4 | −0.200 | 4 |
| 58 | Wisła | Annopol | 51,518 | 261.8 | 44.3 | −0.151 | 4 |
| 59 | Wisła | Dęblin | 68,234 | 227.9 | 46.4 | −0.179 | 4 |
| 60 | Wisła | Toruń | 181,033 | 167.5 | 44.4 | −0.050 | 2 |
| 61 | Wisła | Tczew | 194,376 | 167.3 | 45.4 | −0.124 | 2 |
| 62 | Soła | Oświęcim | 1386 | 473.1 | 45.0 | 0.135 | 4 |
| 63 | Skawa | Sucha Beskidzka | 468 | 507.9 | 43.6 | −0.095 | 4 |
| 64 | Skawa | Wadowice | 836 | 465.0 | 47.9 | 0.061 | 4 |
| 65 | Raba | Proszówki | 1470 | 356.6 | 54.3 | −0.247 * | 4 |
| 66 | Dunajec | Krościenko | 1580 | 634.9 | 45.2 | −0.360 * | 5 |
| 67 | Dunajec | Nowy Sącz | 4341 | 472.8 | 44.9 | −0.466 * | 4 |
| 68 | Poprad | Muszyna | 1514 | 365.9 | 45.4 | −0.220 | 4 |
| 69 | Poprad | Stary Sącz | 2071 | 380.5 | 45.6 | −0.130 | 4 |
| 70 | Biała | Koszyce Wielkie | 957 | 290.5 | 47.8 | −0.254 * | 4 |
| 71 | Nida | Brzegi | 2259 | 177.1 | 56.7 | 0.137 | 2 |
| 72 | Nida | Pińczów | 3352 | 168.2 | 53.9 | 0.218 | 2 |
| 73 | Czarna Nida | Tokarnia | 1216 | 171.4 | 50.2 | 0.091 | 2 |
| 74 | Czarna | Połaniec | 1354 | 149.2 | 44.8 | 0.175 | 3 |
| 75 | Wisłoka | Żółków | 581 | 384.7 | 42.7 | 0.131 | 4 |
| 76 | Ropa | Klęczany | 483 | 406.9 | 67.1 | −0.569 * | 4 |
| 77 | Brzeźnica | Brzeźnica | 484 | 212.5 | 53.8 | −0.066 | 4 |
| 78 | Koprzywianka | Koprzywnica | 502 | 127.1 | 45.9 | −0.010 | 3 |
| 79 | San | Lesko | 1614 | 555.0 | 55.4 | −0.586 * | 4 |
| 80 | San | Przemyśl | 3686 | 444.9 | 39.0 | −0.484 * | 4 |
| 81 | San | Jarosław | 7041 | 312.7 | 48.8 | −0.328 * | 4 |
| 82 | San | Radomyśl | 16,824 | 241.6 | 54.0 | −0.440 * | 4 |
| 83 | Osława | Zagórz | 505 | 509.0 | 38.2 | −0.113 | 4 |
| 84 | Wiar | Krówniki | 789 | 252.7 | 49.0 | −0.162 | 4 |
| 85 | Wisznia | Nienowice | 1185 | 178.6 | 47.7 | 0.016 | 4 |
| 86 | Wisłok | Krosno | 596 | 327.8 | 47.9 | −0.475 * | 4 |
| 87 | Wisłok | Żarnowa | 1427 | 287.3 | 49.0 | −0.384 | 4 |
| 88 | Wisłok | Rzeszów | 2086 | 263.1 | 43.4 | −0.064 | 4 |
| 89 | Wisłok | Tryńcza | 3516 | 227.7 | 51.1 | −0.228 | 4 |
| 90 | Mleczka | Gorliczyna | 529 | 173.2 | 45.3 | −0.076 | 4 |
| 91 | Tanew | Harasiuki | 2034 | 189.7 | 53.9 | −0.030 | 2 |
| 92 | Kamienna | Wąchock | 476 | 192.7 | 44.0 | 0.252 * | 2 |
| 93 | Wieprz | Zwierzyniec | 405 | 160.1 | 66.3 | −0.238 * | 1 |
| 94 | Wieprz | Krasnystaw | 3001 | 129.8 | 59.0 | −0.440 * | 2 |
| 95 | Wieprz | Lubartów | 6364 | 111.7 | 58.8 | −0.196 | 2 |
| 96 | Wieprz | Kośmin | 10,231 | 113.2 | 54.5 | −0.295 * | 2 |
| 97 | Bystrzyca | Sobianowice | 1265 | 125.6 | 59.2 | −0.334 * | 2 |
| 98 | Pilica | Przedbórz | 2536 | 185.9 | 56.6 | 0.430 * | 2 |
| 99 | Pilica | Nowe Miasto | 6717 | 166.9 | 50.8 | 0.415 * | 2 |
| 100 | Pilica | Białobrzegi | 8664 | 160.4 | 49.9 | 0.139 | 2 |
| 101 | Wolbórka | Zawada | 616 | 137.5 | 44.0 | −0.064 | 2 |
| 102 | Drzewiczka | Odrzywół | 1004 | 166.9 | 44.0 | 0.285 * | 2 |
| 103 | Narew | Narew | 1978 | 146.0 | 56.9 | −0.521 * | 3 |
| 104 | Narew | Suraż | 3376 | 139.5 | 62.2 | −0.387 * | 3 |
| 105 | Narew | Strękowa Góra | 7181 | 141.4 | 59.8 | −0.332 * | 3 |
| 106 | Narew | Wizna | 14,308 | 148.4 | 63.6 | −0.248 * | 3 |
| 107 | Narew | Piątnica-Łomża | 15,296 | 150.9 | 65.4 | −0.240 * | 3 |
| 108 | Narew | Nowogród | 20,106 | 152.4 | 58.0 | −0.275 * | 3 |
| 109 | Narew | Ostrołęka | 21,862 | 155.8 | 55.5 | −0.206 | 3 |
| 110 | Narewka | Narewka | 590 | 156.9 | 56.3 | 0.167 | 3 |
| 111 | Supraśl | Fasty | 1817 | 153.3 | 48.6 | −0.258 * | 2 |
| 112 | Biebrza | Sztabin | 846 | 171.5 | 62.1 | 0.005 | 3 |
| 113 | Biebrza | Dębowo | 2322 | 167.3 | 56.7 | −0.226 | 3 |
| 114 | Biebrza | Osowiec | 4365 | 160.0 | 62.2 | −0.051 | 3 |
| 115 | Biebrza | Burzyn | 6900 | 158.0 | 61.1 | −0.192 | 3 |
| 116 | Brzozówka | Karpowicze | 650 | 154.1 | 52.0 | −0.062 | 3 |
| 117 | Pisa | Ptaki | 3562 | 181.6 | 68.5 | −0.058 | 1 |
| 118 | Pisa | Dobrylas | 4061 | 182.4 | 68.2 | −0.016 | 2 |
| 119 | Rozoga | Myszyniec | 231 | 155.2 | 49.0 | −0.024 | 2 |
| 120 | Omulew | Krukowo | 1265 | 170.0 | 49.9 | 0.243 * | 2 |
| 121 | Orzyc | Krasnosielc | 1268 | 142.2 | 49.1 | −0.056 | 2 |
| 122 | Bug | Włodawa | 14,410 | 120.5 | 72.8 | −0.375 * | 3 |
| 123 | Bug | Frankopol | 31,336 | 118.1 | 68.8 | −0.394 * | 3 |
| 124 | Bug | Wyszków | 39,119 | 122.5 | 65.3 | −0.347 * | 3 |
| 125 | Włodawka | Okuninka | 576 | 116.5 | 61.3 | −0.204 | 3 |
| 126 | Krzna | Malowa Góra | 3128 | 108.1 | 52.0 | −0.420 * | 3 |
| 127 | Nurzec | Boćki | 556 | 134.0 | 44.8 | −0.092 | 3 |
| 128 | Nurzec | Brańsk | 1227 | 126.8 | 45.2 | 0.192 | 3 |
| 129 | Liwiec | Łochów | 2466 | 134.1 | 43.0 | −0.149 | 3 |
| 130 | Drwęca | Nowe Miasto Lubawskie | 2725 | 188.9 | 68.9 | −0.144 | 2 |
| 131 | Drwęca | Brodnica | 3526 | 192.5 | 63.9 | 0.093 | 2 |
| 132 | Drwęca | Elgiszewo | 4959 | 173.7 | 69.4 | 0.155 | 2 |
| 133 | Wel | Kuligi | 764 | 206.3 | 56.7 | 0.127 | 1 |
| 134 | Brda | Tuchola | 2462 | 248.6 | 40.5 | 0.143 | 1 |
| 135 | Wda | Czarna Woda | 940 | 210.7 | 57.4 | −0.261 * | 1 |
| 136 | Wierzyca | Brody Pomorskie | 1544 | 175.0 | 49.4 | 0.024 | 2 |
| 137 | Łyna | Sępopol | 3647 | 211.7 | 43.7 | 0.133 | 2 |
| 138 | Guber | Prosna | 1568 | 171.6 | 48.8 | −0.041 | 2 |
| 139 | Gołdapa | Banie Mazurskie | 548 | 266.9 | 54.1 | −0.074 | 3 |
| 140 | Czarna Hańcza | Czerwony Folwark | 454 | 262.6 | 64.6 | −0.033 | 2 |
References
- Döll, P.; Jiménez-Cisneros, B.; Oki, T.; Arnell, N.W.; Benito, G.; Cogley, J.G.; Jiang, T.; Kundzewicz, Z.W.; Mwakalila, S.; Nishijima, A. Integrating risks of climate change into water management. Hydrol. Sci. J. 2015, 60, 4–13. [Google Scholar] [CrossRef]
- Marshall, A.; Grubert, E.; Warix, S. Temperature Overshoot Would Have Lasting Impacts on Hydrology and Water Resources. Water Resour. Res. 2025, 61, e2024WR037950. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W. Climate Change Impacts on the Hydrological Cycle. Ecohydrol. Hydrobiol. 2008, 8, 195–203. [Google Scholar] [CrossRef]
- Ciampittiello, M.; Marchetto, A.; Boggero, A. Water Resources Management under Climate Change: A Review. Sustainability 2024, 16, 3590. [Google Scholar] [CrossRef]
- Wrzesiński, D. Changes in selected characteristics of river regime in Poland under climate warming conditions. Acta Geogr. Lodz. 2024, 115, 175–195. (In Polish) [Google Scholar] [CrossRef]
- Schneider, C.; Laizé, C.L.R.; Acreman, M.C.; Flörke, M. How Will Climate Change Modify River Flow Regimes in Europe? Hydrol. Earth Syst. Sci. 2013, 17, 325–339. [Google Scholar] [CrossRef]
- Bartczak, A.; Krzemiński, M.; Araźny, A. Changes in Evaporation Patterns and Their Impact on Climatic Water Balance and River Discharges in Central Poland, 1961–2020. Reg. Environ. Change 2024, 24, 130. [Google Scholar] [CrossRef]
- Pińskwar, I.; Choryński, A.; Graczyk, D.; Kundzewicz, Z.W. Observed Changes in Precipitation Totals in Poland. Geografie 2019, 124, 237–264. [Google Scholar] [CrossRef]
- Szwed, M. Variability of Precipitation in Poland under Climate Change. Theor. Appl. Climatol. 2019, 135, 1003–1015. [Google Scholar] [CrossRef]
- Wibig, J.; Jędruszkiewicz, J. Recent Changes in the Snow Cover Characteristics in Poland. Int. J. Clim. 2023, 43, 6925–6938. [Google Scholar] [CrossRef]
- Pińskwar, I.; Choryński, A.; Graczyk, D.; Kundzewicz, Z.W. Observed Changes in Extreme Precipitation in Poland: 1991–2015 versus 1961–1990. Theor. Appl. Climatol. 2019, 135, 773–787. [Google Scholar] [CrossRef]
- Łupikasza, E.B.; Małarzewski, Ł. Trends in the Indices of Precipitation Phases under Current Warming in Poland, 1966–2020. Adv. Clim. Change Res. 2023, 14, 97–115. [Google Scholar] [CrossRef]
- Somorowska, U. Assessing the Impact of Climate Change on Snowfall Conditions in Poland Based on the Snow Fraction Sensitivity Index. Resources 2024, 13, 60. [Google Scholar] [CrossRef]
- Wibig, J.; Jędruszkiewicz, J. Are Heatwaves and Drought More Likely to Occur Simultaneously with Warming? EMS Annu. Meet. Abstr. 2023, 20, EMS2023-329. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, Y.; Graf, R.; Wrzesiński, D.; Sojka, M.; Sun, B.; Kong, L.; Ji, Q.; Luo, W. Reconstruction of Long-Term Water Temperature Indicates Significant Warming in Polish Rivers during 1966–2020. J. Hydrol. Reg. Stud. 2022, 44, 101281. [Google Scholar] [CrossRef]
- Sun, J.; Nunno, F.D.; Sojka, M.; Ptak, M.; Zhou, Q.; Luo, Y.; Zhu, S.; Granata, F. Long-Term Daily Water Temperatures Unveil Escalating Water Warming and Intensifying Heatwaves in the Odra River Basin, Central Europe. Geosci. Front. 2024, 15, 101916. [Google Scholar] [CrossRef]
- Zhou, Q.; Nunno, F.D.; Sun, J.; Sojka, M.; Ptak, M.; Qian, J.; Zhu, S.; Granata, F. Characteristics of River Heatwaves in the Vistula River Basin, Europe. Heliyon 2024, 10, e35987. [Google Scholar] [CrossRef] [PubMed]
- Ptak, M.; Olowoyeye, T.; Sojka, M. Trends of Changes in Minimum Lake Water Temperature in Poland. Appl. Sci. 2022, 12, 12601. [Google Scholar] [CrossRef]
- Olowoyeye, T.; Ptak, M.; Sojka, M. How Do Extreme Lake Water Temperatures in Poland Respond to Climate Change? Resources 2023, 12, 107. [Google Scholar] [CrossRef]
- Raczyński, K.; Dyer, J. Changes in Streamflow Drought and Flood Distribution over Poland Using Trend Decomposition. Acta Geophys. 2024, 72, 2773–2794. [Google Scholar] [CrossRef]
- Forzieri, G.; Feyen, L.; Rojas, R.; Flörke, M.; Wimmer, F.; Bianchi, A. Ensemble Projections of Future Streamflow Droughts in Europe. Hydrol. Earth Syst. Sci. 2014, 18, 85–108. [Google Scholar] [CrossRef]
- Piniewski, M.; Szcześniak, M.; Kundzewicz, Z.W.; Mezghani, A.; Hov, Ø. Changes in Low and High Flows in the Vistula and the Odra Basins: Model Projections in the European-scale Context. Hydrol. Process. 2017, 31, 2210–2225. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Piniewski, M.; Mezghani, A.; Okruszko, T.; Pińskwar, I.; Kardel, I.; Hov, Ø.; Szcześniak, M.; Szwed, M.; Benestad, R.E.; et al. Assessment of Climate Change and Associated Impact on Selected Sectors in Poland. Acta Geophys. 2018, 66, 1509–1523. [Google Scholar] [CrossRef]
- Wrzesiński, D.; Marsz, A.A.; Sobkowiak, L.; Styszyńska, A. Response of Low Flows of Polish Rivers to Climate Change in 1987–1989. Water 2022, 14, 2780. [Google Scholar] [CrossRef]
- Lorenc, H. Climatological and meteorological extremes in Poland in relation to the 5th IPCC Report. In Klimat a Społeczeństwo i Gospodarka; Lorenc, H., Ustrnul, Z., Eds.; Wyd. PT Geofizyczne i IMGW-PIB: Warsaw, Poland, 2015; pp. 31–51. (In Polish) [Google Scholar]
- Marsz, A.A.; Sobkowiak, L.; Styszyńska, A.; Wrzesiński, D. Causes and Course of Climate Change and Its Hydrological Consequences in the Greater Poland Region in 1951–2020. Quaest. Geogr. 2022, 41, 183–206. [Google Scholar] [CrossRef]
- Sutton, R.T.; Hodson, D.L.R. Atlantic Ocean forcing of North American and European summer climate. Science 2005, 309, 115–118. [Google Scholar] [CrossRef]
- Sutton, R.T.; Dong, B. Atlantic Ocean influence on a shift in European climate in the 1990s. Nat. Geosci. 2012, 5, 788–792. [Google Scholar] [CrossRef]
- Wrzesiński, D.; Marsz, A.; Styszyńska, A.; Sobkowiak, L. Effect of the North Atlantic Thermohaline Circulation in Changes in Climate Conditions and River Flow in Poland. Water 2019, 11, 1622. [Google Scholar] [CrossRef]
- Pociask-Karteczka, J.; Limanówka, D.; Nieckarz, Z. Impact of North Atlantic oscillation on the flows of the Carpathian rivers (1951–2000). Folia Geogr. Ser. Geogr. Phys. 2003, 33–34, 89–104. (In Polish) [Google Scholar]
- Pociask-Karteczka, J. River runoff response to climate changes in Poland (East-Central Europe). In Hydro-Climatology: Variability and Change (Proceedings of Symposium J-H02 Held During IUGG 2011 in Melbourne, Australia, July 2011); IAHS Publ.: Maastricht, The Netherlands, 2011; Volume 344. [Google Scholar]
- Piniewski, M.; Laizé, C.L.; Acreman, M.C.; Okruszko, T.; Schneider, C. Effect of climate change on environmental flow indicators in the Narew Basin, Poland. J. Environ. Qual. 2014, 43, 155–167. [Google Scholar] [CrossRef] [PubMed]
- Malinowski, Ł.; Skoczko, I. Impacts of Climate Change on Hydrological Regime and Water Resources Management of the Narew River in Poland. J. Ecol. Eng. 2018, 19, 4. [Google Scholar] [CrossRef]
- Gizińska, J.; Sojka, M. How Climate Change Affects River and Lake Water Temperature in Central-West Poland—A Case Study of the Warta River Catchment. Atmosphere 2023, 14, 330. [Google Scholar] [CrossRef]
- Okołowicz, W. General Climatology; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1976; pp. 1–422. (In Polish) [Google Scholar]
- Kędziora, A. Fundamentals of Agro-Meteorology; Państwowe Wydawnictwo Rolnicze i Leśne: Warsaw, Poland, 1999; pp. 1–364. (In Polish) [Google Scholar]
- Kędziora, A. Water balance of Konin strip mine landscape in changing climatic conditions. Rocz. Glebozn. 2008, 59, 104–118. (In Polish) [Google Scholar]
- Radzka, E. Climatic water balance for the vegetation season (according to Ivanov’s equation) in Central-Eastern Poland. Woda-Środowisko-Obsz. Wiej. 2014, 14, 67–76. (In Polish) [Google Scholar]
- Okoniewska, M.; Szumińska, D. Changes in Potential Evaporation in the Years 1952–2018 in North-Western Poland in Termsof the Impact of Climatic Changes on Hydrological an Hydrochemical Condotions. Water 2020, 12, 877. [Google Scholar] [CrossRef]
- Raczyński, K.; Dyer, J. Development of an Objective Low Flow Identification Method Using Breakpoint Analysis. Water 2022, 14, 2212. [Google Scholar] [CrossRef]
- Stahl, K.; Vidal, J.-P.; Hannaford, J.; Tijdeman, E.; Laaha, G.; Gauster, T.; Tallaksen, L.M. The Challenges of Hydrological Drought Definition, Quantification and Communication: An Interdisciplinary Perspective. Proc. Int. Assoc. Hydrol. Sci. 2020, 383, 291–295. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Grabiński, T.; Wydymus, S.; Zeliaś, A. Numerical Taxonomy Methods in Modeling Socio-Economic Phenomena; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1989; pp. 1–278. (In Polish) [Google Scholar]
- Mojena, R. Hierarchical grouping methods and stopping rules: An evaluation. Comput. J. 1977, 20, 359–363. [Google Scholar] [CrossRef]
- Rotnicka, J. Typology of Hydrological Periods for Use in River Regime Studies. Quaest. Geogr. 1993, 15/16, 77–95. [Google Scholar]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Marsz, A.A.; Styszyńska, A.; Bryś, K.; Bryś, T. Role of internal variability in climate system in increase of air temperature in Wrocław (Poland) in the years 1951–2018. Quaest. Geogr. 2021, 40, 109–124. [Google Scholar] [CrossRef]
- Wrzesiński, D. Flow Regime Patterns and Their Changes. In Management of Water Resources in Poland; Zeleňáková, M., Kubiak-Wójcicka, K., Negm, A.M., Eds.; Springer: New York, NY, USA, 2021; pp. 163–180. [Google Scholar] [CrossRef]
| Significance Level (p) | 1951–2020 (70 Years) | 1951–1988 (38 Years) | 1988–2020 (33 Years) |
|---|---|---|---|
| 0.05 | 0.232 | 0.213 | 0.334 |
| 0.01 | 0.302 | 0.403 | 0.430 |
| 0.001 | 0.380 | 0.501 | 0.532 |
| Group | Mean | BSS | Standard Deviation (σ) | Median | Min. | Max. | Lower Quartile | Upper Quartile |
|---|---|---|---|---|---|---|---|---|
| A (SE Poland) | 36.07 | 3.47 | 29.05 | 30.61 | 0.42 | 127.97 | 13.42 | 49.70 |
| B1 (N Poland) | 35.98 | 4.19 | 35.05 | 21.83 | 0.15 | 136.28 | 10.70 | 52.38 |
| B2 (SW Poland) | 35.56 | 3.97 | 37.25 | 25.36 | 1.21 | 124.63 | 8.96 | 58.60 |
| Group | 1951–1988 | 1988–2020 | ||
|---|---|---|---|---|
| Average NDLF | BSS | Average NDLF | BSS | |
| A (SE Poland) | 42.17 | 5.29 | 28.81 | 3.86 |
| B1 (N Poland) | 36.42 | 6.10 | 34.40 | 5.66 |
| B2 (SW Poland) | 27.55 | 4.37 | 44.09 | 6.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wrzesiński, D.; Marsz, A.A.; Styszyńska, A.; Perz, A.E.; Brzezińska, W.; Sobkowiak, L. Spatial Regularities of Changes in the Duration of Low River Flows in Poland Under Climate Warming Conditions. Water 2025, 17, 243. https://doi.org/10.3390/w17020243
Wrzesiński D, Marsz AA, Styszyńska A, Perz AE, Brzezińska W, Sobkowiak L. Spatial Regularities of Changes in the Duration of Low River Flows in Poland Under Climate Warming Conditions. Water. 2025; 17(2):243. https://doi.org/10.3390/w17020243
Chicago/Turabian StyleWrzesiński, Dariusz, Andrzej A. Marsz, Anna Styszyńska, Adam Edmund Perz, Wiktoria Brzezińska, and Leszek Sobkowiak. 2025. "Spatial Regularities of Changes in the Duration of Low River Flows in Poland Under Climate Warming Conditions" Water 17, no. 2: 243. https://doi.org/10.3390/w17020243
APA StyleWrzesiński, D., Marsz, A. A., Styszyńska, A., Perz, A. E., Brzezińska, W., & Sobkowiak, L. (2025). Spatial Regularities of Changes in the Duration of Low River Flows in Poland Under Climate Warming Conditions. Water, 17(2), 243. https://doi.org/10.3390/w17020243






