Dynamic Co-Optimization of Features and Hyperparameters in Object-Oriented Ensemble Methods for Wetland Mapping Using Sentinel-1/2 Data
Abstract
1. Introduction
2. Materials and Methods
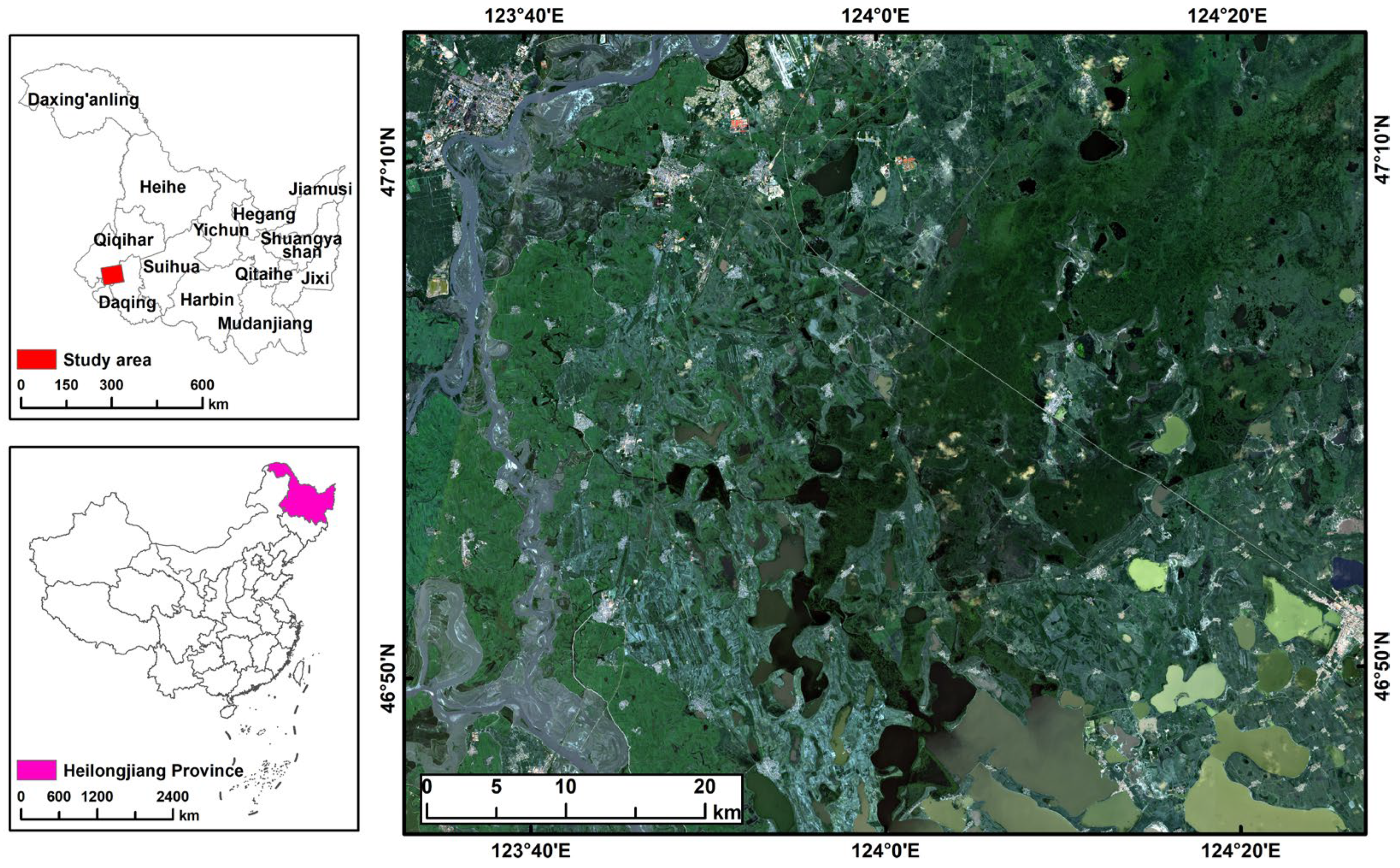
2.1. Study Area
2.2. Datasets
2.2.1. Sentinel-1 and Sentinel-2 Image Acquisition
2.2.2. Field Survey Data Collection
2.3. Shapley Additive Explanations Method
2.4. Feature Selection Techniques
2.5. Ensemble Algorithms and Hyperparameters Tuning
2.5.1. Tree-Based Ensemble Algorithms
2.5.2. Hyperparameters Tuning
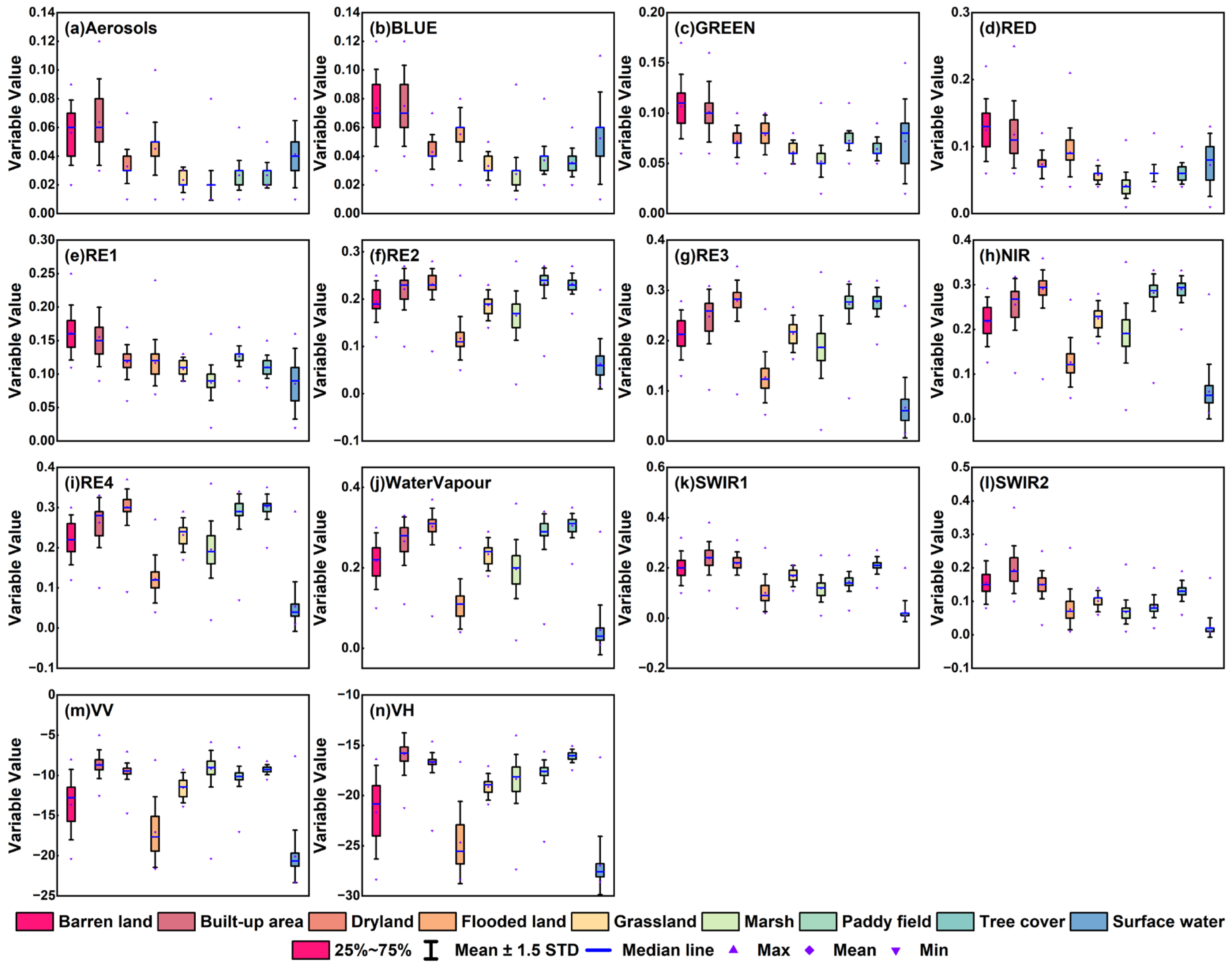
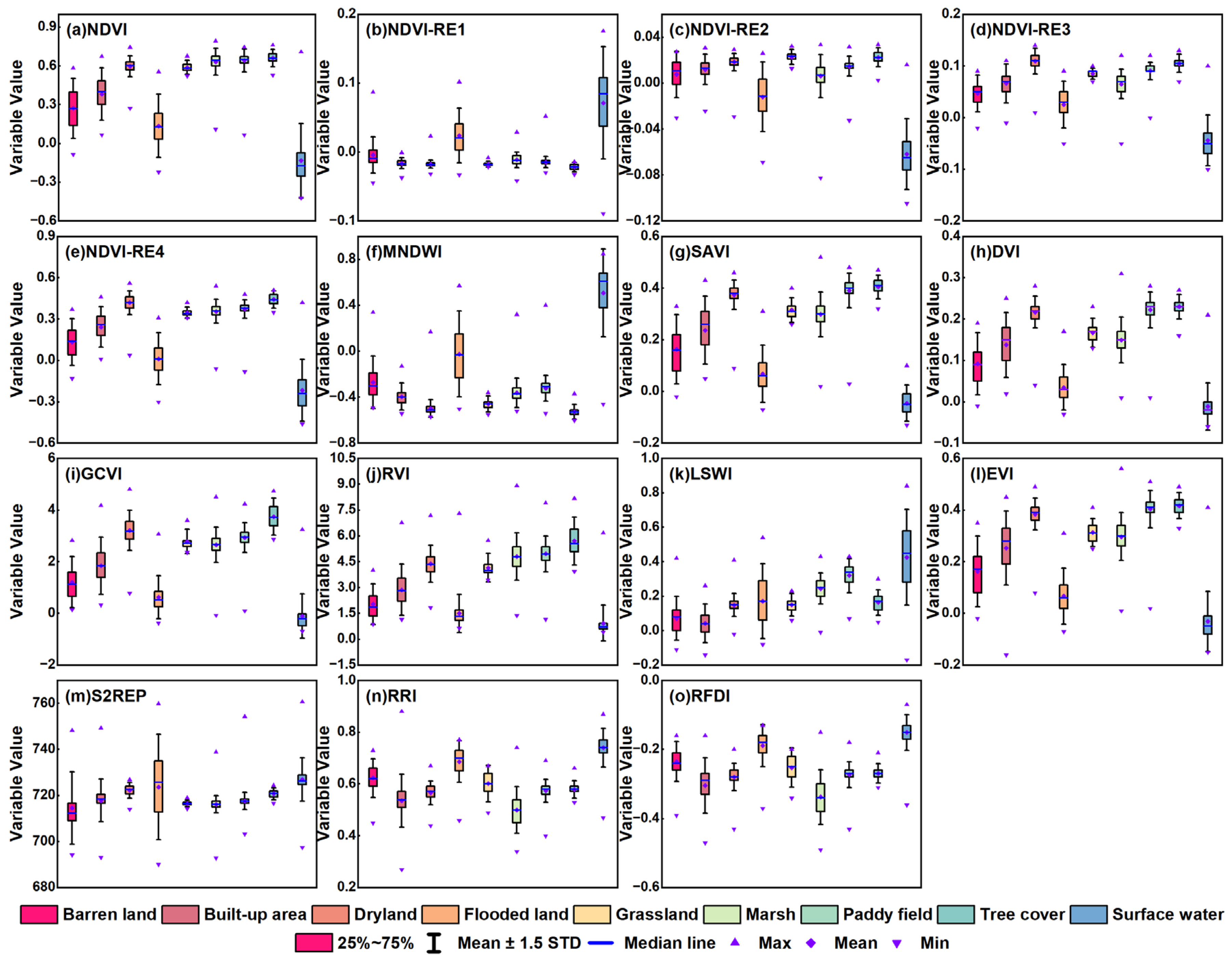
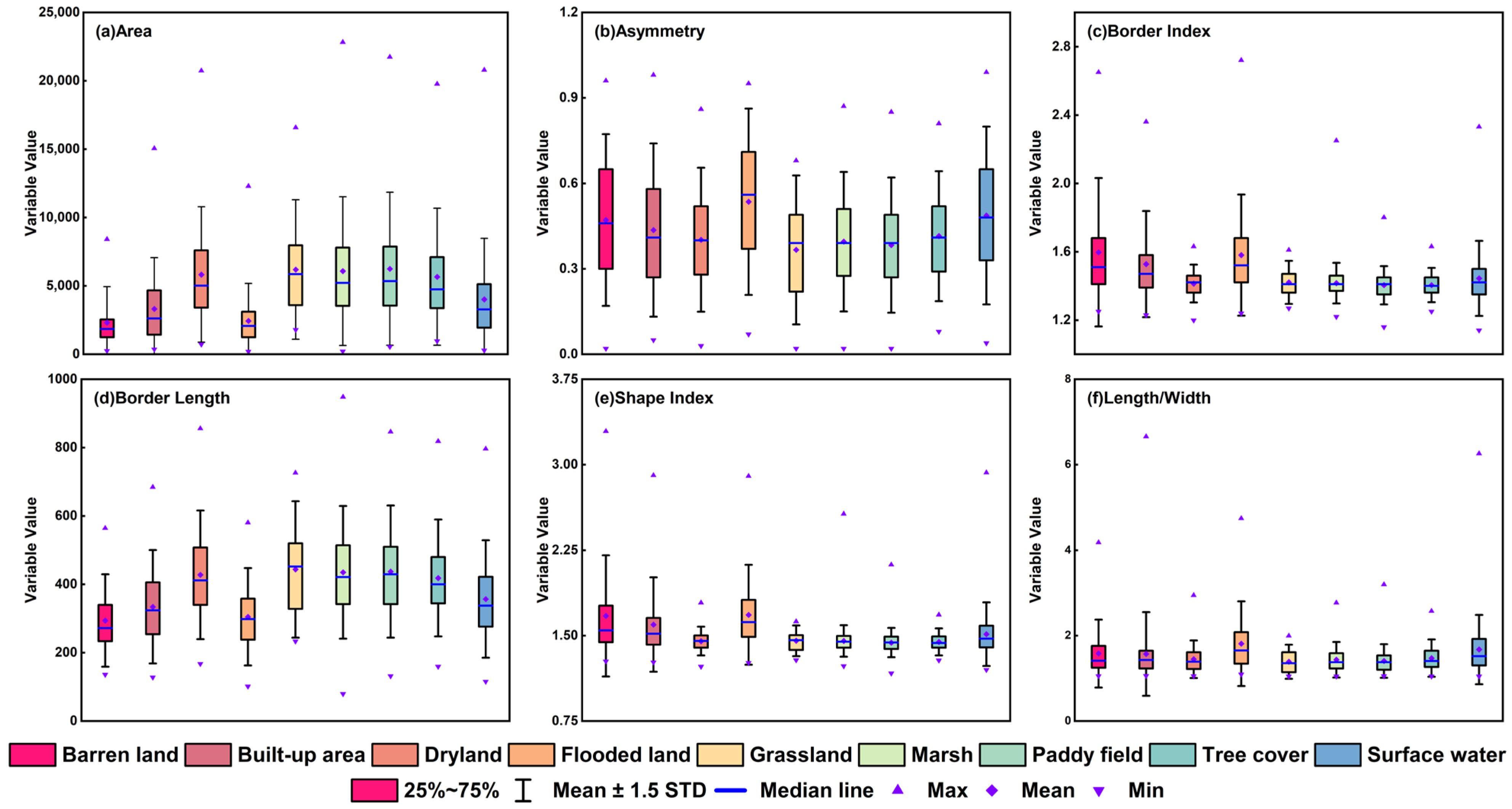
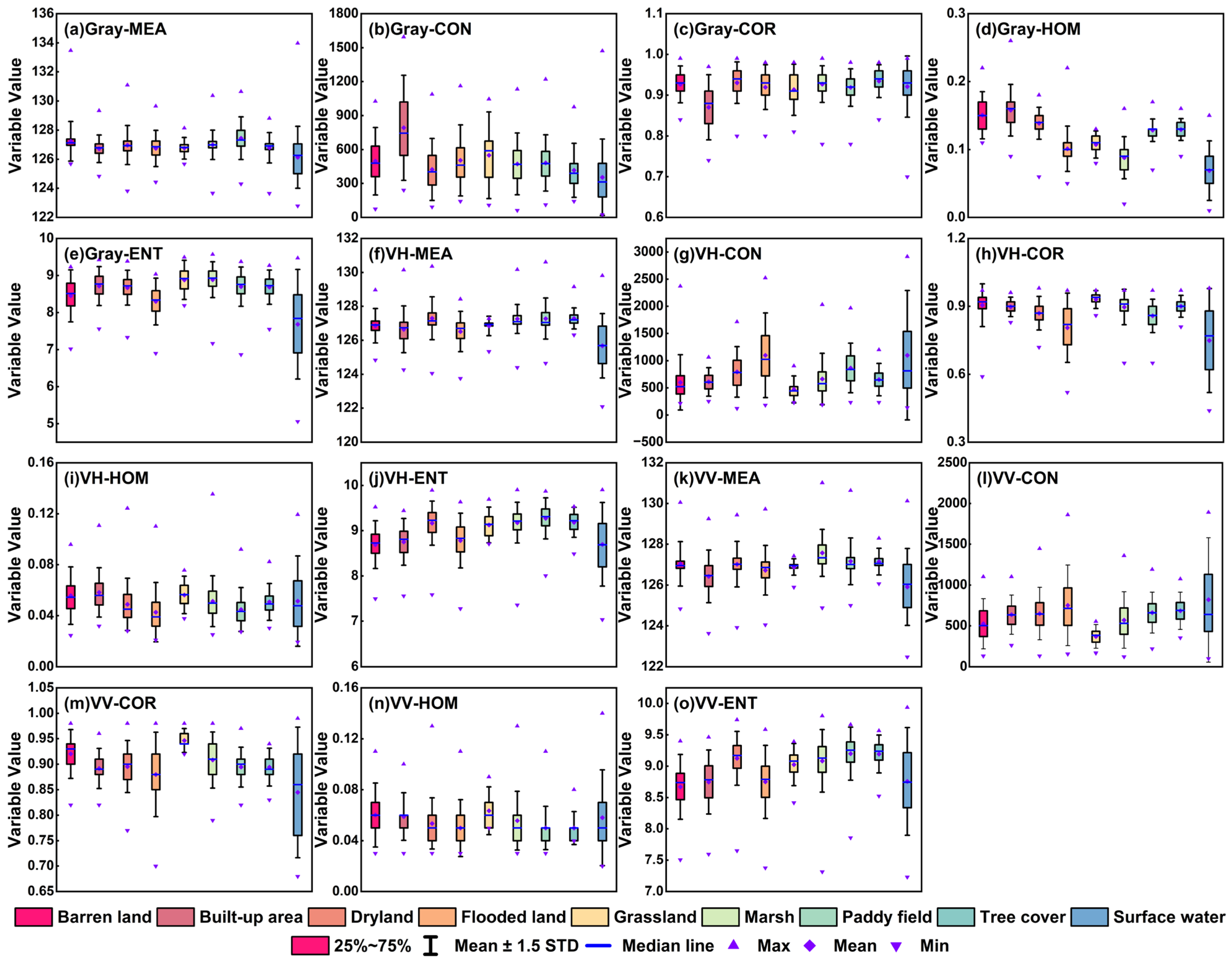
2.6. Feature Extraction from Sentinel-1 and Sentinel-2 Images
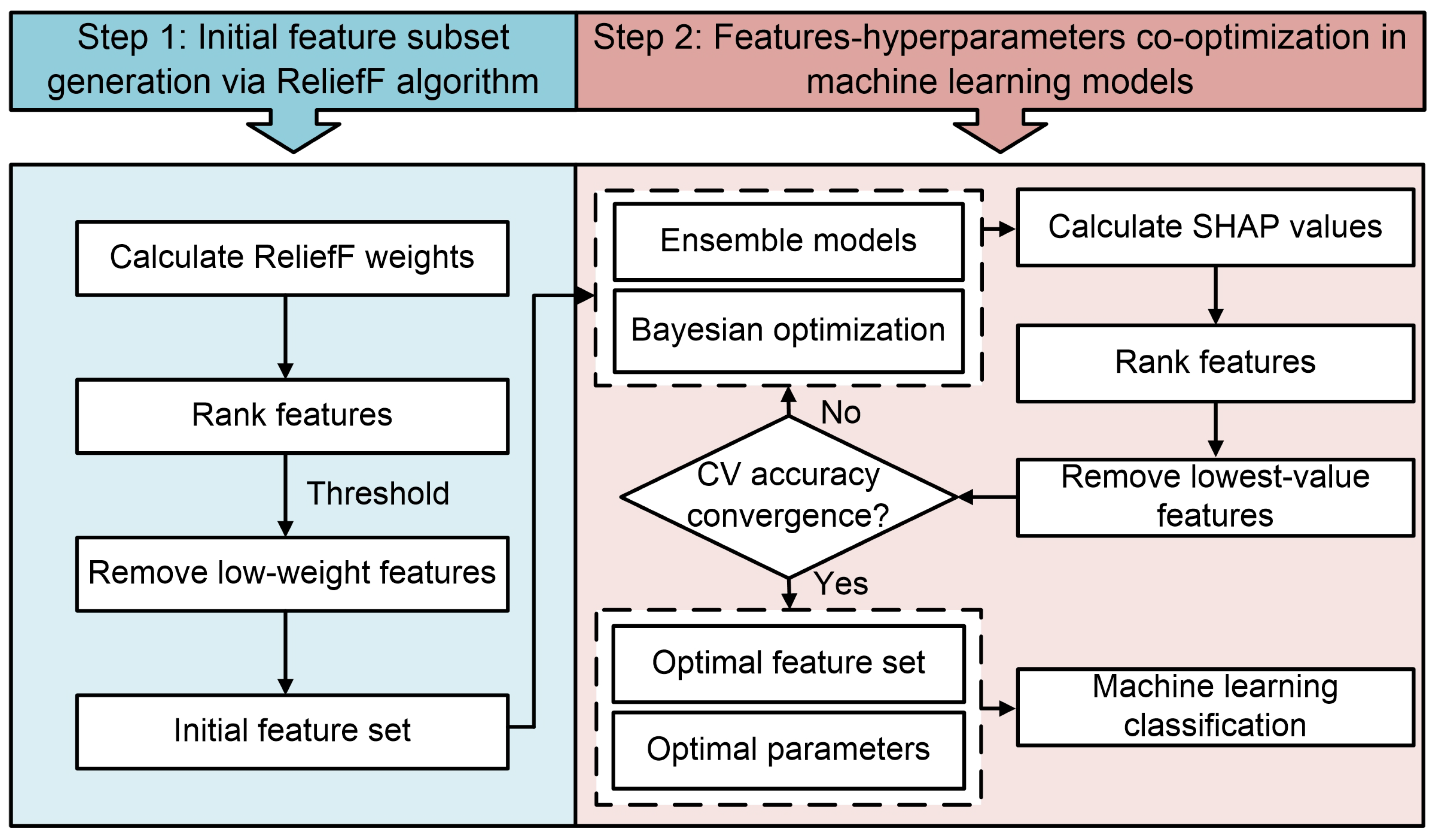
2.7. Dynamic Hybrid Method for Wetland Mapping
2.8. Accuracy Assessment
3. Results and Discussion
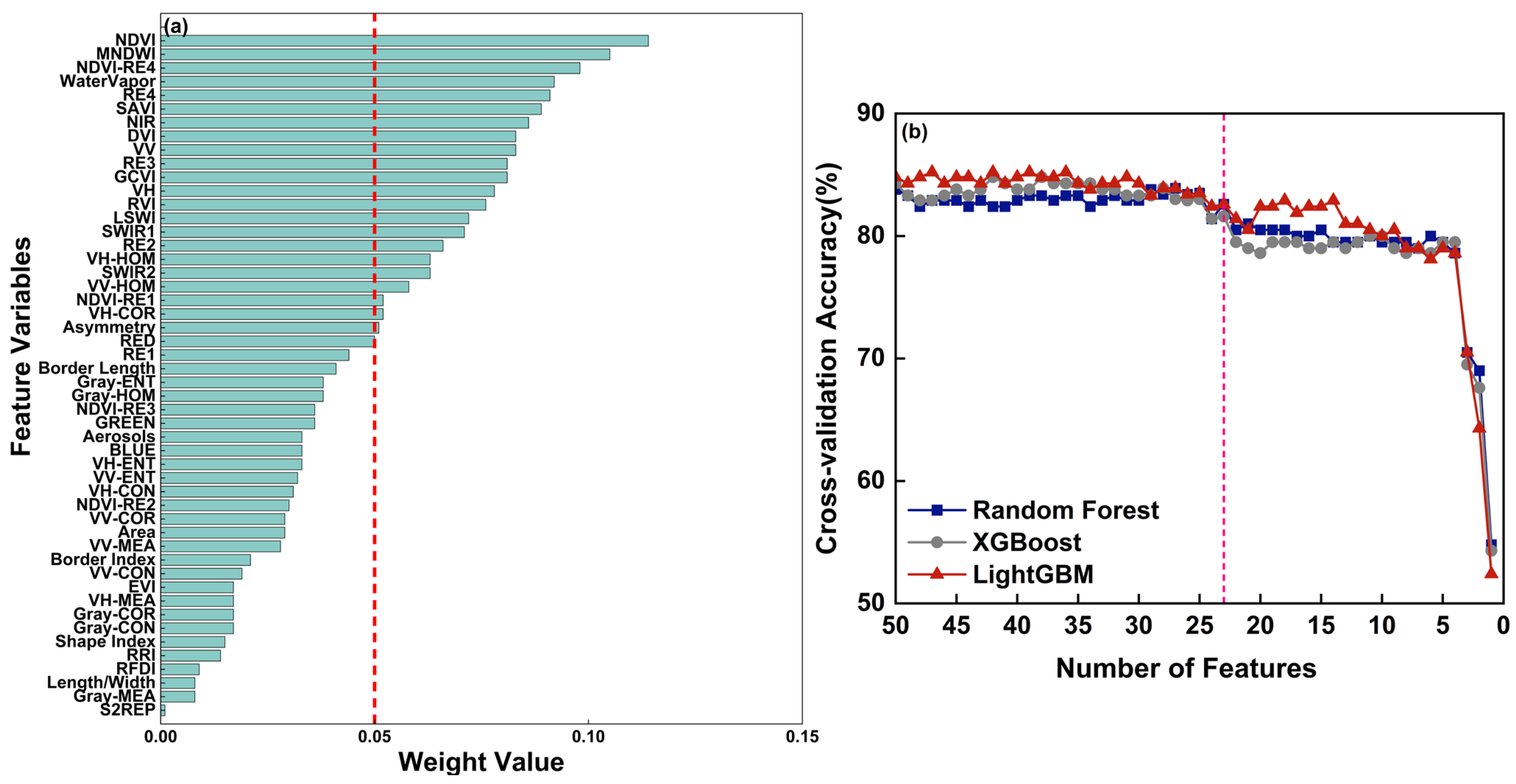
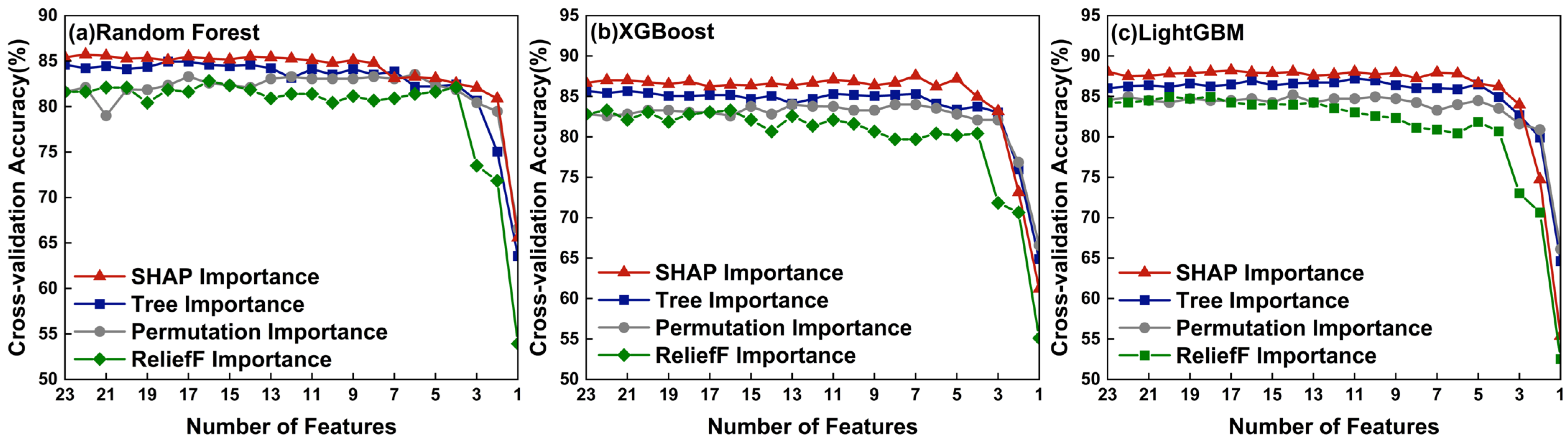
3.1. Feature Ranking and Accuracy Assessment Based on the ReliefF Algorithm
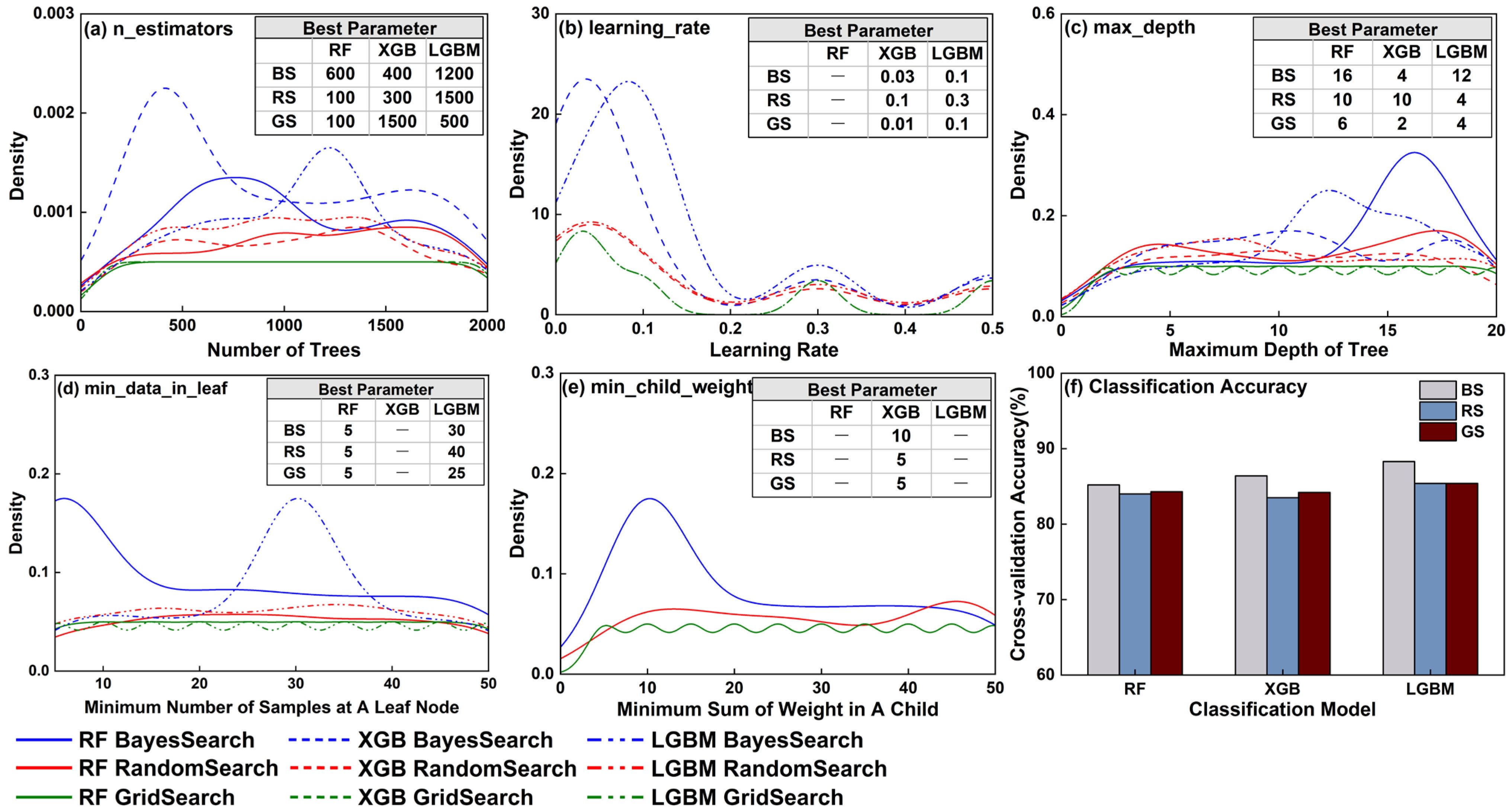
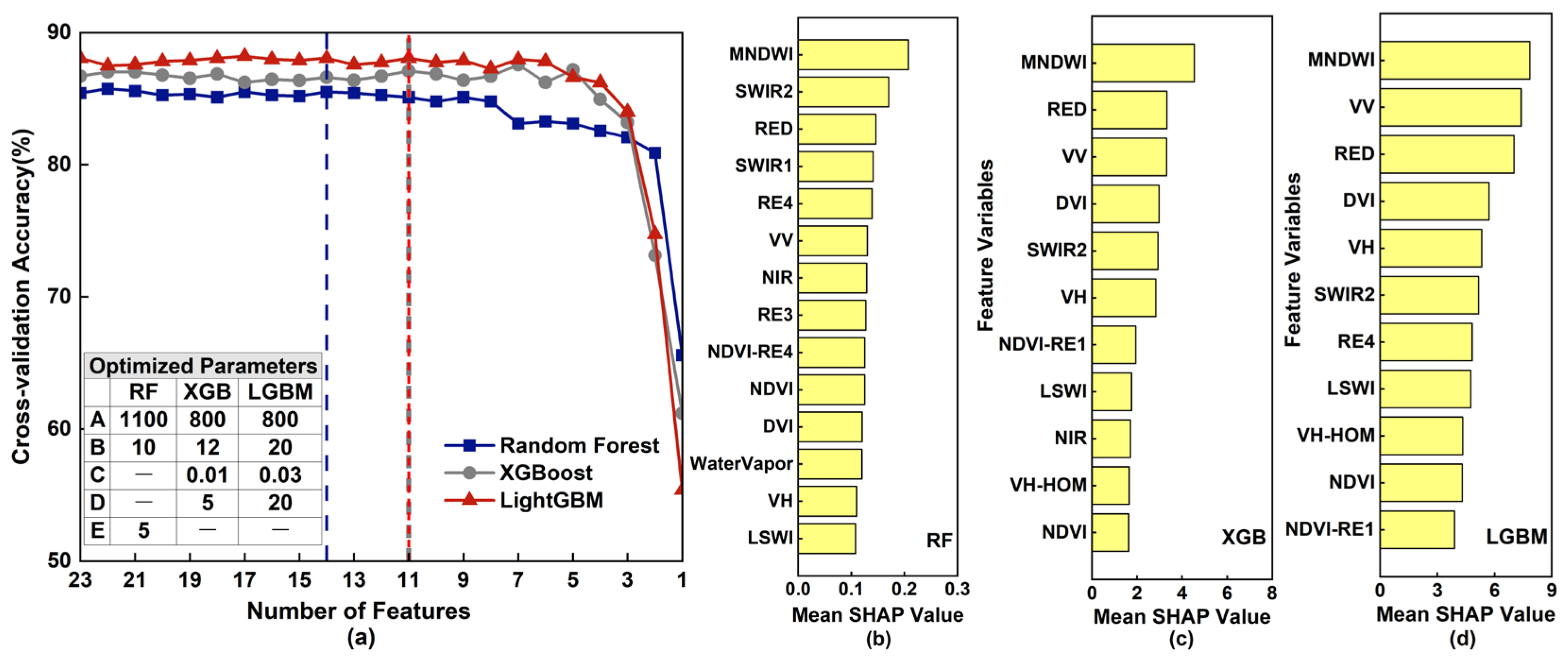
3.2. Evaluation of Hyperparameter Tuning Methods
3.3. Evaluation of Dynamic Hybrid Methods
3.4. Assessment of Computational Efficiency
3.5. Classification Results
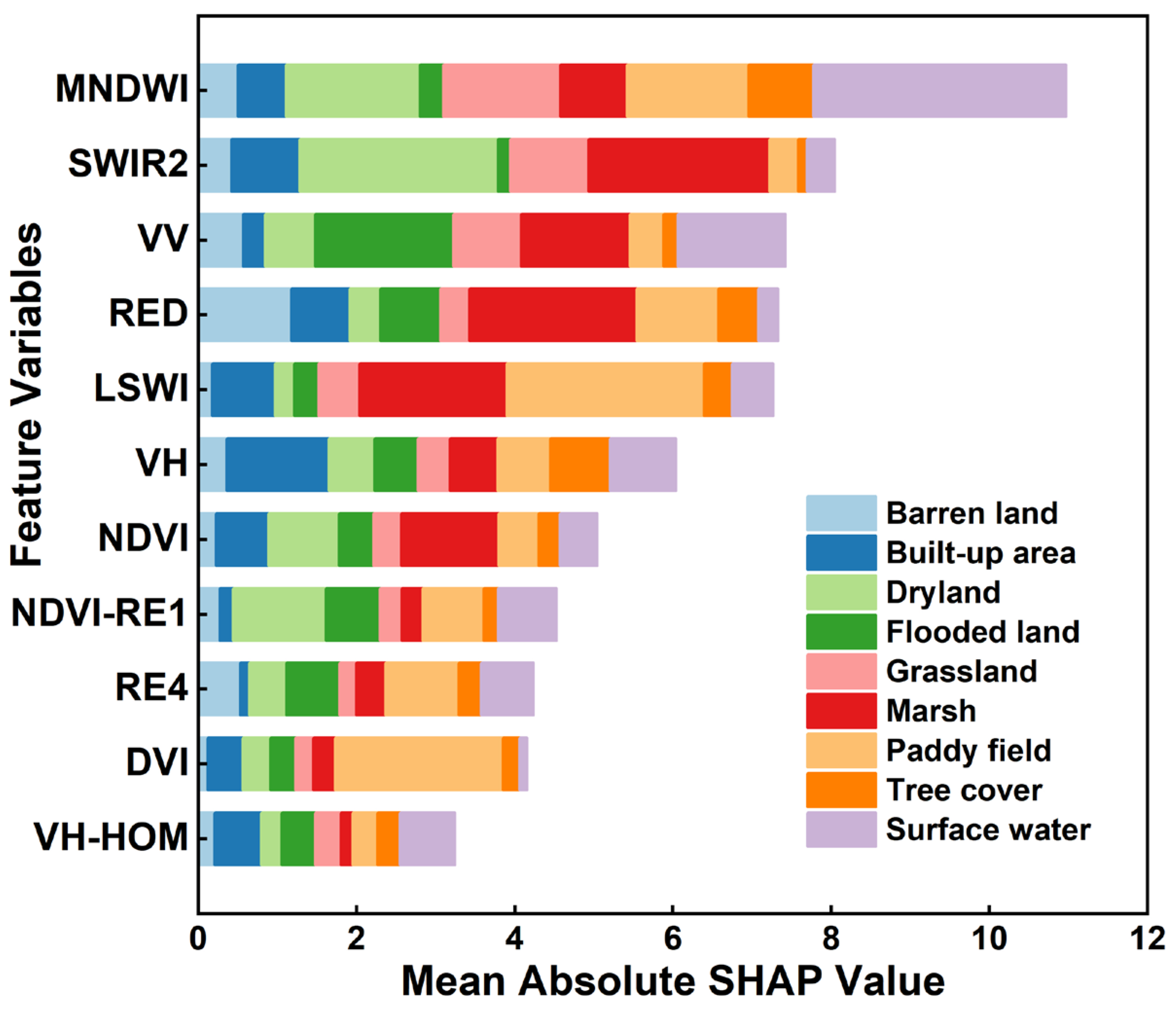
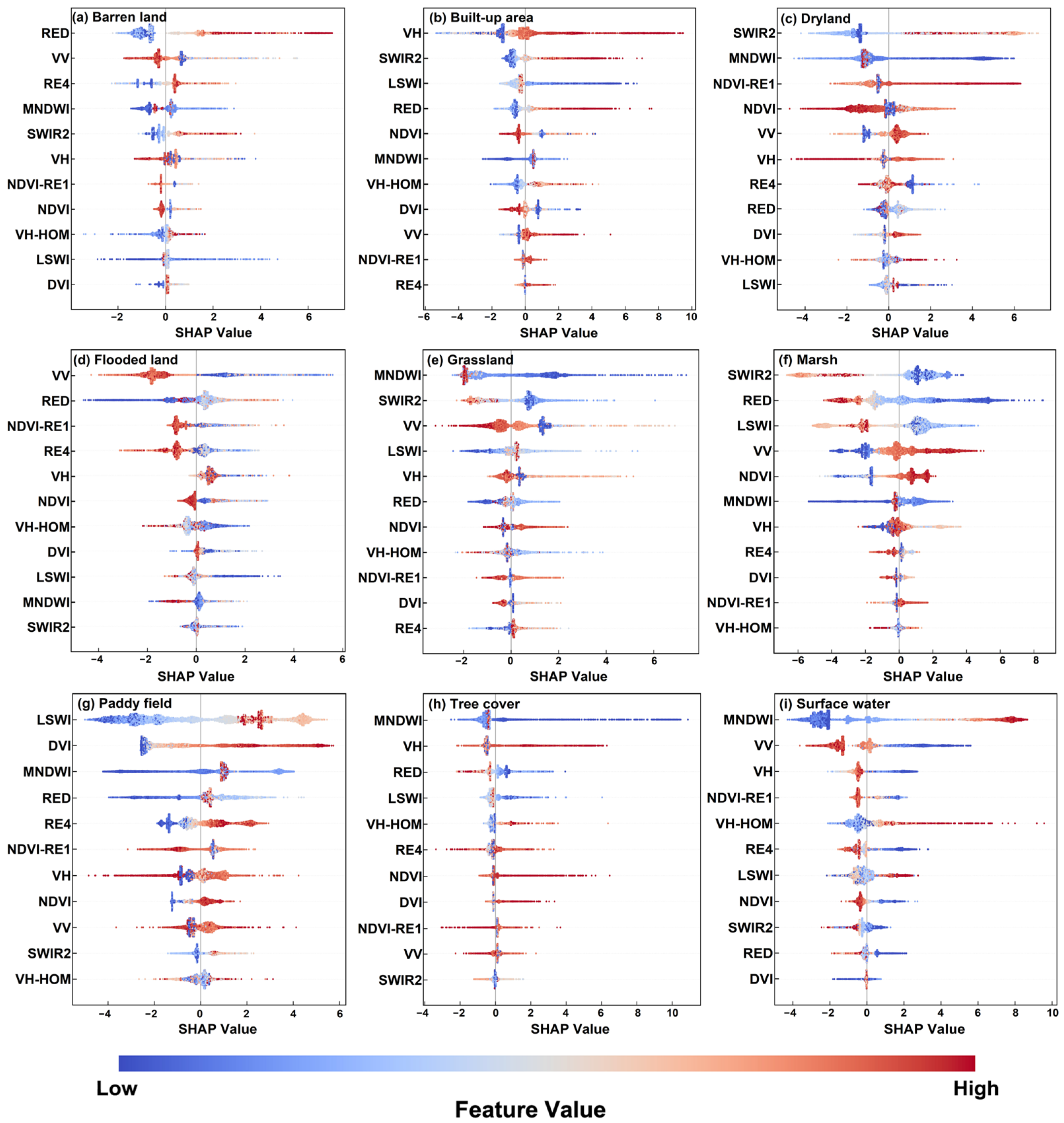
3.6. Explanation of Variable Importance for Wetland Classification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bridgewater, P.; Kim, R.E. The Ramsar convention on wetlands at 50. Nat. Ecol. Evol. 2021, 5, 268–270. [Google Scholar] [CrossRef]
- Ramsar, C.S. The Ramsar Convention Manual: A Guide to the Convention on Wetlands (Ramsar, Iran, 1971), 6th ed.; Ramsar Convention Secretariat: Gland, Switzerland, 2013. [Google Scholar]
- Liu, H.; Jiang, Q.; Ma, Y.; Yang, Q.; Shi, P.; Zhang, S.; Tan, Y.; Xi, J.; Zhang, Y.; Liu, B.; et al. Object-Based Multigrained Cascade Forest Method for Wetland Classification Using Sentinel-2 and Radarsat-2 Imagery. Water 2022, 14, 82. [Google Scholar] [CrossRef]
- Xu, T.; Weng, B.; Yan, D.; Wang, K.; Li, X.; Bi, W.; Li, M.; Cheng, X.; Liu, Y. Wetlands of International Importance: Status, Threats, and Future Protection. Int. J. Environ. Res. Public Health 2019, 16, 1818. [Google Scholar] [CrossRef] [PubMed]
- Mahdavi, S.; Salehi, B.; Granger, J.; Amani, M.; Brisco, B.; Huang, W. Remote sensing for wetland classification: A comprehensive review. Gisci. Remote Sens. 2017, 55, 623–658. [Google Scholar] [CrossRef]
- Eppink, F.V.; van den Bergh, J.C.; Rietveld, P. Modelling biodiversity and land use: Urban growth, agriculture and nature in a wetland area. Ecol. Econ. 2004, 51, 201–216. [Google Scholar] [CrossRef]
- Mondal, B.; Dolui, G.; Pramanik, M.; Maity, S.; Biswas, S.S.; Pal, R. Urban expansion and wetland shrinkage estimation using a GIS-based model in the East Kolkata Wetland, India. Ecol. Indic. 2017, 83, 62–73. [Google Scholar] [CrossRef]
- Guo, M.; Li, J.; Sheng, C.; Xu, J.; Wu, L. A review of wetland remote sensing. Sensors 2017, 17, 777. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Puri, L.; Acharya, A.K.; Aryal, R. Wetland mapping and monitoring with Sentinel-1 and Sentinel-2 data on the Google Earth Engine. J. For. Nat. Resour. Manag. 2023, 3, 1–21. [Google Scholar] [CrossRef]
- Peng, K.; Jiang, W.; Hou, P.; Wu, Z.; Ling, Z.; Wang, X.; Niu, Z.; Mao, D. Continental-scale wetland mapping: A novel algorithm for detailed wetland types classification based on time series Sentinel-1/2 images. Ecol. Indic. 2023, 148, 110113. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, Z.Y.; Avdan, U. Mapping and monitoring wetland dynamics using thermal, optical, and SAR remote sensing data. Wetl. Manag. Assess. Risk Sustain. Solut. 2019, 87, 86–107. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, L.; Xiong, S.; You, L.; He, Z.; Huang, Y.; Lu, J. C-band synthetic aperture radar time-series for mapping of wetland plant communities in China’s largest freshwater lake. J. Appl. Remote Sens. 2025, 19, 021006. [Google Scholar] [CrossRef]
- Grings, F.; Ferrazzoli, P.; Karszenbaum, H.; Salvia, M.; Kandus, P.; Jacobo-Berlles, J.; Perna, P. Model investigation about the potential of C band SAR in herbaceous wetlands flood monitoring. Int. J. Remote Sens. 2008, 29, 5361–5372. [Google Scholar] [CrossRef]
- Prasad, P.; Loveson, V.J.; Kotha, M. Probabilistic coastal wetland mapping with integration of optical, SAR and hydro-geomorphic data through stacking ensemble machine learning model. Ecol. Inform. 2023, 77, 102273. [Google Scholar] [CrossRef]
- Landuyt, L.; Verhoest, N.E.; Van Coillie, F.M. Flood mapping in vegetated areas using an unsupervised clustering approach on sentinel-1 and-2 imagery. Remote Sens. 2020, 12, 3611. [Google Scholar] [CrossRef]
- Konapala, G.; Kumar, S.V.; Ahmad, S.K. Exploring Sentinel-1 and Sentinel-2 diversity for flood inundation mapping using deep learning. ISPRS J. Photogramm. 2021, 180, 163–173. [Google Scholar] [CrossRef]
- Slagter, B.; Tsendbazar, N.-E.; Vollrath, A.; Reiche, J. Mapping wetland characteristics using temporally dense Sentinel-1 and Sentinel-2 data: A case study in the St. Lucia wetlands, South Africa. Int. J. Appl. Earth Obs. 2020, 86, 102009. [Google Scholar] [CrossRef]
- Mohseni, F.; Amani, M.; Mohammadpour, P.; Kakooei, M.; Jin, S.; Moghimi, A. Wetland mapping in great lakes using Sentinel-1/2 time-series imagery and DEM data in Google Earth Engine. Remote Sens. 2023, 15, 3495. [Google Scholar] [CrossRef]
- Gallant, A.L. The challenges of remote monitoring of wetlands. Remote Sens. 2015, 7, 10938–10950. [Google Scholar] [CrossRef]
- Wen, L.; Hughes, M. Coastal wetland mapping using ensemble learning algorithms: A comparative study of bagging, boosting and stacking techniques. Remote Sens. 2020, 12, 1683. [Google Scholar] [CrossRef]
- Ferreira, C.S.; Kašanin-Grubin, M.; Solomun, M.K.; Sushkova, S.; Minkina, T.; Zhao, W.; Kalantari, Z. Wetlands as nature-based solutions for water management in different environments. Curr. Opin. Environ. Sci. Health 2023, 33, 100476. [Google Scholar] [CrossRef]
- Carlson, K.; Buttenfield, B.P.; Qiang, Y. Wetland Classification, Attribute Accuracy, and Scale. ISPRS Int. J. Geo-Inf. 2024, 13, 103. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Yuling, H.; Gang, Y.; Weiwei, S.; Lin, Z.; Ke, H.; Xiangchao, M. Wetlands mapping in typical regions of South America with multi-source and multi-feature integration. J. Remote Sens. 2023, 27, 1300–1319. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Granger, J.E.; Brisco, B.; Hanson, A. Wetland classification using multi-source and multi-temporal optical remote sensing data in Newfoundland and Labrador, Canada. Can. J. Remote Sens. 2017, 43, 360–373. [Google Scholar] [CrossRef]
- Beniwal, S.; Arora, J. Classification and feature selection techniques in data mining. Int. J. Eng. Res. Technol. 2012, 1, 1–6. [Google Scholar]
- Bruzzone, L. An approach to feature selection and classification of remote sensing images based on the Bayes rule for minimum cost. IEEE T. Geosci. Remote 2000, 38, 429–438. [Google Scholar] [CrossRef]
- Tang, J.L.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–64. [Google Scholar]
- Wah, Y.B.; Ibrahim, N.; Hamid, H.A.; Abdul-Rahman, S.; Fong, S. Feature selection methods: Case of filter and wrapper approaches for maximising classification accuracy. Pertanika J. Sci. Tech. 2018, 26, 329–340. [Google Scholar]
- Liu, H.; Zhou, M.; Liu, Q. An embedded feature selection method for imbalanced data classification. IEEE-CAA J. Automatic. 2019, 6, 703–715. [Google Scholar] [CrossRef]
- Prastyo, P.H.; Ardiyanto, I.; Hidayat, R. A review of feature selection techniques in sentiment analysis using filter, wrapper, or hybrid methods. In Proceedings of the 2020 6th International Conference on Science and Technology (ICST), Yogyakarta, Indonesia, 7–8 September 2020; pp. 1–6. [Google Scholar]
- Stańczyk, U. Feature evaluation by filter, wrapper, and embedded approaches. In Feature Selection for Data and Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2014; pp. 29–44. [Google Scholar]
- Hira, Z.M.; Gillies, D.F. A review of feature selection and feature extraction methods applied on microarray data. Adv. Bioinform. 2015, 2015, 198363. [Google Scholar] [CrossRef] [PubMed]
- Xiong, M.; Fang, X.; Zhao, J. Biomarker identification by feature wrappers. Genome Res. 2001, 11, 1878–1887. [Google Scholar] [CrossRef] [PubMed]
- Santana, L.E.A.d.S.; de Paula Canuto, A.M. Filter-based optimization techniques for selection of feature subsets in ensemble systems. Expert Syst. Appl. 2014, 41, 1622–1631. [Google Scholar] [CrossRef]
- Ansari, G.; Ahmad, T.; Doja, M.N. Hybrid filter–wrapper feature selection method for sentiment classification. Arab. J. Sci. Eng. 2019, 44, 9191–9208. [Google Scholar] [CrossRef]
- Stańczyk, U. Ranking of characteristic features in combined wrapper approaches to selection. Neural Comput. Appl. 2015, 26, 329–344. [Google Scholar] [CrossRef]
- Amani, M.; Mahdavi, S.; Berard, O. Supervised wetland classification using high spatial resolution optical, SAR, and LiDAR imagery. J. Appl. Remote Sens. 2020, 14, 024502. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Ruiz, L.F.C.; Guasselli, L.A.; Simioni, J.P.D.; Belloli, T.F.; Fernandes, P.C.B. Object-based classification of vegetation species in a subtropical wetland using Sentinel-1 and Sentinel-2A images. Sci. Remote Sens. 2021, 3, 100017. [Google Scholar] [CrossRef]
- Azhand, D.; Pirasteh, S.; Varshosaz, M.; Shahabi, H.; Abdollahabadi, S.; Teimouri, H.; Pirnazar, M.; Wang, X.; Li, W. Sentinel 1a-2a incorporating an object-based image analysis method for flood mapping and extent assessment. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2024, 10, 7–17. [Google Scholar] [CrossRef]
- Chen, Y.; He, X.; Xu, J.; Zhang, R.; Lu, Y. Scattering feature set optimization and polarimetric SAR classification using object-oriented RF-SFS algorithm in coastal wetlands. Remote Sens. 2020, 12, 407. [Google Scholar] [CrossRef]
- Zheng, J.Y.; Hao, Y.Y.; Wang, Y.C.; Zhou, S.Q.; Wu, W.B.; Yuan, Q.; Gao, Y.; Guo, H.Q.; Cai, X.X.; Zhao, B. Coastal wetland vegetation classification using pixel-based, object-based and deep learning methods based on RGB-UAV. Land 2022, 11, 2039. [Google Scholar] [CrossRef]
- Guo, S.; Feng, Z.; Wang, P.; Chang, J.; Han, H.; Li, H.; Chen, C.; Du, W. Mapping and classification of the liaohe estuary wetland based on the combination of object-oriented and temporal features. IEEE Access 2024, 12, 60496–60512. [Google Scholar] [CrossRef]
- Marjani, M.; Mahdianpari, M.; Mohammadimanesh, F.; Gill, E.W. CVTNet: A fusion of convolutional neural networks and vision transformer for wetland mapping using Sentinel-1 and Sentinel-2 satellite data. Remote Sens. 2024, 16, 2427. [Google Scholar] [CrossRef]
- Hosseiny, B.; Mahdianpari, M.; Brisco, B.; Mohammadimanesh, F.; Salehi, B. WetNet: A spatial–temporal ensemble deep learning model for wetland classification using Sentinel-1 and Sentinel-2. IEEE T. Geosci. Remote 2021, 60, 4406014. [Google Scholar] [CrossRef]
- Onojeghuo, A.O.; Onojeghuo, A.R. Wetlands Mapping with Deep ResU-Net CNN and Open-Access Multisensor and Multitemporal Satellite Data in Alberta’s Parkland and Grassland Region. Remote Sens. Earth Syst. Sci. 2023, 6, 22–37. [Google Scholar] [CrossRef]
- Krichen, M. Convolutional neural networks: A survey. Computers 2023, 12, 151. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE T. Neur. Net. Lear. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Jamali, A.; Mahdianpari, M.; Karaş, İ.R. A comparison of tree-based algorithms for complex wetland classification using the google earth engine. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2021, 46, 313–319. [Google Scholar] [CrossRef]
- Govil, S.; Lee, A.J.; MacQueen, A.C.; Pricope, N.G.; Minei, A.; Chen, C. Using hyperspatial LiDAR and multispectral imaging to identify coastal wetlands using gradient boosting methods. Remote Sens. 2022, 14, 6002. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Shen, W. A review of ensemble learning algorithms used in remote sensing applications. Appl. Sci. 2022, 12, 8654. [Google Scholar] [CrossRef]
- Fu, B.L.; Liu, M.; He, H.C.; Lan, F.W.; He, X.; Liu, L.L.; Huang, L.K.; Fan, D.L.; Zhao, M.; Jia, Z.L. Comparison of optimized object-based RF-DT algorithm and SegNet algorithm for classifying Karst wetland vegetation communities using ultra-high spatial resolution UAV data. Int. J. Appl. Earth Obs. 2021, 104, 102533. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, C.; Li, E.; Cai, X.; Yang, J.; Xia, Y. Object-Based Wetland Vegetation Classification Using Multi-Feature Selection of Unoccupied Aerial Vehicle RGB Imagery. Remote Sens. 2021, 13, 4910. [Google Scholar] [CrossRef]
- Fu, B.L.; Xie, S.Y.; He, H.C.; Zuo, P.P.; Sun, J.; Liu, L.L.; Huang, L.K.; Fan, D.L.; Gao, E.T. Synergy of multi-temporal polarimetric SAR and optical image satellite for mapping of marsh vegetation using object-based random forest algorithm. Ecol. Indic. 2021, 131, 108173. [Google Scholar] [CrossRef]
- Ke, L.N.; Tan, Q.; Lu, Y.; Wang, Q.M.; Zhang, G.S.; Zhao, Y.; Wang, L. Classification and spatio-temporal evolution analysis of coastal wetlands in the Liaohe Estuary from 1985 to 2023: Based on feature selection and sample migration methods. Front. For. Glob. Chang. 2024, 7, 1406473. [Google Scholar] [CrossRef]
- Feng, K.; Mao, D.; Zhen, J.; Pu, H.; Yan, H.; Wang, M.; Wang, D.; Xiang, H.; Ren, Y.; Luo, L. Potential of Sample Migration and Explainable Machine Learning Model for Monitoring Spatiotemporal Changes of Wetland Plant Communities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 9894–9906. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, B.; Sun, X.; Yao, H.; Zhang, S.; Wu, Y.; Kuang, H.; Deng, T. Effects of multi-growth periods UAV images on classifying karst wetland vegetation communities using object-based optimization stacking algorithm. Remote Sens. 2023, 15, 4003. [Google Scholar] [CrossRef]
- Aydin, H.E.; Iban, M.C. Predicting and analyzing flood susceptibility using boosting-based ensemble machine learning algorithms with SHapley Additive exPlanations. Nat. Hazards 2023, 116, 2957–2991. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Na, X.; Zang, S.; Liu, L.; Li, M. Wetland mapping in the Zhalong National Natural Reserve, China, using optical and radar imagery and topographical data. J. Appl. Remote Sens. 2013, 7, 073554. [Google Scholar] [CrossRef]
- Ekanayake, I.; Meddage, D.; Rathnayake, U. A novel approach to explain the black-box nature of machine learning in compressive strength predictions of concrete using Shapley additive explanations (SHAP). Case Stud. Constr. Mat. 2022, 16, e01059. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. Explainable AI for trees: From local explanations to global understanding. arXiv 2019, arXiv:1905.04610. [Google Scholar] [CrossRef] [PubMed]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In Proceedings of the European Conference on Machine Learning, Catania, Italy, 6–8 April 1994; pp. 171–182. [Google Scholar]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Chen, R.C.; Dewi, C.; Huang, S.W.; Caraka, R.E. Selecting critical features for data classification based on machine learning methods. J. Big Data 2020, 7, 52. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 52. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Shi, T.L.; Wang, C.; Zhang, W.; He, J.J. Classification of coastal wetlands in the Liaohe Delta with multi-source and multi-feature integration. Environ. Monit. Assess. 2025, 197, 247. [Google Scholar] [CrossRef]
- Gangat, R.; Van Deventer, H.; Naidoo, L.; Adam, E. Estimating soil moisture using Sentinel-1 and Sentinel-2 sensors for dryland and palustrine wetland areas. S. Afr. J. Sci. 2020, 116, 49–57. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Tassi, A.; Vizzari, M. Object-Oriented LULC Classification in Google Earth Engine Combining SNIC, GLCM, and Machine Learning Algorithms. Remote Sens. 2020, 12, 3776. [Google Scholar] [CrossRef]
- Iqbal, N.; Mumtaz, R.; Shafi, U.; Zaidi, S.M.H. Gray level co-occurrence matrix (GLCM) texture based crop classification using low altitude remote sensing platforms. PeerJ Comput. Sci. 2021, 7, e536. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.; Deering, D. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA: Washington, DC, USA, 1973.
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Tucker, C.J.; Sellers, P. Satellite remote sensing of primary production. Int. J. Remote Sens. 1986, 7, 1395–1416. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Chandrasekar, K.; Sesha Sai, M.; Roy, P.; Dwevedi, R. Land Surface Water Index (LSWI) response to rainfall and NDVI using the MODIS Vegetation Index product. Int. J. Remote Sens. 2010, 31, 3987–4005. [Google Scholar] [CrossRef]
- Huete, A.; Liu, H.; Batchily, K.; Van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Vreugdenhil, M.; Wagner, W.; Bauer-Marschallinger, B.; Pfeil, I.; Teubner, I.; Rüdiger, C.; Strauss, P. Sensitivity of Sentinel-1 backscatter to vegetation dynamics: An Austrian case study. Remote Sens. 2018, 10, 1396. [Google Scholar] [CrossRef]
- Wagner, F.H.; Dalagnol, R.; Tarabalka, Y.; Segantine, T.Y.; Thomé, R.; Hirye, M.C. U-net-id, an instance segmentation model for building extraction from satellite images—Case study in the Joanópolis city, Brazil. Remote Sens. 2020, 12, 1544. [Google Scholar] [CrossRef]


| Index | Formula | References |
|---|---|---|
| NDVI | [78] | |
| NDVI-RE1 | ||
| NDVI-RE2 | ||
| NDVI-RE3 | ||
| NDVI-RE4 | ||
| MNDWI | [79] | |
| SAVI | [80] | |
| DVI | [81] | |
| GCVI | [82] | |
| RVI | [83] | |
| LSWI | [84] | |
| EVI | [85] | |
| S2REP | [86] | |
| RRI | [87] | |
| RFDI | [88] | |
| Gray | [76] |
| Machine Learning Models | Hyperparameters | Search Range | Step |
|---|---|---|---|
| RF | n_estimators | [100, 2100] | 100 |
| max_depth | [2, 22] | 2 | |
| min_samples_leaf | [5, 55] | 5 | |
| XGBoost | n_estimators | [100, 2100] | 100 |
| learning_rate | [0.1, 0.3, 0.5, 0.01, 0.03, 0.05] | - | |
| max_depth | [2, 22] | 2 | |
| min_child_weight | [5, 55] | 5 | |
| LightGBM | n_estimators | [100, 2100] | 100 |
| learning_rate | [0.1, 0.3, 0.5, 0.01, 0.03, 0.05] | - | |
| max_depth | [2, 22] | 2 | |
| min_data_in_leaf | [5, 55] | 5 |
| Model | Without Feature Selection | Feature Selection | |||||
|---|---|---|---|---|---|---|---|
| ReliefF | Optimization Method | ReliefF | Tree | Permutation | SHAP | Optimization Method | |
| Random Forest | 3.628 | Grid Search | 1.208 | 1.306 | 1.171 | 1.237 | Bayesian Search |
| XGBoost | 4.371 | 1.118 | 1.408 | 1.214 | 1.244 | ||
| LightGBM | 2.172 | 0.943 | 0.880 | 0.952 | 0.904 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Ma, Y.; Zheng, Q.; Chen, Q. Dynamic Co-Optimization of Features and Hyperparameters in Object-Oriented Ensemble Methods for Wetland Mapping Using Sentinel-1/2 Data. Water 2025, 17, 2877. https://doi.org/10.3390/w17192877
Ma Y, Ma Y, Zheng Q, Chen Q. Dynamic Co-Optimization of Features and Hyperparameters in Object-Oriented Ensemble Methods for Wetland Mapping Using Sentinel-1/2 Data. Water. 2025; 17(19):2877. https://doi.org/10.3390/w17192877
Chicago/Turabian StyleMa, Yue, Yongchao Ma, Qiang Zheng, and Qiuyue Chen. 2025. "Dynamic Co-Optimization of Features and Hyperparameters in Object-Oriented Ensemble Methods for Wetland Mapping Using Sentinel-1/2 Data" Water 17, no. 19: 2877. https://doi.org/10.3390/w17192877
APA StyleMa, Y., Ma, Y., Zheng, Q., & Chen, Q. (2025). Dynamic Co-Optimization of Features and Hyperparameters in Object-Oriented Ensemble Methods for Wetland Mapping Using Sentinel-1/2 Data. Water, 17(19), 2877. https://doi.org/10.3390/w17192877






