Bayesian Analysis of Stormwater Pump Failures and Flood Inundation Extents
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Study
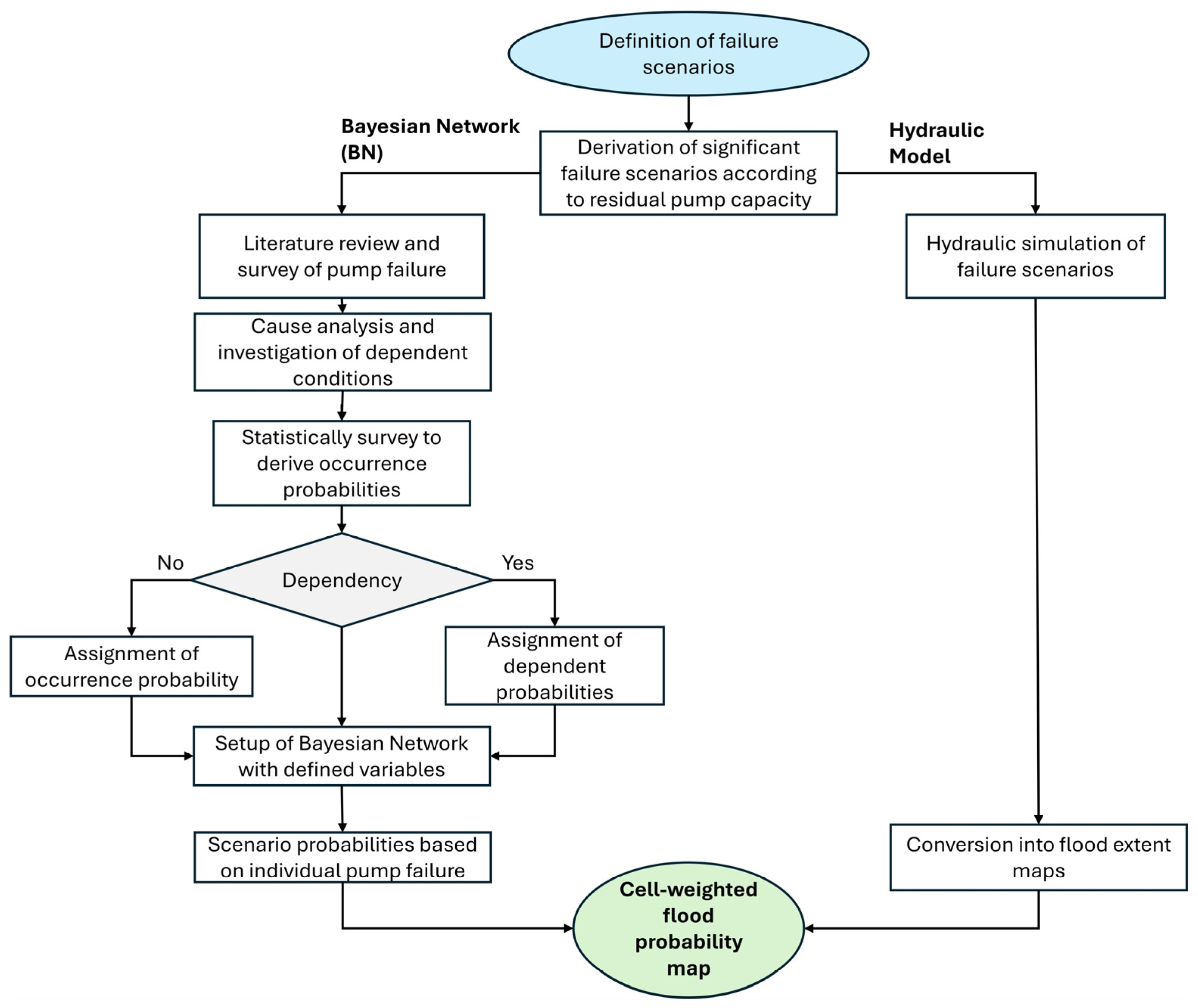
2.2. Framework for Pump Failure Assessment
2.3. Framework to Determine Pumping Failure Scenarios
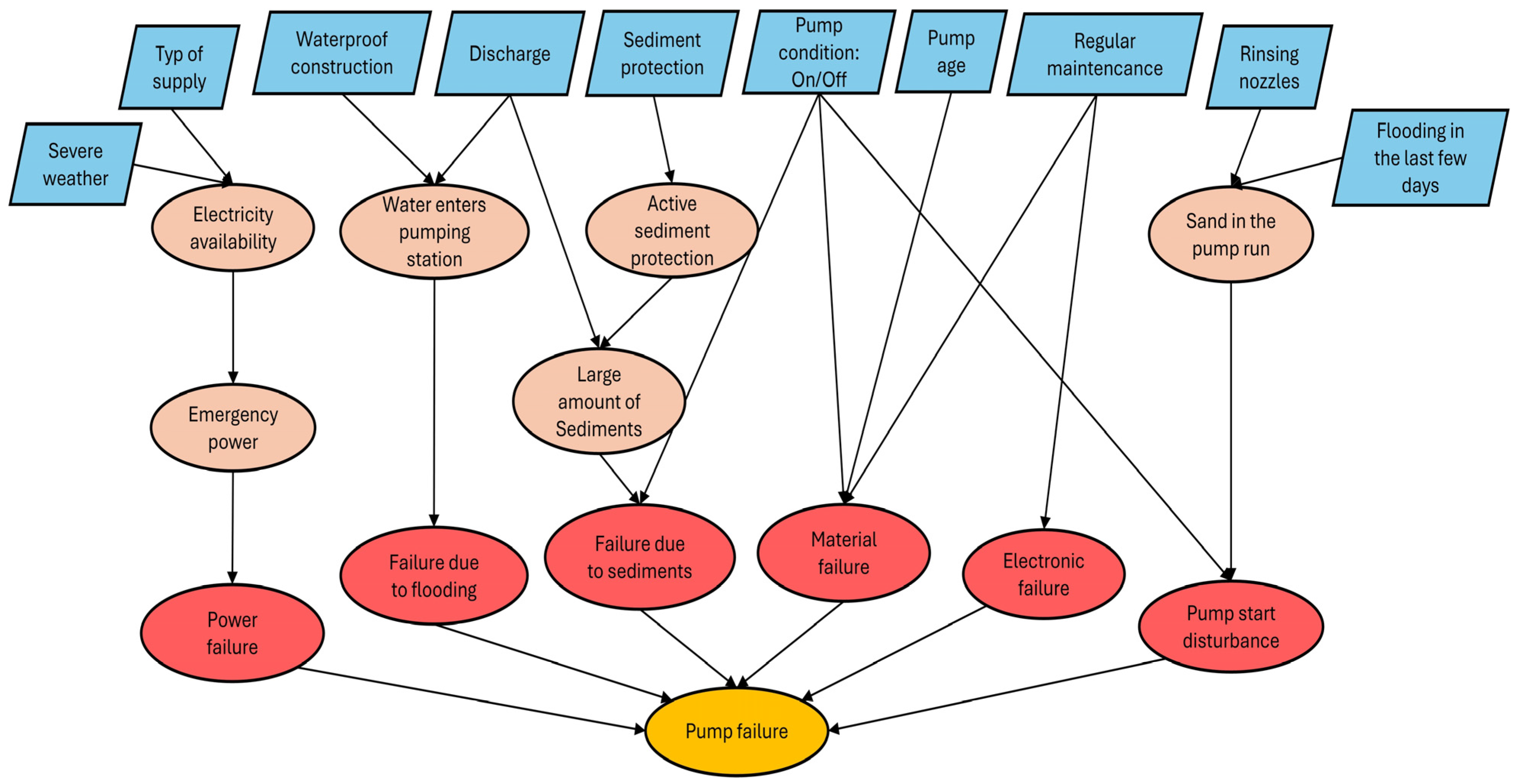
2.4. Pump Failure Mechanisms
- Power failure (external): Power failures are more likely to occur during thunderstorms and are strongly influenced by the type of power supply. Pumping stations typically include redundancy. The more redundancies, the less likely a total power failure is. The existence of an emergency generator that can supply the pumping station with electricity in case of an emergency reduces the likelihood of failure [25].
- Failure due to flooding (external): There is a significant increase in the likelihood of damage or complete destruction of the technical components of the pumping station in the event of flooding. This is primarily influenced by the type of structure (e.g., waterproof design) and the incoming discharge [25,42].
- Failure due to sediments (external): A riverbed is characterized by the transport of sediments. During periods of high discharge, more sediments are carried into the river and transported downstream. The more sediments are present, the greater the risk that they enter the pump and cause a blockage. This scenario is primarily affected by the amount of incoming discharge and the presence of a sediment protection system, such as nozzles, at the entrance to the pumping station.
- Material failure (internal): Mechanical disturbances are a main cause of pump failure. Consequently, a pump may fail during regular operation, causing an abrupt change in available discharge capacity. The likelihood of mechanical failure depends on the pump’s age and condition, both of which can be improved through regular maintenance [16,43,44].
- Electronic failure (internal): In addition to the mechanical components, pumping stations consist of a wide range of electronic components that have a limited lifetime and are therefore at risk of malfunctioning. These components control the operation of a pump with sensors and transmission of information, and thus can lead, in case of malfunction, to complete failure. As with mechanical components, maintenance services can prevent malfunctions and reduce the risk of pump failure [45].
- Pump start disturbance (external): Pumps are activated when a certain discharge or water level threshold is exceeded. In the event of a high discharge, sediments can enter the pump and hinder the starting process. For example, after past flood events, large quantities of sediments may be carried into the pump inlets that have been turned off. This may block the rotor blades and prevent the pump from starting when needed. Flushing nozzles can reduce the risk of pumps becoming blocked by cleaning out sediments.
2.5. Pump Failure Mechanisms and Failure Probability
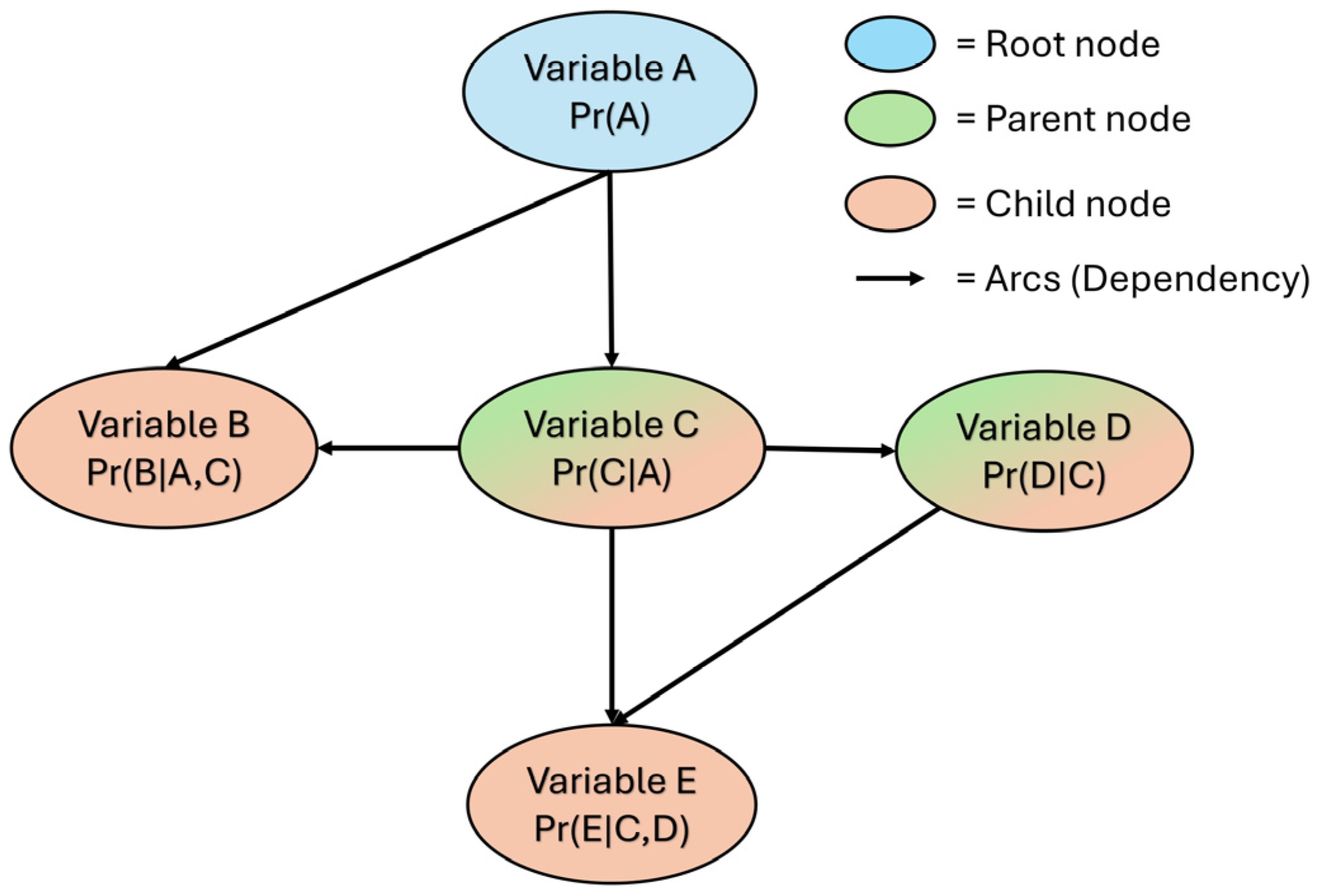
2.6. Bayesian Network for Individual Pump Failure Probability
2.7. Dual-Drainage 1D/2D Model
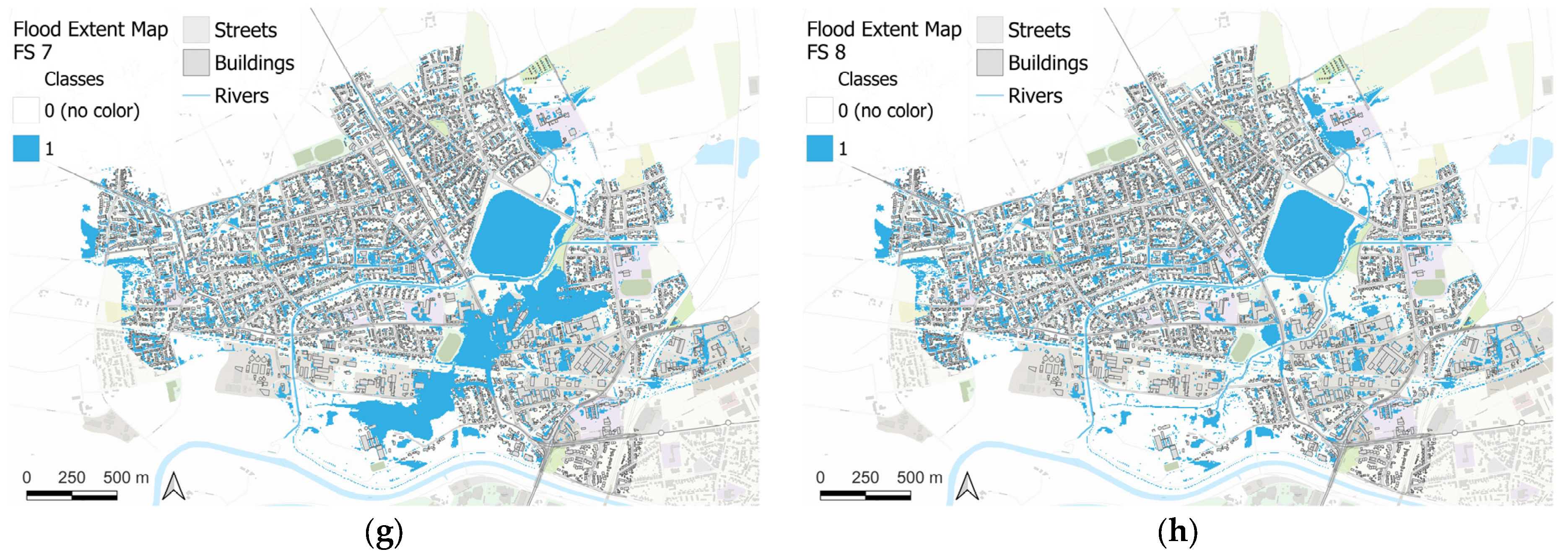
2.8. Flood Inundation Probability Map
3. Results
3.1. Pump Failure Scenarios
3.2. Pump Failure Assessment
3.2.1. Pump Failure Mechanisms—Survey Results
3.2.2. Derivation of the Probability Distribution
3.2.3. Bayesian Network
3.3. Flood Probability Map
4. Discussion
4.1. Pump Failure Scenarios
4.2. Pump Failure Assessment
4.2.1. Pump Failure Mechanisms
4.2.2. Bayesian Network
4.3. Flood Probability Map
4.4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| DAG | Directed acyclic graph |
| FTA | Fault Tree Analysis |
| ML | Machine Learning |
| PC | Pump discharge capacity |
| PFM | Probabilistic Flood Maps |
| FS | Failure scenario |
| S | Scenario |
References
- Emschergenossenschaft und Lippeverband. Lippeverband: Flussgebietsmanagement an der Lippe. Available online: https://www.eglv.de/emscher-lippe/lippeverband/ (accessed on 20 August 2025).
- Emschergenossenschaft und Lippeverband. Emschergenossenschaft: Flussgebietsmanagement von Anfang an. Available online: https://www.eglv.de/emscher-lippe/emschergenossenschaft/ (accessed on 20 August 2025).
- Emschergenossenschaft und Lippeverband. PuwaSTAR: Pumpwerkeswarnung für Starkregen und Hochwasser im Urbanen Raum. Available online: https://www.eglv.de/puwastar/ (accessed on 20 August 2025).
- Mays, L.W. Review of Advances in Risk and Reliability Analysis for Hydraulic Structures. In Application of Frequency and Risk in Water Resources; Singh, V.P., Ed.; Springer: Dordrecht, The Netherlands, 1987; pp. 227–262. ISBN 978-94-009-3955-4. [Google Scholar]
- Wang, Q.-A.; Chen, J.; Ni, Y.; Xiao, Y.; Liu, N.; Liu, S.; Feng, W. Application of Bayesian networks in reliability assessment: A systematic literature review. Structures 2025, 71, 108098. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, K.-F.; Wood, R.R.; Ludwig, R. A scalable flood-resilience-index for measuring climate change adaptation: Munich city. Water Res. 2020, 173, 115502. [Google Scholar] [CrossRef] [PubMed]
- ten Veldhuis, J.A.E.; Clemens, F.H.L.R.; van Gelder, P.H.A.J.M. Fault tree analysis for urban flooding. Water Sci. Technol. 2009, 59, 1621–1629. [Google Scholar] [CrossRef] [PubMed]
- Korving, H.; Geise, M.; Clemens, F. Failure of sewage pumps: Statistical modelling and impact assessment. Water Sci. Technol. 2006, 54, 119–126. [Google Scholar] [CrossRef]
- Anbari, M.; Tabesh, M. Failure Event Probability Calculation in Wastewater Collection Systems Using the Bayesian Network. J. Water Wasewater 2015, 27, 48–61. [Google Scholar]
- Li, J. Probabilistic risk analysis of dyke failure modes using FTA. Saf. Reliab. 2017, 37, 128–147. [Google Scholar] [CrossRef]
- Rikkert, S.J.H.; Kok, M.; Lendering, K.; Jongejan, R. A pragmatic, performance-based approach to levee safety assessments. J Flood Risk Manag. 2022, 15, e12836. [Google Scholar] [CrossRef]
- Briggs, E.K.; Hodkiewicz, M. Maintenance and Reliability of a Water Pumping Station; Engineers Australia: Hobart, Australia, 2005. [Google Scholar]
- Cousineau, D. Fitting the three-parameter weibull distribution: Review and evaluation of existing and new methods. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 281–288. [Google Scholar] [CrossRef]
- Rizwan, S.; Nabhani, H.; Rahbi, Y.; Alagiriswamy, S. Reliability Analysis of a Three-unit Pumping System. Int. J. Eng. Trends Technol. 2022, 70, 24–31. [Google Scholar] [CrossRef]
- Ibe, O.C. (Ed.) Markov Processes for Stochastic Modeling, 2nd ed.; Elsevier: Oxford, UK, 2013; ISBN 978-0-12-407795-9. [Google Scholar]
- Piri, J.; Pirzadeh, B.; Keshtegar, B.; Givehchi, M. Reliability Analysis of Pumping Station for Sewage Network Using Hybrid Neural Networks—Genetic Algorithm and method of Moment. Process Saf. Environ. Prot. 2020, 145, 39–51. [Google Scholar] [CrossRef]
- Rasinojehdehi, R.; Cirovic, G. Enhancing water pump failure prediction using machine learning: A focus on less-explored variables. Comput. Algorithms Numer. Dimens. 2023, 2, 124–135. [Google Scholar] [CrossRef]
- Kabir, S.; Papadopoulos, Y. Applications of Bayesian networks and Petri nets in safety, reliability, and risk assessments: A review. Saf. Sci. 2019, 115, 154–175. [Google Scholar] [CrossRef]
- Lei, G.; Wang, W.; Liang, Y.; Yin, J.; Wang, H. Failure risk assessment of discharge system of the Hanjiang-to-Weihe River Water Transfer Project. Nat. Hazards 2021, 108, 3159–3180. [Google Scholar] [CrossRef]
- ten Veldhuis, M.-C.; Clemens, F.; Gelder, P. Quantitative fault tree analysis for urban water infrastructure flooding. Struct. Infrastruct. Eng. 2011, 7, 809–821. [Google Scholar] [CrossRef]
- Bi, Z.; Li, C.; Li, X.; Gao, H. Research on Fault Diagnosis for Pumping Station Based on T-S Fuzzy Fault Tree and Bayesian Network. J. Electr. Comput. Eng. 2017, 2017, 6175429. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Song, H.; Zhang, H.-Y.; Chan, C.W. Fuzzy fault tree analysis based on T–S model with application to INS/GPS navigation system. Soft Comput. 2009, 13, 31–40. [Google Scholar] [CrossRef]
- Jacobs, J.A.; Mathews, M.J.; Kleingeld, M. Failure Prediction of Mine De-watering Pumps. J. Fail. Anal. Prev. 2018, 18, 927–938. [Google Scholar] [CrossRef]
- Bold, S.; Pfeiffer, E. Analyse und Management des Hochwasserrisikos im Emschergebiet. In Risiken bei der Bemessung und Bewirtschaftung von Fließgewässern und Stauanlagen, Dresden; Technische Universität Dresden, Institut für Wasserbau und Technische Hydromechanik: Dresden, Germany, 2004; pp. 191–206. [Google Scholar]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Bates, P.D.; Pappenberger, F.; Romanowicz, R.J. Uncertainty in Flood Inundation Modelling. In Applied Uncertainty Analysis for Flood Risk Management; Imperial College Press: London, UK, 2014; pp. 232–269. ISBN 978-1-84816-270-9. [Google Scholar] [CrossRef]
- Merz, B.; Thieken, A.H. Separating natural and epistemic uncertainty in flood frequency analysis. J. Hydrol. 2005, 309, 114–132. [Google Scholar] [CrossRef]
- Hosseini-Shakib, I.; Alipour, A.; Seiyon Lee, B.; Srikrishnan, V.; Nicholas, R.E.; Keller, K.; Sharma, S. What drives uncertainty surrounding riverine flood risks? J. Hydrol. 2024, 634, 131055. [Google Scholar] [CrossRef]
- Rehan, B.; Hall, J. Uncertainty and sensitivity analysis of flood risk management decisions based on stationary and nonstationary model choices. E3S Web Conf. 2016, 7, 20003. [Google Scholar] [CrossRef]
- Aitken, G.; Beevers, L.; Christie, M.A. Multi-Level Monte Carlo Models for Flood Inundation Uncertainty Quantification. Water Resour. Res. 2022, 58, e2022WR032599. [Google Scholar] [CrossRef]
- Delenne, C.; Cappelaere, B.; Guinot, V. Uncertainty analysis of river flooding and dam failure risks using local sensitivity computations. Reliab. Eng. Syst. Saf. 2012, 107, 171–183. [Google Scholar] [CrossRef]
- Beevers, L.; Collet, L.; Aitken, G.; Maravat, C.; Visser, A. The influence of climate model uncertainty on fluvial flood hazard estimation. Nat. Hazards 2020, 104, 2489–2510. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Quintana-Romero, T.; Leandro, J. A method to devise multiple model structures for urban flood inundation uncertainty. J. Hydrol. 2022, 604, 127246. [Google Scholar] [CrossRef]
- Alfonso, L.; Mukolwe, M.; Di Baldassarre, G. Probabilistic Flood Maps to support decision-making: Mapping the Value of Information. Water Resour. Res. 2016, 52, 1026–1043. [Google Scholar] [CrossRef]
- Alfonso, L.; Tefferi, M.A. Effects of Uncertain Control in Transport of Water in a River-Wetland System of the Low Magdalena River, Colombia. In Transport of Water Versus Transport over Water; Springer: Cham, Switzerland, 2015; Volume 58, pp. 131–144. [Google Scholar] [CrossRef]
- Stephens, T.A.; Bledsoe, B.P. Probabilistic mapping of flood hazards: Depicting uncertainty in streamflow, land use, and geomorphic adjustment. Anthropocene 2020, 29, 100231. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Vorogushyn, S.; Castellarin, A.; Merz, B.; Brath, A. Probabilistic flood hazard mapping: Effects of uncertain boundary conditions. Hydrol. Earth Syst. Sci. 2013, 17, 3127–3140. [Google Scholar] [CrossRef]
- Information und Technik Nordrhein-Westfalen, Statistisches Landesamt. Kommunalprofil Dorsten, Stadt. Available online: https://www.dorsten.de/_Resources/Persistent/d/f/1/e/df1ece0363d5c37b4d29f45e25e50a9e7db9516e/Kommunalprofil%20Dorsten%20Langfassung_.pdf (accessed on 11 May 2025).
- Ogie, R.I.; Dunn, S.; Holderness, T.; Turpin, E. Assessing the vulnerability of pumping stations to trash blockage in coastal mega-cities of developing nations. Sustain. Cities Soc. 2017, 28, 53–66. [Google Scholar] [CrossRef]
- Korving, H.; Ottenhoff, E.C. Analysis of the causes of pump failure and differences of failure characteristics. Water Sci. Technol. 2008, 57, 1271–1276. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, X.; Yu, A.; Speitel, M.; Yu, X. Assessment of the impacts of climat change on water supply system pipe failures. Sci. Rep. 2023, 13, 7349. [Google Scholar] [CrossRef]
- Dutta, N.; Kaliannan, P.; Paramasivam, S. A comprehensive review on fault detection and analysis in the pumping system. Int. J. Ambient Energy 2022, 43, 6878–6898. [Google Scholar] [CrossRef]
- Roscoe, K.; Hanea, A.; Jongejan, R.; Vrouwenvelder, T. Levee System Reliability Modeling: The Length Effect and Bayesian Updating. Safety 2020, 6, 7. [Google Scholar] [CrossRef]
- Jensen, F.V. Bayesian networks. WIREs Comp. Stat. 2009, 1, 307–315. [Google Scholar] [CrossRef]
- Torres-Toledano, J.; Sucar, L. Bayesian Networks for Reliability Analysis of Complex Systems. Lect. Notes Comput. Sci. 1998, 1484, 195–206. [Google Scholar] [CrossRef]
- Khakzad, N.; Khan, F.; Amyotte, P. Safety analysis in process facilities: Comparison of fault tree and Bayesian network approaches. Reliab. Eng. Syst. Saf. 2011, 96, 925–932. [Google Scholar] [CrossRef]
- Bulti, D.T.; Abebe, B.G. A review of flood modeling methods for urban pluvial flood application. Model. Earth Syst. Environ. 2020, 6, 1293–1302. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, L.; Li, R.; Yin, J.; Yu, D. Linking a Storm Water Management Model to a Novel Two-Dimensional Model for Urban Pluvial Flood Modeling. Int. J. Disaster Risk Sci. 2020, 11, 508–518. [Google Scholar] [CrossRef]
- Leandro, J.; Martins, R. A methodology for linking 2D overland flow models with the sewer network model SWMM 5.1 based on dynamic link libraries. Water Sci. Technol. 2016, 73, 3017–3026. [Google Scholar] [CrossRef]
- Chang, T.-J.; Wang, C.-H.; Chen, A.S. A novel approach to model dynamic flow interactions between storm sewer system and overland surface for different land covers in urban areas. J. Hydrol. 2015, 524, 662–679. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.S.; Schumann, A.H. A 2D parallel diffusive wave model for floodplain inundation with variable time step (P-DWave). J. Hydrol. 2014, 517, 250–259. [Google Scholar] [CrossRef]
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model(SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Krieger, K.; Schmitt, T.; Illgen, M. Risikomanagement in der kommunalen Überflutungsvorsorge nach DWA-Merkblatt M 119. GWF Wasser-Abwasser 2017, 158, 34–39. [Google Scholar]
- Horritt, M.S. A methodology for the validation of uncertain flood inundation models. J. Hydrol. 2006, 326, 153–165. [Google Scholar] [CrossRef]
| Pump ID | Pump Discharge Capacity [m3/s] |
|---|---|
| Pump 1 | 2 |
| Pump 2 | 4.5 |
| Pump 3 | 4.5 |
| Pump 4 | 4.5 |
| Scenario | Pump Discharge Capacity [m3/s] Pump ID 1 | Pump Discharge Capacity [m3/s] Pump ID 2 | Pump Discharge Capacity [m3/s] Pump ID 3 | Pump Discharge Capacity [m3/s] Pump ID 4 | Total-Pumping Discharge Capacity [m3/s] |
|---|---|---|---|---|---|
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2 | 2.0 | 4.5 | 4.5 | 0.0 | 11.0 |
| 3 | 2.0 | 4.5 | 0.0 | 4.5 | 11.0 |
| 4 | 2.0 | 0.0 | 4.5 | 4.5 | 11.0 |
| 5 | 0.0 | 4.5 | 4.5 | 4.5 | 13.5 |
| 6 | 2.0 | 4.5 | 0.0 | 0.0 | 6.5 |
| 7 | 2.0 | 0.0 | 4.5 | 0.0 | 6.5 |
| 8 | 2.0 | 0.0 | 0.0 | 4.5 | 6.5 |
| 9 | 0.0 | 4.5 | 4.5 | 0.0 | 9.0 |
| 10 | 0.0 | 4.5 | 0.0 | 4.5 | 9.0 |
| 11 | 0.0 | 0.0 | 4.5 | 4.5 | 9.0 |
| 12 | 2.0 | 0.0 | 0.0 | 0.0 | 2.0 |
| 13 | 0.0 | 4.5 | 0.0 | 0.0 | 4.5 |
| 14 | 0.0 | 0.0 | 4.5 | 0.0 | 4.5 |
| 15 | 0.0 | 0.0 | 0.0 | 4.5 | 4.5 |
| Scenario | Total-Pumping Discharge Capacity [m3/s] |
|---|---|
| 1 | 0 |
| 2 | 11 |
| 3 | 13.5 |
| 4 | 6.5 |
| 5 | 9 |
| 6 | 2 |
| 7 | 4.5 |
| Type of Supply | ||
|---|---|---|
| Severe weather | Single | Dual |
| Yes | 92% | 97% |
| No | 98% | 99% |
| Variable | Regular Operation (Pump 1–4) | Flood Scenario (Pump 1–4) | Extreme Scenario (Pump 1–4) |
|---|---|---|---|
| Pump state (on/off) | On | On | Off |
| Power supply | Dual power supply | Dual power supply | Dual power supply |
| severe weather | No | Yes | Yes |
| Waterproof construction | Yes | Yes | Yes |
| Incoming discharge | below design discharge | above design discharge | above design discharge |
| Age of Pumps (1–4) | (3, 8, 20, 14) | (3, 8, 20, 14) | (3, 8, 20, 14) |
| Sediment protection | Yes | Yes | Yes |
| Rinsing nozzles | Yes | Yes | Yes |
| Flooding in the past few days | No | No | Yes |
| Regular maintenance | Yes | Yes | No |
| Scenarios/Failure Probability | Regular Operation [%] | Flood Scenario [%] | Extreme Scenario [%] |
|---|---|---|---|
| Pump 1 | 1 | 23 | 62 |
| Pump 2 | 2 | 25 | 64 |
| Pump 3 | 5 | 29 | 78 |
| Pump 4 | 3 | 27 | 70 |
| Pumps/State (Flood Scenario) | Operating Probability [%] | Failure Probability [%] |
|---|---|---|
| Pump 1 | 77 | 23 |
| Pump 2 | 75 | 25 |
| Pump 3 | 71 | 29 |
| Pump 4 | 73 | 27 |
| Scenario | Pump 1 [%] | Pump 2 [%] | Pump 3 [%] | Pump 4 [%] | Scenario Probability [%] | Total-Pumping Discharge Capacity [m3/s] |
|---|---|---|---|---|---|---|
| 1 | 23.0 | 25.0 | 29.0 | 27.0 | 0.5 | 0.0 |
| 2 | 77.0 | 75.0 | 71.0 | 27.0 | 11.1 | 11.0 |
| 3 | 77.0 | 75.0 | 29.0 | 73.0 | 12.2 | 11.0 |
| 4 | 77.0 | 25.0 | 71.0 | 73.0 | 10.0 | 11.0 |
| 5 | 23.0 | 75.0 | 71.0 | 73.0 | 8.9 | 13.5 |
| 6 | 77.0 | 75.0 | 29.0 | 27.0 | 4.5 | 6.5 |
| 7 | 77.0 | 25.0 | 71.0 | 27.0 | 3.7 | 6.5 |
| 8 | 77.0 | 25.0 | 29.0 | 73.0 | 4.1 | 6.5 |
| 9 | 23.0 | 75.0 | 71.0 | 27.0 | 3.3 | 9.0 |
| 10 | 23.0 | 75.0 | 29.0 | 73.0 | 3.7 | 9.0 |
| 11 | 23.0 | 25.0 | 71.0 | 73.0 | 3.0 | 9.0 |
| 12 | 77.0 | 25.0 | 29.0 | 27.0 | 1.5 | 2.0 |
| 13 | 23.0 | 75.0 | 29.0 | 27.0 | 1.4 | 4.5 |
| 14 | 23.0 | 25.0 | 71.0 | 27.0 | 1.1 | 4.5 |
| 15 | 23.0 | 25.0 | 29.0 | 73.0 | 1.2 | 4.5 |
| Scenario | Total-Pumping Discharge Capacity [m3/s] | Residual-Pumping Discharge Capacity [%] | Occurrence Probability [%] |
|---|---|---|---|
| 1 | 0 | 0.0 | 0.5 |
| 2 | 11 | 71.0 | 33.3 |
| 3 | 13.5 | 87.1 | 8.9 |
| 4 | 6.5 | 41.9 | 12.3 |
| 5 | 9 | 58.1 | 9.9 |
| 6 | 2 | 12.9 | 1.5 |
| 7 | 4.5 | 29.0 | 3.7 |
| 8 | 15.5 | 100.0 | 29.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramsauer, S.; Schmid, F.; Johann, G.; Falter, D.; Eckers, H.; Leandro, J. Bayesian Analysis of Stormwater Pump Failures and Flood Inundation Extents. Water 2025, 17, 2876. https://doi.org/10.3390/w17192876
Ramsauer S, Schmid F, Johann G, Falter D, Eckers H, Leandro J. Bayesian Analysis of Stormwater Pump Failures and Flood Inundation Extents. Water. 2025; 17(19):2876. https://doi.org/10.3390/w17192876
Chicago/Turabian StyleRamsauer, Sebastian, Felix Schmid, Georg Johann, Daniela Falter, Hannah Eckers, and Jorge Leandro. 2025. "Bayesian Analysis of Stormwater Pump Failures and Flood Inundation Extents" Water 17, no. 19: 2876. https://doi.org/10.3390/w17192876
APA StyleRamsauer, S., Schmid, F., Johann, G., Falter, D., Eckers, H., & Leandro, J. (2025). Bayesian Analysis of Stormwater Pump Failures and Flood Inundation Extents. Water, 17(19), 2876. https://doi.org/10.3390/w17192876







