Beyond Local Indicators: Integrating Aggregated Runoff into Rainwater Harvesting Potential Mapping

Abstract

Water scarcity, driven by over-consumption, population growth, climate change, and pollution, poses severe threats to both human health and ecosystems. Rainwater harvesting (RWH) has emerged as a sustainable solution to mitigate these impacts, offering environmental, social, and economic benefits. Traditional RWH site selection methods rely heavily on GIS-based Multi-Criteria Approaches, such as the Analytical Hierarchy Process, which typically assess runoff potential at the pixel scale using proxy indicators like runoff coefficients or drainage density. However, these methods often overlook horizontal water fluxes and temporal variability, leading to underestimation of the actual runoff available for harvesting. This study introduces an innovative enhancement to AHP/GIS-based methodologies for rainwater harvesting (RWH) site selection by incorporating Aggregated Runoff (AR) as a key criterion. Unlike traditional approaches, the use of AR—representing the total upstream surface water collected at each pixel—enables a more realistic and accurate assessment of RWH potential without increasing data or computational requirements. The proposed criterion is independent of the specific methodology or data layers adopted, making it broadly applicable and easily integrable into existing frameworks. The methodology is applied to the upper Tiber River catchment in Central Italy, demonstrating that AR-based assessments yield more realistic RWH potential maps compared to conventional methods. Additionally, the study proposes a quantile-based scoring system to account for inter-annual hydrological variability, enhancing the robustness of site selection under changing climate conditions.

1. Introduction

Freshwater scarcity is a global issue affecting human communities mainly in developing countries or arid regions. It is estimated that about half of the world population lives in water-scarce regions, and a quarter of the planet population faces extreme water stress conditions, using more than 80% of the annually renewable potable water; at the same time, there is an increasing demand for water human activities [1]. Natural water resources degradation by over-consumption coupled with increasing population and climate crisis escalates the risk of water scarcity [2], while water pollution exacerbates the problem. Although the lack of drinking water is the most immediate threat to human health, water scarcity also has environmental consequences, like, e.g., the depletion of lakes and aquifers, increased seawater intrusion and vulnerability of ecosystems.

Rainwater harvesting ($RWH$) has emerged as a promising practice worldwide to address water scarcity and to adapt to the impacts of climate change and socio-economic shifts [3,4]. $RWH$ serves as an effective strategy for collecting water, particularly for non-potable applications; moreover, when properly collected, rainwater is typically of high quality and can often be used with minimal or no treatment. The implementation of $RWH$ offers environmental, social, and economic benefits [5,6]. Furthermore, $RWH$ structures mitigate runoff rates and soil erosion while enhancing the aquifer recharge [7,8] or providing surface water storage, compensating seasonal or inter-annual water availability. Water harvesting is generally defined as the collection of rainfall as runoff and its storage for beneficial use [9].

Although precipitation or runoff—both directly linked to water availability—are recognized as the primary variables in the design of $RWH$ systems, the implemented solutions must be adapted to the specific characteristics of the study area, this includes the consideration of physiographic features and existing infrastructure, both in urban and rural environments [10,11]. The Food and Agriculture Organization (FAO), as cited by Kahinda et al. [12], proposed six main criteria for the identification of suitable RWH sites: climate, hydrology, topography, agronomy, and socioeconomics. However, the specific metrics associated with each criterion may vary depending on the methodological approach, local features, and it is also subject to a certain degree of subjectivity; to date, a clear and standardized methodology is still lacking.

Past studies focused mainly on topographic and hydrological characteristics such as rainfall, slope, soil type, drainage network, while more recent studies include additional parameters related to socio-economic aspects such as distance to settlements or roads and cost;, in general, a variety of methods can be used to integrate the different criteria into a tool for selecting suitable sites for $RWH$ (see, e.g., Singh et al. [13], Husen et al. [14], Jha et al. [15], Mahmood et al. [16], Mahmoud et al. [17], Mbilinyi et al. [18], Preeti et al. [19], Saleem et al. [20], Shadmehri Toosi et al. [3], Mohajerani et al. [21]); a classification of the main criteria can be found in [3]. A popular approach for $RWH$ site selection is based on Multi-Criteria Approaches (MCA) like the Analytical Hierarchy Process (AHP) [22] implemented in a GIS platform. The success of GIS procedure in $RWH$ site selection relies on the large database of hydrologic and general information available and in the possibility to analyze a large portion of space. The analyses are typically conducted on a pixel scale: for each pixel the criteria selected are combined and then scored accordingly with the rules defined. The final output consists of a spatially variable Rainwater Harvesting Potential index, which classifies the whole catchment area based on its suitability for the implementation of $RWH$ structures. Despite its availability, the quantity of rainwater is the main constraint in rainwater harvesting, the procedures proposed in the literature, with some exceptions [23], do not consider the water balance along the hydrological model, but aim at an indirect assessment of the available runoff potential through proxy quantities such as curve number or local runoff coefficient. Methodologies that rely on water balance equations can be found in the recent literature and are receiving increasing attention; however, they are typically based on 0-D or 1-D modeling approaches sometimes aggregated over urban catchments or small districts [24,25]. The adoption of such methodologies need a more detailed dataset including information on hydraulic infrastructures present in the area.

All the standard approaches using GIS-based methods for large-scale analysis introduce a direct or indirect assessment of runoff; the latter is typically evaluated at pixel scale without considering the horizontal fluxes (0-D model), namely the water exchange between adjacent cells, which is an underestimated aspect. The accumulation of water along the flow paths is a critical process: runoff accumulates along flow paths, and then the actual quantity of runoff available for $RWH$ is generally higher than the one predicted by local, pixel-scale 0-D models; the aggregated runoff can be assessed with the local runoff only in the headwaters, which usually represent a small portion of the catchment.

In this study, we propose to improve the popular AHP/GIS-based methodologies for the assessment of rainwater harvesting potential by introducing information on the aggregated runoff ($AR$). It considers the total actual surface water collected upstream of each of the cells of the domain instead of the local contribution to runoff in the evaluation of the $RWH$ potential index. This new quantity enables a more realistic and accurate assessment of available runoff without increasing calculation complexity or data requirements. We would also like to emphasize that the introduction of the $AR$ layer is not dependent on the particular methodology or layers considered alongside the runoff, and it can be implemented in all frameworks.

For illustrative purposes, we apply the procedure based on aggregated runoff to the upper part of the Tiber River catchment (Central Italy), comparing it with the standard approach based on local runoff coefficients. We extend existing methodologies through runoff aggregation, significantly enhancing their effectiveness without requiring any expansion of the dataset. The proposed approach is easily transferable and applicable to any region or catchment worldwide.

Furthermore, an often underestimated aspect in the methodologies proposed for $RWH$ site selection is the temporal variability associated with hydrological variables. This variability significantly influences the performance and efficiency of the selected $RWH$ structures. The adoption on a standard year or a limited number of observation years is another critical aspect of standard procedures which may compromise the robustness of site selection outcomes: the same procedure applied to runoff from different years may result in very different $RWH$ Potential scores; nevertheless, the careful selection of evaluation criteria and the assignment of appropriate weights within multi-criteria decision-making frameworks may help in mitigate the limitations introduced by temporal averaging. This aspect will be carefully investigated and a score based on the quantile will be proposed for the aggregated runoff layer. By adopting a quantile-based scoring approach, it is possible to derive a robust $RWH$ Potential index while mitigating the effects of temporal variability. This latter aspect is particularly relevant in the context of climate crisis scenarios, where hydrological patterns are increasingly unpredictable. We emphasize that the main objective of our work is not urban water harvesting, that usually requires a different approach, more focused on the local scale, but rather a simple and preliminary screening of the rainwater harvesting potential carried out at the basin scale.

The structure of the paper is as follows: First, the methodology is introduced, with a detailed description of the rationale of the new aggregated runoff potential layer. This is followed by the presentation of a case study of the upper Tiber River catchment, closed at the Ponte Felcino gauge station. The practical derivation of the layers is illustrated in this section. The discussion then compares the $RWH$ Potential index obtained using a standard methodology with that derived from the new aggregated runoff layer. The choice of the Upper Tiber catchment allows an in-depth analysis of the results and highlights the influence of temporal variability of hydrological variables. Finally, the conclusions summarize the main findings and implications of the study.

2. Methodology

As stated above, herein, we propose an improvement of the popular AHP/GIS-based methodologies for the evaluation of the rainwater harvesting potential index (hereinafter indicated as $\rho$) by incorporating the aggregated runoff through a simple hydrological model, providing an effective assessment of the total runoff; the latter will be adopted as a criterion in the structure of the MCA/AHP, while the selection of the other criteria is left to the user. The methodology is somewhat similar to the one adopted in Fiori et al. [26] for different purposes.

As we will show in the following sections, the use of an albeit simple, hydrologic model for runoff assessment has several advantages over the traditional use of proxy quantities like the local runoff coefficient or similar, without increasing the computational effort required. The hydrological model is based on a standard geomorphological approach commonly performed on GIS platform.

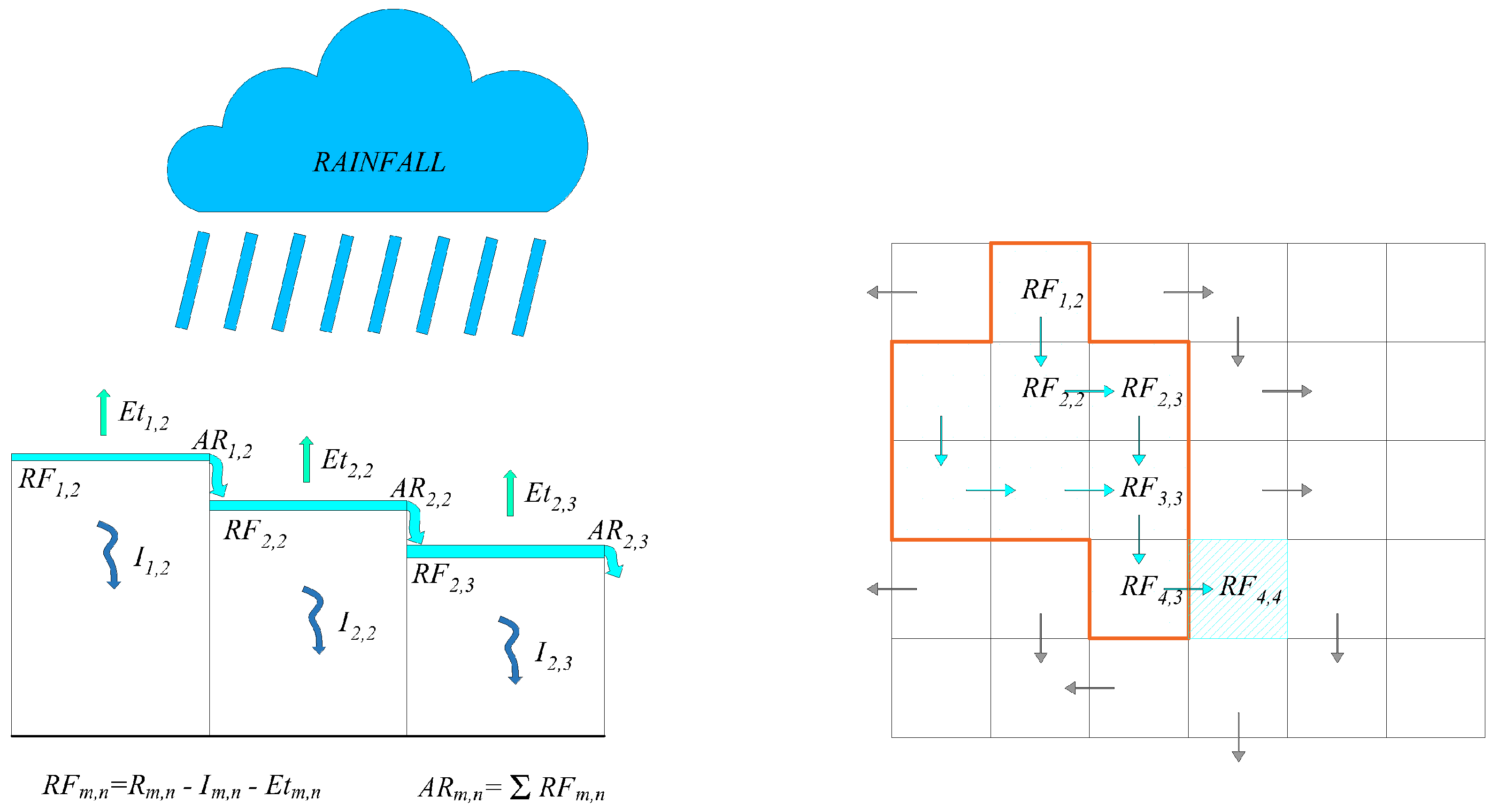
A schematic diagram of the geomorphological framework for the accumulated runoff assessment is shown in Figure 1, where panel (a) shows a vertical section including vertical fluxes (rainfall and infiltration) while panel (b) shows surface runoff aggregation. The area of interest is divided into N cells of equal size. The total amount of rainfall falling on a given cell $(m,n)$ is partitioned into three main components: (i) Infiltration $I_{m,n}$, the portion that infiltrate into the soil; (ii) Runoff $R{F}_{m,n}$, the portion that flows over the surface; (iii) evapotranspiration $E{t}_{m,n}$, the portion that returns to the atmosphere. The surface runoff generated in a cell flows toward the downstream cell, following the direction of the higher gradient up to the stream. As it moves, it accumulates with the runoff generated in the downstream cell. Therefore, the water quantity available for rainwater harvesting, is that pertaining to the sub-catchment which is greater than that pertaining to single cell runoff. The water quantity available for rainwater harvesting, $A{R}_{m,n}$ is that pertaining to the sub-catchment which is greater than that pertaining to single cell ($R{F}_{m,n}$), the latter constituting the relative contribution of the single cell. That quantity is the aggregated runoff $A{R}_{m,n}$ which in a given cell is obtained by adding the local runoff with the contributions from all upstream cells (as an example $A{R}_{2,3}=A{R}_{1,2}+A{R}_{2,2}+A{R}_{2,3}$). The rationale of the proposed methodology stands in this more effective evaluation of the total runoff that can be potentially collected by a rainwater harvesting structure located by the cell. The above quantity can be calculated first by evaluating the surface runoff ($R{F}_{m,n}$) for each cell of the study area then aggregating the runoff along the surface flow paths. The aggregated runoff ($A{R}_{m,n}$) can be evaluated by calculating the flow directions and then the flow accumulation by weighing each cell with the local runoff, along standard geomorphological analysis (e.g., [27]). All the above quantities can be easily evaluated by standard tools pre-implemented in the GIS platform. With the previous simple passages, it is possible to introduce an effective assessment of the runoff as criterion in the AHP for the selection of $RWH$ sites. The methodology described above has (i) the advantage of providing an effective estimate of runoff that considers the dynamics of water transfer within the basin, and is therefore representative of the entire basin subtended by the cell and not by local quantities such as the runoff coefficient, and (ii) provides an estimate, standing the limits of model uncertainty, of the maximum amount of water that can be harvested in the selected time period analysis.

The $AR$, combined with other criteria (e.g., slope, drainage density and others), can be used in AHP to rank the N cells of the study area by the $RWH$ index $\rho$. The proposed criterion can be easily integrated into the wide range of methods proposed in the literature for the index $\rho$ such as the ones proposed by Jha et al. [14], Preeti et al. [18]. Although the adoption of the $AR$ instead of the local runoff is an important conceptual change, it does not imply a substantial modification of the AHP structure, but only a redefinition of the classes. In fact, the modification of the classes is necessary because of the relevant difference that arises in the values of $AR$ and $RF$, the latter of which will be discussed in detail in the following section in the application example.

Hence, the $AR$ is introduced in a standard AHP/GIS procedure for rainwater harvesting potential, which is briefly summarized here. In AHP, when considering M criteria for the definition of $RWH$ potential index, a pairwise comparison matrix $M\times M$ is created, where each criterion is compared to every other criterion, using a numerical scale to represent relative importance. The scale typically goes from 1 to 9, where 1 indicates equal importance, 5 indicates strong importance, and 9 indicates extreme importance [22]. Once the pairwise comparison matrix is completed, the relative weights of each criterion $w_i$ are derived based on the literature and expert opinion. This typically involves calculating the eigenvector corresponding to the largest eigenvalue of the comparison matrix. The eigenvector is then normalized obtaining $w_i$. The consistency of weights in a pairwise comparison matrix is calculated using a consistency ratio ($CR$). The $CR<$ 0.1 indicates consistency of weights, while a $CR>$ 0.1 denotes inconsistency which must be revised. For each criterion i (with $i=1,\dots M$) the values associated with the feature are reclassified in classes and a score $S_i$ is associated with each class. A detailed description of the procedure is provided by Saaty [22]. The overall value of the index ($\rho$) in a specific position ($x,y$) is obtained by the linear combination of the feature scores $S_i$ and the criteria weights $w_i$. The final equation is as follows

$$\rho (x,y)=\sum _i^N{w}_{i}S{(x,y)}_i$$

(1)

In this study, we propose an improvement to popular AHP/GIS-based methodologies for assessing RWH potential by introducing the concept of aggregated runoff (AR). Unlike traditional approaches that rely on local runoff contributions, AR accounts for the total surface water collected upstream of each cell within the domain. By incorporating horizontal fluxes, this approach enables a more realistic and accurate estimation of available runoff, without increasing computational complexity or data requirements. The proposed procedure is particularly well-suited for large-area assessments, where detailed hydrological modeling may be impractical, and where preliminary screening is essential for identifying promising zones for RWH implementation.

3. Application Example: The Rainwater Harvesting Potential Index for the Catchment of Tiber at Ponte Felcino

To develop an application example and discuss the main advantages of adopting the $AR$, we use the basic methodology and criteria provided by Jha et al. [14] as the reference study, making suitable changes to the proposed procedure as required. We remark that the choice of the reference study is only for the sake of illustration, and any choice of the M criteria is possible. The discussion will describe the impact of aggregated runoff and the benefits of using a long (71-year) hydrological dataset. The standard procedure will be used as a reference case to discuss the improvements associated with the use of the $AR$ criterion. In that work, the authors include three criteria ($M=3$) for the definition of $\rho$: runoff coefficient, slope and drainage density. The index $\rho$ is obtained by the following linear combination:

$$\rho (x,y)=w_R{S}_R+w_S{S}_S+w_{DD}{S}_{DD}$$

(2)

with $w_i$ the weight of the i-criteria and $S_i$ the score; in the previous equation the subscripts R, S and $DD$ indicate runoff (local coefficient in the original formulation or spatially aggregated in the present work), slope and drainage density, respectively. In the following, ${\rho }_{RC}$ indicates the $RWH$ potential index calculated by using the local runoff coefficient $RC$ while ${\rho }_{AR}$ indicates the index calculated by using the aggregated runoff $AR$.

The classes and the pertaining score, with the exception of the new aggregated runoff parameter, as well as the criteria weights, are taken from the reference study and summarized in

Table 1. Summary of criteria and normalized weights.

Thematic Layers	Criteria Weights	Normalized Weights
Slope	8	0.35
Drainage Density	6	0.26
Runoff Coefficient	9	0.39

; for additional details on the AHP parameters and the consistency of the weights refer to Jha et al. [14]. The classes of the new parameters will be deeply discussed in the following.

After the weights and classes are defined, a GIS software is used to combine the weighted layers to produce $\rho$ accordingly with Equation (2). After the calculation the $\rho$ values are reclassified into 6 suitability classes from “Very poor” up to “Very good”.

The study area selected for the methodological test is the Upper Tiber River basin close to the Ponte Felcino hydrometric gauge station. The area is located in central Italy and extends between the regions of Tuscany, Umbria and Emilia Romagna. The study area is about 2073 km², the main watercourse is about 113 km long. The altitude ranges from 190 to 1453 m asl, with an average altitude of 518 m asl and an average slope of 29%. The basin is mainly located on the western Apennines. The area has a heterogeneous lithology mainly consisting of clay and flysch, most of which have very low hydraulic conductivity. Rainfall in the region is relatively abundant and unevenly distributed throughout the year. Annual rainfall ranges from about 900 to 1200 mm. The seasonal distribution of rainfall is characteristic of central Italy; autumn and winter are the wettest seasons, spring tends to be moderately wet, while summer is usually the driest season.

The spatial datasets used to develop the criteria maps are as follows: (i) the Digital Elevation Model (DEM) [28], depicted in panel (a) of Figure 2, and (ii) the BIGBANG database [29]. Both datasets are open access and cover the whole Italian territory. Specifically, the BIGBANG model is a national-scale hydrological balance framework developed by the Institute for Environmental Protection and Research (ISPRA) within a geographic information system (GIS) environment. It enables the estimation of key components of the hydrological balance, such as precipitation and runoff, on a monthly basis across a uniform spatial grid with a resolution of 1 km², spanning the period from 1951 to 2022 (BIGBANG 7.0). This extensive temporal and spatial dataset has made it possible to conduct a robust analysis of the uncertainties in $\rho$ linked to the temporal variability of runoff.

All maps presented below have been generated using QGIS an open-source GIS environment [30]. In the following, we provide a brief description for each one of the criteria and the pertaining maps.

3.1. Slope Map

The topography of the catchment and, in particular, the slope, influences both runoff and infiltration. A steep slope is more prone to runoff generation, but steep slopes result in rapid water flow, reducing water storage capacity and sediment accumulation, while flat slopes lead to slow water flow, allowing for larger water storage capacity and more effective RWH techniques [31]. The slope map is generated from the DEM using the GDAL raster slope algorithm tool in QGIS. In this catchment, the slope value ranges from 0 to 175%, with very pronounced prevalence on the medium-high values. The criterion has an assigned total weight of $w_S=0.35$, the total slope range is classified into six classes characterized by a suitability rank and a relative weight. Suitability rank and class weights are inversely proportional to slope values; the relationship is non-linear. The following table shows the classes and relative weights normalized (

Table 2. Classified spatial distribution of percentage of slope with its criteria and feature class weights.

Thematic Layers	Classes	Suitability Rank	Criteria Weight	Feature Class Weights	Normalized Weights	Area (%)
Slope percentage			8		0.35
	0–1%	Very High		8	0.31	4.4
	1–3%	High		7	0.27	5.2
	3–5%	Medium		5	0.19	2.4
	5–10%	Low		3	0.12	4.8
	10–15%	Very Low		2	0.08	7.2
	>15%	Extremely Low		1	0.04	76

). The last column refers to the percentage of the catchment area that falls into the class. The slope map is shown in panel (b) of Figure 2.

3.2. Drainage Density Map

Higher drainage density ($DD$) values are associated with greater runoff volumes because water is quickly conveyed to the channel [32], this makes surface runoff less susceptible to infiltration. Furthermore, high dissection is typically associated with geological formations that are more prone to runoff generation. Moreover, greater drainage density implies more efficient runoff concentration and transport towards harvesting structures. Dense drainage networks enable multiple localized interventions throughout the watershed and facilitate micro-catchment $RWH$ systems, which are particularly useful in semi-arid and arid areas [33]. These characteristics are positive when dealing with surface water harvesting structures (as in this work), but negative when considering infiltration-based solutions. The $DD$ map is generated from the stream network map; the latter was sampled in circular subareas with a radius of 1 km. The algorithm is the GDAL line density tool [34]. The definition of the river network is a prerequisite for the assessment of the drainage density, and it is defined from the DEM and the flow accumulation map; different rules exist in the literature; however, the differences are limited to the first cells of the network. This aspect, together with the limited weight of the criterion, has suggested the adoption of a simpler approach. The river network is defined by introducing the threshold of 100,000 cells corresponding to 10 km² on the flow accumulation. From an operational point of view the procedure includes a few passages such as sink fill and flow directions evaluation. The weight associated with the criteria is $w_D=$ 0.26; the values associated with the drainage density range from 0 to 0.5 km/km², with the prevalence of intermediate values. The suitability rank is defined over four classes, the relative weights are chosen proportional to the drainage density values. All information are reported in

Table 3. Classified spatial distribution of drainage density with its criteria and feature class weights.

Thematic Layers	Classes	Suitability Rank	Criteria Weight	Feature Class Weights	Normalized Weights	Area (%)
Drainage density			6		0.26
	<0.75 km/km2	Low		3	0.13	20
	0.75–1.5 km/km2	Medium		5	0.22	47.9
	1.5–2.25 km/km2	High		7	0.30	27.3
	>2.25 km/km2	Very High		8	0.35	4.8

. The maps are shown in panel (c) of Figure 2.

3.3. Runoff Coefficient

The runoff coefficient $RC$–defined as the percentage of total precipitation that contributes to runoff—is a key parameter in rainwater harvesting. The $RC$, associated with a catchment area, can be assessed directly from hydrological record analysis, evaluated using physically based methods, or obtained by correlating it with local catchment characteristics, such as geology, slope gradient, and land use [35]. The use of modeling approaches (e.g., SCS-CN, Green-Ampt Model) may lead to a reliable assessment of the efficiency of $RWH$ structures. Although $RC$ is usually considered as a given property of the catchment/pixel, it evolves in time, reflecting the non-linearity of infiltration processes and rainfall pattern, and it can be considered to be a fraction of the rainfall just as a rough approximation. In particular, wet years are characterized by higher runoff coefficients than dry years. Although $RC$ temporal variability is a key factor for $RWH$ with an evident impact on dry years, it is often underestimated in studies which often rely on a few years of test period or temporally averaged quantities. The standard approach to generate spatial maps of the runoff coefficient requires the application of the water balance equation, typically at the 0-D scale, to evaluate local runoff from precipitation [3,7,14]. In this study, we took advantage of the BIGBANG model, in which precipitation and surface runoff are already provided in the form of monthly scale spatial maps. The availability of that extensive database has certainly simplified the calculation but more importantly it has allowed extensive analysis of the effects of temporal variability of rainfall. The runoff coefficient is then estimated at pixel scale simply as the ratio of runoff volume to precipitation volume. 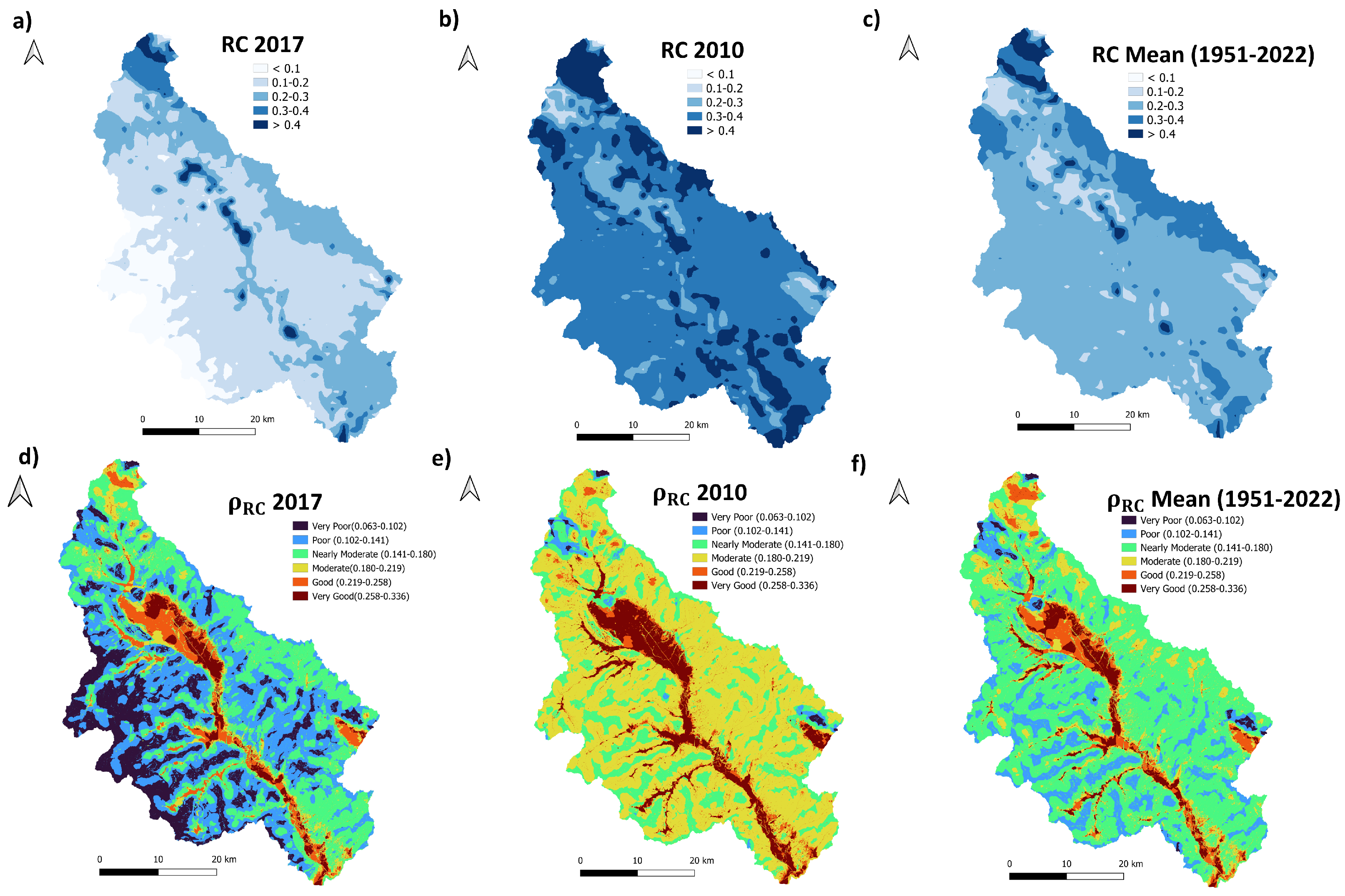The In Figure 3, in panels (a–c) 3 maps of the $RC$ are shown, the first one pertains to the 2017 a dry year, characterized by an average precipitation on the basin of 674 mm; the second maps are for 2010, a wet year, with an average precipitation of 1347 mm. The last map is obtained by taking the average of the runoff coefficient over the whole 72 years observation periods, while the three maps exhibit the same general pattern, significant differences can be observed in the values with higher values pertaining to the water-rich year and the lower values to the water poor year. The criteria weight is $w_R=0.39$; values ranges between 0.1 and 0.5, five classes are defined from the suitability rank with higher weights associated with higher runoff coefficient values, the classes and the weights are summarized in

Table 4. Classified spatial distribution of variables runoff coefficient with its criteria and feature class weights.

Thematic Layers	Classes	Suitability Rank	Criteria Weight	Feature Class Weights	Normalized Weights	Area (%)
Runoff coefficients mean (1951–2022)			9		0.39
	<0.1	Very Low		1	0.04	0.04
	0.1–0.2	Low		3	0.13	7.14
	0.2–0.3	Medium		5	0.22	70.88
	0.3–0.4	High		6	0.26	19.49
	>0.4	Very High		8	0.35	2.45

.

3.4. Aggregated Runoff Map

The aggregated runoff $AR$ is the novel contribution of this work. It is the amount of runoff, available at a given location, resulting from both precipitations falling on the cell and surface flow from adjacent cells. The $AR$ has some similarities with the flow accumulation which represents the area of the subcatchment drained by a given cell. The evaluation of surface flow directions within the domain is a preliminary step, which can be performed using simple geomorphological tools (e.g., [27]). In this work, we used the D8 algorithm [36] to determine flow direction, assigning each pixel a downslope neighbor among the eight adjacent cells based on the steepest descent. From an operational perspective, the procedure includes a few steps also required for drainage density map generation, such as sink filling. Once the flow direction has been evaluated, the aggregated runoff ($AR$) for pixel k is calculated as follows (see Figure 1):

$$AR(x_k,y_k)=\sum _j^{M_k}RF(x_j,y_j)$$

(3)

where $RF(x_j,y_j)$ is the runoff that belongs to the cells $j=1:M_k$ that contributes to the sub-basin closed pertaining to the cell k. In other words, the $AR$ can be evaluated as the flow accumulation when considering runoff instead of cell area during the calculation. In the evaluation of aggregated runoff, all cells belonging to the stream network were excluded. This study is primarily focused on RWH structures located on hillslopes, which collect surface runoff before it reaches the river network. Although the inclusion of the stream network in the framework is technically feasible, it would require the consideration of additional hydrological processes such as subsurface flow contributing to baseflow; furthermore, the use of in-channel RWH structures require would require a more specific analysis.

The aggregated runoff exhibits a higher spatial variability with respect to the runoff coefficient; in the case of $AR$ the range of variability is strictly dependent on the threshold which define the separation between hillslopes and channels which determines the higher boundary of the quantity. This fact requires a new standard procedure for the identification of the classes which cannot be defined by universal values (such as in the case of $RC$). An effective procedure is to set the classes boundary by the adoption of a series of thresholds on the quantiles. The classified aggregated runoff map is generated by dividing the whole range of variability, for each year, into five classes with an probability. As shown in Section 4, the adoption of quantiles allows a significant improvement of the procedure through a more robust classification, although this approach does not allow a universal definition of the class boundaries.

As for the runoff, the criteria weight is $w_R=0.39$, the class limits reproduced in

Table 5. Classified spatial distribution of variable aggregated runoff potential with its criteria and feature class weights.

Thematic Layers	Classes (Quantiles)	Suitability Rank	Criteria Weight	Feature Class Weights	Normalized Weights	Area (%)
Aggregated Runoff mean (1951–2022) in m3			9		0.39
	<1731	Very Low		1	0.04	20
	1731–2422	Low		3	0.13	20
	2422–3878	Medium		5	0.22	20
	3878–7064	High		6	0.26	20
	>7064	Very High		8	0.35	20

refer to the mean scenario obtained by averaging the $AR$ over 72 years. Reclassified $AR$ maps are reproduced in panel (a–c) of Figure 4, the three panels refer to the dry year, the wet year and the average conditions as in Figure 3.

4. Results and Discussion

The capabilities and results of our improved model are discussed by comparing the final results obtained using the standard runoff coefficient-based model with those obtained using the aggregated runoff model. In the following, the two rainwater harvesting potentials will be indicated as ${\rho }_{RC}$ and ${\rho }_{AR}$, respectively. Although these results were obtained for a specific catchment area, the methodology is general and can be applied to any basin. We would also like to reiterate that the method’s main contribution is the definition of the aggregated runoff layer, which is independent of the choice of other layers to be used in combination with it.

We start the discussion by analyzing the ${\rho }_{RC}$. The adoption of the BIGBANG dataset allows a detailed analysis of the hydrological regimes and the temporal variability of the rainfall, which results in the temporal variability of the $RC$. The latter is not a fixed quantity, but depends on rainfall and soil dynamics, with evapotranspiration, infiltration and storage being the more important processes. The soil determines the available runoff by a typical non-linear behavior. As a consequence in each year the $RC$ assumes different values. In the series of panels in Figure 3 we illustrate the analysis for the years 2017 and 2010, a water poor and a water-rich year, respectively. Figure 3 shows the runoff coefficient maps for 2010 and 2017, panels (a) and (b) while panel (c) shows the map obtained by applying the same procedure to a ‘standard year’, for which the RC is calculated by taking the time average over the period 1951–2022. The total precipitation values are 670, 1347 and 951 mm/year, respectively.

The series of figures clearly emphasizes the effect of the runoff coefficient. As expected, ${\rho }_{RC}$ (panels d–f) generally assumes values proportional to the rainfall. Focusing on the spatial distribution the water poor year, panel (a), shows a high spatial heterogeneity of the runoff coefficient, determined by the spatial variability of the soil characteristics and the saturation dynamics, while the water-rich year, panel (b), shows a low spatial variability of the $RC$, probably due to a more homogeneous temporal distribution of rainfall and soil saturation. The high spatial variability of the $RC$ obtained for 2017 is also reflected in a more pronounced variability of the ${\rho }_{RC}$. When comparing the scenarios, significant differences in $RWH$ values are immediately evident especially in the western and central parts of the basin. These differences should not be underestimated when selecting the optimal locations for $RWH$ potential index. The latter is particularly important considering that during drought periods, rainwater harvesting structures can play a strategic role in water resource management.

As for the impact of the other criteria, ${\rho }_{RC}$ is highest near streams due to low slopes, with a clear correlation between slope and ${\rho }_{RC}$. Gentle slopes help, but their effect can be offset if water quickly returns to streams. Drainage density also peaks near watercourses, mainly influencing moderate ${\rho }_{RC}$ values.

Using aggregated runoff, slope and drainage density in Equation (3) we can calculate the Aggregated Rainwater Harvesting Potential ${\rho }_{AR}$; results are reproduced in Figure 4, the analyzed cases are the same presented in Figure 3. The general pattern of ${\rho }_{AR}$ exhibits some similarities with the ${\rho }_{RC}$ analyzed before: the zone located in south-eastern part of the catchment are confirmed to be the less suitable for rainwater harvesting while the zones close to the stream network and the floodplain are still the more appropriate. However, the difference between the two indexes ${\rho }_{AR}$ and ${\rho }_{RC}$ maps is about the 64% of the total area for all three cases considered. 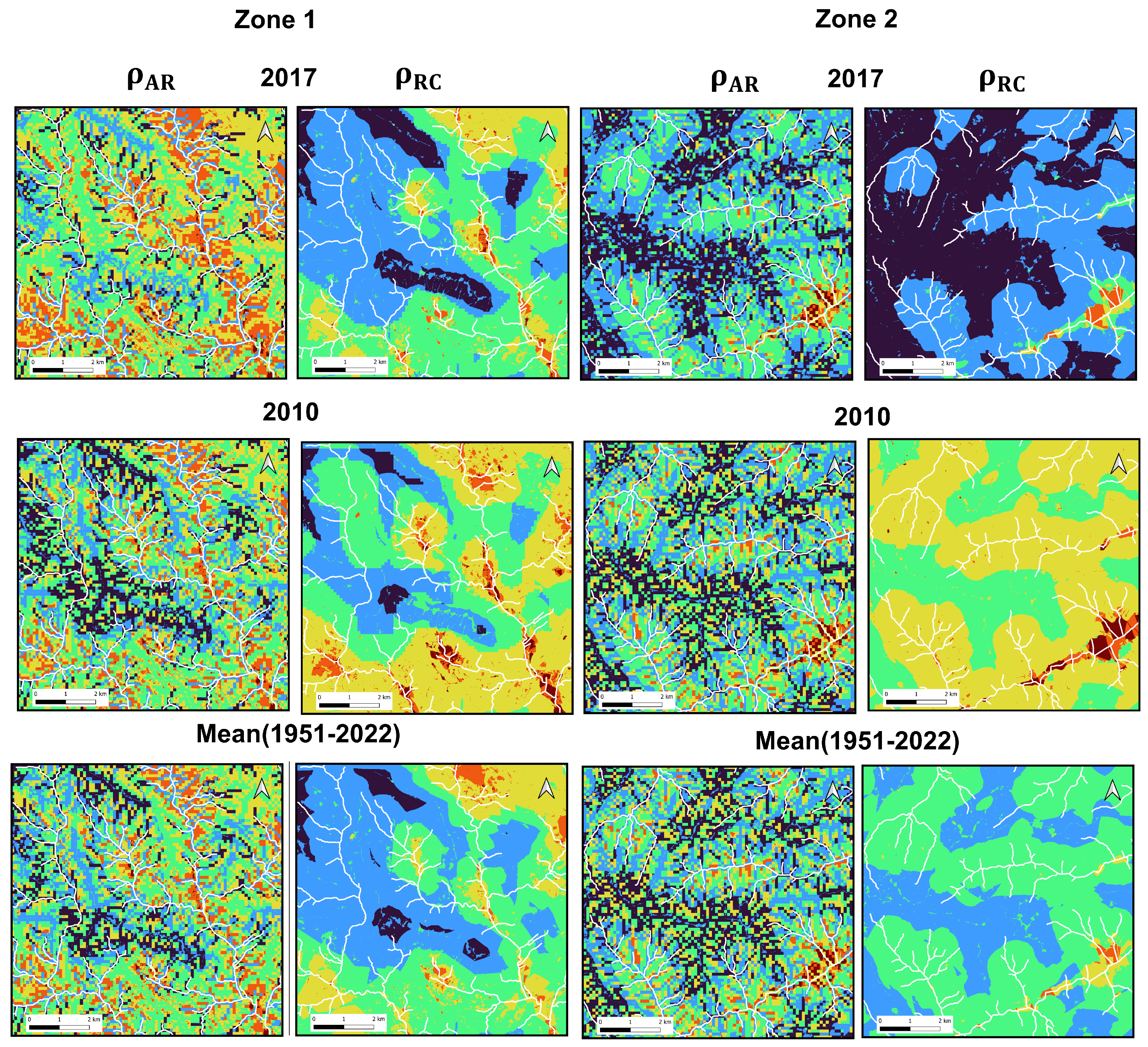This result is very significant if we consider that the ${\rho }_{AR}$ and ${\rho }_{RC}$ are carried out using the same slope and drainage density maps, which contribute to the total value for 35% and 26%, respectively. Differences clearly emerge when focusing on specific areas. A selection of magnifications are shown in Figure 5. The first feature that emerges is the greater spatial variability of ${\rho }_{AR}$ compared to ${\rho }_{RC}$, as a consequence of the variability of $AR$, which increases along the surface flow lines.

Figure 5 clearly shows the increase in water availability that is obtained proceeding from the top of the slopes towards the streams identifies areas that are gradually more productive and then more suitable for $RWH$ structures. The possibility of using an $RWH$ structure strictly depends on the water available quantity, and in fact, all the existing indices rely on runoff assessments; however in standard methodologies this passage is carried out at local scale, using a single pixel or even larger areas as a support. Our analysis shows that procedures that rely on $RC$ are more prone to error. For example, two cells with similar characteristics, one located upstream and the other downstream in a sub-basin, would receive the same ${\rho }_{RC}$ score, even though the downstream cell clearly has greater potential. That characteristic feature can be correctly cached by evaluating the actual water availability of the entire subcatchment belonging to a given cell using the new ${\rho }_{AR}$, which gives a robust classification. Furthermore, as shown in Figure 5, a more accurate spatial identification of the area can be seen.

As in the previous case we observe a dependence of the final ${\rho }_{AR}$ on the annual rainfall, with higher or lower values in water-rich and water poor years, those differences are quite intuitive and do not need additional discussion. However, in the case of ${\rho }_{AR}$, the effect of the temporal variability of rainfall is less pronounced than in the ${\rho }_{RC}$ case. The large differences observed in Zone 2, where the ${\rho }_{RC}$ classification changes completely, are not present in the ${\rho }_{AR}$ map. This map is characterized by greater stability, which is partially related to the use of quantiles in the classes definition.

The stability of the classification obtained through the use of aggregate runoff and quantiles, together with its lower dependence on precipitation in the three cases analyzed above, is also reflected in the percentages of basin area belonging to each class, as shown in

Table 6. Relative amount of the catchment area in each class as predicted by the two indices ${\rho }_{RC}$ and ${\rho }_{AR}$ for the three scenarios presented.

	${\mathit{\rho }}_{\mathit{RC}}$			${\mathit{\rho }}_{\mathit{AR}}$
Class	2017	2010	Mean	2017	2010	Mean
Very poor	17.3	0.4	0.6	14.9	14.1	13.5
Poor	41.0	1.5	20.5	18.3	18.3	18.3
Nearly moderate	24.4	21.0	59.0	31.7	32.3	32.5
Moderate	7.3	61.9	13.3	21.8	22.9	23.8
Good	7.5	5.0	5.6	7.8	7.7	7.4
Very good	2.6	10.2	1.0	5.5	4.7	4.6

.

In Figure 6, we present an additional analysis of the time variability of the ${\rho }_{RC}$ and ${\rho }_{AR}$, those analyses aim to highlight the performances and the general benefits from the implementation of RWH structures at catchment scale. Panels (a) and (b) show general spatial statistics of the indexes for the years from 1951 to 2022. Panels (c) and (d) show the percentage/total area in each class for the 2 indices, different colors pertain to different classes. In the processing of the first two graphs, the index values have not been reclassified, i.e., they are those obtained from Equation (3). When looking at the average values, the indices at the catchment scale are very similar (more or less 0.18), corresponding to nearly moderate class to moderate range. Both indices evolve over time, reflecting the annual rainfall variability, with a higher variation associated with the ${\rho }_{RC}$; the analysis of the mean values is of little significance and will not be discussed further. More interesting is the temporal variability of the indices, which is shown by the coefficient of variation, panel (b). In general, the spatial variability of the ${\rho }_{AR}$ is greater than that of the corresponding ${\rho }_{RC}$; this result must be interpreted as a higher resolution and sensitivity of ${\rho }_{AR}$, which embeds more information than ${\rho }_{RC}$, and not as a lack of robustness of the index. In fact, ${\rho }_{AR}$ is characterized by a higher degree of robustness, which is reflected in the greater stability of the observed coefficients of variation for different years.

Now we move to the analysis of the variability of the area fraction in the different classes depicted in panels (c) and (d); as in the previous analysis, the percentages associated with ${\rho }_{RC}$ are characterized by a high temporal variability with the values significantly depending on the total amount of rainfall, values varies up to tens of units in percentage, such as for the “Moderate” class, while the percentage of the “Very good” class varies from a minimum of 1% to a maximum of 10%. On the other hand, the area classification by the ${\rho }_{RC}$ shows very stable values, identifying 4% of the catchment area as “Very good”. The stability of the values indicates the reduction in uncertainty in the selection of areas for the implementation of $RWH$ structures; this feature makes the new index particularly suitable as a tool for the planning of basin management policies and the optimal allocation of economic resources.

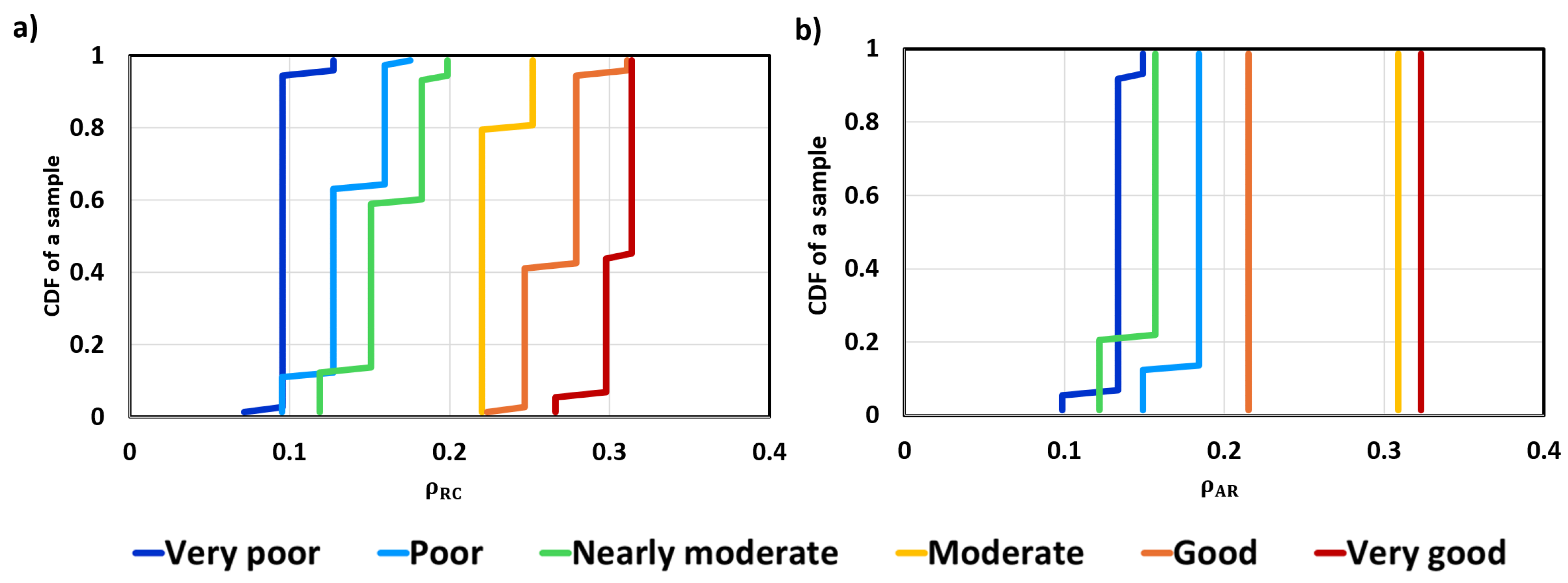
The analysis is now extended at the pixel scale. Figure 7 shows the empirical frequency curves for 6 pixels associated with the sample of local $RWH$ potential index and ${\rho }_{AR}$ values were obtained over the 72 years from 1951 to 2022. A pixel sample is randomly chosen from each class (based on the average year). Then empirical frequency analysis was carried out for the non-classified values (Equations (2) and (3)). The finite number of values that $RWH$ potential index and ${\rho }_{AR}$ can assume reflects in the discrete distributions shown in Figure 7. Focusing on panel (a), we can see that each pixel is characterized by a certain variability of the $RWH$ potential index, which means that the classification score of the analyzed pixel is not unique but depends on the particular year. We can also see how the pixel classified as “Moderate” according to $RWH$ potential changes its score to “Very good” when considering the new classification based on the aggregated runoff, while the pixel classified as “Good” moves in the “Moderate” class. Variability is much less pronounced in the same analysis carried out for ${\rho }_{AR}$, depicted in panel (b), where a very low level of variability can be observed, the latter turns into a deterministic value for higher scored sites. This latest analysis highlights the low sensitivity of our approach to annual precipitation values, even at the pixel scale. This property is particularly important given that detailed precipitation datasets are often not available, and the observation period used for the $RWH$ potential assessment is often limited to a few years.

5. Summary and Conclusions

The core idea behind this work is that rainwater harvesting potential at a given site depends on the runoff that is generated upstream. Runoff increases during surface flow as more and more areas contribute to it, as function of the basin geomorphology. However, runoff aggregation is generally overlooked in procedures for selecting optimal RWH structure locations. In this study, we propose the introduction of a new criterion—aggregated runoff $AR$—into site classification procedures, replacing traditional indicators that evaluate only local water availability, such as the runoff coefficient.

Aggregated runoff can easily be integrated into existing methodologies proposed in the literature, together with other established parameters, such as slope, drainage density or others possible criteria for selecting RWH potential locations. Aggregated runoff can be assessed on a large scale using a geomorphological approach and simple tools that are commonly available on GIS platforms. This new criterion, which allows for a more accurate estimation of the actual water availability, has a highly significant impact on the final outcome.

We applied this approach to the Tiber River basin at Ponte Felcino, comparing it with a standard method based on the runoff coefficient. The study was extended over a 72-year period to account for the effects of annual rainfall variability. The subsequent analyses were carried out using the BIGBANG database developed by ISPRA [29]. In the example we show how to apply the proposed criteria, with simple and practical guidelines. The analysis performed, despite based on specific catchment, highlights some general issues related to rainwater site selection when using AHP/GIS-based methodologies, which can be overcome by adopting the proposed approach and by addressing rainfall time variability. The results are quite general and can be extended to other catchments and methodologies. The main results can be summarized as follows.

• The integration of aggregated runoff substantially modifies the RHP potential $\rho$ maps, increasing the scores of areas located at the base of hillslopes and decreasing the scores of sites located on the top. This spatial pattern could not be adequately captured by models relying solely on local runoff.
• Moreover, the use of aggregated runoff has enhanced the accuracy, determining a more precise identification of zones most suitable for the installation of RWH structures.
• Since the aggregate runoff maximum value is influenced by rainfall and catchment dimensions, a novel classification system is required. In this study, thresholds were defined through a quantile-based analysis of the spatial distribution of runoff values across grid cells. The latter resulted in a marked improvement in the robustness of the methodology, as demonstrated by the computation of key basin-scale aggregated statistics. In particular, the use of aggregated runoff and quantile-based classification produced highly stable baseline statistics, with minimal sensitivity to annual rainfall variability. By contrast, the conventional approach, which is based on runoff coefficients and rigid classification schemes, exhibited significant temporal variability. This makes our criterion particularly relevant, given that RWH systems are usually chosen based on long-term average parameters, but they are crucial during drought periods.
• The pixel-scale analysis, conducted on annual values for individual grid cells, confirmed the improvement of the performance on the evaluation of the RWH potential. The empirical frequency distributions of the local $\rho$ values revealed that, when using the runoff coefficient approach, class assignment uncertainty is significant with changes in classes assignment from year to year. This variability, however, is much more less pronounced when applying the new criterion, which yields nearly deterministic class assignments.

Summarizing, the introduction of aggregated runoff as one of the main criteria for assessing RWH potential zones by popular AHP/GIS-based methodologies is a simple and potentially useful improvement of such methods. It enables a more realistic and accurate assessment of RWH potential and the available runoff without increasing calculation complexity or data requirements. We emphasize again that the proposed criteria is independent on the particular methodology or layers considered in the AHP/GIS-based method and it can be implemented in all frameworks.