Machine Learning Models of the Geospatial Distribution of Groundwater Quality: A Systematic Review
Abstract
1. Introduction
1.1. Groundwater and Contamination Hazard
1.2. Geospatial Analysis and Models
1.3. Machine Learning
1.4. Scope and Objectives
- (i)
- (ii)
- (iii)
- Provide a systematic and comprehensive review of published MLGHM articles meeting stated inclusion criteria.
- Provide a descriptive analysis of MLGHM articles with respect to geographic distribution, target and predictive variables, and ML approaches.
- Consider the criteria to be sensibly considered in selecting the best ML model for a particular purpose.
- Ultimately, provide optimization-oriented suggestions to improve the effectiveness/efficiency of MLGHM.
2. Materials and Methods
2.1. Survey and Criteria
- (i)
- Only original research articles that were published in Scopus-Indexed journals (December 2024 list [45]) were considered.
- (ii)
- With some notable exceptions, only those articles in which ML analysis led to generalizing the prediction to unsampled subareas (i.e., GHM) were included. A few articles that did not satisfy this criterion were retained as they included a clear representation of the contaminant distribution in addition to presenting useful comparisons among controversial ML models (e.g., Ref. [46]). Hence, studies that were bound to merely numerical groundwater quality analysis were not included.
- (iii)
- (iv)
- Articles in which it was not immediately clear whether the used models were ML-based (e.g., Ref. [49]) were excluded, as were articles that, notwithstanding that their models were categorized as unsupervised techniques, nevertheless described techniques that are widely considered not to be unsupervised ML. Such techniques included entropy model averaging (EMA) in Ref. [50], fuzzy-catastrophe framework (FCF) in Ref. [51], fuzzy membership framework (FMF) in Ref. [30], as well as the GA and Wilcoxon test in Ref. [52]. Note that the use of metaheuristic techniques such as the genetic algorithm (GA) for optimizing predefined frameworks (e.g., DRASTIC) is considered a popular, yet non-ML, approach for GHM. Examples of these studies will be discussed later.
2.2. Meta-Data
3. Trend Analysis
- (i)
- There has been a consistent rise in the rate of MLGHM publications over the period of 2005–2024.
- (ii)
- Iran, India, and the United States are the countries with the highest number of MLGHM case studies.
- (iii)
- was the most studied target variable.
- (iv)
- Chemical characteristics of water and, to a lesser extent, textural and chemical characteristics of overlying soils were the most commonly used predictive variables.
- (v)
- Tree-based models (mostly RF) were the most favored feature selection technique.
4. Machine Learning—Review of Model Types
4.1. Supervised Models
4.1.1. Artificial Neural Networks
4.1.2. Neuro-Fuzzy Models
4.1.3. Tree-Based Models
4.1.4. Support Vector-Based Models
4.1.5. Regression Models
4.1.6. Probabilistic Models
4.1.7. Ensembles
- (i)
- Group 1: Meta-models (MMs) comprising committee and stacking learning that exhibit two-level predictions, i.e., the outputs of the models in Level 1 are considered inputs for another model in Level 2 (A.K.A. Levels 0 and 1). Fijani, et al. [105] presented the first application of such models (SCMAI) in 2013.
- (ii)
- Group 2: Metaheuristic optimization algorithm (MOA)-based models in which an MOA optimizes a baseline ML. MOAs are known as global optimizers that can tackle complicated problems [106,107]. These algorithms employ search operators to systematically update the solution in the search space through exploiting and exploring the knowledge. Such strategies ensure the final solution is globally optimum, i.e., protected from getting stuck in local minima [108]. The use of GA for optimizing CMAI by Fijani, Nadiri, Moghaddam, Tsai, and Dixon [105] in 2013 was the first appearance of MOAs in the surveyed literature.
- (iii)
- Group 3: Dual hybrids (DHs) are created by integrating two baseline ML models. These models usually deliver stronger solutions than single conventional models, due to benefiting from the computational advantages of both models simultaneously. The first representative of this group was Cubist—as a hybrid of DT and LR—used by Band, et al. [109] in 2020.
4.1.8. Others
4.2. Unsupervised Models
4.2.1. Clustering Models
4.2.2. Self-Organizing Map
4.2.3. Unsupervised Deep Learning
5. What Defines a Better Model?
5.1. Model Design and Data Handling
- (i)
- Role of assumptions: Many data-driven models are able to satisfactorily learn and reproduce intrinsic non-linear patterns. There is overwhelming evidence of the suitability of ML models for exploring the relationship between GWQ and its influencing factors. But an overlooked question regarding many ML-based efforts is ’To what extent can the performance of an ML be influenced by the modeling assumptions?’
- (ii)
- Feature selection: As shown in Section S1.5, many MLGHM studies have benefited from feature selection to optimize the models in terms of dimensionality. These techniques can help ML models by improving learning performance, preventing overfitting, and/or reducing computational costs [137].
- (iii)
- Dataset adjustment: The data splitting ratio, which specifies what portions of the dataset are dedicated to the training and testing phases [39], is an important factor that can impact the quality of training, and consequently, the quality of the prediction results. In addition, data-centric cross-validation techniques (e.g., K-Fold) [138] can be regarded as addressing the stability of the model.
5.2. Model’s Performance and Reliability
- (iv)
- Accuracy and validation: Accuracy assessment is one of the most important steps of any modeling. In MLGHM efforts, scientists have extensively used accuracy metrics (e.g., RMSE, AUC, and R2) to validate and compare the performance of their models.
- (v)
- Hyperparameters (tuning and presentation): Recognizing and proper determination of models’ hyperparameters is vital as they can impact the quality of the prediction. ML models, therefore, should ideally be hyperparameter-tuned to maximize the model’s potential and to be hyperparameter-transparent to support reproducible research.
- (vi)
- Stability: Stability of an ML model can be defined as its ability to maintain consistent performance when exposed to small perturbations. In this sense, recognizing the sources of uncertainty, as well as assessing the models’ repeatability and ensuring the results’ reproducibility, can be helpful.
- (vii)
- (viii)
- Explainability (transparency/interpretability): Many of the reviewed ML models lack explainability, i.e., a clear presentation of the internal processes, and so are labeled here as ‘opaque-box’ models. In contrast, explainable artificial intelligence (XAI) is an increasingly used term to describe more explainable ML models that enable human users to better understand and so better trust [142].
- (ix)
- Optimizability: optimizing an ML model can be conducted with respect to data and dimension, the model’s architecture, hyperparameters, and the training algorithms, and can lead to a more applicable model.
5.3. Computational Efficiency
- (x)
- Computation time: Particularly for models of large datasets, reducing the computation time to attain a target accuracy may be an important model characteristic [143] necessitating a computationally efficient model. This factor should be evaluated with respect to the operating system’s characteristics (e.g., RAM and CPU frequency) to reflect the models’ computational demand fairly.
- (xi)
- Penalizing for complexity: Penalty functions aim to address a trade-off between the model’s fitness and its complexity. To this end, the model is penalized (sometimes partly) with respect to the number of its computational parameters (e.g., the number of intercepts, coefficients, and error variance in MLR).
5.4. Practical Application
- (xii)
- Informed hazard zonation (IHZ): Once a GHM is produced, it is essential to correctly classify the study area into different hazard classes for optimizing decision-making and cost estimations. Popular methods for doing so are based on statistical methods (e.g., Equal Intervals) and/or regulatory standards; however, more recent studies explicitly consider model accuracy and purpose-related model-informed cost-benefit balances.
6. Machine Learning Models—Comparative Assessment
- Label A focuses on comparing mostly conventional models, including (but not limited to) ANNs, NFs, SVMs, and simple tree-based models,
- Label B focuses on the competition between tree-based and Ensemble 1 models,
- Label C addresses the competency of DL, asserting itself as a competitive model to the above two groups,
- Label D focuses on MM ensembles (Ensemble 2—Group 1),
- Label E evaluates MOA-based ensembles (Ensemble 2—Group 2) versus relevant baseline models.
- (i)
- Data Adjustment: Many studies considered feature selection (and/or importance assessment) using popular models (e.g., tree-based MLs, PDP, and PCA) to delineate the role of predictive variables. As an interesting idea, some studies (e.g., Refs [145,180]) created and imposed various combinations of predictive variables that led to identifying the most accurate prediction scenarios. Many works also took advantage of data-centric cross-validation (mostly the K-fold technique) as part of data adjustment. Nevertheless, a few studies (e.g., Refs. [46,116]) paid attention to optimizing the data splitting ratio that reportedly can be an accuracy-determinant factor.
- (ii)
- Hyperparameters: Reporting the used hyperparameters was inconsistent, i.e., present in many articles but missing in many others. Most studies, however, benefit from automatic methods such as the GS algorithm and manual methods such as T&E to ensure proper assignment of hyperparameters.
- (iii)
- Computational efficiency: Some studies considered documenting computational details (e.g., computation time [135,155,171,182,183] and the used operating system [171,176,180]). These two factors can reflect important information regarding an informed selection of efficient MLs, due to the complexities of some MLs and occasional limitations in computer facilities. Moreover, utilizing penalty functions to constrain the model’s complexity is another promising direction for proper selection of the model (and predictive variables). However, it was observed in a small portion of the surveyed articles (e.g., Refs. [152,158,163,182]). To exemplify, in Refs. [135,171], the outstanding model not only achieved the highest accuracy, but also was quicker in terms of training time (and convergence of the solution [183]). Further, Ref. [158] indicated that its superior model achieved these merits along with the lowest penalty expressed by AIC and BIC.
- (iv)
- Others: Many studies leveraged internal and external techniques (e.g., XGBoost’s inherent regularisation [159] and Dropout for DL [171]) to prevent overfitting. In contrast, quantitative evaluation of prediction uncertainty was explored in a few studies (e.g., using statistical indices of PICP [156] and U95% [180]). Models’ explainability, generalizability, and results’ reproducibility likewise received limited attention, as they were often discussed in brief. Last but not least, IHZ remained almost underexplored despite its great importance. The vast majority of the reviewed studies employed well-established methods (e.g., natural breaks, equal hazard interval, and WHO standards) to classify the studied aquifers in terms of hazard. Only a few studies (e.g., Ref. [157] from Table 1 and others [185,186,187]) identified AUC-based cutoff optimization for determining hazardous areas.
6.1. Accuracy Comparison
6.1.1. Label A
6.1.2. Label B
- (i)
- XGBoost > LGBM, AdB, CatBoost in Ref. [161],
- (ii)
- XGBoost > GBM, LGBM in Ref. [159],
- (iii)
- CatBoost > XGBoost, LGBM in Ref. [158],
- (iv)
- CatBoost > AdB in Ref. [162],
- (v)
- AdB > XGBoost, LGBM in Ref. [178],
- (vi)
- GBR > XGBoost, AdB in Ref. [156].
- (i)
- (ii)
6.1.3. Label C
6.1.4. Label D
- (i)
- KNN-SEL > GBDT, XGBoost, RF in Ref. [172],
- (ii)
- LDA-SEL > RF, ERT, DT, XGBoost, AdB, GBDT in Ref. [173],
- (iii)
- AdB-Ens > AdB, XGBoost, LGBM, RF in Ref. [178],
- (iv)
- GP-Ens, SVR-Ens > ANN-Ens, supervised and unsupervised DLs in Ref. [135],
- (v)
- NB-SEL > RF, AdB, XGBoost, LGBM, CatBoost, GBDT, BA-DT in Ref. [179].
6.1.5. Label E
- (i)
- ANFIS-PSO, ANFIS-DE, ANFIS-GA > ANFIS in Ref. [181],
- (ii)
- ANFIS-AO, ANFIS-SMA, ANFIS-ACO > LsR, ANFIS in Ref. [180],
- (iii)
- RF-FA, RF-MOE, RF-Ant, RF-GWO, RF-PSO > RF in Ref. [183],
- (iv)
- RF-GOA, RF-GWO, RF-PSO > RF in Ref. [184],
- (v)
- ANN-PSO, ANN-GWO > ANN in Ref. [217],
- (vi)
- PSO-ANN > SVM, MLR in Ref. [182].
- (i)
- (ii)
- Since each study considers only one baseline ML (ANN/ANFIS/RF), cross-category comparisons are required to assess the power of a given MOA in optimizing different baseline MLs in the same study, e.g., ANN-PSO vs. ANFIS-PSO vs. RF-PSO.
6.2. Overall Comparison
- (i)
- Very Fast to Fast: MLR, LgR, DT, ERT, KNN, and LDA.
- (ii)
- Moderate to Slow: RF, NFs, shallow ANNs, SVMs, Ensemble 1, and M5.
- (iii)
- Slow to Very Slow: GP, DLs, and MOA-based models.
7. Informed Model Selection
8. Discussion, Conceptual Framework, and Future Work
8.1. Conceptual Framework
8.1.1. Stage 0
- (a)
- Spatial heterogeneity of data: How does the model deal with the heterogeneous distribution of the relationship between target and predictor variables? For large study areas, a possible solution can be found in Ref. [124] wherein the study area was partitioned into three sub-domains to account for the area’s heterogeneity.
- (b)
- Temporal variations (upon occurrence): How does the model account for temporal changes in contaminant concentrations and environmental conditions? Performing separate seasonal assessments (as in Ref. [233]) and considering temporal predictive variables (e.g., precipitation and temperature seasonality, as in Ref. [234]) may help address this issue.
- (c)
- Data quality and representativeness: To what extent can the provided dataset represent the sampling frame in the study area? Proper selection of predictive variables can assist the model in obtaining a deeper understanding of the relationship between contaminant and environmental conditions. For instance, aquifer dynamics can be expressed in terms of both physical and chemical characteristics [235], necessitating the inclusion of predictive variables such as time-dependent flow and water pH. Moreover, testing for multicollinearity in the data can address another significant question: Does each factor effectively (and independently) represent an aspect of the problem? Removing unnecessary factors can improve model stability and interpretability.
- (d)
- Problem’s non-linearity: How to ensure the model can capture any non-linear dependency of a contaminant target variable on various factors simultaneously? Comparing the accuracy of the candidate ML models to benchmark linear models (e.g., MLR in Ref. [163]) can reflect the relative capability of the models in handling MLGHM non-linearities. Plus, some linear models have pre-implementation conditions to be satisfied (e.g., ensuring the normal distribution of the target variable when using MLR).
- (e)
- Model verification: How to ensure a satisfactorily trained model has been protected against undesirable phenomena such as local minima and overfitting? (See Table 1).
8.1.2. Stage 1
8.1.3. Stage 2
8.1.4. Stage 3
- (i)
- Possible reasons: Apart from the presence of noise in data and having a limited number of training samples (but with many predictive variables), it is established that the higher a model’s complexity (referred to as high-variance models), the higher the susceptibility to overfitting [250].
- (ii)
- Indicator: An indicator of overfitting is a considerable difference between the training and testing accuracies (AccuracyTraining >> AccuracyTesting). Moreover, one may estimate the proneness to overfitting by monitoring accuracy during area-centric and/or data-centric cross-validations.
- (iii)
- Possible solutions: Feasible solutions to overfitting can include leveraging data augmentation techniques in the event of data insufficiency (as in Ref. [253]); applying feature selection in the case of high dimensionality; using regularization methods (See Table 1); trying simpler (shallower) versions if the current models are too complex (deep); and employing models that are known for being more immune to overfitting (e.g., XGBoost, See Table 1).
8.1.5. Stage 4
8.2. Future Directions
- (i)
- Although XAI was discussed earlier (e.g., Section 8.1.4), increasing the transparency is still considered a significant emerging direction towards enhancing stakeholders’ trust in modeling outcomes. This study offered an example of moving from opaque-box to transparent-box for DL (see Text S3 and Figure S7). However, other methods, such as SHAP, along with monotonic constraints [264], can be helpful to elucidate models’ calculations.
- (ii)
- Employing PIML models—embedding physical laws into learning algorithms—is another growing frontier to enhance scientific plausibility and reliability of the model under extrapolation [265,266]. An example of this in MLGHM works can be incorporating hydrogeological rules (e.g., groundwater flow directs contamination, hence, no upgradient contamination movement) into the mathematical computations of the predictive model.
- (iii)
- (iv)
- Transfer learning (e.g., fine-tuning a pre-trained model with limited data from the new to-be-assessed region) [269] and federated learning (e.g., collaborative training of models without sharing raw data) [270] are two approaches that can contribute to tackling challenges stemming from data scarcity and data privacy.
- (v)
- While many traditional hazard zonation models are easily accessible in software such as GIS, more recent models may require external tools (and more statistical knowledge) to implement, making them challenging to use for some. Hence, future efforts should also focus on developing user-friendly graphical user interfaces (GUIs) to facilitate the use of GHM models and new hazard classification methods.
9. Conclusions
- (i)
- There has been an exponential increase in published applications of MLGHM models over the past two decades.
- (ii)
- Iran, India, the US, and China are the countries most modeled in these studies, but there are many other countries that would benefit from (further) MLGHM.
- (iii)
- Nitrate, water quality index, and arsenic featured as the most studied target groundwater quality indicators. The most frequently considered categories of predictive variables were groundwater chemical characteristics and geomorphological factors.
- (iv)
- Tree-based ML was the most popular feature selection method.
- (v)
- Tree-based ML (mostly RF) was the most popular MLGHM model.
- (vi)
- Published evaluations of model superiority have been largely based on accuracy. On the basis of many articles, resampling-improved ensembles, meta-model ensembles, and tree-based models outperformed a wide variety of models, including (but not limited to) shallow ANNs, SVMs, NFs, and regression models. A more detailed accuracy comparison (based on the existing pieces of evidence) then reflected a close competition among boosting ensembles, random forest, and deep learning as the most promising members of their families.
- (vii)
- Aside from accuracy, other key factors—notably including model complexity and predictability—have been largely overlooked in assessing ML model quality, notwithstanding their often key importance in determining what are better models for particular types of problems.
- (viii)
- We present a flowchart that can inform GHM researchers to help better select the most appropriate popular ML models on the basis of requirements for (a) accuracy, (b) transparency, (c) training speed, and (d) number of hyperparameters, as well as (e) the intended modeling scale and (f) required user’s expertise.
- (ix)
- Notable gaps that were identified in the surveyed studies were discussed in depth, and several ideas were suggested for optimizing MLGHM models by emphasizing the features of a ‘better model’.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ryder, G. The United Nations World Water Development Report; Wastewater: The Untapped Resource; UNESCO Pub.: London, UK, 2017. [Google Scholar]
- Rodella, A.-S.; Zaveri, E.; Bertone, F. The Hidden Wealth of Nations: The Economics of Groundwater in Times of Climate Change; World Bank: Washington, DC, USA, 2023. [Google Scholar]
- Hasan, M.F.; Smith, R.; Vajedian, S.; Pommerenke, R.; Majumdar, S. Global land subsidence mapping reveals widespread loss of aquifer storage capacity. Nat. Commun. 2023, 14, 6180. [Google Scholar] [CrossRef]
- Jasechko, S.; Perrone, D. Global groundwater wells at risk of running dry. Science 2021, 372, 418–421. [Google Scholar] [CrossRef]
- Fan, Y.; Li, H.; Miguez-Macho, G. Global patterns of groundwater table depth. Science 2013, 339, 940–943. [Google Scholar] [CrossRef]
- Niazi, H.; Wild, T.B.; Turner, S.W.; Graham, N.T.; Hejazi, M.; Msangi, S.; Kim, S.; Lamontagne, J.R.; Zhao, M. Global peak water limit of future groundwater withdrawals. Nat. Sustain. 2024, 7, 413–422. [Google Scholar] [CrossRef]
- Podgorski, J.; Berg, M. Global threat of arsenic in groundwater. Science 2020, 368, 845–850. [Google Scholar] [CrossRef] [PubMed]
- Podgorski, J.; Berg, M. Global analysis and prediction of fluoride in groundwater. Nat. Commun. 2022, 13, 4232. [Google Scholar] [CrossRef]
- Foster, S.; Garduno, H.; Kemper, K.; Tuinhof, A.; Nanni, M.; Dumars, C. Groundwater Quality Protection: Defining Strategy and Setting Priorities; The World Bank: Washington, DC, USA, 2003. [Google Scholar]
- Hassan, M.M. Arsenic in Groundwater: Poisoning and Risk Assessment; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Muhib, M.I.; Ali, M.M.; Tareq, S.M.; Rahman, M.M. Nitrate Pollution in the Groundwater of Bangladesh: An Emerging Threat. Sustainability 2023, 15, 8188. [Google Scholar] [CrossRef]
- Shaji, E.; Sarath, K.; Santosh, M.; Krishnaprasad, P.; Arya, B.; Babu, M.S. Fluoride contamination in groundwater: A global review of the status, processes, challenges, and remedial measures. Geosci. Front. 2024, 15, 101734. [Google Scholar] [CrossRef]
- Haldar, D.; Duarah, P.; Purkait, M.K. MOFs for the treatment of arsenic, fluoride and iron contaminated drinking water: A review. Chemosphere 2020, 251, 126388. [Google Scholar] [CrossRef]
- Zheng, Y. Global solutions to a silent poison. Science 2020, 368, 818–819. [Google Scholar] [CrossRef]
- Fendorf, S.; Michael, H.A.; Van Geen, A. Spatial and temporal variations of groundwater arsenic in South and Southeast Asia. Science 2010, 328, 1123–1127. [Google Scholar] [CrossRef]
- Nations, T.U. Goal 6: Ensure Access to Water and Sanitation for All. Available online: https://www.un.org/sustainabledevelopment/water-and-sanitation/#:~:text=Goal%206:%20Ensure%20access%20to%20water%20and%20sanitation%20for%20all&text=Access%20to%20safe%20water%2C%20sanitation,cent%20to%2073%20per%20cent (accessed on 1 June 2025).
- Bhattacharya, P.; Polya, D.; Jovanovic, D. Best Practice Guide on the Control of Arsenic in Drinking Water; IWA Publishing: London, UK, 2017. [Google Scholar]
- UNICEF. Arsenic Primer: Guidance on the Investigation & Mitigation of Arsenic Contamination; UNICEF: New York, NY, USA, 2018. [Google Scholar]
- Dewan, A.; Dewan, A.M. Hazards, Risk, and Vulnerability; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Xiong, H.; Wang, Y.; Guo, X.; Han, J.; Ma, C.; Zhang, X. Current status and future challenges of groundwater vulnerability assessment: A bibliometric analysis. J. Hydrol. 2022, 615, 128694. [Google Scholar] [CrossRef]
- Abegeja, D.; Nedaw, D. Identification of groundwater potential zones using geospatial technologies in Meki Catchment, Ethiopia. Geol. Ecol. Landsc. 2024, 1–16. [Google Scholar] [CrossRef]
- Machiwal, D.; Cloutier, V.; Güler, C.; Kazakis, N. A review of GIS-integrated statistical techniques for groundwater quality evaluation and protection. Environ. Earth Sci. 2018, 77, 681. [Google Scholar] [CrossRef]
- Jain, H. Groundwater vulnerability and risk mitigation: A comprehensive review of the techniques and applications. Groundw. Sustain. Dev. 2023, 22, 100968. [Google Scholar] [CrossRef]
- Nistor, M.-M. Groundwater vulnerability in Europe under climate change. Quat. Int. 2020, 547, 185–196. [Google Scholar] [CrossRef]
- Al-Abadi, A.M. The application of Dempster–Shafer theory of evidence for assessing groundwater vulnerability at Galal Badra basin, Wasit governorate, east of Iraq. Appl. Water Sci. 2017, 7, 1725–1740. [Google Scholar] [CrossRef]
- Neshat, A.; Pradhan, B. An integrated DRASTIC model using frequency ratio and two new hybrid methods for groundwater vulnerability assessment. Nat. Hazards 2015, 76, 543–563. [Google Scholar] [CrossRef]
- Abbasi, S.; Mohammadi, K.; Kholghi, M.; Howard, K. Aquifer vulnerability assessments using DRASTIC, weights of evidence and the analytic element method. Hydrol. Sci. J. 2013, 58, 186–197. [Google Scholar] [CrossRef]
- Goudarzi, S.; Jozi, S.A.; Monavari, S.M.; Karbasi, A.; Hasani, A.H. Assessment of groundwater vulnerability to nitrate pollution caused by agricultural practices. Water Qual. Res. J. 2015, 52, 64–77. [Google Scholar] [CrossRef]
- Kang, J.; Zhao, L.; Li, R.; Mo, H.; Li, Y. Groundwater vulnerability assessment based on modified DRASTIC model: A case study in Changli County, China. Geocarto Int. 2017, 32, 749–758. [Google Scholar] [CrossRef]
- Msaddek, M.H.; Moumni, Y.; Ayari, A.; El May, M.; Chenini, I. Artificial intelligence modelling framework for mapping groundwater vulnerability of fractured aquifer. Geocarto Int. 2022, 37, 10480–10510. [Google Scholar] [CrossRef]
- El Naqa, I.; Murphy, M.J. What Is Machine Learning; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ayodele, T.O. Types of machine learning algorithms. New Adv. Mach. Learn. 2010, 3, 19–48. [Google Scholar]
- Morales, E.F.; Escalante, H.J. A brief introduction to supervised, unsupervised, and reinforcement learning. In Biosignal Processing and Classification Using Computational Learning and Intelligence; Elsevier: Amsterdam, The Netherlands, 2022; pp. 111–129. [Google Scholar]
- Wachniew, P.; Zurek, A.J.; Stumpp, C.; Gemitzi, A.; Gargini, A.; Filippini, M.; Rozanski, K.; Meeks, J.; Kværner, J.; Witczak, S. Toward operational methods for the assessment of intrinsic groundwater vulnerability: A review. Crit. Rev. Environ. Sci. Technol. 2016, 46, 827–884. [Google Scholar] [CrossRef]
- Tung, T.M.; Yaseen, Z.M. A survey on river water quality modelling using artificial intelligence models: 2000–2020. J. Hydrol. 2020, 585, 124670. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, J.; Yang, X.; Zhang, Y.; Zhang, L.; Ren, H.; Wu, B.; Ye, L. A review of the application of machine learning in water quality evaluation. Eco-Environ. Health 2022, 1, 107–116. [Google Scholar] [CrossRef]
- Ewuzie, U.; Bolade, O.P.; Egbedina, A.O. Application of deep learning and machine learning methods in water quality modeling and prediction: A review. In Current Trends and Advances in Computer-Aided Intelligent Environmental Data Engineering; Academic Press: Cambridge, MA, USA, 2022; pp. 185–218. [Google Scholar] [CrossRef]
- Hanoon, M.S.; Ahmed, A.N.; Fai, C.M.; Birima, A.H.; Razzaq, A.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Application of artificial intelligence models for modeling water quality in groundwater: Comprehensive review, evaluation and future trends. Water Air Soil Pollut. 2021, 232, 411. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, C.; Wang, Y.; Lyu, G.; Lin, S.; Liu, W.; Niu, H.; Hu, Q. Application of machine learning models in groundwater quality assessment and prediction: Progress and challenges. Front. Environ. Sci. Eng. 2024, 18, 29. [Google Scholar] [CrossRef]
- Chowdhury, T.N.N.; Battamo, A.Y.; Nag, R.; Zekker, I.; Salauddin, M. Impacts of climate change on groundwater quality: A systematic literature review of analytical models and machine learning techniques. Environ. Res. Lett. 2025, 20, 033003. [Google Scholar] [CrossRef]
- Haggerty, R.; Sun, J.; Yu, H.; Li, Y. Application of machine learning in groundwater quality modeling-A comprehensive review. Water Res. 2023, 233, 119745. [Google Scholar] [CrossRef]
- Pandya, H.; Jaiswal, K.; Shah, M. A comprehensive review of machine learning algorithms and its application in groundwater quality prediction. Arch. Comput. Methods Eng. 2024, 31, 4633–4654. [Google Scholar] [CrossRef]
- Haghbin, M.; Sharafati, A.; Dixon, B.; Kumar, V. Application of soft computing models for simulating nitrate contamination in groundwater: Comprehensive review, assessment and future opportunities. Arch. Comput. Methods Eng. 2021, 28, 3569–3591. [Google Scholar] [CrossRef]
- Kumari, N.; Pathak, G.; Prakash, O. A review of application of artificial neural network in ground water modeling. In Proceedings of the International Conference on Recent Advances in Mathematics, Statistics and Computer Science 2015, Bihar, India, 29–31 May 2015; pp. 393–402. [Google Scholar] [CrossRef]
- Scopus. Scopus-Indexed Journals. Available online: https://www.scopus.com/ (accessed on 1 February 2025).
- Singha, S.; Pasupuleti, S.; Singha, S.S.; Singh, R.; Kumar, S. Prediction of groundwater quality using efficient machine learning technique. Chemosphere 2021, 276, 130265. [Google Scholar] [CrossRef]
- Masoud, A.A. Groundwater quality assessment of the shallow aquifers west of the Nile Delta (Egypt) using multivariate statistical and geostatistical techniques. J. Afr. Earth Sci. 2014, 95, 123–137. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, S.; Wang, Q.; Hu, S.; Qin, G.; Yu, H. Response of a Coastal Groundwater System to Natural and Anthropogenic Factors: Case study on east coast of laizhou bay, china. Int. J. Environ. Res. Public Health 2020, 17, 5204. [Google Scholar] [CrossRef]
- Romero, J.M.; Salazar, D.C.; Melo, C.E. Hydrogeological spatial modelling: A comparison between frequentist and Bayesian statistics. J. Geophys. Eng. 2023, 20, 523–537. [Google Scholar] [CrossRef]
- Gharekhani, M.; Nadiri, A.A.; Khatibi, R.; Nikoo, M.R.; Barzegar, R.; Sadeghfam, S.; Moghaddam, A.A. Quantifying the groundwater total contamination risk using an inclusive multi-level modelling strategy. J. Environ. Manag. 2023, 332, 117287. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Norouzi, H.; Khatibi, R.; Gharekhani, M. Groundwater DRASTIC vulnerability mapping by unsupervised and supervised techniques using a modelling strategy in two levels. J. Hydrol. 2019, 574, 744–759. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Gharekhani, M.; Khatibi, R. Mapping aquifer vulnerability indices using artificial intelligence-running multiple frameworks (AIMF) with supervised and unsupervised learning. Water Resour. Manag. 2018, 32, 3023–3040. [Google Scholar] [CrossRef]
- Vesselinov, V.V.; Alexandrov, B.S.; O’Malley, D. Contaminant source identification using semi-supervised machine learning. J. Contam. Hydrol. 2018, 212, 134–142. [Google Scholar] [CrossRef]
- Tiwari, A. Supervised learning: From theory to applications. In Artificial Intelligence and Machine Learning for EDGE Computing; Elsevier: Amsterdam, The Netherlands, 2022; pp. 23–32. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Proceedings of the Numerical analysis: Proceedings of the Biennial Conference Held at Berlin, Heidelberg, Germany, 28 June–1 July 1977; Springer: Berlin/Heidelberg, Germany, 2006; pp. 105–116. [Google Scholar]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A review of the artificial neural network models for water quality prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Boo, K.B.W.; El-Shafie, A.; Othman, F.; Khan, M.M.H.; Birima, A.H.; Ahmed, A.N. Groundwater level forecasting with machine learning models: A review. Water Res. 2024, 252, 121249. [Google Scholar] [CrossRef]
- Almasri, M.N.; Kaluarachchi, J.J. Modular neural networks to predict the nitrate distribution in ground water using the on-ground nitrogen loading and recharge data. Environ. Model. Softw. 2005, 20, 851–871. [Google Scholar] [CrossRef]
- Wang, M.; Liu, G.; Wu, W.; Bao, Y.; Liu, W. Prediction of agriculture derived groundwater nitrate distribution in North China Plain with GIS-based BPNN. Environ. Geol. 2006, 50, 637–644. [Google Scholar] [CrossRef]
- Ouifak, H.; Idri, A. Application of neuro-fuzzy ensembles across domains: A systematic review of the two last decades (2000–2022). Eng. Appl. Artif. Intell. 2023, 124, 106582. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Mehrabi, M.; Pradhan, B.; Moayedi, H.; Alamri, A. Optimizing an adaptive neuro-fuzzy inference system for spatial prediction of landslide susceptibility using four state-of-the-art metaheuristic techniques. Sensors 2020, 20, 1723. [Google Scholar]
- Ang, Y.K.; Talei, A.; Zahidi, I.; Rashidi, A. Past, present, and future of using neuro-fuzzy systems for hydrological modeling and forecasting. Hydrology 2023, 10, 36. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Dixon, B. Applicability of neuro-fuzzy techniques in predicting ground-water vulnerability: A GIS-based sensitivity analysis. J. Hydrol. 2005, 309, 17–38. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on typical tabular data? Adv. Neural Inf. Process. Syst. 2022, 35, 507–520. [Google Scholar]
- Januschowski, T.; Wang, Y.; Torkkola, K.; Erkkilä, T.; Hasson, H.; Gasthaus, J. Forecasting with trees. Int. J. Forecast. 2022, 38, 1473–1481. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Mendes, M.P.; Garcia-Soldado, M.J.; Chica-Olmo, M.; Ribeiro, L. Predictive modeling of groundwater nitrate pollution using Random Forest and multisource variables related to intrinsic and specific vulnerability: A case study in an agricultural setting (Southern Spain). Sci. Total Environ. 2014, 476, 189–206. [Google Scholar] [CrossRef]
- Nolan, B.T.; Gronberg, J.M.; Faunt, C.C.; Eberts, S.M.; Belitz, K. Modeling nitrate at domestic and public-supply well depths in the Central Valley, California. Environ. Sci. Technol. 2014, 48, 5643–5651. [Google Scholar] [CrossRef]
- Cortes, C. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Wang, L. Support Vector Machines: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 177. [Google Scholar]
- Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Zendehboudi, A.; Baseer, M.A.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Kok, Z.H.; Shariff, A.R.M.; Alfatni, M.S.M.; Khairunniza-Bejo, S. Support vector machine in precision agriculture: A review. Comput. Electron. Agric. 2021, 191, 106546. [Google Scholar] [CrossRef]
- Ammar, K.; Khalil, A.; McKee, M.; Kaluarachchi, J. Bayesian deduction for redundancy detection in groundwater quality monitoring networks. Water Resour. Res. 2008, 44, W08412. [Google Scholar] [CrossRef]
- Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B.; Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B. Regression Models; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ma, X.; Zou, B.; Deng, J.; Gao, J.; Longley, I.; Xiao, S.; Guo, B.; Wu, Y.; Xu, T.; Xu, X. A comprehensive review of the development of land use regression approaches for modeling spatiotemporal variations of ambient air pollution: A perspective from 2011 to 2023. Environ. Int. 2024, 183, 108430. [Google Scholar] [CrossRef]
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-w. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Twarakavi, N.K.; Kaluarachchi, J.J. Aquifer vulnerability assessment to heavy metals using ordinal logistic regression. Groundwater 2005, 43, 200–214. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef]
- Bharadiya, J.P. A review of Bayesian machine learning principles, methods, and applications. Int. J. Innov. Sci. Res. Technol. 2023, 8, 2033–2038. [Google Scholar]
- Krapu, C.; Borsuk, M. Probabilistic programming: A review for environmental modellers. Environ. Model. Softw. 2019, 114, 40–48. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. A review of machine learning concepts and methods for addressing challenges in probabilistic hydrological post-processing and forecasting. Front. Water 2022, 4, 961954. [Google Scholar] [CrossRef]
- Nolan, B.T.; Fienen, M.N.; Lorenz, D.L. A statistical learning framework for groundwater nitrate models of the Central Valley, California, USA. J. Hydrol. 2015, 531, 902–911. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Ting, K.M.; Witten, I.H. Stacking Bagged and Dagged Models; Working paper 97/09; University of Waikato, Department of Computer Science: Hamilton, New Zealand, 1997; Available online: https://researchcommons.waikato.ac.nz/entities/publication/37f19edd-e874-4b2c-a26b-0b4a202ca555 (accessed on 8 August 2025).
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, L.; Suganthan, P.N. Ensemble classification and regression-recent developments, applications and future directions. IEEE Comput. Intell. Mag. 2016, 11, 41–53. [Google Scholar] [CrossRef]
- Mahajan, P.; Uddin, S.; Hajati, F.; Moni, M.A. Ensemble learning for disease prediction: A review. Healthcare 2023, 11, 1808. [Google Scholar] [CrossRef]
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- Sakib, M.; Mustajab, S.; Alam, M. Ensemble deep learning techniques for time series analysis: A comprehensive review, applications, open issues, challenges, and future directions. Clust. Comput. 2025, 28, 73. [Google Scholar] [CrossRef]
- Wen, L.; Hughes, M. Coastal wetland mapping using ensemble learning algorithms: A comparative study of bagging, boosting and stacking techniques. Remote Sens. 2020, 12, 1683. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Shen, W. A review of ensemble learning algorithms used in remote sensing applications. Appl. Sci. 2022, 12, 8654. [Google Scholar] [CrossRef]
- Zaresefat, M.; Derakhshani, R. Revolutionizing groundwater management with hybrid AI models: A practical review. Water 2023, 15, 1750. [Google Scholar] [CrossRef]
- Kumar, V.; Yadav, S. A state-of-the-Art review of heuristic and metaheuristic optimization techniques for the management of water resources. Water Supply 2022, 22, 3702–3728. [Google Scholar] [CrossRef]
- Fijani, E.; Nadiri, A.A.; Moghaddam, A.A.; Tsai, F.T.-C.; Dixon, B. Optimization of DRASTIC method by supervised committee machine artificial intelligence to assess groundwater vulnerability for Maragheh–Bonab plain aquifer, Iran. J. Hydrol. 2013, 503, 89–100. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic algorithms: A comprehensive review. Comput. Intell. Multimed. Big Data Cloud Eng. Appl. 2018, 185–231. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Bristol, UK, 2010. [Google Scholar]
- Akay, B.; Karaboga, D.; Akay, R. A comprehensive survey on optimizing deep learning models by metaheuristics. Artif. Intell. Rev. 2022, 55, 829–894. [Google Scholar] [CrossRef]
- Band, S.S.; Janizadeh, S.; Pal, S.C.; Chowdhuri, I.; Siabi, Z.; Norouzi, A.; Melesse, A.M.; Shokri, M.; Mosavi, A. Comparative analysis of artificial intelligence models for accurate estimation of groundwater nitrate concentration. Sensors 2020, 20, 5763. [Google Scholar] [CrossRef]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L., Jr. Discriminatory Analysis-Nonparametric Discrimination: Small Sample Performance; (No. UCB11). 1952. Available online: https://www.semanticscholar.org/paper/Discriminatory-Analysis-Nonparametric-Small-Sample-Fix-Hodges/1fa93fb4aa010d46b22393131bc61a0a0d041da0 (accessed on 8 August 2025).
- Halder, R.K.; Uddin, M.N.; Uddin, M.A.; Aryal, S.; Khraisat, A. Enhancing K-nearest neighbor algorithm: A comprehensive review and performance analysis of modifications. J. Big Data 2024, 11, 113. [Google Scholar] [CrossRef]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- Motevalli, A.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R.; Pradhan, B.; Gholami, V. Inverse method using boosted regression tree and k-nearest neighbor to quantify effects of point and non-point source nitrate pollution in groundwater. J. Clean. Prod. 2019, 228, 1248–1263. [Google Scholar] [CrossRef]
- Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Ahmad, B.B. Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and UNEEC methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef]
- Díaz-Alcaide, S.; Martínez-Santos, P. Mapping fecal pollution in rural groundwater supplies by means of artificial intelligence classifiers. J. Hydrol. 2019, 577, 124006. [Google Scholar] [CrossRef]
- Al-Sahaf, H.; Bi, Y.; Chen, Q.; Lensen, A.; Mei, Y.; Sun, Y.; Tran, B.; Xue, B.; Zhang, M. A survey on evolutionary machine learning. J. R. Soc. N. Z. 2019, 49, 205–228. [Google Scholar] [CrossRef]
- Zhong, J.; Feng, L.; Ong, Y.-S. Gene expression programming: A survey. IEEE Comput. Intell. Mag. 2017, 12, 54–72. [Google Scholar] [CrossRef]
- Banzhaf, W.; Machado, P.; Zhang, M. Handbook of Evolutionary Machine Learning; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Telikani, A.; Tahmassebi, A.; Banzhaf, W.; Gandomi, A.H. Evolutionary machine learning: A survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Batista, J.E.; Silva, S. Evolutionary Machine Learning in Environmental Science. Handb. Evol. Mach. Learn. 2023, 563–590. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. Complex Syst. 2001, 13, 87–129. [Google Scholar]
- Gao, W.; Moayedi, H.; Shahsavar, A. The feasibility of genetic programming and ANFIS in prediction energetic performance of a building integrated photovoltaic thermal (BIPVT) system. Sol. Energy 2019, 183, 293–305. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Gharekhani, M.; Khatibi, R.; Sadeghfam, S.; Moghaddam, A.A. Groundwater vulnerability indices conditioned by supervised intelligence committee machine (SICM). Sci. Total Environ. 2017, 574, 691–706. [Google Scholar] [CrossRef]
- Meray, A.; Wang, L.; Kurihana, T.; Mastilovic, I.; Praveen, S.; Xu, Z.; Memarzadeh, M.; Lavin, A.; Wainwright, H. Physics-informed surrogate modeling for supporting climate resilience at groundwater contamination sites. Comput. Geosci. 2024, 183, 105508. [Google Scholar] [CrossRef]
- Ghahramani, Z. Unsupervised learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 72–112. [Google Scholar]
- Makhzani, A.; Frey, B.J. Winner-take-all autoencoders. Adv. Neural Inf. Process. Syst. 2015, 28, 2791–2799. [Google Scholar]
- Narvaez-Montoya, C.; Mahlknecht, J.; Torres-Martínez, J.A.; Mora, A.; Bertrand, G. Seawater intrusion pattern recognition supported by unsupervised learning: A systematic review and application. Sci. Total Environ. 2023, 864, 160933. [Google Scholar] [CrossRef]
- Drogkoula, M.; Kokkinos, K.; Samaras, N. A comprehensive survey of machine learning methodologies with emphasis in water resources management. Appl. Sci. 2023, 13, 12147. [Google Scholar] [CrossRef]
- Kalteh, A.M.; Hjorth, P.; Berndtsson, R. Review of the self-organizing map (SOM) approach in water resources: Analysis, modelling and application. Environ. Model. Softw. 2008, 23, 835–845. [Google Scholar] [CrossRef]
- Das, M.; Kumar, A.; Mohapatra, M.; Muduli, S. Evaluation of drinking quality of groundwater through multivariate techniques in urban area. Environ. Monit. Assess. 2010, 166, 149–157. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef]
- Choi, B.-Y.; Yun, S.-T.; Kim, K.-H.; Kim, J.-W.; Kim, H.M.; Koh, Y.-K. Hydrogeochemical interpretation of South Korean groundwater monitoring data using Self-Organizing Maps. J. Geochem. Explor. 2014, 137, 73–84. [Google Scholar] [CrossRef]
- Faal, F.; Nikoo, M.R.; Ashrafi, S.M.; Šimůnek, J. Advancing aquifer vulnerability mapping through integrated deep learning approaches. J. Clean. Prod. 2024, 481, 144112. [Google Scholar] [CrossRef]
- Fisher, A.; Rudin, C.; Dominici, F. All models are wrong, but many are useful: Learning a variable’s importance by studying an entire class of prediction models simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [Google Scholar]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. (CSUR) 2017, 50, 94. [Google Scholar] [CrossRef]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Ludwig, M.; Moreno-Martinez, A.; Hölzel, N.; Pebesma, E.; Meyer, H. Assessing and improving the transferability of current global spatial prediction models. Glob. Ecol. Biogeogr. 2023, 32, 356–368. [Google Scholar] [CrossRef]
- Wenger, S.J.; Olden, J.D. Assessing transferability of ecological models: An underappreciated aspect of statistical validation. Methods Ecol. Evol. 2012, 3, 260–267. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Overfitting, model tuning, and evaluation of prediction performance. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer: Berlin/Heidelberg, Germany, 2022; pp. 109–139. [Google Scholar]
- Dwivedi, R.; Dave, D.; Naik, H.; Singhal, S.; Omer, R.; Patel, P.; Qian, B.; Wen, Z.; Shah, T.; Morgan, G. Explainable AI (XAI): Core ideas, techniques, and solutions. ACM Comput. Surv. 2023, 55, 194. [Google Scholar] [CrossRef]
- Al-Jarrah, O.Y.; Yoo, P.D.; Muhaidat, S.; Karagiannidis, G.K.; Taha, K. Efficient machine learning for big data: A review. Big Data Res. 2015, 2, 87–93. [Google Scholar] [CrossRef]
- Khan, I.; Ayaz, M. Sensitivity analysis-driven machine learning approach for groundwater quality prediction: Insights from integrating ENTROPY and CRITIC methods. Groundw. Sustain. Dev. 2024, 26, 101309. [Google Scholar] [CrossRef]
- Esmaeilbeiki, F.; Nikpour, M.R.; Singh, V.K.; Kisi, O.; Sihag, P.; Sanikhani, H. Exploring the application of soft computing techniques for spatial evaluation of groundwater quality variables. J. Clean. Prod. 2020, 276, 124206. [Google Scholar] [CrossRef]
- Kerketta, A.; Kapoor, H.S.; Sahoo, P.K. Groundwater fluoride prediction modeling using physicochemical parameters in Punjab, India: A machine-learning approach. Front. Soil Sci. 2024, 4, 1407502. [Google Scholar] [CrossRef]
- Boudibi, S.; Fadlaoui, H.; Hiouani, F.; Bouzidi, N.; Aissaoui, A.; Khomri, Z.-E. Groundwater salinity modeling and mapping using machine learning approaches: A case study in Sidi Okba region, Algeria. Environ. Sci. Pollut. Res. 2024, 31, 48955–48971. [Google Scholar] [CrossRef] [PubMed]
- Khiavi, A.N.; Tavoosi, M.; Kuriqi, A. Conjunct application of machine learning and game theory in groundwater quality mapping. Environ. Earth Sci. 2023, 82, 395. [Google Scholar] [CrossRef]
- Javidan, R.; Javidan, N. A novel artificial intelligence-based approach for mapping groundwater nitrate pollution in the Andimeshk-Dezful plain, Iran. Geocarto Int. 2022, 37, 10434–10458. [Google Scholar] [CrossRef]
- Tavakoli, M.; Motlagh, Z.K.; Sayadi, M.H.; Ibraheem, I.M.; Youssef, Y.M. Sustainable Groundwater management using machine learning-based DRASTIC model in rurbanizing riverine region: A case study of Kerman Province, Iran. Water 2024, 16, 2748. [Google Scholar] [CrossRef]
- Chahid, M.; El Messari, J.E.S.; Hilal, I.; Aqnouy, M. Application of the DRASTIC-LU/LC method combined with machine learning models to assess and predict the vulnerability of the Rmel aquifer (Northwest, Morocco). Groundw. Sustain. Dev. 2024, 27, 101345. [Google Scholar] [CrossRef]
- El-Rawy, M.; Wahba, M.; Fathi, H.; Alshehri, F.; Abdalla, F.; El Attar, R.M. Assessment of groundwater quality in arid regions utilizing principal component analysis, GIS, and machine learning techniques. Mar. Pollut. Bull. 2024, 205, 116645. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, X.; Sun, Y.; Yao, L.; Gan, L.; Wu, J.; Chen, S.; Li, J.; Wang, J. Enhanced groundwater vulnerability assessment to nitrate contamination in Chongqing, Southwest China: Integrating novel explainable machine learning algorithms with DRASTIC-LU. Hydrol. Res. 2024, 55, 663–682. [Google Scholar] [CrossRef]
- Bordbar, M.; Busico, G.; Sirna, M.; Tedesco, D.; Mastrocicco, M. A multi-step approach to evaluate the sustainable use of groundwater resources for human consumption and agriculture. J. Environ. Manag. 2023, 347, 119041. [Google Scholar] [CrossRef]
- Bakhtiarizadeh, A.; Najafzadeh, M.; Mohamadi, S. Enhancement of groundwater resources quality prediction by machine learning models on the basis of an improved DRASTIC method. Sci. Rep. 2024, 14, 29933. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, X.; Gan, L.; Chen, S.; Zhao, S.; Ding, J.; Kang, W.; Yang, H. Mapping specific groundwater nitrate concentrations from spatial data using machine learning: A case study of chongqing, China. Heliyon 2024, 10, e27867. [Google Scholar] [CrossRef]
- Sarkar, S.; Das, K.; Mukherjee, A. Groundwater salinity across India: Predicting occurrences and controls by field-observations and machine learning modeling. Environ. Sci. Technol. 2024, 58, 3953–3965. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.A.; Tsujimura, M.; Ha, N.T.; Van Binh, D.; Dang, T.D.; Doan, Q.-V.; Bui, D.T.; Ngoc, T.A.; Thuc, P.T.B.; Pham, T.D. Evaluating the predictive power of different machine learning algorithms for groundwater salinity prediction of multi-layer coastal aquifers in the Mekong Delta, Vietnam. Ecol. Indic. 2021, 127, 107790. [Google Scholar] [CrossRef]
- Huang, P.; Hou, M.; Sun, T.; Xu, H.; Ma, C.; Zhou, A. Sustainable groundwater management in coastal cities: Insights from groundwater potential and vulnerability using ensemble learning and knowledge-driven models. J. Clean. Prod. 2024, 442, 141152. [Google Scholar] [CrossRef]
- Aju, C.; Achu, A.; Mohammed, M.P.; Raicy, M.; Gopinath, G.; Reghunath, R. Groundwater quality prediction and risk assessment in Kerala, India: A machine-learning approach. J. Environ. Manag. 2024, 370, 122616. [Google Scholar] [CrossRef]
- Barzegar, R.; Razzagh, S.; Quilty, J.; Adamowski, J.; Pour, H.K.; Booij, M.J. Improving GALDIT-based groundwater vulnerability predictive mapping using coupled resampling algorithms and machine learning models. J. Hydrol. 2021, 598, 126370. [Google Scholar] [CrossRef]
- Tachi, S.E.; Bouguerra, H.; Djellal, M.; Benaroussi, O.; Belaroui, A.; Łozowski, B.; Augustyniak, M.; Benmamar, S.; Benziada, S.; Woźnica, A. Assessing the Risk of Groundwater Pollution in Northern Algeria through the Evaluation of Influencing Parameters and Ensemble Methods. In Doklady Earth Sciences; Pleiades Publishing: Moscow, Russia, 2023; pp. 1233–1243. [Google Scholar]
- Knoll, L.; Breuer, L.; Bach, M. Large scale prediction of groundwater nitrate concentrations from spatial data using machine learning. Sci. Total Environ. 2019, 668, 1317–1327. [Google Scholar] [CrossRef]
- Pal, S.C.; Ruidas, D.; Saha, A.; Islam, A.R.M.T.; Chowdhuri, I. Application of novel data-mining technique based nitrate concentration susceptibility prediction approach for coastal aquifers in India. J. Clean. Prod. 2022, 346, 131205. [Google Scholar] [CrossRef]
- Sun, X.; Cao, W.; Pan, D.; Li, Y.; Ren, Y.; Nan, T. Assessment of aquifer specific vulnerability to total nitrate contamination using ensemble learning and geochemical evidence. Sci. Total Environ. 2024, 912, 169497. [Google Scholar] [CrossRef]
- Bordbar, M.; Khosravi, K.; Murgulet, D.; Tsai, F.T.-C.; Golkarian, A. The use of hybrid machine learning models for improving the GALDIT model for coastal aquifer vulnerability mapping. Environ. Earth Sci. 2022, 81, 402. [Google Scholar] [CrossRef]
- Islam, A.R.M.T.; Pal, S.C.; Chowdhuri, I.; Salam, R.; Islam, M.S.; Rahman, M.M.; Zahid, A.; Idris, A.M. Application of novel framework approach for prediction of nitrate concentration susceptibility in coastal multi-aquifers, Bangladesh. Sci. Total Environ. 2021, 801, 149811. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Yan, Y.; Jing, H.; Baloch, M.Y.J.; Du, S.; Du, S. Large-scale groundwater pollution risk assessment research based on artificial intelligence technology: A case study of Shenyang City in Northeast China. Ecol. Indic. 2024, 169, 112915. [Google Scholar] [CrossRef]
- Gholami, V.; Booij, M. Use of machine learning and geographical information system to predict nitrate concentration in an unconfined aquifer in Iran. J. Clean. Prod. 2022, 360, 131847. [Google Scholar] [CrossRef]
- Kumar, S.; Pati, J. Machine learning approach for assessment of arsenic levels using physicochemical properties of water, soil, elevation, and land cover. Environ. Monit. Assess. 2023, 195, 641. [Google Scholar] [CrossRef]
- Karimanzira, D.; Weis, J.; Wunsch, A.; Ritzau, L.; Liesch, T.; Ohmer, M. Application of machine learning and deep neural networks for spatial prediction of groundwater nitrate concentration to improve land use management practices. Front. Water 2023, 5, 1193142. [Google Scholar] [CrossRef]
- Li, X.; Liang, G.; Wang, L.; Yang, Y.; Li, Y.; Li, Z.; He, B.; Wang, G. Identifying the spatial pattern and driving factors of nitrate in groundwater using a novel framework of interpretable stacking ensemble learning. Environ. Geochem. Health 2024, 46, 482. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, Z.; Fu, Y.; Zhao, L.; Ren, Y.; Nan, T.; Guo, H. Prediction of arsenic and fluoride in groundwater of the North China Plain using enhanced stacking ensemble learning. Water Res. 2024, 259, 121848. [Google Scholar] [CrossRef]
- Moazamnia, M.; Hassanzadeh, Y.; Nadiri, A.A.; Sadeghfam, S. Vulnerability indexing to saltwater intrusion from models at two levels using artificial intelligence multiple model (AIMM). J. Environ. Manag. 2020, 255, 109871. [Google Scholar] [CrossRef]
- Bordbar, M.; Neshat, A.; Javadi, S.; Pradhan, B.; Dixon, B.; Paryani, S. Improving the coastal aquifers’ vulnerability assessment using SCMAI ensemble of three machine learning approaches. Nat. Hazards 2022, 110, 1799–1820. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Deo, R.; Fijani, E.; Tziritis, E. Mapping groundwater contamination risk of multiple aquifers using multi-model ensemble of machine learning algorithms. Sci. Total Environ. 2018, 621, 697–712. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Baghban, H. A supervised committee machine artificial intelligent for improving DRASTIC method to assess groundwater contamination risk: A case study from Tabriz plain aquifer, Iran. Stoch. Environ. Res. Risk Assess. 2016, 30, 883–899. [Google Scholar] [CrossRef]
- Jafarzadeh, F.; Moghaddam, A.A.; Razzagh, S.; Barzegar, R.; Cloutier, V.; Rosa, E. A meta-ensemble machine learning strategy to assess groundwater holistic vulnerability in coastal aquifers. Groundw. Sustain. Dev. 2024, 26, 101296. [Google Scholar] [CrossRef]
- Usman, U.S.; Salh, Y.H.M.; Yan, B.; Namahoro, J.P.; Zeng, Q.; Sallah, I. Fluoride contamination in African groundwater: Predictive modeling using stacking ensemble techniques. Sci. Total Environ. 2024, 957, 177693. [Google Scholar] [CrossRef] [PubMed]
- Jamei, M.; Karbasi, M.; Malik, A.; Abualigah, L.; Islam, A.R.M.T.; Yaseen, Z.M. Computational assessment of groundwater salinity distribution within coastal multi-aquifers of Bangladesh. Sci. Rep. 2022, 12, 11165. [Google Scholar] [CrossRef]
- Elzain, H.E.; Chung, S.Y.; Park, K.-H.; Senapathi, V.; Sekar, S.; Sabarathinam, C.; Hassan, M. ANFIS-MOA models for the assessment of groundwater contamination vulnerability in a nitrate contaminated area. J. Environ. Manag. 2021, 286, 112162. [Google Scholar] [CrossRef]
- De Jesus, K.L.M.; Senoro, D.B.; Dela Cruz, J.C.; Chan, E.B. Neuro-particle swarm optimization based in-situ prediction model for heavy metals concentration in groundwater and surface water. Toxics 2022, 10, 95. [Google Scholar] [CrossRef]
- Pham, Q.B.; Tran, D.A.; Ha, N.T.; Islam, A.R.M.T.; Salam, R. Random forest and nature-inspired algorithms for mapping groundwater nitrate concentration in a coastal multi-layer aquifer system. J. Clean. Prod. 2022, 343, 130900. [Google Scholar] [CrossRef]
- Saha, A.; Pal, S.C.; Chowdhuri, I.; Roy, P.; Chakrabortty, R. Effect of hydrogeochemical behavior on groundwater resources in Holocene aquifers of moribund Ganges Delta, India: Infusing data-driven algorithms. Environ. Pollut. 2022, 314, 120203. [Google Scholar] [CrossRef]
- Wu, R.; Alvareda, E.M.; Polya, D.A.; Blanco, G.; Gamazo, P. Distribution of groundwater arsenic in Uruguay using hybrid machine learning and expert system approaches. Water 2021, 13, 527. [Google Scholar] [CrossRef]
- Wu, R.; Podgorski, J.; Berg, M.; Polya, D.A. Geostatistical model of the spatial distribution of arsenic in groundwaters in Gujarat State, India. Environ. Geochem. Health 2021, 43, 2649–2664. [Google Scholar] [CrossRef]
- Yang, N.; Winkel, L.H.; Johannesson, K.H. Predicting geogenic arsenic contamination in shallow groundwater of South Louisiana, United States. Environ. Sci. Technol. 2014, 48, 5660–5666. [Google Scholar] [CrossRef] [PubMed]
- Nourani, V.; Ghaffari, A.; Behfar, N.; Foroumandi, E.; Zeinali, A.; Ke, C.-Q.; Sankaran, A. Spatiotemporal assessment of groundwater quality and quantity using geostatistical and ensemble artificial intelligence tools. J. Environ. Manag. 2024, 355, 120495. [Google Scholar] [CrossRef] [PubMed]
- Taşan, S. Estimation of groundwater quality using an integration of water quality index, artificial intelligence methods and GIS: Case study, Central Mediterranean Region of Turkey. Appl. Water Sci. 2023, 13, 15. [Google Scholar] [CrossRef]
- Karandish, F.; Darzi-Naftchali, A.; Asgari, A. Application of machine-learning models for diagnosing health hazard of nitrate toxicity in shallow aquifers. Paddy Water Environ. 2017, 15, 201–215. [Google Scholar] [CrossRef]
- Gholami, V.; Khaleghi, M.; Pirasteh, S.; Booij, M.J. Comparison of self-organizing map, artificial neural network, and co-active neuro-fuzzy inference system methods in simulating groundwater quality: Geospatial artificial intelligence. Water Resour. Manag. 2022, 36, 451–469. [Google Scholar] [CrossRef]
- Sahour, S.; Khanbeyki, M.; Gholami, V.; Sahour, H.; Kahvazade, I.; Karimi, H. Evaluation of machine learning algorithms for groundwater quality modeling. Environ. Sci. Pollut. Res. 2023, 30, 46004–46021. [Google Scholar] [CrossRef]
- Chakraborty, M.; Sarkar, S.; Mukherjee, A.; Shamsudduha, M.; Ahmed, K.M.; Bhattacharya, A.; Mitra, A. Modeling regional-scale groundwater arsenic hazard in the transboundary Ganges River Delta, India and Bangladesh: Infusing physically-based model with machine learning. Sci. Total Environ. 2020, 748, 141107. [Google Scholar] [CrossRef]
- Alkindi, K.M.; Mukherjee, K.; Pandey, M.; Arora, A.; Janizadeh, S.; Pham, Q.B.; Anh, D.T.; Ahmadi, K. Prediction of groundwater nitrate concentration in a semiarid region using hybrid Bayesian artificial intelligence approaches. Environ. Sci. Pollut. Res. 2022, 29, 20421–20436. [Google Scholar] [CrossRef]
- Uddameri, V.; Silva, A.L.B.; Singaraju, S.; Mohammadi, G.; Hernandez, E.A. Tree-based modeling methods to predict nitrate exceedances in the Ogallala aquifer in Texas. Water 2020, 12, 1023. [Google Scholar] [CrossRef]
- Arabgol, R.; Sartaj, M.; Asghari, K. Predicting nitrate concentration and its spatial distribution in groundwater resources using support vector machines (SVMs) model. Environ. Model. Assess. 2016, 21, 71–82. [Google Scholar] [CrossRef]
- Rokhshad, A.M.; Khashei Siuki, A.; Yaghoobzadeh, M. Evaluation of a machine-based learning method to estimate the rate of nitrate penetration and groundwater contamination. Arab. J. Geosci. 2021, 14, 40. [Google Scholar] [CrossRef]
- Mishra, D.; Chakrabortty, R.; Sen, K.; Pal, S.C.; Mondal, N.K. Groundwater vulnerability assessment of elevated arsenic in Gangetic plain of West Bengal, India; Using primary information, lithological transport, state-of-the-art approaches. J. Contam. Hydrol. 2023, 256, 104195. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, M.A.; Kaya, F.; Mohamed, A.; Alarifi, S.S.; Abdelrady, A.; Keshavarzi, A.; Szabó, N.P.; Szűcs, P. Application of GIS-based machine learning algorithms for prediction of irrigational groundwater quality indices. Front. Earth Sci. 2023, 11, 1274142. [Google Scholar] [CrossRef]
- Mahboobi, H.; Shakiba, A.; Mirbagheri, B. Improving groundwater nitrate concentration prediction using local ensemble of machine learning models. J. Environ. Manag. 2023, 345, 118782. [Google Scholar] [CrossRef]
- Mousavi, M.; Qaderi, F.; Ahmadi, A. Spatial prediction of temporary and permanent hardness concentrations in groundwater based on chemistry parameters by artificial intelligence. Int. J. Environ. Sci. Technol. 2023, 20, 6665–6684. [Google Scholar] [CrossRef]
- Mirchooli, F.; Motevalli, A.; Pourghasemi, H.R.; Mohammadi, M.; Bhattacharya, P.; Maghsood, F.F.; Tiefenbacher, J.P. How do data-mining models consider arsenic contamination in sediments and variables importance? Environ. Monit. Assess. 2019, 191, 777. [Google Scholar] [CrossRef]
- Rafiei-Sardooi, E.; Azareh, A.; Ghazanfarpour, H.; Parteli, E.J.R.; Faryabi, M.; Barkhori, S. An integrated modeling framework for groundwater contamination risk assessment in arid, data-scarce environments. Acta Geophys. 2024, 73, 1865–1889. [Google Scholar] [CrossRef]
- Gharekhani, M.; Nadiri, A.A.; Khatibi, R.; Sadeghfam, S.; Moghaddam, A.A. A study of uncertainties in groundwater vulnerability modelling using Bayesian model averaging (BMA). J. Environ. Manag. 2022, 303, 114168. [Google Scholar] [CrossRef]
- Alizadeh, Z.; Mahjouri, N. A spatiotemporal Bayesian maximum entropy-based methodology for dealing with sparse data in revising groundwater quality monitoring networks: The Tehran region experience. Environ. Earth Sci. 2017, 76, 436. [Google Scholar] [CrossRef]
- Abba, S.; Yassin, M.A.; Jibril, M.M.; Tawabini, B.; Soupios, P.; Khogali, A.; Shah, S.M.H.; Usman, J.; Aljundi, I.H. Nitrate concentrations tracking from multi-aquifer groundwater vulnerability zones: Insight from machine learning and spatial mapping. Process Saf. Environ. Prot. 2024, 184, 1143–1157. [Google Scholar] [CrossRef]
- Shadrin, D.; Nikitin, A.; Tregubova, P.; Terekhova, V.; Jana, R.; Matveev, S.; Pukalchik, M. An automated approach to groundwater quality monitoring—Geospatial mapping based on combined application of Gaussian Process Regression and Bayesian Information Criterion. Water 2021, 13, 400. [Google Scholar] [CrossRef]
- Pal, S.C.; Islam, A.R.M.T.; Chakrabortty, R.; Islam, M.S.; Saha, A.; Shit, M. Application of data-mining technique and hydro-chemical data for evaluating vulnerability of groundwater in Indo-Gangetic Plain. J. Environ. Manag. 2022, 318, 115582. [Google Scholar]
- Mosavi, A.; Hosseini, F.S.; Choubin, B.; Abdolshahnejad, M.; Gharechaee, H.; Lahijanzadeh, A.; Dineva, A.A. Susceptibility prediction of groundwater hardness using ensemble machine learning models. Water 2020, 12, 2770. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Opitz, D.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Perović, M.; Šenk, I.; Tarjan, L.; Obradović, V.; Dimkić, M. Machine learning models for predicting the ammonium concentration in alluvial groundwaters. Environ. Model. Assess. 2021, 26, 187–203. [Google Scholar] [CrossRef]
- Nosair, A.M.; Shams, M.Y.; AbouElmagd, L.M.; Hassanein, A.E.; Fryar, A.E.; Abu Salem, H.S. Predictive model for progressive salinization in a coastal aquifer using artificial intelligence and hydrogeochemical techniques: A case study of the Nile Delta aquifer, Egypt. Environ. Sci. Pollut. Res. 2022, 29, 9318–9340. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Sedghi, Z.; Khatibi, R.; Gharekhani, M. Mapping vulnerability of multiple aquifers using multiple models and fuzzy logic to objectively derive model structures. Sci. Total Environ. 2017, 593, 75–90. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Gharekhani, M.; Khatibi, R.; Moghaddam, A.A. Assessment of groundwater vulnerability using supervised committee to combine fuzzy logic models. Environ. Sci. Pollut. Res. 2017, 24, 8562–8577. [Google Scholar] [CrossRef]
- Hamamin, D.F.; Nadiri, A.A. Supervised committee fuzzy logic model to assess groundwater intrinsic vulnerability in multiple aquifer systems. Arab. J. Geosci. 2018, 11, 176. [Google Scholar] [CrossRef]
- Sahour, S.; Khanbeyki, M.; Gholami, V.; Sahour, H.; Karimi, H.; Mohammadi, M. Particle swarm and grey wolf optimization: Enhancing groundwater quality models through artificial neural networks. Stoch. Environ. Res. Risk Assess. 2024, 38, 993–1007. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Antoniadis, A.; Lambert-Lacroix, S.; Poggi, J.-M. Random forests for global sensitivity analysis: A selective review. Reliab. Eng. Syst. Saf. 2021, 206, 107312. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Wu, L.; Li, J.; Wang, Y.; Meng, Q.; Qin, T.; Chen, W.; Zhang, M.; Liu, T.-Y. R-drop: Regularized dropout for neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 10890–10905. [Google Scholar]
- Molnar, C. Interpretable Machine Learning; Lulu. com: Durham, NC, USA, 2020. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Li, Q.; Liu, S.-Y.; Yang, X.-S. Influence of initialization on the performance of metaheuristic optimizers. Appl. Soft Comput. 2020, 91, 106193. [Google Scholar] [CrossRef]
- Malakar, P.; Balaprakash, P.; Vishwanath, V.; Morozov, V.; Kumaran, K. Benchmarking machine learning methods for performance modeling of scientific applications. In Proceedings of the 2018 IEEE/ACM Performance Modeling, Benchmarking and Simulation of High Performance Computer Systems (PMBS), Dallas, TX, USA, 12 November 2018; pp. 33–44. [Google Scholar]
- Akinola, S.O.; Oyabugbe, O.J. Accuracies and training times of data mining classification algorithms: An empirical comparative study. J. Softw. Eng. Appl. 2015, 8, 470–477. [Google Scholar] [CrossRef]
- Caruana, R.; Karampatziakis, N.; Yessenalina, A. An empirical evaluation of supervised learning in high dimensions. In Proceedings of the 25th international conference on Machine learning, Helsinki, Finland, 5–9 July 2008; pp. 96–103. [Google Scholar]
- Wang, P.; Fan, E.; Wang, P. Comparative analysis of image classification algorithms based on traditional machine learning and deep learning. Pattern Recognit. Lett. 2021, 141, 61–67. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Araya, D.; Podgorski, J.; Berg, M. Groundwater salinity in the Horn of Africa: Spatial prediction modeling and estimated people at risk. Environ. Int. 2023, 176, 107925. [Google Scholar] [CrossRef] [PubMed]
- Scorzato, L. Reliability and Interpretability in Science and Deep Learning. Minds Mach. 2024, 34, 27. [Google Scholar] [CrossRef]
- Berhanu, K.G.; Lohani, T.K.; Hatiye, S.D. Spatial and seasonal groundwater quality assessment for drinking suitability using index and machine learning approach. Heliyon 2024, 10, e30362. [Google Scholar] [CrossRef] [PubMed]
- Podgorski, J.; Kracht, O.; Araguas-Araguas, L.; Terzer-Wassmuth, S.; Miller, J.; Straub, R.; Kipfer, R.; Berg, M. Groundwater vulnerability to pollution in Africa’s Sahel region. Nat. Sustain. 2024, 7, 558–567. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Lun, Z.; Gu, Z.; Li, Z. Unveiling the beneficial effects of N2 as a CO2 impurity on fluid-rock reactions during carbon sequestration in carbonate reservoir aquifers: Challenging the notion of purer is always better. Environ. Sci. Technol. 2024, 58, 22980–22991. [Google Scholar] [CrossRef]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machine learning. ACM Comput. Surv. (CSUR) 2021, 54, 115. [Google Scholar] [CrossRef]
- Mehrabi, M.; Nalivan, O.A.; Scaioni, M.; Karvarinasab, M.; Kornejady, A.; Moayedi, H. Spatial mapping of gully erosion susceptibility using an efficient metaheuristic neural network. Environ. Earth Sci. 2023, 82, 459. [Google Scholar] [CrossRef]
- Mahanty, B.; Lhamo, P.; Sahoo, N.K. Inconsistency of PCA-based water quality index–Does it reflect the quality? Sci. Total Environ. 2023, 866, 161353. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the IJCAI, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1145. [Google Scholar]
- Agrawal, T. Hyperparameter Optimization in Machine Learning: Make Your Machine Learning and Deep Learning Models More Efficient; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Mosavi, A.; Hosseini, F.S.; Choubin, B.; Goodarzi, M.; Dineva, A.A. Groundwater salinity susceptibility mapping using classifier ensemble and Bayesian machine learning models. IEEE Access 2020, 8, 145564–145576. [Google Scholar] [CrossRef]
- Sze, V.; Chen, Y.-H.; Yang, T.-J.; Emer, J.S. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Christin, S.; Hervet, É.; Lecomte, N. Applications for deep learning in ecology. Methods Ecol. Evol. 2019, 10, 1632–1644. [Google Scholar] [CrossRef]
- Sivakumar, M.; Parthasarathy, S.; Padmapriya, T. A simplified approach for efficiency analysis of machine learning algorithms. PeerJ Comput. Sci. 2024, 10, e2418. [Google Scholar] [CrossRef] [PubMed]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Kuha, J. AIC and BIC: Comparisons of assumptions and performance. Sociol. Methods Res. 2004, 33, 188–229. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Ding, J. Information criteria for model selection. Wiley Interdiscip. Rev. Comput. Stat. 2023, 15, e1607. [Google Scholar] [CrossRef]
- Yates, L.A.; Aandahl, Z.; Richards, S.A.; Brook, B.W. Cross validation for model selection: A review with examples from ecology. Ecol. Monogr. 2023, 93, e1557. [Google Scholar] [CrossRef]
- Ying, X. An overview of overfitting and its solutions. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; p. 022022. [Google Scholar]
- Rice, L.; Wong, E.; Kolter, Z. Overfitting in adversarially robust deep learning. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 8093–8104. [Google Scholar]
- Jabbar, H.; Khan, R.Z. Methods to avoid over-fitting and under-fitting in supervised machine learning (comparative study). Comput. Sci. Commun. Instrum. Devices 2015, 70, 978–981. [Google Scholar]
- Qi, S.; He, M.; Hoang, R.; Zhou, Y.; Namadi, P.; Tom, B.; Sandhu, P.; Bai, Z.; Chung, F.; Ding, Z. Salinity modeling using deep learning with data augmentation and transfer learning. Water 2023, 15, 2482. [Google Scholar] [CrossRef]
- Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), Virtual, 13–18 July 2018; pp. 80–89. [Google Scholar]
- Holm, E.A. In defense of the black box. Science 2019, 364, 26–27. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Uszkoreit, H.; Du, Y.; Fan, W.; Zhao, D.; Zhu, J. Explainable AI: A brief survey on history, research areas, approaches and challenges. In Proceedings of the Natural Language Processing and Chinese Computing: 8th CCF International Conference, NLPCC 2019, Dunhuang, China, 9–14 October 2019; pp. 563–574. [Google Scholar]
- Saha, S.; Roy, J.; Hembram, T.K.; Pradhan, B.; Dikshit, A.; Abdul Maulud, K.N.; Alamri, A.M. Comparison between deep learning and tree-based machine learning approaches for landslide susceptibility mapping. Water 2021, 13, 2664. [Google Scholar] [CrossRef]
- Costache, R.; Arabameri, A.; Blaschke, T.; Pham, Q.B.; Pham, B.T.; Pandey, M.; Arora, A.; Linh, N.T.T.; Costache, I. Flash-flood potential mapping using deep learning, alternating decision trees and data provided by remote sensing sensors. Sensors 2021, 21, 280. [Google Scholar] [CrossRef] [PubMed]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-metaheuristic ensembles for spatial assessment of forest fire susceptibility. J. Environ. Manag. 2020, 260, 109867. [Google Scholar] [CrossRef]
- Asadi Nalivan, O.; Mousavi Tayebi, S.A.; Mehrabi, M.; Ghasemieh, H.; Scaioni, M. A hybrid intelligent model for spatial analysis of groundwater potential around Urmia Lake, Iran. Stoch. Environ. Res. Risk Assess. 2023, 37, 1821–1838. [Google Scholar] [CrossRef]
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Cantarino, I.; Carrion, M.A.; Goerlich, F.; Martinez Ibañez, V. A ROC analysis-based classification method for landslide susceptibility maps. Landslides 2019, 16, 265–282. [Google Scholar] [CrossRef]
- Wu, R.; Polya, D.A. Objective cost-informed cutoff criteria improve the utility of machine learning models of environmental hazards: A case study of groundwater arsenic distribution in India. Expo. Health 2024, 16, 619–631. [Google Scholar] [CrossRef]
- Bramm, A.M.; Matrenin, P.V.; Khalyasmaa, A.I. A Review of XAI Methods Applications in Forecasting Runoff and Water Level Hydrological Tasks. Mathematics 2025, 13, 2830. [Google Scholar] [CrossRef]
- Schuster, G.T.; Chen, Y.; Feng, S. Review of physics-informed machine-learning inversion of geophysical data. Geophysics 2024, 89, T337–T356. [Google Scholar] [CrossRef]
- Bhasme, P.; Vagadiya, J.; Bhatia, U. Enhancing predictive skills in physically-consistent way: Physics informed machine learning for hydrological processes. J. Hydrol. 2022, 615, 128618. [Google Scholar] [CrossRef]
- Jayaraman, P.; Nagarajan, K.K.; Partheeban, P.; Krishnamurthy, V. Critical review on water quality analysis using IoT and machine learning models. Int. J. Inf. Manag. Data Insights 2024, 4, 100210. [Google Scholar] [CrossRef]
- Singh, Y.; Walingo, T. Smart water quality monitoring with IOT wireless sensor networks. Sensors 2024, 24, 2871. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 12. [Google Scholar] [CrossRef]
- Chang, F.-J.; Kao, L.-s.; Kuo, Y.-M.; Liu, C.-W. Artificial neural networks for estimating regional arsenic concentrations in a blackfoot disease area in Taiwan. J. Hydrol. 2010, 388, 65–76. [Google Scholar] [CrossRef]
- Al-Mahallawi, K.; Mania, J.; Hani, A.; Shahrour, I. Using of neural networks for the prediction of nitrate groundwater contamination in rural and agricultural areas. Environ. Earth Sci. 2012, 65, 917–928. [Google Scholar] [CrossRef]
- Nourani, V.; Alami, M.T.; Vousoughi, F.D. Self-organizing map clustering technique for ANN-based spatiotemporal modeling of groundwater quality parameters. J. Hydroinform. 2016, 18, 288–309. [Google Scholar] [CrossRef]
- Baghapour, M.A.; Fadaei Nobandegani, A.; Talebbeydokhti, N.; Bagherzadeh, S.; Nadiri, A.A.; Gharekhani, M.; Chitsazan, N. Optimization of DRASTIC method by artificial neural network, nitrate vulnerability index, and composite DRASTIC models to assess groundwater vulnerability for unconfined aquifer of Shiraz Plain, Iran. J. Environ. Health Sci. Eng. 2016, 14, 13. [Google Scholar] [CrossRef]
- Wagh, V.; Panaskar, D.; Muley, A.; Mukate, S.; Gaikwad, S. Neural network modelling for nitrate concentration in groundwater of Kadava River basin, Nashik, Maharashtra, India. Groundw. Sustain. Dev. 2018, 7, 436–445. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Sedghi, Z.; Khatibi, R.; Sadeghfam, S. Mapping specific vulnerability of multiple confined and unconfined aquifers by using artificial intelligence to learn from multiple DRASTIC frameworks. J. Environ. Manag. 2018, 227, 415–428. [Google Scholar] [CrossRef]
- Jang, W.S.; Engel, B.; Yeum, C.M. Integrated environmental modeling for efficient aquifer vulnerability assessment using machine learning. Environ. Model. Softw. 2020, 124, 104602. [Google Scholar] [CrossRef]
- Elzain, H.E.; Chung, S.Y.; Senapathi, V.; Sekar, S.; Park, N.; Mahmoud, A.A. Modeling of aquifer vulnerability index using deep learning neural networks coupling with optimization algorithms. Environ. Sci. Pollut. Res. 2021, 28, 57030–57045. [Google Scholar] [CrossRef]
- Roostaei, J.; Colley, S.; Mulhern, R.; May, A.A.; Gibson, J.M. Predicting the risk of GenX contamination in private well water using a machine-learned Bayesian network model. J. Hazard. Mater. 2021, 411, 125075. [Google Scholar] [CrossRef]
- Elzain, H.E.; Chung, S.Y.; Senapathi, V.; Sekar, S.; Lee, S.Y.; Roy, P.D.; Hassan, A.; Sabarathinam, C. Comparative study of machine learning models for evaluating groundwater vulnerability to nitrate contamination. Ecotoxicol. Environ. Saf. 2022, 229, 113061. [Google Scholar] [CrossRef] [PubMed]
- Nadiri, A.A.; Moazamnia, M.; Sadeghfam, S.; Gnanachandrasamy, G.; Venkatramanan, S. Formulating Convolutional Neural Network for mapping total aquifer vulnerability to pollution. Environ. Pollut. 2022, 304, 119208. [Google Scholar] [CrossRef] [PubMed]
- Ijlil, S.; Essahlaoui, A.; Mohajane, M.; Essahlaoui, N.; Mili, E.M.; Van Rompaey, A. Machine learning algorithms for modeling and mapping of groundwater pollution risk: A study to reach water security and sustainable development (Sdg) goals in a mediterranean aquifer system. Remote Sens. 2022, 14, 2379. [Google Scholar] [CrossRef]
- Ruidas, D.; Pal, S.C.; Saha, A.; Chowdhuri, I.; Shit, M. Hydrogeochemical characterization based water resources vulnerability assessment in India’s first Ramsar site of Chilka lake. Mar. Pollut. Bull. 2022, 184, 114107. [Google Scholar] [CrossRef] [PubMed]
- Nadiri, A.A.; Barzegar, R.; Sadeghfam, S.; Rostami, A.A. Developing a Data-Fused Water Quality Index Based on Artificial Intelligence Models to Mitigate Conflicts between GQI and GWQI. Water 2022, 14, 3185. [Google Scholar] [CrossRef]
- Akakuru, O.C.; Akaolisa, C.C.Z.; Aigbadon, G.O.; Eyankware, M.O.; Opara, A.I.; Obasi, P.N.; Ofoh, I.J.; Njoku, A.O.; Akudinobi, B.E.B. Integrating machine learning and multi-linear regression modeling approaches in groundwater quality assessment around Obosi, SE Nigeria. Environ. Dev. Sustain. 2023, 25, 14567–14606. [Google Scholar] [CrossRef]
- Gani, A.; Singh, M.; Pathak, S.; Hussain, A. Groundwater quality index development using the ANN model of Delhi Metropolitan City, India. Environ. Sci. Pollut. Res. 2023, 32, 7269–7284. [Google Scholar] [CrossRef]
- El Yousfi, Y.; Himi, M.; El Ouarghi, H.; Aqnouy, M.; Benyoussef, S.; Gueddari, H.; Ait Hmeid, H.; Alitane, A.; Chaibi, M.; Zahid, M. Assessment and Prediction of the Water Quality Index for the Groundwater of the Ghiss-Nekkor (Al Hoceima, Northeastern Morocco). Sustainability 2022, 15, 402. [Google Scholar] [CrossRef]
- Smida, H.; Tarki, M.; Gammoudi, N.; Dassi, L. GIS-based multicriteria and artificial neural network (ANN) investigation for the assessment of groundwater vulnerability and pollution hazard in the Braga shallow aquifer (Central Tunisia): A critical review of generic and modified DRASTIC models. J. Contam. Hydrol. 2023, 259, 104245. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Bordbar, M.; Nikoo, M.R.; Silabi, L.S.S.; Senapathi, V.; Xiao, Y. Assessing vulnerability of coastal aquifer to seawater intrusion using Convolutional Neural Network. Mar. Pollut. Bull. 2023, 197, 115669. [Google Scholar] [CrossRef]
- Ahn, S.H.; Jeong, D.H.; Kim, M.; Lee, T.K.; Kim, H.-K. Prediction of groundwater quality index to assess suitability for drinking purpose using averaged neural network and geospatial analysis. Ecotoxicol. Environ. Saf. 2023, 265, 115485. [Google Scholar] [CrossRef] [PubMed]
- Gaagai, A.; Aouissi, H.A.; Bencedira, S.; Hinge, G.; Athamena, A.; Heddam, S.; Gad, M.; Elsherbiny, O.; Elsayed, S.; Eid, M.H. Application of water quality indices, machine learning approaches, and GIS to identify groundwater quality for irrigation purposes: A case study of Sahara Aquifer, Doucen Plain, Algeria. Water 2023, 15, 289. [Google Scholar] [CrossRef]
- Sajib, A.M.; Diganta, M.T.M.; Rahman, A.; Dabrowski, T.; Olbert, A.I.; Uddin, M.G. Developing a novel tool for assessing the groundwater incorporating water quality index and machine learning approach. Groundw. Sustain. Dev. 2023, 23, 101049. [Google Scholar] [CrossRef]
- Mohammed, M.; Mohamed, A.; Szabó, N.; Szűcs, P. Development of machine-learning-based models for identifying the sources of nitrate and fluoride in groundwater and predicting their human health risks. Int. J. Energy Water Resour. 2023, 8, 161–180. [Google Scholar] [CrossRef]
- Anjum, R.; Ali, S.A.; Siddiqui, M.A. Assessing the impact of land cover on groundwater quality in a smart city using gis and machine learning algorithms. Water Air Soil Pollut. 2023, 234, 182. [Google Scholar] [CrossRef]
- Omeka, M.E. Evaluation and prediction of irrigation water quality of an agricultural district, SE Nigeria: An integrated heuristic GIS-based and machine learning approach. Environ. Sci. Pollut. Res. 2023, 31, 54178–54203. [Google Scholar] [CrossRef]
- Dhaoui, O.; Antunes, I.M.; Benhenda, I.; Agoubi, B.; Kharroubi, A. Groundwater salinization risk assessment using combined artificial intelligence models. Environ. Sci. Pollut. Res. 2024, 31, 33398–33413. [Google Scholar] [CrossRef]
- Thanh, N.N.; Chotpantarat, S.; Ngu, N.H.; Thunyawatcharakul, P.; Kaewdum, N. Integrating machine learning models with cross-validation and bootstrapping for evaluating groundwater quality in Kanchanaburi province, Thailand. Environ. Res. 2024, 252, 118952. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, L.; Pan, H.; Li, Y.; Shao, Y.; Li, J.; Xie, X. Spatio-temporal prediction of groundwater vulnerability based on CNN-LSTM model with self-attention mechanism: A case study in Hetao Plain, northern China. J. Environ. Sci. 2024, 153, 128–142. [Google Scholar] [CrossRef]
- Dasgupta, R.; Banerjee, G.; Hidayetullah, S.M.; Saha, N.; Das, S.; Mazumdar, A. A comparative analysis of statistical, MCDM and machine learning based modification strategies to reduce subjective errors of DRASTIC models. Environ. Earth Sci. 2024, 83, 211. [Google Scholar] [CrossRef]
- Bordbar, M.; Heggy, E.; Jun, C.; Bateni, S.M.; Kim, D.; Moghaddam, H.K.; Rezaie, F. Comparative study for coastal aquifer vulnerability assessment using deep learning and metaheuristic algorithms. Environ. Sci. Pollut. Res. 2024, 31, 24235–24249. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Keshtkar, M.; Samaei, M.R.; Isazadeh, S.; Khaneghah, A.M. Assessing water quality index and health risk using deterministic and probabilistic approaches in Darab County, Iran; A machine learning for fluoride prediction. Chemosphere 2024, 352, 141284. [Google Scholar] [CrossRef]
- Gholami, V.; Sahour, H.; Khaleghi, M.R.; Ghajari, Y.E.; Sahour, S. Combining artificial neural networks and genetic algorithms to model nitrate contamination in groundwater. Nat. Hazards 2024, 120, 4789–4809. [Google Scholar] [CrossRef]
- Iqbal, J.; Su, C.; Ahmad, M.; Baloch, M.Y.J.; Rashid, A.; Ullah, Z.; Abbas, H.; Nigar, A.; Ali, A.; Ullah, A. Hydrogeochemistry and prediction of arsenic contamination in groundwater of Vehari, Pakistan: Comparison of artificial neural network, random forest and logistic regression models. Environ. Geochem. Health 2024, 46, 14. [Google Scholar] [CrossRef]
- Tian, L.; Hu, L.; Wang, D.; Cao, X. Site-scale groundwater pollution risk assessment using surrogate models and statistical analysis. J. Contam. Hydrol. 2024, 261, 104288. [Google Scholar] [CrossRef]
- Das, C.R.; Das, S. Coastal groundwater quality prediction using objective-weighted WQI and machine learning approach. Environ. Sci. Pollut. Res. 2024, 31, 19439–19457. [Google Scholar] [CrossRef]
- Sakizadeh, M.; Zhang, C.; Milewski, A. Spatial distribution pattern and health risk of groundwater contamination by cadmium, manganese, lead and nitrate in groundwater of an arid area. Environ. Geochem. Health 2024, 46, 80. [Google Scholar] [CrossRef]
- Eid, M.H.; Mikita, V.; Eissa, M.; Ramadan, H.S.; Mohamed, E.A.; Abukhadra, M.R.; El-Sherbeeny, A.M.; Kovács, A.; Szűcs, P. An advanced approach for drinking water quality indexing and health risk assessment supported by machine learning modelling in Siwa Oasis, Egypt. J. Hydrol. Reg. Stud. 2024, 56, 101967. [Google Scholar] [CrossRef]
- Jacob, C.; Masilamani, U.S. Performance evaluation of different machine learning algorithms for prediction of nitrate in groundwater in Thiruvannamalai District. CLEAN–Soil Air Water 2025, 43, 2400060. [Google Scholar] [CrossRef]
- Khan, I.; Umar, R. Machine Learning-driven Optimization of Water Quality Index: A Synergistic ENTROPY-CRITIC Approach Using Spatio-Temporal Data. Earth Syst. Environ. 2024, 8, 1453–1475. [Google Scholar] [CrossRef]
- Gad, M.; Gaagai, A.; Agrama, A.A.; El-Fiqy, W.F.; Eid, M.H.; Szűcs, P.; Elsayed, S.; Elsherbiny, O.; Khadr, M.; Abukhadra, M.R. Comprehensive evaluation and prediction of groundwater quality and risk indices using quantitative approaches, multivariate analysis, and machine learning models: An exploratory study. Heliyon 2024, 10, e36606. [Google Scholar] [CrossRef]
- Saha, A.; Pal, S.C.; Islam, A.R.M.T.; Islam, A.; Alam, E.; Islam, M.K. Hydro-chemical based assessment of groundwater vulnerability in the Holocene multi-aquifers of Ganges delta. Sci. Rep. 2024, 14, 1265. [Google Scholar] [CrossRef]
- Egbueri, J.C.; Abu, M.; Agbasi, J.C. An integrated appraisal of the hydrogeochemistry and the potential public health risks of groundwater nitrate and fluoride in eastern Ghana. Groundw. Sustain. Dev. 2024, 26, 101264. [Google Scholar] [CrossRef]
- Best, K.B.; Miro, M.E.; Kirpes, R.M.; Kaynar, N.; Chesler, A.N. Data-driven decision support tools for assessing the vulnerability of community water systems to groundwater contamination in Los Angeles County. Environ. Sci. Policy 2021, 124, 393–400. [Google Scholar] [CrossRef]
- Nolan, B.T.; Malone, R.W.; Gronberg, J.A.; Thorp, K.R.; Ma, L. Verifiable metamodels for nitrate losses to drains and groundwater in the Corn Belt, USA. Environ. Sci. Technol. 2012, 46, 901–908. [Google Scholar] [CrossRef]
- Gholami, V.; Khaleghi, M.; Sebghati, M. A method of groundwater quality assessment based on fuzzy network-CANFIS and geographic information system (GIS). Appl. Water Sci. 2017, 7, 3633–3647. [Google Scholar] [CrossRef]
- Jebastina, N.; Prince Arulraj, G. Spatial prediction of nitrate concentration using GIS and ANFIS modelling in groundwater. Bull. Environ. Contam. Toxicol. 2018, 101, 403–409. [Google Scholar] [CrossRef]
- Asghari Moghaddam, A.; Nouri Sangarab, S.; Kadkhodaie Ilkhchi, A. Assessing groundwater vulnerability potential using modified DRASTIC in Ajabshir Plain, NW of Iran. Environ. Monit. Assess. 2023, 195, 497. [Google Scholar] [CrossRef]
- Amini, M.; Abbaspour, K.C.; Berg, M.; Winkel, L.; Hug, S.J.; Hoehn, E.; Yang, H.; Johnson, C.A. Statistical modeling of global geogenic arsenic contamination in groundwater. Environ. Sci. Technol. 2008, 42, 3669–3675. [Google Scholar] [CrossRef]
- Amini, M.; Mueller, K.; Abbaspour, K.C.; Rosenberg, T.; Afyuni, M.; Møller, K.N.; Sarr, M.; Johnson, C.A. Statistical modeling of global geogenic fluoride contamination in groundwaters. Environ. Sci. Technol. 2008, 42, 3662–3668. [Google Scholar] [CrossRef]
- Bindal, S.; Singh, C.K. Predicting groundwater arsenic contamination: Regions at risk in highest populated state of India. Water Res. 2019, 159, 65–76. [Google Scholar] [CrossRef]
- Wheeler, D.C.; Nolan, B.T.; Flory, A.R.; DellaValle, C.T.; Ward, M.H. Modeling groundwater nitrate concentrations in private wells in Iowa. Sci. Total Environ. 2015, 536, 481–488. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Luque-Espinar, J.A.; Chica-Olmo, M.; Mendes, M.P. Feature selection approaches for predictive modelling of groundwater nitrate pollution: An evaluation of filters, embedded and wrapper methods. Sci. Total Environ. 2018, 624, 661–672. [Google Scholar] [CrossRef]
- Khosravi, K.; Sartaj, M.; Tsai, F.T.-C.; Singh, V.P.; Kazakis, N.; Melesse, A.M.; Prakash, I.; Bui, D.T.; Pham, B.T. A comparison study of DRASTIC methods with various objective methods for groundwater vulnerability assessment. Sci. Total Environ. 2018, 642, 1032–1049. [Google Scholar] [CrossRef]
- Adnan, S.; Iqbal, J.; Maltamo, M.; Bacha, M.S.; Shahab, A.; Valbuena, R. A simple approach of groundwater quality analysis, classification, and mapping in Peshawar, Pakistan. Environments 2019, 6, 123. [Google Scholar] [CrossRef]
- Podgorski, J.; Wu, R.; Chakravorty, B.; Polya, D.A. Groundwater arsenic distribution in India by machine learning geospatial modeling. Int. J. Environ. Res. Public Health 2020, 17, 7119. [Google Scholar] [CrossRef] [PubMed]
- Norouzi, H.; Moghaddam, A.A. Groundwater quality assessment using random forest method based on groundwater quality indices (case study: Miandoab plain aquifer, NW of Iran). Arab. J. Geosci. 2020, 13, 912. [Google Scholar] [CrossRef]
- Lahjouj, A.; El Hmaidi, A.; Bouhafa, K.; Boufala, M.h. Mapping specific groundwater vulnerability to nitrate using random forest: Case of Sais basin, Morocco. Model. Earth Syst. Environ. 2020, 6, 1451–1466. [Google Scholar] [CrossRef]
- Chakrabortty, R.; Roy, P.; Chowdhuri, I.; Pal, S.C. Groundwater vulnerability assessment using random forest approach in a water-stressed paddy cultivated region of West Bengal, India. Groundw. Geochem. Pollut. Remediat. Methods 2021, 392–410. [Google Scholar] [CrossRef]
- Norouzi, H.; Moghaddam, A.A.; Celico, F.; Shiri, J. Assessment of groundwater vulnerability using genetic algorithm and random forest methods (case study: Miandoab plain, NW of Iran). Environ. Sci. Pollut. Res. 2021, 28, 39598–39613. [Google Scholar] [CrossRef]
- Cardenas-Martinez, A.; Rodriguez-Galiano, V.; Luque-Espinar, J.A.; Mendes, M.P. Predictive modelling benchmark of nitrate Vulnerable Zones at a regional scale based on Machine learning and remote sensing. J. Hydrol. 2021, 603, 127092. [Google Scholar] [CrossRef]
- Khan, Q.; Liaqat, M.U.; Mohamed, M.M. A comparative assessment of modeling groundwater vulnerability using DRASTIC method from GIS and a novel classification method using machine learning classifiers. Geocarto Int. 2022, 37, 5832–5850. [Google Scholar] [CrossRef]
- Sarkar, S.; Mukherjee, A.; Gupta, S.D.; Bhanja, S.N.; Bhattacharya, A. Predicting regional-scale elevated groundwater nitrate contamination risk using machine learning on natural and human-induced factors. Acs EsT Eng. 2022, 2, 689–702. [Google Scholar] [CrossRef]
- Judeh, T.; Almasri, M.N.; Shadeed, S.M.; Bian, H.; Shahrour, I. Use of GIS, statistics and machine learning for groundwater quality management: Application to nitrate contamination. Water Resour. 2022, 49, 503–514. [Google Scholar] [CrossRef]
- Sarkar, S.; Mukherjee, A.; Senapati, B.; Duttagupta, S. Predicting potential climate change impacts on groundwater nitrate pollution and risk in an intensely cultivated area of South Asia. ACS Environ. Au 2022, 2, 556–576. [Google Scholar] [CrossRef]
- Singha, S.S.; Singha, S.; Pasupuleti, S.; Venkatesh, A. Knowledge-driven and machine learning decision tree-based approach for assessment of geospatial variation of groundwater quality around coal mining regions, Korba district, Central India. Environ. Earth Sci. 2022, 81, 36. [Google Scholar] [CrossRef]
- Islam, A.R.M.T.; Pal, S.C.; Chakrabortty, R.; Idris, A.M.; Salam, R.; Islam, M.S.; Zahid, A.; Shahid, S.; Ismail, Z.B. A coupled novel framework for assessing vulnerability of water resources using hydrochemical analysis and data-driven models. J. Clean. Prod. 2022, 336, 130407. [Google Scholar] [CrossRef]
- He, S.; Wu, J.; Wang, D.; He, X. Predictive modeling of groundwater nitrate pollution and evaluating its main impact factors using random forest. Chemosphere 2022, 290, 133388. [Google Scholar] [CrossRef]
- Aind, D.A.; Malakar, P.; Sarkar, S.; Mukherjee, A. Controls on groundwater fluoride contamination in eastern parts of India: Insights from Unsaturated zone fluoride profiles and AI-based modeling. Water 2022, 14, 3220. [Google Scholar] [CrossRef]
- Madani, A.; Hagage, M.; Elbeih, S.F. Random Forest and Logistic Regression algorithms for prediction of groundwater contamination using ammonia concentration. Arab. J. Geosci. 2022, 15, 1619. [Google Scholar] [CrossRef]
- Biswas, T.; Pal, S.C.; Chowdhuri, I.; Ruidas, D.; Saha, A.; Islam, A.R.M.T.; Shit, M. Effects of elevated arsenic and nitrate concentrations on groundwater resources in deltaic region of Sundarban Ramsar site, Indo-Bangladesh region. Mar. Pollut. Bull. 2023, 188, 114618. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Niknam, A.R.R.; Barzkar, A.; Niazkar, M.; Zare Mehrjerdi, Y.; Abedi, M.J.; Heydari Pour, M. Water quality index estimations using machine learning algorithms: A case study of Yazd-Ardakan Plain, Iran. Water 2023, 15, 1876. [Google Scholar] [CrossRef]
- Elzain, H.E.; Chung, S.Y.; Venkatramanan, S.; Selvam, S.; Ahemd, H.A.; Seo, Y.K.; Bhuyan, M.S.; Yassin, M.A. Novel machine learning algorithms to predict the groundwater vulnerability index to nitrate pollution at two levels of modeling. Chemosphere 2023, 314, 137671. [Google Scholar] [CrossRef]
- Motlagh, Z.K.; Derakhshani, R.; Sayadi, M.H. Groundwater vulnerability assessment in central Iran: Integration of GIS-based DRASTIC model and a machine learning approach. Groundw. Sustain. Dev. 2023, 23, 101037. [Google Scholar] [CrossRef]
- Thanh, N.N.; Chotpantarat, S.; Ha, N.-T.; Trung, N.H. Determination of conditioning factors for mapping nickel contamination susceptibility in groundwater in Kanchanaburi Province, Thailand, using random forest and maximum entropy. Environ. Geochem. Health 2023, 45, 4583–4602. [Google Scholar] [CrossRef]
- Wu, R.; Richards, L.A.; Roshan, A.; Polya, D.A. Artificial Intelligence Modelling to Support the Groundwater Chemistry-Dependent Selection of Groundwater Arsenic Remediation Approaches in Bangladesh. Water 2023, 15, 3539. [Google Scholar] [CrossRef]
- Subbarayan, S.; Thiyagarajan, S.; Karuppannan, S.; Panneerselvam, B. Enhancing groundwater vulnerability assessment: Comparative study of three machine learning models and five classification schemes for Cuddalore district. Environ. Res. 2024, 242, 117769. [Google Scholar] [CrossRef]
- Chu, Y.; He, B.; He, J.; Zou, H.; Sun, J.; Wen, D. Revealing the drivers and genesis of NO3-N pollution classification in shallow groundwater of the Shaying River Basin by explainable machine learning and pathway analysis method. Sci. Total Environ. 2024, 918, 170742. [Google Scholar] [CrossRef]
- Chen, K.; Liu, Q.; Yang, T.; Ju, Q.; Zhu, M. Risk assessment of nitrate groundwater contamination using GIS-based machine learning methods: A case study in the northern Anhui plain, China. J. Contam. Hydrol. 2024, 261, 104300. [Google Scholar] [CrossRef] [PubMed]
- Apogba, J.N.; Anornu, G.K.; Koon, A.B.; Dekongmen, B.W.; Sunkari, E.D.; Fynn, O.F.; Kpiebaya, P. Application of machine learning techniques to predict groundwater quality in the Nabogo Basin, Northern Ghana. Heliyon 2024, 10, e28527. [Google Scholar] [CrossRef] [PubMed]
- Elzain, H.E.; Abdalla, O.; Ahmed, H.A.; Kacimov, A.; Al-Maktoumi, A.; Al-Higgi, K.; Abdallah, M.; Yassin, M.A.; Senapathi, V. An innovative approach for predicting groundwater TDS using optimized ensemble machine learning algorithms at two levels of modeling strategy. J. Environ. Manag. 2024, 351, 119896. [Google Scholar] [CrossRef]
- Raj, A.; Sinha, A.; Singh, A.; Pasupuleti, S. Assessment and prediction of hexavalent chromium vulnerability in groundwater by Geochemical modelling, NOBLES Index and Random Forest Model. Sci. Total Environ. 2024, 906, 167570. [Google Scholar]
- Saha, A.; Pal, S.C. Modelling groundwater vulnerability in a vulnerable deltaic coastal region of Sundarban Biosphere Reserve, India. Environ. Geochem. Health 2024, 46, 8. [Google Scholar] [CrossRef]
- Khusulio, K.; Sharma, N.R.; Das, I.C.; Setia, R.; Pathak, A.; Kumar, R. Hydrochemical assessment of groundwater with special emphasis on fluoride in parts of Punjab and fluoride prediction using GIS and ML. Environ. Earth Sci. 2024, 83, 570. [Google Scholar] [CrossRef]
- Gómez-Escalonilla, V.; Martínez-Santos, P. A Machine Learning Approach to Map the Vulnerability of Groundwater Resources to Agricultural Contamination. Hydrology 2024, 11, 153. [Google Scholar] [CrossRef]
- Gómez-Escalonilla, V.; Montero-González, E.; Díaz-Alcaide, S.; Martín-Loeches, M.; del Rosario, M.R.; Martínez-Santos, P. A machine learning approach to site groundwater contamination monitoring wells. Appl. Water Sci. 2024, 14, 250. [Google Scholar] [CrossRef]
- Arafa, N.A.; El-Said Salem, Z.; Abdeldayem, A.L.; Ghorab, M.A.; Moustafa, Y.M.; Soliman, S.A.; Farag, M.H.; Purohit, S.; Elhag, M.; Youssef, Y.M. Advancing Deltaic Aquifer Vulnerability Mapping to Seawater Intrusion and Human Impacts in Eastern Nile Delta: Insights from Machine Learning and Hydrochemical Perspective. Earth Syst. Environ. 2024, 9, 2481–2506. [Google Scholar] [CrossRef]
- Nandi, R.; Mondal, S.; Mandal, J.; Bhattacharyya, P. From fuzzy-TOPSIS to machine learning: A holistic approach to understanding groundwater fluoride contamination. Sci. Total Environ. 2024, 912, 169323. [Google Scholar] [CrossRef] [PubMed]
- Jalali, R.; Tishehzan, P.; Hashemi, H. A machine learning framework for spatio-temporal vulnerability mapping of groundwaters to nitrate in a data scarce region in Lenjanat Plain, Iran. Environ. Sci. Pollut. Res. 2024, 31, 42088–42110. [Google Scholar] [CrossRef]
- Raisa, S.S.; Sarkar, S.K.; Sadiq, M.A. Advancing groundwater vulnerability assessment in Bangladesh: A comprehensive machine learning approach. Groundw. Sustain. Dev. 2024, 25, 101128. [Google Scholar] [CrossRef]
- Lombard, M.A.; Bryan, M.S.; Jones, D.K.; Bulka, C.; Bradley, P.M.; Backer, L.C.; Focazio, M.J.; Silverman, D.T.; Toccalino, P.; Argos, M. Machine learning models of arsenic in private wells throughout the conterminous United States as a tool for exposure assessment in human health studies. Environ. Sci. Technol. 2021, 55, 5012–5023. [Google Scholar] [CrossRef]
- Soriano, M.A., Jr.; Deziel, N.C.; Saiers, J.E. Regional scale assessment of shallow groundwater vulnerability to contamination from unconventional hydrocarbon extraction. Environ. Sci. Technol. 2022, 56, 12126–12136. [Google Scholar] [CrossRef]
- Hamlin, Q.; Martin, S.; Kendall, A.; Hyndman, D. Examining relationships between groundwater nitrate concentrations in drinking water and landscape characteristics to understand health risks. GeoHealth 2022, 6, e2021GH000524. [Google Scholar] [CrossRef]
- Bulka, C.M.; Bryan, M.S.; Lombard, M.A.; Bartell, S.M.; Jones, D.K.; Bradley, P.M.; Vieira, V.M.; Silverman, D.T.; Focazio, M.; Toccalino, P.L. Arsenic in private well water and birth outcomes in the United States. Environ. Int. 2022, 163, 107176. [Google Scholar] [CrossRef]
- Liu, C.; Bartelt-Hunt, S.; Li, Y. Precipitation, temperature, and landcovers drive spatiotemporal variability of groundwater nitrate concentration across the Continental United States. Sci. Total Environ. 2024, 945, 174040. [Google Scholar] [CrossRef]
- Tesoriero, A.J.; Wherry, S.A.; Dupuy, D.I.; Johnson, T.D. Predicting redox conditions in groundwater at a national scale using random forest classification. Environ. Sci. Technol. 2024, 58, 5079–5092. [Google Scholar] [CrossRef] [PubMed]
- Tesoriero, A.J.; Gronberg, J.A.; Juckem, P.F.; Miller, M.P.; Austin, B.P. Predicting redox-sensitive contaminant concentrations in groundwater using random forest classification. Water Resour. Res. 2017, 53, 7316–7331. [Google Scholar] [CrossRef]
- Gharechaee, H.; Samani, A.N.; Sigaroodi, S.K.; Sadeghi, S.M.M.; Sharifitabesh, S.; Mousavi, M.S.; Marcu, M.V.; Hubbart, J.A. Introducing a novel approach for assessment of groundwater salinity hazard, vulnerability, and risk in a semiarid region. Ecol. Inform. 2024, 81, 102647. [Google Scholar] [CrossRef]
- Rosecrans, C.Z.; Nolan, B.T.; Gronberg, J.M. Prediction and visualization of redox conditions in the groundwater of Central Valley, California. J. Hydrol. 2017, 546, 341–356. [Google Scholar] [CrossRef]
- Canion, A.; McCloud, L.; Dobberfuhl, D. Predictive modeling of elevated groundwater nitrate in a karstic spring-contributing area using random forests and regression-kriging. Environ. Earth Sci. 2019, 78, 271. [Google Scholar] [CrossRef]
- Bentekhici, N.; Benkesmia, Y.; Bouhlala, M.A.; Saad, A.; Ghabi, M. Mapping and assessment of groundwater pollution risks in the main aquifer of the Mostaganem plateau (Northwest Algeria): Utilizing the novel vulnerability index and decision tree model. Environ. Sci. Pollut. Res. 2024, 31, 45074–45104. [Google Scholar] [CrossRef]
- Jeihouni, M.; Toomanian, A.; Mansourian, A. Decision tree-based data mining and rule induction for identifying high quality groundwater zones to water supply management: A novel hybrid use of data mining and GIS. Water Resour. Manag. 2020, 34, 139–154. [Google Scholar] [CrossRef]
- Podgorski, J.; Araya, D.; Berg, M. Geogenic manganese and iron in groundwater of Southeast Asia and Bangladesh–machine learning spatial prediction modeling and comparison with arsenic. Sci. Total Environ. 2022, 833, 155131. [Google Scholar] [CrossRef]
- Araya, D.; Podgorski, J.; Kumi, M.; Mainoo, P.A.; Berg, M. Fluoride contamination of groundwater resources in Ghana: Country-wide hazard modeling and estimated population at risk. Water Res. 2022, 212, 118083. [Google Scholar] [CrossRef]
- Ling, Y.; Podgorski, J.; Sadiq, M.; Rasheed, H.; Eqani, S.A.M.A.S.; Berg, M. Monitoring and prediction of high fluoride concentrations in groundwater in Pakistan. Sci. Total Environ. 2022, 839, 156058. [Google Scholar] [CrossRef]
- Joodavi, A.; Aghlmand, R.; Podgorski, J.; Dehbandi, R.; Abbasi, A. Characterization, geostatistical modeling and health risk assessment of potentially toxic elements in groundwater resources of northeastern Iran. J. Hydrol. Reg. Stud. 2021, 37, 100885. [Google Scholar] [CrossRef]
- Podgorski, J.E.; Labhasetwar, P.; Saha, D.; Berg, M. Prediction modeling and mapping of groundwater fluoride contamination throughout India. Environ. Sci. Technol. 2018, 52, 9889–9898. [Google Scholar] [CrossRef]
- Sarkar, S.; Mukherjee, A.; Chakraborty, M.; Quamar, M.T.; Duttagupta, S.; Bhattacharya, A. Prediction of elevated groundwater fluoride across India using multi-model approach: Insights on the influence of geologic and environmental factors. Environ. Sci. Pollut. Res. 2023, 30, 31998–32013. [Google Scholar] [CrossRef] [PubMed]
- Affum, A.O.; Kwaansa-Ansah, E.E.; Osae, S.D. Estimating groundwater geogenic arsenic contamination and the affected population of river basins underlain mostly with crystalline rocks in Ghana. Environ. Chall. 2024, 15, 100898. [Google Scholar]
- Nath, B.; Chowdhury, R.; Ni-Meister, W.; Mahanta, C. Predicting the distribution of arsenic in groundwater by a geospatial machine learning technique in the two most affected districts of Assam, India: The public health implications. GeoHealth 2022, 6, e2021GH000585. [Google Scholar] [CrossRef] [PubMed]
- Xiangcao, Z.; Su, C.; Xianjun, X.; Ge, W.; Xiao, Z.; Yang, L.; Pan, H. Employing machine learning to predict the occurrence and spatial variability of high fluoride groundwater in intensively irrigated areas. Appl. Geochem. 2024, 167, 106000. [Google Scholar] [CrossRef]
- Knoll, L.; Breuer, L.; Bach, M. Nation-wide estimation of groundwater redox conditions and nitrate concentrations through machine learning. Environ. Res. Lett. 2020, 15, 064004. [Google Scholar] [CrossRef]
- Hájek, M.; Jiménez-Alfaro, B.; Hájek, O.; Brancaleoni, L.; Cantonati, M.; Carbognani, M.; Dedić, A.; Dítě, D.; Gerdol, R.; Hájková, P. A European map of groundwater pH and calcium. Earth Syst. Sci. Data Discuss. 2020, 2020, 1–41. [Google Scholar]
- Abba, S.I.; Yassin, M.A.; Mubarak, A.S.; Shah, S.M.H.; Usman, J.; Oudah, A.Y.; Naganna, S.R.; Aljundi, I.H. Drinking water resources suitability assessment based on pollution index of groundwater using improved explainable artificial intelligence. Sustainability 2023, 15, 15655. [Google Scholar] [CrossRef]
- Ammar, K.; McKee, M.; Kaluarachchi, J. Bayesian method for groundwater quality monitoring network analysis. J. Water Resour. Plan. Manag. 2011, 137, 51–61. [Google Scholar] [CrossRef]
- Sajedi-Hosseini, F.; Malekian, A.; Choubin, B.; Rahmati, O.; Cipullo, S.; Coulon, F.; Pradhan, B. A novel machine learning-based approach for the risk assessment of nitrate groundwater contamination. Sci. Total Environ. 2018, 644, 954–962. [Google Scholar] [CrossRef] [PubMed]
- Awais, M.; Aslam, B.; Maqsoom, A.; Khalil, U.; Ullah, F.; Azam, S.; Imran, M. Assessing nitrate contamination risks in groundwater: A machine learning approach. Appl. Sci. 2021, 11, 10034. [Google Scholar] [CrossRef]
- Wei, A.; Bi, P.; Guo, J.; Lu, S.; Li, D. Modified DRASTIC model for groundwater vulnerability to nitrate contamination in the Dagujia river basin, China. Water Supply 2021, 21, 1793–1805. [Google Scholar] [CrossRef]
- Agrawal, P.; Sinha, A.; Kumar, S.; Agarwal, A.; Banerjee, A.; Villuri, V.G.K.; Annavarapu, C.S.R.; Dwivedi, R.; Dera, V.V.R.; Sinha, J. Exploring artificial intelligence techniques for groundwater quality assessment. Water 2021, 13, 1172. [Google Scholar] [CrossRef]
- Abu El-Magd, S.A.; Ismael, I.S.; El-Sabri, M.A.S.; Abdo, M.S.; Farhat, H.I. Integrated machine learning–based model and WQI for groundwater quality assessment: ML, geospatial, and hydro-index approaches. Environ. Sci. Pollut. Res. 2023, 30, 53862–53875. [Google Scholar] [CrossRef]
- Twarakavi, N.K.; Kaluarachchi, J.J. Sustainability of ground water quality considering land use changes and public health risks. J. Environ. Manag. 2006, 81, 405–419. [Google Scholar] [CrossRef]
- Asadi, P.; Hosseini, S.M.; Ataie-Ashtiani, B.; Simmons, C.T. Fuzzy vulnerability mapping of urban groundwater systems to nitrate contamination. Environ. Model. Softw. 2017, 96, 146–157. [Google Scholar] [CrossRef]
- Jmal, I.; Ayed, B.; Boughariou, E.; Allouche, N.; Saidi, S.; Hamdi, M.; Bouri, S. Assessing groundwater vulnerability to nitrate pollution using statistical approaches: A case study of Sidi Bouzid shallow aquifer, Central Tunisia. Arab. J. Geosci. 2017, 10, 364. [Google Scholar] [CrossRef]
- Rizeei, H.M.; Azeez, O.S.; Pradhan, B.; Khamees, H.H. Assessment of groundwater nitrate contamination hazard in a semi-arid region by using integrated parametric IPNOA and data-driven logistic regression models. Environ. Monit. Assess. 2018, 190, 633. [Google Scholar] [CrossRef]
- El Baba, M.; Kayastha, P.; Huysmans, M.; De Smedt, F. Groundwater vulnerability and nitrate contamination assessment and mapping using DRASTIC and geostatistical analysis. Water 2020, 12, 2022. [Google Scholar] [CrossRef]
- Adiat, K.; Akeredolu, B.; Akinlalu, A.; Olayanju, G. Application of logistic regression analysis in prediction of groundwater vulnerability in gold mining environment: A case of Ilesa gold mining area, southwestern, Nigeria. Environ. Monit. Assess. 2020, 192, 577. [Google Scholar] [CrossRef]
- Jaydhar, A.K.; Pal, S.C.; Saha, A.; Islam, A.R.M.T.; Ruidas, D. Hydrogeochemical evaluation and corresponding health risk from elevated arsenic and fluoride contamination in recurrent coastal multi-aquifers of eastern India. J. Clean. Prod. 2022, 369, 133150. [Google Scholar] [CrossRef]
- Mohammaddost, A.; Mohammadi, Z.; Rezaei, M.; Pourghasemi, H.R.; Farahmand, A. Assessment of groundwater vulnerability in an urban area: A comparative study based on DRASTIC, EBF, and LR models. Environ. Sci. Pollut. Res. 2022, 29, 72908–72928. [Google Scholar] [CrossRef] [PubMed]
- Jang, C.-S. Geostatistical estimates of groundwater nitrate-nitrogen concentrations with spatial auxiliary information on DRASTIC-LU-based aquifer contamination vulnerability. Environ. Sci. Pollut. Res. 2023, 30, 81113–81130. [Google Scholar] [CrossRef] [PubMed]
- Twarakavi, N.K.C.; Kaluarachchi, J.J. Arsenic in the shallow ground waters of conterminous United States: Assessment, health risks, and costs for mcl compliance 1. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 275–294. [Google Scholar] [CrossRef]
- Gurdak, J.J.; Qi, S.L. Vulnerability of recently recharged groundwater in principle aquifers of the United States to nitrate contamination. Environ. Sci. Technol. 2012, 46, 6004–6012. [Google Scholar] [CrossRef]
- Nolan, B.T.; Hitt, K.J. Vulnerability of shallow groundwater and drinking-water wells to nitrate in the United States. Environ. Sci. Technol. 2006, 40, 7834–7840. [Google Scholar] [CrossRef]
- Podgorski, J.E.; Eqani, S.A.M.A.S.; Khanam, T.; Ullah, R.; Shen, H.; Berg, M. Extensive arsenic contamination in high-pH unconfined aquifers in the Indus Valley. Sci. Adv. 2017, 3, e1700935. [Google Scholar] [CrossRef]
- LaMotte, A.; Greene, E. Spatial analysis of land use and shallow groundwater vulnerability in the watershed adjacent to Assateague Island National Seashore, Maryland and Virginia, USA. Environ. Geol. 2007, 52, 1413–1421. [Google Scholar] [CrossRef]
- Bretzler, A.; Lalanne, F.; Nikiema, J.; Podgorski, J.; Pfenninger, N.; Berg, M.; Schirmer, M. Groundwater arsenic contamination in Burkina Faso, West Africa: Predicting and verifying regions at risk. Sci. Total Environ. 2017, 584, 958–970. [Google Scholar] [CrossRef]
- Ayotte, J.D.; Medalie, L.; Qi, S.L.; Backer, L.C.; Nolan, B.T. Estimating the high-arsenic domestic-well population in the conterminous United States. Environ. Sci. Technol. 2017, 51, 12443–12454. [Google Scholar] [CrossRef]
- Winkel, L.; Berg, M.; Amini, M.; Hug, S.J.; Annette Johnson, C. Predicting groundwater arsenic contamination in Southeast Asia from surface parameters. Nat. Geosci. 2008, 1, 536–542. [Google Scholar] [CrossRef]
- Rodríguez-Lado, L.; Sun, G.; Berg, M.; Zhang, Q.; Xue, H.; Zheng, Q.; Johnson, C.A. Groundwater arsenic contamination throughout China. Science 2013, 341, 866–868. [Google Scholar] [CrossRef]
- Pal, S.C.; Biswas, T.; Jaydhar, A.K.; Ruidas, D.; Saha, A.; Chowdhuri, I.; Mandal, S.; Islam, A.; Islam, A.R.M.T.; Pande, C.B. Source identification and potential health risks from elevated groundwater nitrate contamination in Sundarbans coastal aquifers, India. Sci. Rep. 2024, 14, 4153. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Rodriguez-Lado, L.; Liu, J.; Johnson, C.A.; Zheng, Q.; Sun, G. Coupling predicted model of arsenic in groundwater with endemic arsenism occurrence in Shanxi Province, Northern China. J. Hazard. Mater. 2013, 262, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Atashi Yazdi, S.S.; Motamedvaziri, B.; Hosseini, S.Z.; Ahmadi, H. Reciprocal analysis of groundwater potentiality and vulnerability modeling in the Bahabad Plain, Iran. Environ. Sci. Pollut. Res. 2023, 30, 39586–39604. [Google Scholar] [CrossRef] [PubMed]
- Nolan, B.T.; Green, C.T.; Juckem, P.F.; Liao, L.; Reddy, J.E. Metamodeling and mapping of nitrate flux in the unsaturated zone and groundwater, Wisconsin, USA. J. Hydrol. 2018, 559, 428–441. [Google Scholar] [CrossRef]
- Ghosh, T. Groundwater hydro-geochemical inferences and eXplainable Artificial Intelligence augmented groundwater quality prediction in arid and semi-arid segment of Rajasthan, India. Groundw. Sustain. Dev. 2024, 26, 101272. [Google Scholar]
- Uddin, M.G.; Rana, M.S.P.; Diganta, M.T.M.; Bamal, A.; Sajib, A.M.; Abioui, M.; Shaibur, M.R.; Ashekuzzaman, S.; Nikoo, M.R.; Rahman, A. Enhancing Groundwater Quality Assessment in Coastal Area: A Hybrid Modeling Approach. Heliyon 2024, 10, e33082. [Google Scholar] [CrossRef]
- Guo, X.; Xiong, H.; Li, H.; Gui, X.; Hu, X.; Li, Y.; Cui, H.; Qiu, Y.; Zhang, F.; Ma, C. Designing dynamic groundwater management strategies through a composite groundwater vulnerability model: Integrating human-related parameters into the DRASTIC model using LightGBM regression and SHAP analysis. Environ. Res. 2023, 236, 116871. [Google Scholar] [CrossRef]
- Yang, S.; Luo, D.; Tan, J.; Li, S.; Song, X.; Xiong, R.; Wang, J.; Ma, C.; Xiong, H. Spatial Mapping and Prediction of Groundwater Quality Using Ensemble Learning Models and SHapley Additive exPlanations with Spatial Uncertainty Analysis. Water 2024, 16, 2375. [Google Scholar] [CrossRef]
- Erickson, M.L.; Elliott, S.M.; Brown, C.J.; Stackelberg, P.; Ransom, K.M.; Reddy, J.E. Machine learning predicted redox conditions in the glacial aquifer system, northern continental United States. Water Resour. Res. 2021, 57, e2020WR028207. [Google Scholar] [CrossRef]
- Ransom, K.M.; Nolan, B.T.; Stackelberg, P.; Belitz, K.; Fram, M.S. Machine learning predictions of nitrate in groundwater used for drinking supply in the conterminous United States. Sci. Total Environ. 2022, 807, 151065. [Google Scholar] [CrossRef]
- Ransom, K.M.; Nolan, B.T.; Traum, J.A.; Faunt, C.C.; Bell, A.M.; Gronberg, J.A.M.; Wheeler, D.C.; Rosecrans, C.Z.; Jurgens, B.; Schwarz, G.E. A hybrid machine learning model to predict and visualize nitrate concentration throughout the Central Valley aquifer, California, USA. Sci. Total Environ. 2017, 601, 1160–1172. [Google Scholar] [CrossRef]
- DeSimone, L.A.; Pope, J.P.; Ransom, K.M. Machine-learning models to map pH and redox conditions in groundwater in a layered aquifer system, Northern Atlantic Coastal Plain, eastern USA. J. Hydrol. Reg. Stud. 2020, 30, 100697. [Google Scholar] [CrossRef]
- Erickson, M.L.; Elliott, S.M.; Brown, C.J.; Stackelberg, P.E.; Ransom, K.M.; Reddy, J.E.; Cravotta, C.A., III. Machine-learning predictions of high arsenic and high manganese at drinking water depths of the glacial aquifer system, northern continental United States. Environ. Sci. Technol. 2021, 55, 5791–5805. [Google Scholar] [CrossRef] [PubMed]
- Knierim, K.J.; Kingsbury, J.A.; Belitz, K.; Stackelberg, P.E.; Minsley, B.J.; Rigby, J.R. Mapped predictions of manganese and arsenic in an alluvial aquifer using boosted regression trees. Groundwater 2022, 60, 362–376. [Google Scholar] [CrossRef] [PubMed]
- Stackelberg, P.E.; Belitz, K.; Brown, C.J.; Erickson, M.L.; Elliott, S.M.; Kauffman, L.J.; Ransom, K.M.; Reddy, J.E. Machine learning predictions of pH in the glacial aquifer system, Northern USA. Groundwater 2021, 59, 352–368. [Google Scholar] [CrossRef] [PubMed]
- Erickson, M.L.; Elliott, S.M.; Christenson, C.; Krall, A.L. Predicting geogenic arsenic in drinking water wells in glacial aquifers, north-central USA: Accounting for depth-dependent features. Water Resour. Res. 2018, 54, 10172–10187. [Google Scholar] [CrossRef]
- DeSimone, L.A.; Ransom, K.M. Manganese in the Northern Atlantic Coastal Plain aquifer system, eastern USA—Modeling regional occurrence with pH, redox, and machine learning. J. Hydrol. Reg. Stud. 2021, 37, 100925. [Google Scholar] [CrossRef]
- Attia, M.; Tsai, F.T.-C. Successive bootstrapping deep learning approach and airborne EM-borehole data fusion to understand salt water in the Mississippi River Valley Alluvial Aquifer. Sci. Total Environ. 2024, 932, 172950. [Google Scholar] [CrossRef]
- Tokranov, A.K.; Ransom, K.M.; Bexfield, L.M.; Lindsey, B.D.; Watson, E.; Dupuy, D.I.; Stackelberg, P.E.; Fram, M.S.; Voss, S.A.; Kingsbury, J.A. Predictions of groundwater PFAS occurrence at drinking water supply depths in the United States. Science 2024, 386, 748–755. [Google Scholar] [CrossRef]
- Meray, A.O.; Sturla, S.; Siddiquee, M.R.; Serata, R.; Uhlemann, S.; Gonzalez-Raymat, H.; Denham, M.; Upadhyay, H.; Lagos, L.E.; Eddy-Dilek, C. PyLEnM: A machine learning framework for long-term groundwater contamination monitoring strategies. Environ. Sci. Technol. 2022, 56, 5973–5983. [Google Scholar] [CrossRef] [PubMed]
- Wood, W.W.; Smedley, P.L.; Lindsey, B.D.; Wood, W.T.; Kirchheim, R.E.; Cherry, J.A. Global groundwater solute composition and concentrations. Groundwater 2022, 60, 714–720. [Google Scholar] [CrossRef] [PubMed]
- Güler, C.; Kurt, M.A.; Alpaslan, M.; Akbulut, C. Assessment of the impact of anthropogenic activities on the groundwater hydrology and chemistry in Tarsus coastal plain (Mersin, SE Turkey) using fuzzy clustering, multivariate statistics and GIS techniques. J. Hydrol. 2012, 414, 435–451. [Google Scholar] [CrossRef]
- Zghibi, A.; Merzougui, A.; Zouhri, L.; Tarhouni, J. Understanding groundwater chemistry using multivariate statistics techniques to the study of contamination in the Korba unconfined aquifer system of Cap-Bon (North-east of Tunisia). J. Afr. Earth Sci. 2014, 89, 1–15. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K. Identifying sources of groundwater contamination in a hard-rock aquifer system using multivariate statistical analyses and GIS-based geostatistical modeling techniques. J. Hydrol. Reg. Stud. 2015, 4, 80–110. [Google Scholar] [CrossRef]
- Javadi, S.; Hashemy, S.; Mohammadi, K.; Howard, K.; Neshat, A. Classification of aquifer vulnerability using K-means cluster analysis. J. Hydrol. 2017, 549, 27–37. [Google Scholar] [CrossRef]
- Mohammadrezapour, O.; Kisi, O.; Pourahmad, F. Fuzzy c-means and K-means clustering with genetic algorithm for identification of homogeneous regions of groundwater quality. Neural Comput. Appl. 2020, 32, 3763–3775. [Google Scholar] [CrossRef]
- Marín Celestino, A.E.; Ramos Leal, J.A.; Martínez Cruz, D.A.; Tuxpan Vargas, J.; De Lara Bashulto, J.; Morán Ramírez, J. Identification of the hydrogeochemical processes and assessment of groundwater quality, using multivariate statistical approaches and water quality index in a wastewater irrigated region. Water 2019, 11, 1702. [Google Scholar] [CrossRef]
- Yang, J.; Ye, M.; Tang, Z.; Jiao, T.; Song, X.; Pei, Y.; Liu, H. Using cluster analysis for understanding spatial and temporal patterns and controlling factors of groundwater geochemistry in a regional aquifer. J. Hydrol. 2020, 583, 124594. [Google Scholar] [CrossRef]
- Rahmani, B.; Javadi, S.; Shahdany, S.M.H. Evaluation of aquifer vulnerability using PCA technique and various clustering methods. Geocarto Int. 2021, 36, 2117–2140. [Google Scholar] [CrossRef]
- Javadi, S.; Hashemy Shahdany, S.M.; Neshat, A.; Chambel, A. Multi-parameter risk mapping of Qazvin aquifer by classic and fuzzy clustering techniques. Geocarto Int. 2022, 37, 1160–1182. [Google Scholar] [CrossRef]
- Fashina, L.; Luffman, I.; Joyner, T.A.; Nandi, A. Geospatial assessment of karst spring water quality in Northeast Tennessee, USA. Geosciences 2022, 12, 303. [Google Scholar] [CrossRef]
- Nourani, V.; Ghaneei, P.; Kantoush, S.A. Robust clustering for assessing the spatiotemporal variability of groundwater quantity and quality. J. Hydrol. 2022, 604, 127272. [Google Scholar] [CrossRef]
- Uzcategui-Salazar, M.; Lillo, J. A new approach to pollution vulnerability assessment in aquifers using K-means analysis. Environ. Earth Sci. 2022, 81, 495. [Google Scholar] [CrossRef]
- Wang, W.; Li, W.; Xue, M.; Gu, X.; Ye, C.; Jiao, Y.; Liu, B.; Han, Y.; Tong, Y.; Zhang, X. Spatial-temporal characteristics and influencing factors of lake water and groundwater chemistry in Hulun Lake, Northeast China. Water 2023, 15, 937. [Google Scholar] [CrossRef]
- Guo, X.; Yang, Z.; Li, C.; Xiong, H.; Ma, C. Combining the classic vulnerability index and affinity propagation clustering algorithm to assess the intrinsic aquifer vulnerability of coastal aquifers on an integrated scale. Environ. Res. 2023, 217, 114877. [Google Scholar]
- Halder, S.; Bhattacharya, S.; Roy, M.B.; Roy, P.K. Application of fuzzy C-means clustering and fuzzy EDAS to assess groundwater irrigation suitability and prioritization for agricultural development in a complex hydrogeological basin. Environ. Sci. Pollut. Res. 2023, 30, 57529–57557. [Google Scholar] [CrossRef]
- Eid, M.H.; Eissa, M.; Mohamed, E.A.; Ramadan, H.S.; Czuppon, G.; Kovács, A.; Szűcs, P. Application of stable isotopes, mixing models, and K-means cluster analysis to detect recharge and salinity origins in siwa oasis, Egypt. Groundw. Sustain. Dev. 2024, 25, 101124. [Google Scholar] [CrossRef]
- Panagiotou, C.F.; Chekirbane, A.; Eliades, M.; Papoutsa, C.; Akylas, E.; Stylianou, M.; Stathopoulos, N. Assessing the groundwater quality of El Fahs aquifer (NE Tunisia) using multivariate statistical techniques and geostatistical modeling. Appl. Water Sci. 2024, 14, 170. [Google Scholar] [CrossRef]
- Page, R.M.; Huggenberger, P.; Lischeid, G. Multivariate analysis of groundwater-quality time-series using self-organizing maps and sammon’s mapping. Water Resour. Manag. 2015, 29, 3957–3970. [Google Scholar]
- Yang, X.; Jia, C.; Yang, F.; Yang, H.; Yao, Y. Spatio-temporal variation of groundwater pollution in urban wetlands and management strategies for zoning. J. Environ. Manag. 2023, 342, 118318. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Wu, Y.; Yu, Y.; Wang, L.; Qi, P.; Sun, Y.; Fu, Q.; Zhang, G. Assessment of groundwater quality variation characteristics and influencing factors in an intensified agricultural area: An integrated hydrochemical and machine learning approach. J. Environ. Manag. 2024, 371, 123233. [Google Scholar] [CrossRef]
- Gholami, V.; Sahour, H. A Hybrid Approach of Supervised Self-organizing Maps and Genetic Algorithms for Predictive Mapping of Arsenic Pollution in Groundwater Resources. Expo. Health 2023, 16, 775–790. [Google Scholar] [CrossRef]
- Gholami, V.; Khaleghi, M.R.; Taghvaye Salimi, E. Groundwater quality modeling using self-organizing map (SOM) and geographic information system (GIS) on the Caspian southern coasts. J. Mt. Sci. 2020, 17, 1724–1734. [Google Scholar] [CrossRef]
- Rezaei, F.; Ahmadzadeh, M.R.; Safavi, H.R. SOM-DRASTIC: Using self-organizing map for evaluating groundwater potential to pollution. Stoch. Environ. Res. Risk Assess. 2017, 31, 1941–1956. [Google Scholar] [CrossRef]
- Lee, K.-J.; Yun, S.-T.; Yu, S.; Kim, K.-H.; Lee, J.-H.; Lee, S.-H. The combined use of self-organizing map technique and fuzzy c-means clustering to evaluate urban groundwater quality in Seoul metropolitan city, South Korea. J. Hydrol. 2019, 569, 685–697. [Google Scholar] [CrossRef]
- Nandi, R.; Mondal, S.; Mandal, J.; Bhattacharyya, P. Deciphering geochemical fingerprints and health implications of groundwater fluoride contamination in mica mining regions using machine learning tactics. Environ. Geochem. Health 2024, 46, 400. [Google Scholar] [CrossRef]

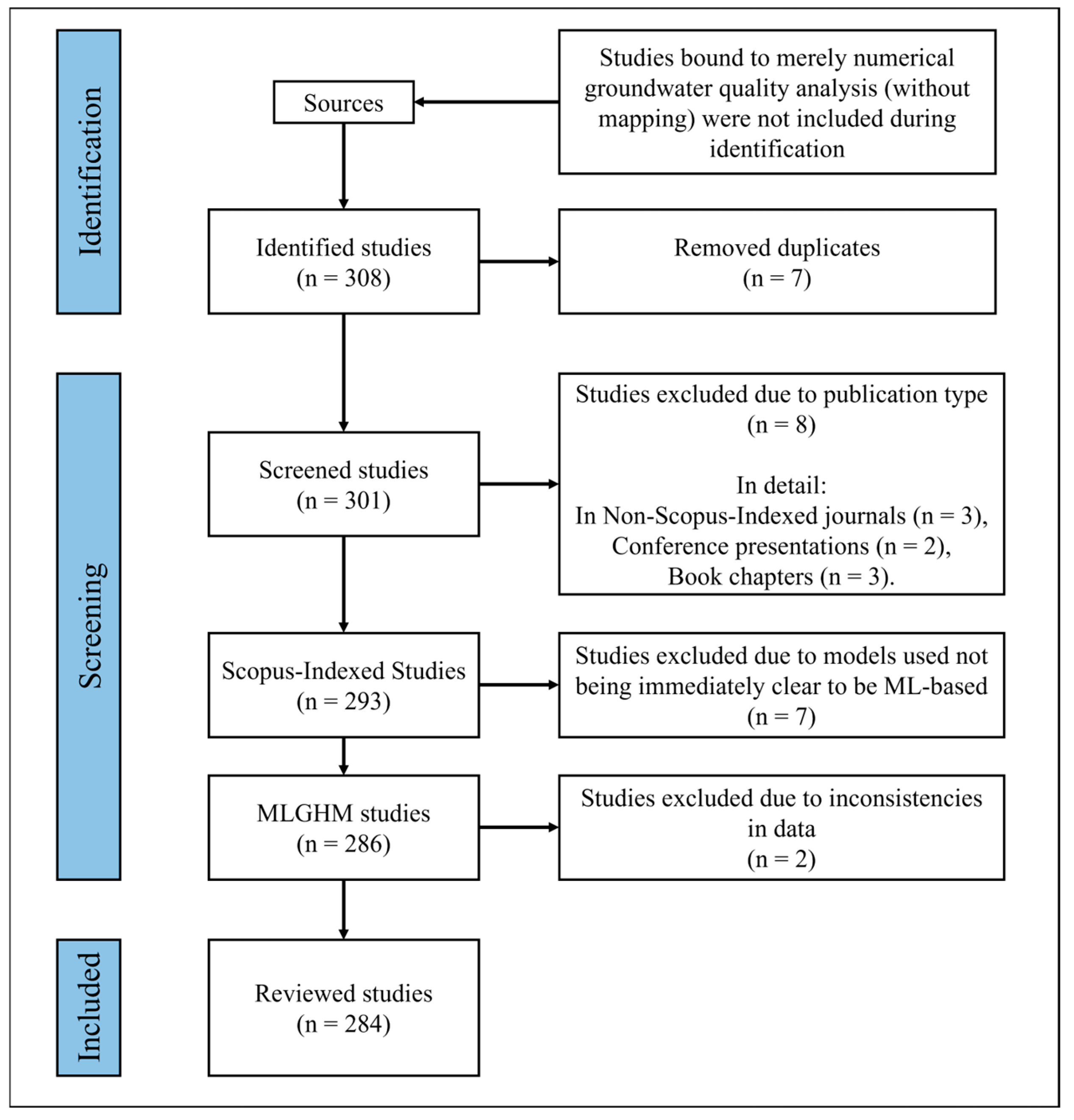
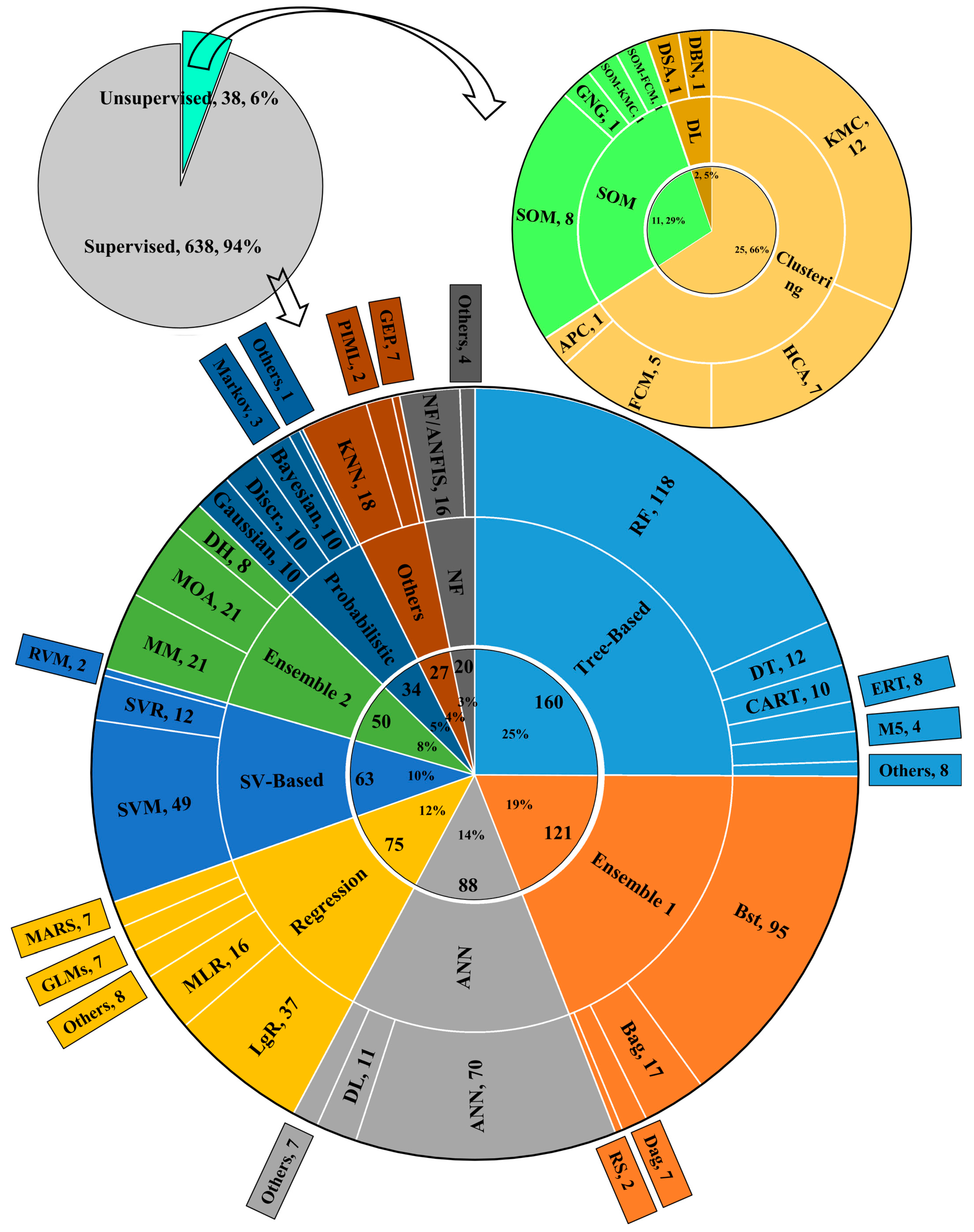
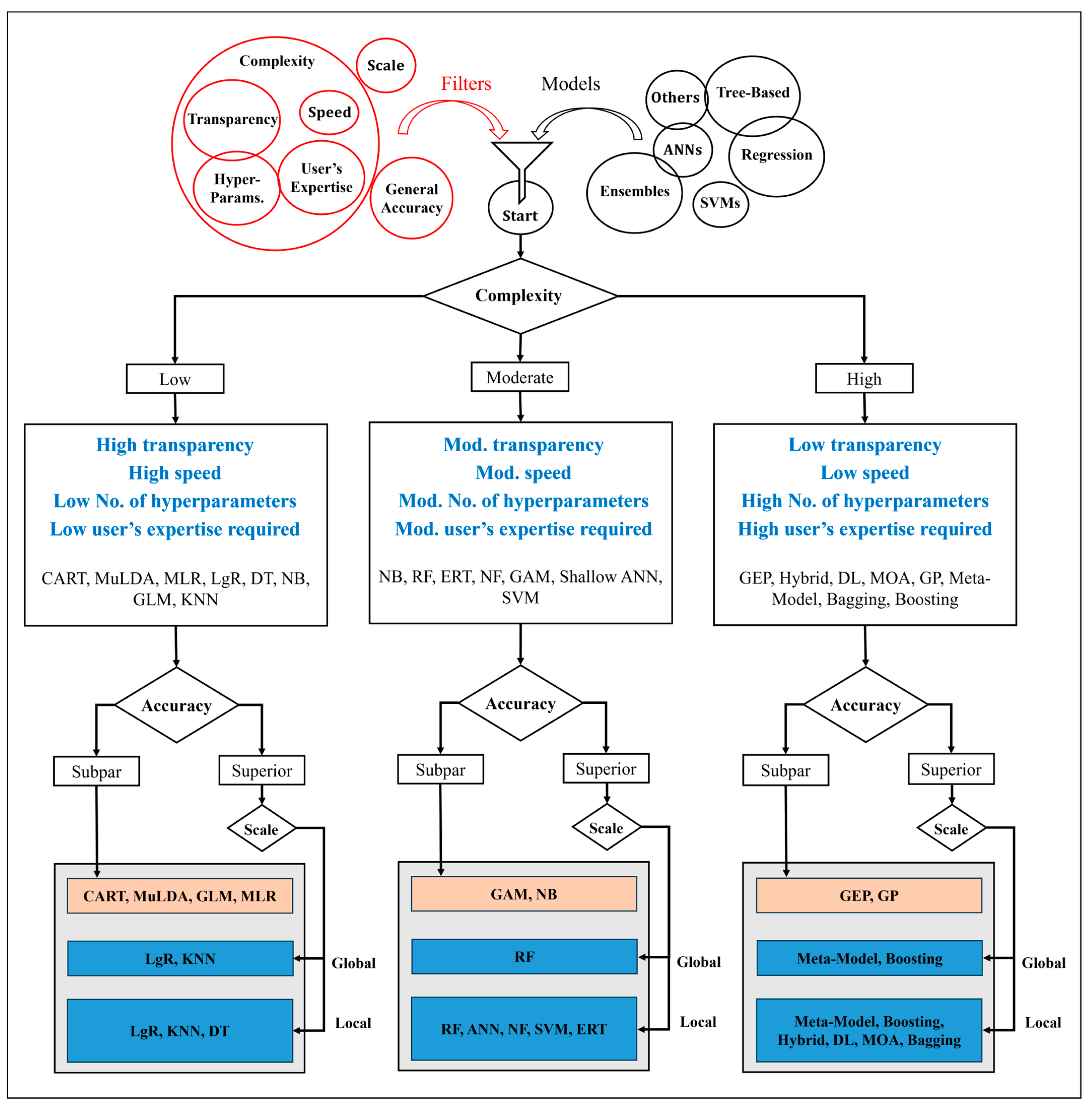
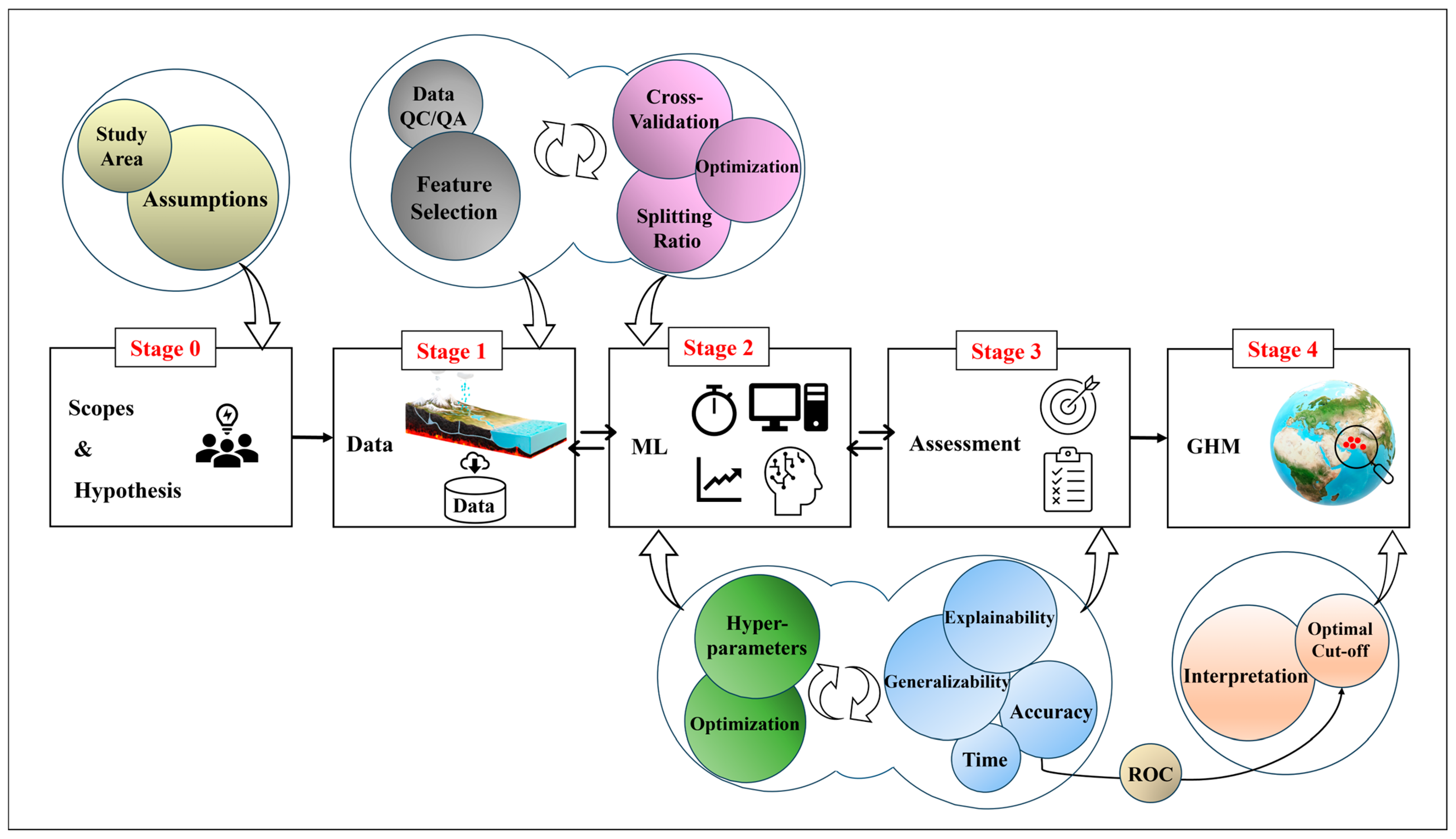
| L. | Reference | Target Parameter | Country | Models (Most Accurate > Others) | Criteria Considered | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data Adjustment | Hyperpa. | Comp. Efficiency | Others/Comments | ||||||||||
| TSR | CV | FS/IA | Opt | Rep | CT | OS | PF | ||||||
| A | Khan and Ayaz [144] | WQI | India | ANN > MLR, GP, SVM, RT, BRT | ★✖ | - Addressing uncertainty | |||||||
| Esmaeilbeiki, et al. [145] | H, EC | India | DENFIS, GEP > GMDH, MARS, M5 | ✖ | - Considering input scenarios | ||||||||
| Kerketta, et al. [146] | F− | India | ELM > XGBoost, SVM, RF, ANN | ✖ | ✚ | ⃞ ✔✖ | ✔ | - POF by various inherent features - Using MOAs (GA) for model optimization | |||||
| Boudibi, et al. [147] | Salinity (EC) | Algeria | RF > HyFIS, KNN, Cubist, SVM | ✔ | ✖ | ✖ | ✔ | ||||||
| Khiavi, et al. [148] | WQI | Iran | RF > NB, SVM, KNN | ★✔ | - Using game theory for model assessment | ||||||||
| Javidan and Javidan [149] | Iran | CMMRF > RF, MMRF, FMRF | ✖ | - Using cutoff-dependent accuracy metrics - Briefly discussing transferability | |||||||||
| Tavakoli, et al. [150] | RI (TDS) | Iran | RF > BRT, SVM, MARS, GLM | ✔ | - Briefly discussing transferability | ||||||||
| Chahid, et al. [151] | VI () | Morocco | ERT > BA, ANN, KNN | ✖ | ✖ | ✔ | - Using evolutionary algorithms for model optimization - POF by various inherent features | ||||||
| El-Rawy, et al. [152] | WQI | Egypt | RR > RF, XGBoost, DT, KNN | ★✖❄ | ✔ | - Considering input scenarios - POF by various inherent features | |||||||
| Liang, et al. [153] | China | RF > XGBoost, SVM | ✔ | O | ⃞ | - Using SHAP to address explainability - POF by XGBoost’s inherent features - Addressing uncertainty by statistical analysis | |||||||
| Bordbar, et al. [154] | SWI, WQI | Italy | RF, SVM > BRT | ✖✔ | - Briefly discussing transferability | ||||||||
| Bakhtiarizadeh, et al. [155] | Iran | GEP, GA-PolyR > PSO-MARS, M5 | ✔ | ✚ | ✖ | ✔ | ✔ | - POF by various techniques - Discussing explainability | |||||
| B | Díaz-Alcaide and Martínez-Santos [116] | Fecal cont. | Mali | RF > LgR, ANN, SVM, DT, KNN, LDA, NB, AdB, QDA, GBC, GP | ✔ | ✚ | ⃞ | ⃟ | - Ensembling the elite models - Addressing uncertainty - Briefly discussing transferability and explainability | ||||
| Liang, et al. [156] | China | GBR > RF, XGBoost, AdB | ✔ | ✔★ | ⃞ ✖ | - POF by XGBoost’s inherent features - Addressing uncertainty using PICP and MPI | |||||||
| Sarkar, et al. [157] | Salinity (EC) | India | RF > GBoost, LgR | ✔ | ▲✖ ✔★ | ✖ | ✔ | - Using DSRM to address the issue of imbalanced data - IHZ using cutoff point - Addressing transferability by large-scale modeling | |||||
| Tran, et al. [158] | Salinity (Cl−) | Vietnam | CatBoost > RF, XGBoost, LGB | ✔ | ✔ | ⃞ | ✔ | ⃟ | ✔ | - GHM classified based on WHO standards - Superior model achieved lowest penalty and fastest training | |||
| Huang, et al. [159] | China | XGBoost > CART, GBM, RF, LGBM | ✔ | O✔ | ✖ | ✔ | - Using SHAP to address explainability - POF by XGBoost’s inherent features | ||||||
| Aju, et al. [160] | WQI | India | RF > XGBoost, SVR, ANN | O | ✖ | - POF by XGBoost’s inherent features - Using SHAP to address explainability | |||||||
| Barzegar, et al. [161] | TDS | Iran | XGBoost > R, LGBM, AdB, CatBoost | ✔ | ★ | ⃞ | ✔ | - POF by XGBoost’s inherent regularization - Addressing reproducibility | |||||
| Tachi, et al. [162] | Algeria | CatBoost > AdB, RF | ★✔ | - POF by various inherent features | |||||||||
| Knoll, et al. [163] | Germany | RF > BRT, CART, MLR | ✔ | ✚ | ✔ | ✔ | ✔ | - Using stratified random sampling for data division - POF by various inherent features - Briefly discussing transferability - Addressing transferability by large-scale modeling | |||||
| Pal, et al. [164] | India | Bst > Bag, RF | ✔ | ✔ | ✔ | ✔ | - POF by various inherent features | ||||||
| Sun, et al. [165] | China | Bag > Bst, GBDT, RF, SVM, ANN, | ✔ | ★O✔ | - POF by various inherent features - Using SHAP to address explainability | ||||||||
| Bordbar, et al. [166] | VI (TDS) | Iran | BA-LMT > DA-LMT, BA-NBT, DA-NBT, RS-NBT, RS-LMT, LMT, NBT | - POF by various inherent features | |||||||||
| Islam, et al. [167] | Bangladesh | Bst > Bag, RF | ✔ | ✖ | ✔ | ✔ | - POF by various inherent features | ||||||
| C | Singha, Pasupuleti, Singha, Singh, and Kumar [46] | WQI | India | DL > XGBoost, ANN, RF | ✔ | ✔ | ✚ | ⃞ ✔✖ | ✔ | - POF by Dropout, mini-batch size, and L2 regularization | |||
| Meng, et al. [168] | RI () | China | DL > RF, ANN | ✔ | ✚ | - Stability analysis by coefficient of variation - Assessing prediction symmetry by OEE/UEE | |||||||
| Gholami and Booij [169] | Iran | XGBoost > DL, MLR | ★✔ | ✔ | ✔ | - POF by XGBoost’s inherent features | |||||||
| Kumar and Pati [170] | As | India | DL > XGBoost, RF, GBM, DT, NB | ★ | ⃞ | ✔ | |||||||
| Karimanzira, et al. [171] | Germany | RF > various DLs | ✔ | ▲✔ | ✖ | ✔ | ✔ | ✔ | - Using leave-one-out encoding technique - POF in DL using Dropout technique - Addressing uncertainty using PICP and MPIW - Briefly discussing transferability - Addressing explainability - Superior model achieved fastest training | ||||
| D | Li, et al. [172] | England | KNN-SEL > GBDT, XGBoost, RF, ERT, KNN | ✔ | ★O | ✖ | ✔ | - Ensembling using KNN - Using SHAP to address explainability - Addressing stability and generalizability through CV - Superior model achieved better generalizability and stability | |||||
| Cao, et al. [173] | As, F− | China | LDA-SEL > RF, ERT, DT, XGBoost, AdB, GBDT, SVM, KNN, LDA, LgR, ANN | ✔ | ✖ | - Ensembling using LDA - Using optimal entropy-weighted to select SEL components | |||||||
| Moazamnia, et al. [174] | VI (Salinity) | Iran | SVM-AIMM > ANN, NF | ✔ | - Ensembling using SVM | ||||||||
| Nadiri, Gharekhani, Khatibi, Sadeghfam, and Moghaddam [124] | Iran | ANN-SICM > SVM, NF, GEP | ✔ | ✔ | - Ensembling using ANN - Yielding an explicit formula from GEP - Dividing study area into three parts due to heterogeneity | ||||||||
| Bordbar, et al. [175] | VI (SWI) | Iran | ANN-SCMAI > NF, SVM, ANN | ✔ | ✔ | - Ensembling using ANN - Assessing statistical significance of models’ differences by Friedman’s and WSR tests | |||||||
| Fijani, Nadiri, Moghaddam, Tsai, and Dixon [105] | VI () | Iran | ANN-SCMAI > ANN, ANFIS, | ✖ | ✔ | ✔ | - Ensembling using ANN - Using MOA (GA) to train the ensemble model | ||||||
| Barzegar, et al. [176] | RI () | Iran | ANN-Committee > SVR, M5 Tree, ELM, MARS | ✖ | ⃞ ✔✖ | ✔ | ✔ | ✖ | - Ensembling using ANN - POF by various inherent features - Briefly discussing explainability | ||||
| Barzegar, et al. [177] | VI () | Iran | ANN-SCMAI > ANN, NF | ✖ | ✔ | ✔ | - Ensembling using ANN - Using MOA (GA) to train the ensemble model | ||||||
| Jafarzadeh, et al. [178] | , TDS | Iran | AdB-Ens > AdB, XGBoost, LGBM, RF | ✔ | ⃞ | ✔ | - Ensembling using AdB - POF by various inherent features - Performing holistic GVM by integrating DRASTIC and GALDIT | ||||||
| Faal, Nikoo, Ashrafi, and Šimůnek [135] | Salinity (TDS) | Iran | GP-Ens > SVR-Ens, ANN-Ens, DNN, CNN, DBN, DSA | ✔ | ✔ | ✔ | - Ensembling using GP, SVR, ANN - POF by various inherent features - Superior model achieved fastest training | ||||||
| Usman, et al. [179] | F− | Africa | NB-SEL > LgR, DT, RF, SVM, NB, KNN, AdB, XGBoost, LGBM, CatBoost, GBDT, BA-DT, ANN, ERT, LDA | ✔ | ✖ | - Ensembling using NB - Briefly discussing transferability - POF by various inherent features - Addressing transferability by large-scale modeling | |||||||
| E | Jamei, et al. [180] | Salinity | Bangladesh | ANFIS-AO > ANFIS-SMA, ANFIS-ACO, LsR, ANFIS, | ✔ | ✔ ⃞ | ✔ | ✔ | - Addressing uncertainty by U95% - POF by Monte Carlo technique - Using MOAs (AO, ACO, SMA) for model optimization - Considering input scenarios | ||||
| Elzain, et al. [181] | VI () | S. Korea | ANFIS-PSO > ANFIS-DE, ANFIS-GA, ANFIS | ✔ | ★ | ✔ | ✔ | ✔ | - Using various MOAs for model optimization - Superior model achieved fastest training (amid MOAs) - Briefly discussing transferability | ||||
| De Jesus, et al. [182] | Cr, Cd, Fe, Mn, Zn, Ni, Pb, Cu | Philippines | PSO-ANN > SVM, MLR | ★✖ | ✔ | ✔ | ✔ | ✔ | - Using MOAs (PSO) for model optimization - Using KGE for model assessment - POF using early stopping approach | ||||
| Pham, et al. [183] | Vietnam | RF-FA > RF-MOE, RF-Ant, RF-GWO, RF-PSO, RF | ★ | ✔ | ✔ | - Using various MOAs for model optimization - Briefly discussing transferability - Superior model achieved fastest convergence (amid MOAs) | |||||||
| Saha, et al. [184] | VI | India | RF-GOA > RF-GWO, RF-PSO, RF | ❄✔★ | ✔ | - Using various MOAs for model optimization - Briefly discussing transferability | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrabi, M.; Polya, D.A.; Han, Y. Machine Learning Models of the Geospatial Distribution of Groundwater Quality: A Systematic Review. Water 2025, 17, 2861. https://doi.org/10.3390/w17192861
Mehrabi M, Polya DA, Han Y. Machine Learning Models of the Geospatial Distribution of Groundwater Quality: A Systematic Review. Water. 2025; 17(19):2861. https://doi.org/10.3390/w17192861
Chicago/Turabian StyleMehrabi, Mohammad, David A. Polya, and Yang Han. 2025. "Machine Learning Models of the Geospatial Distribution of Groundwater Quality: A Systematic Review" Water 17, no. 19: 2861. https://doi.org/10.3390/w17192861
APA StyleMehrabi, M., Polya, D. A., & Han, Y. (2025). Machine Learning Models of the Geospatial Distribution of Groundwater Quality: A Systematic Review. Water, 17(19), 2861. https://doi.org/10.3390/w17192861







