Comparative Study of Shallow and Deep Learning-Based Data-Driven Models for Monthly Runoff Simulation in the Yalong River Basin
Abstract
1. Introduction
2. Methodology
2.1. Shallow Data-Driven Models
2.1.1. ANN
2.1.2. SVM
2.1.3. ELM
2.2. Deep Learning Models
2.2.1. LSTM
2.2.2. CNN
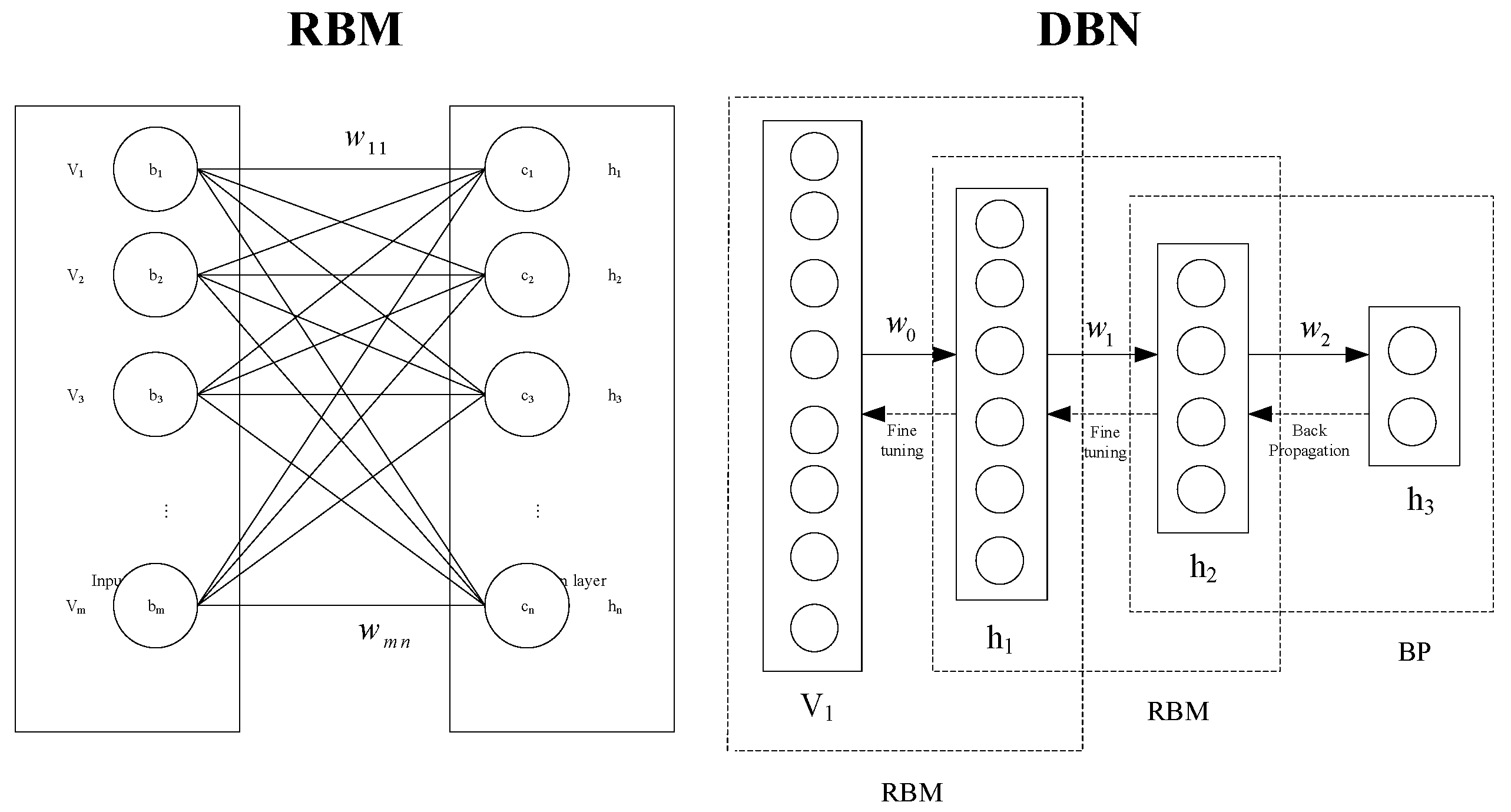
2.2.3. DBN
2.3. Evaluation Criteria
3. Study Region and Data
4. Results and Discussion
4.1. Data Pre-Processing
4.2. Factors Selection Results
4.3. Parameters Settings
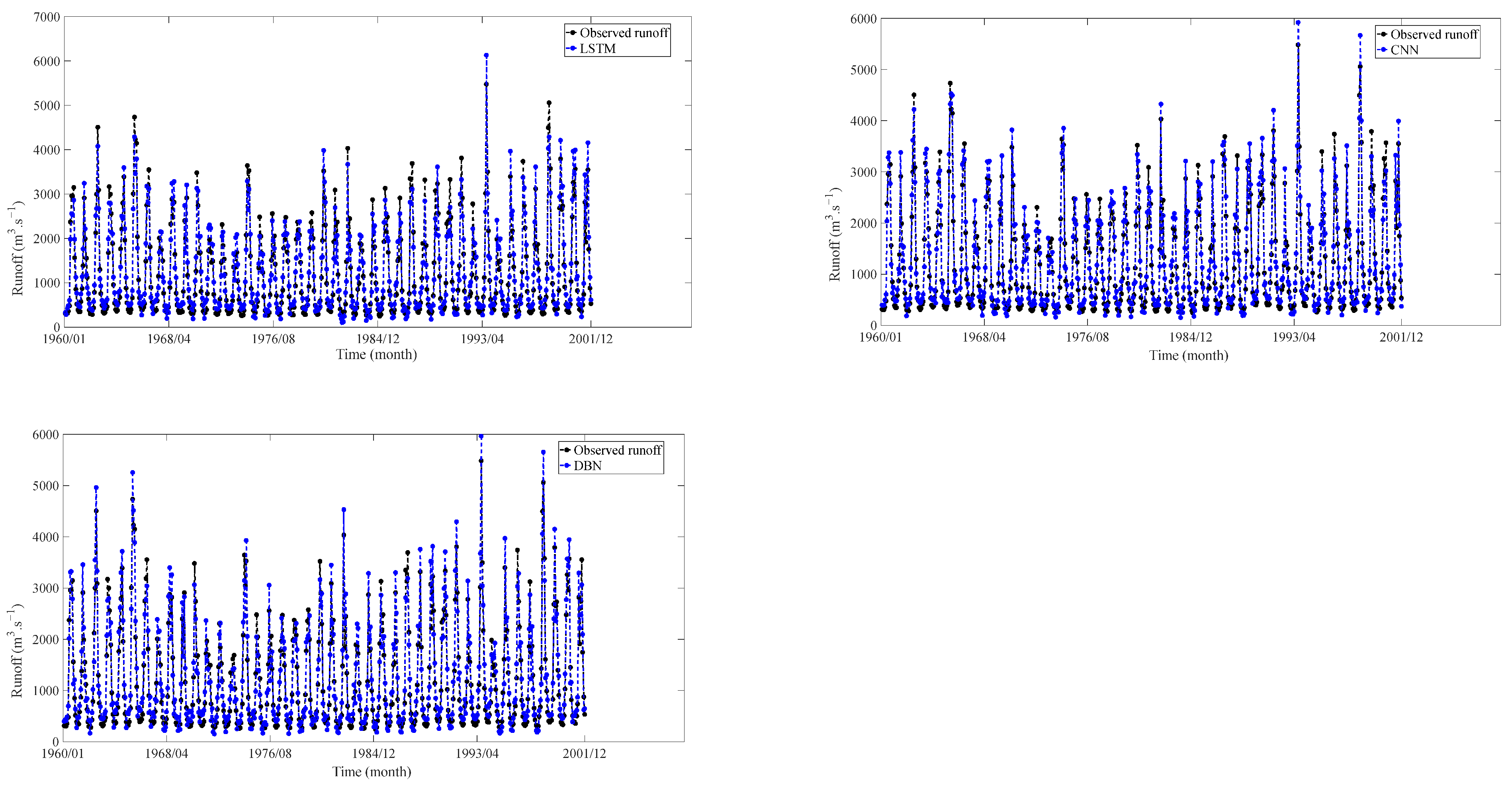
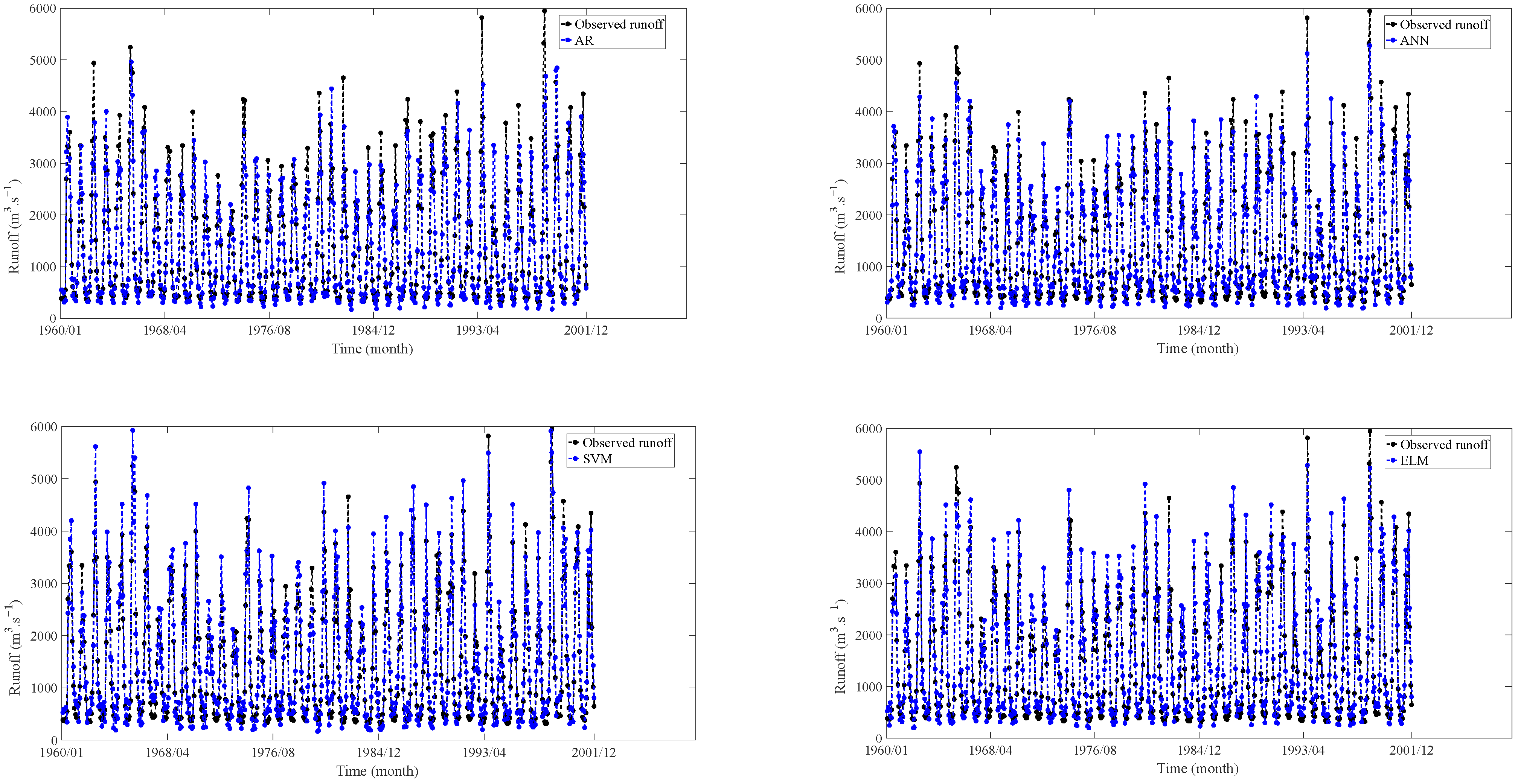
4.4. Monthly Runoff Training Results
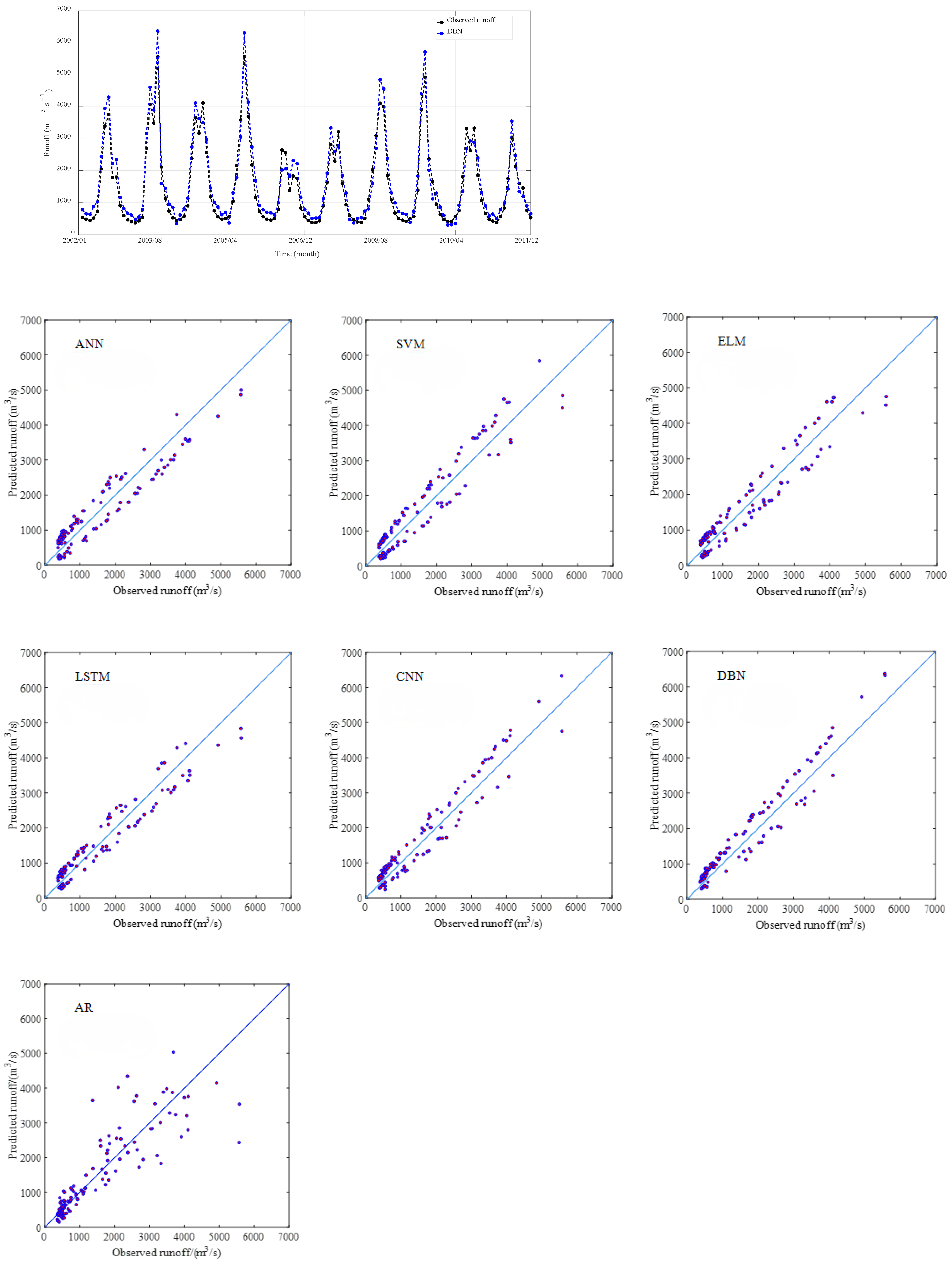
4.5. Monthly Runoff Validation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, Q.F.; Lei, X.H.; Wang, X.; Wang, H.; Wen, X.; Ji, Y.; Kang, A.Q. An adaptive middle and long-term runoff forecast model using EEMD-ANN hybrid approach. J. Hydrol. 2018, 567, 767–780. [Google Scholar] [CrossRef]
- Yue, Z.; Ai, P.; Xiong, C.; Hong, M.; Song, Y. Mid-to long-term runoff prediction by combining the deep belief network and partial least-squares regression. J. Hydroinform. 2020, 22, 1283–1305. [Google Scholar] [CrossRef]
- Yue, Z.; Ai, P.; Yuan, D.; Xiong, C. Ensemble approach for mid-long term runoff forecasting using hybrid algorithms. J. Ambient Intell. Humaniz. Comput. 2020, 13, 5103–5122. [Google Scholar] [CrossRef]
- Barge, J.T.; Sharif, H.O. An Ensemble Empirical Mode Decomposition, Self-Organizing Map, and Linear Genetic Programming Approach for Forecasting River Streamflow. Water 2016, 8, 247. [Google Scholar] [CrossRef]
- Yue, Z.; Liu, H.; Zhou, H. Monthly Runoff Forecasting Using Particle Swarm Optimization Coupled with Flower Pollination Algorithm-Based Deep Belief Networks: A Case Study in the Yalong River Basin. Water 2023, 15, 2704. [Google Scholar] [CrossRef]
- Tripathy, K.P.; Mishra, A.K. Deep learning in hydrology and water resources disciplines: Concepts, methods, applications, and research directions. J. Hydrol. 2024, 628, 130458. [Google Scholar] [CrossRef]
- Islam, Z. A Review on Physically Based Hydrologic Modeling; University of Alberta: Edmonton, AB, Canada, 2011. [Google Scholar]
- Kim, T.; Yang, T.; Gao, S.; Zhang, L.; Ding, Z.; Wen, X.; Gourley, J.J.; Hong, Y. Can artificial intelligence and data-driven machine learning models match or even replace process-driven hydrologic models for streamflow simulation?: A case study of four watersheds with different hydro-climatic regions across the CONUS. J. Hydrol. 2021, 598, 126423. [Google Scholar] [CrossRef]
- Jiang, Z.; Lu, B.; Zhou, Z.; Zhao, Y. Comparison of Process-Driven SWAT Model and Data-Driven Machine Learning Techniques in Simulating Streamflow: A Case Study in the Fenhe River Basin. Sustainability 2024, 16, 6074. [Google Scholar] [CrossRef]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of rainfall-runoff models: Application of global optimization to the Sacramento Soil Moisture Accounting Model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Moreda, F.; Koren, V.; Zhang, Z.; Reed, S.; Smith, M. Parameterization of distributed hydrological models: Learning from the experiences of lumped modeling. J. Hydrol. 2006, 320, 218–237. [Google Scholar] [CrossRef]
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 397, 225–237. [Google Scholar] [CrossRef]
- Chu, W.; Gao, X.; Sorooshian, S. Improving the shuffled complex evolution scheme for optimization of complex nonlinear hydrological systems: Application to the calibration of the Sacramento soil moisture accounting model. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, X. The Xinanjiang Model, Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: California City, CA, USA, 1995; pp. 215–232. [Google Scholar]
- Xu, H.; Xu, C.Y.; Chen, H.; Zhang, Z.; Li, L. Assessing the influence of rain gauge density and distribution on hydrological model performance in a humid region of China. J. Hydrol. 2013, 505, 1–12. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, H.; Xu, C.Y.; Jie, M.-X.; Chen, J.; Guo, S.-L.; Liu, J. The effect of rain gauge density and distribution on runoff simulation using a lumped hydrological modelling approach. J. Hydrol. 2018, 563, 106–122. [Google Scholar] [CrossRef]
- Fang, Y.H.; Zhang, X.; Corbari, C.; Mancini, M.; Niu, G.-Y.; Zeng, W. Improving the Xin’anjiang hydrological model based on mass–energy balance. Hydrol. Earth Syst. Sci. 2017, 21, 3359–3375. [Google Scholar] [CrossRef]
- Xu, D.; Wang, W.; Chau, K.; Cheng, C.-T.; Chen, S.-Y. Comparison of three global optimization algorithms for calibration of the Xinanjiang model parameters. J. Hydroinform. 2013, 15, 174–193. [Google Scholar] [CrossRef]
- Sheng, Z.; Wen, S.; Feng, Z.K.; Gong, J.; Shi, K.; Guo, Z.; Yang, Y.; Huang, T. A survey on data-driven runoff forecasting models based on neural networks. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 1083–1097. [Google Scholar] [CrossRef]
- Mohammadi, B. A review on the applications of machine learning for runoff modeling. Sustain. Water Resour. Manag. 2021, 7, 98. [Google Scholar] [CrossRef]
- Yazdani, M.R.; Saghafian, B.; Mahdian, M.H.; Soltani, S. Monthly runoff estimation using artificial neural networks. J. Agric. Sci. Technol. 2009, 11, 335–362. [Google Scholar]
- Samantaray, S.; Das, S.S.; Sahoo, A.; Satapathy, D.P. Monthly runoff prediction at Baitarani river basin by support vector machine based on Salp swarm algorithm. Ain Shams Eng. J. 2022, 13, 101732. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- He, C.; Chen, F.; Long, A.; Qian, Y.; Tang, H. Improving the precision of monthly runoff prediction using the combined non-stationary methods in an oasis irrigation area. Agric. Water Manag. 2023, 279, 108161. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Zeng, S.; Tang, Z.; Liu, L.; Zhang, Q.; Tang, Z.; Hua, X. Predicting Monthly Runoff of the Upper Yangtze River Based on Multiple Machine Learning Models. Sustainability 2022, 14, 11149. [Google Scholar] [CrossRef]
- Sit, M.A.; Demiray, B.Z.; Xiang, Z.; Ewing, G.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep learning convolutional neural network in rainfall–runoff modelling. J. Hydroinform. 2020, 22, 541–561. [Google Scholar] [CrossRef]
- Wang, W.C.; Wang, B.; Chau, K.W.; Xu, D.M. Monthly runoff time series interval prediction based on WOA-VMD-LSTM using non-parametric kernel density estimation. Earth Sci. Inform. 2023, 16, 2373–2389. [Google Scholar] [CrossRef]
- Jain, A.; Mao, J.; Mohiuddin, K. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Haykin, S.; Network, N. A comprehensive foundation. Neural Netw. 2004, 2, 41. [Google Scholar]
- Huang, G.B.; Zuo, B.; Gong, W.Y.; Kasun, L.L.C.; Vong, C.M. Local receptive fields based extreme learning machine. IEEE Comput. Intell. Mag. 2015, 10, 18–29. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2018, 569, 387–408. [Google Scholar] [CrossRef]
- Schmidhuber, J.; Hochreiter, S. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Khan, A.; Zhang, Y.-K.; Kuang, X.; Liang, X.; Taccari, M.L.; Nuttall, J. Daily runoff forecasting by deep recursive neural network. J. Hydrol. 2021, 596, 126067. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Shu, X.; Ding, W.; Peng, Y.; Wang, Z.; Wu, J.; Li, M. Monthly Streamflow Forecasting Using Convolutional Neural Network. Water Resour. Manag. 2021, 35, 5089–5104. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, X.; Xie, J.; Zhang, X.; Liu, S. Monthly Runoff Interval Prediction Based on Fuzzy Information Granulation and Improved Neural Network. Water 2022, 14, 3683. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Ai, P.; Song, Y.; Xiong, C.; Chen, B.; Yue, Z. A novel medium-and long-term runoff combined forecasting model based on different lag periods. J. Hydroinform. 2022, 24, 367–387. [Google Scholar] [CrossRef]
- Erdem, O.; Ceyhan, E.; Varli, Y. A new correlation coefficient for bivariate time-series data. Phys. A Stat. Mech. Its Appl. 2014, 414, 274–284. [Google Scholar] [CrossRef]
- Deng, W.; Yao, R.; Zhao, H.; Yang, X.; Li, G. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 2019, 23, 2445–2462. [Google Scholar] [CrossRef]





















| Statistical Measures (m3·s−1) | ||||||
|---|---|---|---|---|---|---|
| Station | Time Periods | Samples | Min. | Max. | Ave. | Stdev. |
| LHK | 1960.01–2011.12 | All samples | 108 | 2860 | 661.54 | 557.25 |
| 1960.01–2001.12 | Training samples | 108 | 2860 | 662.68 | 551.84 | |
| 2002.01–2011.12 | Validation samples | 124 | 2800 | 656.77 | 581.76 | |
| JP | 1960.01–2011.12 | All samples | 243 | 5480 | 1208.65 | 1032.63 |
| 1960.01–2001.12 | Training samples | 243 | 5480 | 1208.59 | 1036.85 | |
| 2002.01–2011.12 | Validation samples | 285 | 4660 | 1208.89 | 1019.01 | |
| GD | 1960.01–2011.12 | All samples | 303 | 5950 | 1416.25 | 1187.83 |
| 1960.01–2001.12 | Training samples | 303 | 5950 | 1413.29 | 1189.56 | |
| 2002.01–2011.12 | Validation samples | 329 | 5200 | 1428.65 | 1185.41 | |
| ET | 1960.01–2011.12 | All samples | 365 | 6920 | 1617.32 | 1375.17 |
| 1960.01–2001.12 | Training samples | 369 | 6920 | 1643.14 | 1398.9 | |
| 2002.01–2011.12 | Validation samples | 365 | 5574 | 1508.85 | 1270.44 | |
| Hydrological Stations | Factors Selection Results |
|---|---|
| LHK | cli31 (m-1), rf (m-1), mar (m-1), cli43 (m-6), cli29 (m-12), cli44 (m-12), mar (m-12) |
| JP | cli14 (m-1), rf (m-1), mar (m-1), cli43 (m-6), cli44 (m-6), cli44 (m-12), rf (m-12) |
| GD | cli14 (m-1), cli21 (m-1), rf (m-1), mar (m-1), cli43 (m-7), cli29 (m-8), cli33 (m-8), cli44 (m-12), rf (m-12) |
| ET | rf (m-1), mar (m-1), cli43 (m-7), cli44 (m-7), cli29 (m-8), cli33 (m-8) |
| Key Factors | Interpretation |
|---|---|
| mar | Monthly average runoff |
| rf | Constructing the rain factor via the Tyson Polygon algorithm based on the 22 meteorological stations in the YRB |
| cli14 | North African–North Atlantic–North American Subtropical High Intensity Index (110° W-60° E) |
| cli21 | North American–North Atlantic Subtropical High Intensity Index (110° W-20° W) |
| cli29 | Asia Polar Vortex Intensity Index (1, 60° E-150° E) |
| cli31 | North American Polar Vortex Intensity Index (3, 120° W-30° W) |
| cli33 | Northern Hemisphere Polar Vortex Intensity Index (5, 0-360) |
| cli43 | Tibet Plateau Region Index (25° N-35° N, 80° E-100° E) |
| cli44 | Tibet Plateau Region Index (30° N-40° N, 75° E-105° E) |
| Hydrological Station | Model | MAPE (%) | RMSE (m3·s−1) | NSE | R2 |
|---|---|---|---|---|---|
| LHK | AR | 26.65 | 287.8 | 0.7275 | 0.7309 |
| ANN | 28.79 | 231.43 | 0.8238 | 0.8424 | |
| SVM | 24.28 | 223.6 | 0.8355 | 0.8461 | |
| ELM | 21.17 | 214.01 | 0.8439 | 0.8768 | |
| LSTM | 21.78 | 178.46 | 0.8952 | 0.9123 | |
| CNN | 21.83 | 180.09 | 0.8933 | 0.9144 | |
| DBN | 16.81 | 163.53 | 0.912 | 0.9353 | |
| JP | AR | 24.27 | 486.55 | 0.7794 | 0.781 |
| ANN | 25.3 | 296.51 | 0.9181 | 0.9208 | |
| SVM | 28.27 | 304.33 | 0.9137 | 0.9194 | |
| ELM | 26.84 | 291.58 | 0.9208 | 0.9335 | |
| LSTM | 28.53 | 288.73 | 0.9223 | 0.925 | |
| CNN | 28.17 | 272.57 | 0.9308 | 0.9391 | |
| DBN | 28.29 | 286.35 | 0.9236 | 0.9309 | |
| GD | AR | 23.63 | 550.51 | 0.7854 | 0.7868 |
| ANN | 30.93 | 357.2 | 0.9097 | 0.9104 | |
| SVM | 34.43 | 380.32 | 0.8976 | 0.9108 | |
| ELM | 30.04 | 358.08 | 0.9092 | 0.9216 | |
| LSTM | 27.41 | 328.4 | 0.9236 | 0.9292 | |
| CNN | 25.75 | 307.4 | 0.9331 | 0.9457 | |
| DBN | 28.04 | 334.09 | 0.921 | 0.9424 | |
| ET | AR | 24.21 | 637.25 | 0.7921 | 0.7933 |
| ANN | 27.48 | 366.27 | 0.9313 | 0.9387 | |
| SVM | 29.37 | 378.85 | 0.9265 | 0.9361 | |
| ELM | 27.91 | 365.09 | 0.9318 | 0.9319 | |
| LSTM | 27.79 | 340.98 | 0.9405 | 0.9414 | |
| CNN | 24.43 | 329.35 | 0.9445 | 0.9508 | |
| DBN | 30.88 | 346.71 | 0.9384 | 0.9576 |
| Hydrological Station | Model | MAPE (%) | RMSE (m3·s−1) | NSE | R2 |
|---|---|---|---|---|---|
| LHK | AR | 28.94 | 311.61 | 0.7107 | 0.714 |
| ANN | 45.73 | 258.06 | 0.8016 | 0.8061 | |
| SVM | 44.42 | 254.87 | 0.8065 | 0.841 | |
| ELM | 42.31 | 245.98 | 0.8197 | 0.8524 | |
| LSTM | 40.41 | 236.48 | 0.8334 | 0.8495 | |
| CNN | 38.26 | 231.04 | 0.841 | 0.8639 | |
| DBN | 33.62 | 224.65 | 0.8496 | 0.8836 | |
| JP | AR | 31.63 | 629.04 | 0.6157 | 0.6515 |
| ANN | 39.54 | 381.64 | 0.8586 | 0.8589 | |
| SVM | 32.63 | 348.27 | 0.8822 | 0.9127 | |
| ELM | 37.46 | 342.92 | 0.8858 | 0.8926 | |
| LSTM | 30.38 | 303.81 | 0.9104 | 0.9178 | |
| CNN | 30 | 298.51 | 0.9135 | 0.9146 | |
| DBN | 29.56 | 306.51 | 0.9088 | 0.9396 | |
| GD | AR | 26.89 | 615.36 | 0.7283 | 0.7343 |
| ANN | 41.1 | 441.42 | 0.8602 | 0.868 | |
| SVM | 33.62 | 358.03 | 0.908 | 0.9312 | |
| ELM | 35.13 | 353.72 | 0.9102 | 0.9318 | |
| LSTM | 29.6 | 334.56 | 0.9197 | 0.9242 | |
| CNN | 30.12 | 361.21 | 0.9064 | 0.9233 | |
| DBN | 28.67 | 336.91 | 0.9185 | 0.9371 | |
| ET | AR | 25.93 | 641.98 | 0.7425 | 0.7503 |
| ANN | 38.89 | 411.87 | 0.894 | 0.9051 | |
| SVM | 33.02 | 403.43 | 0.8983 | 0.9134 | |
| ELM | 33.3 | 384.01 | 0.9079 | 0.9081 | |
| LSTM | 29.33 | 352.17 | 0.9225 | 0.9266 | |
| CNN | 28.65 | 351.49 | 0.9228 | 0.9385 | |
| DBN | 28.31 | 361.67 | 0.9183 | 0.9452 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Z.; Wang, L.; Zhu, J.; Zhou, H. Comparative Study of Shallow and Deep Learning-Based Data-Driven Models for Monthly Runoff Simulation in the Yalong River Basin. Water 2025, 17, 2735. https://doi.org/10.3390/w17182735
Yue Z, Wang L, Zhu J, Zhou H. Comparative Study of Shallow and Deep Learning-Based Data-Driven Models for Monthly Runoff Simulation in the Yalong River Basin. Water. 2025; 17(18):2735. https://doi.org/10.3390/w17182735
Chicago/Turabian StyleYue, Zhaoxin, Li Wang, Jun Zhu, and Hui Zhou. 2025. "Comparative Study of Shallow and Deep Learning-Based Data-Driven Models for Monthly Runoff Simulation in the Yalong River Basin" Water 17, no. 18: 2735. https://doi.org/10.3390/w17182735
APA StyleYue, Z., Wang, L., Zhu, J., & Zhou, H. (2025). Comparative Study of Shallow and Deep Learning-Based Data-Driven Models for Monthly Runoff Simulation in the Yalong River Basin. Water, 17(18), 2735. https://doi.org/10.3390/w17182735








