Abstract
Nowadays, climate change is one of the significant threats humanity faces. Many researchers have documented its effects on water availability and vulnerable systems. This study examines the long-term precipitation record (1965–2019) from the Tulcea station, located just 4 km from the Danube Delta Biosphere Reserve (DDBR), to evaluate the impact of climate change on precipitation variability, which can significantly affect biodiversity in this protected area. We integrated change point detection (CPD), stationarity tests, trend analysis, and series decomposition to characterize shifts and patterns in the time series. The Lee & Heghinian test detected a change point (CP) in all data series, whereas the Hubert segmentation methods and Cumulative Sum Method (CUSUM) found fewer series that present at least a CP. The Mann–Kendall (MK) trend test and Innovative Trend Analysis (ITA) indicated an increasing trend in the annual, monthly, and October precipitation series. The Seasonal-Trend decomposition using Loess STL decomposition found the highest seasonality indices in June and July. The Ensemble Empirical Mode Decomposition (EEMD) emphasizes a substantial difference in the seasonal cycle. The results indicate a high variability in the precipitation pattern, with periods of high precipitation followed by dry periods.
1. Introduction
Climate change has emerged as one of the most pressing environmental challenges of our time, profoundly influencing water resources and hydrological systems across the globe [1]. Understanding the induced changes’ mechanisms, timing, and spatial patterns is essential for ensuring sustainable water management, safeguarding public access to fresh water, and minimizing adverse impacts on water quality and ecosystems [2,3]. The modification in precipitation regime directly affects water availability and quality, ecosystem health, agriculture, and human activities [4,5,6,7].
Over recent decades, observational data and climate model simulations have documented significant alterations in precipitation intensity, frequency, and spatial distribution, primarily driven by evolving atmospheric circulation and humidity patterns [8,9,10]. These changes have increased hydrological variability, with some regions experiencing intensified flooding and others enduring prolonged droughts. Such shifts present growing challenges for freshwater management and ecosystem resilience [11,12,13].
To better understand and respond to these threats, robust statistical tools are needed to analyze hydro-meteorological time series data. Time series analysis plays a central role in hydrology, climatology, and meteorology, particularly for studying long-term temperature and precipitation series, key indicators of climate variability and change. Identifying trends, seasonal cycles, and structural changes in these variables is critical for interpreting underlying climate dynamics [14,15,16].
An important concern when studying time series evolution is the determination of breakpoints or change points, i.e., detecting the moments where there are modifications of the series’ statistical properties or distribution. They are widely utilized across disciplines, including hydrometeorology [17,18,19,20], healthcare [21], signal processing [22,23], etc.
Trend detection and seasonal decomposition methods enable the separation of intra-annual cycles from longer-term patterns and random noise, thereby enhancing insights into seasonal behavior and its evolution over time [24,25,26,27].
Precipitation variability has substantial environmental and socio-economic implications, especially in regions where water resources are already constrained or climate conditions are highly variable. One such area is DDBR, a UNESCO World Heritage Site and Ramsar Wetland of international importance, one of Europe’s most dynamic and ecologically valuable wetland systems. Belonging to the Dobrogea region in southeastern Romania, DDBR is particularly sensitive to climatic fluctuations due to its low elevation, fragile ecosystems, and strong dependency on hydrological regimes [28,29,30,31].
Most of the previous research primarily focused on analyzing extreme weather events in Dobrogea in general. For instance, a Generalized Pareto Distribution was applied to the extreme monthly precipitation series [32], and 11 rainfall extreme indices were calculated using daily precipitation data from January 1961 to December 2005 [33]. The studies [34,35] have indicated a significant increase in drought events in Romania, particularly in Dobrogea, from 1980 to 2000, with more than 50% of those years experiencing below-average rainfall, whereas SPI12 and SPEI12 readings at Sulina indicate an increase in the frequency and duration of droughts, especially since the early 1980s [36].
Despite existing analyses of the broader Dobrogea region, few have specifically addressed precipitation dynamics in the Danube downstream area, and none have utilized extended time series data reaching up to the recent years. Therefore, this research aims to address the long-term precipitation variability at the mouth of the Danube, with a focus on the DDBR, an area that has received limited attention in previous studies [37,38,39]. This paper seeks to fill that gap by examining long-term precipitation records from Tulcea, at the boundary of the Danube Delta, to detect structural breaks, trends, and seasonal shifts. These changes may indicate broader hydrological transformations, with significant implications for water resource management, ecosystem resilience, and flood or drought risk in the DDBR. In doing so, the research provides critical insights into the climate sensitivity of one of Europe’s most ecologically vulnerable wetland systems.
2. Study Area and Data Series
Dobrogea is located in the southeastern part of Romania. It is bounded by the Danube River to the west and north, the Black Sea to the east, and Bulgaria to the south. It covers approximately 23,000 km2 and includes Constanța and Tulcea counties [34] and the Danube Delta. Its topography is a combination of low-lying plains, hills, and the Măcin Mountains. Climatically, Dobrogea (Figure 1, left) lies in a transition zone between temperate-continental and maritime influences, with steppe characteristics particularly evident in its central and southern areas. Dobrogea is one of the driest regions in Romania.
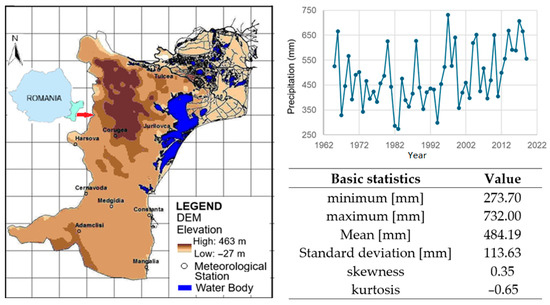
Figure 1.
(left) Dobrogea region; (top right) Annual precipitation series spanning 1965–2019 recorded at Tulcea; (bottom right) Basic statistics of the annual series recorded at Tulcea.
The mean annual precipitation recorded at ten main hydrometeorological stations in the region varied between 350 and 450 mm during the period 1965–2005 [12,32]. Rainfall is irregular, seasonally concentrated. The climate is often marked by prolonged dry spells and sudden, intense convective events, posing significant challenges to agriculture, water resource management, and ecosystem stability [40,41,42,43].
The Danube Delta is the Europe’s second largest and one of the most intact deltaic systems. It is a biodiversity hotspot that hosts over 5000 species, including numerous rare and endangered taxa. Its complex mosaic of freshwater, brackish, and terrestrial habitats, offers a unique natural laboratory for studying ecosystem function, species interactions, and environmental change. The Delta is a critical migratory corridor for over 300 avian species (including threatened taxa such as the white-tailed eagle, red-breasted goose, and Dalmatian pelican). It also contains the world’s largest continuous reed bed system, which plays a vital role in water filtration, habitat provision, and sediment stabilization. Hydrology is a key driver of ecological processes in the Delta. Seasonal flooding, particularly in spring, reshapes habitats, enriches nutrient availability, and sustains the reproductive cycles of many species. These temporal dynamics underpin the Delta’s exceptional biological productivity. Recognized as a UNESCO World Heritage Site and Ramsar Wetland, the Danube Delta deserves detailed investigation to sustain its conservation and management efforts in the face of ongoing climate change and anthropogenic pressures [44].
Tulcea is in inland Dobrogea, at the western edge of the DDBR. The distance to ecologically sensitive wetland zones is 3 to 5 km, and that to the strictly protected areas around 10 km from. Tulcea serves as the administrative center and logistical gateway to the DDBR. It is designed as the primary observation site for monitoring climate-induced changes in water systems [45]. It offers long-term climate records to the European Climate Assessment & Dataset. This makes it strategically important for understanding regional climate variability and hydrological dynamics in the Danube Delta. Due to its geographical position, Tulcea is exposed to maritime and deltaic influences. In 2019, at Tulcea, about 271 days were without rain. The number of rainy days was between 3 and 8 per month, with the highest average precipitation in June (about 80 mm) and the lowest in August (23 mm).
Although there are other main meteorological stations in Dobrogea, all are situated inland, at least 65 km from the Danube Delta. Therefore, the climate at those stations is not the same as in the DDBR. Extrapolating the results of the analysis performed for the precipitation series from those stations to the Danube Delta would not be correct. So, the study of the data collected at Tulcea is essential for understanding the variability in the DDBR. The analyzed series consists of precipitations recorded at Tulcea from 1965 to 2019 as follows:
- -
- the total annual precipitation series, denoted by ANTOT (Figure 1 (top, right));
- -
- the total monthly precipitation series that spans January 1965 to December 2019, denoted by MTOT (Figure 2a);
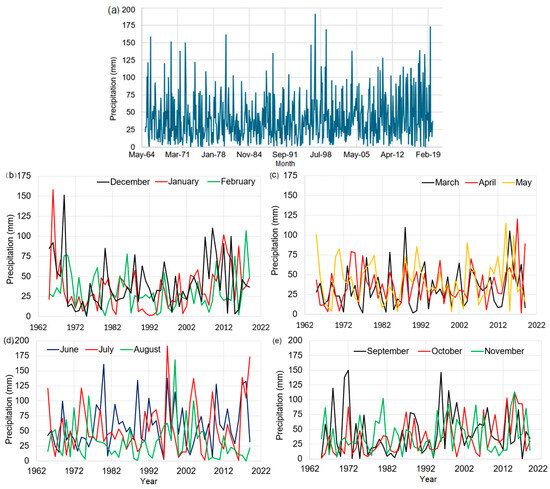 Figure 2. (a) MTOT, (b) Precipitation series recorded in December, January, and February. (c) Precipitation series recorded in March, April, and May. (d) Precipitation series recorded in June, July, and August. (e) Precipitation series recorded in September, October, and November.
Figure 2. (a) MTOT, (b) Precipitation series recorded in December, January, and February. (c) Precipitation series recorded in March, April, and May. (d) Precipitation series recorded in June, July, and August. (e) Precipitation series recorded in September, October, and November. - -
- the monthly series recorded each month (e.g., January series, formed by the precipitation recorded in January from 1965 to 2019, February series, etc.) (Figure 2b–e).
The series are sourced from the National Institute of Meteorology, where they were checked for accuracy. No series contains missing values.
3. Methodology
The study involved the stages summarized in the flowchart in Figure 3.
Figure 3.
A flowchart of the study.
The below steps were followed:
- (1)
- Computation of the basic statistics and detection of outliers.
- (2)
- Testing the hypothesis that the series is Gaussian against non-normality by the Shapiro-Wilks test [46]. This step is important when applying the CPD and trend tests, given that some of them rely on the normality hypothesis.
- (3)
- Build the autocorrelation function to evaluate the series autocorrelation.
- (4)
- Test the hypothesis that the series presents a unit root against stationarity by the Augmented Dickey–Fuller (ADF) test [47], and the trend- or level-stationarity against the trend- or level-nonstationarity by the KPSS [48] test.
- (5)
- Determine the CPs.
Given that various statistical techniques involve the series stationarity, CPs’ identification is essential for ensuring the high accuracy of the models and reliable forecasts. CPD methods offer a robust statistical framework for identifying transitions between different climatic regimes.
The CPs’ existence was first tested by the Buishand [49], Pettitt [50], and Lee & Heghinian [51] tests. All these methods check the hypothesis that there is a CP against no CP. The first and third tests can be utilized only when the series is Gaussian, or the normality can be reached after a Box–Cox transformation. By contrast, Hubert’s segmentation procedure [52] and CUSUM [53] can detect multiple CPs and have the advantage that there is no restriction to the series distribution. In the case of the last procedure, for a given segmentation, Scheffé’s test [54] assesses whether adjacent segments have statistically distinct means, validating the segmentation. We shall focus on the CUSUM algorithm implemented in the CPA [55] software.
Given a data series, the steps of the CUSUM are as follows:
- Compute the average of the data series, ;
- Initiate the cumulative sum by zero and compute recurrently these sums by adding to the previous one the deviation of the series value from the mean;
- Determine the range and amplitude of the series sums (i.e., the difference between the maximum and minimum sums).
- Bootstrap the data series.
- Determine the amplitude of the new sums’ series.
- Determine the confidence level of the CP apparition CL(%) as the ratio between the number of samples for which the value obtained at v. is smaller than that from iii.
When the autocorrelation hypothesis was rejected, the nonparametric version of the test, in which the median replaced the average, was used.
- (6)
- Study of trend existence.
Alongside abrupt changes, gradual trends and seasonal variability are essential to understanding precipitation dynamics. Nonparametric trend detection techniques are employed to assess monotonic trends in climate data due to their robustness to non-normal distributions and data irregularities [24,25]. Therefore, we used the classical Mann–Kendall (MK) test and the Hirsh-Slack (seasonal Mann–Kendall) (SMK) test [56] to test the series randomness against the existence of a monotonic trend. The series trend, if significant, was determined by Sen’s nonparametric method [57].
The results were compared to those of Şen’s innovative trend analysis (ITA) [58], which involved dividing the series into two halves, sorting each in ascending order, and plotting the second subseries versus the first one. If the points are situated around the first bisector of the coordinate axes, there is no trend in the data series. Grouping the points below this line indicates a decreasing tendency, while clustering above the line implies an increasing trend.
- (7)
- Decompose the MTOT to emphasize the trend and seasonality.
STL [26] is an adaptive method for analyzing time series data. It decomposes a series into three additive components: a long-term trend, a seasonal component that captures periodic fluctuations, and a residual term representing irregular variation. Unlike classical decomposition methods, STL employs locally estimated scatterplot smoothing (LOESS), enabling it to model nonlinear trends and seasonality that may vary over time. Additionally, STL is robust to outliers, ensuring that anomalous observations exert minimal influence on the estimated components [59].
- (8)
- Decompose the MTOT into IMFs using the Empirical Mode Decomposition method, to determine the short and long-term variation in the precipitation series [60,61], by the following procedure.
- Build the lower and upper envelopes by interpolating the local minima and maxima, respectively;
- Build the average of the lower and upper envelopes;
- Compute the detail component, h, as the difference between the series and the mean envelope;
- Check if h is an IMF, i.e.,
- o
- There is an equal number of zero-crossings and extrema, or the difference between them is 1;
- o
- The average of the lower and upper envelopes of h is zero everywhere;
- If h does not fulfill the IMF conditions, repeat all stages with h instead of the raw series.
- If h fulfills the IMF conditions, stop. At that moment, the series will be written as a sum of IMFs and a residual.
EMD enables the extraction of oscillatory components from nonstationary signals and reveals how these variations evolve across different time scales.
4. Results
The basic statistics of the monthly series are presented in Table 1. The highest amplitude of the monthly series corresponds to July, June, and January. The highest standard deviation was found in July, followed by September and June.

Table 1.
Basic statistics of the monthly series.
By comparison, ANTOT and MTOT have amplitudes (i.e., maximum–minimum) of 458.30 mm and 190.40 mm, means of 484.19 mm and 40.35, and standard deviations of 113.63 mm and 32.28 mm, respectively.
The highest number of outliers was detected in October, indicating years with high precipitation compared to similar months in other years. All series are right-skewed, and all but November are leptokurtic. November is the only series without aberrant values. MTOT also has outliers, indicating a high variability of the entire monthly series. The boxplots are presented in Figure 4.
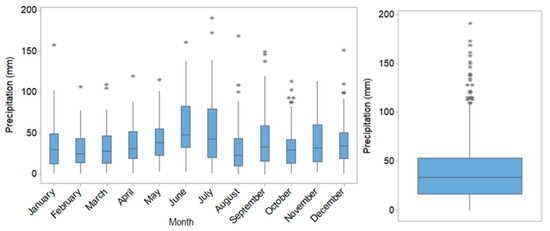
Figure 4.
The boxplot of the series by month (left) and the box of MTOT (right).
The presence of numerous outliers in the October precipitation series in Tulcea, in contrast to the absence of outliers in November, can be attributed to the distinct atmospheric dynamics characterizing the two months. October represents a transitional period between the warm season and the onset of winter, during which residual high sea surface temperatures in the Black Sea and incursions of cold air from northern latitudes frequently interact. This interaction fosters conditions favorable for convective activity and cyclogenesis, leading to occasional episodes of intense rainfall and high variability in daily or monthly precipitation totals. These extreme events contribute to a broader distribution of values and the emergence of statistical outliers. In contrast, November is typically characterized by more stable atmospheric conditions, lower temperatures, and reduced convective potential, resulting in more uniform and moderate precipitation. Consequently, the November precipitation series tends to exhibit lower variability and lacks the extreme values necessary to generate statistical outliers. This seasonal contrast underscores the impact of regional climatic dynamics and transitional weather patterns on precipitation variability in the lower Danube and Black Sea regions.
The distribution of ANTOT is almost symmetric, is slightly platykurtic (Figure 1), and has no outliers. MTOT is right-skewed and leptokurtic. The hypothesis of series normality was rejected for all series. The series distribution was almost Gaussian after various transformations. The third column in Table 2 contains the type of transformation and the corresponding parameter, if applicable.

Table 2.
Autocorrelation, transformations to reach normality, and results of stationarity tests.
According to the article of Wang et al. [62], the transformations improve the power of detection methods and increase the accuracy in identifying shifts in data patterns. The raw data series were used for other tests, so that the physical significance of the data was not impacted.
The last three columns of the same table contain the ADF and KPSS tests’ results and the corresponding p-values (inside the brackets) for trend- and level-stationarity. In the second column of Table 2, ‘yes’ indicates the existence of the series autocorrelation. In the third column, ‘Box–Cox’ followed by a number, indicates the parameter in the Box–Cox transformation utilized to reach the series’ normality. ‘Yes’ in the last three columns means the rejection of the hypothesis.
The ADF test did not reject the unit root hypothesis for February, April, August, September, and December, for which the non-stationarity was expected. Taking the first-order differences and performing the same tests for these five series, the unit-root hypothesis could be rejected. The KPSS test rejected the level-stationarity only for October, MTOT, and ANTOT. So, these series are expected to be non-stationary around a certain level. The January series is not trend stationary.
The output of stationarity tests shows that the series that require attention when studying the CP in the mean are mainly those that are level nonstationary. When studying the change in trend, the series for which the ADF did not reject the null hypothesis, and the KPSS-trend test rejected the null hypothesis simultaneously should also be considered.
Pettitt and Buishand’s tests rejected the hypothesis of CPs’ existence for all but the January, October, ANTOT, and MTOT series. In Table 3, ‘yes’ in the column of the Buishand test means that the test could not reject the hypothesis of a CP existence.

Table 3.
The results of the CP tests.
The numbers in the table’s columns indicate the year (month) when the CPs were found. It is no surprise that different tests detected different CPs, given their different mathematical background on which the computation relies. For example, 1965 is the first year in the data series, so detecting it as a CP means that the corresponding value is an outlier. Similarly, June 1991 and July 1991 (the row before the last one, the last column) show that the values recorded in those months are aberrant, masking the real CPs. The Lee & Heghinian algorithm detected the most probable CPs of the series March, April, and November in 2011–2013 (specifically, January 2011, March, April, and November 2013) and 2016–2017 (July and February). They are reflected in the CP of the annual series (in 2012). July 1996 was found as a CP of MTOT by the same test. This finding concurs with those of the Hubert procedure and Lee & Heghinian for February, April, July, December, and ANTOT.
Since the autocorrelation hypothesis was rejected for October, ANTOT, and MTOT, the non-parametric CUSUM was applied when searching for CPs. The CUSUM advantage is that it can also detect CPs in the standard deviation and the coefficient of variation. The algorithm identified CPs in the mean for January, October, December, MTOT, and ANTOT Series, and in variance for March, August, October, and ANTOT (Table 4), with confidence levels exceeding 94%.

Table 4.
CPs of the Tulcea series.
We remark that some CPs found with the previous methods are among those found by CUSUM. We note that in this last case, using the non-parametric version (which confirmed the finding of the parametric version), which is less sensitive to outliers than the other methods, improved the finding accuracy. The CUSUM charts for the monthly series are presented in Figure 5.
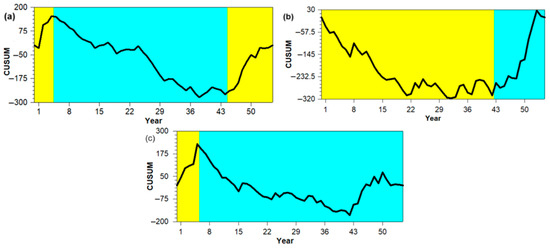
Figure 5.
CUSUM charts for (a) January, (b) October, and (c) December series.
As a general remark, in for Gaussian data with a single CP, the most powerful choices are Lee & Heghinian or CUSUM. For a single change in non-Gaussian data, Pettitt’s test provides robustness at some cost in power. For multiple change points, either CUSUM-based segmentation algorithm (especially rank-based) or Hubert’s segmentation is most appropriate.
The MK test followed by the Sen procedure detected an increasing trend in the October series (slope = 0.667), ANTOT (slope = 2.555), and MTOT (slope = 0.015). The Hirsch–Slack test provided a p-value of 0.00514 and a positive z-value, confirming the existence of a positive trend in the MTOT series. The results of the ITA are presented in Figure 6. The position of the dots around the first bisector of the coordinate axes (represented by the red lines in Figure 6) for all but the October series indicates no trend in the data series.
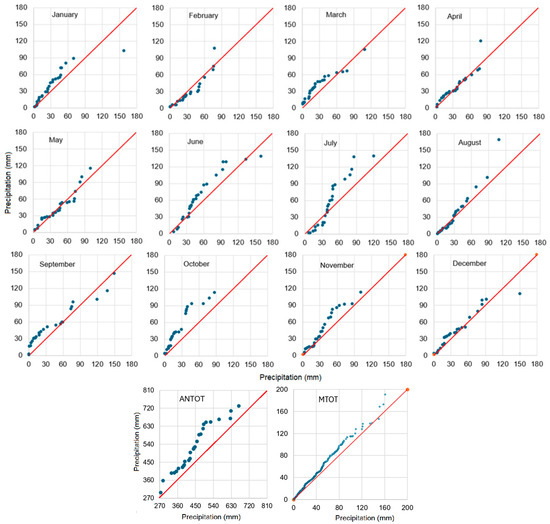
Figure 6.
Results of the ITA trend test.
The position of the dots above the first bisector indicates a positive trend in the October series. This means that the single month for which an increase in precipitation over time is October, whereas for the rest of the series, no increasing or decreasing tendency was detected. These results confirm the output of the MK test.
Figure 7 presents MTOT, its trend, seasonal factors, and the remainder obtained by the STL decomposition.
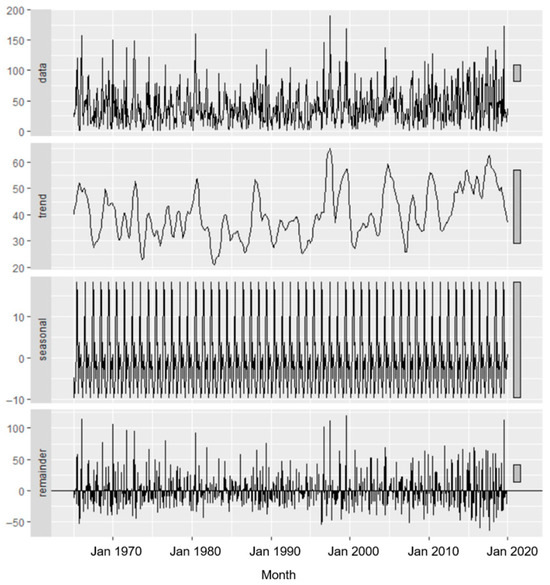
Figure 7.
STL decomposition of MTOT series. From top to bottom, the rectangles contain data series, trend, seasonality, and remainder.
The trend obtained by Lowess (i.e., by a more general method than that of Sen) has an undulating pattern showing the long-term behavior of the series. The rising trend around 2007–2015 suggests increased rainfall during that period. The period 1980–1995 is characterized by some regularity in precipitation increase and decrease, with the lowest minima and maxima compared to other periods. The trend attenuation is noticed after 2015. These modifications indicate a non-stationarity in the series trend, which can be due to climatic change and modifications in land use.
The Seasonal Component exhibits consistent peaks and troughs, characteristic of climates that experience distinct wet and dry seasons. The seasonal amplitude, measuring approximately 10–15 mm, is notably smaller than the overall rainfall variability, indicating that while seasonality is present, it is not the predominant factor.
The highest indices of seasonality correspond to June and July, showing the highest seasonal variability in precipitation during these months. In contrast, the indices’ absolute values are lowest in November, December, and May, with values ranging from 0.68 to 1.64, suggesting much lower seasonal variability during these months. Consequently, the seasonal pattern highlights a rainy season in the summer and drier weather in November and December.
The Residual reflects the unexplained variability within the data series, which may include unusual droughts, isolated dry months, or extreme rainfall events. Notably, spikes in this variability are more frequent and intense following the year 2000, indicating an increase in climate volatility. In the context of the MTOT analysis, EMD decomposes the series into IMFs that represent the precipitation behavior at different scales (Figure 8).
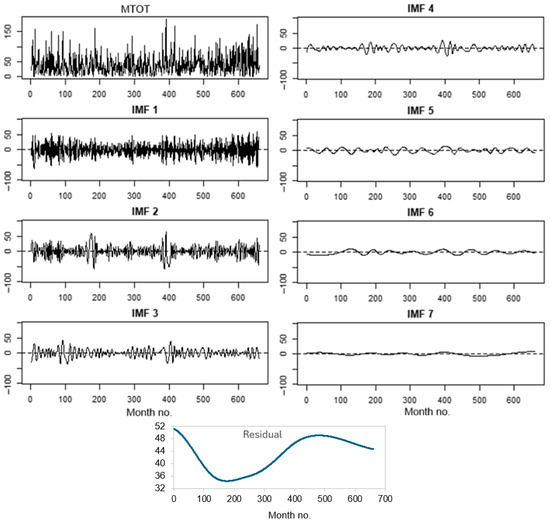
Figure 8.
EMD decomposition of MTOT series: IMFs 1–7 and the residual.
IMF 1 and IMF 2 present high frequency. IMF 1 captures very short-term rainfall variability (1–2 months), characterized by unusually wet or dry months. Such fluctuations often arise from transient weather systems and are not linked to specific seasonal patterns, appearing more as random noise in the climate data. IMF 2 displays short-term swings (2–4 months) in rainfall amounts, which may indicate intra-seasonal oscillations. These oscillations can lead to noticeable changes in precipitation within a single season, affecting local weather patterns.
IMFs 3 and 4 present a medium frequency. IMF3, with a time scale of about 4–8 months, starts to reveal seasonal variability, shedding light on the patterns of wet and dry periods throughout the year. It captures the rhythmic changes in rainfall associated with different times of the year, reflecting the climate seasonality. There is a clear sine-decrease in this IMF’s values, followed by an opposite behavior from month 80 (September 1971) to about 356 (August 1994), followed by a diminishing variation amplitude until 2015. IMF 4 reflects the annual cycle of rainfall, capturing consistent patterns tied to wet and dry seasons. It provides a clear indication of seasonal behavior, illustrating the predictable shifts in precipitation that occur as the year progresses. The highest seasonal variability was noticed in August 1976–March 1988 (a subperiod September 1971–August 1994, reflected in the variation in IMF 3).
The IMF 5 shows the interannual variability in rainfall reflecting longer-term climate influences. We talk about a period of 1.5 to 3 years when the frequency appears low. An almost regular sine wave is still present, highlighting trends that extend beyond single seasons.
The last two IMFs, with lower and much lower frequencies than those of IMF 5, capture stronger interannual signals for 3–7 years and 8–12 years, respectively. In the case of IMF 6, the timeframe allows for analysis of regional climate variability, revealing how rainfall patterns may shift over several years. In the case study, two periods of significant increase were followed by a sine-damped decrease. IMF 7 reflects decadal-scale variability, illustrating long-term climate cycles or persistent drought or wet conditions patterns that can last for many years. For the Tulcea series, the amplitude of these periods is higher after 2000, with the lengths moving toward 12 years.
Residual represents long-term climate trends, such as gradual drying or wetting phenomena, and exhibits the same sine pattern. These shifts may stem from climate change (at least after 1990) or land use transformations.
5. Discussion
5.1. Discussions of the Results
This study provides evidence of statistically significant and non-stationary behavior in precipitation time series, particularly for October and for the aggregated series, MTOT and ANTOT. These findings align with regional studies reporting enhanced autumn precipitation across southeastern Europe and the Romanian territory in recent decades. For example, Spinoni et al. [63] documented increases in heavy precipitation events and precipitation totals during autumn, especially after the 1990s, consistent with broader climate shifts in the Balkans and Mediterranean.
The upward trends in ANTOT and MTOT, in addition to October-specific changes, indicate that precipitation increases are not limited to isolated months but may reflect a broader shift in the annual precipitation regime. These can be interpreted as a manifestation of enhanced climate variability, particularly due to increased contributions from extreme precipitation events rather than uniform increases in daily or monthly rainfall. This distinction is crucial: rising totals may result from a lower number but more intense rainfall events, a dynamic frequently observed in Mediterranean and Balkan climates [64].
Unlike Western Europe, where atmospheric teleconnections like the North Atlantic Oscillation (NAO) have heavy climatological influence, in the Dobrogea and the Danube Delta, regional and local climatic drivers are more important in shaping extreme weather and hydrological patterns. One such driver is the frequent formation of Eastern Mediterranean cyclonic systems, especially during spring and autumn. These low-pressure systems transport moist air masses from the Aegean and Levantine basins into southeastern Europe, where they can produce heavy precipitation and flash flooding, particularly in the low-lying regions [65].
The Black Sea plays a central role in modulating regional climate. During periods of anomalously warm sea surface temperatures, evaporation rates increase, contributing to greater atmospheric instability over the coastal region. This can enhance local convective activity, resulting in heavy rainfall events or localized storms. In late summer and early autumn, this mechanism is especially influential when warm marine air interacts with polar air intrusions descending over Eastern Europe [66,67,68].
The STL decomposition of MTOT revealed a high variability in the seasonal components. At the same time, the Remainder showed augmented irregularity and volatility post-2000, suggesting increasing influence from high-frequency disturbances and short-duration extremes. These findings align with those of Irașoc et al. [69], who reported rising maximum rainfall events in Dobrogea, especially during the autumn months. The presence of more outliers and shifts in distribution skewness in October’s monthly precipitation supports the hypothesis that climate variability in the region is intensifying, even when mean values show only moderate increases. The concentration of significant changes in October may point to a seasonal reorganization of precipitation regimes, with autumn becoming increasingly important in annual water budgets. Given the location of Tulcea near the Danube Delta, a sensitive socio-ecological system, such shifts may have implications for flood risk, agriculture, and water resource management. Similar concerns have been raised by Zaharia et al. [70], who projected that stronger seasonal contrasts and unpredictable rainfall patterns will mark the future hydrological regime of southeastern Romania.
The change-point detected by multiple statistical tests further confirmed an abrupt shift around the early 2000s in precipitation behavior. This period has also been identified in other Romanian hydrological studies as a pivot for changes in streamflow regimes and the frequency of hydrological extremes. These abrupt changes are often linked to broader atmospheric teleconnections, including shifts in the Mediterranean Oscillation, and sea surface temperature anomalies in the Black Sea and eastern Mediterranean [71,72,73].
Although only October and the aggregated series (ANTOT and MTOT) exhibited statistically significant trends, other months (March and August) showed alterations in the variance that trend analysis alone cannot fully capture. This reinforces the idea that climate change in southeastern Europe is increasingly expressed through greater intra-seasonal and interannual variability [72,74].
The decomposition via Empirical Mode Decomposition (EEMD) indicated the influence of both interannual variability and longer-term low-frequency patterns. These oscillations are consistent with previous findings in the Balkan and Mediterranean domains, where climate signals are known to be modulated by multi-decadal oscillations and synoptic-scale variability [75].
5.2. Comparative Discussions with the Results for the Monthly Sulina Series
To complement the actual study, we compared the CPs detected for the MTOT with the monthly precipitation series spanning the period January 1965–December 2019 collected at Sulina, a station which is situated 13 km offshore. This new data series was retrieved from the European Climate Assessment & Dataset (https://www.ecad.eu/ (accessed on 12 May 2025)). This comparison will give an idea about the monthly precipitation variability at different points in the DDBR.
The interquartile range method (IQRM) detected 50 outliers of the Sulina monthly series (denoted STOT in the following). The Hubert method detected as CPs the months August 1992, September 1992, June 2013, and May 2014. The parametric CUSUM found three CPs for the same series (Table 5), compared to only one (August 1996) for Tulcea. The same method identified two CPs (November 1972 and July 2009) in standard deviation of STOT, compared to only one CP (March 2017) for MTOT.

Table 5.
CPs in mean and standard deviation for Sulina STOT series determined by the nonparametric CUSUM.
The existence of such a high number of outliers could bias the CPs’ detection. For example, in the Hubert method, two consecutive months were determined as CPs (August 1992, September 1992) given that they are outlies. However, the nonparametric CUSUM, which is less sensitive to the aberrant values, detected only two CPs in mean and one in standard deviation for STOT.
The MK test did not find a significant trend for any of the segments delimited by the CPs of STOT. Therefore, the CPs are due to a high precipitation variability and the intensification of the extreme events, and not to a slow increase/decrease in the precipitation quantity.
A summary of CPs in mean determined for the monthly and annual series are presented in Table 6. No matter which version of CUSUM was used, the number of CPs and the moment of their apparition are not the same for the series registered at Sulina and Tulcea. The difference between the CPs detected at the two stations situated at only 15 km distance can be explained only by the most pregnant climatic influences—more accentuated continental for Tulcea, and more humid maritime at Sulina—as well as to the atmospheric circulation. They will be deeply investigated in a future work.

Table 6.
CPs in mean and for Sulina and Tulcea monthly series determined by the nonparametric CUSUM.
5.3. Implications of the Study for Regional Planning
5.3.1. Implications for Planning in the Danube Delta Resulted from the Statistical Analysis
The Danube Delta, with its complex network of water channels, wetlands, and biologically rich habitats, is uniquely vulnerable to changes in hydrological input and precipitation variability.
The statistical analysis indicated that the DDBR is likely to experience increasing hydrological irregularity, as evidenced by the break points, seasonal shifts, and rising variability detected in precipitation records. These changes can lead to fluctuating water levels, altered sedimentation dynamics, and disrupted aquatic habitats, which threaten both ecological integrity and human activities such as fishing, agriculture, and navigation.
The DDBR requires proactive and integrated environmental management tailored to increasing precipitation variability and changing water dynamics. Planning mechanisms must be flexible and adaptive, incorporating feedback from ecological monitoring and climate trend analyses to adjust priorities over time. Climate variability must be treated not as an episodic disturbance but as a central consideration in all levels of territorial development forecast.
The spatial planning should incorporate climate scenarios and hydrological projections derived from advanced data decomposition methods, which will enable authorities to prepare for long-term shifts in water regimes rather than respond only to immediate pressures. Policies must prioritize long-term monitoring and research, particularly into the decadal and interannual cycles revealed by EMD analysis. The STL and EMD results can inform predictive models that forecast rainfall anomalies and guide infrastructure lifespan planning.
The results of this study, particularly the identification of variance shifts and CPs in key months, highlight the growing complexity of water regime changes that cannot be addressed through static management approaches. Therefore, the Delta’s water management strategy should be guided by:
- Dynamic hydrological models that integrate local precipitation trends and Danube River discharge;
- Ecological flow maintenance policies to support wetland biodiversity during dry periods;
- Flexible flood control mechanisms that prioritize nature-based solutions over hard infrastructure alone;
- Real-time hydrometeorological monitoring systems that provide actionable intelligence for basin-scale coordination
5.3.2. Restoring and Rewilding Solutions for European River Delta
Europe’s deltas and estuaries are remarkable landscapes, home to rich biodiversity, productive ports, and vital wetlands. Yet, these areas face mounting pressures from urban growth, infrastructure, and climate-related risks. Balancing human activity with ecological preservation is a challenge. Different projects, among which DeltaNet [76], offered practical examples of how to achieve it. Active from 2010 to 2013, DeltaNet brought together nine delta regions across seven EU countries to share knowledge and develop sustainable policies for sensitive areas. The project focused on restoring and maintaining healthy delta ecosystems, improving flood and sediment management, and fostering public engagement. The key approaches were:
- Integrated Delta Management: Combining economic development in port areas with ecological conservation.
- Flood and Sediment Control: Restoring natural sediment flows and reducing flood risks.
- Wetland and Habitat Restoration: Reconnecting rivers to floodplains and reviving wetlands.
- Public Awareness and Policy Coordination: Engaging stakeholders and harmonizing regional strategies.
Notable good practices included:
- Elbe Estuary, Germany, and Severn Estuary, UK: Developed integrated management plans that merge ecological and economic objectives.
- Ebro River, Spain: Restored sediment flux to the delta, revitalizing wetlands and river habitats.
- Danube Delta, Romania: Reconnected abandoned polders to the river, enhancing floodplain wetlands and ecological function.
Nature-based solutions in European river deltas demonstrate the potential of ecosystem restoration to simultaneously mitigate climate risks, enhance biodiversity, and sustain local livelihoods [77]. Hydrological reconnection projects, such as the restoration of the Babina polder in the Danube Delta, have shown rapid recovery of ecological functions and socio-economic activities once natural processes are re-established [78]. Rewilding initiatives in the Danube Delta, including the reintroduction of water buffalo, horses, and deer, have revived natural grazing dynamics, enhanced habitat diversity, and contributed to fire risk reduction [79]. In the Ebro Delta, sediment augmentation and lagoon reconnection have increased resilience against sea-level rise while improving habitats for endangered species [80,81].
Across all cases, integrated and participatory governance emerges as essential, with stakeholder engagement and adaptive legal frameworks providing flexibility and societal support for long-term management [77]. Complementary initiatives in the Po Delta (Italy) [82], the Nida River Inland Delta (Poland) [83], and under the DaWetRest [84] program in the Danube Delta highlight the added value of coupling ecological restoration with cultural heritage preservation and innovative business models. Collectively, these examples confirm that leveraging natural processes is a cost-effective and sustainable pathway for the resilient management of European deltas under accelerating environmental change.
From a planning perspective, the DDBR requires a tailored, hydro-ecologically sensitive approach. Critical infrastructure (e.g., sluices, levees, and embankments) must be evaluated and upgraded to respond to both flash flooding risks and extended low-water periods. Strategic planning should preserve and enhance the Delta’s natural capacity to regulate water through restoration and protection of flood retention areas, reedbeds, and natural levees. It must also reconcile its ecological significance with the socio-economic roles. Settlement expansion must be strictly limited in flood-prone zones, while tourism infrastructure should be subject to strict environmental assessments. Conservation zoning, aligned with the seasonal and decadal hydrological dynamics revealed in this study, can support the long-term resilience of wetlands and aquatic ecosystems.
Considering the Danube Delta’s exposure to upstream influences, transboundary water governance and coordinated cross-sectoral policy are indispensable pillars of an effective climate adaptation framework. Participation in the International Commission for the Protection of the Danube River should be strengthened to ensure regional coherence in managing flow variability and ecological pressures.
6. Conclusions
In this study, we examined the long-term precipitation record (1965–2019) from the Tulcea station, located at the mouth of the Danube Delta in Romania, to provide a comprehensive evaluation of temporal precipitation variability. This comprehensive analysis reveals a complex interplay of seasonal, interannual, and long-term climatic dynamics. High variability, especially in the summer months, alongside significant skewness and kurtosis in most monthly series, highlights the irregular nature of rainfall events in the region. The presence of CPs, detected by various statistical methods, underscores modifications in precipitation regimes, notably around the years 1965, 1996, and 2012. The application of STL and EMD confirms the presence of multi-scale oscillations and long-term trends, with increasing climate volatility observed particularly after 2000. These findings indicate a departure from stationarity in both mean and variance, likely driven by climate change. The detection of positive trends in series such as October, MTOT, and ANTOT highlights a gradual intensification of rainfall, underscoring the need for adaptive water resource management and further investigation into regional climate drivers. EMD, while powerful, lacks a formal statistical framework for significance testing, and the subjective interpretation of IMFs may introduce bias.
Despite the robustness of the multi-method approach, some limitations should be acknowledged. First, change point detection methods have various degrees of sensitivity to outliers and sample length, leading to inconsistencies in CP identification across techniques. They also rely on various mathematical or statistical methodologies. The biased CP detection can significantly affect the quality of the models that could be built for the data series, and, especially, the forecast based on them. Therefore, the analysis should also be complemented by the knowledge of climate evolution on the region and metadata, which should support the acceptance of the CP existence. Second, the narrow database limits the results extrapolation to the entire Danube Delta. Therefore, for a full understanding of climate variability in the DDBR, the precipitation evolution (e.g., trend, CPs in mean and variance) should be analyzed considering the data series from other meteorological points in the region.
High-resolution spatial data and remote sensing could help assess the changes. Moreover, future work should focus on integrating physically based climate models to better interpret the statistical findings in the context of atmospheric dynamics. A deeper analysis of the connections with physical mechanisms of atmospheric circulation (e.g., NAO) could strengthen the interpretation of the statistical results. Furthermore, the use of more advanced machine learning techniques, such as deep learning-based time series models, could enhance trend and anomaly detection. Finally, extending the analysis to include other data series (e.g., temperature and evapotranspiration), updated to 2025, would provide a better view of regional water cycle shifts in response to climate change. The results would support the water resources management and planning.
Author Contributions
Conceptualization, A.B. and C.Ș.D.; methodology, A.B. and C.Ș.D.; software, A.B.; validation, C.Ș.D.; formal analysis, C.Ș.D.; investigation, A.B. and C.Ș.D.; resources, A.B.; data curation, A.B.; writing—original draft preparation, A.B.; writing—review and editing, C.Ș.D.; visualization, A.B.; supervision, A.B.; project administration, A.B.; funding acquisition, A.B. and C.Ș.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data can be freely downloaded from: European Climate Assessment & Data: https://www.ecad.eu/dailydata/index.php (accessed on 12 May 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANTOT | Annual total precipitation series RECORDED AT Tulcea |
| CP | Change Point |
| CPD | Change Point Detection |
| CUSUM | Cumulative Sum |
| DDBR | Danube Delta Biosphere Reserve |
| ITA | Innovative trend analysis |
| MK | Mann–Kendall |
| MTOT | Tulcea monthly precipitation series |
| SMK | Seasonal Mann–Kendall |
| STOT | Sulina monthly precipitation series |
References
- IPCC Sixth Assessment Report. Impacts, Adaptation and Vulnerability. 2022. Available online: https://www.ipcc.ch/report/sixth-assessment-report-working-group-ii/ (accessed on 22 June 2025).
- The Global Water Monitor. 2024. Available online: https://www.globalwater.online/globalwater/report/index.html (accessed on 22 June 2025).
- Do, H.X.; Mei, Y.; Gronewold, A.D. To what extent are changes in flood magnitude related to changes in precipitation extremes? Geophys. Res. Lett. 2020, 47, e2020GL088684. [Google Scholar] [CrossRef]
- Impact of Climate Change on Water Availability and Quality. Available online: https://www.unicef.org/serbia/en/impact-of-climate-change-on-water-availability-and-quality (accessed on 22 June 2025).
- van Vliet, M.T.H.; Thorslund, J.; Strokal, M.; Hofstra, N.; Flörke, M.; Macedo, H.E.; Nkwasa, A.; Tang, T.; Kaushal, S.S.; Kumar, R.; et al. Global river water quality under climate change and hydroclimatic extremes. Nat. Rev. Earth Environ. 2023, 4, 687–702. [Google Scholar] [CrossRef]
- Barbulescu, A.; Barbes, L.; Dumitriu, C.S. Assessing the Water Pollution of the Brahmaputra River Using Water Quality Indexes. Toxics 2021, 9, 297. [Google Scholar] [CrossRef] [PubMed]
- Sjerps, R.M.A.; ter Laak, T.L.; Zwolsman, G.J.J.G. Projected impact of climate change and chemical emissions on the water quality of the European rivers Rhine and Meuse: A drinking water perspective. Sci. Total Environ. 2017, 601–602, 1682–1694. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Maftei, C. Modeling the climate in the area of Techirghiol Lake (Romania). Rom. J. Phys. 2015, 60, 1163–1170. [Google Scholar]
- Berg, A.; Findell, K.; Lintner, B.; Giannini, A.; Seneviratne, S.I.; Van Den Hurk, B.; Lorenz, R.; Pitman, A.; Hagemann, S.; Meier, A.; et al. Land–atmosphere feedbacks amplify aridity increase over land under global warming. Nat. Clim. Change 2016, 6, 869–874. [Google Scholar] [CrossRef]
- Brunner, M.I.; Hingray, B.; Zappa, M.; Favre, A.-C. Future Trends in the Interdependence Between Flood Peaks and Volumes: Hydro-Climatological Drivers and Uncertainty. Water Resour. Res. 2019, 55, 4745–4759. [Google Scholar] [CrossRef]
- Slater, L.J.; Anderson, B.; Buechel, M.; Dadson, S.; Han, S.; Harrigan, S.; Kelder, T.; Kowal, K.; Lees, T.; Matthews, T.; et al. Nonstationary weather and water extremes: A review of methods for their detection, attribution, and management. Hydrol. Earth Syst. Sci. 2021, 25, 3897–3935. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Maftei, C. Evaluating the Probable Maximum Precipitation. Rom. Rep. Phys. 2023, 75, 704. [Google Scholar] [CrossRef]
- Sun, W.; Li, J.; Yu, R.; Li, N.; Zhang, Y. Exploring changes of precipitation extremes under climate change through global variable-resolution modeling. Sci. Bull. 2024, 69, 237–247. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Raman, A.; Gründemann, G.J.; Kumar, M.; Pietroniro, A.; Shen, C.; Song, Y.; Thébault, C.; van Werkhoven, K.; Wood, A.W.; et al. Technical note: How many models do we need to simulate hydrologic processes across large geographical domains? Hydrol. Earth Syst. Sci. 2025, 29, 2361–2375. [Google Scholar] [CrossRef]
- Alifujiang, Y.; Abuduwaili, J.; Maihemuti, B.; Emin, B.; Groll, M. Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan. Atmosphere 2020, 11, 332. [Google Scholar] [CrossRef]
- Cao, S.; Li, X.; You, R.; Diao, Y.; Wang, J.; Liu, Y. Investigation of the trend and cycles using the long-term records of annual precipitation in Shandong, China. J. Water Clim. Change 2022, 13, 3761–3775. [Google Scholar]
- Bărbulescu, A.; Deguenon, J. Change point detection and models for precipitation evolution. Case study. Rom. J. Phys. 2014, 59, 590–600. [Google Scholar]
- Conte, L.C.; Bayer, M.D.; Bayer, F.M. Bootstrap Pettitt test for detecting change points in hydroclimatological data: Case study of Itaipu Hydroelectric Plant, Brazil. Hydrol. Sci. J. 2019, 64, 1312–1326. [Google Scholar] [CrossRef]
- Valderrama Balaguera, J.C. Precipitation forecast estimation applying the change point method and ARIMA. Cogent Eng. 2024, 11, 2340191. [Google Scholar] [CrossRef]
- Getahun, Y.S.; Li, M.-H.; Pun, I.-F. Trend and change-point detection analyses of rainfall and temperature over the Awash River basin of Ethiopia. Heliyon 2021, 7, e08024. [Google Scholar] [CrossRef] [PubMed]
- Fotoohinasab, A.; Hocking, T.; Afghah, F. A Graph-constrained Changepoint Detection Approach for ECG Segmentation. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 332–336. [Google Scholar]
- Shvetsov, N.; Buzun, N.; Dylov, D.V. Unsupervised Non-Parametric Change Point Detection in Quasi-Periodic Signals. 2020. Available online: https://arxiv.org/abs/2002.02717 (accessed on 22 June 2020).
- Alawadhi, F.A.; Alhulail, D. Bayesian change points analysis for earthquakes body wave magnitude. J. Appl. Stat. 2016, 43, 1567–1582. [Google Scholar] [CrossRef]
- Jiqin, H.; Gelata, F.T.; Gemeda, S.C. Application of MK trend and test of Sen’s slope estimator to measure impact of climate change on the adoption of conservation agriculture in Ethiopia. J. Water Clim. Change 2023, 14, 977–988. [Google Scholar] [CrossRef]
- Kliengchuay, W.; Mingkhwan, R.; Kiangkoo, N.; Suwanmanee, S.; Sahanavin, N.; Kongpran, J.; WaiAung, H.; Tantrakarnapa, K. Analyzing temperature, humidity, and precipitation trends in six regions of Thailand using innovative trend analysis. Sci. Rep. 2024, 14, 7800. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I.J. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–33. [Google Scholar]
- Bush, E.R.; Abernethy, K.A.; Jeffery, K.; Tutin, C.; White, L.; Dimoto, E.; Dikangadissi, J.-T.; Jump, A.S.; Bunnefeld, N. Fourier analysis to detect phenological cycles using long-term tropical field data and simulations. Methods Ecol. Evol. 2017, 8, 530–540. [Google Scholar]
- Bandoc, G.; Prăvălie, R. Climatic water balance dynamics over the last five decades in Romania’s most arid region, Dobrogea. J. Geogr. Sci. 2015, 25, 1307–1327. [Google Scholar] [CrossRef]
- Cheval, S.; Dumitrescu, A.; Birsan, M.-V. Variability of the aridity in the South-Eastern Europe over 1961–2050. Catena 2017, 151, 74–86. [Google Scholar] [CrossRef]
- Bădăluță, C.A.; Haliuc, A.; Bădăluță, G.; Scriban, R.E. Spatiotemporal variability of drought in Romania during 1901–2021 using the Standardized Precipitation Evapotranspiration Index (SPEI). Ann. Univ. Oradea Ser. Geogr. 2024, 34, 33–44. [Google Scholar]
- Petre, M.J. Assessment of the UTCI and HSI Biometeorological Indices for Constanța and Tulcea. Available online: https://riscurisicatastrofe.reviste.ubbcluj.ro/Volume/XXIV_Nr_34_2024/PetreMJ_RCJ2024_5.pdf (accessed on 20 June 2025).
- Deguenon, J.; Bărbulescu, A.; Sarr, M. GPD Models for extreme rainfall with cyclic trend detection over ten stations in Dobrudja. Comput. Eng. Syst. Appl. 2011, 2, 131–136. [Google Scholar]
- Deguenon, J.; Bărbulescu, A. Trends of extreme precipitation events in Dobrudja. Ovidius Univ. Ann. Ser. Civ. Eng. 2011, 7, 73–80. [Google Scholar]
- Maftei, C.; Dobrica, G.; Cerneaga, C.; Buzgaru, N. Drought Land Degradation and Desertification—Case Study of Nuntasi-Tuzla Lake in Romania. In Water Safety, Security and Sustainability. Advanced Sciences and Technologies for Security Applications; Vaseashta, A., Maftei, C., Eds.; Springer: Cham, Switzerland, 2021; pp. 583–597. [Google Scholar] [CrossRef]
- Preoteasa, L.; Vespremeanu-Stroe, A.; Hanganu, D.; Katona, O.; Timar-Gabor, A. Coastal changes from open coast to present lagoon system in Histria region (Danube delta). J. Coast. Res. 2013, 65, 564–569. [Google Scholar] [CrossRef]
- Nagavciuc, V.; Ionita, M.; Roibu, C.-C. Extreme Aridity in the South-Eastern Part of Romania. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Băutu, E. Mathematical models of climate evolution in Dobrudja. Theor. Appl. Climatol. 2010, 100, 29–44. [Google Scholar]
- Bărbulescu, A.; Dumitriu, C.S.; Dragomir, F. Detecting Aberrant Values and Their Influence on the Time Series Forecast. In Proceedings of the 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, Mauritius, 7–8 October 2021. [Google Scholar] [CrossRef]
- Saliba, Y.; Bărbulescu, A. A Multi-Method Approach to Analyzing Precipitation Series and Their Change Points in Semi-Arid Climates: The Case of Dobrogea. Water 2025, 17, 391. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Maftei, C.; Dumitriu, C.S. The modeling of the climatic process that participates at the sizing of an irrigation system. Bull. Appl. Comput. Math. 2002, CII-2048, 11–20. [Google Scholar]
- Trif, A.; Mihai, D. Effect of climate change on Dobrogea agricultural area. Sci. Pap. Ser. E. Land Reclam. Earth Obs. Surv. Environ. Eng. 2014, 3, 137–140. [Google Scholar]
- Bărbulescu, A.; Dumitriu, C.S.; Maftei, C. On the Probable Maximum Precipitation Method. Rom. J. Phys. 2022, 67, 801. [Google Scholar]
- Prăvălie, R.; Bandoc, G. Aridity Variability in the Last Five Decades in the Dobrogea Region, Romania. Arid Land Res. Manag. 2015, 29, 265–287. [Google Scholar] [CrossRef]
- RESTORE4CS. Available online: https://www.restore4cs.eu/case-pilots/danube-delta/ (accessed on 27 July 2025).
- Tătui, F. Potential usage of met mast datasets for climatic parameters monitoring in Tulcea County, Romania. Forum Geogr. 2015, 14, 22–29. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [PubMed]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root. J. Econ. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Buishand, T.A. Tests for detecting a shift in the mean of hydrological time series. J. Hydrol. 1984, 73, 51–69. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change point problem. J. R. Stat. Soc. Ser. C. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Lee, A.F.S.; Heghinian, S.M. A Shift of the Mean Level in a Sequence of Independent Normal Random Variables—A Bayesian Approach. Technometrics 1977, 19, 503–506. [Google Scholar] [CrossRef]
- Hubert, P. Segmentation Procedure as a Tool for Discrete Modeling of Hydro-Meteorological Regimes. Stoch. Environ. Res. Risk Assess. 2000, 14, 297–304. [Google Scholar]
- Stapenhurst, T. Mastering Statistical Process Control, 1st ed.; Routledge: London, UK, 2005. [Google Scholar] [CrossRef]
- Scheffe, H. The Analysis of Variance; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Taylor, W.A. Change-Point Analysis: A Powerful New Tool for Detecting Changes. 2000. Available online: https://variation.com/wp-content/uploads/change-point-analyzer/change-point-analysis-a-powerful-new-tool-for-detecting-changes.pdf (accessed on 4 June 2025).
- Hirsch, R.M.; Slack, J.R. A Nonparametric Trend Test for Seasonal Data With Serial Dependence. Water Resour. Res. 1984, 20, 727–732. [Google Scholar] [CrossRef]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; Van Nostrand Reinhold Company: New York, NY, USA, 1987. [Google Scholar]
- Şen, Z. Innovative trend analysis methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2021; Available online: https://otexts.com/fpp3/ (accessed on 25 June 2025).
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang Transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46, RG2006. [Google Scholar]
- Kim, D.; Kim, K.-O.; Oh, H.-S. Extending the Scope of Empirical Mode Decomposition using Smoothing. EURASIP J. Adv. Signal Process. 2012, 168, 168. [Google Scholar] [CrossRef]
- Wang, X.L.; Chen, H.; Wu, Y.; Feng, Y.; Pu, Q. New Techniques for the Detection and Adjustment of Shifts in Daily Precipitation Data Series. J. Appl. Meteor. Climatol. 2010, 49, 2416–2436. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.V. Pan-European Seasonal Trends and Variability of Precipitation and Temperature in Europe (1951–2010). Glob. Planet. Change 2017, 148, 113–130. [Google Scholar] [CrossRef]
- Zittis, G. Observed rainfall trends and precipitation uncertainty in the vicinity of the Mediterranean, Middle East and North Africa. Theor. Appl. Climatol. 2018, 134, 1207–1230. [Google Scholar] [CrossRef]
- Birsan, M.V. Trends in Monthly Natural Streamflow in Romania and Linkages to Atmospheric Circulation in the North Atlantic. Water Resour. Manag. 2015, 29, 3305–3313. [Google Scholar] [CrossRef]
- Meredith, E.; Semenov, V.; Maraun, D.; Park, W.; Chernokulsky, A. Crucial role of Black Sea warming in amplifying the 2012 Krymsk precipitation extreme. Nat. Geosci. 2015, 8, 615–619. [Google Scholar] [CrossRef]
- Mohamed, B.; Ibrahim, O.; Nagy, H. Sea Surface Temperature Variability and Marine Heatwaves in the Black Sea. Remote Sens. 2022, 14, 2383. [Google Scholar]
- Gavrikov, A.V.; Zolina, O.G.; Razorenova, O.A.; Aleksandrova, M.P.; Gulev, S.K.; Stenchikov, G.L. Extreme Precipitation in June 2021 over the Black Sea in the Context of Long-Term Climate Change. Oceanology 2022, 62, 303–309. [Google Scholar] [CrossRef]
- Irașoc, A.; Ionac, N.Ș.; Dumitrescu, A.; Beteringhe, A. Extreme Rainfall Intensities at Sub-Hourly Temporal Scale in Dobrudja, Romania. Geogr. Tech. 2024, 19, 103–122. [Google Scholar] [CrossRef]
- Zaharia, L.; Ioana-Toroimac, G.; Perju, E.R. Hydrological Impacts of Climate Changes in Romania. In Water Resources Management in Romania; Negm, A., Romanescu, G., Zeleňáková, M., Eds.; Springer: Cham, Switzerland, 2020; pp. 309–351. [Google Scholar] [CrossRef]
- Ionita, M.; Chelcea, S.; Rimbu, N.; Adler, M.-J. Spatial and temporal variability of winter streamflow over Romania and its relationship to large-scale atmospheric circulation. J. Hydrol. 2014, 519, 1339–1349. [Google Scholar] [CrossRef]
- Ioniță, M.; Lohmann, G.; Rimbu, N.; Chelcea, S.; Dima, M. Interannual to decadal summer drought variability over Europe and its relationship to global sea surface temperature. Clim. Dyn. 2012, 38, 363–377. [Google Scholar] [CrossRef]
- Cramer, W.; Guiot, J.; Fader, M.; Garrabou, J.; Gattuso, J.–P.; Iglesias, A.; Lange, M.A.; Lionello, P.; Llasat, M.C.; Paz, S.; et al. Climate change and interconnected risks to sustainable development in the Mediterranean. Nat. Clim. Change 2018, 8, 972–980. [Google Scholar] [CrossRef]
- Danilovich, I.S.; Loginov, V.F.; Groisman, P.Y. Changes of Hydrological Extremes in the Center of Eastern Europe and Their Plausible Causes. Water 2023, 15, 2992. [Google Scholar] [CrossRef]
- Zampieri, M.; Toreti, A.; Schindler, A.; Scoccimarro, E.; Gualdi, S. Atlantic multi-decadal oscillation influence on weather regimes over Europe and the Mediterranean in spring and summer. Glob. Planet. Change 2017, 151, 92–100. [Google Scholar] [CrossRef]
- Network of European Delta Regions-Sustainable Delta Governance. Available online: https://keep.eu/projects/423/Network-of-European-Delta-Reg-EN/ (accessed on 8 September 2025).
- European Commission: Directorate-General for Research and Innovation. Evaluating the Impact of Nature-Based Solutions—A Handbook for Practitioners; Publications Office of the European Union: Luxembourg, 2021; Available online: https://data.europa.eu/doi/10.2777/244577 (accessed on 15 May 2025).
- Natural Water Retention Measures. The Babina Restoration Project (Danube Delta, Romania). 2014. Available online: https://www.nwrm.eu (accessed on 8 September 2025).
- Rewilding Danube Delta. Available online: https://rewilding-danube-delta.com/ (accessed on 8 September 2025).
- Spanish Climate Change Adaption Platform. Habitat Restoration and Management in the Ebro Delta Coastal Lagoons. Available online: https://adaptecca.es/en/casos-practicos/habitat-restoration-and-management-ebro-delta-coastal-lagoons (accessed on 8 September 2025).
- Rodríguez-Santalla, I.; Navarro, N. Main Threats in Mediterranean Coastal Wetlands. The Ebro Delta Case. J. Mar. Sci. Eng. 2021, 9, 1190. [Google Scholar] [CrossRef]
- Conservation Programme for the Po Delta Park Geographical Areas (Second Phase). Available online: https://econservation.jrc.ec.europa.eu/project/2000338 (accessed on 8 September 2025).
- Project LIFE4DELTA_PL. Available online: https://life4delta.pl/?lang=en (accessed on 8 September 2025).
- DaWetRest. Available online: https://dawetrest.eu/ (accessed on 8 September 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).