Research on Acceleration Methods for Hydrodynamic Models Integrating a Dynamic Grid System, Local Time Stepping, and GPU Parallel Computing
Abstract
1. Introduction
2. High Performance Hydrodynamic Model
2.1. Base Model
2.2. Performance Optimization
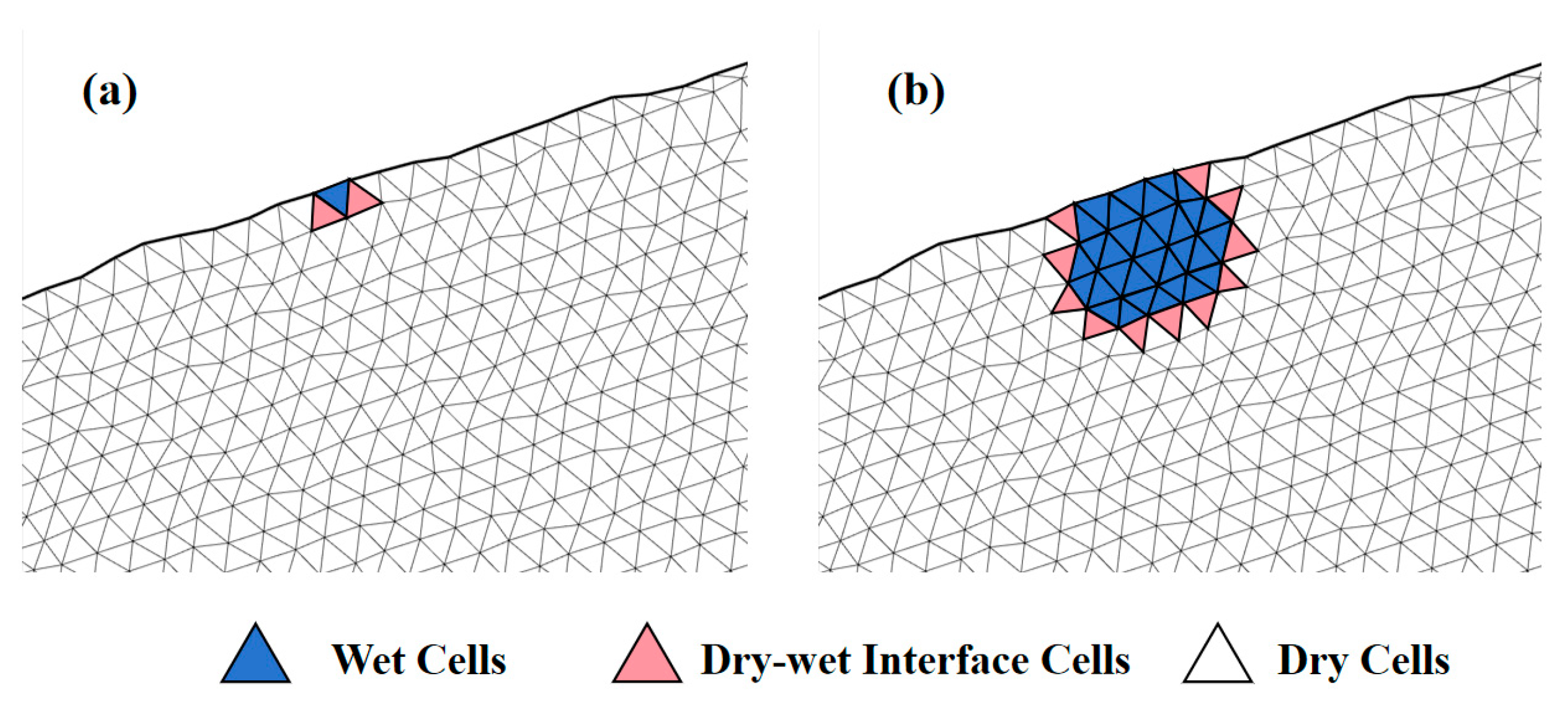
2.2.1. Dynamic Grid System
2.2.2. Local Time Step Technology
2.2.3. GPU Parallelization
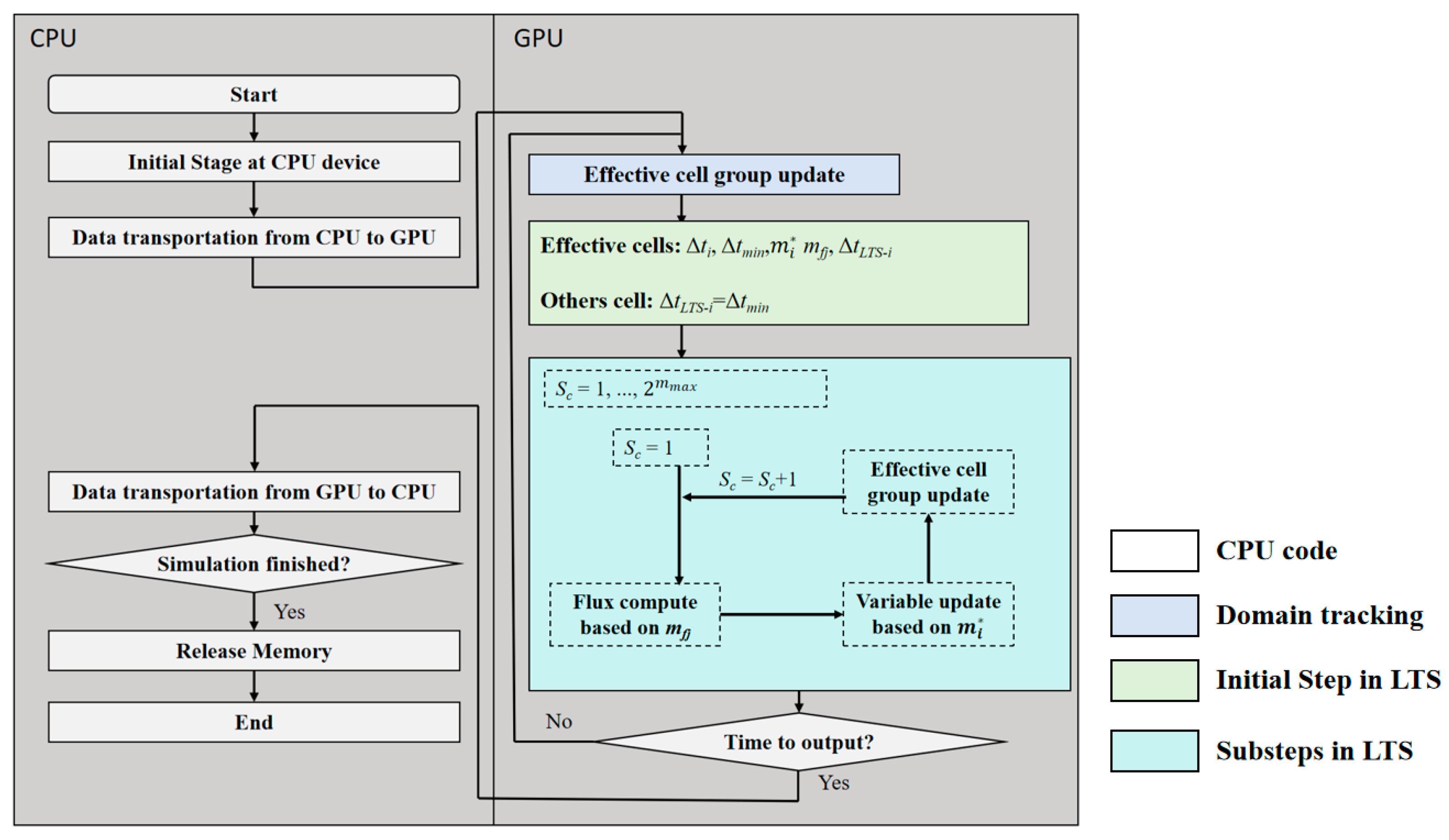
2.2.4. Fusion Method of Dynamic Mesh, Local Time-Stepping, and GPU Parallel Acceleration
3. Numerical Test
3.1. Dam Break Flow over Three Humps
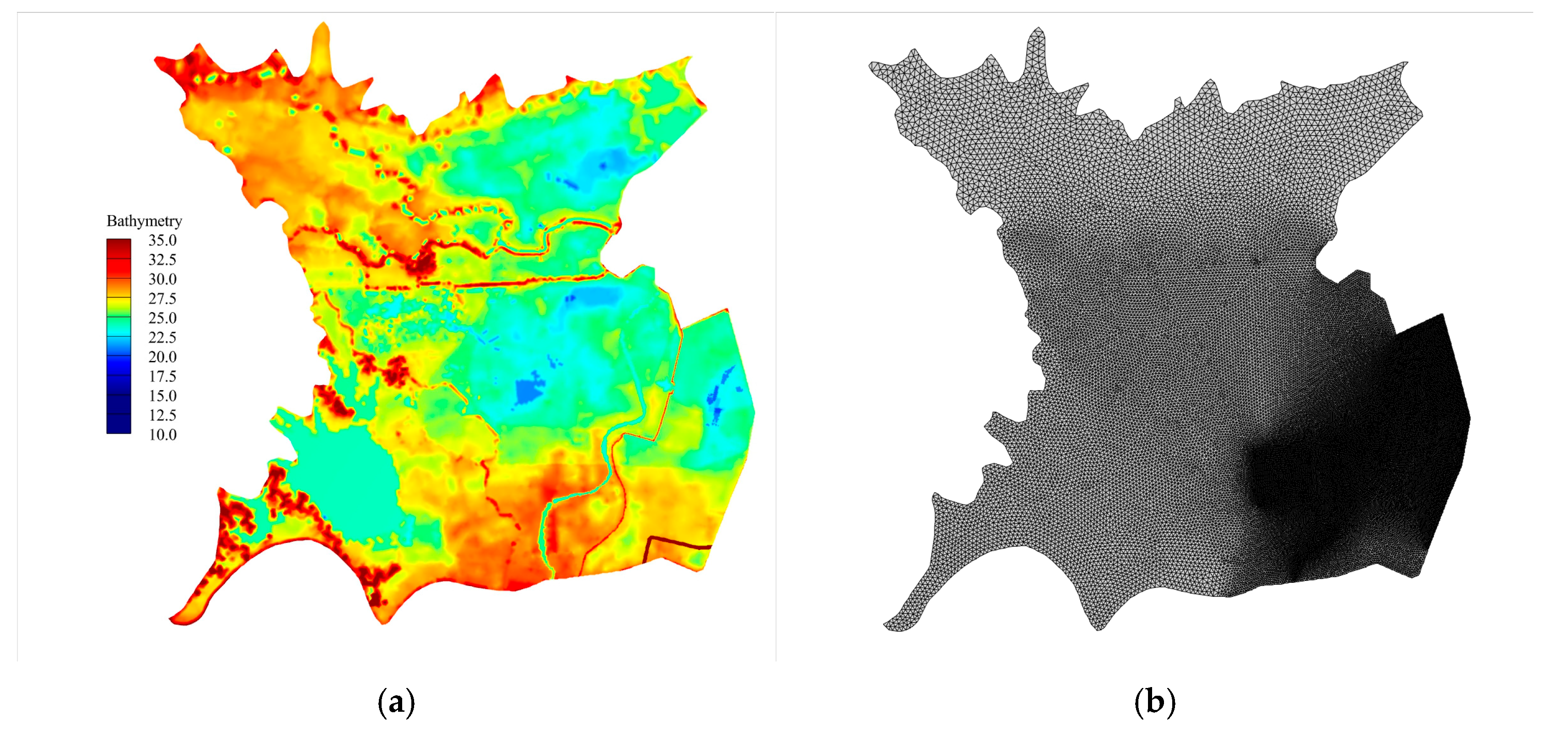
3.2. Simulation of Inundation Caused by Tuanzhouyuan Dyke Breach
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Güneralp, B.; Güneralp, I.; Liu, Y. Changing global patterns of urban exposure to flood and drought hazards. Glob. Environ. Change 2015, 31, 217–225. [Google Scholar] [CrossRef]
- Rentschler, J.; Salhab, M.; Jafino, B.A. Flood exposure and poverty in 188 countries. Nat. Commun. 2022, 13, 3527. [Google Scholar] [CrossRef]
- Cea, L.; Sañudo, E.; Montalvo, C.; Farfán, J.; Puertas, J.; Tamagnone, P. Recent advances and future challenges in urban pluvial flood modelling. Urban Water J. 2025, 22, 149–173. [Google Scholar] [CrossRef]
- Kim, B.; Sanders, B.F.; Famiglietti, J.S.; Guinot, V. Urban flood modeling with porous shallow-water equations: A case study of model errors in the presence of anisotropic porosity. J. Hydrol. 2015, 523, 680–692. [Google Scholar] [CrossRef]
- Pal, D.; Marttila, H.; Ala-Aho, P.; Lotsari, E.; Ronkanen, A.-K.; Gonzales-Inca, C.; Croghan, D.; Korppoo, M.; Kämäri, M.; van Rooijen, E.; et al. Blueprint conceptualization for a river basin’s digital twin. Hydrol. Res. 2025, 56, 197–212. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; García-Navarro, P. An Efficient GPU Implementation of a Coupled Overland-Sewer Hydraulic Model with Pollutant Transport. Hydrology 2021, 8, 146. [Google Scholar] [CrossRef]
- Mignot, E.; Dewals, B. Hydraulic modelling of inland urban flooding: Recent advances. J. Hydrol. 2022, 609, 127763. [Google Scholar] [CrossRef]
- USACE 2024b. HEC-RAS Version 6.6 Release Notes. Available online: https://www.hec.usace.army.mil/confluence/rasdocs/rasrn/latest (accessed on 8 October 2024).
- Judi, D.R.; Burian, S.J.; McPherson, T.N. Two-Dimensional Fast-Response Flood Modeling: Desktop Parallel Computing and Domain Tracking. J. Comput. Civ. Eng. 2011, 25, 184–191. [Google Scholar] [CrossRef]
- Hou, J.-M.; Wang, R.; Jing, H.-X.; Zhang, X.; Liang, Q.-H.; Di, Y.-Y. An efficient dynamic uniform Cartesian grid system for inundation modeling. Water Sci. Eng. 2017, 10, 267–274. [Google Scholar] [CrossRef]
- Sanders, B.F. Integration of a shallow water model with a local time step. J. Hydraul. Res. 2008, 46, 466–475. [Google Scholar] [CrossRef]
- Hu, P.; Lei, Y.; Han, J.; Cao, Z.; Liu, H.; He, Z.; Yue, Z. Improved Local Time Step for 2D Shallow-Water Modeling Based on Unstructured Grids. J. Hydraul. Eng. 2019, 145, 06019017. [Google Scholar] [CrossRef]
- Tao, J.; Hu, P.; Xie, J.; Ji, A.; Li, W. Application of the tidally averaged equilibrium cohesive sediment concentration for determination of physical parameters in the erosion-deposition fluxes. Estuar. Coast. Shelf Sci. 2024, 300, 108721. [Google Scholar] [CrossRef]
- Li, W.; Liu, B.; Hu, P. Fast modeling of vegetated flow and sediment transport over mobile beds using shallow water equations with anisotropic porosity. Water Resour. Res. 2023, 59, e2021WR031896. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Hu, P. Fully coupled morphological modelling under the combined action of waves and currents. Adv. Water Resour. 2025, 195, 104875. [Google Scholar] [CrossRef]
- Sanders, J.; Kandrot, E. CUDA by Example: An Introduction to General-Purpose GPU Programming; Addison-Wesley: Boston, MA, USA, 2010. [Google Scholar]
- Saleem, A.H.; Norman, M.R. Accelerated numerical modeling of shallow water flows with MPI, OpenACC, and GPUs. Environ. Model. Softw. 2024, 180, 11. [Google Scholar] [CrossRef]
- Dong, B.; Huang, B.; Tan, C.; Xia, J.; Lin, K.; Gao, S.; Hu, Y. Multi-GPU parallelization of shallow water modelling on unstructured meshes. J. Hydrol. 2025, 657, 133105. [Google Scholar] [CrossRef]
- Qasaimeh, M.; Denolf, K.; Lo, J.; Vissers, K.; Zambreno, J.; Jones, P.H. Comparing Energy Efficiency of CPU, GPU and FPGA Implementations for Vision Kernels. In Proceedings of the 2019 IEEE International Conference on Embedded Software and Systems (ICESS), Las Vegas, NV, USA, 2–3 June 2019. [Google Scholar] [CrossRef]
- Lastovetsky, A.; Manumachu, R.R. Energy-Efficient Parallel Computing: Challenges to Scaling. Information 2023, 14, 248. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Xu, W.-J.; Tian, F.-Q.; Du, X.-H. A Multi-GPUs based SWE algorithm and its application in the simulation of flood routing. Adv. Water Resour. 2025, 201, 104985. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, P.; Li, W.; Cao, Z.; Li, Y. An engineering-oriented Shallow-water Hydro-Sediment-Morphodynamic model using the GPU-acceleration and the hybrid LTS/GMaTS method. Adv. Eng. Softw. 2024, 200, 103821. [Google Scholar] [CrossRef]
- Hu, X.; Song, L. Hydrodynamic modeling of flash flood in mountain watersheds based on high-performance GPU computing. Nat. Hazards 2017, 91, 567–586. [Google Scholar] [CrossRef]
- Guo, K.; Guan, M.; Yu, D. Urban surface water flood modelling—A comprehensive review of current models and future challenges. Hydrol. Earth Syst. Sci. 2021, 25, 2843–2860. [Google Scholar] [CrossRef]
- Hoshino, T.; Maruyama, N.; Matsuoka, S.; Takaki, R. CUDA vs. OpenACC: Performance Case Studies with Kernel Benchmarks and a Memory-Bound CFD Application. In Proceedings of the 2013 13th IEEE/ACM International Symposium on Cluster, Cloud, and Grid Computing, Delft, The Netherlands, 13–16 May 2013; pp. 136–143. [Google Scholar] [CrossRef]


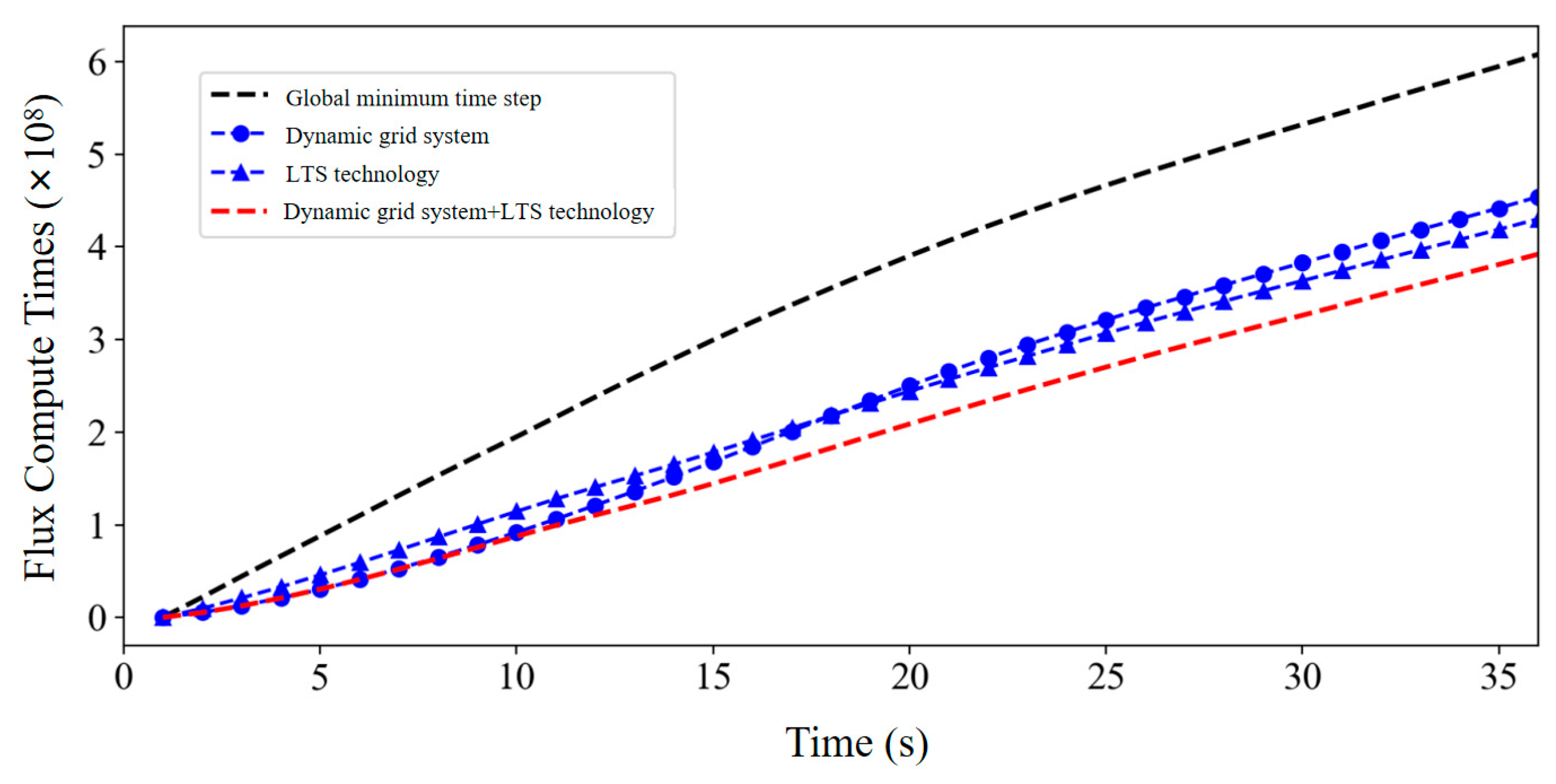


| Case | Mesh Info | Computational Costs for Base Model/min | Speed Up Ratio | |||||
|---|---|---|---|---|---|---|---|---|
| Number | Minimum Size | Dynamic Grid | LTS Technology | GPU | Dynamic Grid + LTS | Dynamic Grid + LTS + GPU | ||
| Uniform | 129486 | 0.2 | 2.63 | 1.18 | 1.29 | 15.8 | 1.41 | 16.21 |
| Non-uniform | 243790 | 0.1 | 11.34 | 1.09 | 1.36 | 38.45 | 1.33 | 41.58 |
| Non-uniform | 474276 | 0.05 | 39.92 | 1.18 | 1.56 | 49.06 | 1.78 | 62.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ping, Y.; Xu, H.; Song, L.; Chen, J.; Zhang, Z.; Hu, Y. Research on Acceleration Methods for Hydrodynamic Models Integrating a Dynamic Grid System, Local Time Stepping, and GPU Parallel Computing. Water 2025, 17, 2662. https://doi.org/10.3390/w17182662
Ping Y, Xu H, Song L, Chen J, Zhang Z, Hu Y. Research on Acceleration Methods for Hydrodynamic Models Integrating a Dynamic Grid System, Local Time Stepping, and GPU Parallel Computing. Water. 2025; 17(18):2662. https://doi.org/10.3390/w17182662
Chicago/Turabian StylePing, Yang, Hao Xu, Lixiang Song, Jie Chen, Zhenzhou Zhang, and Yuying Hu. 2025. "Research on Acceleration Methods for Hydrodynamic Models Integrating a Dynamic Grid System, Local Time Stepping, and GPU Parallel Computing" Water 17, no. 18: 2662. https://doi.org/10.3390/w17182662
APA StylePing, Y., Xu, H., Song, L., Chen, J., Zhang, Z., & Hu, Y. (2025). Research on Acceleration Methods for Hydrodynamic Models Integrating a Dynamic Grid System, Local Time Stepping, and GPU Parallel Computing. Water, 17(18), 2662. https://doi.org/10.3390/w17182662






