Simulation and Prediction of Soil–Groundwater Pollution: Current Status and Challenges

Abstract

Soil–groundwater pollution is a complex environmental phenomenon formed by the coupling of multiple processes. Due to the concealment of pollution, the persistence of harm, and the complexity of the system, soil–groundwater pollution has become a major environmental issue of increasing concern. The simulation and prediction of different types of models, different pollutants, and different scales in soil and groundwater have always been the research hotspots for pollution prevention and control. Starting from the mathematical mechanism of pollutant transport in soil and groundwater, this study reviews the method models represented by empirical models, analytical models, statistical models, numerical models, and machine learning, and expounds the characteristics and applications of the various representative models. Our Web of Science analysis (2015–2025) identifies 3425 relevant studies on soil–groundwater pollution models. Statistical models dominated (n = 1155), followed by numerical models (n = 878) and machine learning (n = 703). Soil pollution studies (n = 1919) outnumber groundwater research (n = 1506), with statistical models being most prevalent for soil and equally common as numerical models for groundwater. Then this study summarizes the research status of soil–groundwater pollution simulation and prediction at the level of multi-scale numerical simulation and the pollutant transport mechanism. It also discusses the development trend of artificial intelligence innovation applications such as machine learning in soil–groundwater pollution, looks forward to the challenges and measures to cope with them, and proposes to systematically respond to core challenges in soil and groundwater pollution simulation and remediation through new technology development, multi-scale and multi-interface coupling, intelligent optimization algorithms, and pollution control collaborative optimization methods for pollution management, so as to provide references for the future simulation, prediction, and remediation of soil–groundwater pollution.

1. Introduction

With the acceleration of global urbanization and the continuous enhancement of social productivity, soil and groundwater pollution has become increasingly widespread, posing significant environmental challenges. Many countries have recognized the potential hazards of soil–groundwater contamination and prioritized its prevention and control in environmental management strategies. Researchers have made substantial progress in understanding pollution mechanisms, developing simulation and prediction methods, and advancing related technologies. This study, based on the current status of soil and groundwater pollution, systematically reviews the mathematical mechanisms governing the transport of pollutants in soil and groundwater. It provides a comprehensive overview of existing models and methods for pollution simulation and prediction, critically analyzes recent research advancements, highlights the innovative breakthroughs brought by artificial intelligence (AI) technologies in this field, and discusses future development trends and the challenges that remain. The roadmap of the research is shown in Figure 1.

2. Overview of Soil and Groundwater Pollution

Pollutants in soil and groundwater pose significant threats to human health through multiple exposure pathways, including inhalation of volatile compounds, ingestion of contaminated groundwater, soil intake, dermal contact, and bioaccumulation in the food chain. Among these pollutants, a substantial proportion are known to be carcinogenic, teratogenic, or mutagenic [1]. The nature of soil–groundwater pollution is inherently complex, involving the coupling of physical transport and transformation, geochemical evolution, biodegradation, and hydrogeological processes.

From the perspective of soil pollution, some developed countries report industrial land contamination rates exceeding 20% [2]. In the United States, 10–30% of underground storage tanks have experienced varying degrees of leakage [3]. In England and Wales, nearly 100,000 sites are known to be contaminated, affecting approximately 300,000 hectares of land due to industrial activities and natural causes [4]. It is estimated that Europe has 2.8 million potentially contaminated sites, of which 19% require or may require remediation or risk mitigation measures [5]. Nearly two-thirds of point-source soil pollution in Europe is attributed to industrial and commercial activities as well as waste disposal and treatment practices [6].

In China, the soil pollution situation has shown signs of improvement. According to the 2023 China Ecological and Environmental Status Bulletin [7], the overall soil environmental risk has been effectively controlled, and the trend of worsening soil pollution has been preliminarily curbed. The safe utilization rate of agricultural land reached 91%, with the soil conditions of farmland remaining generally stable. Targeted measures have been implemented to control heavy metal pollution, such as cadmium, at the source, resulting in a downward trend in heavy metal concentrations in remediated plots. The safe use of land designated for key construction projects has also been effectively ensured.

In contrast, groundwater pollution remains a serious concern. As declared at the 30th International Geological Congress held in Beijing in 1996, “Half of the world’s groundwater is polluted” [1]. In China, the situation is similarly alarming, with monitoring data indicating that 90% of groundwater is polluted to varying degrees, and 60% is severely contaminated [8]. Trend analysis indicates that the scope of groundwater pollution continues to expand, with two-thirds of Chinese cities experiencing a general decline in groundwater quality. Localized areas face severe deterioration, and over 300 cities suffer from water supply shortages due to groundwater contamination [2]. According to the 2023 China Ecological and Environmental Status Bulletin [7], among 1888 national groundwater quality assessment points, 77.8% were classified as Class I–IV, while 22.2% were Class V. The primary exceedance indicators included iron, sulfate, and chloride, indicating an urgent need for groundwater quality improvement.

It is important to note the concealed nature of soil and groundwater systems. Compared to air and surface water pollution, the environmental response of subsurface pollution is significantly delayed, resulting in more prolonged and far-reaching risks to ecosystems and human health. Furthermore, due to the complexity of hydrogeological conditions, pollutant migration in the soil–groundwater system involves multi-interface, multiphase, and multi-process interactions, which pose significant challenges to research. Given these conditions, the importance of simulation and predicting pollutant behavior in soil and groundwater becomes evident. Such efforts are essential for providing scientific and technical support for effective pollution management and prevention. Studies have demonstrated that numerical modeling approaches can provide reliable predictions of heavy metal contamination risks at polluted sites [9]. Furthermore, machine learning can identify the key factors governing metal migration in soils [10]; it holds broad application prospects for modeling and predicting soil–groundwater pollution.

Based on the mathematical principles of soil–groundwater pollution modeling, this study systematically classifies existing models and analyzes the characteristics of representative model types. A comprehensive review is presented on the current research status and developmental trends of modeling technologies, with a focused discussion on the application of machine learning in soil–groundwater pollution studies. Research findings indicate that machine learning algorithms enable more refined characterization of soil–groundwater pollution [11]. Furthermore, the study identifies five critical challenges: information acquisition, prediction accuracy, computational cost, unclear multi-interface mechanisms, and pollution remediation. Corresponding countermeasures are proposed to address these challenges, aiming to advance the field toward more efficient and accurate pollution simulation and management.

3. Processes of Pollutant Fate and Transport: Key Models and Frameworks

3.1. Mathematical Mechanisms Based on Transport Processes

To investigate the sources, migration pathways, and potential impacts of pollutants, mathematical theories are employed to simulate and predict the transport and transformation processes of pollutants in soil and groundwater, based on the current pollution conditions. This approach, which helps in developing effective pollution control strategies, has become a widely used and efficient method. These mathematical models are based on the principles of mass conservation and motion equations, incorporating various physical and chemical processes, including convection, diffusion, adsorption, attenuation, and transformation [12].

(1)

Convection

Convection typically occurs when a fluid, during its flow, transports itself and the pollutants it contains to a specific spatial location, resulting in relative motion. In porous media systems, as the flow rate of the fluid increases, the flow velocity also increases, which enhances convection and dilutes the pollutants. The convective transport of pollutants is commonly described using the convective flux, denoted as $J_v$.

$$J_v=nuC$$

(1)

Here, $J_v$ represents the convective flux, with units of kg·m⁻²·s⁻¹; $n$ is the porosity of the porous medium; $u$ is the average flow velocity of the fluid through the pore spaces of the porous medium, with units of m·s⁻¹; and $C$ is the average concentration of the pollutant, with units of kg·m⁻³.

(2)

Diffusion

Diffusion refers to the natural spreading of pollutants in soil and groundwater due to concentration gradients. The diffusion process is typically described by Fick’s First Law, which states that the rate of pollutant transport is directly proportional to the concentration gradient.

$$J_s= -D_s^{\prime }{\displaystyle \frac{dC}{dx}}$$

(2)

Here, $J_s$ represents the diffusion flux of the solute, with units of kg·m⁻²·s⁻¹. $D_s^{\prime }$ D_s′ is the effective diffusion coefficient of the solute, with units of m²·s⁻¹; and ${\displaystyle \frac{dC}{dx}}$ is the concentration gradient, with units of kg·m⁻⁴.

To describe the temporal variation in concentration in non-steady-state diffusion processes, Fick’s Second Law is required. If the diffusion coefficient $D_s^{\prime }$ is independent of concentration $C$, it can be expressed as

$${\displaystyle \frac{\partial C}{\partial t}}={ D}_s^{\prime }{\nabla }^{2}C$$

(3)

Here, $D_s^{\prime }$ is the effective diffusion coefficient of the solute, with units of m²·s⁻¹, and $C$ is the average concentration of the pollutant, with units of kg·m⁻³.

(3)

Adsorption

Adsorption refers to the process by which pollutants adhere to and desorb from the surface of soil particles. Adsorption is typically described by adsorption isotherm models, which consider the adsorption sites on the soil particle surfaces and the adsorption isotherms. Among these, the Langmuir isotherm and the Freundlich isotherm are the most widely applied:

The Langmuir isotherm is typically expressed as

$$q_e=q_{max}{\displaystyle \frac{K_L{C}_e}{1+K_L{C}_e}}$$

(4)

Here, $q_e$ represents the amount of adsorbate per unit mass of the adsorbent, $q_{max}$ is the maximum adsorption capacity of the adsorbent, $K_L$ is the adsorption equilibrium constant, with units of m³·kg⁻¹, and $C_e$ is the equilibrium concentration of the pollutant, in units of kg·m⁻³.

The Freundlich isotherm is typically expressed as the following mathematical formula:

$$q_e={ K}_F{C}_e^{1/n}$$

(5)

Here, $q_e$ represents the amount of adsorbate per unit mass of the adsorbent, $K_F$ is the adsorption equilibrium constant, with units of m³·kg⁻¹, $C_e$ is the equilibrium concentration of the pollutant, in units of kg·m⁻³, and n is a constant.

The Temkin isotherm is typically expressed as

$$q_e={\displaystyle \frac{RT}{b}}ln(A·C_e)$$

(6)

Here, $q_e$ represents the amount of adsorbate per unit mass of the adsorbent, $R$ is the gas constant, with units of J·mol⁻¹·K⁻¹, $T$ is the absolute temperature, with units of K, $b$ is the Temkin constant related to adsorption heat, with units of J·mol⁻¹, $A$ is the adsorption equilibrium constant, with units of L·mol⁻¹, $C_e$ is the equilibrium concentration of the pollutant, in units of kg·m⁻³.

(4)

Attenuation

Attenuation refers to the process by which pollutants decrease in soil and groundwater due to biodegradation, chemical reactions, or other factors. Attenuation is typically described by a first-order kinetic model, which considers the attenuation rate constant. The differential form of the pollutant concentration degradation rate in the first-order kinetic model is

$${\displaystyle \frac{dC}{dt}}=kC$$

(7)

Here, $k$ is the attenuation rate constant, with units of s⁻¹, $C$ is the concentration of the pollutant in the solution, in units of kg·m⁻³, and ${\displaystyle \frac{dC}{dt}}$ is the attenuation rate, with units of kg·m⁻³·s⁻¹.

(5)

Transformation

Transformation refers to the process by which pollutants undergo changes in soil and groundwater due to chemical reactions or other factors. Transformation is typically described by a reaction kinetics model, which considers the transformation rate constant and the reaction mechanism. The transformation reaction rate equation can be expressed as

$$\begin{array}{c}-r_A=k{C}_A^{{\mathsf{\alpha }}_1}{C}_B^{{\mathsf{\alpha }}_2}\end{array}$$

(8)

Here, $r_A$ is the reaction rate, with units of kg·m⁻³·s⁻¹, $k$ is the second-order reaction rate constant (Suppose α1 + α2 = 2), with units of m³·kg⁻¹·s⁻¹, $C$ is the concentration of the pollutant in the solution, in units of kg·m⁻³, and $\alpha$ is the reaction order.

The systematic integration of soil–groundwater pollutant migration and transformation processes lays the theoretical foundation for constructing multi-physical field coupling mathematical models. Mathematical models can be used to simulate and predict the migration and transformation of pollutants across different spatial and temporal scales, effectively revealing the mechanisms of pollutant transport. This forms the basis for numerical simulation control equations, providing scientific support for environmental management and pollution remediation.

3.2. Introduction to Representative Models

The mathematical theories, construction methods, applicable scenarios, and approaches to representing pollutant migration and transformation processes vary among soil and groundwater pollution models. The mathematical foundation is a core element, and based on differences in theoretical approaches, these models can be classified into five categories: empirical models, analytical models, numerical models, statistical models, and machine learning.

(1)

Empirical Models

Empirical models are established based on observed data and empirical patterns, and are typically used to describe known pollution conditions and trends. These models determine the relationships between variables through statistical analysis of experimental data. However, they may lack accuracy when describing complex environmental systems due to unclear mechanisms and limited precision. Empirical models are generally suitable for rapid assessments or scenarios where the underlying mechanisms are not well understood, such as initial pollutant screening or concentration prediction at specific sites.

(2)

Analytical Models

Analytical models describe the transport processes of soil and groundwater pollution through analytical solutions of pollutant migration equations. These models typically require simplified boundary conditions and are often used for theoretical research and simulations of idealized systems, such as long-term plume dispersion in homogeneous aquifers. Analytical models are characterized by theoretical rigor and computational efficiency, making them one of the more mature modeling approaches used in soil and groundwater pollution studies.

(3)

Numerical Models

Numerical models use computer simulations to approximate solutions to complex equations through discretization and iterative algorithms, simulating the transport of pollutants in soil and groundwater. These models are typically based on numerical methods such as the finite element method or finite difference method and can support multi-interface and multi-process coupled simulations—for example, coupling between the unsaturated and saturated zones. Numerical models are capable of accurately capturing system heterogeneity and nonlinear processes, and they are currently the most widely used type of model in soil and groundwater pollution research.

(4)

Statistical Models

Statistical models analyze historical data and trends using probability theory and statistical methods to quantify the uncertainty and spatial variability of pollutant distribution. These models can help identify potential pollution sources and high-risk areas, playing an important role in risk assessment and planning management. In the future, integrating machine learning (ML) and other artificial intelligence techniques may uncover hidden patterns from multi-source data, offering broad application prospects.

(5)

Machine learning

Building upon the aforementioned four model categories, machine learning represents an emerging class of models. Its underlying principle involves utilizing diverse algorithms to optimize model construction. In soil–groundwater pollution research, machine learning has been primarily applied to pollution source identification, pollutant concentration prediction, and contamination risk assessment.

A literature search targeting the aforementioned five models was conducted in the Web of Science (WOS) Core Collection database, covering the period from 1 January 2015 to 29 April 2025, with the search conducted on 29 April 2025. The search was carried out using the topic (TS) field with the following search query: “TS = (Empirical Models) AND TS = (soil) OR TS = (groundwater) AND TS = (pollution); TS = (Analytical Models) AND TS = (soil) OR TS = (groundwater) AND TS = (pollution); TS = (Numerical Models) AND TS = (soil) OR TS = (groundwater) AND TS = (pollution); TS = (Statistical Models) AND TS = (soil) OR TS = (groundwater) AND TS = (pollution); TS = (Machine learning) AND TS = (soil) OR TS = (groundwater) AND TS = (pollution)”.

The initial search yielded 3595 potentially relevant studies. After excluding review articles (n = 170), a total of 3425 research articles were retained for analysis. Among these, the distribution of modeling approaches was as follows: empirical models (n = 305), analytical models (n = 384), numerical models (n = 878), statistical models (n = 1155), and machine learning (n = 703). In terms of pollution types, soil pollution was addressed in 1919 studies, while groundwater pollution was investigated in 1506 studies. The specific distribution is presented in Figure 2.

The results indicate that statistical models were the most frequently employed approach, followed by numerical Models and machine learning. Regarding pollution categories, studies on soil pollution outnumbered those on groundwater pollution. Notably, statistical models were the most widely used method in soil pollution research, whereas numerical models and statistical models were equally prevalent in groundwater pollution studies.

The following table (

Table 1. Classification table of representative models for soil and groundwater pollution studies.

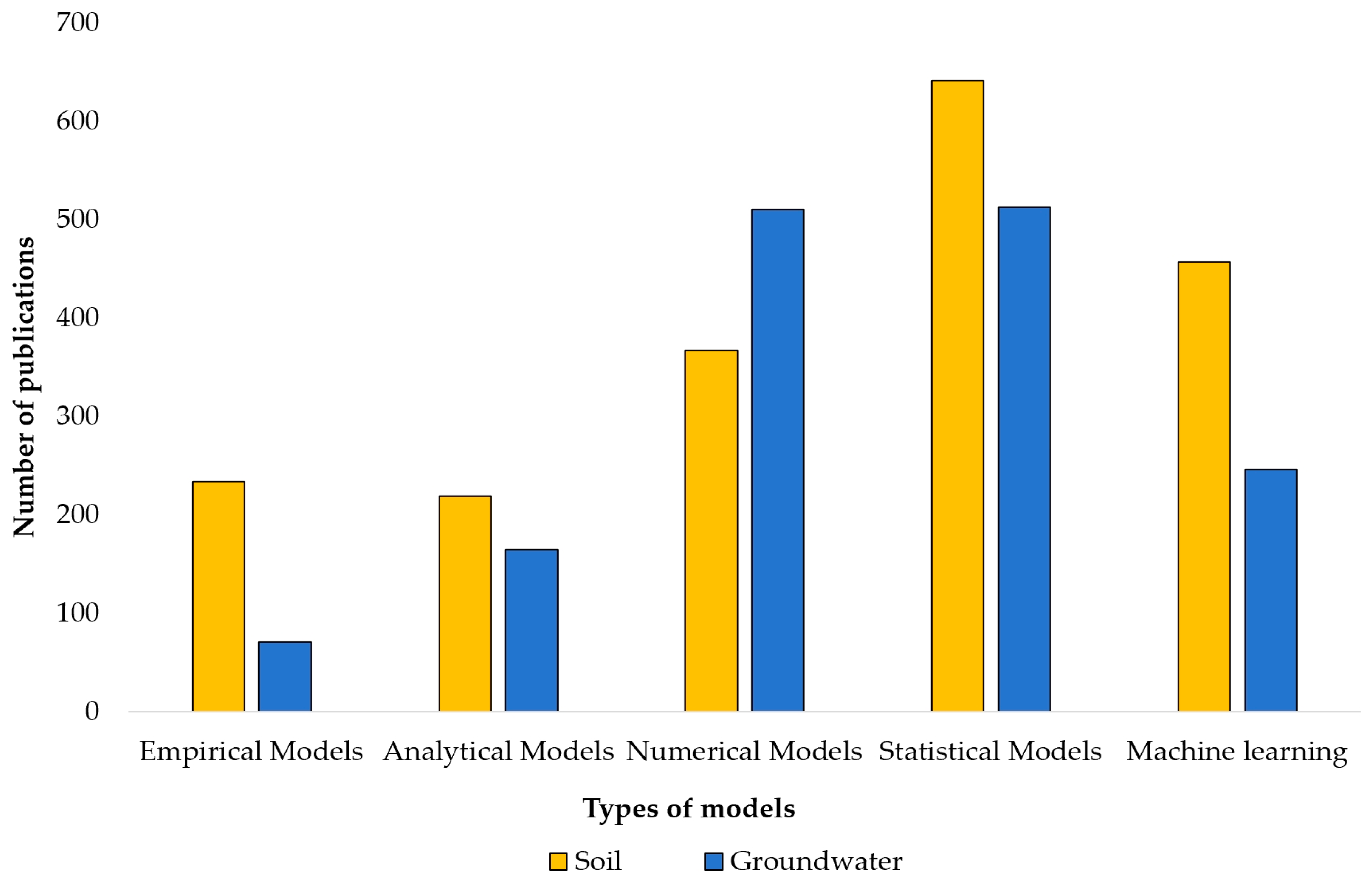
Classification	Representative Models	Model Overview	Main Features of the Model	Evaluation Index	References
Empirical Models	Johnson and Ettinger Model	The commonly used indoor and outdoor vapor intrusion models	The statistical model is simple and easy to use, but its computational results tend to be overly conservative	Accuracy, Precision, Recall, F1 Score	[13]
	DED Model	The binary equilibrium desorption model	Optimize the phase distribution process of VOCs in soil		[14]
	Volasoil Model	The model for actual risk assessment of contaminated soil	Both scientifically reasonable and practical		[15]
	CLEA Model	Models used for risk assessment	Evaluating the impact of contaminated soil on human health		[16]
	DRASTIC Model	Models used for groundwater vulnerability assessment	The most mature and widely used model in the method of nested index		[17]
Analytical Models	EPACMTP Model	Models used to simulate the migration of pollutants in soil and groundwater	The mature analytical models widely recognized both domestically and internationally	MSE, R2, Runtime	[18]
	PHREEQC Model	Models used for hydrogeochemical modeling	Use for one-dimensional advection–dispersion solute transport situations		[19]
Numerical Models	MODFLOW Model	The model that uses the three-dimensional finite difference method for numerical simulation	The most widely used three-dimensional groundwater flow model in the world	Accuracy, MSE, R2, AUC-ROC, Runtime	[20]
	FEMWAT-ER Model	The finite element model used for numerical modeling of groundwater and surface water	Simulate the coupled flow and contaminant transport driven by density in both saturated and unsaturated zones		[21]
	MT3D Model	The three-dimensional solute transport model used to simulate convection, dispersion, and chemical reactions of individual dissolved components in groundwater	Simulate the transport process of different chemicals in groundwater, suitable for complex groundwater systems		[22]
	RT3D Model	The numerical model used to describe the transport and reaction processes of groundwater and solutes	Fully consider the impact of chemical reactions in groundwater on pollutant transport		[23]
	DFN Model	The model used to describe the discrete fracture network structure of rocks	Accurately describe the migration paths of fluids and pollutants in fractured rock masses		[24]
	NIHM Model	The standard integrated hydrological model	Able to reduce the dimensionality of flow and transport problems		[25]
Statistical Models	MIM Model	The moving-static model	Solve the two-dimensional non-equilibrium solute transport problem in groundwater	Accuracy, Precision, F1 Score, MSE, R2	[26]
	ISSHM Model	The surface–subsurface integrated hydrological model	The solute transport solver in the model can easily encounter numerical dispersion errors		[27]
	2D RTMs Model	Two-dimensional reactive transport model	A new method for identifying and evaluating the potential contribution of arsenic sources in soil and water systems		[28]
Machine learning	ANNs Model	The basic deep learning model	Effective for modeling nonlinear relationships in complex pollution systems	Accuracy, Precision, Recall, F1 Score, AUC-ROC	[29]
	RF Model	The ensemble learning model in machine learning	Demonstrate outstanding performance in pollution source identification and risk assessment		[30]
	SVM Model	The classical supervised learning algorithm model	Applicable for assessing groundwater contamination probability and classifying pollution risk levels		[31]

) presents an analysis of some representative models from these five categories in the study of soil and groundwater pollution.

When evaluating the accuracy and performance of different models in a table, the following statistical metrics can be used to demonstrate model quality:

Accuracy: measures the proportion of correct predictions made by the model.

Precision: calculates the ratio of true positive predictions to all positive predictions.

Recall: represents the ratio of true positives correctly identified among all actual positives.

F1 Score: the harmonic mean of precision and recall, balancing both metrics.

AUC-ROC (Area Under the ROC Curve): Evaluates binary classification performance, especially for imbalanced data. A higher AUC value indicates better model discrimination.

Mean Squared Error (MSE): Used in regression tasks to quantify the average squared difference between predicted and actual values. Lower values denote higher precision.

R-squared (R²): Assesses how well the model fits the data. Values closer to 1 indicate stronger predictive capability.

Runtime: Measures the time required for model training or prediction. A critical performance factor for large-scale datasets or real-time applications.

In practical applications, different types of models are often combined for comprehensive analysis and evaluation in order to better manage and address soil and groundwater pollution issues. When selecting a model, it is essential to consider factors such as the availability of data, the complexity and accuracy requirements of the model, its adaptability, computational efficiency, as well as the specific goals and scope of the application to choose the most suitable model.

4. Research Status and Development Trends

4.1. Multi-Scale Numerical Simulation Technology

In recent years, numerical models have dominated pollutant migration simulation, capable of handling heterogeneous media, multiphase flow, and complex chemical reaction processes. On the international level, a relatively complete multi-scale numerical simulation technology system has been developed. For example, a coupled model based on the Richards equation and solute transport equation has been developed for the solute migration process in the unsaturated–saturated soil at medium and small scales, with dynamic simulation of water flow and pollutant migration achieved through finite difference or finite element methods. In large-scale groundwater pollutant migration, a combination of the analytical element method and streamline method has been shown to have good simulation effects [32]. Additionally, a series of innovative methods have been proposed: enhancing groundwater inversion accuracy through particle tracking models [33], addressing system uncertainty through stochastic modeling [34], and optimizing fracture medium simulation using fracture mass accumulation technology [35]. Domestic scholars have also innovatively established a multi-level risk assessment system for contaminated sites and developed risk-based control technologies [36]. New breakthroughs have been made in three-dimensional grid modeling and pollutant source tracking methods: a unified modeling technique for complex geological bodies has been proposed, enabling grid generation for complex reverse faults [37]. Pollution source tracking based on numerical simulation involves constructing grid models, combining pollution data for tracking, and improving the accuracy of pollutant path detection through optimization algorithms [38]. However, challenges remain, such as distortion in heterogeneity representation when extending from medium- and small-scale models to regional scales, and the difficulty of accurately capturing the spatial distribution characteristics of pollutants in large-scale simulations.

4.2. Study of Pollutant Migration Mechanisms

Since the 20th century, foreign countries have systematically carried out research on the migration and transformation mechanisms of soil and groundwater pollutants, achieving breakthroughs in many areas. In terms of microscopic molecular mechanisms, the “dual-mode” adsorption theory for hydrophobic organic pollutants was proposed to replace the traditional Langmuir/Freundlich models, more accurately reflecting the nonlinear adsorption behavior of hydrophobic organic compounds [39]. In the multiphase transport process, a control and evaluation model for multiphase flow and migration of nonaqueous phase liquids (NAPLs) has been developed [40]. In multi-interface reactions, the solute transport in both solid-phase kinetic adsorption and gas–water interface adsorption was explained for the first time [41]. Domestically, recent research has focused on the multiphase migration patterns of heavy metals and organic pollutants. A pollutant simulation framework has been established that takes into account geological characteristics, soil types, climate conditions, and other factors. Additionally, multi-scale groundwater flow and pollutant migration simulation methods have been developed and improved, overcoming key modeling challenges in the transport of density-variable, multi-component, and multiphase pollutants [42]. However, research on multi-process coupling mechanisms remains insufficient. Existing models still inadequately represent complex mechanisms such as unsaturated–saturated zone coupling transport and the interaction between biogeochemical processes and hydrological processes. There is a significant lag in the development of multi-medium migration models for emerging pollutants, particularly in the case of volatile organic compounds (VOCs), where there is a lack of assessment standards for phase-transition-migration coupling simulations [43].

4.3. Application of Artificial Intelligence Methods

Under the wave of the new era, AI has made significant progress in modeling research related to soil and groundwater pollution. Machine learning, a subset of AI [44], utilizes supervised learning, unsupervised learning, and reinforcement learning algorithms to build predictive models, significantly improving the analytical accuracy of multiphase pollutant transport mechanisms. Neural networks, as one of the most widely used machine learning algorithms, have achieved breakthroughs in precision through error backpropagation mechanisms, particularly in the inverse prediction of groundwater pollutant concentrations, and have begun to show great promise in the groundwater domain [45]. Due to their powerful nonlinear mapping capabilities, neural networks have gradually become mainstream tools for groundwater quality simulation. Further studies have shown that machine learning techniques are also being applied to support pollution source identification and probabilistic risk assessment. Convolutional neural networks (CNNs) can be integrated into machine learning frameworks to address the identification of groundwater pollution sources under given aquifer monitoring networks [46]. CNNs have emerged as the preferred architecture for dynamic simulation of groundwater quality [47].

In the simulation of soil and groundwater pollutant transport, ensemble learning algorithms exhibit distinct advantages in innovation, breakthrough potential, and efficiency through collaborative multi-model mechanisms. For instance, Huang et al. creatively combined self-organizing neural networks with K-means clustering algorithms, providing a basis for precise zoning and control of groundwater pollution in contaminated sites [48]. Tian et al. integrated Random Forest regression with stochastic parameter models to enable rapid pollution risk assessments [49]. This method demonstrated a breakthrough in simulating the migration of NAPL plumes by optimizing parameter selection through feature importance analysis, reducing computational time by two orders of magnitude, and offering a new paradigm for pollutant migration studies in heterogeneous aquifers [30]. The efficiency of this method provides strong technical support for sustainable water resource management, with significant engineering value in remediation plan optimization and early risk warning [50].

However, current AI applications in soil and groundwater pollution research still face many challenges. Firstly, the quality of training data varies, and the sparsity of monitoring data for emerging pollutants lowers model accuracy. Secondly, most AI models remain at the data-driven level, lacking deep integration with the physical and chemical processes of pollutant migration and transformation. Additionally, although deep learning methods can handle high-dimensional data in soil and groundwater environments, they often suffer from limited model interpretability, which restricts their application in pollution forecasting and environmental management.

5. Challenges and Countermeasures

5.1. Information Acquisition Challenges

Information acquisition is the first and fundamental step in model-based simulation and prediction. The construction of a conceptual model for groundwater pollution relies on three primary categories of data: basic background information of the assessment area, data required for hydrodynamic field generalization, and data required for pollution site characterization. For the latter, essential information includes the attributes and locations of pollution sources, the physicochemical properties of major contaminants, types, and concentrations of pollutants exceeding the standards, parameters related to pollutant transport and transformation, and the migration pathways of contaminant discharge [51]. However, due to complex site conditions, the lack of historical site data, and measurement errors in model parameters, it is often difficult to obtain accurate and reliable data. This lack of critical information negatively impacts the accuracy and reliability of soil and groundwater pollution simulation and prediction.

In the future, emerging technologies can be employed to improve the efficiency of information acquisition. These include multi-source data fusion, intelligent interpolation techniques, and the integration of high-resolution remote sensing with machine learning methods—such as combining Interferometric synthetic aperture radar (InSAR) technology with machine learning to monitor land subsidence [52]. These approaches enable real-time acquisition of hydrological and geological dynamic data such as groundwater levels, conductivity, and pollutant concentrations. Additionally, geostatistical methods can be used to infer the spatial distribution of parameters in unsampled regions, while Bayesian inversion techniques can integrate historical data to reduce the impact of missing information.

5.2. Prediction Accuracy Challenges

Numerical models are the most commonly used tools in groundwater pollution simulation. However, due to the inherent complexity of hydrogeological conditions and the uncertainty in conceptual models and fitting data, numerical models often exhibit randomness in their calibration parameters, leading to reduced simulation accuracy [53]. For example, seasonal fluctuations in groundwater levels or anthropogenic water use can alter groundwater flow fields, yet models often assume steady or quasi-steady states, causing a lag in the model’s response to dynamic pollution processes.

Despite the progress made in modeling soil and groundwater pollutants, several challenges persist. The uncertainty of certain model parameters limits their applicability and predictive capability. For instance, hydraulic conductivity is affected by spatial heterogeneity, such as pore structure and fracture development, which is often overlooked in model predictions, thereby increasing the uncertainty of simulation results. Additionally, due to the limitations inherent in each model, its application scope is narrow, and the accuracy often fails to meet practical requirements. In China, the standard system for groundwater pollution simulation and prediction is relatively underdeveloped, lacks enforcement, and suffers from insufficient refinement [54].

Looking forward, integrating hydrogeological conditions with hydrogeochemical processes to develop multi-scale coupled hydrogeochemical models could significantly improve prediction accuracy. These models would combine groundwater flow fields, pollutant transport fields, and geochemical reaction fields into a cohesive framework. Advancements in heterogeneous characterization techniques can also help reduce model errors—for example, the use of DFN models to describe preferential flow paths in fractured media, thereby enabling the study of coupled groundwater flow and solute transport in fractured rock masses [55]. To address the lag in model response caused by seasonal water level fluctuations or human water use, dynamic boundary conditions can be introduced to better capture these effects. Furthermore, it is recommended to integrate geological, hydrological, and pollution monitoring data to establish a national-scale groundwater pollution database that supports standardized data sharing.

5.3. Computational Cost Challenges

Uncertainty analysis in model predictions is a critical step in ensuring the reliability of simulation results. However, the high computational cost associated with such analyses significantly limits their widespread application in engineering practices and scientific research. Sources of uncertainty in soil and groundwater models can be categorized into three types: parameter uncertainty, model uncertainty, and data uncertainty [56]. Global sensitivity analysis is one of the methods used to analyze parameter uncertainty, but it is generally based on Monte Carlo sampling and Latin Hypercube sampling, which require thousands to tens of thousands of sampling iterations, making them highly labor-intensive and limiting their practicality in groundwater numerical models [57]. For example, the Sobol index method requires variance decomposition to quantify the contribution of parameters to the output, typically requiring N × (D + 2) model runs (where D is the number of parameters and N is the sample size). For instance, when D = 10 and N = 10³, it requires 1.2 × 10⁴ simulations. Even if each simulation takes just one minute, the total time required would be eight days. Monte Carlo simulations, which involve random sampling to statistically estimate the output distribution, require even more samples, especially for low-probability, high-risk events, with sampling numbers exceeding hundreds of thousands to stabilize the probability distribution, further exacerbating the computational burden.

In the future, adopting comprehensive groundwater modeling methods for computation can significantly reduce the computational cost of uncertainty analysis and prediction [58]. In recent years, the increasing computational power and the application of high-performance parallel computing have made a significant impact on reducing the computational costs associated with model prediction uncertainty [59]. Parallel computing can efficiently implement global sensitivity analysis, improve the efficiency of model parameter optimization [60], accelerate Monte Carlo simulations, and speed up the training and validation of surrogate models. Additionally, using surrogate models to replace original models is a novel approach to addressing the computational cost issue. Surrogate models greatly enhance the computational efficiency of numerical models and have been applied in six major areas: groundwater pollution source identification, groundwater remediation design, coastal aquifer management, groundwater uncertainty analysis, groundwater monitoring network design, and groundwater transport parameter inversion [61]. However, the challenge remains of how to optimize the inversion of numerical model parameters using surrogate models or parallel computation optimization algorithms, which is a problem to be solved in the future [60].

5.4. Unclear Mechanisms in Multi-Interface and Multiphase Systems

In terms of the scientific problems to be solved, the existing research in China on the interaction mechanisms of heavy metals and organic pollutants in soil–groundwater systems, the interfacial mass transfer processes and coupling models in these systems, and the driving mechanisms and regulatory principles of multiphase processes in soil–groundwater systems is still not sufficiently clear [42]. In actual complex media sites, although related modeling methods and applications have a certain foundation, the modeling difficulty remains high due to the complexity of the soil structure, groundwater distribution, and the distribution of volatile organic pollutants across phases in complex media such as loose porous media and fractured (karst) media, which exhibit significant heterogeneity. As a result, there has been limited research on the multiphase transport and diffusion flux of volatile organic pollutants in such sites, especially in terms of the diffusion flux from soil, aqueous phase, and free phase to the gas phase.

In the future, more in-depth research and exploration can be conducted on the interaction mechanisms of pollutants, the coupling processes across multiple interfaces, and the driving mechanisms in soil–groundwater systems. For the study of interaction mechanisms, research can start from the multiphase distribution of pollutants (NAPL—aqueous-air), and the TMVOC module in the TOUGH2 (v.2.1) numerical simulation software can be used to simulate the multiphase and multi-interface transport processes of pollutants [62]. The study of coupling mechanisms can be achieved by coupling the fugacity model with the HYDRUS-1D (v.4.17)model to simulate the dynamic processes of pollutant solute adsorption, degradation, and leaching [63]. The gas-phase diffusion behavior of VOCs in the unsaturated zone has been incorporated into the fugacity model, quantifying the air–liquid–solid multiphase distribution coefficients and providing new methods for predicting the extent of contamination. The driving mechanisms can be explored by further investigating the physical–chemical driving factors and biogeochemical driving networks. Deepening the study of multiphase and multi-interface processes could break through the traditional model bottlenecks related to multiphysical field coupling, preferential flow paths in heterogeneous media, and the characterization of air–liquid–solid multiphase distribution.

5.5. Challenges in Pollution Remediation

Soil and groundwater pollution remediation technologies are closely linked with model simulation predictions, and both dynamically interact. Remediation measures can serve as input conditions for models, while models can validate the results of pollution remediation. Groundwater remediation technologies have been continuously improved and innovated through extensive practical applications. Currently, the most typical groundwater pollution remediation technologies include the following three: pump-and-treat (P&T) technology, monitor natural attenuation (MNA) technology, and in situ remediation technology [64]. In addition, permeable reactive barriers (Bio-PRBs) are an emerging groundwater pollution remediation technology that is still under development. Advanced knowledge of pollutant migration and the reactions within Bio-PRBs is crucial for the successful practical application of this technology [34]. However, the remediation process for soil and groundwater pollution also faces many challenges, such as how to achieve integrated water and soil management, the management and control of large and complex contaminated sites, the rebound of pollutants during groundwater remediation, and the pollution migration and risk control methods for karst fissure water [65]. These are the issues that soil and groundwater pollution remediation will need to address in the future. Additionally, due to the limited research on the effectiveness of models for complex medium sites, it is difficult to assess the validity of model predictions, making it hard to propose effective and precise pollution risk management strategies and develop optimized remediation plans.

To address the challenges of soil and groundwater pollution remediation, it is necessary to combine different types of groundwater and soil from complex sites for integrated remediation. The selection of remediation methods should prioritize economically effective emerging remediation technologies. Furthermore, consideration could be given to combining MNA technology with P&T and in situ technologies, as well as deepening research into the application of PRB technology [58]. From a long-term perspective, physical–chemical–biological multi-layer integrated remediation should be pursued to achieve long-term stability in pollution remediation, and further development and optimization of smart remediation technologies are essential.

6. Conclusions and Outlook

The research on soil–groundwater pollution simulation and prediction has made significant progress in the areas of multi-scale numerical simulation, pollutant migration mechanisms, and the application of artificial intelligence methods. However, there are still notable challenges in five areas: model information acquisition, prediction accuracy, computational costs, multi-interface and multiphase mechanisms, and pollution remediation. By developing new technologies, multi-scale and multi-interface coupling, intelligent optimization algorithms, and synergistic optimization of pollution control, we can systematically address the core challenges in soil and groundwater pollution simulation and remediation. A literature survey over the past decade on five different models for soil–groundwater pollution reveals that numerical models and statistical models are the most frequently cited and widely applied approaches. For different types of soil–groundwater models, appropriate evaluation metrics can be utilized to assess their accuracy and performance, thereby demonstrating the quality of the models. When evaluating the accuracy and performance of different models in the assessment table, evaluation indices such as accuracy, precision, recall, F1 score, AUC-ROC, MSE, R², and runtime can be used to demonstrate model quality; different types of models emphasize a distinct evaluation index based on their specific characteristics and applications.

There is a need to accelerate the establishment of a soil–groundwater pollution simulation and prediction standard system, enhance its constraints, and improve its refinement to provide technical support for the remediation of soil and groundwater pollution in China, thus promoting the transformation of society towards green development. In the future, continuous optimization and innovation of models and research methods for soil and groundwater pollution simulation and prediction, combined with high-performance parallel computing, will enable more accurate and efficient pollution control of soil and groundwater, forming a complete technical system of simulation–prediction–remediation. This will protect the environment and benefit humanity.