Numerical Study of Downstream Sediment Scouring of the Slotted Roller Bucket System
Abstract
1. Introduction
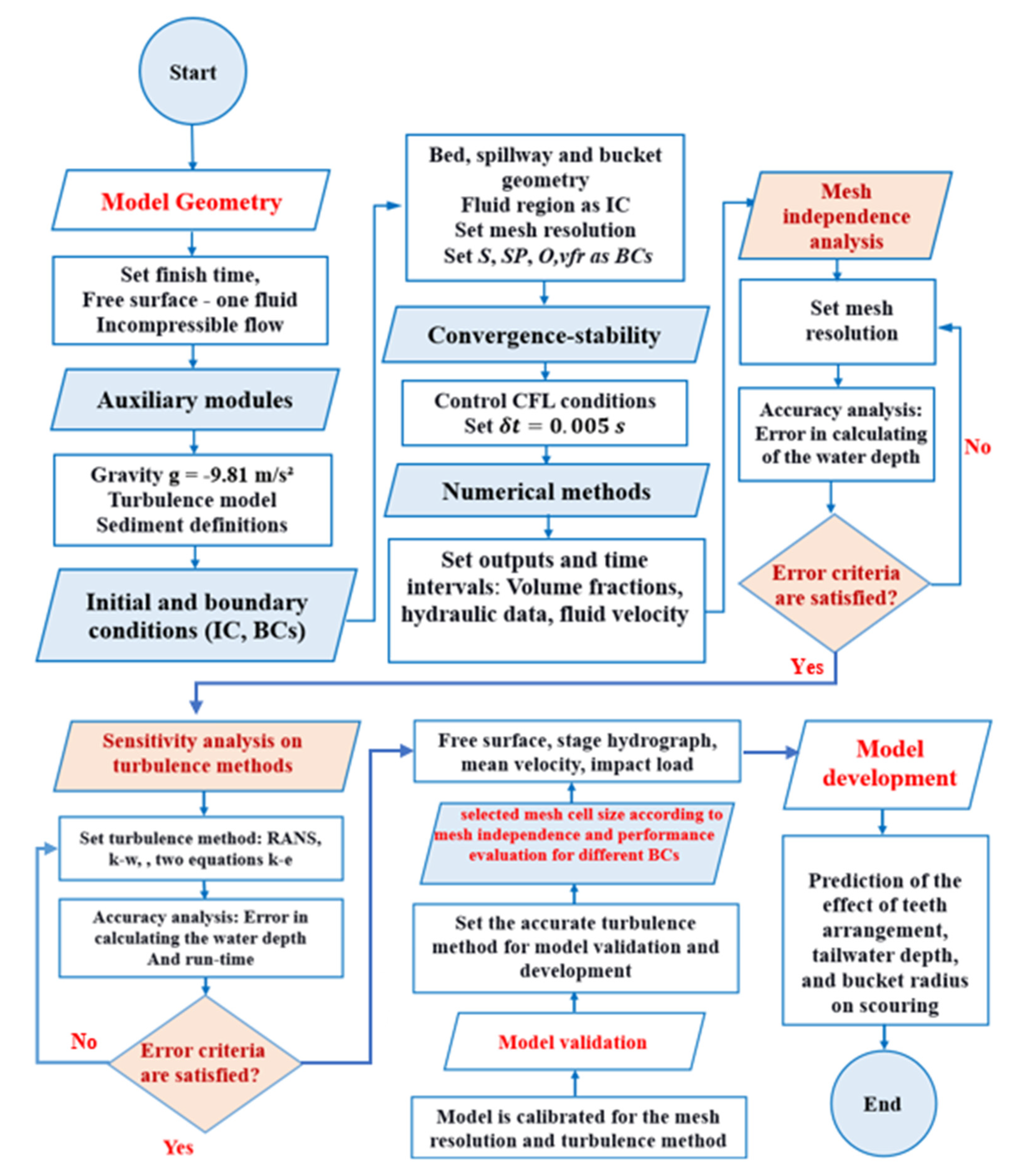
2. Materials and Methods
2.1. Governing Equations
2.2. Sediment Scour and Bed-Material Transport Model
2.3. Geometry, Initial and Boundary Conditions
2.4. Calibration and Validation
3. Results and Discussion
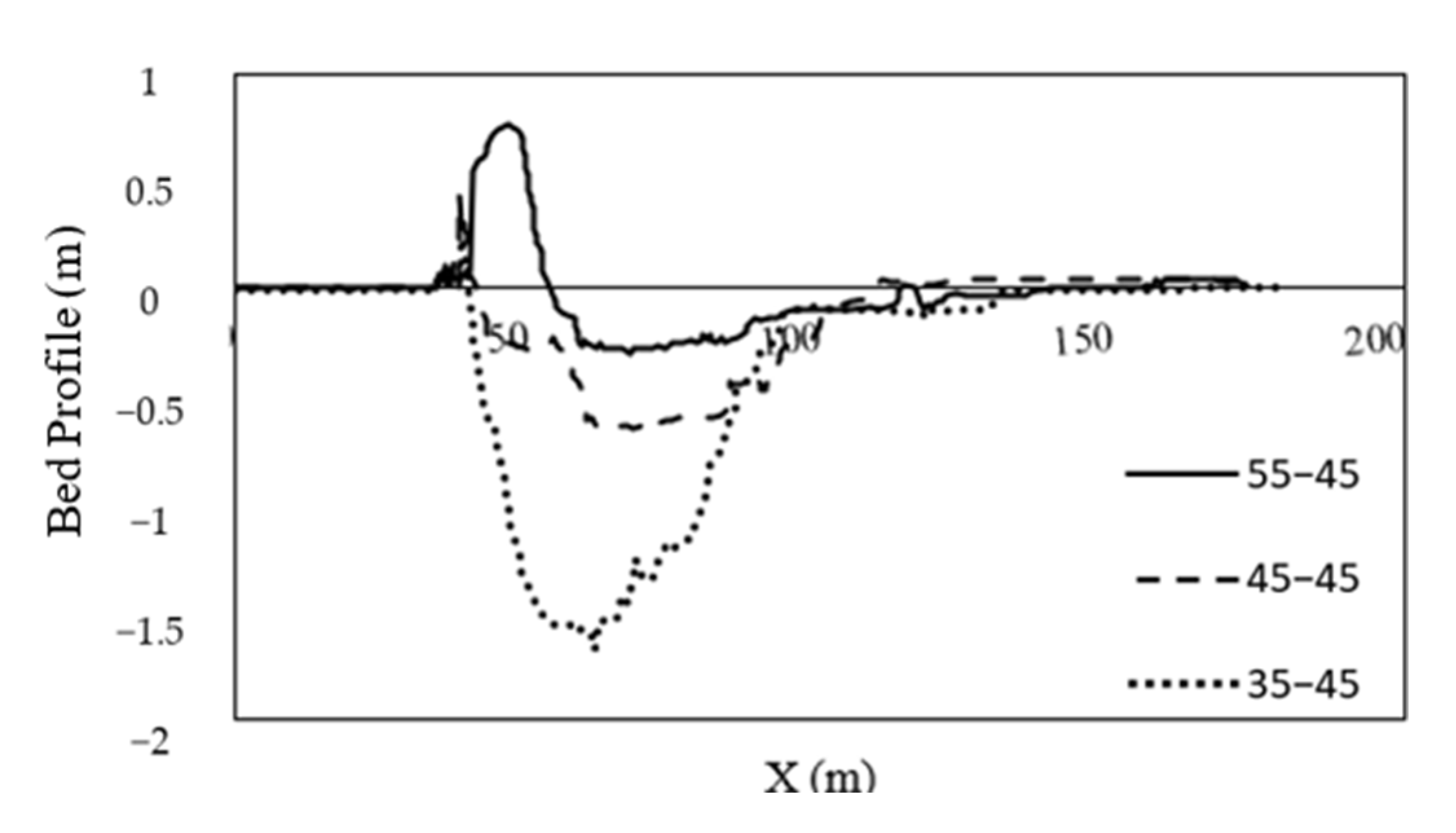
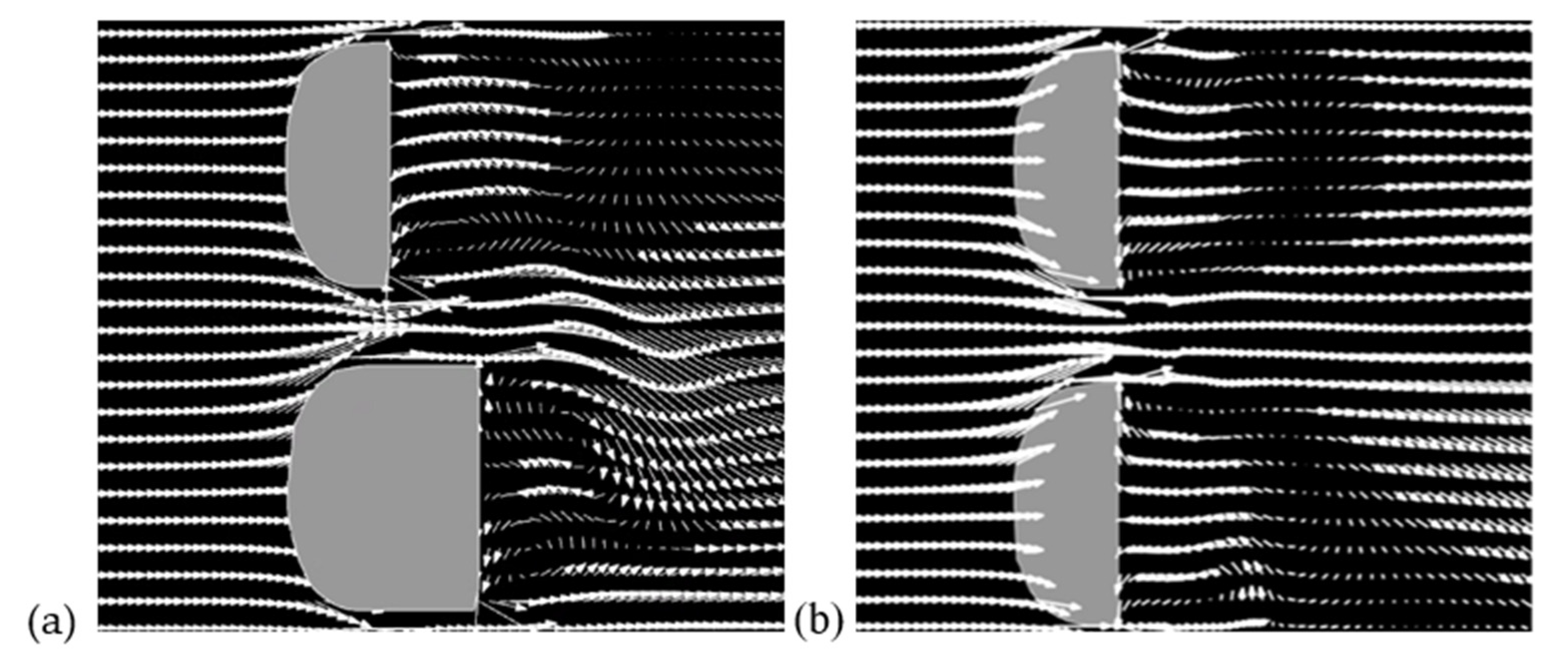
3.1. Group P (Different Lip Angles)
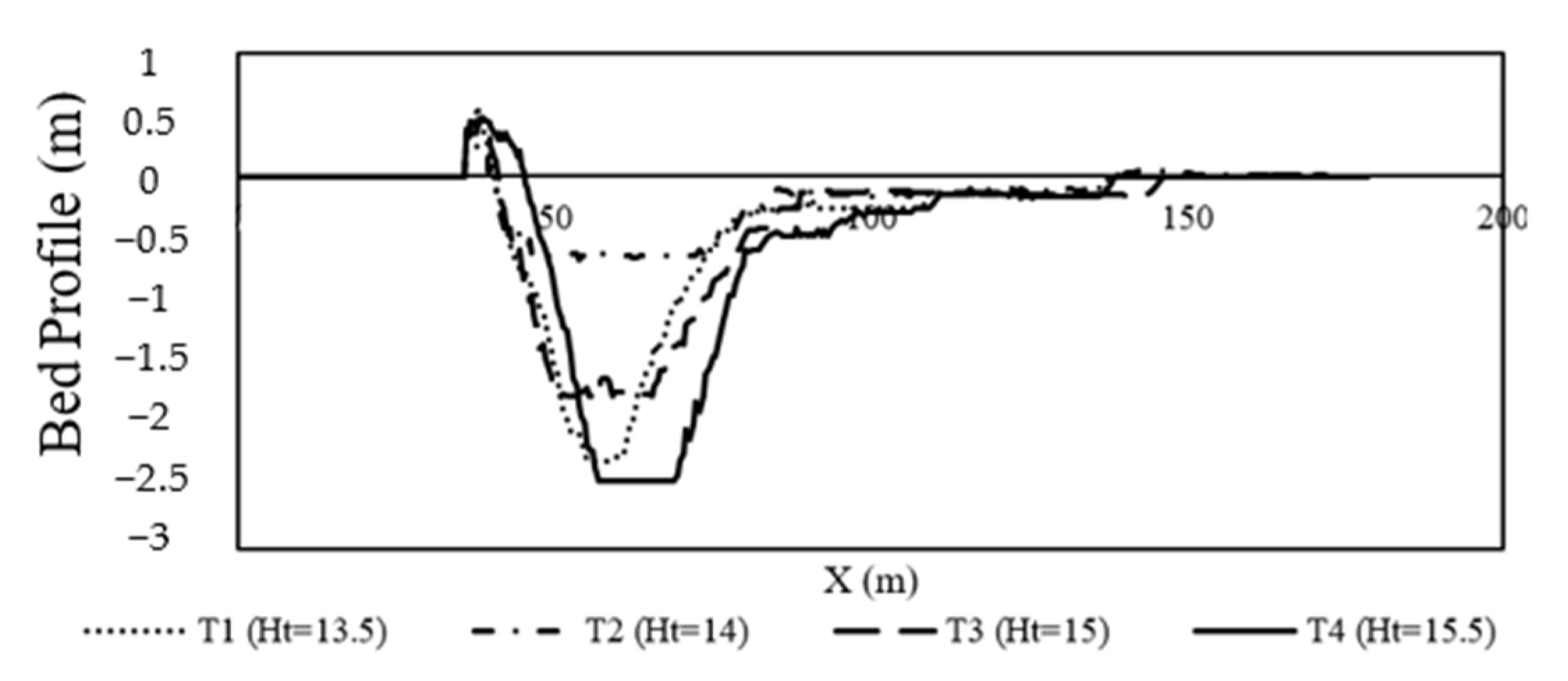
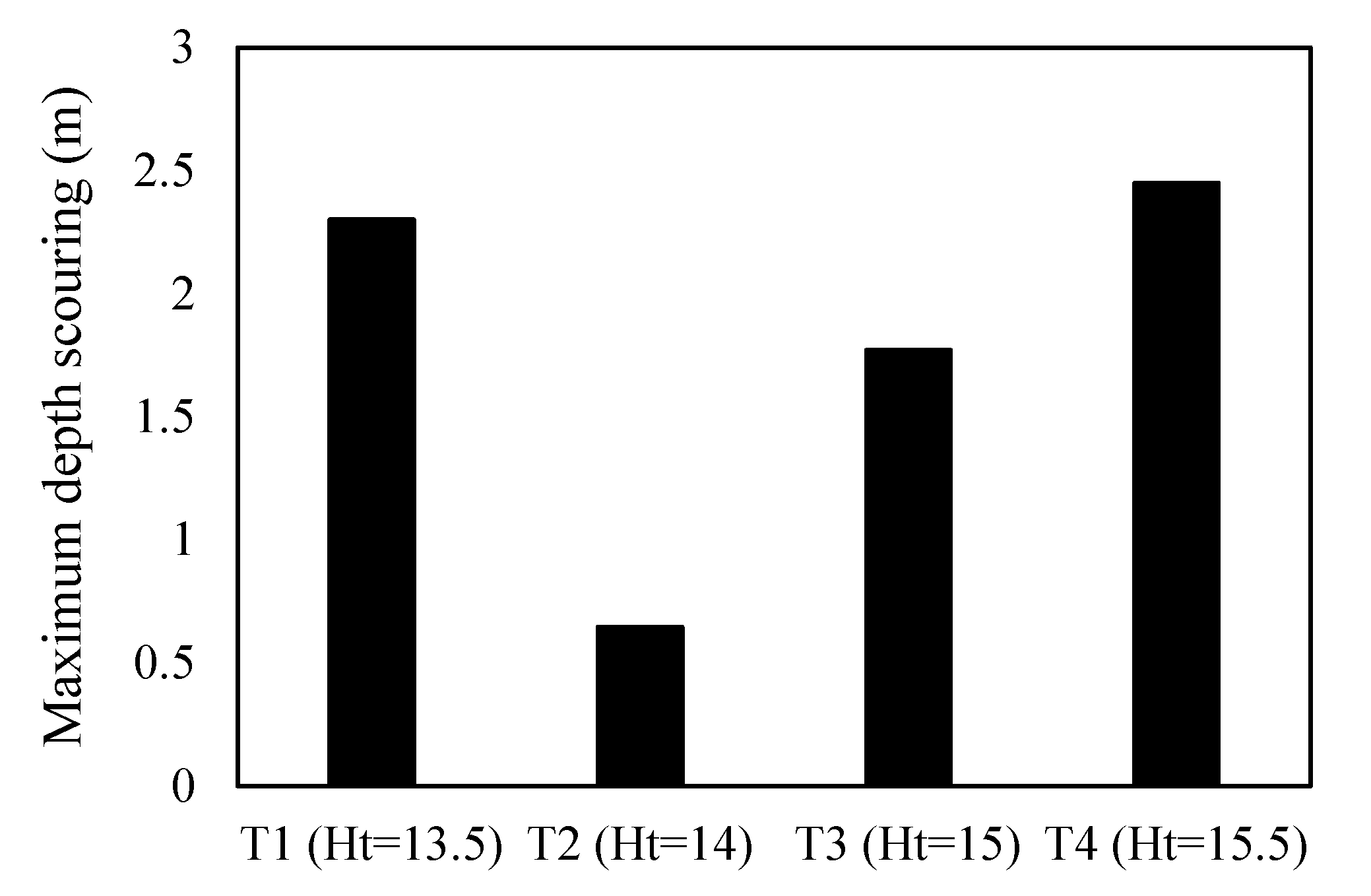
3.2. Group T (Tailwater Depth)
3.3. Group R (Different Bucket Radii)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arjenaki, M.O.; Sanayei, H.R.Z. Numerical investigation of energy dissipation rate in stepped spillways with lateral slopes using experimental model development approach. Model. Earth Syst. Environ. 2020, 6, 605–616. [Google Scholar] [CrossRef]
- Khatsuria, R.M. Hydraulics of Spillways and Energy Dissipators; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Latifi, A.; Hosseini, S.A.; Saneie, M. Comparison of downstream scour of single and combined free-fall jets in co-axial and non-axial modes. Model. Earth Syst. Environ. 2018, 4, 1271–1284. [Google Scholar] [CrossRef]
- El Amri, A.; Verrette, J. Variations of the hydrodynamic efforts on horizontal and eroded base plates downstream in a trough-type energy dissipator. Can. J. Civ. Eng. 2007, 34, 890–894. [Google Scholar]
- Fuladipanah, M.; Azamathulla, H.M.; Tota-Maharaj, K.; Mandala, V.; Chadee, A. Precise forecasting of scour depth downstream of flip bucket spillway through data-driven models. Results Eng. 2023, 20, 101604. [Google Scholar] [CrossRef]
- Eskandari, A.; Heidarnejad, M.; Masjedi, A.; Purmohammadi, M.H.; Kamanbedast, A. Experimental investigation on the effect of different slot shapes and configurations on scour dimension downstream of flip buckets. Water SA 2020, 46, 458–464. [Google Scholar] [CrossRef]
- Ramarao, V.; Joshi, P.; Inamdar, A.; Sanghvi, S.S. Assessment of ski-jump bucket parameters for sluice spillway of Himalayan dam by hydraulic model studies. Int. J. Adv. Res. Ideas Innov. Technol. 2019, 5, 1156–1161. [Google Scholar]
- Ramarao, V.S.; Kulhare, A. Effect of Deficient Tailwater on the Performance of Slotted Roller Bucket of Indira Sagar Dam, Madhya Pradesh. In Proceedings of the 9th IAHR International Symposium on Hydraulic Structures—9th ISHS, Roorkee, India, 24–27 October 2022. [Google Scholar]
- Nangare, P.B.; Kote, A.S. Enhancement of energy dissipation using combination of solid roller bucket and type II stilling basin for ogee stepped spillway. In River Hydraulics: Hydraulics, Water Resources and Coastal Engineering; Springer International Publishing: Cham, Switzerland, 2021; Volume 2, pp. 97–101. [Google Scholar]
- Hafnaoui, M.A.; Debabeche, M. Numerical modeling of the hydraulic jump location using 2D Iber software. Model. Earth Syst. Environ. 2021, 7, 1939–1946. [Google Scholar] [CrossRef]
- Kote, A.S.; Nangare, P.B. Hydraulic model investigation on stepped spillway’s plain and slotted roller bucket. Eng. Technol. Appl. Sci. Res. 2019, 9, 4419–4422. [Google Scholar] [CrossRef]
- Nangare, P.; Kote, A. Experimental investigation of an ogee stepped spillway with plain and slotted roller bucket for energy dissipation. Int. J. Civ. Eng. Technol. 2017, 8, 1549–1555. [Google Scholar]
- Heidarian, P.; Neyshabouri, S.A.A.S.; Khoshkonesh, A.; Bahmanpouri, F.; Nsom, B.; Eidi, A. Numerical study of flow characteristics and energy dissipation over the slotted roller bucket system. Model. Earth Syst. Environ. 2022, 8, 5337–5351. [Google Scholar] [CrossRef]
- Rahmani Firozjaei, M.; Salehi Neyshabouri, S.A.A.; Amini Sola, S.; Mohajeri, S.H. Numerical simulation on the performance improvement of a lateral intake using submerged vanes. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 167–177. [Google Scholar] [CrossRef]
- Khani, S.; Moghadam, M.; Nikookar, M. Pressure fluctuations investigation on the curve of flip buckets using analytical and numerical methods. Comput. Res. Prog. Appl. Sci. Eng. 2017, 3, 165–171. [Google Scholar]
- Mirzaei, H.; Heydari, Z.; Fazli, M. Predicting the scour around open groyne using different models of turbulence & vortices flow in variety of open & close groyne. Model. Earth Syst. Environ. 2019, 5, 101–118. [Google Scholar]
- Morais, V.H.P.d.; Gireli, T.Z.; Vatavuk, P. Modelagem numérica e experimental aplicada a um vertedouro de superfície composto por um perfil Creager e um dissipador do tipo roller bucket. RBRH 2020, 25, e18. [Google Scholar] [CrossRef]
- Movahedi, A.; Kavianpour, M.; Aminoroayaie Yamini, O. Experimental and numerical analysis of the scour profile downstream of flip bucket with change in bed material size. ISH J. Hydraul. Eng. 2019, 25, 188–202. [Google Scholar] [CrossRef]
- Rahmani Firozjaei, M.; Hajebi, Z.; Naeeni, S.T.O.; Akbari, H. Experimental and numerical investigation of bottom intake structure for desalination plants. Numer. Methods Civ. Eng. 2024, 8, 1–9. [Google Scholar] [CrossRef]
- Sharif, N.; Ravori, A.R. Experimental and numerical study of the effect of flow separation on dissipating energy in compound bucket. APCBEE Procedia 2014, 9, 334–338. [Google Scholar] [CrossRef]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.; Speziale, C. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A Fluid Dyn. 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Amini, A.A.; Sarkardeh, H.; Jabbari, E.; Eidi, A. Understanding vortex characteristics in hydraulic systems: A temperature-driven analysis. Model. Earth Syst. Environ. 2024, 10, 3559–3571. [Google Scholar] [CrossRef]
- Mastbergen, D.R.; Van Den Berg, J.H. Breaching in fine sands and the generation of sustained turbidity currents in submarine canyons. Sedimentology 2003, 50, 625–637. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of Marine Sands; Thomas Telford Publications: London, UK, 1997. [Google Scholar]
- Meyer-Peter, E. Formulas for bed-load transport. In Proceedings of the 2nd IAHR Meeting, Stockholm, Sweden, 7–9 June 1948. [Google Scholar]
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Pétursson, G.S. Model Investigation of a Low Froude Number Roller Bucket at Urriðafoss HEP. Master’s Thesis, School of Engineering and Natural Sciences, University of Iceland, Reykjavik, Iceland, 2013. [Google Scholar]
- Okhravi, S.; Gohari, S.; Alemi, M.; Maia, R. Numerical modeling of local scour of non-uniform graded sediment for two arrangements of pile groups. Int. J. Sediment Res. 2023, 38, 597–614. [Google Scholar] [CrossRef]
- Oodi, S.; Gohari, S.; Di Francesco, S.; Nazari, R.; Nikoo, M.R.; Heidarian, P.; Eidi, A.; Khoshkonesh, A. Wave–Structure Interaction Modeling of Transient Flow Around Channel Obstacles and Contractions. Water 2025, 17, 424. [Google Scholar] [CrossRef]
- Flow Science, Inc. FLOW-3D® Version 2023R1 Users Manual; Flow Science, Inc.: Santa Fe, NM, USA, 2023; Available online: https://www.flow3d.com (accessed on 23 April 2023).
- Karr, M.H.F.E.L. Bucket-Type Energy Dissipator Characteristics. Lehigh University Fritz Lab Report, 1956. Available online: https://preserve.lehigh.edu/lehigh-scholarship/faculty-and-staff-publications/fritz-lab-reports/bucket-type-energy-dissipator (accessed on 23 April 2023).
- Zhang, M.-L.; Shen, Y.-M. Three-dimensional simulation of meandering river based on 3-D RNG κ-ε turbulence model. J. Hydrodyn. Ser. B 2008, 20, 448–455. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Nsom, B.; Bahmanpouri, F.; Dehrashid, F.A.; Adeli, A. Numerical study of the dynamics and structure of a partial dam-break flow using the VOF method. Water Resour. Manag. 2021, 35, 1513–1528. [Google Scholar] [CrossRef]
- Bahmanpouri, F.; Daliri, M.; Khoshkonesh, A.; Namin, M.M.; Buccino, M. Bed compaction effect on dam break flow over erodible bed; experimental and numerical modeling. J. Hydrol. 2021, 594, 125645. [Google Scholar] [CrossRef]
- Bhosekar, V.; Patnaik, S.; Bhajantri, M.; Sunderlal, B. Limitations of spillway roller bucket. Water Energy Int. 2012, 69, 47–54. [Google Scholar]
- Saghravani, F.; Salehi Neyshabouri, S.A.A. Investigation of Scour Downstream of Flip Bucket. Master’s Thesis, Tarbiat Modares University, Tehran, Iran, 1992. [Google Scholar]
- Peterka, J.A. Hydraulic Model Studies of Scour Holes and Bed Vortices Under Jets; Technical Note No. 59, WMO-No. 147; U.S. Water Resources Council: Washington, DC, USA, 1964. [Google Scholar]
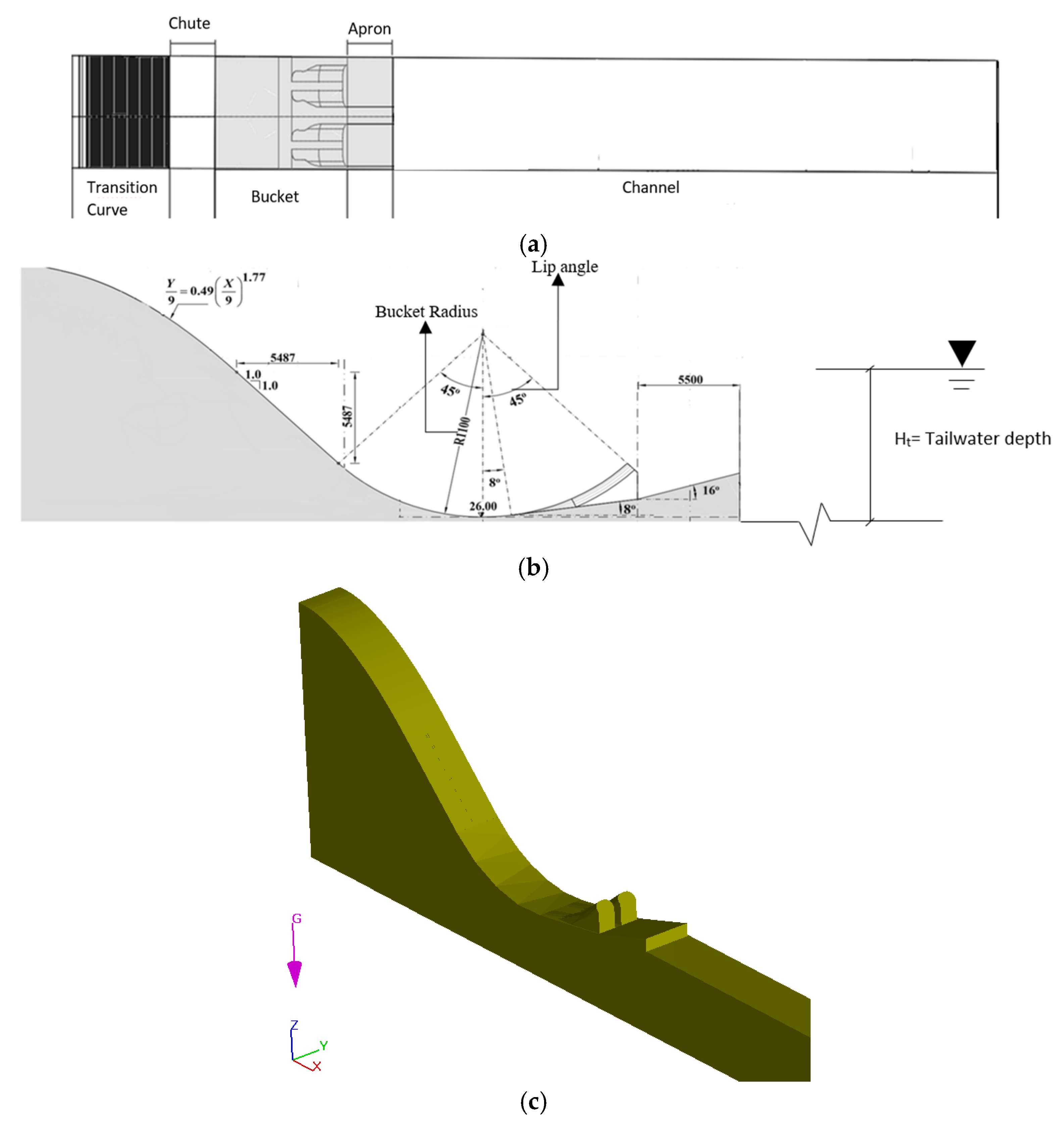
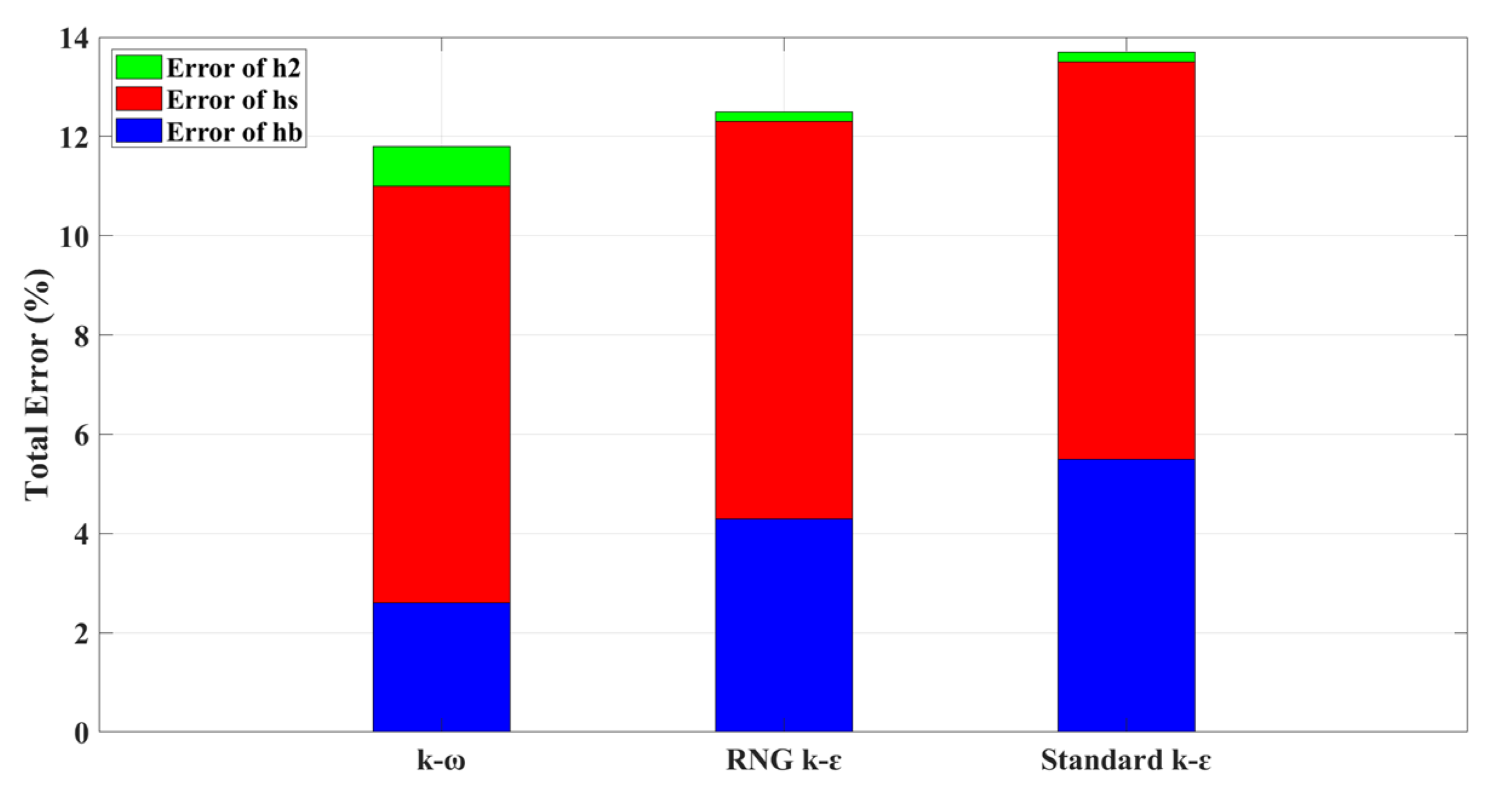



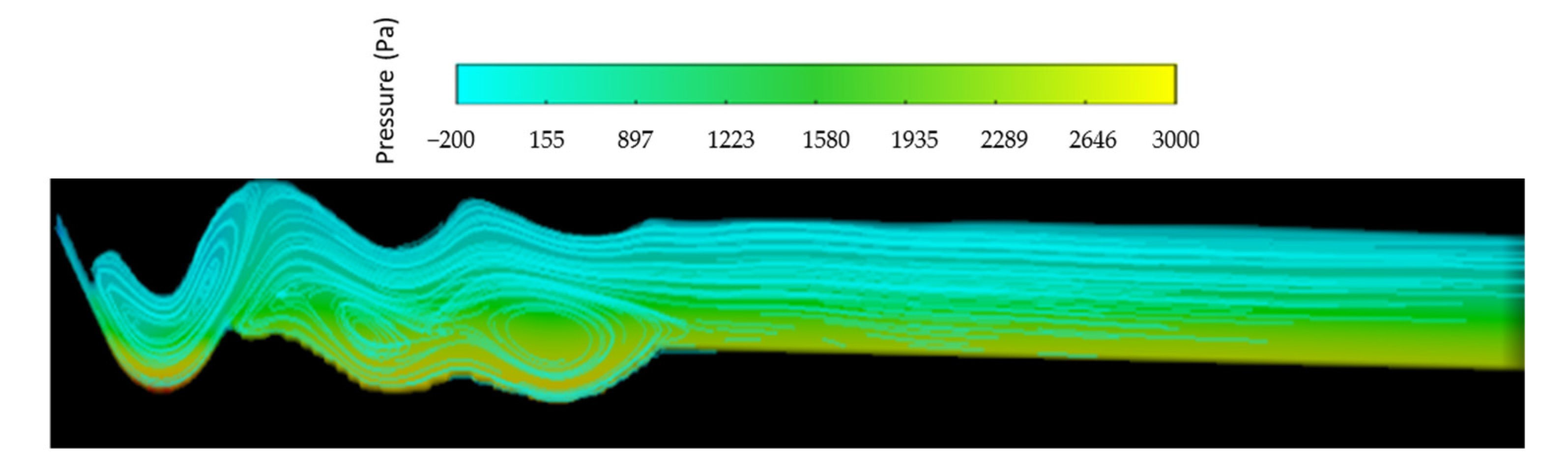

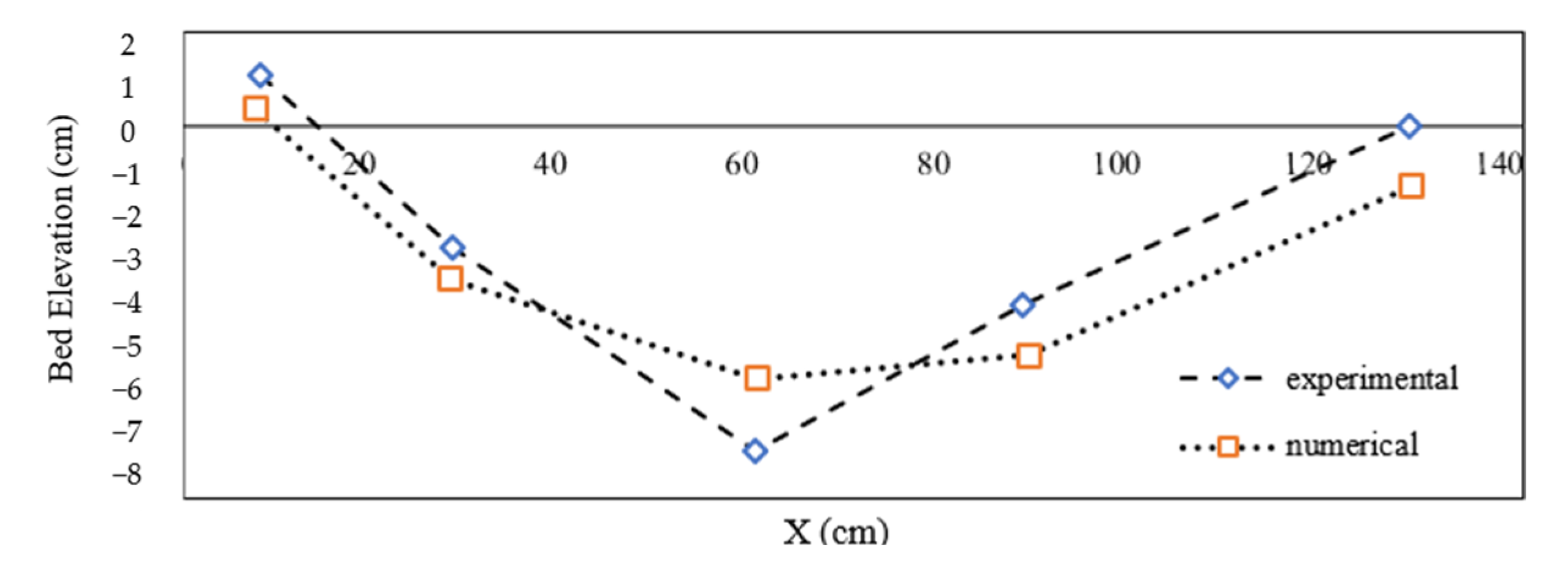
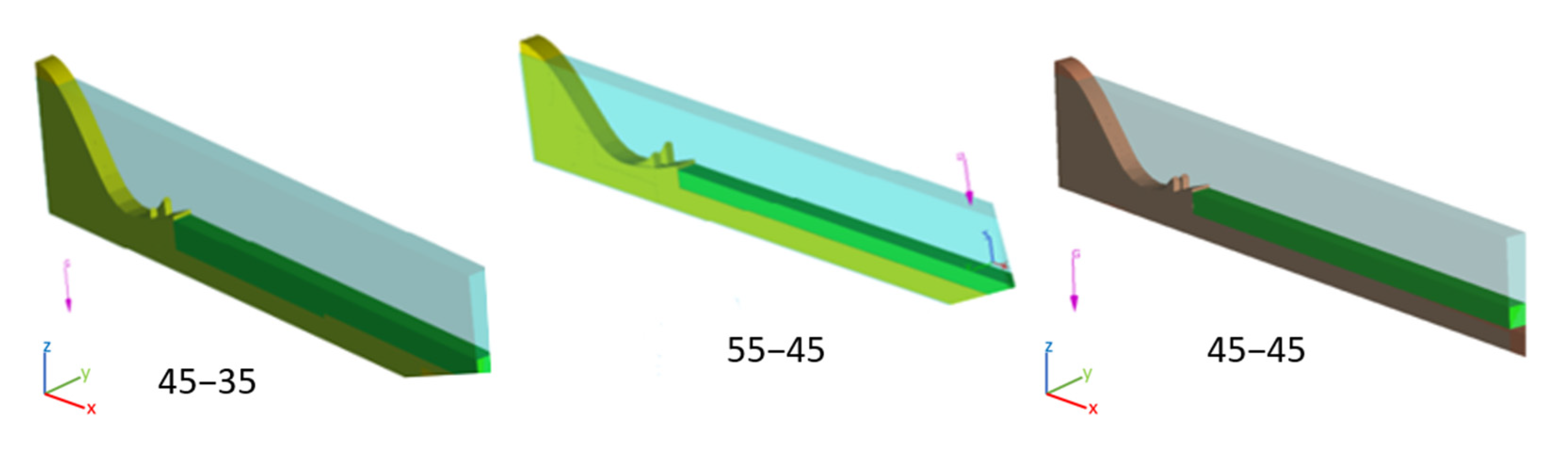




| Group | Model | Teeth Angle | Radius | Tailwater Depth |
|---|---|---|---|---|
| P | A | 45–55 | 11 | 14 |
| B | 45–45 | |||
| C | 45–35 | |||
| T | T1 | 45–45 | 11 | 13.5 |
| T2 | 14 | |||
| T3 | 15 | |||
| T4 | 15.5 | |||
| R | R1 | 45–45 | 9 | 14 |
| R2 | 11 | |||
| R3 | 13 |
| Group | P | T | R | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | A (55–45) | B (45–45) | C (45–35) | T1 | T2 | T3 | T4 | R1 | R2 | R3 |
| Discharge (m3/s) | 184 | 183 | 181 | 180 | 183 | 179 | 182 | 178 | 183 | 185 |
| Boundaries | Condition |
|---|---|
| xmin | Specified pressure |
| xmax | Outflow |
| ymin | Free slip |
| ymax | Free slip |
| zmin | Wall |
| zmax | Free slip |
| Boundary Name | Condition |
|---|---|
| Xmin | Initial discharge |
| Xmax | Specified pressure |
| Ymin | Wall |
| Ymax | Wall |
| Zmin | Wall |
| Zmax | Free slip |
| Number of Cells | Error of hb% | Error of hs% | Error of h2% | Total of Error % |
|---|---|---|---|---|
| 1 × 105 | 8.6 | 12.2 | 10.6 | 31.4 |
| 3 × 105 | 5.1 | 8 | 6.8 | 19.9 |
| 6 × 105 | 4.3 | 6.3 | 4.9 | 15.5 |
| 10 × 105 | 3.8 | 5.7 | 3.7 | 13.2 |
| Numerical (ft) | 2.98 | 2.77 | 3.14 | 0.37 | 0.40 | 0.42 | 0.93 | 0.04 |
| Experimental (ft) | 3.00 | 2.95 | 3.35 | 0.40 | 0.41 | 0.45 | 0.98 | 0.04 |
| Error (%) | 0.7 | 6.1 | 6.3 | 6.3 | 0.5 | 6.2 | 5.2 | 1.4 |
| Model | Angle of Teeth Lips | Area of Downstream Roller (m2) |
|---|---|---|
| A | 45–55 | 98.1 |
| B | 45–45 | 165.1 |
| C | 45–35 | 112 |
| Model | Tailwater Depth (m) | Area of Downstream Roller (m2) |
|---|---|---|
| T1 | 13.5 | 145 |
| T2 | 14 | 187 |
| T3 | 15 | 89.6 |
| T4 | 15.5 | 205 |
| Model | Bucket Radius (m) | Area of Downstream Roller (m2) |
|---|---|---|
| R1 | 9 | 129 |
| R2 | 11 | 121 |
| R3 | 13 | 190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heidarian, P.; Neyshabouri, S.A.A.S.; Khoshkonesh, A.; Nazari, R.; Okhravi, S.; Di Francesco, S. Numerical Study of Downstream Sediment Scouring of the Slotted Roller Bucket System. Water 2025, 17, 2471. https://doi.org/10.3390/w17162471
Heidarian P, Neyshabouri SAAS, Khoshkonesh A, Nazari R, Okhravi S, Di Francesco S. Numerical Study of Downstream Sediment Scouring of the Slotted Roller Bucket System. Water. 2025; 17(16):2471. https://doi.org/10.3390/w17162471
Chicago/Turabian StyleHeidarian, Payam, Seyed Ali Akbar Salehi Neyshabouri, Alireza Khoshkonesh, Rouzbeh Nazari, Saeid Okhravi, and Silvia Di Francesco. 2025. "Numerical Study of Downstream Sediment Scouring of the Slotted Roller Bucket System" Water 17, no. 16: 2471. https://doi.org/10.3390/w17162471
APA StyleHeidarian, P., Neyshabouri, S. A. A. S., Khoshkonesh, A., Nazari, R., Okhravi, S., & Di Francesco, S. (2025). Numerical Study of Downstream Sediment Scouring of the Slotted Roller Bucket System. Water, 17(16), 2471. https://doi.org/10.3390/w17162471







