Potential Effects of Grassland Restoration on the Water Resources in Nango-Dani, Aso, Japan
Abstract
1. Introduction
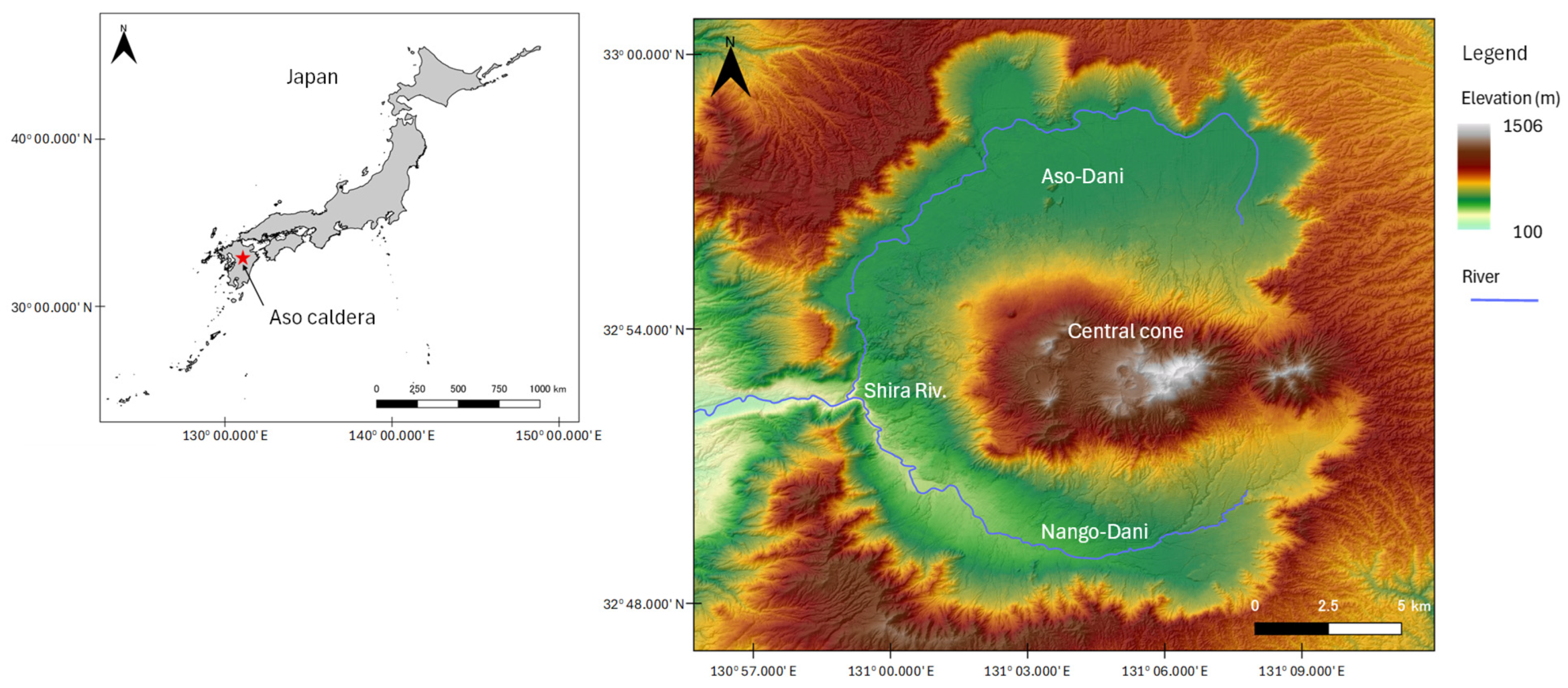
2. Study Area
3. Materials and Methods
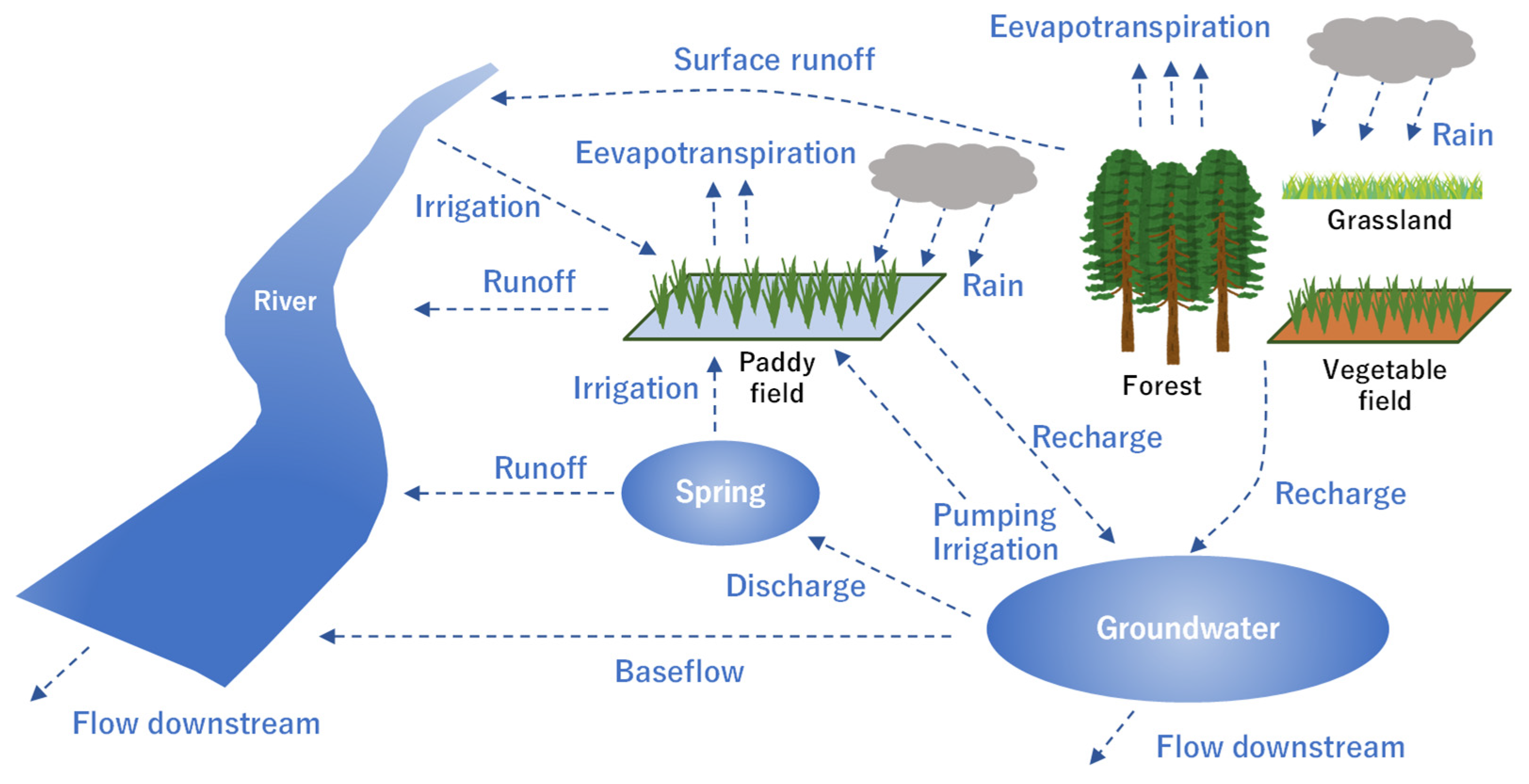
3.1. Conceptual Model
3.2. Water Budget Calculations
3.2.1. Water Budget of Each Tank
3.2.2. Groundwater Inflow and Outflow Between Tanks
3.2.3. Groundwater Recharge and Surface Runoff Volumes
3.2.4. Evapotranspiration
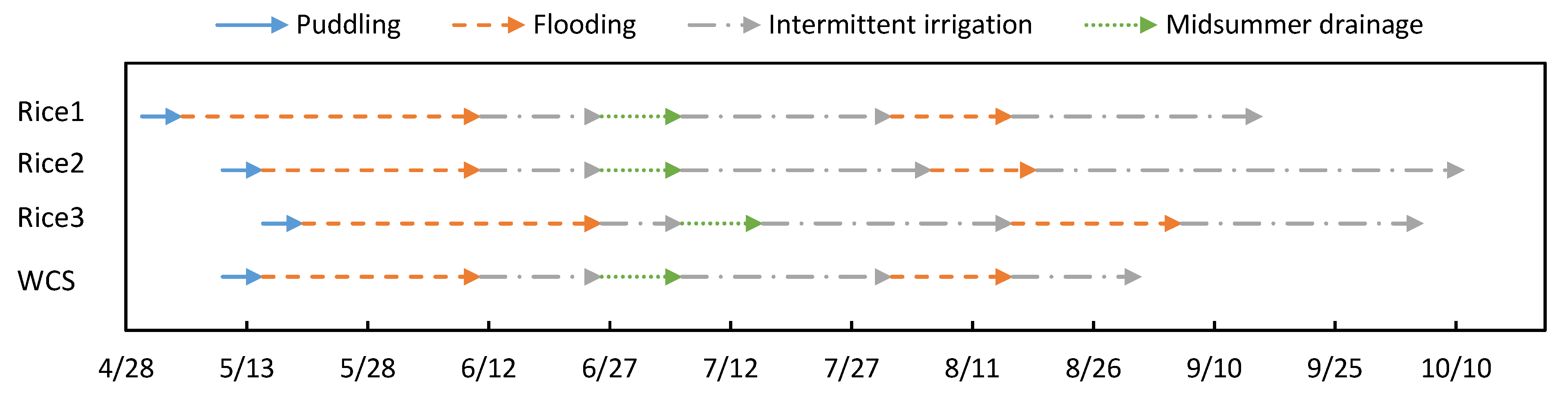
3.2.5. Irrigation Water Volume for Rice Paddies
3.2.6. Spring Water and Baseflow Discharge
3.2.7. Model Calibration and Validation Assessment
3.3. Grassland Restoration Patterns
4. Results and Discussion
4.1. Model Validation and Groundwater Recharge
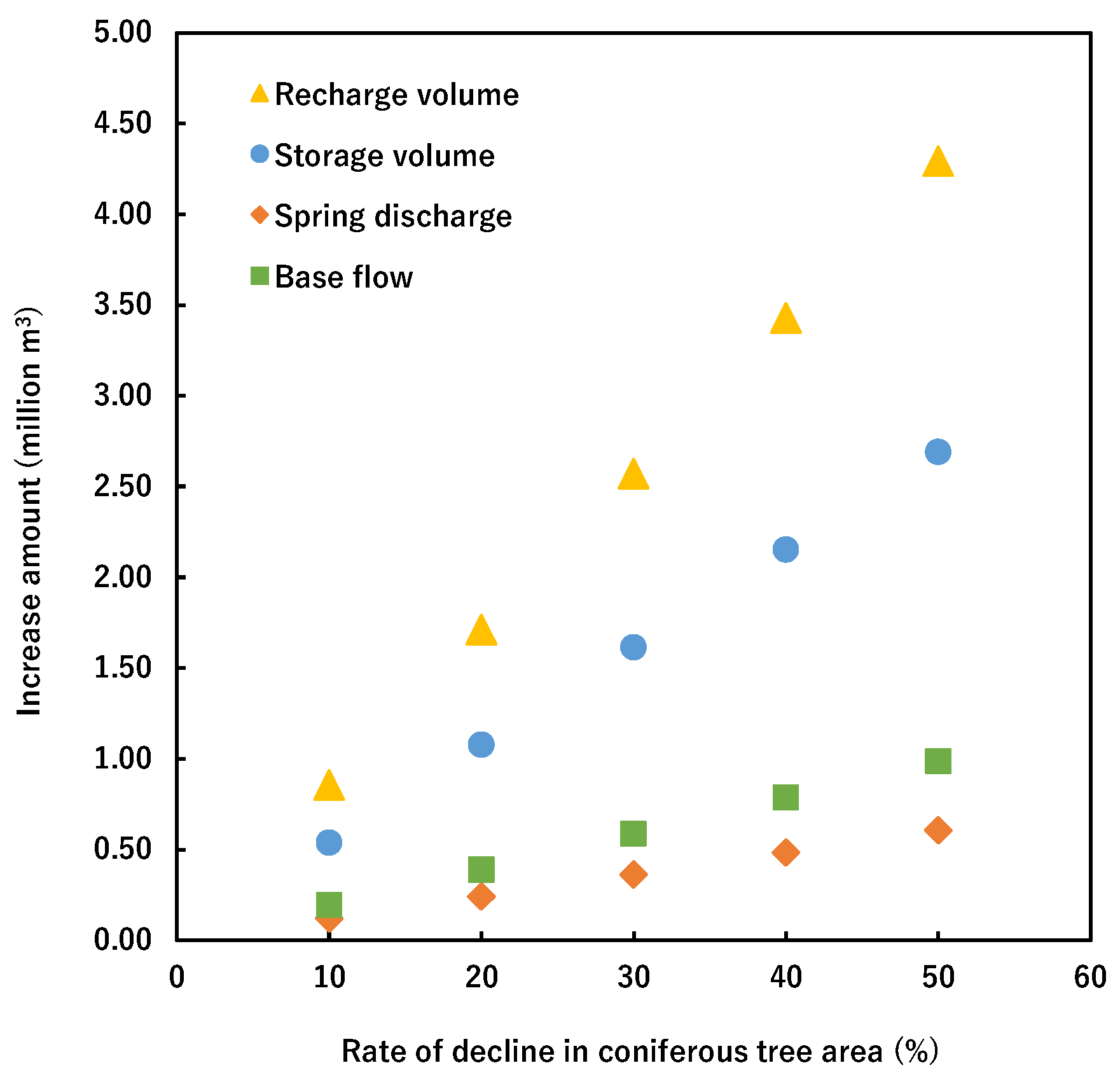
4.2. Potential Effects of Grassland Restoration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jha, M.K. Impacts of Landscape Changes on Water Resources. Water 2020, 12, 2244. [Google Scholar] [CrossRef]
- Martins, M.S.d.M.; Valera, C.A.; Zanata, M.; Santos, R.M.B.; Abdala, V.L.; Pacheco, F.A.L.; Fernandes, L.F.S.; Pissarra, T.C.T. Potential Impacts of Land Use Changes on Water Resources in a Tropical Headwater Catchment. Water 2021, 13, 3249. [Google Scholar] [CrossRef]
- Azo Grassland Restoration Council. Aso Grasslands for the Future, 2nd ed.; Ministry of the Environment: Kumamoto, Japan, 2014; 60p.
- Kudo, K.; Shimada, J.; Maruyama, A.; Tanaka, N. The quantitative evaluation of groundwater recharge rate using Displacement Flow Model with stable isotope ratio in the soil water of difference vegetation cover. J. Groundw. Hydrol. 2016, 58, 21–45. [Google Scholar] [CrossRef]
- Takahashi, Y. Conservation and restoration of grassland landscape by collaborative management: A case of Aso Grassland. Landsc. Ecol. Manag. 2009, 14, 5–14. [Google Scholar] [CrossRef]
- Amano, H.; Iwasaki, Y. Land Cover Classification by Integrating NDVI Time Series and GIS Data to Evaluate Water Circulation in Aso Caldera, Japan. Int. J. Environ. Res. Public Health 2020, 17, 6605. [Google Scholar] [CrossRef] [PubMed]
- Kumamoto Prefecture; Water Supply in Kumamoto Prefecture. Available online: https://www.pref.kumamoto.jp/soshiki/51/220285.html (accessed on 9 August 2025).
- Shimano, Y. Hydro-chemical study of spring water in the Aso caldera, central Kyushu. Bunsei Bull 1997, 8, 43–67. [Google Scholar]
- Ono, K.; Watanabe, K. Geological map of Aso volcano 1:50,000. In Geological Map of Volcanos; Geological Survey of Japan: Ibaraki, Japan, 1985; No. 4; Available online: https://www.gsj.jp/Map/JP/volcano.html (accessed on 4 July 2025).
- Ministry of Land, Infrastructure, Transport and Tourism; Water Information System. Available online: https://www1.river.go.jp/cgi-bin/SiteInfo.exe?ID=309091289912015 (accessed on 9 August 2025).
- Japan Meteorological Agency. Historical Weather Data. Available online: https://www.data.jma.go.jp/stats/etrn/index.php?prec_no=86&block_no=1660&year=&month=&day=&view= (accessed on 4 July 2025).
- Amano, H.; Ichikawa, T.; Nakagawa, K. Assessment of impact of Kumamoto earthquake in Aso Nangou-Dani using water budget simulation. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2021, 2, I_133–I_138. [Google Scholar] [CrossRef] [PubMed]
- Kokusai Kogyo Co., Ltd. FY2014 Groundwater Survey Report for the Nango-Dani Region and Surrounding Areas; Kokusai Kogyo Co., Ltd.: Tokyo, Japan, 2015; 94p. [Google Scholar]
- Hattori, S.; Abe, T. Characteristic of Canopy Interception in a Bamboo Stand. Water Sci. 1989, 33, 34–53. [Google Scholar]
- Yoshi, T. Infiltration and Recharge Characteristics of Forests and Vegetable Fields in the Takayubaru Plateau, Kumamoto. Master’s Thesis, Tokai University, Kumamoto, Japan, 2009. [Google Scholar]
- Japan Road Association. Guidelines for Road Earthworks, 2009th ed.; Maruzen: Tokyo, Japan, 2009; 450p. [Google Scholar]
- Ministry of Agriculture, Forestry and Fisheries. eMAFF Farmland Information System. Available online: https://map.maff.go.jp/ (accessed on 9 July 2025).
- Amano, H.; Ichikawa, T. Quantitative Assessment of Groundwater Recharge Amount by Winter Flooding in Minamiaso Village, Kumamoto Prefecture. Bull. Sch. Humanit. Sci. Tokai Univ. 2022, 1, 18–23. [Google Scholar]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A comparison of six potential evapotranspiration methods for regional use in the Southeastern United States. J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar]
- Asia Air Survey Co., Ltd. FY2012 Survey Report on the Impact of Grassland Afforestation on River Discharge in the Aso Region; Asia Air Survey Co., Ltd.: Tokyo, Japan, 2013; 103p. [Google Scholar]
- Japan Society of Civil Engineers Committee on Hydraulics; Subcommittee for the Revision of the Hydraulic Formula Handbook. Hydraulic Formula Handbook, 1999th ed.; Maruzen: Tokyo, Japan, 1999; pp. 339–357. [Google Scholar]
- Kumamoto City: Environment in Kumamoto City. Available online: https://www.city.kumamoto.jp/kankyo/kiji00320533/index.html (accessed on 14 July 2025).
- Minamiaso Village. The Number of Population and Households. Available online: https://www.vill.minamiaso.lg.jp/kiji003739/index.html (accessed on 14 July 2025).



| Grassland | Coniferous Tree | Broadleaf Tree | Paddy Field | Vegetable Field | |
|---|---|---|---|---|---|
| α | 0.91 | 0.80 | 0.85 | 1.00 | 1.00 |
| I | 2.4 | 3.0 | 4.7 | 0.029~0.086 | 1.2 |
| Grassland Coniferous Tree Broadleaf Tree (Tank1) | Grassland Coniferous Tree Broadleaf Tree (Tank2) | Golf Course | Bare Land Building | Water Body | |
|---|---|---|---|---|---|
| β | 0.2 | 0.4 | 0.3 | 0.95 | 1.0 |
| Permeability Coefficient (m/s) | Discharge Coefficient kt1 | Discharge Coefficient kt2 | Runoff Coefficient δ | Effective Porosity | |
|---|---|---|---|---|---|
| Initial value | 2.10 × 10−5 ~6.30 × 10−4 | 2.0 × 10−3 | 0.1 | 0.02 | 0.20 |
| Calibrated value | 5.00 × 10−5 ~7.85 × 10−3 | 4.5 × 10−4 ~8.0 × 10−4 | 0.25 | 0.07 | 0.25 |
| Case-0 | Case-1 | Case-2 | Case-3 | Case-4 | Case-5 | |
|---|---|---|---|---|---|---|
| % | 0 | 10 | 20 | 30 | 40 | 50 |
| Grassland | Paddy Field | Vegetable Field | Broadleaf Trees | Coniferous Trees | Bare Land | Buildings | Golf Course | Water Body | Total | |
|---|---|---|---|---|---|---|---|---|---|---|
| Area (km2) | 18.6 | 11.6 | 20.9 | 42.8 | 41.4 | 5.3 | 7.7 | 0.4 | 0.9 | 149.6 |
| Recharge volume (million m3) | 28.2 | 95.8 | 56.9 | 60.1 | 60.8 | 0.7 | 1.0 | 0.9 | 1.9 | 306.2 |
| Recharge height (mm) | 1513 | 8248 | 2728 | 1406 | 1469 | 127 | 127 | 1961 | 2197 | 2047 |
| % of total recharge | 9.2 | 31.3 | 18.6 | 19.8 | 19.6 | 0.2 | 0.3 | 0.3 | 0.6 | 100.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amano, H.; Nakagawa, K.; Ichikawa, T.; Berndtsson, R. Potential Effects of Grassland Restoration on the Water Resources in Nango-Dani, Aso, Japan. Water 2025, 17, 2466. https://doi.org/10.3390/w17162466
Amano H, Nakagawa K, Ichikawa T, Berndtsson R. Potential Effects of Grassland Restoration on the Water Resources in Nango-Dani, Aso, Japan. Water. 2025; 17(16):2466. https://doi.org/10.3390/w17162466
Chicago/Turabian StyleAmano, Hiroki, Kei Nakagawa, Tsutomu Ichikawa, and Ronny Berndtsson. 2025. "Potential Effects of Grassland Restoration on the Water Resources in Nango-Dani, Aso, Japan" Water 17, no. 16: 2466. https://doi.org/10.3390/w17162466
APA StyleAmano, H., Nakagawa, K., Ichikawa, T., & Berndtsson, R. (2025). Potential Effects of Grassland Restoration on the Water Resources in Nango-Dani, Aso, Japan. Water, 17(16), 2466. https://doi.org/10.3390/w17162466







