Evaluation of Infiltration Swale Media Using Small-Scale Testing Techniques and Its SWMM Modeling Considerations
Abstract
1. Introduction
2. Materials and Methods
2.1. Apparatus Design and Construction
2.2. Testing Procedures
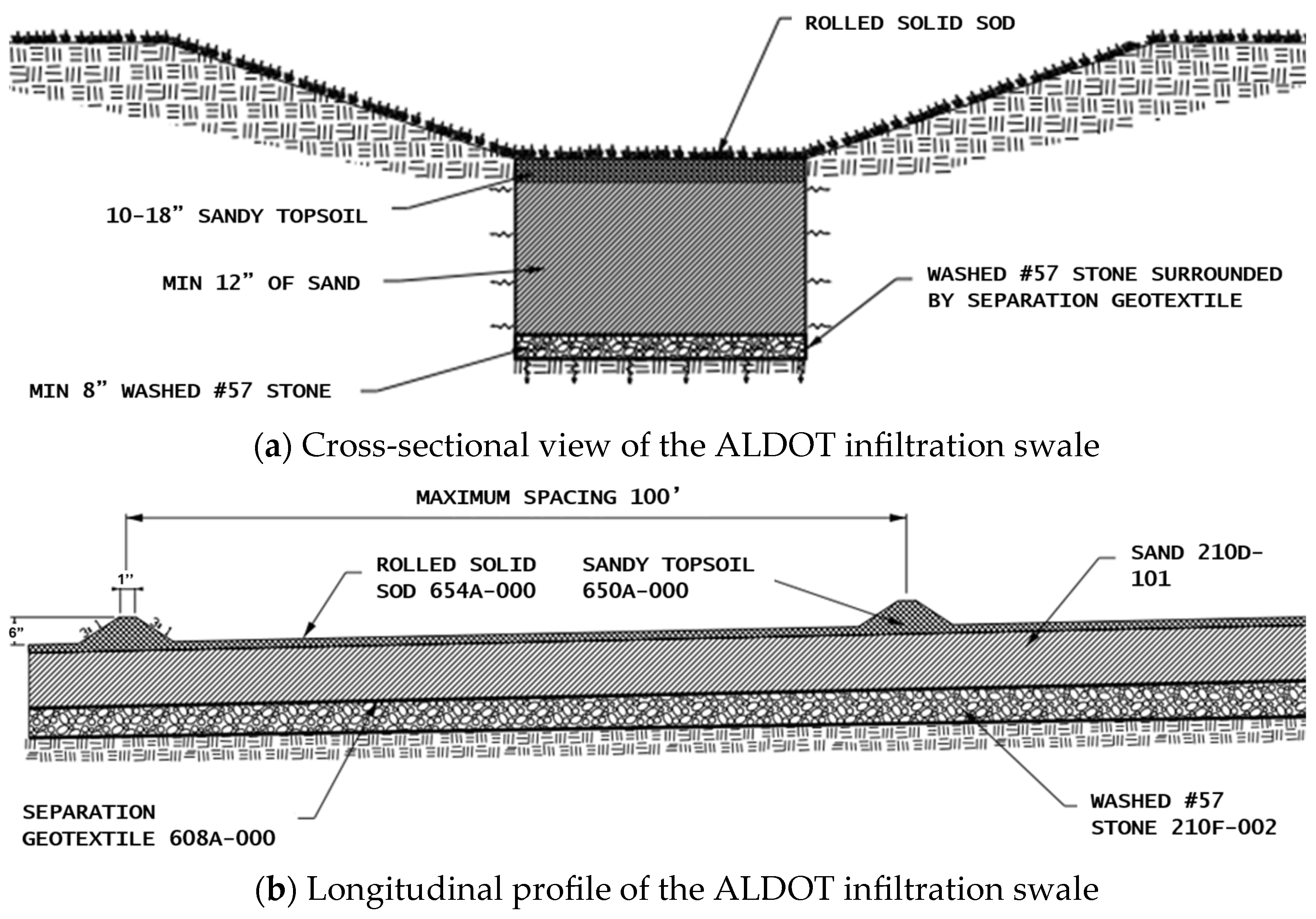
2.3. Infiltration Swale Media Design
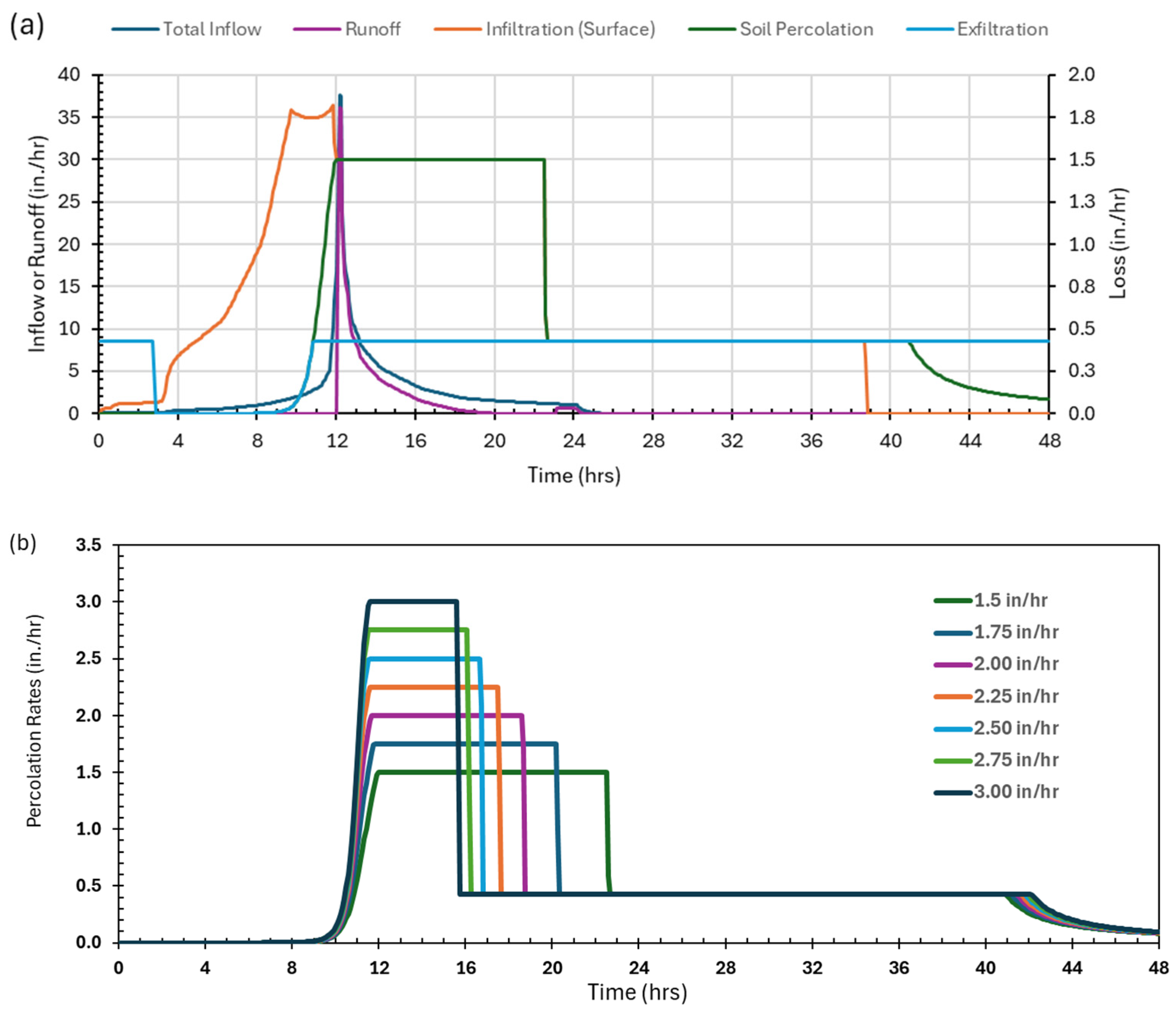
2.4. SWMM Infiltration Swale Modeling
3. Results and Discussion
3.1. Material Properties
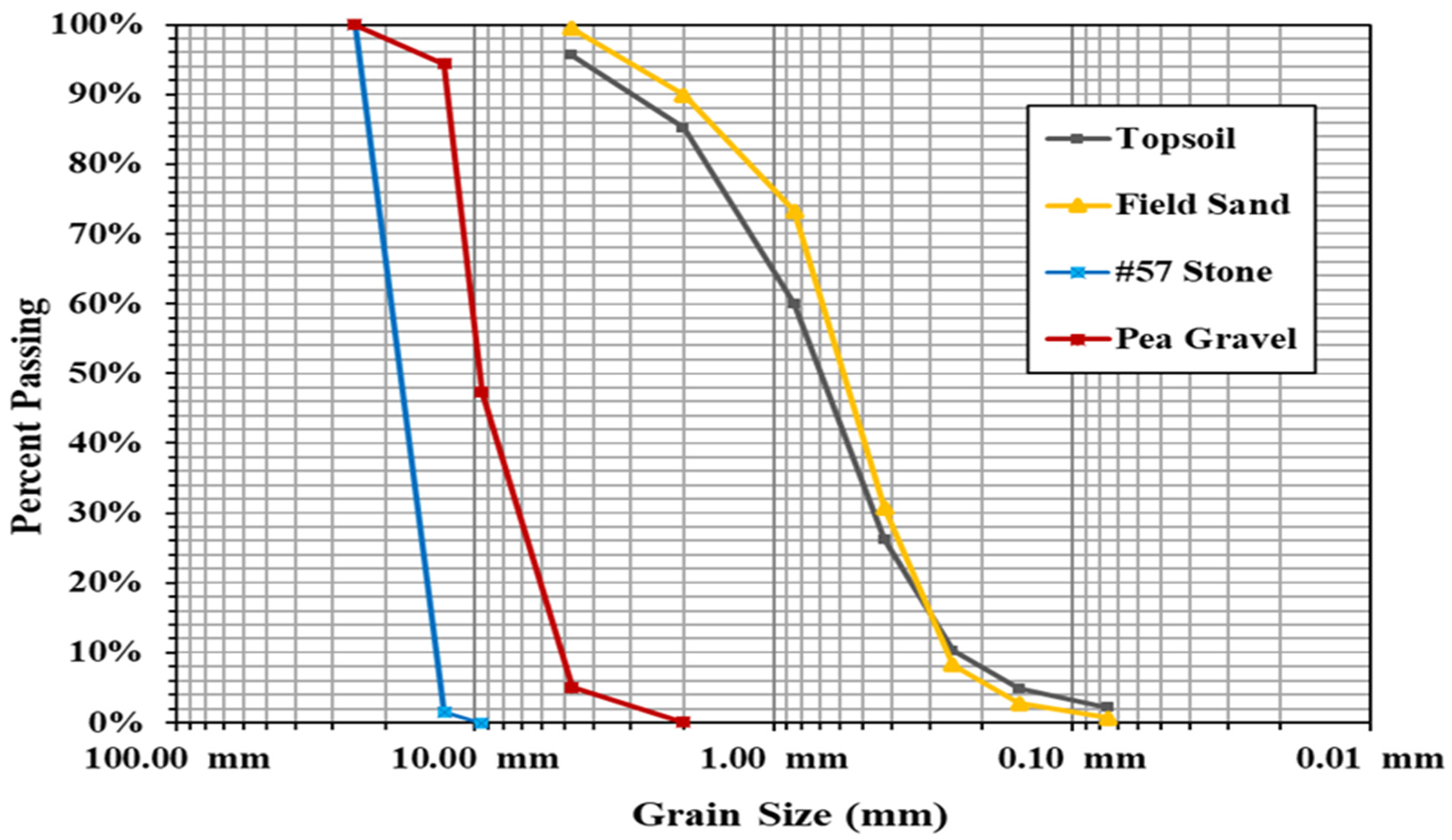
Particle Size Distribution
3.2. Modified Laboratory Testing for Constant Head Permeability
3.2.1. Permeability Evaluation of Infiltration Swale Media
3.2.2. Evaluation of Field Sand Permeability Across Varying Densities
3.2.3. Comparative Permeability Testing of GDOT and ALDOT Infiltration Swale Designs
3.3. Infiltration Rate Tests
3.3.1. Infiltration Rates of Infiltration Swale Materials
3.3.2. Infiltration Testing of Swale Design Alternatives Using the Falling-Head Method
3.3.3. Constant Head Infiltration Rate Tests
3.3.4. Comparison with Infiltration Rates in Other Studies
3.4. Modeling Infiltration Swales and Challenges
3.4.1. Swale’s Infiltration Process Simulated by SWMM
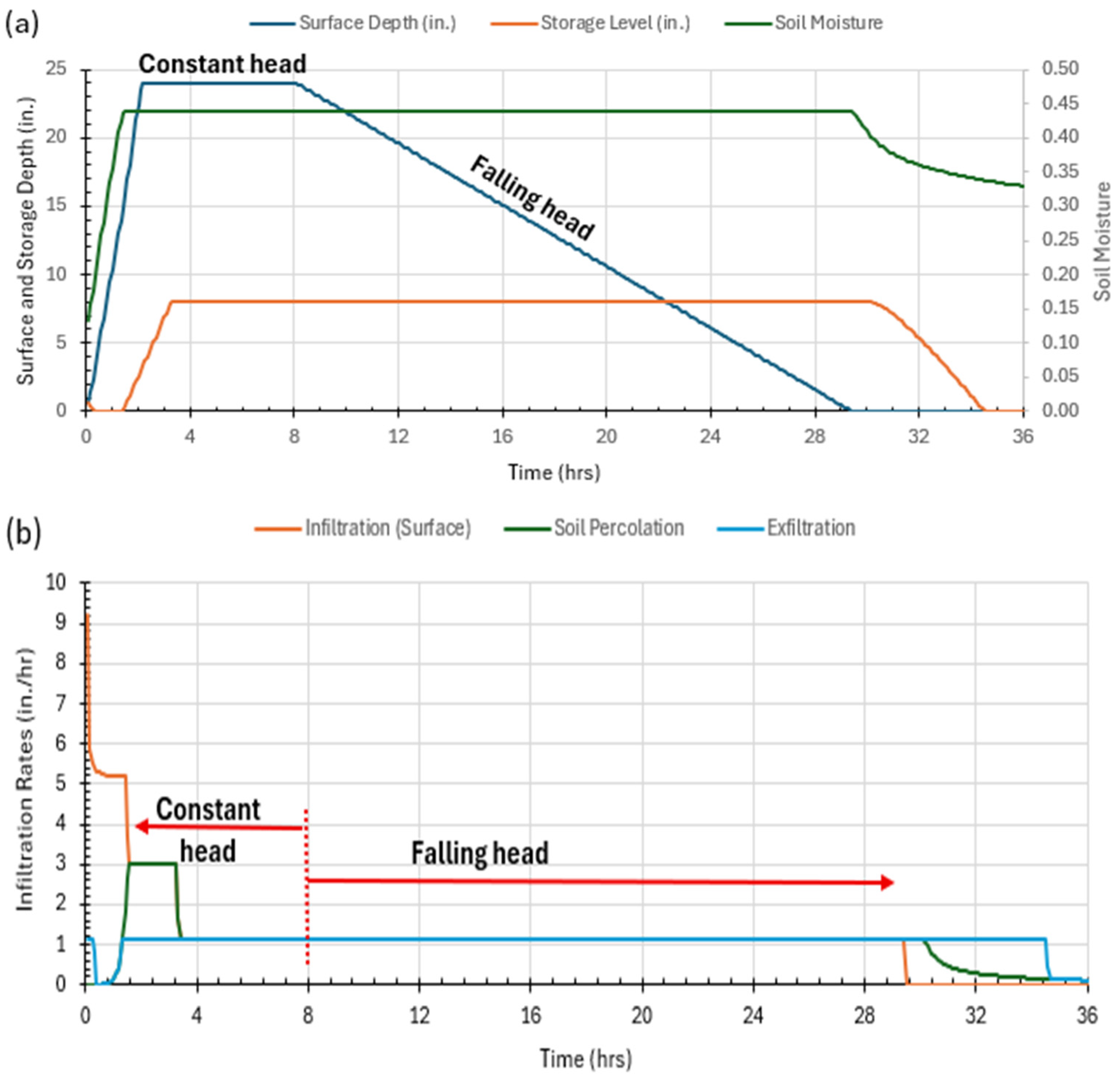


3.4.2. Comparison Between Measured and Estimated Infiltration Rates
3.4.3. Swale Performance Sensitive to Estimated Hydraulic Conductivities
4. Summary and Conclusions
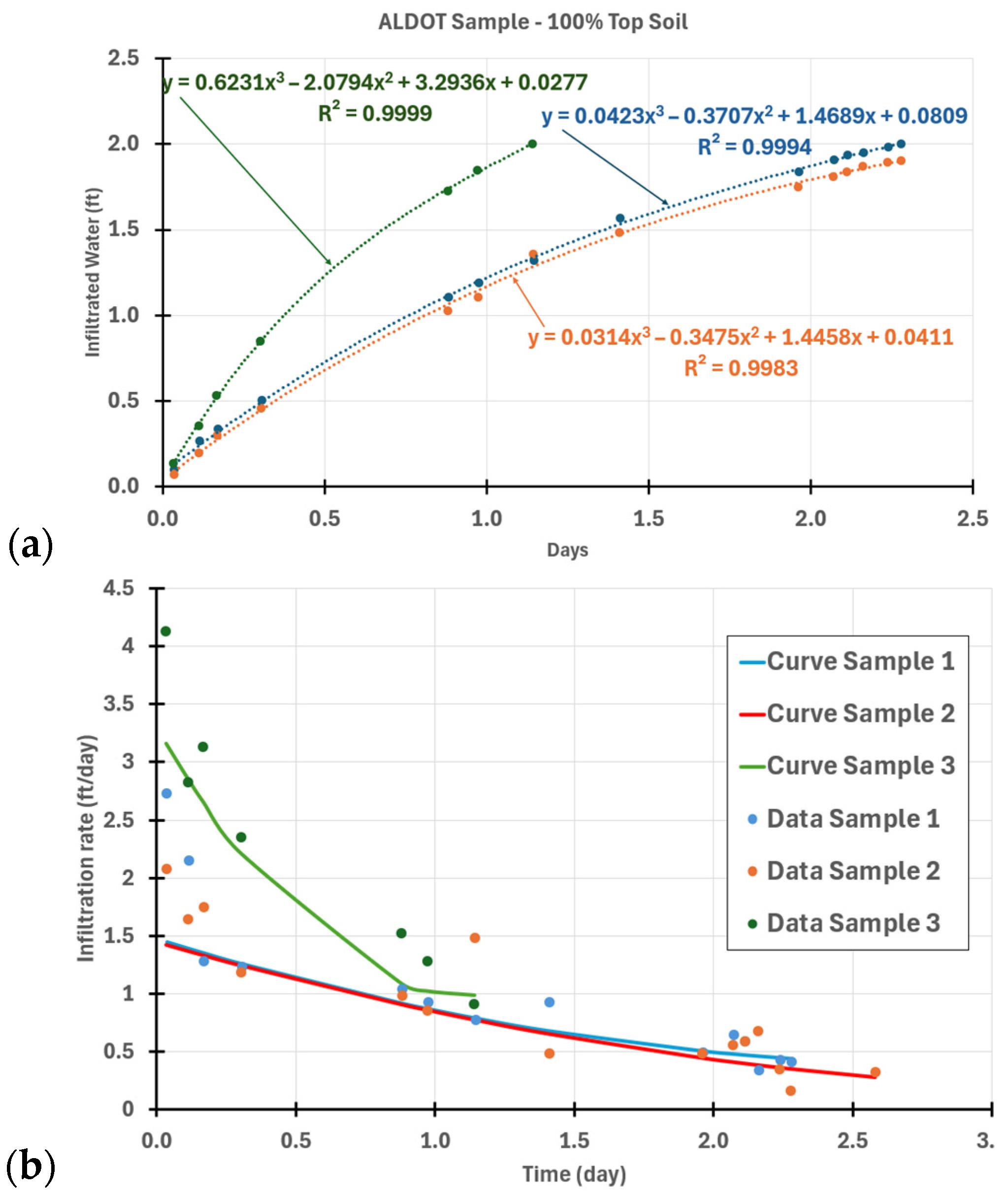
- The permeability of the topsoil used in this study (~88% sand content) as the top layer in the existing ALDOT infiltration swale design was measured as 0.58 m/day (1.90 ft/day), only about 1% of the field sand’s permeability (Table 2). The average measured infiltration rate of topsoil under falling head tests was 0.63 ft/day (0.19 m/day). Low permeability and infiltration rate of topsoil is the limiting factor of the low permeabilities (0.02–0.69 m/day or 0.07–2.26 ft/day) of several ALDOT and GDOT swale designs (Table 3). The topsoil based on ASTM D 5268 could contain 10–90% silt and clay and could even have much lower permeability than the topsoil used in this study; therefore, using a topsoil layer in the infiltration swale designs is not recommended and can potentially greatly reduce the infiltration capacity/rate of the swales.
- An amended topsoil mixture, consisting of pine bark fines and topsoil, was proposed to replace the topsoil layer. Infiltration rates of the mixtures with 5–75% of pine bark fines by weight were determined and ranged from 0.23 to 7.81 m/day (0.75 to 25.62 ft/day). An amended topsoil with 20% pine bark fines and 80% topsoil by weight (or 50% by volume for each) was used for new infiltration swale designs, and its average infiltration rate is 1.71 m/day (5.60 ft/day), which is much larger than the ALDOT swale’s drainage rate of 1 ft/day (0.3 m/day).
- There were 15 different infiltration swale designs (Table 7, including existing ALDOT design) that were tested using 2 ft (0.6 m) constant-head and falling-head columns. Even replacing the geotextile at the column bottom with stainless-steel wire mesh and replacing the geotextile between sand and #57 stones with 6 in. (15.2 cm) of pea gravel increased the swale infiltration performance, while using 6–10 in. (15.2–25.4 cm) of amended topsoil significantly increased the swale infiltration rates (Table 6).
- The F3 design with grass, consisting of 6 in. (15.2 cm) of amended topsoil, 10 in. (25.4 cm) sand, 6 in. (15.2 cm) peak gravel, and 9 in. (22.9 cm) #57 stone, has average infiltration rates of 11.66 ft/day (3.55 m/day) under falling-head tests and 13.73 ft/day (4.18 m/day) under constant-head tests, which are 37.6 and 15.1 times larger, respectively, than the existing ALDOT design with grass under the same tests (Table 6).
- SWMM modeling of the column test cases reveal that measured infiltration rates from constant-head and falling-head column tests give the soil’s saturated hydraulic conductivities if the pea gravel layer between sand and stone layers and the wire mesh at the column bottom do not restrict the vertical flow; otherwise, they indicate the overall average infiltration rates for the particular swale design.
- Sensitivity of the surface runoff from a southern Alabama project site shows that the infiltration capacity of the swale design linearly increases with the estimated saturated hydraulic conductivity below 0.91 m/day (1.5 in./h). Once the saturated hydraulic conductivity exceeds 0.91 m/day (1.5 in./h), the runoff volume stabilizes at approximately 50% of the total inflow volume. The recommended optimal design F3 (Table 6) has a conductivity greater than 3.52 ft/day (1.07 m/day), so selecting the conductivity may not be an issue for the SWMM modeling on F3 swale.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Symbols
| ALDOT | Alabama Department of Transportation |
| A | Cross-sectional area of specimen in Equation (1) |
| ASTM | American Society for Testing and Materials |
| D1 | Freeboard height for surface ponding |
| D2 | Thickness of the soil layer |
| D3 | Thickness of the storage layer |
| d1 | Surface depth |
| f1 | Infiltration rate of surface water into the soil layer |
| f2 | Percolation rate of water through the soil layer into the storage layer |
| f3 | Exfiltration rate of water from the storage layer into the native soil |
| F | Cumulative infiltration volume per unit area over a storm event |
| GDOT | Georgia Department of Transportation |
| HCO | Decay constant derived from moisture retention curve data |
| h | Difference in the water head on manometers |
| h1 h2 | Layer thickness |
| i | Precipitation rate falling directly on the surface layer |
| k | Coefficient of permeability |
| K2s Ks | Saturated hydraulic conductivity |
| L | Distance between manometers |
| LID | Low-impact development |
| PVC | Polyvinyl chloride |
| Q | Volume of water discharged |
| q0, q1 | Inflow to LID and runoff outflow from LID |
| SWMM | Storm Water Management Model by USEPA |
| t | Total measured time of discharge |
| USEPA | United States Environmental Protection Agency |
| θ2o | Moisture content at the top of the soil layer |
| θ2 | Soil layer moisture content |
| μ | Water viscosity |
| ψ | Suction head at the infiltration wetting front formed |
| ϕ2 | Porosity or void fraction of the soil layer |
| ϕ3 | Porosity or void fraction of the storage layer |
References
- Bell, C.D.; Wolfand, J.M.; Panos, C.L.; Bhaskar, A.S.; Gilliom, R.L.; Hogue, T.S.; Hopkins, K.G.; Jefferson, A.J. Stormwater control impacts on runoff volume and peak flow: A meta-analysis of watershed modelling studies. Hydrol. Process. 2020, 34, 3134–3152. [Google Scholar] [CrossRef]
- Novotny, V. Nonpoint Pollution and Urban Stormwater Management, Volume IX (Water Quality Management Library, V. 9); CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Paule-Mercado, M.A.; Lee, B.Y.; Memon, S.A.; Umer, S.R.; Salim, I.; Lee, C.H. Influence of land development on stormwater runoff from a mixed land use and land cover catchment. Sci. Total Environ. 2017, 599–600, 2142–2155. [Google Scholar] [CrossRef]
- Alabama (SWCC). Alabama Handbook for Erosion Control, Sediment Control and Stormwater Management on Construction Sites and Urban Areas, Volume 1 Developing Plans and Designing Best Management Practices; Alabama Soil and Water Conservation Committee (SWCC): Montegomery, AL, USA, 2018. [Google Scholar]
- Davis, A.P.; Traver, R.G.; Hunt, W.F. Improving Urban Stormwater Quality: Applying Fundamental Principles. J. Contemp. Water Res. Educ. 2010, 146, 3–10. [Google Scholar] [CrossRef]
- Chen, T.; Wang, M.; Su, J.; Li, J. Unlocking the Positive Impact of Bio-Swales on Hydrology, Water Quality, and Biodiversity: A Bibliometric Review. Sustainability 2023, 15, 8141. [Google Scholar] [CrossRef]
- USEPA. Technical Guidance on Implementing the Stormwater Runoff Requirements for Federal Projects Under Section 438 of the Energy Independence and Security Act; United States Environmental Protection Agency (USEPA): Washington, DC, USA, 2009. [Google Scholar]
- LeFevre, G.H.; Paus, K.H.; Natarajan, P.; Gulliver, J.S.; Novak, P.J.; Hozalski, R.M. Review of Dissolved Pollutants in Urban Storm Water and Their Removal and Fate in Bioretention Cells. J. Environ. Eng. 2015, 141, 04014050. [Google Scholar] [CrossRef]
- Stinshoff, P.; Busse, L.; Kick, D.; Helmreich, B. Stormwater treatment in infiltration swales with an engineered and planted soil media—Results of a pilot-scale approach. J. Environ. Manag. 2025, 385, 125693. [Google Scholar] [CrossRef] [PubMed]
- ALDOT. Guidelines for Operation. Subject: Post Development Stormwater Runoff Management for Small Frequent Rain Events; Alabama Department of Transportation (ALDOT): Montgomery, AL, USA, 2014. [Google Scholar]
- Dietz, M.E. Low Impact Development Practices: A Review of Current Research and Recommendations for Future Directions. Water Air Soil Pollut. 2007, 186, 351–363. [Google Scholar] [CrossRef]
- MPCA. Minnesota Stormwater Manual: Engineered (Bioretention) Media Mixes for Stormwater Applications; Minnesota Pollution Control Agency (MPCA): St. Paul, MN, USA, 2023. [Google Scholar]
- Eben, P.; Stinshoff, P.; Knoll, S.; Busse, L.; Kick, D.; Duthweiler, S.; Moning, C.; Pauleit, S.; Helmreich, B. Are infiltration swales all-rounders? An interdisciplinary field study on multifunctionality. Ecol. Eng. 2025, 215, 107597. [Google Scholar] [CrossRef]
- Crittenden, J.C.; Berrigan, J.K.; Hand, D.W. Design of Rapid Small-Scale Adsorption Tests for a Constant Diffusivity. J. (Water Pollut. Control Fed.) 1986, 58, 312–319. [Google Scholar]
- ASTM. D2434-68(2000); Standard Test Method for Permeability of Granular Soils (Constant Head). American Society of Testing and Materials (ASTM) International: West Conshohocken, PA, USA, 2000.
- Ma, Y.Z. Permeability Modeling. In Quantitative Geosciences: Data Analytics, Geostatistics, Reservoir Characterization and Modeling; Springer: Cham, Switzerland, 2019; pp. 495–515. [Google Scholar]
- Elhakim, A. Estimation of soil permeability. AEJ—Alex. Eng. J. 2016, 55, 2631–2638. [Google Scholar] [CrossRef]
- Verruijt, A. Soil Mechanics; Delft University of Technology: Delft, The Netherlands, 2001. [Google Scholar]
- Sánchez, F. Flujo en Medios Porosos: Ley de Darcy. Departamento de Geología, Universidad de Salamanca, España. 2008. Available online: http://agronomia.criba.edu.ar/carreras/ia/archivos/Materias/579/archivos/aguassubterraneas/DARCY.pdf (accessed on 10 January 2023).
- Lucas, W.C.; Medina, D.E.; Montalto, F.A.; Skripnik, S.; Sokolovskaya, N. Computational Methods in Low Impact Development Stormwater Control Measures; American Society of Civil Engineers: Reston, VA, USA, 2023. [Google Scholar]
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual, Volume III—Water Quality; National Risk Management Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2016. [Google Scholar]
- Frias, R.A.; Maniquiz-Redillas, M. Modelling the applicability of Low Impact Development (LID) technologies in a university campus in the Philippines using Storm Water Management Model (SWMM). IOP Conf. Ser. Mater. Sci. Eng. 2021, 1153, 012009. [Google Scholar] [CrossRef]
- Bragg, M.A.; Poudel, A.; Vasconcelos, J.G. Comparing SWMM and HEC-RAS Hydrological Modeling Performance in Semi-Urbanized Watershed. Water 2025, 17, 1331. [Google Scholar] [CrossRef]
- Burszta-Adamiak, E.; Mrowiec, M. Modelling of Green roofs’ hydrologic performance using EPA’s SWMM. Water Sci. Technol. A J. Int. Assoc. Water Pollut. Res. 2013, 68, 36–42. [Google Scholar] [CrossRef] [PubMed]
- Rosa, D.J.; Clausen, J.C.; Dietz, M.E. Calibration and verification of SWMM for low impact development. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 746–757. [Google Scholar] [CrossRef]
- Ramirez Florez, D.A. Evaluation of Infiltration Swale Media Using Small- and Intermediate-Scale Testing Techniques. Master’s Thesis, Auburn University, Auburn, AL, USA, 2024. [Google Scholar]
- Viessman, W.; Lewis, G.L. Introduction to Hydrology, 5th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2003; p. 612. [Google Scholar]
- Jiang, C.; Li, J.; Li, H.; Li, Y. An improved approach to design bioretention system media. Ecol. Eng. 2019, 136, 125–133. [Google Scholar] [CrossRef]
- Austin, P.J. Constructing and Evaluating Large-Scale Infiltration Swales for Retaining and Infiltrating Roadway Stormwater Runoff. Master’s Thesis, Auburn University, Auburn, AL, USA, 2024. [Google Scholar]
- Austin, P.J.; Florez, D.A.R.; Ji, Y.; Perez, M.A.; Fang, X.; Donald, W.N. Designing and Evaluating Infiltration Swales for Retaining and Infiltrating Roadway Stormwater Runoff; Highway Research Center at Auburn University: Auburn, AL, USA, 2025. [Google Scholar]
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual, Volume I—Hydrology (Revised); National Risk Management Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2016. [Google Scholar]
- ASTM D698-12; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort. American Society of Testing and Materials (ASTM) International: West Conshohocken, PA, USA, 2021.
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-Ampt infiltration parameters from soils data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Kozlowski, T.; Ludynia, A. Permeability Coefficient of Low Permeable Soils as a Single-Variable Function of Soil Parameter. Water 2019, 11, 2500. [Google Scholar] [CrossRef]
- ALDOT. Standard Specifications for Highway Construction; Alabama Department of Transportation (ALDOT): Montgomery, AL, USA, 2022. [Google Scholar]
- Dylewski, K.L.; Brown, J.T.R.; LeBleu, C.M.; Brantley, D.E.F. Low Impact Development Handbook for the State of Alabama; Alabama Department of Environmental Management: Montgomery, AL, USA, 2007. [Google Scholar]
- Le Coustumer, S.; Fletcher, T.D.; Deletic, A.; Barraud, S.; Lewis, J.F. Hydraulic performance of biofilter systems for stormwater management: Influences of design and operation. J. Hydrol. 2009, 376, 16–23. [Google Scholar] [CrossRef]
- Thompson, A.M.; Paul, A.C.; Balster, N.J. Physical and Hydraulic Properties of Engineered Soil Media for Bioretention Basins. Trans. ASABE 2008, 51, 499–514. [Google Scholar] [CrossRef]
- DCLCD. Dane County Erosion Control and Stormwater Management Manual, 1st ed.; Dane County Land Conservation Department (DCLCD): Madison, WI, USA, 2001. [Google Scholar]
- Carlisle, V.W.; Sodek, F.; Collins, M.E.; Hammond, L.C.; Harris, W.G. Characterization Data for Selected Florida Soils; University of Florida, Institute of Food and Agricultural Sciences: Gainesville, FL, USA, 1989. [Google Scholar]
- Gregory, J.H.; Dukes, M.; Jones, P.; Miller, G. Effect of Urban Soil Compaction on Infiltration Rate. J. Soil. Water Conserv. 2006, 61, 117–124. [Google Scholar] [CrossRef]
- Hussain, R.; Ghosh, K.K.; Ravi, K. Influence of biochar particle size on the hydraulic conductivity of two different compacted engineered soils. Biomass Convers. Biorefinery 2023, 13, 801–811. [Google Scholar] [CrossRef]
- MPCA. Minnesota Stormwater Manual: Design Criteria for Infiltration; Minnesota Pollution Control Agency (MPCA): St. Paul, MN, USA, 2022. [Google Scholar]





| Material | Bulk Density | Porosity 2 | |
|---|---|---|---|
| Loose Sample | After Consolidation | ||
| Topsoil | 88.8 lb/ft3 (1.42 g/cm3) | 96.8 lb/ft3 (1.55 g/cm3) | 43% |
| #57 stone | 98.6 lb/ft3 (1.58 g/cm3) | N/A | 46% |
| Pea gravel | 101.1 lb/ft3 (1.62 g/cm3) | N/A | 41% |
| Field sand | 93.6 lb/ft3 (1.50 g/cm3) | See Figure 5 | 33% |
| Pine bark fine | 22.2 lb/ft3 (0.36 g/cm3) | N/A | 73.5% |
| Amended topsoil 1 | 61.2 lb/ft3 (0.98 g/cm3) | 68.7 lb/ft3 (1.10 g/cm3) | 58% |
| Materials | Permeability, k, at 20 °C | ||
|---|---|---|---|
| in./min | cm/min | m/day | |
| Topsoil | 0.016 | 0.04 | 0.58 |
| Field sand | 1.56 | 3.95 | 557.06 |
| #57 stone | 2403.03 | 6103.76 | 87,894.29 |
| Pea gravel | 215.31 | 546.98 | 7875.27 |
| Design | Materials | |||
|---|---|---|---|---|
| Topsoil Layer Height in. (cm) | Field Sand Layer Height in. (cm) | #57 Stone Layer Height in. (cm) | Permeability, k (20 °C) ft/day (m/day) | |
| ALDOT 1 | 9.4 (24) | 14.2 (36) | 9.4 (24) | 2.28 (0.69) |
| ALDOT 2 | 11.8 (30) | 12.6 (32) | 8.7 (22) | 1.80 (0.55) |
| ALDOT 3 | 8.3 (21) | 16.5 (42) | 7.9 (20) | 1.56 (0.48) |
| ALDOT 4 | 8.3 (21) | 16.5 (42) | 8.3 (21) | 0.48 (0.14) |
| ALDOT 5 | 10.6 (27) | 15.0 (38) | 7.5 (19) | 0.24 (0.07) |
| GDOT 1 | 22.4 (57) | 1.6 (4) | 9.1 (23) | 0.12 (0.04) |
| GDOT 2 | 22.0 (56) | 2.4 (6) | 8.7 (22) | 0.24 (0.07) |
| Topsoil Sample | Falling-Head Test | Average | Overall Average | ||
|---|---|---|---|---|---|
| Test 1 | Test 2 | Test 3 | |||
| Sample 1 | 0.76 ft/day (0.23 m/day) | 0.35 ft/day (0.11 m/day) | 0.27 ft/day (0.08 m/day) | 0.46 ft/day (0.14 m/day) | 0.63 ± 0.36 ft/day (0.19 ± 0.11 m/day) |
| Sample 2 | 0.86 ft/day (0.26 m/day) | 0.41 ft/day (0.12 m/day) | 0.28 ft/day (0.09 m/day) | 0.52 ft/day (0.16 m/day) | |
| Sample 3 | 1.39 ft/day (0.42 m/day) | 0.94 ft/day (0.29 m/day) | 0.39 ft/day (0.11 m/day) | 0.91 ft/day (0.28 m/day) | |
| Sample Composition by Weight | Infiltration Rate, ft/day (m/day) | ||||
|---|---|---|---|---|---|
| Topsoil (%) | Pine Bark Fines (%) | First Test | Second Test | Third Test | Average |
| 100 | 0 | 1.00 (0.30) | 0.57 (0.17) | 0.31(0.09) | 0.63 (0.19) |
| 95 | 5 | 0.87 (0.27) | 0.55 (0.17) | 0.87 (0.27) | 0.76 (0.23) |
| 93 | 7 | 0.96 (0.29) | 1.67 (0.51) | 0.03 (0.01) | 0.89 (0.27) |
| 90 | 10 | 0.92 (0.28) | 0.87 (0.27) | 1.63 (0.50) | 1.14 (0.35) |
| 85 | 15 | 1.50 (0.45) | 2.32 (0.71) | 3.29 (1.00) | 2.37 (0.72) |
| 80 1 | 20 | 5.70 (1.73) | 3.40 (1.04) | 7.70 (2.35) | 5.60 (1.71) |
| 75 | 25 | 14.3 (4.35) | 17.0 (5.19) | 21.3 (6.50) | 17.5 (5.35) |
| 70 | 30 | 12.9 (3.94) | 30.6 (9.34) | 35.1 (10.7) | 26.2 (7.99) |
| 60 | 40 | 45.0 (13.7) | 15.7 (4.77) | 16.3 (4.96) | 25.6 (7.81) |
| 50 | 50 | 222 (67.2) | 411.4 (125.4) | 320 (97.5) | 318 (96.8) |
| 25 | 75 | 262 (79.8) | 320.0 (97.54) | 411 (125.4) | 331 (101) |
| 0 | 100 | 2160 (658.4) | 1440 (438.9) | 1920 (585.2) | 1840 (560.8) |
| Description | Designs 2 | Measured Infiltration Rates (ft/day) | Estimated ks (ft/day) | |
|---|---|---|---|---|
| Falling Head | Constant Head | |||
| 10″ topsoil, 12″ sand, 9″ #57 stone | A_geo_geo | 0.31 ± 0.14 (0.16–0.54) | N/A 3 | 1.81 ± 0.706 (0.59–3.02) |
| 10″ topsoil, 12″ sand, 8″ #57 stone | A-1G_geo_swm | 0.62 ± 0.28 (0.34–1.18) | 0.46 ± 0.06 (0.40–0.56) | 1.81 ± 0.706 (0.59–3.02) |
| 10″ topsoil, 12″ sand, 9″ #57 stone | A*_geo_geo_con | 0.49 ± 0.31 (0.23–1.29) | 1.73 ± 0.45 (1.16–2.31) | 1.81 ± 0.706 (0.59–3.02) |
| 10″ topsoil, 12″ sand, 9.5″ #57 stone | A*_geo_geo_con_grass | 0.31 ± 0.07 (0.24–0.43) | 0.91 ± 0.08 (0.79–1.04) | 1.81 ± 0.706 (0.59–3.02) |
| 10″ mixture 12″ sand, 8″ #57 stone | B_geo_geo | 2.25 ± 1.94 (0.33–6.46) | N/A | 11.51 ± 2.465 (7.19–15.82) |
| 10″ mixture 12″ sand, 9.5″ #57 stone | B*_geo_geo_con | 1.10 ± 0.64 (0.46–2.25) | 5.38 ± 1.23 (3.46–7.69) | 11.51 ± 2.465 (7.19–15.82) |
| 6″ mixture 16″ sand, 8″ #57 stone | C_geo_geo | 1.32 ± 0.36 (0.86–1.94) | N/A | 17.93 ± 3.616 (11.43–24.40) |
| 6″ mixture 15″ sand, 1″ peag 1, 8″ #57 stone | D_pea1_geo | 0.92 ± 0.17 (0.67–1.23) | N/A | 17.24 ± 3.500 (10.96–23.49) |
| 6″ mixture, 4″ peag, 18″ #57 stone | E_pea4_geo | 1.60 ± 1.01 (0.45–3.30) | N/A | 5.55 ± 1.253 (3.4–7.7) |
| 10″ mixture 12″ sand, 6″ peag, 8″ #57 stone | F_pea6_swm | 5.99 ± 2.72 (2.26–11.08) | 7.66 ± 1.97 (4.80–9.45) | 11.51 ± 2.465 (7.19–15.82) |
| 10″ mixture 12″ sand, 6″ peag, 4″ #57 stone | F*_pea6_swm_con | 1.26 ± 0.46 (0.73–2.03) | 5.31 ± 0.76 (4.18–6.43) | 11.51 ± 2.465 (7.19–15.82) |
| 6″ mixture 16″ sand, 6″ peag, 7″ #57 stone | F1_pea6_swm | 1.11 ± 0.16 (0.89–1.35) | 4.75 ± 1.36 (3.32–7.41) | 17.93 ± 3.616 (11.43–24.40) |
| 8″ mixture 14″ sand, 6″ peag, 7″ #57 stone | F2_pea6_swm | 1.58 ± 0.38 (1.17–2.17) | 6.73 ± 1.39 (5.22–8.82) | 14.02 ± 2.934 (8.82–19.20) |
| 6″ mixture 10″ sand, 6″ peag, 9″ #57 stone | F3*_pea6_swm_con | 2.24 ± 0.31 (1.94–2.98) | 5.75 ± 0.89 (4.52–7.48) | 13.65 ± 2.866 (8.58–18.70) |
| 6″ mixture 10″ sand, 6″ peag, 9″ #57 stone | F3*_pea6_swm_con_grass | 11.66 ± 5.69 (3.52–24.26) | 13.73 ± 4.78 (7.48–21.31) | 13.65 ± 2.866 (8.58–18.70) |
| Name | Conductivity ft/day (m/day) | Runoff ft3 (m3) | Runoff/Inflow (%) | Infiltration ft3 (m3) | Percolated ft3 (m3) | Max Storage Level, in. (cm) | Water into Native Soil, in. (cm) |
|---|---|---|---|---|---|---|---|
| Design A | 0.32 (0.10) | 17,072 (483) | 80.0% | 3514 (100) | 1425 (40) | 2.5 (6.4) | 5.4 (13.8) |
| 0.48 (0.15) | 16,592 (470) | 77.8% | 4580 (130) | 2491 (71) | 2.5 (6.4) | 8.6 (21.9) | |
| 0.64 (0.20) | 16,155 (458) | 75.7% | 5177 (147) | 3351 (95) | 2.5 (6.4) | 11.2 (28.4) | |
| 0.80 (0.24) | 15,724 (445) | 73.7% | 5608 (159) | 3938 (112) | 2.5 (6.4) | 13.0 (32.9) | |
| Design B | 0.50 (0.15) | 16,304 (462) | 76.4% | 4947 (140) | 2400 (68) | 2.5 (6.4) | 8.4 (21.2) |
| 1.00(0.30) | 14,993 (425) | 70.3% | 6340 (180) | 4326 (123) | 3.3 (8.3) | 14.1 (35.8) | |
| 1.50 (0.46) | 13,728 (389) | 64.4% | 7604 (215) | 5752 (163) | 13.7 (34.9) | 16.7 (42.5) | |
| 2.00 (0.61) | 12,499 (354) | 58.6% | 8833 (250) | 7078 (200) | 23.1 (58.8) | 17.1 (43.4) | |
| 2.50 (0.76) | 11,384 (322) | 53.4% | 9949 (282) | 8178 (232) | 26.0 (66.0) | 17.3 (43.9) | |
| 3.00 (0.91) | 10,693 (303) | 50.1% | 10,640 (301) | 8806 (249) | 26.0 (66.0) | 17.4 (44.2) | |
| 3.50 (1.07) | 10,675 (302) | 50.0% | 10,658 (302) | 8855 (251) | 26.0 (66.0) | 17.4 (44.3) | |
| 4.00 (1.22) | 10,666 (302) | 50.0% | 10,667 (302) | 8890 (252) | 26.0 (66.0) | 17.5 (44.4) | |
| 4.50 (1.37) | 10,660 (302) | 50.0% | 10,672 (302) | 8919 (253) | 26.0 (66.0) | 17.5 (44.4) | |
| 5.00 (1.52) | 10,654 (302) | 49.9% | 10,678 (302) | 8945 (253) | 26.0 (66.0) | 17.5 (44.5) | |
| 5.50 (1.68) | 10,649 (302) | 49.9% | 10,683 (303) | 8968 (254) | 26.0 (66.0) | 17.5 (44.5) | |
| 6.00 (1.83) | 10,645 (301) | 49.9% | 10,688 (303) | 8989 (255) | 26.0 (66.0) | 17.5 (44.5) | |
| 6.50 (1.98) | 10,640 (301) | 49.9% | 10,692 (303) | 9009 (255) | 26.0 (66.0) | 17.6 (44.6) | |
| Design F | 2.50 (0.76) | 11,384 (322) | 53.4% | 9949 (282) | 8164 (231) | 26.0 (66.0) | 17.3 (43.8) |
| 5.00 (1.52) | 10,758 (305) | 50.4% | 10,574 (299) | 8841 (250) | 26.0 (66.0) | 17.5 (44.4) | |
| 7.50 (2.29) | 10,737 (304) | 50.3% | 10,596 (300) | 8940 (253) | 26.0 (66.0) | 17.5 (44.6) | |
| 9.00 (2.74) | 10,726 (304) | 50.3% | 10,606 (300) | 8984 (254) | 26.0 (66.0) | 17.6 (44.6) | |
| 11.50 (3.51) | 10,712 (303) | 50.2% | 10,620 (301) | 9043 (256) | 26.0 (66.0) | 17.6 (44.7) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez Flórez, D.A.; Ji, Y.; Austin, P.J.; Perez, M.A.; Fang, X.; Donald, W.N. Evaluation of Infiltration Swale Media Using Small-Scale Testing Techniques and Its SWMM Modeling Considerations. Water 2025, 17, 2390. https://doi.org/10.3390/w17162390
Ramírez Flórez DA, Ji Y, Austin PJ, Perez MA, Fang X, Donald WN. Evaluation of Infiltration Swale Media Using Small-Scale Testing Techniques and Its SWMM Modeling Considerations. Water. 2025; 17(16):2390. https://doi.org/10.3390/w17162390
Chicago/Turabian StyleRamírez Flórez, Diego Armando, Yuting Ji, Parker J. Austin, Michael A. Perez, Xing Fang, and Wesley N. Donald. 2025. "Evaluation of Infiltration Swale Media Using Small-Scale Testing Techniques and Its SWMM Modeling Considerations" Water 17, no. 16: 2390. https://doi.org/10.3390/w17162390
APA StyleRamírez Flórez, D. A., Ji, Y., Austin, P. J., Perez, M. A., Fang, X., & Donald, W. N. (2025). Evaluation of Infiltration Swale Media Using Small-Scale Testing Techniques and Its SWMM Modeling Considerations. Water, 17(16), 2390. https://doi.org/10.3390/w17162390








