Next Article in Journal
RETRACTED: Yang et al. Biological Activated Carbon Filtration Controls Membrane Fouling and Reduces By-Products from Chemically Enhanced Backwashing During Ultrafiltration Treatment. Water 2023, 15, 3803
Previous Article in Journal
Could the Presence of Ferrihydrite in a Riverbed Impacted by Mining Leachates Be Linked to a Reduction in Contamination and Health Indexes?
Previous Article in Special Issue
Asymmetric Impacts of Urbanization on Extreme Hourly Precipitation Across the Yangtze River Delta Urban Agglomeration During 1978–2012
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 15
10.3390/w17152168
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Climatology of Errors in HREF MCS Precipitation Objects

by
William A. Gallus, Jr.
*,
Anna Duhachek
,
Kristie J. Franz
and
Tyreek Frazier
Department of Earth, Atmosphere, and Climate, Iowa State University, Ames, IA 50011, USA
*
Author to whom correspondence should be addressed.
Water 2025, 17(15), 2168; https://doi.org/10.3390/w17152168
Submission received: 29 May 2025 / Revised: 16 July 2025 / Accepted: 17 July 2025 / Published: 22 July 2025
(This article belongs to the Special Issue Analysis of Extreme Precipitation Under Climate Change)
Browse Figures
Versions Notes

Abstract

Numerical weather prediction of warm season rainfall remains challenging and skill at achieving this is often much lower than during the cold season. Prior studies have shown that displacement errors play a large role in the poor skill of these forecasts, but less is known about how such errors compare to other sources of error, particularly within forecasts from convection-allowing ensembles. The present study uses the Method for Object-based Diagnostic Evaluation to develop a climatology of errors for precipitation objects from High-Resolution Ensemble Forecasting forecasts for mesoscale convective systems during the warm seasons from 2018 to 2023 in the United States. It is found that displacement errors in all ensemble members are generally not systematic, and on average are between 100 and 150 km. Errors are somewhat smaller in September, possibly reflecting increased forcing from synoptic-scale systems. Although most ensemble members have a negative error for the 10th percentile of rainfall intensity, the error becomes positive for heavier amounts. However, the total system rainfall is less than that observed for all members except the 12 UTC NAM. This is likely due to the negative errors for area that are present in all models, except again in the 12 UTC NAM.

1. Introduction

Flash flooding causes on average of 64 fatalities annually in the United States, and as the population grows, more flood-prone land is being developed into residential areas, increasing risk to life and property [1,2]. From 2007 to 2017, 95% of flash floods were associated with nontropical heavy rainstorms without snowmelt [1]. Most heavy rainfall events within the central and eastern contiguous United States (CONUS) are caused by large, long-lived multicellular storm complexes known as mesoscale convective systems (MCSs) [3,4].
Most MCSs in the central and eastern CONUS occur during the warm season with a peak during the summer in June, July, and August [4,5,6]. Consequently, flash floods are also more frequent during the warm season [1,7]. Flash-flood-related casualties are particularly common in small watersheds because smaller watersheds tend to react more quickly and dramatically to heavy precipitation [7]. Quantitative precipitation forecasts (QPFs) are a potentially critical source of early flood warning information; unfortunately, errors in QPFs limit their applicability for the forecasting of small watersheds [7,8,9,10].
The poor skill of warm season QPFs persists at least in part because such precipitation often comes from convection that is small in scale and often forced by other small-scale features like outflow boundaries that are not resolved well by existing observational networks (e.g., [11,12,13]). MCSs that form in more strongly forced synoptic environments have been found to be simulated with more accuracy [14,15]. Even these events, however, often exhibit forecast errors due to inaccurately simulated mesoscale features [16].
In the past, most models could not resolve convection explicitly, so they depended on a convective parameterization scheme [12,17,18], which often introduced error and led to substantially different solutions depending on what parameterization was used [19]. Improved computer resources now allow many convection-allowing models (CAMs) to be run, including ensembles of CAMs such as the HREF (High-Resolution Ensemble Forecast; [20]) using horizontal grid spacings of roughly 4 km or less that allow convective parameterizations to be neglected. Ref. [21] found that models with 2 km and 4 km horizontal grid spacings and no convective parameterization schemes performed significantly better than a model with 12 km grid spacing and parameterized convection for next-day precipitation events.
Refining the horizontal resolution will not always improve the accuracy of the model [21,22,23]. Ref. [24] found that reducing the grid spacing of a model from 3 km to 1 km improved the simulated climatological frequency of different storm types but did not improve the accuracy of the forecast when considering the evolution of storm types within individual events. As an extreme example of a case where coarser grid spacing worked much better, ref. [25] found that in simulations of the 2020 Midwestern derecho, simulations using 13 km and 25 km grid spacings did show intense convection in roughly the right areas at the right times, but 3 km simulations failed to do this due to their production of preceding spurious convection. CAMs typically forecast properties of storms such as their type better than simulations using convective parameterizations but are less skilled at predicting details such as convective location and structure [12]. Ref. [26] examined multiple CAMs and found the average displacement of the initiation of an MCS was approximately 75–110 km.
Ref. [27] examined displacement errors in the centroids of the total precipitation footprint and that of the first hour of precipitation in MCSs simulated by two CAM ensembles, the HREF and the High-Resolution Rapid Refresh Ensemble (HRRRE; [28]) to better understand the potential for bias correction. The HRRRE, an ensemble made of perturbations of the same model, had more agreement in the displacement errors among members, and a statistically significant western displacement trend, whereas the HREF, an ensemble made of different models, had less agreement and more random errors. In addition, ref. [27] found that the displacement error of the accumulated precipitation forecast improved by shifting the forecast centroid east or west and north or south based on the direction of the displacement error in the first hour. Ref. [8] used the distribution of QPF displacement errors from [27] to randomly select shifts (both direction and distance) for the HRRRE QPFs prior to inputting the precipitation forecasts into a hydrologic model. The members were also weighed by the object’s displacement error at the time of convective initiation. The resulting ensemble streamflow predictions showed improvement over using the non-shifted HRRRE as input. The above studies focused on mitigating displacement errors, even though errors in intensity and areal coverage also exist in QPFs, because at least one prior study that looked at small ensembles with 15 km and 4 km horizontal grid spacing [29] implied that displacement errors were a larger problem for QPFs.
The purpose of the present work is to expand upon [27,29] to create an object-based climatology of QPF errors associated with warm-season MCSs. Using the HREF members, the HRRR (High-Resolution Rapid Refresh), HRW ARW (High-Resolution Window Advanced Research Weather Research and Forecasting), HRW NSSL (High-Resolution Window National Severe Storms Laboratory), and NAM CONUS Nest (North American Model Contiguous United States Nested domain) numerical models, QPFs from 2018 to 2023 were compared to observations using the Method for Object-based Diagnostic Evaluation (MODE; [30]). Displacement, area, and intensity errors are examined to gain more insight, with a state-of-the-art operational CAM ensemble, into the relative importance of these different types of error on precipitation forecasts. This work is intended to inform the use of QPFs for extreme precipitation forecasting, as well as their application in hydrologic prediction.

2. Data and Methods

2.1. Data

Observed precipitation data were accessed from the National Severe Storms Laboratory’s (NSSL) Multi-Radar/Multi-Sensor System (MRMS; [31]). MRMS combines data from multiple sources including 146 radar sites in the United States and 30 in Canada, along with 7000 hourly rain gauge readings to provide 1 km horizontal grid spacing depictions of weather events with a 2 min temporal resolution. Quantitative precipitation estimate products are available for 1, 3, 6, 12, 24, 48, and 72 h periods. MRMS is widely used by various government agencies to monitor water resources and flash flooding, as evidenced by its use as the main source of verification data for QPF-related experiments, like FFAIR (J. Correia, CIRES, 2024 personal communication). MRMS also provides reflectivity mosaics that assist in the verification and forecasting of severe thunderstorm hazards such as hail, lightning, and tornadoes [32].
HREF precipitation forecasts produced by the HRRR, HRW ARW, HRW NSSL, and NAM CONUS Nest numerical models from 2018 to 2023 were included in this study. The first three members use the same dynamic core [33], while the NAM uses a different core [34]. The fifth HREF model, the HRW FV3 [35], was not included as its output was not available until May 2021. Each of the models has either a 3.0 km or 3.2 km horizontal resolution. The HRW ARW uses initial conditions (ICs) from the RAP [36], the lateral boundary conditions (LBCs) from the GFS (e.g., [37]), the WSM6 microphysics scheme [38], and the YSU planetary boundary layer (PBL) parameterization scheme [39]. The HRRR uses LBCs from the RAP, the Thompson microphysics scheme [40], and the MYNN PBL parameterization scheme [41]. HRRR uses ICs from RAP prior to 11 May 2021, and HRRRDAS thereafter. The NAM CONUS Nest and the HRW NSSL both use the NAM for the ICs and LBCs and the MYJ PBL parameterization scheme [42]. They differ as the NAM CONUS Nest uses the Ferrier–Aligo microphysics scheme [43] and the current NAM run for LBCs while the HRW NSSL uses the WSM6 microphysics scheme and a NAM run from six hours before for initialization.

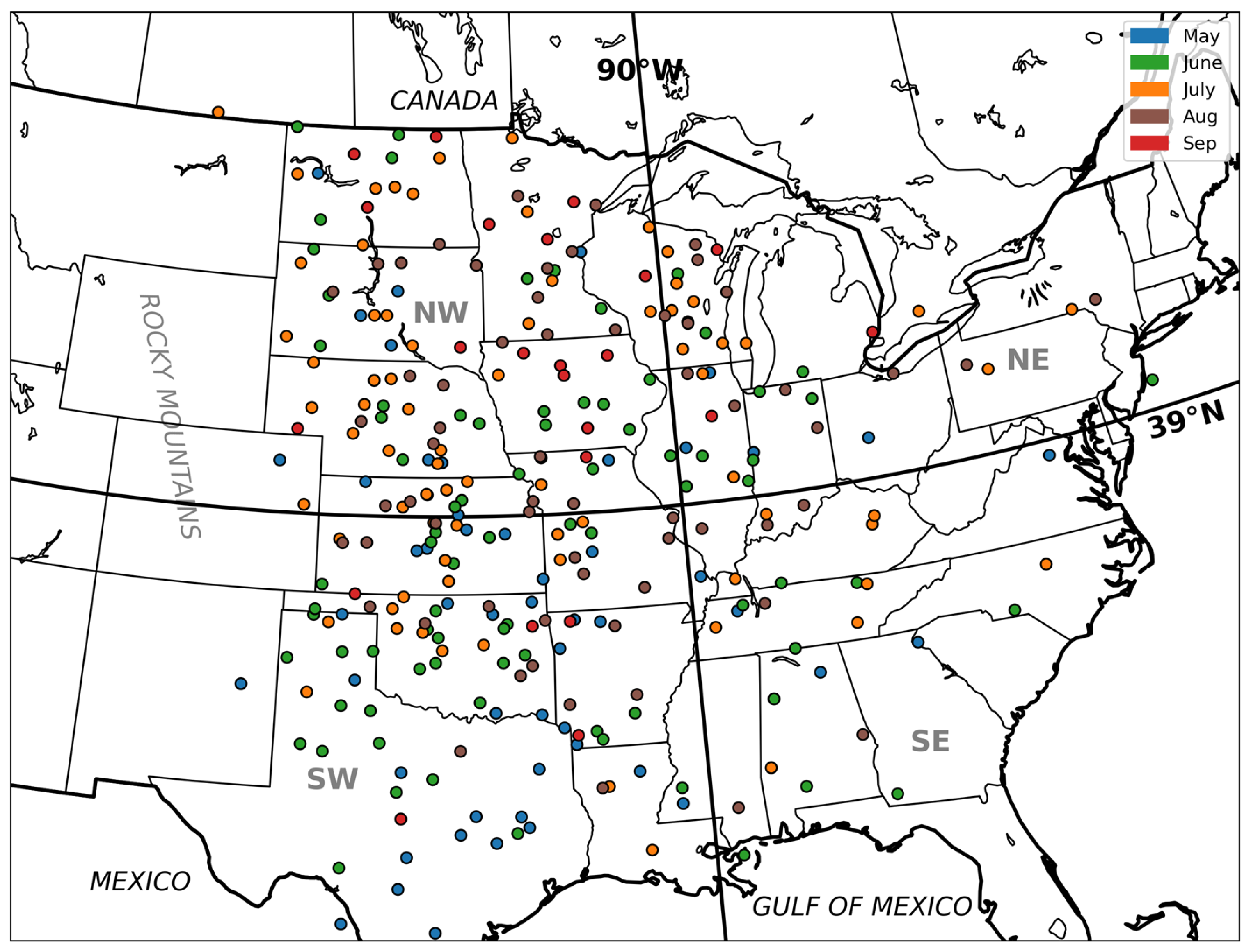
2.2. Case Selection

Cases were identified by examining archived composite NEXRAD radar reflectivity data for the period from May–September 2018–2023 for convective events over 100 km long in at least one direction and lasting over 6 h. This resulted in 499 MCSs being identified over the CONUS with all but one of these cases occurring east of the Rocky Mountains, as would be expected from the previously reported climatologies of such systems (e.g., [6]). Because MCSs typically develop in the late afternoon and persist through the night, we chose to examine the HREF members from the 12 UTC cycles immediately preceding MCS formation, and to focus on the 24 h QPF ending at 12 UTC the next morning. The HREF comprises a current member of each model and a time-lagged member [44]. Because of this time lagging, we used the 12 UTC run of each model and the time-lagged member, which was the 00 UTC run for the HRW ARW, HRW NSSL, and NAM CONUS Nest, and the 06 UTC run for the HRRR. To most fairly compare the forecasts to the observations, the observation data were coarsened from their 1 km horizontal grid spacing to 3 km, and the forecasts were re-gridded to match the observation grid point locations.

2.3. MODE Processing

The eight HREF member QPFs and the MRMS observation data were processed with MODE [30]. MODE determines the precipitation objects present in the input fields, in this case, the 24 h accumulated precipitation. MODE uses both convolution and thresholding to determine objects, where the threshold is supplied by the user. In the present study, MODE was calibrated by manually adjusting its configuration and examining its output for a sample of cases. The configuration that produced objects that best resembled the MCSs observed in radar data used a rainfall threshold of 13.7 mm in 24 h. MODE matches forecast objects to those observed by using a calculation called the interest function to assign each forecast–observation pair a value that represents how likely they are to correspond to each other. The weight MODE gives to each attribute of a forecast–observation pair in this calculation must be calibrated. This calibration was performed by picking the forecast–observation pairs that we determined were most likely correct for a sample of cases and adjusting the weight of each attribute until the interest function best agreed with our assessment. Even with the interest function calibrated to perform best at identifying MCS precipitation footprints, MODE sometimes broke a single event into multiple forecasted or observed objects, so a single observed object could correspond with several forecasted objects or vice versa. Because of this, we visually inspected the MODE results and adjusted the object pairings as follows: First, we matched the composite reflectivity of the MCS event to an observed object or objects. Next, the forecasted object(s) most likely to be associated with the observed object(s) were determined. While the object with the highest interest function value was considered, it was also disregarded if other forecast object(s) were deemed a more likely match.
Many of the original cases needed to be discarded during the matching process. Several cases were unusable because other precipitation events overlapped the observations or forecasts for the MCS of interest during the 24 h accumulation period. This made collecting data corresponding to an individual MCS impossible. Occasionally, a case simply had no forecast object corresponding to the observations. For some cases, only the forecast for a particular ensemble member had to be discarded while the other members could still be used. This led to each ensemble member having a slightly different number of cases in the analyses, although the number was generally around 300. All these remaining cases occurred east of the Rocky Mountains. In the analyses that followed, statistics for the HRRR runs were subdivided into a pre- and a post-11 May 2021 group, since the HRRR changed the source of its ICs on this day, and this change noticeably impacted the skill of the forecasts.
MODE calculates several parameters for each individual object and forecast–observation object pair. For the present study, the focus was on centroid location, intensity of rainfall, areal coverage, and rain volume within the MCS (referred to as intensity sum in MODE). Centroids represent the center of mass of the precipitation systems. For cases where several objects made up the forecast or observations, the parameters for each object had to be combined. The centroid latitude, centroid longitude, and three of the five intensity percentiles computed by MODE that represented the distribution well (10th, 50th, and 90th) were combined by taking an average weighted by the area of each object. The area and intensity sum parameters were combined by summing the objects together. The correlation between errors in displacement or intensity with errors in other parameters was investigated using the Pearson correlation coefficient. Distributions of errors in these parameters were also examined by month and region. The four regions considered (northwest, northeast, southwest, and southeast) are shown in Figure 1, which also shows the spatial and monthly distribution of events for one of the HREF members, the 00 UTC ARW. Statistical significance of differences among the eight model members for a given MODE parameter was evaluated using a Nemenyi [45] post hoc test after the application of the global Friedman [46] test. Significance of variations by region or month for a particular model was first evaluated with a two-way ANOVA test [47] to determine global significance and then Tukey’s Honestly Significant Difference test [48] was used for post hoc testing for pairwise significance between individual months or regions. Significance is noted in the following results if the p-value is less than 0.05 (95% confidence).

3. Results

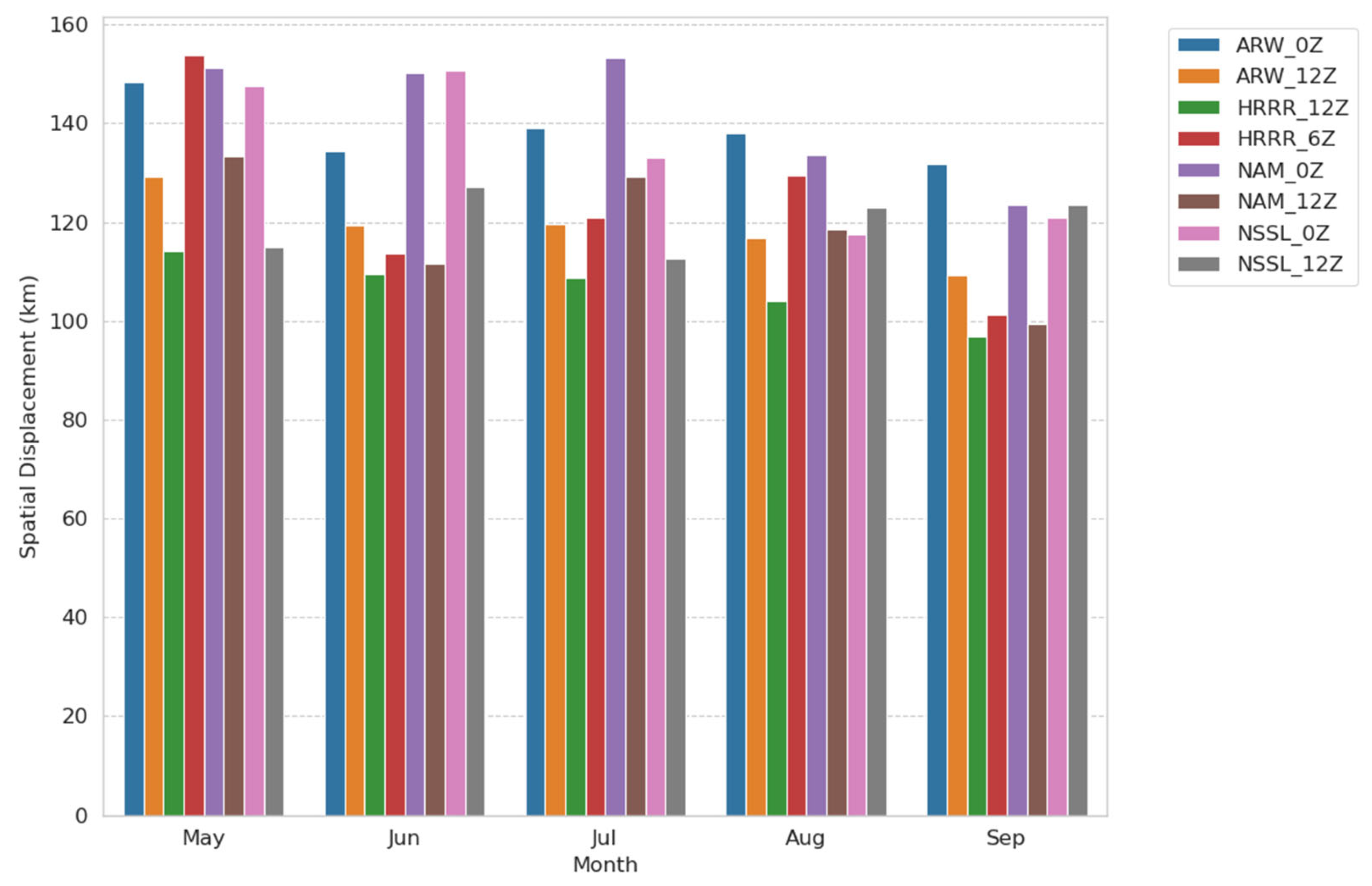
3.1. Displacement Errors

First, errors in the forecast location of the MCSs were evaluated. The Wilcoxon rank sum test showed no evidence of a significant difference between the displacement distribution from cases before and after 11 May 2021 for the ARW, NSSL, and NAM models, suggesting the entire six years of data from these models could be compared to the HRRR output, even though the HRRR output was restricted to the period from 11 May 2021 through 2023 because of the change in initialization procedure that took place in 2021. For all models, the displacement errors were smaller for the 12 UTC runs compared to the time-lagged 00/06 UTC runs (Figure 2). The only differences that were statistically significant, however, were between the 12 UTC HRRR and the 00 UTC NAM and ARW members, with the HRRR having significantly less displacement error. At 12 UTC, all four models had a median displacement around 100 km, roughly 20 km less on average than in the time-lagged members. Over 75% of cases were displaced by over 50 km for all members, with time-lagged members displaced more than 175 km over 25% of the time. Although [43] found that time-lagging could help with forecasts of precipitation and increase the spread in ensemble forecasts, for these MCS cases, the time-lagged members had noticeably reduced skill for the location of the precipitation centroids. The improved displacement errors with less lead time were consistent with typical error growth over time in forecast models. It is also worth noting that more MCSs were always identified in the 12 UTC runs than in the time-lagged runs, with the biggest difference present in the NSSL runs. It is possible that the greater number of systems identified in the 12 UTC runs reflects the decreased lead time in these runs, which typically results in improved QPF skill and should allow MODE to find more forecast systems that it considers a match with the observed ones.
The ARW members tended to displace events to the northeast (Figure 3) with 32% of cases displaced to this quadrant in the 00 UTC run and 39% of cases in the 12 UTC run. The HRRR had systems too far north in the 06 UTC run, with 29% of cases being displaced to the northeast and 31% of cases being displaced to the northwest. In the 12 UTC HRRR run, the error toward the northeast was greater, with 37% of cases displaced in this direction.
Though the total displacement errors tended to decrease in the 12 UTC model runs, the directional errors in the ARW and HRRR became more pronounced. The NAM model had errors toward the northwest with 41% of 00 UTC cases and 40% of 12 UTC cases displaced to this quadrant. The NSSL had a weak western error in the 00 UTC run, with 29% of cases displaced to the northwest and 28% to the southwest. This trend was replaced by a weak northeastern trend in the 12 UTC run with 28% of cases displaced to this quadrant. The weakness of the trends in the NSSL and the lack of consistency between the 00 UTC and 12 UTC runs suggest that systematic directional error is not a problem in this model. However, in the other model runs, a relatively consistent directional error toward the north occurred. Although prior studies have investigated a few characteristics of forecast errors for the HREF ensemble (e.g., [20,49]), it does not appear that location errors have been studied previously for a large sample of MCSs. Ref. [27] examined a much smaller set of 0–18 h QPFs for MCSs, all of which led to flash flood warnings, and did show some tendency for northward displacement errors in the NAM and NSSL HREF members, but overall did not find systematic trends in the HREF.
Regarding regional variations in displacement errors (Figure 4), the ARW and HRRR both performed worst in the southeast and best in the southwest. The NSSL changed little from region to region. The errors of the HRRR varied greatly from region to region. A comparison of the medians of each model shows that most models typically had better agreement in the northern regions than in the southern ones. The southeastern U.S. is well-known for presenting challenges for accurate QPFs (e.g., [50]), as small-scale weakly forced thunderstorms are common in the summer, and orography can influence such convection. It must be noted, however, that no differences between regions for any model were statistically significant using Tukey’s test.
Errors in displacement evidence some variation by month over the May–September study period (Figure 5). It should be noted that while the other models had 22–26 cases for the month of September, the 06 UTC HRRR only had seven cases, and the 12 UTC HRRR only had three, since our analysis only used the HRRR output after the change to use HRRDAS for initialization. Because of this, caution should be used in interpreting the results for the HRRR in September. None of the differences between months for most models, in general, appeared substantial and none were statistically significant, although there was a hint of there being smaller errors in September. It is well known that summer QPFs have the lowest skill (e.g., [9,11]), at least partly due to weaker synoptic-scale forcing, and thus it is possible that increased large-scale forcing may improve skill for some centroid locations by September.

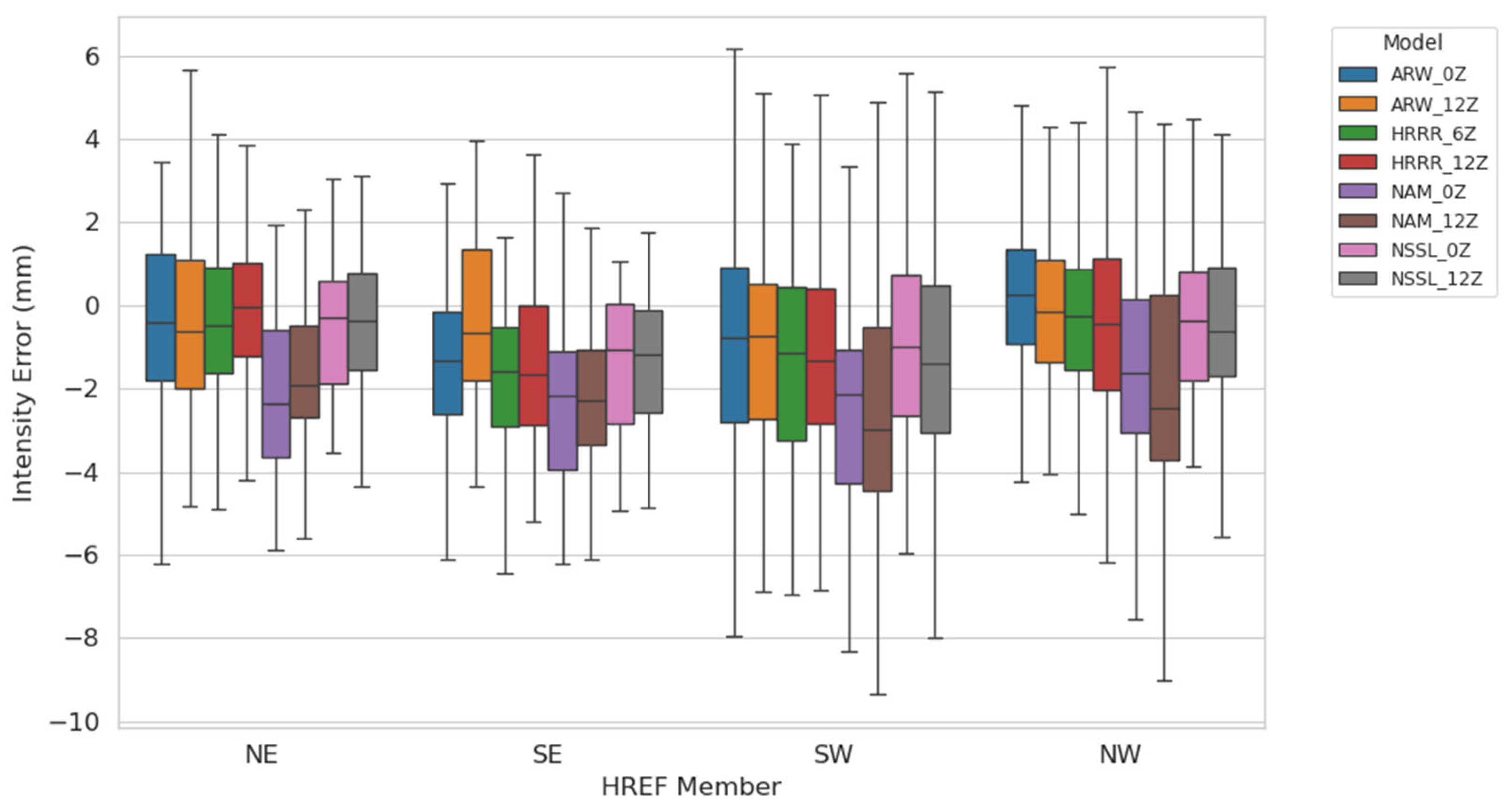
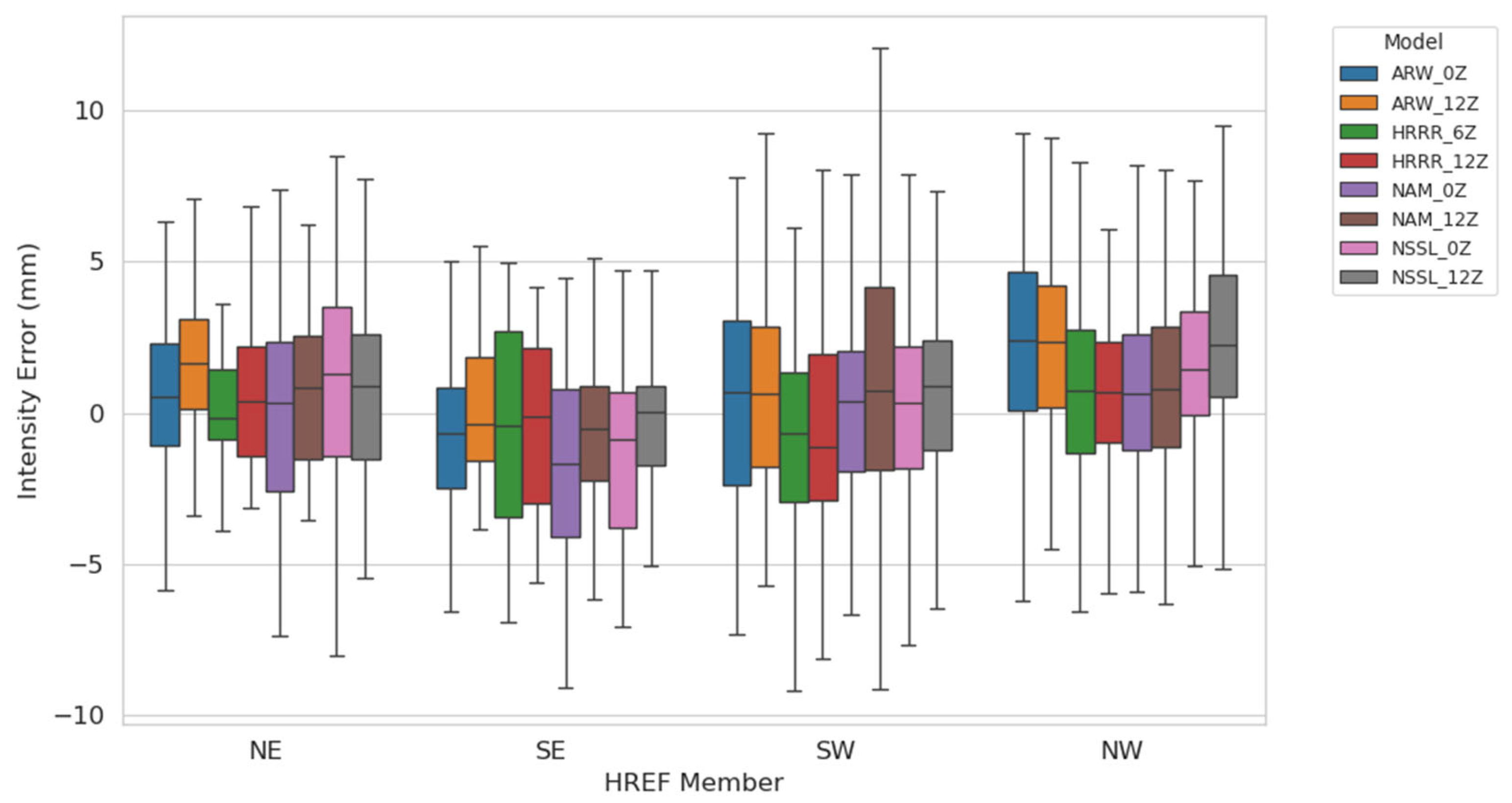
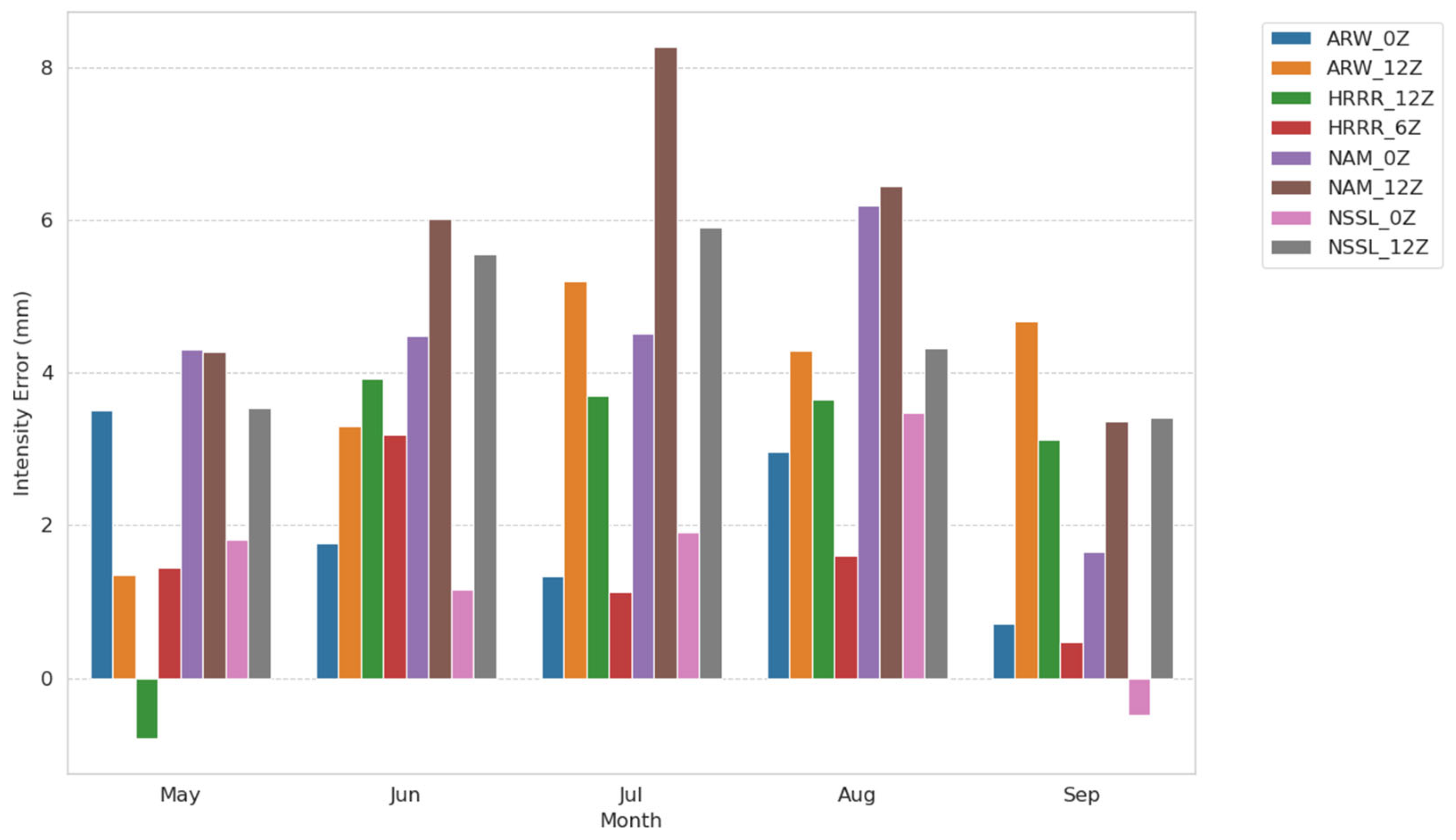
3.2. Intensity Errors

Unlike for displacement errors, errors for the 10th, 50th, and 90th intensity percentiles had at least one model other than the HRRR show evidence of a significant change in the skill between the sample of cases before 11 May 2021 and those after. This means that caution must be used in comparing the results for the intensity of rainfall between the HRRR and other models, since some differences may be attributed to the statistics for the ARW, NAM, and NSSL being computed from a longer time period.
All models except for the 06 UTC HRRR had negative errors for the 10th percentile of intensity (Figure 6), with the NAM being the worst, as it forecast too little precipitation for over 75% of cases. There was little change in errors between the 00 UTC and 12 UTC runs for the ARW and NSSL, but the NAM and HRRR had a greater negative error for the 12 UTC runs, although the difference compared to the time-lagged member was not significant (Table 1). Statistically significant differences were more common with the NAM runs compared to the other models (Table 1), with the NAM being drier, and were more common with most of the NSSL runs compared to the HRRR, although Figure 6 suggests the practical significance of the difference was small. The average 10th percentile intensity value from all observed objects was around 8 mm, meaning that for most models, errors were less than 25% of the magnitude of the intensity.
Examining the monthly errors in the 10th percentile of intensity, the smaller negative errors in the ARW and HRRR compared to the NAM and NSSL models are apparent in all months, but especially for the HRRR in May and the ARW in September. The NAM had the greatest negative error, especially from June through September (Figure 7). The only statistically significant differences between months occurred with the 00 UTC NAM member, where the negative errors in June and July were both significantly greater than those in May.
The northern regions generally had less negative errors than the southern regions for models other than the NAM (Figure 8). For the 06 and 12 UTC HRRR models, the magnitude of the errors in both the SW and SE regions were significantly greater than those of the NW region. The differences among regions were not statistically significant for any of the other models. The median of the HRRR and ARW was close to zero or even positive in these regions. The ARW, HRRR, and NSSL had similar errors in the southwest.
The errors for the 50th percentile of intensity (Figure 9) were generally larger than the 10th intensity percentile errors, likely due at least in part to overall heavier precipitation amounts (the average 50th percentile intensity for observed objects was 21.5 mm). The exception was with the NAM, where the magnitude of positive errors for the 50th percentile was not as large as those for the negative errors at the 10th percentile. The HRRR had errors close to zero while the NAM had a slight positive error. The NSSL and ARW members had larger positive errors. None of the differences between the models were statistically significant, except for the 06 UTC HRRR compared to the 12 UTC ARW. In general, all models showed a shift from being too light, with precipitation amounts at the 10th percentile, to being too heavy, with amounts at the 50th percentile. The relative magnitude of errors for the 50th percentile intensity was much less than that for the 10th percentile, generally around 5%.
Despite models generally having positive errors overall for the 50th percentile of intensity, all models except for the 12 UTC NSSL had negative errors for the median in the southeast region (Figure 10). Of note, no model except the HRRR had a negative error in any other region for the 50th percentile of intensity. The HRRR generally had much smaller errors in the northern regions than in the southern ones. The northeast and southwest regions had errors closest to zero with most models. The northwest region had a larger positive error, with both runs of the ARW and NSSL overpredicting intensity in over 75% of cases. In four different models, the differences between some regions were statistically significant. In the 12 UTC ARW, the 00 UTC NAM, and the 00 UTC NSSL models, errors in the northwest were significantly more positive that those in the SW and SE. For the 12 UTC NSSL, the errors in the NW were significantly more positive than all three other regions. Regarding performance by month, no notable differences were present in any of the models.
For 90th percentile intensity errors, the HRRR once again had almost no error (Figure 11). The other models, especially the NAM, had positive errors that were much larger than those for the 10th and 50th percentiles, as would be expected since the 90th percentile intensity represents the areas of heaviest precipitation within the MCS. In fact, the average 90th percentile intensity value for the observed objects was 46.8 mm. Because these areas would present the greatest danger of excessive rainfall and flash flooding, any errors present here would be more impactful to public safety. The 12 UTC NAM, for instance, had a positive error of around 8 mm. Most of the differences between the models were not statistically significant (Table 2) except for the 06 UTC HRRR, which often had significantly less error than the other model members. These results suggest that, except for the HRRR, the HREF members would tend to overestimate the risk of flash flooding due to excessive rainfall. In a relative sense, however, these errors are not as large as those with the 10th percentile, averaging around 10% for most models.
The positive errors in the NAM and NSSL members were greater during the summer months (June, July, August) than in May or September (Figure 12). The positive error was largest in August for the ARW and HRRR. The only model to show any negative error in any month was the HRRR, but these negative errors were very small, in the order of 1 mm or less. None of the differences between months for any of the models were statistically significant.
Regionally, all models except the HRRR in the northwest had positive errors in all regions (Figure 13), which were greatest in the northwestern region. For the 12 UTC NSSL model, the difference between the error in the NW region and that of the SW region was statistically significant. Other differences between regions were not significant. The southeast region generally had the least variability among cases, but this was likely due to it having the fewest cases. Except for the southeast region, some cases had overestimates exceeding 30 mm and underestimates exceeding 20 mm. Of note, most models in most regions had larger positive errors in their 12 UTC runs than in the time-lagged runs.

3.3. Water Volume and Area Errors

Errors in MODE’s intensity sum parameter, which measures the total amount of water that falls as precipitation within the object, correlated strongly with errors in the areal coverage (Figure 14) with a Pearson correlation coefficient of at least 0.9 for all models. This implies that errors in the total amount of precipitation are far more heavily impacted by errors in the size of the event than by errors in intensity. Because of this relationship, we examined errors in the forecasted area and forecasted intensity sum together. Errors in both parameters were not found to significantly change between cases occurring before 11 May 2021 and cases occurring after in any of the models.
All models except the 12 UTC NSSL had at least a slight negative error for both the area and the total system precipitation amount. The errors were especially severe in the HRRR which forecasted too small an event for 73% of the 06 UTC cases and 72% of the 12 UTC cases. The underestimates of the total system precipitation amount were likely accentuated by the fact HRRR did not have the large positive errors at the 50th and 90th intensity percentiles that were common in the other models. The underestimate in total system rainfall occurred despite the generally positive errors in the 50th and 90th percentile of intensity for most models because the area coverage was too small. Thus, it seems these models create areas of heavy rain more intense than observed, but over smaller regions than those observed. In addition, although amounts at the 10th intensity percentile are small and might be assumed to not contribute much to the system total rainfall, because the areal coverage of the light amounts is so large, the underestimates discussed earlier for the 10th percentile intensity in most models also likely play a role in the underestimates in the total system rainfall.
Model errors in areal coverage (and thus total system rainfall) agree better in the western regions while the eastern regions have more variability (Figure 15), despite the western regions having more cases. The ARW members have positive errors in system rainfall amounts and areal coverage in the eastern regions, with negative errors in the west, while the HRRR members have especially large negative errors in the northeast. Otherwise, no systematic trends are apparent among the regions in the 00 UTC NAM and NSSL models. However, statistically significant differences are present in the 12 UTC NAM between the NE region and all other regions, with the NE having much larger positive errors in area. For the 12 UTC NSSL model, area errors are statistically significantly more positive in the NE compared to both the NW and SW, while the SE region also has significantly more positive errors than the NW. No other differences between regions for the other models were significant. In addition, no meaningful trends or statistically significant differences were present in the monthly analysis of both fields.

4. Discussion

A climatology of precipitation object errors was developed for the HREF ensemble using MODE, focusing on displacement, intensity, and areal coverage errors for MCSs that occurred during the warm seasons of 2018–2023 in the United States. A threshold of 13.7 mm for 24 h precipitation was used to define the MCS precipitation objects in MODE. Prior studies with much smaller samples of cases had shown that large displacement errors are common in QPFs for warm season events. The present work extends those prior works to a much larger sample of cases, roughly 300 for each of the eight HREF members evaluated, and compares the displacement errors to other errors that often result in poor QPF skills during the warm season.
It was found that the median displacement errors among all eight members, the 12 UTC runs of the NAM CONUS Nest, HRRR, HRW ARW and HRW NSSL, and a time-lagged version of each, were between 100 and 150 km for the centroids of 24 h precipitation within the MCSs. No strong systematic errors exist consistently among all members in the direction of the displacement errors, although a weak tendency toward a north displacement is present in many members. Displacement error magnitudes tend to be largest in the southeastern portion of the United States, a region known for weakly forced summertime precipitation that results in low QPF skill.
Intensity errors were evaluated for the 10th, 50th, and 90th percentiles of precipitation at grid points within the precipitation objects identified by MODE. Negative errors are common for the 10th percentile, but this switches to positive errors for the heavier thresholds, except in the HRRR runs, which have errors near zero. The positive errors are most severe in the 12 UTC NAM CONUS Nest member, where they are around 8 mm, and statistically significantly worse than those of both HRRR members. The negative error at the 10th percentile is most pronounced in the southern regions, where it is significantly worse than in the northern regions in both HRRR members, and the positive error at the 50th percentile, albeit relatively small, is least intense in the southeast region. The northwest region is generally the wettest in the models, with either the greatest positive errors or smallest negative errors depending on the model and the intensity threshold.
Despite the positive errors generally present for the heaviest rainfall amounts in most models, the total system rainfall is underestimated by all models except the 12 UTC NSSL. A strong correlation is found between the total system rainfall and the areas of the objects. Thus, to a large extent, this underestimate of total system rainfall is due to an underestimate of the areal coverage of the objects.

5. Conclusions

Because the types of errors examined in the present study reflect different aspects of a forecast, it is difficult to determine if one type of error is more harmful to the forecast skill than another. Yet, such information is valuable for model developers to understand where the greatest needs are and where limited resources would best be used to improve QPF. The present study’s use of a state-of-the-art operational CAM ensemble could provide insights to facilitate improvements that would likely benefit weather forecasting well into the future.
Despite the challenge mentioned above, a rough idea of the relative importance of the different types of errors can be obtained by considering that the median footprint of 24 h precipitation from the MCSs in the present study has an area of roughly 100,000 km2, or 10,940 model grid boxes for the HREF. If one assumes a circle for the object, the diameter would be around 350 km, meaning the typical displacement errors are about 35% of the diameter of the objects. The median precipitation amount (50th percentile) for all grid points in the objects was 21.5 mm; thus the typical intensity errors at this threshold, roughly 1 mm, are only about 5% of the average rainfall amount. Finally, regarding areal coverage, the typical errors of roughly 1000 model grid boxes would be approximately 10% of the area of the observed objects.
This analysis would suggest that although errors in all these aspects of a rainfall forecast do contribute noticeably to the total QPF error, displacement errors may exert the greatest negative influence on forecast skill, and both forecasters and model developers may benefit from focusing their attention on the reasons for the large displacement errors in MCS forecasts. Object-based verification approaches should continue to be used to allow for the different types of errors to be isolated within QPFs. We also recommend an exploration of alternative ensemble designs that might mitigate the large but generally random displacement errors present in CAMs. In ongoing work, we investigate the use of artificial intelligence (AI) as a tool to anticipate displacement errors and correct them. Related to this, we are examining whether near-storm environmental weather conditions are correlated with specific directions or magnitudes of displacement error.

Author Contributions

Conceptualization, W.A.G.J. and K.J.F.; methodology, W.A.G.J. and K.J.F.; software, A.D.; validation, W.A.G.J., A.D. and K.J.F.; formal analysis, A.D. and T.F.; investigation, W.A.G.J., A.D. and K.J.F.; resources, W.A.G.J. and K.J.F.; data curation, A.D.; writing—original draft preparation, W.A.G.J., A.D. and K.J.F.; writing—review and editing, W.A.G.J. and K.J.F.; visualization, A.D. and T.F.; supervision, W.A.G.J. and K.J.F.; project administration, W.A.G.J. and K.J.F.; funding acquisition, W.A.G.J. and K.J.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by NOAA grant number NA23OAR4590377-T1-01.

Data Availability Statement

Data available in a publicly accessible repository that does not issue DOIs (https://meteor.geol.iastate.edu/~tyreek/Parsed_MODE_Output/, accessed on 15 July 2025).

Acknowledgments

Thanks are given to Kent Knopfmeier at NSSL for some assistance in finding the archived HREF output. Thanks are also given to the two anonymous reviewers who provided feedback that allowed the paper to be improved.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Ahmadalipour, A.; Moradkhani, H. A Data-Driven Analysis of Flash Flood Hazard, Fatalities, and Damages over the CONUS during 1996–2017. J. Hydrol. 2019, 578, 124106. [Google Scholar] [CrossRef]
  2. Cutter, S.L.; Emrich, C.T.; Gall, M.; Reeves, R. Flash Flood Risk and the Paradox of Urban Development. Nat. Hazards Rev. 2018, 19, 1–12. [Google Scholar] [CrossRef]
  3. Jirak, I.L.; Cotton, W.R.; McAnelly, R.L. Satellite and Radar Survey of Mesoscale Convective System Development. Mon. Weather Rev. 2003, 131, 2428–2449. [Google Scholar] [CrossRef]
  4. Stevenson, S.N.; Schumacher, R.S. A 10-Year Survey of Extreme Rainfall Events in the Central and Eastern United States Using Gridded Multisensor Precipitation Analyses. Mon. Weather Rev. 2014, 142, 3147–3162. [Google Scholar] [CrossRef]
  5. Hitchens, N.M.; Baldwin, M.E.; Trapp, R.J. An Object-Oriented Characterization of Extreme Precipitation-Producing Convective Systems in the Midwestern United States. Mon. Weather Rev. 2012, 140, 1356–1366. [Google Scholar] [CrossRef]
  6. Fritsch, J.M.; Kane, R.J.; Chelius, C.R. The Contribution of Mesoscale Convective Weather Systems to the Warm-Season Precipitation in the United States. J. Appl. Meteorol. Climatol. 1986, 25, 1333–1345. [Google Scholar] [CrossRef]
  7. Špitalar, M.; Gourley, J.J.; Lutoff, C.; Kirstetter, P.E.; Brilly, M.; Carr, N. Analysis of Flash Flood Parameters and Human Impacts in the US from 2006 to 2012. J. Hydrol. 2014, 519, 863–870. [Google Scholar] [CrossRef]
  8. Hugeback, K.K.; Franz, K.J.; Gallus, W.A. Short-Term Ensemble Streamflow Prediction Using Spatially Shifted QPF Informed by Displacement Errors. J. Hydrometeorol. 2023, 24, 21–34. [Google Scholar] [CrossRef]
  9. Adams, T.E., III; Dymond, R. The effect of QPF on real-time deterministic hydrologic forecast uncertainty. J. Hydrometeorol. 2019, 20, 1687–1705. [Google Scholar] [CrossRef]
  10. Seo, B.-C.; Quintero, F.; Krajewski, W.F. High-resolution QPF uncertainty and its implications for flood prediction: A case study for the Eastern Iowa flood of 2016. J. Hydrometeorol. 2018, 19, 1289–1304. [Google Scholar] [CrossRef]
  11. Olson, D.A.; Junker, N.W.; Korty, B. Evaluation of 33 Years of Quantitative Precipitation Forecasting at the NMC. Weather Forecast. 1995, 10, 498–511. [Google Scholar] [CrossRef]
  12. Fritsch, J.M.; Carbone, R.E. Improving Quantitative Precipitation Forecasts in the Warm Season: A USWRP Research and Development Strategy. Bull. Am. Meteorol. Soc. 2004, 85, 955–965. [Google Scholar] [CrossRef]
  13. Gallus, W.A., Jr. The Challenge of Warm-Season Convective Precipitation Forecasting. In Rainfall Forecasting; Wong, T.S.W., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2012; pp. 129–160. ISBN 978-61942-134-9. [Google Scholar]
  14. Keil, C.; Heinlein, J.; Craig, G.C. The convective adjustment time-scale as indicator of predictability of convective precipitation. Q. J. R. Meteorol Soc. 2014, 140, 480–490. [Google Scholar] [CrossRef]
  15. Wapler, K.; James, P. Thunderstorm occurrence and characteristics in Central Europe under different synoptic conditions. Atmos. Res. 2015, 158–159, 231–244. [Google Scholar] [CrossRef]
  16. Nielsen, E.R.; Schumacher, R.S. Using Convection-Allowing Ensembles to Understand the Predictability of an Extreme Rainfall Event. Mon. Weather Rev. 2016, 144, 3651–3676. [Google Scholar] [CrossRef]
  17. Stensrud, D.J.; Fritsch, J.M. Mesoscale Convective Systems in Weakly Forced Large-Scale Environments. Part II: Generation of a Mesoscale Initial Condition. Mon. Weather Rev. 1994, 122, 2068–2083. [Google Scholar] [CrossRef]
  18. Stensrud, D.J.; Fritsch, J.M. Mesoscale Convective Systems in Weakly Forced Large-Scale Environments. Part III: Numerical Simulations and Implications for Operational Forecasting. Mon. Weather Rev. 1994, 122, 2084–2104. [Google Scholar] [CrossRef]
  19. Gallus, W.A. Eta Simulations of Three Extreme Precipitation Events: Sensitivity to Resolution and Convective Parameterization. Weather Forecast. 1999, 14, 405–426. [Google Scholar] [CrossRef]
  20. Roberts, B.; Gallo, B.T.; Jirak, I.L.; Clark, A.J.; Dowell, D.C.; Wang, X.; Wang, Y. What Does a Convection-Allowing Ensemble of Opportunity Buy Us in Forecasting Thunderstorms? Weather Forecast. 2020, 35, 2293–2316. [Google Scholar] [CrossRef]
  21. Schwartz, C.S.; Kain, J.S.; Weiss, S.J.; Xue, M.; Bright, D.R.; Kong, F.; Thomas, K.W.; Levit, J.J.; Coniglio, M.C. Next-Day Convection-Allowing WRF Model Guidance: A Second Look at 2-km versus 4-km Grid Spacing. Mon. Weather Rev. 2009, 137, 3351–3372. [Google Scholar] [CrossRef]
  22. Kain, J.S.; Weiss, S.J.; Bright, D.R.; Baldwin, M.E.; Levit, J.J.; Carbin, G.W.; Schwartz, C.S.; Weisman, M.L.; Droegemeier, K.K.; Weber, D.; et al. Some Practical Considerations Regarding Horizontal Resolution in the First Generation of Operational Convection-Allowing NWP. Weather Forecast. 2008, 23, 931–952. [Google Scholar] [CrossRef]
  23. Clark, A.J.; Weiss, S.J.; Kain, J.S.; Jirak, I.L.; Coniglio, M.; Melick, C.J.; Siewert, C.; Sobash, R.A.; Marsh, P.T.; Dean, A.R.; et al. An Overview of the 2010 Hazardous Weather Testbed Experimental Forecast Program Spring Experiment. Bull. Am. Meteorol. Soc. 2012, 93, 55–74. [Google Scholar] [CrossRef]
  24. Thielen, J.E.; Gallus, W.A. Influences of Horizontal Grid Spacing and Microphysics on WRF Forecasts of Convective Morphology Evolution for Nocturnal MCSs in Weakly Forced Environments. Weather Forecast. 2019, 34, 1495–1517. [Google Scholar] [CrossRef]
  25. Gallus, W.A.; Harrold, M.A. Challenges in Numerical Weather Prediction of the 10 August 2020 Midwestern Derecho: Examples from the FV3-LAM. Weather Forecast. 2023, 38, 1429–1445. [Google Scholar] [CrossRef]
  26. Stelten, S.; Gallus, W.A. Pristine Nocturnal Convective Initiation: A Climatology and Preliminary Examination of Predictability. Weather Forecast. 2017, 32, 1613–1635. [Google Scholar] [CrossRef]
  27. Kiel, B.M.; Gallus, W.A.; Franz, K.J.; Erickson, N. A Preliminary Examination of Warm Season Precipitation Displacement Errors in the Upper Midwest in the HRRRE and HREF Ensembles. J. Hydrometeorol. 2022, 23, 1007–1024. [Google Scholar] [CrossRef]
  28. Kalina, E.A.; Jankov, I.; Alcott, T.; Olson, J.; Beck, J.; Berner, J.; Dowell, D.; Alexander, C. A Progress Report on the Development of the High-Resolution Rapid Refresh Ensemble. Weather Forecast. 2021, 36, 791–804. [Google Scholar] [CrossRef]
  29. Gallus, W.A. Application of Object-Based Verificaiton Techniques to Ensemble Precipitation Forecasts. Wea. Forecast. 2010, 25, 144–158. [Google Scholar] [CrossRef]
  30. Davis, C.A.; Brown, B.; Bullock, R. Object-Based Verification of Precipitation Forecasts. Part I: Application to Convective Rain Systems. Mon. Weather Rev. 2006, 134, 1785–1795. [Google Scholar] [CrossRef]
  31. Zhang, J.; Howard, K.; Langston, C.; Kaney, B.; Qi, Y.; Tang, L.; Grams, H.; Wang, Y.; Cockcks, S.; Martinaitis, S.; et al. Multi-Radar Multi-Sensor (MRMS) Quantitative Precipitation Estimation: Initial Operating Capabilities. Bull. Am. Meteorol. Soc. 2016, 97, 621–638. [Google Scholar] [CrossRef]
  32. Smith, T.M.; Lakshmanan, V.; Stumpf, G.J.; Ortega, K.L.; Hondl, K.; Cooper, K.; Calhoun, K.M.; Kingfield, D.M.; Manross, K.L.; Toomey, R.; et al. Multi-Radar Multi-Sensor (MRMS) Severe Weather and Aviation Products: Initial Operating Capabilities. Bull. Amer. Meteor. Soc. 2016, 97, 1617–1630. [Google Scholar] [CrossRef]
  33. Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.; Duda, M.G.; Powers, J.G. A Description of the Advanced Research WRF Version 3, NCAR Technical Note; National Center for Atmospheric Research: Boulder, CO, USA, 2008; p. 125. [Google Scholar]
  34. Janjic, Z.; Gall, R. Scientific Documentation of the NCEP Nonhydrostatic Multiscale Model on the B Grid (NMMB). Part 1 Dynamics; National Center for Atmospheric Research: Boulder, CO, USA, 2012; p. 75. [Google Scholar]
  35. Putman, W.M.; Lin, S.J. Finite-Volume Transport on Various Cubed-Sphere Grids. J. Comput. Phys. 2007, 227, 55–78. [Google Scholar] [CrossRef]
  36. Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell, D.C.; Grell, G.A.; et al. A North American Hourly Assimilation and Model Forecast Cycle: The Rapid Refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
  37. Zhou, X.; Juang, H.M.H. A Model Instability Issue in the National Centers for Environmental Prediction Global Forecast System Version 16 and Potential Solutions. Geosci. Model Dev. 2023, 16, 3263–3274. [Google Scholar] [CrossRef]
  38. Hong, S.Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
  39. Hong, S.; Lim, J. The WRF Single-Moment 6-Class Microphysics Scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
  40. Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
  41. Nakanishi, M.; Niino, H. Development of an Improved Turbulence Closure Model for the Atmospheric Boundary Layer. J. Meteorol. Soc. Jpn. 2009, 87, 895–912. [Google Scholar] [CrossRef]
  42. Janjić, Z.I. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
  43. Aligo, E.A.; Ferrier, B.; Jacob, R. Carley Modified NAM Microphysics for Forecasts of Deep Convective Storms. Mon. Weather Rev. 2018, 146, 4115–4153. [Google Scholar] [CrossRef]
  44. Mittermaier, M.P. Improving Short-range High-resolution Model Precipitation Forecast Skill Using Time-Lagged Ensembles. Q. J. R. Meteorol. Soc. 2007, 133, 1487–1500. [Google Scholar] [CrossRef]
  45. Nemenyi, P.B. Distribution-free Multiple Comparisons. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1963. [Google Scholar]
  46. Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
  47. Fisher, R.A. Statistical Methods for Research Workers. In Breakthroughs in Statistics: Methodology and Distribution; Springer: New York, NY, USA, 1970; pp. 66–70. [Google Scholar]
  48. Tukey, J. Comparing individual means in the Analysis of Variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef] [PubMed]
  49. Wade, A.R.; Jirak, I.L.; Lyza, A.W. Regional and Seasonal Biases in Convection-Allowing Model Forecasts of Near-Surface Temperature and Moisture. Weather Forecast. 2023, 38, 2415–2426. [Google Scholar] [CrossRef]
  50. Moore, B.J.; Mahoney, K.M.; Sukovich, E.M.; Cifelli, R.; Hamill, T.M. Climatology and Environmental Characteristics of Extreme Precipitation Events in the Southeastern United States. Mon. Weather Rev. 2015, 143, 718–741. [Google Scholar] [CrossRef]
Water 17 02168 g001
Figure 1. Distribution of cases used in this study for the 00 UTC ARW member of the HREF, showing the four regions of the United States (northwest, northeast, southwest, southeast) used for spatial analysis (defined relative to the 39° N latitude and 90° W longitude lines shown), and color-coded (see legend at upper right) by month.
Figure 1. Distribution of cases used in this study for the 00 UTC ARW member of the HREF, showing the four regions of the United States (northwest, northeast, southwest, southeast) used for spatial analysis (defined relative to the 39° N latitude and 90° W longitude lines shown), and color-coded (see legend at upper right) by month.
Water 17 02168 g001
Water 17 02168 g002
Figure 2. Boxplots of centroid displacement (km) of all HREF members, with median indicated by horizontal black line, and boxes showing values between the 25th and 75th percentiles. Number of cases for each HREF member is shown below each plot.
Figure 2. Boxplots of centroid displacement (km) of all HREF members, with median indicated by horizontal black line, and boxes showing values between the 25th and 75th percentiles. Number of cases for each HREF member is shown below each plot.
Water 17 02168 g002
Water 17 02168 g003
Figure 3. Scatterplots of the displacement (km) of the centroid for all models.
Figure 3. Scatterplots of the displacement (km) of the centroid for all models.
Water 17 02168 g003
Water 17 02168 g004
Figure 4. Median centroid displacement (km) of all models (see color legend at upper right) by region.
Figure 4. Median centroid displacement (km) of all models (see color legend at upper right) by region.
Water 17 02168 g004
Water 17 02168 g005
Figure 5. Median centroid displacement (km) of all models (see color legend at upper right) by month.
Figure 5. Median centroid displacement (km) of all models (see color legend at upper right) by month.
Water 17 02168 g005
Water 17 02168 g006
Figure 6. Boxplots of difference (intensity error) between the forecast and observed 10th percentile intensity (mm) for all models.
Figure 6. Boxplots of difference (intensity error) between the forecast and observed 10th percentile intensity (mm) for all models.
Water 17 02168 g006
Water 17 02168 g007
Figure 7. Difference (intensity error) between the forecast and observed 10th percentile intensity (mm) for all models by month.
Figure 7. Difference (intensity error) between the forecast and observed 10th percentile intensity (mm) for all models by month.
Water 17 02168 g007
Water 17 02168 g008
Figure 8. Boxplots of difference (intensity error) between the forecast and observed 10th percentile intensity (mm) for all models by region.
Figure 8. Boxplots of difference (intensity error) between the forecast and observed 10th percentile intensity (mm) for all models by region.
Water 17 02168 g008
Water 17 02168 g009
Figure 9. As in Figure 6, except showing the 50th percentile intensity.
Figure 9. As in Figure 6, except showing the 50th percentile intensity.
Water 17 02168 g009
Water 17 02168 g010
Figure 10. As in Figure 8, except for showing the 50th percentile intensity.
Figure 10. As in Figure 8, except for showing the 50th percentile intensity.
Water 17 02168 g010
Water 17 02168 g011
Figure 11. As in Figure 6, except showing 90th percentile intensity.
Figure 11. As in Figure 6, except showing 90th percentile intensity.
Water 17 02168 g011
Water 17 02168 g012
Figure 12. As in Figure 7, except showing 90th percentile intensity.
Figure 12. As in Figure 7, except showing 90th percentile intensity.
Water 17 02168 g012
Water 17 02168 g013
Figure 13. As in Figure 8, except showing the 90th percentile intensity.
Figure 13. As in Figure 8, except showing the 90th percentile intensity.
Water 17 02168 g013
Water 17 02168 g014
Figure 14. Scatterplot of mean area errors (9 km2 model grid boxes) and mean total system rainfall errors (mm) for the eight HREF members (see color legend at upper left).
Figure 14. Scatterplot of mean area errors (9 km2 model grid boxes) and mean total system rainfall errors (mm) for the eight HREF members (see color legend at upper left).
Water 17 02168 g014
Water 17 02168 g015
Figure 15. Boxplots of differences between the forecasted and observed system area (9 km2 model grid boxes) for all models (see color bar at right) by region.
Figure 15. Boxplots of differences between the forecasted and observed system area (9 km2 model grid boxes) for all models (see color bar at right) by region.
Water 17 02168 g015
Table 1. p-values for differences between the models for errors in the 10th percentile of intensity (mm), with values less than 0.05 in bold. Numbers in the model names refer to time in UTC.
Table 1. p-values for differences between the models for errors in the 10th percentile of intensity (mm), with values less than 0.05 in bold. Numbers in the model names refer to time in UTC.
ARW_0ARW_12HRRR_12HRRR_6NAM_0NAM_12NSSL_0NSSL_12
ARW_0
ARW_120.978
HRRR_120.8840.284
HRRR_60.2280.0150.959
NAM_00.0010.045<0.001<0.001
NAM_12<0.0010.002<0.001<0.0010.984
NSSL_00.9941.0000.4010.0290.024<0.001
NSSL_120.3160.9050.008<0.0010.6300.1200.819
Table 2. p-values for differences between the models for errors in the 90th percentile intensity (mm) with values less than 0.05 in bold. Numbers in the model name refer to times in UTC.
Table 2. p-values for differences between the models for errors in the 90th percentile intensity (mm) with values less than 0.05 in bold. Numbers in the model name refer to times in UTC.
ARW_0ARW_12HRRR_12HRRR_6NAM_0NAM_12NSSL_0NSSL_12
ARW_0
ARW_120.819
HRRR_120.9150.112
HRRR_60.138<0.0010.860
NAM_00.8191.0000.112<0.001
NAM_120.3660.9970.014<0.0010.997
NSSL_00.8840.0901.0000.8950.0900.010
NSSL_120.9870.9990.3830.0090.9990.9050.332
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gallus, W.A., Jr.; Duhachek, A.; Franz, K.J.; Frazier, T. A Climatology of Errors in HREF MCS Precipitation Objects. Water 2025, 17, 2168. https://doi.org/10.3390/w17152168

AMA Style

Gallus WA Jr., Duhachek A, Franz KJ, Frazier T. A Climatology of Errors in HREF MCS Precipitation Objects. Water. 2025; 17(15):2168. https://doi.org/10.3390/w17152168

Chicago/Turabian Style

Gallus, William A., Jr., Anna Duhachek, Kristie J. Franz, and Tyreek Frazier. 2025. "A Climatology of Errors in HREF MCS Precipitation Objects" Water 17, no. 15: 2168. https://doi.org/10.3390/w17152168

APA Style

Gallus, W. A., Jr., Duhachek, A., Franz, K. J., & Frazier, T. (2025). A Climatology of Errors in HREF MCS Precipitation Objects. Water, 17(15), 2168. https://doi.org/10.3390/w17152168

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop