Development of Open-Source Tools for Event-Based Hydrological Modelling Using GIS and Python
Abstract
1. Introduction
2. Materials and Methods
2.1. GIS Operations
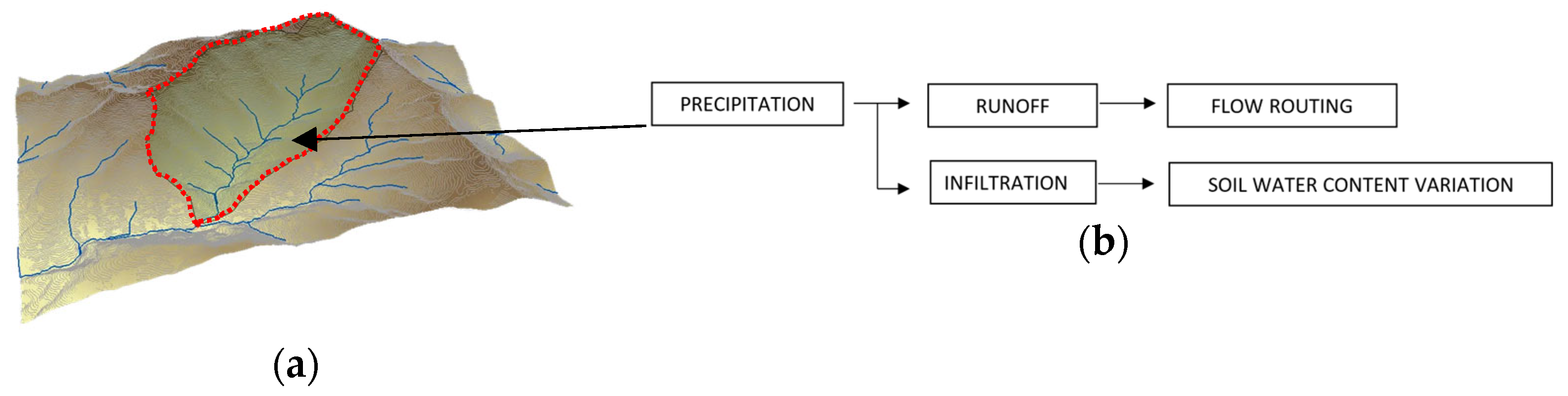
2.2. Integration with Hydrological Models
- Land uses, soil physical properties and soil moisture influencing infiltration/abstractions generation.
- Topographical information for delineating catchments and determining the transient time and flow routing downstream.
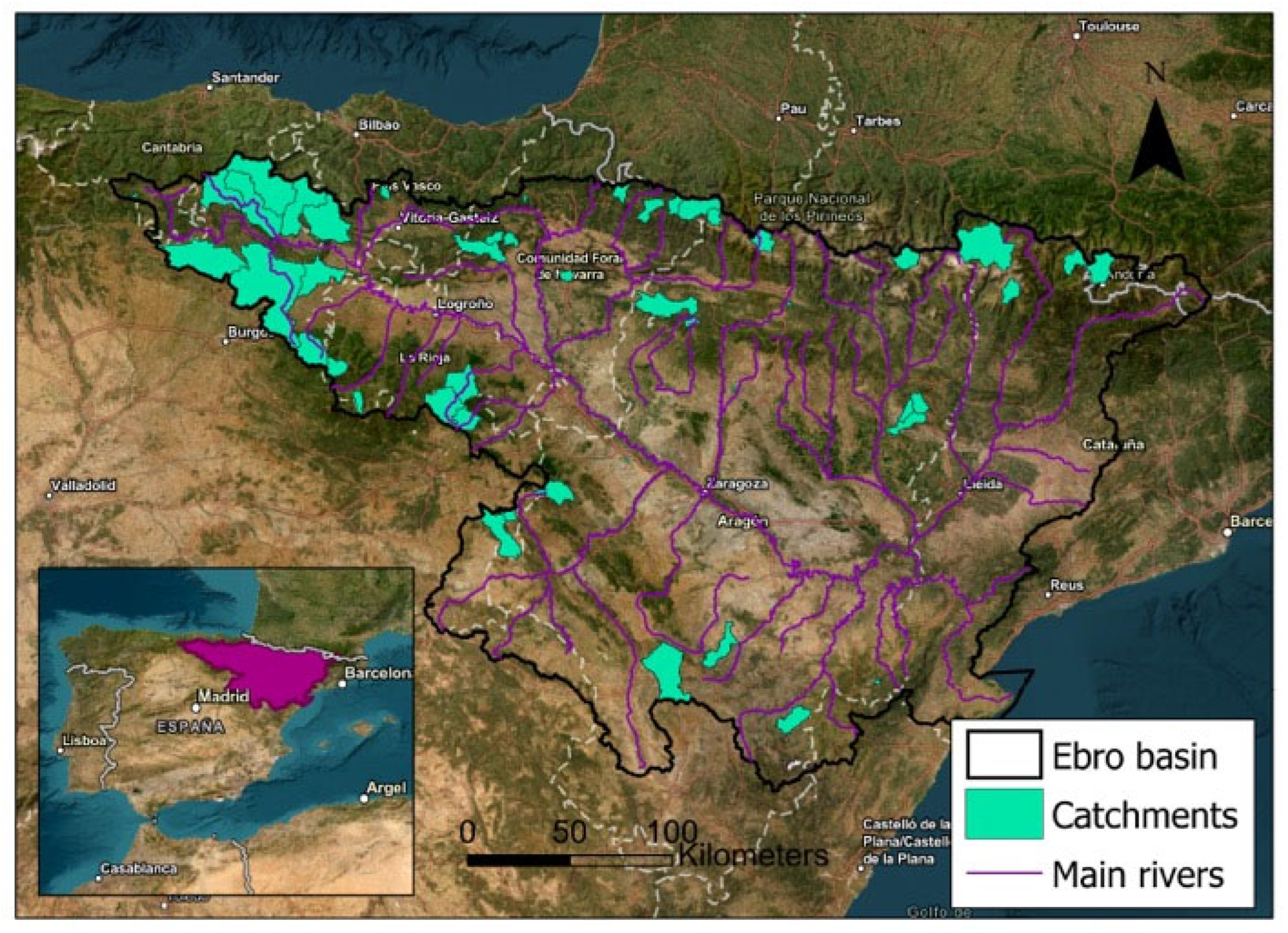
2.3. Case Study
3. Results and Discussion
3.1. GIS-Based Processes
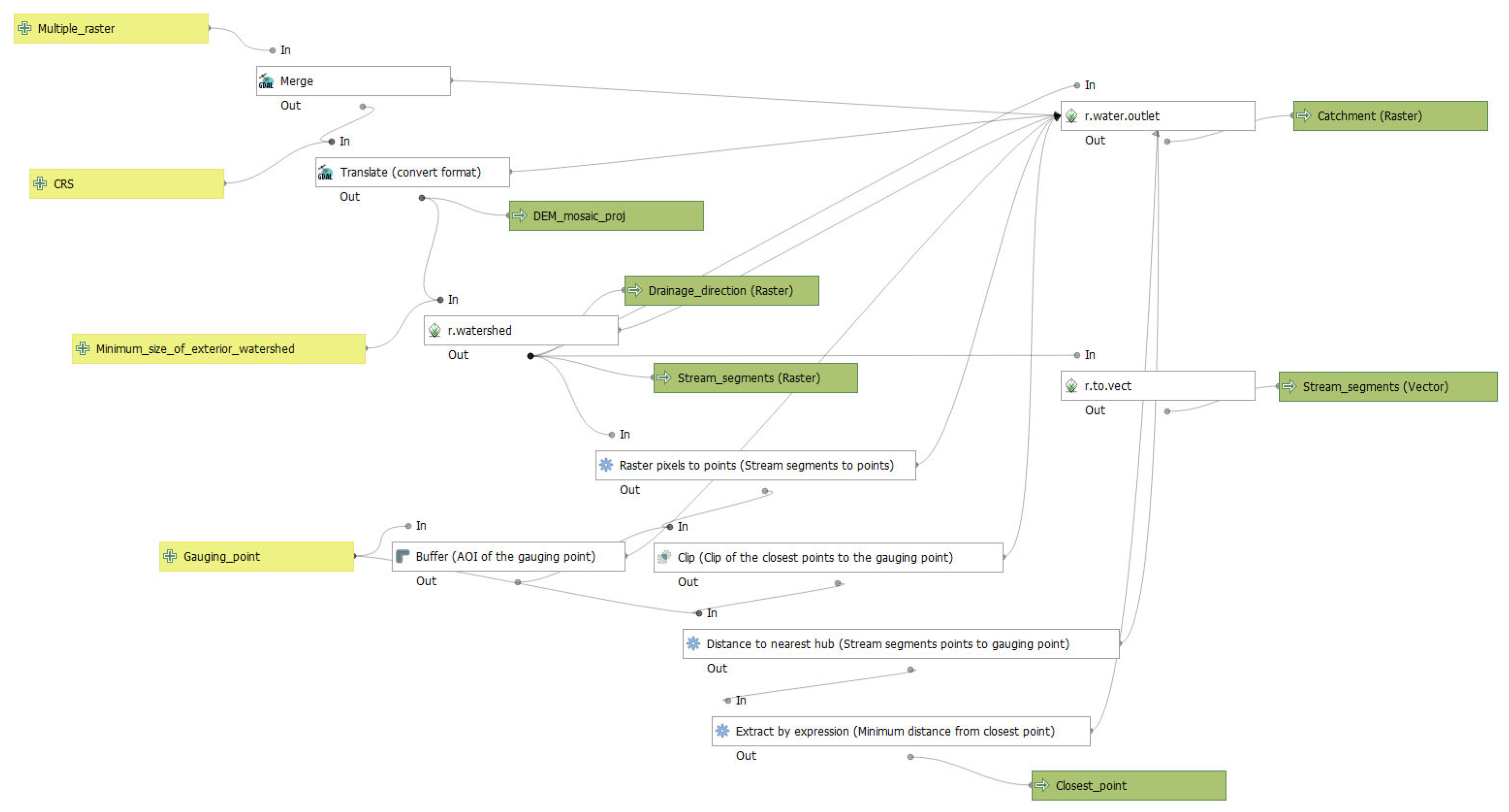
3.1.1. Catchment Delineation
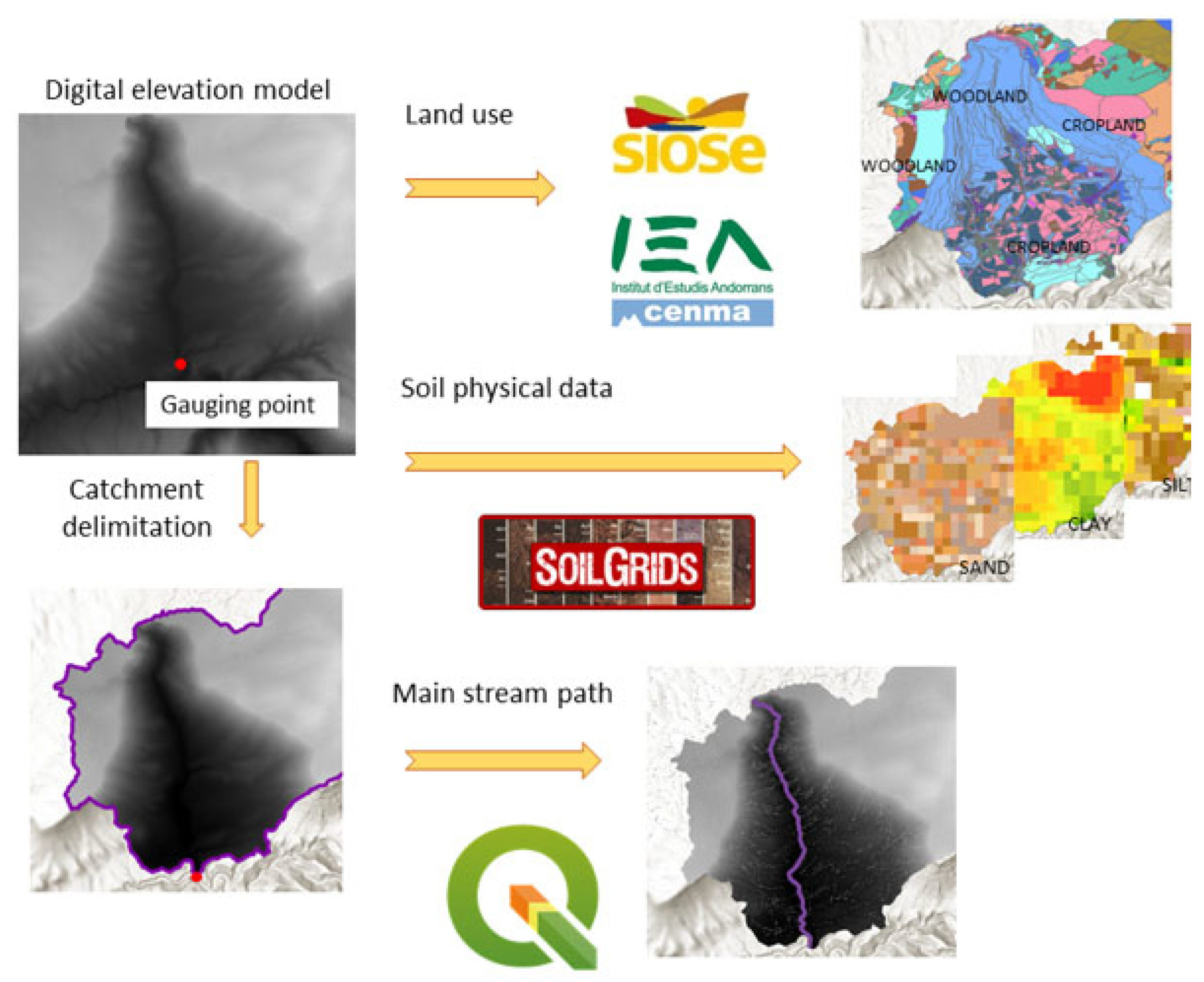
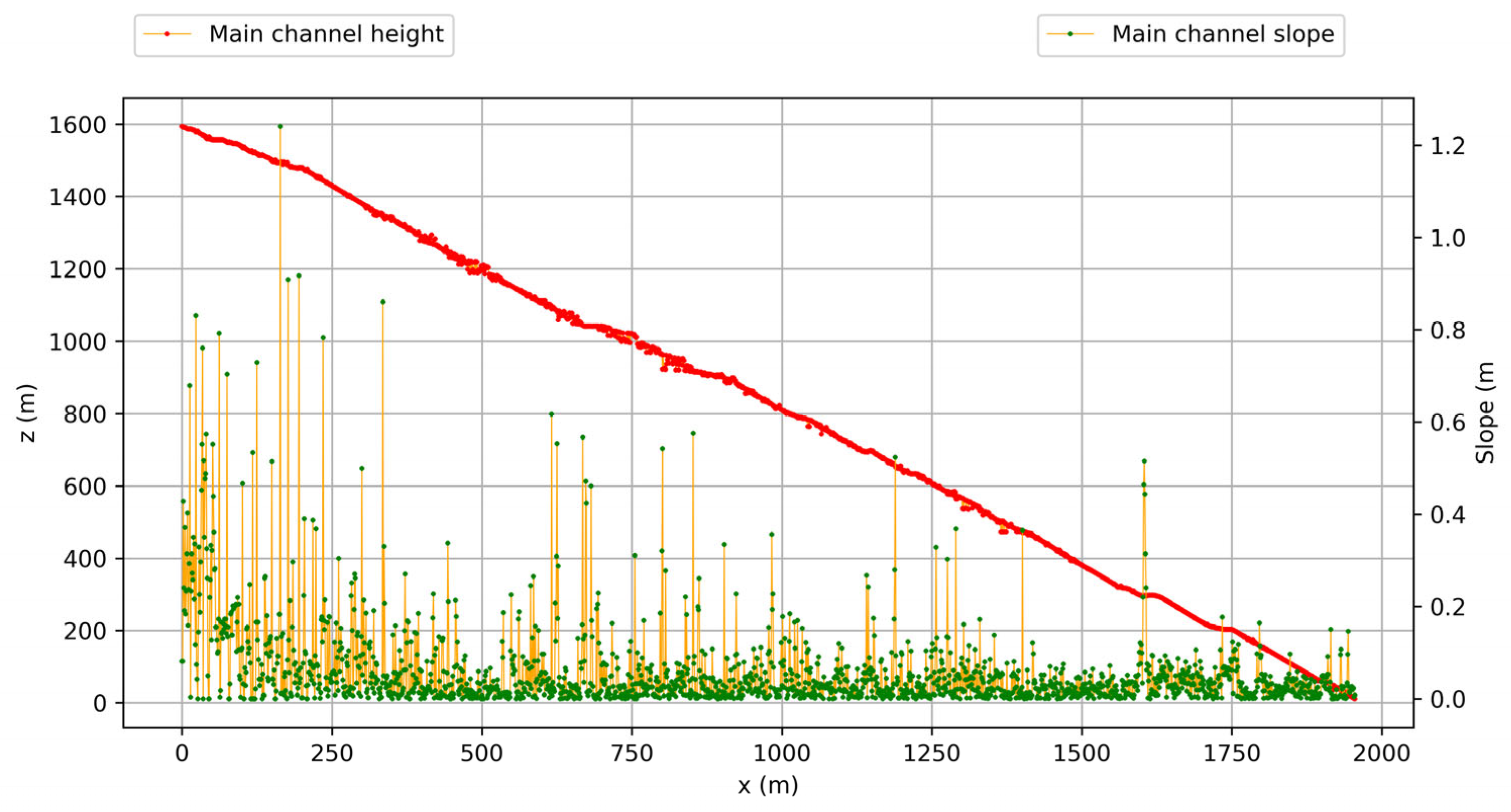
3.1.2. Topography and Land Uses
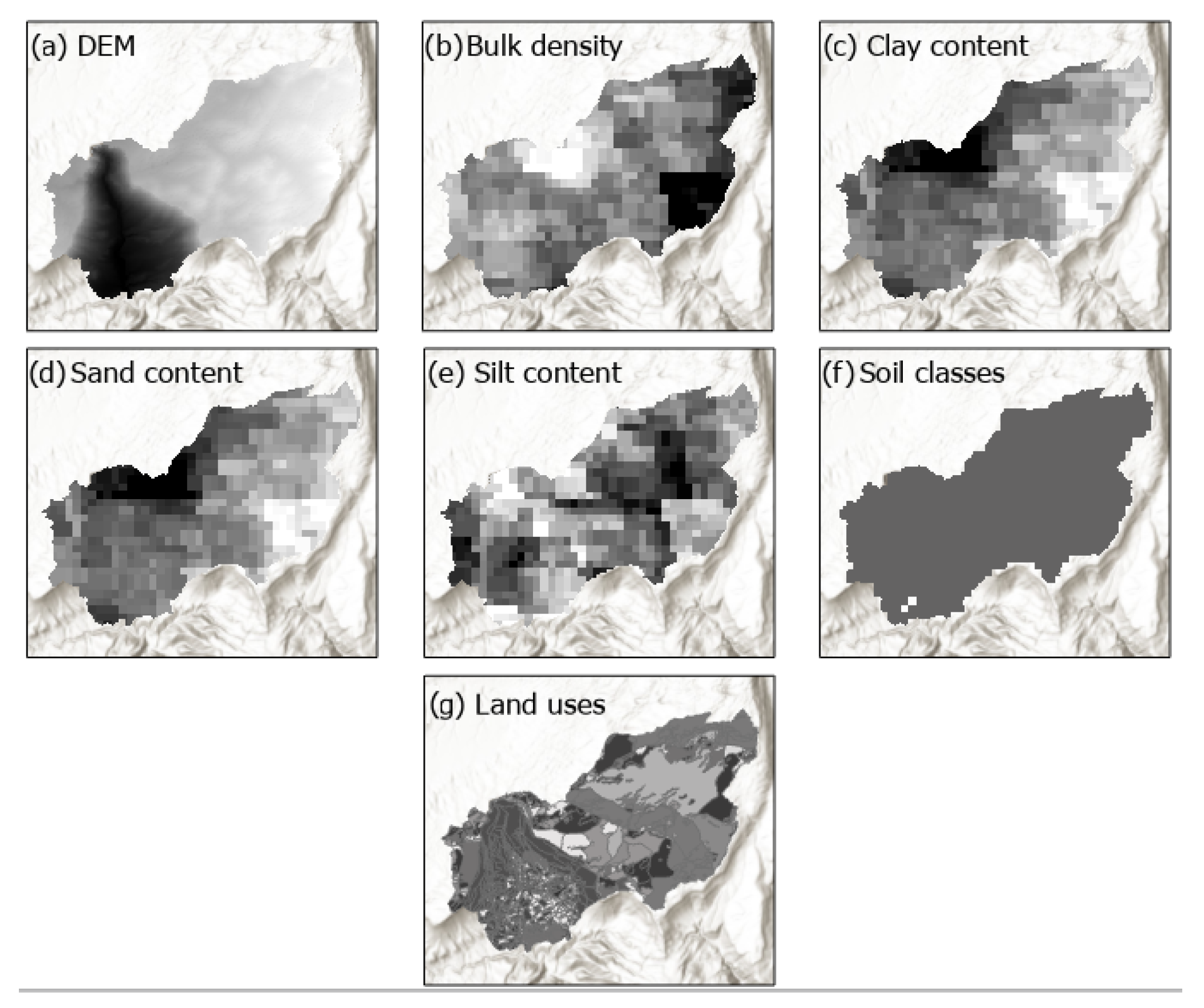
3.1.3. Spatial Homogenisation
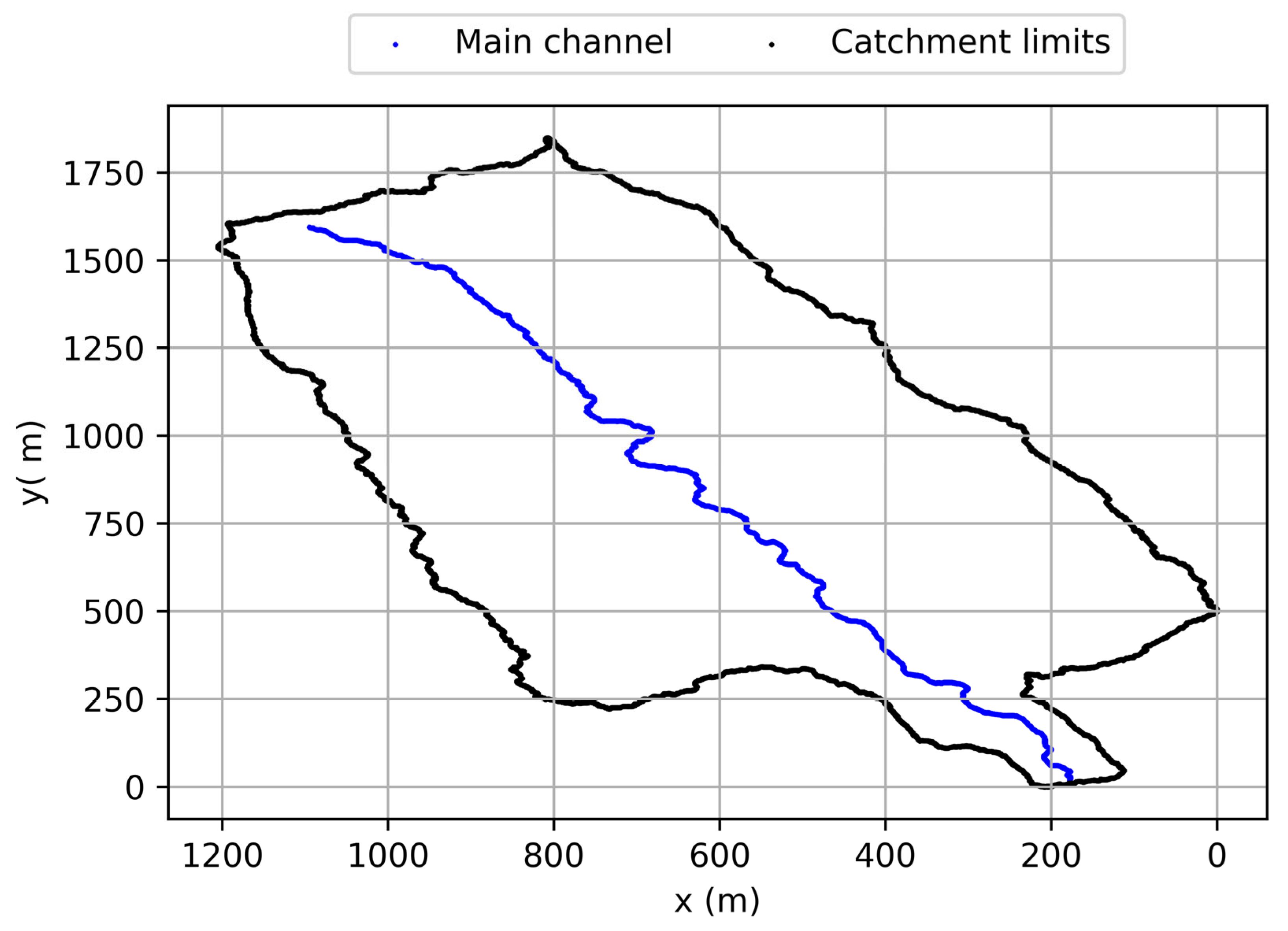
3.1.4. Flow Pathways
3.1.5. Catchment Characterisation and Exchangeable Files
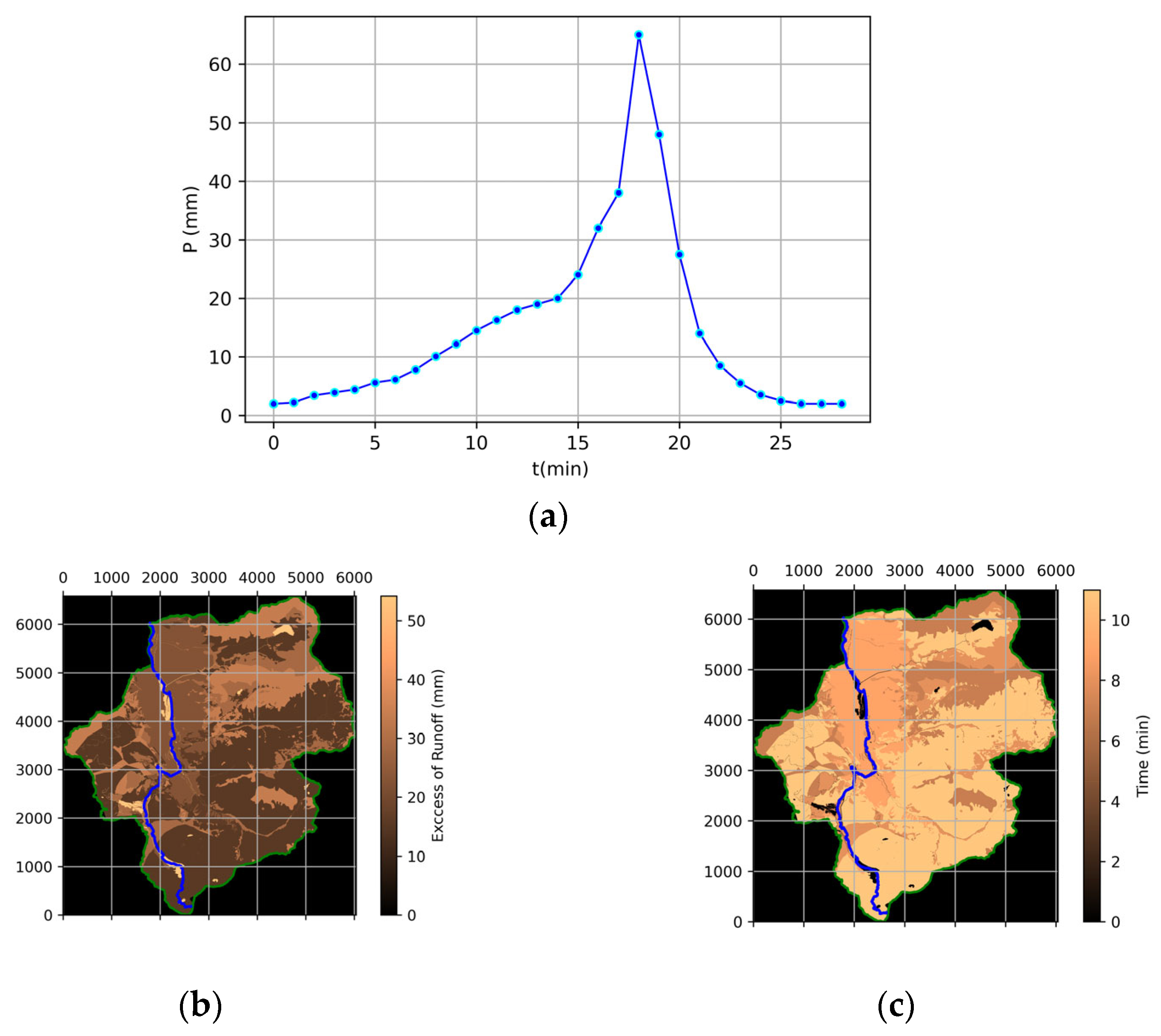
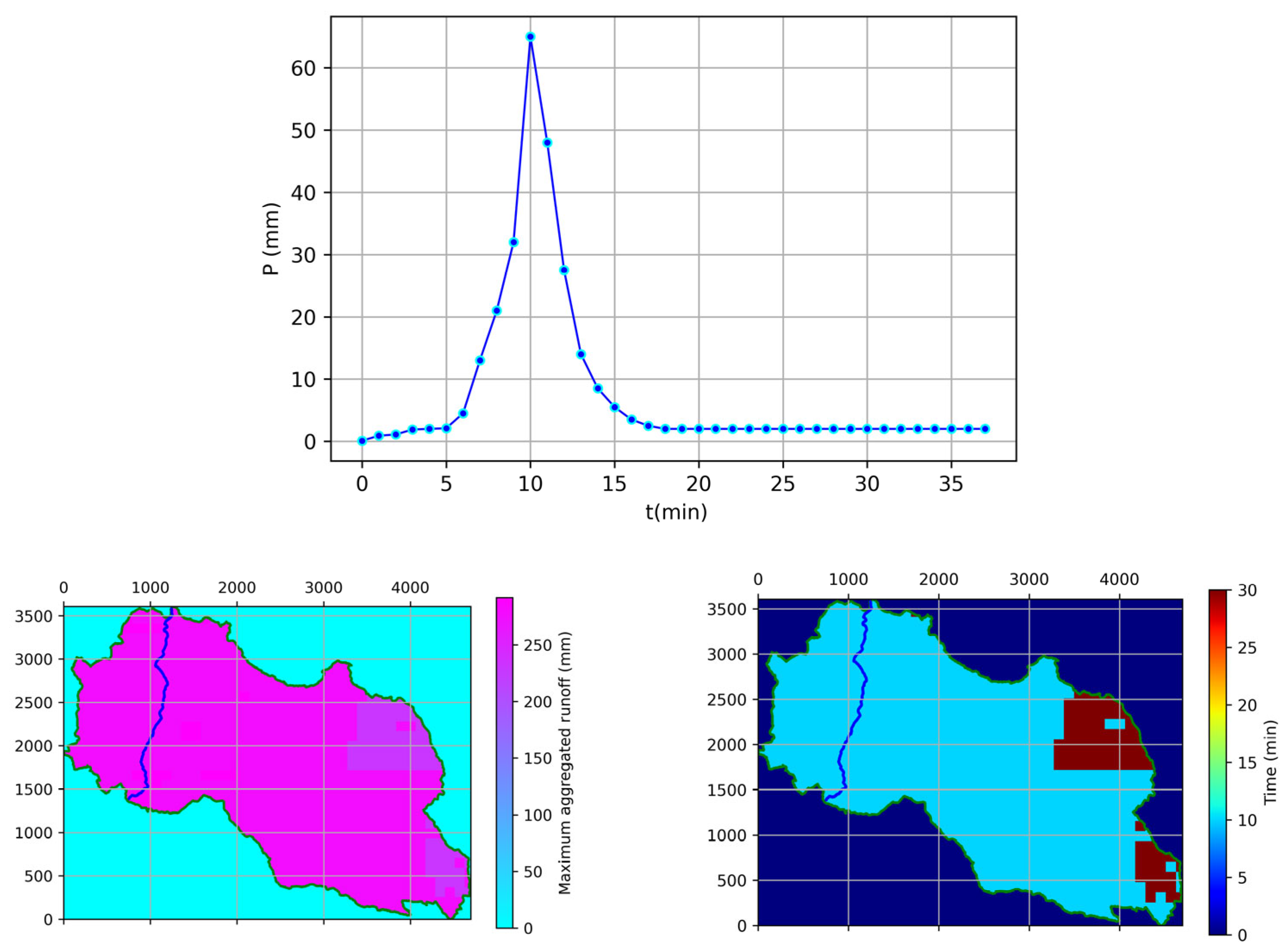
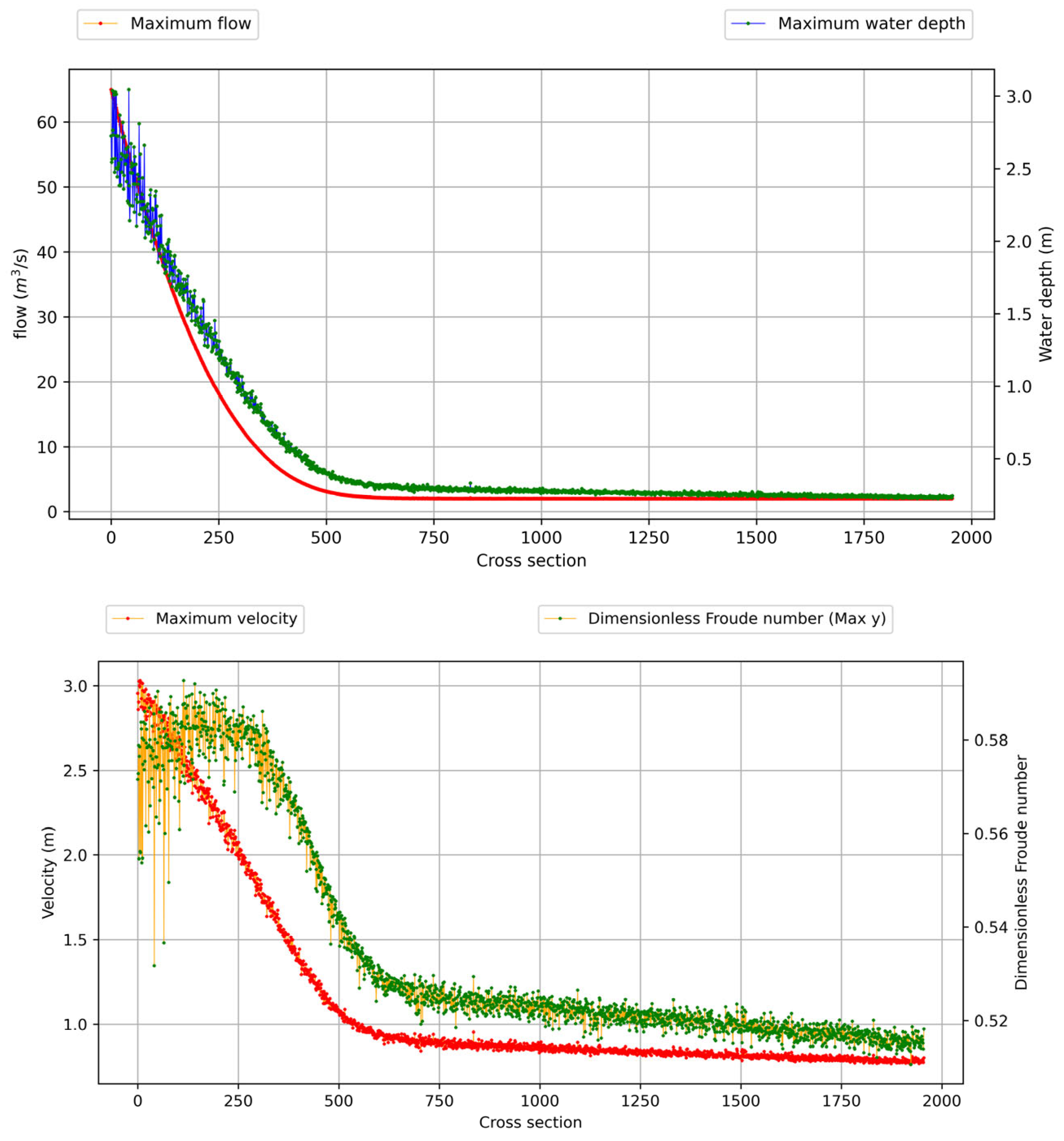
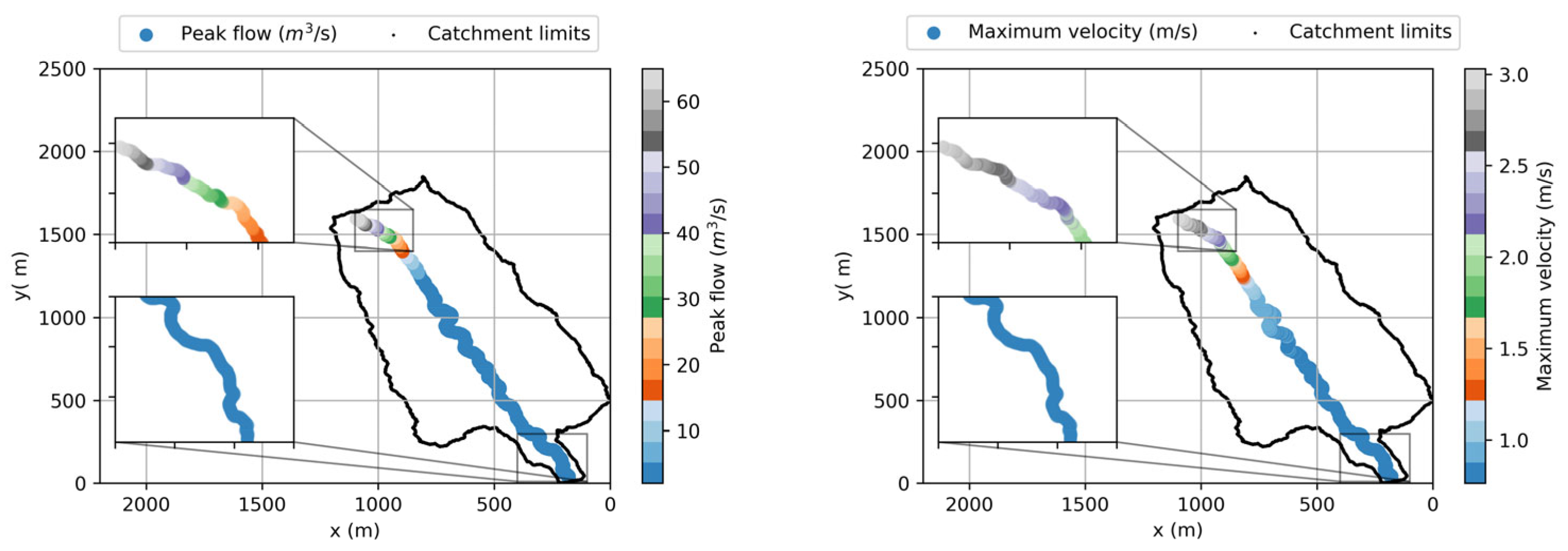
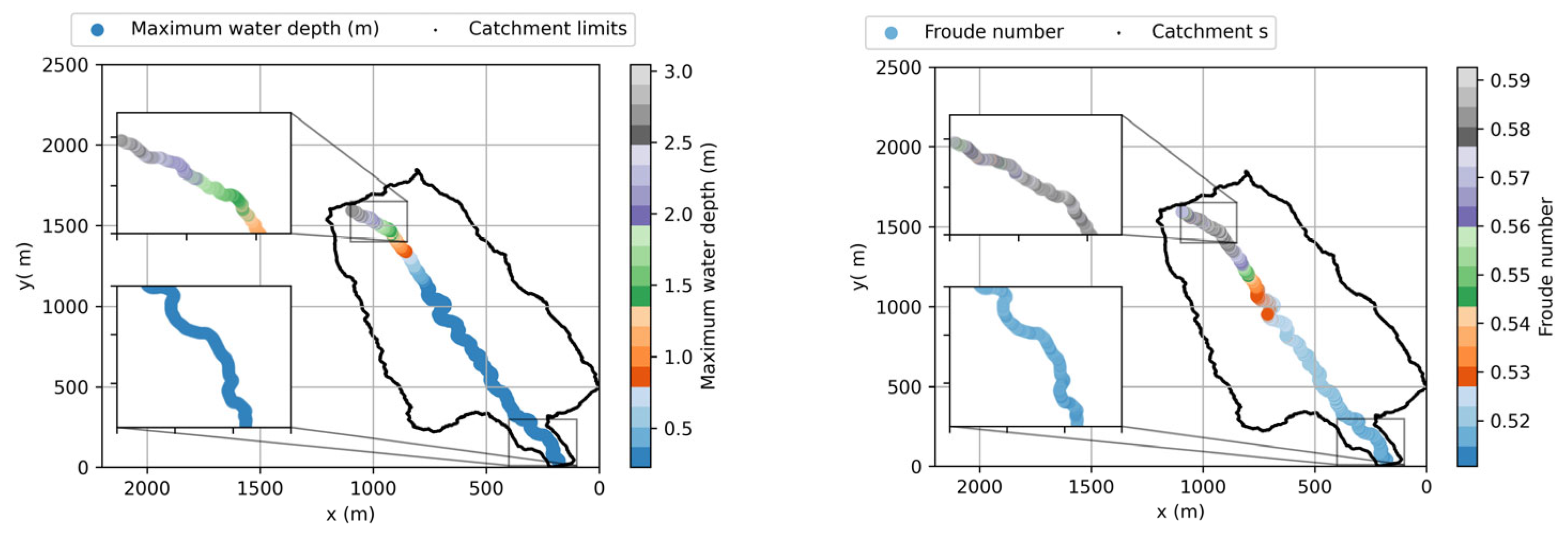
3.2. General Overview and Application Example
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herrera, P.A.; Marazuela, M.A.; Hofmann, T. Parameter estimation and uncertainty analysis in hydrological modeling. Wiley Interdiscip. Rev. Water 2022, 9, e1569. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43, 1–18. [Google Scholar] [CrossRef]
- Oreskes, N.; Shrader-Frechette, K.; Belitz, K. Verification, Validation, and Confirmation of Numerical Models in the Earth Sciences. Science 1979, 263, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Hrozencik, R.A.; Manning, D.T.; Suter, J.F.; Goemans, C.; Bailey, R.T. The Heterogeneous Impacts of Groundwater Management Policies in the Republican River Basin of Colorado. Water Resour. Res. 2017, 53, 10757–10778. [Google Scholar] [CrossRef]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Wada, Y.; Bierkens, M.F.P.; de Roo, A.; Dirmeyer, P.A.; Famiglietti, J.S.; Hanasaki, N.; Konar, M.; Liu, J.; Müller Schmied, H.; Oki, T.; et al. Human-water interface in hydrological modelling: Current status and future directions. Hydrol. Earth Syst. Sci. 2017, 21, 4169–4193. [Google Scholar] [CrossRef]
- Chang, F.-J.; Wang, Y.-C.; Tsai, W.P. Modelling Intelligent Water Resources Allocation for Multi-users. Water Resour. Manag. 2016, 30, 1395–1413. [Google Scholar] [CrossRef]
- Letcher, R.A.; Croke, B.F.W.; Jakeman, A.J. Integrated assessment modelling for water resource allocation and management: A generalised conceptual framework. Environ. Model. Softw. 2007, 22, 733–742. [Google Scholar] [CrossRef]
- Nousiainen, R.; Warsta, L.; Turunen, M.; Huitu, H.; Koivusalo, H.; Pesonen, L. Analyzing subsurface drain network performance in an agricultural monitoring site with a three-dimensional hydrological model. J. Hydrol. 2015, 529, 82–93. [Google Scholar] [CrossRef]
- Ursulak, J.; Coulibaly, P. Integration of hydrological models with entropy and multi-objective optimization based methods for designing specific needs streamflow monitoring networks. J. Hydrol. 2021, 593, 125876. [Google Scholar] [CrossRef]
- Hagemann, S.; Chen, C.; Clark, D.B.; Folwell, S.; Gosling, S.N.; Haddeland, I.; Hanasaki, N.; Heinke, J.; Ludwig, F.; Voss, F.; et al. Climate change impact on available water resources obtained using multiple global climate and hydrology models. Earth Syst. Dyn. 2013, 4, 129–144. [Google Scholar] [CrossRef]
- Xu, C.Y. Modelling the effects of climate change on water resources in central Sweden. Water Res. Manag. 2000, 14, 177–189. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Massari, C.; Crow, W.; Brocca, L. An assessment of the accuracy of global rainfall estimates without groundbased observations. Hydrol. Earth Syst. Sci. 2017, 21, 4347–4361. [Google Scholar] [CrossRef]
- Manfreda, S.; Caylor, K.K.; Good, S.P. An ecohydrological framework to explain shifts in vegetation organization across climatological gradients. Ecohydrology 2017, 10, e1809. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, H.; Tong, C.; Liu, W.; Du, B.T. Evaluation of ESA Active, Passive and Combined Soil Moisture Products Using Upscaled Ground Measurements. Sensors 2019, 19, 2718. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Mao, K.; Meng, F.; Shen, X.; Xu, T.; Cao, M. Long-Term Spatiotemporal Variations in Soil Moisture in North East China Based on 1-km Resolution Downscaled PassiveMicrowave Soil Moisture Products. Sensors 2019, 19, 3527. [Google Scholar] [CrossRef] [PubMed]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Castellví, F.; Cammalleri, C.; Ciraolo, G.; Maltese, A.; Rossi, F. Daytime sensible heat flux estimation over heterogeneous surfaces using multitemporal land-surface temperature observations. Water Resour. Res. 2016, 52, 3457–3476. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Domeneghetti, A. Exploiting the proliferation of current and future satellite observations of rivers. Hydrol. Process. 2016, 30, 2891–2896. [Google Scholar]
- Domeneghetti, A.; Castellarin, A.; Tarpanelli, A.; Moramarco, T. Investigating the uncertainty of satellite altimetry products for hydrodynamic modelling. Hydrol. Process. 2008, 29, 4908–4918. [Google Scholar] [CrossRef]
- Schneider, R.; Godiksen, P.N.; Villadsen, H.; Madsen, H.; Bauer-Gottwein, P. Application of CryoSat-2 altimetry data for river analysis and modelling. Hydrol. Earth Syst. Sci. 2017, 21, 751–764. [Google Scholar] [CrossRef]
- Tourian, M.J.; Tarpanelli, A.; Elmi, O.; Qin, T.; Brocca, L.; Moramarco, T.; Sneeuw, N. Spatiotemporal densification of river water level time series by multimission satellite altimetry. Water Resour. Res. 2016, 52, 1140–1159. [Google Scholar] [CrossRef]
- Schumann, A.H.; Funke, R.; Schultz, G.A. Application of a geographic information system for conceptual rainfall–runoff modeling. J. Hydrol. 2000, 240, 45–61. [Google Scholar] [CrossRef]
- Durand, M.; Andreadis, K.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Moller, D.; Wilson, M. Estimation of bathymetric depth and slope from data assimilation of swath altimetry into a hydrodynamic model. Geophys. Res. Lett. 2008, 10, L20401. [Google Scholar] [CrossRef]
- Schlosser, C.A.; Houser, P.R. Assessing a satellite-era perspective of the global water cycle. J. Clim. 2017, 20, 1316–1338. [Google Scholar] [CrossRef]
- Levizzani, V.; Cattani, E. Satellite remote sensing of precipitation and the terrrestrial water cycle in a changing climate. Remote Sens. 2019, 11, 2301. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G.; Maggioni, V.; Chambon, P.; Oki, R. The global satellite precipitation constellation: Current status and future requirement. Bull. Amer. Meteorol. Soc. 2021, 102, E1844–E1861. [Google Scholar] [CrossRef]
- Fang, J.; Yang, W.; Luan, Y.; Du, J.; Lin, A.; Zhao, L. Evaluation of the TRMM 3B42 and GPMIMERG products for extreme precipitation analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.S.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Chen, H.; Yong, B.; Shen, Y.; Liu, J.; Hong, Y.; Zhang, J. Comparison analysis of six purely satellite-derived global precipitation estimates. J. Hydrol. 2020, 581, 124376. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Güntner, A.; Hübner, C.; Kusche, J.; Jonard, F.; Vey, S.; Vereecken, H. Emerging methods for noninvasive sensing of soil moisture dynamics from field to catchment scale: A review. WIREs Water 2015, 2, 635–647. [Google Scholar] [CrossRef]
- Jain, M.K.; Kothyari, U.C.; Raju, K.G.R. A GIS based distributed rainfall–runoff model. J. Hydrol. 2004, 299, 107–135. [Google Scholar] [CrossRef]
- Zollweg, J.A.; Gburek, W.J.; Steenhuis, T.S. SMoRMod—A GIS-integrated rainfall-runoff model. Trans. ASAE 1996, 39, 1299–1307. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on soil physics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Cunge, J.A. On the subject of a flood propagation computation method (Muskingum method). J. Hydraul. Res. 1969, 7, 205–230. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L. Applied Hydrology; McGrawHill: New York, NY, USA, 1988. [Google Scholar]
- Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Mualem, Y. Hydraulic conductivity of unsaturated soils: Prediction and formulas. Methods Soil Anal. Part 1 Phys. Mineral. Methods 1986, 5, 799–823. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Maidment, D.R. ArcHydro: GIS for Water Resources; ESRI Press: Redlands, CA, USA, 2002. [Google Scholar]
- USACE. HEC-GeoHMS User’s Manual, Version 4.2; U.S. Army Corps of Engineers; Hydrologic Engineering Center: Davis, CA, USA, 2009.
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Kirpich, Z.P. Time of concentration of small agricultural watersheds. Civ. Civil. Eng. 1940, 10, 362. [Google Scholar]
- NRCS (National Research Conservation Service). Ponds—Planning, Design, Construction; Agriculture Handbook no 590; US Natural Resources Conservation Service: Washington DC, USA, 1997.
- Giandotti, M. Previsione Delle Piene e Delle Magre dei Corsid’acqua; Istituto Poligrafico dello Stato: Rome, Italy, 1934; Volume 8, pp. 107–117.
- Johnstone, D.; Cross, W.P. Elements of Applied Hydrology; Ronald Press: New York, NY, USA, 1949. [Google Scholar]
- Philip, J.R. Theory of infiltration. Adv. Hydrosci. 1969, 5, 215–305. [Google Scholar]
- Horton, R.E. An approach toward physical interpretation of infiltration capacity. Soil Sci. Soc. Am. Proc. 1940, 5, 399–417. [Google Scholar] [CrossRef]
- Ross, P.J.; Haverkamp, R.; Parlange, J.Y. Calculating parameters for infiltration equations from soil hydraulic functions. Transp. Porous Media 1996, 24, 315–339. [Google Scholar] [CrossRef]
- Brutsaert, W. Vertical infiltration in dry soil. Water Resour. Res. 1977, 13, 363–368. [Google Scholar] [CrossRef]
- Smith, R.E.; Parlange, J.Y. A parameter-efficient hydrologic infiltration model. Water Resour. Res. 1978, 14, 533–538. [Google Scholar] [CrossRef]



| Steps | Inputs | Outputs | Tools |
|---|---|---|---|
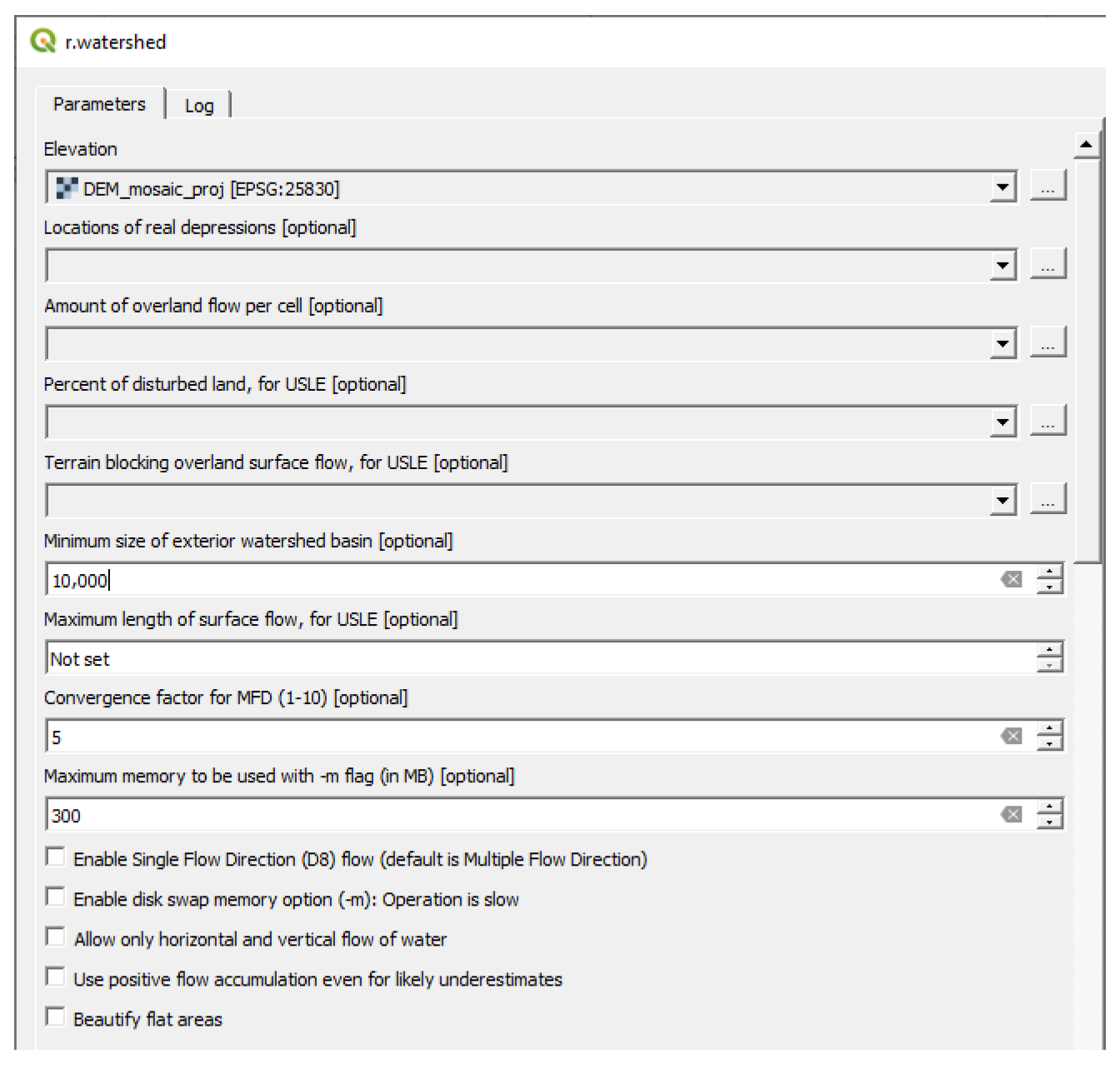
| Catchment delineation Model: 1. Catchment_delimitation | DEM rasters, coordinate reference system (CRS), minimum size of watershed and gauging point | DEM_mosaic (raster), drainage_direction (raster), stream_segments (raster) and catchment area (raster) | QGIS (raster pixel to points, clip, distance to the nearest hub, extract by expression), GDAL (merge, translate), GRASS (r.watershed, r.water.outlet and r.to.vect) |
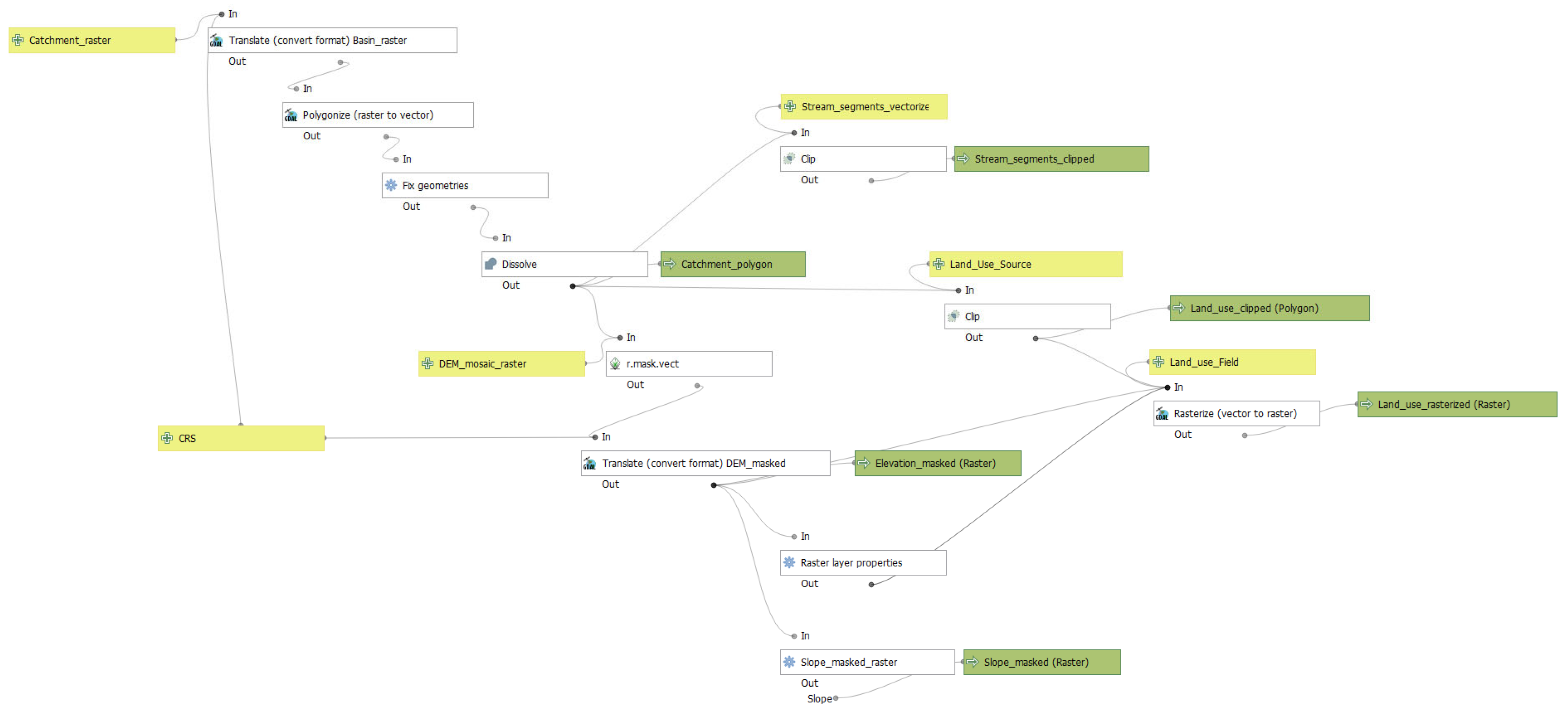
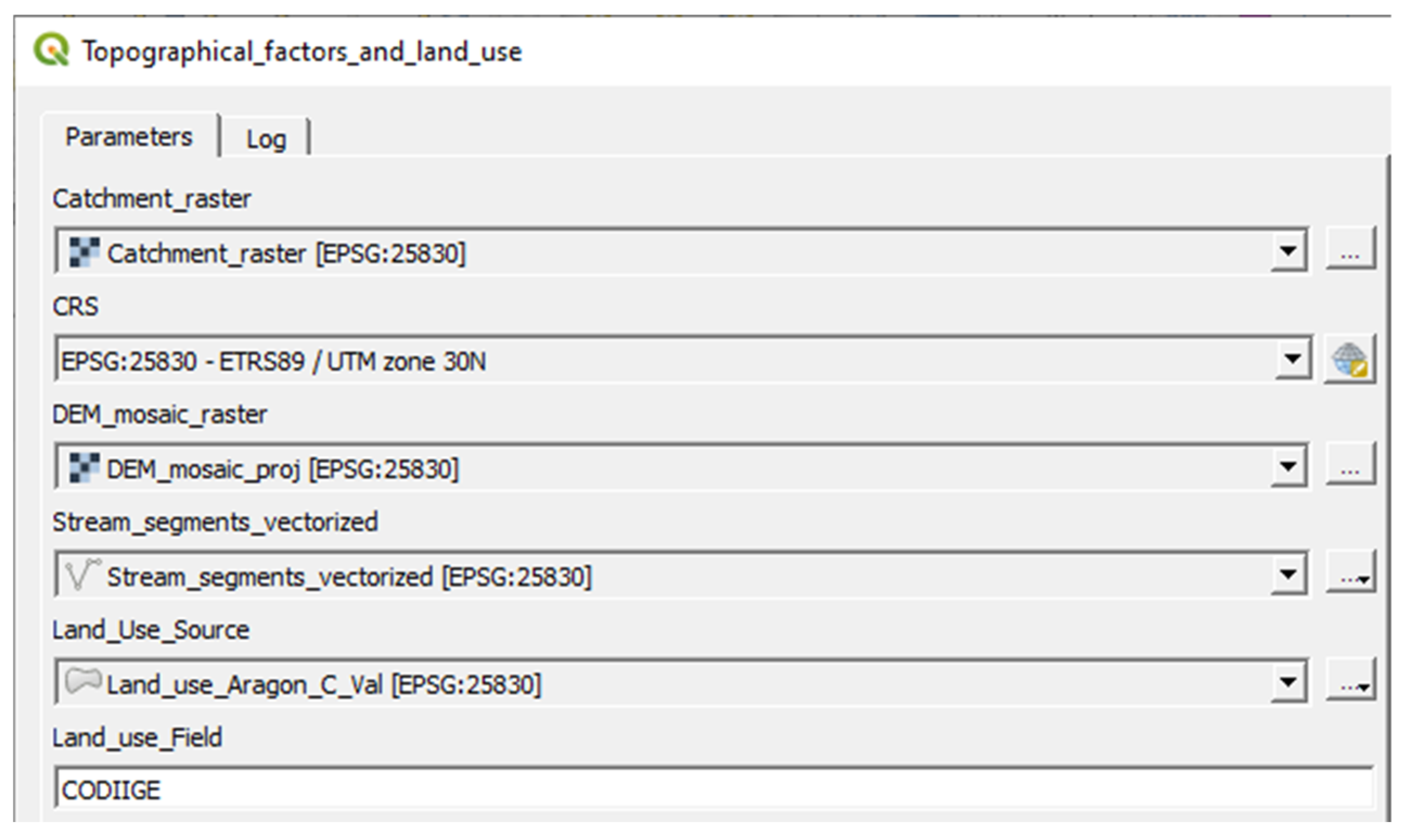
| Topography and land use Model: 2. Topographical_factors_and_land_use | Catchment (raster), CRS, DEM_mosaic (Raster), Land use source (polygon), stream_segments (raster) | Catchment (polygon vector layer), Elevation (Raster), Slope (Raster), Land_use (Polygon—vector—and raster), stream_segments (vector) | QGIS (dissolve, slope, clip and raster layer properties), GDAL (translate, olygonise and rasterise), GRASS (r.mask.vect) |
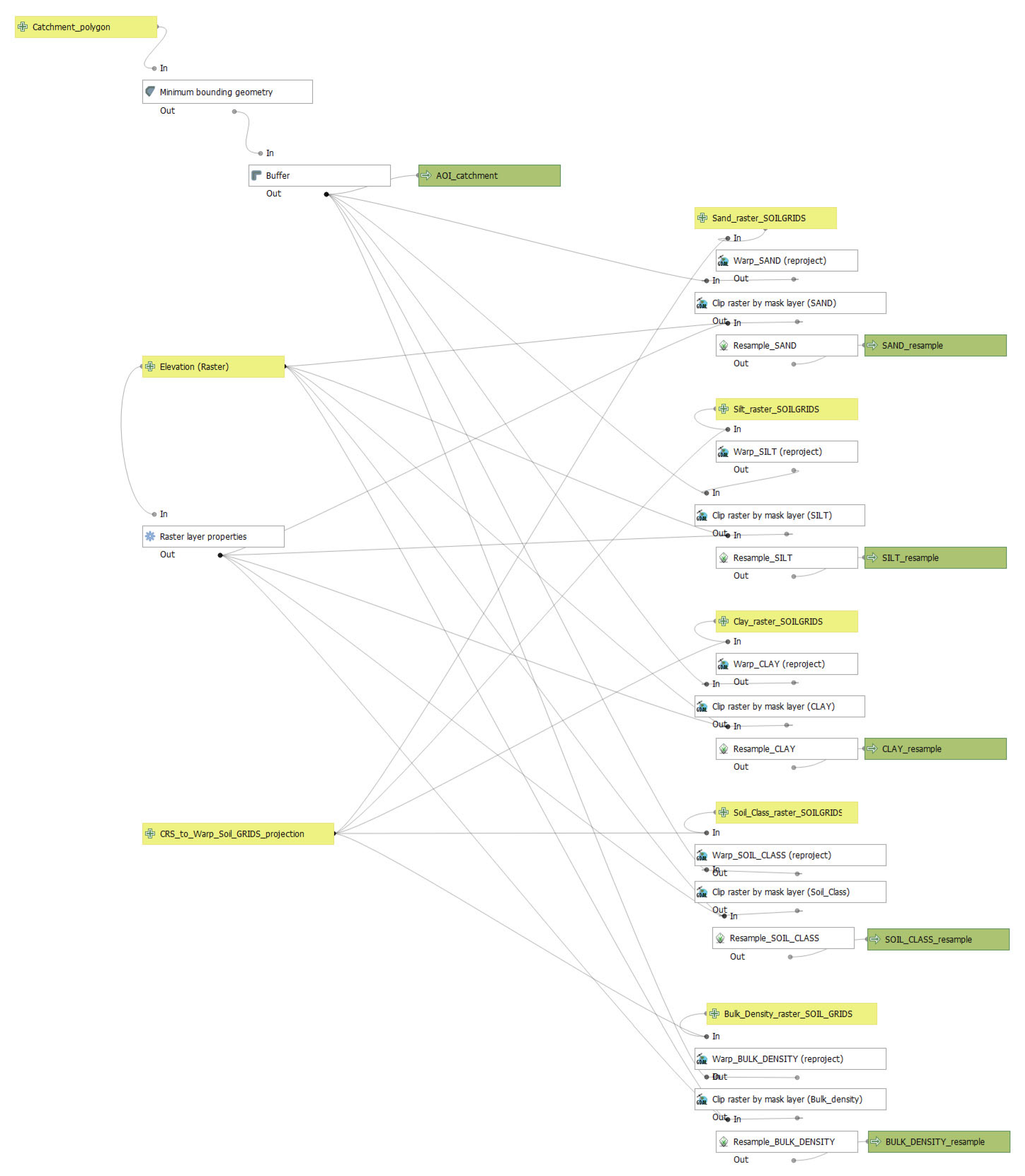
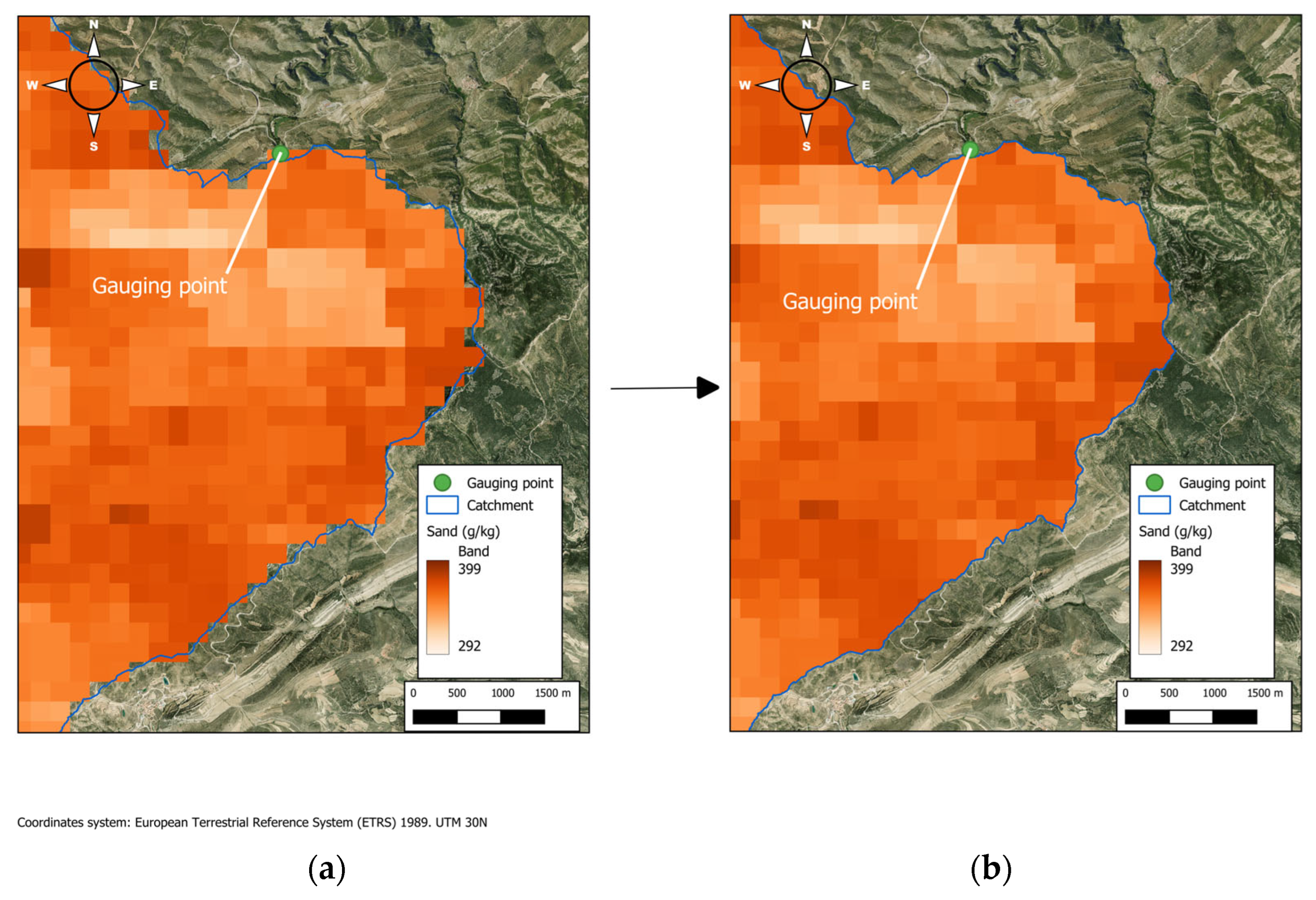
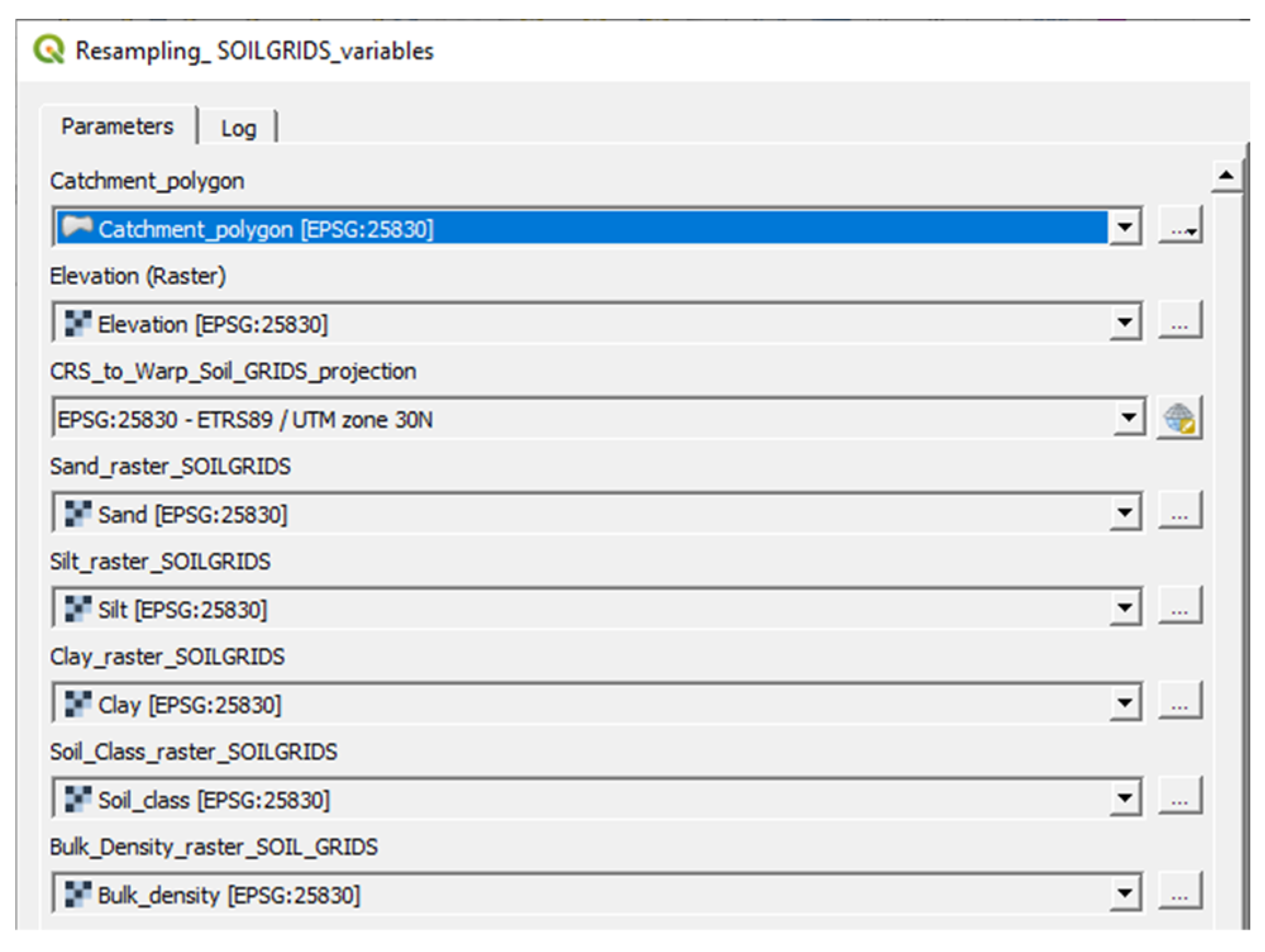
| Spatial homogenisation Model: 3. Resampling_SOILGRIDS_ variables | Sand, silt, clay, soil classes and bulk density SOILGRIDS rasters and elevation (raster) | Sand, silt, clay, soil classes and bulk density resampled (raster) | QGIS (minimum bounding geometry, buffer and raster layer properties), GDAL (warp), GRASS (r.resample) |
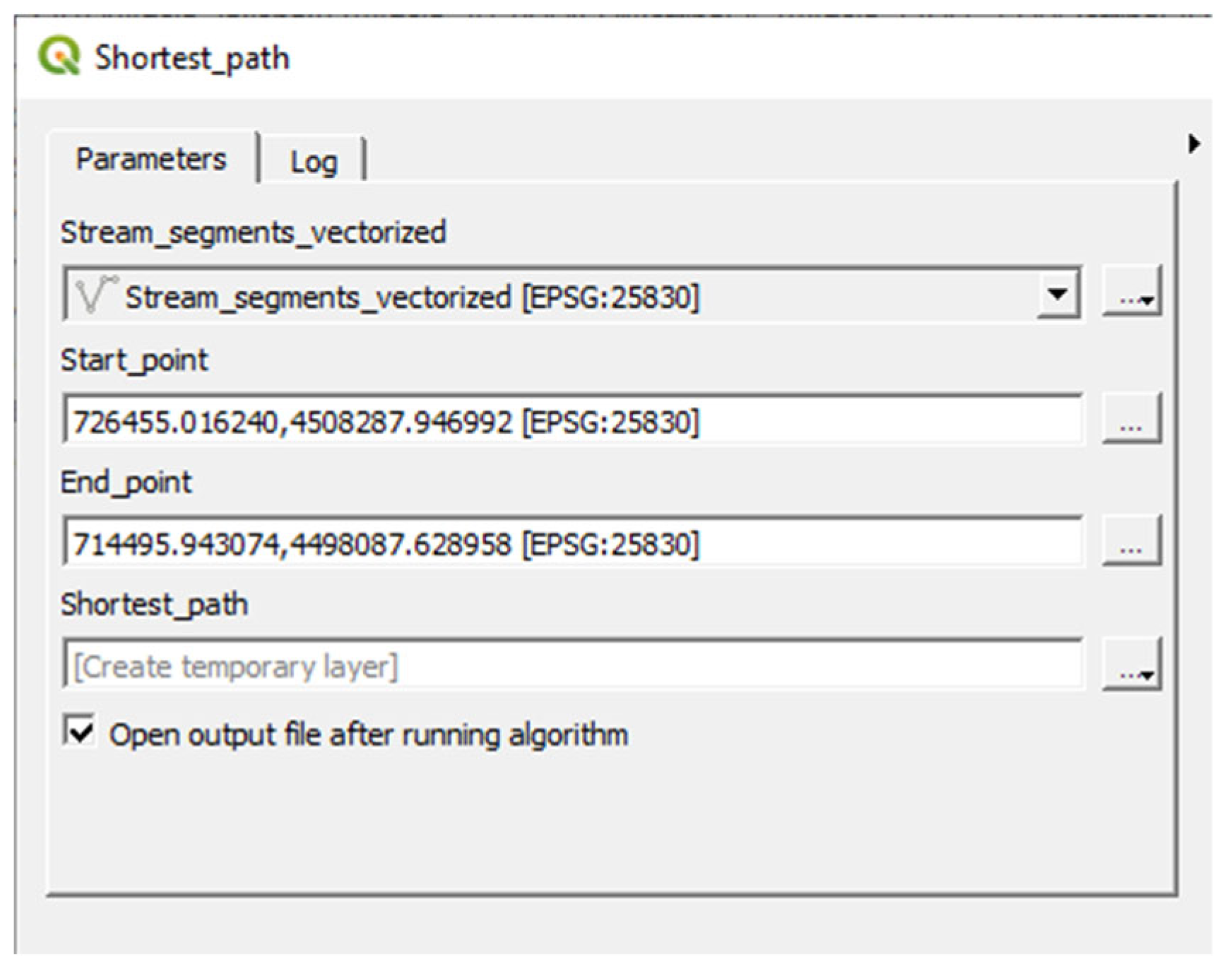
| Flow pathways Model: 4. Shortest_ path Catchment characterisation Model: 5. Catchment_ characterisation | Stream_segments (vector), start point and end point Catchment (polygon), slope (raster), Land_use (raster) and shortest path length (vector) | Shortest_path (vector line layer) Catchment_characteristics (polygon vector) | QGIS (shortest path point to point) QGIS (zonal statistics, field calculator) |
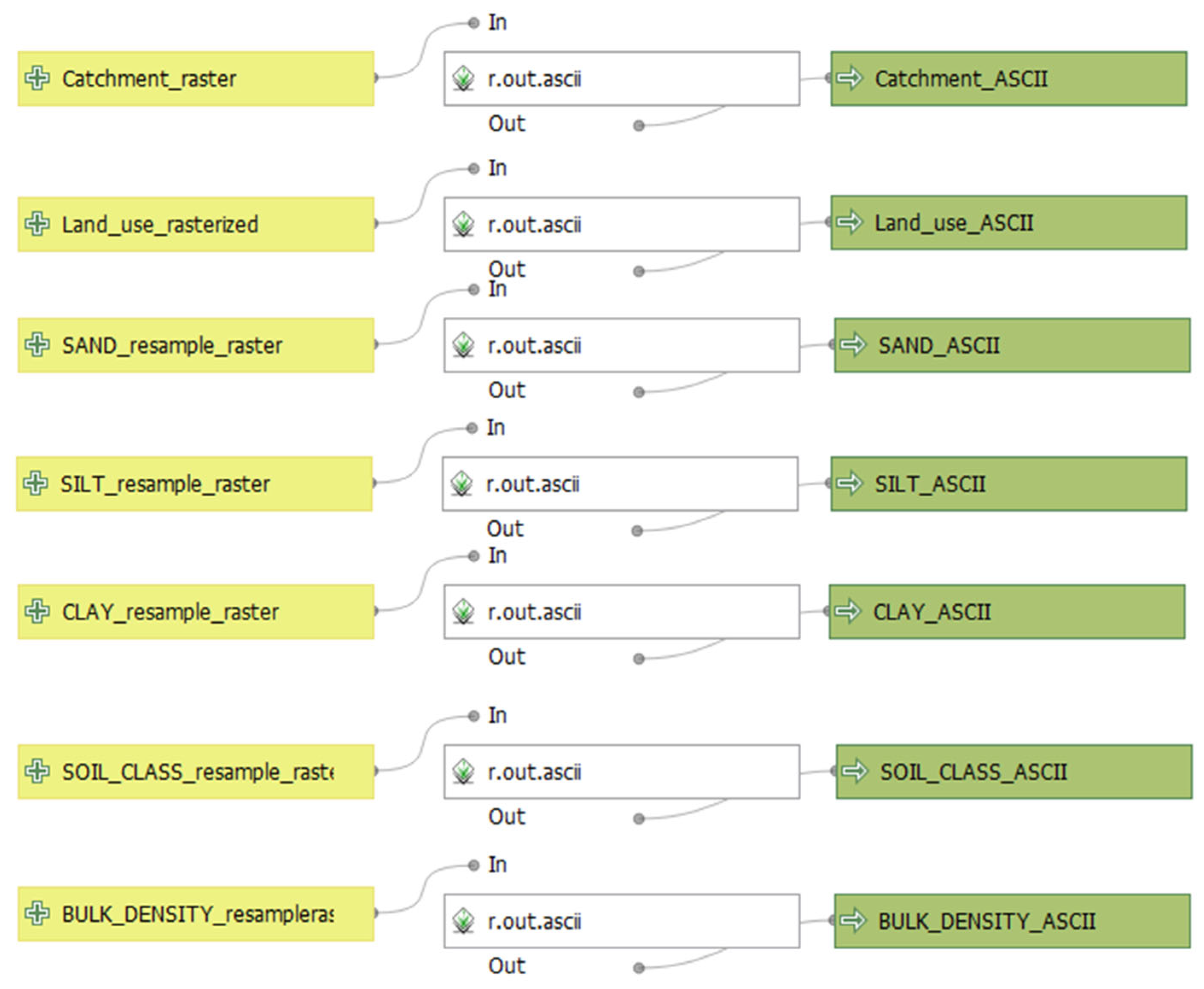
| Exchangeable files Model: 6. ASCII_ conversion | Catchment, land use, elevation, slope, sand, silt, clay, soil class and bulk density (raster layers) | Catchment, land use, sand, silt, clay, soil class and bulk density (.asc file) | GRASS (r.aout.ascii) |
| Catchment | z Max (masl) | z Min (masl) | Channel Length | Catchment Area |
|---|---|---|---|---|
| Aragón at Canfranc | 2160.03 | 1041.91 | 18,987.66 | 18,254,694 |
| Bailin at Sabiñanigo | 1078.86 | 743.675 | 4651.442 | 4,508,212 |
| Cidacos at Arnedillo | 1607.32 | 647.671 | 28,141.38 | 176,407,587 |
| Cidacos at Yanguas | 1607.32 | 943.343 | 26,049.78 | 230,120,488 |
| Deza at EmbidDeAriza | 1091.97 | 780.169 | 40,193.02 | 207,366,324 |
| Flamisell at Cabdella | 2670.56 | 1275.38 | 17,336.71 | 72,034,834 |
| Garona at Bossost | 2577.25 | 710.235 | 47,696.3 | 440,715,489 |
| Isuela at Trasobares | 1580.56 | 636.852 | 28,743.83 | 116,994,476 |
| Izalzu at Anduña | 1501.12 | 796.684 | 12,066.23 | 47,171,880 |
| Larraun at Iribas | 697.602 | 560.652 | 3067.464 | 5,825,444 |
| Nela at Villarcayo | 1495.34 | 1065.76 | 16,309.96 | 105,146,261 |
| Linares at SanPedroManrique | 947.97 | 593.783 | 51,586.01 | 254,733,836 |
| Oca at Oña | 1235.93 | 572.718 | 90,988.14 | 1,038,283,932 |
| Oja at Azurrulla | 1895.08 | 919.251 | 14,463.59 | 73,822,908 |
| Omecillo at Berengueda | 940.005 | 477.69 | 37,291.6 | 342,161,356 |
| Oroncillo at Oron | 1031.87 | 477.678 | 39,005.88 | 215,597,179 |
| Pancrudo at Navarrete | 1301.75 | 899.522 | 46,608.72 | 381,876,679 |
| Rudron at Valdelateja | 971.635 | 651.205 | 50,960.24 | 505,378,148 |
| Sanguesa at Onsella | 1104.98 | 408.293 | 57,150.27 | 233,627,436 |
| Subialde at Larrinoa | 976.08 | 593.27 | 9730.708 | 21,360,782 |
| Tiron at SanMiguelPedroso | 1943.81 | 805.105 | 27,491.29 | 190,327,545 |
| Trueba at MedinaDePomar | 1361.59 | 578.945 | 53,004.09 | 468,549,100 |
| Ubagua at Riezu | 1212.42 | 491.038 | 91,333.75 | 35,536,916 |
| Urederra at Barindano | 736.78 | 500.118 | 6083.276 | 37,063,648 |
| Urriobi at Espinal | 1347.52 | 856.52 | 11,611.5 | 4,846,596 |
| Vallfarrera at Alins | 2601.49 | 1071.4 | 20,319.19 | 82,741,803 |
| Veral at Zuriza | 2093.41 | 1188.19 | 12,843.68 | 46,176,842 |
| Zatoya at Ochagavia | 1175.03 | 789.745 | 20,686.8 | 72,702,728 |
| Zidacos at Garinoiain | 636.188 | 485.35 | 7164.723 | 27,097,980 |
| Material | Pixel Resolution |
|---|---|
| Digital elevation model (DEM) | 5 m |
| SoilGrids: silt, sand, clay and bulk density | 250 m |
| Spanish Land Use System (SIOSE) | Polygon shapefile (minimum polygon size: 1 m2). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida-Ñauñay, A.F.; Sanz, E.; Berlanga, A.; Patricio, M.Á.; Molina, J.M.; Zubelzu, S. Development of Open-Source Tools for Event-Based Hydrological Modelling Using GIS and Python. Water 2025, 17, 2160. https://doi.org/10.3390/w17142160
Almeida-Ñauñay AF, Sanz E, Berlanga A, Patricio MÁ, Molina JM, Zubelzu S. Development of Open-Source Tools for Event-Based Hydrological Modelling Using GIS and Python. Water. 2025; 17(14):2160. https://doi.org/10.3390/w17142160
Chicago/Turabian StyleAlmeida-Ñauñay, Andrés F., Ernesto Sanz, Antonio Berlanga, Miguel Ángel Patricio, José M. Molina, and Sergio Zubelzu. 2025. "Development of Open-Source Tools for Event-Based Hydrological Modelling Using GIS and Python" Water 17, no. 14: 2160. https://doi.org/10.3390/w17142160
APA StyleAlmeida-Ñauñay, A. F., Sanz, E., Berlanga, A., Patricio, M. Á., Molina, J. M., & Zubelzu, S. (2025). Development of Open-Source Tools for Event-Based Hydrological Modelling Using GIS and Python. Water, 17(14), 2160. https://doi.org/10.3390/w17142160









