Evaluating CHIRPS and ERA5 for Long-Term Runoff Modelling with SWAT in Alpine Headwaters
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Input Datasets
| Data Type | Data Source | Resolution/No. Stations |
|---|---|---|
| Land | ||
| Digital elevation model (DEM) | Copernicus—EU DEM v 1.1 [107], https://land.copernicus.eu/imagery-in-situ/eu-dem/eu-dem-v1.1 (accessed on 10 September 2018) | 25 m × 25 m |
| Soil | EEA—European Soil Data Centre (ESDAC) [108], https://esdac.jrc.ec.europa.eu/ (accessed on 11 September 2018) | 1 km × 1 km |
| Land use | European Environment Agency [109], Corine Land Cover (CLC) 2006 ver. 20, https://land.copernicus.eu/pan-european/corine-land-cover/clc-2006 (accessed on 11 September 2018) | 100 m × 100 m |
| Weather and discharge observations | ||
| Air temperature, precipitation, snow depth | European Climate Assessment & Dataset (ECA&D) [101] Data available at https://www.ecad.eu (accessed on 20 March 2019) | 4 stations |
| Precipitation | Bundesministerium für Nachhaltigkeit und Tourismus—eHYD [110], https://ehyd.gv.at/#, (accessed on 18 March 2019) Autonome Provinz Bozen, http://weather.provinz.bz.it | 29 stations |
| Discharge | Bundesministerium für Nachhaltigkeit und Tourismus—eHYD [110], https://ehyd.gv.at/# (accessed on 18 March 2019) | 9 stations |
| Climate products | ||
| Temperature, wind speed, solar radiation, humidity (CFSR) | National Centers for Environmental Prediction (NCEP) [52,62,63] https://www.uoguelph.ca/watershed/w3s (accessed on 25 April 2021) | 0.5° × 0.5° |
| Precipitation CHIRPS-V2.0 | Climate Hazards Group InfraRed Precipitation with Station [38], ftp://ftp.chg.ucsb.edu/pub/org/chg/products/CHIRPS-2.0 (accessed on 25 April 2021) | 0.05° × 0.05° |
| Precipitation ERA5 | Grid—European Centre for Medium-Range Weather Forecasts—ERA5 [50,105,106], https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form (accessed on 25 April 2021) | 0.25° × 0.25° |
2.3. Evaluation Methods
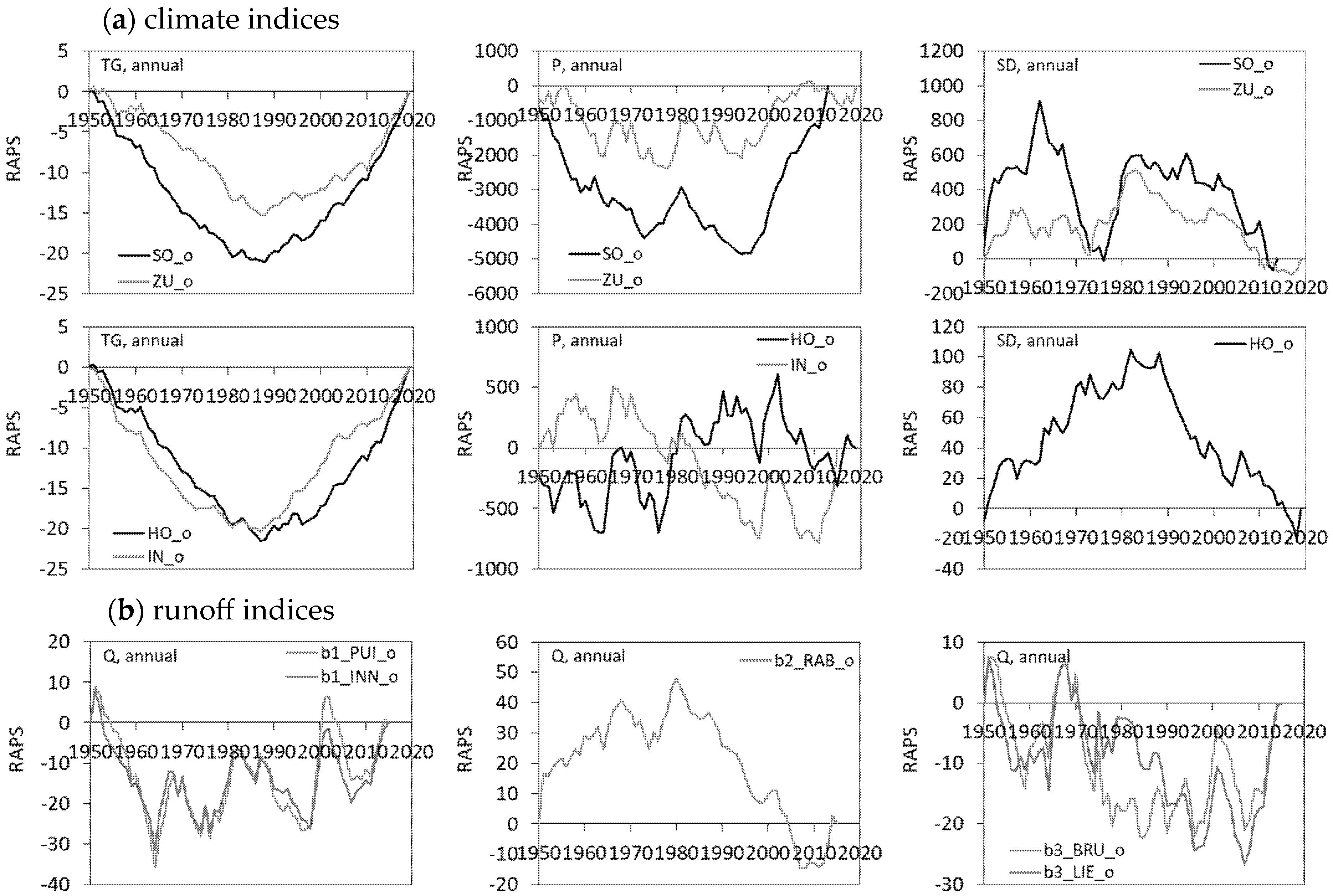
2.4. Long-Term Climate and Runoff Variations
2.5. Evaluation Using Hydrological Model
3. Results
3.1. Performance Evaluation Using Gauge Observations
3.2. Performance Evaluation Using Hydrological Model
4. Discussion
4.1. Evaluation Using Precipitation Observations
4.2. Evaluation Using Hydrological Modelling
5. Conclusions
- Both gridded precipitation products (GPPs) effectively replicate the observed precipitation patterns and reproduce the observed runoff regime. CHIRPS generally outperforms ERA5, showing lower RMAE in annual (25% CHIRPS, 37% ERA5) and monthly (40% CHIRPS, 44% ERA5) precipitation estimates. This translates into improved runoff performance, with CHIRP achieving lower RMAE in annual (12% CHIRPS, 20% ERA5) and monthly (20% CHIRPS, 26% ERA5) runoff. Despite its higher bias in precipitation and runoff, ERA5 demonstrates a higher correlation and a more consistent performance in precipitation amounts and trends across elevation bands and pilot catchments. This consistency likely stems from ERA5’s reanalysis framework, but it is limited by coarser resolution. The comparable performance of CHIRPS and ERA5 aligns with findings from earlier studies in the Alps [51,58,94].
- The evaluation of GPP precipitation trend performance has received limited research attention. Trend analysis shows that both GPPs generally follow observed precipitation trends and are capable of reproducing observed long-term runoff trends. Their performance in capturing precipitation trends is comparable to that for precipitation amounts. While precipitation trends are generally overestimated, CHIRPS shows lower precipitation trend bias at annual, seasonal, and monthly scales. This cascaded GPP performance, from precipitation amounts to precipitation trends, has been reported previously, including similar precipitation trend performance between CHIRPS and ERA-Interim (Error_TP = 1.87% y−1 CHIRPS, 1.97% y−1 ERA-Interim) [80].
- CHIRPS’s lower RMAE in annual precipitation corresponds to a lower annual runoff error than ERA5, while ERA5’s higher cold season precipitation results in elevated runoff RMAE relative to CHIRPS. Similarly, spatial patterns of precipitation trend errors are reflected in the corresponding runoff trend errors in the respective catchments. Seasonal precipitation trend error is likewise mirrored by seasonal runoff trend error. These consistent cascade of errors from precipitation and precipitation trends to runoff and runoff trends highlight the substantial impact of precipitation performance on hydrological model outputs in the pilot area.
- Some systematic overestimations of precipitation and precipitation trends are evident. Both products overestimate precipitation at lower elevations and during cold season. These biases likely stem from challenges in capturing winter precipitation from non-convective systems and snow-covered surfaces, particularly in complex alpine terrain. Additionally, both GPPs tend to overestimate precipitation trends during the warm season.
- The spatial resolution of GPPs substantially influences hydrological model performance in mountainous areas, independent of GPP performance in representing precipitation amounts and trends. CHIRPS’s finer spatial resolution (0.05°), gauge correction, and enhanced ability to capture orographically induced precipitation make it more suitable for complex mountainous terrain. CHIRPS’s more reliable runoff trend estimates and fewer missed trend significance counts at the monthly scale strengthen its advantage for long-term hydrological simulations in multiple mountainous catchments, particularly smaller ones. In contrast, ERA5’s coarser grid may limit its ability to accurately resolve orographic precipitation patterns in smaller catchments. However, its strong performance in catchment b3, where grid alignment is more centrally located, emphasizes the importance of spatial alignment between GPP resolution and catchment morphology. Given its lower error and finer spatial resolution, CHIRPS can be recommended for hydrological modelling in catchments smaller than 1000 km2, whereas ERA5 can be comparably suitable for applications in larger catchments, though this requires further confirmation.
- ERA5 demonstrates a higher correlation with observed precipitation despite exhibiting a larger precipitation bias than CHIRPS. This suggests that ERA5 more accurately captures precipitation temporal variability, indicating the potential for improved runoff generation if bias correction techniques are applied. While CHIRPS shows better raw precipitation and runoff estimates due to its finer spatial resolution and lower initial biases, ERA5 could ultimately generate improved model performance after appropriate debiasing. Future work should explicitly investigate the impacts of bias correction on the ERA5 generated model performance in catchments with complex topography.
- Model runoffs generated with measured precipitation outperform those generated using the best GPPs by a relatively small margin. This indicates that GPPs are not only viable substitutes for ground-based data but may, under certain conditions, outperform sparse or biased observational datasets in estimating both runoff and runoff trends. However, in this study, the GPP runoff was generated by a hydrologic model developed based on observed precipitation, so the GPP-generated runoff would perform differently if the model had been developed based on precipitation products.
- Scale discrepancies between precipitation gauges and GPPs are a common challenge. Although interpolation techniques (simple averaging, inverse distance weighting, Thiessen polygons) are often used to mitigate these mismatches, no single method proves universally optimal across all areas [51]. This study observed better performance with selected point-to-point comparisons rather than with spatially averaged precipitation. This highlights the importance of the careful selection of gauge–grid pairs in mountainous regions, where orographic effects are significant. Further research on preprocessing techniques for GPP assessments in complex terrains is recommended to enhance accuracy and applicability.
- The performance of GPPs in representing precipitation amounts and trends cascades directly into the accuracy of simulated runoff and runoff trends. CHIRPS exhibits lower uncertainties in runoff estimates for catchments b1 and b2, while ERA5 performs better in catchment b3. Beyond precipitation data quality, the performance of runoff simulations is also influenced by local geomorphological and hydroclimatic conditions. Therefore, careful consideration of these site-specific factors is essential when evaluating the long-term suitability of GPPs for hydrological applications in mountainous regions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, S.; Liu, D.; Wang, Z.; Zhao, Q.; Zou, H.; Hou, Y.; Liu, P.; Xiong, L. Runoff Responses to Climate and Land Use/Cover Changes under Future Scenarios. Water 2017, 9, 475. [Google Scholar] [CrossRef]
- KlemeŠ, V. Operational Testing of Hydrological Simulation Models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Bronstert, A. Rainfall-Runoff Modeling for Assessing Impacts of Climate and Land Use Change. In Encyclopedia of Hydrological Sciences; John Wiley & Sons, Ltd.: Chichester, UK, 2005. [Google Scholar]
- Blöschl, G.; Montanari, A. Climate Change Impacts—Throwing the Dice? Hydrol. Process. 2010, 24, 374–381. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Time Stability of Catchment Model Parameters: Implications for Climate Impact Analyses. Water Resour. Res. 2011, 47, W02531. [Google Scholar] [CrossRef]
- Addor, N.; Rössler, O.; Köplin, N.; Huss, M.; Weingartner, R.; Seibert, J. Robust Changes and Sources of Uncertainty in the Projected Hydrological Regimes of Swiss Catchments. Water Resour. Res. 2014, 50, 7541–7562. [Google Scholar] [CrossRef]
- Duethmann, D.; Bloschl, G.; Parajka, J. Why Does a Conceptual Hydrological Model Fail to Correctly Predict Discharge Changes in Response to Climate Change? Hydrol. Earth Syst. Sci. 2020, 24, 3493–3511. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.; Arsenault, R. Uncertainty of Gridded Precipitation and Temperature Reference Datasets in Climate Change Impact Studies. Hydrol. Earth Syst. Sci. 2021, 25, 3331–3350. [Google Scholar] [CrossRef]
- Ivezic, V.; Bekic, D.; Horvat, B. Modelling of Basin Wide Daily Evapotranspiration with a Partial Integration of Remote Sensing Data. Atmosphere 2018, 9, 120. [Google Scholar] [CrossRef]
- Ivezic, V.; Bekic, D.; Kerin, I. Estimating Basin-Wide Air Temperature by Partial Integration of Remote Sensing Data. Can. J. Earth Sci. 2018, 55, 1196–1206. [Google Scholar] [CrossRef]
- Bekić, D.; Halkijević, I.; Gilja, G.; Lončar, G.; Carević, D.; Potočki, K. Examples of Trends in Water Management Systems under Influence of Modern Technologies. Gradjevinar 2019, 71, 833–842. [Google Scholar] [CrossRef]
- Birsan, M.V.; Molnar, P.; Burlando, P.; Pfaundler, M. Streamflow Trends in Switzerland. J. Hydrol. 2005, 314, 312–329. [Google Scholar] [CrossRef]
- Beniston, M.; Rebetez, M.; Giorgi, F.; Marinucci, M.R. An Analysis of Regional Climate Change in Switzerland. Theor. Appl. Climatol. 1994, 49, 135–159. [Google Scholar] [CrossRef]
- Auer, I.; Böhm, R.; Jurkovic, A.; Lipa, W.; Orlik, A.; Potzmann, R.; Schöner, W.; Ungersböck, M.; Matulla, C.; Briffa, K.; et al. HISTALP—Historical Instrumental Climatological Surface Time Series of the Greater Alpine Region. Int. J. Climatol. 2007, 27, 17–46. [Google Scholar] [CrossRef]
- Widmann, M.; Schär, C. A Principal Component and Long-Term Trend Analysis of Daily Precipitation in Switzerland. Int. J. Climatol. 1997, 17, 1333–1356. [Google Scholar] [CrossRef]
- Matiu, M.; Crespi, A.; Bertoldi, G.; Maria Carmagnola, C.; Marty, C.; Morin, S.; Schöner, W.; Cat Berro, D.; Chiogna, G.; De Gregorio, L.; et al. Observed Snow Depth Trends in the European Alps: 1971 to 2019. Cryosphere 2021, 15, 1343–1382. [Google Scholar] [CrossRef]
- Scherrer, S.C.; Appenzeller, C.; Laternser, M. Trends in Swiss Alpine Snow Days: The Role of Local- and Large-Scale Climate Variability. Geophys. Res. Lett. 2004, 31, L13215. [Google Scholar] [CrossRef]
- Laternser, M.; Schneebeli, M. Long-Term Snow Climate Trends of the Swiss Alps (1931–99). Int. J. Climatol. 2003, 23, 733–750. [Google Scholar] [CrossRef]
- Klein, G.; Vitasse, Y.; Rixen, C.; Marty, C.; Rebetez, M. Shorter Snow Cover Duration since 1970 in the Swiss Alps Due to Earlier Snowmelt More than to Later Snow Onset. Clim. Change 2016, 139, 637–649. [Google Scholar] [CrossRef]
- Fatichi, S.; Rimkus, S.; Burlando, P.; Bordoy, R.; Molnar, P. Elevational Dependence of Climate Change Impacts on Water Resources in an Alpine Catchment. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 3743–3794. [Google Scholar] [CrossRef]
- Bliss, A.; Hock, R.; Radić, V. Global Response of Glacier Runoff to Twenty-First Century Climate Change. J. Geophys. Res. Earth Surf. 2014, 119, 717–730. [Google Scholar] [CrossRef]
- Radić, V.; Hock, R. Glaciers in the Earth’s Hydrological Cycle: Assessments of Glacier Mass and Runoff Changes on Global and Regional Scales. Surv. Geophys. 2014, 35, 813–837. [Google Scholar] [CrossRef]
- Filippa, G.; Cremonese, E.; Galvagno, M.; Isabellon, M.; Bayle, A.; Choler, P.; Carlson, B.Z.; Gabellani, S.; di Cella, U.M.; Migliavacca, M. Climatic Drivers of Greening Trends in the Alps. Remote Sens. 2019, 11, 2527. [Google Scholar] [CrossRef]
- Carlson, B.Z.; Corona, M.C.; Dentant, C.; Bonet, R.; Thuiller, W.; Choler, P. Observed Long-Term Greening of Alpine Vegetation—A Case Study in the French Alps. Environ. Res. Lett. 2017, 12, 114006. [Google Scholar] [CrossRef]
- Zierl, B.; Bugmann, H. Global Change Impacts on Hydrological Processes in Alpine Catchments. Water Resour. Res. 2005, 41, W02028. [Google Scholar] [CrossRef]
- Bavay, M.; Grünewald, T.; Lehning, M. Response of Snow Cover and Runoff to Climate Change in High Alpine Catchments of Eastern Switzerland. Adv. Water Resour. 2013, 55, 4–16. [Google Scholar] [CrossRef]
- Leitinger, G.; Tasser, E.; Newesely, C.; Obojes, N.; Tappeiner, U. Seasonal Dynamics of Surface Runoff in Mountain Grassland Ecosystems Differing in Land Use. J. Hydrol. 2010, 385, 95–104. [Google Scholar] [CrossRef]
- Hohmann, C.; Kirchengast, G.; Birk, S. Alpine Foreland Running Drier? Sensitivity of a Drought Vulnerable Catchment to Changes in Climate, Land Use, and Water Management. Clim. Change 2018, 147, 179–193. [Google Scholar] [CrossRef]
- European Environment Agency. EEA Regional Climate Change and Adaptation—The Alps Facing the Challenge of Changing Water Resources; EEA Report; Office for Official Publications of the European Communities: Luxembourg, 2009; pp. 1–143. [Google Scholar] [CrossRef]
- Viviroli, D.; Archer, D.R.; Buytaert, W.; Fowler, H.J.; Greenwood, G.B.; Hamlet, A.F.; Huang, Y.; Koboltschnig, G.; Litaor, M.I.; López-Moreno, J.I.; et al. Climate Change and Mountain Water Resources: Overview and Recommendations for Research, Management and Policy. Hydrol. Earth Syst. Sci. 2011, 15, 471–504. [Google Scholar] [CrossRef]
- Fehlmann, M.; Gascón, E.; Rohrer, M.; Schwarb, M.; Stoffel, M. Improving Medium-Range Forecasts of Rain-on-Snow Events in Prealpine Areas. Water Resour. Res. 2019, 55, 7638–7661. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff Conditions in the Upper Danube Basin under an Ensemble of Climate Change Scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Toreti, A.; Masante, D.; Acosta Navarro, J.; Bavera, D.; Cammalleri, C.; De Jager, A.; Di Ciollo, C.; Hrast Essenfelder, A.; Maetens, W.; Magni, D.; et al. Drought in Europe July 2022; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar] [CrossRef]
- Barontini, S.; Grossi, G.; Kouwen, N.; Maran, S.; Scaroni, P.; Ranzi, R. Impacts of Climate Change Scenarios on Runoff Regimes in the Southern Alps. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 3089–3141. [Google Scholar] [CrossRef]
- Jain, S.K.; Jain, S.K.; Jain, N.; Xu, C.-Y. Hydrologic Modeling of a Himalayan Mountain Basin by Using the SWAT Mode. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–26. [Google Scholar] [CrossRef]
- Farinotti, D.; Usselmann, S.; Huss, M.; Bauder, A.; Funk, M. Runoff Evolution in the Swiss Alps: Projections for Selected High-Alpine Catchments Based on ENSEMBLES Scenarios. Hydrol. Process. 2012, 26, 1909–1924. [Google Scholar] [CrossRef]
- Leskovar, K.; Mrakužić, P.; Meaški, H. Evaluation of Remotely Sensed Precipitation Product in a Hydrological Model of the Bednja Watershed. Gradjevinar 2021, 73, 335–348. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Thirel, G.; Notarnicola, C.; Kalas, M.; Zebisch, M.; Schellenberger, T.; Tetzlaff, A.; Duguay, M.; Mölg, N.; Burek, P.; de Roo, A. Assessing the Quality of a Real-Time Snow Cover Area Product for Hydrological Applications. Remote Sens. Environ. 2012, 127, 271–287. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s New Land Surface Precipitation Climatology Based on Quality-Controlled in Situ Data and Its Role in Quantifying the Global Water Cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing Objective Techniques for Gauge-Based Analyses of Global Daily Precipitation. J. Geophys. Res. 2008, 113, D04110. [Google Scholar] [CrossRef]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Durand, Y.; Brun, E.; Merindol, L.; Guyomarc’h, G.; Lesaffre, B.; Martin, E. A Meteorological Estimation of Relevant Parameters for Snow Models. Ann. Glaciol. 1993, 18, 65–71. [Google Scholar] [CrossRef]
- Hiebl, J.; Frei, C. Daily Temperature Grids for Austria since 1961—Concept, Creation and Applicability. Theor. Appl. Climatol. 2016, 124, 161–178. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a Natural Rain Gauge: Estimating Global Rainfall from Satellite Soil Moisture Data. J. Geophys. Res. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Bruster-Flores, J.L.; Ortiz-Gómez, R.; Ferriño-Fierro, A.L.; Guerra-Cobián, V.H.; Burgos-Flores, D.; Lizárraga-Mendiola, L.G. Evaluation of Precipitation Estimates CMORPH-CRT on Regions of Mexico with Different Climates. Water 2019, 11, 1722. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 Reanalysis 2017. Available online: https://rda.ucar.edu/datasets/d630000/ (accessed on 25 April 2021).
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of Eight High Spatial Resolution Gridded Precipitation Products in Adige Basin (Italy) at Multiple Temporal and Spatial Scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring; U.S. Geological Survey: Reston, VA, USA, 2014; Volume 832, p. 4. [Google Scholar]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; Van Dijk, A.I.J.M.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily Evaluation of 26 Precipitation Datasets Using Stage-IV Gauge-Radar Data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global Precipitation Measurement: Methods, Datasets and Applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Derin, Y.; Yilmaz, K.K. Evaluation of Multiple Satellite-Based Precipitation Products over Complex Topography. J. Hydrometeorol. 2014, 15, 1498–1516. [Google Scholar] [CrossRef]
- Sharifi, E.; Eitzinger, J.; Dorigo, W. Performance of the State-of-the-Art Gridded Precipitation Products over Mountainous Terrain: A Regional Study over Austria. Remote Sens. 2019, 11, 2018. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.H.; Delrieu, G.; Hong, Y.; Hsu, Y.C.; et al. Multiregional Satellite Precipitation Products Evaluation over Complex Terrain. J. Hydrometeorol. 2016, 17, 1817–1836. [Google Scholar] [CrossRef]
- Katsanos, D.; Retalis, A.; Michaelides, S. Validation of a High-Resolution Precipitation Database (CHIRPS) over Cyprus for a 30-Year Period. Atmos. Res. 2016, 169, 459–464. [Google Scholar] [CrossRef]
- Maggioni, V.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Modeling Satellite Precipitation Errors over Mountainous Terrain: The Influence of Gauge Density, Seasonality, and Temporal Resolution. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4130–4140. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; Macalister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as Weather Input Data for Watershed Models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR Climate Data for Hydrologic Prediction in Data-Scarce Watersheds: An Application in the Blue Nile River Basin. J. Am. Water Resour. Assoc. 2014, 50, 1226–1241. [Google Scholar] [CrossRef]
- Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of Precipitation Input for SWAT Modeling in Alpine Catchment: A Case Study in the Adige River Basin (Italy). Sci. Total Environ. 2016, 573, 66–82. [Google Scholar] [CrossRef] [PubMed]
- Mei, Y.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Evaluating Satellite Precipitation Error Propagation in Runoff Simulations of Mountainous Basins. J. Hydrometeorol. 2016, 17, 1407–1423. [Google Scholar] [CrossRef]
- Grusson, Y.; Anctil, F.; Sauvage, S.; Sánchez Pérez, J. Testing the SWAT Model with Gridded Weather Data of Different Spatial Resolutions. Water 2017, 9, 54. [Google Scholar] [CrossRef]
- Raimonet, M.; Oudin, L.; Thieu, V.; Silvestre, M.; Vautard, R.; Rabouille, C.; Le Moigne, P. Evaluation of Gridded Meteorological Datasets for Hydrological Modeling. J. Hydrometeorol. 2017, 18, 3027–3041. [Google Scholar] [CrossRef]
- Guo, J.; Su, X. Parameter Sensitivity Analysis of SWAT Model for Streamflow Simulation with Multisource Precipitation Datasets. Hydrol. Res. 2019, 50, 861–877. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Using High-Resolution Satellite Rainfall Products to Simulate a Major Flash Flood Event in Northern Italy. J. Hydrometeorol. 2013, 14, 171–185. [Google Scholar] [CrossRef]
- Ashouri, H.; Nguyen, P.; Thorstensen, A.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D. Assessing the Efficacy of High-Resolution Satellite-Based PERSIANN-CDR Precipitation Product in Simulating Streamflow. J. Hydrometeorol. 2016, 17, 2061–2076. [Google Scholar] [CrossRef]
- Duan, Z.; Tuo, Y.; Liu, J.; Gao, H.; Song, X.; Zhang, Z.; Yang, L.; Mekonnen, D.F. Hydrological Evaluation of Open-Access Precipitation and Air Temperature Datasets Using SWAT in a Poorly Gauged Basin in Ethiopia. J. Hydrol. 2019, 569, 612–626. [Google Scholar] [CrossRef]
- Luo, X.; Wu, W.; He, D.; Li, Y.; Ji, X. Hydrological Simulation Using TRMM and CHIRPS Precipitation Estimates in the Lower Lancang-Mekong River Basin. Chin. Geogr. Sci. 2019, 29, 13–25. [Google Scholar] [CrossRef]
- Musie, M.; Sen, S.; Srivastava, P. Comparison and Evaluation of Gridded Precipitation Datasets for Streamflow Simulation in Data Scarce Watersheds of Ethiopia. J. Hydrol. 2019, 579, 124168. [Google Scholar] [CrossRef]
- Satgé, F.; Ruelland, D.; Bonnet, M.-P.; Molina, J.; Pillco, R. Consistency of Satellite Precipitation Estimates in Space and over Time Compared with Gauge Observations and Snow-Hydrological Modelling in the Lake Titicaca Region. Hydrol. Earth Syst. Sci. Discuss. 2018, 23, 595–619. [Google Scholar] [CrossRef]
- Dhanesh, Y.; Bindhu, V.M.; Senent-Aparicio, J.; Brighenti, T.M.; Ayana, E.; Smitha, P.S.; Fei, C.; Srinivasan, R. A Comparative Evaluation of the Performance of CHIRPS and CFSR Data for Different Climate Zones Using the SWAT Model. Remote Sens. 2020, 12, 3088. [Google Scholar] [CrossRef]
- Le, M.H.; Lakshmi, V.; Bolten, J.; Bui, D.D. Adequacy of Satellite-Derived Precipitation Estimate for Hydrological Modeling in Vietnam Basins. J. Hydrol. 2020, 586, 124820. [Google Scholar] [CrossRef]
- Kolluru, V.; Kolluru, S.; Konkathi, P. Evaluation and Integration of Reanalysis Rainfall Products under Contrasting Climatic Conditions in India. Atmos. Res. 2020, 246, 105121. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 Reanalysis as a Potential Reference Dataset for Hydrological Modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Roth, V.; Lemann, T. Comparing CFSR and Conventional Weather Data for Discharge and Soil Loss Modelling with SWAT in Small Catchments in the Ethiopian Highlands. Hydrol. Earth Syst. Sci. 2016, 20, 921–934. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; Van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-Scale Evaluation of 22 Precipitation Datasets Using Gauge Observations and Hydrological Modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Le, A.M.; Pricope, N.G. Increasing the Accuracy of Runoffand Streamflow Simulation in the Nzoia Basin, Western Kenya, through the Incorporation of Satellite-Derived CHIRPS Data. Water 2017, 9, 114. [Google Scholar] [CrossRef]
- Zeiger, S.; Hubbart, J. An Assessment of Mean Areal Precipitation Methods on Simulated Stream Flow: A SWAT Model Performance Assessment. Water 2017, 9, 459. [Google Scholar] [CrossRef]
- Ledesma, J.L.J.; Futter, M.N. Gridded Climate Data Products Are an Alternative to Instrumental Measurements as Inputs to Rainfall–Runoff Models. Hydrol. Process. 2017, 31, 3283–3293. [Google Scholar] [CrossRef]
- Sirisena, T.A.J.G.; Maskey, S.; Ranasinghe, R.; Babel, M.S. Effects of Different Precipitation Inputs on Streamflow Simulation in the Irrawaddy River Basin, Myanmar. J. Hydrol. Reg. Stud. 2018, 19, 265–278. [Google Scholar] [CrossRef]
- Dalla Torre, D.; Di Marco, N.; Menapace, A.; Avesani, D.; Righetti, M.; Majone, B. Suitability of ERA5-Land Reanalysis Dataset for Hydrological Modelling in the Alpine Region. J. Hydrol. Reg. Stud. 2024, 52, 101718. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A Continental-Scale Hydrology and Water Quality Model for Europe: Calibration and Uncertainty of a High-Resolution Large-Scale SWAT Model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Rahman, K.; Maringanti, C.; Beniston, M.; Widmer, F.; Abbaspour, K.; Lehmann, A. Streamflow Modeling in a Highly Managed Mountainous Glacier Watershed Using SWAT: The Upper Rhone River Watershed Case in Switzerland. Water Resour. Manag. 2013, 27, 323–339. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Tuo, Y.; Marcolini, G.; Disse, M.; Chiogna, G. Calibration of Snow Parameters in SWAT: Comparison of Three Approaches in the Upper Adige River Basin (Italy). Hydrol. Sci. J. 2018, 63, 657–678. [Google Scholar] [CrossRef]
- Koycegiz, C.; Buyukyildiz, M. Calibration of SWAT and Two Data-Driven Models for a Data-Scarce Mountainous Headwater in Semi-Arid Konya Closed Basin. Water 2019, 11, 147. [Google Scholar] [CrossRef]
- Kang, K.; Lee, J.H. Hydrologic Modelling of the Effect of Snowmelt and Temperature on a Mountainous Watershed. J. Earth Syst. Sci. 2014, 123, 705–713. [Google Scholar] [CrossRef]
- Bieger, K.; Hörmann, G.; Fohrer, N. Analyse Spatiale Détaillée Du Ruissellement et de l’apport de Sédiments Simulés Par SWAT Dans Un Bassin Versant Montagneux En Chine. Hydrol. Sci. J. 2015, 60, 784–800. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Yang, X.; Haywood, J. A Review of SWAT Applications, Performance and Future Needs for Simulation of Hydro-Climatic Extremes. Adv. Water Resour. 2020, 143, 103662. [Google Scholar] [CrossRef]
- Bandhauer, M.; Isotta, F.; Lakatos, M.; Lussana, C.; Båserud, L.; Izsák, B.; Szentes, O.; Tveito, O.E.; Frei, C. Evaluation of Daily Precipitation Analyses in E-OBS (V19.0e) and ERA5 by Comparison to Regional High-Resolution Datasets in European Regions. Int. J. Climatol. 2022, 42, 727–747. [Google Scholar] [CrossRef]
- Monteiro, D.; Morin, S. Multi-Decadal Analysis of Past Winter Temperature, Precipitation and Snow Cover Data in the European Alps from Reanalyses, Climate Models and Observational Datasets. Cryosphere 2023, 17, 3617–3660. [Google Scholar] [CrossRef]
- Mei, Y.; Anagnostou, E.N.; Nikolopoulos, E.I.; Borga, M. Error Analysis of Satellite Precipitation Products in Mountainous Basins. J. Hydrometeorol. 2014, 15, 1778–1793. [Google Scholar] [CrossRef]
- Kormann, C.; Francke, T.; Bronstert, A. Detection of Regional Climate Change Effects on Alpine Hydrology by Daily Resolution Trend Analysis in Tyrol, Austria. J. Water Clim. Change 2015, 6, 124–143. [Google Scholar] [CrossRef]
- Frei, C.; Schär, C. A Precipitation Climatology of the Alps from High-Resolution Rain-Gauge Observations. Int. J. Climatol. 1998, 18, 873–900. [Google Scholar] [CrossRef]
- Messerli, B.; Viviroli, D.; Weingartner, R. Mountains of the World: Vulnerable Water Towers for the 21 St Century. Ambio 2004, 33, 29–34. [Google Scholar] [CrossRef]
- Keiler, M.; Knight, J.; Harrison, S. Climate Change and Geomorphological Hazards in the Eastern European Alps. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 2461–2479. [Google Scholar] [CrossRef] [PubMed]
- Klein Tank, A.M.G.; Wijngaard, J.B.; Können, G.P.; Böhm, R.; Demarée, G.; Gocheva, A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C.; et al. Daily Dataset of 20th-Century Surface Air Temperature and Precipitation Series for the European Climate Assessment. Int. J. Climatol. 2002, 22, 1441–1453. [Google Scholar] [CrossRef]
- Peterson, T.C.; Vose, R.S. An Overview of the Global Historical Climatology Network Temperature Database. Bull. Am. Meteorol. Soc. 1997, 78, 2837–2849. [Google Scholar] [CrossRef]
- Janowiak, J.E.; Joyce, R.J.; Yarosh, Y. A Real-Time Global Half-Hourly Pixel-Resolution Infrared Dataset and Its Applications. Bull. Am. Meteorol. Soc. 2001, 82, 205–217. [Google Scholar] [CrossRef]
- Wan, Z. New Refinements and Validation of the Collection-6 MODIS Land-Surface Temperature/Emissivity Product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Radu, R.; Schepers, D.; Simmons, A.; Soci, C.; et al. Global Reanalysis: Goodbye ERA-Interim, Hello ERA5. ECMWF Newsl. 2019, 159, 17–24. [Google Scholar] [CrossRef]
- Hoffmann, L.; Günther, G.; Li, D.; Stein, O.; Wu, X.; Griessbach, S.; Heng, Y.; Konopka, P.; Müller, R.; Vogel, B.; et al. From ERA-Interim to ERA5: The Considerable Impact of ECMWF’s next-Generation Reanalysis on Lagrangian Transport Simulations. Atmos. Chem. Phys. 2019, 19, 3097–3214. [Google Scholar] [CrossRef]
- EU-DEM — Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/imagery-in-situ/eu-dem (accessed on 10 September 2018).
- Panagos, P.; Van Liedekerke, M.; Jones, A.; Montanarella, L. European Soil Data Centre: Response to European Policy Support and Public Data Requirements. Land Use Policy 2012, 29, 329–338. [Google Scholar] [CrossRef]
- CORINE Land Cover—Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/pan-european/corine-land-cover (accessed on 11 September 2018).
- Bundesministerium für Nachhaltigkeit und Tourismus eHYD. Available online: https://ehyd.gv.at/# (accessed on 18 March 2019).
- Sriwongsitanon, N.; Kaprom, C.; Tantisuvanichkul, K.; Prasertthonggorn, N.; Suiadee, W.; Bastiaanssen, W.G.M.; Williams, J.A. The Combined Power of Double Mass Curves and Bias Correction for the Maximisation of the Accuracy of an Ensemble Satellite-Based Precipitation Estimate Product. Hydrology 2023, 10, 154. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Kendall, M.; Gibbons, J. Rank Correlation Methods—Charles Griffin Book, 5th ed.; Oxford University Press: London, UK, 1990; ISBN 0-19-520837-4. [Google Scholar]
- Garbrecht, J.; Fernandez, G.P. Visualization of Trends and Fluctuations in Climatic Records. JAWRA J. Am. Water Resour. Assoc. 1994, 30, 297–306. [Google Scholar] [CrossRef]
- Fontaine, T.A.; Cruickshank, T.S.; Arnold, J.G.; Hotchkiss, R.H. Development of a Snowfall-Snowmelt Routine for Mountainous Terrain for the Soil Water Assessment Tool (SWAT). J. Hydrol. 2002, 262, 209–223. [Google Scholar] [CrossRef]
- Grusson, Y.; Sun, X.; Gascoin, S.; Sauvage, S.; Raghavan, S.; Anctil, F.; Sáchez-Pérez, J.M. Assessing the Capability of the SWAT Model to Simulate Snow, Snow Melt and Streamflow Dynamics over an Alpine Watershed. J. Hydrol. 2015, 531, 574–588. [Google Scholar] [CrossRef]
- Yacoub, C.; Foguet, A.P. Slope Effects on SWAT Modeling in a Mountainous Basin. J. Hydrol. Eng. 2013, 18, 1663–1673. [Google Scholar] [CrossRef]
- Rango, A.; Martinec, J. Revisiting the Degree-Day Method for Snowmelt Computations. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 657–669. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool User’s Manual Version 2005; Texas Water Resources Institute: Temple, TX, USA, 2011. [Google Scholar]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute of Aquatic Science and Technology, Eawag: Dübendorf, Switzerland, 2011; p. 106. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Veith Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ahl, R.S.; Woods, S.W.; Zuuring, H.R. Hydrologic Calibration and Validation of SWAT in a Snow-Dominated Rocky Mountain Watershed, Montana, U.S.A. J. Am. Water Resour. Assoc. 2008, 44, 1411–1430. [Google Scholar] [CrossRef]
- Schmucki, E.; Marty, C.; Fierz, C.; Weingartner, R.; Lehning, M. Impact of Climate Change in Switzerland on Socioeconomic Snow Indices. Theor. Appl. Climatol. 2017, 127, 875–889. [Google Scholar] [CrossRef]
- Hadi, S.J.; Tombul, M. Long-Term Spatiotemporal Trend Analysis of Precipitation and Temperature over Turkey. Meteorol. Appl. 2018, 25, 445–455. [Google Scholar] [CrossRef]
- Lakson, M.; Post, P.; Sepp, M. The Impact of Atmospheric Circulation on Air Temperature Rise in Estonia. Front. Earth Sci. 2019, 7, 131. [Google Scholar] [CrossRef]
- Kolendowicz, L.; Czernecki, B.; Półrolniczak, M.; Taszarek, M.; Tomczyk, A.M.; Szyga-Pluga, K. Homogenization of Air Temperature and Its Long-Term Trends in Poznań (Poland) for the Period 1848–2016. Theor. Appl. Climatol. 2019, 136, 1357–1370. [Google Scholar] [CrossRef]
- Hafizi, H.; Sorman, A.A. Assessment of 13 Gridded Precipitation Datasets for Hydrological Modeling in a Mountainous Basin. Atmosphere 2022, 13, 143. [Google Scholar] [CrossRef]
- Napoli, A.; Crespi, A.; Ragone, F.; Maugeri, M.; Pasquero, C. Variability of Orographic Enhancement of Precipitation in the Alpine Region. Sci. Rep. 2019, 9, 13352. [Google Scholar] [CrossRef] [PubMed]
- Dhawan, P.; Dalla Torre, D.; Niazkar, M.; Kaffas, K.; Larcher, M.; Righetti, M.; Menapace, A. A Comprehensive Comparison of Bias Correction Methods in Climate Model Simulations: Application on ERA5-Land across Different Temporal Resolutions. Heliyon 2024, 10, e40352. [Google Scholar] [CrossRef] [PubMed]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing Bias Correction Methods in Downscaling Meteorological Variables for a Hydrologic Impact Study in an Arid Area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Wang, Y.; Bian, J.; Wang, S.; Tang, J.; Ding, F. Evaluating SWAT Snowmelt Parameters and Simulating Spring Snowmelt Nonpoint Source Pollution in the Source Area of the Liao River. Pol. J. Environ. Stud. 2016, 25, 2177–2185. [Google Scholar] [CrossRef] [PubMed]











| Dataset | Variables | Spatial Coverage | Temporal Coverage | Spatial Resolution | Temporal Resolution | Category |
|---|---|---|---|---|---|---|
| CFSR | P,T | global | 1979–2017 | 0.3125° | Daily | gauge + reanalysis |
| CHIRPS-V2.0 | P | 50° N–50° S | 1981-present | 0.05° | Daily | gauge + satellite + reanalysis |
| CMORPH-BLD | P | 50° N–50° S | 1998-present | 0.25° | 3-Hourly | gauge + satellite |
| CMORPH-CRT | P | 50° N–50° S | 1998-present | 0.25° | 3-Hourly | gauge + satellite |
| CMORPH-RAW | P | 50° N–50° S | 1998-present | 0.25° | 3-Hourly | satellite |
| E-OBS | P,T | 25° N–71.5° N–25° W–45° E | 1950–2024 | 0.1° | Daily | gauge |
| ERA5 | P,T | global | 1940-present | 0.28125° | Hourly | gauge + reanalysis |
| ERA-Interim | P | global | 1979–2019 | 0.72° | 6-Hourly | gauge + reanalysis |
| MSWEP-2.2 | P | global | 1979-present | 0.1° | 3-Hourly | gauge + satellite + reanalysis |
| PERSIANN-CDR | P | 60° N–60° S | 1983-present | 0.25° | Daily | gauge + satellite |
| PGF | P | 90° N–90° S | 1948–2011 | 0.25° | 3-Hourly | gauge + reanalysis |
| SAFRAN | P,T | France | 1991-present | 0.1° | Hourly | gauge + reanalysis |
| SM2RAIN | P | Land | 2007–2021 | 0.5° | Daily | near-surface soil moisture |
| SPARTACUS | P,T | Austria | 1961-present | 1 km | Daily | gauge data interpolation |
| TRMM | P | 50° N–50° S | 1998–2019 | 0.25° | 3-Hourly | satellite |
| Dataset | Variable | Author(s) | Study Area | Assessment |
|---|---|---|---|---|
| CFSR | P,T P,T P,T P,T P P P,T P T P P,T P | Fuka et al. [62] Dile & Srinivasan [63] Roth & Lemann [79] Grusson et al. [66] Le et al. [81] Sun et al. [56] Duan et al. [71] Guo et al. [68] Luo et al. [72] Musie et al. [73] Dhanesh et al. [75] Tarek et al. [8] | Catskill Mountains, (USA); Blue Nile (Ethiopia) Lake Tanana, Ethiopia Blue Nile (Ethiopia) Garonne basin, France Kenya Global Ethiopia Shiyang River (China) Lancang-Mekong River (China) Ketar and Meki basins (Ethiopia) USA, Brazil, Spain, Ethiopia, India Africa | m (SWAT) m (SWAT) o+m (SWAT) m (SWAT) o+m (SWAT) o o+m (SWAT) m (SWAT) m (SWAT) o+m (SWAT) o+m (SWAT) m (GR4J, HMETS) |
| CHIRPS-V2.0 | P P P P P P P P P P P P P,T P P P P,T P | Duan et al. [51] Katsanos et al. [60] Tuo et al. [64] Beck et al. [80] Le et al. [81] Zeiger et al. [82] Sirisena et al. [84] Duan et al. [71] Guo et al. [68] Luo et al. [72] Musie et al. [73] Satge et al. [74] Beck et al. [54] Dhanesh et al. [75] Le et al. [76] Venkatesh et al. [77] Tarek et al. [8] Leskovar et al. [37] | Upper Adige basin, Italy Cyprus (and Europe) Upper Adige basin, Italy Global Kenya Missouri (USA) Irrawaddy (Myanmar) Ethiopia Shiyang River (China) Lancang-Mekong River (China) Ketar and Meki basins (Ethiopia) Lake Titicaca (Peru/Bolivia) USA USA, Brazil, Spain, Ethiopia, India Vietnam India Africa Croatia | o o m (SWAT) o+m (HBV) o+m (SWAT) o+m (SWAT) o+m (SWAT) o+m (SWAT) m (SWAT) o+m (SWAT) m (SWAT) o+m (GR4J) o o+m (SWAT) o+m (SWAT) o+m (SWAT) m (GR4J, HMETS) o+m (SWAT) |
| CMORPH-BLD | P P P | Duan et al. [51] Derin et al. [59] Stage et al. [74] | Upper Adige basin, Italy Swiss and Italian Alps, French Cevennes, etc. Lake Titicaca (Peru/Bolivia) | o o o+m (GR4J) |
| CMORPH-CRT | P P P P P | Duan et al. [51] Derin et al. [59] Beck et al. [80] Satge et al. [74] Beck et al. [54] | Upper Adige basin, Italy Swiss and Italian Alps, French Cevennes, etc. Global Lake Titicaca (Peru/Bolivia) USA | o o o+m (HBV) o+m (GR4J) o |
| CMORPH-RAW | P P P P P | Nikolopoulos et al. [69] Duan et al. [51] Maggioni et al. [61] Mei et al. [65] Stage et al. [74] | Fella basin, north-east Italy Upper Adige basin, Italy Trentino-Alto, Adige region, Italy Upper Adige basin, Italy Lake Titicaca (Peru/Bolivia) | o+m (tRIBS) o o m (ICHYMOD) o+m (GR4J) |
| E-OBS | P,T P,T | Ledesma and Futter [83] Raimonet et al. [67] | Sweden France | o+m (PERSiST, HBV) m (GR4J) |
| ERA5 | P P,T P,T P,T P,T P P,T P,T | Sharifi et al. [58] Tarek et al. [78] Fehlmann et al. [31] Venkatesh et al. [77] Tarek et al. [8] Bandhauer et al. [94] Monteiro and Morin [95] Dalla Torre et al. [85] | Austria North America Bernese (Switzerland) India Africa Europe (Alps) Europe (Alps) Upper Adige basin, Italy | o o+m (GR4J, HMETS) m (HBV-3) o+m (SWAT) m (GR4J, HMETS) o o o+m (ICHYMOD) |
| ERA-Interim | P P,T P,T P P,T | Derin et al. [59] Tarek et al. [78] Beck et al. [80] Beck et al. [54] Tarek et al. [8] | Swiss and Italian Alps, French Cevennes, etc. North America Global USA Africa | o o+m (HMETS, GR4J) o+m (HBV) o m (GR4J, HMETS) |
| MSWEP-2.2 | P P | Beck et al. [80] Sharifi et al. [58] | Global Austria | o+m (HBV) o |
| PERSIANN-CDR | P P P P P P P P P P P P,T | Duan et al. [51] Nikolopoulos et al. [69] Derin et al. [59] Maggioni et al. [61] Mei et al. [65] Ashouri et al. [70] Sirisena et al. [84] Musie et al. [73] Stage et al. [74] Beck [54] Le et al. [76] Tarek et al. [8] | Upper Adige basin, Italy Fella basin, north-east Italy Swiss and Italian Alps, French Cevennes, etc. Trentino-Alto, Adige region, Italy Upper Adige basin, Italy Oklahoma/Arkansas (USA) Irrawaddy (Myanmar) Ketar and Meki basins (Ethiopia) Lake Titicaca (Peru/Bolivia) USA Vietnam Africa | o o+m (tRIBS) o o m (ICHYMOD) o+m (HL-RDHM) o+m (SWAT) m (SWAT) o+m (GR4J) o o+m (SWAT) m (GR4J, HMETS) |
| PGF | P P | Duan et al. [51] Guo et al. [68] | Upper Adige basin, Italy Shiyang River (China) | o m (SWAT) |
| SAFRAN | P P | Grusson et al. [66] Raimonet et al. [67] | Garonne basin, France France | m (SWAT) m (GR4J) |
| SM2RAIN | P P P P | Brocca et al. [48] Beck et al. [80] Sharifi et al. [58] Beck et al. [54] | Global Global Austria USA | o o+m (HBV) o o |
| TRMM | P P P P P P P P P P P P | Nikolopoulos et al. [69] Duan et al. [51] Katsanos et al. [60] Tuo et al. [64] Ashouri et al. [70] Zeiger et al. [82] Duan et al. [71] Guo et al. [68] Luo et al. [72] Musie et al. [73] Satge et al. [74] Beck et al. [54] | Fella basin, north-east Italy Upper Adige basin (Italy) Cyprus (and Europe) Upper Adige basin (Italy) Oklahoma/Arkansas (USA) Missouri (USA) Ethiopia Shiyang River (China) Lancang-Mekong River (China) Ketar and Meki basins (Ethiopia) Lake Titicaca (Peru/Bolivia) USA | o+m (tRIBS) o o m (SWAT) o+m (HL-RDHM) o+m (SWAT) o+m (SWAT) m (SWAT) o+m (SWAT) m (SWAT) o+m (GR4J) o |
| Catchment | Area | Mean Discharge | Orthic Podzols | Dystric Cambisols | Lithosols | Evergreen Forest | Bare Rock | Moors and Heathland |
|---|---|---|---|---|---|---|---|---|
| (b1) Sill River | 853 km2 | 25.1 m3 s−1 | 39% | 20% | 15% | 31% | 26% | 23% |
| (b2) Drava River | 669 km2 | 13.7 m3 s−1 | 17% | 31% | 15% | 46% | 25% | 17% |
| (b3) Isel River | 1197 km2 | 39.9 m3 s−1 | 40% | 21% | 21% | 26% | 40% | 23% |
| Catchment | b1_ | Sill | b2_ | Drava | b3_ | Isel | Average Elev. (m a.s.l.) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gauges | Name | Dresdner Hütte | Trins | Schönberg im Stubaital | Hochberg | Kartitsch | Toblach | Felbertauerntunnel-Süd | Prägraten | St.Johann im Walde | b1 | b2 | b3 |
| ID | b1_DH | b1_SS | b1_TR | b2_HO | b2_KA | b2_TO | b3_FT | b3_PR | b3_SJ | ||||
| Elevation | 2290 | 1235 | 1009 | 1672 | 1374 | 1219 | 1637 | 1340 | 750 | 1511 | 1422 | 1242 | |
| CHIRPS points | Y coord. | 46.975 | 47.075 | 47.175 | 46.825 | 46.725 | 46.725 | 47.099 | 47.025 | 46.882 | |||
| X coord. | 11.125 | 11.425 | 11.425 | 12.375 | 12.525 | 12.225 | 12.539 | 12.375 | 12.653 | ||||
| Elevation | 2984 | 1355 | 971 | 2128 | 1724 | 1211 | 2154 | 1323 | 839 | 1770 | 1688 | 1439 | |
| ERA5 points | Y coord. | 47.030 | 47.000 | 47.230 | 46.800 | 46.800 | 46.800 | 47.220 | 47.000 | 46.200 | |||
| X coord. | 11.250 | 11.500 | 11.500 | 12.250 | 12.500 | 12.250 | 12.520 | 12.510 | 12.830 | ||||
| Elevation | 2665 | 1556 | 907 | 2011 | 1684 | 1050 | 2078 | 1231 | 868 | 1864 | 1582 | 1392 | |
| Statistical Metric | Equation | Optimal Value |
|---|---|---|
| Bias (B) | 0 | |
| Percent bias (PB) | 0 | |
| Mean absolute error (MAE) | 0 | |
| Relative mean absolute error (RMAE) | 0 | |
| Coefficient of determination (R2) | 1 | |
| Nash–Sutcliffe efficiency (NSE) | 1 |
| Indicator | Station | Annual | Warm | Cold | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg | LinT | Avg | LinT | Avg | LinT | |||||
| TG | SO | −5.2 | 0.31 | *** | −0.3 | 0.31 | *** | −10.7 | 0.34 | *** |
| (°C 10y−1) | ZU | −4.4 | 0.20 | *** | 0.4 | 0.22 | *** | −9.6 | 0.19 | * |
| HO | 7.0 | 0.30 | *** | 12.4 | 0.30 | *** | 1.5 | 0.31 | *** | |
| IN | 9.8 | 0.29 | *** | 15.9 | 0.25 | *** | 4.1 | 0.33 | *** | |
| P | SO | 1664 | 91 | *** | 847 | 48 | *** | 540 | 25 | ** |
| (mm 10y−1) | ZU | 2006 | 26 | 960 | 20 | * | 714 | −1 | ||
| HO | 1162 | 2 | 772 | 8 | 261 | −7 | ||||
| IN | 886 | 3 | 587 | 10 | + | 193 | −6 | |||
| SD | SO | 272 | −11 | + | 256 | −13 | * | 348 | −15 | |
| (cm 10y−1) | ZU | 214 | −5 | 169 | 0 | 317 | −9 | + | ||
| HO | 19 | −1 | * | 6 | 0 | 21 | −2 | * | ||
| Q | b1_INN | 24.7 | 0.34 | + | 37.8 | 0.23 | 10.5 | 0.31 | * | |
| (m3 s−1 10y−1) | b2_RAB | 9.0 | −0.22 | + | 12.5 | −0.42 | * | 4.9 | −0.08 | ** |
| b3_LIE | 39.3 | 0.33 | 66.0 | 0.11 | 10.3 | 0.39 | * | |||
| Parameter | Description | Calibration Range | |||||
|---|---|---|---|---|---|---|---|
| V_TLAPS.sub | Temperature lapse rate (°C/km) | −8–−2 | |||||
| V_PLAPS.sub | Precipitation lapse rate (mm/1000 m) | 0–100 | |||||
| V_SFTMP.bsn | Snowfall temperature (°C) | −5–5 | |||||
| V_SMTMP.bsn | Snowmelt temperature (°C) | −5–5 | |||||
| V_SMFMX.bsn | Maximal snowmelt factor—21st of June (mm/day) | 5–10 | |||||
| V_SMFMN.bsn | Minimal snowmelt factor—21st of December (mm/day) | 0–5 | |||||
| V_TIMP.bsn | Snow temperature lag factor (-) | 0–1 | |||||
| b1 Sill | b2 Drava | b3 Isel | |||||
| Calibration range | Fitted value | Calibration range | Fitted value | Calibration range | Fitted value | ||
| R_CN2.mgt | Soil conservation services (SCS) runoff curve number | −0.2–0.2 | 0.081 | −0.2–0.2 | −0.143 | −0.2–0.2 | −0.066 |
| A_GWQMN.gw | Threshold depth of water in shallow aquifer for return flow (mm) | 0–300 | 250.50 | −300–300 | 145.80 | −300–0 | −90.30 |
| R_ESCO.hru | Soil evaporation compensation coefficient | −0.25–0.25 | 0.103 | −0.25–0.25 | 0.151 | −0.25–0.25 | 0.019 |
| V_GW_DELAY.gw | Delay time for aquifer recharge (days) | 0–300 | 33.90 | 0–300 | 24.90 | 0–300 | 23.10 |
| A_SLSUBBSN.hru | Average slope length (m) | −9–115 | 13.44 | −9–115 | 90.324 | −9–115 | 2.53 |
| R_GW_REVAP.gw | Groundwater “revap” coefficient | 0–0.2 | 0.028 | −0.2–0.2 | 0.199 | −0.2–0 | −0.183 |
| R_REVAPMN.gw | Threshold depth of water in the shallow aquifer for “revap” or percolation to occur (mm H20) | −0.2–0 | −0.109 | −0.2–0.2 | −0.058 | 0–0.2 | 0.067 |
| V_ALPHA_BF.gw | Baseflow alpha factor (1/days) | 0–1 | 0.427 | 0–1 | 0.147 | 0–1 | 0.177 |
| R_SOL_AWC().sol | Available water capacity of the soil layer (mm H20/mm soil) | −0.05–0.05 | 0.034 | −0.05–0.05 | 0.04 | −0.05–0.05 | −0.047 |
| V_RCHRG_DP.gw | Deep aquifer percolation fraction | 0–1 | 0.251 | 0–1 | 0.543 | 0–1 | 0.155 |
| Station | b1_KRO | b1_PUI | b1_INN | b2_AUS | b2_RAB | b2_LIE | b3_HOP | b3_BRU | b3_LIE | |
|---|---|---|---|---|---|---|---|---|---|---|
| Drainage area (km2) | 127 | 342 | 853 | 62 | 375 | 669 | 268 | 514 | 1197 | |
| Calibration | p-factor | 0.73 | 0.73 | 0.76 | 0.58 | 0.76 | 0.77 | 0.77 | 0.69 | 0.79 |
| r-factor | 0.70 | 1.02 | 1.00 | 1.05 | 0.99 | 1.03 | 0.58 | 0.43 | 0.54 | |
| R2 | 0.81 | 0.89 | 0.93 | 0.27 | 0.73 | 0.78 | 0.91 | 0.96 | 0.95 | |
| NSE | 0.76 | 0.87 | 0.90 | 0.21 | 0.71 | 0.67 | 0.87 | 0.91 | 0.93 | |
| Validation | p-factor | 0.63 | 0.80 | 0.77 | 0.62 | 0.70 | 0.73 | 0.68 | 0.70 | 0.67 |
| r-factor | 0.61 | 0.91 | 0.84 | 1.17 | 1.14 | 1.19 | 0.61 | 0.45 | 0.52 | |
| R2 | 0.88 | 0.88 | 0.91 | 0.33 | 0.47 | 0.51 | 0.84 | 0.96 | 0.93 | |
| NSE | 0.78 | 0.84 | 0.85 | 0.31 | 0.44 | 0.50 | 0.80 | 0.89 | 0.90 | |
| Matrix | Product | mean a | Annual | mean w | Warm | mean c | Cold | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (H) | Elev_3 | Elev_2 | Elev_1 | Elev_3 | Elev_2 | Elev_1 | Elev_3 | Elev_2 | Elev_1 | |||||
| P | OBS | 1022 | 1266 | 945 | 807 | 674 | 811 | 634 | 550 | 348 | 456 | 312 | 257 | |
| (mm) | CHIRPS | 1175 | 1273 | 1085 | 1207 | 775 | 868 | 710 | 765 | 400 | 405 | 375 | 443 | |
| ERA5 | 1397 | 1537 | 1314 | 1354 | 878 | 976 | 825 | 838 | 519 | 561 | 490 | 516 | ||
| PB | CHIRPS | 15% | 1% | 15% | 50% | 15% | 7% | 12% | 39% | 15% | −11% | 20% | 72% | |
| ERA5 | 37% | 21% | 39% | 68% | 30% | 20% | 30% | 52% | 49% | 23% | 57% | 101% | ||
| MAE | CHIRPS | 258 | 221 | 215 | 401 | 156 | 106 | 164 | 215 | 134 | 145 | 99 | 186 | |
| (mm) | ERA5 | 376 | 271 | 369 | 547 | 208 | 171 | 195 | 288 | 176 | 114 | 181 | 258 | |
| RMAE | CHIRPS | 25% | 17% | 23% | 50% | 23% | 13% | 26% | 39% | 39% | 32% | 32% | 72% | |
| ERA5 | 37% | 21% | 39% | 68% | 31% | 21% | 31% | 52% | 51% | 25% | 58% | 101% | ||
| (V) | b1 Sill | b2 Drava | b3 Isel | b1 Sill | b2 Drava | b3 Isel | b1 Sill | b2 Drava | b3 Isel | |||||
| P | OBS | 1022 | 1050 | 966 | 1048 | 674 | 665 | 662 | 694 | 348 | 385 | 304 | 354 | |
| (mm) | CHIRPS | 1175 | 1018 | 982 | 1525 | 775 | 694 | 650 | 980 | 400 | 324 | 332 | 545 | |
| ERA5 | 1397 | 1471 | 1224 | 1497 | 878 | 931 | 775 | 928 | 519 | 540 | 449 | 569 | ||
| PB | CHIRPS | 15% | −3% | 2% | 45% | 15% | 4% | −2% | 41% | 15% | −16% | 9% | 54% | |
| ERA5 | 37% | 40% | 27% | 43% | 30% | 40% | 17% | 34% | 49% | 40% | 48% | 61% | ||
| MAE | CHIRPS | 258 | 197 | 101 | 477 | 156 | 79 | 102 | 287 | 134 | 135 | 68 | 199 | |
| (mm) | ERA5 | 376 | 421 | 258 | 449 | 208 | 265 | 122 | 236 | 176 | 162 | 149 | 216 | |
| RMAE | CHIRPS | 25% | 19% | 10% | 45% | 23% | 12% | 15% | 41% | 39% | 35% | 22% | 56% | |
| ERA5 | 37% | 40% | 27% | 43% | 31% | 40% | 18% | 34% | 51% | 42% | 49% | 61% | ||
| Monthly | mean m | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
| P | OBS | 85 | 42 | 36 | 55 | 66 | 89 | 124 | 140 | 129 | 94 | 97 | 95 | 54 |
| (mm) | CHIRPS | 98 | 52 | 51 | 62 | 78 | 148 | 130 | 147 | 134 | 115 | 101 | 95 | 63 |
| ERA5 | 116 | 64 | 61 | 91 | 105 | 133 | 169 | 176 | 164 | 120 | 115 | 116 | 82 | |
| R2 | CHIRPS | 0.83 | 0.76 | 0.70 | 0.65 | 0.72 | 0.84 | 0.89 | 0.92 | 0.93 | 0.86 | 0.84 | 0.84 | 0.75 |
| ERA5 | 0.91 | 0.89 | 0.87 | 0.87 | 0.88 | 0.93 | 0.93 | 0.92 | 0.92 | 0.93 | 0.92 | 0.91 | 0.89 | |
| PB | CHIRPS | 15% | 23% | 40% | 13% | 18% | 66% | 5% | 5% | 4% | 22% | 4% | 1% | 17% |
| ERA5 | 37% | 51% | 69% | 66% | 59% | 49% | 36% | 25% | 27% | 28% | 19% | 23% | 53% | |
| MAE | CHIRPS | 34 | 22 | 24 | 30 | 35 | 64 | 35 | 33 | 28 | 37 | 35 | 36 | 27 |
| (mm) | ERA5 | 37 | 24 | 26 | 38 | 42 | 46 | 50 | 48 | 46 | 32 | 30 | 34 | 31 |
| RMAE | CHIRPS | 40% | 52% | 67% | 56% | 53% | 71% | 28% | 24% | 22% | 39% | 36% | 38% | 50% |
| ERA5 | 44% | 56% | 72% | 71% | 63% | 52% | 41% | 34% | 36% | 34% | 31% | 36% | 57% |
| Matrix | Product | mean a | Annual | mean w | Warm | mean c | Cold | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (H) | Elev_3 | Elev_2 | Elev_1 | Elev_3 | Elev_2 | Elev_1 | Elev_3 | Elev_2 | Elev_1 | |||||
| TP | OBS | 51 | 57 | 52 | 42 | 18 | 34 | 6 | 18 | 33 | 23 | 46 | 24 | |
| (mm 10y-1) | CHIRPS | 64 | 52 | 64 | 83 | 49 | 42 | 50 | 57 | 15 | 10 | 14 | 26 | |
| ERA5 | 68 | 67 | 64 | 80 | 36 | 46 | 30 | 34 | 32 | 21 | 34 | 46 | ||
| B | CHIRPS | 13 | −5 | 12 | 41 | 31 | 8 | 44 | 39 | −18 | −13 | −31 | 2 | |
| (mm 10y-1) | ERA5 | 17 | 10 | 12 | 38 | 18 | 12 | 24 | 17 | −1 | −2 | −12 | 21 | |
| PB | CHIRPS | 25% | −10% | 24% | 98% | 170% | 22% | 707% | 221% | −54% | −57% | −69% | 7% | |
| ERA5 | 33% | 17% | 23% | 91% | 101% | 35% | 388% | 93% | −4% | −9% | −26% | 89% | ||
| MAE | CHIRPS | 25 | 9 | 25 | 48 | 38 | 21 | 48 | 45 | 24 | 25 | 33 | 3 | |
| (mm 10y-1) | ERA5 | 25 | 27 | 17 | 38 | 25 | 23 | 29 | 19 | 16 | 4 | 23 | 21 | |
| (V) | b1 Sill | b2 Drava | b3 Isel | b1 Sill | b2 Drava | b3 Isel | b1 Sill | b2 Drava | b3 Isel | |||||
| TP | OBS | (+)51 | 39 | (+)60 | 55 | (*)18 | (*)38 | (*)−15 | (*)31 | (+)33 | 1 | (+)75 | 24 | |
| (mm 10y-1) | CHIRPS | 64 | (+)37 | 83 | (*)73 | (*)49 | 29 | (*)53 | 64 | (+)15 | 8 | (+)30 | (+)8 | |
| ERA5 | 68 | (+)49 | 87 | (*)69 | 36 | 39 | 28 | 42 | 32 | 10 | 59 | 28 | ||
| B | CHIRPS | 13 | −2 | 23 | 17 | 31 | −9 | 68 | 33 | −18 | 7 | −45 | −16 | |
| (mm 10y-1) | ERA5 | 17 | 10 | 27 | 14 | 18 | 1 | 43 | 11 | −1 | 9 | −16 | 3 | |
| PB | CHIRPS | 25% | −6% | 39% | 31% | 170% | −24% | −457% | 107% | −54% | 618% | −60% | −65% | |
| ERA5 | 33% | 25% | 45% | 26% | 101% | 3% | −289% | 35% | −4% | 807% | −21% | 14% | ||
| MAE | CHIRPS | 25 | 6 | 27 | 42 | 38 | 9 | 68 | 38 | 24 | 7 | 45 | 19 | |
| (mm 10y-1) | ERA5 | 25 | 10 | 33 | 32 | 25 | 9 | 43 | 22 | 16 | 9 | 21 | 19 | |
| Monthly | mean m | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
| TP | OBS | 4.2 | (*)17.9 | (*)12.4 | −2.3 | (+)−9.7 | (+)10.1 | −5.8 | −3.3 | (*)26.6 | 0.5 | −13.0 | 15.7 | 1.9 |
| (mm 10y-1) | CHIRPS | 5.4 | (*)17.2 | (*)10.7 | −6.2 | (*)−17.1 | 1.9 | (*)7.7 | 2.3 | (**)20.1 | (*)9.4 | 7.4 | 7.4 | 3.4 |
| ERA5 | 5.7 | (*)23.5 | (*)19.6 | −0.5 | (+)−19.9 | 12.3 | −2.5 | 6.3 | (*)24.6 | −0.6 | −3.8 | 7.4 | 2.1 | |
| R2 | CHIRPS | 0.37 | 0.89 | 0.83 | 0.19 | 0.79 | 0.12 | 0.24 | 0.03 | 0.85 | 0.06 | 0.39 | 0.78 | 0.35 |
| ERA5 | 0.63 | 0.89 | 0.84 | 0.78 | 0.78 | 0.90 | 0.17 | 0.31 | 0.86 | 0.35 | 0.43 | 0.68 | 0.40 | |
| B | CHIRPS | 0.7 | −0.7 | −1.7 | −3.9 | −7.4 | −8.2 | 13.5 | 5.6 | −6.5 | 8.9 | 17.2 | −8.3 | 1.5 |
| (mm 10y-1) | ERA5 | 1.5 | 5.6 | 7.1 | 1.9 | −10.2 | 2.3 | 3.3 | 9.6 | −2.0 | −1.0 | 9.2 | −8.4 | 0.2 |
| PB | CHIRPS | 16% | −4% | −14% | 166% | 76% | −81% | −231% | −171% | −24% | 1925% | −133% | −53% | 81% |
| ERA5 | 35% | 31% | 57% | −80% | 105% | 22% | −57% | −292% | −7% | −227% | −71% | −53% | 12% | |
| MAE | CHIRPS | 9.5 | 5.2 | 4.6 | 9.6 | 9.0 | 8.2 | 13.8 | 7.6 | 10.6 | 10.1 | 20.3 | 10.5 | 4.0 |
| (mm 10y-1) | ERA5 | 7.5 | 7.3 | 7.8 | 4.8 | 10.5 | 3.8 | 7.2 | 11.5 | 9.4 | 3.4 | 10.9 | 9.1 | 4.0 |
| Matrix | Product | mean a | Annual | mean w | Warm | mean c | Cold | mean m | Monthly | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| outlets | b1_INN | b3_LIE | b1_INN | b3_LIE | b1_INN | b3_LIE | b1_INN | b3_LIE | ||||||
| Q | OBS | 990 | 929 | 1050 | 784 | 698 | 870 | 201 | 228 | 175 | 82 | 77 | 87 | |
| (mm) | CHIRPS | 877 | 824 | 930 | 734 | 650 | 817 | 143 | 173 | 113 | 73 | 68 | 78 | |
| ERA5 | 1069 | 1185 | 952 | 831 | 830 | 831 | 238 | 356 | 121 | 89 | 98 | 80 | ||
| MEAS | 854 | 811 | 896 | 702 | 635 | 769 | 152 | 176 | 128 | 71 | 67 | 75 | ||
| PB | CHIRPS | −11% | −11% | −11% | −6% | −7% | −6% | −30% | −24% | −35% | −11% | −11% | −11% | |
| ERA5 | 9% | 28% | −9% | 7% | 19% | −5% | 13% | 56% | −31% | 10% | 28% | −9% | ||
| MEAS | −14% | −13% | −15% | −10% | −9% | −12% | −25% | −22% | −27% | −13% | −12% | −14% | ||
| MAE | CHIRPS | 123 | 105 | 141 | 78 | 56 | 100 | 58 | 55 | 61 | 17 | 14 | 19 | |
| (mm) | ERA5 | 186 | 261 | 112 | 106 | 135 | 78 | 92 | 130 | 54 | 21 | 25 | 17 | |
| MEAS | 136 | 118 | 154 | 84 | 66 | 102 | 51 | 52 | 49 | 15 | 13 | 16 | ||
| RMAE | CHIRPS | 12% | 11% | 13% | 10% | 8% | 11% | 30% | 24% | 35% | 20% | 19% | 21% | |
| ERA5 | 19% | 28% | 11% | 14% | 19% | 9% | 44% | 57% | 31% | 26% | 33% | 20% | ||
| MEAS | 14% | 13% | 15% | 11% | 10% | 12% | 25% | 23% | 28% | 18% | 17% | 19% | ||
| NSE | CHIRPS | 0.865 | 0.871 | 0.860 | ||||||||||
| ERA5 | 0.758 | 0.646 | 0.871 | |||||||||||
| MEAS | 0.881 | 0.877 | 0.885 | |||||||||||
| Monthly | all stations | mean m | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| Q | OBS | 80 | 29 | 26 | 30 | 50 | 128 | 165 | 142 | 112 | 83 | 69 | 55 | 69 |
| (mm) | CHIRPS | 72 | 16 | 11 | 14 | 46 | 127 | 147 | 133 | 104 | 76 | 63 | 54 | 69 |
| ERA5 | 100 | 40 | 32 | 45 | 89 | 142 | 169 | 164 | 143 | 115 | 97 | 86 | 83 | |
| MEAS | 70 | 17 | 11 | 14 | 45 | 118 | 141 | 125 | 98 | 82 | 71 | 56 | 66 | |
| R2 | CHIRPS | 0.93 | 0.91 | 0.86 | 0.80 | 0.94 | 0.96 | 0.99 | 0.98 | 0.97 | 0.97 | 0.93 | 0.96 | 0.92 |
| ERA5 | 0.94 | 0.92 | 0.88 | 0.90 | 0.95 | 0.95 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.97 | 0.87 | |
| MEAS | 0.95 | 0.89 | 0.86 | 0.85 | 0.94 | 0.98 | 0.98 | 0.98 | 0.99 | 0.98 | 0.99 | 0.99 | 0.94 | |
| PB | CHIRPS | −17% | −45% | −55% | −52% | −8% | 0% | −11% | −6% | −7% | −8% | −9% | 0% | −1% |
| ERA5 | 34% | 38% | 24% | 51% | 77% | 11% | 3% | 16% | 28% | 40% | 40% | 58% | 19% | |
| MEAS | −17% | −42% | −57% | −53% | −11% | −8% | −15% | −12% | −13% | −1% | 4% | 3% | −5% | |
| MAE | CHIRPS | 15 | 13 | 14 | 16 | 10 | 18 | 23 | 17 | 17 | 11 | 15 | 10 | 19 |
| (mm) | ERA5 | 25 | 14 | 10 | 17 | 40 | 30 | 17 | 26 | 32 | 33 | 28 | 32 | 27 |
| MEAS | 14 | 12 | 14 | 16 | 10 | 16 | 25 | 21 | 15 | 9 | 6 | 7 | 15 | |
| RMAE | CHIRPS | 26% | 45% | 55% | 54% | 19% | 14% | 14% | 12% | 15% | 14% | 22% | 18% | 27% |
| ERA5 | 40% | 49% | 37% | 58% | 80% | 23% | 10% | 18% | 28% | 40% | 40% | 58% | 39% | |
| MEAS | 24% | 43% | 57% | 53% | 21% | 13% | 15% | 14% | 13% | 10% | 9% | 13% | 22% |
| Matrix | Product | mean a | Annual | mean w | Warm | mean c | Cold | mean m | Monthly | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| outlet | b1_INN | b3_LIE | b1_INN | b3_LIE | b1_INN | b3_LIE | b1_INN | b3_LIE | ||||||
| TQ | OBS | 40.2 | 30.4 | 50.0 | 19.8 | 9.9 | 29.6 | (*)20.5 | (+)20.6 | (*)20.3 | 3.4 | 2.6 | 4.2 | |
| (mm 10y−1) | CHIRPS | (*)46.9 | 26.3 | (*)67.5 | (+)30.2 | 6.8 | (+)53.6 | (+)16.7 | 19.5 | (+)13.9 | 3.9 | 2.2 | 5.6 | |
| ERA5 | 43.2 | 22.9 | 63.6 | 24.1 | −2.5 | 50.6 | 19.2 | 25.4 | 13.0 | 3.6 | 1.9 | 5.3 | ||
| MEAS | (+)44.9 | 18.1 | (+)71.8 | (+)27.9 | 4.0 | (+)51.8 | 17.0 | 14.0 | 19.9 | 3.7 | 1.5 | 6.0 | ||
| B | CHIRPS | 6.7 | −4.0 | 17.5 | 10.4 | −3.1 | 24.0 | −3.8 | −1.1 | −6.4 | 0.5 | −0.4 | 1.4 | |
| (mm 10y−1) | ERA5 | 3.0 | −7.5 | 13.6 | 4.3 | −12.4 | 21.0 | −1.3 | 4.7 | −7.3 | 0.2 | −0.7 | 1.1 | |
| MEAS | 4.7 | −12.3 | 21.8 | 8.2 | −5.9 | 22.2 | −3.5 | −6.6 | −0.4 | 0.4 | −1.1 | 1.8 | ||
| PB | CHIRPS | 17% | −13% | 35% | 53% | −31% | 81% | −18% | −5% | −32% | 10% | −14% | 34% | |
| ERA5 | 8% | −25% | 27% | 22% | −125% | 71% | −6% | 23% | −36% | 0% | −26% | 26% | ||
| MEAS | 12% | −41% | 44% | 41% | −59% | 75% | −17% | −32% | −2% | 1% | −41% | 43% | ||
| MAE | CHIRPS | 10.8 | 4.0 | 17.5 | 13.5 | 3.1 | 24.0 | 3.8 | 1.1 | 6.4 | 3.0 | 3.2 | 2.9 | |
| (mm 10y−1) | ERA5 | 10.6 | 7.5 | 13.6 | 16.7 | 12.4 | 21.0 | 6.0 | 4.7 | 7.3 | 4.1 | 4.3 | 4.0 | |
| MEAS | 17.0 | 12.3 | 21.8 | 14.0 | 5.9 | 22.2 | 3.5 | 6.6 | 0.4 | 2.7 | 2.4 | 3.1 | ||
| monthly | all stations | mean m | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| TQ | OBS | 2.2 | 1.3 | 0.7 | −0.4 | (*)9.4 | 12.3 | 2.3 | −10.5 | (+)1.4 | (+)6.3 | −3.6 | 5.6 | 1.9 |
| (mm 10y−1) | CHIRPS | 3.3 | 2.0 | 1.4 | 0.0 | (*)9.1 | (+)20.2 | −0.4 | (*)−9.1 | 2.0 | 6.4 | 3.3 | 2.7 | 1.9 |
| ERA5 | 3.5 | (*)4.7 | 2.3 | 1.0 | (*)11.5 | (*)18.9 | (+)11.9 | −7.9 | −0.3 | 1.2 | −2.6 | 1.8 | −0.8 | |
| MEAS | 3.8 | (*)2.1 | 1.6 | −0.3 | 9.7 | (*)16.9 | (*)12.8 | (+)−10.4 | 4.5 | 7.1 | −2.3 | 3.2 | 1.0 | |
| R2 | CHIRPS | 0.55 | 0.96 | 0.77 | 0.03 | 0.71 | 0.92 | 0.03 | 0.65 | 0.54 | 0.99 | 0.24 | 0.76 | 0.74 |
| ERA5 | 0.43 | 0.96 | 0.89 | 0.00 | 0.66 | 0.90 | 0.19 | 0.63 | 0.01 | 0.75 | 0.72 | 0.87 | 0.14 | |
| MEAS | 0.52 | 0.81 | 0.72 | 0.06 | 0.95 | 0.80 | 0.23 | 0.60 | 0.45 | 0.84 | 0.51 | 0.71 | 0.82 | |
| B | CHIRPS | 1.1 | 0.7 | 0.7 | 0.3 | −0.3 | 7.9 | −2.7 | 1.4 | 0.7 | 0.0 | 7.0 | −2.8 | 0.0 |
| (mm 10y−1) | ERA5 | 1.3 | 3.4 | 1.5 | 1.4 | 2.2 | 6.6 | 9.6 | 2.6 | −1.6 | −5.1 | 1.0 | −3.7 | −2.6 |
| MEAS | 1.6 | 0.8 | 0.8 | 0.1 | 0.3 | 4.6 | 10.4 | 0.1 | 3.1 | 0.8 | 1.4 | −2.3 | −0.9 | |
| PB | CHIRPS | 48% | 52% | 95% | −91% | −3% | 64% | −117% | −13% | 48% | 0% | −192% | −50% | −2% |
| ERA5 | 57% | 264% | 208% | −380% | 23% | 54% | 412% | −24% | −120% | −80% | −28% | −67% | −140% | |
| MEAS | 72% | 64% | 111% | −18% | 3% | 38% | 449% | −1% | 225% | 12% | −37% | −42% | −45% | |
| MAE | CHIRPS | 4.0 | 0.7 | 0.8 | 0.5 | 5.0 | 7.9 | 10.5 | 6.4 | 4.6 | 0.9 | 7.0 | 3.5 | 0.8 |
| (mm 10y−1) | ERA5 | 5.0 | 3.4 | 1.5 | 1.4 | 7.2 | 6.6 | 14.1 | 5.1 | 6.8 | 5.5 | 2.2 | 3.7 | 2.6 |
| MEAS | 4.0 | 0.9 | 0.9 | 0.6 | 1.7 | 7.2 | 13.8 | 8.1 | 5.2 | 2.8 | 2.4 | 3.4 | 1.0 |
| Catchment | Area 1990 (km2) | Area 2006 (km2) | Area 2012 (km2) | Area 2018 (km2) | 1990–2018 Difference (km2) | 1990–2018 Difference (%) |
|---|---|---|---|---|---|---|
| b1 Sill | 29.47 | 19.48 | 20.33 | 19.35 | 10.12 | 34% |
| b3 Isel | 86.44 | 51.00 | 49.32 | 48.40 | 38.04 | 44% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekić, D.; Leskovar, K. Evaluating CHIRPS and ERA5 for Long-Term Runoff Modelling with SWAT in Alpine Headwaters. Water 2025, 17, 2116. https://doi.org/10.3390/w17142116
Bekić D, Leskovar K. Evaluating CHIRPS and ERA5 for Long-Term Runoff Modelling with SWAT in Alpine Headwaters. Water. 2025; 17(14):2116. https://doi.org/10.3390/w17142116
Chicago/Turabian StyleBekić, Damir, and Karlo Leskovar. 2025. "Evaluating CHIRPS and ERA5 for Long-Term Runoff Modelling with SWAT in Alpine Headwaters" Water 17, no. 14: 2116. https://doi.org/10.3390/w17142116
APA StyleBekić, D., & Leskovar, K. (2025). Evaluating CHIRPS and ERA5 for Long-Term Runoff Modelling with SWAT in Alpine Headwaters. Water, 17(14), 2116. https://doi.org/10.3390/w17142116








