Attribution Analysis on Runoff Reduction in the Upper Han River Basin Based on Hydro-Meteorologic and Land Use/Cover Change Data Series
Abstract
1. Introduction
2. Study Area and Data
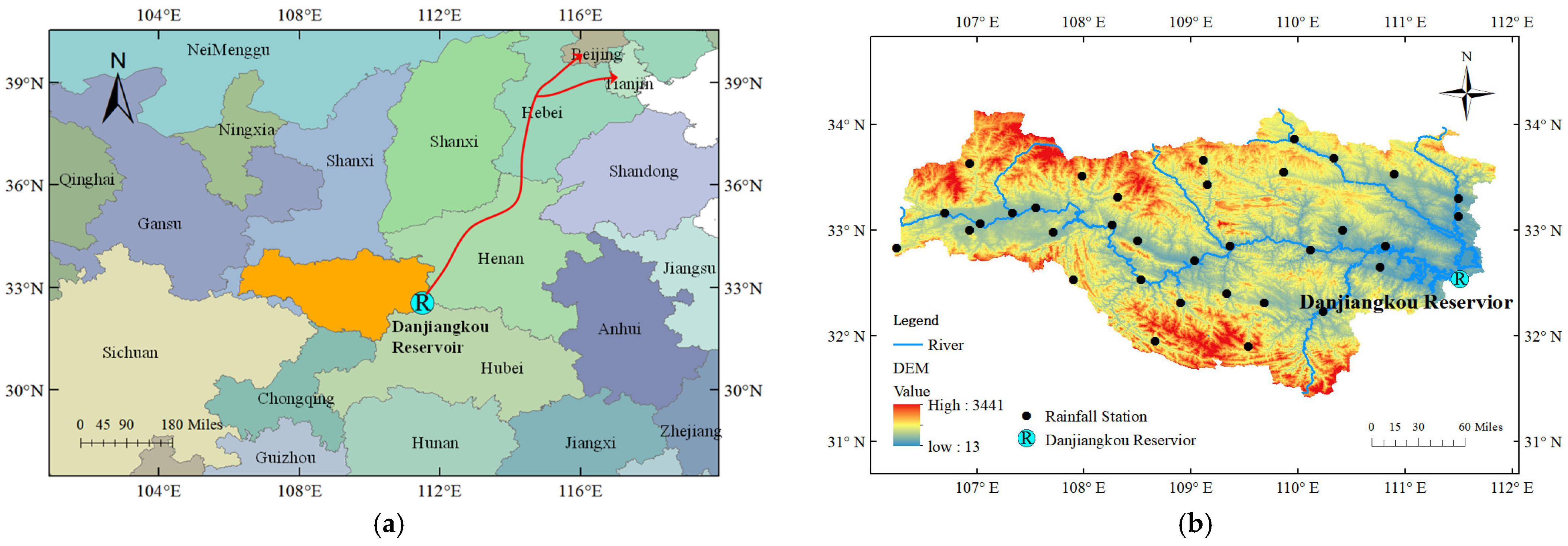
2.1. Study Area
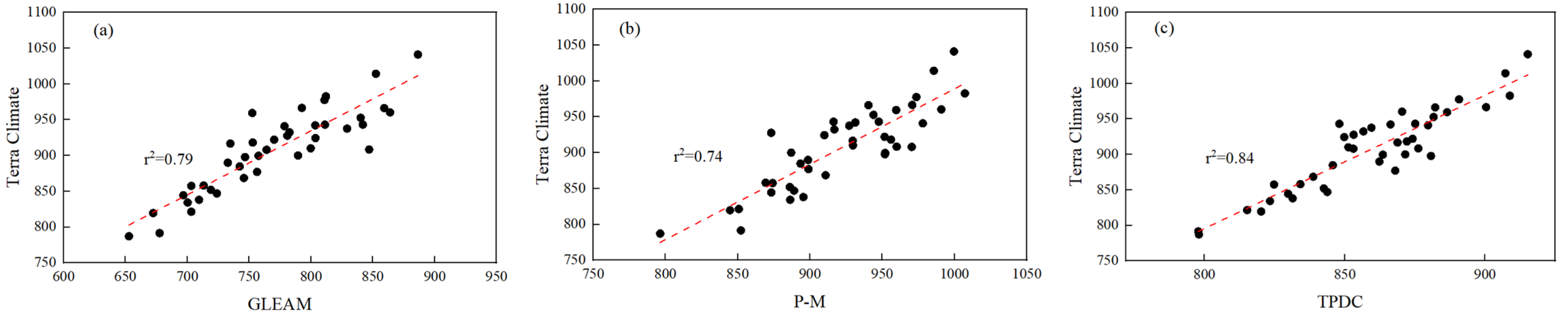
2.2. Data Collection
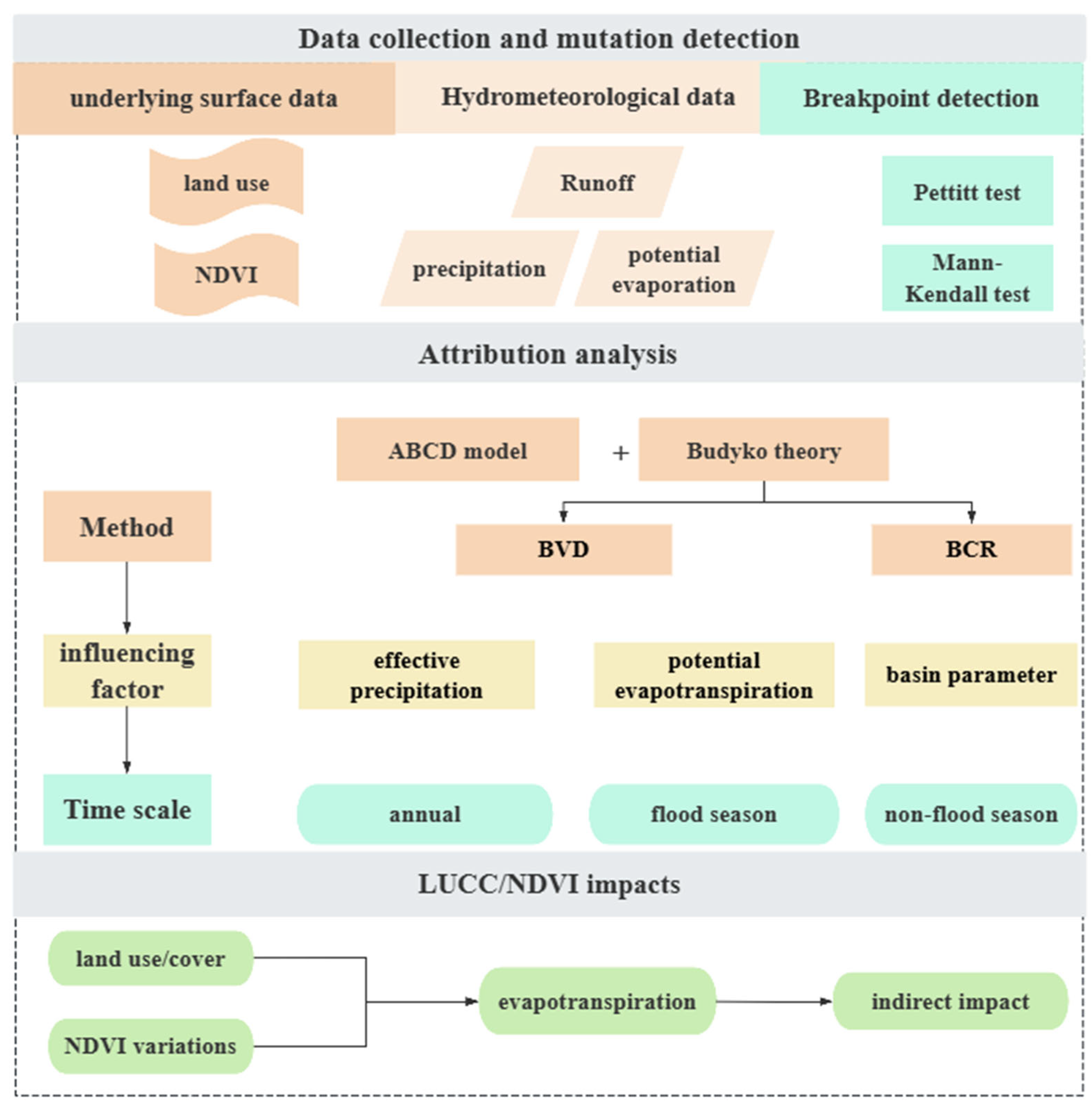
3. Methodology
3.1. Mutation Analysis
3.2. Runoff Sensitivity
3.3. Attribution Analysis of Runoff Change
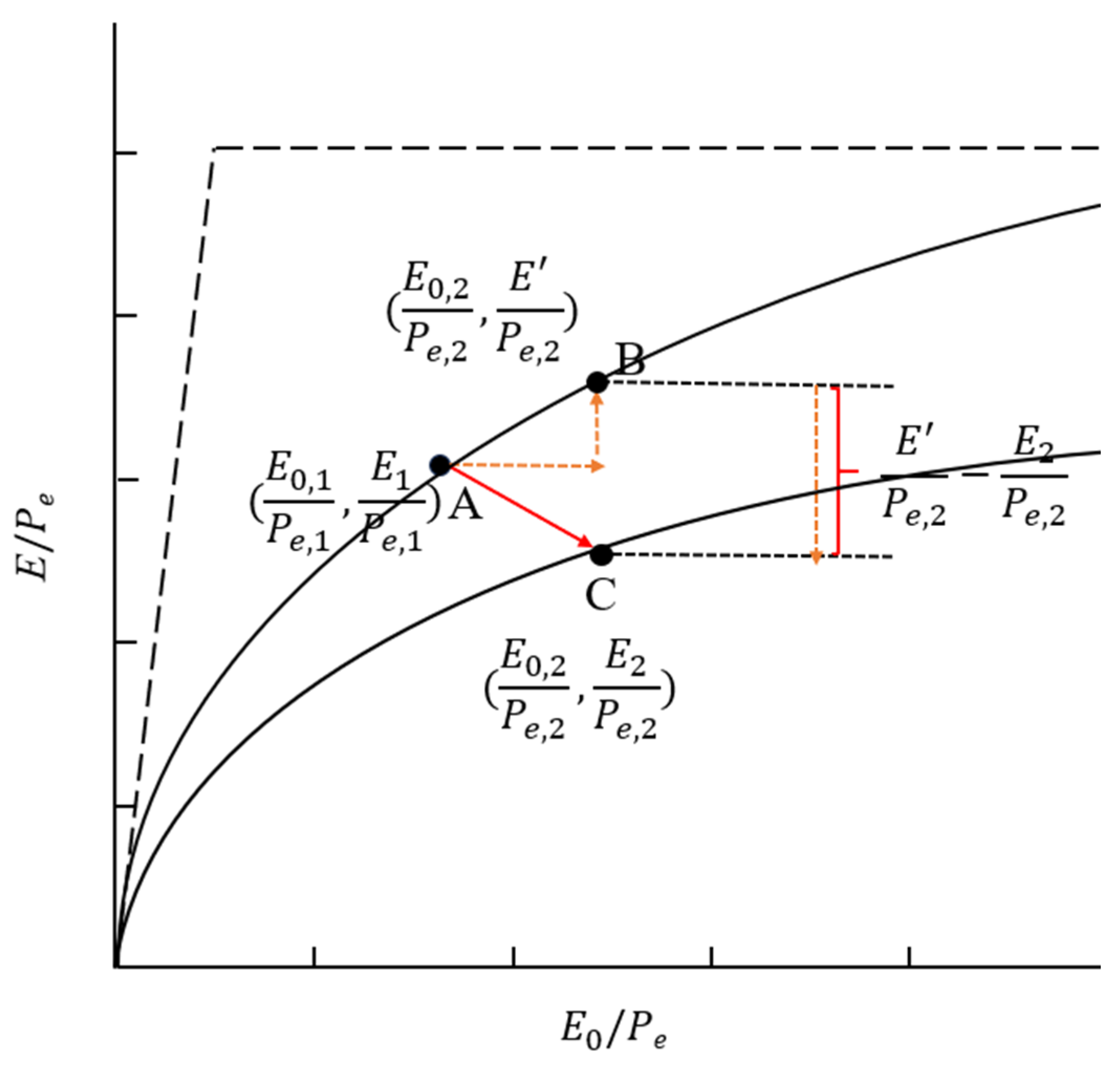
3.3.1. Budyko Vertical Decomposition with Total Differential Method
3.3.2. Budyko Complementary Relationship Method
3.4. Water Storage Simulation
3.5. Land Use/Cover Changes (LUCC)
3.5.1. LUCC Transfer Matrix
3.5.2. LUCC Dynamic Degree
4. Results
4.1. Trend in Runoff and Its Influencing Factors
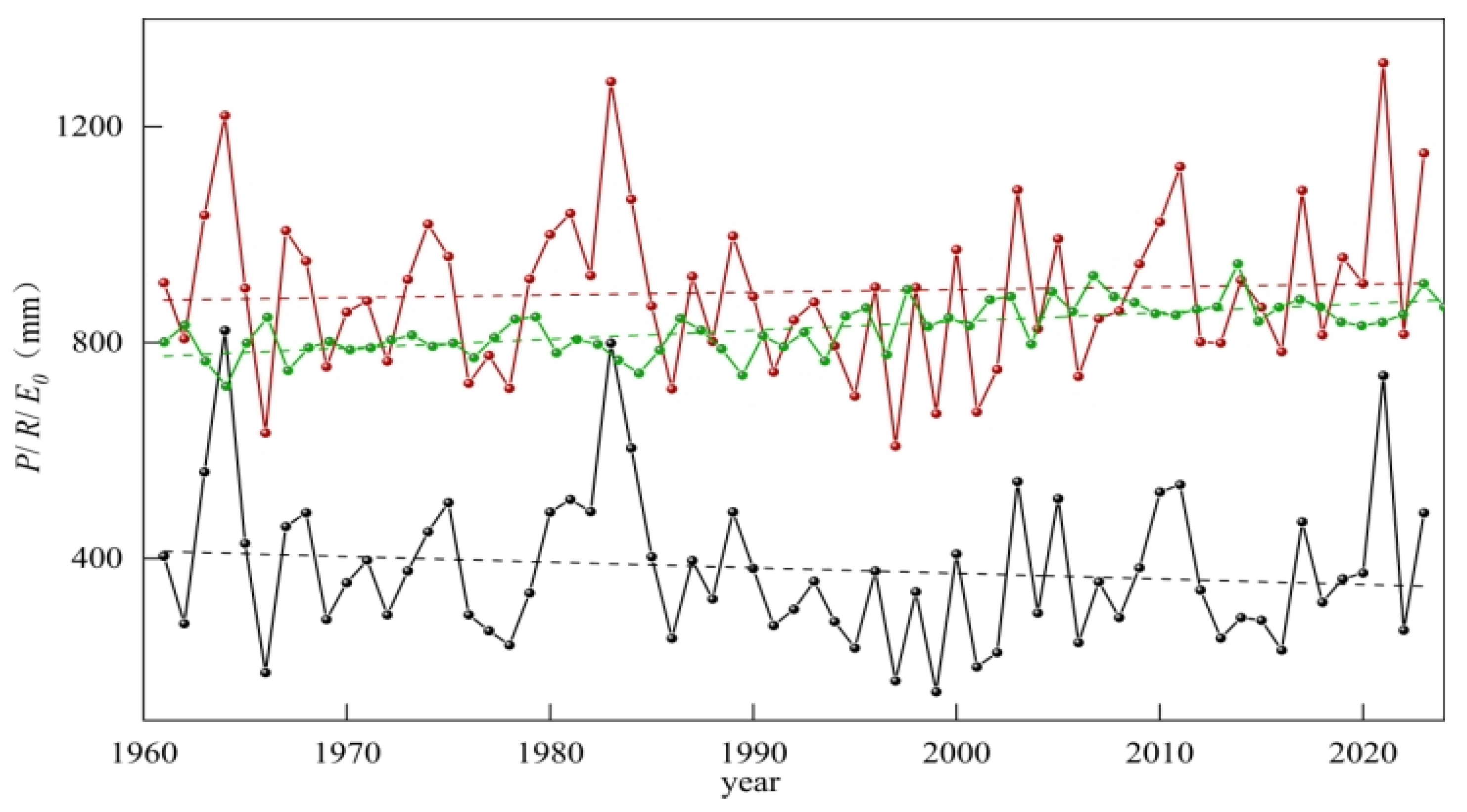
4.1.1. Interannual Variability
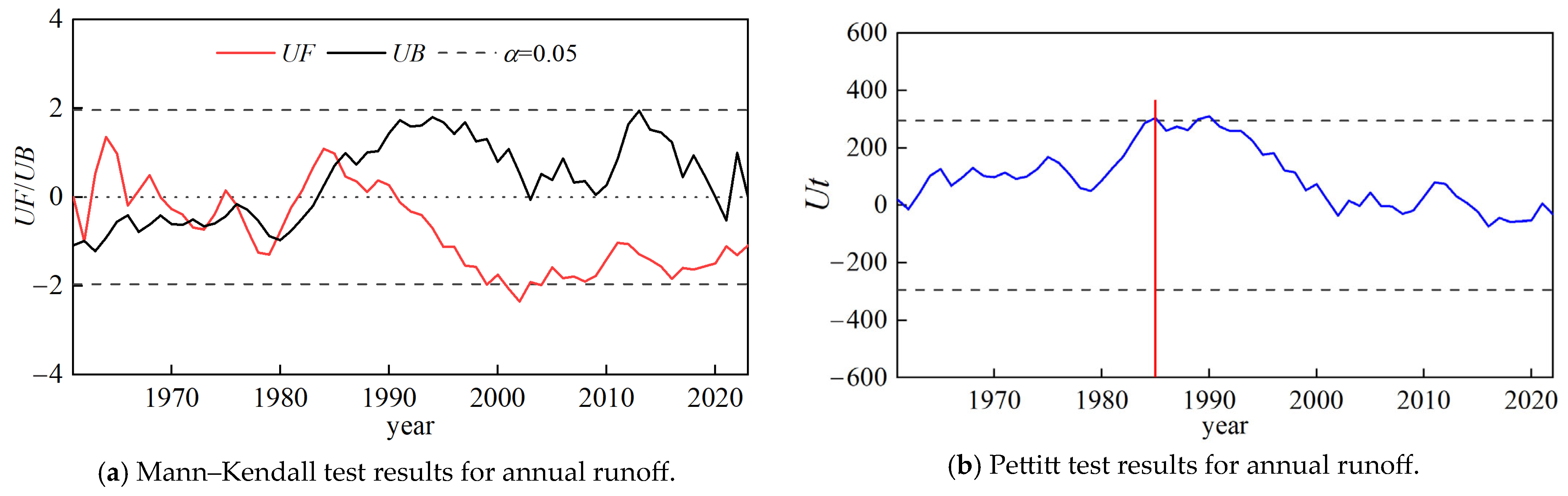
4.1.2. Runoff Mutation Point Detection
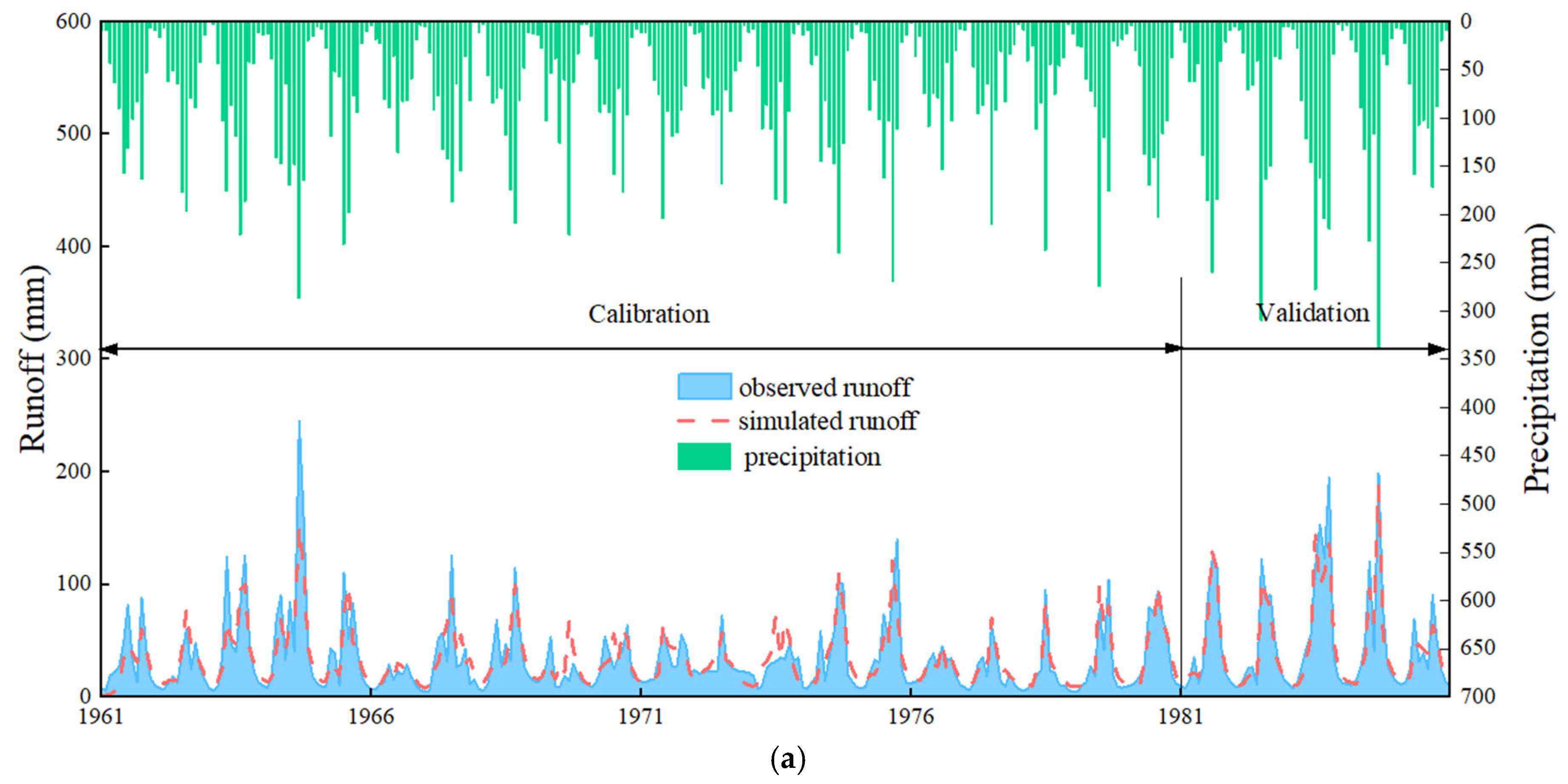
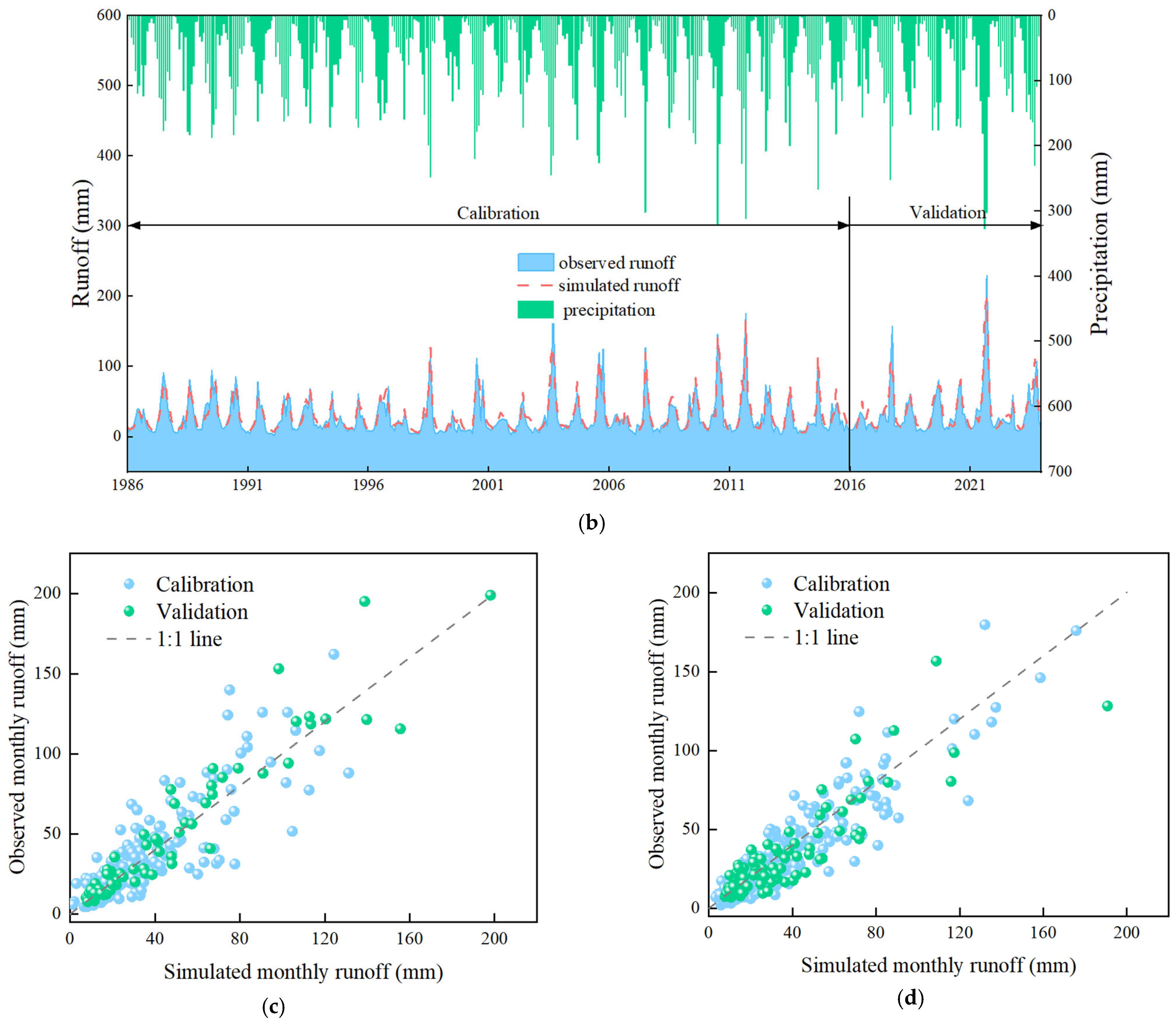
4.2. Calibration and Validation of ABCD Model
4.3. Runoff Attribution Results
4.3.1. Sensitivity Analysis of Runoff Changes
4.3.2. Attribution Analysis Results at Annual and Seasonal Time Scales
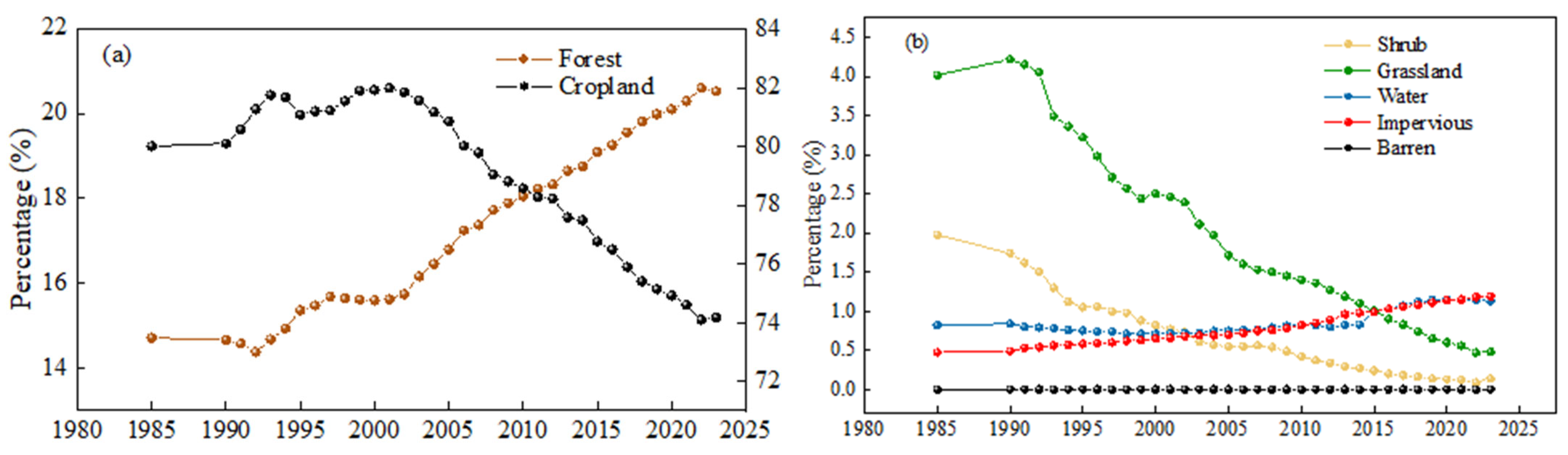
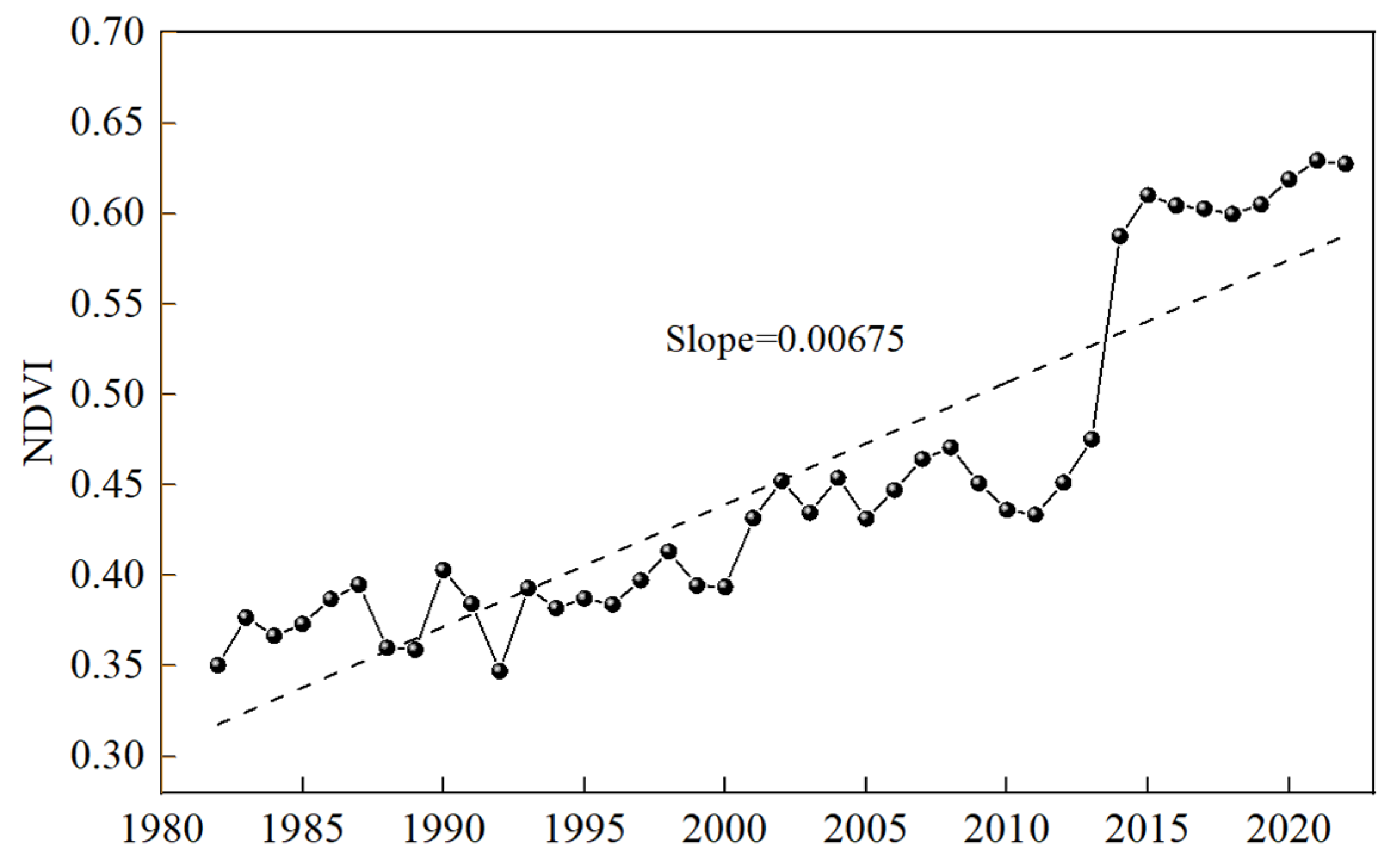
4.4. LUCC and NDVI Variations
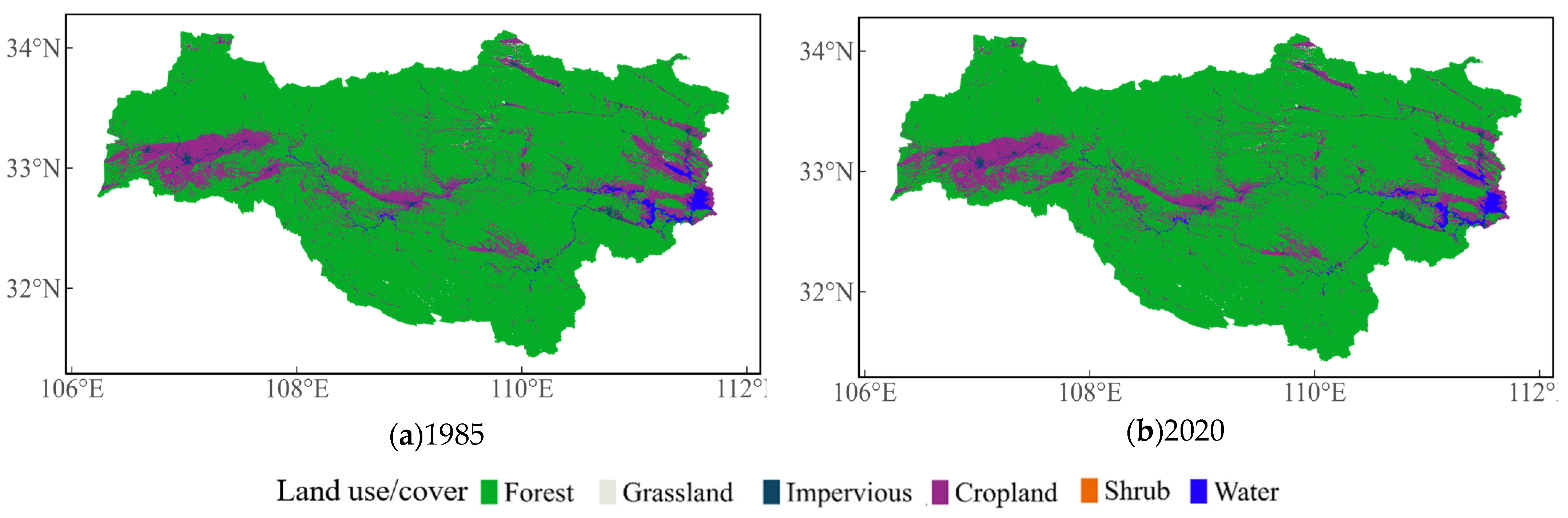
4.4.1. LUCC Variations
4.4.2. NDVI Variations
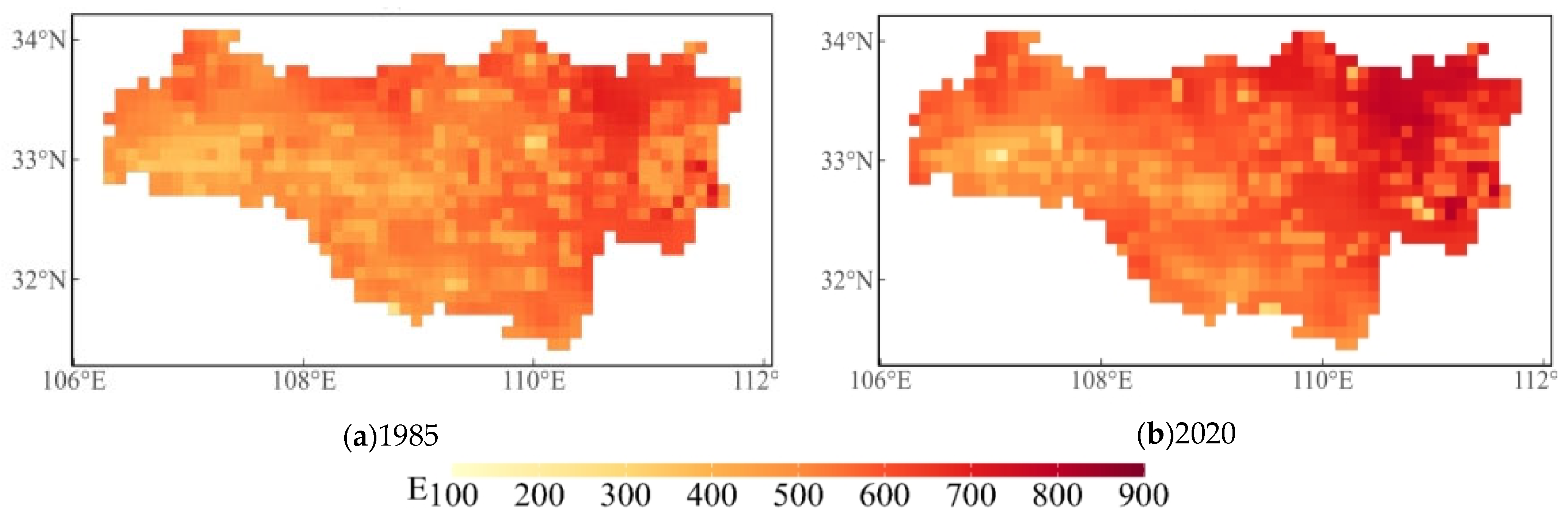
4.5. Estimated Evapotranspiration Variations
5. Discussion
6. Conclusions
- (1)
- The annual runoff of the Danjiangkou Reservoir showed a decreasing trend of 1.71 mm/year from 1961 to 2023 and changed abruptly in 1985. Compared to the reference period, runoff and precipitation decreased while potential evapotranspiration increased during the change period at both the annual and seasonal time scales. Additionally, it is suggested that the dry season accounted for most of the annual runoff reduction.
- (2)
- The proposed BVD-TD and BCR methods yielded consistent results but differed in magnitude, with the BVD-TD method generally overestimating the influence of potential evapotranspiration. Averaging the results of both methods, the annual runoff reduction was attributed mainly to the basin parameter (38.99%), followed by potential evapotranspiration (32.84%), and finally effective precipitation (28.17%).
- (3)
- Meteorological factors were the primary contributors to runoff reduction in the Danjiangkou Reservoir at both the annual and seasonal scales. Effective precipitation exerted a stronger influence during the flood season while potential evapotranspiration played a more significant role in the dry season.
- (4)
- LULC showed that the area of cropland decreased, while the area of forest increased, and the whole basin showed a greening trend as the NDVI increased. Due to land use/cover changes in the upper Han River basin, the annual average actual evapotranspiration increased by 1.163 billion m3 from 1985 to 2023.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wigley, T.M.L.; Jones, P.D. Influences of Precipitation Changes and Direct CO2 Effects on Streamflow. Nature 1985, 314, 149–152. [Google Scholar] [CrossRef]
- Zhan, C.S.; Jiang, S.S.; Sun, F.B.; Jia, Y.W.; Niu, C.W.; Yue, W.F. Quantitative Contribution of Climate Change and Human Activities to Runoff Changes in the Wei River Basin, China. Hydrol. Earth Syst. Sci. 2014, 18, 3069–3077. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global Pattern of Trends in Streamflow and Water Availability in a Changing Climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef]
- Gu, B.; Zhou, S.; Yu, B.; Findell, K.L.; Lintner, B.R. Multifaceted Changes in Water Availability with a Warmer Climate. npj Clim. Atmos. Sci. 2025, 8, 31. [Google Scholar] [CrossRef]
- Xu, X.; Yang, D.; Yang, H.; Lei, H. Attribution Analysis Based on the Budyko Hypothesis for Detecting the Dominant Cause of Runoff Decline in Haihe Basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Lv, X.; Zuo, Z.; Ni, Y.; Sun, J.; Wang, H. The Effects of Climate and Catchment Characteristic Change on Streamflow in a Typical Tributary of the Yellow River. Sci. Rep. 2019, 9, 14535. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Paramaputra, K.; Mousa, A.; Kong, S.Y.; Garg, A.; Anggraini, V. Field Based Analysis of Vegetation and Climate Impacts on the Hydrological Properties of Urban Vegetated Slope. Sci. Rep. 2025, 15, 7702. [Google Scholar] [CrossRef]
- Nadal-Romero, E.; Vicente-Serrano, S.; Lana-Renault, N.; López-Moreno, J.I.; Regües, D.; Lasanta, T.; García-Ruiz, J.M. Plant Cover Determines Runoff Generation in Response to Dry and Wet Conditions. J. Hydrol. 2025, 660, 133495. [Google Scholar] [CrossRef]
- Sankarrao, L.; Rathinasamy, M. Impacts of Agricultural Intensification on the Hydrologic Components for a Coastal River Basin Using Coupled Hydrological Model. Groundw. Sustain. Dev. 2025, 29, 101440. [Google Scholar] [CrossRef]
- Wu, L.; Wang, L.; Li, C.; Zhang, Y.; Wei, J.; Xie, X.; Lv, J. Separating the Contributions of Climate Change and Human Activities to Regional AET Variability by Using a Developed Analytical Framework. Stoch. Environ. Res. Risk Assess. 2020, 34, 1831–1845. [Google Scholar] [CrossRef]
- Xie, M.; Ren, Z.; Li, Z.; Zhang, X.; Ma, X.; Li, P.; Shen, Z. Evolution of the Precipitation–Stream Runoff Relationship in Different Precipitation Scenarios in the Yellow River Basin. Urban Clim. 2023, 51, 101609. [Google Scholar] [CrossRef]
- Bai, X.; Zhao, W. Impacts of Climate Change and Anthropogenic Stressors on Runoff Variations in Major River Basins in China since 1950. Sci. Total Environ. 2023, 898, 165349. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Krysanova, V.; Gong, Y.; Gao, M.; Treu, S.; Chen, Z.; Jiang, T. The Recent Trends of Runoff in China Attributable to Climate Change. Clim. Change 2024, 177, 159. [Google Scholar] [CrossRef]
- Senbeta, T.B.; Romanowicz, R.J. The Role of Climate Change and Human Interventions in Affecting Watershed Runoff Responses. Hydrol. Process. 2021, 35, e14448. [Google Scholar] [CrossRef]
- Álamos, N.; Alvarez-Garreton, C.; Muñoz, A.; González-Reyes, Á. The Influence of Human Activities on Streamflow Reductions during the Megadrought in Central Chile. Hydrol. Earth Syst. Sci. 2024, 28, 2483–2503. [Google Scholar] [CrossRef]
- Bai, H.; Zhong, Y.; Ma, N.; Kong, D.; Mao, Y.; Feng, W.; Wu, Y.; Zhong, M. Changes and Drivers of Long-Term Land Evapotranspiration in the Yangtze River Basin: A Water Balance Perspective. J. Hydrol. 2025, 653, 132763. [Google Scholar] [CrossRef]
- Wiebe, A.J.; Rudolph, D.L.; Craig, J.R. Quantifying Uncertainty in Groundwater Recharge Due to Spatiotemporal Rainfall and Temporal Evapotranspiration Variability. J. Hydrol. 2025, 657, 133089. [Google Scholar] [CrossRef]
- Birylo, M.; Błaszczak-Bąk, W.; Suchocki, C. Application of GLDAS Models and ALS Point Clouds in Assessing the Impact of Modified Evapotranspiration on the Water Budget. Water Res. 2025, 283, 123746. [Google Scholar] [CrossRef]
- Li, J.; Ai, P.; Xiong, C.; Song, Y. Leveraging Multi-Source Data and Teleconnection Indices for Enhanced Runoff Prediction Using Coupled Deep Learning Models. Sci. Rep. 2025, 15, 14732. [Google Scholar] [CrossRef]
- Wang, D.; Shu, L.; Jin, J.; Chen, J.M. Spatiotemporal Variations and Drivers of Runoff in China Based on a High-Quality Continuous Runoff Dataset. J. Hydrol. Reg. Stud. 2025, 59, 102398. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, A.; Zhang, Y.; Yang, F. The Quantitative Attribution of Climate Change to Runoff Increase over the Qinghai-Tibetan Plateau. Sci. Total Environ. 2023, 897, 165326. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Wu, X.; Yang, Y.; Zheng, Y. Impacts of LULC Changes on Runoff from Rivers through a Coupled SWAT and BiLSTM Model: A Case Study in Zhanghe River Basin, China. Ecol. Inform. 2024, 84, 102866. [Google Scholar] [CrossRef]
- Mei, J.; Yong, B.; Lyu, Y.; Qi, W.; Wen, Y.; Wang, G.; Zhang, J. Runoff Evolution Responses to Climate Change: A Case Study in the Headwater Area of Yellow River, China. J. Environ. Manag. 2025, 384, 125512. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo, F.; Cory, N.; Arheimer, B.; Laudon, H.; van der Velde, Y.; Hasper, T.B.; Teutschbein, C.; Uddling, J. Dominant Effect of Increasing Forest Biomass on Evapotranspiration: Interpretations of Movement in Budyko Space. Hydrol. Earth Syst. Sci. 2018, 22, 567–580. [Google Scholar] [CrossRef]
- Choudhury, B.J. Evaluation of an Empirical Equation for Annual Evaporation Using Field Observations and Results from a Biophysical Model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of Mean Annual Evapotranspiration to Vegetation Changes at Catchment Scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Wang, D.; Tang, Y. A One-Parameter Budyko Model for Water Balance Captures Emergent Behavior in Darwinian Hydrologic Models. Geophys. Res. Lett. 2014, 41, 4569–4577. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Jia, Z.; Zou, J.; Xiao, P. Applicability of Attribution Methods for Identifying Runoff Changes in Changing Environments. Sci. Rep. 2024, 14, 26100. [Google Scholar] [CrossRef]
- Tsao, J.; Lee, C.-H.; Yeh, H.-F. Attribution of Streamflow Variations in Southern Taiwan. Water 2020, 12, 2465. [Google Scholar] [CrossRef]
- Melo, P.A.; Alvarenga, L.A.; Tomasella, J.; de Mello, C.R.; Martins, M.A.; Coelho, G. Analysis of Hydrological Impacts Caused by Climatic and Anthropogenic Changes in Upper Grande River Basin, Brazil. Environ. Earth Sci. 2022, 81, 504. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, J.; Yang, Q.; Wang, G. Quantifying the Effects of Climate and Watershed Structure Changes on Runoff Variations in the Tao River Basin by Using Three Different Methods under the Budyko Framework. Theor. Appl. Climatol. 2023, 151, 953–966. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, L.; Huang, Y.; Pan, M.; Wang, G. A New Method to Partition Climate and Catchment Effect on the Mean Annual Runoff Based on the Budyko Complementary Relationship. Water Resour. Res. 2016, 52, 7163–7177. [Google Scholar] [CrossRef]
- Wang, D.; Hejazi, M. Quantifying the Relative Contribution of the Climate and Direct Human Impacts on Mean Annual Streamflow in the Contiguous United States. Water Resour. Res. 2011, 47, W00J12. [Google Scholar] [CrossRef]
- Liu, X.; Liu, C.; Luo, Y.; Zhang, M.; Xia, J. Dramatic Decrease in Streamflow from the Headwater Source in the Central Route of China’s Water Diversion Project: Climatic Variation or Human Influence? J. Geophys. Res. Atmos. 2012, 117, D06113. [Google Scholar] [CrossRef]
- Zhang, B.; Zheng, L.; Wang, Y.; Li, N.; Li, J.; Yang, H.; Bi, Y. Multiscale Ecosystem Service Synergies/Trade-Offs and Their Driving Mechanisms in the Han River Basin, China: Implications for Watershed Management. Environ. Sci. Pollut. Res. 2023, 30, 43440–43454. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Zhang, J.; Chen, J. The Impact of Multi-Projects on the Alteration of the Flow Regime in the Middle and Lower Course of the Hanjiang River, China. Water 2020, 12, 2301. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, W.; Yang, H.; Hong, F.; Yang, K.; Guo, W. The Ecological–Hydrological Regime of the Han River Basin under Changing Conditions: The Coupled Influence of Human Activities and Climate Change. Ecohydrology 2024, 17, e2632. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, W.; Ma, Y.; Bai, X.; Huang, L.; Cheng, S.; Yang, H.; Guo, W. Spatiotemporal Dislocation of Ecosystem Supply and Demand Services from Habitat Quality under Different Development Scenarios. Ecol. Indic. 2023, 157, 111230. [Google Scholar] [CrossRef]
- Han, P.; Yang, G.; Wang, Z.; Liu, Y.; Chen, X.; Zhang, W.; Zhang, Z.; Wen, Z.; Shi, H.; Lin, Z.; et al. Driving Factors and Trade-Offs/Synergies Analysis of the Spatiotemporal Changes of Multiple Ecosystem Services in the Han River Basin, China. Remote Sens. 2024, 16, 2115. [Google Scholar] [CrossRef]
- Shah, S.A.; Jehanzaib, M.; Yoo, J.; Hong, S.; Kim, T.-W. Investigation of the Effects of Climate Variability, Anthropogenic Activities, and Climate Change on Streamflow Using Multi-Model Ensembles. Water 2022, 14, 512. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, W.; Chen, W.; Hong, F.; Bai, X.; Guo, W. Response of Hydrological Regimes to Land Use Change: A Case Study of the Han River Basin. J. Water Clim. Change 2023, 14, 4708–4728. [Google Scholar] [CrossRef]
- Cui, G.; Li, X.; Li, Q.; Huang, J.; Tao, Y.; Li, S.; Zhang, J. Damming Effects on Dissolved Inorganic Carbon in Different Kinds of Reservoirs in Jialing River, Southwest China. Acta Geochim. 2017, 36, 581–597. [Google Scholar] [CrossRef]
- Wang, X.; Guo, S.; Zhong, S.; Wang, M.; Xiang, X. Flood Season Division Using Statistical Analysis Methods and Verifying by Regional Rainy Characteristics. Water 2024, 16, 3677. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, Z.; Lai, C.; He, S.; Jiang, J.; Wang, Z. Attribution and Scarcity Analysis of Blue and Green Water Resources in a River Basin under Climate and Environmental Change. Ecol. Indic. 2025, 175, 113574. [Google Scholar] [CrossRef]
- Qin, Z.; Peng, T.; Singh, V.P.; Chen, M. Spatio-Temporal Variations of Precipitation Extremes in Hanjiang River Basin, China, during 1960–2015. Theor. Appl. Climatol. 2019, 138, 1767–1783. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, N.; Li, Y.; Liu, Z. Impact of Large-Scale Water Transfer Projects on the Ecological Flow and Its Value of Rivers in the Water-Receiving Area: Case Study of the Han River-to-Wei River Water Transfer Project. Nat. Resour. Res. 2025, 34, 271–298. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a High-Resolution Global Dataset of Monthly Climate and Climatic Water Balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. The 30m Annual Land Cover Dataset and Its Dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Dong, S.; Huang, W.; Li, X.; Tao, S. Study on Temporal and Spatial Characteristics of Cold Waves in Shandong Province of China. Nat. Hazards 2017, 88, 191–219. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Society. Ser. C (Appl. Stat.) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Arora, V.K. The Use of the Aridity Index to Assess Climate Change Effect on Annual Runoff. J. Hydrol. 2002, 265, 164–177. [Google Scholar] [CrossRef]
- Lv, X.; Liu, S.; Li, S.; Ni, Y.; Qin, T.; Zhang, Q. Quantitative Estimation on Contribution of Climate Changes and Watershed Characteristic Changes to Decreasing Streamflow in a Typical Basin of Yellow River. Front. Earth Sci. 2021, 9, 752425. [Google Scholar] [CrossRef]
- Chen, X.; Alimohammadi, N.; Wang, D. Modeling Interannual Variability of Seasonal Evaporation and Storage Change Based on the Extended Budyko Framework. Water Resour. Res. 2013, 49, 6067–6078. [Google Scholar] [CrossRef]
- Xin, Z.; Li, Y.; Zhang, L.; Ding, W.; Ye, L.; Wu, J.; Zhang, C. Quantifying the Relative Contribution of Climate and Human Impacts on Seasonal Streamflow. J. Hydrol. 2019, 574, 936–945. [Google Scholar] [CrossRef]
- Yan, B.; Gu, Y.; Li, E.; Xu, Y.; Ni, L. Runoff Prediction of Tunxi Basin under Projected Climate Changes Based on Lumped Hydrological Models with Various Model Parameter Optimization Strategies. Sustainability 2024, 16, 6897. [Google Scholar] [CrossRef]
- Aragão, L.; Mentaschi, L.; Pinardi, N.; Verri, G.; Senatore, A.; Di Sabatino, S. The Freshwater Discharge into the Adriatic Sea Revisited. Front. Clim. 2024, 6, 1368456. [Google Scholar] [CrossRef]
- Wu, Y.; Qin, F.; Dong, X.; Li, L. Investigating the Spatio-Temporal Evolution of Land Cover and Ecosystem Service Value in the Kuye River Basin. Water 2024, 16, 2456. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Y.; Niu, X.; Yan, H.; Zhen, L. Land Use/Cover Change and Its Driving Mechanism in Thailand from 2000 to 2020. Land 2022, 11, 2253. [Google Scholar] [CrossRef]
- Zhao, L.; Fan, X. Effects of Land Use Changes on Ecosystem ServiceValues: A Case Study in Guilin, China. Pol. J. Environ. Stud. 2020, 29, 1483–1492. [Google Scholar] [CrossRef]
- Li, Y.; Cai, Y.; Fu, Q.; Zhang, X.; Wan, H.; Yang, Z. Dynamics of Land Use/Land Cover Considering Ecosystem Services for a Dense-Population Watershed Based on a Hybrid Dual-Subject Agent and Cellular Automaton Modeling Approach. Engineering 2024, 37, 182–195. [Google Scholar] [CrossRef]
- Guo, W.; Hong, F.; Yang, H.; Huang, L.; Ma, Y.; Zhou, H.; Wang, H. Quantitative Evaluation of Runoff Variation and Its Driving Forces Based on Multi-Scale Separation Framework. J. Hydrol. Reg. Stud. 2022, 43, 101183. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, Z.; Zhao, G.; Zhu, J.; Zhao, B.; Sun, Y.; Gao, J.; Zhang, Y. Evapotranspiration Increase Is More Sensitive to Vegetation Greening than to Vegetation Type Conversion in Arid and Semi-Arid Regions of China. Glob. Planet. Change 2025, 244, 104634. [Google Scholar] [CrossRef]
- Liang, X.; Wang, D.; Ye, Q.; Zhang, J.; Liu, M.; Liu, H.; Yu, K.; Wang, Y.; Hou, E.; Zhong, B.; et al. Stomatal Responses of Terrestrial Plants to Global Change. Nat. Commun. 2023, 14, 2188. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Shao, W.; Liu, J.; Su, H.; Zhang, G.; Fu, X. Exploring Spatio-Temporal Dynamics of Future Extreme Precipitation, Runoff, and Flood Risk in the Hanjiang River Basin, China. Remote Sens. 2024, 16, 3980. [Google Scholar] [CrossRef]
- Niu, P.; Wang, Z.; Wang, J.; Cao, Y.; Peng, P. Estimation and Prediction of Water Conservation in the Upper Reaches of the Hanjiang River Basin Based on InVEST-PLUS Model. PeerJ 2024, 12, e18441. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Liu, W.; Scanlon, B.R.; Zhang, L.; Pan, M. Local and Global Factors Controlling Water-Energy Balances within the Budyko Framework. Geophys. Res. Lett. 2013, 40, 6123–6129. [Google Scholar] [CrossRef]
- Cheng, C.; Liu, W.; Mu, Z.; Zhou, H.; Ning, T. Lumped Variable Representing the Integrative Effects of Climate and Underlying Surface System: Interpreting Budyko Model Parameter from Earth System Science Perspective. J. Hydrol. 2023, 620, 129379. [Google Scholar] [CrossRef]

| Period | Model Parameters | Evaluation Metrics | ||||||
|---|---|---|---|---|---|---|---|---|
| a | b | c | d | Calibration | Validation | |||
| NSE | KEG | NSE | KEG | |||||
| Reference period | 0.90 | 344.43 | 0.13 | 0.48 | 0.80 | 0.85 | 0.90 | 0.89 |
| Change period | 0.92 | 356.20 | 0.21 | 0.62 | 0.85 | 0.90 | 0.84 | 0.89 |
| Time Scale | Period | R | Pe | E0 | ω | |||
|---|---|---|---|---|---|---|---|---|
| Annual | 1961~2023 | 380.89 | 890.80 | 894.53 | 1.94 | 1.67 | −0.67 | −1.19 |
| 1961~1985 | 429.02 | 912.48 | 853.91 | 1.86 | ||||
| 1985~2023 | 349.22 | 876.54 | 921.26 | 2.01 | ||||
| Change/Δ | −79.81 | −35.94 | 67.35 | 0.15 | ||||
| Change rate/% | −18.60 | −3.94 | 7.89 | 7.88 | ||||
| Flood season | 1961~2023 | 209.25 | 503.73 | 453.04 | 2.14 | 1.76 | −0.76 | −1.02 |
| 1961~1985 | 226.77 | 512.54 | 440.10 | 2.08 | ||||
| 1985~2023 | 197.71 | 497.93 | 461.55 | 2.19 | ||||
| Change/Δ | −29.06 | −14.62 | 21.44 | 0.11 | ||||
| Change rate/% | −12.81 | −2.85 | 4.87 | 5.17 | ||||
| Dry season | 1961~2023 | 171.64 | 387.07 | 441.49 | 1.78 | 1.58 | −0.58 | −1.38 |
| 1961~1985 | 202.25 | 399.93 | 413.81 | 1.67 | ||||
| 1985~2023 | 151.50 | 378.61 | 459.71 | 1.86 | ||||
| Change/Δ | −50.75 | −21.32 | 45.91 | 0.19 | ||||
| Change rate/% | −25.09 | −5.33 | 11.09 | 11.14 |
| Method | Contributions/% | Pe | E0 | ω |
|---|---|---|---|---|
| BCR | Annual | 24.05 | 41.59 | 34.36 |
| Flood season | 30.56 | 39.15 | 30.29 | |
| Dry season | 17.76 | 34.07 | 48.17 | |
| BVD-TD | Annual | 43.63 | 32.29 | 24.08 |
| Flood season | 36.88 | 37.02 | 26.10 | |
| Dry season | 49.99 | 29.62 | 20.38 | |
| Mean value | Annual | 28.17 | 32.84 | 38.99 |
| Flood season | 33.79 | 32.63 | 33.59 | |
| Dry season | 23.69 | 27.23 | 49.08 |
| LULC | LUCC Dynamic Degree | |||||||
|---|---|---|---|---|---|---|---|---|
| 1985–1990 | 1990–1995 | 1995–2000 | 2000–2005 | 2005–2010 | 2010–2015 | 2015–2020 | 2020–2023 | |
| Cropland | 0.06 | 0.71 | 0.58 | −0.72 | −1.60 | −1.37 | −1.50 | −1.10 |
| Forest | −0.02 | 0.28 | 0.09 | 0.46 | 0.48 | 0.38 | 0.37 | 0.25 |
| Shrub | −2.34 | −7.93 | −4.38 | −6.59 | −4.73 | −8.57 | −9.17 | 2.56 |
| Grassland | 1.00 | −4.74 | −4.47 | −6.32 | −3.63 | −5.57 | −8.12 | −6.67 |
| Water | 0.49 | −2.14 | −1.07 | 1.13 | 1.87 | 4.15 | 3.23 | −0.58 |
| Impervious | 0.85 | 3.67 | 2.41 | 1.54 | 3.43 | 4.15 | 3.03 | 1.46 |
| Comprehensive | 0.06 | 0.36 | 0.20 | 0.36 | 0.40 | 0.37 | 0.36 | 0.22 |
| Year | LULC | 2023 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Cropland | Forest | Shrub | Grassland | Water | Barren | Impervious | Total | ||
| 1985 | Cropland | 10,575.37 | 6118.98 | 6.40 | 113.10 | 232.87 | 0.19 | 629.67 | 17,676.57 |
| Forest | 2632.29 | 64,751.19 | 53.87 | 32.23 | 20.96 | 0.05 | 68.94 | 67,559.54 | |
| Shrub | 85.56 | 1655.40 | 42.27 | 32.02 | 0.03 | 0.02 | 0.15 | 1815.45 | |
| Grassland | 631.39 | 2740.58 | 22.24 | 260.08 | 16.75 | 0.08 | 21.92 | 3693.03 | |
| Water | 26.81 | 7.88 | 0.01 | 1.23 | 700.37 | 0.01 | 19.52 | 755.82 | |
| Barren | 0.22 | 0.00 | 0.00 | 0.03 | 0.21 | 0.00 | 0.50 | 0.97 | |
| Impervious | 9.72 | 0.25 | 0.00 | 0.07 | 70.02 | 0.00 | 354.70 | 434.76 | |
| Total | 13,961.35 | 75,274.27 | 124.79 | 438.77 | 1041.22 | 0.35 | 1095.40 | 91,936.14 | |
| LULC | Cropland | Forest | Shrub | Grassland | Water | Impervious | |
|---|---|---|---|---|---|---|---|
| E0/mm | 776.57 | 792.98 | 771.27 | 774.90 | 819.33 | 807.05 | |
| Kc | 0.6 | 0.8 | 0.4 | 0.7 | 1.0 | 0.1 | |
| 1985 | area/(km2) | 17,676.57 | 67,559.54 | 1815.45 | 3693.03 | 755.82 | 434.76 |
| E/(×108 m3) | 82.36 | 428.59 | 5.60 | 20.03 | 6.19 | 0.35 | |
| 2023 | area/(km2) | 13,961.35 | 75,274.27 | 124.79 | 438.77 | 1041.22 | 1095.40 |
| E/(×108 m3) | 65.05 | 477.53 | 0.38 | 2.38 | 8.53 | 0.88 | |
| 1985–2023 | Δarea/(km2) | −3715.22 | 7714.73 | −1690.67 | −3254.27 | 285.40 | 660.64 |
| ΔE/(×108 m3) | −17.31 | 48.94 | −5.22 | −17.65 | 2.34 | 0.53 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Guo, S.; Wang, M.; He, X.; Wang, W. Attribution Analysis on Runoff Reduction in the Upper Han River Basin Based on Hydro-Meteorologic and Land Use/Cover Change Data Series. Water 2025, 17, 2067. https://doi.org/10.3390/w17142067
Wang X, Guo S, Wang M, He X, Wang W. Attribution Analysis on Runoff Reduction in the Upper Han River Basin Based on Hydro-Meteorologic and Land Use/Cover Change Data Series. Water. 2025; 17(14):2067. https://doi.org/10.3390/w17142067
Chicago/Turabian StyleWang, Xiaoya, Shenglian Guo, Menyue Wang, Xiaodong He, and Wei Wang. 2025. "Attribution Analysis on Runoff Reduction in the Upper Han River Basin Based on Hydro-Meteorologic and Land Use/Cover Change Data Series" Water 17, no. 14: 2067. https://doi.org/10.3390/w17142067
APA StyleWang, X., Guo, S., Wang, M., He, X., & Wang, W. (2025). Attribution Analysis on Runoff Reduction in the Upper Han River Basin Based on Hydro-Meteorologic and Land Use/Cover Change Data Series. Water, 17(14), 2067. https://doi.org/10.3390/w17142067







